Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular and pore-scale structure evolution in amorphous solid water
Zachary
Amato
 *ab,
Sabrina
Gärtner
ab,
Pierre
Ghesquière
b,
Thomas F.
Headen
*ab,
Sabrina
Gärtner
ab,
Pierre
Ghesquière
b,
Thomas F.
Headen
 a,
Tristan G. A.
Youngs
a,
Daniel T.
Bowron
a,
Leide P.
Cavalcanti
a,
Tristan G. A.
Youngs
a,
Daniel T.
Bowron
a,
Leide P.
Cavalcanti
 a,
Sarah E.
Rogers
a,
Sarah E.
Rogers
 a,
Natalia
Pascual
b,
Olivier
Auriacombe
a,
Natalia
Pascual
b,
Olivier
Auriacombe
 b,
Ellen
Daly
b,
Rachael E.
Hamp
b,
Ellen
Daly
b,
Rachael E.
Hamp
 b,
Catherine R.
Hill
b,
T. P.
Ragesh Kumar
b and
Helen J.
Fraser
b,
Catherine R.
Hill
b,
T. P.
Ragesh Kumar
b and
Helen J.
Fraser
 b
b
aISIS Facility, Rutherford Appleton Laboratory, Harwell Oxford, Didcot, Oxon OX11 0QX, UK. E-mail: zachary.amato@stfc.ac.uk
bDepartment of Physical Sciences, The Open University, Walton Hall, Milton Keynes MK7 6AA, UK
First published on 28th November 2025
Abstract
The pore structure of vapour deposited amorphous solid water (ASW) is of both fundamental interest and astrophysical importance, where the system's properties are believed to play a major role in processes such as star and planetary body formation. Here we report a comprehensive characterisation of D2O ASW in the temperature range of 20 to 180 K, using combined total and small-angle neutron scattering. Significant changes to the ice morphology are observed across the temperature range 100 to 150 K, whereby there is a significant loss of specific surface area and porosity; the transition of 3D to 2D dominated pore shapes and a general compaction of the ice. The initial structure of nanometer scale microporous islands with voids between them at low temperature evolves with annealing into compact islands with larger voids. Even past crystallisation, there is still porosity present until desorption due to persisting void volume.
1 Introduction
Amorphous solid water (ASW) is a disordered form of water ice, formed via vapour deposition at low temperatures and pressures, that lacks long-range crystalline order while maintaining local tetrahedral ordering. It is one of the most common solid materials in the Universe. Experimental and theoretical studies over the last few decades have shown that low temperature depositions of ASW are usually very porous, depending on the deposition conditions, giving ASW a large capacity to incorporate trace gases in a sponge-like structure.1–6 This therefore influences processes as varied as the formation of complex chemicals or the cooling of star-forming regions. The very different collisional properties of porous versus compact materials are also thought to affect crucial steps in the formation of planets from the small grains in accretion disks around young stars.7 Understanding the multi-scale structure of ASW is thus not only of fundamental interest, but also underpins our understanding of three aspects of the origins of life as we know it: the formation of complex organic molecules, of a suitable planet, and a suitable star.ASW is a complex material, whereby the problem with nailing down its structure is twofold: (1) the structure of the material depends on growth conditions – rate, composition and directionality of the gas flow, as well as substrate temperature and cooling rates all affect the porosity and crystallinity/amorphicity of the deposited ice.3–5,8–17 (2) ASW is metastable; its structure changes with temperature and to a debated degree with time to reach an energetically preferable state by crystallizing and/or losing porosity. These changes again depend on the environmental conditions the ice is experiencing, where the heating rate likely has the biggest impact.
Experimental studies aiming to study the evolving porosity of ASW upon annealing typically use indirect methods such as tracking the adsorption/release of gases using mass spectrometry (technique referred to as temperature programmed desorption (TPD)) and observing changing features in IR spectra (e.g. dangling OH bonds – used as a proxy for porosity).3,10,15,18–31 Unfortunately, these methods are limited in their ability to measure porosity. For example, using a probe gas relies on the gas’ accessibility to both pore sites and specific binding sites on the ASW surface. Pores that are closed off to the surface will therefore not be included in the measurements. There have been a few positron annihilation spectroscopy studies that have been able to also measure closed off pores; for example, Wu et al. (2011) provided qualitative information on the formation and evolution of micropores and mesopores, but have yet to be able to assign quantitative values to sizes and concentrations of these pores.17,32–34 ASW is neither conductive nor easy to image, so methods such as AFM, TEM and STEM are also not viable, and even if they were, they are mostly surface rather than bulk probes of matter.35–37
To address these shortcoming, we developed a methodology using neutron scattering, a direct and non-interacting method of probing structure and porosity, to study the impact of deposition temperature on the structure of ASW.1 At low deposition temperatures, we showed that ASW is highly porous with large surface areas. With increasing deposition temperature, the structure of ASW becomes more similar to a compact ice – there is less surface area and a difference in porosity. We provided direct experimental evidence that the ASW structure itself grows as microporous islands/grains with voids between them, meaning that the porosity of ASW is a combination of the void volume between the islands and the micropores within the islands themselves. These two populations of pores were impacted differently depending on the deposition temperature. The term microporous in our work follows the IUPAC definition, noting that the pores are in the nm not µm range.38 All of the samples studied in Amato et al. (2025) were annealed, replicating increasing temperatures during star-formation processes, to track the evolution of the structure and porosity – which is the basis of this study.
Prior studies have found that annealing ASW leads to a loss of porosity and surface area, along with a general compaction. TPD studies have shown that warming ASW towards 60 K leads to the trapping of co-deposited gases as the ice is restructuring and closing off pores to the surface. Further warming, through the 60–120 K range, triggers the collapse of pores, which would allow some adsorbates to escape, while others still remain trapped in isolated nanopores.27 These trapped gases only escape once the ice goes through the glass transition (136 K) and then crystallisation past 140 K.8,22,29,39–43 With these structural changes, it has been shown that there is a significant reduction in specific surface area (SSA) – from several hundred m2 cm−3 for low temperature porous ASW to less than 1 m2 cm−3 in compact ASW.14,28
The structure and dynamics of the pore collapse and loss of surface area however remains unresolved. There are still many open questions such as do the pores continuously shrink until they disappear? Or do they merge and grow bigger before eventually being destroyed? Do cracks open up throughout? Using combined total neutron scattering (TNS) and small-angle neutron scattering (SANS), as well as standalone SANS, we have undertaken an unparalleled study of the evolution of ASW porosity and structure upon annealing to answer these open questions.
2 Methodology
The method of growing the ASW samples that are annealed for this study and the results of the impact of deposition temperature on the structures is described in detail within Amato et al. (2025).1In summary, a dedicated deposition setup was developed that allows for the ASW to be grown in situ on the instruments NIMROD and SANS2d, at the ISIS Neutron and Muon Source. NIMROD is a total neutron scattering instrument that can obtain structural information on continuously probed length scales in the range of <1 to 300 Å.44 This is possible as a result of the wide range of momentum transfer, Q, over which this instrument measures (0.02 Å−1 ≤ Q ≤ 50 Å−1). Q is defined as Q = (4π/λ)sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, where λ is the neutron wavelength and 2θ is the scattering angle. The resulting data therefore allows for the simultaneous investigation of the ice phase, bulk pore structure and surface properties. Q can be interpreted as an inverse size metric, meaning that low Q (known as SANS region) carries information on the porosity of the ASW and the high Q (diffraction region) carries that of the short- and intermediate-range atomic and molecular structure, which tells us the extent of periodic ordering of the water molecules. In addition to using NIMROD, the specialised SANS instrument SANS2d was used to cover length scales much larger than what NIMROD can probe, however it does not have the high Q diffraction region to give information on crystallinity. These larger length scales were needed as our experiments on NIMROD showed structural features in ASW that were too large for NIMROD to reliably study, as seen throughout Amato et al. (2025) and in this work.1 SANS2d covers a Q-range of 0.002–3 Å−1 and therefore can access length scales between 2.5 and 3000 Å−1.45
θ, where λ is the neutron wavelength and 2θ is the scattering angle. The resulting data therefore allows for the simultaneous investigation of the ice phase, bulk pore structure and surface properties. Q can be interpreted as an inverse size metric, meaning that low Q (known as SANS region) carries information on the porosity of the ASW and the high Q (diffraction region) carries that of the short- and intermediate-range atomic and molecular structure, which tells us the extent of periodic ordering of the water molecules. In addition to using NIMROD, the specialised SANS instrument SANS2d was used to cover length scales much larger than what NIMROD can probe, however it does not have the high Q diffraction region to give information on crystallinity. These larger length scales were needed as our experiments on NIMROD showed structural features in ASW that were too large for NIMROD to reliably study, as seen throughout Amato et al. (2025) and in this work.1 SANS2d covers a Q-range of 0.002–3 Å−1 and therefore can access length scales between 2.5 and 3000 Å−1.45
Here we present data on eight samples that were deposited at temperatures ranging from 20 to 120 K (see Table 1). The methodology and setup was carefully kept the same for each sample in order to ensure consistency across a long time period. Each sample was grown by vapour-depositing D2O onto a cold vanadium plate over 12 hours, at an average growth rate of the ice film thickness of 1.45 × 10−9 m s−1 (3.625 ML s−1), under high vacuum (4 × 10−7 mbar). This grows ice thicknesses of 51 to 92 µm by the end of deposition, depending on the deposition temperature.
| Year | Instrument | Sample deposition temperature (K) |
|---|---|---|
| 2015 | NIMROD | 30 |
| 50 | ||
| 80 | ||
| 2016 | NIMROD | 20 |
| 40 | ||
| 60 | ||
| 100 | ||
| 120 | ||
| 2022 | SANS2d | 30 |
| 80 | ||
| 120 | ||
| 2023 | SANS2d | 50 |
| 60 | ||
| 100 |
D2O, rather than H2O, is used as its neutron scattering properties are more suitable for the investigations presented here. There are of course differences between D2O and H2O. Tomberli et al. (2000) used high-energy electromagnetic radiation scattering to find that liquid D2O is slightly more ordered than H2O. Both the works of Soper and Benmore (2008) (X-ray and neutron diffraction) and Liang et al. (2023) (molecular dynamics) similarly found that D2O is a more structured liquid than H2O, even though D2O's structural properties like bond angle and length are slightly smaller than those of H2O.46,47 It was also found that the hydrogen bonding of D2O is stronger than that of H2O. Overall, the differences are less than 4% and it is therefore reasonable to make the swap as the benefits of using D2O for neutron scattering far outweigh these small differences.
Once deposition was complete, the samples were all subsequently annealed to 180 K in 10 K steps and held isothermally at each step for either 30 minutes (samples run on NIMROD) or 1 hour (samples run on SANS2d). A longer isothermal hold was needed on SANS2d in order to get comparable data quality. Temperatures are monitored using thermocouples attached to the side of the vanadium plate and on the cryostat. The temperature control relies on feedback from the surface thermocouple to ensure the ice temperature is as close to the reported substrate temperature as possible, as is standard practice in surface science experiments of this type.
Neutron scattering data was taken continuously throughout the annealing process, but it is important to note that the annealing process was not paused even if the neutron beam went down, as can happen for a spallation neutron source, so that our work is consistent across samples and comparable to TPD experiments, hence why there is data missing at certain temperature points for some samples. After the temperature reaches 180 K, a sample is then flash heated to 250 K and checked to ensure that there is no ice left on the surface before beginning the deposition of the next sample. Prior to 180 K, there is no experimental evidence that our ices have started desorbing. We cannot detect a pressure rise in the vacuum system (usual with desorption) and the strength of the neutron scattering signal is not diminished (indicative of material loss).
Fig. 1 shows an example of the entire deposition and annealing process for the sample deposited at 20 K.
For NIMROD, the data was reduced and calibrated using the software Gudrun, which obtains the differential cross section (DCS), with units of bars per sr per atom, as a function of Q.48 SANS2d data was reduced and calibrated with the Mantid software, giving absolute units of cm−1 that is integrated over the circumference across the 2D detectors to obtain 1D data of intensity as a function of Q.49,50 By normalising to the atomic density, I(Q) and DCS (Q) are easily translated between one another.51
3 Qualitative analysis of structural changes upon annealing
Even prior to analysing the data, we can gain a qualitative understanding of the structural changes during annealing from the original processed data of DCS as a function of Q, shown in Fig. 2 for every sample throughout the annealing process. First, it shows that there is consistency between our samples even though they were created at different beamtime visits several years apart. The broad peak on the curve in the low Q region, around 0.1 Å−1, which we can observe at low temperatures is slowly disappearing upon annealing. This is indicative of a loss in porosity as the pores are changing and being destroyed. In the high Q region that is zoomed in, past 120 K there is the appearance of Bragg peaks that indicate the samples are starting to crystallise. Full crystallisation ensues at 140 K for every sample. These changes mirror what we expect based on the wider literature.8,9,13,22,28,39,52,53 However, it is important to note that even past the crystallisation point, we see that our samples are still granular and do not melt into a thin film. As the resolution of the Bragg peaks are not what would be expected for a crystallography study, we do not analyse them quantitatively.An important feature of ASW is its metastable nature. It is never in equilibrium, unless it goes through a phase change that turns it into a different form. This was very evident in our molecular dynamics simulations where we annealed ASW systems and saw that there was a unique pathway and outcome, regardless of whether the starting and simulation conditions were identical.54 Our neutron data herein shows the same behaviour, as shown in Fig. 3, where the curves are not identical between the samples at the same temperature points, but from different deposition temperatures. This is more evident for the lower temperature when the system is amorphous as we can see that past crystallisation (bottom panel at 160 K), the high Q data merges far more compared to the data at 80 K (top panel).
4 Analysis
As our reduced data shows information and trends that align with the wider literature, we feel confidence in being able to continue with quantitatively analysing the data. All of the analysis methods, apart from the diffuse interface model (described below), are identical to what was used for the deposition data, which is described in detail within Amato et al. (2025).1 The main goal of the models used is to obtain information about the porosity, pore sizes and shapes, as well as surface area throughout the annealing process. As with the deposition study, we chose a range of fitting methods with differing balance regarding the number of prior assumptions and richness of resulting data, which all give a consistent picture of the changes in the ASW porous structure as a function of annealing temperature.14.1 Microporosity
To study the evolution of microporosity, which is the nanometer scale pores within the islands of the ASW, only the NIMROD data is needed rather than the merged NIMROD and SANS2d SANS data.Surface properties of the scattering particles (pores) in ASW have been derived from the slope of the low Q NIMROD data by employing the Porod and diffuse interface models. The Porod model was fitted between 0.015 and 0.3 Å−1 and obtains the specific surface area (SSA) by calculating a Porod constant from the intercept of the quasi-plateau of an I(Q)·Q4 plot.
As our earlier works on non-porous water ice found evidence of a diffuse interface building up with increasing temperature, we also applied the diffuse interface model, which is able to fit a wider range of the low Q data than the Porod model. This model fits the data well and not only provides a sanity check, but also yields additional information in providing the thickness of the diffuse interface. In the case of diffuse interfaces, the SSA is obtained from fitting
| I(Q) = 2π(Δρ)2SSA·Q−4e−Q2t2, | (1) |
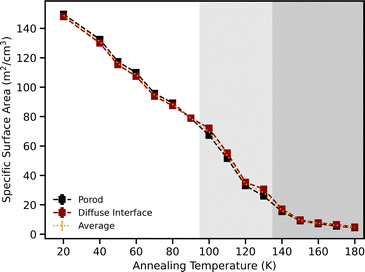
Both models yielded closely matching SSA values. While the Porod model uses only one fit parameter, it is applicable only to that part of the low Q slope that best matches Q−4. The diffuse interface model fits the whole low Q range to the right of the knee (where the slope turns over to Q−2 at the lowest Q values), but requires two parameters to do so. Thus, we have decided to subsequently average SSA values from both fits and across samples at each annealing temperature (example shown in Fig. 4).
Two models were chosen to obtain information about the pore structure of the ice samples: a widely applicable shape-independent Guinier–Porod (GP) model and a shape-based 2D slit pore model. The 2D slit pore model was chosen as the SANS curve slope indicates the presence of slit dominated shapes by following a Q−2 dependence at the lowest Q section.
The GP model can get information about pore size, shape and surface roughness by extracting the radius of gyration, Rg, the s parameter (s = 0 indicates spheres, s = 1 indicates cylinders and s = 2 indicates platelets) and the d parameter, respectively.1,59 The d parameter is related to surface roughness, where values of 3–4 indicate roughness on nanometer length scales, 4 represents a smooth surface, and ≥4 indicate diffuse surfaces.60,61
In the low temperature scans, structural features are shown in two Q-ranges (∼0.02 and 0.15 Å−1). To reproduce both features in the GP analysis, we fitted a double GP function:
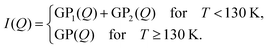 | (2) |
As the GP model cannot calculate the overall volume of scattering centres (porosity), another model was applied to obtain this – the 2D slit pore model. This model extracts the porosity (pore volume divided by total sample volume – i.e. the volume fraction the pores occupy in the whole sample volume) and pore widths, when assuming randomly oriented 2D slit pores. We created this model by summing SASView's inbuilt Lamellar pore model and its inbuilt Gaussian model to obtain:
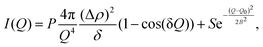 | (3) |
The Porod, diffuse interface and GP models were fitted using Python codes, while the slit pore model was created and fitted using SASView, a program for the analysis of small angle scattering data.62,63
4.2 Full Q range data analysis
It was found that there is good overlap between the SANS regions from each instrument, once translated to the same units. This means that the pore structures are comparable. Therefore, to obtain a much wider low Q-range than is possible with either instrument, with good resolution all across, the SANS slopes of each were merged together. Full details of this procedure are described in Amato et al. (2025).1The low Q data at each annealing step of all samples with the same deposition temperatures were merged, weighted by the uncertainties of each instrument.
To obtain a full pore size distribution from the merged NIMROD and SANS2d SANS data of every ASW sample throughout the annealing process, the computer routine MAXE was implemented. Details of this are fully outlined in Amato et al. (2025).1 Briefly, MAXE uses the maximum entropy algorithm to perform an inverse transform of the SANS intensity into real space to yield a pore size distribution (assuming spherical pores). This is done by fitting the most featureless and disordered distribution (highest entropy) that it can to the data via an iterative procedure, accounting for the chi-squared statistic. Compared to the GP, slit and Porod models, MAXE covers the full measured Q range. Additionally, the advantage of MAXE is that it avoids the need to assume any prior model of the size distribution of inhomogeneous scatterers (pores). MAXE yields the fractional volume distribution C(D), where C(D)δD gives the volume fraction V(D) of pores with diameters comprised in [D, D + δD], normalised over the total pore volume. From this pore size distribution, the total porosity and specific surface areas are also calculated.
5 Results and discussion
5.1 NIMROD
For data obtained from NIMROD, the porosity discussed is microporosity due to NIMROD's inability to access certain larger features as the minimum Q is around 0.015 Å−1.Using the surface analysis methods of the Porod/diffuse interface and slit pore models, the porosity and specific surface areas were extracted. Fig. 5 shows that with increasing annealing temperature, the samples generally lose porosity and surface area. The surface area decreases linearly with increasing temperature, while the porosity decreases until a broad peak past 120 K, before decreasing again past 150 K. This broad peak is likely caused by the significant global structural changes brought on by the glass transition at 136 K before crystallisation at 140 K.64 The slit pore model is thus likely ‘switching’ between small and larger pores as the larger pores come to dominate, and so the data from these simplified models should be treated with caution in this region.
Although after this ‘bump’ the SSA approaches the compact ice value, there is still significant porosity remaining that could be explained by the ice transforming into compact islands with the void volume remaining as porosity. A linear decrease in SSA is similarly found in experimental (e.g. gas adsorption study of Boxe et al. (2007) and TPD study of Bar-Nun et al. (1985)) and Monte Carlo simulation (e.g. Cazaux et al. (2015) and He et al. (2019)) studies.23,53,65,66 Li et al. (2021) used X-ray scattering to follow the structural evolution of porous ASW upon heating from 80 K.13 They found the same collapse of micropores when heating up to 130 K. After 130 K, they similarly observe crystallisation through the emergence of Bragg peaks at Q = 2.79 and 3.28 Å−1 (related to both Ic and Ih), with a peak at 3.04 Å−1 strictly related to Ih at higher temperatures.67–69 They conclude that their ASW transforms from low-density amorphous ice (LDA) to the so-called stacking disordered ice I at 140 K.
Our study of ASW deposition showed that the ice features two main populations of pores – micropores within islands/grains which are themselves separated by larger voids.1 We see this again within this study when we fit our models to the NIMROD DCS curves. Fig. 6 shows the pore sizes as a function of annealing temperature, obtained from the two different methods using the GP and slit pore models. The double GP model encompasses the two pore features seen in the curves and so there are two sets of length scales, whereas the slit pore model has only one set. Clearly there are significant differences in size between the two length scales from the GP data set and they behave differently when the ice is annealed. The micropores within the islands disappear past 120 K whereas the larger void volume persists even past crystallisation.
Initially at the lower temperatures, the slit pore model pore widths are most similar to the Rgmicropore values (small-scale island pores). With increasing temperature, they significantly increase in size past 90 K, by 121 Å, as the model ‘switches’ from small to larger pores, meaning that the ice becomes dominated by the voids. This was also seen with the deposition results, whereby the samples deposited at the lower temperatures are dominated by micropores and therefore the slit pore model pore widths were very similar to the Rgmicropore values.1
Due to the void volume hitting the size limit that NIMROD can reliably measure, only the micropores data will be discussed from now on. Fig. 7 shows the GP results as a function of annealing temperature for these small scale pores within each sample. There are more significant changes in pore shape than size as seen in the radius of gyration and s parameter results. At low deposition temperatures, the pores start at sizes between 5 and 10 Å before increasing with annealing temperature. In some cases, the pores double in size before disappearing after 120 K, as seen with all the samples. Most of these drastic global changes start to occur from 100 K where the onset of the glass transition begins and finalises at 136 K, before crystallisation at 140 K.64
Their shapes generally start as mostly cylindrical and transition to 2D slit pores as the ice is annealed. This transition from more 3D to 2D dominated pore shapes may have interesting astrophysical implications, such as impacting the rate of H2 formation as an example.14 Confining H atoms between slit pores may force them to recombine as there is no possibility of desorbing from the surface. If the pores are initially filled with gases (e.g. CO2 or CH4 as for cometary nuclei), the 3D to 2D transition could also provide a natural explanation for the formation of clathrate hydrates as there would be a build of internal pressure when the gases are trapped.70 Formation of clathrate hydrates would then become thermodynamically feasible, despite the vacuum environment.
These changes in the pores are accompanied by a restructuring of the ice surface, which transforms from a rough to a diffuse interface for every sample, as seen with the d parameter in Fig. 7. This restructuring is in agreement with earlier observations of a loss in dangling bonds between 15 and 120 K.3Fig. 8 shows the thickness of the diffuse interface throughout annealing and it is clear that the diffuse interface becomes more important as the ice goes through the glass transition and crystallisation phase changes. After these phase changes, the diffuse interface thickness more than doubles in some cases, becoming a couple monolayers thick.
5.2 Combined SANS
The NIMROD data has given us a good indication that the two populations of pores seem to evolve differently with annealing temperature. To elucidate this, we used the instrument SANS2d to access larger length scales, which will cover the voids with better resolution.Fig. 9 shows the merged SANS data from NIMROD and SANS2d (raw SANS2d data found in SI). As seen with the deposition results, the merging of the SANS region from NIMROD and SANS2d has increased the Q-range and the size of objects we can observe.1 It has particularly helped improve the resolution of the characteristic features observed, which is the shoulder at low temperature that corresponds to small length scale pores (a few nm) and larger structures of a few 10–100 nm at higher temperatures. However, the merging has not been able to fix the inconsistency of the low temperature SANS2d data for the sample deposited at 100 K. This behaviour was not seen for the 100 K sample on NIMROD, which is trusted as the high Q region can be used to check the amount of and phase of the sample. This section of the 100 K sample data was therefore omitted from further analysis.
For all the samples, the curves exhibit a Porod curve that is characteristic of the presence of scattering surfaces. Qualitatively, it is observed that there is the presence of a shoulder moving to lower Q when the temperature is increased, from ≃0.1 Å−1 at 40 K to 0.05 Å−1 at 170 K. This is indicative of the presence of pores that shift position towards larger length scales. At 180 K, the water is desorbing off the surface and so the total amount of scattering is low, creating the very noisy data observed.
At lower temperatures, the distributions exhibit two distinct populations of pores, with some showing this more clearly than others. For example, the sample deposited at 80 K displays one main red/white ‘peak’, whereas other samples show two. This multi-contribution character of this distribution shows again that the ice samples have two major populations of scattering voids – the small scale pores in the islands and the voids between them. Upon annealing to ≥110 K, the distributions each only have one major contribution (voids between islands) that dramatically increases in size to a few hundred angstrom, reaching a plateau of over 1000 Å above 160 K.
In Fig. 10, there is a corresponding cumulative porosity plot next to each pore size distribution plot. At low temperatures, the major contributors to pore volume are the small pores (diameters less than 70 Å). As the ice is annealed, the major contributor sizes increases and, even at high temperatures, the large pores still yield a high amount of pore volume and therefore porosity.
Fig. 11 shows the volume fraction as a function of pore size for every sample. The samples deposited at 30 and 60 K have two populations starting at around 16 Å and 35 Å; the 80 K has one major population at 24 Å and another less-intense one at 60 Å; the 100 K sample has two populations at 34 and 50 Å, and the 120 K sample has two populations at 26 and 264 Å. When annealed, all samples show a significant increase in pore size for all populations. Above 150 K, all samples have pore sizes of a few hundred angstroms, with sizes reaching over 1000 Å at the highest temperatures. At 180 K, there is surprisingly still some contribution at the low length scales (≤50 Å) that could be explained by a loss of statistics or disturbance of the ice from significant water desorption at such high temperatures. Overall, the two populations of pores are clearer at the lowest temperatures, with very large voids only becoming clear at the higher temperatures. Raut et al. (2007) used IR spectroscopy and found that their ices also have a dual pore structure, having both micro- and mesopores whereby the micropores are destroyed by 140 K, but some mesopores remain, in line with what we see with our work.10 This has been interpreted as either coalescence of smaller pores into larger ones, preferential destruction of small pores or decrease of surface roughness of the pores.
 | ||
| Fig. 11 Volume fraction as a function of pore size for every sample. Trace colours represent annealing temperature as indicated by the colourbar on the right hand side. | ||
We cannot say whether or not it is only above a certain thickness that our small pores and voids model is valid as we cannot test thinner films with neutrons. In our molecular dynamics studies, we create much smaller ASW systems and find that it still reproduces the small pore volume from the neutrons very well, despite there being much less material (thicknesses of up to 40 Å).54 We also see qualitatively in our previous deposition work with neutrons that the small pores and voids are present within the 1st hour of deposition (thickness only around 25 µm) as the line profile is the same as towards the end.1 Additionally, the work of Bu et al. (2016) shows cracking and separation during growth at smaller thicknesses than ours, ranging from 1–5 µm, with a higher thickness threshold for cracking at higher growth temperature (10–50 K used).71
It is important to note that although the thickness of our ASW samples are on the micron scale, the length scales we are sensitive to are on the nanometer scale, so there may be even larger void volume than what we have observed.
The porosity of each sample as a function of annealing temperature is shown in Fig. 12. It shows that there is a global porosity decrease during annealing for all samples and that there is good consistency between samples. Porosity generally goes down for all samples (apart from the 120 K sample) until a temperature of 110 K and then increases throughout the glass transition (with a lot of deviation at this point) and past crystallisation. After 170 K, the ice is undergoing desorption which leads to a loss in porosity and sample generally. As discussed previously, the initial decrease at low temperatures is likely due to the small scale porosity within the islands being destroyed. As these pores are destroyed, there comes a point where the void volume starts to dominate and so the porosity increases again. Eventually, the outcome of annealing is compact islands with larger voids between them. For most samples, apart from the samples deposited at 80 and 120 K, there is still significant porosity at the highest temperatures, meaning there is still void volume and that the ice does not melt into a uniform film across the surface.
Although the merged porosities are higher than that of pure NIMROD data, due to the merged data encompassing larger pores from SANS2d that are outside NIMROD's range, they are still smaller at low temperatures than other experimental studies. For example, Mitchell et al. (2017) measured porosity loss, calculated using density from a quartz crystal microbalance (QCM), and obtained a porosity of 35% that decreased to 20% upon annealing from 10 to 140 K.72 Raut et al. (2007) also used a QCM to measure porosity change and obtained a porosity change of 40% to 13% from 40 to 140 K for samples deposited at 77°, with respect to the normal to the surface, and a porosity of 21% at 40 K for background deposition.10 The porosity percentages found in this work are likely lower than those found in the literature as our porosity calculation is limited to the size range covered by the instrument and differences in deposition.
Fig. 13 shows the SSA as a function of annealing for every sample and it shows that the SSA decreases linearly with increasing temperature. This indicates that it is the small scale population of pores that mainly contributes to SSA and therefore, when they disappear with increasing temperature, so does the SSA, regardless of whether there is void volume still left at high temperatures.
Our SSA results generally compare well with that of gas adsorption studies across the literature, as shown in Fig. 14. Some studies do observe far larger surface areas, such as for example Ghormley et al. (1967) who report SSAs of 500 m2 cm−3 at 20 K, whereas this work obtains SSAs that are less than half of that value.73 These discrepancies are likely due to differences in the experimental apparatus and method. The deposition setup used herein grows relatively thick films of up to 100 µm compared to thin films of less than 1 µm commonly used for porosity measurements.5
 | ||
| Fig. 14 Specific surface area as a function of annealing temperature from our work and that of Ghormley (1967), Mayer & Pletzer (1986), Schmitt et al. (1987), Bar-Nun et al. (1987), Murray & Plane (2003), and Boxe et al. (2007).6,23,31,73–75 | ||
6 Conclusions
This work employed total neutron scattering and SANS to understand how the structure and porosity of ASW evolves upon annealing. Overall, the ice network is globally porous with a very high surface area at low temperature, which decreases to a very low value upon annealing. This is well known from a wide variety of studies of porous ASW.4,8,10,15,17,18,20,30,39,52,57 We have provided further direct experimental evidence but with a higher level of detail and new insights.Our results show significant changes to the ice structure occur across the temperature range of 100 to 150 K, which is set around the glass transition temperature where an enhanced mobility of the water molecules kicks in ref. 64. This results in the loss of SSA and porosity; the transition from 3D to 2D dominated pore shapes and a general compaction of the ice. While none of these effects occur at a specific onset temperature and they become significant at slightly different temperature points, they are all notable between 100 and 150 K.
We wanted to answer the open questions of whether the pores continuously shrink or merge and grow bigger before they disappear? According to our results, both of these are true to some degree as our two populations of pores, of differing scales, evolve independently and differently with annealing temperature. Fig. 15 summarises what our results show in terms of the evolution of the ASW structure and porosity. Initially, the ice is dominated by the micropores within the island that grow slightly bigger before disappearing past 120 K. Although the total pore volume decreases throughout annealing, the voids significantly increase in size after 120 K and come to dominate the ice. Even past crystallisation, there is still void volume persisting – meaning there is still porosity at the higher temperatures until desorption.
The next step is to understand the underlying mechanism of this pore collapse, which is the focus of our follow-up work.
Author contributions
Z. Amato: formal analysis, investigation, software, visualization, writing – original draft and writing – review & editing. S. Gärtner: formal analysis, investigation, methodology, software and validation. T. F. Headen and H. J. Fraser: conceptualization, funding acquisition, investigation, methodology, project administration, resources, supervision, validation and writing – review & editing. P. Ghesquiere: formal analysis, investigation, methodology and software. T. Youngs, D. Bowron, L. Cavalcanti, S. Rogers: investigation, methodology, resources and software. N. Pascual, O. Auriacombe, E. Daly, R. E. Hamp, R. K. TP: investigation. C. R. Hill: investigation, methodology and software.Conflicts of interest
There are no conflicts to declare.Data availability
Data for this article are available at: https://doi.org/10.5286/ISIS.E.RB1510246;https://doi.org/10.5286/ISIS.E.RB1610318; https://doi.org/10.5286/ISIS.E.RB2010205. The data analysis scripts are found at: https://github.com/ZacAmato/Batch_Analysis_ASW.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. The SI includes the raw SANS2d intensity as a function of Q curves throughout the annealing of each sample. See DOI: https://doi.org/10.1039/d5cp03851k.
Acknowledgements
Astrochemistry at the Open University is currently supported by STFC under grant agreement numbers ST/X001164/1, ST/T005424/1 and ST/Z510087/1 and Z. Amato also thanks The Open University for funding his PhD studentship in part. Earlier research leading to the original experimental work presented in this paper was undertaken at the OU and previously supported by UK Space Agency, EU COST Action CM1401 and UKRI – STFC under grant agreement numbers ST/M003051/1 and ST/P000584/1. We thank the STFC ISIS Neutron and Muon Source for award of beamtime allocations RB151024676 and RB161031877 on NIMROD and RB201020578 on SANS2D, and for partly funding Z. Amato through the ‘ISIS Facilities Development Studentship’ scheme. We would like to acknowledge and thank the ‘Pressure and Furnace’, ‘Cryogenics’, ‘Electronics’ and ‘Soft Matter’ groups at the ISIS Neutron and Muon Source as their setting up/maintaining of the dedicated deposition setup is vital to our work. We especially thank Chris Goodway for his help in the design and construction of the deposition setup. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no 654000.References
- Z. Amato, T. F. Headen, S. Gartner, P. Ghesquiere, T. G. A. Youngs, D. T. Bowron, L. Cavalcanti, S. E. Rogers, N. Pascual, O. Auriacombe, E. Daly, R. E. Hamp, C. R. Hill, R. K. TP and H. J. Fraser, Phys. Chem. Chem. Phys., 2025, 27, 6616–6627 RSC.
- A. Al-Halabi, H. J. Fraser, G. J. Kroes and E. F. V. Dishoeck, Astron. Astrophys., 2004, 422, 777–791 CrossRef CAS.
- J. B. Bossa, K. Isokoski, M. S. D. Valois and H. Linnartz, Astron. Astrophys., 2012, 545, A82 CrossRef.
- K. P. Stevenson, G. A. Kimmel, Z. Dohnalek, R. S. Smith and B. D. Kay, Science, 1999, 283, 1505–1507 CrossRef CAS PubMed.
- D. E. Brown, S. M. George, C. Huang, E. K. L. Wong, K. B. Rider, R. S. Smith and B. D. Kay, J. Phys. Chem., 1996, 100, 4988–4995 CrossRef CAS.
- A. Bar-Nun, J. Dror, E. Kochavi and D. Laufer, Phys. Rev. B:Condens. Matter Mater. Phys., 1987, 35, 2427–2435 CrossRef CAS PubMed.
- S. Gartner, B. Gundlach, T. F. Headen, J. Ratte, J. Oesert, S. N. Gorb, T. G. A. Youngs, D. T. Bowron, J. Blum and H. J. Fraser, Astrophys. J., 2017, 848, 96 CrossRef.
- D. J. Burke and W. A. Brown, Phys. Chem. Chem. Phys., 2010, 12, 5947–5969 RSC.
- A. R. Clements, B. Berk, I. R. Cooke and R. T. Garrod, Phys. Chem. Chem. Phys., 2018, 20, 5553–5568 RSC.
- U. Raut, M. Fama, B. D. Teolis and R. A. Baragiola, J. Chem. Phys., 2007, 127(20), 204713 CrossRef CAS PubMed.
- N. Watanabe and A. Kouchi, Prog. Surf. Sci., 2008, 83, 439–489 CrossRef CAS.
- N. Horimoto, H. S. Kato and M. Kawai, J. Chem. Phys., 2002, 116, 4375–4378 CrossRef CAS.
- H. Li, A. Karina, M. Ladd-Parada, A. Spah, F. Perakis, C. Benmore and K. Amann-Winkel, J. Phys. Chem. B, 2021, 125, 13320–13328 CrossRef CAS PubMed.
- C. Mitterdorfer, M. Bauer, T. G. Youngs, D. T. Bowron, C. R. Hill, H. J. Fraser, J. L. Finney and T. Loerting, Phys. Chem. Chem. Phys., 2014, 16, 16013–16020 RSC.
- O. Galvez, B. Mate, V. J. Herrero and R. Escribano, Icarus, 2008, 197, 599–605 CrossRef CAS.
- M. P. Collings, M. A. Anderson, R. Chen, J. W. Dever, S. Viti, D. A. Williams and M. R. McCoustra, Mon. Not. R. Astron. Soc., 2004, 354, 1133–1140 CrossRef.
- Y. C. Wu, J. Jiang, S. J. Wang, A. Kallis and P. G. Coleman, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 064123 CrossRef.
- K. Isokoski, J. B. Bossa, T. Triemstra and H. Linnartz, Phys. Chem. Chem. Phys., 2014, 16, 3456–3465 RSC.
- J. J. Shephard, J. S. Evans and C. G. Salzmann, J. Phys. Chem. Lett., 2013, 4, 3672–3676 CrossRef CAS.
- B. Mate, Y. Rodriguez-Lazcano and V. J. Herrero, Phys. Chem. Chem. Phys., 2012, 14, 10595–10602 RSC.
- G. Malenkov, J. Phys.: Condens. Matter, 2009, 21, 283101 CrossRef PubMed.
- S. Malyk, G. Kumi, H. Reisler and C. Wittig, J. Phys. Chem. A, 2007, 111, 13365–13370 CrossRef CAS PubMed.
- C. S. Boxe, B. R. Bodsgard, W. Smythe and M. T. Leu, J. Colloid Interface Sci., 2007, 309, 412–418 CrossRef CAS PubMed.
- C. Manca, C. Martin and P. Roubin, Chem. Phys., 2004, 300, 53–62 CrossRef CAS.
- Z. Dohnalek, G. A. Kimmel, P. Ayotte, R. S. Smith and B. D. Kay, J. Chem. Phys., 2003, 118, 364–372 CrossRef CAS.
- S. Mitlin and K. T. Leung, J. Phys. Chem. B, 2002, 106, 6234–6247 CrossRef CAS.
- J. P. Devlin, J. Geophys. Res.:Planets, 2001, 106, 33333–33349 CrossRef CAS.
- G. A. Kimmel, Z. Dohnalek, K. P. Stevenson, R. S. Smith and B. D. Kay, J. Chem. Phys., 2001, 114, 5295–5303 CrossRef CAS.
- V. Sadtchenko, K. Knutsen, C. F. Giese and W. R. Gentry, J. Phys. Chem. B, 2000, 104, 4894–4902 CrossRef CAS.
- P. Jenniskens and D. F. Blake, Structural Transitions in Amorphous Water Ice and Astrophysical Implications, 1994 Search PubMed.
- E. Mayer and R. Pletzer, Nature, 1986, 319, 298–301 CrossRef CAS.
- M. Eldrup, A. Vehanen, P. J. Schultz and K. G. Lynn, Phys. Rev. Lett., 1983, 51, 2007–2010 CrossRef CAS.
- M. Eldrup, A. Vehanen, P. J. Schultz and K. G. Lynn, Phys. Rev. B:Condens. Matter Mater. Phys., 1985, 32, 7048–7064 CrossRef CAS PubMed.
- Y. C. Wu, A. Kallis, J. Jiang and P. G. Coleman, Structural and phase changes in amorphous solid water films revealed by positron beam spectroscopy Search PubMed.
- A. Kouchi, T. Hama, Y. Kimura, H. Hidaka, R. Escribano and N. Watanabe, Chem. Phys. Lett., 2016, 658, 287–292 CrossRef CAS.
- T. Tomaru, H. Hidaka, A. Kouchi and N. Watanabe, Phys. Chem. Chem. Phys., 2024, 26, 15232–15239 RSC.
- J. H. E. Cartwright, B. Escribano and C. I. Sainz-Diaz, Astrophys. J., 2008, 687, 1406 CrossRef.
- I. U. of Pure and A. C. (IUPAC), Micropore, 2025, https://goldbook.iupac.org/terms/view/M03906, Accessed: 05-06-2025.
- M. P. Collings, J. W. Dever, H. J. Fraser and M. R. S. McCoustra, Astrophys. Space Sci., 2003, 285, 633–659 CrossRef CAS.
- R. S. Smith, R. A. May and B. D. Kay, J. Phys. Chem. B, 2016, 120, 1979–1987 CrossRef CAS PubMed.
- P. Jenniskens, S. F. Banham, D. F. Blake and M. R. S. Mccoustra, Liquid water in the domain of cubic crystalline ice I c, 1997.
- R. A. May, R. S. Smith and B. D. Kay, The molecular volcano revisited: Determination of crack propagation and distribution during the crystallization of nanoscale amorphous solid water films, 2012.
- T. Zubkov, R. S. Smith, T. R. Engstrom and B. D. Kay, J. Chem. Phys., 2007, 127, 184707 CrossRef PubMed.
- D. T. Bowron, A. K. Soper, K. Jones, S. Ansell, S. Birch, J. Norris, L. Perrott, D. Riedel, N. J. Rhodes, S. R. Wakefield, A. Botti, M. A. Ricci, F. Grazzi and M. Zoppi, Rev. Sci. Instrum., 2010, 81, 033905 CrossRef CAS PubMed.
- R. K. Heenan, S. E. Rogers, D. Turner, A. E. Terry, J. Treadgold and S. M. King, Neutron News, 2011, 22, 19–21 CrossRef.
- A. K. Soper and C. J. Benmore, Phys. Rev. Lett., 2008, 101, 065502 CrossRef CAS PubMed.
- C. Liang, A. Rayabharam and N. R. Aluru, J. Phys. Chem. B, 2023, 127(29), 6532–6542 CrossRef CAS PubMed.
- A. Soper, Gudrun Software, 2024, https://www.isis.stfc.ac.uk/Pages/Gudrun.aspx, Accessed: 2024-06-25.
- Mantid, Software, 2024, https://www.mantidproject.org/, Accessed: 2024-06-25.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- B. Hammouda, Probing Nanoscale Structures – the SANS toolbox, 2008, https://api.semanticscholar.org/CorpusID:139951325.
- R. A. Baragiola, Planet. Space Sci., 2003, 51, 953–961 CrossRef CAS.
- J. He, A. R. Clements, S. M. Emtiaz, F. Toriello, R. T. Garrod and G. Vidali, Astrophys. J., 2019, 878, 94 CrossRef CAS.
- Z. Amato, T. F. Headen, P. Ghesquiere and H. J. Fraser, Phys. Chem. Chem. Phys., 2025, 27, 14864–14883 RSC.
- L. Feigin and D. Svergun, Structure Analysis by Small-Angle X-Ray and Neutron Scattering, Springer US, Boston, MA, 1987 Search PubMed.
- NIST, Neutron activation and scattering calculator, https://www.ncnr.nist.gov/resources/activation/, 2025, Accessed: 2025-01-14.
- P. Ehrenfreund, H. J. Fraser, J. Blum, J. H. Cartwright, J. M. Garcia-Ruiz, E. Hadamcik, A. C. Levasseur-Regourd, S. Price, F. Prodi and A. Sarkissian, Planet. Space Sci., 2003, 51, 473–494 CrossRef CAS.
- T. Loerting, I. Kohl, W. Schustereder, K. Winkel and E. Mayer, ChemPhysChem, 2006, 7, 1203–1206 CrossRef CAS PubMed.
- B. Hammouda, J. Appl. Crystallogr., 2010, 43, 716–719 CrossRef CAS.
- T. J. Su, J. R. Lu, Z. F. Cui, R. K. Thomas and R. K. Heenan, Langmuir, 1998, 14, 5517–5520 CrossRef CAS.
- R. Strey, J. Winkler and L. Magid, J. Phys. Chem., 1991, 95, 7502–7507 CrossRef CAS.
- SasView, Software, 2024, https://www.sasview.org/, Accessed: 2024-06-25.
- Z. Amato, Batch Analysis ASW, 2025, https://github.com/ZacAmato/Batch_Analysis_ASW, Accessed: 2025-01-03.
- C. R. Hill, C. Mitterdorfer, T. G. Youngs, D. T. Bowron, H. J. Fraser and T. Loerting, Phys. Rev. Lett., 2016, 116, 215501 CrossRef PubMed.
- A. Bar-nun, G. Herman, D. Laufer and M. L. Rappaport, Icarus, 1985, 63, 317–332 CrossRef CAS.
- S. Cazaux, J. B. Bossa, H. Linnartz and A. G. G. M. Tielens, Astron. Astrophys., 2015, 573, A16 CrossRef.
- L. del Rosso, M. Celli, F. Grazzi, M. Catti, T. C. Hansen, A. D. Fortes and L. Ulivi, Nat. Mater., 2020, 19, 663–668 CrossRef CAS PubMed.
- W. F. Kuhs, C. Sippel, A. Falenty and T. C. Hansen, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 21259–21264 CrossRef CAS PubMed.
- T. L. Malkin, B. J. Murray, A. V. Brukhno, J. Anwar and C. G. Salzmann, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1041–1045 CrossRef CAS PubMed.
- D. Blake, L. Allamandola, S. Sandford, D. Hudgins and F. Freund, Science, 1991, 254, 548–551 CrossRef CAS PubMed.
- C. Bu, C. A. Dukes and R. A. Baragiola, Appl. Phys. Lett., 2016, 109, 201902 CrossRef.
- E. H. Mitchell, U. Raut, B. D. Teolis and R. A. Baragiola, Icarus, 2017, 285, 291–299 CrossRef CAS.
- J. A. Ghormley, J. Chem. Phys., 1967, 46, 1321–1325 CrossRef CAS.
- B. Schmitt, J. Ocampo and J. Klinger, J. Phys. Colloq., 1987, 48, C1-519–C1-525 Search PubMed.
- B. J. Murray and J. M. C. Plane, Phys. Chem. Chem. Phys., 2003, 5, 4129–4138 RSC.
- H. J. Fraser, Understanding Structural Changes in Amorphous Solid Water (ASW) on Heating, 2015 DOI:10.5286/ISIS.E.RB1510246.
- H. J. Fraser, What really governs porosity in Amorphous Solid Water (ASW)?, 2016 DOI:10.5286/ISIS.E.RB1610318.
- P. Ghesquiere, Evolution of porosity and structure of Amorphous Solid Water (ASW), 2022 DOI:10.5286/ISIS.E.RB2010205.
| This journal is © the Owner Societies 2026 |