31P NMR chemical shift of phosphine oxides measures the total strength of multiple anticooperative H-bonds formed between the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/h2_char_e001.gif) O group and proton donors
O group and proton donors
Omar
Alkhuder
 ,
Mikhail A.
Kostin
,
Mikhail A.
Kostin
 and
Peter M.
Tolstoy
and
Peter M.
Tolstoy
 *
*
Institute of Chemistry, St. Petersburg State University, St. Petersburg, Russia. E-mail: peter.tolstoy@spbu.ru
First published on 17th November 2025
Abstract
In this work, experimental 31P NMR chemical shifts of triphenylphosphine oxide are used to evaluate the strength of P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O⋯H–O hydrogen bonds. Complexes featuring either one or two H-bonds (1
O⋯H–O hydrogen bonds. Complexes featuring either one or two H-bonds (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, respectively) formed between Ph3P
2 complexes, respectively) formed between Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and 24 substituted phenols are investigated by low-temperature liquid-state NMR spectroscopy in CDF3/CDF2Cl solution. We demonstrate that the 31P NMR chemical shift changes upon complexation, ΔδP, correlate well with the total strength of all hydrogen bonds formed by the P
O and 24 substituted phenols are investigated by low-temperature liquid-state NMR spectroscopy in CDF3/CDF2Cl solution. We demonstrate that the 31P NMR chemical shift changes upon complexation, ΔδP, correlate well with the total strength of all hydrogen bonds formed by the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. This allows one to use ΔδP as a tool for estimating overall binding energies in compounds containing phosphine oxides. Additionally, using DFT calculations with implicit (PCM) and explicit (2–3 solvent molecules) solvation models we reached a semi-quantitative agreement between calculated and experimental ΔδP values. The anticooperativity effects in 1
O group. This allows one to use ΔδP as a tool for estimating overall binding energies in compounds containing phosphine oxides. Additionally, using DFT calculations with implicit (PCM) and explicit (2–3 solvent molecules) solvation models we reached a semi-quantitative agreement between calculated and experimental ΔδP values. The anticooperativity effects in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes were estimated to be ca. 15–20% both in experiment and calculations.
2 complexes were estimated to be ca. 15–20% both in experiment and calculations.
Introduction
In modern chemistry, various molecules containing the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functionality have demonstrated considerable practical utility due to the exceptional electron-donating ability of the P
O functionality have demonstrated considerable practical utility due to the exceptional electron-donating ability of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygen atom, allowing one to tune and enhance the properties of such molecules as participants in various non-covalent interactions: hydrogen bonding, halogen bonding and other σ-hole interactions, coordination bonding and others. For example, the presence of a proton-accepting P
O oxygen atom, allowing one to tune and enhance the properties of such molecules as participants in various non-covalent interactions: hydrogen bonding, halogen bonding and other σ-hole interactions, coordination bonding and others. For example, the presence of a proton-accepting P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group was shown to facilitate the formation of effective hydrogen bond networks for proton transfer, as observed in various proton-conducting materials.1–3 It is also able to impart superior mechanical and thermal properties to polymers.4,5 Besides, the P
O group was shown to facilitate the formation of effective hydrogen bond networks for proton transfer, as observed in various proton-conducting materials.1–3 It is also able to impart superior mechanical and thermal properties to polymers.4,5 Besides, the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group was employed in the design of a wide range of polymeric biomedical materials used in drug delivery, tissue engineering, dental applications, etc.6,7 In particular, surface phosphorylation was used to increase the adhesion and biocompatibility of materials.8,9 Interactions between phosphine oxides and the surfaces of nanoparticles10,11 or quantum dots12,13 are also utilized for their stabilization. In engineering applications, the introduction of the P
O group was employed in the design of a wide range of polymeric biomedical materials used in drug delivery, tissue engineering, dental applications, etc.6,7 In particular, surface phosphorylation was used to increase the adhesion and biocompatibility of materials.8,9 Interactions between phosphine oxides and the surfaces of nanoparticles10,11 or quantum dots12,13 are also utilized for their stabilization. In engineering applications, the introduction of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety and the structural tunability around it were shown to occasionally improve properties such as flame retardation,14,15 UV resistance,16 and mechanical strength.17 In catalysis, P
O moiety and the structural tunability around it were shown to occasionally improve properties such as flame retardation,14,15 UV resistance,16 and mechanical strength.17 In catalysis, P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-containing molecules have several applications, among which the most common ones are perhaps their usage as bifunctional ligands in cross-coupling reactions,18–21 as chiral catalysts for asymmetric organocatalysis,22,23 and as stabilization agents for peroxides formed at various stages of reaction.24–27
O-containing molecules have several applications, among which the most common ones are perhaps their usage as bifunctional ligands in cross-coupling reactions,18–21 as chiral catalysts for asymmetric organocatalysis,22,23 and as stabilization agents for peroxides formed at various stages of reaction.24–27
One of the prominent fields in which materials involving P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups excel is extraction and separation.28 The P
O groups excel is extraction and separation.28 The P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group is considered one of the most effective functional groups in designing extractants for f-block elements, due to its strong coordination ability with highly charged metal ions.29–31 Various compounds containing the P
O group is considered one of the most effective functional groups in designing extractants for f-block elements, due to its strong coordination ability with highly charged metal ions.29–31 Various compounds containing the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group—either phosphine oxides or phosphinic/phosphoric acids29,32—have demonstrated high efficiency in selective extraction of various metals, including lanthanides and actinides, for reprocessing of metallurgical waste33 and spent nuclear fuel.34 Phosphine-oxide-based extractants are usually able to perform extraction in acidic media, which is linked to the high polarity of the P
O group—either phosphine oxides or phosphinic/phosphoric acids29,32—have demonstrated high efficiency in selective extraction of various metals, including lanthanides and actinides, for reprocessing of metallurgical waste33 and spent nuclear fuel.34 Phosphine-oxide-based extractants are usually able to perform extraction in acidic media, which is linked to the high polarity of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond.31,33 For example, the first extractant with high selectivity between Americium and Curium—two of the most challenging elements to separate chemically due to their similar properties—was a tridentate ligand with two P
O bond.31,33 For example, the first extractant with high selectivity between Americium and Curium—two of the most challenging elements to separate chemically due to their similar properties—was a tridentate ligand with two P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O groups.35
O groups.35
The P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O functionality is an excellent NMR and IR spectroscopic probe. In IR spectroscopy, changes in the stretching frequency of the P
O functionality is an excellent NMR and IR spectroscopic probe. In IR spectroscopy, changes in the stretching frequency of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond, ΔνP
O bond, ΔνP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O, were previously used to characterize the strength of hydrogen bonding in phosphine oxide complexes with proton donors.36 In recent studies of R3PO complexes with substituted phenols in organic solutions a non-linear relationship between hydrogen bond strength and the shift in P
O, were previously used to characterize the strength of hydrogen bonding in phosphine oxide complexes with proton donors.36 In recent studies of R3PO complexes with substituted phenols in organic solutions a non-linear relationship between hydrogen bond strength and the shift in P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O frequency was proposed.37 Quantum chemical calculations revealed that the P
O frequency was proposed.37 Quantum chemical calculations revealed that the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O vibrational frequency is affected by additional weak interactions with surrounding solvent molecules.38,39
O vibrational frequency is affected by additional weak interactions with surrounding solvent molecules.38,39
In NMR spectroscopy, it was shown that 31P NMR chemical shift, δP, is strongly affected by the geometry of hydrogen bonds involving the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, as well as other structural and electronic parameters, reflecting the high sensitivity of δP to the surrounding environment,40–42 including various weaker C–H⋯O interactions.43 In a homologous series of complexes, the shift of the 31P NMR signal upon complexation was shown to correlate well with the hydrogen bond strength.44,45 Similar correlations, obtained by quantum-chemical calculations, were also proposed for halogen-bonded complexes.46 On a more qualitative level, experimental 31P NMR spectra were instrumental in proving the stoichiometry of self-associates formed by phosphinic, phosphoric and phosphonic acids: cyclic dimers and trimers,47 cyclic tetramers48 and cage-like tetramers.49 The solid-state 31P NMR spectra of R3PO molecules adsorbed on silica/zeolites were used to describe the translational mobility of guest molecules in the host matrix50 and the acidity of the surface.51 Finally, no account on 31P NMR spectroscopy of phosphine oxides would be complete without mentioning the Gutmann–Beckett method,52,53 in which triethylphosphine oxide (TEPO) is used as a spectroscopic probe to establish so-called Acceptor Numbers (ANs) as a measure of the electron-accepting ability of Lewis acids54–56 or Brønsted acids.57–60 The Gutmann–Beckett methodology, originally developed for liquid solutions, was later on extended to solids61 and to ionic liquids,62 and also the usage of ΔνP
O group, as well as other structural and electronic parameters, reflecting the high sensitivity of δP to the surrounding environment,40–42 including various weaker C–H⋯O interactions.43 In a homologous series of complexes, the shift of the 31P NMR signal upon complexation was shown to correlate well with the hydrogen bond strength.44,45 Similar correlations, obtained by quantum-chemical calculations, were also proposed for halogen-bonded complexes.46 On a more qualitative level, experimental 31P NMR spectra were instrumental in proving the stoichiometry of self-associates formed by phosphinic, phosphoric and phosphonic acids: cyclic dimers and trimers,47 cyclic tetramers48 and cage-like tetramers.49 The solid-state 31P NMR spectra of R3PO molecules adsorbed on silica/zeolites were used to describe the translational mobility of guest molecules in the host matrix50 and the acidity of the surface.51 Finally, no account on 31P NMR spectroscopy of phosphine oxides would be complete without mentioning the Gutmann–Beckett method,52,53 in which triethylphosphine oxide (TEPO) is used as a spectroscopic probe to establish so-called Acceptor Numbers (ANs) as a measure of the electron-accepting ability of Lewis acids54–56 or Brønsted acids.57–60 The Gutmann–Beckett methodology, originally developed for liquid solutions, was later on extended to solids61 and to ionic liquids,62 and also the usage of ΔνP![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O instead of δP was suggested.63
O instead of δP was suggested.63
One of the defining features of phosphine oxides is the ability of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygen atom to simultaneously form multiple hydrogen bonds, a phenomenon for which phosphine oxides were previously called “ambidextrous hydrogen bond acceptors”.64 This capability to interact with multiple proton donors at once enhances the versatility of phosphine oxides in molecular recognition and supramolecular assembly. Despite the experimental evidence confirming the formation of multiple hydrogen bonds with the same P
O oxygen atom to simultaneously form multiple hydrogen bonds, a phenomenon for which phosphine oxides were previously called “ambidextrous hydrogen bond acceptors”.64 This capability to interact with multiple proton donors at once enhances the versatility of phosphine oxides in molecular recognition and supramolecular assembly. Despite the experimental evidence confirming the formation of multiple hydrogen bonds with the same P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group—both in solution and in the crystalline state60,64–67—the previously established numerical correlations between 31P NMR spectra and the complexation energy were constructed only for 1
O group—both in solution and in the crystalline state60,64–67—the previously established numerical correlations between 31P NMR spectra and the complexation energy were constructed only for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (except for our recent computational work, ref. 39). Therefore, the primary objective of this work is to conduct both experimental and quantum chemical investigations to establish correlations between hydrogen bond energies and 31P NMR parameters of 1
1 complexes (except for our recent computational work, ref. 39). Therefore, the primary objective of this work is to conduct both experimental and quantum chemical investigations to establish correlations between hydrogen bond energies and 31P NMR parameters of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 phosphine oxide complexes with proton donors, as well as to explore the cooperativity effects within the pairs of mutually coupled hydrogen bonds in these complexes.
2 phosphine oxide complexes with proton donors, as well as to explore the cooperativity effects within the pairs of mutually coupled hydrogen bonds in these complexes.
For this purpose, here we focus on 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
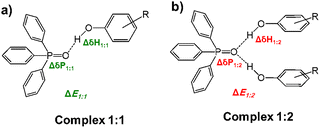
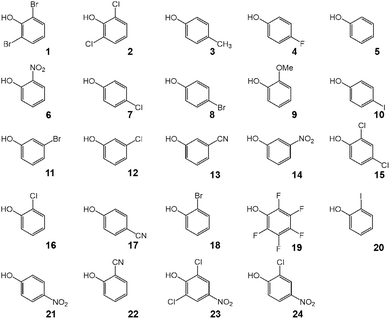
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrogen-bonded complexes composed of triphenylphosphine oxide (Ph3PO) and substituted phenols as OH proton donors. See schematic structures of complexes in Fig. 1 and chemical structures of studied phenols in Fig. 2. Substituted phenols were chosen because they do not have a strong proton-accepting site and provide a decent variety of proton-donating abilities. The complexes were experimentally investigated using 1H and 31P NMR spectroscopy in solution in a mixture of deuterated Freonic gases CDF3/CDF2Cl at 100 K. For each complex we used the value of 1H NMR chemical shift of bridging protons to estimate the hydrogen bond energy, which was then correlated with the 31P NMR chemical shifts. The primary goal was to find a way to use changes in 31P chemical shifts upon complexation, ΔδP, to predict the strength of the complexes. Additionally, we conducted a series of DFT calculations to determine complexation energies ΔE and NMR parameters and compared the results with experimental data. In computations, the effects of P
2 hydrogen-bonded complexes composed of triphenylphosphine oxide (Ph3PO) and substituted phenols as OH proton donors. See schematic structures of complexes in Fig. 1 and chemical structures of studied phenols in Fig. 2. Substituted phenols were chosen because they do not have a strong proton-accepting site and provide a decent variety of proton-donating abilities. The complexes were experimentally investigated using 1H and 31P NMR spectroscopy in solution in a mixture of deuterated Freonic gases CDF3/CDF2Cl at 100 K. For each complex we used the value of 1H NMR chemical shift of bridging protons to estimate the hydrogen bond energy, which was then correlated with the 31P NMR chemical shifts. The primary goal was to find a way to use changes in 31P chemical shifts upon complexation, ΔδP, to predict the strength of the complexes. Additionally, we conducted a series of DFT calculations to determine complexation energies ΔE and NMR parameters and compared the results with experimental data. In computations, the effects of P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O complexation with the neighboring solvent molecules via additional CH⋯O hydrogen bonds were explicitly considered.
O complexation with the neighboring solvent molecules via additional CH⋯O hydrogen bonds were explicitly considered.
Experimental and computational details
Sample preparation
Triphenylphosphine oxide (Ph3PO), substituted phenols 1–24 and chloroform (CHCl3) were purchased from companies listed in Table S1 in the SI and used without further purification. Ph3PO (5.37 mg, 19.3 µmol) was dissolved in 1 mL of CHCl3. Then the weighted amount of substituted phenol (or the corresponding volume for liquid substances) calculated according to the desired stoichiometric composition of the sample (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 1
1 or 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) was added. Subsequently, using an Eppendorf pipette 0.1 mL of the solution was transferred into a thick-walled NMR sample tube with a J. Young valve (Wilmad 522-LPV-7) and CHCl3 was removed in vacuo. Finally, ca. 0.2 mL of the mixture of deuterated freonic gases CDF3/CDF2Cl, synthesized by a modified method of ref. 68, was added by vacuum transfer (at ca. 10−6 mbar), resulting in a Ph3PO concentration of ca. 0.01 M. Prior to the addition to the sample the freonic mixture was additionally dried over alumina in a cold ethanol bath (ca. 140 K). The resulting composition of the sample was controlled by measuring NMR signal intensities of CH protons of Ph3PO and phenols at room temperature. It should be noted that in some cases the composition of the sample at low temperature differs significantly from that initially prepared at room temperature due to the poor and varying solubility of phenols in Freons.
2) was added. Subsequently, using an Eppendorf pipette 0.1 mL of the solution was transferred into a thick-walled NMR sample tube with a J. Young valve (Wilmad 522-LPV-7) and CHCl3 was removed in vacuo. Finally, ca. 0.2 mL of the mixture of deuterated freonic gases CDF3/CDF2Cl, synthesized by a modified method of ref. 68, was added by vacuum transfer (at ca. 10−6 mbar), resulting in a Ph3PO concentration of ca. 0.01 M. Prior to the addition to the sample the freonic mixture was additionally dried over alumina in a cold ethanol bath (ca. 140 K). The resulting composition of the sample was controlled by measuring NMR signal intensities of CH protons of Ph3PO and phenols at room temperature. It should be noted that in some cases the composition of the sample at low temperature differs significantly from that initially prepared at room temperature due to the poor and varying solubility of phenols in Freons.
NMR measurements
All NMR measurements were performed at the Center of Magnetic Resonance in the Saint-Petersburg State University Research Park. The room-temperature and low-temperature (100 ± 1 K) liquid-state 1H and 31P NMR spectra were recorded using a Bruker Avance III 500 MHz spectrometer (11.7 T, 499.91 MHz for 1H, 202.4 MHz for 31P). For 1H NMR spectra 30° pulses, an acquisition time of 2.6 s, a relaxation delay of 1 s, and 128 scans were used. For 31P NMR spectra 30° pulses, an acquisition time of 0.8 s, a relaxation delay of 2 s, and 256 scans were used. All 31P NMR spectra were recorded with broadband proton decoupling. 1H NMR chemical shifts were calibrated to the TMS scale using the central signal of the CHClF2 triplet as an internal secondary standard set to 7.21 ppm. The 31P NMR spectra were referenced to H3PO4 (85% in H2O) using the unified scale, according to IUPAC recommendations.69 The spectra were processed using MestReNova70 and TopSpin software.71Computational details
DFT calculations were carried out at the Computing Center of St. Petersburg State University Research Park. For individual compounds and complexes of Ph3PO with proton donors 1–24 and/or explicit solvent molecules, the calculations of optimized geometries and harmonic vibration frequencies were performed using the Gaussian 16 software package72 at the PW6B95/def2-TZVPD level of theory.73–76 The Grimme dispersion correction GD3 was included.77 This level of theory was chosen because it follows the recent “best practice protocol” recommendations78 and benchmarks,79 combining a meta-hybrid generalized gradient approximation functional (mGGA) with a triple-ζ basis set and dispersion correction. In a large-scale benchmark study80 PW6B95-D3 was found to be the most robust and accurate general-purpose hybrid-functional, based on its performance in the combined evaluation of basic molecular properties, reaction energies and non-covalent interactions.Unless specified in the text, the polarizable continuum model (PCM, ε = 40)81 was used for implicit solvent effects. All structures were checked for the absence of imaginary harmonic vibrational frequencies. For each complex several chemically reasonable starting geometries were tested, which differed by the relative orientations of Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and proton donors pre-positioned to form hydrogen bonds with the P
O and proton donors pre-positioned to form hydrogen bonds with the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and preoptimized at the B3LYP/6-311++G(d,p) level of theory. In all cases, in the final optimized structures the CH⋯O and the OH⋯O hydrogen bonds stayed intact. The structures with the lowest electronic energies were selected for further analysis. For more on that see Fig. 8 and the corresponding text.
O group and preoptimized at the B3LYP/6-311++G(d,p) level of theory. In all cases, in the final optimized structures the CH⋯O and the OH⋯O hydrogen bonds stayed intact. The structures with the lowest electronic energies were selected for further analysis. For more on that see Fig. 8 and the corresponding text.
The complexation energies for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (ΔE1
1 complexes (ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were calculated as the difference between the full electronic energies of the complex and its constituting fragments in their relaxed geometries: ΔE1
1) were calculated as the difference between the full electronic energies of the complex and its constituting fragments in their relaxed geometries: ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 = Ecomplex
1 = Ecomplex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 – (EPh3PO + Efree
1 – (EPh3PO + Efree![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) proton
proton![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) donor). In a similar way, the complexation energies for 1
donor). In a similar way, the complexation energies for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (ΔE1
2 complexes (ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) were defined as ΔE1
2) were defined as ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 = Ecomplex
2 = Ecomplex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 – (EPh3PO + 2·Efree
2 – (EPh3PO + 2·Efree![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) proton
proton![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) donor). In case if explicit solvent molecules were used in the calculation, the expressions for complexation energies were modified accordingly. Namely, all energy values were taken for complexes of the corresponding species with the required number of solvent molecules. For example, ΔE1
donor). In case if explicit solvent molecules were used in the calculation, the expressions for complexation energies were modified accordingly. Namely, all energy values were taken for complexes of the corresponding species with the required number of solvent molecules. For example, ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 = Ecomplex
2 = Ecomplex![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2+CHF3 + 2·ECHF3 − EPh3PO+3×CHF3 − 2·Efree
2+CHF3 + 2·ECHF3 − EPh3PO+3×CHF3 − 2·Efree![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) proton
proton![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) donor, see one of the following subsections for more details. The complexation energies were calculated without correction for the basis set superposition error (BSSE).
donor, see one of the following subsections for more details. The complexation energies were calculated without correction for the basis set superposition error (BSSE).
For each species optimized at the abovementioned level of theory, the set of NMR parameters were calculated using the GIAO approach at the WP04/pcSseg-2 level of theory. The pcSseg-2 basis set was extensively benchmarked for nuclear shielding calculations for a wide set of atoms.82 The WP04 functional was previously shown to perform especially well for 1H NMR chemical shifts.83 The NMR shielding constants σfree were calculated for isolated proton donors (for 1H) or isolated Ph3PO (for 31P) in their relaxed geometries. The NMR shielding constants σcomplex were computed for the same moieties in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes. Changes in 1H and 31P NMR chemical shifts upon complexation, ΔδH1
2 complexes. Changes in 1H and 31P NMR chemical shifts upon complexation, ΔδH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (or ΔδH1
1 (or ΔδH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and ΔδP1
2) and ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (or ΔδP1
1 (or ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2), were calculated as Δδ = σfree – σcomplex.
2), were calculated as Δδ = σfree – σcomplex.
Results
NMR spectra
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
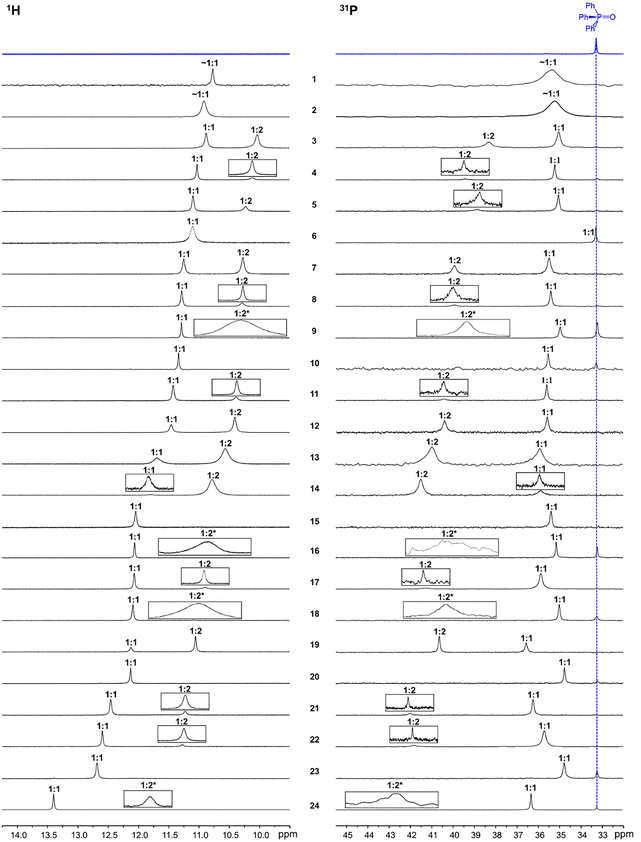
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes. This assignment is based on the following. The signals of 1
2 complexes. This assignment is based on the following. The signals of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes were identified by studying NMR spectra of additional samples at different Ph3PO/phenol ratios: when the concentration of substituted phenol is decreased this signal remains the only one in the spectrum. Fig. S1 in the SI gives an example of a series of such measurements for the Ph3PO complex with 4-chlorophenol 7. The stoichiometry of 1
1 complexes were identified by studying NMR spectra of additional samples at different Ph3PO/phenol ratios: when the concentration of substituted phenol is decreased this signal remains the only one in the spectrum. Fig. S1 in the SI gives an example of a series of such measurements for the Ph3PO complex with 4-chlorophenol 7. The stoichiometry of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes was identified by comparing the relative integrated intensities of signals in the 1H and 31P spectra, as shown in Fig. S1 in the SI.
2 complexes was identified by comparing the relative integrated intensities of signals in the 1H and 31P spectra, as shown in Fig. S1 in the SI.
For the Ph3PO complex with phenols 9, 16, 18 and 24 it is hard to find conditions for simultaneous observation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, so it is done for separate samples, see Fig. S2–S5 in the SI.
2 complexes, so it is done for separate samples, see Fig. S2–S5 in the SI.
In cases of 2,6-disubstituted phenols with bulky substituents (1, 2, and 23) and in several other cases (10, 15, and 20) we were unable to obtain convincing spectra with resolved signals, which could be assigned to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes. In most of cases this was at least partially due to the low solubility of these phenols at low temperatures. Besides, steric hindrance imposed by two ortho-substituents might preclude the formation of stable 1
2 complexes. In most of cases this was at least partially due to the low solubility of these phenols at low temperatures. Besides, steric hindrance imposed by two ortho-substituents might preclude the formation of stable 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (for more on this, see the Discussion). Moreover, for 2,6-disubstituted phenols 1 and 2 the observed 1H and 31P signals keep shifting when the composition of the samples is changed, indicating a fast exchange regime between free species and weakly H-bonded complexes, see Fig. S6 and S7 in the SI. For this reason, as the closest approximation to the spectra of 1
2 complexes (for more on this, see the Discussion). Moreover, for 2,6-disubstituted phenols 1 and 2 the observed 1H and 31P signals keep shifting when the composition of the samples is changed, indicating a fast exchange regime between free species and weakly H-bonded complexes, see Fig. S6 and S7 in the SI. For this reason, as the closest approximation to the spectra of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes we took 1H NMR spectra of the samples with the lowest amounts of 1 (2), and 31P NMR spectra of the samples with the ratio of Ph3PO and 1 (2) closest to 1
1 complexes we took 1H NMR spectra of the samples with the lowest amounts of 1 (2), and 31P NMR spectra of the samples with the ratio of Ph3PO and 1 (2) closest to 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. We felt that this is more appropriate than to discard these data entirely.
1. We felt that this is more appropriate than to discard these data entirely.
Under the conditions used – no more than 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratio of phosphine oxide to phenol – there was no detectable formation of 1
2 molar ratio of phosphine oxide to phenol – there was no detectable formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes. It should be mentioned, however, that during the course of the experiments for 4-fluorophenol (4), phenol (5), 2,4-dichlorophenol (15), 2-chlorophenol (16), 2-bromophenol (18), 2-iodophenol (20), and 2,6-dichloro-4-nitrophenol (23) we tested higher relative concentrations and noticed that the excess phenol tends to precipitate at low temperatures. This might indicate that for these particular phenols the formation of 1
3 complexes. It should be mentioned, however, that during the course of the experiments for 4-fluorophenol (4), phenol (5), 2,4-dichlorophenol (15), 2-chlorophenol (16), 2-bromophenol (18), 2-iodophenol (20), and 2,6-dichloro-4-nitrophenol (23) we tested higher relative concentrations and noticed that the excess phenol tends to precipitate at low temperatures. This might indicate that for these particular phenols the formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes is suppressed either by steric reasons or by the low solubility of the phenol, which is true for the majority of studied phenols in the CDF3/CDF2Cl mixture (note that already 1
3 complexes is suppressed either by steric reasons or by the low solubility of the phenol, which is true for the majority of studied phenols in the CDF3/CDF2Cl mixture (note that already 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes are rarely in majority or even entirely absent, as for 15, 20, and 23).
2 complexes are rarely in majority or even entirely absent, as for 15, 20, and 23).
In 1H NMR spectra there are no OH signals that could be assigned to free (uncomplexed) phenols with one notable exception. In the 31P NMR spectrum of the sample containing Ph3PO and 2-nitrophenol 6 the position of the signal of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group is unchanged, indicating that there is no clearly detectable complexation between the species. Thus, the corresponding 1H NMR signal at 11.11 ppm is likely due to the formation of an intramolecular hydrogen bond between –OH and –NO2 groups of 6. In the Discussion section the corresponding data point will be omitted from the construction of various correlations. In all other cases the OH chemical shifts of 1
O group is unchanged, indicating that there is no clearly detectable complexation between the species. Thus, the corresponding 1H NMR signal at 11.11 ppm is likely due to the formation of an intramolecular hydrogen bond between –OH and –NO2 groups of 6. In the Discussion section the corresponding data point will be omitted from the construction of various correlations. In all other cases the OH chemical shifts of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 species in the range 10.5–13.5 ppm are characteristic of medium–strong hydrogen bonds with Ph3PO. The further downfield the signal appears, the stronger the corresponding hydrogen bond.84 The OH signals of 1
1 species in the range 10.5–13.5 ppm are characteristic of medium–strong hydrogen bonds with Ph3PO. The further downfield the signal appears, the stronger the corresponding hydrogen bond.84 The OH signals of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes are shifted upfield with respect to the signals of 1
2 complexes are shifted upfield with respect to the signals of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, which is indicative of anticooperative coupling of two hydrogen bonds,85 competing for the electron density at the central oxygen atom, RO–H⋯O(P)⋯H–OR. In turn, 31P NMR signals shift further to the low field as the number of hydrogen bonds and/or their strength increases. Therefore, it could be suggested that while OH chemical shifts are markers of the strength of each hydrogen bond individually, the 31P NMR chemical shift of phosphine oxide could be a marker of the total (combined) strength of all hydrogen bonds formed with the P
1 complexes, which is indicative of anticooperative coupling of two hydrogen bonds,85 competing for the electron density at the central oxygen atom, RO–H⋯O(P)⋯H–OR. In turn, 31P NMR signals shift further to the low field as the number of hydrogen bonds and/or their strength increases. Therefore, it could be suggested that while OH chemical shifts are markers of the strength of each hydrogen bond individually, the 31P NMR chemical shift of phosphine oxide could be a marker of the total (combined) strength of all hydrogen bonds formed with the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. This hypothesis will be examined in detail in the Discussion. The numerical values of 1H and 31P NMR chemical shifts of 1
O group. This hypothesis will be examined in detail in the Discussion. The numerical values of 1H and 31P NMR chemical shifts of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (δH1
2 complexes (δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, δH1
1, δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, δP1
2, δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and δP1
1 and δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively) and their changes upon complexation with respect to free individual species (ΔδP1
2, respectively) and their changes upon complexation with respect to free individual species (ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔδP1
1 and ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) are collected in Table 1.
2) are collected in Table 1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes formed between Ph3PO and substituted phenols in CDF3/CDF2Cl at 100 K. Chemical shifts δH1
2 complexes formed between Ph3PO and substituted phenols in CDF3/CDF2Cl at 100 K. Chemical shifts δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, δH1
1, δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, δP1
2, δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and δP1
1, and δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in ppm. Changes in NMR chemical shifts upon complexation ΔδP1
2 in ppm. Changes in NMR chemical shifts upon complexation ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔδP1
1 and ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in ppm. Complexation energies (estimated using eqn (1) as described in the text), ΔE1
2 in ppm. Complexation energies (estimated using eqn (1) as described in the text), ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ΔE1
1, ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 in kJ mol−1
2 in kJ mol−1
| No. | Proton donor | Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
||||||
|---|---|---|---|---|---|---|---|---|---|
δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
δP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
||
| 1 | 2,6-Dibromophenol | 10.77 | 35.31 | 2.06 | 27.29 | — | — | — | — |
| 2 | 2,6-Dichlorophenol | 10.92 | 35.23 | 1.98 | 27.90 | — | — | — | — |
| 3 | 4-Methylphenol | 10.88 | 35.03 | 1.78 | 27.75 | 10.03 | 38.30 | 5.05 | 48.43 |
| 4 | 4-Fluorophenol | 11.03 | 35.22 | 1.97 | 28.38 | 10.11 | 39.41 | 6.16 | 49.10 |
| 5 | Phenol | 11.10 | 35.04 | 1.79 | 28.66 | 10.23 | 38.84 | 5.59 | 50.06 |
| 6 | 2-Nitrophenol | 11.11 | 33.29 | 0.04 | 28.70 | — | — | — | — |
| 7 | 4-Chlorophenol | 11.25 | 35.47 | 2.22 | 29.30 | 10.27 | 39.92 | 6.67 | 50.43 |
| 8 | 4-Bromophenol | 11.28 | 35.40 | 2.15 | 29.43 | 10.28 | 39.91 | 6.66 | 50.49 |
| 9 | 2-Methoxyphenol | 11.29 | 34.96 | 1.71 | 29.45 | 10.30 | 39.35 | 6.10 | 50.66 |
| 10 | 4-Iodophenol | 11.33 | 35.51 | 2.26 | 29.65 | — | — | — | — |
| 11 | 3-Bromophenol | 11.43 | 35.59 | 2.34 | 30.03 | 10.39 | 40.42 | 7.17 | 51.38 |
| 12 | 3-Chlorophenol | 11.46 | 35.56 | 2.31 | 30.16 | 10.40 | 40.40 | 7.15 | 51.54 |
| 13 | 3-Cyanophenol | 11.69 | 35.90 | 2.65 | 31.15 | 10.56 | 40.96 | 7.71 | 52.85 |
| 14 | 3-Nitrophenol | 11.81 | 35.88 | 2.63 | 31.63 | 10.78 | 41.50 | 8.25 | 54.68 |
| 15 | 2,4-Dichlorophenol | 12.04 | 35.38 | 2.13 | 32.61 | — | — | — | — |
| 16 | 2-Chlorophenol | 12.06 | 35.14 | 1.89 | 32.69 | 10.85 | 40.27 | 7.02 | 55.27 |
| 17 | 4-Cyanophenol | 12.07 | 35.87 | 2.62 | 32.72 | 10.90 | 41.31 | 8.06 | 55.66 |
| 18 | 2-Bromophenol | 12.09 | 35.01 | 1.76 | 32.81 | 11.00 | 40.37 | 7.12 | 56.53 |
| 19 | 2,3,4,5,6-Pentafluorophenol | 12.12 | 36.56 | 3.31 | 32.94 | 11.05 | 40.64 | 7.39 | 56.95 |
| 20 | 2-Iodophenol | 12.13 | 34.76 | 1.51 | 32.97 | — | — | — | — |
| 21 | 4-Nitrophenol | 12.45 | 36.23 | 2.98 | 34.33 | 11.22 | 42.03 | 8.78 | 58.37 |
| 22 | 2-Cyanophenol | 12.59 | 35.71 | 2.46 | 34.92 | 11.27 | 41.83 | 8.58 | 58.78 |
| 23 | 2,6-Dichloro-4-nitrophenol | 12.68 | 34.77 | 1.52 | 35.27 | — | — | — | — |
| 24 | 2-Chloro-4-nitrophenol | 13.40 | 36.31 | 3.06 | 38.28 | 11.80 | 42.63 | 9.38 | 63.23 |
QC calculations
To find out how much solvation influences the observed correlation between 31P NMR chemical shift and hydrogen bond strength, we have performed a series of quantum-chemical calculations including implicit and explicit solvent models. The full set of considered structures is schematically shown in Fig. S8 in the SI, while here we will focus primarily on the most relevant cases.![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O). This matches the distribution of electron localization function (ELF) previously described for (CH3)3PO.39
O). This matches the distribution of electron localization function (ELF) previously described for (CH3)3PO.39
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes with and without solvent molecules on the examples of complexes with 3-chlorophenol 12. Optimized structures of other complexes are qualitatively similar and collected in the SI as sets of xyz coordinates.
2 complexes with and without solvent molecules on the examples of complexes with 3-chlorophenol 12. Optimized structures of other complexes are qualitatively similar and collected in the SI as sets of xyz coordinates.
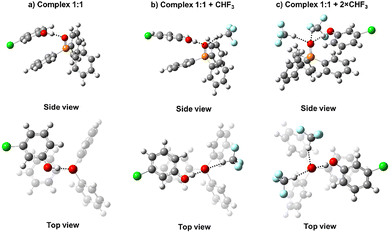 | ||
Fig. 5 The optimized structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes of Ph3PO with 3-chlorophenol 12 in an aprotic medium (ε = 40) without explicit solvent molecules (a) and with one (b) or two (c) solvent molecules. 1 complexes of Ph3PO with 3-chlorophenol 12 in an aprotic medium (ε = 40) without explicit solvent molecules (a) and with one (b) or two (c) solvent molecules. | ||
 | ||
Fig. 6 The optimized structures of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes of Ph3PO with 3-chlorophenol 12 in an aprotic medium (ε = 40) without (a) and with one (b) explicit solvent molecule. 2 complexes of Ph3PO with 3-chlorophenol 12 in an aprotic medium (ε = 40) without (a) and with one (b) explicit solvent molecule. | ||
The structures of all complexes exhibit several similarities: the intermolecular OHO hydrogen bonds are nearly linear and formed along one of the lone pairs of the oxygen atom of Ph3PO, while solvent molecules fill other vacancies around the PO group. Note that in the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes without the solvent molecule the dihedral angle between two OHO hydrogen bonds (more precisely, the angle between two PO(H)O planes) is close to 120°, which also corresponds to the localization of lone pairs characteristic of sp3 hybridization of the PO oxygen.
2 complexes without the solvent molecule the dihedral angle between two OHO hydrogen bonds (more precisely, the angle between two PO(H)O planes) is close to 120°, which also corresponds to the localization of lone pairs characteristic of sp3 hybridization of the PO oxygen.
As it will be justified in the Discussion, as the main complexation reaction we have considered the reaction schematically shown in Fig. 7. Here, the oxygen atom of Ph3PO in its “free” state forms three hydrogen bonds with CHF3 solvent molecules, which are being substituted one by one with phenols upon formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes. Addition of each subsequent solvent molecule is energetically favorable due to the formation of an extra CH⋯O hydrogen bond. Moreover, replacing any solvent molecule with phenols 1–24 is also energetically favorable mainly because the newly formed OH⋯O hydrogen bonds are stronger than the replaced CH⋯O ones. This is demonstrated in Fig. S9 as an energy diagram on the example of 2-chloro-4-nitrophenol 24. The calculations indicate that for the smaller phenols (with the possible exception of 2,6-disubstituted one) there is sufficient space around the P
2 complexes. Addition of each subsequent solvent molecule is energetically favorable due to the formation of an extra CH⋯O hydrogen bond. Moreover, replacing any solvent molecule with phenols 1–24 is also energetically favorable mainly because the newly formed OH⋯O hydrogen bonds are stronger than the replaced CH⋯O ones. This is demonstrated in Fig. S9 as an energy diagram on the example of 2-chloro-4-nitrophenol 24. The calculations indicate that for the smaller phenols (with the possible exception of 2,6-disubstituted one) there is sufficient space around the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group for a third phenol molecule to replace the remaining CHF3 solvent molecule and to form a third OH⋯O hydrogen bond; as an example, see the structure of the 1
O group for a third phenol molecule to replace the remaining CHF3 solvent molecule and to form a third OH⋯O hydrogen bond; as an example, see the structure of the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complex with phenol 24 below Fig. S9. The third OH⋯O bond remains stronger than the CH⋯O bond it replaces, and the complex gains additional stability. However, the 1
3 complex with phenol 24 below Fig. S9. The third OH⋯O bond remains stronger than the CH⋯O bond it replaces, and the complex gains additional stability. However, the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 complexes were not considered in this work, as their experimental counterparts were not detected.
3 complexes were not considered in this work, as their experimental counterparts were not detected.
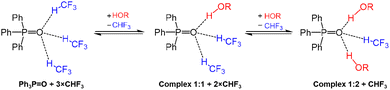 | ||
Fig. 7 Reaction of formation of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1 1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes between Ph3PO and ROH including explicit solvation of Ph3PO by CHF3 molecules. 2 complexes between Ph3PO and ROH including explicit solvation of Ph3PO by CHF3 molecules. | ||
In all cases the complexes were also surrounded by a polarizable medium. Other possible reactions are listed in Fig. S10 in the SI, and they will be briefly mentioned in the Discussion as well.
The full electronic energy values and the NMR shielding constants for all species considered are included in Tables S2–S4 in the SI. For convenience, using the data for the species shown in Fig. 7, we have prepared a separate table (Table 2) containing changes in electronic energies (ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔE1
1 and ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) and the corresponding changes in NMR observables (ΔδH1
2) and the corresponding changes in NMR observables (ΔδH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ΔδH1
1, ΔδH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, ΔδP1
2, ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and ΔδP1
1, and ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) along the complexation reaction. In this way, Table 2 is analogous to the experimental table (Table 1).
2) along the complexation reaction. In this way, Table 2 is analogous to the experimental table (Table 1).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, ΔδH1
1, ΔδH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, ΔδP1
2, ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔδP1
1 and ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2) in ppm, complexation energy, ΔE1
2) in ppm, complexation energy, ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔE1
1 and ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, in kJ mol−1
2, in kJ mol−1
| No. | Proton donor | Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 + 2 × CHF3 1 + 2 × CHF3 |
Complexes 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 + 2 × CHF3 2 + 2 × CHF3 |
||||
|---|---|---|---|---|---|---|---|
δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
−ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
δH1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
ΔδP1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
−ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 2 |
||
| a Iodine element is not included in the pcSseg-2 basis set used in this work. | |||||||
| 1 | 2,6-Dibromophenol | 3.55 | 5.86 | 33.17 | 2.98 | 8.75 | 63.87 |
| 2 | 2,6-Dichlorophenol | 3.48 | 5.37 | 31.91 | 3.06 | 9.09 | 57.55 |
| 3 | 4-Methylphenol | 5.23 | 3.17 | 27.86 | 5.29 | 6.61 | 44.78 |
| 4 | 4-Fluorophenol | 5.04 | 3.45 | 29.43 | 5.35 | 7.51 | 46.42 |
| 5 | Phenol | 5.23 | 3.31 | 28.01 | 5.35 | 6.99 | 45.27 |
| 6 | 2-Nitrophenol | 5.92 | 4.86 | 37.30 | 5.50 | 9.31 | 63.25 |
| 7 | 4-Chlorophenol | 5.26 | 3.40 | 30.70 | 5.49 | 7.42 | 47.95 |
| 8 | 4-Bromophenol | 5.27 | 3.39 | 31.15 | 5.49 | 7.94 | 48.35 |
| 9 | 2-Methoxyphenol | 5.08 | 3.41 | 29.08 | 5.00 | 7.33 | 51.52 |
| 10 | 4-Iodophenola | — | — | — | — | — | — |
| 11 | 3-Bromophenol | 5.30 | 3.82 | 30.92 | 5.51 | 7.78 | 49.04 |
| 12 | 3-Chlorophenol | 5.24 | 4.03 | 30.64 | 5.49 | 7.54 | 48.58 |
| 13 | 3-Cyanophenol | 5.63 | 4.45 | 32.15 | 5.59 | 8.63 | 49.96 |
| 14 | 3-Nitrophenol | 5.46 | 4.40 | 33.38 | 5.65 | 9.13 | 50.77 |
| 15 | 2,4-Dichlorophenol | 5.76 | 4.34 | 35.59 | 5.73 | 9.80 | 54.84 |
| 16 | 2-Chlorophenol | 5.56 | 3.28 | 32.59 | 5.67 | 8.84 | 52.32 |
| 17 | 4-Cyanophenol | 5.65 | 3.96 | 33.48 | 5.78 | 9.15 | 51.27 |
| 18 | 2-Bromophenol | 5.42 | 4.26 | 33.15 | 5.68 | 9.30 | 53.51 |
| 19 | 2,3,4,5,6-Pentafluorophenol | 5.97 | 4.11 | 41.56 | 4.55 | 8.86 | 67.30 |
| 20 | 2-Iodophenola | — | — | — | — | — | — |
| 21 | 4-Nitrophenol | 5.92 | 4.27 | 35.42 | 5.82 | 10.21 | 52.66 |
| 22 | 2-Cyanophenol | 5.92 | 4.15 | 35.42 | 5.91 | 10.17 | 55.66 |
| 23 | 2,6-Dichloro-4-nitrophenol | 4.70 | 6.28 | 36.95 | 3.42 | 9.37 | 67.18 |
| 24 | 2-Chloro-4-nitrophenol | 6.47 | 4.79 | 40.21 | 6.23 | 11.70 | 60.16 |
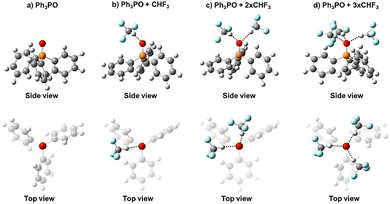
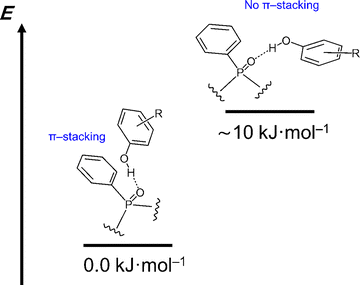
As a side note it should be mentioned that for some 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes we have obtained more than one stable structure. These structures differ in relative orientations of phenyl rings in Ph3P
1 complexes we have obtained more than one stable structure. These structures differ in relative orientations of phenyl rings in Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and phenol: π-stacking lowers the complexation energy by ca. 10 kJ mol−1, as shown schematically in Fig. 8. As an example, Fig. S11a and S10b in the SI illustrate two structures of the Ph3PO complex with 2,4-dichlorophenol 15 in the presence of two CHF3 molecules, while Fig. S11c in the SI shows the energy difference between the structures with and without the π-stacking for all complexes in which this phenomenon was observed. Throughout this work we always used the structures with the lowest energy.
O and phenol: π-stacking lowers the complexation energy by ca. 10 kJ mol−1, as shown schematically in Fig. 8. As an example, Fig. S11a and S10b in the SI illustrate two structures of the Ph3PO complex with 2,4-dichlorophenol 15 in the presence of two CHF3 molecules, while Fig. S11c in the SI shows the energy difference between the structures with and without the π-stacking for all complexes in which this phenomenon was observed. Throughout this work we always used the structures with the lowest energy.
Discussion
In the following, we attempt to construct and discuss the relationships between the energy of complexation and the experimental 1H and 31P NMR chemical shifts of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrogen-bonded complexes formed by Ph3PO and substituted phenols 1–24. We also discuss the construction of an appropriate computational model, which is able to quantitatively reproduce the experimental findings, mainly by evaluating implicit and explicit solvation effects on the calculated parameters. Additionally, we study and discuss the anticooperativity of hydrogen bonds in the case of 1
2 hydrogen-bonded complexes formed by Ph3PO and substituted phenols 1–24. We also discuss the construction of an appropriate computational model, which is able to quantitatively reproduce the experimental findings, mainly by evaluating implicit and explicit solvation effects on the calculated parameters. Additionally, we study and discuss the anticooperativity of hydrogen bonds in the case of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes.
2 complexes.
Experimental correlations between δH, ΔδP and ΔE
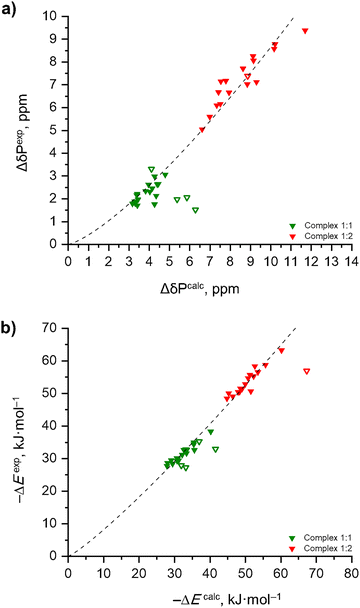
Fig. 9a shows the experimental correlations between δH and ΔδP for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (green circles) and the 1
1 complexes (green circles) and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (red circles). At first glance, the two data sets seem to follow independent trends (the solid curves shown in Fig. 9a will be explained below). However, the situation changes if one converts the experimental 1H NMR chemical shifts, δH, into the complexation energy, ΔE, using the linear equation previously proposed by T. Schaefer in ref. 86 for intramolecular O–H⋯O hydrogen bonds formed within ortho-substituted phenols:
2 complexes (red circles). At first glance, the two data sets seem to follow independent trends (the solid curves shown in Fig. 9a will be explained below). However, the situation changes if one converts the experimental 1H NMR chemical shifts, δH, into the complexation energy, ΔE, using the linear equation previously proposed by T. Schaefer in ref. 86 for intramolecular O–H⋯O hydrogen bonds formed within ortho-substituted phenols:| –ΔE (in kJ mol−1) = 4.18·(δH − δHfree) (in ppm) + 1.67 | (1) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, the ΔE1
1 complexes, the ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 values calculated using eqn (1) range from ∼26 kJ mol−1 to ∼40 kJ mol−1. For 1
1 values calculated using eqn (1) range from ∼26 kJ mol−1 to ∼40 kJ mol−1. For 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes, the ΔE1
2 complexes, the ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 values, determined as the sum of energies of two hydrogen bonds, each calculated using eqn (1), range from ∼48 kJ mol−1 to ∼70 kJ mol−1. The ΔE1
2 values, determined as the sum of energies of two hydrogen bonds, each calculated using eqn (1), range from ∼48 kJ mol−1 to ∼70 kJ mol−1. The ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔE1
1 and ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 values are added to Table 1, while the resulting ΔE(ΔδP) plot is shown in Fig. 9b.
2 values are added to Table 1, while the resulting ΔE(ΔδP) plot is shown in Fig. 9b.
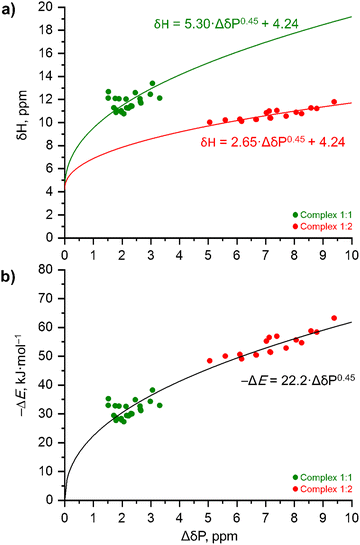 | ||
Fig. 9 The experimental correlations between ΔδP and (a) δH and (b) ΔE (estimated using eqn (1)) for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (green circles) and the 1 1 complexes (green circles) and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (red circles) formed between Ph3PO with substituted phenols based on the NMR experimental data set listed in Table 1. 2 complexes (red circles) formed between Ph3PO with substituted phenols based on the NMR experimental data set listed in Table 1. | ||
At this point it seems appropriate to say a couple of words about the applicability and validity of eqn (1). Over the last several decades there were at least a dozen of experimental and theoretical publications dedicated to the construction of correlations between hydrogen bond strength and bridging proton NMR chemical shifts, see examples in ref. 87–91. Somewhat surprisingly, in all of these works a linear relationship was established/proposed. Depending on the type of the hydrogen bond (OHO, OHN, FHF, etc.) and the set of studied complexes, various slopes and free terms were listed. Based on this collection of works, the following could be summarized: for medium strong hydrogen bonds formed between OH acids and organic proton acceptors the downfield shift of the 1H NMR signal by 1 ppm typically corresponds to ca. 4–7 kJ mol−1 of hydrogen bond strengthening. In turn, the free term, which logically should be zero in an ideal case, tends to be relatively small, correcting the results by a couple of kJ mol−1. For more on this, see ref. 81. There are no publications perfectly matching the set of complexes considered here. Two of the close matches are our previous works, ref. 45 and 39, where based on theoretical calculations for trimethylphosphine oxide complexes with various organic acids the slope of ca. 6 kJ mol−1 ppm−1 was proposed. Nevertheless, in the spirit of this essentially experimental work we decided to rely on the experimental results reported in ref. 83 and given by eqn (1), which has an additional advantage of dealing specifically with hydrogen bonds involving phenolic OH groups. Previously, eqn (1) was also successfully applied to the study on phenol complexes with C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O acceptors.82
O acceptors.82
Coming back to the ΔE(ΔδP) plot shown in Fig. 9b, now the data points for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes could be simultaneously and reasonably well fit by a single power function:
2 complexes could be simultaneously and reasonably well fit by a single power function:
| –ΔE (in kJ mol−1) = 22.2·ΔδP0.45 (in ppm) | (2) |
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. A caution should be exercised, however, when interpreting ΔδP values for 1
O group. A caution should be exercised, however, when interpreting ΔδP values for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes alone, due to significant scattering of the data points. All the hydrogen bond energies of 1
1 complexes alone, due to significant scattering of the data points. All the hydrogen bond energies of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes are relatively close to each other within the 25–35 kJ mol−1 range and the chemical shifts are scattered over the 1.5–3.5 ppm region. The overall cloud of data points is somewhat elongated along the correlation curve and the general upward trend is well reproduced by the calculations (see below), but the scattering of experimental data points is clear. As a result, not much could be concluded about the relative hydrogen bond energies for a random pair of 1
1 complexes are relatively close to each other within the 25–35 kJ mol−1 range and the chemical shifts are scattered over the 1.5–3.5 ppm region. The overall cloud of data points is somewhat elongated along the correlation curve and the general upward trend is well reproduced by the calculations (see below), but the scattering of experimental data points is clear. As a result, not much could be concluded about the relative hydrogen bond energies for a random pair of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes from their 31P NMR chemical shifts, besides the rough estimate that both hydrogen bonds are around 30 kJ mol−1. The situation is somewhat better for 1
1 complexes from their 31P NMR chemical shifts, besides the rough estimate that both hydrogen bonds are around 30 kJ mol−1. The situation is somewhat better for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes. While the range of hydrogen bond energies is twice as wide, the ΔδP ranges three times larger, so that the data points are better stretched along the correlation curve, giving more confidence in the curve itself and in the resulting estimates of hydrogen bond energies.
2 complexes. While the range of hydrogen bond energies is twice as wide, the ΔδP ranges three times larger, so that the data points are better stretched along the correlation curve, giving more confidence in the curve itself and in the resulting estimates of hydrogen bond energies.
Previously the functional dependence of type ΔE = α·ΔδPβ was found computationally for hydrogen-bonded complexes of trimethylphosphine oxide ((CH3)3PO, TMPO) with stoichiometries 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 145 and 1
145 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 239 and also for various halogen-bonded complexes of TMPO.46 It could be expected that for other phosphine oxides, such as popular thiethylphosphine oxide (TEPO), a similar functional dependence would be observed, with some variations in coefficients α and β reflecting different spans of 31P NMR chemical shifts and bond energies available for TEPO. We find it too early to speculate about the exact α and β values for other phosphine oxides prior to the experiments/calculations.
239 and also for various halogen-bonded complexes of TMPO.46 It could be expected that for other phosphine oxides, such as popular thiethylphosphine oxide (TEPO), a similar functional dependence would be observed, with some variations in coefficients α and β reflecting different spans of 31P NMR chemical shifts and bond energies available for TEPO. We find it too early to speculate about the exact α and β values for other phosphine oxides prior to the experiments/calculations.
It is intriguing to check the possibility of reproducing quantitatively the results shown in Fig. 9b using quantum-chemical calculations. Clearly, the 31P NMR chemical shift is quite sensitive to hydrogen bonds formed by the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. Thus, it could be argued that in the case of weakly CH–proton donating solvents, such as CHF3, a careful account for specific solvent–solute interactions is required to achieve the quantitative match. We explore this in the following section.
O group. Thus, it could be argued that in the case of weakly CH–proton donating solvents, such as CHF3, a careful account for specific solvent–solute interactions is required to achieve the quantitative match. We explore this in the following section.
Quantum-chemical correlations between ΔE and ΔδP
The set of optimized structures described in Results allows one to consider complexation between Ph3PO and substituted phenols in vacuum or in a polarizable continuum (Fig. S10a in the SI), as well as additionally explicitly taking into account solvent molecules forming CH⋯O hydrogen bonds with P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O oxygen: two solvent molecules (if sp2 hybridization dominates, Fig. S10b in the SI) or three solvent molecules (if sp3 hybridization dominates, Fig. 7). Using the data from Tables S2–S4 in the SI, for each of these models one could generate −ΔE(ΔδP) plots, which are shown in Fig. S13a–c in the SI and Fig. 11, respectively, superimposed with experimental data points (several data points in Fig. 11 are shown as open symbols for the reason that will be explained in one of the following paragraphs). In all cases, the general trends are qualitatively consistent with the experiment: ΔδP increases with increasing overall ΔE for the majority of compounds. Quantitatively, clearly, both implicit and explicit solvent models consequently and significantly improve the quality of the match between theory and experiment. Going from vacuum to PCM and then subsequently adding two or three explicit solvent molecules brings the calculated data points closer and close to the experimental ones. Table 3 illustrates the decrease in the mean absolute error for both ΔE and ΔδP in the 1
O oxygen: two solvent molecules (if sp2 hybridization dominates, Fig. S10b in the SI) or three solvent molecules (if sp3 hybridization dominates, Fig. 7). Using the data from Tables S2–S4 in the SI, for each of these models one could generate −ΔE(ΔδP) plots, which are shown in Fig. S13a–c in the SI and Fig. 11, respectively, superimposed with experimental data points (several data points in Fig. 11 are shown as open symbols for the reason that will be explained in one of the following paragraphs). In all cases, the general trends are qualitatively consistent with the experiment: ΔδP increases with increasing overall ΔE for the majority of compounds. Quantitatively, clearly, both implicit and explicit solvent models consequently and significantly improve the quality of the match between theory and experiment. Going from vacuum to PCM and then subsequently adding two or three explicit solvent molecules brings the calculated data points closer and close to the experimental ones. Table 3 illustrates the decrease in the mean absolute error for both ΔE and ΔδP in the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes of Ph3PO with substituted phenols. The sequential improvement of the computational data is additionally visualized in Fig. S14 and S15 in the SI, where the mismatches between experimental and calculated hydrogen bond energies and 31P NMR chemical shifts are shown as histograms for all four complexation reactions. Finally, in TOC graphics we attempted to depict it as an arrow hitting the target closer and closer to the bull's eye.
2 complexes of Ph3PO with substituted phenols. The sequential improvement of the computational data is additionally visualized in Fig. S14 and S15 in the SI, where the mismatches between experimental and calculated hydrogen bond energies and 31P NMR chemical shifts are shown as histograms for all four complexation reactions. Finally, in TOC graphics we attempted to depict it as an arrow hitting the target closer and closer to the bull's eye.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes of Ph3PO with substituted phenols, obtained using various solvation models
2 complexes of Ph3PO with substituted phenols, obtained using various solvation models
| Solvent model | 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes 1 complexes |
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes 2 complexes |
||
|---|---|---|---|---|
| Error in ΔδP | Error in ΔE | Error in ΔδP | Error in ΔE | |
| Gas phase | 8.9 | 37.6 | 14.6 | 73.0 |
| Polarizable medium (ε = 40) | 4.4 | 21.2 | 6.0 | 41.1 |
| Aprotic medium with 2 solvent molecules | 3.2 | 2.0 | 0.9 | 5.2 |
| Aprotic medium with 3 solvent molecules | 1.9 | 1.8 | 1.3 | 3.6 |
For the best-performed model (polarizable continuum and three explicit solvent molecules) we have plotted a direct comparison between calculated and experimental 31P NMR chemical shifts (Fig. 10a) and hydrogen bond energies (Fig. 10b). In both cases there is a decent slightly non-linear correlation. The largest scattering of data points is observed for the ΔδP of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes, especially for those with 2,6-disubstituted phenol (open symbols in Fig. 10).
1 complexes, especially for those with 2,6-disubstituted phenol (open symbols in Fig. 10).
The calculated data points in Fig. 11 (PCM + three solvent molecules) could be fitted with the following equation:
| –ΔE (in kJ mol−1) = 15.0·ΔδP0.57 (in ppm) | (3) |
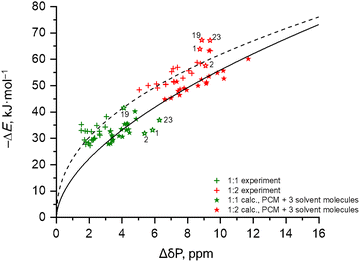 | ||
Fig. 11 The calculated ΔE(ΔδP) correlation constructed for the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes (green stars) and the 1 1 complexes (green stars) and the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (red stars) for the complexation reaction shown in Fig. 7 (see the numerical data in Table 2). The experimental data points are shown as crosses for comparison. The dashed and solid curves correspond to eqn (2) and (3), respectively. Note: “PCM + 3 solvent molecules” in the legend refers to the initial state of Ph3PO subsequently forming hydrogen bonds with phenols. In other words, the P 2 complexes (red stars) for the complexation reaction shown in Fig. 7 (see the numerical data in Table 2). The experimental data points are shown as crosses for comparison. The dashed and solid curves correspond to eqn (2) and (3), respectively. Note: “PCM + 3 solvent molecules” in the legend refers to the initial state of Ph3PO subsequently forming hydrogen bonds with phenols. In other words, the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group is forming three hydrogen bonds at all times, as shown in Fig. 7. O group is forming three hydrogen bonds at all times, as shown in Fig. 7. | ||
To construct this correlation, we have excluded from the fitting the data points for the complexes of Ph3PO with 2,6-disubstituted phenols (1, 2, 19 and 23; open symbols in Fig. 11). These data points look like clear outlier, though by looking at the optimized structures it is hard to pinpoint which particular geometric feature might be responsible for that.
Chemical intuition suggests that it could have something to do with the interference of intramolecular H-bonds with ortho-substituents and steric hinderances; we leave this question for future studies. The deviation of eqn (3) from eqn (2) and the corresponding deviations of calculated data points from the experimental ones seem to be systematic, but at the moment it is hard to tell what would decrease these deviations: improvements in chemical modelling (inclusion of motion averaging or further solvation effects) or improvements in computational modelling (usage of more advanced functionals and/or basis sets). In any case, the match between calculated and experimental data is fine and it seems reasonable to conclude that Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O in solution tends to form three hydrogen bonds whenever possible, occupying all electron-donating sites on the oxygen atom, thus indicating a significant P+–O− character of the P
O in solution tends to form three hydrogen bonds whenever possible, occupying all electron-donating sites on the oxygen atom, thus indicating a significant P+–O− character of the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond. Finally, we note that in calculations the correlation between ΔδP and ΔE for 1
O bond. Finally, we note that in calculations the correlation between ΔδP and ΔE for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes is less subjected to the scattering of the data points and the increase of ΔδP could be interpreted as the increase in hydrogen bond strength with more confidence.
1 complexes is less subjected to the scattering of the data points and the increase of ΔδP could be interpreted as the increase in hydrogen bond strength with more confidence.
Anticooperativity of H-bonds in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) 2 complexes
2 complexes
When two hydrogen bonds are formed between a single P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group and two proton donors, these interactions exhibit anticooperativity, meaning that strengthening (shortening) of one bond weakens (lengthens) the other one, as both bonds compete for the electron density of the same oxygen atom. In our study, the mutual influence of two hydrogen bonds in 1
O group and two proton donors, these interactions exhibit anticooperativity, meaning that strengthening (shortening) of one bond weakens (lengthens) the other one, as both bonds compete for the electron density of the same oxygen atom. In our study, the mutual influence of two hydrogen bonds in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes manifests itself as the reduction in the strength of each bond compared to the strength of a single hydrogen bond in 1
2 complexes manifests itself as the reduction in the strength of each bond compared to the strength of a single hydrogen bond in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes. (Nevertheless, the algebraic sum of the strengths of the two hydrogen bonds in 1
1 complexes. (Nevertheless, the algebraic sum of the strengths of the two hydrogen bonds in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes is greater than that of a single hydrogen bond in 1
2 complexes is greater than that of a single hydrogen bond in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes) This is illustrated in Fig. 12, which shows the correlation between the H-bond energy values for 1
1 complexes) This is illustrated in Fig. 12, which shows the correlation between the H-bond energy values for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes (ΔE1
2 complexes (ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and ΔE1
1 and ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, respectively). All data points (both calculated and experimental ones) lie below the “no cooperativity” line ΔE1
2, respectively). All data points (both calculated and experimental ones) lie below the “no cooperativity” line ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 = 2·ΔE1
2 = 2·ΔE1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, demonstrating a 15–20% reduction of individual bond energy.
1, demonstrating a 15–20% reduction of individual bond energy.
If two phenols would form a chain-like complex with Ph3PO, the anticooperativity would switch to cooperativity, as was previously shown in ref. 92 on the example of 2-OH and 2,3-di-OH substituted phenol in complexes with (n-Bu)3PO. In this case adding a second hydrogen bond to a chain nearly doubles the strength of the bond with phosphine oxide, while further additions have diminishing effects. This highlights that hydrogen bond interactions are highly context-dependent: while P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O-centered complexes exhibit competitive weakening due to shared electron density, linear chains can exhibit cooperative reinforcement.
O-centered complexes exhibit competitive weakening due to shared electron density, linear chains can exhibit cooperative reinforcement.
Conclusions
Let us summarize the key findings of this work. We began by experimentally investigating 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 hydrogen-bonded complexes formed between Ph3P
2 hydrogen-bonded complexes formed between Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O and 24 substituted phenols using low-temperature liquid-state NMR spectroscopy.
O and 24 substituted phenols using low-temperature liquid-state NMR spectroscopy.
Despite the noticeable scattering of the experimental data points (especially for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes), the full data set strongly suggests that there is a monotonous interdependence between the change of the 31P NMR chemical shift upon complexation and the combined strength of the hydrogen bonds formed with the P
1 complexes), the full data set strongly suggests that there is a monotonous interdependence between the change of the 31P NMR chemical shift upon complexation and the combined strength of the hydrogen bonds formed with the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group. The larger the ΔδP, the smaller the relative error in hydrogen bond energy estimations. For example, all studied 1
O group. The larger the ΔδP, the smaller the relative error in hydrogen bond energy estimations. For example, all studied 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 complexes cluster around 25–35 kJ mol−1 hydrogen bond energy and are hard to distinguish one from another based on ΔE or ΔδP. In contrast, the data points for 1
1 complexes cluster around 25–35 kJ mol−1 hydrogen bond energy and are hard to distinguish one from another based on ΔE or ΔδP. In contrast, the data points for 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes are stretched over wider ranges of both ΔE and ΔδP and could be interpreted with more confidence.
2 complexes are stretched over wider ranges of both ΔE and ΔδP and could be interpreted with more confidence.
These findings could be seen as experimental evidence of the effect previously predicted computationally.39 The proposed correlation could be used to solve the reverse spectroscopic problem: estimating the complexation energy from experimental 31P NMR chemical shift. The H-bond anticooperativity effects in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 complexes were estimated to be ca. 15% of the individual H-bond energy. Furthermore, we demonstrated that advanced solvation models including both implicit and explicit solvents are necessary to achieve a semi-quantitative match between calculated and experimental 31P NMR parameters. We concluded that in solution Ph3P
2 complexes were estimated to be ca. 15% of the individual H-bond energy. Furthermore, we demonstrated that advanced solvation models including both implicit and explicit solvents are necessary to achieve a semi-quantitative match between calculated and experimental 31P NMR parameters. We concluded that in solution Ph3P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O tends to form three hydrogen bonds, where solvent molecules form CH⋯O hydrogen bonds, occupying all vacant spots, left around the P
O tends to form three hydrogen bonds, where solvent molecules form CH⋯O hydrogen bonds, occupying all vacant spots, left around the P![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety after its complexation with phenols.
O moiety after its complexation with phenols.
Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information is available. See DOI: https://doi.org/10.1039/d5cp03320a.Acknowledgements
This work was financially supported by the Russian Science Foundation (RSF) grant no. 23-13-00095. NMR measurements were performed at the Center for Magnetic Resonance of St. Petersburg State University Research Park. The authors are grateful to Mikhail Vovk for conducting the low-temperature measurements. Quantum-chemical calculations were performed at the Computing Center of St. Petersburg State University Research Park.References
- P. Žguns, K. Klyukin, L. S. Wang, G. Xiong, J. Li, S. M. Haile and B. Yildiz, Energy Environ. Sci., 2024, 17, 5730–5742 RSC.
- F. Jiang, H. Zhu, R. Graf, W. H. Meyer, H. W. Spiess and G. Wegner, Macromolecules, 2010, 43, 3876–3881 CrossRef CAS.
- Y. Hori, T. Chikai, T. Ida and M. Mizuno, Phys. Chem. Chem. Phys., 2018, 20, 10311–10318 RSC.
- O. Petreus, T. Vlad-Bubulac and C. Hamciuc, Eur. Polym. J., 2005, 41, 2663–2670 CrossRef CAS.
- Y. L. Chang, Y. Z. Wang, D. M. Ban, B. Yang and G. M. Zhao, Macromol. Mater. Eng., 2004, 289, 703–707 CrossRef CAS.
- S. Monge, B. Canniccioni, A. Graillot and J. J. Robin, Biomacromolecules, 2011, 12, 1973–1982 CrossRef CAS PubMed.
- Y. Sumiya and T. Uwabe, J. Mater. Chem. B, 2025, 13, 5095–5108 RSC.
- Y. Z. Wan, Y. Huang, C. D. Yuan, S. Raman, Y. Zhu, H. J. Jiang and C. Gao, Mater. Sci. Eng., C, 2007, 27, 855–864 CrossRef CAS.
- M. Kröger, O. Badara, T. Pääkkönen, I. Schlapp-Hackl, S. Hietala and E. Kontturi, Biomacromolecules, 2023, 24, 1318–1328 CrossRef PubMed.
- W. Abdussalam-Mohammed, M. M. Alshaikh, P. Shah and A. Bhattarai, Nanoscale Adv., 2025, 7, 3255–3266 RSC.
- C. J. Abou-Fayssal, C. Fliedel, R. Poli, A. Riisager, K. Philippot and E. Manoury, Mater. Today Chem., 2023, 34, 101752 CrossRef CAS.
- Z. A. Peng and X. Peng, J. Am. Chem. Soc., 2001, 123, 183–184 CrossRef CAS PubMed.
- S. Liang, Z. Tang, S. Li, X. Guo, S. Jia and X. W. Sun, Adv. Opt. Mater., 2025, 13, 2500034 CrossRef CAS.
- E. H. Ablouh, F. Brouillette, M. Taourirte, H. Sehaqui, M. El Achaby and A. Belfkira, RSC Adv., 2021, 11, 24206–24216 RSC.
- B. G. Fiss, L. Hatherly, R. S. Stein, T. Friščić and A. Moores, ACS Sustainable Chem. Eng., 2019, 7, 7951–7959 CrossRef CAS.
- M. A. Velasco-Soto, A. R. Vázquez-Velázquez, S. A. Pérez-García, L. M. Bautista-Carrillo, P. Vorobiev, A. Méndez-Reséndiz and L. Licea-Jiménez, Polymers, 2024, 16, 2705 CrossRef CAS PubMed.
- H. T. Tee, K. Koynov, T. Reichel and F. R. Wurm, ACS Omega, 2019, 4, 9324–9332 CrossRef CAS PubMed.
- P. W. N. M. van Leeuwen, I. Cano and Z. Freixa, ChemCatChem, 2020, 12, 3982–3994 CrossRef CAS.
- I. Cano, L. M. Martínez-Prieto, L. Vendier and P. W. N. M. van Leeuwen, Catal. Sci. Technol., 2018, 8, 221–228 RSC.
- S. E. Denmark, R. C. Smith and S. A. Tymonko, Tetrahedron, 2007, 63, 5730–5738 CrossRef CAS PubMed.
- T. M. Shaikh, C. M. Weng and F. E. Hong, Coord. Chem. Rev., 2012, 256, 771–803 CrossRef CAS.
- D. Parmar, E. Sugiono, S. Raja and M. Rueping, Chem. Rev., 2014, 114, 9047–9153 CrossRef CAS PubMed.
- J. Gramüller, P. Dullinger, D. Horinek and R. M. Gschwind, Chem. Sci., 2022, 13, 14366–14372 RSC.
- S. H. Ahn, D. Lindhardt, N. Bhuvanesh and J. Blümel, ACS Sustainable Chem. Eng., 2018, 6, 6829–6840 CrossRef CAS.
- T. Tsuneda, J. Miyake and K. Miyatake, ACS Omega, 2018, 3, 259–265 CrossRef CAS PubMed.
- F. F. Arp, N. Bhuvanesh and J. Blümel, Dalton Trans., 2019, 48, 14312–14325 RSC.
- F. F. Arp, S. H. Ahn, N. Bhuvanesh and J. Blümel, New J. Chem., 2019, 43, 17174–17181 RSC.
- E. Kukkonen, E. J. Virtanen and J. O. Moilanen, Molecules, 2022, 27, 3465 CrossRef CAS PubMed.
- A. M. Wilson, P. J. Bailey, P. A. Tasker, J. R. Turkington, R. A. Grant and J. B. Love, Chem. Soc. Rev., 2014, 43, 123–134 RSC.
- A. M. Safiulina, N. E. Borisova, A. V. Lizunov, A. V. Golubev, G. V. Bodrin, E. I. Goryunov, I. B. Goryunova, V. K. Brel and I. G. Tananaev, Russ. J. Inorg. Chem., 2023, 68, 1650–1656 CrossRef CAS.
- A. Safiulina, N. Borisova, M. Grigoriev, D. Baulin, V. Baulin and A. Tsivadze, Molecules, 2021, 26, 2217 CrossRef CAS PubMed.
- V. N. H. Nguyen, T. H. Nguyen and M. S. Lee, Metals, 2020, 10, 1105 CrossRef CAS.
- L. Kostenko, N. Kobylinska, S. Khainakov and S. G. Granda, Microchim. Acta, 2019, 186, 474 CrossRef PubMed.
- A. Leoncini, J. Huskens and W. Verboom, Chem. Soc. Rev., 2017, 46, 7229–7273 RSC.
- P. I. Matveev, N. E. Borisova, N. G. Andreadi, G. G. Zakirova, V. G. Petrov, E. V. Belova, S. N. Kalmykov and B. F. Myasoedov, Dalton Trans., 2019, 48, 2554–2559 RSC.
- V. E. Belskii and L. K. Ashrafullina, Zh. Obshch. Khim., 1979, 49, 2241–2245 CAS.
- M. A. Kostin, O. Alkhuder, L. Xu, D. V. Krutin, R. E. Asfin and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2024, 26, 10234–10242 RSC.
- J. O. Jensen, J. Mol. Struct.: THEOCHEM, 2005, 723, 1–8 CrossRef CAS.
- M. A. Kostin, O. Alkhuder, R. E. Asfin and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2025, 27, 1143–1154 RSC.
- I. S. Giba, V. V. Mulloyarova, G. S. Denisov and P. M. Tolstoy, Magn. Reson. Chem., 2021, 59, 465–477 CrossRef CAS PubMed.
- I. G. Shenderovich, J. Phys. Chem. C, 2013, 117, 26689–26702 CrossRef CAS.
- I. G. Shenderovich, J. Chem. Phys., 2020, 153, 184501 CrossRef CAS PubMed.
- I. S. Giba, V. V. Mulloyarova, G. S. Denisov and P. M. Tolstoy, J. Phys. Chem. A, 2019, 123, 2252–2260 CrossRef CAS PubMed.
- I. Alkorta and J. Elguero, J. Phys. Org. Chem., 2017, 30, e3690 CrossRef.
- M. A. Kostin, S. A. Pylaeva and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2022, 24, 7121–7133 RSC.
- A. S. Ostras’, D. M. Ivanov, A. S. Novikov and P. M. Tolstoy, Molecules, 2020, 25, 1406 CrossRef PubMed.
- V. V. Mulloyarova, I. S. Giba, M. A. Kostin, G. S. Denisov, I. G. Shenderovich and P. M. Tolstoy, Phys. Chem. Chem. Phys., 2018, 20, 4901–4910 RSC.
- V. V. Mulloyarova, D. O. Ustimchuk, A. Filarowski and P. M. Tolstoy, Molecules, 2020, 25, 1907 CrossRef CAS PubMed.
- I. S. Giba and P. M. Tolstoy, Symmetry, 2021, 13, 258 CrossRef CAS.
- C. R. Hilliard, S. Kharel, K. J. Cluff, N. Bhuvanesh, J. A. Gladysz and J. Blümel, Chem. – Eur. J., 2014, 20, 17292–17295 CrossRef CAS PubMed.
- D. S. Zasukhin, I. A. Kasyanov, Y. G. Kolyagin, A. I. Bulygina, K. C. Kharas and I. I. Ivanova, ACS Omega, 2022, 7, 12318–12328 CrossRef CAS PubMed.
- U. Mayer, V. Gutmann and W. Gerger, Monatsh. Chem., 1975, 106, 1235–1257 CrossRef CAS.
- V. Gutmann, Coord. Chem. Rev., 1976, 18, 225–255 CrossRef CAS.
- A. Zheng, S. B. Liu and F. Deng, Chem. Rev., 2017, 117, 12475–12531 CrossRef CAS PubMed.
- M. A. Beckett, D. S. Brassington, S. J. Coles and M. B. Hursthouse, Inorg. Chem. Commun., 2000, 3, 530–533 CrossRef CAS.
- M. A. Beckett, G. C. Strickland, J. R. Holland and K. S. Varma, Polymer, 1996, 37, 4629–4631 CrossRef CAS.
- K. M. Diemoz and A. K. Franz, J. Org. Chem., 2019, 84, 1126–1138 CrossRef CAS PubMed.
- J. J. Jennings, M. Milic, K. Targos and A. K. Franz, Eur. J. Med. Chem., 2020, 207, 112693 CrossRef CAS PubMed.
- A. R. Nödling, G. Jakab, P. R. Schreiner and G. Hilt, Eur. J. Org. Chem., 2014, 6394–6398 CrossRef.
- E. Pires and J. M. Fraile, Phys. Chem. Chem. Phys., 2020, 22, 24351–24358 RSC.
- J. P. Osegovic and R. S. Drago, J. Phys. Chem. B, 2000, 104, 147–154 CrossRef CAS.
- J. A. McCune, P. He, M. Petkovic, F. Coleman, J. Estager, J. D. Holbrey, K. R. Seddon and M. Swadźba-Kwaśny, Phys. Chem. Chem. Phys., 2014, 16, 23233–23243 RSC.
- M. C. R. Symons and G. Eaton, J. Chem. Soc., Faraday Trans. 1, 1982, 78, 3033–3044 RSC.
- E. Y. Tupikina, M. Bodensteiner, P. M. Tolstoy, G. S. Denisov and I. G. Shenderovich, J. Phys. Chem. C, 2018, 122, 1711–1720 CrossRef CAS.
- M. Gonschorowsky, K. Merz and M. Driess, Eur. J. Inorg. Chem., 2006, 455–463 CrossRef CAS.
- R. Ahmed, A. Altieri, D. M. D’Souza, D. A. Leigh, K. M. Mullen, M. Papmeyer, A. M. Z. Slawin, J. K. Y. Wong and J. D. Woollins, J. Am. Chem. Soc., 2011, 133, 12304–12310 CrossRef CAS PubMed.
- E. Pires and J. M. Fraile, Phys. Chem. Chem. Phys., 2022, 24, 16755–16761 RSC.
- J. S. Siegel and F. A. L. Anet, J. Org. Chem., 1988, 53, 2629–2630 CrossRef CAS.
- R. K. Harris, E. D. Becker, S. M. Cabral de Menezes, R. Goodfellow and P. Granger, Pure Appl. Chem., 2001, 73, 1795–1818 CrossRef CAS.
- Mesrelab Research MestReNova (Version 14.2.1), https://mestrelab.com/main-product/nmr.
- Bruker BioSpin TopSpin (Version 3.6.5), https://www.bruker.com/en/products-and-solutions/mr/nmr-software/topspin.html.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- Y. Zhao and D. G. Truhlar, J. Phys. Chem. A, 2005, 109, 5656–5667 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065 RSC.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- M. Bursch, J. M. Mewes, A. Hansen and S. Grimme, Angew. Chem., 2022, 134, e202205735 CrossRef.
- U. Ahmed, M. P. Johansson, S. Lehtola and D. Sundholm, Phys. Chem. Chem. Phys., 2025, 27, 8706–8718 RSC.
- L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688 RSC.
- I. G. Shenderovich, A. P. Burtsev, G. S. Denisov, N. S. Golubev and H. H. Limbach, Magn. Reson. Chem., 2001, 39, S91–S99 CrossRef CAS.
- F. Jensen, J. Chem. Theory Comput., 2015, 11, 132–138 CrossRef CAS PubMed.
- K. W. Wiitala, T. R. Hoye and C. J. Cramer, J. Chem. Theory Comput., 2006, 2, 1085–1092 CrossRef CAS PubMed.
- P. M. Tolstoy and E. Y. Tupikina, in Spectroscopy and Computation of Hydrogen-Bonded Systems, ed. M. Wojcik and Y. Ozaki, Wiley-Blackwell, 2022, pp. 345–407 Search PubMed.
- J. Reuben, J. Am. Chem. Soc., 1986, 108, 1735–1738 CrossRef CAS.
- T. Schaefer, J. Phys. Chem., 1975, 79, 1888–1890 CrossRef CAS.
- D. P. Eyman and R. S. Drago, J. Am. Chem. Soc., 1966, 88, 1617–1620 CrossRef CAS.
- K. F. Purcell, J. A. Stikeleather and S. D. Brunk, J. Am. Chem. Soc., 1969, 91, 4019–4027 CrossRef CAS.
- S. E. Odinokov, A. A. Mashkovsky, A. K. Dzizenko and V. P. Glazunov, Spectrosc. Lett., 1975, 8, 157–164 CrossRef CAS.
- G. A. Kumar and M. A. McAllister, J. Org. Chem., 1998, 63, 6968–6972 CrossRef CAS PubMed.
- J. E. Del Bene, S. A. Perera and R. J. Bartlett, J. Phys. Chem. A, 1999, 103, 8121–8124 CrossRef CAS.
- N. Dominelli-Whiteley, J. J. Brown, K. B. Muchowska, I. K. Mati, C. Adam, T. A. Hubbard, A. Elmi, A. J. Brown, I. A. W. Bell and S. L. Cockroft, Angew. Chem., 2017, 129, 7766–7770 CrossRef.
| This journal is © the Owner Societies 2026 |