Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Dissecting non-radiative decay in donor-functionalized radicals with a mode-resolved model
Robert
Toews
 * and
Andreas
Köhn
* and
Andreas
Köhn

Institute for Theoretical Chemistry and Institute of Quantum Science and Technology (IQST), University of Stuttgart, Stuttgart 70569, Germany. E-mail: toews@theochem.uni-stuttgart.de
First published on 4th December 2025
Abstract
Donor-functionalized radicals based on the poly-chlorinated trityl moiety are an emerging class of efficient emitters for next-generation optoelectronics. Their performance is governed by the non-radiative decay of a charge-transfer (CT) state, making its understanding crucial for molecular design. We present a mode-resolved model that links the decay to structural motifs through molecular vibrations. The decisive role of exact exchange in density functional modeling is highlighted, alongside solvation and anharmonic effects. Using representative radical emitters, we show that suppression of non-radiative decay in systems with a perpendicular donor–acceptor arrangement arises from reduced coupling of the promoting mode to the CT exciton and a diminished anharmonic contribution. To elucidate this mechanism, we perform a sensitivity analysis of the contributions of individual modes to the Franck–Condon weighted density of states, including anharmonic effects.
1 Introduction
Organic molecular emitters are widely applied in optoelectronic devices, while ongoing research continues to optimize their photophysical properties through molecular design.1–3 Conventionally, these emitters have a closed-shell ground state and suffer radiative losses due to optically dark triplet states.4 Donor-functionalized radical emitters based on the tris(2,4,6-trichlorophenyl)methyl (TTM) moiety circumvent this issue by having a doublet ground state. In these radical emitters, radiative losses are primarily associated with the non-radiative decay of the intramolecular charge-transfer (CT) state, which arises from electron transfer between the donor and radical (acceptor) moieties.5–7Gaining a theoretical understanding of non-radiative decay is crucial for guiding molecular design. The energy-gap law,8,9 supported by both theory and experiment, dictates that the rate constant knr for non-radiative decay falls off exponentially as the energy gap ΔE increases,
 | (1) |
The transition is driven by high-frequency modes with index μ, which contribute to the reorganization energy by Λμ and are combined into an effective mode with averaged angular frequency ωe. The parameter C describes the coupling between the electronic states involved in the transition.
Donor-functionalized TTM radicals do not conform to the energy-gap law, as they emit in the deep-red/near-infrared region yet exhibit relatively slow non-radiative decay rates.10,11 In addition, chemical modifications of either the donor or the acceptor unit can lead to a further marked reduction of non-radiative decay without substantially altering the energy gap.11,12 This behavior has been attributed to suppressed couplings of the promoting high-frequency vibrations to the CT exciton, either due to the localization of vibrations on the donor or acceptor moiety, or as a consequence of orbital effects arising from molecular symmetry.11,13
Quantitative modeling of non-radiative decay in donor-functionalized radicals has so far relied on the Marcus–Levich–Jortner (MLJ) model,14–18 combining a classical description of low-frequency modes with a harmonic quantum-mechanical treatment of an effective (e) mode representing all high-frequency vibrations,
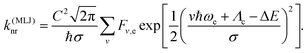 | (2) |
In the above expression, the sum runs over the vibrational quantum number v of the effective mode with harmonic Franck–Condon factor Fv,e. The width parameter σ is related to the classical reorganization energy Λc and the temperature T via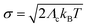 . Due to the size of the radical emitters, only density functional theory (DFT) is practically feasible, and the CT character of these systems requires the use of range-separated hybrid functionals with additional long-range exact exchange (eX).19–22
. Due to the size of the radical emitters, only density functional theory (DFT) is practically feasible, and the CT character of these systems requires the use of range-separated hybrid functionals with additional long-range exact exchange (eX).19–22
Because the effective mode in the MLJ model does not directly correspond to a particular molecular vibration, it is challenging to relate non-radiative decay to molecular design. Here, we present a mode-resolved quantitative model that explicitly connects non-radiative decay to the molecular structure. We begin by addressing key theoretical considerations, covering the effects of long-range eX, solvation, and anharmonicity. Using the systems under investigation, we show that a quantitative and physically sound description of non-radiative decay is possible. The decay mechanism can be related to particular molecular vibrations, allowing the observed trends in rate constants knr to be interpreted in an intuitive manner.
2 Theoretical framework
In the present work, we investigate the non-radiative decay in donor-functionalized radical emitters in solution. The intramolecular charge-transfer (CT) character of the decaying state represents a crucial aspect for theoretical modeling. In addition to discussing the theoretical details of the rate constant knr for non-radiative decay, we also provide remarks on the description of CT states within the (time-dependent) formalism of density functional theory ((TD)-DFT). Furthermore, we briefly address the treatment of solvation effects using state-specific continuum solvation models and include a short note on the rate constant kr for radiative decay.2.1 Non-radiative decay
Our treatment of non-radiative decay by internal conversion is inspired by the MLJ model which combines a classical treatment of low-frequency modes with a (harmonic) quantum mechanical treatment of high-frequency vibrations in terms of an effective mode.14–18 Analogous to the MLJ model, we essentially adopt the classical description from Marcus theory.14,15 For the quantum-mechanical description, however, we abandon the one-effective mode model and explicitly consider the (harmonic) contributions from all quantum-mechanical modes. Moreover, we introduce anharmonic corrections to contributions of selected high-frequency modes based on the Morse potential.23 We note that our approach can be regarded as a reduced linear vibronic coupling model. In this section, we present the complete expression for the rate constant knr (including classical and quantum-mechanical contributions) and focus on the mode-resolved quantum-mechanical treatment of high-frequency vibrations.We note that the quantum-mechanical mode contributions are distinguished as either harmonic or anharmonic. In Section S1.1 of the SI, we provide a detailed derivation of the rate constant considering exclusively harmonic (h) contributions, along with remarks on the complete rate constant, which also includes classical (c) and anharmonic (a) contributions.14–18,24–39 The final and complete expression for the rate constant can be written as
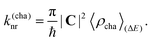 | (3) |
It should be emphasized that this expression relies on the Condon approximation.30–32 In the above expression, the first leading contribution is the squared norm of the first-order non-adiabatic coupling vector C, which is composed of the normal mode projections Cμ,
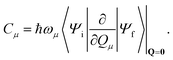 | (4) |
The (dimensionless) normal coordinate and (harmonic) angular frequency of mode μ are denoted as Qμ and ωμ, respectively, and the wavefunctions Ψi and Ψf refer to the initial (i) and final (f) adiabatic electronic state. We remark that C is evaluated at the displacement vector Q = 0, corresponding to the equilibrium geometry of the emitting state.
The second leading contribution in eqn (3) is the total Franck–Condon weighted density of states ρcha (FCWD)31,32,39—including classical, harmonic and anharmonic mode contributions—averaged around the energy gap ΔE of the non-radiative transition. Classifying the normal modes as classical, harmonic, or anharmonic, the total FCWD ρcha can be represented as a convolution of the FCWDs corresponding to the respective mode classes,
| ρcha = ρc ○ ρh ○ ρa = ρc ○ ρq. | (5) |
In the second equality of the previous expression, we summarized the harmonic and anharmonic FCWDs as the overall quantum-mechanical contribution ρq.
In the following, we outline the concepts relevant to a mode-resolved description of non-radiative decay, with the harmonic FCWD ρh as an illustrative example. As shown in Section S1.1 of the SI, ρh is given as a function of the energy gap ΔE by
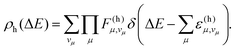 | (6) |
The first summation in the above expression runs over all possible combinations of quantum numbers vμ—corresponding to vibrational states within the final electronic state—associated with the vibrational energies 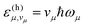 . Assuming non-radiative decay from the vibrational ground state of the emitting state, the harmonic Franck–Condon (FC) factors
. Assuming non-radiative decay from the vibrational ground state of the emitting state, the harmonic Franck–Condon (FC) factors 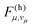 are given by Poisson distributions of the quantum numbers vμ,36
are given by Poisson distributions of the quantum numbers vμ,36
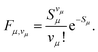 | (7) |
It should be emphasized that the above expression implies the displaced harmonic oscillator model (see also Section S1.1 of the SI). The Huang–Rhys (HR) factor Sμ can be interpreted as a direct measure for the coupling between a mode μ and the exciton.35 Denoting the (dimensionless) displacement of the equilibrium position of mode μ between initial and final vibrational state as Δμ and the corresponding contribution to the total reorganization energy Λ as Λμ, the HR factor Sμ can be expressed as
 | (8) |
Within the displaced harmonic oscillator model, the mode displacements Δμ can be related to the projections Gμ of the initial state electronic gradient G evaluated at the equilibrium geometry of the final electronic state,
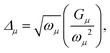 | (9) |
According to eqn (6), a mode μ contributes substantially to ρh if the FC factors 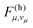 are large at vibrational energies
are large at vibrational energies 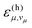 near the gap ΔE. The required vibrational quantum number vμ is relatively small for a high-frequency mode. Hence, a high-frequency mode with significant excitonic coupling Sμ accelerates non-radiative decay due to a large vibronic transition probability
near the gap ΔE. The required vibrational quantum number vμ is relatively small for a high-frequency mode. Hence, a high-frequency mode with significant excitonic coupling Sμ accelerates non-radiative decay due to a large vibronic transition probability 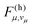 at the gap ΔE of the transition.
at the gap ΔE of the transition.
To conclude our examination of quantum mechanical contributions, we consider the inclusion of anharmonic corrections in terms of displaced Morse oscillators. The concepts introduced above can also be extended to anharmonic oscillators, which are essential for the description of (highly) excited vibrational states. A convenient description of anharmonic vibrations can be achieved by using the Morse potential,23,28,40,41
V(a)μ = ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) e,μ(1 − e−aμQμ)2, e,μ(1 − e−aμQμ)2, | (10) |
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) e,μ and the stiffness aμ.
e,μ and the stiffness aμ.
The anharmonic FCWD, ρa, can be obtained from eqn (7) by substituting 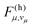 and
and  with the corresponding expressions
with the corresponding expressions  and
and 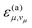 derived for displaced Morse oscillators. The presumably small displacements Δμ between the equilibrium positions of the Morse oscillators are thereby adopted from the displaced harmonic oscillator model (cf.eqn (9)). While the harmonic FC factors
derived for displaced Morse oscillators. The presumably small displacements Δμ between the equilibrium positions of the Morse oscillators are thereby adopted from the displaced harmonic oscillator model (cf.eqn (9)). While the harmonic FC factors  in eqn (7) are invariant with respect to the direction of Δμ due to the symmetry of the harmonic potentials, the sign of Δμ becomes crucial in the anharmonic case.
in eqn (7) are invariant with respect to the direction of Δμ due to the symmetry of the harmonic potentials, the sign of Δμ becomes crucial in the anharmonic case.
In Section S1.2 of the SI, we provide a detailed account on relevant expressions for displaced Morse oscillators and discuss possible effects of the anharmonic contributions.23,28,40–45 The displacements Δμ are defined as positive when the average change in bond lengths, relative to the initial state and determined by projection onto internal coordinates, is positive. For a high-frequency mode, the vibronic transition terminates near the inner turning point of the (final) Morse potential if Δμ > 0, in which case an acceleration of non-radiative decay due to anharmonic contributions can be anticipated (see Section S1.2).
The well-depth for all anharmonic modes is chosen as ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) e,μ = 30
e,μ = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 as suggested by previous works.28,40,41 Section S1.3 of the SI provides a brief discussion of this choice and indicates its justification through a stability analysis of the total FCWD ρcha.28,40,41,46
000 cm−1 as suggested by previous works.28,40,41 Section S1.3 of the SI provides a brief discussion of this choice and indicates its justification through a stability analysis of the total FCWD ρcha.28,40,41,46
2.2 Low-frequency modes
For vibrational modes with sufficiently low frequency, the spacings between adjacent vibrational energy levels are small relative to the thermal energy kBT at relevant temperatures T (room temperature), which motivates a classical description. In analogy to the MLJ model, our distinction between classical (c) and quantum-mechanical (q) modes corresponds to a division of the total reorganization energy Λ for displaced harmonic oscillators,14–18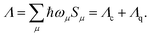 | (11) |
The above summation runs over all normal modes μ and the reorganization energies Λc and Λq collect the contributions from classical and quantum-mechanical modes, respectively.
We adopt the expression for the classical FCWD ρc from Marcus theory, which corresponds to a Gaussian line shape function centered at the classical reorganization energy Λc,14,15
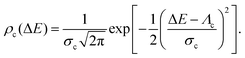 | (12) |
The Gaussian width 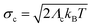 accounts for a thermal broadening of ρc and can be associated with a thermalization of the initial state with respect to the vibrational states of the classical modes.
accounts for a thermal broadening of ρc and can be associated with a thermalization of the initial state with respect to the vibrational states of the classical modes.
2.3 Density functional theory
As indicated earlier, the CT character of the decaying state is an essential aspect of the theoretical description. The difficulties in describing CT states with density functionals is generally related to the many-electron self-interaction error (ME-ESIE), which implies an over-stabilization of fractionally charged subsystems due to semi-local exchange.47–51 Although the admixture of eX into the exchange–correlation functional can presumably cure the ME-ESIE, global hybrid functionals (constant amount of eX) reportedly fail in describing CT states.52–55A general remedy can be found in the (three-parameter) Coulomb-attenuating method (CAM) approach,56,57 which introduces a distant-dependent admixture of eX and a range-separation of the exchange interactions between electrons.58 The Coulomb operator, 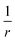 , is divided into a short-range and a long-range part,
, is divided into a short-range and a long-range part,
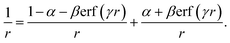 | (13) |
Exchange contributions from the first term on the r.h.s. are evaluated using a semi-local exchange functional, while contributions from the second term are obtained by means of eX. The CAM parameters α and β measure the (additional) amount of eX in the short-range and the long-range limit, respectively. We note in passing that the value of α is typically chosen in accordance with global hybrids (α ≈ 20%). The range-separation parameter γ corresponds to the inverse of the distance distinguishing the short-range from the long-range regime and allows adjustment of the balance between eX and semi-local exchange.59
We recall that the CT states are treated within TD-DFT, and analysis of the corresponding formalism provides a detail essential to our study.60 Under the assumption of zero overlap between the donating orbital ψd and the accepting orbital ψa of the CT excitation, the only non-vanishing element of the electron–hole interaction matrices is given by61
 | (14) |
The orbital energies of ψd and ψa are denoted by εd and εa, and CeX(r) is the coefficient for eX, which generally depends on the distance r = |r1 − r2| between the position vectors r1 and r2. It follows that eX weights the electrostatic attraction between the hole and the particle of the CT excitation, as expressed by the Coulomb integral on the r.h.s. of eqn (14). Discarding the Coulomb integral removes the attraction between hole and particle, allowing large charge separations without energetic penalty, consistent with the tendency toward fractional charges arising from the ME-ESIE.
2.4 Continuum solvation
Solvent effects can be conveniently described by continuum solvation models, which assume the solute molecule to be embedded in a cavity within the bulk dielectric of the solvent.62,63 In the widely adopted apparent surface charge (ASC) method, the solute–solvent interaction is modeled as the interaction between the solute's electrostatic potential and the reaction potential of the bulk dielectric, represented by effective charges on the cavity surface.62,64,65A vertical electronic excitation corresponds to a non-equilibrium situation, in which the electronic degrees of freedom of the solvent relax to the solute's excited-state electrostatic potential, while the nuclear degrees of freedom remain equilibrated with the ground-state potential. Within the ASC method, the non-equilibrium situation is treated by splitting the ASC operator P into an electronic (fast) component Pe and a nuclear (slow) component Pn,62
| P = Pe + Pn, | (15) |
Importantly, the commonly used linear-response (LR) formalism is not admissible for vertical CT excitations with significant change in the solute's electrostatic potential and in such cases the state-specific (SS) formalism should be employed instead.62,66,67 By comparative analysis of the two formalisms, approximate expressions can be derived for the vertical excitation energies E(lr)ve and E(ss)ve within the LR and SS formalism,68,69
| E(lr)ve = E(g)ve − g(d)eμct–gs2, | (16) |
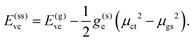 | (17) |
The vertical excitation energy in the gas phase is denoted as E(g)ve, g(d)e and g(s)e are the dynamic (d) and static (s) electronic response functions, respectively, μct–gs is the transition dipole moment of the CT excitation, and μct and μgs are the corresponding permanent dipole moments. It becomes evident that CT excitation energies within the LR formalism can be severely overestimated, since E(lr)ve is corrected in terms of the transition dipole moment, μct–gs, which vanishes for pure CT excitations. We note that while the SS formalism is suited for assessing CT excitation energies in solution, it does not allow for the computation of transition properties, such as μct–gs.70
2.5 Radiative decay
For completeness, we also consider the rate constant kr for radiative decay by fluorescence. The widely known Einstein eq.,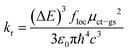 | (18) |
3 Computational details
To reduce computational cost, we assume that neither the gradient and curvature of the potential energy surfaces (PESs) nor the non-adiabatic coupling between electronic states of the same spin multiplicity are influenced by solvation effects. Consideration of solvation effects therefore only introduces a (constant) global shift of the PESs relative to one another.3.1 Density functional
We used the CAM-Becke, 3-parameter, Lee–Yang–Parr56,73–76 (CAM-B3LYP) exchange–correlation functional throughout our study and varied the range-separation parameter γ to adjust the balance between eX and semi-local exchange. The default values α = 19% and β = 46% were adopted for the other two CAM parameters.56 The default value of γ corresponds to γ = 0.33a0−1.56,573.2 Geometries and frequencies
Geometry optimizations and Hessian calculations were performed with a def2-SVP basis set77 for the gas phase at each particular value of γ. No dispersion corrections were added, as changing functional parameters generally requires a re-adjustment of the dispersion coefficients.78 The resolution-of-identity (RI) approximation was employed throughout.79 Geometry optimizations of the first excited electronic state (CT state) were carried out at the corresponding TD-DFT level. The calculations were conducted with version 7.8.1 of the Turbomole program package80 using the m3 grid for numerical integration.81,823.3 Excitation energies
Vertical excitation energies in solution were determined from single-point energy calculations at the respective ground-state equilibrium geometries using the corresponding TD-DFT level with the polarizable continuum model (PCM)63 and the solvent parameters of cyclohexane. Three different variants of PCM were considered: linear-response (PCM-LR),83 corrected linear-response84 (PCM-cLR) and state-specific85,86 (PCM-SS). We note that PCM-SS establishes self-consistency between the solute's excited-state electrostatic potential and the solvent's reaction field, whereas PCM-cLR applies first-order perturbation theory. The calculations were performed with version Rev. C.01 of the Gaussian 16 software87 using a Lebedev integration grid with 45 radial and 434 angular grid points.88 The response-property-optimized def2-SVPD basis set89 was employed throughout and imported into Gaussian 16 via the basis set exchange library.903.4 Excitonic and non-adiabatic couplings
To access vibronic couplings, we evaluated the electronic gradient G of the first excited (CT) state and the derivative coupling vector D at the electronic ground state equilibrium geometry.91 In addition, D was also evaluated at the CT state equilibrium geometry.91 The calculations were performed at the corresponding TD-DFT level using a def2-SVP basis set77 and the RI approximation.79 Relative mode displacements Δμ, Huang–Rhys factors Sμ and non-adiabatic coupling vectors C were obtained from a normal coordinate transformation of G and D, respectively, using the corresponding electronic ground-state Hessian, see Section S2.2 of the SI. Correctly determining the directions of Δμ requires properly orienting the Hessian eigenvectors, as outlined in Section S2.1 of the SI. The calculations were carried out with version 7.8.1 of the Turbomole program package80 using the m3 integration grid.81,823.5 Density of states
The total FCWD, ρcha, was computed with a recursive algorithm for direct state counting, see Section S2.3 of the SI for details.93,94 Modes with frequencies up to 300 cm−1 were treated classically, while the harmonic approximation was applied to modes up to 400 cm−1. Modes with higher frequencies were modeled as displaced Morse oscillators (cf. Section 2.1). The energy gap ΔE of the non-radiative transition was determined by subtracting the total reorganization energy Λ for displaced harmonic oscillators (in the gas phase) from the vertical excitation energy Eve in solution,| ΔE = Eve − Λ. | (19) |
Note that we choose the PCM-SS excitation energy E(ss)ve for evaluating the total FCWD ρcha. The average 〈ρcha〉(ΔE) of ρcha—which omits local fluctuations of the FCWD around ΔE—was obtained using a normal distribution g(ΔE) centered at ΔE,
 | (20) |
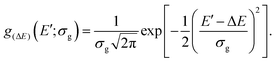 | (21) |
The width was set to σg = 100 cm−1 and the stability analysis of 〈ρcha〉(ΔE) in Section S2.4 of the SI shows that the results are practically not affected by the averaging.
4 Results and discussion
We consider in detail non-radiative decay and vibronic couplings in the three donor-functionalized radical emitters illustrated in Fig. 1. In Sections 4.1–4.3 and 4.6, we examine the relevance of various theoretical aspects to the mode-resolved modeling, viz., balancing eX and semi-local exchange, solvation effects, and anharmonic contributions. This is supplemented by a model calibration in Section 4.4 and an illustrative application linking non-radiative decay to molecular design in Sections 4.5, 4.7 and 4.8.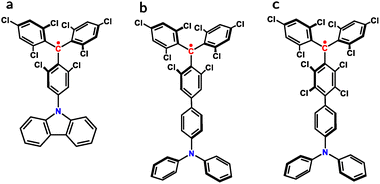 | ||
| Fig. 1 Chemical structural formulas of TTM-1Cz (a), TTM-TPA (b) and TBTM-TPA (c). The radical centers are highlighted in red. | ||
Non-radiative decay in TTM-TPA and TBTM-TPA was previously characterized using a semi-quantitative approach.12 Experimentally, the additional chlorination in TBTM-TPA was found to suppress non-radiative decay relative to TTM-TPA, which can be attributed to the perpendicular orientation between the donor and acceptor planes.12 In the present study, the suppressed decay is explicated by a quantitative, mode-resolved analysis, demonstrating a reasonable overall agreement with experiment.
4.1 Long-range exact exchange
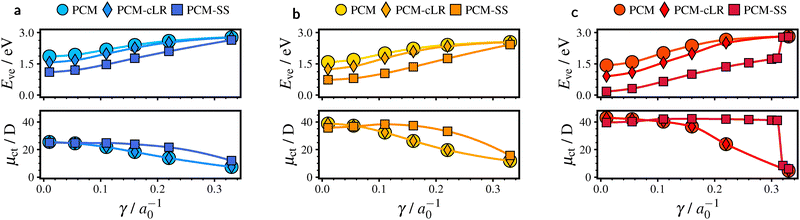
First, we recall the effects of the ME-ESIE on the CT properties in the gas phase, as they play a key role to understand the corresponding effects on (continuum) solvation and vibronic structure. Fig. 2a displays the trend in the CT properties of TTM-1Cz with respect to γ (separation of short-range and long-rang eX) and supporting results for TTM-TPA and TBTM-TPA are provided in Section S3.1 of the SI. As to be expected, frontier orbital energy gap and vertical excitation energy E(g)ve increase with γ. For the CT state dipole moment, μ(g)ct, we observe a notable decline with practically no CT at large γ values.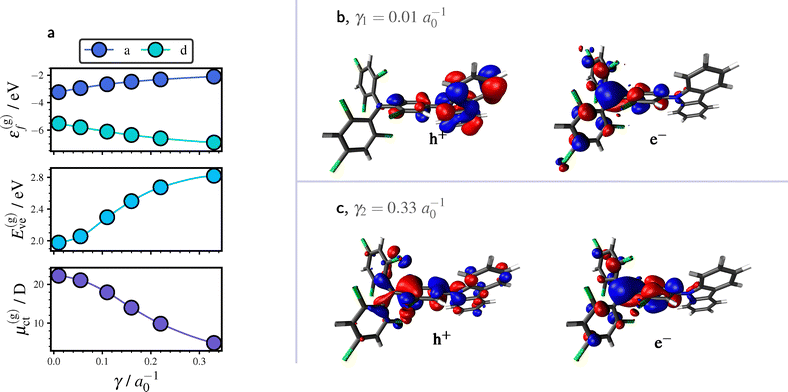 | ||
| Fig. 2 CT properties of TTM-1Cz in the gas phase (g) in dependence on the range-separation parameter γ. (a) Frontier orbital energy ε(g)f (acceptor: a, donor: d), vertical excitation energies E(g)ve and CT state dipole moment μ(g)ct. (b) and (c), Hole (h+) and particle (e−) of the CT exciton obtained by a natural transition orbital analysis92 at γ1 = 0.01a0−1 (contrib.: 99%) and γ2 = 0.33a0−1 (contrib.: 62%). All properties were evaluated at the respective ground state equilibrium geometries. | ||
As can be seen from Fig. 2c, hole and particle are in close proximity at γ2 = 0.33a0−1, which can be comprehended in terms of an increased electrostatic attraction due to long-range eX, cf.eqn (14).61 Accordingly, we observe at γ1 = 0.01a0−1 a confinement of hole and particle to donor and acceptor unit, respectively, as shown Fig. 2b.
The radical emitters therefore clearly demonstrate that long-range eX governs the separation between hole and particle, as reflected in the magnitude of μ(g)ct.61 The trend in μ(g)ct is relevant for solvation effects, and the localization of hole and particle is also expected to have important consequences for excitonic couplings.
4.2 Solvation effects
Large dipole moments μ(g)ct lead to mutual polarization of solvent and solute and result in a considerable decrease of the CT excitation energy Eve in solution. In Fig. 3, we compare the performance of three different versions of PCM, viz. PCM-LR, PCM-cLR and PCM-SS (see also Section 3.3). Note that PCM-cLR yields the same dipole moment μct as PCM-LR, because it applies first-order perturbation theory to PCM-SS and thus leaves the wavefunction unperturbed. For TBTM-TPA (Fig. 3c) we observe significant solvation effects, which can only be captured with PCM-SS. This can be attributed to enhanced particle–hole separation caused by the perpendicular orientation of donor and acceptor planes, along with stronger solute–solvent polarization resulting from an increased CT-state dipole moment. The results for the other systems, TTM-1Cz and TTM-TPA, likewise support the need for state-specific continuum solvation, although the solvation effects are less pronounced. We note that abandoning the state-specific formalism in combination with small long-range eX can potentially lead to error cancellation. In this scenario, excitonic couplings are particularly likely to be underestimated, yielding misleading mode contributions to non-radiative decay, see also Section 4.3.Concerning TBTM-TPA, evaluating excited-state electronic gradients and derivative coupling vectors in the gas phase may introduce considerable errors due to significant solvation effects. In Section S3.2 of the SI, a stability analysis demonstrates that the dominant contribution is the excitation energy, which is properly recovered in our framework. In addition, trends in key quantities, as discussed in Section S3.4 of the SI, indicate that solvation likely induces minor changes in the excitonic couplings and is therefore of secondary importance.
4.3 Vibronic couplings and range-separation
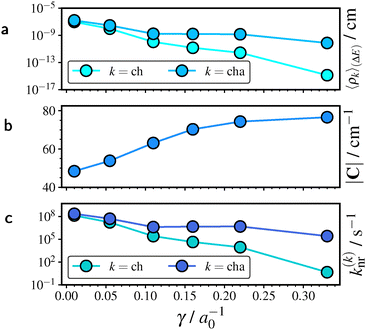
We now examine the relationship between vibronic couplings in the radical emitters and the separation of short-range and long-range eX. We first present a stability analysis of the total rate constant k(cha)nr with respect to γ, followed by an assessment of the excitonic couplings. TTM-1Cz is used as illustrative example and supporting results for TTM-TPA and TBTM-TPA are provided in Section S3.2 of the SI.The two main contributions to k(cha)nr are given by the non-adiabatic coupling |C| and the averaged total FCWD 〈ρcha〉(ΔE), cf.eqn (3). As exemplified by eqn (7), the average 〈ρcha〉(ΔE) consists of two principal contributions, the excitonic couplings Sμ and the energy gap ΔE. Fig. 4 illustrates the trend of the average 〈ρcha〉(ΔE) in relation to the energy gap ΔE and the excitonic couplings, together with a comparison to the averaged FCWD 〈ρch〉(ΔE), where all high-frequency modes are treated harmonically.
In Fig. 4a, we observe a clear exponential decay of 〈ρch〉(ΔE) and 〈ρcha〉(ΔE) with the gap ΔE. Even small variations in ΔE lead to changes by several orders of magnitude. This exponential behavior is consistent with the energy-gap law for non-radiative decay, since the corresponding rate constant knr differs from the FCWD average only by a constant factor (if non-adiabatic couplings are held fixed). Furthermore, the deviation between a harmonic and an anharmonic treatment of the high-frequency modes increases with ΔE and becomes significant at physically relevant gaps of about 2 eV (see also Section 4.6).
Considering the influence of excitonic couplings in Fig. 4b, 〈ρcha〉(ΔE) is shifted relative to 〈ρch〉(ΔE) by approximately a constant offset. In both cases, the FCWD average increases markedly with γ and appears to approach a saturation limit at large γ.
The combined effect of ΔE and excitonic couplings on the averages 〈ρk〉(ΔE) as a function of γ is illustrated in Fig. 5a. We note that the gaps ΔE were computed from the corresponding PCM-SS excitation energies, cf.Fig. 3a. The overall trend is dominated by the gap ΔE, leading to a decrease of 〈ρk〉(ΔE) by several orders of magnitude with increasing γ. The non-adiabatic coupling shown in Fig. 5b increases with γ, although it remains within the same order of magnitude. Consequently, the overall trend in k(k)nr with γ in Fig. 3c can be understood as determined by 〈ρcha〉(ΔE) and hence dominated by the gap ΔE. We note that the stability analyses of TTM-TPA and TBTM-TPA in Section S3.2 of the SI lead to the same conclusions.
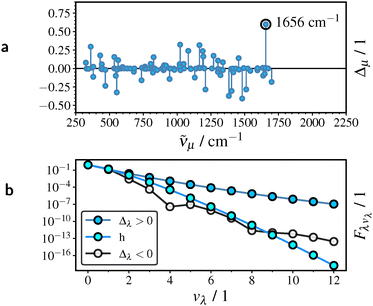
As pointed out in Section 4.7, non-radiative decay in the radical emitters is promoted by a single high-frequency mode owing to its significant contribution to 〈ρcha〉(ΔE)′. To clarify the relationship between long-range eX and excitonic coupling, we examine the mode displacement Δλ and HR factor Sλ (coupling strength) for the promoting mode λ of TTM-1Cz, as shown in Fig. 6. Supporting results for TTM-TPA and TBTM-TPA are provided in Section S3.3 of the SI.
 | ||
| Fig. 6 Dependence of the signed mode displacement Δλ (a) and HR factor Sλ (b) of the promoting mode λ in TTM-1Cz on the range-separation parameter γ. | ||
The promoting mode of TTM-1Cz at approximately 1650 cm−1 is localized on the acceptor moiety in close proximity to the donor unit (see Fig. S9a of the SI). As discussed in detail in Section S3.4 of the SI, the promoting mode perturbs hole and particle simultaneously more readily at larger γ, owing to their increased spatial adjacency resulting from long-range eX. In Fig. 6, we therefore observe a pronounced increase in the positive displacement Δλ and in Sλ with increasing γ, both approaching a saturation limit at large γ. This trend is mirrored by that of 〈ρk〉(ΔE) in Fig. 4b.
Indeed, the results in Section 4.7 show that, with increasing γ, non-radiative decay in the radical emitters is governed almost exclusively by the positively displaced promoting mode. In combination with the trends in the PCM-SS excitation energy shown in Fig. 3, these findings suggest that an accurate description of the CT state energy and the vibronic structure of donor-functionalized radical emitters requires a considerable amount of long-range eX. These findings are supported by the data presented in Section 3.5 of the SI, showing that the observed trends extend to other exchange–correlation functionals.56,95–97
4.4 Model calibration
In Sections 3.1–3.3, we demonstrated that γ significantly influences various properties of radical emitters relevant to the non-radiative decay of the CT state and is hence the central parameter of our model. In the present study, an empirical tuning of γ is performed by requiring that the PCM-SS vertical excitation energy E(ss)ve, cf. Section 3.3, reproduce the experimental absorption maximum. To this end, E(ss)ve is interpolated as a function of γ, and the tuned values γt are obtained by inverting the interpolant and supporting details and an extended discussion are provided in Section S3.6 of the SI.56,57,73–76,95–99 Using γt, equilibrium geometries, Hessians, excited-state electronic gradients, and derivative coupling vectors are evaluated for the gas phase as described in Section 3. For TBTM-TPA, only an approximate tuning of γ was feasible due to computational difficulties arising from its perpendicular arrangement (see also Section S3.6 of the SI).Table 1 compiles relevant properties obtained with the calibrated models together with experimental reference values. While γ was adjusted a posteriori to match the excitation energies, the model also shows good agreement with other experimental properties. In particular, the experimental trend in the non-radiative decay rates is reproduced correctly by the k(cha)nr values. This indicates that the calibrated model provides a reasonable description of the systems. An empirical tuning of γ enables a detailed analysis of the experimental results and is employed here for convenience. Trend analyses of the FCWD (Fig. 4) and, in particular, the coupling between the promoting mode and the CT exciton (Fig. 6) reveal a consistent trend with respect γ suggesting that a non-empirical description could be feasible. Accordingly, alongside a non-empirical tuning of γ, comparative trend analyses of relevant excitonic couplings across different systems may suffice to predict trends in non-radiative decay.
| TTM-1Cz | TTM-TPA | TBTM-TPA | |
|---|---|---|---|
| γ t/a0−1 | 0.211 | 0.251 | 0.310 |
| E (exp)abs/eV | 2.06 | 1.95 | 1.97 |
| E (ss)ve/eV | 2.06 | 1.95 | 1.77 |
| E (exp)ems/eV | 1.97 | 1.70 | 1.70 |
| ΔE/eV | 1.88 | 1.66 | 1.57 |
| k (exp)r/107 s−1 | 1.28 | 1.88 | 2.51 |
| k r/107 s−1 | 1.12 | 1.19 | 1.30 |
| k (exp)nr/s−1 | 1.1 × 107 | 1.4 × 108 | 3.3 × 107 |
| k (cha)nr/s−1 | 1.0 × 107 | 6.8 × 108 | 1.4 × 107 |
| k (ch)nr/s−1 | 2.1 × 104 | 2.1 × 107 | 1.3 × 106 |
Anharmonic contributions are necessary to reach quantitative agreement with experiment, cf.Table 1. Determining the non-adiabatic coupling |C| at the CT state equilibrium geometry is physically sound, as decay proceeds from this geometry and, according to exploratory calculations (not shown), further improves agreement with experiment.
The assumption of distinct accepting and promoting modes was employed in deriving the quantum-mechanical FCWDs37,38 and is well fulfilled by the calibrated models, as shown in Section S3.7 of the SI. We also note that structural relaxation upon non-radiative transition is presumably small and can be reasonably described within the displaced harmonic oscillator framework, as supported by the considerations in Section S3.8 of the SI. To account for anharmonic contributions arising from highly excited vibrational states, the displaced Morse oscillator model is required.
4.5 Mode-resolved analysis
An analysis of vibronic couplings can be performed by examining the spectra of the non-adiabatic couplings Cμ, excitonic couplings Sμ, and reorganization energies Λμ with respect to the normal modes μ, as shown in Fig. 7 (with Sμ omitted for classical modes). The couplings Cμ were evaluated at the CT equilibrium geometry, with further details provided in Section S3.9.101 | ||
Fig. 7 Mode-resolved analysis of the unsigned non-adiabatic couplings |Cμ|, excitonic couplings Sμ and contributions Λμ to the reorganization energy Λ related to a normal mode μ with wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) μ. Results are displayed for TTM-1Cz (a), TTM-TPA (b) and TBTM-TPA (c). Selected more contributions are highlighted. The required calculations were performed with the tuned range-separation parameters γt compiled in Table 1. μ. Results are displayed for TTM-1Cz (a), TTM-TPA (b) and TBTM-TPA (c). Selected more contributions are highlighted. The required calculations were performed with the tuned range-separation parameters γt compiled in Table 1. | ||
The non-radiative transition in the radical emitters is induced by high-frequency skeletal vibrations, with exemplary illustrations provided in Section S3.10 of the SI. For both TTM-1Cz and TTM-TPA (Fig. 7a and b), a single high-frequency mode at around 1650 cm−1 is found that exhibits significant excitonic coupling Sμ and contributes substantially to the reorganization energy. For TBTM-TPA in Fig. 7c, we observe a reduced yet still notable excitonic coupling of the mode at 1627 cm−1, together with a marked coupling at 1342 cm−1.
A comparative analysis of vibronic couplings indicates that variations in non-radiative decay rates are governed by excitonic couplings Sμ, whereas the non-adiabatic couplings Cμ are comparable among the emitters studied. In particular, the suppressed mode in TBTM-TPA at 1627 cm−1 is analogous to the strongly coupled modes of TTM-1Cz and TTM-TPA at approximately 1650 cm−1 (see Section S3.4 of the SI for illustrations). The suppression of non-radiative decay can thus be attributed to the additional chlorination of the TTM moiety. While inspection of the spectra for Sμ already provides insight into the experimental trend of knr, a more refined analysis can be obtained by accounting for anharmonic contributions, as discussed in Section 4.6.
A notable feature in the spectra of Fig. 7 is the absence of both large Cμ and significant Sμ for proton stretching vibrations (above 3000 cm−1). This contrasts with the common view that non-radiative decay proceeds predominantly via such vibrations.9,28,40,41,102 For the radical emitters considered, proton-stretching vibrations—typically localized at the outer edges of the donor or acceptor—have only minor effects on the CT state energy, giving rise to negligible excitonic couplings and making them essentially irrelevant for non-radiative decay (see also Section S3.11). Moreover, previous studies on non-radiative decay in metal–organic complexes emphasize the key role of high-frequency skeletal vibrations.103–107
4.6 Analysis of anharmonic contributions
The analysis in Section 4.5 is restricted to displaced harmonic oscillators. As shown in Table 1, accounting for anharmonic contributions to knr is necessary to achieve quantitative agreement with experiment. We therefore analyze the anharmonic contributions for TTM-1Cz, with particular focus on the promoting mode at 1656 cm−1, and provide a comparison with the harmonic approximation. Supporting results for TTM-TPA and TBTM-TPA are provided in Section S3.12 of the SI. Fig. 8a shows that the promoting mode λ possesses a comparatively large displacement Δλ with positive orientation. We recall that both the magnitude and the orientation of Δλ determine the anharmonic FC factor near the energy gap and thus the relevance of a given mode to nonradiative decay, cf. Section 2.1.For a positive displacement Δλ, the vibronic transition terminates near the inner turning point of the final Morse potential (see also Section S1.2 of the SI), resulting in a relatively slow decrease of the anharmonic FC factor Fλ,vλ with the vibrational quantum number vλ as shown in Fig. 8b. By contrast, the anharmonic Fλ,vλ for a hypothetical negative displacement Δλ, as well as the harmonic Fλ,vλ, are smaller by several orders of magnitude in the relevant range vλ ≥ 9. Consequently, the orientation of promoting mode displacement plays an important role in achieving a quantitative description of non-radiative decay.
Moreover, the increasing deviation of the harmonic Fλ,vλ with vλ underscores the relevance of an anharmonic model for highly excited vibrational states.
The high-frequency mode in TBTM-TPA at 1612 cm−1 not only exhibits a reduced displacement Δλ (weaker excitonic coupling Sλ) but also a negative orientation of this displacement as shown in Section S3.2 of the SI. Both effects lead to a reduction of the (anharmonic) FC factor at relevant vibrational energies. Conversely, the promoting mode in TTM-TPA (1659 cm−1) is positively displaced, leading to faster non-radiative decay. In addition to a reduced excitonic coupling of the promoting mode, non-radiative decay in TBTM-TPA is suppressed due to a diminished anharmonic contribution (Δλ < 0), resulting in a reduced vibronic transition probability. Qualitatively, the reduced Sλ value for TBTM-TPA suffices to explain the suppressed non-radiative decay, as the experimental trend is reproduced correctly at the qualitative level within the harmonic approximation, cf. the k(ch)nr values in Table 1.
4.7 Identification of the promoting mode
The relevance of a quantum-mechanical mode λ to non-radiative decay can be quantified through a sensitivity analysis of the total FCWD average 〈ρcha〉(ΔE). We define the enhancement factor fe,μ of a mode μ as | (22) |
The spectra of enhancement factors fe,μ in Fig. 9 are dominated by a single promoting mode in each case, and the corresponding nuclear motion is visualized. TTM-1Cz and TTM-TPA share the same promoting mode around 1650 cm−1, which is suppressed in TBTM-TPA (1612 cm−1) due to additional chlorination. Instead, non-radiative decay in TBTM-TPA proceeds through a less efficient mode at 1342 cm−1. Thus, sensitivity analysis of 〈ρcha〉(ΔE) provides a reliable means of identifying the promoting mode, whereas simply examining the excitonic couplings Sμ (cf.Fig. 7) may qualitatively agree with the identified promoting modes but does not necessarily make their dominant character sufficiently evident.
 | ||
Fig. 9 Enhancement factors fe,μ measuring the contribution of a single mode μ with wavenumber ![[small nu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e1.gif) μ to the total FCWD average 〈ρcha〉. Results are displayed for TTM-1Cz (a), TTM-TPA (b) and TBTM-TPA (c). The vibrational motions of the dominant modes are visualized. Calculations were performed with the tuned parameters γt compiled in Table 1. μ to the total FCWD average 〈ρcha〉. Results are displayed for TTM-1Cz (a), TTM-TPA (b) and TBTM-TPA (c). The vibrational motions of the dominant modes are visualized. Calculations were performed with the tuned parameters γt compiled in Table 1. | ||
As the FCWD measures the joint probability of all allowed vibronic transitions at a given energy gap ΔE (see Section 2.1), the results of the present section indicate that there is only a single mode with a significant FC factor near ΔE. This large FC factor can be attributed to the large magnitude of the displacement Δλ (i.e., a large HR factor), combined with its positive orientation (see Section 4.7). Intuitively, the dominant role of the promoting mode may be understood from its ability to effectively quench the CT exciton, as discussed in Section 3.4 of the SI.
Since non-radiative decay in the radical emitters is dominated by a single mode, a one-effective-mode model is potentially viable. Section S3.13 of the SI shows that the experimental trend in knr can be quantitatively reproduced with an extended MLJ model, treating the promoting mode as the effective mode. However, this requires explicitly accounting for anharmonic contributions.
It is also worth noting that, the sensitivity analysis of 〈ρcha〉(ΔE) can be applied to groups of (quantum-mechanical) modes. For example, excluding all proton stretching vibrations further supports the conclusion that this class of vibrations is insignificant (see Section S3.14 of the SI).
Finally, we note that long-range eX is crucial for correctly identifying the promoting mode. Insufficient long-range eX, or the use of a global hybrid (corresponding to γ = 0), leads to a fundamentally different non-radiative decay mechanism in which no single mode contributes dominantly, cf. Section S3.15 of the SI.
4.8 Notes on molecular design
A key advantage of the mode-resolved approach is that it enables non-radiative decay to be directly linked to specific structural features through molecular vibrations. Here, we discuss the findings of Sections 4.5–4.7 in the context of molecular design.Our results suggest that the promoting high-frequency mode in donor-functionalized TTM radicals is located at the phenyl ring adjacent to the donor moiety. This mode is strongly coupled to the CT exciton and further accelerates non-radiative decay via anharmonic contributions (Δλ > 0). Together, these effects yield a substantial FC factor near the transition gap, which underlies the dominant role of the promoting mode. In donor-functionalized TBTM radicals, both the excitonic coupling and the anharmonic contribution of this mode are suppressed by the additional chlorination (Δλ < 0), resulting in a diminished FC factor. Non-radiative decay is hence reduced and likely proceeds through a (delocalized) less efficient mode. PTM-based emitters do not exhibit further suppression of non-radiative decay compared to the TBTM analogues,12,108 as the promoting mode is already attenuated, consistent with our findings. Results for additional emitters in Section S3.16 support extending the explanation of suppressed non-radiative decay from TBTM-TPA to the TBTM and PTM series. This section also includes a comprehensive discussion on possible effects influencing non-radiative decay in the radical emitters.
Although localization of vibrations to either the donor or the acceptor moiety may reduce excitonic couplings to some extent,11,13 our study demonstrates that a localized high-frequency vibration can still significantly perturb the CT exciton, since hole and particle may retain considerable overlap due to mutual electrostatic attraction. The introduction of bulky substituents near the donor–acceptor junction can further reduce the excitonic coupling and thereby suppress non-radiative decay.
Moreover, unlike in our earlier study,12 we find that inclusion of contributions from the second, locally excited electronic state is not necessary to achieve a sufficient description of the non-radiative decay.
5 Conclusions
Our study presents a mode-resolved model for the non-radiative decay of the CT state in donor-functionalized radical emitters. The decisive role of additional long-range exact exchange (eX) in density functionals for governing this decay is clearly demonstrated. An adequate amount of eX is essential for a consistent description of excitation energies in solution as well as the couplings of relevant modes to the CT exciton. Importantly, eX amplifies the excitonic coupling of the promoting mode, which becomes evident only at sufficiently large eX contributions. Based on our theoretical analysis, it is likely that the role of exact exchange in governing vibronic transitions from charge-transfer (CT) states also extends to other systems, including closed-shell emitters. We emphasize, however, that confirming this hypothesis would require further computational verification. Moreover, since the non-radiative transition in the radical emitters terminates in an excited vibrational state of the promoting mode, explicit inclusion of anharmonic contributions is imperative for quantitative accuracy.In this study, the model was calibrated through empirical tuning of a functional parameter, with trend analyses suggesting that a non-empirical approach may also be feasible. The calibrated model agrees well with experimental results and accounts for the suppressed decay in the examined radical emitters as a result of the perpendicular orientation of donor and acceptor planes. The sterically demanding substituents required for this arrangement hinder the vibrational motion of the promoting mode, substantially reducing both its coupling to the CT exciton and its anharmonic contribution. In this case, non-radiative decay proceeds via an alternative, less efficient mode. The promoting mode can be identified unambiguously by a sensitivity analysis of the averaged Franck–Condon weighted density of states (FCWD), explicitly accounting for anharmonic contributions. Our approach for identifying modes relevant to non-radiative decay through analysis of the quantum-mechanical FCWD is in principle transferable to other systems, including decay from other types of excited states, e.g., a locally excited state. Such transferability would, in particular, require the Condon approximation to hold and would need further computational verification. We highlight that the key strength of this approach lies in its ability to link non-radiative decay processes to structural features via specific vibrational modes.
Conflicts of interest
There are no conflicts to declare.Data availability
The data that support the findings of this study are available upon reasonable request from the corresponding author, RT.The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: supplementary theoretical and computational details, supplementary results, extended discussion and optimized geometries. See DOI: https://doi.org/10.1039/d5cp03613e.
Acknowledgements
The authors acknowledge support by the state of Baden-Württemberg through bwHPC and the German Research Foundation (DFG) through grant no. INST 40/575-1 FUGG (JUSTUS 2 cluster).Notes and references
- S. R. Forrest and M. E. Thompson, Chem. Rev., 2007, 107, 923–925 CrossRef CAS.
- M. Xu, X. Li, S. Liu, L. Zhang and W. Xie, Mater. Chem. Front., 2023, 7, 4744–4767 RSC.
- L. Lan and H. Zhang, Angew. Chem., Int. Ed., 2025, 64, e202509140 CrossRef CAS.
- R. H. Friend, R. Gymer, A. Holmes, J. Burroughes, R. Marks, C. Taliani, D. Bradley, D. D. Santos, J.-L. Bredas and M. Lögdlund, et al. , Nature, 1999, 397, 121–128 CrossRef CAS.
- Q. Peng, A. Obolda, M. Zhang and F. Li, Angew. Chem., Int. Ed., 2015, 54, 7091–7095 CrossRef CAS.
- A. Obolda, X. Ai, M. Zhang and F. Li, ACS Appl. Mater. Interfaces, 2016, 8, 35472–35478 CrossRef CAS.
- I. Ratera, J. Vidal-Gancedo, D. Maspoch, S. T. Bromley, N. Crivillers and M. Mas-Torrent, J. Mater. Chem. C, 2021, 9, 10610–10623 RSC.
- R. Englman and J. Jortner, Mol. Phys., 1970, 18, 145–164 CrossRef CAS.
- R. Englman and J. Jortner, J. Lumin., 1970, 1, 134–142 CrossRef.
- X. Ai, E. W. Evans, S. Dong, A. J. Gillett, H. Guo, Y. Chen, T. J. Hele, R. H. Friend and F. Li, Nature, 2018, 563, 536–540 CrossRef CAS.
- P. Ghosh, A. M. Alvertis, R. Chowdhury, P. Murto, A. J. Gillett, S. Dong, A. J. Sneyd, H.-H. Cho, E. W. Evans and B. Monserrat, et al. , Nature, 2024, 629, 355–362 CrossRef CAS.
- M. E. Arnold, R. Toews, L. Schneider, J. Schmid, M. H. Putra, M. Busch, A. Groß, F. Deschler, A. Köhn and A. J. Kuehne, Adv. Opt. Mater., 2024, 2500296 Search PubMed.
- M. Maiuri, Nature, 2024, 629, 289–290 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. Marcus, Pure Appl. Chem., 1997, 69, 13–30 CrossRef CAS.
- V. Levich and R. Dogonadze, Dokl. Akad. Nauk SSSR, 1959, 123–126 Search PubMed.
- V. Levich, Adv. Electrochem. Electrochem. Eng., 1966, 4, 249–371 Search PubMed.
- J. Jortner, J. Chem. Phys., 1976, 64, 4860–4867 Search PubMed.
- H. Abroshan, V. Coropceanu and J.-L. Brédas, Adv. Funct. Mater., 2020, 30, 2002916 CrossRef CAS.
- E. Cho, V. Coropceanu and J.-L. Brédas, J. Am. Chem. Soc., 2020, 142, 17782–17786 Search PubMed.
- E. Cho, V. Coropceanu and J.-L. Brédas, J. Mater. Chem. C, 2021, 9, 10794–10801 Search PubMed.
- H. Abroshan, P. Winget, H. S. Kwak, C. T. Brown and M. D. Halls, Phys. Chem. Chem. Phys., 2022, 24, 16891–16899 Search PubMed.
- P. M. Morse, Phys. Rev., 1929, 34, 57 CrossRef CAS.
- P. A. M. Dirac, Proc. R. Soc. London, Ser. A, 1927, 114, 243–265 CAS.
- E. Fermi, Nuclear physics: a course given by Enrico Fermi at the University of Chicago, University of Chicago Press, 1950 Search PubMed.
- A. Messiah, Quantum mechanics, North-Holland Publishing Company, Amsterdam, 1962, vol. 2 Search PubMed.
- M. Born and J. Oppenheimer, Ann. Phys., 1927, 389, 457–484 CrossRef.
- R. Valiev, B. Merzlikin, R. Nasibullin, A. Kurtzevitch, V. Cherepanov, R. Ramazanov, D. Sundholm and T. Kurtén, Phys. Chem. Chem. Phys., 2023, 25, 6406–6415 RSC.
- G. Herzberg and E. Teller, Z. Phys. Chem., 1933, 21, 410–446 CrossRef.
- E. Condon, Phys. Rev., 1926, 28, 1182 CrossRef CAS.
- E. U. Condon, Phys. Rev., 1928, 32, 858 CrossRef CAS.
- E. Condon, Phys. Rev., 1930, 36, 1121 CrossRef CAS.
- S. Mukamel, Principles of nonlinear optical spectroscopy, Oxford University Press, 1995 Search PubMed.
- F. Duschinsky, Acta Physicochim. URSS, 1937, 7, 551–566 Search PubMed.
- K. Huang and A. Rhys, Proc. R. Soc. London, Ser. A, 1950, 204, 406–423 CAS.
- E. S. Medvedev and V. I. Osherov, Radiationless transitions in polyatomic molecules, Springer, 1995, vol. 57 Search PubMed.
- L. Shi, X. Xie and A. Troisi, J. Chem. Phys., 2022, 157, 134106 CrossRef CAS.
- R. P. Fornari, J. Aragó and A. Troisi, J. Chem. Phys., 2015, 142, 184105 CrossRef.
- J. Franck and E. Dymond, Trans. Faraday Soc., 1926, 21, 536–542 Search PubMed.
- R. Valiev, R. Nasibullin, V. Cherepanov, G. V. Baryshnikov, D. Sundholm, H. Ågren, B. F. Minaev and T. Kurtén, Phys. Chem. Chem. Phys., 2020, 22, 22314–22323 RSC.
- V. Plotnikov, Int. J. Quantum Chem., 1979, 16, 527–541 Search PubMed.
- J. López V, A. Rivera, Y. F. Smirnov and A. Frank, Int. J. Quantum Chem., 2002, 88, 280–295 CrossRef.
- E. Laguerre, Bull. Soc. Math., 1878, 6, 72–78 Search PubMed.
- E. Whittaker and G. Watson, A course of modern analysis, Courier Dover Publications, 2020 Search PubMed.
- S. Yeganeh and M. A. Ratner, J. Chem. Phys., 2006, 124, 044108 CrossRef.
- K. M. Ervin, S. Gronert, S. Barlow, M. K. Gilles, A. G. Harrison, V. M. Bierbaum, C. H. DePuy, W. Lineberger and G. B. Ellison, J. Am. Chem. Soc., 1990, 112, 5750–5759 CrossRef CAS.
- T. M. Henderson, B. G. Janesko and G. E. Scuseria, J. Phys. Chem. A, 2008, 112, 12530–12542 Search PubMed.
- J. P. Perdew, R. G. Parr, M. Levy and J. L. Balduz Jr, Phys. Rev. Lett., 1982, 49, 1691 CrossRef CAS.
- J. F. Janak, Phys. Rev. B:Condens. Matter Mater. Phys., 1978, 18, 7165 Search PubMed.
- O. A. Vydrov, G. E. Scuseria and J. P. Perdew, J. Chem. Phys., 2007, 126, 154109 CrossRef.
- A. J. Cohen, P. Mori-Sánchez and W. Yang, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 77, 115123 CrossRef.
- A. Dreuw and M. Head-Gordon, J. Am. Chem. Soc., 2004, 126, 4007–4016 CrossRef CAS.
- A. L. Sobolewski and W. Domcke, Chem. Phys., 2003, 294, 73–83 CrossRef CAS.
- A. Dreuw, G. R. Fleming and M. Head-Gordon, J. Phys. Chem. B, 2003, 107, 6500–6503 CrossRef CAS.
- D. J. Tozer, R. D. Amos, N. C. Handy, B. O. Roos and L. Serrano-Andres, Mol. Phys., 1999, 97, 859–868 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425–8433 CrossRef CAS PubMed.
- T. Leininger, H. Stoll, H.-J. Werner and A. Savin, Chem. Phys. Lett., 1997, 275, 151–160 CrossRef CAS.
- R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109 CrossRef CAS PubMed.
- M. E. Casida, Recent Advances In Density Functional Methods: (Part I), World Scientific, 1995, pp. 155–192 Search PubMed.
- A. Dreuw, J. L. Weisman and M. Head-Gordon, J. Chem. Phys., 2003, 119, 2943–2946 CrossRef CAS.
- J. Tomasi and M. Persico, Chem. Rev., 1994, 94, 2027–2094 CrossRef CAS.
- J. Tomasi, B. Mennucci and R. Cammi, Chem. Rev., 2005, 105, 2999–3094 CrossRef CAS.
- P. Shaw, Phys. Rev. A:At., Mol., Opt. Phys., 1985, 32, 2476 CrossRef CAS.
- P. Shaw, Phys. Rev. A:At., Mol., Opt. Phys., 1987, 35, 2254 CrossRef.
- E. McRae, J. Phys. Chem., 1957, 61, 562–572 CrossRef CAS.
- N. Mataga and T. Kubota, Molecular interactions and electronic spectra, M. Dekker, 1970 Search PubMed.
- S. Corni, R. Cammi, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 123, 134512 CrossRef CAS.
- R. Cammi, S. Corni, B. Mennucci and J. Tomasi, J. Chem. Phys., 2005, 122, 104513 CrossRef CAS.
- D. A. Phan Huu, R. Dhali, C. Pieroni, F. Di Maiolo, C. Sissa, F. Terenziani and A. Painelli, Phys. Rev. Lett., 2020, 124, 107401 CrossRef CAS.
- D. Toptygin, J. Fluoresc., 2003, 13, 201–219 CrossRef CAS.
- A. Einstein, Phys. Z., 1917, 18, 121 CAS.
- P. J. Stephens, F. J. Devlin, C. F. Chabalowski and M. J. Frisch, J. Phys. Chem., 1994, 98, 11623–11627 CrossRef CAS.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B:Condens. Matter Mater. Phys., 1988, 37, 785 CrossRef CAS.
- S. H. Vosko, L. Wilk and M. Nusair, Can. J. Phys., 1980, 58, 1200–1211 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- M. Friede, S. Ehlert, S. Grimme and J.-M. Mewes, J. Chem. Theory Comput., 2023, 19, 8097–8107 CrossRef CAS.
- A. M. Burow, M. Sierka and F. Mohamed, J. Chem. Phys., 2009, 131, 214101 CrossRef.
- TURBOMOLE V7.7 2022, a development of University of Karlsruhe and Forschungszentrum Karlsruhe GmbH, 1989–2007, TURBOMOLE GmbH, https://www.turbomole.com.
- O. Treutler and R. Ahlrichs, J. Chem. Phys., 1995, 102, 346–354 CrossRef CAS.
- K. Eichkorn, F. Weigend, O. Treutler and R. Ahlrichs, Theor. Chem. Acc., 1997, 97, 119–124 Search PubMed.
- G. Scalmani and M. J. Frisch, J. Chem. Phys., 2010, 132, 114110 CrossRef.
- M. Caricato, B. Mennucci, J. Tomasi, F. Ingrosso, R. Cammi, S. Corni and G. Scalmani, J. Chem. Phys., 2006, 124, 124520 CrossRef PubMed.
- R. Improta, V. Barone, G. Scalmani and M. J. Frisch, J. Chem. Phys., 2006, 125, 054103 CrossRef.
- R. Improta, G. Scalmani, M. J. Frisch and V. Barone, J. Chem. Phys., 2007, 127, 074504 CrossRef PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, Gaussian Inc., Wallingford CT, 2016 Search PubMed.
- V. Lebedev, Theory of Cubature Formulas and Computational Mathematics, 1980 Search PubMed.
- D. Rappoport and F. Furche, J. Chem. Phys., 2010, 133, 134105 CrossRef.
- B. P. Pritchard, D. Altarawy, B. Didier, T. D. Gibson and T. L. Windus, J. Chem. Inf. Model., 2019, 59, 4814–4820 CrossRef CAS.
- F. Furche and R. Ahlrichs, J. Chem. Phys., 2002, 117, 7433–7447 CrossRef CAS.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775–4777 CrossRef CAS.
- S. E. Stein and B. Rabinovitch, J. Chem. Phys., 1973, 58, 2438–2445 CrossRef CAS.
- T. Beyer and D. Swinehart, Commun. ACM, 1973, 16, 379 CrossRef.
- M. A. Rohrdanz, K. M. Martins and J. M. Herbert, J. Chem. Phys., 2009, 130, 054112 CrossRef PubMed.
- T. M. Henderson, B. G. Janesko and G. E. Scuseria, J. Chem. Phys., 2008, 128, 194105 Search PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- F. N. Fritsch and J. Butland, SIAM J. Sci. Stat. Comput., 1984, 5, 300–304 CrossRef.
- H. Iikura, T. Tsuneda, T. Yanai and K. Hirao, J. Chem. Phys., 2001, 115, 3540–3544 CrossRef CAS.
- A. Abdurahman, T. J. Hele, Q. Gu, J. Zhang, Q. Peng, M. Zhang, R. H. Friend, F. Li and E. W. Evans, Nat. Mater., 2020, 19, 1224–1229 CrossRef CAS PubMed.
- J. R. Reimers, J. Chem. Phys., 2001, 115, 9103–9109 CrossRef CAS.
- R. R. Valiev, V. N. Cherepanov, R. T. Nasibullin, D. Sundholm and T. Kurten, Phys. Chem. Chem. Phys., 2019, 21, 18495–18500 RSC.
- A. Köhler, A. L. Khan, J. S. Wilson, C. Dosche, M. K. Al-Suti, H. H. Shah and M. S. Khan, J. Chem. Phys., 2012, 136, 094905 CrossRef.
- D. G. Thompson, J. R. Schoonover, C. J. Timpson and T. J. Meyer, J. Phys. Chem. A, 2003, 107, 10250–10260 CrossRef CAS.
- S. D. Cummings and R. Eisenberg, J. Am. Chem. Soc., 1996, 118, 1949–1960 CrossRef CAS.
- E. M. Kober, J. V. Caspar, R. S. Lumpkin and T. J. Meyer, J. Phys. Chem., 1986, 90, 3722–3734 CrossRef CAS.
- J. V. Caspar, E. M. Kober, B. P. Sullivan and T. J. Meyer, J. Am. Chem. Soc., 1982, 104, 630–632 CrossRef CAS.
- S. Dong, W. Xu, H. Guo, W. Yan, M. Zhang and F. Li, Phys. Chem. Chem. Phys., 2018, 20, 18657–18662 RSC.
| This journal is © the Owner Societies 2026 |