The robustness of composite pulses elucidated by classical mechanics: stability around the globe
Jonathan
Berkheim
 * and
David J.
Tannor
* and
David J.
Tannor

Department of Chemical and Biological Physics, Weizmann Institute of Science, 76100, Rehovot, Israel. E-mail: jonathan.berkheim@weizmann.ac.il
First published on 9th December 2025
Abstract
Composite pulses (CPs) are widely used in nuclear magnetic resonance (NMR), optical spectroscopy, optimal control experiments and quantum computing to manipulate systems that are well-described by a two-level Hamiltonian. A careful design of these pulses can allow the refocusing of an ensemble at a desired state, even if the ensemble experiences imperfections in the magnitude of the external field or resonance offsets. Since the introduction of CPs, several theoretical justifications for their robustness have been suggested. In this work, we suggest another justification based on the classical mechanical concept of a stability matrix. The motion on the Bloch sphere is mapped to a canonical system of coordinates and the focusing of an ensemble corresponds to caustics, or the vanishing of an appropriate stability matrix element in the canonical coordinates. Our approach highlights the directionality of the refocusing of the ensemble on the Bloch sphere, revealing how different ensembles refocus along different directions. The approach also clarifies when CPs can induce a change in the width of the ensemble as opposed to simply a rotation of the axes. As a case study, we investigate the 90(x)180(y)90(x) CP introduced by Levitt, where the approach provides a new perspective into why this CP is effective.
I. Introduction: from a purely quantum problem to a purely classical treatment
A. Main goals
Many experiments in atomic, molecular, and optical physics aim to invert a population of particles subjected to an external pulse. For example, in nuclear magnetic resonance (NMR) an ensemble of nuclei that evolves under a constant field and a radiofrequency (RF) field has to undergo a synchronized population inversion between the two spin states in order to detect a considerable signal. In several fields of modern optics (e.g., pump–probe spectroscopy and quantum computing), it is sometimes desirable to invert an ensemble of electrons, initially localized in the ground state, to an excited electronic state in order to maximize the radiative signal or to perform other operations.Consider an idealized ensemble of spins-1/2 in state |a〉 subjected to an external RF field. If one introduces simplifying assumptions so that (1) there are no correlations or couplings between spins, (2) the magnitude of the RF field is homogeneous along the ensemble and (3) the external RF field is on-resonance with the induced level separation, a monochromatic continuous-wave (CW) RF field will invert all spins to state |b〉 in half of the period associated with the Rabi frequency. However, when the ensemble experiences either an inhomogeneity in the magnitude of the RF field or a distribution of resonance offsets, the final state is a superposition of |a〉 and |b〉. The challenge is to find simple sequences of pulses that can produce population inversion under these circumstances for the entire ensemble.
It is with this challenge in mind that composite pulses (CPs) were invented. CPs consist of a short sequence of CW pulses, where each segment in the sequence has a characteristic amplitude, duration and phase. These pulses can compensate for the two imperfections described above: (1) field inhomogeneity and (2) resonance offset. Levitt and Freeman were the first to introduce such a pulse sequence,1 though it was inspired by earlier notions, particularly, Hahn's spin echo2 and the Carr–Purcell–Meiboom–Gill sequence.3,4 Since Levitt's original work, many extensions have been suggested.5–8
The first justification for the success of a CP was provided by Levitt himself, who used perturbation theory to develop an expression for the error caused by the pulse imperfections;9,10 later he developed a figure of merit based on the quaternion formalism of Blümlich and Spiess.11,12 An alternative approach based on optimal control theory was proposed by Boscain and Sugny.13,14 Each of these justifications can serve as a tool to design optimal pulses.
In this work, we suggest another justification based on the classical mechanical concept of a stability matrix. The motion on the Bloch sphere is mapped to a canonical system of coordinates and the focusing of an ensemble corresponds to caustics, or the vanishing of an appropriate stability matrix element in the canonical coordinates. The caustics in CPs are unusual in the sense that each member is governed by a slightly different Hamiltonian, so that averaging is required for the stability analysis. Our approach highlights the directionality of the refocusing of the ensemble on the Bloch sphere, revealing how different ensembles refocus along different directions. As a case study, we investigate the 90(x)180(y)90(x) CP introduced by Levitt, where the approach provides a new perspective into why this CP is effective: the focusing produced by Levitt's CP corresponds to a caustic, as manifested in the elements of the stability matrix. The approach clarifies why the 90(x)180(y)90(x) CP changes the width of the ensemble in the case of resonance offset, as opposed to simply a rotation of the axes in the case of field inhomogeneity. To our knowledge, this work is the first attempt to explore the application of classical stability analysis and caustics to dynamics on the Bloch sphere, formulated in canonical coordinates.
B. Dynamics of two-level system
The evolution of a quantum two-level system is given by the Liouville–von-Neumann equation (LvN) (ħ = 1 is considered throughout work): | (1) |
![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) , in the basis of the states |a〉, |b〉, is a 2 × 2 density matrix:
, in the basis of the states |a〉, |b〉, is a 2 × 2 density matrix: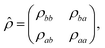 | (2) |
 | (3) |
 for full generality. In the optical nomenclature, ω0 = εb − εa is the level spacing between states |a〉, |b〉 and Ω1(t) plays the role of the time-dependent coupling
for full generality. In the optical nomenclature, ω0 = εb − εa is the level spacing between states |a〉, |b〉 and Ω1(t) plays the role of the time-dependent coupling  , arising from the dipole interaction.15
, arising from the dipole interaction.15
In the SO(3) representation, the matrix ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) is replaced by the so-called Bloch vector r:
is replaced by the so-called Bloch vector r:
| r = (x, y, z)T = (ρba + ρab, i(ρba − ρab), ρbb − ρaa)T, | (4) |
In a similar manner, the Hamiltonian is replaced by the 3-vector Ω:
 | (5) |
| ṙ = Ω × r, | (6) |
Eqn (6) can be also written as:
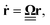 | (7) |
 is a skew-symmetric matrix that represents the cross product of r with the Cartesian components of Ω.
is a skew-symmetric matrix that represents the cross product of r with the Cartesian components of Ω.
Following the standard procedure of moving to the rotating frame and applying the rotating wave approximation (RWA), we can define the resonance offset Δ = ω0 − ω. In the rotating frame, Ω is time-independent. Its norm, denoted Ω, is called the Rabi frequency:
 | (8) |
C. Composite pulses
When CPs in the rotating frame are visualized as a function of time, since the carrier frequency is removed, they appear as a sequence of rectangles.20 Each rectangular segment, enumerated k, in general possesses a characteristic amplitude, duration τk, and phase φk; the latter determines the azimuthal angle of the rotation axis. The general notation τN(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) N)τN−1(
N)τN−1(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) N−1)…τ1(
N−1)…τ1(![[n with combining circumflex]](https://www.rsc.org/images/entities/i_char_006e_0302.gif) 1) represents a series of back-to-back rotations. Also, τk = tk/T where τk is the dimensionless ratio of the clock time tk and the nominal period T = 2π/Ω(0)1; Ω(0)1 is the nominal magnitude of the RF field, which serves as a reference value for the ensemble of fields. As a consequence, we obtain an elegant formula for the overall effect of a CP on an initial state, which also provides the formal solution for the Bloch equations in the rotating frame:
1) represents a series of back-to-back rotations. Also, τk = tk/T where τk is the dimensionless ratio of the clock time tk and the nominal period T = 2π/Ω(0)1; Ω(0)1 is the nominal magnitude of the RF field, which serves as a reference value for the ensemble of fields. As a consequence, we obtain an elegant formula for the overall effect of a CP on an initial state, which also provides the formal solution for the Bloch equations in the rotating frame: | (9) |
 is a general rotation matrix21
is a general rotation matrix21 | (10) |
The CP conceived by Levitt and Freeman is a symmetric sequence comprised of three rectangular segments.1 In Levitt's nomenclature, this sequence is denoted 90°(x)180°(y)90°(x). In the notation of eqn (9):
 | (11) |
Levitt found that this pulse sequence can compensate for two imperfections of the Hamiltonian in eqn (3): (1) field inhomogeneity and (2) resonance offset. In case (1), each member of the ensemble is driven by a slightly different external field, i.e., if the magnitude of the nominal external field is Ω(0)1 = 1, then the magnitude of the RF field felt by the j-th member is Ω(j)1. In case (2), each member of the ensemble has a slightly different offset Δ(j) = ω(j)0 − ω. Following Levitt's work, various extensions have been suggested, many of them consisting of more than just three segments; Levitt himself suggested a five-segment sequence that outperformed his original sequence (eqn (11)).10
These two imperfections lead to variations in the overall effect of the pulse on each member of the ensemble; the effect is two-fold – on the effective rotation axis and the effective flip angle:
 | (12) |
Note that ϑ(j) does not contain the subscript k, since all segments have the same magnitude Ω1 for a certain member j of the ensemble; Ω(j) is the Rabi frequency of the j-th member. In this work, we will treat imperfections (1) and (2) separately; this isolation of variables will put our findings in a clearer context. Fig. 1 shows the effect of these two imperfections.
Levitt found that his pulse sequence can compensate for both imperfections, as seen by the endpoints of the trajectories, which are strikingly close to the antipode of the starting point. We note that these cases are rather different: in case (1), the endpoints are spread along the azimuth ϕ and focused in the polar angle θ, while in case (2) the focusing is apparent in both θ and ϕ. We will return to this difference later in this work.
Throughout this work, we consider: Ω(0)1 = 1, Ω(j)1 ∈ [0.8, 0.9]Ω(0)1 and Δ(j) ∈ [0.4, 0.6] with j = 1, 2, …, 101 and j = 1, 2, …, 201 respectively; these numerical values were considered in the seminal work by Levitt;1 105 time steps were taken per each trajectory. As said, all trajectories start from the north pole. Convergence of trajectories is verified with respect to the time step dt, and stability calculations are converged with respect to the numerical steps dΩ1 and dΔ. Numerical differentiations are done with finite differences.
II. Derivations and methods: a canonical formulation for Bloch equations
A. Non-canonical coordinates
Since we are using SO(3) as a surrogate for SU(2), it is well to revisit the physical interpretation of the Bloch vector r. In classical mechanics, the sets of functions fμ(q, p, t) and gν(q, p, t) define a canonical pair if they provide the following Poisson bracket relations (q and p have the usual meaning of position and momentum, respectively): | (13) |
Spin is an angular momentum and therefore, like any classical angular momentum, satisfies the Poisson bracket relations (μ, ν, λ = 1, 2, 3):
| {rμ, rν} = εμνλrλ ≠ δμν, | (14) |
B. Defining the Hamiltonian for non-canonical coordinates
At this point, we aim to define a classical Hamiltonian. Isomorphically with angular momentum in many situations in classical mechanics, the Hamiltonian takes the form:| H(x, y, z) = Ω·r = Ωxx + Ωyy + Ωzz. | (15) |
This Hamiltonian resembles the quantum Hamiltonian in eqn (3), where now the components of r play the role of Pauli matrices; note that for real-valued electric fields, i.e., Ω = (Ω1, 0, ω0), both the quantum and the classical Hamiltonians have the structure of x-term plus z-term. In this non-canonical representation, the components of r cover the entire phase space; there are no variables conjugate to the components of r. This Hamiltonian is sometimes called the Zeeman Hamiltonian, due to its connection to the Zeeman effect, where a magnetic field interacts with the total angular momentum of a quantum system.21
The EOMs for r have the following form, which is a general Lie–Poisson structure:
 | (16) |
 | (17) |
Since
 | (18) |
| ṙ = −r × Ω = Ω × r, | (19) |
Note that W(r) is the Poisson tensor, the inverse of the two-form dq∧dp;22 for Hamiltonians in canonical form, W(r) is the inverse of the symplectic matrix  , which is independent of r.
, which is independent of r.
C. Canonical coordinates
Now that we have found the classical Hamiltonian in terms of Cartesian coordinates, we will change variables to spherical coordinates, a natural choice for a physical system that lives on a sphere. Given the conventional transformation from Cartesian to spherical coordinates:18 | (20) |
H(θ, ϕ) = Ωx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + Ωy ϕ + Ωy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ θ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + Ωz ϕ + Ωz![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. θ. | (21) |
The Cartesian components of Ω are left as-is intentionally; transforming them to a spherical representation is unnecessary since only the coordinates are of interest to us. Now, we make the following additional change of variables:
 | (22) |
 | (23) |
We may identify the structure of an internal Hamiltonian H0 = Ωzη and an external field  , analogous to the structure of the original quantum Hamiltonian, eqn (3). This classical Hamiltonian is integrable if Ω is time-independent, and the energy is conserved according to Noether's theorem; for CPs, with their piecewise time-dependence, the energy will be piecewise-conserved. If Ω has general time-dependence, then the EOMs are non-autonomous (“1.5D”), and the dynamics might be chaotic under certain circumstances. Previous works showed that this is indeed the case, e.g. if the external field is two-color with incommensurate frequencies chaos can ensue.23,24
, analogous to the structure of the original quantum Hamiltonian, eqn (3). This classical Hamiltonian is integrable if Ω is time-independent, and the energy is conserved according to Noether's theorem; for CPs, with their piecewise time-dependence, the energy will be piecewise-conserved. If Ω has general time-dependence, then the EOMs are non-autonomous (“1.5D”), and the dynamics might be chaotic under certain circumstances. Previous works showed that this is indeed the case, e.g. if the external field is two-color with incommensurate frequencies chaos can ensue.23,24
The variables ϕ and η are in fact canonical. To show this, we calculate their Poisson brackets:
 | (24) |
In the first step, we have used the chain rule for Poisson brackets. In the second step, we used eqn (16). In the third step we used the inverse of eqn (20) to obtain the partial derivatives of ϕ.
We have chosen ϕ as the position and η as its conjugate momentum; we will show later why this choice is natural. In terms of the new canonical coordinates, Hamilton's equations take the form:
 | (25) |
![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) diverges and
diverges and  vanishes there, requiring careful numerical attention around these points.
vanishes there, requiring careful numerical attention around these points.
A bypass for the singularity issue is to obtain the trajectories with the Cartesian Bloch equations (eqn (6)), then to calculate  , and trivially, η(t) = z(t). It can be shown that both the Cartesian components of r and the new canonical coordinates satisfy Liouville's theorem. Liouville's theorem expresses itself in terms of the conservation of area A on the surface of the Bloch sphere. Fig. 2 shows the time-evolution of the populated area in phase space in the case of canonical coordinates; the small deviations from A(t) = π/2 are due to numerical noise.
, and trivially, η(t) = z(t). It can be shown that both the Cartesian components of r and the new canonical coordinates satisfy Liouville's theorem. Liouville's theorem expresses itself in terms of the conservation of area A on the surface of the Bloch sphere. Fig. 2 shows the time-evolution of the populated area in phase space in the case of canonical coordinates; the small deviations from A(t) = π/2 are due to numerical noise.
 | ||
| Fig. 2 Left: Canonical phase space representation of a trajectory starting from (ϕ0, η0) = (0.6π, 0.5), evolving under Levitt's pulse sequence (note that the time-series ϕ(t) is plotted without considering mod 2π). The solution obtained by direct integration of the canonical Bloch eqn (25), and via an indirect calculation based on an integration of the Cartesian Bloch equations are in excellent agreement; such agreement is obtained for any initial conditions, except η = ±1. Right: The time-evolution of the populated area (classical density) in the terms of ϕ and η, starting from an initially rectangular population, showing that Liouville's theorem is satisfied within numerical precision. | ||
D. Stability matrix elements and caustics
In classical mechanics, the stability matrix (or monodromy matrix) describes the stability of the EOMs’ solutions under small changes in the initial conditions. Consider a dynamical system corresponding to the EOMs and let ζ0 be a particular solution of this system. In Hamiltonian dynamics, ζ = (q, p). By linearizing the EOMs about ζ0 we obtain
and let ζ0 be a particular solution of this system. In Hamiltonian dynamics, ζ = (q, p). By linearizing the EOMs about ζ0 we obtain  , where
, where  is the Jacobian matrix. The linearized system provides the stability matrix
is the Jacobian matrix. The linearized system provides the stability matrix  , which satisfies the equation
, which satisfies the equation  with the initial condition
with the initial condition  . Integrating this system gives the stability matrix
. Integrating this system gives the stability matrix  with elements
with elements | (26) |
With the help of the stability matrix, we can define the concept of a caustic, as a position and a time at which a block of the  matrix, specifically ∂qf/∂pi decreases in rank, which in one-dimensional systems means ∂qf/∂pi goes to 0.26 This signifies that locally, the final coordinate is independent of initial momentum, corresponding to a focusing of all the initial momenta in a certain region to a certain final coordinate. The term “caustics” originated in optics, where this focusing of light can lead to burning. The notion of caustics, although originating in coordinate space, can be generalized to the vanishing of other blocks of the stability matrix.27 For example, ∂pf/∂pi and ∂qf/∂qi. We will need both of these objects in the analysis below.
matrix, specifically ∂qf/∂pi decreases in rank, which in one-dimensional systems means ∂qf/∂pi goes to 0.26 This signifies that locally, the final coordinate is independent of initial momentum, corresponding to a focusing of all the initial momenta in a certain region to a certain final coordinate. The term “caustics” originated in optics, where this focusing of light can lead to burning. The notion of caustics, although originating in coordinate space, can be generalized to the vanishing of other blocks of the stability matrix.27 For example, ∂pf/∂pi and ∂qf/∂qi. We will need both of these objects in the analysis below.
The canonical framework of eqn (25) allows an immediate implementation of eqn (26), where q = ϕ and p = η. Formally, we also need to include R, to obtain the following stability matrix:
 | (27) |
Numerically, the calculation of the stability elements is done by considering small separations Δϕi, Δηi and propagating a central swarm and the requisite satellite swarms: each trajectory evolves with its own Hamiltonian and the stability elements are obtained at each moment using finite-difference derivatives. This procedure is based on the suggestion of Heller (ζ = (ϕ, η)):28
 | (28) |
E. Adaptations of the traditional stability analysis
There are three challenges that come up here: (1) contrary to previous works in which ensembles comprise many initial positions and/or momenta, we are interested in the case where all trajectories start from the same initial conditions at ti = 0; (2) contrary to the traditional stability analysis, where all trajectories evolve under the same Hamiltonian, here the Hamiltonian is characterized by slightly different parameters per each trajectory, making the analysis more challenging; (3) the straightforward implementation of the eqn (25) precludes examining ϕ at the poles.In order to overcome challenge (1) for the stability analysis, we take the initial time ti = T/4, where the swarm features maximal spreading, and we consider tf ∈ [T/4, T]. To distinguish ti from the moment when the trajectories actually start, we will denote the latter as t0 = 0.
In order to overcome challenge (2), we bin the stability matrix elements over very small windows:
 | (29) |
We extend the ordinary framework of caustics, and conjecture that the average stability matrix elements shall indicate refocusing. If the refocusing happens close to the desired endpoint, this signifies that the ensemble has undergone a successful population inversion. In particular, if the histogram of the stability matrix element 〈∂ζf/∂ζi〉 collapses into a relatively narrow band, this indicates refocusing in a certain direction in phase space. To measure the size of the band of certain stability element (even before averaging and the absolute value), we define the range parameter hζ
 | (30) |
In order to overcome challenge (3), in calculating ∂ϕf/∂ϕi we launch the central and satellite swarms of trajectories not from η0 = 1 but from η0 = 1 − ε where ε is a parameter much smaller than the shift Δϕ0.
F. The Lagrangian and canonical momentum
Using the canonical coordinates and the Legendre transform, , we may define a Lagrangian. Using eqn (23) and (25) we get:
, we may define a Lagrangian. Using eqn (23) and (25) we get: | (31) |
We may also express η in terms of ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) . Inverting the ϕ-equation in eqn (25) we obtain:
. Inverting the ϕ-equation in eqn (25) we obtain:
 | (32) |
 | (33) |
Identifying the ![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) -terms as those associated with the “kinetic energy” K and the ϕ-terms as those associated with the “potential energy” V:
-terms as those associated with the “kinetic energy” K and the ϕ-terms as those associated with the “potential energy” V:
K(![[small phi (variant), Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a4.gif) ) = (Ωz − ) = (Ωz − ![[small phi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a3.gif) )2, V(ϕ) = −(Ωx )2, V(ϕ) = −(Ωx![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + Ωy ϕ + Ωy![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ)2, ϕ)2, | (34) |
 | (35) |
At this point, we differentiate the Lagrangian in order to obtain the Euler–Lagrange equation. We assume that  , which is valid if Ω is piecewise-constant, as in CPs, except in a finite number of moments; if Ω is strictly time-independent, this approximation is accurate and we obtain:
, which is valid if Ω is piecewise-constant, as in CPs, except in a finite number of moments; if Ω is strictly time-independent, this approximation is accurate and we obtain:
 | (36) |
Eqn (36) is easily checked to be equivalent to Hamilton's equations (eqn (25)) under the assumption on the time-independence of the Lagrangian.
III. Numerical results and analysis
A. The ensemble of RF field inhomogeneity
Fig. 1 (left) shows the evolution of an ensemble under Levitt's pulse sequence with the RF field inhomogeneity. The “initial manifold” at ti = T/4 has a spread in ηi with a single ϕi, while the “final manifold” at tf = T has a spread in ϕf with minimal spread in ηf, corresponding to refocusing in the η-direction.In the rotating frame, we launch at t0 = 0 a central swarm of trajectories, from η0 = 1, and a satellite swarm from η0 − Δη0 = 1–2 × 10−6. From t0 = 0 to ti = T/4, the pulse keeps all trajectories in a line. For each moment tf ∈ [T/4, T], the set ∂ηf/∂ηi is calculated using finite-difference and binned according to eqn (29). Fig. 3 shows representative slices of this time-evolution: from tf = T/4 to tf = T/2, the histogram becomes wider, then it becomes narrower, until tf ≈ 7T/8, where the range of the histogram becomes wider again, and eventually, at tf = T the histogram collapses to a relatively narrow column, compared to the maximal range at tf = T/2. Note that between tf ≈ 3T/4 and tf = 1 the refocusing is somewhat better, but does not take place in the vicinity of η = −1 (note that the histogram plots do not indicate where the refocusing takes place).
For completeness, we repeat the same procedure in the ϕ-direction. At t0 = 0 we launch a central swarm of trajectories, from ϕ0 = 0 and a satellite swarm from ϕ0 + Δϕ0 = 10−6 (and, to overcome the abovmentioned challenge, η0 = 1–10−6). For each moment tf ∈ [T/4, T], the set ∂ϕf/∂ϕi is calculated using finite-difference and binned according to eqn (29). Fig. 4 shows representative slices of this time-evolution: from tf = T/4 to tf = T, the histogram becomes wider, and towards the end its range diverges in width to represent a defocusing in the ϕ-direction.
B. The ensemble of resonance offset
Fig. 1 (right) shows the evolution of an ensemble under Levitt's pulse sequence with resonance offset. The “initial manifold” at ti = T/4 has a spread in both ϕi and ηi, while the “final manifold” at tf = T comprises minimal spread in both ϕi and ηi, corresponding to refocusing in both the ϕ- and η-directions.In the rotating frame, we propagate a central swarm and a satellite swarm with parameters as presented in the previous subsection. In contrast to the ensemble of field inhomogeneity, here, the trajectories are not aligned between t0 = 0 and ti = T/4, in any of the directions. For each moment tf ∈ [T/4, T], the sets ∂ϕf/∂ϕi and ∂ηf/∂ηi are calculated using finite-difference and binned according to eqn (29). Fig. 5 and 6 show representative slices of this time-evolution. At tf = T/4, both histograms are wide, and they become even wider at later times until tf = T/2 (for η) and tf ≈ 5T/8 (for ϕ). At this point, the ranges of both histograms become narrower and eventually, at tf = T, the histograms collapse to narrow bands.
In the η-direction, the tightest refocusing occurs at tf = T, although there are other moments where the refocusing is almost as good; in the ϕ-direction, there is good refocusing at tf = T although there are regions around tf = 0.4T and tf = 0.8T where the refocusing is better.
C. Variation of the ensemble's width
With the classical understanding in hand, we can address the question: why does the imperfection of field inhomogeneity conserve the width of the ensemble along the second and the third segment, while the imperfection of resonance offset expands or contracts the width along all segments?For simplicity, we use a Euclidean measure of the width of an ensemble:
 | (37) |
![[r with combining macron]](https://www.rsc.org/images/entities/b_char_0072_0304.gif) (t) is the mean of the ensemble; N is the total number of trajectories in the ensemble. For convenience, we will suppress the time-parameterization below.
(t) is the mean of the ensemble; N is the total number of trajectories in the ensemble. For convenience, we will suppress the time-parameterization below.
We differentiate σ2 with respect to time to obtain:
 | (38) |
We will now treat each of the four terms. The first term appears as quadratic form with a skew-symmetric operator:
 | (39) |
The second and third terms are cross terms:
 | (40) |
 | (41) |
 | (42) |
 | (43) |
 | (44) |
In the case of field inhomogeneity, all rotations take place about fixed axes. Numerical simulations indicate that along the first segment, σ(t) varies, whereas along the second and the third segment, it is approximately constant. We will explain that.
Along the first segment we have:
 | (45) |
 | (46) |
Note that we could factor out the Ω(k)1 since all the members of the ensemble rotate about the same axis. Along the second segment we have:
 | (47) |
 | (48) |
The approximation is justified as we consider a narrow band of Ω(i)1 around the nominal frequency, and:
z(0)1 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(0)1T/4 = cos Ω(0)1T/4 = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π/2 = 0. π/2 = 0. | (49) |
Now we will examine the third segment, where we have:
 | (50) |
 | (51) |
y(0)2 = y(0)1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(0)1T/2 = sin Ω(0)1T/2 = sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) π/2 = 1, z(0)2 = z(0)1 π/2 = 1, z(0)2 = z(0)1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ω(0)1T/2 = 0, Ω(0)1T/2 = 0, | (52) |
| sin((Ω(i)1 − Ω(k)1)t) ≈ sin(0) = 0. | (53) |
In the case of resonance offset, each trajectory rotates about a different axis which is inclined with respect to the xy plane. For example, in along the first segment, the rotation is specified by the matrix
 | (54) |
In contrast to the former case, we cannot factor out either of the frequency components, so that each sum over i, k is supposed to contain various combinations of trigonometric functions, rather than a single function as before. The prefactors of the summands will contain the initial conditions of each segment, which in general do not vanish, as opposed to the previous case. Altogether, dσ2/dt is not predicted to vanish at any segment.
Fig. 7 demonstrates the numerical results for the Levitt's sequence. The left subfigure corresponds to field inhomogeneity and the right subfigure corresponds to resonance offsets. Note that the width of the ensemble is preserved in second and the third segment of the former case, and not conserved in the latter case.
IV. Conclusion
In this work, we suggest another justification for the robustness of composite pulses, based on the classical mechanical concept of a stability matrix. The motion on the Bloch sphere is mapped to a canonical system of coordinates and the focusing of an ensemble corresponds to caustics, or the vanishing of an appropriate stability matrix element in the canonical coordinates.The caustics in CPs are unusual in the sense that each member is governed by a slightly different Hamiltonian, so that averaging is required for the stability analysis. The average stability matrix elements turned out to be particularly informative: when they collapse to a narrow band, the ensemble refocuses, and when they diverge, the ensemble exhibits a maximal spread. This is a clear, visual, and quantitative way to track robustness.
Our approach highlights the directionality of the refocusing of the ensemble on the Bloch sphere, revealing how different ensembles refocus along different directions. As a case study, we investigated the 90(x)180(y)90(x) CP introduced by Levitt, where the approach provides a new perspective into why this CP is effective: the focusing produced by Levitt's CP corresponds to a caustic, as manifested in the elements of the stability matrix.
The approach clarifies why the 90(x)180(y)90(x) CP changes the width of the ensemble in the case of field inhomogeneity, as opposed to simply a rotation of the axes in the case of resonance offset. In the case of field inhomogeneity, the pulse leads to refocusing in the η-direction, while in the ϕ-direction the ensemble diverges, meaning the refocusing is highly directional. In the case of resonance offsets, refocusing occurs in both directions. This directional aspect goes beyond what was discussed by Levitt.
Although we focused here on the 90(x)180(y)90(x) pulse sequence, our method can be applied to any pulse sequence. In fact, we successfully checked our method in two additional pulses: (1) Levitt's five-segment sequence, which is robust for resonance offsets;10 (2) Dridi's three-segment sequence, which is robust for both ensembles.14 We stress that our method does not rely on a specific form of the pulse or any assumption about the ensemble; all one needs is the pulse sequence and its imperfections. In this sense, we believe that our classical point of view can be useful for analyzing almost all types of CPs.
In summary, we believe that the transfer of ideas from classical mechanics to quantum control is intellectually satisfying, and that notions like stability analysis, manifolds and caustics, can provide new insights into this widely studied system. This ultimately may suggest new pulse sequences for NMR, optical spectroscopy, quantum information processing and quantum computing.
Conflicts of interest
There are no conflicts to declare.Data availability
The MATLAB codes, used to generate the data in this manuscript are publicly available at my GitHub repository: https://github.com/jonathanbrkm/Stability-around-the-globe.Acknowledgements
J. B. and D. J. T. thank Jacob Higer and Ilya Kuprov for helpful discussions. Financial support for this work was provided by the German-Israeli Foundation for Scientific Research and Development (GIF), and the historic generosity of the Harold Perlman family.References
- M. H. Levitt and R. Freeman, J. Magn. Reson., 1979, 33, 473–476 Search PubMed
.
- E. L. Hahn, Phys. Rev., 1950, 80, 580–594 CrossRef
.
- H. Y. Carr and E. M. Purcell, Phys. Rev., 1954, 94, 630–638 CrossRef CAS
.
- S. Meiboom and D. Gill, Rev. Sci. Instrum., 1958, 29, 688–691 CrossRef CAS
.
- S. Wimperis, J. Magn. Reson., 1994, 109, 221–231 CrossRef CAS
.
- H. Cummins and J. Jones, J. Magn. Reson., 2001, 148, 338–342 CrossRef CAS PubMed
.
- B. T. Torosov and N. V. Vitanov, Phys. Rev. A, 2019, 100, 023410 CrossRef CAS
.
- M. Bando, T. Ichikawa, Y. Kondo, N. Nemoto, M. Nakahara and Y. Shikano, Sci. Rep., 2020, 10, 2126 CrossRef CAS PubMed
.
- M. H. Levitt, J. Magn. Reson., 1982, 48, 234–264 CAS
.
- M. H. Levitt, J. Magn. Reson., 1982, 50, 95–110 CAS
.
- C. Counsell, M. Levitt and R. Ernst, J. Magn. Reson., 1985, 63, 133–141 CAS
.
- B. Blümlich and H. Spiess, J. Magn. Reson., 1985, 61, 356–362 Search PubMed
.
- S. J. Glaser, U. Boscain, T. Calarco, C. P. Koch, W. Köckenberger, R. Kosloff, I. Kuprov, B. Luy, S. Schirmer, T. Schulte-Herbrüggen, D. Sugny and F. K. Wilhelm, Eur. Phys. J. D, 2015, 69, 279 CrossRef
.
- G. Dridi, M. Mejatty, S. J. Glaser and D. Sugny, Phys. Rev. A, 2020, 101, 012321 CrossRef CAS
.
-
D. J. Tannor, Introduction to Quantum Mechanics: A Time-Dependent Perspective, University Science Books, 2007, pp. 227–272 Search PubMed
.
- F. Bloch, Phys. Rev., 1946, 70, 460–474 CrossRef CAS
.
-
A. Abragam, The Principles of Nuclear Magnetism, Oxford University Press, 1961 Search PubMed
.
-
C. P. Slichter, Principles of Magnetic Resonance, Springer Berlin Heidelberg, Berlin, Heidelberg, 1990, vol. 1 Search PubMed
.
- R. P. Feynman, F. L. Vernon and R. W. Hellwarth, J. Appl. Phys., 1957, 28, 49–52 CrossRef CAS
.
- M. H. Levitt, Prog. Nucl. Magn. Reson. Spectrosc., 1986, 18, 61–122 CrossRef CAS
.
-
I. Kuprov, Spin, Springer International Publishing, Cham, 2023 Search PubMed
.
-
J. E. Marsden and T. S. Ratiu, Introduction to Mechanics and Symmetry, Springer New York, New York, NY, 1999, vol. 17 Search PubMed
.
- J. Eidson and R. F. Fox, Phys. Rev. A:At., Mol., Opt. Phys., 1986, 34, 3288–3292 CrossRef PubMed
.
- Y. Pomeau, B. Dorizzi and B. Grammaticos, Phys. Rev. Lett., 1986, 56, 681–684 CrossRef PubMed
.
-
E. J. Heller, The Semiclassical Way to Dynamics and Spectroscopy, Princeton University Press, 2018 Search PubMed
.
-
M. C. Gutzwiller, Chaos in Classical and Quantum Mechanics, Springer, 1990 Search PubMed
.
- R. G. Littlejohn, J. Stat. Phys., 1992, 68, 7–50 CrossRef
.
- E. J. Heller, J. Chem. Phys., 1976, 65, 4979–4989 CrossRef CAS
.
- Note that this notation shall be read as one piece.
| This journal is © the Owner Societies 2026 |






