Atomistic simulation study of diamond doping based on machine learning potential
Yiheng
Yan
a,
Yaochen
Yu
a,
Junwei
Hu
a,
Xuecheng
Sun
a,
Qinlan
Luo
bcd,
Zengyong
Chu
 *b,
Jiayu
Dai
*b,
Jiayu
Dai
 *bcd and
Haiyang
Niu
*bcd and
Haiyang
Niu
 *a
*a
aState Key Laboratory of Solidification Processing, International Center for Materials Discovery, School of Materials Science and Engineering, Northwestern Polytechnical University, Xi’an, 710072, China. E-mail: haiyang.niu@nwpu.edu.cn
bCollege of Science, National University of Defense Technology, Changsha, 410073, China. E-mail: Chuzy@nudt.edu.cn
cHunan Key Laboratory of Extreme Matter and Applications, National University of Defense Technology, Changsha, 410073, China
dHunan Research Center of the Basic Discipline for Physical States, National University of Defense Technology, Changsha, 410073, China. E-mail: jydai@nudt.edu.cn
First published on 24th November 2025
Abstract
Diamond is regarded as a highly promising semiconductor material due to its outstanding physical properties. However, achieving efficient p-type and n-type doping remains a significant challenge. In this work, we systematically investigate the B–O and B–S co-doping behaviors in diamond using molecular dynamics and Monte Carlo hybrid simulations based on machine learning potentials. The results indicate that the dopant ratio determines the formation type of impurity complexes, thereby governing the overall electronic properties of the material. Our simulations reveal that a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio of 4
O ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 leads to the exclusive formation of B4O complexes, which exhibit the lowest formation energy (− 1.92 eV) and a low ionization energy (0.11 eV), making them a promising co-doping strategy for high-quality p-type diamond. For B–S co-doping, a B
1 leads to the exclusive formation of B4O complexes, which exhibit the lowest formation energy (− 1.92 eV) and a low ionization energy (0.11 eV), making them a promising co-doping strategy for high-quality p-type diamond. For B–S co-doping, a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of 1
S ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 results in BS complexes with significantly reduced formation energy compared to S single-doping and a low ionization energy (0.56 eV), meeting the requirements for n-type diamond, while a B
1 results in BS complexes with significantly reduced formation energy compared to S single-doping and a low ionization energy (0.56 eV), meeting the requirements for n-type diamond, while a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of 4
S ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is more suitable for p-type diamond. These findings emphasize the critical role of precise dopant ratio control in obtaining high-performance p/n-type diamond semiconductors and provide atomic-scale mechanistic insights for the controllable synthesis of co-doping diamond.
1 is more suitable for p-type diamond. These findings emphasize the critical role of precise dopant ratio control in obtaining high-performance p/n-type diamond semiconductors and provide atomic-scale mechanistic insights for the controllable synthesis of co-doping diamond.
1 Introduction
Diamond exhibits exceptional electrical, mechanical, and thermal properties, including a wide band gap, high carrier mobility, high breakdown field strength, extreme hardness, and superior thermal conductivity.1–7 These characteristics have marked it as one of the most promising semiconductors for radiation-resistant, high-temperature, high-power electronic devices. A primary objective in diamond semiconductor research involves the realization of diamond p–n junction fabrication. However, the preparation of high-quality p-type and n-type diamond remains a significant challenge.8–12As an intrinsic insulator, doping is essential to achieve suitable p-type or n-type semiconductors in diamond. The electron and hole mobilities in pristine diamond are 4000 cm2 V−1 s−1 and 3800 cm2 V−1 s−1,13 respectively. However, it is challenging to achieve these values in practice, primarily due to diamond's exceptionally dense and stiff lattice structure, which creates a significant barrier to efficient doping. Furthermore, as the doping concentration increases, the crystalline quality of diamond degrades.14 Since crystalline quality critically influences the electrical properties of diamond, this degradation leads to a rapid reduction in carrier mobility.15,16 Therefore, achieving a balance between the electrical properties and crystalline quality of diamond requires dopant elements with shallow impurity energy levels and high solid solubility within the diamond lattice.
Boron has been recognized as the predominant dopant for p-type diamond, with typical doping concentrations ranging from 16 to 18 at cm−3.17,18 However, higher doping concentrations invariably introduce significant lattice distortion, thereby degrading the hole mobility.19 Liu et al.20 introduced a limited quantity of sulfur (S) during the growth of boron-doping diamond. It was found that appropriate incorporation of S not only enhanced the boron doping efficiency to 1.2 × 102 at cm−3, but also resulted in a room-temperature hole mobility of 853 cm2 V−1 s−1. Compared to the preparation of p-type diamond, the design and fabrication of n-type diamond semiconductors pose even greater challenges. The primary dopant species for n-type diamond comprise lithium (Li), nitrogen (N), phosphorus (P), and sulfur (S).21–24 Nevertheless, these single-element doping approaches have not yielded satisfactory performance, primarily due to excessively low solid solubility of impurity atoms and the high ionization energies associated with their incorporation. In recent years, increasing research efforts have been dedicated to co-doping with two elements. Using first-principles calculations, Zhou et al.25 demonstrated that in B–N co-doping systems, the solubility of N atoms increases progressively with boron incorporation, achieving a donor energy level of 0.23 eV. Similarly, Fan et al.26 theoretically investigated the B–P system, achieving n-type diamond with a shallow donor level of 109 meV and significantly reduced formation energy compared to single P-doping. These results suggest that co-doping offers a promising solution to the challenges in diamond semiconductor research, as it can lower the formation energy of impurity atoms, improve the crystalline quality of diamond, and enable dopant–dopant interactions that effectively reduce ionization energies.
While previous computational studies have primarily relied on first-principles calculations, this approach limits the ability to sample a wide range of doping configurations. Due to the vast configuration space involved in co-doping, manually enumerating all possible doping configurations is a challenging task. Furthermore, the kinetic evolution of local atomic structures around impurity atoms over extended timescales, as well as their relative stability, remains largely unexplored. This gap in understanding hinders the development of effective co-doping strategies and the accurate prediction of the electronic structures in doped diamond.
Molecular dynamics simulations using machine learning potentials have emerged as powerful tools to address the aforementioned challenges.27–30 This approach combines the accuracy of ab initio methods with the ability to simulate large systems over extended timescales.31–33 In this study, we employ the B–O and B–S co-doping strategies as prototype systems to comprehensively explore the co-doping configuration space, investigate their kinetic evolution, and elucidate their impact on electrical properties. To achieve this, we first developed deep neutral network potentials that can accurately model these B–O and B–S co-doping systems. The local atomic structures around the impurity atoms have been explored through atomistic simulations. Using these potentials, we performed atomistic simulations to characterize the local atomic structures surrounding the impurity atoms. Based on these results and the newly predicted atomic doping complexes, we propose new promising doping strategies in diamond.
2 Method
2.1 DFT setup
All AIMD and DFT calculations were performed using the Vienna Ab initio computational simulation package (VASP)34,35 with projection-enhanced plane waves (PAW),36 using the general gradient approximation (GGA) of Perdew–Burke–Ernzerhof (PBE) functional,37,38 was employed as the exchange–correlation functional. The Grimme's DFT-D3 correction39 was applied to include long-range van der Waals interactions. The energy convergence criterion was set to 10−5 eV. After convergence tests, the K-point mesh was defined as 3 × 5 × 5 and the plane-wave cutoff energy was set to 600 eV (see Fig. S1).2.2 DeepMD setup
Accurate interatomic interaction potential is crucial for molecular dynamics studies of diamond doping. However, the co-doping scheme generates a vast number of possible configurations with highly complex interatomic interactions, so we need to describe the interatomic interactions precisely. In this paper, we mainly choose the DeePMD method developed by Zhang et al.40,41 to construct DNNs, which follows the strategy pioneered by Behler and Parrinello,42,43 and can dramatically improve the computational efficiency of molecular dynamics while maintaining first-principle accuracy. We employed the DeePMD-kit package (v2.2.3)44 to construct two neural networks: an embedding network and a fitting network. The embedding network maps the local environment of each atom to a high-dimensional feature vector, which serves as a descriptor. The fitting network then takes the descriptors output by the embedding network as its direct input and maps these descriptors to the corresponding atomic energy contributions. The architectures of the embedding network and the fitting network were configured as (25, 50, 100) and (240, 240, 240), respectively. The cutoff radius was set to 7.0 Å and the descriptors were smoothly decayed from 6.5 Å to 7.0 Å. These networks were trained using the ADAM optimizer with an exponential decay of the learning rate from 1.0 × 10−3 to 1.0 × 10−8. The loss function was minimized during the training process: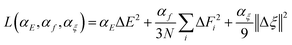 | (1) |
In the loss function of the DeePMD method, αE, αf and αξ represent the pre-factor weights for the energy, force, and virial tensor, respectively. Here, Δ denotes the deviation between the predicted values from the DeePMD model and the training data: N is the total number of atoms in the system, E represents the energy per atom, Fi is the force acting on the i-th atom, and the virial tensor ξ is defined by the formula 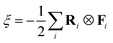 . The weighting coefficients for the energy, force, and virial terms in the loss function are dynamically adjusted within the ranges of 0.02–1, 1000–1, and 0.02–1, respectively. The deep neural network potential employs a training step size of 2.0 × 106 per iteration for parameter optimization.
. The weighting coefficients for the energy, force, and virial terms in the loss function are dynamically adjusted within the ranges of 0.02–1, 1000–1, and 0.02–1, respectively. The deep neural network potential employs a training step size of 2.0 × 106 per iteration for parameter optimization.
2.3 Molecular dynamics simulations
Molecular dynamics simulations were performed using the LAMMPS program,45 employing an isothermal–isobaric (NPT) ensemble with temperature regulated by the Nosé–Hoover thermostat46,47 and pressure controlled via the Parrinello–Rahman barostat,48 utilizing a 2 fs timestep; the simulation system comprised 8000 atoms with periodic boundary conditions applied in all three dimensions.2.4 Hybrid molecular dynamics/Monte Carlo simulation
To efficiently explore stable impurity configurations in co-doping diamond, we employed a hybrid molecular dynamics (MD) and Monte Carlo (MC) simulation strategy implemented in LAMMPS,45 cyclically alternating between two steps: an MD relaxation phase conducting conventional MD simulations to achieve local equilibrium and relax lattice stresses at specified temperature/pressure conditions, followed by an MC atom-swapping using LAMMPS's fix atom/swap command to randomly select impurity atoms and adjacent carbon atoms for attempted atomic-type exchanges, with each swap evaluated via the Metropolis acceptance criterion based on system potential energy changes (ΔE) and simulation temperature (T); this iterative MD/MC cycle enables efficient sampling of diverse impurity spatial configurations while preserving kinetic relaxation, thereby identifying energetically optimal impurity distributions.49–522.5 Formation energy calculation
The magnitude of formation energy determines the solid solubility of impurity atoms in diamond. The formation energy of impurity X in charge state q is defined as:| Ef[qX] = Etot[X,q] − Etot[C,bulk] − ∑ixμx − q[EF + EV + ΔV], | (2) |
2.6 Ionization energy calculations
To directly compare the electrical properties of these configurations and quantify carrier contributions, we calculated ionization energies using the thermodynamic transition level ε(q1/q2) defined as: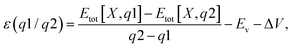 | (3) |
3 Results and discussion
3.1 Training of DNN potential
The reliability of DNN potential crucially depends on the choice of the configurations in the training set. To comprehensively explore the configuration space of the co-doping systems, we implement an active iterative scheme to progressively refine the DNN potentials.53 First, we constructed a 96-atom (2 × 2 × 3) diamond supercell and randomly substituted carbon atoms to generate single-doping configurations with varying concentrations of B, O, and S atoms, as well as B–O and B–S co-doping configurations with different concentrations and stoichiometric ratios, yielding an initial structural ensemble. These structures then underwent ab initio molecular dynamics (AIMD) simulations in the temperature range of 300–4000 K, with approximately 3000 configurations were extracted from trajectories to form the initial training datasets for both the B–O and B–S co-doping systems, from-which the first-generation DNN potentials.We then implement an iterative scheme to progressively improve the accuracy of DNN potentials for the two co-doping systems. This scheme follows a feedback loop wherein continuous iterations optimize and expand the dataset through the following steps: (1) exploration of the configuration space via molecular dynamics simulations employing the DNN potential. Extended-timescale MD simulations are conducted at multiple temperatures; (2) representative configurations are selected from the MD trajectory for DFT single-point energy calculations. Structures exhibiting significant discrepancies between the calculated energies or atomic forces and DNN predictions (ΔE > 5 meV per atom or ΔF > 0.3 eV Å−1) were incorporated into the training set. (3) New potentials are retrained using the updated dataset. Ultimately, the training sets for the B–O and B–S systems consist of 32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 and 22
927 and 22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 714 configurations, respectively. Principal component analysis (PCA) of the training datasets, along with representative local atomic structures, is shown in Fig. 1. Both datasets includes not only the liquid and perfect diamond structures, but also the single-doping, co-doping configurations with various relative sites and compositions, ensuring that the DNN potentials have strong descriptive capabilities.
714 configurations, respectively. Principal component analysis (PCA) of the training datasets, along with representative local atomic structures, is shown in Fig. 1. Both datasets includes not only the liquid and perfect diamond structures, but also the single-doping, co-doping configurations with various relative sites and compositions, ensuring that the DNN potentials have strong descriptive capabilities.
To validate the accuracy of the final DNN potentials, we conducted comparative analyses of energy and atomic forces between the DNN potentials and DFT reference results from test datasets. As shown in Fig. 1(a) and (b), the test set for the B–O co-doping system contains 2053 configurations, while the B–S system comprises 1387 configurations. The root mean square errors (RMSEs) for the B–O co-doping MLP are 4.36 meV per atom for energy and 0.24 eV Å−1 for atomic forces. Corresponding RMSEs for the B–S co-doping MLP are 4.64 meV per atom (energy) and 0.26 eV Å−1 (forces). These results demonstrate the accuracy of the DNN potentials in describing the B–O and B–S co-doping systems.
3.2 Structural analysis of B, O, and S single-doping systems
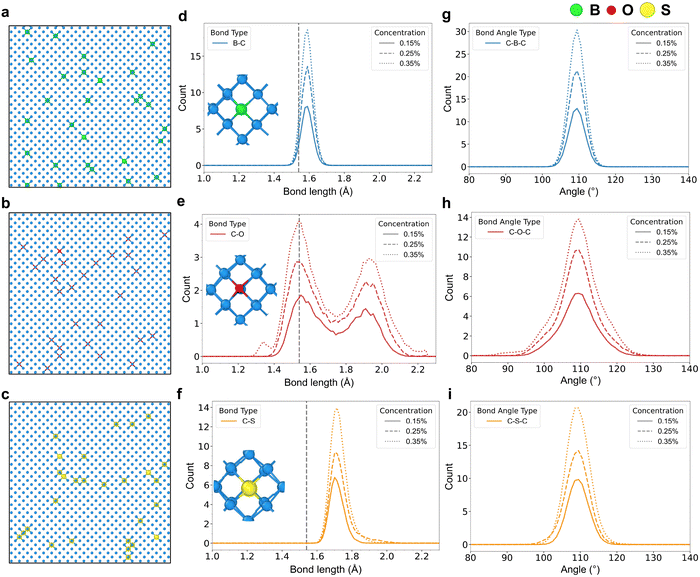
To investigate the effects of doped atoms on the diamond lattice, we first constructed initial structures containing 8000 atoms with three different concentrations of substitutionally single-doping B, O, and S at 0.15%, 0.25%, 0.35%, respectively. These structures were then subjected to 1 ns MD simulations at 300 K under periodic boundary conditions using the NPT ensemble. The resulting configurations are shown in Fig. 2(a)–(c). We conducted a statistical analysis of the average bond-length and bond-angle variations between the impurity atoms and their adjacent carbon atoms during the simulation.As shown in Fig. 2(d)–(f), significant differences are observed in the average bond length variations between impurity atoms and adjacent carbon atoms among the three single-doping systems. The C–O bond exhibits the most pronounced elongation due to the smaller atomic radius of oxygen (∼60 pm) compared to carbon (∼77 pm). This size mismatch induces asymmetric lattice distortion upon substitutional doping, leading to the asymmetrical stretching of the C–O bonds. In contrast, boron (∼85 pm) and sulfur (∼105 pm) incorporation cause more uniform lattice expansion due to their larger radii, resulting in symmetric bond elongation. Sulfur induces the greatest elongation (∼12.06%; weighted average C–S: 1.726 Å) relative to the perfect diamond bond, owing to its largest radius. Boron shows the smallest change (∼3.12%; weighted average B–C: 1.589 Å), consistent with previous computational results.54,55Fig. 2(g)–(i) present the average bond angle variations between impurity atoms and adjacent carbon atoms in the three mono-doping structures. Oxygen doping induces the largest bond-angle fluctuations because surrounding carbon atoms impose the weakest constraints on it, enhancing the thermal vibration amplitude of oxygen atoms at lattice sites. While boron and sulfur atoms are more strongly constrained by neighboring carbon atoms, leading to weaker vibrations at lattice sites and smaller bond-angle variations. In addition, we calculated the radial distribution functions (RDFs) centered on the carbon atoms within the first coordination shell of the dopants in the three monodoped structures at a concentration of 0.35% (see Fig. S2). Our results show that the C–C RDF of the B single-doping structure is closer to that of pristine diamond. Overall, single-doping B exhibits the smallest bond-length and bond-angle changes, resulting in the least lattice distortion. This explains why p-type diamond with boron doping is relatively easy to fabricate.
3.3 B–O co-doping system
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratios of 1
O ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2
3, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 4
1, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. In this way, we can better understand the impact of boron-rich doping on the system. As an example, Fig. 3(a) displays the initial configuration with a 1
1. In this way, we can better understand the impact of boron-rich doping on the system. As an example, Fig. 3(a) displays the initial configuration with a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 B/O ratio, illustrating a random doping distribution.
1 B/O ratio, illustrating a random doping distribution.
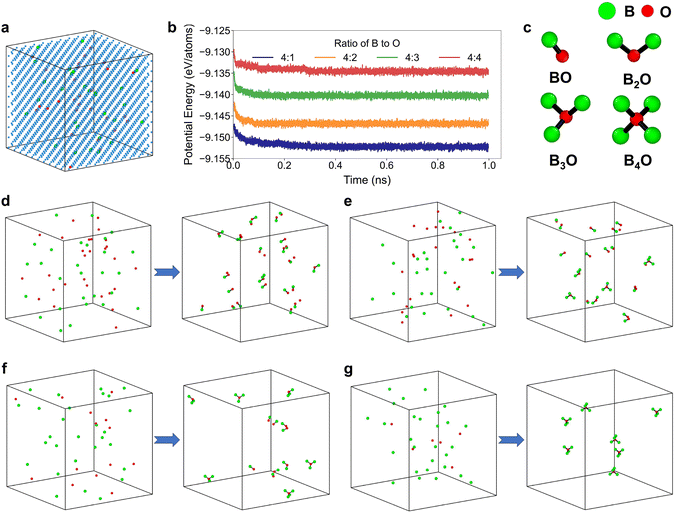
To explore stable configurations, hybrid molecular dynamics (MD) and Monte Carlo (MC) simulations were performed on these four systems at 300 K (Fig. 3(d)–(g)). Initially, B and O atoms were distributed randomly, with almost no direct chemical bonding between them. As the simulation progressed, the energies of all four system decrease progressively and eventually stabilized around a constant value. We extracted configurations after 1 ns simulation, and compared them to their initial states, as shown in Fig. 3(d)–(g). The results indicate that boron atoms tend to form bonds with oxygen atoms with interatomic distance less than 2.0 Å to reduce the system energy, resulting in the formation of four distinct B–O complexes: BO, B2O, B3O, and B4O, as illustrated in Fig. 3(c). Notably, different B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratios yielded distinct B–O complexes. As presented in Table 1, when the B
O ratios yielded distinct B–O complexes. As presented in Table 1, when the B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio is 1
O ratio is 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 78% of oxygen atoms form BO complexes; at a B
1, 78% of oxygen atoms form BO complexes; at a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio of 4
O ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 66.67% of oxygen atoms form BO complexes; for a 2
3, 66.67% of oxygen atoms form BO complexes; for a 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 B
1 B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio, oxygen atoms primarily form BO and B3O configurations; whereas at a 4
O ratio, oxygen atoms primarily form BO and B3O configurations; whereas at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 B
1 B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio, all oxygen atoms form B4O complexes.
O ratio, all oxygen atoms form B4O complexes.
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O O |
O (%) | BO (%) | B2O (%) | B3O (%) | B4O (%) |
|---|---|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
14.29 | 75.00 | 7.14 | 3.57 | 0 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
9.52 | 66.67 | 4.76 | 14.29 | 4.76 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0 | 50 | 7.14 | 35.72 | 7.14 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0 | 0 | 0 | 0 | 100.00 |
In addition, we further computed the C–C RDFs of the systems after hybrid MD/MC simulations at four different doping ratios. By taking the carbon atoms within the first coordination shell of the impurity atoms as centers and statistically evaluating their average RDFs with all surrounding carbon atoms over a 1 ns period (see Fig. S3), the results show that the C–C distribution profiles of the complex structures are closer to those of ideal diamond than those of the monodoped systems. This demonstrates that the formation of such complexes effectively suppresses doping-induced lattice distortion, thereby enhancing the structural integrity of diamond.
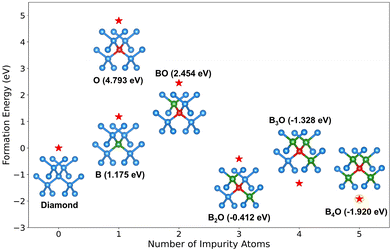 | ||
| Fig. 4 Impurity formation energy of the B-doping, O-doping, and B–O co-doping systems with different BO complexes. | ||
Subsequently, we calculated the band structures of the aforementioned single-doping configurations and four co-doping complexes, as shown in Fig. 5. These results reveal that O single-doping, BO, B2O, and B3O configurations introduce deep-level bands within the bandgap, which is unfavorable for semiconductor device fabrication. Moreover, since oxygen atoms introduce deep-level bands in the bandgap, the B–O co-doping scheme is highly unlikely for n-type diamond synthesis. Conversely, the B4O configuration exhibits not only the lowest formation energy but also excellent p-type semiconductor characteristics (Fig. 5(f)), enabling high-concentration doping while minimizing crystal quality degradation. Therefore, the B–O co-doping scheme appears more suitable for p-type diamond fabrication, with substantially reduced formation energy compared to B mono-doping. Since our MC/MD simulations demonstrate that different B/O ratios yield distinct complex configurations, and only at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O = 4
O = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 does the system exclusively form B4O structures. This highlights that precise stoichiometric control would benefit the synthesis high-performance p-type semiconductors.
1 does the system exclusively form B4O structures. This highlights that precise stoichiometric control would benefit the synthesis high-performance p-type semiconductors.
3.4 B–S co-doping system
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratios of 1
S ratios of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 4
1, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 2
3, 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 4
1, and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, respectively. Hybrid MC/MD simulations reveal that, similar to the B–O system, boron atoms preferentially combine with sulfur to form four different B–S complexes (Fig. 6(c)). The distribution of these complexes depends strongly on the B
1, respectively. Hybrid MC/MD simulations reveal that, similar to the B–O system, boron atoms preferentially combine with sulfur to form four different B–S complexes (Fig. 6(c)). The distribution of these complexes depends strongly on the B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio, as quantified relative to sulfur atoms in Table 2. At a B
S ratio, as quantified relative to sulfur atoms in Table 2. At a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of 1
S ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 75% of sulfur forms BS complexes; at 4
1, 75% of sulfur forms BS complexes; at 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, B2S and B3S dominate; and at 2
3, B2S and B3S dominate; and at 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 85.71% of sulfur forms B2S complexes. While at a 4
1, 85.71% of sulfur forms B2S complexes. While at a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, sulfur exclusively forms both B4S and B3S complexes. We also computed the C–C RDFs for the B–S co-doping system after hybrid MD/MC simulations following the same procedure (see Fig. S4). The results demonstrate that the C–C distribution profile is closer to that of pristine diamond compared to the S single-doping system.
1 ratio, sulfur exclusively forms both B4S and B3S complexes. We also computed the C–C RDFs for the B–S co-doping system after hybrid MD/MC simulations following the same procedure (see Fig. S4). The results demonstrate that the C–C distribution profile is closer to that of pristine diamond compared to the S single-doping system.
B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S S |
S (%) | BS (%) | B2S (%) | B3S (%) | B4S (%) |
|---|---|---|---|---|---|
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
10.71 | 75.00 | 14.29 | 0 | 0 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3 3 |
9.52 | 38.10 | 47.62 | 4.76 | 0 |
2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0 | 14.29 | 85.71 | 0 | 0 |
4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 1 |
0 | 0 | 0 | 42.86 | 57.14 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S stoichiometric ratio plays a crucial role in determining the resulting complex configuration, synthesis of n-type diamond via B–S co-doping requires strict B
S stoichiometric ratio plays a crucial role in determining the resulting complex configuration, synthesis of n-type diamond via B–S co-doping requires strict B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 1
S = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 control, while p-type diamond necessitates B
1 control, while p-type diamond necessitates B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 4
S = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1.
1.
 | ||
| Fig. 7 Impurity formation energy of the B-doping, S-doping, and B–S co-doping systems with different BS complexes. | ||
 | ||
| Fig. 8 Calculated band structures for different systems: (a) S single-doping; B–S co-doping with the complexes of (b) BS, (c) B2S, (d) B3S, and (e) B4S, respectively. | ||
Additionally, we quantified B–C and C–S bond lengths under both ratios. at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 1
S = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the average B–C and C–S bond lengths are 1.562 Å and 1.729 Å, respectively, and at B
1, the average B–C and C–S bond lengths are 1.562 Å and 1.729 Å, respectively, and at B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 4
S = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, they are 1.573 Å and 1.647 Å, respectively. For B
1, they are 1.573 Å and 1.647 Å, respectively. For B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 1
S = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 configurations, C–S bond lengths approximate those in S single-doping systems, while B–C bonds are significantly shorter than in B single-doping diamond. In B
1 configurations, C–S bond lengths approximate those in S single-doping systems, while B–C bonds are significantly shorter than in B single-doping diamond. In B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 4
S = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 configurations, both B–C and C–S bonds are markedly shorter than in their corresponding single-doping systems. This indicates B–S co-doping effectively facilitates impurity incorporation while mitigating lattice distortion. Consequently, the B
1 configurations, both B–C and C–S bonds are markedly shorter than in their corresponding single-doping systems. This indicates B–S co-doping effectively facilitates impurity incorporation while mitigating lattice distortion. Consequently, the B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S stoichiometry plays a crucial role in governing the electrical properties and crystalline quality of diamond.
S stoichiometry plays a crucial role in governing the electrical properties and crystalline quality of diamond.
3.5 Ionization energy calculations
In the B–O co-doping scheme, the B4O configuration is the onley one that avoids introducing deep-level bands within the bandgap while also exhibiting the lowest formation energy, making it the optimal choice for p-type diamond formation. In the B–S co-doping system, the BS configuration demonstrates n-type diamond characteristics, whereas B3S and B4S exhibit p-type behavior, with their formation energies significantly lower than those of S single-doping. To evaluate the electrical properties of these structures, we calculated ionization energies for key configurations as listed in Table 3.The calculated B single-doping ionization energy of 0.31 eV is in close agreement with the value reported in references.57,58 The B4O configuration exhibits an ionization energy of 0.11 eV, representing a 0.20 eV reduction compared to B single-doping. For n-type systems, S single-doping and BS complexes have ionization energies of 0.36 eV and 0.56 eV, respectively. Meanwhile, the p-type B3S and B4S configurations exhibit ionication energies of 0.70 eV and 0.36 eV, respectively, confirming shallow acceptor characteristics. Overall, ionization energy calculations provide further evidence that the B–O co-doping scheme with a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio of 4
O ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is optimal for p-type diamond fabrication. In contrast, within the B–S co-doping system, a B
1 is optimal for p-type diamond fabrication. In contrast, within the B–S co-doping system, a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S ratio of 1
S ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is ideal for synthesizing n-type diamond, while a ratio of 4
1 is ideal for synthesizing n-type diamond, while a ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 favors p-type diamond formation.
1 favors p-type diamond formation.
4 Conclusion
In summary, we developed two distinct DNN potentials that capable of accurate modeling the B–O and B–S co-doping systems. Molecular dynamics simulations using these potentials systematically quantify variations in average bond lengths and angles in B, O, and S single-doping configurations. Hybrid Monte Carlo/molecular dynamics (MC/MD) simulations explored a vast number of configurations under varying stoichiometries for both co-doping systems. First-principles calculations demonstrate that for B–O co-doping at a B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratio of 4
O ratio of 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, the B4O configuration exhibits a 0.11 eV ionization energy and the lowest formation energy (−1.92 eV), confirming its optimal shallow p-type behavior. In the B–S co-doping system, the BS complex (with an ionization energy of approximately 0.56 eV) shows shallow n-type characteristics, while B3S (approximately 0.70 eV) and B4S (approximately 0.36 eV) exhibit shallow p-type properties, all with substantially reduced formation energies compared to S-monodoping. Thus, dopant ratio control governs electrical properties: B
1, the B4O configuration exhibits a 0.11 eV ionization energy and the lowest formation energy (−1.92 eV), confirming its optimal shallow p-type behavior. In the B–S co-doping system, the BS complex (with an ionization energy of approximately 0.56 eV) shows shallow n-type characteristics, while B3S (approximately 0.70 eV) and B4S (approximately 0.36 eV) exhibit shallow p-type properties, all with substantially reduced formation energies compared to S-monodoping. Thus, dopant ratio control governs electrical properties: B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O = 4
O = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 optimizes p-type diamond via B–O co-doping, while B
1 optimizes p-type diamond via B–O co-doping, while B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 1
S = 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 enables n-type, and B
1 enables n-type, and B![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) S = 4
S = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 facilitates p-type diamond in B–S co-doping. This work provides fundamental theoretical support for the synthesis of high-quality p/n-type diamond semiconductors.
1 facilitates p-type diamond in B–S co-doping. This work provides fundamental theoretical support for the synthesis of high-quality p/n-type diamond semiconductors.
Author contributions
Yiheng Yan: writing – original draft, review & editing, conceptualization, investigation, formal analysis, data curation. Yaochen Yu: writing – review & editing, investigation, formal analysis. Junwei Hu: investigation, formal analysis. Xuechen Sun: investigation, formal analysis. Qinlan Luo: writing – review & editing, formal analysis. Zengyong Chu: writing – review & editing, conceptualization, formal analysis, methodology. Jiayu Dai: writing – review & editing, conceptualization, investigation, formal analysis,. Haiyang Niu: writing – review & editing, conceptualization, methodology, formal analysis, funding acquisition, supervision.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Data availability
The data supporting the findings of this study are available within the article and its supplementary information (SI). Supplementary information is available. The Supplementary Information includes DFT convergence test results and radial distribution function (RDF) analyses of different systems. See DOI: https://doi.org/10.1039/d5cp03568f.Additional data can also be obtained from the corresponding author upon reasonable request.
Acknowledgements
H. N. thanks the support from the National Science Fund for Excellent Young Scientist Fund Program (Overseas) of China, and the Research Fund of the State Key Laboratory of Solidification Processing of China (grant no. 2024-ZD-01), and the Fundamental Research Funds for the Central Universities. Q. L. was supported by the National Natural Science Foundation of China (grant no. 22408393), the fund of the State Key Laboratory of Solidification Processing of China (grant no. SKLSP202410). J. D. was supported by the National Natural Science Foundation of China (grant no. 12534013) and the Science and Technology Innovation Program of Hunan Province (grant no. 2025ZYJ001, 2021RC4026).Notes and references
- C. J. Wort and R. S. Balmer, Mater. Today, 2008, 11, 22–28 CrossRef CAS
.
- L. Pan, S. Han, D. Kania, M. Plano and M. Landstrass, Diamond Relat. Mater., 1993, 2, 820–824 CrossRef CAS
.
- M. Kim, J.-H. Seo, U. Singisetti and Z. Ma, J. Mater. Chem. C, 2017, 5, 8338–8354 RSC
.
- H. Bovenkerk, F. Bundy, H. Hall, H. Strong and R. Wentorf, Nature, 1959, 184, 1094–1098 CrossRef CAS
.
- S. Koizumi, K. Watanabe, M. Hasegawa and H. Kanda, Science, 2001, 292, 1899–1901 CrossRef CAS PubMed
.
- J. Isberg, J. Hammersberg, E. Johansson, T. Wikstrom, D. J. Twitchen, A. J. Whitehead, S. E. Coe and G. A. Scarsbrook, Science, 2002, 297, 1670–1672 CrossRef CAS PubMed
.
- E. Ekimov, V. Sidorov, E. Bauer, N. Mel'Nik, N. Curro, J. Thompson and S. Stishov, Nature, 2004, 428, 542–545 CrossRef CAS PubMed
.
- P.-N. Volpe, J. Pernot, P. Muret and F. Omnès, Appl. Phys. Lett., 2009, 94, 092102 CrossRef
.
- V. Mortet, J. Pernot, F. Jomard, A. Soltani, Z. Remes, J. Barjon, J. D'Haen and K. Haenen, Diamond Relat. Mater., 2015, 53, 29–34 CrossRef CAS
.
- R. Rouzbahani, S. S. Nicley, D. E. Vanpoucke, F. Lloret, P. Pobedinskas, D. Araujo and K. Haenen, Carbon, 2021, 172, 463–473 CrossRef CAS
.
- H. Kato, D. Takeuchi, N. Tokuda, H. Umezawa, S. Yamasaki and H. Okushi, Phys. Status Solidi A, 2008, 205, 2195–2199 CrossRef CAS
.
- J. P. Goss, R. J. Eyre and P. R. Briddon, Phys. Status Solidi B, 2008, 245, 1679–1700 CrossRef CAS
.
- F. Zhao, Y. He, B. Huang, T. Zhang and H. Zhu, Materials, 2024, 17, 3437 CrossRef CAS PubMed
.
- D. Das and M. R. Rao, Diamond Relat. Mater., 2022, 128, 109212 CrossRef CAS
.
- N. Tsubouchi, M. Ogura, H. Kato, S. Ri, H. Watanabe, Y. Horino and H. Okushi, Diamond Relat. Mater., 2006, 15, 157–159 CrossRef CAS
.
- M. Hasegawa, T. Teraji and S. Koizumi, Appl. Phys. Lett., 2001, 79, 3068–3070 CrossRef CAS
.
- S. Yamanaka, D. Takeuchi, H. Watanabe, H. Okushi and K. Kajimura, Diamond Relat. Mater., 2000, 9, 956–959 CrossRef CAS
.
- M. Sobaszek, S. Kwon, T. Klimczuk, P. P. Michałowski, J. Ryl, B. Rutkowski, D. Wang, X. Li, M. Bockrath and R. Bogdanowicz,
et al.
, Carbon, 2024, 228, 119337 CrossRef CAS
.
- C. Yap, K. Ansari, S. Xiao, S. Yee, R. Chukka and D. Misra, Diamond Relat. Mater., 2018, 88, 118–122 CrossRef CAS
.
- D. Liu, L. Hao, Z. Chen, W. Zhao, Y. Shen, Y. Bian, K. Tang, J. Ye, S. Zhu and R. Zhang,
et al.
, Appl. Phys. Lett., 2020, 117, 022101 CrossRef CAS
.
- S. Kajihara, A. Antonelli, J. Bernholc and R. Car, Phys. Rev. Lett., 1991, 66, 2010 CrossRef PubMed
.
- Z. M. Shah and A. Mainwood, Diamond Relat. Mater., 2008, 17, 1307–1310 CrossRef CAS
.
- E. Gheeraert, N. Casanova, A. Tajani, A. Deneuville, E. Bustarret, J. Garrido, C. Nebel and M. Stutzmann, Diamond Relat. Mater., 2002, 11, 289–295 CrossRef CAS
.
- M. Nishitani-Gamo, E. Yasu, C. Xiao, Y. Kikuchi, K. Ushizawa, I. Sakaguchi, T. Suzuki and T. Ando, Diamond Relat. Mater., 2000, 9, 941–947 CrossRef CAS
.
- D. Zhou, L. Tang, J. Zhang, R. Yue and Y. Wang, International Conference on Computational Science, 2022, pp. 530-540.
- K. Fan, K. Tang, M. Zhang, K. Wu, G. Zhao, Y. Huang, S. Zhu, J. Ye and S. Gu, Comput. Mater. Sci., 2023, 222, 112113 CrossRef CAS
.
- T. Chen, F. Yuan, J. Liu, H. Geng, L. Zhang, H. Wang and M. Chen, Phys. Rev. Mater., 2023, 7, 053603 CrossRef CAS
.
- A. Y. Pak, V. Sotskov, A. A. Gumovskaya, Y. Z. Vassilyeva, Z. S. Bolatova, Y. A. Kvashnina, G. Y. Mamontov, A. V. Shapeev and A. G. Kvashnin, npj Comput. Mater., 2023, 9, 7 CrossRef CAS
.
- Q. Tong, P. Gao, H. Liu, Y. Xie, J. Lv, Y. Wang and J. Zhao, J. Phys. Chem. Lett., 2020, 11, 8710–8720 CrossRef CAS PubMed
.
- K. Gordiz, S. Vaez Allaei and F. Kowsary, Appl. Phys. Lett., 2011, 99, 251901 CrossRef
.
- H. Niu, L. Bonati, P. M. Piaggi and M. Parrinello, Nat. Commun., 2020, 11, 2654 CrossRef CAS PubMed
.
- L. Zhang, M. Yang, S. Zhang and H. Niu, J. Mater. Sci. Technol., 2024, 185, 23–31 CrossRef CAS
.
- S. Zhang, J. Hu, X. Sun, J. Deng and H. Niu, Phys. Rev. Lett., 2025, 134, 204101 CrossRef CAS PubMed
.
-
J. Hafner and G. Kresse, Properties of Complex Inorganic Solids, Springer, 1997, pp. 69–82 Search PubMed
.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed
.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed
.
- J. Sancho-García, J. Brédas and J. Cornil, Chem. Phys. Lett., 2003, 377, 63–68 CrossRef
.
- Y. Wang and J. P. Perdew, Phys. Rev. B: Condens. Matter Mater. Phys., 1991, 44, 13298 CrossRef PubMed
.
- J. Moellmann and S. Grimme, J. Phys. Chem. C, 2014, 118, 7615–7621 CrossRef CAS
.
- L. Zhang, J. Han, H. Wang, R. Car and W. E, Phys. Rev. Lett., 2018, 120, 143001 CrossRef CAS PubMed
.
- H. Wang, L. Zhang and J. Han,
et al.
, Comput. Phys. Commun., 2018, 228, 178–184 CrossRef CAS
.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed
.
- J. Behler, J. Chem. Phys., 2016, 145, 170901 CrossRef PubMed
.
- J. Zeng, D. Zhang, D. Lu, P. Mo, Z. Li, Y. Chen, M. Rynik, L. Huang, Z. Li and S. Shi,
et al.
, J. Chem. Phys., 2023, 159, 054801 CrossRef CAS PubMed
.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- S. Nosé, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695 CrossRef PubMed
.
- M. Parrinello and A. Rahman, J. Appl. Phys., 1981, 52, 7182–7190 CrossRef CAS
.
- S. Duane, A. D. Kennedy, B. J. Pendleton and D. Roweth, Phys. Lett. B, 1987, 195, 216–222 CrossRef CAS
.
-
R. M. Neal, Bayesian learning for neural networks, Springer Science & Business Media, 2012, vol. 118 Search PubMed
.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, D. J. Srolovitz, P. K. Liaw and Y.-W. Zhang, Nat. Commun., 2021, 12, 4953 CrossRef CAS PubMed
.
- R. Su, J. Yu, P. Guan and W. Wang, Sci. China Mater., 2024, 67, 3298–3308 CrossRef CAS
.
- J. Deng, H. Niu, J. Hu, M. Chen and L. Stixrude, Phys. Rev. B, 2023, 107, 064103 CrossRef CAS
.
- N. Gao, L. Gao and H. Yu, Diamond Relat. Mater., 2023, 132, 109651 CrossRef CAS
.
- S. Breuer and P. Briddon, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 10332 CrossRef CAS PubMed
.
- L. Tang, R. Yue and Y. Wang, Carbon, 2018, 130, 458–465 CrossRef CAS
.
- J. E. Butler, A. Vikharev, A. Gorbachev, M. Lobaev, A. Muchnikov, D. Radischev, V. Isaev, V. Chernov, S. Bogdanov and M. Drozdov,
et al.
, Phys. Status Solidi RRL, 2017, 11, 1600329 CrossRef
.
- Y. Wu, J. Tong, L. Ruan, F. Luo, G. Liu, R. Zhang, X. Han, Y. Zhang, F. Tian and X. Zhang, Comput. Mater. Sci., 2021, 196, 110515 CrossRef CAS
.
- D. Saada, J. Adler and R. Kalish, Appl. Phys. Lett., 2000, 77, 878–879 CrossRef CAS
.
| This journal is © the Owner Societies 2026 |