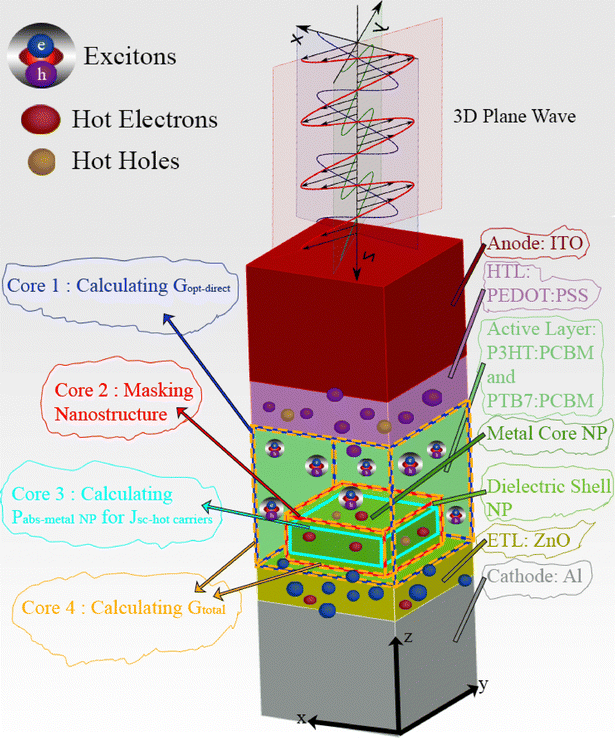
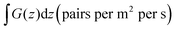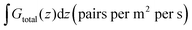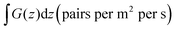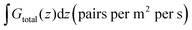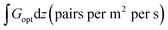Plasmonic vortex-coupled forward emission (PVCFE): a novel light coupling mechanism in aluminium nanostructures for high-efficiency, stable, and cost-effective organic photovoltaics
Mahdi
Aghlmandi Sadigh Bagheri
 *
*
East Azerbaijan Province, Tabriz, Feyziyeh, Iran. E-mail: Mahdi.aghlmandi.sb@gmail.com
First published on 25th November 2025
Abstract
The dual challenge of enhancing power conversion efficiency (PCE) while ensuring long-term stability is paramount for the commercial viability of organic photovoltaics (OSCs). This work confronts these challenges by identifying a novel, material-dependent light coupling mechanism—termed plasmonic vortex-coupled forward emission (PVCFE)—and embedding it within a holistically designed, stable, and cost-effective device architecture. Through a rigorous multiphysics simulation workflow that accurately isolates useful optical generation from parasitic losses, we discover that non-noble metal nanostructures like aluminium (Al) support complex, hybridized plasmon modes. Phase-resolved electromagnetic field analysis reveals that PVCFE involves the synchronous coupling of a vortical near-field with a directional energy channeling component, which actively “pumps” optical energy deep within the organic active layer. Harnessing this discovery, we computationally designed and optimized an inverted OSC based on a high-performance PTB7:PC71BM active layer with a robust AZO ETL and a chemically inert graphite anode. The final, optimized Al-core/Al2O3-shell enhanced device is predicted to exhibit a remarkable 57% relative increase in PCE, reaching a simulated 9.34% compared to the 5.95% intrinsic baseline. This breakthrough is driven by a massive 55.8% increase in short-circuit current to 18.09 mA cm−2, stemming from the PVCFE mechanism and estimated hot carrier contributions, while impressively maintaining the fill factor. Our findings suggest that Al is a potentially superior plasmonic material for high-performance OSCs and introduce PVCFE as a new design paradigm for engineering light–matter interactions in nanophotonic devices.
1 Introduction
The global imperative for a sustainable energy future has intensified research into next-generation photovoltaic technologies capable of delivering clean power at a low cost.1 Organic solar cells (OSCs) represent a highly promising frontier, offering unique advantages such as solution-processability, mechanical flexibility, and lightweight design.2 These features make them ideal for emerging applications from wearable electronics to building-integrated photovoltaics, although significant challenges in device stability and efficiency still need to be overcome to achieve widespread commercialization.3 Despite significant progress, the power conversion efficiencies (PCEs) of OSCs are often constrained by incomplete light absorption within their characteristically thin active layers, a limitation imposed by short exciton diffusion lengths and modest charge carrier mobilities of organic semiconductors.4,5To overcome the absorption bottleneck, advanced light management is essential. The strategic use of polymers and nanostructures continues to be a vibrant area of research for pushing the performance limits of OSCs.6 Plasmonics, which harnesses the resonant interaction of light with collective electron oscillations in metallic nanostructures, has emerged as a particularly powerful approach for enhancing light–matter interactions.7,8 However, the field has been overwhelmingly dominated by noble metals like gold (Au) and silver (Ag), whose prohibitive cost and scarcity fundamentally challenge the low-cost premise of organic photovoltaics, creating a critical need to identify and understand earth-abundant plasmonic alternatives.7,9
Aluminium has emerged as a particularly compelling candidate, with a growing body of experimental work demonstrating its multifaceted benefits. Seminal studies showed that incorporating Al nanoparticles (NPs) into the active layer could yield superior PCE enhancements compared to noble metals, with early work attributing this to improved spectral overlap and increased charge separation at the donor–acceptor interface.10,11 Subsequent research has reinforced these findings, showing significant PCE boosts in PTB7:PC71BM systems by leveraging the localized surface plasmon resonance of Al NPs embedded in the anode buffer layer.12 Critically, beyond just efficiency, the integration of Al NPs has been proven to confer a dramatic advantage in device longevity, extending the operational lifetime of OSCs by up to fivefold by enhancing the structural stability of the active blend and mitigating photo-oxidation.13,14 Concurrently, theoretical explorations by Bagheri into Fe-core/ZnO-shell nanostructures predicted, via optical simulations, that iron could also achieve competitive absorption enhancement over gold, reinforcing the hypothesis that non-noble metals operate via distinct and potentially more advantageous light-coupling mechanisms.15 Yet, despite compelling evidence for Al's benefits to efficiency and stability, a deep, unifying physical understanding of why it so effectively couples and redistributes light within the solar cell cavity has remained elusive.
A significant hurdle in accurately assessing and comparing these plasmonic enhancers has also been methodological. Many computational studies rely on metrics that conflate useful photon absorption within the active layer with parasitic absorption within the metallic nanostructures themselves, leading to potentially inflated performance predictions. Furthermore, beyond direct optical enhancement, plasmon decay is a quantum process that generates energetic “hot” carriers within the metal. This offers a parallel pathway to boost photocurrent, and the fundamental science and application of hot carrier dynamics remains a topic of intense current investigation in fields from photocatalysis to photodetectors.16–19
This study confronts these challenges through a comprehensive multiphysics investigation that bridges the gap between prior experimental observations and fundamental plasmonic theory. We introduce and validate a rigorous “four core” simulation workflow that employs spatial masking to accurately calculate direct optical generation (Gopt_direct) and a phenomenological model to estimate hot carrier contributions (Ghot_carrier). Applying this methodology, we uncover a novel, material-dependent light coupling mechanism, which we term “plasmonic vortex-coupled forward emission” (PVCFE). Phase-resolved electromagnetic field analysis reveals that this mechanism, prominent in Al, involves the synchronous coupling of a vortical near-field with a directional energy channeling component, which “pumps” optical energy deep into the active layer. This is fundamentally different from the asynchronous, near-surface enhancement of noble metals. Harnessing this discovery, our simulations establish aluminium as optically superior to silver and gold in the studied OSC architectures. Finally, we leverage these insights to design and optimize a high-performance, cost-effective inverted OSC—ITO/AZO/PTB7:PC71BM (with Al–Al2O3 NPs)/PEDOT:PSS/graphite—that fully exploits the PVCFE. The final simulated device is predicted to achieve a power conversion efficiency of 9.34%, a remarkable 57% relative enhancement over its intrinsic baseline, driven by a massive increase in short-circuit current from the synergistic action of PVCFE and hot carrier contributions. This work provides a new physical framework for understanding non-noble metal plasmonics and presents a clear design pathway toward ultra-high efficiency, low-cost organic solar cells.
2 Theoretical framework
The performance of the nanostructure-enhanced organic solar cells is analysed through a multiphysics framework that combines classical electromagnetic theory with semiconductor device physics. This section outlines the essential theoretical models for light absorption, carrier generation (including direct optical and plasmon-induced hot carrier pathways), and charge transport.2.1 Optical modelling of nanostructured media
The interaction of light with the device is modelled by solving Maxwell's equations using the finite-difference time-domain (FDTD) method. The material-specific response at optical wavelengths (λ) is governed by the complex relative permittivity, εr(r,λ) = (n(r,λ) + ik(r,λ))2, which dictates the local dispersive and absorptive properties.20,21The local time-averaged power absorption density, Pabs(r,λ), is derived from the Poynting theorem and is given by:22
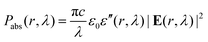 | (1) |
The direct optical carrier generation rate, Gopt_direct(r), within the primary semiconductor active layer is calculated assuming each absorbed photon with energy greater than the material's bandgap (Eg,active) generates one electron–hole pair:23
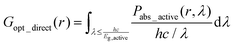 | (2) |
Here, Pabs_active(r,λ) represents the power absorption density occurring exclusively within the semiconductor volume, normalized to the AM1.5G solar spectrum, and h is Planck's constant.
2.2 Plasmon-induced hot carrier generation
In addition to enhancing Gopt_direct, the decay of localized surface plasmons in the metallic nanostructures generates energetic “hot” carriers.16,24 This non-radiative decay creates a non-equilibrium distribution of hot electrons and holes within the metal. Before thermalization, these hot carriers may traverse an ultrathin dielectric shell and inject into the semiconductor, providing a parallel pathway for photocurrent generation.25,26The total current density contribution from this mechanism, Jsc_hot_carrier, is phenomenologically estimated as:27,28
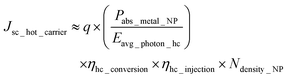 | (3) |
2.3 Electrical modelling of device performance
The solar cell's electrical characteristics are modelled by solving the coupled semiconductor drift-diffusion equations under steady-state conditions.32,33 This framework includes the Poisson equation and the electron/hole continuity equations:34| ∇·(ε(r)∇ψ(r)) = −q[p(r) − n(r) + ND+(r) − NA−(r) + ρtrap(r)] | (4) |
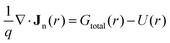 | (5a) |
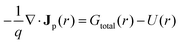 | (5b) |
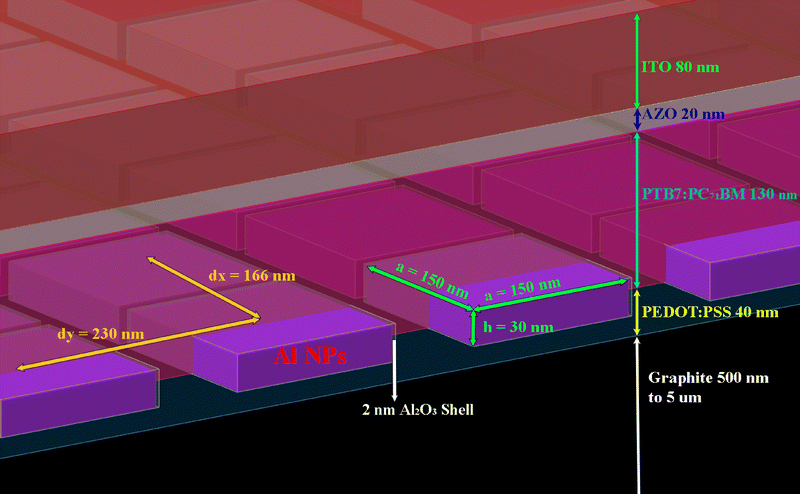
Here, ψ(r) is the electrostatic potential, p(r) and n(r) are the free carrier concentrations, ε(r) is the static permittivity, and U(r) is the net carrier recombination rate. The total generation rate, Gtotal = Gopt_direct + Ghot_carrier(r), serves as the source term. The electron (Jn) and hole (Jp) current densities are described by the drift-diffusion model, accounting for carrier motion due to both electric fields and concentration gradients.32
The net recombination rate, U(r), incorporates contributions from trap-assisted Shockley–Read–Hall (SRH) and bimolecular (Langevin or radiative) recombination processes, which are the dominant loss mechanisms in the organic semiconductors studied.35 Auger recombination is considered a secondary effect and is not included in this model. By solving this system of equations with appropriate boundary conditions at the contacts, the device's current density–voltage (J–V) characteristic is obtained, from which all key performance metrics (Jsc, Voc, FF, PCE, and EQE) are determined.
3 Computational methods
This section details the numerical simulation methodologies used to implement the theoretical models from Section 2, beginning with the optical FDTD framework and the “four core” data processing workflow used to determine the final carrier generation profiles.3.1 Optical simulation workflow: FDTD and the “four core” model
To identify the optimal geometric configuration for maximizing device performance, a particle swarm optimization (PSO) algorithm was employed. The algorithm iteratively adjusts a population of candidate solutions (“particles”) within a multi-dimensional parameter space, with each particle's movement influenced by its own best-known position and the best-known position of the entire swarm.36–38 The objective function for the optimization was the maximization of the Jsc. This automated search was further refined by manual fine-tuning based on the physical insights and trends identified during the optimization process.
Core 1 raw optical absorption calculation: a 3D frequency-domain monitor is used to record the electric fields and material indices throughout the geometric domain of the active layer. From this, the raw, spectrally-resolved power absorption density, Pabs(r,λ), is calculated based on eqn (1). This is then converted to an AM1.5G-normalized raw optical generation rate, Gopt_raw, which at this stage includes contributions from all materials within the monitor (semiconductor, metal, shell).
Core 2 spatial masking for Gopt_direct: the Gopt_raw(r) data is processed by applying a 3D spatial mask based on the precise geometry of the nanostructures. Generation rate values within the volumes of the non-semiconducting metallic cores and dielectric shells are rigorously set to zero. The result is the direct optical generation profile, Gopt_direct_semiconductoreqn (2), which accurately represents carrier generation occurring only within the primary semiconductor absorber.
Core 3 Ghot_carrier estimation & superposition: first, the total AM1.5G-normalized power absorbed solely within the metallic core of a single nanostructure, Pabs_metal_NP (Watts), is calculated using a separate, tightly-bound FDTD monitor. This value serves as the input to the phenomenological hot carrier model (eqn (3)), which estimates the device-level hot carrier current density, Jsc_hot_carrier, based on the efficiencies (η) specified in Section 3.3. This Jsc is then converted into a uniform volumetric generation rate, Ghot_carrier_local, and spatially distributed within the previously defined nanostructure mask volume.
Core 4 Gtotal superposition & final processing: the final total generation rate is computed by superimposing the two distinct generation profiles:
| Gtotal(r) = Gopt_direct_semiconductor(r) + Ghot_carrier_local(r) | (6) |
For simulations of asymmetric nanostructures under unpolarized light, this entire workflow (cores 1–4) is performed independently for two orthogonal polarizations (e.g., transverse electric, TE, and transverse magnetic, TM). The final generation rate is then taken as the average:
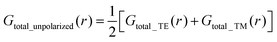 | (7) |
Finally, the 3D Gtotal(r) profile is laterally averaged to produce the 1D Gtotal(z) profile required for device simulation.
3.2 Materials optical database (n, k data)
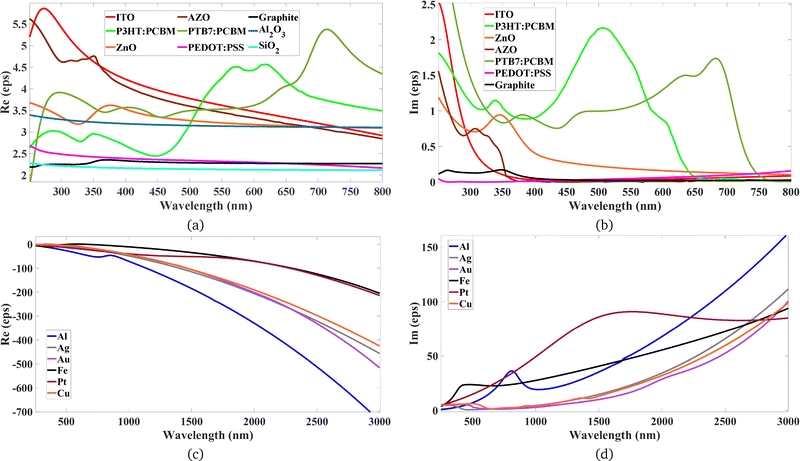
The complex refractive indices (n and k) as a function of wavelength (λ) for all materials used in the optical simulations were obtained from experimental literature or established databases. Fig. 2 graphically presents the n(λ) and k(λ) spectra for the key semiconductor and transparent conductive oxide (TCO) layers (a) and (b), and the metallic components (c) and (d). Specifically: the material stack includes an indium tin oxide (ITO) anode,39 a poly(3,4-ethylenedioxythiophene) polystyrene sulfonate (PEDOT:PSS) HTL,40 and two active semiconductor layers: poly(3-hexylthiophene-2,5-diyl):[6,6]-phenyl-C61 butyric acid methyl ester blend (P3HT:PCBM),41 and poly[[4,8-bis[(2-ethylhexyl)oxy]benzo[1,2-b:4,5-b′]dithiophene-2,6-diyl][3-fluoro-2-[(2-ethylhexyl)carbonyl]thieno[3,4-b]thiophenediyl]]:phenyl-C71-butyric acid methyl ester blend (PTB7:PC71BM).41 The ETLs studied were zinc oxide (ZnO)42 and aluminium-doped zinc oxide (AZO).43 The refractive indices for the metals iron (Fe),44 gold (Au),45 silver (Ag),44 aluminium (Al),46 copper (Cu),45 and platinum (Pt)47 were sourced from the cited literature. Data for aluminum oxide Al2O3 shell and glass (SiO2) were modelled using Palik21 from the Lumerical material database, while data for graphite was taken from ref. 48.3.3 Hot carrier generation estimation parameters
The injection efficiency (ηhc_injection) depends critically on the ultrathin dielectric shell, which serves to prevent charge recombination at the metal surface while allowing for hot carrier tunnelling. For this study, a 2 nm shell is used. We model a self-passivating Al2O3 shell for aluminium nanoparticles, which is known to form naturally. For all other metals, zinc oxide (ZnO) is chosen as a representative, stable, and wide-bandgap dielectric shell, consistent with previous theoretical explorations and its common use as an electron transport layer.The phenomenological model for estimating the hot carrier current density contribution (Jsc_hot_carrier, eqn (3)) requires several key parameters. The total AM1.5G-normalized power absorbed within a single metallic core (Pabs_metal_NP) is directly calculated from the FDTD simulations (Section 3.1.2), and the nanostructure areal density (Ndensity_NP) is defined by the simulated array periodicity. The critical efficiency parameters ηhc_conversion (internal plasmon-to-energetic-carrier conversion) and ηhc_injection (injection through the dielectric shell) are estimated based on a careful review of foundational theoretical and experimental literature. It is emphasized that these efficiencies are highly sensitive to nanoscale geometry, interface chemistry, and material quality; therefore, the values used represent reasoned estimates for an optimized system, intended to explore the relative potential impact of the hot carrier pathway for different materials. An effective average photon energy of Eavg_photon_hc ≈ 1.7–2.0 eV is assumed, representing the energetic portion of the solar spectrum that drives plasmon excitation.24,25,27 The specific efficiencies for each metal, detailed in Table 1, are justified as follows:
| Metal | η hc_conversion | η hc_injection | E avg_photon_hc (eV) |
|---|---|---|---|
| Fe | 0.30 | 0.20 | 2.0 |
| Au | 0.20 | 0.10 | 2.0 |
| Al | 0.30 | 0.20 | 1.7 |
| Cu | 0.15 | 0.10 | 2.0 |
| Ag | 0.40 | 0.10 | 2.0 |
| Pt | 0.20 | 0.15 | 2.0 |
The efficiency of generating energetic hot carriers (ηhc_conversion) is fundamentally dictated by the metal's electronic density of states (EDOS) near the Fermi level.29 For Ag, strong intraband transitions in the visible spectrum make it the most efficient generator of energetic hot electrons, justifying a high ηhc_conversion of 0.40.29,30 In contrast, Au and Cu are dominated by d-band interband transitions for much of the visible spectrum, a process that primarily yields energetic hot holes but low-energy hot electrons. Consequently, their ηhc_conversion for generating useful hot electrons is estimated to be very low, whereas for hot holes, a more moderate value of 0.20–0.15 is used.29,30 Aluminium, with its more free-electron-like EDOS, can support energetic carrier generation via both intraband and interband (>1.5 eV) transitions, warranting a high estimated efficiency of 0.30.29 Transition metals with complex d-bands, Fe and Pt, are predicted to generate both energetic electrons and holes under broadband solar illumination;29 their efficiencies are estimated at 0.30 and 0.20 respectively, reflecting this potential balanced against increased scattering pathways common in d-band metals.16,17,49
The injection efficiency (ηhc_injection) depends critically on the ∼2 nm dielectric shell (Al2O3 for Al, ZnO for others). Based on theoretical models of tunnelling across such thin barriers and the quality of self-passivated interfaces,31 Al is assigned a high potential ηhc_injection of 0.20. Fe and Pt, given their potential for favorable interface energetics with ZnO, are assigned a strong ηhc_injection of 0.20 and 0.15, respectively (with platinum's value being slightly lower because its dominant injection pathway is hot holes, which are less efficiently extracted when injected into the n-type ETL, whereas iron and aluminium are highly efficient injectors of both electrons and holes29). For Au and Cu, a more conservative 0.10 is used, informed by experimental work showing low overall device efficiencies for Au/TiO2 systems.30 Silver's injection efficiency is estimated conservatively at 0.10, as experimental work suggests that injection can be a significant bottleneck despite the high energy of its hot electrons.30,31
To address the inherent uncertainty in these literature-derived efficiency parameters, a comprehensive parametric sensitivity analysis was performed. The results, presented in the SI (Fig. 6), demonstrate how the estimated hot carrier Jsc varies with the total conversion and injection efficiency. This analysis confirms that the relative performance ranking of the materials is robust and primarily dictated by their intrinsic optical absorption properties.
3.4 Electrical device simulation
The final electrical performance of the solar cell was simulated using the SCAPS-1D device simulator (v.3.3.07, University of Gent),50 which numerically solves the fundamental semiconductor device equations. The one-dimensional total generation profile, Gtotal(z), derived from our comprehensive “four core” workflow, was imported to model the creation of charge carriers. The simulation solves the coupled Poisson, continuity, and drift-diffusion equations (eqn (4) and (5)) to generate the device's current density–voltage (J–V) characteristics under steady-state AM1.5G illumination (1000 W m−2) at 300 K.This work focuses on a high-performance inverted architecture: ITO/AZO/PTB7:PC71BM (with Al/Al2O3 NPs)/PEDOT:PSS/graphite. Table 2 details the full set of material and electrical parameters used to model each layer in this stack. These parameters were carefully selected and optimized based on extensive review of established experimental literature to construct a model that is both physically realistic and representative of a high-quality device.51 Standard series (1 Ω cm2) and shunt (5000 Ω cm2) resistances were used.
| Parameter | Unit | ITO (cathode) | AZO (ETL) | PTB7:PC71BM (active) | PEDOT:PSS (HTL) | Graphite (anode) |
|---|---|---|---|---|---|---|
| Global parameters: thermal velocity for all e−/h+ = 1 × 107 cm s−1; interface defect capture cross-sections for all = 1 × 10−19 cm2. | ||||||
| Thickness | nm | 80 | 20 | 130 | 40 | (Contact) |
| Bandgap (Eg) | eV | 3.739,51 | 3.252 | 1.6553 | 1.7754 | N/A |
| Electron affinity (χ) | eV | 4.539 | 4.352 | 3.7053 | 3.354 | N/A |
| Rel. permittivity (εr_static) | 9.039 | 9.052 | 3.853 | 3.554 | N/A | |
| Effective DoS (Nc) | cm−3 | 2.2 × 1018 | 2.2 × 1018 | 2.5 × 1019 | 2.5 × 1019 | N/A |
| Effective DoS (Nv) | cm−3 | 1.8 × 1019 | 1.8 × 1019 | 2.5 × 1019 | 2.5 × 1019 | N/A |
| Mobility (μn/μp) | cm2 V−1 s−1 | 30/10 | 1/0.1 | 2 × 10−3/4 × 10−4 | 1 × 10−4/5 × 10−3 | N/A |
| Doping (ND/NA) | cm−3 | 1 × 1020 (ND) | 1 × 1019 (ND) | 1.7 × 1016 (NA) | 1 × 1019 (NA) | N/A |
| Defect density (Nt) | cm−3 | 1 × 1014 | 1 × 1014 | 1 × 1014 | 1 × 1014 | N/A |
| Contact work function | eV | 4.539 | N/A | N/A | N/A | 4.855 |
| Interface defects (AZO/active) | cm−2 | — | — | 1 × 1012 | — | — |
| Interface defects (active/HTL) | cm−2 | — | — | — | 5 × 1012 | — |
| Interface defects (ITO/AZO) | cm−2 | 5 × 1011 | — | — | — | — |
The parameters in Table 2 were chosen to create a realistic model of a high-performance inverted organic solar cell. The inverted p–i–n architecture (ITO/ETL/active/HTL/anode) was selected for its proven high efficiency and operational stability with modern organic blends.56
Active layer (PTB7:PC71BM): we employ an experimentally verified optical bandgap of 1.65 eV.53 A crucial aspect of this model is treating the active layer not as purely intrinsic, but as a lightly p-doped semiconductor with a shallow acceptor density of NA = 1.7 × 1016 cm−3. This approach models the real-world characteristics of a polymer blend where unintentional doping and small internal gradients exist, allowing for a more accurate prediction of device physics. The charge carrier mobilities of μn = 2 × 10−3 cm2 V−1 s−1 and μp = 4 × 10−4 cm2 V−1 s−1 were chosen to be representative of well-optimized blend morphologies known to facilitate high performance.57
Charge transport layers: an aluminium-doped zinc oxide (AZO) layer serves as the electron transport layer (ETL). The parameters for AZO (Eg = 3.2 eV, χ = 4.3 eV) are chosen to reflect a conductive, n-type TCO that forms an efficient electron-selective contact with a favorable energy cascade from the active layer's LUMO (∼−3.7 eV).58 On the anode side, a heavily p-doped PEDOT:PSS is used as the hole transport layer (HTL). Critically, an experimentally validated electronic bandgap of 1.77 eV was used,54 which, combined with its electron affinity of 3.3 eV, creates a HOMO level of ∼−5.07 eV, providing an excellent energetic match for hole extraction from PTB7's HOMO.
Contacts and interfaces: a cost-effective graphite back contact is used as the anode. Its work function of 4.8 eV forms a near-ohmic contact with the PEDOT:PSS HTL, ensuring a minimal barrier for hole extraction.53 The ITO front contact (cathode) has a work function of 4.5 eV, well-aligned with the AZO ETL for electron collection.39,50,51 To create a realistic model that accounts for primary loss mechanisms, recombination at interfaces was included. Significant defect densities (Nit) were introduced at the critical AZO/active layer (1 × 1012 cm−2) and active layer/HTL (5 × 1012 cm−2) interfaces to account for potential chemical and morphological imperfections that are common in solution-processed devices.59
This comprehensive and physically grounded set of parameters establishes a robust baseline for investigating the impact of plasmonic enhancement on a realistically modelled, high-performance OSC.
4 Results and discussions
4.1 Foundational investigation: a refined analysis of plasmonic enhancement in P3HT:PCBM organic solar cells
Our investigation commences by applying our advanced multiphysics modelling workflow to a P3HT:PCBM based organic solar cell, an architecture that has been instrumental in foundational plasmonics research. This serves to validate our methodology against established systems and to uncover the nuanced physical mechanisms that govern the performance of cost-effective plasmonic materials like Al and Fe. The device architecture, nanostructure dimensions, and material properties are based on the optimized design previously reported by Bagheri,15 with updated, high-accuracy optical constants for all materials.| Analysis | Structure | J sc_opt_direct (mA cm−2) | Injected HC (carriers per s per NP) | J sc_hot_carrier (mA cm−2) | J total (mA cm−2) | ||
|---|---|---|---|---|---|---|---|
| C1:ON | Intrinsic | 6.328 × 1020 | 10.14 | — | — | 6.328 × 1020 | 10.14 |
| C2:OFF | ZnO | 5.675 × 1020 | 9.09 | — | — | 5.675 × 1020 | 9.09 |
| C3:OFF | Al–ZnO | 9.706 × 1020 | 15.55 | — | — | 9.706 × 1020 | 15.55 |
| C4:OFF | Fe–ZnO | 1.022 × 1021 | 16.38 | — | — | 1.022 × 1021 | 16.38 |
| Au–ZnO | 8.198 × 1020 | 13.14 | — | — | 8.198 × 1020 | 13.14 | |
| Ag–ZnO | 8.056 × 1020 | 12.91 | — | — | 8.056 × 1020 | 12.91 | |
| Cu–ZnO | 8.514 × 1020 | 13.64 | — | — | 8.514 × 1020 | 13.64 | |
| Pt–ZnO | 1.032 × 1021 | 16.54 | — | — | 1.032 × 1021 | 16.54 | |
| C1:ON | Intrinsic | 6.328 × 1020 | 10.14 | — | — | 6.328 × 1020 | 10.14 |
| C2:ON | ZnO | 5.292 × 1020 | 8.48 | — | — | 5.292 × 1020 | 8.48 |
| C3:OFF | Al–ZnO | 7.379 × 1020 | 11.82 | — | — | 7.379 × 1020 | 11.82 |
| C4:OFF | Fe–ZnO | 5.617 × 1020 | 9.00 | — | — | 5.617 × 1020 | 9.00 |
| Au–ZnO | 5.743 × 1020 | 9.20 | — | — | 5.743 × 1020 | 9.20 | |
| Ag–ZnO | 6.665 × 1020 | 10.68 | — | — | 6.665 × 1020 | 10.68 | |
| Cu–ZnO | 5.649 × 1020 | 9.05 | — | — | 5.649 × 1020 | 9.05 | |
| Pt–ZnO | 5.997 × 1020 | 9.61 | — | — | 5.997 × 1020 | 9.61 | |
| C1:ON | Intrinsic | 6.328 × 1020 | 10.14 | — | — | 6.328 × 1020 | 10.14 |
| C2:ON | ZnO | 5.292 × 1020 | 8.48 | — | — | 5.292 × 1020 | 8.48 |
| C3:ON | Al–ZnO | 7.379 × 1020 | 11.82 | 9.78 × 105 | 0.928 | 7.958 × 1020 | 12.75 |
| C4:ON | Fe–ZnO | 5.617 × 1020 | 9.00 | 1.75 × 106 | 1.661 | 6.654 × 1020 | 10.66 |
| Au–ZnO | 5.743 × 1020 | 9.20 | 2.08 × 105 | 0.197 | 5.867 × 1020 | 9.40 | |
| Ag–ZnO | 6.665 × 1020 | 10.68 | 7.79 × 104 | 0.074 | 6.712 × 1020 | 10.75 | |
| Cu–ZnO | 5.649 × 1020 | 9.05 | 1.82 × 105 | 0.173 | 5.757 × 1020 | 9.22 | |
| Pt–ZnO | 5.997 × 1020 | 9.61 | 8.55 × 105 | 0.811 | 6.504 × 1020 | 10.42 | |
The initial unmasked analysis (“C1” row set) calculates the apparent Jsc by converting all photon absorption within the active layer's geometric domain—including absorption within the metallic nanostructures—into carrier generation. This method, common in preliminary optical studies, yields significantly inflated current densities, particularly for highly absorbing metals like Pt (16.54 mA cm−2) and Fe (16.38 mA cm−2). While providing an upper limit of total light interaction, this approach fails to distinguish between useful generation in the P3HT:PCBM and parasitic thermal losses in the metal, thereby overestimating the device's true photovoltaic potential and underscoring the necessity for a more refined analytical approach.
Upon applying the “core 2” spatial mask to isolate carrier generation exclusively within the P3HT:PCBM active layer, a physically accurate picture of direct optical enhancement emerges (“C2” row set). The results reveal that aluminium (Al–ZnO) and silver (Ag–ZnO) are the most effective materials for enhancing direct optical generation in this specific P3HT:PCBM architecture, achieving Jsc_opt_direct values of 11.82 mA cm−2 and 10.68 mA cm−2, respectively. These represent significant improvements over both the bare ZnO nanostructure reference (8.48 mA cm−2) and the intrinsic cell. In contrast, Au, Cu, Fe, and Pt nanostructures, in this particular geometric configuration, provide a lower Jsc_opt_direct than the intrinsic cell, indicating that their direct optical coupling into the P3HT:PCBM is less efficient than that of Al and Ag.
The final stage of the analysis (“C3/C4:ON” row set) incorporates the “core 3” hot carrier estimation and the “core 4” superposition to evaluate the total potential photocurrent (Jtotal). Here, the versatility of the different materials becomes evident. Iron (Fe), despite having one of the lowest direct optical contributions (9.00 mA cm−2), exhibits the highest estimated hot carrier current (1.66 mA cm−2), boosting its Jtotal to 10.66 mA cm−2. This substantial hot carrier contribution elevates Fe to be highly competitive with Ag and nearly recovers the performance of the intrinsic cell. Aluminium also shows a strong hot carrier contribution (0.93 mA cm−2), cementing its position as the overall top-performing material with a Jtotal of 12.75 mA cm−2. Conversely, Ag, while optically efficient, is estimated to have a negligible hot carrier contribution (0.07 mA cm−2), and Au's hot carrier potential is also modest (0.20 mA cm−2) due to the less favorable energy distribution of its hot electrons generated from visible light, as discussed in the theory.
This tiered analysis reveals a critical insight: aluminium excels in this system due to its superior ability to enhance direct optical generation in the P3HT:PCBM. Iron, while less effective optically, possesses the largest potential for performance gains via hot carrier harvesting. The subsequent sections will now delve into the underlying physical mechanisms that explain these distinct material-dependent behaviours.
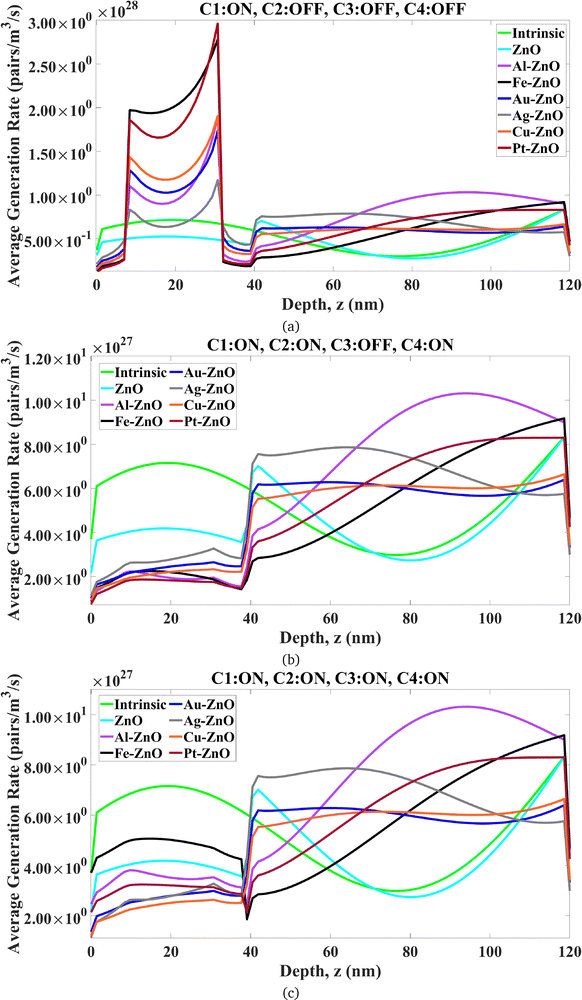
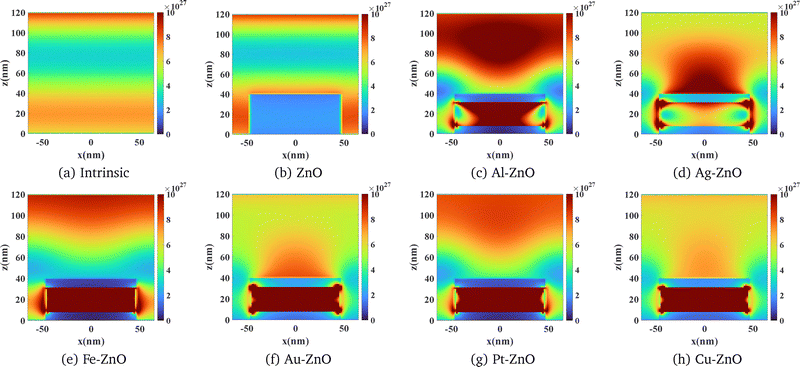
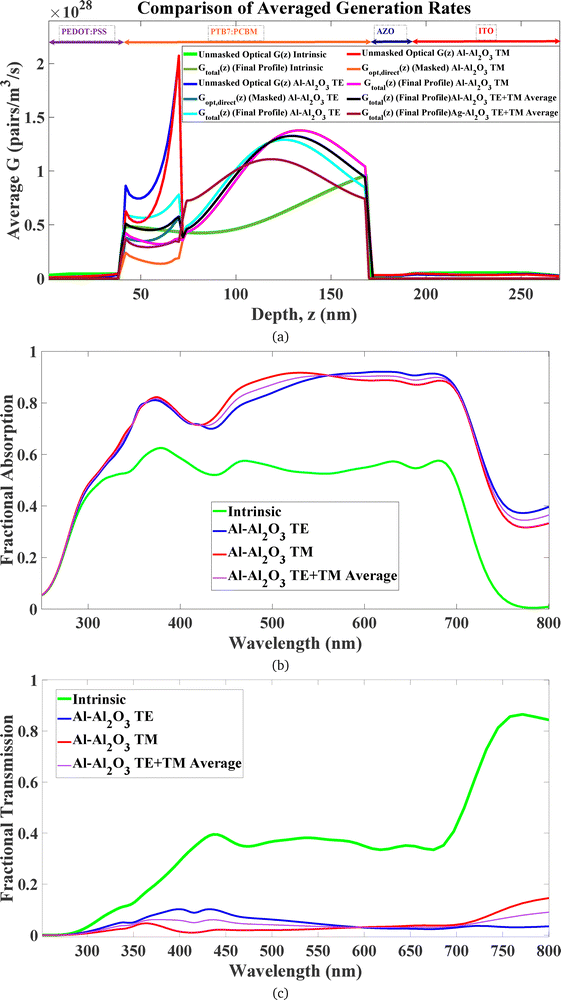
4.1.2.1 The intrinsic cell & the influence of the Al cathode. As shown in Fig. 3a–c (green line), the G(z) profile of the intrinsic device is not a simple exponential decay. It exhibits a complex, sinusoidal-like shape with a prominent generation peak near the front of the active layer (z ≈ [100–120 nm]) and a second peak near the back (z ≈ [0–40 nm]). This structure arises from optical cavity effects, but critically, the intense peak near the back is a signature of surface plasmon polaritons (SPPs) being excited on the smooth Al back cathode. The evanescent fields of these SPPs penetrate into the P3HT:PCBM, strongly enhancing absorption in that region. Thus, the Al cathode in this “intrinsic” reference cell is not merely a reflector but an active plasmonic element, and its SPP-field establishes the baseline optical environment into which the nanoparticles are introduced. The 2D map in Fig. 4a visualizes this combined standing wave and SPP-enhanced field pattern.
4.1.2.2 Nanoparticle-induced perturbation of the optical environment. When ZnO nanostructures are introduced (Fig. 3a–c, sky blue line), they replace a portion of the active material and perturb the local refractive index. As a result, they partially disrupt the SPP-enhanced cavity mode, leading to a suppression of the generation peak near the back contact and an overall reduction in Jsc_opt_direct, as shown in Fig. 3. This establishes that any enhancement by metallic core–shell nanoparticles must overcome this initial disruption and introduce a more potent light-coupling mechanism. Based on the rigorously masked generation profiles calculated for the various metallic nanoparticles (Fig. 3b), two fundamentally different enhancement pathways are revealed.
4.1.2.3 Case 1: LSPR–SPP mode hybridization (noble metals: Au, Ag, Cu). Noble metal nanoparticles, particularly Au and Ag, are characterized by their strong but spectrally narrower LSPR peaks and relatively moderate broadband absorption. This allows a significant portion of incident sunlight, especially outside their primary LSPR wavelength, to penetrate the active layer and still excite the SPPs on the Al back cathode. The resulting generation profile (e.g., silver line for Ag in Fig. 3b) is therefore a superposition of two effects: strong, localized LSPR-driven enhancement in the P3HT:PCBM immediately surrounding the nanoparticle (z ≈ 0–40 nm), combined with the persistent, broader SPP-driven enhancement from the back contact. This is vividly illustrated in the 2D generation map for Ag (Fig. 4d), which shows intense generation “hot spots” localized on the nanoparticle's surface, coexisting with the broader generation pattern deeper in the cell. In this scenario, the LSPRs on the nanoparticles can also be further enhanced by coupling with the backward-propagating SPP field. Among these materials, Ag demonstrates the most effective near-field coupling, leading to the highest Jsc_opt_direct values in this category.
4.1.2.4 Case 2: plasmonic shielding and forward-channeling (non-noble metals: Al, Fe, Pt). A starkly different behaviour is observed for the non-noble metal nanoparticles. Al, Fe, and Pt are potent broadband absorbers. When placed as an array at the front of the active layer, they act as highly effective “plasmonic shields,” intercepting and interacting with the vast majority of incident light. This prevents a significant photon flux from reaching the Al back cathode, leading to a strong suppression of the back-contact SPP mode. Having decoupled the device from the influence of the back-contact SPP, the G(z) profile for these materials is now almost entirely dictated by the intrinsic light-coupling mechanism of the front-side nanoparticles themselves. This mechanism is shown to be a novel form of deep energy deposition. In striking contrast to the noble metals, the generation rate for Al and Fe (purple and black lines, Fig. 3b) is moderate to minimal near the nanoparticle but progressively increases with depth. The 2D G(x,z) map for Al (Fig. 4c) is particularly revealing: instead of hot spots on the NP surface, the dominant feature is a focused, intense “ellipse” of high generation located deep within the active layer, between z ≈ 70–110 nm. This confirms that the Al nanoparticles are actively channelling or “pumping” optical energy to a focal point much deeper than their physical location. Fe and Pt exhibit a similar but weaker deep-generation pumping (Fig. 4e and g).
These G-profiles provide definitive evidence of two competing mechanisms. The choice of nanoparticle material dictates whether the device operates in a hybridized LSPR–SPP mode (with noble metals) or a forward-channelled, nanoparticle-dominated mode (with strongly-absorbing non-noble metals). The subsequent section will use a detailed analysis of local electromagnetic fields to dissect the physical origin of this novel forward-channelling effect.
4.2 A phase-resolved analysis of synchronous and asynchronous plasmon dynamics
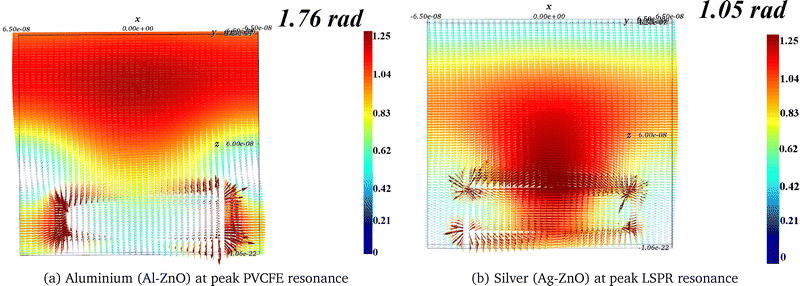
The distinct G(z) profiles of noble versus non-noble metals, particularly the “deep energy deposition” characteristic of aluminium, originate from fundamentally different dynamic behaviours of their plasmonic near-fields. To dissect these mechanisms, a phase-resolved analysis of the electric field (E) vectors was performed for the Al–ZnO and Ag–ZnO nanostructures, representing the champions of their respective classes. Fig. 5 showcases key frames from the full dynamic evolution at 580 nm, where P3HT:PCBM exhibits peak absorption.This asynchronous dynamic—powerful LSPR first, followed by a delayed SPP-coupled channelling—is definitive proof of two weakly-coupled, out-of-phase processes. The time delay is a direct result of the finite travel time of the SPP to the back contact and back. This hybridized mode, while effective, deposits its energy in two separate steps and primarily at the surface, which is fundamentally less efficient than the unified mechanism we observe in Al.
Within this class, aluminium's response is exceptionally efficient and exhibits a unique, synchronous dynamic that we formally term plasmonic vortex-coupled forward emission (PVCFE). This mechanism, which we identify as the archetypal example of the AzizEl effect, is directly linked to aluminium's unique optical properties, which combine the high absorption of non-noble metals with a distinctively large negative real permittivity (Fig. 2c). The key stages of the PVCFE in aluminium are as follows. The process begins with a synchronous build-up (phase 0.5–1.76 radians). Unlike Ag, both the vortical field pattern and the directional “flow-through” energy channelling appear simultaneously. As the phase progresses towards its peak, these two components grow in unison with no time delay. This leads to the peak resonance (phase ≈ 1.76 radians), which is significantly phase-lagged compared to Ag. Critically, at this peak intensity (Fig. 5a), both the vortex and the energy channelling are at their maximum strength simultaneously. The local field intensification is not confined to the surface (non-local) of the nanoparticle but is the visible signature of this powerful, unified mechanism. Finally, during the unified decay (phase > 2.2 radians), both the vortex and channelling components of the PVCFE weaken together as the system dephases.
This synchronicity is the defining feature of the PVCFE. It is not an asynchronous, two-stage process like the LSPR–SPP hybridization seen in silver. Instead, the vortex and the energy channelling are two inseparable facets of the same complex, phase-lagged plasmon mode intrinsic to the nanoparticle. This unified mechanism is exceptionally efficient at both concentrating and directionally steering electromagnetic energy, providing the direct physical explanation for the deep “pumping” of the generation profile, as visualized in the 2D map for Al in Fig. 4c. This discovery moves beyond simple LSPR enhancement, revealing a sophisticated, material-dependent dynamic wherein the localized plasmon itself possesses a strong, intrinsic forward-radiating character, enabling advanced light management in nanophotonic devices.
The results are presented in Fig. 6. This analysis plots the estimated hot carrier Jsc as a linear function of the total hot carrier efficiency (ηtotal = ηhc_conversion × ηhc_injection) for the key plasmonic materials. The slope of each line is a direct measure of a material's intrinsic ability to convert absorbed photon power into injected current, independent of the assumed efficiency. The analysis confirms that the superior potential of Fe and Al is a fundamental consequence of their high optical absorption in this device architecture. While the absolute magnitude of the hot carrier Jsc scales with the assumed efficiencies, the relative performance ranking is robust, solidifying the conclusion that these non-noble metals are exceptional candidates for hot carrier harvesting.
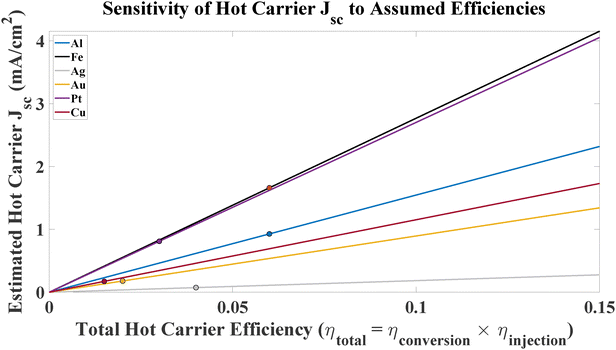 | ||
| Fig. 6 Parametric sensitivity analysis of the estimated hot carrier short-circuit current density (Jsc) as a function of the total assumed hot carrier efficiency (ηtotal). The distinct slope for each material is determined by its total absorbed power under AM1.5G illumination. This demonstrates that the high potential of Fe, Al, and Pt for hot carrier generation is an intrinsic property that is robust against variations in the precise efficiency values. Markers indicate the specific efficiency values used to calculate the results in Table 3. | ||
4.3 Proving the dominance of PVCFE in a high-performance PTB7:PC71BM testbed
The foundational analysis in the P3HT:PCBM system not only revealed the novel plasmonic vortex-coupled forward emission (PVCFE) mechanism but also suggested that it represents a more potent light-coupling strategy than conventional noble metal plasmonics. To definitively test this hypothesis and isolate the mechanism's performance from the electrical limitations of P3HT:PCBM, we transitioned to a higher-performance PTB7:PC71BM active layer. This material system serves as a high-fidelity testbed, characterized by superior charge transport that can accurately reflect the true extent of optical generation enhancements.| Analysis | Structure | J sc_opt_direct (mA cm−2) | Injected HC (carriers per s per NP) | J sc_hot_carrier (mA cm−2) | J total (mA cm−2) | ||
|---|---|---|---|---|---|---|---|
| C1:ON | Intrinsic | 8.986 × 1020 | 14.40 | — | — | 8.986 × 1020 | 14.40 |
| C2:OFF | Al–Al2O3 | 1.326 × 1021 | 21.25 | — | — | 1.326 × 1021 | 21.25 |
| C3/C4:OFF | Ag–Al2O3 | 1.216 × 1021 | 19.48 | — | — | 1.216 × 1021 | 19.48 |
| C1:ON | Intrinsic | 8.986 × 1020 | 14.40 | — | — | 8.986 × 1020 | 14.40 |
| C2:ON | Al–Al2O3 | 1.080 × 1021 | 17.30 | — | — | 1.080 × 1021 | 17.30 |
| C3/C4:OFF | Ag–Al2O3 | 1.061 × 1021 | 17.00 | — | — | 1.061 × 1021 | 17.00 |
| C1:ON | Intrinsic | 8.986 × 1020 | 14.40 | — | — | 8.986 × 1020 | 14.40 |
| C2:ON | Al–Al2O3 | 1.080 × 1021 | 17.30 | 2.22 × 106 | 1.162 | 1.152 × 1021 | 18.46 |
| C3/C4:ON | Ag–Al2O3 | 1.061 × 1021 | 17.00 | 7.19 × 105 | 0.376 | 1.085 × 1021 | 17.38 |
The intrinsic PTB7:PC71BM device, with its strong SPP enhancement from the Al back cathode, establishes a high baseline Jsc of 14.40 mA cm−2. When nanostructures are introduced, the unmasked “C1” analysis again highlights the significant parasitic absorption of Al (apparent Jsc = 21.25 mA cm−2), while the masked analysis reveals the true useful generation.
The rigorously masked results (“C2”) deliver a decisive verdict. The Ag–Al2O3 nanostructures, despite the ideal thin-shell configuration, provide a direct optical Jsc (Jsc_opt_direct) of 17.00 mA cm−2. This is an impressive enhancement, showcasing the power of the hybridized LSPR–SPP coupling mechanism. However, the Al–Al2O3 nanostructures surpass them, achieving a Jsc_opt_direct of 17.30 mA cm−2. This confirms that even under conditions tailored for conventional near-field enhancement, the PVCFE is an intrinsically more powerful mechanism for channelling light and generating carriers deep within this high-performance active layer.
This conclusion is further solidified by the inclusion of hot carrier estimations (“C3/C4”). Due to its superior efficiencies, aluminium adds a substantial 1.16 mA cm−2 of Jsc_hot_carrier, for a final Jtotal of 18.46 mA cm−2. In contrast, silver's much lower hot carrier potential adds only a negligible 0.38 mA cm−2 for a total of 17.38 mA cm−2. This widening performance gap confirms that Al is superior in both primary and secondary enhancement pathways.
Crucially, the ability of Al to actively channel energy deeper into the active layer represents a mechanism that is robustly independent of precise shell thickness, unlike the highly sensitive evanescent near-fields of noble metals. This finding is in complete alignment with previous work by Bagheri on Fe–ZnO and Au–ZnO nanoparticles, which showed that while Au's enhancement decayed significantly with increasing shell thickness, Fe's enhancement remained constant or even improved.15
Beyond its superior optoelectronic performance, aluminium offers a profound advantage in terms of manufacturability and cost-effectiveness. A key challenge in plasmonic device fabrication is the creation of a uniform, ultrathin dielectric shell to prevent quenching and mediate hot carrier injection. For silver, achieving a uniform ∼2 nm shell demands costly and technically sophisticated methods, such as atomic layer deposition.60 In stark contrast, aluminium nanoparticles naturally form a high-quality, self-passivating Al2O3 shell through spontaneous oxidation in ambient conditions. This process requires virtually no additional cost or complex synthesis steps, making the protective and functional oxide shell an integral and economically favourable component of the Al nanoparticle design.12,61,62
Therefore, aluminium emerges as the unequivocal material of choice, offering a trifecta of benefits: a superior light-coupling mechanism (PVCFE), significant hot carrier potential, and a cost-effective, self-passivating shell. Furthermore, its previously identified “plasmonic shield” quality, which renders the device's optical performance largely independent of the back-contact SPP modes, presents a profound opportunity for radical device redesign. Having unequivocally established the superiority of the PVCFE mechanism and aluminium, we are now positioned to design a final, truly innovative OSC. The subsequent section will leverage this knowledge to create an inverted architecture that replaces the expensive, plasmonically-active metal back contact with a low-cost, inert graphite anode. This final design will not only capitalize on aluminium's exceptional optical performance but will also realize the full cost and stability benefits promised by a complete transition to non-noble plasmonics.
4.4 A novel high-performance architecture: decoupling and dominance of PVCFE in a graphite-anode OSC
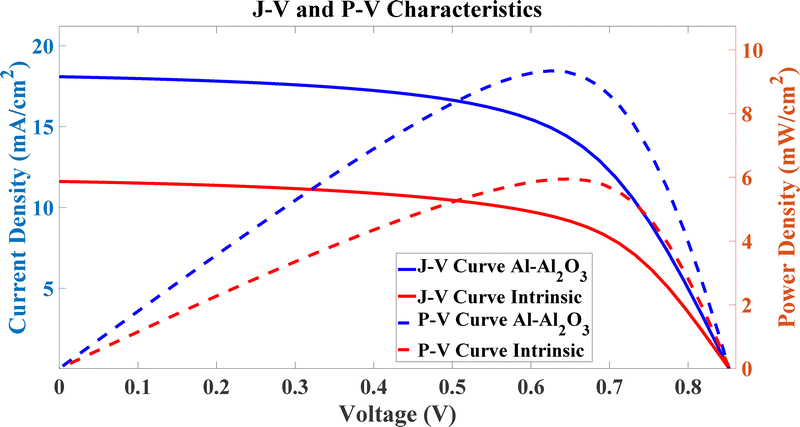
The analysis in Section 4.1 revealed a critical insight: the aluminium back cathode in the conventional device is not an inert reflector but an active plasmonic element, exciting surface plasmon polariton (SPP) modes that significantly contribute to the baseline optical generation. This finding implies that the performance of any front-side nanostructure is intrinsically entangled with this back-side SPP enhancement, leading to complex and sometimes competitive optical effects. While the Al–cathode design was instrumental in discovering the PVCFE, it represents a suboptimal architecture. Based on this insight, we propose that a superior device architecture is one that is optically decoupled from the back contact. This is a novel design principle for plasmonic OSCs, enabled by the “plasmonic shield” nature of the optimized Al–NP array. Fig. 9c provides direct evidence for this shielding effect. While the intrinsic device allows a significant fraction of light to pass through the active layer to be absorbed parasitically by the graphite anode, the introduction of the Al–NP array reduces the average transmission across the active spectrum to less than 5%. This near-complete photon harvesting at the front of the cell renders the back contact's reflectivity non-critical.• Optical decoupling and high efficiency: the PVCFE-driven plasmonic shield ensures maximum light absorption, overcoming the primary limitation of non-reflective anodes. This eliminates LSPR–SPP interference, allowing the intrinsic performance of the front-side nanostructures to be unambiguously harnessed.
• Cost-effectiveness and stability: replacing the conventional vacuum-deposited silver or gold anode with solution-coatable, abundant graphite aligns with the low-cost premise of OSCs. Furthermore, this inverted structure provides significant stability benefits by removing the acidic PEDOT:PSS layer from the vulnerable ITO contact, eliminating a major degradation pathway,64 and by using a robust AZO ETL and a chemically inert graphite anode.
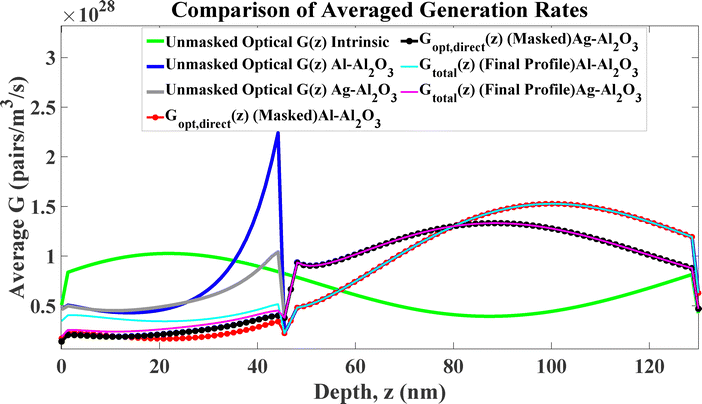
The champion device architecture, illustrated in the 3D schematic in Fig. 8, consists of the following optimized parameters: ITO (80 nm), AZO (20 nm), PTB7:PC71BM (130 nm), PEDOT:PSS (40 nm), and a thick graphite anode (>500 nm). The optimized Al-core/Al2O3-shell nanoparticles embedded at the AZO/active layer interface are cuboids with dimensions of 150 × 150 nm (width/length) and a height of 30 nm.
Table 5 summarizes the comprehensive “four core” analysis for this optimized graphite-anode design, comparing the intrinsic cell with those enhanced by Al–Al2O3 and Ag–Al2O3 nanostructures. The results unequivocally demonstrate the success of this new design. The intrinsic graphite-based device, now free from back-contact SPP enhancement, establishes a true optical baseline Jtotal of 12.11 mA cm−2. The Ag nanostructures, relying on their conventional LSPR mechanism, provide a substantial enhancement, reaching a final TE/TM-averaged Jtotal of 16.21 mA cm−2. This performance is overwhelmingly driven by its strong direct optical generation enhancement (Jsc_opt_direct = 15.87 mA cm−2), while its hot carrier contribution is modest (∼0.35 mA cm−2). The Al nanostructure device emerges as the undisputed champion. In this optically clean environment, the PVCFE mechanism is unleashed. The TE/TM-averaged direct optical Jsc (Jsc_opt_direct) reaches an outstanding 17.59 mA cm−2. Furthermore, aluminium's potent intrinsic absorption and favourable electronic properties lead to a very significant estimated hot carrier contribution of 1.03 mA cm−2.
| Structure | Polarization | J sc_opt_direct (mA cm−2) | J sc_hot_carrier (mA cm−2) | J total (mA cm−2) | |
|---|---|---|---|---|---|
| Intrinsic | TE/TM average | 7.560 × 1020 | 12.11 | — | 12.11 |
| Al–Al2O3 (C1–C4:ON) | TE | 1.113 × 1021 | 17.84 | 1.116 | 18.96 |
| TM | 1.082 × 1021 | 17.33 | 0.942 | 18.27 | |
| TE + TM average | 1.097 × 1021 | 17.59 | 1.030 | 18.62 | |
| Ag–Al2O3 (C1–C4:ON) | TE | 9.498 × 1020 | 15.22 | 0.328 | 15.55 |
| TM | 1.031 × 1021 | 16.52 | 0.363 | 16.88 | |
| TE + TM average | 9.906 × 1020 | 15.87 | 0.345 | 16.21 | |
Combining these two pathways yields a final, TE/TM-averaged total Jsc for the Al-enhanced device of 18.62 mA cm−2. This represents a remarkable 53.7% increase over the new intrinsic baseline of the graphite-based cell. This result, achieved in a cost-effective and stable architecture and explained by a novel, fully characterized physical mechanism (PVCFE), highlights the immense potential of non-noble plasmonics. A detailed analysis of the generation profiles that lead to these results is presented in the following section.
4.4.3.1 Decoupled intrinsic and Ag performance. As hypothesized, the G(z) profile for the intrinsic graphite-based cell (Fig. 9a, green line) is now fundamentally different from the one observed with the Al cathode. The strong, SPP-induced generation peak previously seen near the back interface is completely absent. Instead, the profile shows a more conventional absorption behaviour, with a broad peak near the front that decays into the film. This confirms the critical role of the Al cathode's SPPs in the previous architecture and quantifies its contribution: the total Jsc for the intrinsic cell drops from 14.4 mA cm−2 (with Al cathode) to 12.11 mA cm−2 (with graphite), indicating the back-contact SPP enhancement was responsible for ∼2.3 mA cm−2 of current in the original design. Similarly, the performance of the Ag nanostructures is impacted. Without the backward-propagating SPP field to hybridize with, the G(z) profile for Ag (Fig. 9a, crimson line), while still strongly peaked near the front of the active layer due to its powerful LSPR, is suppressed across the board compared to its potential in a coupled system. This results in a final TE/TM-averaged Jsc for Ag of 16.21 mA cm−2. While this still represents a significant enhancement over the new 12.11 mA cm−2 intrinsic baseline, it confirms that Ag's performance in the previous architecture, in part, relied on synergistic coupling with the back SPP field.
4.4.3.2 Confirmation of Al as a self-contained “plasmonic shield” and PVCFE engine. The results for the Al nanostructures provide the final and definitive proof of the PVCFE mechanism acting as a powerful, self-contained optical engine. The G(z) profiles for Al under both TE and TM polarizations (Fig. 9a, black line) show that its ability to channel energy and create a deep generation peak (now located near z ≈ 120–150 nm in this stack) is fully preserved and even more prominent in the absence of the competing back-SPP mode. Crucially, the TE/TM-averaged total Jsc for the Al-enhanced cell (18.62 mA cm−2) is not diminished by the removal of the optically active Al cathode; its enhancement over the new intrinsic baseline is now even more pronounced. This is clear evidence that the “plasmonic shield” nature of the Al nanoparticle array is so effective that it renders the back contact's optical properties largely irrelevant. As shown in the transmission spectra (Fig. 9c), the PVCFE is powerful enough to manage the incident light entirely on its own, reducing transmission to less than 5%. The total fractional absorption shown in Fig. 9b is also significantly higher for the Al-enhanced cell across the entire active spectrum of PTB7:PC71BM, consistent with its superior Jsc.
4.4.3.3 Conclusion and path to final device analysis. This analysis confirms that Al nanostructures, via the PVCFE mechanism, provide a superior and more robust enhancement strategy than conventional plasmonic materials like Ag. Their “plasmonic shield” quality not only provides exceptional light-trapping but also decouples the device's optical performance from the back contact, enabling the use of low-cost, non-reflective materials like graphite. Given these unequivocal advantages, we now proceed with a full electrical simulation of only the champion Al-enhanced device and the intrinsic baseline to quantify the final power conversion efficiency gains.
4.5 Final device performance: electrical and quantum efficiency analysis
Having established aluminium's superior and novel optical enhancement mechanism (PVCFE) in the optimized graphite-anode architecture, we proceeded to a full electrical device simulation to quantify the final impact on power conversion efficiency (PCE). The one-dimensional total generation profiles (Gtotal(z)) for the calibrated intrinsic and the champion Al–Al2O3 enhanced devices, encompassing both direct optical and estimated hot carrier contributions, were imported into a SCAPS-1D model defined by the realistic device parameters in Table 2. All electrical parameters, including charge mobilities and defect profiles, were held constant between the two simulations to ensure a direct and unambiguous assessment of the plasmonic contribution.The resulting key photovoltaic parameters are summarized in Table 6, with the corresponding current density–voltage (J–V) and power–voltage (P–V) curves plotted in Fig. 10. The calibrated intrinsic reference device, representing a realistic baseline, is predicted to have a PCE of 5.95%, with a Jsc of 11.61 mA cm−2, a Voc of 0.853 V, and a healthy FF of 60.08%. The integration of the optimized Al–Al2O3 nanostructures is predicted to yield a transformative improvement in performance. The short-circuit current density (Jsc) leaps by a massive 55.8% to 18.09 mA cm−2, a direct consequence of the enhanced carrier generation from the synergistic action of the PVCFE mechanism and hot carrier injection. Remarkably, the open-circuit voltage (Voc) remains stable at 0.852 V, indicating that the well-passivated Al/Al2O3 nanostructures do not introduce detrimental recombination pathways.
| Structure | J sc (mA cm−2) | V oc (V) | FF (%) | PCE (%) | V mpp (V) | J mpp (mA cm−2) | P max (mW cm−2) |
|---|---|---|---|---|---|---|---|
| Intrinsic | 11.61 | 0.853 | 60.08 | 5.95 | 0.651 | 9.136 | 5.95 |
| Al–Al2O3 enhanced | 18.09 | 0.852 | 60.57 | 9.34 | 0.625 | 14.938 | 9.34 |
Most significantly, the fill factor (FF) is not only maintained but slightly increases to 60.57%. This is a critical result, demonstrating that the robust inverted device architecture with its highly efficient charge transport layers is capable of extracting the massively increased photocurrent without being limited by space-charge effects or increased recombination losses. The final power conversion efficiency (PCE) for the Al-enhanced device is predicted to reach 9.34%. This constitutes an exceptional 57% relative enhancement over the intrinsic cell, unequivocally demonstrating the success of harnessing the PVCFE mechanism in an electrically optimized architecture.
It is important to contextualize this predicted 57% relative enhancement within the existing experimental landscape. Prior experimental work on Al-based plasmonic OSCs has shown significant, albeit more modest, gains. For instance, notable experimental work from Yang et al.11 and Kakavelakis et al.13 reported PCE enhancements of approximately 30%, while Cui et al.12 demonstrated a 20% improvement. We attribute our significantly higher predicted performance to the holistic design approach that goes beyond simple plasmonic enhancement. Our optimization of the nanostructure array as a functional metasurface is what enables the PVCFE mechanism and the highly effective “plasmonic shield” property. This superior light management, in turn, is what makes the cost-effective and stable graphite anode design viable without compromising efficiency, leading to the large overall performance gain.
Further insight is provided by the simulated external quantum efficiency (EQE) spectra shown in Fig. 11. The intrinsic device exhibits a modest QE whose spectral shape mirrors the natural absorption of the PTB7:PC71BM blend, peaking at ∼680 nm before falling to zero at the bandgap edge. In stark contrast, the Al-enhanced device shows a dramatically boosted QE across the entire 300–750 nm spectrum. Crucially, its peak response is red-shifted to ∼700 nm. This broadband enhancement is a direct result of the PVCFE's superior light coupling. However, the red-shift of the peak is the final, unequivocal evidence of the plasmonic mechanism's dominance. It demonstrates that the enhancement is not merely amplifying the material's inherent absorption; rather, the PVCFE is imprinting its own powerful, lower-energy resonant signature onto the device, fundamentally reshaping its response to light. Thus, our comprehensive opto-electronic model, which synergistically combines the novel PVCFE mechanism for direct optical generation enhancement with a physically-grounded estimation of hot carrier injection, successfully predicts a clear and robust pathway to high-efficiency, stable, and cost-effective organic photovoltaics. The >57% relative improvement in PCE demonstrated herein is a direct result of this multi-faceted enhancement. It is worth noting, however, that the standard drift-diffusion formalism used in the electrical model does not explicitly account for all potential secondary benefits arising from the intense, vortical, and dynamic near-fields characteristic of the PVCFE. Advanced effects, such as field-assisted exciton dissociation or localized carrier ‘steering’ within the organic active layer, could further improve charge collection efficiency. While quantifying these contributions requires advanced quantum transport models beyond the scope of this work, their potential suggests that the experimental realization of this device could yield an even greater performance than the already impressive values predicted by our model. This work therefore not only demonstrates a powerful new plasmonic enhancement strategy but also highlights compelling avenues for future research at the intersection of nanophotonics and advanced device physics. It must be re-emphasized that the hot carrier portion of this enhancement is a theoretical estimate based on the parameters in Table 1. While our sensitivity analysis confirms the robustness of the material ranking, the precise magnitude of this contribution in a real-world device would ultimately require direct experimental calibration.
5 Conclusions
In this comprehensive theoretical and computational study, we have identified, characterized, and leveraged a novel, material-dependent light coupling mechanism in plasmonic organic solar cells, which we term plasmonic vortex-coupled forward emission (PVCFE). The development of a rigorous “four core” simulation workflow, which precisely separates useful semiconductor generation from parasitic metallic absorption and incorporates hot carrier injection estimations, enabled us to move beyond conventional metrics and reveal a deeper layer of plasmonic device physics. Our simulations establish cost-effective aluminium as a potentially superior material to noble metals, driven by the PVCFE mechanism—a synchronous coupling of a vortical near-field with a directional energy channelling component, confirmed via phase-resolved analysis. By translating these fundamental insights into a holistically designed, stable, and inverted OSC architecture (ITO/AZO/PTB7:PC71BM (Al–NPs)/PEDOT:PSS/graphite), we predict a power conversion efficiency of 9.34%, a ∼57% relative improvement over its 5.95% intrinsic counterpart. This exceptional performance stems from a massive Jsc increase to 18.09 mA cm−2 while maintaining the fill factor, a result of co-optimizing the novel PVCFE optical engine with a robust electrical design. This work not only presents a validated pathway to high-efficiency, stable, and low-cost organic photovoltaics but also provides a new fundamental mechanism—the PVCFE—as a powerful design principle for nanophotonics, shifting the focus from simple near-field enhancement to the sophisticated engineering of complex, hybridized plasmon modes for directional energy control.While these simulation results are highly promising, we recognize the challenges and prospects for their experimental validation. A key step would be the synthesis of Al-core/Al2O3-shell nanostructures with dimensional control approaching that of the optimized model, likely through advanced colloidal chemistry or physical deposition methods followed by controlled oxidation. Fabricating the proposed inverted device architecture would then allow for direct comparison of experimental J–V and EQE curves against our predictions. Furthermore, advanced spectroscopic techniques could provide direct evidence of the PVCFE mechanism. For instance, near-field scanning optical microscopy (NSOM) could potentially map the non-local field intensification within the active layer, while ultrafast pump–probe spectroscopy might be used to discern the synchronous, phase-lagged dynamics characteristic of the PVCFE, distinguishing it from the asynchronous response of noble metals. We believe this work provides a strong theoretical motivation for pursuing such challenging but potentially rewarding experimental investigations.
Author contributions
M. A. S. Bagheri is the sole author of this manuscript and was responsible for all aspects of the work, including conceptualization, methodology, simulation, analysis, and manuscript preparation.Conflicts of interest
There are no conflicts to declare.Data availability
The data underlying the results presented in this paper are available in the supplementary information. The custom computational codes generated during the current study are proprietary and are not publicly available.Acknowledgements
The author declares that no funds, grants, or other support were received during the preparation of this manuscript.Notes and references
- N. Kannan and D. Vakeesan, Solar energy for future world:-A review, Renewable Sustainable Energy Rev., 2016, 62, 1092, DOI:10.1016/j.rser.2016.05.022
.
- J. Yi, G. Zhang, H. Yu and H. Yan, Advantages, challenges and molecular design of different material types used in organic solar cells, Nat. Rev. Mater., 2024, 9, 46, DOI:10.1038/s41578-023-00618-1
.
- P. Ding, D. Yang, S. Yang and Z. Ge, Stability of organic solar cells: toward commercial applications, Chem. Soc. Rev., 2024, 53, 2350, 10.1039/D3CS00492A
.
- H. Lin, Z. Xiao, C. Chen, Z. Cai, Y. Liang and W. Zhang, Charge photogeneration and recombination dynamics in non-fullerene solar cells based on a polymer donor with a mono-fluorinated π-bridge, Phys. Chem. Chem. Phys., 2024, 26, 21476, 10.1039/D4CP02014F
.
- L. Sun, Y. Chen, M. Sun and Y. Zheng, Organic solar cells: physical principle and recent advances, Chem. – Asian J., 2023, 18, e202300006, DOI:10.1002/asia.202300006
.
- N. K. Al-Saleem, A. Al-Naghmaish, M. Madani, W. Alfawwar, A. M. Elbasiony, S. Alharthi, M. A. Haque and M. M. Ghobashy, Multifunctional roles and advances of polymers in solar cell technologies: a review, RSC Adv., 2025, 15, 35998, 10.1039/D5RA05820A
.
- P. Mandal, Application of plasmonics in solar cell efficiency improvement: a brief review on recent progress, Plasmonics, 2022, 17, 1247, DOI:10.1007/s11468-022-01616-9
.
- X. Wang, M. She, W. Gu, Y. Bu and X. Yan, Structures, plasmon-enhanced luminescence, and applications of heterostructure phosphors, Phys. Chem. Chem. Phys., 2021, 23, 20765, 10.1039/D1CP01860D
.
- M. Moser, A. Wadsworth, N. Gasparini and I. McCulloch, Challenges to the success of commercial organic photovoltaic products, Adv. Energy Mater., 2021, 11, 2100056, DOI:10.1002/aenm.202100056
.
- V. Kochergin, L. Neely, C. Y. Jao and H. D. Robinson, Aluminum plasmonic nanostructures for improved absorption in organic photovoltaic devices, Appl. Phys. Lett., 2011, 98, 133303, DOI:10.1063/1.3574091
.
- S. P. Yang, M. Yao, T. Jiang, N. Li, Y. Zhang, G. Li, X. W. Li and G. S. Fu, Effect of aluminium nanoparticles on the performance of bulk heterojunction organic solar cells, Chin. Phys. Lett., 2012, 29, 098402, DOI:10.1088/0256-307X/29/9/098402
.
- Y. Cui, D. Huang, Y. Li, W. Huang, Z. Liang, Z. Xu and S. Zhao, Aluminium nanoparticles synthesized by a novel wet chemical method and used to enhance the performance of polymer solar cells by the plasmonic effect, J. Mater. Chem. C, 2015, 3, 4099, 10.1039/C5TC00213C
.
- G. Kakavelakis, E. Stratakis and E. Kymakis, Aluminum nanoparticles for efficient and stable organic photovoltaics, RSC Adv., 2013, 3, 16288, 10.1039/C3RA42792G
.
- M. Sygletou, G. Kakavelakis, B. Paci, A. Generosi, E. Kymakis and E. Stratakis, Enhanced stability of aluminum nanoparticle-doped organic solar cells, ACS Appl. Mater. Interfaces, 2015, 7, 17756, DOI:10.1021/acsami.5b03970
.
- M. A. S. Bagheri, Enhanced absorption in organic solar cells using core-shell iron-ZnO nanoparticles: optical and numerical simulations, J. Nanopart. Res., 2025, 27, 111, DOI:10.1007/s11051-025-06295-1
.
- M. L. Brongersma, N. J. Halas and P. Nordlander, Plasmon-induced hot carrier science and technology, Nat. Nanotechnol., 2015, 10, 25, DOI:10.1038/nnano.2014.311
.
- J. Khurgin, A. Y. Bykov and A. V. Zayats, Hot-electron dynamics in plasmonic nanostructures: fundamentals, applications and overlooked aspects, eLight, 2024, 4, 15, DOI:10.1186/s43593-024-00070-w
.
- J. L. Yang, H. J. Wang, X. Qi, Q. N. Zheng, J. H. Tian, H. Zhang and J. F. Li, Understanding the behaviors of plasmon-induced hot carriers and their applications in photocatalysis, ACS Appl. Mater. Interfaces, 2024, 16, 12149, DOI:10.1021/acsami.4c00709
.
- J. Seok, Y. Jin and K. Yu, Hot carrier-based metal–semiconductor photodetectors: from quantum efficiency models to structural innovations, J. Phys. D: Appl. Phys., 2024, 58, 033002, DOI:10.1088/1361-6463/ad835b
.
-
D. J. Griffiths, Introduction to Electrodynamics, Cambridge University Press, 2023 DOI:10.1017/9781009397735
.
-
Handbook of optical constants of solids, ed. E. D. Palik, Academic Press, 1998. https://books.google.com/books?id=nxoqxyoHfbIC Search PubMed
.
- D. Duche, P. Torchio, L. Escoubas, F. Monestier, J. J. Simon, F. Flory and G. Mathian, Improving light absorption in organic solar cells by plasmonic contribution, Sol. Energy Mater. Sol. Cells, 2009, 93, 1377, DOI:10.1016/j.solmat.2009.02.028
.
- H. Hoppe, N. Arnold, N. S. Sariciftci and D. Meissner, Modeling the optical absorption within conjugated polymer/fullerene-based bulk-heterojunction organic solar cells, Sol. Energy Mater. Sol. Cells, 2003, 80, 105, DOI:10.1016/j.solmat.2003.08.010
.
- C. Clavero, Plasmon-induced hot-electron generation at nanoparticle/metal-oxide interfaces for photovoltaic and photocatalytic devices, Nat. Photonics, 2014, 8, 95, DOI:10.1038/nphoton.2013.238
.
- R. Sundararaman, P. Narang, A. S. Jermyn, W. A. Goddard III and H. A. Atwater, Theoretical predictions for hot-carrier generation from surface plasmon decay, Nat. Commun., 2014, 5, 5788, DOI:10.1038/ncomms6788
.
- S. Linic, P. Christopher and D. B. Ingram, Plasmonic-metal nanostructures for efficient conversion of solar to chemical energy, Nat. Mater., 2011, 10, 911, DOI:10.1038/nmat3151
.
- A. J. Leenheer, P. Narang, N. S. Lewis and H. A. Atwater, Solar energy conversion via hot electron internal photoemission in metallic nanostructures: efficiency estimates, J. Appl. Phys., 2014, 115, 134301, DOI:10.1063/1.4870040
.
- K. Wu, J. Chen, J. R. McBride and T. Lian, Efficient hot-electron transfer by a plasmon-induced interfacial charge-transfer transition, Science, 2015, 349, 632, DOI:10.1126/science.aac5443
.
- T. Gong and J. N. Munday, Materials for hot carrier plasmonics, Opt. Mater. Express, 2015, 5, 2501, DOI:10.1364/OME.5.002501
.
- M. Valenti, A. Venugopal, D. Tordera, M. P. Jonsson, G. Biskos, A. Schmidt-Ott and W. A. Smith, Hot carrier generation and extraction of plasmonic alloy nanoparticles, ACS Photonics, 2017, 4, 1146, DOI:10.1021/acsphotonics.6b01048
.
- A. O. Govorov, H. Zhang and Y. K. Gun’ko, Theory of photoinjection of hot plasmonic carriers from metal nanostructures into semiconductors and surface molecules, J. Phys. Chem. C, 2013, 117, 16616, DOI:10.1021/jp405430m
.
-
S. M. Sze, Y. Li and K. K. Ng, Physics of semiconductor devices, John Wiley & Sons, 2021, https://books.google.co.uk/books?id=pf4VEAAAQBAJ Search PubMed
.
-
A. Jüngel, Transport equations for semiconductors, Springer, 2009, vol. 773. https://books.google.co.uk/books?id=COlsCQAAQBAJ Search PubMed
.
- I. Hwang, C. R. McNeill and N. C. Greenham, Drift-diffusion modeling of photocurrent transients in bulk heterojunction solar cells, J. Appl. Phys., 2009, 106, 093106, DOI:10.1063/1.3247547
.
- J. W. Ryan and E. Palomares, Photo-Induced charge carrier recombination kinetics in small molecule organic solar cells and the influence of film nanomorphology, Adv. Energy Mater., 2017, 7, 1601509, DOI:10.1002/aenm.201601509
.
- J. Robinson and Y. Rahmat-Samii, Particle swarm optimization in electromagnetics, IEEE Trans. Antennas Propag., 2004, 52, 397, DOI:10.1109/TAP.2004.823969
.
-
K. E. Parsopoulos and M. N. Vrahatis, Particle swarm optimization and intelligence: Advances and
Applications, IGI Global, 2010. https://books.google.com/books?id=CSqZW327ekYC Search PubMed
.
- M. Aghlmandi Sadigh Bagheri, R. Yadipour and A. Asgharian, Design and optimization of plasmonic metal nanoantennas on a glass substrate for efficient solar-driven evaporation of seawater: an optical and numerical simulation approach, J. Nanopart. Res., 2024, 26, 260, DOI:10.1007/s11051-024-06125-w
.
- T. A. Konig, P. A. Ledin, J. Kerszulis, M. A. Mahmoud, M. A. El-Sayed, J. R. Reynolds and V. V. Tsukruk, Electrically tunable plasmonic behavior of nanocube–polymer nanomaterials induced by a redox-active electrochromic polymer, ACS Nano, 2014, 8, 6182, DOI:10.1021/nn501601e
.
- C. W. Chen, S. Y. Hsiao, C. Y. Chen, H. W. Kang, Z. Y. Huang and H. W. Lin, Optical properties of organometal halide perovskite thin films and general device structure design rules for perovskite single and tandem solar cells, J. Mater. Chem. A, 2015, 3, 9152, 10.1039/C4TA05237D
.
- C. Stelling, C. R. Singh, M. Karg, T. A. König, M. Thelakkat and M. Retsch, Plasmonic nanomeshes: their ambivalent role as transparent electrodes in organic solar cells, Sci. Rep., 2017, 7, 42530, DOI:10.1038/srep42530
.
- O. Aguilar, S. de Castro, M. P. Godoy and M. Rebello Sousa Dias, Optoelectronic characterization of Zn1-xCdxO thin films as an alternative to photonic crystals in organic solar cells, Opt. Mater. Express, 2019, 9, 3638, DOI:10.1364/OME.9.003638
.
-
R. E. Treharne, A. Seymour-Pierce, K. Durose, K. Hutchings, S. Roncallo and D. Lane, Optical design and fabrication of fully sputtered CdTe/CdS solar cells, Journal of Physics: Conference Series, IOP Publishing, 2011, vol. 286, p. 012038 DOI:10.1088/1742-6596/286/1/012038
.
- W. S. Werner, K. Glantschnig and C. Ambrosch-Draxl, Optical constants and inelastic electron-scattering data for 17 elemental metals, J. Phys. Chem. Ref. Data, 2009, 38, 1013, DOI:10.1063/1.3243762
.
- P. B. Johnson and R. W. Christy, Optical constants of the noble metals, Phys. Rev. B, 1972, 6, 4370, DOI:10.1103/PhysRevB.6.4370
.
- K. M. McPeak, S. V. Jayanti, S. J. Kress, S. Meyer, S. Iotti, A. Rossinelli and D. J. Norris, Plasmonic films can easily be better: rules and recipes, ACS Photonics, 2015, 2, 326, DOI:10.1021/ph5004237
.
- A. Tselin, M. Pogodaeva, S. Levchenko, A. Kalmykov, K. Garbuzov, A. Smirnov and V. Drachev, Exploring the dielectric function of platinum, Phys. Rev. B, 2024, 110, 195130, DOI:10.1103/PhysRevB.110.195130
.
- A. B. Djurišić and E. H. Li, Optical properties of graphite, J. Appl. Phys., 1999, 85, 7404, DOI:10.1063/1.369370
.
- A. P. Manuel and K. Shankar, Hot electrons in TiO2–noble metal nano-heterojunctions: fundamental science and applications in photocatalysis, Nanomaterials, 2021, 11, 1249, DOI:10.3390/nano11051249
.
- M. Burgelman, P. Nollet and S. Degrave, Modelling polycrystalline semiconductor solar cells, Thin Solid Films, 2000, 361–362, 527, DOI:10.1016/S0040-6090(99)00825-1
.
- A. N. Alahmadi, Design of an efficient PTB7:PC70BM-based polymer solar cell for 8% efficiency, Polymers, 2022, 14, 889, DOI:10.3390/polym14050889
.
- L. Dejam, S. Solaymani, A. Achour, S. Stach, Ş. Ţălu, N. B. Nezafat, V. Dalouji, A. A. Shokri and A. Ghaderi, Correlation between surface topography, optical band gaps and crystalline properties of engineered AZO and CAZO thin films, Chem. Phys. Lett., 2019, 719, 78, DOI:10.1016/j.cplett.2019.01.042
.
- M. T. Khan, Investigation of the electrical, optical and photophysical properties of PTB7:PCBM-thin films, J. Mater. Sci.: Mater. Electron., 2023, 34, 2016, DOI:10.1007/s10854-023-11366-x
.
- R. Bhujel, S. Rai, U. Deka, G. Sarkar, J. Biswas and B. P. Swain, Bandgap engineering of PEDOT:PSS/rGO a hole transport layer for SiNWs hybrid solar cells, Bull. Mater. Sci., 2021, 44, 72, DOI:10.1007/s12034-021-02376-8
.
-
P. Simonov, Physicochemical aspects of preparation of carbon-supported noble metal catalysts, Catalysis by supported complexes, Marcel Dekker, Inc., New York, NY, 2003, pp. 409–454 DOI:10.1201/9780203912713.ch12
.
- K. Wang, C. Liu, T. Meng, C. Yi and X. Gong, Inverted organic photovoltaic cells, Chem. Soc. Rev., 2016, 45, 2937, 10.1039/C5CS00831J
.
- B. Ebenhoch, S. A. Thomson, K. Genevičius, G. Juška and I. D. Samuel, Charge carrier mobility of the organic photovoltaic materials PTB7 and PC71BM and its influence on device performance, Org. Electron., 2015, 22, 62, DOI:10.1016/j.orgel.2015.03.013
.
- F. Azri, A. Meftah, N. Sengouga and A. Meftah, Electron and hole transport layers optimization by numerical simulation of a perovskite solar cell, Sol. Energy, 2019, 181, 372, DOI:10.1016/j.solener.2019.02.017
.
- H. Tang, Y. Bai, H. Zhao, X. Qin, Z. Hu, C. Zhou, F. Huang and Y. Cao, Interface engineering for highly efficient organic solar cells, Adv. Mater., 2024, 36, 2212236, DOI:10.1002/adma.202212236
.
- L. Shang, J. Qu, Z. Wang, M. Zhang and C. Li, Optical absorption property and photo-thermal conversion performance of Ag@Al2O3 plasmonic nanofluids with Al2O3 nano-shell fabricated by atomic layer deposition, J. Mol. Liq., 2021, 326, 115388, DOI:10.1016/j.molliq.2021.115388
.
- S. Kaushal, M. D. Zeeshan, M. I. Ansari and D. Sharma, Progress in tribological research of Al2O3 ceramics: a review, Mater. Today: Proc., 2023, 82, 163, DOI:10.1016/j.matpr.2022.12.116
.
- R. Liu, B. Zhao, N. Sheng and C. Zhu, Synthesis of Al@Al2O3 microcapsules by a triple-coating method for high-temperature thermal energy storage, J. Energy Storage, 2023, 68, 107843, DOI:10.1016/j.est.2023.107843
.
- R. Po, C. Carbonera, A. Bernardi, F. Tinti and N. Camaioni, Polymer-and carbon-based electrodes for polymer solar cells: Toward low-cost, continuous fabrication over large area, Sol. Energy Mater. Sol. Cells, 2012, 100, 97–114, DOI:10.1016/j.solmat.2011.12.022
.
- S. K. Gupta, S. Banerjee, A. Singh, L. S. Pali and A. Garg, Modeling of degradation in normal and inverted OSC devices, Sol. Energy Mater. Sol. Cells, 2019, 191, 329, DOI:10.1016/j.solmat.2018.11.039
.
| This journal is © the Owner Societies 2026 |