Tailoring the electronic and thermoelectric properties of the SnSe monolayer via vacancy defects: insights from density functional theory
Erik Bhekti
Yutomo
 *,
Suci
Faniandari
and
Muhammad
Fahmi
*,
Suci
Faniandari
and
Muhammad
Fahmi
Department of Physics, Faculty of Science and Mathematics, Diponegoro University, Semarang 50275, Indonesia. E-mail: erikbhekti@fisika.fsm.undip.ac.id
First published on 19th November 2025
Abstract
Vacancy-defect engineering has been recognized as an effective strategy for tailoring the electronic and thermoelectric properties of 2D materials. In this study, we employed density functional theory (DFT) to investigate the impact of vacancies on the electronic and thermoelectric properties of the SnSe monolayer. Four models were considered: perfect SnSe monolayer, Sn0.94Se monolayer (Sn vacancy), SnSe0.94 monolayer (Se vacancy), and Sn0.94Se0.94 monolayer (Sn–Se vacancies). Structural analysis revealed that the Sn vacancy induces the most significant lattice rearrangement, followed by the Se and Sn–Se vacancies. From an electronic perspective, the SnSe monolayer is a semiconductor with an indirect bandgap of 0.908 eV. Introducing the Sn vacancy transforms it into a p-type conductor with high electrical conductivity, while the Se vacancy reduces the bandgap to 0.508 eV but preserves its semiconducting nature. In contrast, Sn–Se vacancies enlarge the bandgap to 1.039 eV. A strong correlation between the electronic and thermoelectric transport properties was also observed. Systems with larger bandgaps exhibit higher Seebeck coefficients, with the Sn0.94Se0.94 monolayer achieving the maximum value of 1.510 × 10−3 V K−1. Thermoelectric performance optimization shows that the Sn0.94Se monolayer is the most promising candidate at low temperatures (300–400 K), reaching a peak power factor of 2.226 × 10−3 W m−1 K−2. Moreover, vacancy introduction significantly reduces the electronic and thermal conductivity, further reinforcing the Sn0.94Se monolayer as an optimal candidate for thermoelectric applications in the low-temperature range.
1. Introduction
In recent years, research on two-dimensional (2D) materials, beyond graphene and hexagonal boron nitride (h-BN), has progressed rapidly.1–3 The main driver of this effort is the need to discover materials with unique physical properties that can open up new opportunities for technological applications. 2D materials with superior electronic, optical, transport, and thermal properties enable significant advances in various fields, ranging from optoelectronics, catalysis, energy conversion, and biomedical applications.4–6 One group of materials that has attracted attention is group-IV monochalcogenides, which are binary compounds with the general formula of MX (M = Ge or Sn, X = S or Se) that have a structure similar to that of black phosphorus.7,8 Experimental studies have shown that thin films of GeSe exhibit anisotropic spin transport and polarization behavior, high Hall mobility (∼85 cm2 V−1 s−1), anisotropic ferroelectric and ferroelastic properties, significant optical absorption coefficients (∼104 cm−1), and a moderate bandgap of about 1.3 eV.9–12 These characteristics make it a potential candidate for solar cell and infrared detector applications.13–15 Theoretical calculations indicate that MX monolayers possess good dynamic stability, high electrical conductivity and Seebeck coefficients, and low thermal conductivity, suggesting that their thermoelectric performance could surpass those of their bulk structures.16 Furthermore, GeX monolayers, with their wider bandgap than their bulk counterparts, larger surface area, auxetic mechanical properties, highly tunable electronic properties, and significant charge-carrier mobility, present a fascinating area for further exploration in photovoltaic and water-splitting applications.17,18As a member of this group, tin selenide (SnSe) is known for its outstanding combination of electronic, optical, and thermoelectric properties, making it a strong candidate for heat-to-electricity energy conversion.19–22 SnSe has a layered orthorhombic structure with weak van der Waals bonding between the layers, contributing to its extremely low lattice thermal conductivity.23,24 Its anisotropic character is reflected in different electronic and optical behaviors along the zigzag and armchair directions.25 Several studies have reported a high figure of merit (ZT), reaching ∼2.6 for single-crystal p-type samples.26,27 This value can still be improved through strategies, such as band structure engineering, halogen doping, alloying with heavy elements, or adjusting the crystal symmetry to converge band structures.25,28,29 These approaches not only increase the power factor but can also maintain or reduce the thermal conductivity, thereby strengthening the prospects of the SnSe in environmentally friendly thermoelectric and optoelectronic devices.
Additionally, the layered nature of the SnSe allows it to be exfoliated into thin sheets or synthesized in the form of nanosheets. The synthesis of the SnSe nanosheets has been reported using solution-mediated growth methods and high-vacuum thermal evaporation.30,31 These results open up great opportunities to explore the unique properties of the SnSe monolayer. Interestingly, the SnSe monolayer has been shown to exhibit superior electronic and thermoelectric performance compared to the bulk SnSe.32–35 Various studies have confirmed that these properties can be further tuned by external engineering, such as doping or strain application. Pham et al. (2023) reported that transition metal doping (e.g., Fe) can tailor the SnSe monolayer for specific applications, such as SO2 gas sensing, achieving a recovery time of ∼27 seconds at 373 K and sensitivity up to 73% while maintaining a suitable bandgap for thermoelectric applications.36 Other studies have shown that applying a slight uniaxial strain (1–2%) to the SnSe monolayer can improve its thermoelectric properties, achieving increased Seebeck coefficients and modified energy band structures.37 Zhou et al. (2021) also revealed that P, In, and Br doping in the SnSe monolayer can enhance its hydrogen evolution reaction (HER) performance by lowering the hydrogen adsorption energy to close to zero, whereas doping with K and Te reduces the performance.38 Insawang et al. (2024) showed that structural engineering using RF sputtering and vacuum annealing can improve the crystallinity and thermoelectric performance of the SnSe thin film, especially when heat treatment is applied at an optimal temperature of 400 °C.39
Although these various approaches have succeeded in improving the performance of the SnSe monolayer, the influence of intrinsic defects, especially atomic vacancies, on their electronic and thermoelectric properties remains relatively underexplored. However, defects are often unavoidable in 2D materials and can affect their fundamental properties. Shang et al. (2025) demonstrated that vacancies in the MoSSe monolayer modify the interplay between external pressure and thermoelectric efficiency, where sulfur and selenium vacancies differently affect the power factor and thermal conductivity, leading to either enhancement or suppression of ZT depending on the applied pressure.40 Similarly, Zheng et al. (2019) showed that introducing oxygen vacancies into a MoO3 monolayer creates sharp peaks in the density of states near the Fermi level, which effectively improves the ZT compared to the pristine system.41 In contrast, Kumar et al. (2021) found that selenium vacancies in MoSe2 monolayers reduce the band gap and power factor due to the emergence of dangling states within the band gap region, thereby deteriorating thermoelectric performance.42 Collectively, these findings highlight that vacancy engineering not only alters the fundamental electronic properties but also serves as a powerful strategy to tune the thermoelectric response of 2D materials, enabling both the enhancement and reduction of ZT depending on defect type and external conditions.
For the SnSe monolayer, a recent comprehensive study by Yue et al. (2024) using scanning tunneling microscopy (STM) and density functional theory (DFT) calculations reported that the Sn vacancy with a low formation energy (0.382 eV) significantly modifies the electronic structure, causes p-type doping, and impacts electron transport.43 Nevertheless, the effects of vacancies on key thermoelectric parameters, such as the thermal conductivity and power factor, are still not well understood. In this work, we aim to systematically investigate the influence of vacancy defects on the electronic and thermoelectric properties of a SnSe monolayer. Specifically, three types of vacancy configurations are considered, namely, Sn, Se, and combined Sn–Se vacancies. Our analysis begins with a structural examination to determine the most energetically favorable vacancy sites and to understand how such defects modify the geometric configuration of the lattice. We then perform an in-depth exploration of the resulting electronic structure to elucidate the defect-induced modifications in the band characteristics. Finally, the thermoelectric performance of the defective systems is evaluated through key transport parameters, including the Seebeck coefficient, electrical conductivity, power factor, and electronic thermal conductivity. This comprehensive approach provides new insights into the defect–property relationship in SnSe monolayers, offering valuable guidance for the design of optimized thermoelectric materials.
2. Computational methodology
In this study, four configurations were used to explore the influence of vacancy defects on the electronic and thermoelectric properties of the SnSe monolayer. The first system is a perfect SnSe monolayer that serves as a reference, as shown in Fig. 1(a) for the top view and Fig. 1(b) for the side view. The second model was built by removing one Sn atom (Sn0.94Se monolayer), and the third model by removing one Se atom (SnSe0.94 monolayer); the fourth model includes double vacancies, which remove one Sn atom and one Se atom (Sn0.94Se0.94 monolayer) simultaneously. The perfect SnSe monolayer was modeled using a 3 × 3 supercell consisting of 18 Sn atoms and 18 Se atoms. To avoid interlayer interactions due to periodic conditions, a vacuum space of about 20 Å was added along the normal direction relative to the monolayer plane.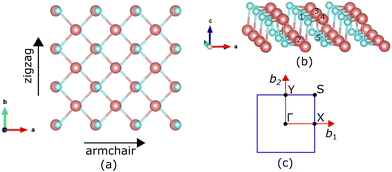 | ||
| Fig. 1 Top view (a) and side view (b) of the crystal structure, and (c) high-symmetry points in the first-order Brillouin zone of the SnSe monolayer. | ||
The density functional theory (DFT)-based calculations were performed with the Quantum ESPRESSO code, which has been widely used for the study of 2D systems due to its efficiency and accuracy.44,45 The core–valence electron interactions were represented by the projector augmented wave (PAW) pseudopotential.46 For the exchange–correlation interactions, the generalized gradient approximation (GGA) approach with the Perdew–Burke–Ernzerhof (PBE) parameterization was used, which has proven to be reliable in describing the electronic properties of 2D materials.47–49 Geometry optimization was performed using the Broyden–Fletcher–Goldfarb–Shanno (BFGS) algorithm until the total force and energy in the system were smaller than 10−3 Ry Bohr−1 (∼25 meV Å−1) and 10−4 Ha (∼3 meV), respectively.50–53 In the optimization stage, the lattice parameters along the plane-parallel axes (a and b axes) were allowed to relax, while the inter-plane distance (c-axis) was kept constant by maintaining the vacuum thickness. After optimization, self-consistent field (SCF) calculations were performed with a cut-off kinetic energy of 65 Ry (0.952 keV) for the wave function and 560 Ry (7.619 keV) for the charge density. The Brillouin zone was sampled using the Monkhorst–Pack scheme. The k-point convergence test was performed for the SnSe monolayer, and the results confirmed that a 7 × 7 × 1 k-point grid ensures well-converged total energy. The detailed results of the k-point convergence test can be seen in Fig. S1 in the SI. To obtain more detailed information on the electronic properties, including the band structure and projected density of states (PDOS), non-self-consistent field (NSCF) calculations were performed using a denser k-point grid, namely, 16 × 16 × 1. The band structure was calculated along the standard path in the orthorhombic monolayer Brillouin zone, namely, Γ–X–S–Y–Γ, as can be seen in Fig. 1(c). Meanwhile, the PDOS was calculated using the atomic orbital projection technique so that the specific contributions of Sn and Se atoms to the density of states can be analyzed. Spin–orbit coupling (SOC) was not included in the present calculations. Although SOC may slightly reduce the band gap of the SnSe monolayer due to relativistic effects, previous studies35 have reported that the influence is relatively small (approximately 0.05–0.1 eV) and does not significantly alter the band dispersion. Hence, neglecting SOC is reasonable for the purpose of comparing the relative effects of different vacancy configurations on the electronic and thermoelectric properties.
To connect electronic properties with thermoelectric performance, the calculated band structure and PDOS were then processed using the BoltzTraP package based on a semi-classical Boltzmann transport theory approach in the constant-time relaxation limit.54,55 In this step, the energy–wave number (E–k) data from the NSCF calculations were extracted and used to calculate various transport coefficients, including electrical conductivity σ, Seebeck coefficient S, and electronic thermal conductivity κe. The σ, S, and κe parameters were then calculated using eqn (1)–(3), respectively.
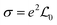 | (1) |
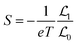 | (2) |
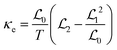 | (3) |
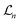 (n = 0, 1, and 2) are thermoelectric integrals, and T is the absolute temperature. The thermoelectric integral was calculated using eqn (4).
(n = 0, 1, and 2) are thermoelectric integrals, and T is the absolute temperature. The thermoelectric integral was calculated using eqn (4).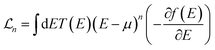 | (4) |
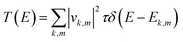 | (5) |
3. Result and discussion
3.1 Structural properties
Based on the geometry optimization of the SnSe monolayer, the bond length between the Se1 atom and the Sn3 atom, l13, and the bond length between the Se1 atom and the Sn2 atom, l12 (see Fig. 1(b)), are 2.896 Å and 2.731 Å, respectively. Furthermore, the bond angle formed by the Sn2–Se1–Se3 and Sn2–Se1–Se4 atoms is 94.292°. These structural parameters are consistent with those obtained in previous computational56,57 and experimental43 studies; thus, the accuracy of the simulation parameters in this study can be validated. Before analyzing the effect of vacancies on the physical properties of the SnSe monolayer, the most stable vacancy model is determined by calculating the formation energy (Ef) based on eqn (6).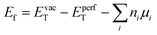 | (6) |
| Defect types | E f (eV) | S 0 (Å) | Δr‖ (Å) | Δr⊥ (Å) |
|---|---|---|---|---|
| TAL/BAL is the top/bottom atomic layer. | ||||
| SnSe monolayer | — | 166.301 | — | — |
| Sn0.94Se monolayer with Sn vacancy in TAL | 4.720 | 161.859 | 0.031–0.674 | 0.049–0.388 |
| Sn0.94Se monolayer with Sn vacancy in BAL | 4.721 | 161.757 | 0.112–0.481 | 0.047–0.399 |
| SnSe0.94 monolayer with Se vacancy in TAL | 4.696 | 164.228 | 0.009–0.564 | 0.024–0.194 |
| SnSe0.94 monolayer with Se vacancy in BAL | 4.667 | 164.245 | 0.049–0.426 | 0.015–0.200 |
| Sn0.94Se0.94 monolayer with vacancies of Sn in TAL and Se in BAL | 7.814 | 165.522 | 0.059–0.339 | 0.001–0.069 |
| Sn0.94Se0.94 monolayer with vacancies of Sn in BAL and Se in TAL | 7.828 | 164.613 | 0.058–0.380 | 0.000–0.065 |
Moreover, the phonon spectrum of the SnSe monolayer, reported in our previous study,37 exhibits no imaginary frequencies, confirming its dynamic stability. The introduction of vacancies causes only local atomic lattice rearrangements without significantly altering the overall bonding network, suggesting that the defective configurations remain dynamically stable. This inference is also supported by previous studies on vacancy-defected MoS2,59 which demonstrated that similar vacancy configurations preserve the dynamic stability of the lattice. Fig. 2 shows the optimized structure of the SnSe monolayers with vacancies. We find that the presence of vacancies induces only local atomic lattice rearrangements around the vacancy centers in the Sn0.94Se, SnSe0.94, and Sn0.94Se0.94 monolayers. To quantify the atomic lattice rearrangements, we calculate the atomic displacements from their positions in the perfect system using eqn (7) and (8).
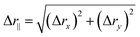 | (7) |
| Δr⊥ = |Δrz| | (8) |
Δ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = = ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) v − v − ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) p p | (9) |
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) v and
v and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) p are the position vectors of atoms in the vacancy systems and the perfect system, respectively. Δr‖ and Δr⊥ are calculated for only the 10 nearest neighbor atoms of the vacancy centers. The calculated Δr‖ and Δr⊥ summarized in Table 1 show that the Sn0.94Se monolayer has a larger value than the SnSe0.94 monolayer. This result indicates that the Sn vacancy can induce a more significant atomic lattice rearrangement than the Se vacancy. This condition can occur because the missing Sn atom has a larger atomic radius than the Se atom (the atomic radius of the Sn atom = 217 pm, while that of the Se atom = 190 pm). Interestingly, the atomic lattice rearrangement in the Sn0.94Se0.94 monolayer is not significant compared to that in the other two vacancy models, even though the number of atoms lost is greater. This condition is predicted because the simultaneous formation of Sn and Se vacancies does not overcharge or undercharge the system, unlike the case in the other two vacancy models. Similar conditions were also observed in previous experimental and computational studies.43,60 Furthermore, the atomic lattice rearrangement induces a decrease in the surface area (S0) of the SnSe monolayer, as can be seen in Table 1. The greater the atomic lattice rearrangement, the greater the reduction in the S0 of the SnSe monolayer. This condition certainly results in atomic distortion, which will significantly affect the physical properties of the material.
p are the position vectors of atoms in the vacancy systems and the perfect system, respectively. Δr‖ and Δr⊥ are calculated for only the 10 nearest neighbor atoms of the vacancy centers. The calculated Δr‖ and Δr⊥ summarized in Table 1 show that the Sn0.94Se monolayer has a larger value than the SnSe0.94 monolayer. This result indicates that the Sn vacancy can induce a more significant atomic lattice rearrangement than the Se vacancy. This condition can occur because the missing Sn atom has a larger atomic radius than the Se atom (the atomic radius of the Sn atom = 217 pm, while that of the Se atom = 190 pm). Interestingly, the atomic lattice rearrangement in the Sn0.94Se0.94 monolayer is not significant compared to that in the other two vacancy models, even though the number of atoms lost is greater. This condition is predicted because the simultaneous formation of Sn and Se vacancies does not overcharge or undercharge the system, unlike the case in the other two vacancy models. Similar conditions were also observed in previous experimental and computational studies.43,60 Furthermore, the atomic lattice rearrangement induces a decrease in the surface area (S0) of the SnSe monolayer, as can be seen in Table 1. The greater the atomic lattice rearrangement, the greater the reduction in the S0 of the SnSe monolayer. This condition certainly results in atomic distortion, which will significantly affect the physical properties of the material.
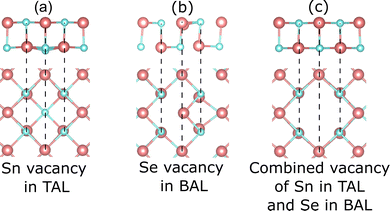 | ||
| Fig. 2 Optimized crystal structures of the (a) Sn0.94Se, (b) SnSe0.94, and (c) Sn0.94Se0.94 monolayers with the most stable vacancy positions. | ||
3.2 Electronic properties
The analysis of electronic and thermoelectric properties was only carried out on the perfect SnSe monolayer and the vacancy systems with the best stability: the Sn0.94Se monolayer with Sn vacancy in TAL, the SnSe0.94 monolayer with Se vacancy in BAL, and the Sn0.94Se0.94 monolayer with Sn vacancy in TAL and Se vacancy in BAL. Fig. 3(a) shows the band structure of a perfect SnSe monolayer. Based on the calculation results, the perfect SnSe monolayer has semiconductor properties with an indirect band gap of 0.908 eV, which is formed between the valence band maximum (VBM) at point X′ and the conduction band minimum (CBM) at point Y′. In addition, two extrema bands in the valence band and two extrema bands in the conduction band are observed, each located along the Γ–X and Y–Γ paths, respectively. In our previous study, through the application of strain, we were able to modify the position of these extrema bands.37 The bandgap of 0.908 eV obtained in this study is within the bandgap range reported by various previous studies. The previous study reported a bandgap of 0.986 eV using generalized gradient approximation (GGA), 1.067 eV using strongly constrained and appropriately normed (SCAN) meta-GGA, and 1.471 eV using HSE06 hybrid functional.61 Other studies also mentioned bandgap values of 0.93 eV,35 1.12 eV,62 0.92 eV,63 1.13 eV,64 1.20 eV,65 and 0.90 eV,66 which generally used the GGA approach. Meanwhile, experimental results show that the SnSe thin films with a thickness of 2–100 µm have a bandgap of 1.047 eV.67 Based on this comparison, it can be said that the calculation results using the GGA functional are closer to the experimental values compared with the results obtained with other functionals, so that GGA is considered more suitable for calculating the electronic properties of the SnSe monolayers efficiently and realistically. When compared with other Sn-based monochalcogenide materials, such as SnTe and SnS, it is known that SnTe has a bandgap of around 1.05 eV,68 while SnS has a larger bandgap of around 1.36 eV.69 For thermoelectric applications, the ideal bandgap is generally in the range of 0.1–1.0 eV, because it can provide a balance between the electrical conductivity and Seebeck coefficient.70 In this context, SnSe and SnTe monolayers, with band gaps of 0.908 eV and 1.05 eV, respectively, are in a more suitable range than SnS, which has a relatively large band gap.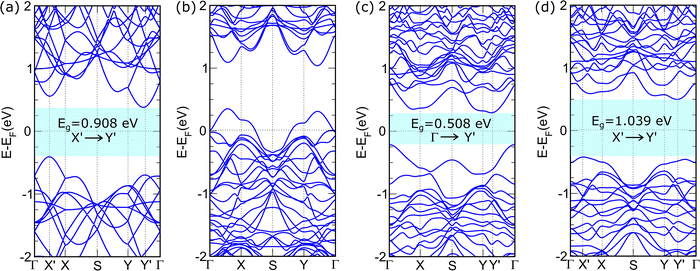 | ||
| Fig. 3 Band structures of the (a) SnSe, (b) Sn0.94Se, (c) SnSe0.94, and (d) Sn0.94Se0.94 monolayers. The energy (E) was set relative to the Fermi energy (EF). | ||
Fig. 3(b) shows the band structure of the Sn0.94Se monolayer, where it is observed that the Fermi level crosses the valence band, indicating the transition of electronic properties from a semiconductor to a p-type conductor. This result suggests that Sn vacancies act as hole doping, which increases the concentration of positive charge carriers, thus contributing significantly to the increase in electrical conductivity. The emergence of this electronic property transformation can be explained by the formation of Sn vacancies, which can cause the surrounding Se atoms to lack about 0.67 electrons, creating a defect state and shifting the Fermi level toward the valence band. In addition, the extreme energy bands on the Γ–X and Y–Γ paths are observed to be almost completely degenerate, which is suspected to be caused by lattice distortion due to the presence of a vacancy. This phenomenon is consistent with the results of previous studies,37 where the application of strain on the SnSe monolayer also causes the degeneration of extreme energy bands. Furthermore, Fig. 3(c) shows the band structure of the SnSe0.94 monolayer. In contrast to the Sn vacancy, the semiconducting property of the SnSe monolayer is still maintained, with the indirect band gap reduced to 0.508 eV. It is observed that the VBM shifts to the Γ point, while the CBM is at the Y′ point on the Y–Γ path. This band gap reduction is caused by the excess charge of 0.67 electrons on the Sn atoms around the Se vacancy site, which induces defect states in the valence band and contributes to the formation of the new VBM. In addition, a flattening of the extreme conduction band is observed, indicating the emergence of localized states around the Fermi level due to the vacancy. This band flattening phenomenon is in line with the results of several previous studies showing that the vacancy can induce localized electron states, and this has important implications for transport properties, especially in reducing charge-carrier mobility. Fig. 3(d) shows the band structure of the Sn0.94Se0.94 monolayer. This system maintains the semiconductor properties with an indirect band gap that is actually widened compared to a perfect SnSe monolayer, which is 1.039 eV. The VBM and CBM are located at the X′ and Y′ points, respectively. This band gap widening can be attributed to the interaction between defect states due to the offsetting Sn and Se vacancies, thus reducing the density of states around the Fermi level. In addition, a band flattening phenomenon is observed in both the valence and conduction band extrema.
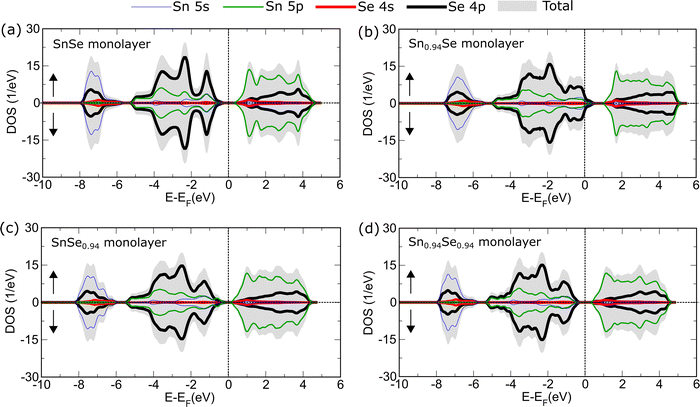
Total density of state (TDOS) and projected density of state (PDOS) calculations considering spin polarization for a more in-depth analysis of the electronic properties of the SnSe, Sn0.94Se, SnSe0.94, and Sn0.94Se0.94 monolayers have been performed, with the results shown in Fig. 4. Based on Fig. 4(a), the TDOS of the SnSe monolayer shows a zero value at the Fermi level, which clearly indicates a semiconducting character. This result confirms the band structure calculation results in Fig. 3(a). Then, there are four prominent peaks at energies of −7.382 eV, −3.595 eV, −2.326 eV, and −1.182 eV in the valence band, where the highest peaks at −2.326 eV and −1.182 eV indicate localized electronic states. This localized state at an energy of −1.182 eV is essential in increasing the Seebeck coefficient because it creates a steep DOS gradient near the Fermi level.71,72 In the conduction band, there are three prominent peaks at 1.169 eV, 2.708 eV, and 3.728 eV, with the peaks at 1.169 eV and 3.728 eV having almost the same DOS intensity. In addition, the symmetric TDOS of spin up and spin down over the entire energy range confirms that this system is non-magnetic, which ensures electronic stability and minimizes the effect of spin on charge transport.73 Furthermore, PDOS analysis shows that the deep valence band is dominated by Sn 5s orbitals, which are strongly hybridized with Se 4p orbitals. In contrast, the shallow valence band is dominated by Se 4p orbitals, which are strongly hybridized with Sn 5s and Sn 5p orbitals. On the conduction band side, Sn 5p orbitals are very dominant and undergo substantial hybridization with Se 4p orbitals. Therefore, Se 4p orbitals and Sn 5p orbitals play crucial roles in charge-carrier transport in the SnSe monolayer.
Furthermore, Fig. 4(b) displays the TDOS and PDOS of the Sn0.94Se monolayer. Unlike the perfect system, the TDOS value at the Fermi level is no longer zero. This result confirms the band-structure calculation results in Fig. 3(b), which indicate a transition from semiconductor to metal properties. In addition, there is a blue shift in the positions of the four prominent TDOS peaks of the valence band, which are now located at energies of −6.808 eV, −2.991 eV, −1.881 eV, and −0.727 eV. Compared with the perfect SnSe monolayer system, these four peaks not only shift closer to higher energy levels but also experience a decrease in intensity, indicating that the electronic states become delocalized due to the loss of Sn atoms in the crystal lattice. Interestingly, a new peak appears at −0.283 eV, which is not found in the perfect system. This peak reflects the defect state that arises due to the Sn vacancy. The existence of a defect peak near the Fermi level is essential because it can act as an electronic acceptor, thus directly impacting the electrical conductivity and Seebeck value. Meanwhile, the three prominent peaks in the conduction band also experience a shift to higher energies at 1.692 eV, 3.311 eV, and 4.399 eV, respectively. Although the band structure changes, the spin-up and spin-down symmetries are maintained, indicating that these Sn0.94Se monolayers are still non-magnetic, despite the presence of structural defects.
Fig. 4(c) shows the TDOS and PDOS of the SnSe0.94 monolayer. In this system, the TDOS is zero at the Fermi level, indicating that the semiconducting properties of the SnSe monolayer are maintained despite the presence of the Se vacancy. A red shift is observed in the four prominent peaks of the valence band, which are located at energies of −7.540 eV, −3.590 eV, −2.525 eV, and −1.326 eV. These four peaks also exhibit a decrease in intensity, indicating the delocalization of electronic states resulting from the Se vacancy. On the other hand, the TDOS in the valence band near the Fermi level experiences a slight increase, which can be attributed to the presence of defect states resulting from the Se vacancy. The presence of defect states results in a decrease in the energy gap, as shown in Fig. 3(b). Meanwhile, the three prominent peaks in the conduction band shift to energies of 1.004 eV, 2.557 eV, and 3.644 eV. The spin-up and spin-down TDOSs exhibit perfect symmetry, confirming that the system remains non-magnetic. PDOS analysis reveals that the contributions of the orbitals composing the valence and conduction bands generally do not experience significant changes compared to the SnSe monolayer system. The valence band remains dominated by the Sn 5s orbital hybridized with Se 4p, while the Sn 5p dominates the conduction band. However, an important insight obtained from PDOS is that the defect state appearing near the Fermi level originates from the Sn 5p orbital. The presence of a charge imbalance due to the loss of a Se atom can explain this phenomenon, which causes the surrounding Sn atoms to become overcharged. This result opens up the possibility of local charge engineering that can be utilized for controlling electronic and thermoelectric properties.74
Fig. 4(d) shows the TDOS and PDOS for the Sn0.94Se0.94 monolayer. In this configuration, the TDOS remains zero at the Fermi level. The positions of the prominent peaks in the valence band and conduction band do not experience significant shifts compared to those in the perfect system, located at −7.385 eV, −3.546 eV, −2.337 eV, and −1.171 eV for the valence band and 1.157 eV, 2.834 eV, and 3.735 eV for the conduction band, respectively. The PDOS characteristics of the Sn0.94Se0.94 monolayer also show strong similarities with the perfect system. The valence band is still dominated by the interaction between the Sn 5s and Se 4p orbitals, while the conduction band remains dominated by the Sn 5p orbital, which hybridises with the Se 4p orbital. This result indicates that, despite the presence of Sn and Se vacancies, their influence on the band structure and orbital character is relatively minimal, allowing the electronic structure to remain stable and the semiconductor properties to be maintained.
Next, the effective mass of the charge carriers (m*) is calculated using eqn (10).
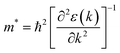 | (10) |
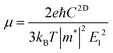 | (11) |
| Charge carriers | Transport parameters | SnSe monolayer | Sn0.94Se monolayer | SnSe0.94 monolayer | Sn0.94Se0.94 monolayer |
|---|---|---|---|---|---|
| Electron | m* (m0) | 0.127 | 0.112 | 0.224 | 0.254 |
| μ (cm2 V−1 s−1) | 473.360 | 374.529 | 271.904 | 159.713 | |
| τ (fs) | 34.213 | 23.840 | 34.618 | 23.074 | |
| Hole | m* (m0) | 0.118 | 0.133 | 0.207 | 0.294 |
| μ (cm2 V−1 s−1) | 381.088 | 345.239 | 129.448 | 155.064 | |
| τ (fs) | 25.555 | 26.068 | 15.265 | 25.939 |
3.3 Thermoelectric transport properties
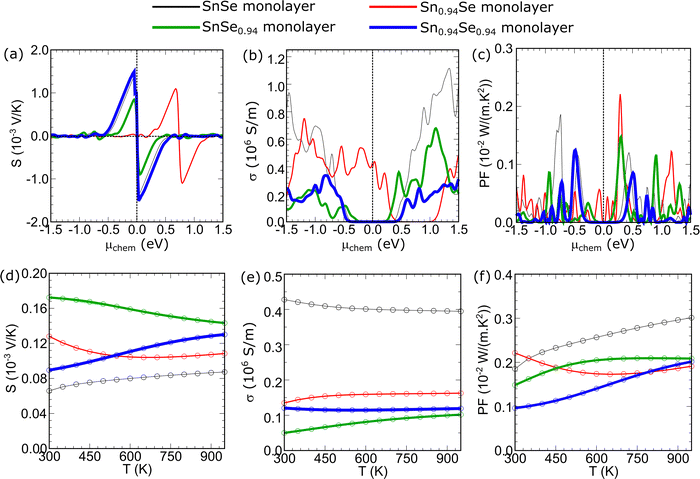
The effect of vacancies on thermoelectric transport properties, such as the Seebeck coefficient (S) and electrical conductivity (σ) of the SnSe monolayer, was evaluated at room temperature (T = 300 K). Fig. 5(a) shows the S curves as a function of the chemical potential (μchem), indicating that the bandgap of each system strongly influences the S behavior. The Sn0.94Se0.94 monolayer, with the largest bandgap, exhibits the highest S compared to other systems with a maximum S of 1.510 × 10−3 V K−1. These results suggest that S optimization can be achieved through electronic structure modifications, such as bandgap engineering or band convergence approaches. In particular, the Sn0.94Se monolayer with p-type conductor behavior shows a significant potential increase in S upon n-type doping, with a maximum S of 1.098 × 10−3 V K−1. Fig. 5(b) displays σ as a function of μchem. Similar to S, σ also strongly depends on the bandgap. The bandgap describes the energy range around the Fermi level (μchem = 0) with σ = 0. For the Sn0.94Se monolayer, σ remains high even at the Fermi level (4.231 × 105 S m−1), confirming the metallic behavior of the system. It is important to note that the τ value used to calculate the σ is obtained from deformation potential theory, which assumes that carrier scattering is mainly governed by acoustic phonons, an assumption generally valid for defect-free crystals. However, in systems containing vacancies, additional scattering mechanisms, such as defect and impurity scattering, can significantly influence τ. As a result, the calculated transport properties for defective systems may slightly overestimate the absolute values of the σ. To mitigate this limitation, we also evaluated the normalized σ/τ as functions of μchem (see Fig. S2(a) in the SI). The consistent trends between σ/τ and the potential deformation theory-based σ indicate that the vacancy-induced variations in the electronic transport are primarily governed by modifications in the electronic structure rather than the absolute value of τ. This confirms that the comparative analysis among different vacancy configurations remains valid within the constant-τ framework. In addition, we calculated the normalized electronic thermal conductivity, κe/τ, as a function of μchem, as shown in Fig. S2(b) in SI. The observed trend of κe/τ follows that of σ/τ, confirming that the Wiedemann–Franz law holds for all investigated systems. This consistency further supports the reliability of the transport behavior obtained within the constant-τ approximation.In the present study, the thermoelectric performance of defective SnSe monolayers was evaluated in terms of the power factor (PF = S2σ), which represents the intrinsic electronic contribution to the overall thermoelectric efficiency. Although the figure of merit (ZT) is the most relevant descriptor of the thermoelectric performance, its accurate determination requires both electronic and lattice thermal conductivities. Since our calculations were carried out under the constant relaxation time approximation without explicit consideration of phonon transport, the lattice thermal conductivity could not be evaluated. Therefore, the discussion is limited to PF, which remains a meaningful descriptor for comparing the relative electronic performance of different vacancy configurations. The calculated PF as a function of μchem is shown in Fig. 5(c). Of the four systems reviewed, the Sn0.94Se monolayer exhibits the highest PF of 2.212 × 10−3 W m−1 K−2 (n-type doping), followed by SnSe monolayer (1.861 × 10−3 W m−1 K−2, p-type doping), SnSe0.94 monolayer (1.477 × 10−3 W m−1 K−2, n-type doping), and Sn0.94Se0.94 monolayer (1.246 × 10−3 W m−1 K−2, p-type doping).
The doping position that yields the maximum PF for each system was used to evaluate the thermoelectric transport properties as a function of T. Fig. 5(d) shows that the four systems have distinct S values at T = 300 K. The SnSe0.94 monolayer exhibits the highest S of about 0.173 × 10−3 V K−1, followed by the Sn0.94Se monolayer at 0.129 × 10−3 V K−1, while the Sn0.94Se0.94 and SnSe monolayers are lower at 0.090 × 10−3 V K−1 and 0.066 × 10−3 V K−1, respectively. With increasing temperature, contrasting trends emerge. The SnSe0.94 and Sn0.94Se monolayers display a gradual decline in S, reaching 0.144 × 10−3 V K−1 and 0.109 × 10−3 V K−1 at 950 K. In contrast, the Sn0.94Se0.94 and SnSe monolayers exhibit an increasing trend, with S values rising to 0.131 × 10−3 V K−1 and 0.088 × 10−3 V K−1, respectively. These findings indicate that proper selection of doping type and concentration can optimize the Seebeck coefficient. Fig. 5e shows that σ is dominated by the SnSe monolayer across the entire temperature range. At 300 K, the SnSe monolayer reaches about 4.288 × 105 S m−1, which is higher than those of the Sn0.94Se monolayer (1.365 × 105 S m−1), Sn0.94Se0.94 monolayer (1.236 × 105 S m−1), and SnSe0.94 monolayer (0.524 × 105 S m−1) systems. Importantly, the SnSe monolayer maintains a nearly constant σ with temperature, slightly decreasing to 3.961 × 105 S m−1 at 950 K. The other three systems also remain nearly temperature-independent, with conductivities fluctuating only slightly in the range of 1.7–1.0 × 105 S m−1. Such a high σ of the SnSe monolayer is advantageous for thermoelectric applications, although it must be balanced with a sufficiently high S to maximize the PF.
Fig. 5(f) shows the PF as a function of temperature. At 300 K, the Sn0.94Se monolayer exhibits the largest PF of about 2.226 × 10−3 W m−1 K−2, followed closely by the SnSe monolayer (1.869 × 10−3 W m−1 K−2) and SnSe0.94 monolayer (1.512 × 10−3 W m−1 K−2) systems, whereas the Sn0.94Se0.94 monolayer trails behind at 0.957 × 10−3 W m−1 K−2. However, the temperature evolution of PF reveals strikingly different behaviors. As the temperature increases to 950 K, the SnSe monolayer significantly improves, reaching the highest PF of 3.026 × 10−3 W m−1 K−2. The Sn0.94Se0.94 monolayer system also shows a strong enhancement, rising steadily to 2.019 × 10−3 W m−1 K−2 at 950 K. In contrast, the SnSe0.94 and Sn0.94Se monolayers exhibit a monotonic decline, with PF values dropping to 2.099 × 10−3 W m−1 K−2 and 1.917 × 10−3 W m−1 K−2, respectively, at 950 K. These result indicate that the combination of moderate electrical conductivity and a high Seebeck coefficient makes the Sn0.94Se monolayer suitable for low-temperature thermoelectric applications (300–400 K).
This crossover behavior between the Sn0.94Se and SnSe monolayer systems can be understood in terms of the dominant charge-transport mechanisms at different temperature regimes. At low temperatures (300–400 K), the Sn0.94Se monolayer exhibits a degenerate carrier distribution due to the formation of shallow defect states near the Fermi level induced by Sn vacancies. These defect-induced states increase the carrier concentration and enhance electrical conductivity while maintaining a reasonably large Seebeck coefficient because of the asymmetric density of states around the Fermi level. As a result, the Sn0.94Se monolayer displays a relatively large PF in the low-temperature region. In contrast, the SnSe monolayer behaves as a typical narrow-gap semiconductor, where the number of thermally excited carriers increases exponentially with temperature. Although carrier mobility decreases slightly due to enhanced phonon scattering, this reduction is overcompensated by the rapid rise in carrier concentration, leading to improved electrical conductivity and a higher PF at elevated temperatures. Consequently, above approximately 600 K, the SnSe monolayer surpasses the defective systems in PF performance. Such temperature-dependent crossover transport has also been reported in other defect-engineered chalcogenides, such as GeSe,79 where moderate vacancy concentrations enhance low-temperature PF but lead to increased carrier scattering at high temperatures.
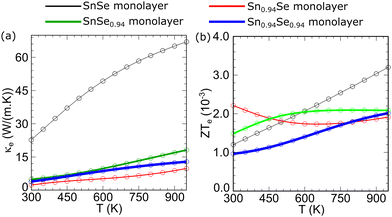
Although the figure of merit (ZT) was not explicitly calculated in this study, thermoelectric performance analysis was still carried out through the evaluation of PF combined with the analysis of the electronic thermal conductivity (κe) as a function of T, as shown in Fig. 6(a). It can be seen that the system with vacancies, either Sn, Se, or both, has a much lower κe than the perfect SnSe monolayer. This condition indicates that the introduction of vacancies can effectively suppress the contribution of thermal conductivity from charge carriers, a crucial aspect in improving thermoelectric efficiency. Therefore, even though the PF of defective systems decreases slightly at elevated temperatures, the combination of the higher PF of the Sn0.94Se monolayer at low temperatures and the strong suppression of κe suggests that the overall ZT still improves, particularly in the low-temperature region, where the PF enhancement is most evident. Moreover, previous studies65 have shown that the lattice thermal conductivity (κl) of the SnSe monolayer is substantially lower than κe. Considering this, the total thermal conductivity of the vacancy-containing systems is expected to be smaller, reinforcing the notion that Sn-vacancy engineering can effectively enhance thermoelectric performance. For a more comprehensive evaluation of the thermoelectric behavior, the electronic figure of merit (ZTe = PF/κe) was calculated, as depicted in Fig. 6(b). The ZTe of the Sn0.94Se monolayer exhibits the highest value in the low-temperature range (300–400 K), consistent with its superior power factor (PF) in this region (see Fig. 5(f)). This suggests that moderate Sn vacancies can improve the balance between electrical conductivity and Seebeck coefficient, enhancing the low-temperature thermoelectric performance. In contrast, at higher temperatures (above 600 K), the SnSe monolayer shows a more pronounced increase in ZTe due to its rapidly increasing PF despite its higher κe.
To further validate our theoretical results, we compared them with recent experimental observations. Wu et al.80 demonstrated that introducing Sn vacancy defects can significantly improve the thermoelectric efficiency of polycrystalline SnSe, increasing the ZT value by up to 66.7% (from 0.36 to 0.6 at 773 K). Likewise, Lee et al.81 found that the high PF observed in hole-doped SnSe is strongly correlated with the Sn vacancy concentration, which is determined by the cooling rate during single-crystal growth. Although these experimental studies were performed on bulk or polycrystalline SnSe, while the present work focuses on the monolayer system, the overall trends in electronic transport enhancement due to Sn vacancies remain consistent. It is worth noting that in this study, we did not calculate the full ZT, since the κl was not considered. Therefore, the discussion is restricted to the electronic contribution (PF and ZTe) and their qualitative consistency with the experimental findings. This comparison still provides valuable insights into how vacancy-induced carrier tuning can effectively improve thermoelectric performance in both bulk and low-dimensional SnSe systems. Therefore, engineering the Sn vacancies in the SnSe monolayers has been proven to be an effective strategy for optimizing their thermoelectric performance.
4. Conclusion
The structural, electronic, and thermoelectric properties of the SnSe monolayer with various vacancy configurations have been systematically investigated using density functional theory combined with Boltzmann transport calculations. Structural analysis reveals that the Sn vacancy produces the most pronounced lattice distortion compared to Se or combined Sn–Se vacancies, as evidenced by the larger atomic displacements in the Sn0.94Se monolayer. Interestingly, in the case of the Sn–Se vacancies, atomic displacements are relatively small despite the higher number of missing atoms, due to the charge compensation that stabilizes the system. These distortions are accompanied by a reduction in the monolayer surface area, which directly influences the electronic and transport properties.From the electronic property perspective, the perfect SnSe monolayer behaves as a semiconductor with an indirect band gap of 0.908 eV. The creation of the Sn vacancy transforms the system into a p-type conductor with high electrical conductivity, while the Se vacancy reduces the band gap to 0.508 eV, and the Sn–Se double vacancies instead widen the gap to 1.039 eV. These electronic transitions are attributed to the appearance of defect states around the Fermi level, as confirmed by the PDOS analysis. A clear correlation is also established between the band gap and thermoelectric properties: larger band gaps lead to higher Seebeck coefficients, with the Sn0.94Se0.94 monolayer exhibiting the maximum value of 1.510 × 10−3 V K−1. In contrast, the transition to a p-type conductor in the Sn0.94Se monolayer results in the highest electrical conductivity of 4.231 × 105 S m−1. The superior power factor performance of the Sn0.94Se monolayer at low-to-medium temperatures (300–400 K), with a maximum of 2.226 × 10−3 W m−1 K−2, was observed, which arises from the optimal balance between a relatively high Seebeck coefficient and a moderate electrical conductivity. Furthermore, the introduction of vacancy defects effectively reduces the electronic thermal conductivity, which theoretically contributes to an enhanced thermoelectric figure of merit.
Finally, vacancy-defect engineering emerges as a powerful strategy for tailoring the thermoelectric performance of the SnSe monolayers. Among the studied systems, the Sn0.94Se monolayer can be identified as the most promising candidate for low-temperature thermoelectric applications. Beyond these findings, this study provides valuable theoretical insights that can serve as a guide for experimental efforts focused on synthesizing and optimizing vacancy-controlled SnSe-based thermoelectric materials, particularly through identifying defect configurations that balance structural stability, electronic transitions, and transport efficiency.
Author contributions
E. B. Y., S. F., and M. F. designed and conceived the study. E. B. Y. conducted the simulation, analyzed the data and wrote the initial draft. S. F., and M. F. revised the paper. E. B. Y. wrote proposal and acquired project funding. All authors confirmed the final manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article, including the Quantum ESPRESSO input and output files, are available from the corresponding author upon reasonable request.Supplementary information is available. The Supplementary Information includes convergence testing of k-point sampling and additional transport-property data for the SnSe-based monolayers. See DOI: https://doi.org/10.1039/d5cp03391h.
Acknowledgements
This research was supported by “Riset Dosen Muda (RDM)” research grant with contract number: 222-185/UN7.D2/PP/IV/2025.References
- J. Wei, M. Sajjad, J. Zhang, D. Li and Z. Mao, The rise of novel 2D materials beyond graphene: A comprehensive review of their potential as supercapacitor electrodes, Surf. Interfaces, 2023, 42, 103334 CrossRef CAS.
- M. Zhao, C. Casiraghi and K. Parvez, Electrochemical exfoliation of 2D materials beyond graphene, Chem. Soc. Rev., 2024, 53, 3036–3064 RSC.
- D. Zhu, L. Zhang, L. Wang, H. Q. Fu, Z. Wu, M. Dong, Y. Zou, Y. Lei, X. Zhang, Y. L. Zhong and L. Wang, Electrochemical Engineering of Emerging 2D Materials beyond Graphene: Progress and Prospects, Small Methods, 2025, 2500197 CrossRef CAS PubMed.
- R. Kurapati, K. Kostarelos, M. Prato and A. Bianco, Biomedical Uses for 2D Materials Beyond Graphene: Current Advances and Challenges Ahead, Adv. Mater., 2016, 28, 6052–6074 CrossRef CAS PubMed.
- W. Yu, K. Gong, Y. Li, B. Ding, L. Li, Y. Xu, R. Wang, L. Li, G. Zhang and S. Lin, Flexible 2D Materials beyond Graphene: Synthesis, Properties, and Applications, Small, 2022, 18, 2105383 CrossRef CAS.
- R. Gusmão, M. Veselý and Z. Sofer, Recent Developments on the Single Atom Supported at 2D Materials Beyond Graphene as Catalysts, ACS Catal., 2020, 10, 9634–9648 CrossRef.
- Y. Pu, J. Zhang, P. Li, G. Wan, J. Pan, Y.-F. Zhang and S. Du, Unveiling the Mechanism of Negative Poisson's Ratio in Phosphorus-like 2D MX Materials Driven by Geometric and Electronic Structures, J. Phys. Chem. Lett., 2025, 16, 5820–5826 CrossRef CAS PubMed.
- M. Kang, T. Liu, H. Sun, L. Li and K. Wang, Blue phosphorus phase GeSe monolayer for nitrogenous toxic gas sensing: A DFT study, Sens. Actuators, A, 2024, 365, 114861 CrossRef CAS.
- S. Guan, C. Liu, Y. Lu, Y. Yao and S. A. Yang, Tunable ferroelectricity and anisotropic electric transport in monolayer β-GeSe, Phys. Rev. B, 2018, 97, 144104 CrossRef.
- E. Sutter, K. Kisslinger, L. Wu, Y. Zhu, S. Yang, F. Camino, C.-Y. Nam and P. Sutter, Single Crystalline GeSe van der Waals Ribbons With Uniform Layer Stacking, High Carrier Mobility, and Adjustable Edge Morphology, Small, 2024, 20, 2406129 CrossRef CAS PubMed.
- D. M. Kennes, L. Xian, M. Claassen and A. Rubio, One-dimensional flat bands in twisted bilayer germanium selenide, Nat. Commun., 2020, 11, 1124 CrossRef CAS.
- E. Sutter, J. S. French and P. Sutter, Free-standing large, ultrathin germanium selenide van der Waals ribbons by combined vapor–liquid–solid growth and edge attachment, Nanoscale, 2022, 14, 6195–6201 RSC.
- Y. Mao, X. Wu, H. Chen and J. Deng, Controllable preparation of ultrathin GeSe nanosheets for infrared photodetection, Infrared Phys. Technol., 2023, 132, 104736 CrossRef CAS.
- J. Zhou, L. Gao, S. Yang, Z. Qu, Y. Cao, J. Pang, J. Ni and J. Zhang, Enhancing photovoltaic performance of GeSe thin film solar cells by photogenerated carriers redistribution via Cu doping, Appl. Surf. Sci., 2025, 682, 161675 CrossRef CAS.
- Y. Shi, M. Yuan, M. Wei, Y. Wang, M. Qin, Z. Wei, Y. Chen and J. Lian, Thickness modulated optical and bandgap properties at visible frequencies of GeSe thin films, Phys. B, 2025, 705, 417085 CrossRef CAS.
- A. Shafique and Y.-H. Shin, Thermoelectric and phonon transport properties of two-dimensional IV–VI compounds, Sci. Rep., 2017, 7, 506 CrossRef PubMed.
- X. Lv, W. Wei, Q. Sun, F. Li, B. Huang and Y. Dai, Two-dimensional germanium monochalcogenides for photocatalytic water splitting with high carrier mobility, Appl. Catal., B, 2017, 217, 275–284 CrossRef CAS.
- H. Huang, J. Wang, Z. Xiang, Q. Li, X. Zhu, L.-L. Wang and H. Zhang, Two-dimensional γ-GeSe/BlueP heterojunctions for efficient solar energy conversion applications, Surf. Interfaces, 2025, 62, 106119 CrossRef CAS.
- Z. Cheng, J. Zhang, L. Lin, Z. Zhan, Y. Ma, J. Li, S. Yu and H. Cui, Pressure-Induced Modulation of Tin Selenide Properties: A Review, Molecules, 2023, 28, 7971 CrossRef CAS PubMed.
- S. M. Ali, H. Kassim, Z. M. Alaizeri and M. Shahabuddin, Enhanced electrochemical performance of novel nanoarchitectonics tin selenide (SnSe/rGO) pseudocapacitive material for energy storage application, J. Energy Storage, 2023, 73, 109163 CrossRef.
- Y. Hao, J. Ren, M. Sun, X. Geng, Y. Gu, Y. Li and Y. Hao, Borax-Assisted Ball Milling Produces High-Yield Tin Selenide Quantum Dots for Efficient Perovskite Solar Cell Applications, ACS Sustainable Chem. Eng., 2025, 13, 4631–4640 CrossRef CAS.
- H. Zheng, M. Jia, P. Che and Z. Li, The Fabrication of Tin Selenide Films with Different Preferred Crystal Planes by a Molten Salt Electrolysis Method, J. Electron. Mater., 2025, 54, 7927–7934 CrossRef CAS.
- Z. Zhang, C. Yu, S. Lu, S. Volz and J. Chen, Low thermal conductivity and promising thermoelectric performance induced by resonant bonding in a two-dimensional lead-tin-selenide ordered alloy, Phys. Rev. Appl., 2024, 22, 054013 CrossRef CAS.
- V. P. Zhukov and E. V. Chulkov, Comparative ab initio study of the electronic structure and thermoelectric properties of tin selenide with electron and hole conductivity, Phys. B, 2024, 695, 416529 CrossRef CAS.
- T.-E. Shi, X. Yang, W.-J. Li, Z. Li, Z.-Y. Wang, Y.-X. Zhang, J. Feng and Z.-H. Ge, Multiscale-defects simultaneous optimization of thermoelectric performance in the n-type polycrystalline SnSe via (Zr,Cl) Co-doping, J. Alloys Compd., 2025, 1026, 180535 CrossRef CAS.
- P. Mandal, S. Maitra, U. K. Ghorui, P. Chakraborty, B. Adhikary and D. Banerjee, Effects of codoping on tin selenide nanomaterials to enhance the thermoelectric performance above the ambient temperature range, J. Mater. Chem. C, 2023, 11, 8577–8589 RSC.
- L. Shi, J. Ding, X. Chen, X. Qu, Z. Chen and M. Jiang, High thermoelectric performance of polycrystalline SnSe prepared by cold sintering, Ceram. Int., 2025, 51, 21979–21986 CrossRef.
- Z. Xu, M. Nisar, J. Zhang, F. Li, S. Chen, G. Liang, J. Luo, Z. Zheng and Y.-X. Chen, Copper iodide doping on SnSe polycrystalline with enhanced thermoelectric properties, J. Eur. Ceram. Soc., 2025, 45, 117292 CrossRef CAS.
- H. Shi, Y. Wen, S. Bai, C. Chang, L. Su, T. Gao, S. Liu, D. Liu, B. Qin, Y. Qin, H. Liang, X. Qian, Z. Hou, X. Gao, T. Zhou, Q. Tan and L.-D. Zhao, Crystal symmetry modification enables high-ranged in-plane thermoelectric performance in n-type SnSe crystals, Nat. Commun., 2025, 16, 1788 CrossRef CAS PubMed.
- W. Yang, C. Zhao, B. Du, R. Wu, X. Lai, Y. He and J. Jian, SnSe nanosheet arrays film for trace NO2 detection at room temperature, Sens. Actuators, B, 2022, 370, 132407 CrossRef CAS.
- D. Sun and R. E. Schaak, Solution-Mediated Growth of Two-Dimensional SnSe@GeSe Nanosheet Heterostructures, Chem. Mater., 2017, 29, 817–822 CrossRef CAS.
- N. Ghobadi and E. Gholami Hatam, Investigation the optical band gap of self-assembled monolayer of tin selenide synthesized by chemical solution deposition, Opt. Quantum Electron., 2019, 51, 269 CrossRef.
- Y. J. Zheng, Q. Zhang, O. Odunmbaku, Z. Ou, M. Li and K. Sun, Tuning the carrier type and density of monolayer tin selenide via organic molecular doping, J. Phys.: Condens. Matter, 2021, 34, 085001 CrossRef PubMed.
- K. Ahmad, Z. Almutairi, S. M. Ali, R. Almuzaiqer, C. Wan and A. Sayeed, Synthesis, Characterization and Power Factor Estimation of SnSe Thin Film for Energy Harvesting Applications, Processes, 2024, 12, 665 CrossRef CAS.
- M. Anshory and M. A. U. Absor, Strain-controlled spin-splitting in the persistent spin helix state of two-dimensional SnSe monolayer, Phys. E, 2020, 124, 114372 CrossRef CAS.
- K. D. Pham, T.-D. Hoang, Q.-T. Nguyen and D.-Q. Hoang, Fe-doped SnSe monolayer: A promising 2D material for reusable SO2 gas sensor with high sensitivity, J. Alloys Compd., 2023, 940, 168919 CrossRef CAS.
- E. B. Yutomo, F. A. Noor and T. Winata, Uniaxial strain effects on the electronic and thermoelectric properties of SnSe monolayer: A density functional theory study, Comput. Theor. Chem., 2025, 1248, 115184 CrossRef CAS.
- H. Zhou, W. Zhang, L. Li, F. Sun and A. Hong, Doping engineering: Highly improving hydrogen evolution reaction performance of monolayer SnSe, Int. J. Hydrogen Energy, 2021, 46, 37907–37914 CrossRef CAS.
- M. Insawang, S. Ruamruk, A. Vora-ud, K. Singsoog, S. Inthachai, K. Chaarmart, S. Boonkirdram, M. Horprathum, M. S. Muntini, S. Park, T. B. Phan and T. Seetawan, Investigation on thermoelectric properties of SnSe thin films as prepared by RF magnetron sputtering, Radiat. Phys. Chem., 2024, 222, 111789 CrossRef CAS.
- Y. Shang, X. Pan, Y. Jia, Y. Wu and M. Sun, Effect of pressure on the thermoelectric performance of monolayer Janus MoSSe materials with different native vacancy defects, Nanoscale, 2025, 17, 13861–13868 RSC.
- W. Zheng, W. Cao, Z. Wang, H. Deng, J. Shi and R. Xiong, Improvement of the thermoelectric properties of a MoO3 monolayer through oxygen vacancies, Beilstein J. Nanotechnol., 2019, 10, 2031–2038 CrossRef CAS PubMed.
- R. Kumar, Ab initio study of effect of Se vacancies on the electronic and thermoelectric properties of the two-dimensional MoSe2 monolayer, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 635 CrossRef CAS.
- C. Yue, Z. Huang, W.-L. Wang, Z. Gao, H. Lin, J. Liu and K. Chang, Identification and Manipulation of Atomic Defects in Monolayer SnSe, ACS Nano, 2024, 18, 25478–25488 CrossRef CAS PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. B. Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. D. Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H.-Y. Ko, A. Kokalj, E. Küçükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H.-V. Nguyen, A. Otero-de-la-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, Advanced capabilities for materials modelling with Quantum ESPRESSO, J. Phys.: Condens. Matter, 2017, 29, 465901 CrossRef CAS PubMed.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. D. Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, QUANTUM ESPRESSO: a modular and open-source software project for quantum simulations of materials, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- E. B. Yutomo, F. A. Noor and T. Winata, Effect of the number of nitrogen dopants on the electronic and magnetic properties of graphitic and pyridinic N-doped graphene – a density-functional study, RSC Adv., 2021, 11, 18371–18380 RSC.
- E. B. Yutomo, F. A. Noor, T. Winata, B. Yuliarto and H. Abdullah, Theoretical insights on the effect of alloying with Co in the mechanism of graphene growth on a CuCo (1 1 1) catalyst, Appl. Surf. Sci., 2023, 631, 157500 CrossRef CAS.
- C. G. Broyden, The Convergence of a Class of Double-rank Minimization Algorithms 1. General Considerations, IMA J. Appl. Math., 1970, 6, 76–90 CrossRef.
- R. Fletcher, A new approach to variable metric algorithms, Comput. J., 1970, 13, 317–322 CrossRef.
- D. Goldfarb, A family of variable-metric methods derived by variational means, Math. Comput., 1970, 24, 23–26 CrossRef.
- D. F. Shanno, Conditioning of quasi-Newton methods for function minimization, Math. Comput., 1970, 24, 647–656 CrossRef.
- G. K. H. Madsen and D. J. Singh, BoltzTraP. A code for calculating band-structure dependent quantities, Comput. Phys. Commun., 2006, 175, 67–71 CrossRef CAS.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- L.-C. Zhang, G. Qin, W.-Z. Fang, H.-J. Cui, Q.-R. Zheng, Q.-B. Yan and G. Su, Tinselenidene: a Two-dimensional Auxetic Material with Ultralow Lattice Thermal Conductivity and Ultrahigh Hole Mobility, Sci. Rep., 2016, 6, 19830 CrossRef CAS PubMed.
- H. L. Shi, Q. Z. Han, J. Yang, L. J. Gong, Y. H. Ren, Y. H. Zhao, H. Yang, Q. H. Liu and Z. T. Jiang, Unveiling the temperature-dependent thermoelectric properties of the undoped and Na-doped monolayer SnSe allotropes: a comparative study, Nanotechnology, 2024, 35, 195705 CrossRef CAS PubMed.
- Y. Cheng, L. Zhu, G. Wang, J. Zhou, S. R. Elliott and Z. Sun, Vacancy formation energy and its connection with bonding environment in solid: A high-throughput calculation and machine learning study, Comput. Mater. Sci., 2020, 183, 109803 CrossRef CAS.
- Y. Gan and H. Zhao, Chirality and vacancy effect on phonon dispersion of MoS2 with strain, Phys. Lett. A, 2016, 380, 745–752 CrossRef CAS.
- Y. Zhou, W. Li, M. Wu, L.-D. Zhao, J. He, S.-H. Wei and L. Huang, Influence of defects on the thermoelectricity in SnSe: A comprehensive theoretical study, Phys. Rev. B, 2018, 97, 245202 CrossRef CAS.
- N. Al Bouzieh, M. A. Sattar, M. Benkraouda and N. Amrane, A Comparative Study of Electronic, Optical, and Thermoelectric Properties of Zn-Doped Bulk and Monolayer SnSe Using Ab Initio Calculations, Nanomaterials, 2023, 13, 2084 CrossRef CAS PubMed.
- G. Ding, Y. Hu, D. Li and X. Wang, A comparative study of thermoelectric properties between bulk and monolayer SnSe, Results Phys., 2019, 15, 102631 CrossRef.
- M. Luo, Y. Xu and Y. Shen, Magnetic properties of SnSe monolayer doped by transition-metal atoms: A first-principle calculation, Results Phys., 2020, 17, 103126 CrossRef.
- J. Wu, X. Li, L. Huang, T. Liang, X. Xing and A. Luo, SnSe Monolayer-Based heavy metal sensors with high Sensitivity, Selectivity, and Reusability: Insights from first principle calculation, Results Phys., 2023, 53, 106973 CrossRef.
- N. Veronica, F. Millah, M. S. Muntini, E. H. Hasdeo, N. Amalia and S. A. Wella, Strain-induced high thermoelectric performance of monolayer SnSe: a DFT study, Phys. Scr., 2025, 100, 075950 CrossRef CAS.
- T. V. Vu, H. D. Tong, T. K. Nguyen, C. V. Nguyen, A. A. Lavrentyev, O. Y. Khyzhun, B. V. Gabrelian, H. L. Luong, K. D. Pham, P. T. Dang and D. D. Vo, Enhancement of monolayer SnSe light absorption by strain engineering: A DFT calculation, Chem. Phys., 2019, 521, 5–13 CrossRef CAS.
- M. Parenteau and C. Carlone, Influence of temperature and pressure on the electronic transitions in SnS and SnSe semiconductors, Phys. Rev. B:Condens. Matter Mater. Phys., 1990, 41, 5227–5234 CrossRef CAS PubMed.
- Y. Li, M. N. Wu, T. Ding, K. Ma, F. S. Liu, W. Q. Ao and J. Q. Li, Promising thermoelectric properties and anisotropic electrical and thermal transport of monolayer SnTe, Appl. Phys. Lett., 2019, 114, 083901 CrossRef.
- A. Shukla and N. K. Gaur, Adsorption of O3, SO3 and CH2O on two dimensional SnS monolayer: A first principles study, Phys. B, 2019, 572, 12–17 CrossRef CAS.
- A. I. Popoola, Y. A. Odusote, S. T. Ogunjo and R. A. Distasio, Exploring the suitability of narrow-bandgap compounds for thermoelectric application, Phys. Scr., 2023, 98, 075501 CrossRef CAS.
- N. T. Hung, J. M. Adhidewata, A. R. T. Nugraha and R. Saito, Enhanced thermoelectric performance by van Hove singularities in the density of states of type-II nodal-line semimetals, Phys. Rev. B, 2022, 105, 115142 CrossRef CAS.
- I. M. R. Verzola, R. A. B. Villaos, W. Purwitasari, Z.-Q. Huang, C.-H. Hsu, G. Chang, H. Lin and F.-C. Chuang, Prediction of van Hove singularities, excellent thermoelectric performance, and non-trivial topology in monolayer rhenium dichalcogenides, Mater. Today Commun., 2022, 33, 104468 CrossRef CAS.
- P. Trocha, Spin-dependent thermoelectric properties of a hybrid ferromagnetic metal/quantum dot/topological insulator junction, Sci. Rep., 2025, 15, 4904 CrossRef CAS PubMed.
- E. B. Yutomo, F. A. Noor and T. Winata, The effect of vacancies on the magnetic and optical properties of monolayer alpha lead oxide (α-PbO): A density functional theory study, Micro Nanostruct., 2022, 163, 107125 CrossRef.
- L.-B. Shi, M. Yang, S. Cao, Q. You, Y.-Y. Niu and Y.-Z. Wang, Elastic behavior and intrinsic carrier mobility for monolayer SnS and SnSe: First-principles calculations, Appl. Surf. Sci., 2019, 492, 435–448 CrossRef CAS.
- H. Y. Lv, W. J. Lu, D. F. Shao and Y. P. Sun, Enhanced thermoelectric performance of phosphorene by strain-induced band convergence, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 90, 085433 CrossRef CAS.
- S. Ghorui, J. Kangsabanik, M. Aslam and A. Alam, Optoelectronic and transport properties of vacancy-ordered double-perovskite halides: A first-principles study, Phys. Rev. Appl., 2024, 21, 024036 CrossRef CAS.
- P. Yu and B. Pan, Effect of vacancy defects on thermal transport properties of tungsten nitride compounds on divertor surface in ITER, Commun. Phys., 2024, 7, 27 CrossRef CAS.
- T. Lyu, X. Li, Q. Yang, J. Cheng, Y. Zhang, C. Zhang, F. Liu, J. Li, W. Ao, H. Xie and L. Hu, Stepwise Ge vacancy manipulation enhances the thermoelectric performance of cubic GeSe, Chem. Eng. J., 2022, 442, 136332 CrossRef.
- C. Wu, X.-L. Shi, M. Li, Z. Zheng, L. Zhu, K. Huang, W.-D. Liu, P. Yuan, L. Cheng, Z.-G. Chen and X. Yao, Argon Plasma Bombardment Induces Surface-Rich Sn Vacancy Defects to Enhance the Thermoelectric Performance of Polycrystalline SnSe, Adv. Funct. Mater., 2024, 34, 2402317 CrossRef CAS.
- J.-E. Lee, K. Kim, V. Q. Nguyen, J. Hwang, J. D. Denlinger, B. I. Min, S. Cho, H. Ryu, C. Hwang and S.-K. Mo, Enhanced thermoelectric performance of SnSe by controlled vacancy population, Nano Convergence, 2023, 10, 32 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |