Theoretical study of Si/C alternately substituted annulenes with a belt structure
Takako
Kudo
 *ab,
Katherine N.
Ferreras
c,
Taiji
Nakamura
bd,
Akira
Imanishi
b,
Ryuta
Ikutomo
b and
Mark S.
Gordon
*ab,
Katherine N.
Ferreras
c,
Taiji
Nakamura
bd,
Akira
Imanishi
b,
Ryuta
Ikutomo
b and
Mark S.
Gordon
 *c
*c
aGunma Study Center, The Open University of Japan, Maebashi, Gunma 371-0032, Japan. E-mail: t-kudo@ouj.ac.jp
bDepartment of Pure and Applied Science, Graduate School of Science and Technology, Gunma University, Kiryu 376-8515, Japan. E-mail: tkudo@gunma-u.ac.jp
cDepartment of Chemistry and Ames National Laboratory, Iowa State University, Ames, Iowa 50011, USA. E-mail: mgordon@iastate.edu
dFukui Institute for Fundamental Chemistry, Kyoto University, Takano, Nishihiraki-cho 34-4, Sakyo-ku, Kyoto 606-8103, Japan. E-mail: nakamura.taiji.6d@kyoto-u.ac.jp
First published on 11th December 2025
Abstract
Alternating Si/C belt-shaped annulenes, H2nSinCn (n = 3, 4, 5, 6, and 10), representing a third class of annulenes beyond the planar and Möbius types, were investigated through quantum chemical calculations. Notably, the Si–C bond length alternation is not observed regardless of the number of π electrons (e.g., 4n or 4n + 2). For the smaller molecules (n = 3 and 4), the belt-shaped isomers were found to be less thermodynamically stable than their planar counterparts, benzene (n = 3) and cyclooctatetraene (n = 4), due to distorted π orbitals and strained ring structures. The quasi-atomic orbital (QUAO) analysis reveals that the planar n = 3 Si/C annulene exhibits delocalized π bonding with weak aromatic stabilization, while its belt-shaped counterpart shows hybridization-induced π localization and antiaromatic character. Both n = 4 systems (planar and belt-shaped) are intrinsically antiaromatic, although geometric distortion in the belt isomer partially alleviates this destabilization. As the ring size increases (n ≥ 5), the Si–C π orbitals become increasingly localized due to geometric constraints, in contrast with the uniform delocalization observed in the all-carbon analog H20C20. Notably, in the larger annulenes (n = 5, 6, and 10), the curvature of the belt structure imposes a ceiling on π conjugation. These results underscore the key role of geometry and QUAO asymmetry in modulating antiaromaticity in Si/C belt systems.
1. Introduction
Annulenes are a fascinating group of compounds that are of considerable interest in organic chemistry. There is a vast literature on the properties and behavior of annulenes, ranging from benzene to polyaromatic hydrocarbons1,2 to macrocycles3–6 to substitutions with heteroatoms. For example, borazine (B3N3H6)7–12 is isoelectronic with benzene and there are valence isoelectronic benzene analogs that contain heavier group 14 elements such as Si and Ge.13–18 In addition to their fundamental interest, Si/C π-conjugated systems are increasingly relevant to the design of novel semiconducting and optoelectronic materials, owing to the tunable electronic properties offered by heavier main-group elements like silicon.19–21Kudo and co-workers22,23 have previously investigated the structure in the ground and low-lying excited electronic states of the Si/C-alternately substituted analogs of cyclobutadiene, benzene, cyclooctatetraene (COT), and cyclodecapentaene. The 4-, 6-, and 8-membered compounds were found to have equal-bond planar structures in the ground S0 state that are not always observed in the all-carbon or all-silicon congeners. These previous results have spurred the present investigation of alternating mixed Si/C analogs of polyenes or saturated polyhedral compounds.24,25
The target of the present study is the Si/C alternately substituted annulenes with a belt structure, sometimes called the third type of annulenes26,27 after the well-known planar species and the twisted ring structure Möbius annulenes.28,29 The rings in the belt structures are not twisted but H (or other substituents) attached to the heavy atoms are almost perpendicular to the ring plane and alternating up and down (see Fig. 1), so the structures look like a band or belt. The ring sizes considered in this study are relatively small: 6, 8, 10, 12, and 20-membered rings with the formula H2nSinCn (n = 3, 4, 5, 6, and 10).
 | ||
| Fig. 1 Belt-shaped annulene (H20C20, left) and the Si/C analog with formula H2nSinCn for n = 10 (right). | ||
Because of the unusual structures of the compounds of interest, the quasi-atomic orbital (QUAO) analysis developed by Ruedenberg et al.30–43 is employed in this work to provide detailed insights into how electron populations, hybridization, and bond strengths vary between planar and belt-shaped systems. For the 6- and 8-membered rings, the properties investigated here are discussed in comparison with 1,3,5-trisilabenzene and 1,3,5,7-tetrasilacyclooctatetraene, respectively. Furthermore, comparison with the all-carbon analog (H20C20) was carried out for the 20-membered ring. These comparisons help to identify the unique characteristics of the new Si/C alternating compounds, as well as to provide deeper insights into the regular annulene chemistry as well.
2. Computational methods
2.1. Theoretical background of QUAOs analysis
The quasi-atomic orbitals (QUAOs) for a self-consistent field molecular wave function are constructed in a two-step process. The first step uses accurate atomic minimal basis set (AAMBS)44–46 orbitals, which are obtained from highly accurate self-consistent field calculations performed on isolated atoms. The AAMBS serve as a template to generate precursor QUAOs using the singular value decomposition (SVD30,47,48). The precursor QUAOs are then orthogonalized, while ensuring maximum overlap with the AAMBS orbitals, thereby exhibiting minimal deviation from the original free atom orbitals.In the second step, precursor QUAOs are combined to construct oriented QUAOs that adapt most effectively to the chemical environment by minimizing the number of significant off-diagonal elements (i.e., bond orders) of the density matrix. The oriented QUAOs are consequently aligned spatially and reflect typical molecular bonding patterns. Further details on the computation of QUAOs have been discussed in previous papers.30–34 The QUAO analysis generates three primary sets of data: (1) a list of hybridization characters (calculated by overlap integrals between QUAOs and the respective AAMBS orbitals on the same atom) and orbital occupations for each atom; (2) a list of QUAO populations in descending order; (3) a table of QUAO pairs with their respective bond orders and kinetic bond orders (defined below).
In terms of QUAOs the first order density matrix, r(1,2), is expressed as follows:
 | (1) |
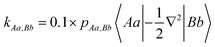 | (2) |
The scale factor of 0.1 was introduced to compensate for the omission of potential energy contributions.52 Generally, a negative KBO indicates an attractive (bonding) interaction, and positive KBOs correspond to repulsive (antibonding) interactions. One can think of KBOs as energy-weighted bond orders and therefore more closely aligned than simple bond orders with bond energies.
The label of each QUAO has several components. The first component is the atom symbol with a subscripted number that indicates the atom on which the QUAO is centered. If the QUAO participates in bonding, the second components of the label, are lower-case atom symbols with subscripted numbers, indicating the atoms toward which the QUAO is directed. The last component of the label is a sigma or pi symbol, characterizing the type of bond in which the QUAO participates, namely, a σ or π bond. For example, C1c2σ is a QUAO in which a sigma QUAO is centered on the atom C1 and is oriented toward atom C2. A bond, pair of interacting QUAOs, is depicted by two labels separated by a dash, for example, C1c2σ–C2c1σ. If the systems studied have symmetry the subscripted numbers identifying the atoms for equivalent QUAOs are dropped, for example, the label C1c2σ would be referred as Ccσ. The QUAO calculations were carried out at the RHF/6-311++G(d,p) level of theory at both the optimized MP2 and DFT geometries (see following subsection) using the GAMESS53–56 software suite. The QUAOs were plotted using the MacMolPlot57 visualization software.
2.2. Computational details
The target molecules of the present study are the Si/C alternately mixed annulenes, H2nSinCn (n = 3, 4, 5, 6, and 10), and H20C20 with a belt-type structure. For comparison, 1,3,5-trisilabenzene (H6Si3C3) and 1,3,5,7-tetrasilacyclooctatetraene (H8Si4C4) are investigated as well. Geometry optimizations of all molecules were carried out using second order perturbation theory (MP2).58–60 The cc-pVDZ basis set61 was used for the level of theory.As an assessment of their aromaticity, the nucleus independent chemical shift (NICS) index62,63 of the annulenes was calculated using B3LYP64,65/6-311++G(2d,p)66 at the MP2/cc-pVDZ optimized geometries. In general, a large negative NICS is taken to indicate aromatic character, whereas a large positive NICS is an indication of antiaromaticity.
For the isomerization pathways between the belt-type and planar n = 3 and 4 annulenes, CASSCF(6,6) and CASSCF(8,8) calculations67 were carried out, respectively, with the 6-311G(d,p)68,69 basis set. Each active space was constructed using the 6 and 8, respectively, frontier π orbitals and the related electrons. For example, n = 3 (6,6) means that 6 electrons and 6 frontier π orbitals are involved in the active space. Intrinsic reaction coordinate (IRC) calculations were carried out to confirm the connectivity of the transition state and equilibrium structures.70,71 To improve the relative energies, single point energies were calculated at every stationary point using multi-reference second order perturbation theory (MR-MP2)72 with the 6-311G(d,p) basis set. All optimized structures considered here were characterized as minima or transition states by a normal mode vibrational analysis.
The electronic structure calculations described in this subsection were performed using Gaussian 16.73 The molecular structures and related MOs were drawn by GuassView v.6.73 KNF and MSG did not use the Gaussian software, nor would they.
3. Results and discussion
3.1. n = 3 (6-membered ring)
The structure of the belt-type H6Si3C3 is shown together with the regular type, 1,3,5-trisilabenzene in Fig. 2. As seen from the HSiCH angle (167.7°) the plane of the HSiCH unit is almost perpendicular to that of the molecular framework consisting of 6 heavy elements. All Si–C bond lengths are equal in the belt type structure, as for benzene. The Si–C bond length of 1.826 Å is shorter than a typical Si–C bond of methyl silane (1.893 Å) but longer than that of trisilabenzene (1.778 Å), suggesting the extent of π electron delocalization is small compared to the benzene. The Si–H and C–H bond lengths are similar in both isomers.The MP2/cc-pVDZ belt-type isomer is significantly higher in energy than the planar isomer by 127.6 (125.2 free energy) kcal mol−1. This is in agreement with the fact that the large positive NICS value (18.2, see Table 1) does not indicate the existence of aromaticity, in contrast with the benzene congener.
| Compound n | Regular annulene (H2nSinCn) | Belt annulene (H2nSinCn) | Belt annulene (H20C20) | |||||
|---|---|---|---|---|---|---|---|---|
| 3 | 4 | 3 | 4 | 5 | 6 | 10 | 20 | |
| r(Si–C) | 1.778 | 1.770 | 1.826 | 1.813, 1.799 | 1.793 | 1.787 | 1.778 | |
| r(Si–H) | 1.487 | 1.488 | 1.480 | 1.489 | 1.488 | 1.487 | 1.486 | |
| r(C–H) | 1.096 | 1.101 | 1.126 | 1.106 | 1.104 | 1.101 | 1.098 | 1.100 |
| <CSiC | 118.000 | 124.600 | 127.800 | 129.500 | 131.000 | |||
| <SiCSi | 95.700 | 103.000 | 103.400 | 106.500 | 113.100 | |||
| <HSiCH | 0.000 | 0.000 | 167.700 | 175.200 | 176.200 | 176.100 | 177.100 | |
| NICS(0) | −6.162 | 7.578 | 18.196 | 5.094 | 0.950 | 0.770 | −0.083 | 26.664 |
| r(C–C) | 1.447, 1.378 | |||||||
| <CCC | 121.286 | |||||||
| <HCCH | 176.700 | |||||||
The frontier MOs of the n = 3 belt-type structure are shown in Fig. 3. The highest occupied molecular orbital is a degenerate pair. The same is true for the LUMO+1 pair. As one would expect due to the relative electronegativities of C and Si, the occupied MOs have larger LCAO (linear combination of atomic orbitals) coefficients on the carbons, while the reverse is true for the unoccupied MOs. The lowest unoccupied molecular orbital (LUMO) energy (−0.8077 eV) is significantly lower than that of the benzene isomer (2.080 eV), while the degenerate highest occupied molecular orbitals (HOMOs) of the belt-type isomer (−8.362 eV) are also slightly lower in energy than that of benzene (−8.121 eV). These observations may indicate that a single configuration description of the belt type structure is not sufficient.
3.2. n = 4 (8-membered ring)
The structure of the belt-type H8Si4C4 is also depicted in Fig. 2. As reported previously,22 the Si/C alternately substituted COT (cyclooctatetraene) analog has a planar structure with all Si–C bond lengths being 1.770 Å. For the belt-type structure, however, small Si–C bond alternation (1.813 Å and 1.799 Å) is observed, with both sets of bonds being longer than the one in Si/C COT. Interestingly, a weak interaction might exist among the four silicon atoms in the n = 4 belt structure, as the distances between the Si atoms are 2.681 and 2.817 Å, compared with a typical Si–Si single bond distance (2.362 Å) in disilane at the same level of theory. The HSiCH dihedral angle is 175.2°, similar to that in the n = 3 structure. In comparison with the COT analog, there is greater variation in the bond distances, suggesting less delocalization; the NICS value (5.094) is also smaller than the 7.578 of COT suggesting weaker antiaromaticity. However, as for n = 3, the belt type isomer is still higher in energy by 70.5 (70.4 free energy) kcal mol−1 than the COT analog, suggesting the benefit of the π conjugation in the regular planar structure of the latter.As shown in Fig. 4, the mixing of the π character of the frontier MOs seems clearer than for n = 3, possibly because the belt plane is closer to 180° than for n = 3 (167.7°) as mentioned above.
3.3. The larger rings (n = 5, 6, and 10)
Depicted in Fig. 5 are the structures of the belt type Si/C alternately substituted annulenes of the larger n = 5, 6, and 10 rings and the belt type carbon analog, H20C20. The geometrical and NICS data are also summarized in Table 1.In the Si/C compounds the Si–C bond distances are equal or nearly so (see Table 1), in contrast with the carbon ring in H20C20 in which bond alternation is clearly observed. This suggests that remarkable electron delocalization exists in the Si/C mixed belt annulenes. The Si–C bond length shortens as the ring size increases, similar to the regular annulenes. On the other hand, the Si–H and C–H bond lengths are relatively constant regardless of the ring size. Interestingly, unlike the smaller Si/C mixed rings, the belt plane of the H20Si10C10 (n = 10) is inclined by ca. 18° relative to the normal to the heavy atom plane, as shown in Fig. 6.
 | ||
| Fig. 6 A sideview of the structure of H20Si10C10. The numbers are the inclination angles in degrees. | ||
The repulsion among the H atoms seems to prevent the inclination of the belt plane for the smaller rings, but this repulsion apparently decreases enough as the ring size increases to permit the inclination. Therefore, the structural trend may suggest a completely planar ring structure in the larger rings. Based on these results, the belt-type Si/C mixed annulenes seem to be more similar to acyclic polyenes than to the regular annulenes.
The NICS values for the belt-type structures are shown in Table 1. The n = 3 belt structure has the largest NICS (18.196), compared with −6.162 for the isoelectronic benzene analog. The calculated NICS values decrease in magnitude monotonically as the ring size increases, indicating a decrease in antiaromatic character. The n = 10 belt structure NICS is the smalling currents suggesting considerable anti-aromaticity of this compound. As a whole, the effect of “aromaticity” on the stability of the belt-type annulenes does not seem important based on the NICS values.
The frontier orbitals of the compounds of interest, for larger values of n, in this work are shown in Fig. SI1 of the SI. The Si–C π orbitals in the Si/C belt structures are increasingly localized as n increases. In contrast, the π orbitals spread equally on each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in H20C20. The HOMOs are degenerate in the belt annulenes with odd n (3, 5). As seen from Fig. SI1, the orbital energy of the LUMO of these Si/C mixed rings are much larger than in the smaller rings (n = 3 and 4), so a single configuration description is likely reasonable for the larger rings. The internal C–Si–C angles widen from 118° in n = 3 to 131.0° in n = 10, reflecting a reduction in angular strain and consequently improved orbital alignment.
C bond in H20C20. The HOMOs are degenerate in the belt annulenes with odd n (3, 5). As seen from Fig. SI1, the orbital energy of the LUMO of these Si/C mixed rings are much larger than in the smaller rings (n = 3 and 4), so a single configuration description is likely reasonable for the larger rings. The internal C–Si–C angles widen from 118° in n = 3 to 131.0° in n = 10, reflecting a reduction in angular strain and consequently improved orbital alignment.
3.4. Isomerization to the regular type for n = 3 and 4
For both n = 3 and n = 4, CASSCF calculations were carried out to explore the potential energy surface of the isomerization that connects the belt and regular isomers (see Fig. 7), followed by single point multi-reference second order perturbation theory (MR-MP2) energies. For n = 3, the energy decreases almost monotonically from the belt type to the benzene analog. The calculated barrier for the isomerization is so low (0.3 kcal mol−1) that the belt species may be kinetically unstable as one might expect.For n = 4, an intermediate (labelled iv in Fig. 7) with one (C)H significantly out of the plane was found between the belt type and COT analog. The molecular structure shown in Fig. SI2 has almost Cs symmetry; the molecular framework containing most H atoms is nearly flat except for the one out-of-plane C–H bond noted above. The predicted MR-MP2 isomerization barrier is a more substantial 7 kcal mol−1 relative to n = 3. An intermediate with a similar structure was also located at the MP2/cc-pVDZ level of theory, with an energy relative to the COT analog of 11.1 kcal mol−1. Interestingly, the structural characteristics of the intermediate iv resembles that of one of the isomers of Si/C alternately substituted cyclodecapentaene, H10Si5C5.22
Both n = 4 energy barriers from the belt to the intermediate and between the intermediate and COT are low, suggesting that the belt-type and the intermediate are not kinetically stable. An animation of the minimum energy path for the n = 4 potential energy surface is provided in the SI. Based on the intrinsic reaction coordinate the movements of the (C)H seem relatively larger than those of the (Si)H through the whole process of the transformation. The movements of the hydrogen substituents appear to be important for the isomerization. Therefore, the introduction of bulky substituents might increase the kinetic stability of the belt-type annulenes.
3.5. QUAO analysis of n = 3 and 4 Si/C annulenes
The QUAO analysis of planar and belt-shaped Si/C annulenes reveals important differences between the electronic structures of the n = 3 and n = 4 systems. The QUAOs of each Si/C annulene structure are shown in Fig. 8 and 9, respectively, with belt-shaped annulenes labeled (A) and regular (planar) structures labeled (B). Below each QUAO a label and a number identify the QUAO within each molecular system. The number represents the population in electron units, corresponding to the diagonal elements of the first order density matrix, pAaAa in eqn (1). Each σ QUAO is localized and directed towards a single bonding atom, whereas the π QUAOs are delocalized over two adjacent atoms, reflecting their conjugated nature. Accordingly, the π QUAOs are labeled Csisiπ and Siccπ to denote the atomic centers and their bonding character. In Fig. 9(A), two population values are reported for the Csisiπ QUAO of the n = 4 belt-shaped annulene, corresponding to the two types of chemically distinct carbon environments in this molecule (Fig. 10). | ||
| Fig. 8 Oriented quasi-atomic orbitals of (A) belt and (B) planar H6Si3C3 isomers. The QUAO populations are in bold face. | ||
Initially, the σ-framework is analyzed for the four systems, the n = 3 and n = 4 regular and belt-shaped annulenes. Then, to separate the effects of geometry and electron count, the regular and belt-shaped annulenes for n = 3 are compared. Although both n = 3 isomers are formally aromatic (6 π electrons), the belt-shaped structure exhibits clear magnetic evidence (NICS(0) = 18.196) of antiaromatic destabilization, likely influenced by its constrained nonplanar geometry. For the n = 4 structures antiaromaticity in the belt-shaped structure gives rise to electronic asymmetry among similar atoms (e.g., C atoms or Si atoms) within a formally symmetric framework. Parallels are also drawn between the two sets of annulenes, n = 3 and n = 4, to evaluate how geometry and electron count together shape the electronic structure in these Si/C hybrid annulenes.
To establish a baseline for bonding behavior, first consider the σ framework in the context of the hybridization patterns, orbital populations, and bond orders and kinetic bond orders of the oriented QUAOs. As shown in Table 2, the σ QUAOs for the C–H, Si–H, and C–Si interactions, in both planar and belt-shaped annulenes exhibit consistent hybridization trends, namely ∼65–70% p-character and ∼30–35% s-character, consistent with sp2-like hybridization on carbon and silicon atoms. Similarly, the population data presented in Fig. 8 and 9, show minimal variation in the populations of key σ QUAOs. For example, the Csiσ populations range from 1.22 to 1.26, and the Sicσ populations range from 0.74 to 0.77 across all four systems, values that are consistent with the expected electronegativity differences between carbon and silicon. The corresponding bond orders and kinetic bond orders for these σ interactions also show little variation between planar and belt-type geometries, with Csiσ–Sicσ BOs ranging from 0.91 to 0.94 and KBOs between −27.0 and −30.2 kcal mol−1. Similarly, strong BO and KBO values are maintained for C–H and Si–H interactions, with BOs consistently above 0.95 and KBOs ranging from 23.4 to 36.6 kcal mol−1 (Table 3). Together, the consistent hybridization, population symmetry, and the similar bond order (BO)s and kinetic bond order (KBO) values confirm that a strong and consistent σ-bonding framework is preserved in both geometries and ring sizes.
| Compound | H6Si3C3 | H8Si4C4 | ||||||
|---|---|---|---|---|---|---|---|---|
| QUAO label | Planar | Belt | Planar | Belt | ||||
| s | p | s | p | s | p | s | p | |
| Values in parenthesis for the n = 4 belt-shaped isomer correspond to atoms C1/C2 (C1sisiπ), the values listed outside parenthesis correspond to C3/C4 (C3sisiπ). See Fig. 10 for atom numbers. | ||||||||
| Csiσ | 0.31 | 0.69 | 0.33 | 0.67 | 0.33 | 0.6 | 0.33 (0.31) | 0.67 (0.69) |
| Sicσ | 0.34 | 0.66 | 0.33 | 0.67 | 0.35 | 0.65 | 0.33 (0.31) | 0.67 (0.69) |
| Csisiπ | 0.00 | 1.00 | 0.09 | 0.91 | 0.00 | 1.00 | 0.00 (0.05) | 1.00 (0.95) |
| Siccπ | 0.00 | 1.00 | 0.01 | 0.99 | 0.00 | 1.00 | 0.03 | 0.97 |
| Chσ | 0.26 | 0.74 | 0.15 | 0.85 | 0.23 | 0.77 | 0.22 | 0.78 |
| Sihσ | 0.32 | 0.68 | 0.29 | 0.71 | 0.29 | 0.71 | 0.28 | 0.72 |
| Hcσ | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| Hsiσ | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 |
| Compound | H6Si3C3 | H8Si4C4 | ||||||
|---|---|---|---|---|---|---|---|---|
| QUAO pair | Planar | Belt | Planar | Belt | ||||
| BO | KBO | BO | KBO | BO | KBO | BO | KBO | |
| Values in parentheses for the n = 4 belt-shaped isomer correspond to C1sisiπ QUAOs, on carbon atoms C1/C2. | ||||||||
| Csiσ–Sicσ | 0.94 | −28.8 | 0.91 | −27.0 | 0.94 | −30.2 | 0.93 | −28.6, (−28.2) |
| Csisiπ–Siccπ | 0.64 | −9.4 | 0.48 | −3.9 | 0.58 | −9.0 | 0.61 (0.51) | −7.9, (−5.6) |
| Chσ–Hcσ | 0.97 | −36.6 | 0.95 | −31.9 | 0.96 | −34.8 | 0.97 | −34.7, (−34.2) |
| Sihσ–Hsiσ | 0.97 | −25.4 | 0.95 | −23.4 | 0.97 | −24.5 | 0.96 | −23.7 |
Now, consider the π space for n = 3 and n = 4. The n = 3 Si/C annulene systems have six π-electrons, corresponding to (4n + 2) with n = 2. In principle, 4n + 2 π electrons in a ring system correspond to an aromatic molecule. In contrast to the σ-framework, the π-systems of these annulenes exhibit geometry-dependent variations in hybridization, electron distribution, and bonding strength. As shown in Table 2, the planar isomer maintains ideal p-character (100%) in both Csisiπ and Siccπ QUAOs, enabling effective overlap and delocalization across the ring. In the belt-shaped isomer, however, due to its nonplanarity, the Csisiπ QUAO incorporates 9% s-character, while the Siccπ QUAO retains nearly pure p-character (99%). The introduction of s-character into the carbon π orbital reduces its directionality, thereby weakening the overlap with adjacent silicon π orbitals. This deviation is interpreted as an electronic response to angular strain and nonplanarity, in which s–p mixing compensates for the geometric distortion. As a result, the π bond order decreases from 0.64 in the regular isomer to 0.48 in the belt-shaped analog, and the kinetic bond order drops from −9.4 to −3.9 kcal mol−1 (Table 3), indicating a significant loss in π conjugation strength. The bond orders of the planar isomer are consistent with well-established aromatic systems such as benzene and naphthalene, underscoring the stabilizing influence of planarity and uninterrupted π conjugation.43 Taken together, these findings indicate that although the belt-type isomer retains some delocalization, π conjugation is significantly weakened due to hybridization asymmetry (between C and Si) and curvature-induced distortion.
The belt-type structure of the n = 3 system exhibits significant geometric distortion relative to its planar counterpart. This constrained, nonplanar geometry disrupts π delocalization, as reflected by the reduced BO and KBO, and the strongly positive NICS(0) value (+18.2 ppm). These features indicate pronounced antiaromatic character, despite the presence of 4n + 2 π electrons that suggests aromaticity according to Hückel's rule. In contrast, the n = 3 regular (planar) isomer has a negative NICS, ideal π orbital alignment, and BO/KBO values that are consistent with aromatic stabilization. Together, these results highlight how curvature and hybridization asymmetry can disrupt conjugation, even in systems that satisfy aromatic electron-count rules. As shown next, the n = 4 system presents a different situation: although both isomers possess positive NICS values consistent with antiaromaticity, the planar structure maintains a symmetric geometry and ideal π hybridization, while the belt-type isomer responds to its antiaromatic configuration through adaptive orbital asymmetry and selective π localization thereby mitigating the extent of electronic destabilization.
In the n = 4 systems, the impact of antiaromatic destabilization becomes more pronounced, particularly in the belt-shaped structure. As shown in Table 2, the regular H8C4Si4 annulene maintains ideal p-character in both Csisiπ and Siccπ QUAOs, consistent with a delocalized π-system. However, in the belt-shaped isomer, the Csisiπ QUAO adopts two distinct hybridization profiles: one set of carbon atoms (C3/C4) retains pure p-character, while the other (C1/C2) incorporates 5% s-character reflecting chemically and electronically inequivalent environments. This hybridization asymmetry is mirrored in the QUAO electronic populations: Csisiπ in C1/C2 carries 1.51 electrons and C3/C4 contains 1.37 electrons. These values suggest a partial localization of electron density in specific C–Si–C segments of the ring, likely adopted to relieve the electronic strain imposed by the 8 π-electron configuration. While the Siccπ QUAOs can adopt two distinct profiles due to symmetry, the differences in the electronic populations appear in only the seventh decimal place, making all Siccπ QUAO essentially electronically equivalent. With the molecular geometry retaining overall C2v symmetry, the emergence of a subtle (0.014 Å) bond length alternation and hybridization differences reflect an adaptive electronic reorganization aimed at mitigating the destabilizing effects of antiaromaticity.
The electronic asymmetry observed in the QUAO analysis of the belt-shaped n = 4 system is consistent with subtle geometric features in the optimized structure. While distances remain uniform from each carbon atom to adjacent silicon atoms, the Si–C distances from each silicon to its two neighboring carbons differ slightly (∼0.014 Å). This small geometric variation coincides with asymmetries in π QUAO populations and hybridization (Fig. 9A, and Table 2), where chemically distinct carbon atoms exhibit electronically different bonding interactions with silicon. As a result, the silicon atoms engage in asymmetric π bonding, while carbon atoms maintain symmetric bonding environments. This redistribution of π electron density also manifests in bond order and kinetic bond order (KBO) variations. Although the asymmetry is geometrically subtle, it is the electronic adjustment of the carbon atoms, rather than direct Si—Si bonding differences, that drives the weakening of antiaromaticity. Together, these findings suggest that the belt-shaped H8Si4C4 annulene adopts a nonuniform bonding arrangement as an adaptive mechanism to reduce the destabilization associated with its 4n π-electron configuration.
The effects of π hybridization and population asymmetry in the belt-shaped H8Si4C4 annulene are further reflected in the bond orders and kinetic bond orders derived from the interacting QUAOs. Shown in Table 3, the bond order between Csisiπ and Siccπ QUAOs in the planar structure is 0.58, with a corresponding KBO of −9.0 kcal mol−1, indicating moderately strong π conjugation similar to the planar n = 3 analog. In contrast, the belt-shaped isomer exhibits two distinct π bond orders, 0.61 (C3/C4) and 0.51 (C1/C2), depending on the specific Csisiπ orbital involved, with corresponding KBOs of −7.9 (C3/C4) and −5.6 (C1/C2) kcal mol−1. This variation highlights the asymmetric bonding interactions between silicon and the chemically distinct carbon atoms identified earlier. The directional asymmetry of the QUAOs, illustrated in Fig. 9, confirms that while π bonding persists across the ring, the extent of conjugation differs locally. This asymmetry of the π-system, driven by somewhat unusual hybridization (s–p mixing) due to the partial nonplanarity, may serve to stabilize the belt-type structure by selectively localizing electron density and partially relieving antiaromatic destabilization.
As noted in the earlier discussion of the n = 4 system, there are relatively short Si—Si distances between non directly bonded Si atoms in the belt isomer that could imply weak Si–Si bonding. Additional insight into the bonding topology of the belt-shaped n = 4 annulene provided by the presence of weak π-type (1,3) Siccπ–Siccπ interactions between vicinal silicon atoms. Fig. 11 illustrates this type of interaction. The BOs and KBOs of each of these weaker interactions whose KBO magnitudes are greater than 0.60 kcal mol−1 are shown in Table SI1, of the SI. The (nonbonding) Si–Si π interactions exhibit modest bond orders, 0.19 in n = 3 and 0. 25–0. 27 in n = 4 belt annulenes and very slightly bonding kinetic bond orders (−1.9 kcal mol−1) in n = 3 and (−3.2 and −2.3 kcal mol−1) in n = 4, consistent with weak π conjugation. Although these values are small, their occurrence in both n = 3 and n = 4 belt-shaped isomers, with larger values for the larger system, suggests a recurring structural motif in which vicinal Si atoms engage in weak π overlap. In the n = 4 system, these interactions occur between silicon atoms separated by ∼2.8 and 2.7 Å; these distances fall well below the typical Si–Si van der Waals contact (∼4.2 kcal mol−1) but are longer than conventional Si–Si single bond distances (∼2.35–2.40 Å).74 The ability of these atoms to sustain such long-range interactions is attributed to the radial extent of Si 3p orbitals, which allow limited π overlap even at extended distances.75,76 These (Siccπ–Siccπ) interactions are negligible in the corresponding regular structures, thus highlighting the role of belt-induced curvature and strain in promoting long-range Si–Si orbital overlap. While weak, the presence of these long-range interactions across both n = 3 and n = 4 belt-shaped systems suggests that they contribute a secondary layer of π interactions (secondary π-network) that subtly influences the electronic distribution and structural preferences of these Si/C hybrid rings.
Taken together, the QUAO analysis reveals that both geometries and π-electron count play critical roles in determining the electronic structure and aromatic character of Si/C annulenes. In the n = 3 systems, where 6 π electrons formally satisfy the (4n + 2) Hückel rule, the regular (planar) isomer supports delocalized π conjugation and exhibits a modestly negative NICS value, consistent with the aromatic stabilization enabled by efficient Si and C overlap. However, this overlap is intrinsically limited by the diffuse nature of the silicon 3p orbitals relative to the more compact carbon 2p orbitals, which constrains the extent of π delocalization even in the more favorable planar geometry.76,77 The belt-shaped analog, while geometrically distorted, retains only partial delocalization due to hybridization asymmetry and reduced π overlap, resulting in a strongly positive NICS value indicative of antiaromatic character. In the n = 4 systems, both isomers exhibit positive NICS values, confirming the destabilizing influence of a 4n π-electron configuration. However, the regular (planar) structure preserves delocalization and symmetry, resulting in a stronger antiaromatic response. In contrast, the belt-shaped isomer exhibits π hybridization asymmetry, bond order splitting, and population imbalance, that together point to a localized π -framework. This reduced delocalization correlates with a weaker NICS value and suggests the system alleviates antiaromaticity by concentrating π density in selected C–Si–C regions. These results underscore how antiaromatic instability can be alleviated through structural adaptation, and how hybridization, orbital populations, and bond orders collectively govern the magnetic and electronic behavior of π-conjugated Si/C rings. Nonetheless, the belt isomers are much higher in energy than the regular isomers, suggesting that the geometric distortions and the consequent impact on electronic structure are not sufficient to significantly stabilize the belt isomers.
3.6. QUAO analysis of n = 5, 6, 10 belt-shaped H2nSinCn annulenes and all-carbon belt-shaped H20C20 annulene
The QUAO analysis was applied to the n = 5, 6, 10 optimized geometries of the belt-shaped Si/C annulene (H2nSinCn) systems, as well as the belt-shaped H20C20 all-carbon analog. These extended conjugated rings enable a broader assessment of how ring size, curvature, and substitution modulate bonding symmetry, hybridization, and aromaticity. The geometric parameters, and magnetic properties indices are summarized in Table 1. As in the smaller systems, each QUAO is characterized by its directional orientation and electron population, shown in Table 4. All four annulenes analyzed here consist of an even number of π-contributing atoms, with π-bonding described in terms of QUAOs that span two adjacent atoms, sharing approximately two electrons between them. The H10Si5C5 annulene has a formal count of 10 π electrons, consistent with Hückel aromaticity (4n + 2), whereas the n = 6 and n = 10 Si/C systems, as well as the H20C20 analog, have 12 and 20 π electrons, respectively, and are formally antiaromatic (4n). The H20C20 system serves as a reference for fully carbon delocalization in curved π-systems, enabling direct comparison with the Si/C frameworks. The following discussion examines first the σ framework stability across these larger belts, followed by trends in π delocalization, population asymmetry, and aromatic response.| Compound | 5 | 6 | 10 | H20C20 | ||||
|---|---|---|---|---|---|---|---|---|
| Label | s | p | s | p | s | p | s | p |
| Csisiπ | 0.01 | 0.98 | 0.00 | 1.00 | 0.00 | 1.00 | ||
| Csiσ | 0.32 | 0.68 | 0.31 | 0.69 | 0.31 | 0.69 | ||
| Chσ | 0.24 | 0.76 | 0.25 | 0.75 | 0.26 | 0.74 | ||
| Siccπ | 0.03 | 0.97 | 0.01 | 0.99 | 0.01 | 0.99 | ||
| Sicσ | 0.33 | 0.67 | 0.34 | 0.66 | 0.35 | 0.65 | ||
| Sihσ | 0.28 | 0.72 | 0.28 | 0.72 | 0.28 | 0.72 | ||
| Hcσ | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | ||
| Hsiσ | 1.00 | 0.00 | 1.00 | 0.00 | 1.00 | 0.00 | ||
| Cccπ | 0.00 | 1.00 | ||||||
| C1c20σ (long) | 0.29 | 0.71 | ||||||
| C1c3σ (short) | 0.33 | 0.67 | ||||||
| Chσ | 0.26 | 0.74 | ||||||
| Hcσ | 1.00 | 0.00 | ||||||
To evaluate the σ bonding network across the larger belt-shaped annulenes, the hybridization patterns, orbital populations, and bond order metrics of the σ-type QUAOs were examined. As shown in Table 4, the σ orbitals associated with C–H, Si–H, and Si–C interactions exhibit hybrid compositions consistent with sp2-like bonding across all three Si/C systems, with ∼30% s-character and ∼70% p-character. The populations of the QUAOs involved in these interactions change little as the ring size increases, with Csiσ and Sicσ values ranging from 1.24 to 1.25 and 0.76 to 0.75, respectively. These values are in agreement with the relative electronegativities of the bonded atoms, with the more electronegative carbon centers accumulating greater electron density. Similar population trends are observed for the remaining σ QUAOs: Chσ and Hsiσ range from 1.14–1.15 and 1.13–1.16, respectively, while the less electronegative Sihσ and Hcσ fall in the 0.87–0.85 and 0.86–0.83 range. These consistent patterns across σ QUAOs reflect local bonding environments that are preserved with increasing ring size. BOs and KBOs (Table 5) further support this interpretation, with CSiσ–Sicσ BO values nearly unchanged, 0.93–0.94, and KBOs in the −29.1 to −30.1 kcal mol−1 range across n = 5, 6, and 10. Comparable trends are observed in the all-carbon H20C20 system, where the two types of C–Cσ bonds maintain high BO and KBO values. Collectively, these findings confirm that the σ framework remains robust and well-defined across the full series of belt-shaped annulenes.
| Compound | 5 | 6 | 10 | H20C20 | ||||
|---|---|---|---|---|---|---|---|---|
| Interacting QUAOs | BO | KBO | BO | KBO | BO | KBO | BO | KBO |
| a Cc–Cc over shorter carbon–carbon bond length. b Cc–Cc over longer carbon–carbon bond length. | ||||||||
| Csiσ–Sicσ | 0.93 | −29.1 | 0.94 | −29.5 | 0.94 | −30.1 | ||
| Csisiπ–Siccπ | 0.58 | −7.7 | 0.59 | −8.0 | 0.60 | −8.6 | ||
| Chσ–Hcσ | 0.97 | −35.2 | 0.97 | −35.6 | 0.97 | −36.2 | 0.97 | −37.3 |
| Sihσ–Hsiσ | 0.96 | −23.6 | 0.96 | −23.5 | 0.96 | −23.4 | ||
| C1c3π–C3c1πa | 0.87 | −20.7 | ||||||
| C1c3π–C20c18πb | 0.37 | −6.7 | ||||||
| C1c3σ–C3c1σa | 0.99 | −54.8 | ||||||
| C1c20σ–C20c1σb | 0.98 | −51.4 | ||||||
The π-bonding interactions in the larger belted Si/C annulenes also have a consistent pattern despite their different π-electron counts. These annulenes (n = 5–10) exhibit a uniform π-electronic landscape across ring sizes. The QUAO hybridizations for the Csisiπ and Siccπ orbitals consistently exhibit nearly 99% p-character, with only minor deviations (3% s-character in the Siccπ QUAO of n = 5). As Table 6 shows, electron populations are similarly constant, with Csisiπ QUAOs ranging from 1.38–1.40 and Siccπ from 0.61–0.62, suggesting an absence of asymmetry. Csisiπ–Siccπ bond orders and kinetic bond orders fall within narrow ranges (BO = 0.58–0.60, KBO = −7.7 to −8.6 kcal mol−1), indicative of a modest yet continuous π-delocalization network with no sign of population asymmetry. Despite formally satisfying (4n + 2) or (4n) π-electron rules these results suggest that despite variations in ring size and formal π-electron count, the Si/C belts maintain an uninterrupted conjugated framework. In the Si/C belt-shaped annulenes the vicinal π interactions between Si⋯Si peak at n = 4 (Table 7), indicating that a curvature corresponding to this ring size provides an optimal geometry for overlap of Si 3p orbitals. Beyond this point, as the belt flattens (n ≥ 5) the interaction weakens due to the increasing interatomic separation. In contrast, the vicinal C⋯C π interactions are negligible under strong curvature at n = 3, and increase monotonically with increasing ring size, reflecting the geometric preference of carbon for in-plane π conjugation over curved overlap.
| Label | 5 | 6 | 10 | H20C20 |
|---|---|---|---|---|
| Csisiπ | 1.40 | 1.39 | 1.38 | |
| Csiσ | 1.24 | 1.25 | 1.25 | |
| Chσ | 1.14 | 1.14 | 1.15 | 1.13 |
| Siccπ | 0.61 | 0.62 | 0.62 | |
| Sicσ | 0.76 | 0.75 | 0.75 | |
| Sihσ | 0.87 | 0.86 | 0.85 | |
| Hcσ | 0.86 | 0.83 | 0.83 | 0.87 |
| Hsiσ | 1.13 | 1.16 | 1.16 | |
| Cccπ | 1.00 | |||
| C1c3σ | 1.00 | |||
| C1c20σ | 1.00 |
| Interacting QUAOs | 3 | 4 | 5 | 6 | 10 |
|---|---|---|---|---|---|
| Siccπ–Siccπ | −1.90 | −3.23, −2.29 | −1.91 | −1.80 | −0.98 |
| Csisiπ–Csisiπ | <−0.6 | −1.38 | −1.47 | −1.56 | −1.58 |
In contrast, the all-carbon H20C20 system displays features typical of antiaromatic strain. Two distinct classes of π bonding are observed: one over shorter C–C bonds with higher BO (0.87) and KBO (−20.7 kcal mol−1), resembling ethylene-like localization, and another spanning longer bonds (BO = 0.37) and (KBO = −6.7 kcal mol−1) with π QUAOs delocalized across four carbon centers. This bifurcation of π-bond character reflects an incomplete conjugation pathway characteristic of strained antiaromatic systems and is supported by the large NICS(0) value of 26.664 ppm. Together, these features highlight the contrast in how Si/C and all-carbon belts manage antiaromaticity: the former moderates it through uniform delocalization and hybridization balance, while the latter relies on bond alternation and π-localization to relieve strain.
4. Conclusions
The belt-shaped alternating Si/C annulenes, H2nSinCn (n = 3, 4, 5, 6, and 10), were investigated and compared with their planar (regular) isomers. For the smaller systems with n = 3 and 4, compared with the regular annulenes benzene (n = 3) and cyclooctatetraene (n = 4), the belt-type isomers were found to be significantly less stable thermodynamically as expected from the distorted π orbitals and strained ring structures. The NICS value of both n = 3 and 4 belt annulenes are positive suggesting that they have antiaromatic character despite the Hückel 4n + 2 rule. All of the Si–C bond lengths in every Si/C mixed annulene investigated is equal or nearly equal within each molecular structure. This behavior seems to be a characteristic of the Si/C alternately mixed annulenes. As the ring size increases to n ≥ 5, the Si–C π orbitals in the Si/C belt structures are increasingly localized, in contrast with the fact that the π orbitals spread equally on each C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond in the all-carbon analog, H20C20.
C bond in the all-carbon analog, H20C20.
The QUAO framework is employed to probe localized orbital populations, hybridization patterns, and directional bonding symmetries, all features not readily discernible from frontier orbital energies alone. Through this analysis, the belt- and regular- (planar) type annulenes reveal distinct electronic responses to their π-electron counts and geometries. In the n = 3 series, in which aromatic stabilization is expected, even modest s-character in the π QUAOs of the belt-shaped isomer disrupts conjugation, weakening aromatic delocalization. In contrast, the emergence of s-character in π QUAOs in the n = 4 belt-shaped species, serves not as a perturbation, but as an adaptive response that facilitates π localization in select regions of the ring and attenuates destabilization.
In general, in the belt-shaped Si/C annulenes with larger n, a combination of structural curvature and orbital mismatch between silicon and carbon limits the extent of π-delocalization. While silicon can contribute to π systems through its 3p orbitals, these orbitals are more diffuse and less directional than the carbon 2p orbitals, resulting in weaker overlap. This orbital mismatch becomes especially consequential in non-planar systems, where the strain already constrains effective conjugation. As a result, Si/C alternately substituted annulenes reach a limit in how much their π electrons can spread out, showing that silicon atoms control π conjugation by adjusting orbital overlap, hybridization, and structural (curvature) adaptation. A consequence of these structural and electronic distortions is that in the Si/C belt structures with larger values of n that have 4n π electrons (e.g., n = 10), the tendency toward antiaromaticity is decreased. In contrast, the corresponding planar isomer (e.g., H8Si4C4) is significantly antiaromatic. Because the all-carbon H20C20 system lacks the Si–C orbital mismatch and is free of hybridization limitations, this molecule mitigates strain via localization and bond alternation.
Author contributions
T. K. conceptualized the idea, wrote the initial draft, revised the manuscript, contributed to discussion and approved the final manuscript, K. N. F. conducted the QUAO analysis, wrote the initial draft, revised the manuscript, and contributed to discussion, T. N. conducted the ab initio molecular orbital calculations, and contributed to discussion, A. I., and R. K. conducted the ab initio molecular orbital calculations, and M. S. G. conducted the review, editing, contributed to discussion and approved the final manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the supplementary information (SI). Supplementary information: the frontier orbitals of the bigger Si/C and H20C20 belt-type annulenes, the structure of an intermediate of n = 4 isomerization, an animation of n = 4 isomerization, tables of the coordinates and energies of the calculated molecules. See DOI: https://doi.org/10.1039/d5cp03030g.Acknowledgements
This work was supported by a grant from the Air Force Office of Scientific Research (MSG, KNF), AFOSR FA9550-18-1-0321.Notes and references
- A. T. Lawal, Polycyclic aromatic hydrocarbons. A review, Cogent Environ. Sci., 2017, 3(1), 1339841, DOI:10.1080/23311843.2017.1339841.
- F. Barbosa Jr., B. A. Rocha, M. C. O. Souza, M. Z. Bocato, L. F. Azevedo, J. A. Adeyemi, A. Santana and A. D. Campiglia, Polycyclic aromatic hydrocarbons (PAHs): Updated aspects of their determination, kinetics in the human body, and toxicity, J. Toxicol. Environ. Health, Part B, 2023, 26(1), 28–65, DOI:10.1080/10937404.2022.2164390.
- M. Iyoda, J. Yamakawa and M. J. Rahman, Conjugated Macrocycles: Concepts and Applications, Angew. Chem., Int. Ed., 2011, 50, 10522–10553, DOI:10.1002/anie.201006198.
- K. Miki and K. Ohe, π-Conjugated Macrocycles Bearing Angle-Strained Alkynes, Chem. – Eur. J., 2020, 26, 2529–2575, DOI:10.1002/chem.201904114.
- G. Li, T. Y. Gopalakrishna, H. Phan, T. S. Herng, J. Ding and J. Wu, From Open-Shell Singlet Diradicaloid to Closed-Shell Global Antiaromatic Macrocycles, Angew. Chem., Int. Ed., 2018, 57, 7166–7170, DOI:10.1002/anie.201803949.
- M. Piccardo, A. Soncini and P. W. Fowler, Design of annulene-within-an-annulene systems by the altanisation approach. A study of altan-[n]annulenes, Phys. Chem. Chem. Phys., 2020, 22, 5476–5486, 10.1039/c9cp06835j.
- A. Stock, E. Pohland and I. X. Borwasserstoffe, B3N3H6, Ber. Dtsch. Chem. Ges., 1926, 59, 2215–2223, DOI:10.1002/cber.19260590907.
- R. Boese, A. H. Maulitz and P. Stellberg, Solid-State Borazine: Does it Deserve to be Entiteled Inorganic “Benzene”?, Chem. Ber., 1994, 127, 1887–1889 CrossRef CAS.
- R. Steudel, The Chemistry of Inorganic Ring Systems; Studies in Inorganic Chemistry, Elsevier, 1992, vol. 14, pp. 486 Search PubMed.
- N. Matsunaga and M. S. Gordon, Stabilities and energetics of inorganic benzene isomers: prismanes, J. Am. Chem. Soc., 1994, 116, 11407–11419, DOI:10.1021/ja00104a021.
- M. D. R. Merino-García, L. A. Soriano-Agueda, J. D. D. Guzmán-Hernández, D. Martínez-Otero, B. L. Rivera, F. Cortés-Guzmán, J. E. Barquera-Lozada and V. Jancik, Benzene and Borazine, so Different, yet so Similar: Insight from Experimental Charge Density Analysis, Inorg. Chem., 2022, 61(18), 6785–6798, DOI:10.1021/acs.inorgchem.1c03923.
- S. Grenda, N. Claiser, A. Barbon, F. Guégan, B. Toury and D. Luneau, An Open-Shell Functionalization of Inorganic Benzene, J. Am. Chem. Soc., 2024, 146(48), 32906–32911, DOI:10.1021/jacs.4c10736.
- S. Nagase, K. Kobayashi and T. Kudo, Theoretical study of the aromatic and polyhedral compounds with Ge, Sn and Pb skeletons, Main Group Met. Chem., 1994, 17(1–4), 171–181, DOI:10.1515/MGMC.1994.17.1-4.171.
- S. Fujimori, Y. Mizuhata and N. Tokitoh, Recent progress in the chemistry of heavy aromatics, Proc. Jpn. Acad., Ser. B, 2023, 99, 480–512, DOI:10.2183/pjab.99.027.
- D. A. Clabo, Jr. and H. F. Schaefer, III, The silicon analog of benzene–hexasilabenzene (Si6H6), J. Chem. Phys., 1986, 84, 1664–1669, DOI:10.1063/1.450462.
- S. Nagase, H. Teramae and T. Kudo, Hexasilabenzene (Si6H6). Is the benzene-like D6h structure stable?, J. Chem. Phys., 1987, 86, 4513–4517, DOI:10.1063/1.452726.
- M. Moteki, S. Maeda and K. Ohno, Systematic Search for Isomerization Pathways of Hexasilabenzene for Finding its Kinetic Stability, Organometallics, 2009, 28, 2218–2224 CrossRef CAS.
- T. Nakamura and T. Kudo, The planarity of heteroatom analogues of benzene: energy component analysis and the planarization of hexasilabenzene, J. Comput. Chem., 2019, 40, 581–590, DOI:10.1002/jcc.25743.
- H. F. Schaefer III, 1,3,5-Trisilabenzene: has it been synthesized?, J. Mol. Struct.:THEOCHEM, 1995, 358, 1–14, DOI:10.1016/0166-1280(95)04334-9.
- K. K. Baldridge, O. Uzan and J. M. L. Martin, The Silabenzenes: Structure, Properties, and Aromaticity, Organometallics, 2000, 19, 1477–1487, DOI:10.1021/om9903745.
- A. S. Ivanov and A. I. Boldyrev, Si6−nCnH6 (n = 0–6) Series; When do Silabenzenes Become Planar and Global Minima?, J. Phys. Chem. A, 2012, 116, 9591–9598, DOI:10.1021/jp307722q.
- T. Kudo, M. W. Schmidt and N. Matsunaga, Ab initio molecular orbital study of the first four Si/C alternately substituted Annulenes, J. Phys. Chem. A, 2019, 123, 4588–4598, DOI:10.101/acs.jpca.9b02631.
- T. Nakamura, A. Mesuda and T. Kudo, Theoretical study of the Si/C mixed benzenes and their major valence isomers, Organometallics, 2020, 39, 3041–3049, DOI:10.1021/acs.organomet.0c00440.
- T. Uchiyama, T. Nakamura, M. Hiyama and T. Kudo, Theoretical study of Si/C equally mixed dodecahedrane analogues, Molecules, 2023, 28, 2769, DOI:10.3390/molecules28062769.
- T. Uchiyama, T. Nakamura, M. Hiyama and T. Kudo, Theoretical study of Si/C mixed analogues of platonic hydrocarbons, Comput. Theor. Chem., 2025, 1246, 115116, DOI:10.1016/j.comptc.2025.115116.
- K. Tahara and Y. Tobe, Molecular Loops and Belts, Chem. Rev., 2006, 106, 5274–5290, DOI:10.1021/cr050556a.
- T. Kawase and H. Kuwata, Ball-, Bowl-, and Belt-Shaped Conjugated Systems and Their Complexing Abilities: Exploration of the Concave-Convex π–π Interaction, Chem. Rev., 2006, 106, 5250–5273, DOI:10.1021/cr0509657.
- E. Heilbronner, Hűckel molecular orbitals of Mőbius-type conformations of annulenes, Tetrahedron Lett., 1964, 5, 1923–1928, DOI:10.1016/S0040-4039(01)89474-0.
- C. Castro, C. M. Isoborn, W. L. Karney, M. Mauksch and P. V. R. Schleyer, Aromaticity with a Twist: Mobius [4n]Annulenes, Org. Lett., 2002, 4(20), 3431–3434, DOI:10.1021/ol026610g.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A comprehensive analysis of molecule-intrinsic quasi-atomic, bonding, and correlating orbitals. I. Hartree-Fock wave functions, J. Chem. Phys., 2013, 139, 234107, DOI:10.1063/1.4840776.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. II. Strongly Correlated MCSCF Wave Functions, J. Phys. Chem. A, 2015, 119, 10360–10367, DOI:10.1021/acs.jpca.5b03399.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic, Quasi-Atomic Orbitals. III. The Covalent Bonding Structure of Urea, J. Phys. Chem. A, 2015, 119, 10368–10375, DOI:10.1021/acs.jpca.5b03400.
- A. C. West, M. W. Schmidt, M. S. Gordon and K. Ruedenberg, A Comprehensive Analysis in Terms of Molecule-Intrinsic Quasi-Atomic Orbitals. IV. Bond Breaking and Bond Forming along the Dissociative Reaction Path of Dioxetane, J. Phys. Chem. A, 2015, 119, 10376–10389, DOI:10.1021/acs.jpca.5b03402.
- A. C. West, J. J. Duchimaza-Heredia, M. S. Gordon and K. Ruedenberg, Identification and Characterization of Molecular Bonding Structures by ab initio Quasi-Atomic Orbital Analyses, J. Phys. Chem. A, 2017, 121, 8884–8898, DOI:10.1021/acs.jpca.7b07054.
- J. J. Duchimaza Heredia, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bonding Analysis of Xe-Containing Compounds, J. Phys. Chem. A, 2018, 122, 3442–3454, DOI:10.1021/acs.jpca.8b00115.
- J. J. Duchimaza Heredia, A. D. Sadow and M. S. Gordon, A Quasi-Atomic Analysis of Three-Center Two-Electron Zr–H–Si Interactions, J. Phys. Chem. A, 2018, 122, 9653–9669, DOI:10.1021/acs.jpca.8b09530.
- G. Schoendorff, M. W. Schmidt, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bond Analyses in the Sixth Period: II. Bond Analyses of Cerium Oxides, J. Phys. Chem. A, 2019, 123, 5249–5256, DOI:10.1021/acs.jpca.9b04024.
- E. B. Guidez, M. S. Gordon and K. Ruedenberg, Why is Si2H2 Not Linear? An Intrinsic Quasi-Atomic Bonding Analysis, J. Am. Chem. Soc., 2020, 142, 13729–13742, DOI:10.1021/jacs.0c03082.
- J. L. Galvez Vallejo, J. D. Heredia and M. S. Gordon, Bonding analysis of water clusters using quasi-atomic orbitals, Phys. Chem. Chem. Phys., 2021, 23, 18734–18743, 10.1039/D1CP02301B.
- T. Harville and M. S. Gordon, Intramolecular hydrogen bonding analysis, J. Chem. Phys., 2022, 156, 174302, DOI:10.1063/5.0090648.
- D. Del Angel Cruz, J. L. Galvez Vallejo and M. S. Gordon, Analysis of the bonding in tetrahedrane and phosphorus substituted tetrahedranes, Phys. Chem. Chem. Phys., 2023, 25, 27276–27292, 10.1039/d3cp03619g.
- D. Del Angel Cruz, K. N. Ferreras, T. Harville, G. Schoendorf and M. S. Gordon, Analysis of bonding motifs in unusual molecules I: planar hexacoordinated carbon atoms, Phys. Chem. Chem. Phys., 2024, 26, 21395–21406, 10.1039/D4CP01800A.
- K. N. Ferreras, T. Harville, D. Del Angel Cruz and M. S. Gordon, Analysis of Bonding Motifs in Unusual Molecules: II. Infinitene, Phys. Chem. Chem. Phys., 2024, 26, 21407–21418, 10.1039/D4CP01802H.
- M. W. Schmidt, E. A. Hull and T. L. Windus, Valence Virtual Orbitals: An Unambiguous ab Initio Quantification of the LUMO Concept, J. Phys. Chem. A, 2015, 119, 10408–10427, DOI:10.1021/acs.jpca.5b06893.
- G. Schoendorff, A. C. West, M. W. Schmidt, K. Ruedenberg and M. S. Gordon, Quasi-Atomic Bond Analyses in the Sixth Period: I. Relativistic Accurate Atomic Minimal Basis Sets for the Elements Cesium to Radon, J. Phys. Chem. A, 2019, 123, 5242–5248, DOI:10.1021/acs.jpca.9b04023.
- G. Schoendorff, A. C. West, M. W. Schmidt, K. Ruedenberg, A. K. Wilson and M. S. Gordon, Relativistic ab Initio Accurate Atomic Minimal Basis Sets: Quantitative LUMOs and Oriented Quasi-Atomic Orbitals for the Elements Li–Xe, J. Phys. Chem. A, 2017, 121, 3588–3597, DOI:10.1021/acs.jpca.7b01916.
- G. W. Stewart, On the Early History of the Singular Value Decomposition, SIAM Rev., 1993, 35, 551–566, DOI:10.1137/1035134.
- H. F. King, R. E. Stanton, H. Kim, R. E. Wyatt and R. G. Parr, Corresponding Orbitals and the Nonorthogonality Problem in Molecular Quantum Mechanics, J. Chem. Phys., 1967, 47, 1936–1941, DOI:10.1063/1.1712221.
- J. Ivanic, G. J. Atchity and K. Ruedenberg, Intrinsic local constituents of molecular electronic wave functions. I. Exact representation of the density matrix in terms of chemically deformed and oriented atomic minimal basis set orbitals, Theor. Chem. Acc., 2008, 120, 281–294, DOI:10.1007/s00214-007-0308-4.
- K. Ruedenberg, The Physical Nature of the Chemical Bond, Rev. Mod. Phys., 1962, 34, 326–376, DOI:10.1103/RevModPhys.34.326.
- M. W. Schmidt, J. Ivanic and K. Ruedenberg, Covalent bonds are created by the drive of electron waves to lower their kinetic energy through expansion, J. Chem. Phys., 2014, 140, 204104, DOI:10.1063/1.4875735.
- K. Ruedenberg, Atoms and interatomic bonding synergism inherent in molecular electronic wave functions, J. Chem. Phys., 2022, 157, 024111, DOI:10.1063/5.0094609.
- F. Zahariev, P. Xu, B. M. Westheimer, S. Webb, J. Galvez Vallejo, A. Tiwari, V. Sundriyal, M. Sosonkina, J. Shen, G. Schoendorff, M. Schlinsog, T. Sattasathuchana, K. Ruedenberg, L. B. Roskop, A. P. Rendell, D. Poole, P. Piecuch, B. Q. Pham, V. Mironov, J. Mato, S. Leonard, S. S. Leang, J. Ivanic, J. Hayes, T. Harville, K. Gururangan, E. Guidez, I. S. Gerasimov, C. Friedl, K. N. Ferreras, G. Elliott, D. Datta, D. D. A. Cruz, L. Carrington, C. Bertoni, G. M. J. Barca, M. Alkan and M. S. Gordon, The General Atomic and Molecular Electronic Structure System (GAMESS): Novel Methods on Novel Architectures, J. Chem. Theory Comput., 2023, 19, 7031–7055, DOI:10.1021/acs.jctc.3c00379.
- M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery, General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363, DOI:10.1002/jcc.540141112.
- M. S. Gordon and M. W. Schmidt, Theory and Applications of Computational Chemistry, Elsevier, 2005, pp. 1167–1189 Search PubMed.
- G. M. J. Barca, C. Bertoni, L. Carrington, D. Datta, N. De Silva, J. E. Deustua, D. G. Fedorov, J. R. Gour, A. O. Gunina, E. Guidez, T. Harville, S. Irle, J. Ivanic, K. Kowalski, S. S. Leang, H. Li, W. Li, J. J. Lutz, I. Magoulas, J. Mato, V. Mironov, H. Nakata, B. Q. Pham, P. Piecuch, D. Poole, S. R. Pruitt, A. P. Rendell, L. B. Roskop, K. Ruedenberg, T. Sattasathuchana, M. W. Schmidt, J. Shen, L. Slipchenko, M. Sosonkina, V. Sundriyal, A. Tiwari, J. L. Galvez Vallejo, B. Westheimer, M. Włoch, P. Xu, F. Zahariev and M. S. Gordon, Recent developments in the general atomic and molecular electronic structure system, J. Chem. Phys., 2020, 152, 154102, DOI:10.1063/5.0005188.
- B. M. Bode and M. S. Gordon, Macmolplt: a graphical user interface for GAMESS, J. Mol. Graphics Modell., 1998, 16, 133–138, DOI:10.1016/S1093-3263(99)00002-9.
- C. Møller and M. S. Plesset, Note on an approximation treatment for many-Electron systems, Phys. Rev., 1934, 46, 618–622, DOI:10.1103/PhysRev.46.618.
- J. A. Pople, K. Raghavachari, H. B. Schlegel and J. S. Binkley, Derivative studies in Hartree–Fock and Møller–Plesset theories, Int. J. Quantum Chem., 1979, 16(S13), 225–241, DOI:10.1002/qua.560160825.
- M. Head-Gordon, J. A. Pople and M. J. Frisch, MP2 energy evaluation by direct methods, Chem. Phys. Lett., 1988, 153, 503–506, DOI:10.1016/0009-2614(88)85250-3.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- J. P. Foster and F. Weinhold, Natural hybrid orbitals, J. Am. Chem. Soc., 1980, 102, 7211–7218, DOI:10.1021/ja00544a007.
- A. E. Reed, R. B. Weinstock and F. Weinhold, Natural-population analysis, J. Chem. Phys., 1985, 83, 735–746, DOI:10.1063/1.449486.
- A. D. Becke, Density-functional thermochemistry. III. The role of exact exchange, J. Chem. Phys., 1993, 98, 5648–5652, DOI:10.1063/1.464913.
- P. J. Stephens, F. J. Devlin, M. J. Frish and C. F. Chabalowski, Ab initio Calculation of Vibrational Absorption and Circular Dichroism Spectra Using Density Functional Force Fields, J. Phys. Chem., 1994, 98, 11623–11627, DOI:10.1021/j100096a001.
- M. S. Frish, J. A. Pople and J. S. Binkley, Self-Consistent Molecular Orbital Methods. 25. Supplementary Functions for Gaussian Basis Sets, J. Chem. Phys., 1984, 80, 3265–3269, DOI:10.1063/1.447079.
- M. W. Schmidt and M. S. Gordon, The construction and interpretation of MCSCF wavefunction, Annu. Rev. Phys. Chem., 1998, 49, 233–266, DOI:10.1146/annurev.physchem.49.1.233.
- T. H. Dunning, Gaussian basis sets for use in correlated molecular calculations. I. The atoms boron through neon and hydrogen, J. Chem. Phys., 1989, 90, 1007–1023, DOI:10.1063/1.456153.
- P. C. Hariharan and J. A. Pople, The influence of polarization functions on molecular orbital hydrogenation energies, Theor. Chim., 1973, 28, 213–222, DOI:10.1007/BF00533485.
- K. Fukui, The path of chemical reactions – The IRC approach, Acc. Chem. Res., 1981, 14, 363–368, DOI:10.1021/ar00072a001.
- H. P. Hratchian and H. B. Schlegel, in Theory and Applications of Computational Chemistry: The First 40 Years, ed. C. E. Dykstra, G. Frenking, K. S. Kim and G. Scuseria, Elsevier, Amsterdam, 2005, pp. 195–249 Search PubMed.
- K. Hirao, Multireference Moller-Plesset method, Chem. Phys. Lett., 1992, 190, 374–380, DOI:10.1016/0009-2614(92)85354-D.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, Jr, J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Revision A. Gaussian, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- P. Pyykkö and M. Atsumi, Molecular Single-Bond Covalent Radii for Elements 1–118, Chem. – Eur. J., 2009, 15, 186–197, DOI:10.1002/chem.200800987.
- D. Rodrigues Silva, E. Blokker, J. M. van der Schuur, T. A. Hamlin and F. M. Bickelhaupt, Nature and strength of group-14 A–A0 bonds, Chem. Sci., 2024, 15, 1648–1656, 10.1039/D3SC06215E.
- B. Cordero B, V. Gómez, A. E. Platero-Prats, M. Revés, J. Echeverría, E. Cremades, F. Barragán and S. Alvarez, Covalent radii revisited, Dalton Trans., 2018, 40, 2832–2838, 10.1039/B801115J.
- T. Matsuo and N. Hayakawa, π-Electron systems containing Si = Si double bonds, Sci. Technol. Adv. Mater., 2018, 19, 108–129, DOI:10.1080/14686996.2017.1414552.
| This journal is © the Owner Societies 2026 |








