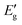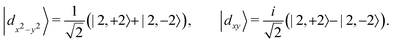Janus VAZ₃H (A = Si, Ge; Z = N, P) single layers exhibiting valley polarization, magnetic anisotropy, and topological transition

Abstract

Using first-principles calculations, we explore the electronic and topological properties of Janus VAZ₃H single layers (A = Si, Ge; Z = N, P) that are dynamically and thermally stable. In the strain-free state, VSiN₃H, VSiP₃H, and VGeN₃H demonstrate direct bandgap ferrovalley (FV) semiconducting properties, while VGeP₃H displays an indirect bandgap. The easy magnetization axis varies among these materials, with VSiN₃H and VGeN₃H preferring in-plane magnetization, whereas VSiP₃H and VGeP₃H favor out-of-plane magnetization. Furthermore, the electronic structure analysis reveals valley polarization at the K and K′ points. When subjected to strain, these systems experience phase transitions, such as direct-to-indirect bandgap shift, the evolution from FV semiconducting to half-valley metal (HVM), and the emergence of a quantum anomalous Hall (QAH) phase within certain strain intervals. The QAH phase is identified by chiral edge states and quantized anomalous Hall conductivity (AHC), supported by an integer AHC plateau of 1e²/h and a Chern number of 1. These results highlight the tunability of VAZ₃H SLs through strain engineering, providing a potential platform for valleytronic and topological applications.

---

1. Introduction

Recent progress in two-dimensional (2D) ferromagnetic materials and valley semiconductors has attracted significant attention for their potential in spintronic and valleytronic devices.^1–5 These breakthroughs offer innovative avenues for controlling quantum properties and stimulate both theoretical research and practical applications.^6–10 Notably, the emergence of ferrovalley (FV) materials represents a major milestone. By breaking time-reversal and spatial-inversion symmetries, FV materials naturally combine ferromagnetism with spontaneous valley polarization.¹¹ By stabilizing valley characteristics through magnetic ordering, this unique combination facilitates efficient valley manipulation and opens avenues for investigating exotic quantum effects such as the anomalous valley Hall effect and the valley-polarized quantum anomalous Hall (QAH) effect.^12–14 Consequently, FV materials present promising opportunities for developing robust, scalable valleytronic devices in next-generation quantum technologies.

With advancements in 2D ferromagnetic and valley semiconductors, the exploration of FV materials has attracted growing attention. Notable examples include 2H-VSe₂,¹¹ LaBr₂,¹⁵ 2H-GdI₂,¹⁶ Nb₃I₈,¹⁷ TiVI₆,¹⁸ NbX₂ (X = S, Se),¹⁹ 2H-FeCl₂,²⁰ Cr₂Se₃,²¹ and VAgP₂Se₆.²² In addition, the development of Janus structures, which break inversion symmetry and provide additional degrees of freedom for tuning electronic and magnetic properties, has further expanded the FV material family. Compositional and structural innovations have led to promising candidates such as 2H-VSSe,^23,24 VClBr,²⁵ LaBrI,²⁶ and GdClF.²⁷ Despite progress, new FV materials remain essential. Existing compounds are promising but limited by stability, tunability, or integration. Novel compositions and structures are needed to enhance performance and uncover quantum phenomena from magnetic ordering and valley polarization.

Recent investigations into VA₂Z₄ (A = Si, Ge; Z = N, P) single layers (SLs) have shown that these materials are promising for valleytronic applications. Specifically, VSi₂N₄ is a ferromagnetic semiconductor with valley-specific physics and strong spin-valley coupling,²⁸ and VSi₂P₄ displays correlation-driven magnetic, topological, and valley features.^29,30 VGe₂P₄, meanwhile, exhibits quasi-half-valley metal behavior that facilitates electron–hole separation via tunable valley polarization.³¹ Motivated by these discoveries, we aim to explore innovative strategies, including the design of Janus structures, to further optimize the valley and topological functionalities of 2D materials.

Here, by performing first-principles calculations, we identify Janus SL VAZ₃H (A = Si, Ge; Z = N, P) as 2D FV semiconductors. Our results indicate that VSiN₃H, VSiP₃H, and VGeN₃H exhibit direct bandgap semiconducting properties, while VGeP₃H is an indirect bandgap semiconductor. The easy magnetization axis differs among these materials, with VSiN₃H and VGeN₃H favoring in-plane magnetization, while VSiP₃H and VGeP₃H prefer out-of-plane magnetization. Owing to their intrinsic ferromagnetism (FM) and spin–orbit coupling (SOC), spontaneous valley polarization emerges at the K and K′ points. By applying strain, phase transitions occur from a FV state to a half-valley metal (HVM), and the QAH phase emerges within specific strain intervals, featuring chiral edge states and quantized Hall conductivity. These findings highlight the potential of SL VAZ₃H materials for next-generation spintronic and valleytronic technologies.

2. Computational details

The calculations are performed using the Vienna Ab initio Simulation Package (VASP), based on density functional theory (DFT).³² Exchange–correlation interactions are treated with the generalized gradient approximation (GGA) using the Perdew–Burke–Ernzerhof (PBE) functional, and the projector augmented-wave (PAW) method is utilized to model the core-electron interactions.³³ A plane-wave cutoff of 500 eV is employed, and the Brillouin zone is sampled within a 13 × 13 × 1 Monkhorst–Pack k-point mesh, ensuring convergence of the total energy within 1 meV per atom. Structural optimization continues until atomic forces are below 0.01 eV Å⁻¹, and the total energy difference is smaller than 10⁻⁶ eV. To capture magnetic effects, spin-polarized calculations are employed, with SOC included as appropriate. The V atom is modeled with an effective Hubbard U_eff of 3.0 eV, consistent with previous works.^14,29,34,35 To ensure accuracy in bandgap calculations, the HSE06 hybrid functional³⁶ is tested, and van der Waals interactions are accounted for using the DFT-D3 method by Grimme. A vacuum of at least 20 Å is added to avoid spurious interactions between periodic images.

To assess thermal stability, ab initio molecular dynamics (AIMD) simulations are carried out using a 4 × 4 × 1 supercell and a Nosé thermostat at 500 K,³⁷ running for 6 ps with a time step of 1.5 fs in the canonical (NVT) ensemble. Additionally, density functional perturbation theory (DFPT) is employed to calculate the phonon dispersion, which helps assess the dynamical stability of the material.³⁸ The Berry curvature is calculated using the maximally localized Wannier functions in Wannier90,^39,40 while the edge states and Chern number are extracted and analyzed with the WannierTools package.⁴¹

To ensure reproducibility of the topological analysis, detailed computational settings are provided. The maximally localized Wannier functions (MLWFs) are constructed from the VASP wavefunctions using Wannier90, with the V-3d orbitals and Z-site p orbitals chosen as the initial projections. A total of 28 Wannier functions are generated. The disentanglement energy window ranged from −7 eV to 10 eV relative to the Fermi level, with a frozen window between −0.5 eV and +0.5 eV, ensuring accurate reproduction of the low-energy bands. The resulting MLWF Hamiltonian is imported into WannierTools for topological analysis. The Chern number is obtained by integrating the Berry curvature over the Brillouin zone using a 200 × 200 × 1 k-mesh, while the anomalous Hall conductivity is computed from the Berry curvature distribution via the Kubo formalism.

3. Results and discussion

As shown in Fig. 1, the crystal structure of the Janus VAZ₃H SLs exhibits hexagonal lattice symmetry, with asymmetry introduced by substituting one Z layer with hydrogen atoms. This modification results in a six-layer atomic configuration, Z–A–Z–V–Z–H, while maintaining the overall hexagonal shape. This tailored structure not only optimizes the atomic arrangement but also fine-tunes the interlayer spacing, leading to a non-uniform electron density distribution at the interfaces. Although the asymmetry alters the properties of the material, the high-symmetry characteristics are still preserved, as shown in the Brillouin zone.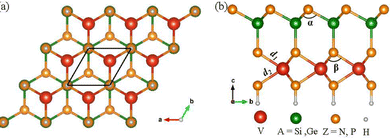

Fig. 1 Side (a) and top (b) views of the crystal structures of SL VAZ₃H (A = Si, Ge; Z = N, P), with dark solid lines marking the primitive unit cell.

The structural parameters of VAZ₃H SLs exhibit a systematic trend influenced by the constituent elements, as summarized in Table 1. The lattice constant (a) and layer thickness (h) increase when Si is replaced by Ge or N by P, consistent with the larger atomic radii of these elements. For example, VSiN₃H has the smallest lattice constant of 2.89 Å, while VGeP₃H has the largest at 3.53 Å. Similarly, the layer thickness increases from 5.60 Å in VSiN₃H to 7.54 Å in VGeP₃H. The bond lengths also follow a similar trend, with V–N and V–Si bonds being shorter than V–P and V–Ge bonds. For instance, in VSiN₃H, the V–N bond length is 2.03 Å, whereas in VGeP₃H, the V–P bond length increases to 2.44 Å. Furthermore, the bond angles α vary across different compositions, with α decreasing from 111.44° in VSiN₃H to 99.17° in VGeP₃H. In contrast, the β angle remains nearly constant across all compositions, fluctuating slightly between 90.70° and 93.57°.

Table 1 Structural and electronic property comparison for VAZ₃H SLs, including lattice constant (a), thickness (h), nearest V–Z bond lengths between V and Z atoms above (d₁) and below (d₂) the V atomic layer, bond angles of A–Z–A (α) and V–Z–A (β), elastic constants (C₁₁, C₁₂), energy difference between AFM and FM states (ΔE_AF), magnetocrystalline anisotropy energy (E_MAE), band gaps calculated without SOC within PBE , 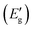with SOC within PBE (E_g), and with SOC within the HSE functional (E^HSE_g), valley polarization for the CBM (C_pol) and VBM (V_pol), and Berry curvature values at K and K′ (Ω(K), Ω (K′)

	a	h	d 1	d 2	α	β	C 11	C 12	ΔEAF	E MAE		E g	E ^HSEg	C pol/Vpol	Ω (K)	Ω (K′)
	(Å)	(Å)	(Å)	(Å)	(°)	(°)	(N m^−1)	(N m^−1)	(meV)	(μ eV)	(eV)	(eV)	(meV)	(Bohr^2)	(Bohr^2)
VSiN3H	2.89	5.60	2.030	2.025	111.44	90.70	337.89	103.41	87.7	−25.43	0.30	0.27	0.34	−1.5/65.3	−367.9	589.6
VSiP3H	3.46	7.41	2.412	2.421	100.94	91.72	126.86	34.66	30.9	4.20	0.22	0.17	0.58	85.5/−2.1	681.9	−275.4
VGeN3H	2.98	5.82	2.057	2.056	108.15	92.58	289.62	96.77	59.0	−2.01	0.17	0.13	0.62	68.4/−1.4	2164.6	−907.4
VGeP3H	3.53	7.54	2.423	2.442	99.17	93.57	125.10	34.28	21.5	6.73	0.48	0.15	0.62	77.9/−1.6	50.3	−32.2

---

The stability of VAZ₃H structures is thoroughly evaluated through mechanical, thermal, and dynamical assessments. Since SL VGeZ₃H yields results similar to SL VSiZ₃ H, only the latter is presented in Fig. 2 for brevity. Mechanical stability is confirmed by the elastic constants in Table 1, which satisfy the Born–Huang criterion (C₁₁ > |C₁₂|), confirming the mechanical stability of the structure. Thermal stability is verified through AIMD simulations shown in Fig. 2(a) and (b), where the atomic structure remains intact for 6 ps at 500 K without significant distortion. Additionally, the phonon dispersion in Fig. 2(c) and (d) reveals no imaginary frequencies throughout the Brillouin zone, confirming dynamical stability and a well-maintained atomic configuration. These findings collectively support the structural stability of VAZ₃H SLs, demonstrating their viability for experimental synthesis, much like the previously realized MoSi₂N₄ and MoAZ₃H, as highlighted in ref. 42–44.

Fig. 2 The evolution of total energy over time during AIMD simulations at 500 K for SL VSiN₃H (a) and VSiP₃H (b), with insets offering snapshots taken at the final stage of AIMD simulations. Panels (c) and (d) display the phonon dispersions for SL VSiN₃H and VSiP₃H, respectively.

To further validate the thermal stability, additional AIMD simulations were performed for VSiN₃H using a larger 5 × 5 × 1 supercell and a longer simulation time of 8 ps. The results show that the atomic structure remains intact, with no bond breaking or collapse, consistent with the original 6 ps simulations of the smaller supercell. These extended simulations confirm that VSiN₃H can withstand finite-temperature fluctuations, providing additional theoretical support for the potential experimental realization of VAZ₃H single layers. Based on the calculated stability, potential synthesis routes may include chemical vapor deposition (CVD) using suitable precursors for V, A-site, and Z-site elements, or exfoliation from bulk materials followed by surface functionalization to achieve the Janus structure. We emphasize that more extensive investigations, such as longer AIMD simulations, larger supercells, and thermodynamic convex hull analyses, will be necessary to fully assess the experimental synthesizability of these materials.

The electron localization function (ELF) analysis indicates that VAZ₃H single layers exhibit similar bonding characteristics across different compositions. For clarity, the ELF distribution of VSiN₃H is shown in Fig. 3(a). The V–N and Si–N bonds display strong covalent bonding with significant electron sharing between the atoms. The introduction of a hydrogen atom in the bottom layer slightly alters the electron distribution around the Si–N bonds, reflecting a subtle influence on the local electronic structure. Furthermore, the V–N bond shows partial ionic character due to the electronegativity difference between V and N, as evidenced by the lower ELF values. Owing to the Janus structure, bonding on both sides of the V atoms in VAZ₃H single layers exhibits directional asymmetry, which in turn affects their chemical and electronic properties.

Fig. 3 (a) Mapping of the electron localization function in SL VSiN₃H. (b) Angular dependence of the MAE for SL VSiP₃H and VGeP₃H, where the polar angle θ is measured with respect to the out-of-plane [001] axis. The MAE is defined as E(θ) − E_min, so that it is zero along the easy axis of magnetization.

To gain deeper insight into the chemical origin of the bonding characteristics in VAZ₃H single layers, Bader charge analysis was carried out for representative systems. In VSiN₃H, the analysis reveals a complex redistribution of electrons among multiple atomic species. Each N atom gains approximately 0.9–1.7e, reflecting their high electronegativity and significant electron accumulation. Meanwhile, the Si atom also loses a substantial amount of charge, and V partially donates electrons as well, indicating that electron transfer is not solely from V to N but involves a collective redistribution among V, Si, and N atoms. This finding is consistent with the ELF analysis, where both V–N and Si–N bonds exhibit strong covalent character with pronounced electron sharing, while the Janus structure introduces directional asymmetry in bonding on either side of the V atoms. When N is replaced by P, the electron gain at the anion sites decreases to roughly 0.4e per P atom, indicating weaker covalency and a more localized electron distribution. In contrast, substituting Si with Ge slightly enhances electron accumulation on the A-site atom and moderately affects the V–Z hybridization. Overall, these results demonstrate that substitutions at both Z and A sites influence the charge redistribution and bonding characteristics in VAZ₃H single layers, thereby shaping their overall electronic structure.

We now proceed to the magnetic properties of VAZ₃H SLs. Since the V–X–V bond angle (β) in all VAZ₃H SLs is close to 90°, it facilitates FM coupling according to the Goodenough–Kanamori–Anderson (GKA) rules.^45–47 Using a 2 × 2 × 1 supercell, we investigated the magnetic properties through nonmagnetic (NM), FM, and stripy antiferromagnetic (AFM) configurations. The energy difference ΔE_AF is defined as the energy of the AFM configuration minus that of the FM state. As seen in Table 1, ΔE_AF decreases progressively as the β angle deviates further from 90°, indicating a gradual reduction in the energy difference between the FM and AFM states, with the FM state remaining the most stable configuration. For instance, in VSiN₃H, the FM state is 347.8 meV lower in energy than the NM state and 87.7 meV lower than the stripy AFM state. The calculated magnetic moments, primarily localized on the V atoms, are approximately 1.0µ_B, reflecting the characteristic d¹ electronic configuration of vanadium among these SLs.

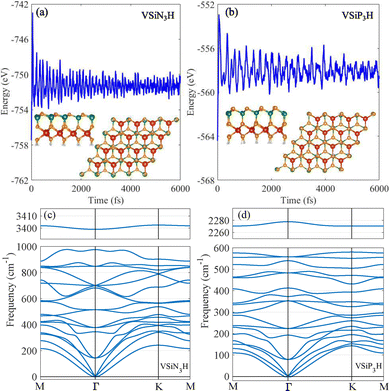
In line with the Mermin–Wagner theorem, a nonzero magnetic anisotropy energy (MAE) is crucial for sustaining long-range ferromagnetic ordering in two-dimensional magnets by counteracting the thermal agitation of magnons. To quantify this effect, the MAE is evaluated as a function of the polar angle θ with respect to the out-of-plane [001] axis,

MAE = E(θ) − E_min, (1)

where E(θ) denotes the total energy when the magnetization is oriented at angle θ, and E_min corresponds to the easy magnetization axis. In this definition, the MAE is zero along the easy axis, while finite values at other directions represent the energy cost to rotate the magnetization away from it. As shown in Fig. 3(b), VSiP₃H and VGeP₃H SLs exhibit their minimum MAE at θ = 0°, indicating an out-of-plane easy axis. In contrast, both VSiN₃H and VGeN₃H are more likely to possess in-plane magnetization, though out-of-plane magnetization may be realized through strain engineering or electrostatic gating.

Having established the magnetic ground state, it is important to investigate the electronic properties of SL VAZ₃H. As the HSE06 hybrid functional results exhibit the same overall trend as those obtained from PBE, the main difference lies in the magnitude of the band gaps (as shown in Table 1). This deviation mainly arises from the different treatments of exchange–correlation effects, where the inclusion of a fraction of exact exchange in HSE06 partially corrects the self-interaction error and leads to a larger band gap compared with PBE. Nevertheless, both methods yield consistent qualitative electronic features, so the PBE results are adopted for subsequent analysis due to their computational efficiency.

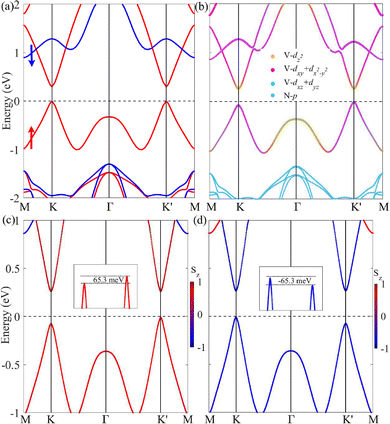
As shown in Fig. 4(a), VSiN₃H possesses magnetic semiconducting properties, where the VBM and CBM are primarily composed of spin-up states. In the absence of SOC, the material exhibits a direct band gap of approximately 0.30 eV, while the band formed by the spin-down states (shown by the blue lines) has a band gap of around 2.20 eV. Remarkably, the K and K′ points in the Brillouin zone host both the VBM and CBM, creating two well-defined valleys.

Fig. 4 (a) Band structure of SL VSiN₃H with spin polarization, excluding SOC effects. (b) Orbital-resolved band structure incorporating SOC. (c) Spin-polarized bands with SOC included. (d) Same as (c) but with reversed magnetization. Enlarged views of the VBM at the K and K′ points, with corresponding V_pol values shown in the insets.

Furthermore, the incorporation of SOC along with the intrinsic FM of the material leads to the spontaneous valley polarization in SL VSiN₃H, as shown in Fig. 4(b). The energy difference between K and K′ in the valence and conduction bands can be defined as V_pol = E_K′ − E_K and C_pol = E_K′ − E_K, where E_K′ and E_K are the energies at the K′ and K points, respectively. Fig. 4(c) shows that VSiN₃H exhibits a valley polarization (V_pol) of 65.3 meV in the valence band, while the valley polarization of CBM (C_pol) is negligible at −1.5 meV. By reversing the magnetic moment, the valley polarization at the K and K′ points is also inverted, leading to the K valley in the VBM having a higher energy compared to the K′ valley, as demonstrated in Fig. 4(d).

The discrepancy in valley polarization between the VBM and CBM is largely due to their differing orbital contributions and the effects of SOC. As shown in Fig. 4(b), for SL VSiN₃H, the d_x²−y²/d_xy orbitals of V dominate the valleys in the valence band, while the d_z² orbital is the main contributor to the conduction band. The SOC Hamiltonian is here approximated by its axial component under the assumption of collinear spin polarization along the z′ direction,

Ĥ_SOC ⋍ λŜ_z′L̂_z

where λ is the atomic SOC constant and 〈Ŝ_z′〉 denotes the spin expectation value. For brevity we define a ≡ λ〈Ŝ_z′〉, so that the effective one-body SOC acting on the orbital sector reads Ĥ^eff_SOC = aL̂_z in the first-order approximation. The SOC-induced energy shift of a given state is therefore determined by its orbital magnetic quantum number m = 〈L̂_z〉.

Although the real-space lobes of d_xy and d_x²−y² differ, these two functions can be expressed as linear combinations of the spherical harmonics |L = 2, m = ±2〉,

The valley Bloch states at K and K′ are well approximated by chiral combinations that project onto |2, ∓2〉, hence they carry m = ∓2 and couple to L̂_z with strength ±2. In this picture the leading SOC contribution to the valley splitting is

ΔE = E_K′ − E_K = 4a,

i.e. four times the effective coupling a. By contrast, the d_z² component corresponds to m = 0 and has negligible first-order shift under L̂_z, which explains the much smaller SOC-induced splitting in the CBM.

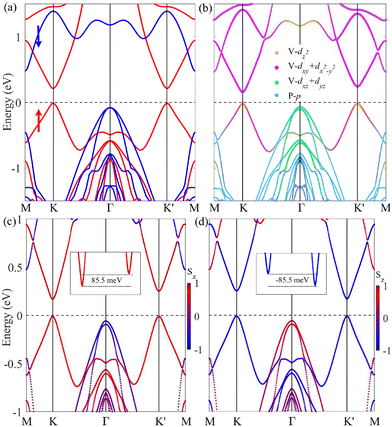
Building upon this understanding, a similar trend is observed in SL VSiP₃H. As illustrated in Fig. 5, although SL VSiP₃H retains a band structure similar to VSiN₃H, its bandgap is significantly reduced. Moreover, the shifts in orbital contributions between the VBM and CBM lead to distinct valley polarization behaviors. At the CBM, the orbital contribution is primarily from the d_x²−y²/d_xy orbitals, which results in a pronounced valley polarization of approximately 85.5 meV. In contrast, the VBM is mainly influenced by the d_z² orbital, where valley polarization is negligible. This trend extends to other VAZ₃H SLs, which share a comparable band structure with slight variations, as shown in Fig. 6. VGeN₃H shares strong similarities with VSiN₃H but features a further reduced bandgap of 0.46 eV and a CBM valley polarization of 68.4 meV. While VGeP₃H preserves the CBM at the K/K′ valleys with a polarization of 77.9 meV, its VBM transitions to the Γ point, demonstrating an indirect bandgap feature.

Fig. 5 (a) Band structure of SL VSiP₃H with spin polarization, excluding SOC effects. (b) Orbital-resolved band structure incorporating SOC. (c) Spin-polarized bands with SOC included. (d) Same as (c) but with reversed magnetization.

Fig. 6 Orbital-resolved (a) and (c) and spin-polarized (b) and (d) band structures with SOC for SL VGeN₃H and SL VGeP₃H, respectively. Enlarged views of the CBM at the K and K′ points, with corresponding C_pol values shown in the insets.

After recognizing the valley polarization in VAZ₃H SLs, we further explore their valley-specific phenomena by calculating and analyzing the Berry curvature, with the results displayed in Fig. 7. As illustrated in Fig. 7(a), the Berry curvature exhibits two pronounced peaks of opposite signs at the K and K′ valleys, reflecting the broken inversion symmetry. For VSiN₃H, the Berry curvature is −367.9 Bohr² at the K point and 589.6 Bohr² at K′. Meanwhile, in VSiP₃H, a sign reversal occurs, shifting the valley contribution from the valence to the conduction band, with Berry curvature values of 681.9 Bohr² at K and −275.4 Bohr² at K′. Similar patterns are observed in VGeN₃H and VGeP₃H, with the values of their Berry curvature summarized in Table 1 for comparison.

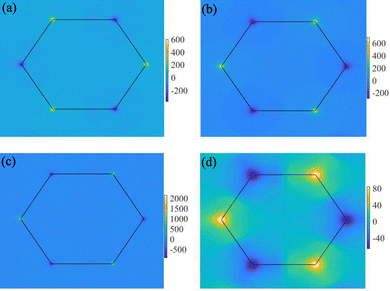Fig. 7 Contour map of Berry curvature for SL VAZ₃H over the entire Brillouin zone. (a)–(d) display the corresponding results for SL VSiN₃H, VSiP₃H, VGeN₃H, and VGeP₃H, respectively.

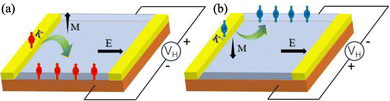
The nonzero Berry curvature (Ω_z(k)) at the K and K′ valleys in VAZ₃H generates an anomalous velocity v(k) in electronic carriers under an applied in-plane electric field E. This effect is described by the relation v(k) ∼ −E × Ω_z(k).⁴⁸ Due to valley polarization induced by intrinsic FM and SOC, carriers from different valleys exhibit distinct transport behaviors. Taking VSi₃PH as an example, electron doping shifts the Fermi level between the K and K′ valleys in the conduction band, which induces an anomalous velocity in spin-up electrons from the K valley. Under an in-plane electric field, the electrons accumulate along the lower edge, giving rise to the anomalous valley Hall effect, as shown in Fig. 8(a). Upon magnetization reversal, as illustrated in Fig. 8(b), a comparable Fermi level shift directs spin-down electrons from the K′ valley to the upper edge. In addition to the anomalous valley Hall effect, this material features charge and spin Hall effects, enabling charge transport modulation via the valley degree of freedom. This highlights the potential of VAZ₃H for valleytronic applications and their broader impact on spintronic technologies.

Fig. 8 (a) Schematic of the anomalous valley Hall effect in electron-doped SL VSiP₃H under an in-plane field with +z magnetization. (b) Same as (a) but with reversed magnetization. Spin-up and spin-down states are marked by red and blue arrows.

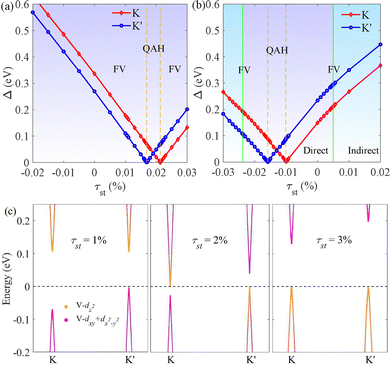
Strain engineering has emerged as a powerful tool for tuning electronic properties in 2D materials, enabling the modulation of band structures, transport characteristics, and even inducing novel quantum phases.⁴⁹ To further understand how strain influences the valleytronic behavior and electronic structures of VAZ₃H SLs, we focus on the effects of in-plane biaxial strain. The strain is defined as τ_st = (a − a₀)/a₀, where a and a₀ are the lattice constants under strain and in the unstrained state, respectively. All four VAN₃H SLs undergo a strain-induced evolution, beginning with the FV state and progressing through the HVM and QAH phases. As a result, we concentrate on VSiN₃H and VSiP₃H for a more detailed discussion.

The strain effects on SL VSiN₃H are depicted in Fig. 9(a). As compressive strain increases, VSiN₃H retains its FV state, with a gradual widening of the bandgap at the K and K′ valleys. When the strain reaches approximately −3.06%, the CBM shifts to the M point, leading to a transition into an indirect bandgap semiconductor while maintaining valley polarization at the VBM. Increasing tensile strain triggers a unique electronic transition. As tensile strain increases, the bandgaps at K and K′ decrease linearly. At 1.69% tensile strain, the bandgap at K′ closes while K retains a small gap, leading to HVM behavior. With further tensile strain, the gap at K′ reopens while the gap at K continues to shrink until it closes at 2.13%. Beyond this point, the bandgaps at both K and K′ gradually increase again, and the material returns to a direct bandgap FV semiconductor.

Fig. 9 Strain-dependent variation of Δ, the energy difference between the top valence and bottom conduction bands at K (red) and K′ (blue) for SL VSiN₃H (a) and VSiP₃H (b). The dashed golden line marks the QAH region, while the solid green lines in (b) indicate the direct–indirect bandgap transition. (c) Orbital-resolved band structure of SL VSiN₃H under τ_st = 1%, 2%, and 3%.

The energy band inversion occurs under strain, as is illustrated in Fig. 9(c). In the absence of strain or with a small strain of 1%, the VBM mainly originates from the d_xy/d_x²−y² orbitals of the V atom, while the CBM originates from its d_z² orbital. During bandgap closure and reopening at K′, their orbital contributions switch. At 2% strain, the VBM and CBM at K are dominated by d_xy + d_x²−y² and d_z² orbitals, respectively. As tensile strain increases like 3% strain, an energy band inversion occurs at K and K′, leading to a QAH phase in the 1.69–2.13% strain range, where SL VSiN₃H exhibits a nontrivial topological phase.

The strain response of SL VSiP₃H reveals some differences from that of VSiN₃H. Under tensile strain, the bandgaps at K and K′ gradually increase. At a tensile strain of about 0.5%, the material transitions into an indirect bandgap semiconductor with the VBM shifting to the Γ point, while the valley of CBM remain preserved. Increasing compressive strain triggers the electronic transition. At −1.0% strain, the closure of the K-point bandgap results in a HVM state. As the strain intensifies beyond −1.0%, the K-point bandgap reopens, while K′ progressively narrows until it vanishes at −1.58%, defining the QAH phase. With further compression, the K′ bandgap reopens, and both valleys exhibit simultaneous bandgap expansion. By −2.38% strain, the CBM relocates to the M point, shifting the system to an indirect bandgap semiconductor.

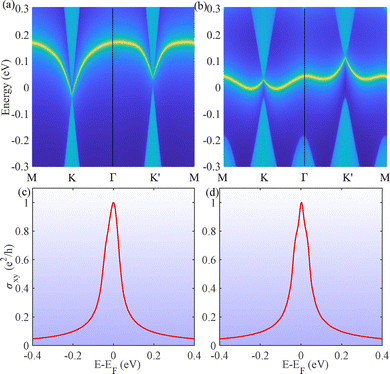
Both strained VSiN₃H and VSiP₃H demonstrate a chiral edge state in the QAH phase, with representative examples at τ_st = 1.9% for VSiN₃H and τ_st = −1.3% for VSiP₃H, as shown in Fig. 10(a) and (b) (highlighted in yellow). This edge state connects the valence and conduction bands, facilitating Bloch electron movement and resulting in Hall conductivity. Moreover, the quantized anomalous Hall conductivity σ_xy near the Fermi level can be obtained by integrating Ω_z(k) over the first Brillouin zone, as described by 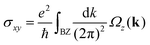. Fig. 10(c) and (d) demonstrate that strained VSiN₃H and VSiP₃H display an integer AHC plateau of 1e²/h at the Fermi level, which aligns with a Chern number of 1, confirming their nontrivial QAH behavior.

Fig. 10 Edge states for SL VSiN₃H (τ_st = 1.9%, (a)) and SL VSiP₃H (τ_st = −1.3%, (b)), with the corresponding calculated QAH conductance for SL VSiN₃H (c) and SL VSiP₃H (d), where E_F denotes the Fermi level.

In addition to VSiN₃H and VSiP₃H, similar trends are observed in other VAZ₃H SLs. For instance, VGeN₃H and VGeP₃H, while exhibiting distinct initial band structures, undergo phase transitions that closely resemble those of VSiP₃H, highlighting the tunable nature of their electronic properties under strain. Under tensile strain, VGeN₃H transitions into an indirect bandgap semiconductor beyond a critical strain while preserving its FV characteristics. Moreover, VGeP₃H maintains FV characteristics in the CBM under tensile strain until it becomes metallic at 3%. Under compressive strain, the QAH phase emerges within −1.04% to −1.42% for VGeN₃H and −4.11% to −3.82% for VGeP₃H, during which the bandgaps at both K′ and K gradually shrink, close, and subsequently reopen. These findings highlight the tunability of the valleytronic and topological properties of VAZ₃H through strain engineering.

4. Summary

This study explores the electronic and topological properties of VAZ₃H SLs, including VSiN₃H, VSiP₃H, VGeN₃H, and VGeP₃H, with a focus on their valley properties and topological transitions under strain. Without strain, VSiN₃H, VSiP₃H, and VGeN₃H exhibit direct bandgap FV semiconductor behavior, while VGeP₃H displays an indirect bandgap. VSiN₃H and VGeN₃H have easy in-plane magnetization axis, whereas VSiP₃H and VGeP₃H prefer easy out-of-plane magnetization. The interplay between intrinsic FM and SOC in the d orbitals of the V atom leads to spontaneous valley polarization at the K and K′ points. This polarization is more evident at the VBM for VSiN₃H and more apparent at the CBM for the other materials. Applying strain induces various phase transitions in these systems, including FV to HVM conversions, direct-to-indirect bandgap shifts, and the emergence of a QAH phase within specific strain intervals. In the QAH phase, chiral edge states connect the valence and conduction bands, resulting in quantum anomalous Hall conductivity, as confirmed by an integer AHC plateau of 1e²/h and a Chern number of 1. These findings underscore the combined role of intrinsic electronic properties and strain tuning in controlling the valleytronic and topological characteristics of VAZ₃H SLs.

Author contributions

Yang Yang and Yanyang Cao conceived the project and designed the research. Yanyang Cao and Shao-Jie Zhang performed the theoretical calculations and analyzed the results. Luogang Xie contributed to the interpretation of the findings and assisted in the literature review. Hong-Yan Lu supervised the project and provided critical insights into the theoretical models. Yang Yang wrote the manuscript with contributions from all authors. All authors reviewed and approved the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request. All relevant data, including computational details and numerical results, have been stored in a publicly accessible repository [if applicable, mention repository and accession details]. Additional information, such as input files for calculations and scripts used for analysis, can be provided upon request.

Acknowledgements

The authors are grateful for support from the Natural Science Foundation of Henan Province (Grant No. 242300420265 and 252300421498), the Training Program for Young Backbone Teachers in Colleges and Universities of Henan Province (Grant No. 2024GGJS081), and the National Natural Science Foundation of China (Grant No. 12074213 and 12404088).

References

1. K. Ando, Science, 2006, 312, 1883–1885.
2. C. Huang, J. Feng, F. Wu, D. Ahmed, B. Huang, H. Xiang, K. Deng and E. Kan, J. Am. Chem. Soc., 2018, 140, 11519–11525.
3. A. Rycerz, J. Tworzydło and C. Beenakker, Nat. Phys., 2007, 3, 172–175.
4. J. R. Schaibley, H. Yu, G. Clark, P. Rivera, J. S. Ross, K. L. Seyler, W. Yao and X. Xu, Nat. Rev. Mater., 2016, 1, 1–15.
5. L. Tao and E. Y. Tsymbal, Phys. Rev. B, 2019, 100, 161110.
6. H.-Z. Lu, W. Yao, D. Xiao and S.-Q. Shen, Phys. Rev. Lett., 2013, 110, 016806.
7. O. L. Sanchez, D. Ovchinnikov, S. Misra, A. Allain and A. Kis, Nano Lett., 2016, 16, 5792–5797.
8. W. Zhou, J. Chen, Z. Yang, J. Liu and F. Ouyang, Phys. Rev. B, 2019, 99, 075160.
9. Z. Zhou, F. Yang, S. Wang, L. Wang, X. Wang, C. Wang, Y. Xie and Q. Liu, Front. Phys., 2022, 17, 1–14.
10. J. Wen, H. Wang, H. Chen, S. Deng and N. Xu, Chin. Phys. B, 2018, 27, 096101.
11. W.-Y. Tong, S.-J. Gong, X. Wan and C.-G. Duan, Nat. Commun., 2016, 7, 13612.
12. H. Hu, W.-Y. Tong, Y.-H. Shen, X. Wan and C.-G. Duan, npj Comput. Mater., 2020, 6, 129.
13. H. Huan, Y. Xue, B. Zhao, G. Gao, H. Bao and Z. Yang, Phys. Rev. B, 2021, 104, 165427.
14. X. Zhou, R.-W. Zhang, Z. Zhang, W. Feng, Y. Mokrousov and Y. Yao, npj Comput. Mater., 2021, 7, 160.
15. P. Zhao, Y. Ma, C. Lei, H. Wang, B. Huang and Y. Dai, Appl. Phys. Lett., 2019, 115, 261605.
16. H.-X. Cheng, J. Zhou, W. Ji, Y.-N. Zhang and Y.-P. Feng, Phys. Rev. B, 2021, 103, 125121.
17. R. Peng, Y. Ma, X. Xu, Z. He, B. Huang and Y. Dai, Phys. Rev. B, 2020, 102, 035412.
18. W. Du, Y. Ma, R. Peng, H. Wang, B. Huang and Y. Dai, J. Mater. Chem. C, 2020, 8, 13220–13225.
19. Y. Zang, Y. Ma, R. Peng, H. Wang, B. Huang and Y. Dai, Nano Res., 2021, 14, 834–839.
20. P. Zhao, Y. Dai, H. Wang, B. Huang and Y. Ma, ChemPhysMater, 2022, 1, 56–61.
21. Z. He, R. Peng, X. Feng, X. Xu, Y. Dai, B. Huang and Y. Ma, Phys. Rev. B, 2021, 104, 075105.
22. Z. Song, X. Sun, J. Zheng, F. Pan, Y. Hou, M.-H. Yung, J. Yang and J. Lu, Nanoscale, 2018, 10, 13986–13993.
23. C. Zhang, Y. Nie, S. Sanvito and A. Du, Nano Lett., 2019, 19, 1366–1370.
24. C. Luo, X. Peng, J. Qu and J. Zhong, Phys. Rev. B, 2020, 101, 245416.
25. Y.-F. Zhao, Y.-H. Shen, H. Hu, W.-Y. Tong and C.-G. Duan, Phys. Rev. B, 2021, 103, 115124.
26. P. Jiang, L. Kang, Y.-L. Li, X. Zheng, Z. Zeng and S. Sanvito, Phys. Rev. B, 2021, 104, 035430.
27. S.-D. Guo, X.-S. Guo, X.-X. Cai and B.-G. Liu, Phys. Chem. Chem. Phys., 2022, 24, 715–723.
28. Q. Cui, Y. Zhu, J. Liang, P. Cui and H. Yang, Phys. Rev. B, 2021, 103, 085421.
29. X. Feng, X. Xu, Z. He, R. Peng, Y. Dai, B. Huang and Y. Ma, Phys. Rev. B, 2021, 104, 075421.
30. S. Li, Q. Wang, C. Zhang, P. Guo and S. A. Yang, Phys. Rev. B, 2021, 104, 085149.
31. S.-D. Guo, Y.-L. Tao, H.-T. Guo, Z.-Y. Zhao, B. Wang, G. Wang and X. Wang, Phys. Rev. B, 2023, 107, 054414.
32. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561.
33. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
34. P. Liu, S. Liu, M. Jia, H. Yin, G. Zhang, F. Ren, B. Wang and C. Liu, Appl. Phys. Lett., 2022, 121, 063103.
35. Y. Wang and Y. Ding, Appl. Phys. Lett., 2021, 119, 193101.
36. J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215.
37. R. N. Barnett and U. Landman, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 48, 2081.
38. S. Baroni, S. De Gironcoli, A. Dal Corso and P. Giannozzi, Rev. Mod. Phys., 2001, 73, 515.
39. A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2008, 178, 685–699.
40. A. A. Mostofi, J. R. Yates, G. Pizzi, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari, Comput. Phys. Commun., 2014, 185, 2309–2310.
41. Q. Wu, S. Zhang, H.-F. Song, M. Troyer and A. A. Soluyanov, Comput. Phys. Commun., 2018, 224, 405–416.
42. Y.-L. Hong, Z. Liu, L. Wang, T. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M.-L. Chen and D.-M. Sun, et al. , Science, 2020, 369, 670–674.
43. X. Cai, G. Chen, R. Li, W. Yu, X. Yang and Y. Jia, Phys. Chem. Chem. Phys., 2023, 25, 29594–29602.
44. X. Cai, G. Chen, R. Li, Z. Pan and Y. Jia, J. Mater. Chem. C, 2024, 12, 4682–4689.
45. J. B. Goodenough, Phys. Rev., 1955, 100, 564.
46. P. W. Anderson, Phys. Rev., 1959, 115, 2.
47. J. Kanamori, J. Appl. Phys., 1960, 31, S14–S23.
48. D. Xiao, M.-C. Chang and Q. Niu, Rev. Mod. Phys., 2010, 82, 1959.
49. F. Guinea, M. I. Katsnelson and A. Geim, Nat. Phys., 2010, 6, 30–33.

---