Effect of variable solubility on reactive convective dissolution
S.
Kabbadj
 ,
A.
De Wit
,
A.
De Wit
 and
L.
Rongy
and
L.
Rongy
 *
*
Université libre de Bruxelles (ULB), Faculté des Sciences, Nonlinear Physical Chemistry Unit, Campus de la Plaine – Boulevard du Triomphe CP231, 1050 Bruxelles, Belgium. E-mail: Sylvain.Kabbadj@ulb.be; Anne.De.Wit@ulb.be; Laurence.Rongy@ulb.be
First published on 3rd December 2025
Abstract
Chemical reactions can influence convective dissolution arising from density changes when a solute A dissolves into a host phase containing a reactant B. In this theoretical study, we examine the conditions that optimize the convective dissolution of A into the host phase when A reacts with B via an A + B → C reaction and the compositional change by the reaction reduces the solubility of A in the solution. Through numerical simulations, we explore how this variable solubility affects the reaction–diffusion–convection (RDC) concentration distributions and the flux of A at the interface. We classify the different density profiles based on key parameters such as the ratio of the initial concentration of B and the initial solubility of A, the individual contributions of each species to the total solution density and a parameter quantifying the influence of the reaction on the solubility of A. Taking into account the variable solubility of A allows to reach new regimes where, for instance, there is no longer any influence of the initial concentration of B on the mass transfer when B is in excess. We also show that, if C strongly decreases the solubility of A, the flux can even be lower than its nonreactive counterpart. These results contribute to understand the conditions where reactions can enhance or reduce the transfer of solutes into a host phase, a question relevant to many applications such as carbon dioxide storage in geological formations.
1 Introduction
Upon dissolution of a solute in a host phase, buoyantly unstable density stratifications can lead to convective dynamics in partially miscible systems. This is the case for two-liquid stratifications,1–6 when a solid dissolves in a liquid7,8 or when a gas enters into an aqueous host phase9–15 for instance. The importance of these physicochemical phenomena has been highlighted, notably in the context of industrial synthesis of chemicals,10,11 to enhance oil recovery techniques16,17 or to optimize the geological sequestration of carbon dioxide (CO2).18–22 In the context of carbon capture and storage (CCS), the dissolution of CO2 is analysed through both experimental12–14,23–26 and theoretical18,19,27–33 studies. Upon dissolution of a solute in a host phase, density changes can arise leading to an unstable stratification of a denser phase above a less dense one in the gravity field, such as in CO2 sequestration. The resulting convective dynamics are influenced by reactions with species dissolved in the host fluid,5,6,10–12,18–21,34–42 salinity,14,43 the presence of impurities,44,45 heterogeneities46 and pressure.14,43In this work, we focus on a reactive system in which a species A dissolves into a host phase containing a reactant B and C is produced in the host phase via a simple A + B → C reaction. The reaction consuming A and B modifies the solute concentrations, which can influence the fluid properties such as the density of the solution.12,34,41 The temporal evolution of the dissolution flux of A is directly influenced by the reaction and by the density stratification leading to the buoyancy-driven convection.11,12,34,41,47–54 The base-state reaction–diffusion (RD) concentration profiles of A, B and C have been compared to the nonreactive diffusive (D) case, leading to a classification of these profiles according to the influence of the parameters of the problem on the density field in the host phase.47–55 Reaction–diffusion–convection (RDC) density profiles have been classified both experimentally and theoretically.1,2,6,10–12,34,50,56 A reaction consuming A can slow down or accelerate the development of the buoyancy-driven convection compared to the nonreactive diffusion–convection (DC) case, leading to stabilizing or destabilizing cases.12,47,50,52,54
In most studies focusing on the convective dissolution between partially miscible phases, the solubility of A in the host phase is considered to be constant in time.5,6,12,34,36,41,43,47,50–56 However the solubility of a species in a solution depends, among others, on the concentration of other solutes.43,57 In the context of CO2 sequestration, for instance, its solubility is known to decrease with an increase of the salinity of the solution.14,43,58–62 Recently, some works48,49 have made the hypothesis that the reactant A is directly and entirely converted into the product C at the interface. In that case, the sum of the concentrations of A and C is a constant. The influence of a variable solubility on the RD dynamics in the host phase has been characterized recently to unify these cases, making the hypothesis that the product C linearly decreases the solubility of A.63 Additionally, the influence of a variable solubility of A on dissolution-driven convection has also been studied in the absence of reaction with a DC model.64
In this framework, our goal is to analyze the influence of a variable solubility on the reactive convective dissolution dynamics. In particular, we show that, if the compositional change by the reaction sufficiently decreases the solubility of A, it inhibits the mass transfer of A into the host phase. We analyze the effect of varying the initial concentration of B in the host phase, which controls the reaction rate. We finally discuss the classifications of the density profiles as a function of the parameter quantifying the decrease of the solubility of A by the reaction.
This work is structured as follows. The model system and the equations are presented in Section 2. The numerical results are discussed in Section 3, with analysis of the influence of three parameters on the dynamics: the variable solubility of A, the initial concentration of B and the contribution to the density of C. The RDC density profiles are reclassified and discussed in Section 4. Finally, Section 5 summarizes the study.
2 Model
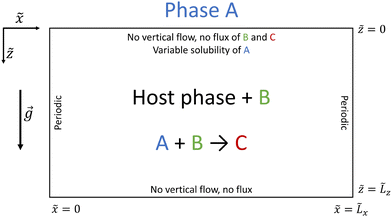
We consider a partially miscible system with a reservoir of A placed above a host phase containing a reactant B and where A dissolves, as shown in Fig. 1. The gravity field g points downwards along the vertical![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) axis perpendicular to the horizontal
axis perpendicular to the horizontal ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) axis. Within the host phase, a bimolecular reaction occurs where species A reacts with B with initial concentration B0, forming product C. The reaction rate of the A + B → C reaction is qÃ
axis. Within the host phase, a bimolecular reaction occurs where species A reacts with B with initial concentration B0, forming product C. The reaction rate of the A + B → C reaction is qÃ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) where q is the kinetic constant and à and
where q is the kinetic constant and à and ![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) are the concentrations of reactants A and B respectively.
are the concentrations of reactants A and B respectively.
We consider that the system is isothermal, isotropic and homogeneous and that the diffusion coefficients are constant. Furthermore, we assume that no mass exchange occurs from the host phase to the reservoir of A and that the interface separating the two phases remains horizontal and located at ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0 in the course of time. This allows to focus on the effects of the reaction on the dynamics in the host phase only. The host phase extends from
= 0 in the course of time. This allows to focus on the effects of the reaction on the dynamics in the host phase only. The host phase extends from ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) = 0 to
= 0 to ![[x with combining tilde]](https://www.rsc.org/images/entities/i_char_0078_0303.gif) =
= ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) x in the horizontal direction and from
x in the horizontal direction and from ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0 to
= 0 to ![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) =
= ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) z along the vertical direction.
z along the vertical direction.
The time, spatial coordinates, velocity, concentrations and pressure are made dimensionless as
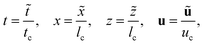 | (1a) |
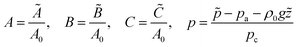 | (1b) |
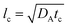 where DA is the diffusion coefficient of A. A0, used to non-dimensionalize the concentrations A, B and C, is the solubility of reactant A in the initial solution of B with concentration B0 when C = 0. We also use the velocity scale
where DA is the diffusion coefficient of A. A0, used to non-dimensionalize the concentrations A, B and C, is the solubility of reactant A in the initial solution of B with concentration B0 when C = 0. We also use the velocity scale 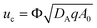 where Φ is the porosity of the medium. We use the ambient pressure pa, the hydrostatic pressure ρ0g
where Φ is the porosity of the medium. We use the ambient pressure pa, the hydrostatic pressure ρ0g![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) and the characteristic pressure
and the characteristic pressure 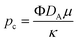 where ρ0 is the density of pure solvent, μ is the dynamic viscosity of the fluid and κ is the permeability of the porous medium.
where ρ0 is the density of pure solvent, μ is the dynamic viscosity of the fluid and κ is the permeability of the porous medium.
The dimensionless equations governing the RDC evolution of the two-dimensional concentrations of A, B and C in the host phase are
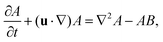 | (2a) |
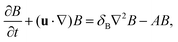 | (2b) |
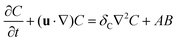 | (2c) |
| ∇p = −u + ρez, | (3a) |
| ∇2p = ∇·(ρez) | (3b) |
![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) of the solution is a linear function of the concentrations of the species:
of the solution is a linear function of the concentrations of the species:![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) = ρ0 (1 + αAÃ + αB = ρ0 (1 + αAÃ + αB![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) + αC + αC![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) ) ) | (4) |
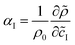 is the solutal expansion coefficient of species I,
is the solutal expansion coefficient of species I, ![[c with combining tilde]](https://www.rsc.org/images/entities/i_char_0063_0303.gif) I being its dimensional concentration. A dimensionless density is computed as
I being its dimensional concentration. A dimensionless density is computed as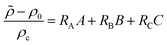 | (5) |
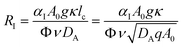 | (6) |
The initial conditions are
A(x, z = 0, t = 0) = 1 + ε![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rand(x), A(x, z > 0, t = 0) = 0, rand(x), A(x, z > 0, t = 0) = 0, | (7a) |
| B(x, z, t = 0) = β, | (7b) |
| C(x, z, t = 0) = 0 | (7c) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) rand(x) is a perturbation of the initial concentration of A introduced at the interface in order to trigger the instability. ε ≪ 1, here chosen as 10−3, is the amplitude of the perturbation while rand(x), a function varying randomly along the horizontal coordinate x between −1 and 1, is the modulation of the perturbation.54
rand(x) is a perturbation of the initial concentration of A introduced at the interface in order to trigger the instability. ε ≪ 1, here chosen as 10−3, is the amplitude of the perturbation while rand(x), a function varying randomly along the horizontal coordinate x between −1 and 1, is the modulation of the perturbation.54
Assuming that the dimensional solubility of A linearly decreases with the presence of species B or C, for the sake of simplicity and generality, it is expressed as
Ã(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0) = Asolvent − σC = 0) = Asolvent − σC![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) − σB − σB![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) | (8) |
![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0) = Asolvent − σC
= 0) = Asolvent − σC![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) − σB
− σB![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) + (σBB0 − σBB0) which leads to
+ (σBB0 − σBB0) which leads toÃ(![[z with combining tilde]](https://www.rsc.org/images/entities/i_char_007a_0303.gif) = 0) = A0 − σC = 0) = A0 − σC![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) − σB ( − σB (![[B with combining tilde]](https://www.rsc.org/images/entities/i_char_0042_0303.gif) − B0) − B0) | (9) |
Using the notations Lz = ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) z/lc and Lx =
z/lc and Lx = ![[L with combining tilde]](https://www.rsc.org/images/entities/i_char_004c_0303.gif) x/lc for the dimensionless height and width of the system, respectively, the boundary conditions for the dimensionless variables are next defined as
x/lc for the dimensionless height and width of the system, respectively, the boundary conditions for the dimensionless variables are next defined as
| uz(z = 0) = 0, uz(z = Lz) = 0 | (10a) |
| u(x = 0) = u(x = Lx), | (10b) |
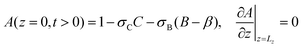 | (10c) |
| A(x = 0) = A(x = Lx), | (10d) |
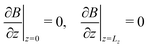 | (10e) |
| B(x = 0) = B(x = Lx), | (10f) |
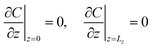 | (10g) |
| C(x = 0) = C(x = Lx) | (10h) |
If all species diffuse at the same rate, i.e. δB = δC = 1, summing eqn (2b) and (2c) with the given boundary and initial conditions evidences the conservation relation:12,54B + C = β. Thanks to this relation, we can reduce the number of dimensionless parameters by defining the dimensionless density ρ as
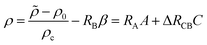 | (11) |
| A(z = 0) = 1 − σCC + σBC = 1 − αC | (12) |
We numerically solve eqn (2), (3) and (11) with eqn (7) and (10) on a domain with Lz = 2048 and Lx = 3072. Note that the choice of Lz does not influence the results provided the system is long enough along the z axis for the reaction front to be far away from the boundary z = Lz over the times studied. We increase the value of Lz to study more unstable cases, while maintaining the same mesh constraints. For instance, the mapped mesh used for Lz = 2048 contains 63![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 140 domain elements and 1026 boundary elements. We integrate Darcy's law on COMSOL Multiphysics version 6.065 with an initial time step of 10−5 and a relative tolerance of 5 × 10−3. A variable time step is chosen by the solver, evolving during the simulation if the tolerance is met. With these values, the iterative convergence errors and the discretization errors on the results were smaller than 5%, which was ensured via a mesh-refinement study. The quantitative measures depend on the random initial noise in eqn (7a). Therefore, we averaged the results over 10 simulations with variable noise realizations for each set of values of the parameters to obtain robust results, with an uncertainty quantified as the 95% confidence interval. Note that increasing the number of simulations does not improve significantly the averages presented in the next sections.
140 domain elements and 1026 boundary elements. We integrate Darcy's law on COMSOL Multiphysics version 6.065 with an initial time step of 10−5 and a relative tolerance of 5 × 10−3. A variable time step is chosen by the solver, evolving during the simulation if the tolerance is met. With these values, the iterative convergence errors and the discretization errors on the results were smaller than 5%, which was ensured via a mesh-refinement study. The quantitative measures depend on the random initial noise in eqn (7a). Therefore, we averaged the results over 10 simulations with variable noise realizations for each set of values of the parameters to obtain robust results, with an uncertainty quantified as the 95% confidence interval. Note that increasing the number of simulations does not improve significantly the averages presented in the next sections.
3 Nonlinear simulations
Let us start by analyzing the nonlinear convective dynamics in the host phase. We first briefly describe the dynamics in nonreactive cases and then, assuming that δB = δC = 1 and RA = 1, we examine the effect of varying the three parameters in reactive cases: α, β and ΔRCB.3.1 Nonreactive cases (β = 0)
Upon dissolution of A in a host phase containing no reagent B (β = 0), the diffusive concentration profile AD(z,t) of A in absence of convection is the classical error function solution of Fick's law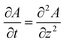 . Since the analytical concentration profile of A is known, the diffusive base-state density profile ρD is simply
. Since the analytical concentration profile of A is known, the diffusive base-state density profile ρD is simply 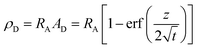 and is a function of RA.
and is a function of RA.
If the density decreases upon dissolution of A or if it does not change (RA ≤ 0), the nonreactive case is stable. The dynamics are controlled only by the diffusion of A and no convection is observed. Most gases dissolving into aqueous solutions correspond to this nonreactive stable case,54 as well as CO2 dissolving in nitrobenzene for example.66
For CO2 sequestration in saline aquifers for instance, its dissolution into brine typically corresponds to a convectively unstable case where the solute A increases the density of the host phase (RA > 0). It has been characterized in the literature in absence of reaction.7,19,31,32,40,43,67,68 The dissolution creates an unstable density stratification in the gravity field with a denser fluid on top of a less dense one, which is at the origin of buoyancy-driven convection. At first, fingers of the denser fluid sink in the host phase without interacting significantly with each other.7,31,54 A merging phenomenon between fingers then starts and increases over time, leading to a decrease in time of the number of fingers. Small fingers appearing near the interface, also called protoplumes, finally develop in the reinitiation regime32,54,68 and join the other fingers. In this work, we focus on these unstable cases by maintaining RA = 1 and consider the effect of a variable solubility on the reactive-convective dissolution of A in a host phase.
3.2 Reactive cases (β ≠ 0) for RA = 1
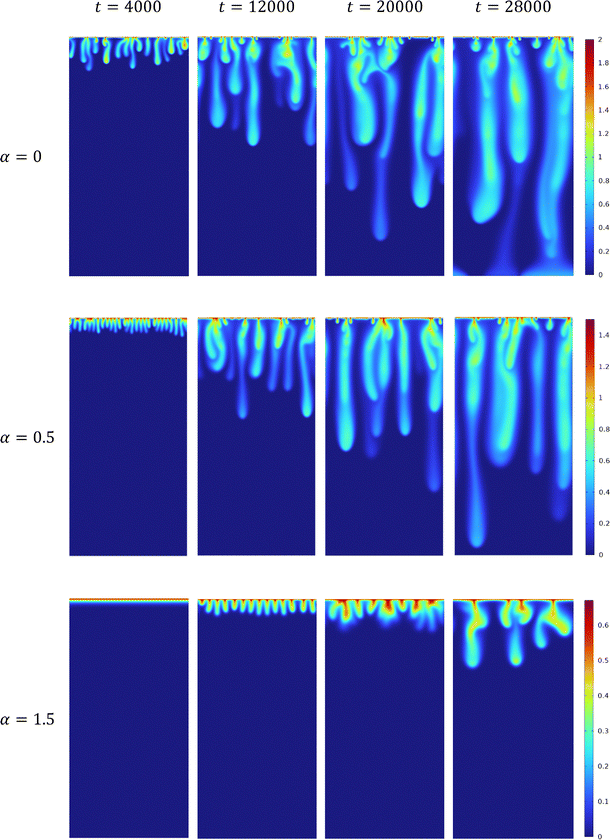
We vary α, β and ΔRCB to understand their influence on the density profiles and on the flux of A through the interface. In particular, we compare the results of the reactive cases with those of the unstable nonreactive (NR) case. The main objective of this section is to determine for which value of these parameters the dynamics are stabilized or destabilized.The influence of the variable solubility of A on the density distribution is presented in Fig. 2 for three different values of α. For any nonzero value of α, the dynamics are more stable than the corresponding reactive case with α = 0. Indeed, it has been shown in a reaction–diffusion system that when α > 0 increases, the reaction front invades the host phase more slowly.63 Consequently, A and C are smaller at a given depth z while B is larger. The density field being directly correlated to the concentration fields through eqn (11), increasing α leads to a decrease of ρ, which stabilizes the dynamics compared to the α = 0 case.
The stabilization of the dynamics due to an increase of α results in a decrease in the initial number of fingers and an increase of the onset time. The dynamics feature less merging or splitting between the fingers. Finally, we note that the maximal amplitude of the change of density decreases when α increases.
The RDC dynamics are also visualized in Fig. 3 using the horizontally-averaged density profile ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) (z,t) computed as
(z,t) computed as
 | (13) |
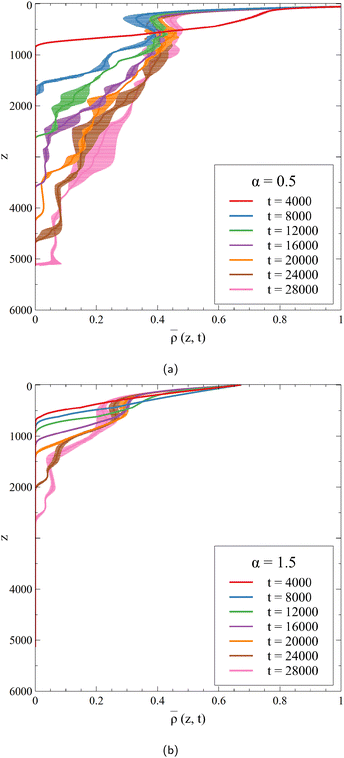 | ||
Fig. 3 Horizontally-averaged density profiles of the 2D dynamics of Fig. 2 at different times for (a) α = 0.5 and (b) α = 1.5. Note that the maximum values of the density in the host phase, obtained at the interface (z = 0), are ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) max = 1.50 when α = 0.5 and max = 1.50 when α = 0.5 and ![[small rho, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d1.gif) max = 0.67 when α = 1.5. Each curve is averaged over 10 simulations, for which the standard deviation is shown. max = 0.67 when α = 1.5. Each curve is averaged over 10 simulations, for which the standard deviation is shown. | ||
At early times, before the onset time of the convection, the density profile is similar to its RD counterpart as convection has not affected the concentration profiles yet.41 When the formation of the fingers starts, deviations are observed and the density profile is deformed. At a given depth z, the averaged density increases over time, an increase that is less marked when α increases because C is produced in smaller quantities, which corresponds to the stabilization of the dynamics when C inhibits the dissolution of A.
Space-time plots of the density at a given depth (z = 64) are given in Fig. 4 for two values of α. This location is chosen to be sufficiently below the fixed interface so that the convective dynamics are easily observed. The differences in terms of the number of fingers sinking to the bottom of the host phase or in terms of the onset time of the convection are visualized at early times. The lateral drift of fingers69 as well as merging and splitting phenomena result in branches in the space-time plots.
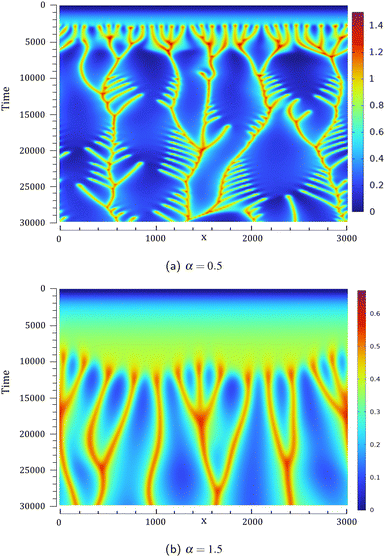 | ||
| Fig. 4 Space-time plots of the density computed at a horizontal line at z = 64 below the interface for the unstable reactive cases of Fig. 2 with (a) α = 0.5 and (b) α = 1.5. The density scale varies from 0 (blue) to its maximum value (red). | ||
To quantify the storage rate of A into the host phase, we compute the temporal evolution of the dissolution flux of A through the interface. Eqn (14) present the known solutions of the flux: JD is the analytical diffusive flux of A in absence of reaction and convective dynamics; JRD is the reaction–diffusion flux that can be computed analytically when α = 0 or numerically when α ≥ 0 in absence of convection;63 the RDC flux of A is computed numerically using eqn (14d).
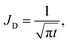 | (14a) |
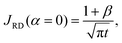 | (14b) |
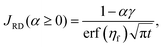 | (14c) |
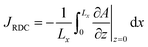 | (14d) |
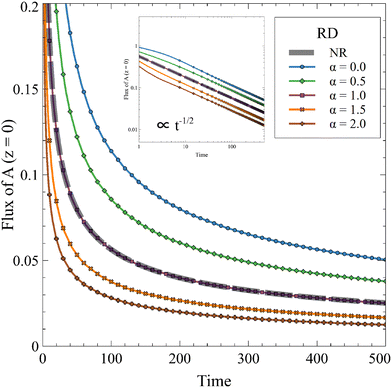
For a constant solubility of A (α = 0), the flux of A is always increased by the reaction.52,54 However, it has been shown, in the absence of convection, that increasing α decreases this effect until the reaction does not improve the mass transfer anymore when α = 1.63 We compute the temporal evolution of the flux of A in a one-dimensional RD system for 0 ≤ α ≤ 2 in Fig. 5.
The RD flux decreases with time, following a diffusive t−1/2 dependence, because the concentration gradient of A decreases over time. When α increases, C hinders the dissolution of A and the flux tends to the value of the nonreactive case when α = 1. As a reminder, A is then fully converted to C while the asymptotic concentration profile of the product is the same as the nonreactive profile of A. Interestingly, we see that the reaction can decrease the flux of A compared to the nonreactive case if α > 1.
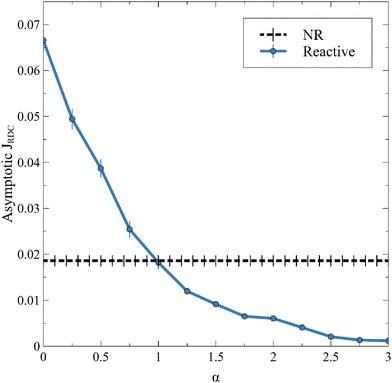
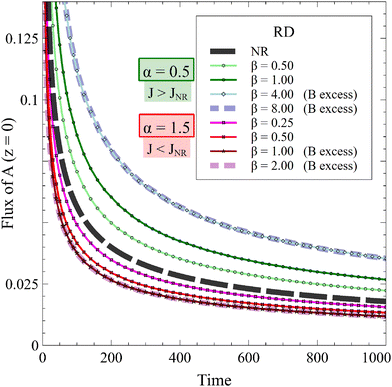
This new result is also observed in the presence of convection, as seen on the temporal evolution of JRDC in Fig. 6. Again, the flux of A first decreases with time. When the convective dynamics start, i.e. at the onset time of convection t0, the flux increases because the destabilization of the dynamics makes A sink faster in the host solution. The following changes of the flux are due to the merging and splitting of the fingers. After some time, the RDC flux fluctuates around an asymptotic value. This is well known both in NR dynamics31 and in the reactive case where the solubility is constant.54 We average the values of the flux at later times (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ≤ t ≤ 30
000 ≤ t ≤ 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) to calculate an asymptotic flux. This asymptotic flux decreases with increasing α, as seen in Fig. 7.
000) to calculate an asymptotic flux. This asymptotic flux decreases with increasing α, as seen in Fig. 7.
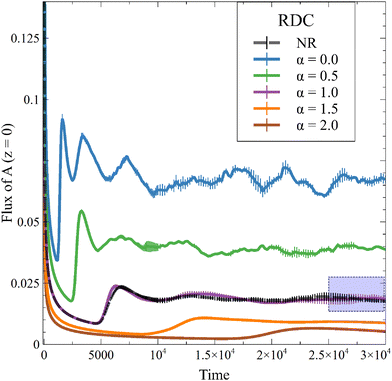 | ||
| Fig. 6 Temporal evolution of the RDC flux of A through the interface for different values of α and β = ΔRCB = 1 compared to the nonreactive (NR) case. The area framed in blue represents the time range over which the flux is averaged to give the asymptotic JRDC in Fig. 7. Each curve is averaged over 10 simulations, for which the standard deviation is shown. | ||
As in the RD cases (Fig. 5), the reaction can either increase the mass transfer if 0 ≤ α < 1 or decrease it if α > 1 compared to the nonreactive case. This result changes the conception of the RDC dynamics, given that it is no longer possible to consider that the reaction always improves the mass transfer if the presence of the product sufficiently decreases the solubility of A. Finally, we observe that, for a high value of α, the inhibition of the dissolution of A by the reaction tends to saturate, since increasing α does not significantly decrease the flux anymore. Note that the stabilization of the dynamics when α increases is also seen from the standard deviation (Fig. 3), which decreases with increasing α.
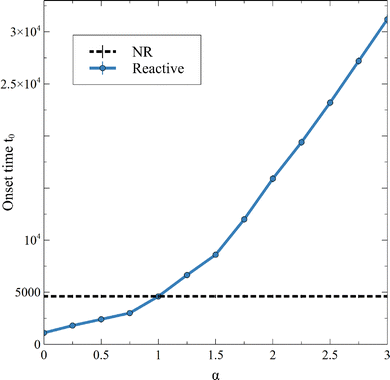
When convection starts, the flux of A deviates from its RD counterpart and increases. The onset time of convection t0 is computed as the time when the flux starts to depart from the diffusive decay, i.e. here when JRDC − JRD > 10−5. Note that, over the times studied in this work, the flux at t0 is the global minimum of the flux because convection increases the mass transfer at the interface and JRDC > JRD. The dependence of the onset time of the convection t0 on α shown in Fig. 8 corroborates the fact that the larger α, the later convection starts. Again, the value α = 1 separates cases where convection starts earlier than in absence of reaction (α < 1) from cases where convection starts later (α > 1).
In previous works where A(z = 0) = 1 at all times, B was always the species limiting the reaction, hence the consumption of A was directly linked to β.52,54 Here, we consider that A(z = 0) decreases when C is produced. The species limiting the reaction is then A in some cases and B in others, depending on the values of α and β. To determine which reactant is in excess in the (β, α) space of parameters, we consider the boundary condition (12) and state that the minimal value of A (Amin) is obtained for the maximal value of C (Cmax), i.e.:
| Amin = 1 − αCmax at z = 0. | (15) |
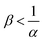 , which is always the case when α = 0. Conversely, if B is in excess
, which is always the case when α = 0. Conversely, if B is in excess 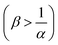 then Amin = 0 and
then Amin = 0 and 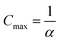 .
.
The temporal evolution of the RD flux of A is presented for two values of α as a function of β in Fig. 9. If α < 1, the reaction increases the flux of A compared to its NR counterpart, while the flux is decreased by the reaction if α > 1 because the solutes strongly inhibit the entrance of A in the host phase. In both cases, the effect of the reaction is stronger with increasing β, until B is in excess.
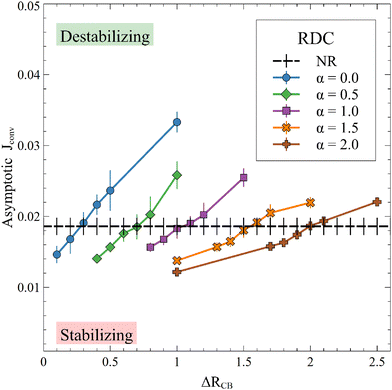
In Fig. 10, we present the asymptotic RDC flux of A and compare it to the nonreactive case for variable (β, α).
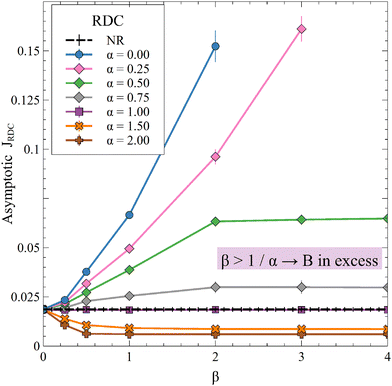 | ||
Fig. 10 Asymptotic (25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ≤ t ≤ 30 000 ≤ t ≤ 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000) averaged RDC flux of A for different values of α and β while ΔRCB = 1. Each point is averaged over 10 simulations, for which the standard deviation is shown. 000) averaged RDC flux of A for different values of α and β while ΔRCB = 1. Each point is averaged over 10 simulations, for which the standard deviation is shown. | ||
The reaction increases the flux compared to the nonreactive flux for all values of α < 1. In these cases, as long as 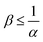 , increasing β enhances the influence of the reaction on the mass transfer which results in an increase of JRDC, because the concentration gradient increases. Once the reactant B is in excess (β > 1/α) the flux is not influenced by β any longer, the reaction being limited by the solubility of A and not by the initial amount of B anymore. Conversely, increasing β decreases the mass transfer for all values of α > 1. The product strongly decreases the solubility of A in these cases, hence the reaction is quickly limited by A and the asymptotic flux is again not influenced by β once
, increasing β enhances the influence of the reaction on the mass transfer which results in an increase of JRDC, because the concentration gradient increases. Once the reactant B is in excess (β > 1/α) the flux is not influenced by β any longer, the reaction being limited by the solubility of A and not by the initial amount of B anymore. Conversely, increasing β decreases the mass transfer for all values of α > 1. The product strongly decreases the solubility of A in these cases, hence the reaction is quickly limited by A and the asymptotic flux is again not influenced by β once 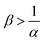 , i.e. when B is in excess. We recall that A + C = ρ = 1 at the interface when α = ΔRCB = 1 so JRDC = JNR for any value of β in that case.
, i.e. when B is in excess. We recall that A + C = ρ = 1 at the interface when α = ΔRCB = 1 so JRDC = JNR for any value of β in that case.
To summarize, the initial concentration of B does not have any influence on the mass transfer of A if B is in excess. The possibility of B being in excess is a novel specific feature of dissolution with variable solubility. Indeed, if α = 0, A is always the limiting species in excess as no substance in the host phase inhibits its continuous dissolution. If A is in excess, the influence of the reaction on the dynamics is directly correlated to β as studied previously in RD systems63 and in the presence of convection.52,54 If B is in excess (β > 1/α), then the dynamics give a RDC asymptotic flux which saturates.
It is possible to calculate the direct effect of the consumption of A on the mass transfer in the absence of convection. For a fixed solubility of A (α = 0), the RD flux is always larger than its nonreactive diffusive counterpart and the ratio JRD/JD = 1 + β is constant over time.54 For any positive value of α, the concentrations are calculated numerically and the ratio is a function of α. To quantify the direct effect of the convection on the flux of A, we divide the RDC flux by this ratio as
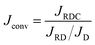 | (16) |
We define ΔRcrit such that Jconv = JNR if ΔRCB = ΔRcrit. We compute Jconv for 0 ≤ α ≤ 4 using different values of ΔRCB and obtain the value of ΔRCB = ΔRcrit when there is no direct effect of the convective dynamics on the flux. As shown in Fig. 12, we observe that ΔRcrit is a function of α as
| ΔRcrit ≃ 0.615 (±0.011) α + 0.345 (±0.015) for 0 ≤ α < 1, | (17a) |
| ΔRcrit ≃ 1.000 (±0.009) α + 0.010 (±0.004) for 1 ≤ α ≤ 4. | (17b) |
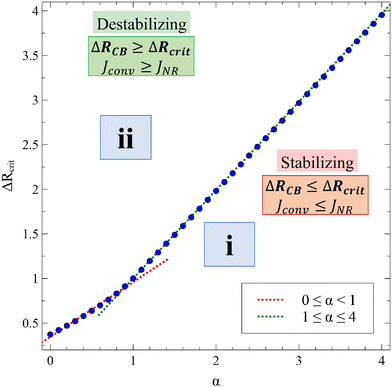 | ||
| Fig. 12 Classification of the RDC regimes in the (ΔRCB, α) space when β = 1: regime i (reaction stabilizes the dynamics compared to the nonreactive case) and regime ii (reaction destabilizes the dynamics compared to the nonreactive case). The red and green dotted lines are eqn (17a) and (17b) respectively. | ||
To summarise, when the solubility of A is affected by the reaction, that reaction can inhibit the convective dynamics and decrease the flux relative to the NR case if ΔRCB < ΔRcrit. Note that the direct effect of the convection, studied via ΔRCB, must then be coupled to the direct effect of the consumption of A depending on α to study the overall effects of the reaction on the flux.
4 Discussion
We summarize here the results presented in Section 3 and classify the density profiles based on the influence of the parameters on the mass transfer. We first analyze the RD density profiles reconstructed from the concentration fields, then we present the different regimes in the (β, α) and (ΔRCB, α) spaces of parameters. For each space, the other parameters are kept unitary.When α < 1, the consumption of A by the reaction increases the transfer of A into the host phase and increasing β increases this effect, provided A is in excess which is the case if 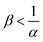 (Fig. 10). The density of the solution increases with β and is larger at a given depth for all reactive cases compared to the nonreactive case. The RD density profiles are not affected by β if α = ΔRCB = 1 and the reaction does not influence the mass transfer or the density profiles. Conversely, the direct effect of the reaction is a decrease of the flux and of the density when α > 1. Most importantly, we observe that in all cases where α ≠ 1, increasing β does not influence the flux if B is in excess (Fig. 10).
(Fig. 10). The density of the solution increases with β and is larger at a given depth for all reactive cases compared to the nonreactive case. The RD density profiles are not affected by β if α = ΔRCB = 1 and the reaction does not influence the mass transfer or the density profiles. Conversely, the direct effect of the reaction is a decrease of the flux and of the density when α > 1. Most importantly, we observe that in all cases where α ≠ 1, increasing β does not influence the flux if B is in excess (Fig. 10).
We recall that the RD concentration fields, from which the density profiles are constructed, are not affected by ΔRCB. The specific reactive case in which α = ΔRCB = ΔRcrit = 1 again corresponds to the diffusive case. We observe that when ΔRCB < ΔRcrit, the density is smaller at a given depth than its nonreactive value. In these stabilizing cases, the convective dynamics reduce the flux in a RDC system. On the other hand, if the contribution of C to the density is large enough (ΔRCB > ΔRcrit), the convective dynamics are more important than in a nonreactive case and the dynamics are destabilized because the density, which is the driving-force of the convection, is then larger at a given depth (Fig. 11).
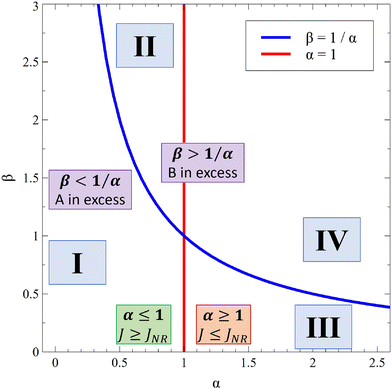
Fig. 13 summarizes the RDC regimes in the (β, α) parameter space. We identify four regimes of interest. In regime I, i.e. α < 1 and 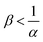 , the consumption of A by the reaction increases the flux relative to the nonreactive case. Since A is in excess, increasing β results in an increase of the effect of the reaction, which improves the mass transfer. In regime II, i.e. α < 1 and
, the consumption of A by the reaction increases the flux relative to the nonreactive case. Since A is in excess, increasing β results in an increase of the effect of the reaction, which improves the mass transfer. In regime II, i.e. α < 1 and 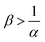 , the reaction still directly increases the flux (JRDC > JNR) but increasing β does not influence the mass transfer anymore because B is in excess. Conversely in regime III, i.e. α > 1 and
, the reaction still directly increases the flux (JRDC > JNR) but increasing β does not influence the mass transfer anymore because B is in excess. Conversely in regime III, i.e. α > 1 and 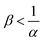 , the reaction decreases the flux relative to the NR case which is a major difference from the previously studied reactive cases.52,54 In this regime, increasing β decreases the flux even more. Finally the reaction decreases the flux but the influence of the reaction is not influenced by β in regime IV, i.e. α > 1 and
, the reaction decreases the flux relative to the NR case which is a major difference from the previously studied reactive cases.52,54 In this regime, increasing β decreases the flux even more. Finally the reaction decreases the flux but the influence of the reaction is not influenced by β in regime IV, i.e. α > 1 and 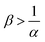 .
.
The relation between ΔRCB and α is summarized in Fig. 12 with two regimes of interest. In regime i, i.e. ΔRCB < ΔRcrit, the density is mostly controlled by the concentration of A. The decrease of A over time, due to its consumption by the reaction as well as the inhibition of its solubility by the solutes, leads to a stabilization of the dynamics and a decrease of the flux relative to the nonreactive case. In regime ii, ΔRCB > ΔRcrit, the contribution of C to the density is large enough to compensate for the consumption of A by the reaction. Even if the product inhibits the dissolution of A, it is produced in a sufficient quantity to destabilize the dynamics and increase the mass transfer compared to the nonreactive case.
5 Conclusions
Upon dissolution of a reactant A in a host phase containing a species B in which an A + B → C reaction generates a product C, the solubility of A can be affected by the compositional changes in the host phase. We have computed theoretically the reaction–diffusion–convection concentration profiles (eqn (2)) of the species and the density profile (eqn (11)) when the solubility of A linearly decreases with C (eqn (12)), i.e. A(z = 0) = 1 − αC. To explore the optimal conditions for the transfer of A into the host phase, we have quantified the influence on the flux of A of the variable solubility (α), of the initial concentration of B (β) and of the contribution of C to the density (ΔRCB). The mass transfer of A is enhanced by the reaction if 0 ≤ α < 1 because the consumption of A increases the gradient of its concentration. We show that the flux is the same as its nonreactive counterpart when α = ΔRCB = 1 because A is consumed as soon as it enters the host phase. In this limit case, A = 1 − C and ρ = A + C = 1 at the interface. Furthermore, we observe that the mass transfer is decreased by the reaction with regard to the nonreactive flux when α > 1. This new result changes our understanding of reactive convective dissolution since the reaction is not always increasing the flux anymore if the influence of the reaction on the solubility of A is large enough.Whether the reaction increases the flux (α < 1) or decreases it (α > 1), this effect is enhanced if the initial solution is more concentrated in B, i.e. if β increases. Because the solubility of A can change with the reaction, we may reach cases where A becomes the limiting reactant. This occurs when 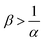 . As B is then in excess, increasing β does not influence the mass transfer. In the context of CO2 sequestration, this result highlights the importance of the choice of the sequestration site. Indeed, our results show that it is not always best to choose a concentrated aquifer if the reaction decreases the mass transfer (α > 1) or if B is in excess (no influence of β on the flux) for instance. With regard to the convective dynamics, we observe that an increase of ΔRCB destabilizes the dynamics and increases the flux for a fixed value of α. Note that below a value of ΔRCB = ΔRcrit = f(α), the reaction stabilizes the dynamics. This helps our understanding of the direct link between the influence of the variable solubility on the RD concentration profiles and the influence of the consumption of A on the convective dynamics.
. As B is then in excess, increasing β does not influence the mass transfer. In the context of CO2 sequestration, this result highlights the importance of the choice of the sequestration site. Indeed, our results show that it is not always best to choose a concentrated aquifer if the reaction decreases the mass transfer (α > 1) or if B is in excess (no influence of β on the flux) for instance. With regard to the convective dynamics, we observe that an increase of ΔRCB destabilizes the dynamics and increases the flux for a fixed value of α. Note that below a value of ΔRCB = ΔRcrit = f(α), the reaction stabilizes the dynamics. This helps our understanding of the direct link between the influence of the variable solubility on the RD concentration profiles and the influence of the consumption of A on the convective dynamics.
The classification of the RDC dynamics provided in this study opens perspectives for future research. Upon dissolution of CO2 into an aquifer for instance, CO2 may precipitate through a mineralisation reaction.40 It could be valuable to extend the framework to account for situations where precipitation decreases salinity, thereby increasing the solubility of CO2, corresponding to α < 0. The influence of the precipitation of C could be investigated using the relations found in the (β, α) and (ΔRCB, α) space of parameters. Furthermore, the influence of the diffusivity of the species on the RDC flux of A could also be studied for a variable solubility of A. Beyond these aspects, while the present model assumes isothermal conditions, future studies could address the role of heat release or absorption that may further impact solubility variations and convective dynamics.
Conflicts of interest
There are no conflicts to declare.Data availability
We hereby state that all the data supporting this article have been included as part of the manuscript, and raw data are available from the corresponding author upon reasonable request.Acknowledgements
We acknowledge the financial support of the ARC programme via the project CREDI and of the Fondation ULB.Notes and references
- M. A. Budroni, C. Thomas and A. De Wit, Phys. Chem. Chem. Phys., 2017, 19, 7936–7946 RSC.
- M. A. Budroni, L. A. Riolfo, L. Lemaigre, F. Rossi, M. Rustici and A. De Wit, J. Phys. Chem. Lett., 2014, 5, 875–881 CrossRef CAS PubMed.
- K. Eckert and A. Grahn, Phys. Rev. Lett., 1999, 82, 4436–4439 CrossRef CAS.
- R. Sczech, K. Eckert and M. Acker, J. Phys. Chem. A, 2008, 112, 7357–7364 CrossRef CAS PubMed.
- S. S. S. Cardoso and J. T. H. Andres, Nat. Commun., 2014, 5, 5743 CrossRef CAS PubMed.
- I. Cherezov and S. S. S. Cardoso, Phys. Chem. Chem. Phys., 2016, 18, 23727 RSC.
- A. C. Slim, M. M. Bandi, J. C. Miller and L. Mahadevan, Phys. Fluids, 2013, 25, 024101 CrossRef.
- J. Philippi, M. Berhanu, J. Derr and S. Courrech du Pont, Phys. Rev. Fluids, 2019, 4, 103801 CrossRef.
- M. A. Bees, A. J. Pons, P. G. Sørensen and F. Sagués, Chem. Phys., 2001, 114, 1932–1943 CAS.
- C. Wylock, A. Rednikov, B. Haut and P. Colinet, J. Phys. Chem. B, 2014, 118, 11323–11329 CrossRef CAS PubMed.
- C. Wylock, A. Rednikov, P. Colinet and B. Haut, Chem. Eng. Sci., 2017, 157, 232–246 CrossRef CAS.
- V. Loodts, C. Thomas, L. Rongy and A. De Wit, Phys. Rev. Lett., 2014, 113, 114501 CrossRef CAS PubMed.
- A. Vreme, F. Nadal, B. Pouligny, P. Jeandet, G. Liger-Belair and P. Meunier, Phys. Rev. Fluids, 2016, 1, 064301 CrossRef.
- C. Thomas, S. Dehaeck and A. De Wit, Int. J. Greenhouse Gas Control, 2018, 72, 105–116 CrossRef CAS.
- H. Liu and A. F. Taylor, J. Phys. Chem. B, 2022, 126, 10136–10145 CrossRef CAS PubMed.
- Z. Dai, H. Viswanathan, T. Xiao, R. Middleton, F. Pan, W. Ampomah, C. Yang, Y. Zhou, W. Jia, S.-Y. Lee, M. Cather, R. Balch and B. McPherson, Energy Procedia, 2017, 114, 6957–6967 CrossRef CAS.
- Z. Dai, R. Middleton, H. Viswanathan, J. Fessenden-Rahn, J. Bauman, R. Pawar, S.-Y. Lee and B. McPherson, Environ. Sci. Technol. Lett., 2014, 1, 49–54 CrossRef CAS.
- H. E. Huppert and J. A. Neufeld, Annu. Rev. Fluid Mech., 2014, 46, 255–272 CrossRef.
- H. Emami-Meybodi, H. Hassanzadeh, C. P. Green and J. Ennis-King, Int. J. Greenhouse Gas Control, 2015, 40, 238–266 CrossRef CAS.
- D. R. Hewitt, Proc. R. Soc. A, 2020, 476, 20200111 CrossRef CAS PubMed.
- M. De Paoli, Eur. Phys. J. E:Soft Matter Biol. Phys., 2023, 46, 129 CrossRef CAS PubMed.
- A. Firoozabadi and P. C. Myint, AIChE J., 2010, 56, 1398–1405 CrossRef CAS.
- T. J. Kneafsey and K. Pruess, Transp. Porous Media, 2010, 82, 123–139 CrossRef CAS.
- T. F. Faisal, S. Chevalier and M. Sassi, Energy Procedia, 2013, 37, 5323–5330 CrossRef CAS.
- R. Outeda, C. El Hasi, A. D'Onofrio and A. Zalts, Chaos, 2014, 24, 013135 CrossRef CAS PubMed.
- C. Thomas, L. Lemaigre, A. Zalts, A. D'Onofrio and A. De Wit, Int. J. Greenhouse Gas Control, 2015, 42, 525–533 CrossRef CAS.
- A. Riaz, M. Hesse, H. A. Tchelepi and F. M. Orr, J. Fluid Mech., 2006, 548, 87–111 CrossRef CAS.
- D. P. Schrag, Science, 2007, 315, 812–813 CrossRef CAS PubMed.
- S. Bachu, Prog. Energy Combust. Sci., 2008, 34, 254–273 CrossRef CAS.
- J. A. Neufeld and H. E. Huppert, J. Fluid Mech., 2009, 625, 353–370 CrossRef CAS.
- M. T. Elenius and K. Johannsen, Comput. Geosci., 2012, 16, 901–911 CrossRef.
- A. C. Slim, J. Fluid Mech., 2014, 741, 461–491 CrossRef CAS.
- L. Rongy, K. B. Haugen and A. Firoozabadi, AIChE J., 2012, 58, 1336–1345 CrossRef CAS.
- C. Thomas, V. Loodts, L. Rongy and A. De Wit, Int. J. Greenhouse Gas Control, 2016, 53, 230–242 CrossRef CAS.
- J. Ennis-King and L. Paterson, Int. J. Greenhouse Gas Control, 2007, 1, 86–93 CrossRef CAS.
- J. T. H. Andres and S. S. S. Cardoso, Phys. Rev. E:Stat., Nonlinear, Soft Matter Phys., 2011, 83, 046312 CrossRef PubMed.
- K. Ghesmat, H. Hassanzadeh and J. Abedi, J. Fluid Mech., 2011, 673, 480–512 CrossRef CAS.
- Y. Jun, D. E. Giammar and C. J. Werth, Environ. Sci. Technol., 2013, 47, 3–8 CrossRef CAS PubMed.
- L. Binda, C. El Hasi, A. Zalts and A. D'Onofrio, Chaos, 2017, 27, 053111 CrossRef CAS PubMed.
- C. Thomas, S. Dehaeck and A. De Wit, Phys. Rev. Fluids, 2020, 5, 113505 CrossRef.
- V. Loodts, P. M. J. Trevelyan, L. Rongy and A. De Wit, Phys. Rev. E, 2016, 94, 043115 CrossRef CAS PubMed.
- R. Tanaka, C. Almarcha, Y. Nagatsu, Y. Méheust and P. Meunier, Phys. Rev. Lett., 2024, 132, 084002 CrossRef CAS PubMed.
- V. Loodts, L. Rongy and A. De Wit, Chaos, 2014, 24, 043120 CrossRef CAS PubMed.
- J. Wang, Z. Wang, D. Ryan and C. Lan, Int. J. Greenhouse Gas Control, 2015, 42, 132–137 CrossRef CAS.
- S. M. Jafari Raad and H. Hassanzadeh, Int. J. Greenhouse Gas Control, 2017, 63, 350 CrossRef CAS.
- R. Benhammadi, P. Meunier and J. J. Hidalgo, Phys. Rev. Fluids, 2025, 10, 043501 CrossRef.
- P. Ghoshal and S. S. S. Cardoso, Phys. Chem. Chem. Phys., 2018, 20, 21617–21628 RSC.
- M. C. Kim and S. S. S. Cardoso, Phys. Fluids, 2018, 30, 094102 CrossRef.
- M. C. Kim and S. S. S. Cardoso, Phys. Fluids, 2019, 31, 084101 CrossRef.
- V. Loodts, L. Rongy and A. De Wit, Phys. Chem. Chem. Phys., 2015, 17, 29814–29823 RSC.
- V. Loodts, H. Saghou, B. Knaepen, L. Rongy and A. De Wit, Fluids, 2018, 3, 83 CrossRef CAS.
- M. Jotkar, A. De Wit and L. Rongy, Phys. Chem. Chem. Phys., 2019, 21, 6432–6442 RSC.
- M. Jotkar, L. Rongy and A. De Wit, Phys. Rev. Fluids, 2020, 5, 104502 CrossRef.
- V. Loodts, B. Knaepen, L. Rongy and A. De Wit, Phys. Chem. Chem. Phys., 2017, 19, 18565–18579 RSC.
- P. Ghoshal, M. C. Kim and S. S. S. Cardoso, Phys. Chem. Chem. Phys., 2017, 19, 644–655 RSC.
- M. C. Kim and C. Wylock, Can. J. Chem. Eng., 2017, 95, 589–604 CrossRef CAS.
- V. Savary, G. Berger, M. Dubois, J.-C. Lacharpagne, A. Pages, S. Thibeau and M. Lescanne, Int. J. Greenhouse Gas Control, 2012, 10, 123–133 CrossRef CAS.
- W. M. Haynes, D. R. Lide and T. J. Bruno, CRC Handbook of Chemistry and Physics 2012–2013, CRC Press, London, 2012 Search PubMed.
- H. Zhao, R. M. Dilmore and S. N. Lvov, AIChE J., 2015, 61, 2286–2297 CrossRef CAS.
- R. Khosrokhavar, G. Elsinga, R. Farajzadeh and H. Bruining, J. Pet. Sci. Eng., 2014, 122, 230–239 CrossRef CAS.
- M. Babaei and A. Islam, Water Resour. Res., 2018, 54, 9585–9604 CrossRef CAS.
- A. Islam, A. Y. Sun and C. Yang, Sci. Rep., 2016, 6, 24768 CrossRef CAS PubMed.
- S. Kabbadj, L. Rongy and A. De Wit, Phys. Rev. E, 2023, 107, 065109 CrossRef CAS PubMed.
- S. M. Jafari Raad, H. Emami-Meybodi and H. Hassanzadeh, Adv. Water Resour., 2019, 126, 40–54 CrossRef.
- COMSOL AB, COMSOL Multiphysics v. 6.0, Stockholm (Sweden), 2023, https://www.comsol.com.
- A. Okhotsimskii and M. Hozawa, Chem. Eng. Sci., 1998, 53, 2547–2573 CrossRef CAS.
- G. S. Pau, J. B. Bell, K. Pruess, A. S. Almgren, M. J. Lijewski and K. Zhang, Adv. Water Resour., 2010, 33, 443–455 CrossRef CAS.
- D. R. Hewitt, J. A. Neufeld and J. R. Lister, J. Fluid Mech., 2013, 719, 551–586 CrossRef CAS.
- D. Fernandez, L. Binda, A. Zalts, C. El Hasi and A. D'Onofrio, Chaos, 2018, 28, 013108 CrossRef CAS PubMed.
| This journal is © the Owner Societies 2026 |