Study on terahertz spectroscopy and weak intermolecular interactions of methylparaben under temperature effects

Abstract

Herein, terahertz time-domain spectroscopy (THz-TDS) is used to measure the terahertz spectra of methylparaben (MeP) in the frequency range of 0.5–3.0 THz at different temperatures of 300 K, 330 K, 360 K, and 390 K. Theoretical calculations were conducted using the quasi-harmonic approximation (QHA) method at temperatures of 180 K, 240 K, 300 K, and 360 K. The influence of temperature on the terahertz response of MeP molecules was explored in depth. Both the experimental and theoretical results indicate that as the temperature increases, the terahertz spectrum of this frequency band tends to shift towards the low-frequency region. To further explore the mechanism of this phenomenon, we further used the VMARD method combined with atomic displacement maps to allocate and analyze the vibration modes of each absorption peak at different temperatures. The results indicate that with changes in temperature, there are significant differences in the dominant mechanisms and motion distribution characteristics of each vibration mode, but their motion is still mainly concentrated in the rotational motion of molecules or functional groups. In addition, we used an independent gradient model based on the Hirshfeld partition (IGMH) method combined with atoms in molecules (AIM) theory to explore the effect of temperature on weak interactions in MeP crystals. It was found that the strength of hydrogen bonds varies with temperature, which in turn affects the basic characteristics of weak interactions. This study not only deepens the understanding of the thermodynamic behavior of MeP molecules, but also provides an important theoretical basis and technical support for the thermal stability regulation of materials in the food, cosmetics, and pharmaceutical industries.

---

1. Introduction

Terahertz (THz) waves, as a unique frequency band located between microwaves and infrared waves in the electromagnetic spectrum, have shown great potential for applications in food safety,¹ chemical industry,² biomedicine³ and other fields in recent years due to their unique physical and chemical properties. It is worth noting that this technological advantage is gradually extending to new fields such as agriculture and environmental monitoring, and geological research. For example, N. Menchu et al.⁴ used continuous wave terahertz spectroscopy technology to establish a quantitative relationship model between leaf moisture content and the terahertz absorption coefficient, achieving the non-destructive and accurate detection of the moisture content in different colored Indian almond leaves, providing a new non-destructive testing method for dynamic monitoring of agricultural moisture. H. Huang et al.⁵ innovatively introduced terahertz time-domain spectroscopy to address the complex correlation between the mineral crystal structure and the chemical composition, providing a mineral analysis system based on lattice dynamics response for geological exploration. Terahertz waves not only cover the characteristic energy levels of molecular vibrations and rotations, but also have high sensitivity to weak intermolecular interactions,^6,7 making terahertz spectroscopy an important tool for revealing the microstructure and interaction mechanisms of matter.

Herein, methylparaben (MeP) was selected as the research object, and its crystal structure is shown in Fig. 1. As a widely used preservative, MeP holds an important position in the food, cosmetics, and pharmaceutical industries due to its antibacterial and antifungal properties.^8,9 However, although MeP has been widely applied in multiple fields, the understanding of its molecular structure and interaction mechanism is still limited, especially the influence of temperature on its molecular vibration modes and weak interactions has not been fully studied. Temperature, as one of the key factors affecting the properties of materials, can significantly alter the thermal motion state of molecules, thereby affecting their intermolecular interactions and vibration modes.^10,11 These changes are typically manifested as frequency shifts and intensity variations in absorption peaks in terahertz spectra. Traditionally, techniques such as fluorescence spectroscopy,¹² single-crystal X-ray diffraction,¹³ and liquid chromatography¹⁴ have been used to detect and study MeP. However, these methods have limitations in describing complex intermolecular interactions in crystals, particularly in the study of temperature effects. Therefore, this study proposes a method for detecting and studying MeP using terahertz time-domain spectroscopy technology combined with theoretical simulation. Compared with traditional detection methods, THz-TDS technology is more accurate, efficient, and safe in the detection process. By using THz-TDS technology, it is possible to effectively capture the characteristic absorption peaks of MeP in the terahertz band and observe their changes with temperature, thereby revealing the mechanism of the influence of temperature on its molecular vibration modes and weak interactions.

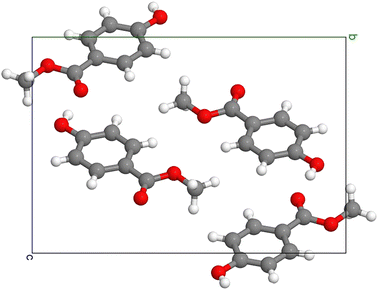Fig. 1 Crystal structure of MeP, with the red, gray, and white spheres representing oxygen atoms, carbon atoms, and hydrogen atoms, respectively.

In recent years, significant progress has been made in simulating and interpreting terahertz spectra using first principles calculations based on density functional theory (DFT).^15–17 The DFT method describes multi-electron systems through electron density rather than wave function, greatly simplifying the calculation process, while maintaining high computational accuracy. By combining the quasi-harmonic approximation (QHA),^18–21 the influence of temperature on molecular vibrations and weak interactions can be further studied, thus providing a more comprehensive understanding of the thermodynamic behavior of matter. This study not only fills the gap in the research on the effects of temperature on MeP in terahertz spectroscopy, but also provides a new perspective for a deeper understanding of its molecular structure and interaction mechanism.

2. Experimental

2.1. Experimental apparatus

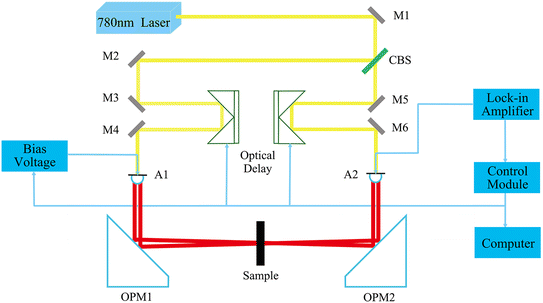
The experimental data in this study were obtained through transmission measurements using a CCT-1800 terahertz time-domain spectrometer developed by China Communications Technology Co., Ltd. The spectral measurement range of the system is 0.1–4.5 THz, with a dynamic measurement range of 75 dB. In the terahertz frequency band used in this study (0.5–3.0 THz), the signal-to-noise ratio is not less than 30 dB. A schematic^22,23 of the CCT-1800 THz-TDS system is shown in Fig. 2.

Fig. 2 Schematic of the THz-TDS system.

2.2. Sample preparation

The MeP and polyethylene powders used in this experiment were purchased from Sigma-Aldrich (Shanghai) Trading Co., Ltd. MeP has a purity of 99% and is a white crystal that meets the experimental requirements. It can be used directly without further purification. The sample was dried in a vacuum oven at 50 °C for about 2 h to remove residual moisture. Then, the sample and polyethylene powder were weighed using an electronic balance, mixed and ground in a mass ratio of 3 : 1. Subsequently, the sample was compressed into uniform thin sheets with a thickness of 1.0 mm and a diameter of 13 mm using an FW-4A tablet press.

Given the strong absorption properties of water towards terahertz waves, to ensure the accuracy of the terahertz spectral measurement experimental data, the entire experimental process was carried out in an orderly manner under strictly controlled environmental conditions. To avoid interference from atmospheric moisture on the measurement results during all terahertz spectroscopy measurements, a nitrogen purging system was specially used to keep the sample chamber in a dry nitrogen environment at all times. During the measurement process, nitrogen gas was continuously introduced to maintain a dry environment, effectively ensuring the accuracy and repeatability of the measurement. Besides, the terahertz optical path was completely closed during the entire experimental process, and the interior was filled with dry nitrogen gas, which kept the relative humidity in the sample chamber at a level of less than 2%, minimizing the influence of moisture in the air on terahertz wave absorption.

3. Theoretical calculation models and methods

3.1. Independent gradient model based on Hirshfeld partition

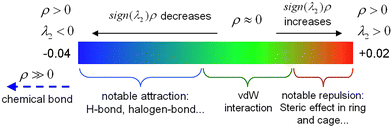
The independent gradient model based on Hirshfeld partition (IGMH)^24–26 is a sophisticated analysis method that combines electron density partitioning and gradient analysis, which is mainly used to characterize intermolecular interactions. This method is based on the Hirshfeld partition scheme, which divides the total electron density of a molecular system into the contributions from each atom, thereby effectively separating independent gradients associated with each atomic region.

The electron density function ρ(r) is used to describe the strength of weak interactions. To further describe the types and strengths of weak interactions, the sign(λ₂) function defined by the IRI method²⁷ was introduced. Multiplying the strength ρ function used to describe weak interactions and the sign(λ₂) used to describe interaction types to obtain the sign(λ₂)ρ function, and projecting it onto the corresponding iso-surfaces in different colors can intuitively display the position, strength, and type of weak interactions. The color scale used in this method is shown in Fig. 3. The blue area on the left side of the figure represents weak interactions with attractive effects. The larger the value of ρ(r), the darker the blue, indicating stronger attraction. The small value of ρ(r) in the middle green area indicates weak interaction strength, and the sign of λ₂ can be positive or negative. The red area on the right represents the region with mutual exclusion (steric hindrance) effect. The larger the value of ρ(r), the darker the red color, indicating a stronger steric hindrance effect.

Fig. 3 Color scale of functions based on IGMH method.

3.2. The theory of atoms in molecules

The theory of atoms in molecules (AIM)^28–30 is a theoretical model in quantum chemistry that describes the structure of molecules. It divides atomic regions within molecules by analyzing the topological properties of electron density gradient fields. The electron density gradient field has many topological features, and the critical point is one of the key ones, which plays an important role in revealing the internal structure of molecules. The critical point (CP) refers to the point where the magnitude of the function gradient is zero, and these critical points reveal the interactions between different atoms.

The Hessian matrix stands as a crucial instrument for dissecting electron density distributions. By computing the eigenvalues of the Hessian matrix (denoted as λ₁ > λ₂ > λ₃), one can ascertain the properties and classifications of electron density critical points. These critical points are predominantly categorized into four types, as follows: (3, −3), (3, −1), (3, +1), and (3, +3). Here, the first parameter of the coordinates represents the total number of non-zero eigenvalues of the Hessian matrix, while the second parameter represents the sum of the sign functions of these eigenvalues. Notably, the (3, −1) critical point typically corresponds to a bond critical point (BCP), characterized by one positive eigenvalue (λ₁ > 0) and two negative eigenvalues (λ₂ < 0, λ₃ < 0). Through AIM topological analysis, the hydrogen bond energy can be estimated based on the electron density at the BCP, with the strength and nature of hydrogen bonds directly correlated with these topological descriptors. The formula for calculating the binding energy of hydrogen bonds is as follows:

ΔE ≈ −223.08 × ρ(r_BCP) + 0.7423 (1)

where ρ(r_BCP) represents the electron density at the BCP. This method based on AIM topology analysis not only provides a new perspective for understanding the nature of hydrogen bonds, but also enables the prediction of hydrogen bond strength through simple electron density measurements, greatly simplifying the complexity of hydrogen bond research.

4. Results and discussion

4.1. Analysis of terahertz spectroscopy based on temperature effects

This study utilizes a CCT-1800 THz-TDS system and its accompanying transmission heating module to measure the terahertz spectra of MeP at temperatures of 300 K, 330 K, 360 K, and 390 K. To ensure the high reproducibility and robustness of the experimental results, this study independently prepared two different batches of MeP samples (lot number: LRAD5896 and LRAE0392). The spectral data obtained from the experiment is based on the average of five independent measurements as the final result, as shown in Fig. 4(a) and (b), respectively.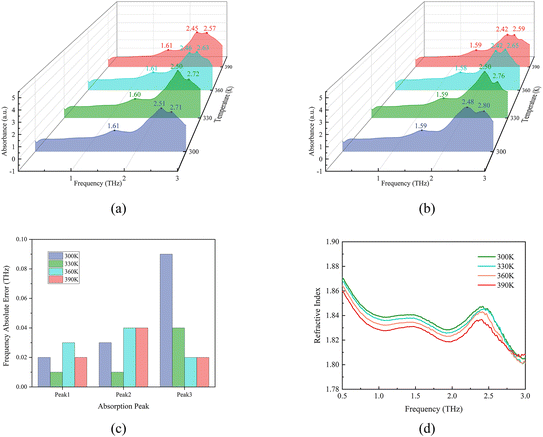

Fig. 4 Experimentally measured THz spectra of MeP at different temperatures of (a) batch number LRAD5896 and (b) batch number LRAE0392, (c) frequency errors, and (d) refractive index spectra.

In different temperature environments, the terahertz spectrum of MeP always exhibits three distinct absorption peaks. For the convenience of subsequent description, we label these three absorption peaks from left to right as peak 1, peak 2, and peak 3. Among them, the MeP sample with lot number LRAD5896 (as shown in Fig. 4(a)) maintains a relatively stable absorption peak 1 position near 1.61 THz in its terahertz spectrum. As the temperature gradually increases, absorption peak 2 shows a trend towards lower frequencies, specifically shifting from 2.51 THz at 300 K to 2.45 THz at 390 K. Meanwhile, absorption peak 3 also shows a trend of shifting towards lower frequencies, gradually changing from 2.71 THz at 300 K to 2.57 THz at 390 K. The absorption peaks in the terahertz spectra of the MeP sample (lot number: LRAE0392), as illustrated in Fig. 4(b), exhibit high consistency across various temperatures compared to the preceding batch (LRAD5896). Fig. 4(c) illustrates the frequency errors for three absorption peaks in the two batches of MeP samples, revealing that the maximum error (0.09 THz) occurs at absorption peak 3 under 300 K conditions. The above-mentioned experimental results clearly indicate that the terahertz absorption characteristics of MeP are significantly affected by temperature changes, especially the frequency shift phenomenon of absorption peaks 2 and 3, which is likely closely related to the temperature sensitivity of its intermolecular interactions. Given the high spectral similarity between the two sample batches, subsequent measurements and data processing utilized the MeP samples from batch LRAD5896.

The significant advantage of THz-TDS technology lies in its ability to simultaneously obtain the absorption characteristics and refractive index of substances. In this study, the refractive index spectra of MeP in the terahertz frequency band were extracted through experiments (as shown in Fig. 4(d)), and it was found that their fluctuation amplitude was small in the 0.5–3.0 THz frequency band, which is less than 5%, indicating that MeP has relatively stable dispersion characteristics. In the temperature range of 300 K to 390 K, the refractive index shows a gradual decreasing trend as the temperature increases. This phenomenon may be attributed to the combined effects of changes in molecular polarization caused by an increase in temperature, material density reduction caused by thermal expansion, and negative thermal optical coefficient characteristics. It is worth noting that the trend of refractive index change is inherently consistent with the phenomenon of absorption peak shifting towards lower frequencies mentioned earlier, indicating that the temperature sensitivity of intermolecular interactions may simultaneously affect the polarization response and vibration energy level of materials. This provides a key material parameter basis for the design of terahertz functional devices based on temperature regulation.

To further investigate the effect of temperature on the terahertz absorption peaks, this study introduces temperature factors in the theoretical calculations. Considering that experimental spectra can only obtain data at room temperature and above, expanding the calculation temperature range can help to more clearly reveal the impact of temperature changes on the spectra. This study is based on the QHA method, calculating the lattice parameters at different temperatures, and performing restrictive geometric optimization by fixing the lattice parameters. Using these data, the theoretical terahertz spectra at temperatures of 180 K, 240 K, 300 K, and 360 K were further calculated. The temperature-related theoretical calculated spectra are shown in Fig. 5. The results indicate that the theoretical spectra based on QHA can well simulate the terahertz absorption spectra under temperature changes. It accurately predicts the three absorption peaks that exist in the experiment.

Fig. 5 Theoretically calculated THz spectra of MeP at different temperatures.

According to Fig. 5, it can be seen that as the temperature increases, each absorption peak shift towards lower frequencies. Except for absorption peak 1, the temperature change trend of the calculated spectra is basically consistent with the experimental spectra. The difference between absorption peak 1 in the experimental spectrum and the calculated spectrum may be due to the difficulty of the instrument to capture small frequency shifts when measuring small temperature spacing changes. To quantitatively analyze the frequency shift caused by temperature, Table 1 lists the absorption peak frequencies calculated for MeP at different temperatures. In addition, the experimentally measured 300 K and 360 K terahertz spectra were compared with the calculated spectra in the same graph to further verify the accuracy of the theoretical calculations.

Table 1 Frequency distribution of the theoretical absorption peaks of MeP at different temperatures

Temperature (K)	Absorption peak 1 (THz)	Absorption peak 2 (THz)	Absorption peak 3 (THz)
180	1.57	2.46	2.90
240	1.57	2.43	2.85
300	1.52	2.41	2.81
360	1.50	2.40	2.76

---

A comparison of the experimental and theoretical spectral results for MeP at 300 K and 360 K is shown in Fig. 6. This figure shows that at 300 K, the calculated frequencies of absorption peak 1 and absorption peak 2 are slightly lower than the experimentally measured values, while the calculated frequency of absorption peak 3 is slightly higher than the experimental values. At 360 K, the calculated frequencies of absorption peaks 1 and 2 are also slightly lower than the experimental values, and the calculated frequency of absorption peak 3 is also slightly higher than the experimental values. However, overall, the frequency deviation between the experimental and theoretical absorption peaks at 300 K and 360 K is approximately 0.1 THz, indicating good consistency between the experimental and theoretical calculation results. Meanwhile, the error between the experimental and theoretical calculation results is inevitable, mainly due to the following two reasons. Firstly, the QHA calculation assumes that the lattice vibration is a simple harmonic vibration, and describes the anharmonic effect through volume change approximation. This processing method ignores the high-order interactions between phonons, especially under high temperature conditions, which may lead to insufficient calculation accuracy. Secondly, due to the inertial nature of temperature measurement, there may be temperature fluctuations during the experimental process, which can also have a certain impact on the experimental results. These factors collectively lead to small deviations between the experimental and theoretical spectra.

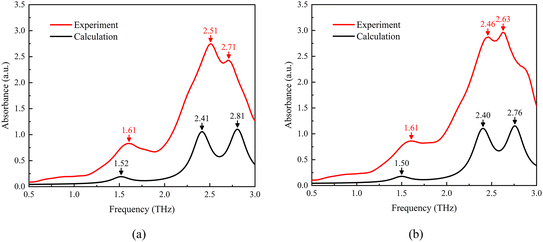Fig. 6 Comparison of the experimental and theoretical THz spectra of MeP at (a) 300 K and (b) 360 K.

4.2. Analysis of vibration modes induced by thermal effect

Absorption peaks in the terahertz band are often caused by the coupling of intermolecular and intramolecular vibrations. Thus, to further investigate the source of the terahertz spectral absorption peaks of MeP, this study used the VMARD³¹ method for vibration mode allocation, and combined the vibration mode atomic displacement map to analyze the temperature-induced molecular motion. By comparing the vibration mode distribution and atomic displacement characteristics at different temperatures (180 K, 240 K, 300 K, and 360 K), the regulatory effect of temperature changes on the molecular vibration modes and their motion directions was systematically studied. As shown in Tables 2–5, the frequencies of all the vibration modes exhibit significant temperature dependence within the temperature range of 180 K to 360 K, and show varying degrees of frequency reduction with an increase in temperature. This phenomenon is consistent with the trend of the characteristic peak of the experimental terahertz spectrum moving towards lower frequencies, indicating that an increase in temperature leads to a weakening of intermolecular interactions and intensification of molecular motion.

Table 2 Assignment results of vibration mode 1 for MeP

Temperature (K)	Mode (THz)	Vibrational mode assignment	Mode assignment
Note: the υ, δ, γ and τ symbols in the table represent key length extension, key angle bending, out-of-plane angle bending, and dihedral angle torsion, respectively. The percentage in parentheses represents the maximum contribution ratio of the vibration mode.
180	1.57	δH(59)C(51)H(63) (7.2%)	υ(45.7%), δ(52.2%)
			γ(0.3%), τ(1.8%)
240	1.56	δH(59)C(51)H(63) (7.2%)	υ(45.7%), δ(52.2%)
			γ(0.3%), τ(1.8%)
300	1.52	δH(57)C(49)H(61) (7.4%)	υ(40.2%), δ(56.8%)
			γ(0.6%), τ(2.4%)
360	1.50	δH(57)C(49)H(61) (9.0%)	υ(41.7%), δ(54.6%)
			γ(0.5%), τ(3.2%)

---

Table 3 Assignment results of vibration mode 2 for MeP

Temperature (K)	Mode (THz)	Vibrational mode assignment	Mode assignment
Note: υ, δ, γ and τ in the table represent key length extension, key angle bending, out-of-plane angle bending, and dihedral angle torsion, respectively. The percentage in parentheses represents the maximum contribution ratio of the vibration mode.
180	2.45	τO(4)C(16)C(20)C(40) (6.0%)	υ(10.6%), δ(12.4%)
			γ(12.2%), τ(64.8%)
240	2.40	δH(54)C(49)H(61) (13.1%)	υ(11.4%), δ(45.8%)
		δH(56)C(51)H(63) (12.6%)	γ(2.6%), τ(40.1%)
300	2.39	δC(40)C(20)C(24)C(68) (6.3%)	υ(8.9%), δ(12.0%)
			γ(12.5%), τ(66.7%)
360	2.37	δC(40)C(20)C(24)C(68) (5.5%)	υ(4.9%), δ(14.5%)
			γ(13.9%), τ(66.7%)

---

Table 4 Assignment results of vibration mode 3 for MeP

Temperature (K)	Mode (THz)	Vibrational mode assignment	Mode assignment
Note: the υ, δ, γ and τ symbols in the table represent key length extension, key angle bending, out-of-plane angle bending, and dihedral angle torsion, respectively. The percentage in parentheses represents the maximum contribution ratio of the vibration mode.
180	2.47	δH(54)C(49)H(61) (11.4%), δH(56)C(51)H(63) (11.3%)	υ(12.6%), δ(39.3%)
			γ(2.4%), τ(45.7%)
240	2.44	τO(4)C(16)C(20)C(40) (6.0%)	υ(5.9%), δ(13.6%)
			γ(12.1%), τ(68.4%)
300	2.43	δH(54)C(49)H(61) (11.4%), δH(56)C(51)H(63) (11.3%)	υ(12.5%), δ(39.5%)
			γ(6.0%), τ(41.9%)
360	2.42	δH(54)C(49)H(61) (11.4%), δH(56)C(51)H(63) (11.4%)	υ(12.5%), δ(39.7%)
			γ(6.0%), τ(41.8%)

---

Table 5 Assignment results of vibration mode 4 for MeP

Temperature (K)	Mode (THz)	Vibrational mode assignment	Mode assignment
Note: the υ, δ, γ and τ symbols in the table represent key length extension, key angle bending, out-of-plane angle bending, and dihedral angle torsion, respectively. The percentage in parentheses represents the maximum contribution ratio of the vibration mode.
180	2.90	τO(2)C(14)C(18)C(38) (7.9%)	υ(5.1%), δ(8.3%)
			γ(19.3%), τ(67.4%)
240	2.85	τO(3)C(15)C(19)C(39) (7.8%)	υ(6.6%), δ(8.9%)
			γ(20.8%), τ(63.7%)
300	2.81	τO(3)C(15)C(19)C(39) (7.7%)	υ(6.4%), δ(8.5%)
			γ(18.8%), τ(66.3%)
360	2.76	τO(3)C(15)C(19)C(39) (7.6%)	υ(6.8%), δ(8.7%)
			γ(18.2%), τ(66.3%)

---

Table 2 shows the VMARD analysis results of the first absorption peak of MeP. The analysis shows that absorption peak 1 is mainly dominated by vibration mode 1, and its vibration characteristics mainly come from the contributions of bond length stretching vibration and bond angle bending vibration. As the temperature increases, the dominant mechanism of vibration mode 1 changes. The contribution rate of bond length stretching vibration decreases from 45.7% to 41.7%, while the contribution rate of bond angle bending vibration increases from 52.2% to 54.6%. Specifically, the dominant role of the corresponding maximum contribution of C₍₅₂₎H₍₆₀₎ bond length stretching vibration is gradually replaced by H₍₅₇₎C₍₄₉₎H₍₆₁₎ bond angle bending vibration. However, due to the fact that the maximum contribution value of the defined internal coordinates only accounts for 9.0% of the entire vibration mode contribution, it indicates that the motion of vibration mode 1 is relatively dispersed in the internal coordinate space. However, as shown in Fig. 7, the overall motion of vibration mode 1 exhibits a characteristic of rotation around the a-axis, mainly manifested as methyl rotation bending vibration. When the temperature is low, the molecules of O¹ and O² tend to rotate clockwise around the a-axis, while the molecules of O³ and O⁴ tend to rotate counterclockwise around the a-axis. When the temperature increases above 300 K, the rotation direction of the molecules is reversed, and the molecules of O¹ and O² rotate counterclockwise around the a-axis, while the molecules of O³ and O⁴ rotate clockwise around the a-axis.

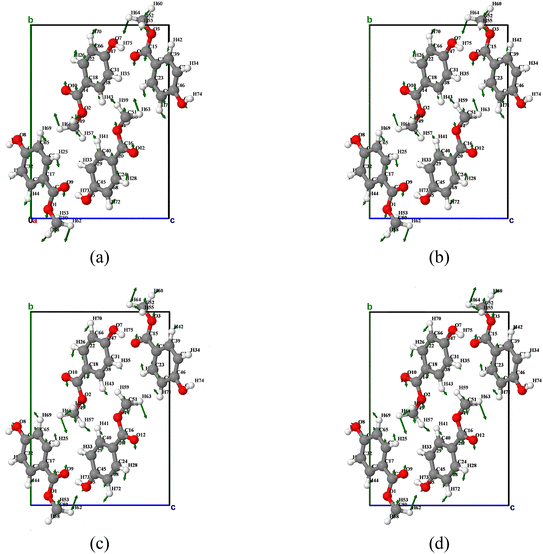Fig. 7 Atomic displacement diagrams of the vibration mode 1 of MeP at temperatures of (a) 180 K, (b) 240 K, (c) 300 K, and (d) 360 K.

The second absorption peak of MeP is mainly formed by the coupling effect of vibration modes 2 and 3. The VMARD analysis results of vibration mode 2 with temperature variation are shown in Table 3. At 180 K, the vibration contribution of vibration mode 2 mainly comes from dihedral angle torsion, with contribution rate of 64.8%. However, the maximum contribution of dihedral angle torsion only accounts for 6.0% of the entire vibration contribution, indicating that the motion distribution of vibration mode 2 is relatively dispersed at this temperature. When the temperature increases to 240 K, the dominant mechanism of vibration mode 2 shifts to bond angle bending and dihedral angle torsion, with their vibration contribution rates accounting for 45.8% and 40.1%, respectively. The maximum contribution still comes from bond angle bending of H₍₅₄₎C₍₄₉₎H₍₆₁₎ and H₍₅₆₎C₍₅₁₎H₍₆₃₎. When the temperature further increased to 300 K and 360 K, the dominant mechanism of vibration mode 2 shifted again to dihedral angle torsion, which accounted for 66.7% of the total vibration contribution, while the maximum contribution of dihedral angle torsion (dihedral angle torsion of C) was only 6.3% and 5.5%, respectively, further confirming the significant dispersion of the motion distribution of vibration mode 2.

In summary, as the temperature changes, vibration mode 2 does not exhibit a single dominant motion mode throughout. According to the analysis of the atomic displacement diagram (as shown in Fig. 8), vibration mode 2 exhibits more pronounced methyl rotation motion compared to vibration mode 1. Specifically, at 240 K, the methyl groups of molecules O² and O⁴ exhibit a counterclockwise rotation trend around the a-axis, while the methyl groups of molecules O¹ and O³ exhibit a clockwise rotation trend around the a-axis. At 180 K, 300 K, and 360 K, the methyl groups of molecules O¹ and O² rotate in the same direction around the a-axis, and the methyl groups of molecules O³ and O⁴ also rotate in the same direction around the a-axis, exhibiting a counterclockwise rotation trend.

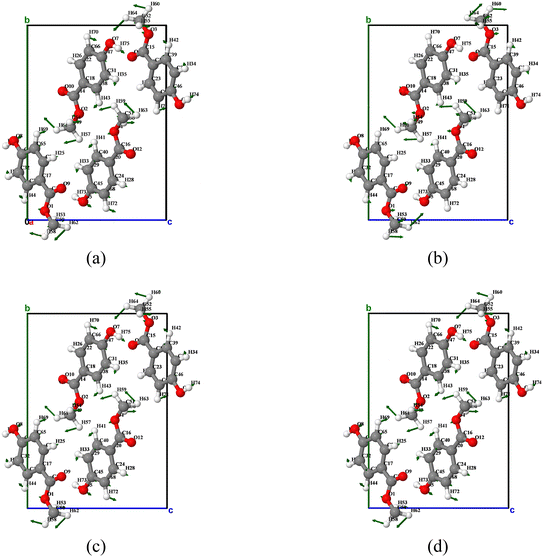Fig. 8 Atomic displacement diagrams of the vibration mode 2 of MeP at temperatures of (a) 180 K, (b) 240 K, (c) 300 K, and (d) 360 K.

Table 4 shows the VMARD analysis results of vibration mode 3 as a function of temperature. Unlike vibration mode 2, vibration mode 3 is dominated by dihedral angle torsion throughout the entire temperature range, but its contribution decreases with an increase in temperature. When the temperature increases from 180 K to 360 K, the contribution rate of dihedral angle torsion significantly decreases from 45.7% to 41.8%. It is worth noting that at 180 K, 300 K, and 360 K, the vibration contribution of bond angle bending is close to that of dihedral angle torsion, only slightly lower than the latter. Moreover, at these temperature points, the maximum proportion of vibration contribution comes from the bond angle bending modes of H₍₅₄₎C₍₄₉₎H₍₆₁₎ and H₍₅₆₎C₍₅₁₎H₍₆₃₎, with contribution rates of 11.4% and 11.3%, respectively, rather than dihedral angle torsion. However, at 240 K, the vibration contribution of bond angle bending significantly decreased, and dihedral angle torsion dominated the vibration contribution, with the maximum contribution coming from the dihedral angle torsion of O₍₄₎C₍₁₆₎C₍₂₀₎C₍₄₀₎, which was 6.0% (240 K). In summary, although dihedral angle torsion remains dominant throughout the entire temperature range, its maximum contribution rate is only 6.0%, and the maximum vibration contribution rate does not always come from dihedral angle torsion of O₍₄₎C₍₁₆₎C₍₂₀₎C₍₄₀₎.

Fig. 9 shows the atomic displacement diagram corresponding to vibration mode 3. Vibration mode 3 mainly exhibits rotational motion of methyl groups throughout the temperature change process, showing similar motion at 180 K and 240 K. The main motion is that the methyl groups of molecules O¹ and O² rotate clockwise around the a-axis, while the methyl groups of molecules O³ and O⁴ rotate counterclockwise around the a-axis. The motion of the molecules at 300 K and 360 K is slightly different from that at 180 K and 240 K. The motion of the methyl groups in molecules O² and O⁴ is similar, but the motion of the methyl groups in molecules O¹ and O³ is opposite, that is, the methyl groups of molecules O¹ and O⁴ rotate counterclockwise around the a-axis, and the methyl groups of molecules O² and O³ rotate clockwise around the a-axis.

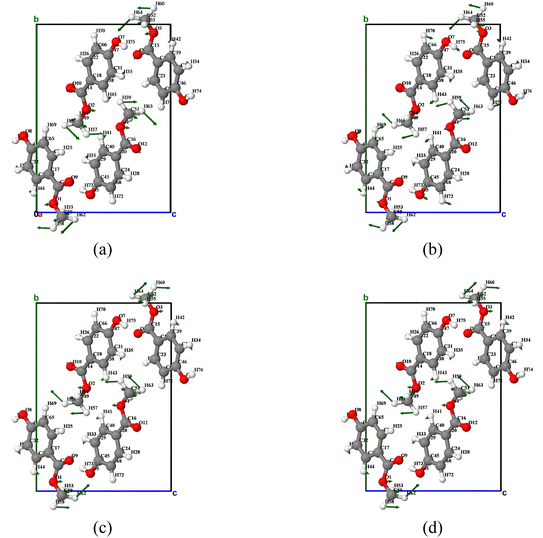Fig. 9 Atomic displacement diagrams of the vibration mode 3 of MeP at temperatures of (a) 180 K, (b) 240 K, (c) 300 K, and (d) 360 K.

The third absorption peak of MeP is mainly dominated by vibration mode 4, and Table 5 shows the VMARD analysis results of vibration mode 4 with a variation in temperature. Throughout the temperature range, the vibration mode is dominated by dihedral angle torsion, and the main vibration contribution comes from the dihedral angle torsion of O₍₃₎C₍₁₅₎C₍₁₉₎C₍₃₉₎. However, its maximum contribution value is only 7.9%. This result indicates that although the motion characteristics of vibration mode 4 are mainly dihedral angle torsion, its vibration motion is not concentrated on specific functional groups, but presents a dispersed distribution.

By analyzing the atomic displacement diagram corresponding to vibration mode 4 (as shown in Fig. 10), it can be found that except for 180 K, molecules O¹ and O² exhibit a counterclockwise rotation trend around the c-axis (viewed from the c-axis ab plane), while molecules O³ and O⁴ exhibit a clockwise rotation trend around the c-axis. At 180 K, the rotation direction of molecules O¹ and O² changes to clockwise, while molecules O³ and O⁴ change to counterclockwise rotation. It is worth noting that compared with the aforementioned vibration modes, the overall rotation trend of vibration mode 4 is weaker, and thus the directional arrows in the atomic displacement diagram are shorter.

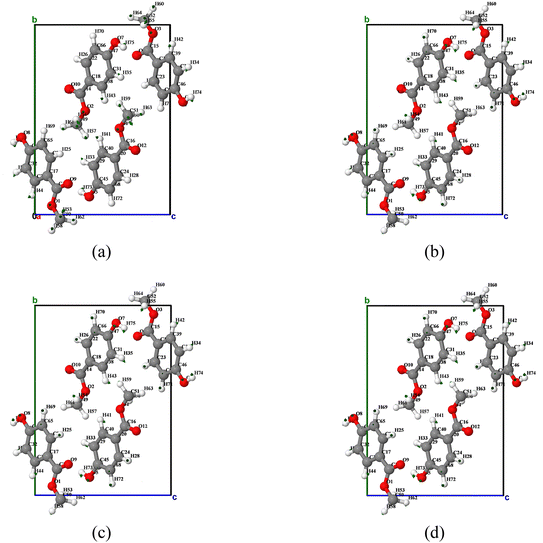Fig. 10 Atomic displacement diagrams of the vibration mode 4 of MeP at temperatures of (a) 180 K, (b) 240 K, (c) 300 K, and (d) 360 K.

By comparing and analyzing the temperature response behavior of multiple vibration modes, it was found that there are differences in the sensitivity of the different modes to temperature changes, which may be related to the molecular motion types and spatial orientations involved in each vibration mode. Vibration modes 1, 2, 3, and 4 exhibit different dominant mechanisms and motion distribution characteristics, with their motion modes mainly focused on the rotational motion of molecules or functional groups (such as methyl). It is worth noting that as the temperature changes, the direction of motion of some vibration modes remains unchanged, while others undergo significant reversal. These findings provide important theoretical basis for a deeper understanding of the molecular dynamics behavior and temperature dependence of MeP.

4.3. Analysis of weak interactions induced by temperature effect

Terahertz spectroscopy is closely related to the vibrational behavior of molecules, and in molecular crystals, this correlation is usually manifested as intermolecular weak interactions. This study used the IGMH method and AIM topology analysis method to study intermolecular interactions, both of which are implemented using the Multiwfn³² software and visualized using the VMD software. Fig. 11 shows the IGMH analysis results of MeP at different temperatures (180 K, 240 K, 300 K, and 360 K). According to the two-dimensional scatter plot, it can be observed that the data distribution at all temperatures is basically consistent, showing four characteristic peaks, a blue peak on the left, two pure green peaks in the middle, and a brown mixed peak on the right. This phenomenon indicates that under different temperature conditions, the distribution and intensity of weak interactions in the crystals of MeP are highly similar, and the overall characteristics of the weak interactions remain relatively stable under temperature changes.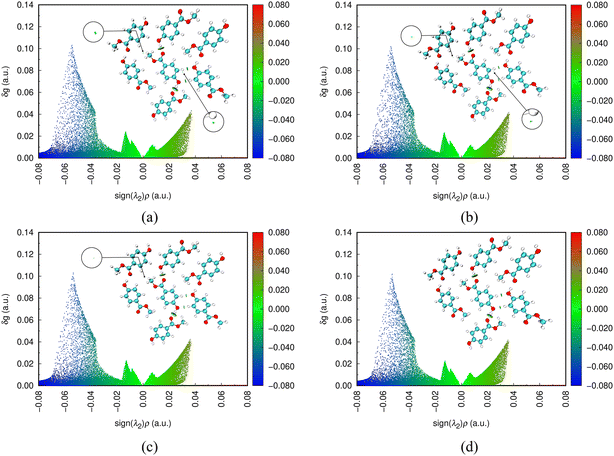

Fig. 11 IGMH analysis results for MeP at temperatures of (a) 180 K, (b) 240 K, (c) 300 K, and (d) 360 K (the iso-value of the three-dimensional iso-surface map is 0.015).

Through in-depth analysis of the 3D iso-surface map with an iso-value of 0.015 (corresponding to the upper right corner of the 2D scatter plot), it can be observed that the weak interaction distribution map in MeP crystal shows two green regions at 180 K. These regions significantly decrease in area at 240 K, only one remains at 300 K, and they completely disappear at 360 K. The existence of these green areas is closely related to van der Waals interactions, and their dynamic behavior with temperature changes indicates that van der Waals interactions are highly sensitive to temperature changes and gradually weaken with an increase in temperature until they disappear. Through further analysis of the two-dimensional scatter plot, it can be found that although the overall distribution area of van der Waals interactions maintains high similarity at the macroscopic scale when the iso-value is 0.015, there are still a few differences in data points at the microscopic scale, indicating that the influence of temperature changes on van der Waals interactions is mainly reflected in local details. In addition, when the iso-value is large, due to the wide distribution area of the blue peak, the intensity change of hydrogen bonding interaction is more significant compared to van der Waals interaction, and this change is easier to observe. However, this change is still extremely subtle in 2D scatter plots and difficult to capture directly, requiring systematic observation by continuously adjusting iso-value and combining them with 3D contour maps.

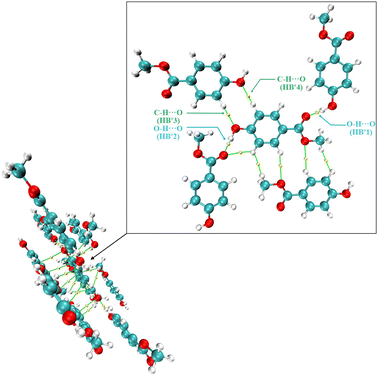
To further quantify the effect of temperature changes on the strength of weak interactions, this study systematically analyzed the weak interactions in methyl paraben crystals using the AIM theoretical method. The AIM method can accurately characterize the strength of weak interactions and their temperature dependence by calculating the topological parameters of electron density, such as the electron density at the critical point of the bond. The results of the AIM topology analysis are shown in Fig. 12, and the layer where the intermediate molecule is located is magnified. The critical points of AIM calculation results in MeP occur at HB^#1, HB^#2, HB^#3, and HB^#4. HB^#1 in MeP is mainly formed by the interaction between –CO– on the central ester group and H– on the surrounding hydroxyl groups, while HB^#2 is mainly formed by the interaction between H on the central molecule and –CO– on the surrounding ester groups. Therefore, HB^#1 and HB^#2 are of the same type of hydrogen bond. HB^#3 is mainly formed by the interaction between the O on the hydroxyl group of the central molecule and the H on the benzene ring of the surrounding molecule, while HB^#4 is mainly formed by the interaction between the H on the benzene ring of the central molecule and the O on the hydroxyl group of the surrounding molecule. Therefore, HB^#3 and HB^#4 should be classified as another type of hydrogen bond.

Fig. 12 The AIM analysis results for MeP. The red, blue, and white spheres represent oxygen, carbon, and hydrogen atoms, respectively. The yellow sphere represents the critical point and the green line represents the bond diameter.

Tables 6–9 show the AIM analysis results of HB^#1, HB^#2, HB^#3, and HB^#4 regions at different temperatures, respectively. According to these tables, it can be seen that the electron density in the HB^#1 and HB^#2 regions significantly decreases with an increase in temperature, which is consistent with the trend of weakening weak interactions caused by an increase in temperature in the IGMH analysis. As the electron density decreases, the hydrogen bonding energy of HB^#1 and HB^#2 also decreases accordingly, but their strength remains in the weak to moderate range, and electrostatic interaction remains their main driving force. In contrast, under temperature changes, the interaction strength between the HB^#3 and HB^#4 regions is still lower than the interaction strength between HB^#1 and HB^#2, but its trend of change is consistent with that of HB^#1 and HB^#2. As the temperature increases, the electron density of HB^#3 and HB^#4 also decreases, leading to a further decrease in their hydrogen bonding energy. It is worth noting that the interaction strength between HB^#3 and HB^#4 gradually changes from weak to moderate, and then to very weak, and their mechanism of action gradually shifts from mainly electrostatic interaction to mainly dispersion and electrostatic interaction. This transformation indicates that the increase in temperature not only weakens the strength of hydrogen bonds, but also changes the fundamental characteristics of interactions.

Table 6 Topological parameters, predicted binding energy and suggested classification for HB^#1 hydrogen bonds

Temperature (K)	ρ (a.u.)	ΔE (kcal mol^−1)	Strength	Major nature
180	0.0544	−11.3992	Weak to medium	Electrostatic
240	0.0539	−11.2709	Weak to medium	Electrostatic
300	0.0536	−11.2089	Weak to medium	Electrostatic
360	0.0531	−11.0960	Weak to medium	Electrostatic

---

Table 7 Topological parameters, predicted binding energy and suggested classification for HB^#2 hydrogen bonds

Temperature (K)	ρ (a.u.)	ΔE (kcal mol^−1)	Strength	Major nature
180	0.0543	−11.3780	Weak to medium	Electrostatic
240	0.0539	−11.2706	Weak to medium	Electrostatic
300	0.0535	−11.1944	Weak to medium	Electrostatic
360	0.0530	−11.0826	Weak to medium	Electrostatic

---

Table 8 Topological parameters, predicted binding energy and suggested classification for HB^#3 hydrogen bonds

Temperature (K)	ρ (a.u.)	ΔE (kcal mol^−1)	Strength	Major nature
180	0.0133	−2.2154	Very weak	Dispersion and electrostatic
240	0.0130	−2.1658	Very weak	Dispersion and electrostatic
300	0.0128	−2.1094	Very weak	Dispersion and electrostatic
360	0.0125	−2.0540	Very weak	Dispersion and electrostatic

---

Table 9 Topological parameters, predicted binding energy and suggested classification for HB^#4 hydrogen bonds

Temperature (K)	ρ (a.u.)	ΔE (kcal mol^−1)	Strength	Major nature
180	0.0133	−2.2314	Very weak	Dispersion and electrostatic
240	0.0131	−2.1744	Very weak	Dispersion and electrostatic
300	0.0128	−2.1199	Very weak	Dispersion and electrostatic
360	0.0126	−2.0624	Very weak	Dispersion and electrostatic

---

The research results indicate that a change in temperature has a certain impact on the weak interactions in different regions of MeP crystals, which exhibit varying degrees of temperature dependence. Through quantitative analysis using the AIM theory method, it was found that as the temperature increases, the electron density, ρ, in the hydrogen bonding region decreases. This not only directly weakens the strength of hydrogen bonds, but also may change the essential characteristics of weak interactions, mainly manifested in the HB^#3 and HB^#4 regions. The decrease in electron density leads to a reduction in hydrogen bond binding energy, and at the same time, the interaction mechanism in some regions gradually shifts from being dominated by electrostatic interactions to being dominated by both dispersion and electrostatic interactions. This discovery is highly consistent with the results of the IGMH analysis, further verifying weak interactions, especially van der Waals interactions, which are highly sensitive to temperature changes.

5. Conclusions

This study uses terahertz time-domain spectroscopy (THz-TDS) technology combined with quasi harmonic approximation theory (QHA) to systematically reveal the regulatory mechanism of temperature on the terahertz spectral characteristic absorption peaks, molecular vibration modes, and weak interactions of methyl para-hydroxybenzoate (MeP). Experiments have found that within the temperature range of 300–390 K, the three characteristic absorption peaks of MeP exhibit a red shift phenomenon, with the frequency shifts of absorption peak 2 and peak 3 being particularly significant, which is highly consistent with the temperature dependence of lattice parameters predicted by QHA theory. Vibration mode analysis shows that an increase in temperature leads to dynamic changes in the contribution ratio of intramolecular bond length stretching and bond angle bending, and some vibration modes even have reverse rotation directions, while the rotational motion of methyl groups remains the dominant vibration form. The study of weak interactions further confirms that the electron density in the hydrogen bond region decreases linearly with an increase in temperature, leading to weakening of the hydrogen bond binding energy. At the same time, van der Waals interactions exhibit stronger temperature sensitivity, and their range of action significantly shrinks at high temperatures. These findings not only deepen our understanding of the thermodynamic behavior of MeP molecules, but also provide a new theoretical paradigm for analyzing intermolecular interactions through terahertz spectroscopy. They have important guiding value for regulating the thermal stability of MeP in the fields of food, cosmetics, and pharmaceuticals.

Author contributions

Yuan Tang: writing – original draft, writing – review & editing, methodology, formal analysis, conceptualization, funding acquisition. Xiaojie Wang: writing – review & editing, data curation, investigation, software. Tao Chen: writing – review & editing, funding acquisition, project administration, validation, methodology, resources. Daoguo Yang: methodology, visualization, supervision, resources. Yueting Huang: writing – review & editing, validation, funding acquisition. Xianyan Huang: software, data curation, funding acquisition.

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Data availability

We would like to submit the enclosed manuscript entitled “Study on terahertz spectroscopy and weak intermolecular interactions of methylparaben under temperature effects”, which we wish to be considered for publication in “CrystEngComm”. The data that support the findings of this study are available from the corresponding author upon reasonable request.

Acknowledgements

This research is supported by the National Natural Science Foundation of China (Grant No. 62261012 and 61841502), the Middle-aged and Young Teachers' Basic Ability Promotion Project of Guangxi under Grant No. 2024KY1735, the Guangxi Key Laboratory of Automatic Detecting Technology and Instruments under Grant No. YQ24103, and the Innovation Project of Guangxi Graduate Education under Grant YCSW2025366.

References

1. S. Khushbu, M. Yashini and A. Rawson, et al., Recent advances in terahertz time-domain spectroscopy and imaging techniques for automation in agriculture and food sector, Food Anal. Methods, 2021, 15(2), 498–526.
2. E. M. Kleist and M. T. Ruggiero, Advances in low-frequency vibrational spectroscopy and applications in crystal engineering, Cryst. Growth Des., 2022, 22(2), 939–953.
3. P. Bawuah and J. A. Zeitler, Advances in terahertz time-domain spectroscopy of pharmaceutical solids: A review, TrAC, Trends Anal. Chem., 2021, 139, 116272.
4. N. Menchu and A. K. Chaudhary, Cost-effective assessment of water content in Indian almond (Catappa) of various colored leaves using continuous-wave terahertz spectroscopy and principal component analysis, J. Opt. Photonics Res., 2025,(6), 1–8.
5. H. Huang, Z. Liu and M. T. Ruggiero, et al., Terahertz geoscience: THz time-domain spectroscopy for mineral materials, Cryst. Growth Des., 2025, 25(10), 3578–3594.
6. Y. Tang, Z. Li and S. Tu, et al., Qualitative and quantitative study of intermolecular weak interactions for aminosalicylic acid isomers by terahertz spectroscopy, Int. J. Quantum Chem., 2022, e26971.
7. T. Chen, Y. Huang and Z. Tang, et al., Terahertz spectral vibrational properties and weak interactions analysis of caffeic acid and ferulic acid, J. Mol. Struct., 2022, 1270, 133960.
8. J. Wen, J. Hu and X. Yang, et al., Effective analysis of Alzheimer's disease and mechanisms of methyl-4-hydroxybenzoate using network toxicology, molecular docking, and machine learning strategies, Curr. Alzheimer Res., 2025, 22(6), 456–475.
9. J. Neis, A. Zamberlan and E. Saraiva, et al., Simultaneous assay of pyrimethamine and methylparaben in extemporaneous pediatric suspensions by an isocratic stability-indicating UPLC-DAD method, J. Liq. Chromatogr. Relat. Technol., 2024, 47(6–10), 171–180.
10. M. P. Davis and T. M. Korter, Low-frequency vibrational spectroscopy and quantum mechanical simulations of the crystalline polymorphs of the antiviral drug ribavirin, Mol. Pharmaceutics, 2022, 19(9), 3385–3393.
11. J. Navkiran, L. Josephine and B. William, et al., Fundamentally intertwined: anharmonic intermolecular interactions dictate both thermal expansion and terahertz lattice dynamics in molecular crystals, Chem. Commun., 2024, 60(84), 12169–12172.
12. X. He, M. Wang and J. You, et al., Detection of adulteration of non-transgenic soybean oil with transgenic soybean oil by integrating absorption, scattering with fluorescence spectroscopy, J. Food Meas. Charact., 2025, 19(2), 1–12.
13. A. Sharfalddin, B. Davaasuren and A. H. Emwas, et al., Single crystal, Hirshfeld surface and theoretical analysis of methyl 4-hydroxybenzoate, a common cosmetic, drug and food preservative-experiment versus theory, PLoS One, 2020, 15(10), e0239200.
14. J. B. de Oliveira, L. S. Lopes and F. C. de Costa, et al., Study on the combination of multi-wavelength calibration and liquid chromatography with UV-vis detector for the determination of the synthetic dye sunset yellow FCF in soft drinks, Chromatographia, 2024, 87(2), 137–144.
15. F. Huang, M. Liu and M. Xie, et al., A combined study on the skeletal vibration of aminopyrine by terahertz time-domain spectroscopy and DFT simulation, Optik, 2020, 208, 163913.
16. L. Xu, Y. Li and P. Jing, et al., Terahertz spectroscopic characterizations and DFT calculations of indomethacin cocrystals with nicotinamide and saccharin, Spectrochim. Acta, Part A, 2021, 249, 119309.
17. Y. Tang, Z. Li and H. Zhang, et al., Chemical bonds and weak interactions of methoxysalicylic acid isomers investigated by terahertz spectroscopy and density functional theory, AIP Adv., 2022, 12(5), 055015.
18. O. Vasiliev, Thermodynamic properties of tungsten disulfide from first principles in quasi-harmonic approximation, Powder Metall. Met. Ceram., 2021, 59(9), 1–9.
19. R. Ali, S. Muhammad and K. Muhammad, et al., Temperatures and pressure-dependent thermostructural properties of Ti2AlC MAX-phase using quasi-harmonic debye approximation, Glass Phys. Chem., 2023, 49(5), 493–502.
20. P. Giacomo, C. Nikhil and S. Bob, Non-local thermoelasticity based on equilibrium statistical thermodynamics, J. Thermoelasticity, 2020, 139(14), 37–59.
21. C. Zhu, Z. Liu and S. Li, et al., Novel ReSe semiconductor designed by structure prediction and phase diagram calculation, J. Mater. Sci., 2021, 56(11), 1–13.
22. T. Chen, X. Wang and H. Su, Low-frequency vibrational modes and weak interactions of 4-hydroxybenzoic acid and methylparaben studied by terahertz spectroscopy combined with solid-state density functional theory, J. Mol. Struct., 2025, 1331, 141583.
23. T. Chen, X. Zhong and Z. Li, et al., Analysis of intermolecular weak interactions and vibrational characteristics for vanillin and ortho-vanillin by terahertz spectroscopy and density functional theory, IEEE Trans. Terahertz Sci. Technol., 2021, 11(3), 318–329.
24. T. Lu and Q. Chen, Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical systems, J. Comput. Chem., 2022, 43(8), 539–555.
25. X. Jing, L. Chen and Y. Liu, et al., Molecular dynamics simulation of CO2 hydrate growth and intermolecular weak interaction analysis, Chem. Technol. Fuels Oils, 2022, 58(2), 410–421.
26. M. Soleymani and M. Goudarzi, A DFT study on the Sc(OTf)3 catalyzed hetero Diels–Alder reaction of N-tosylhydrazones and ortho-quinone methides: energetic aspects, selectivities, and molecular mechanism, Struct. Chem., 2023, 35(2), 497–509.
27. T. Lu and Q. Chen, Interaction Region Indicator (IRI): A simple real space function clearly revealing both chemical bonds and weak interactions, Chem.: Methods, 2021, 1, 231–239.
28. S. Scheiner, On the reliability of atoms in molecules, noncovalent index, and natural bond orbital to identify and quantify noncovalent bonds, J. Comput. Chem., 2022, 43(26), 1814–1824.
29. Z. Li, Y. Yang and T. Xu, et al., Next generation quantum theory of atoms in molecules for the design of emitters exhibiting thermally activated delayed fluorescence with laser irradiation, J. Comput. Chem., 2021, 43(3), 206–214.
30. S. Emamian, T. Lu and H. Kruse, et al., Exploring nature and predicting strength of hydrogen bonds: a correlation analysis between atoms-in-molecules descriptors, binding energies, and energy components of symmetry-adapted perturbation theory, J. Comput. Chem., 2019, 40(32), 2868–2881.
31. F. Teixeira and M. N. D. S. Cordeiro, Improving vibrational mode interpretation using bayesian regression, J. Chem. Theory Comput., 2018, 15(1), 456–470.
32. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33(5), 580–592.

---