Investigation of the homogeneity of BGO single crystals, a promising X-ray diffraction standard
Polina S.
Serebrennikova
 *ab,
Vladimir N.
Shlegel
b and
Sergey A.
Gromilov
ab
*ab,
Vladimir N.
Shlegel
b and
Sergey A.
Gromilov
ab
aNovosibirsk State University, Pirogova Street, 2, Novosibirsk, 630090, Russian Federation
bNikolaev Institute of Inorganic Chemistry of the Siberian Branch of the Russian Academy of Science, Lavrentyev Avenue, 3, Novosibirsk, 630090, Russian Federation. E-mail: serebrennikova@niic.nsc.ru
First published on 4th November 2025
Abstract
This article demonstrates the application of an original technique for single crystal unit cell parameter determination during the certification of a new X-ray diffraction standard Bi4Ge3O12 (BGO) using a conventional laboratory diffractometer equipped with a 2D detector. A BGO crystal weighing 51.86 kg and over 50 cm in length was grown using the LTG CZ method. The dynamics of structural characteristics was studied in the temperature range of 140–480 K by single crystal X-ray diffraction analysis. The cubic unit cell parameters of nine BGO single crystals taken from different areas of the initial sample were determined using the original technique based on the calibration of the goniometer equatorial circumference of small segments according to external standard doublets. The measurements were carried out in the diffraction angle range of 2θ ∼ 120° (MoKα-radiation), and the relative error was no more than 5 × 10−5. It was found that the initial BGO sample is homogeneous, and its unit cell parameter values are in the range of 10.5176–10.5183 Å, 〈a〉 = 10.5180(5) Å. The thermal expansion of BGO was studied in the range of 100–500 K. It was shown that the absolute increase in cell volume is 8.1 Å3 with a relative increase of 0.7%. The thermal expansion coefficient of BGO at room temperature is 6.39 × 10−6 K−1. The potential use of BGO single crystals as an external and internal standard is demonstrated in the test refinement of Si and Ge poly- and single crystal unit cell parameters.
Introduction
The determination of unit cell parameters (UCPs) from individual single crystals is necessary when a high degree of line overlapping in powder diffraction patterns makes it impossible to reliably determine their centres. Such a situation is inherent mainly to low-symmetry phases with unit cell parameters exceeding 10 Å. The Rietveld method is frequently used in such cases, but the correct estimation of actual accuracy achieved in UCP determination with this approach can be quite difficult. It is related to the correlation of parameters being refined, which contributes to the positions and shapes of overlapping diffraction lines. The study of individual single crystals, for which there is no such problem, seems to be a solution in these situations.Modern laboratory single-crystal diffractometers that are focused on single crystal X-ray diffraction structural analysis (SCXRD) do not demonstrate high accuracy of UCP measurement.1–3 A factor that significantly reduces the accuracy of measurements is the sample eccentricity – the inaccuracy of setting the geometric centre of the crystal in the ω and φ axes, which is associated with the inevitable centering error.3 Other sources of errors may be: large pixel sizes that do not allow obtaining a sufficient number of points per peak for high-quality processing of its shape and peak-background area which is important for determining its centre of gravity, errors in the detector plane installation, the lack of a fast and standardized calibration procedure in the majority of data collection and integration programs, incorrect processing of radiation doublets at high angles using an average wavelength, etc. The differences in the UCP values, determined on different devices during the SCXRD by the least squares method (LSM), were previously estimated for experimental samples and corresponded to 10−2–10−3 relative error.4
One of these methods, which makes it possible to determine the single crystal peak positions with high accuracy, is the refinement of experimental geometric parameters by eight reflections.5 The SINGLE program6 is implemented based on this method. In these studies, it was shown that with this approach it is possible to achieve a relative error in UCP determination of 1/30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 (∼3 × 10−5). However, this method requires a four-circle goniometer to move eight symmetrically related reflections to reflective positions and the ability to record rocking curves using a point detector or a pixel of a two-dimensional detector, which limits its use on conventional modern devices. Dudka et al.3 proposed a computational complex that makes it possible to determine single crystals' UCPs with a relative error of at least 5 × 10−5, but it was also designed for the use of a point detector.
000 (∼3 × 10−5). However, this method requires a four-circle goniometer to move eight symmetrically related reflections to reflective positions and the ability to record rocking curves using a point detector or a pixel of a two-dimensional detector, which limits its use on conventional modern devices. Dudka et al.3 proposed a computational complex that makes it possible to determine single crystals' UCPs with a relative error of at least 5 × 10−5, but it was also designed for the use of a point detector.
For the precise determination of single crystals' UCPs, including the development of new X-ray diffraction standards, specialized methods have been used, discussed in detail by Lider.7 Among them, the method of two coplanar reflections and the Bond method are relatively suitable for implementation on a standard laboratory X-ray diffractometer. These methods provide a relative error in UCPs of ∼10−5–10−8, depending on the accuracy of the goniometer used and the error in the wavelength value. The method of coplanar vectors, however, is not universal for phases of any crystal systems; additionally, its use is complicated by the need to select reflection planes that simultaneously meet the conditions of quasi-multiple X-ray diffraction and are available for moving to a reflective position in the geometry of the setup for registering them synchronously.8 Taking into account the fact that conventional single-crystal devices are often equipped with only two- or three-circle goniometers, the selection of such reflections can be extremely complicated. The Bond method seems to be quite implementable on laboratory devices; the restrictions are due to the number of goniometer degrees of freedom and the need to install the detector at the same angle in the positive and negative directions. However, the design of most single crystal diffractometers allows this operation to be performed only up to certain angle values. For example, in our case, on a Bruker D8 Venture diffractometer, the maximum achievable angle in the positive direction is 100°, and in the negative direction, it is 120°. Thus, the implementation of the methods on laboratory devices is possible only with certain restrictions.
Despite all the above disadvantages, modern single-crystal diffractometers are usually equipped with goniometers of angle setting reproducibility up to 0.0001° and axes converging into a sphere less than 7 μm, which makes them potentially suitable for precision experiments. In recent work, we have proposed a technique for refining the UCPs of single crystals on conventional diffractometers equipped with 2D detectors. The technique is based on the refinement of the dependence between the angular pixel size γ and the equatorial coordinate of the goniometer X according to the diffraction pattern of a single-crystalline standard obtained under the same geometric conditions as a studied phase.9–11 The general form of the dependence is:
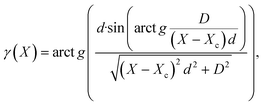 | (1) |
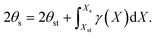 | (2) |
To achieve the best accuracy, this approach is used in conjunction with the method of taking into account the eccentricity.12 While using the technique, the error in UCP determination does not exceed the error estimated from the goniometer accuracy. The most precise values were obtained using the angular pixel size calculated from the interdoublet distances of reference reflections. The main advantages of the technique are its compatibility with standard laboratory devices, since it makes possible to work with a fixed position of the detector in the high-angle diffraction region, does not require special parameters of the radiation source, and is based on the use of widespread 2D detectors. The main requirement for the samples studied by this method is sufficient crystal quality. In particular, the level of mosaicity, microstress, and possible twinning should not interfere with the good spatial resolution of radiation doublets at the high angle region (the gap between the Kα1- and Kα2-components is at least half the height of the Kα2-component). In this paper, we describe the use of this technique to refine single crystals' UCPs at the maximum available detector angle of the device we use (120°) in order to achieve a minimum relative error and to certify a new single-crystal X-ray diffraction standard. The need for such standards is due to their low diversity: the main standard for calibration of a single-crystal diffractometer is currently α-Al2O3 (NIST SRM-1990, ruby spheres).2 Test single crystals (for example, ylid), which are usually supplied with diffractometers, cannot be considered as standards, since there is no information about measuring their UCPs using independent precision methods. They can be good candidates for conducting such experiments and certifications to improve the quality of laboratory equipment settings.
Bi4Ge3O12 (BGO) was chosen as a potential X-ray diffraction standard. Its structure was first described by Durif:13 space group I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d, a = 10.497(8) Å. A large difference in the UCP values of BGO given in the literature is observed.13–19 The range of these values at room temperature is 0.024 Å (10.495–10.524 Å). The most precise value is a = 10.5187(2) Å, obtained by NIST17 on a polycrystalline sample (complete X-ray data are deposited in the PDF database,20 no. 00-034-0416). In this work, the scanning was carried out on an instrument equipped with an X-ray tube with a copper anode (λCuKα1 = 1.540598 Å), the internal standard Si SRM-640a (a = 5.430825 Å) was used, and the UCP calculation was carried out using a set of single reflections in the 2θ range of 115–118°. The values obtained on single crystals differ significantly from the NIST result, despite the fact that almost all of them were obtained on diffractometers equipped with point detectors, i.e., ones more suitable for accurate determination of UCPs than modern devices. The data14,18,19 coincide best with the value from NIST,17 but the difference between them still exceeds the error values estimated by the authors. We have not found any examples of precision measurements of the BGO UCP on single crystals, so its refinement using our technique and comparison with high-precision NIST data is interesting.
3d, a = 10.497(8) Å. A large difference in the UCP values of BGO given in the literature is observed.13–19 The range of these values at room temperature is 0.024 Å (10.495–10.524 Å). The most precise value is a = 10.5187(2) Å, obtained by NIST17 on a polycrystalline sample (complete X-ray data are deposited in the PDF database,20 no. 00-034-0416). In this work, the scanning was carried out on an instrument equipped with an X-ray tube with a copper anode (λCuKα1 = 1.540598 Å), the internal standard Si SRM-640a (a = 5.430825 Å) was used, and the UCP calculation was carried out using a set of single reflections in the 2θ range of 115–118°. The values obtained on single crystals differ significantly from the NIST result, despite the fact that almost all of them were obtained on diffractometers equipped with point detectors, i.e., ones more suitable for accurate determination of UCPs than modern devices. The data14,18,19 coincide best with the value from NIST,17 but the difference between them still exceeds the error values estimated by the authors. We have not found any examples of precision measurements of the BGO UCP on single crystals, so its refinement using our technique and comparison with high-precision NIST data is interesting.
A comparative analysis of BGO, Si and α-Al2O3 theoretical diffraction patterns showed that the first one has a significantly higher intensity of reflections. In addition, the angular position of the first BGO reflection (~20.7° for CuKα radiation) is less than that of SRM-1990 (25.57°)2 and of Si (28.44°).21 The advantage of BGO in comparison with α-Al2O3 is also its high symmetry, because the hexagonal system of α-Al2O3 provides additional uncertainty (two unit cell parameters with their own errors affect the positions of its lines). This situation makes BGO a promising X-ray standard, including for average diffraction angles. The advantage of using BGO as a single-crystal reference also lies in a higher number of the reflections in the diffraction pattern. For example, in the angle range from 20 to 80° there are 29 BGO lines with different positions and only 6 lines of Si (for CuKα radiation). It allows us to expect a better calibration of the goniometer according to the techniques described in previous studies.9–11,22,23 The availability of a well-developed method for obtaining BGO crystals of high perfection24,25 with reproducible characteristics also makes BGO a promising standard.
In addition to the metrological application, BGO crystals can also be used as ionizing radiation detectors in various climatic zones in wide temperature ranges due to their scintillation properties. In an article by Tsuchida et al.,26 the dependences of the scintillation attenuation time profile under gamma radiation excitation and the light output of BGO in the temperature range of −20–20 °C were studied to simulate its behavior in space. The authors have shown that both parameters depend significantly on temperature. At the same time, studies of the BGO thermal expansion tensor, which determines the linked thermodynamic properties and structural features of the material application under various external conditions, are quite rare in the literature and the results contradict each other. Thus, the dependence of UCPs on T for BGO was studied during an in situ X-ray diffraction experiment on a polycrystal in the temperature range of 300–900 K,27 and a discontinuity in the graph in the region of 400 K corresponded to a sharp change in the linear thermal expansion coefficient (TEC) from 3.9 × 10−6 to 6.8 × 10−6 K−1. Conclusions to refute this result were made by Radaev et al.;18 however, their measurements of the BGO UCP by single crystal neutron diffraction studies were only at two temperatures – 293 and 573 K, which did not allow complete tracing of the dynamics. Radaev et al.18 also compared the structural parameters of BGO at these two temperatures and showed that the (GeO4) tetrahedron metrics do not change noticeably with increasing temperature. Thermal expansion occurs mainly due to an increase in Bi–O distances in the (BiO6) distorted octahedron, with negligible changes in the bonding angles. According to dilatometry data,28 there is also no phase transition at 400 K and the linear TEC increases from 5.75 × 10−6 K−1 at 140 K to 7.81 × 10−6 K−1 at 800 K according to a law close to quadratic. At the same time, Rao et al.29 observed that the linear TEC increased from 6.9 × 10−6 to 16.5 × 10−6 K−1 in a much smaller range of 293–573 K. Thus, an independent determination of the temperature dynamics of the BGO TEC is also interesting.
The purpose of this work is the X-ray certification of BGO for further use as a reference for X-ray diffractometry of poly- and single crystals. The minor tasks are to examine the homogeneity of the synthesized large BGO crystal and to study its thermal expansion.
Experimental
Synthesis and chemical analysis
BGO crystals were grown by the low-thermal gradient Czochralski method (LTG Cz).24,25 An essential feature of the crystal synthesis technology is the low temperature gradients in the growth zone. The axial and radial temperature gradients in the melt and crystal are maintained within a range of no more than 1 degree per cm. The approach enables the synthesis of high-quality BGO crystals without inclusions, weighing up to 75 kg. It was shown25 that they have a high radiation resistance (∼106 rad) and unique optical uniformity (attenuation length ∼10 m, λ = 480 nm), as well as high uniformity of scintillation characteristics in the axial direction (shown by the example of irradiation of 30 × 35 × 38 mm3 blocks with γ-radiation of 662 keV energy).The obtained BGO sample was a transparent colorless crystal with a longitudinal size of about 55 cm and a weight of 51.86 kg (Fig. 1a). An 11.5 cm long fragment was cut from it, which had a base in the shape of a triangle with concave sides at the base (Fig. 1b). Atomic emission spectral analysis of its fragment was carried out using a spectrometer iCAP-6500 Thermo Scientific (inductively coupled plasma): Ag – (2.4 ± 0.4) × 10−5 % mass fraction; Al, Mo, Ni, As, Au, Ca, Hf, Na, B, P, Pb, Rb, Sb, Se, Sn, Te, Ba, Li, Sr, Be, Mg, Mn, Ti, V, Zr, Co, Cu, Hg, Re, Ta, Ga, In, and W were below the detection levels.
For the X-ray diffraction study, 9 crystals (hereinafter samples 1–9) with linear sizes of about 50 microns were extracted from different areas of the fragment (as marked in Fig. 1c). These regions were selected to study the effect of both the axial and radial temperature gradients on homogeneity. In addition, to check for reproducibility, one more crystal (sample 10) was selected from another sample grown under the same conditions.
X-ray diffraction structural analysis
XRD studies of BGO single crystal 1 were performed using a Bruker D8 Venture diffractometer (the description was given earlier). An Oxford Cryosystems Cryostream 800 plus nitrogen flow cryostat provided the temperatures with a stability of 0.1°. The calculation of data collection strategy, as well as raw data integration, absorption correction, and global refinement of UCPs, were carried out using the Bruker APEX3 V2019.1-0 software package.30 The obtained Fhkl arrays were processed in Olex2 v.1.5 (ref. 31) using SHELXT32 and SHELXL33 to solve and refine the structural model. The atomic displacement parameters were refined in the anisotropic approximation. The main refinement results are shown in Table S1. In the same way, the SCXRD of crystal 1 was carried out at temperatures in the range from 140 to 480 K with increments of 40°. All obtained cif files were deposited to the CCDC. The CCDC numbers and the results are shown in Table S2, and the designations of bonding distances and angles are given according to Fig. 4 (and S1).Calibration of the goniometer equator – γ(X) approximation
A Si single crystal certified using the Bond scheme on a single-crystal spectrometer21 was used as an external standard. Its UCP was recalculated using the recommended wavelength λCuKα1 = 1.5405929 Å (ref. 34) and was found to be aSi = 5.431042 Å. The Si single crystal standard was a ball with a diameter of ∼50 microns. After mounting it on the goniometer and careful centering, including rotations around the ω-axis by ±90°, the orientation of the crystal was determined. For this purpose, a scan series was carried out in the ϕ-rotation mode (0–360° range, 0.5° step, 1 s exposure time) at three different values of ω. The corresponding detector positions were 2θD = 0, ±50° (D = 70 mm). The calculation of the single crystal orientation matrix relative to the axes of the goniometer and the angles for moving reflections on the goniometer equatorial circle was performed using the APEX3 program.30 Based on the maximum available detector setting angle of 120° on the used device, (12 4 4)Si with the theoretical positions of Kα1- and Kα2-components of 120.070 and 121.283° correspondingly was taken. For these calculations, the values of the wavelengths of characteristic molybdenum radiation were used: λMoKα1 = 0.70931715(41) and λMoKα2 = 0.713607(12) Å.34 The calibration of the inter-doublet interval was performed based on the results of the scanning conducted at the detector position: 2θD = −120°, D = 109 mm. The sample–detector distance was chosen to be 109 mm, because it is the optimal one for obtaining the best intensity/half-width ratio on our device.9 The exposure time was selected in such a value as to obtain at least 104 counts at the maximum above the background. The coordinates of the Kα1/Kα2-components' centres of gravity were found by their approximation by two 2D Gaussian functions using the Origin program.35 Calibration was carried out according to the proposed approach,9 and the results of angular pixel size calculation are given in Table 1.| Si | |||||
|---|---|---|---|---|---|
| N | X Kα1, pix.a | Y Kα1, pix.a | X Kα2, pix.a | Y Kα2, pix.a | g,b ° |
| 1 | 389.549(4) | 504.929(3) | 406.643(8) | 504.998(6) | 0.07096(5) |
| 2 | 389.676(4) | 503.452(3) | 406.738(8) | 503.402(6) | 0.07109(5) |
| 3 | 389.550(4) | 504.925(3) | 406.615(8) | 504.965(6) | 0.07108(5) |
| 4 | 389.673(4) | 505.158(3) | 406.715(8) | 505.274(6) | 0.07118(5) |
| 5 | 389.559(4) | 504.055(3) | 406.611(8) | 504.068(6) | 0.07114(5) |
| 6 | 389.719(4) | 504.780(3) | 406.776(8) | 504.776(8) | 0.07111(5) |
| 7 | 389.609(6) | 505.180(5) | 406.637(12) | 505.355(9) | 0.07124(5) |
| 8 | 389.637(5) | 504.746(4) | 406.691(10) | 504.832(8) | 0.07113(5) |
| 9 | 389.554(5) | 502.822(4) | 406.657(9) | 502.925(7) | 0.07092(5) |
| 10 | 389.773(5) | 504.500(3) | 406.763(9) | 504.557(8) | 0.07139(5) |
| BGO | |||||
|---|---|---|---|---|---|
| N | X Kα1, pix.a | Y Kα1, pix.a | 2θKα1,b ° | d,c Å | a,c Å |
a The standard deviation of the 2D-Gaussian profile processing is shown.
b The error is calculated based on the standard deviation in determining the coordinates of the peak centres.
c The errors are calculated from the accuracy of the goniometer (0.005°) and the diffraction angle used (∼120°) by the formula Δd/d = ctg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θΔθ. θΔθ.
|
|||||
| 1 | 393.638(13) | 507.382(10) | 120.360(5) | 0.40879(2) | 10.5178(5) |
| 2 | 393.648(10) | 506.245(8) | 120.352(5) | 0.40880(2) | 10.5182(5) |
| 3 | 393.565(11) | 506.173(9) | 120.360(5) | 0.40880(2) | 10.5180(5) |
| 4 | 393.706(10) | 506.936(9) | 120.357(5) | 0.40879(2) | 10.5179(5) |
| 5 | 393.486(11) | 501.034(9) | 120.349(5) | 0.40881(2) | 10.5183(5) |
| 6 | 393.675(12) | 504.003(10) | 120.351(5) | 0.40880(2) | 10.5182(5) |
| 7 | 393.724(14) | 503.324(10) | 120.363(5) | 0.40878(2) | 10.5178(5) |
| 8 | 393.665(13) | 501.853(11) | 120.357(5) | 0.40879(2) | 10.5180(5) |
| 9 | 393.566(18) | 502.801(14) | 120.355(5) | 0.40880(2) | 10.5181(5) |
| 10 | 393.769(10) | 508.217(12) | 120.355(5) | 0.40880(2) | 10.5180(5) |
| Average value | 120.356 | 0.40880 | 10.5180 | ||
| Standard deviation | 0.004 | 8 × 10−6 | 0.0002 | ||
To use the calibration for measuring the BGO UCP, a reflection of 2θ in the range of 120.070–121.283° is required. Since the studies of nine BGO single crystals were performed on different days, a new calibration was obtained before or after scanning each crystal.
Refinement of the UCP of BGO single crystals
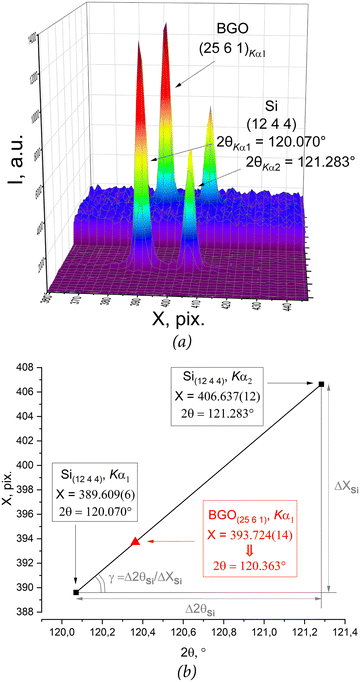
BGO single crystals 1–10 had linear dimensions corresponding to the diameter of the external Si standard used (i.e. approximately 50 microns) to minimize errors associated with absorption and eccentricity. The (25 6 1) reflection with 2θ = 120.331° (calculated from SCXRD data at 300 K) was chosen to determine their UCP. It falls into the interval between the Kα1- and Kα2-components of the (12 4 4)Si and has the highest intensity among other reflections with the same angular position 2θ: (21 11 10), (18 17 7), (18 13 13), (21 14 5) and (22 13 3).At the first stage of each UCP measurement, the orientation matrix of the single crystal corresponding to the goniometer axes and the conditions for the movement of one of the 48 symmetrically related (25 6 1)BGO reflections to the reflecting position on the goniometer equatorial circumference were determined. When choosing indices, we were guided by the maximum matching of the reflection scanning conditions (12 4 4)Si and (25 6 1)BGO. First of all, this is about the coincidence of the detector positions, and secondly, the proximity of the ω angles. The rotation of the sample around this axis makes the greatest contribution to the error associated with the eccentricity of the sample. For both single crystals (Si and BGO), the differences in the values of ω were no more than 10°. The relative position of the (12 4 4)Si and (25 6 1)BGO doublets for crystal 7 is shown in Fig. 2.
The angular position of the (25 6 1)BGO reflection was determined according to the proposed approach (linear approximation of γ(X) in formulas (1) and (2)):9
| 2θ(Kα1(25 6 1)BGO) = 2θ(Kα1(12 4 4)Si) + ΔX × γ, | (3) |
The BGO UCP dependence on temperature study
The temperature studies were carried out using crystals 9 and 10. After scanning the (12 4 4)Si reference reflection, the pre-oriented crystal was mounted on a goniometer, and the (25 6 1)BGO reflection was measured sequentially at different temperatures. Crystal 9 was studied in the range of 100–500 K, and crystal 10 in the range of 100–430 K (with a step of 20 K in both cases). The temperature stability was provided by the Oxford Cryosystems Cryostream 800plus nitrogen flow cryostat (with an accuracy of 0.1 K). After reaching each target temperature, a pause of 5 minutes was to provide thermal equilibrium of the sample. Further processing was carried out in a similar way to determine the UCP of crystals 1–10 at room temperature. The results of the experiments are shown in Table S3.Results and discussion
BGO crystal structure
The crystal structure of BGO is constructed from distorted octahedra (BiO6) connected through common edges and distorted tetrahedra (GeO4) isolated from each other and having common angles with (BiO6) (see Fig. 3).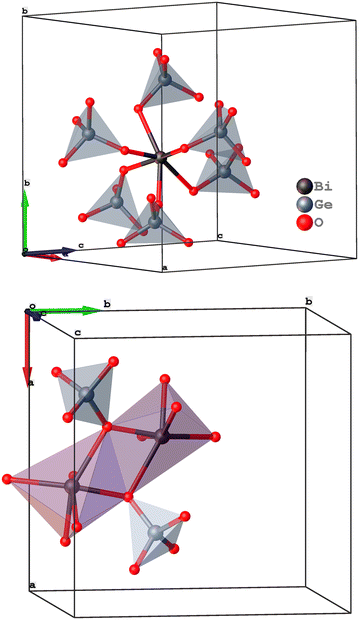 | ||
| Fig. 3 Fragments of the BGO structure – the relative position of distorted (BiO6) octahedra and distorted (GeO4) tetrahedra. | ||
The structural characteristics obtained at different temperatures are given in Table S2 according to the designations of Fig. 4, which is also duplicated in the SI as Fig. S1. Table S2 shows that many structural parameters in the temperature range of 140–480 K do not change within the error. In particular, the difference observed between the min and max values does not exceed 3σ (where σ is the standard deviation) for all studied parameters. Fig. 5 shows the temperature dependence of selected parameters that exhibit the most noticeable changes. Thus, the distance Bi1–O5 in the distorted octahedron (BiO6) increases by 0.4% when the temperature changes from 140 to 480 K (2.6σ), while the distance Bi1–O6 shows little change (1.4σ). Among the bonding angles in (BiO6), the angles O3–Bi1–O6 and O2–Bi1–O4 increase noticeably by 0.25 and 0.47%, respectively (2σ in both cases). There is also no increase in the Ge–O distance in the tetrahedron (GeO4) – 0.8σ, but the angles O8–Ge–O6 and O7–Ge–O6 change in opposite directions: the angle O8–Ge–O6 decreases by 0.35% (2σ), and O7–Ge–O6 increases by 0.22% (1.9σ). The angles Bi1–O6–Bi2, Bi1–O6–Ge and Bi2–O6–Ge, which determine the relative positions of (BiO6) and (GeO4) polyhedra, show minimal change – 1σ, 1.7σ and 1.5σ, respectively. These factors, combined with an increase in thermal oscillations of Bi, Ge and O by almost three times, lead to an increase in the volumes of polyhedra (BiO6) and (GeO4) by 0.57 (2.7σ) and 0.55% (0.7σ), respectively. As a result, the BGO UCP increases by 0.19%.
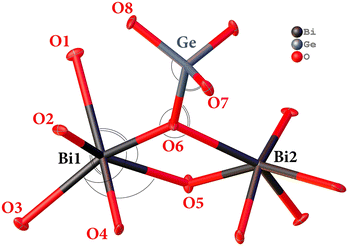 | ||
| Fig. 4 A fragment of the BGO structure with the indicated designations of atoms. All the same element atoms are linked-connected. | ||
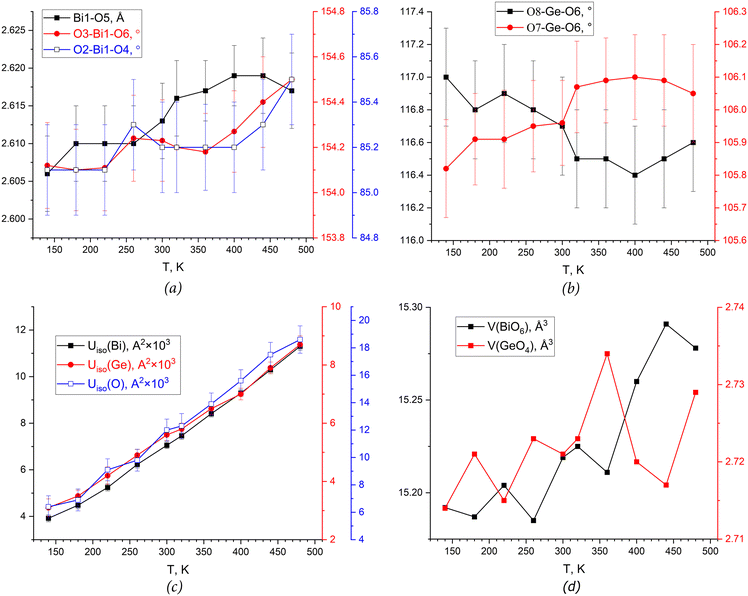 | ||
| Fig. 5 Changes in some crystal-structural characteristics of BGO in the temperature range of 140–480 K, obtained according to the SCXRD data (the designations are given according to Fig. 6): polyhedron (BiO6) parameters (a); polyhedron (GeO4) parameters (b); equivalent isotropic displacement parameters (c); volumes of polyhedra (BiO6) and (GeO4) (d). | ||
The data obtained confirm the conclusion18 that thermal expansion occurs mainly due to an increase in the (BiO6) distorted octahedron with little-changing (GeO4) metrics.
The UCP of BGO at room temperature
The range of UCPs for BGO in Table 1 goes from 10.5178(5) to 10.5183(5) Å. The average value is 10.5180 Å.The conclusion about the homogeneity of the initial crystal can be made by the coincidence of the UCP values of its individual fragments within the measurement error. Therefore, this error should be estimated. The error can be most correctly estimated using a well-known mathematical apparatus for the geometry of a single-crystal diffractometer (for example, King & Finger5). However, applying these models requires precise values of some instrument characteristics, in particular, the accuracy of the goniometer. In the technical specifications of our instrument, the absolute accuracy of the goniometer is not specified, there is only the reproducibility of the angle setting – 0.0001°. We can conclude about the absolute accuracy of our goniometer along the ω axis from the measurement results of reference polycrystalline samples on Bruker D8 Advance diffractometers (0.005°) equipped with similar goniometers, and about the total accuracy only from experiments conducted with reference single crystals.
In previous work,22 we estimated the error in determining the angles of 2θ, calculated based on the results of full area detector calibration according to the external standard – Si single crystal. For this purpose, the positions of a large number of standard reflections, registered at different positions of the crystal, but at the same position of the detector were measured.
The information obtained about this detector position (sample–detector distance, angle 2θD, slope angles of the detector plane relative to the goniometer axes) enables conversion of reflection coordinates of the observed reflections to the values of 2θ. It was shown that with this approach, the measurement errors of 2θ angles reach 0.009°. The main errors are systematic – they are caused by the displacement of the crystal during rotations around the φ and ω axes (eccentricity of the sample). To reduce errors, an approach was proposed, when calibration is conducted not for the entire area of the detector, but only for a small central zone at the equator.9–11 Sample displacement effects are minimized by scanning the experimental and the reference samples under identical geometric conditions. As previous studies have shown, this method significantly improves measurement accuracy: for example, the relative measurement error of the InSb single crystal's UCP (with a well-known UCP value from the literature) was 7 × 10−5 according to our method at diffraction angles of about 100°, which corresponds to an error in determining the angular position equal to 0.005°.22 This level of angle determination error has been repeatedly confirmed in our experiments in previous studies.9–11,22,23
When using reflections with diffraction angles of ∼120° and Δθ = 0.005°, the relative measurement error calculated by the formula Δd/d = ctg![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θΔθ is 5 × 10−5. It should be noted that for the Bruker D8 Venture diffractometer used, the detector setting angle of 120° is the maximum achievable. It would be possible to use reflections at the edge of the detector (as described in previous work),10 but this requires more complex calibration procedures. Thus, in our case, the absolute measurement error can be estimated to be ±0.0005 Å from the relative error of 5 × 10−5 and the resulting UCP values. The values of parameter a of the ten BGO single crystals coincide within this range (see Fig. 6). The average value of the BGO UCP obtained from the 10 crystals is 10.5180 Å. The range of UCP deviations of the 10 crystals from their average value is 7.2 × 10−6–4.0 × 10−4 Å. Thus, within the estimated measurement accuracy, the initial BGO sample is homogeneous, and the BGO UCP is 10.5180(5) Å. Also, based on the UCP results for the tenth crystal selected from another synthesis, the possibility of obtaining high-perfection BGO crystals with reproducible characteristics in independent experiments can be assumed.
θΔθ is 5 × 10−5. It should be noted that for the Bruker D8 Venture diffractometer used, the detector setting angle of 120° is the maximum achievable. It would be possible to use reflections at the edge of the detector (as described in previous work),10 but this requires more complex calibration procedures. Thus, in our case, the absolute measurement error can be estimated to be ±0.0005 Å from the relative error of 5 × 10−5 and the resulting UCP values. The values of parameter a of the ten BGO single crystals coincide within this range (see Fig. 6). The average value of the BGO UCP obtained from the 10 crystals is 10.5180 Å. The range of UCP deviations of the 10 crystals from their average value is 7.2 × 10−6–4.0 × 10−4 Å. Thus, within the estimated measurement accuracy, the initial BGO sample is homogeneous, and the BGO UCP is 10.5180(5) Å. Also, based on the UCP results for the tenth crystal selected from another synthesis, the possibility of obtaining high-perfection BGO crystals with reproducible characteristics in independent experiments can be assumed.
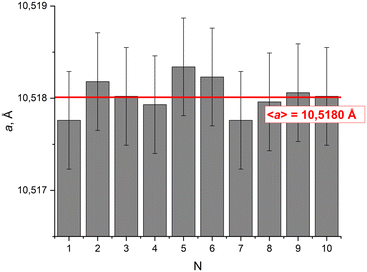 | ||
| Fig. 6 The obtained BGO UCP for crystals 1–10. The absolute error bars of 0.0005 Å are shown. The average value for the 10 crystals is given by the red line. | ||
Comparing the obtained aBGO value with those known in the literature (see Table 2), it can be noted that the work carried out on single crystals demonstrates a wide range of values of 0.033 Å (from 10.491(1) to 10.524(3) Å). The largest measurement errors and the largest deviations from a value of 10.5180(5) Å are demonstrated in works,13,15,16 where the UCPs were determined by the LSM when solving the Bi4Ge3O12 structure. The data obtained by SCXRD14,18 and the Rietveld method on polycrystals19 for different types of radiation coincide with our value better, but the difference still does not correspond to the estimated measurement errors. The best coincidence is demonstrated by the data of NBS USA,17 obtained on the polycrystal: the difference is 0.0007 Å. Thus, our data and the data of NBS coincide within the estimated measurement errors.
| References | T, K | a, Å | Sample and experiment/peak registration and determination/procedure (standard, method, program) | Number of peaks/range sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ/λ, Å−1/UCP calculation method θ/λ, Å−1/UCP calculation method |
Δa, Å |
|---|---|---|---|---|---|
| SC – single crystal; PC – polycrystal; XRD – X-ray diffraction; ND – neutron diffraction; LSM – the least squares method.a The single crystal was annealed. | |||||
| Durif, 1982 (ref. 13) | 298 | 10.497(8) | SC, XRD/— | —/—/LSM | −0.021 |
| Milenov et al., 2007 (ref. 14) | 293.2 | 10.510(2) | SC, XRD/ω/2θ technique, Nonius diffractometer control software40 | 22/0.43–0.53/LSM | −0.008 |
| 10.512(0) | −0.006 | ||||
| Philipsborn, 1971 (ref. 15) | 300 | 10.495 | SC, XRD/— | —/—/the Laue method | −0.023 |
| Kuz'micheva et al., 2018 (ref. 16) | 298 | 10.497(2) | SC, XRD/Enraf-Nonius CAD-4, WinGX program41 | 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 009/up to 1.02/LSM 009/up to 1.02/LSM |
−0.021 |
| 10.491(1)a | 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 412/up to 1.02/LSM 412/up to 1.02/LSM |
−0.027 | |||
| Morris et al., 1984 (ref. 17) | 298 | 10.5187(2) | PC, XRD/internal standard, diffraction pattern processing in JCPDS-NBS POWDER-PATTERN software, determination of peak positions by the second derivative algorithm of Savitzky & Golay (1964),42 taking into account the doublet | 53/0.23–0.57/LSM | 0.0007 |
| Radaev et al., 1990 (ref. 18) | 293 | 10.524(3) | SC, ND/“Syntex P-1” diffractometer | 4200/up to 0.79 Å−1/LSM | 0.006 |
| 573 | 10.540(4) | — | |||
| Fisher & Waldner, 1982 (ref. 19) | 298 | 10.513(5) | PC, ND/Saphir reactor | 43/—/Rietveld's method | −0.005 |
Table 2 shows that in the cases of single crystal studies, the errors indicated by the authors (mainly standard deviations) are several times higher than those estimated by our group for the doublet technique. Thus, in this paper, the BGO UCP is determined with a relative accuracy of 5 × 10−5 for the first time for the single crystal. Of course when using devices with better characteristics (a more accurate goniometer, parallel beam, smaller pixel sizes, etc.), it would be possible to increase accuracy.
When certifying BGO, its high absorption makes it advisable to shape the studied crystals into spheres. However, this presents certain technical challenges due to the small size of samples suitable for laboratory diffractometers. At the current stage, when selecting crystals 1–10, we have chosen the most isometric samples with linear dimensions of approximately 50 microns in all three directions.
Temperature studies
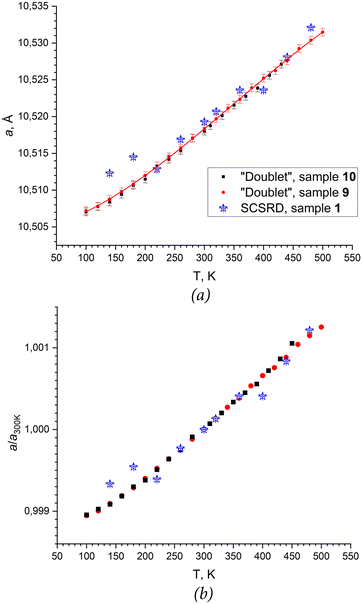
Temperature studies were carried out on crystal 1 using SCXRD and on crystals 9 and 10 using the “doublet” technique, following the same procedure as for UCP refinement at room temperature. Fig. 7 shows that the temperature dependencies obtained for crystals 9 and 10 coincide within the estimated error. The SCXRD data generally follow the same trend, but the level of oscillation turns out to be much higher. It should be noted that the uncertainties reported in SCXRD are the standard deviations when averaging the UCP over a large data set I(X, Y) and are based on the positions of the detector and the crystal determined by the program with some error. Such errors reflect the internal consistency of the array used (random errors), and do not capture systematic errors in the UCP determined, therefore, they are not plotted in Fig. 7.The approximation of the obtained UCP(T) dependence for crystal 9 was carried out in the Origin program.35 A third-degree polynomial was chosen (Fig. 7a, adjusted R-square = 0.99977):
| a(T) = −1.5(2) × 10−10T3 + 1.6(2) × 10−7T2 + 1.2(5) × 10−5T + 10.5044(4). |
| αij(i = j) = −4.369(1) × 10−11T2 + 3.067(1) × 10−8T + 1.121(1) × 10−6, αij(i ≠ j) = 0. |
 | ||
| Fig. 8 BGO TEC(T) dependence in comparison with literature data.27–29 | ||
The BGO TEC at room temperature is similar to other oxides studied – Gd2O3 (α11 = 5.83 × 10−6 K−1) and Y2O3 (α11 = 5.75 × 10−6 K−1 (ref. 37)), as well as common diffractometric standards, for example, Si (α11 = 2.69 × 10−6 K−1).38 This makes BGO less suitable as a temperature reference than, for example, sulfur. The sulfur α-33S TEC, which we determined earlier,39 turn out to be higher at room temperature: α11 = 15.35 × 10−5, α22 = 8.56 × 10−5, and α33 = 9.12 × 10−5 K−1.
Test determination of Si and Ge UCPs using BGO as the external standard
The test determination of the Si and Ge UCPs was carried out to demonstrate the effectiveness of BGO as an X-ray standard and to verify the correctness of the determined UCP value for it. BGO samples from random areas of the initial sample were ground in heptane and then a reference Si polycrystal certified earlier in the Bond scheme on a single-crystal spectrometer21 was added to the powder. After homogenization, the sample was applied to the polished side of a standard sample holder, and after heptane evaporation the sample was a thin, even layer (thickness ∼100 microns). The experiment was carried out using a Bruker D8 Advance diffractometer (CuKα radiation, LYNXEYE XE-T linear detector, Bragg–Brentano scheme) in the 5–75° range with a 0.03° step and an accumulation time of 2 seconds (Fig. 9). The refinement of the Si UCP was carried out on the (3 1 1) reflection with a theoretical angular position of the Kα1-component of 56.121°. The correction was introduced according to the BGO (6 2 0) and (5 4 1) reflections, and their positions (55.186 and 56.670°) were calculated based on the previously obtained aBGO = 10.5180 Å. Similarly, the refinement was carried out on the (4 0 0) Si reflection (69.128°), with the correction for BGO (6 4 2) and (7 3 2) reflections with calculated angular positions of 66.4664 and 70.4320°. The Kα1-components' centers of gravity of the selected reflections were determined by their processing by the Gauss function in the powder diffraction mode (taking into account the Kα2-component) in the Fityk program.43 Then the graphs of the Δθ(θ) dependence were plotted for each case using two BGO reflections, and the correction for the Si reflection angular position was made. Finally, the Si UCP was calculated. The Si UCP, determined by the (3 1 1) reflection, was 5.4307(9), and by the (4 0 0) reflection – 5.4309(7) Å. The errors are calculated based on the accuracy of the goniometer 0.005°. The difference between the obtained values and the reference one aSi = 5.431042 (ref. 21) is 0.0003 and 0.0001 Å, correspondingly, which is noticeably better than the expected measurement error. Furthermore, the high quality of the obtained BGO diffraction pattern should be emphasized, demonstrating its potential as a promising X-ray diffraction standard: for example, the FWHM of the Kα1-components at diffraction angles of 56–57° is 0.073° for the (3 1 1) Si peak and 0.087° for the (5 4 1) BGO (Fig. 9).The BGO single crystal was also used as an external standard to refine the Ge single crystal's UCP. The average aGe value calculated from the measurement data by single-crystal spectrometer and multiple reflection methods21 is 5.65777 Å. The Ge (14 2 0) reflection with a theoretical position of 124.87° 2θ was selected to measure its UCP. This value is within the inter-doublet interval of the BGO (7 14 21) reflection: Kα1 = 124.052 and Kα2 = 125.371° 2θ. The experiment, reflection processing, and UCP calculation were carried out following the procedure described earlier. The calculated value of aGe = 5.6577(3) Å, and the difference from the reference value is 0.00007 Å.
Another promising application may be the use of BGO as a standard for the entire detector plane calibration: both using powder and single crystals. Fig. 10 shows the calibration result for the D = 139 mm, 2θD = 120° position of the Bruker D8 Venture detector (CuKα radiation), performed on Si and BGO single crystals based on the results of identical experiments. Calibration was obtained in the SearchXY-2θ program22 based on the PyFAI library.44 The calibration results obtained are in poor agreement, presumably because of the low statistics of Si reflections. Nevertheless, Fig. 10 clearly demonstrates the advantages of using a large-cell standard when calibrating diffractometers.
 | ||
| Fig. 10 The result of the D = 139 mm, 2θ = 120° position calibration of the Bruker D8 Venture detector (CuKα radiation), performed on Si and BGO single crystals based on the results of identical experiments. Calibration was obtained in the SearchXY-2θ program22 based on the PyFAI library.44 When the calibration arcs approximation, both components of the doublets are used. | ||
Thus, the conducted studies confirm that BGO is a promising X-ray diffraction standard. In the future, we plan to certify BGO single crystals obtained according to technical specifications. At the current stage, fragments of the BGO single crystal studied in this work can be obtained from the authors free of charge.
Conclusions
In this work, the X-ray certification of the new Bi4Ge3O12 (BGO) standard was carried out. BGO demonstrates several advantages over traditional commercial mono- and polycrystalline standards. Some aspects of the accuracy of determining single crystals' UCPs on serial laboratory diffractometers were considered. Literature data analysis revealed that the variation in reported BGO UCP values obtained by X-ray and neutron diffraction of poly- and single crystals significantly exceeds the measurement errors given. The BGO UCP a = 10.5180(5) Å was determined using the original technique, and the relative measurement error was 5 × 10−5. The homogeneity of the initial large BGO crystal was confirmed by the analysis of the UCPs of nine samples from its different regions: they coincided within the estimated measurement error. Furthermore, based on the UCP results for the tenth crystal selected from another synthesis, the possibility of obtaining BGO crystals of high perfection with reproducible characteristics in independent experiments was demonstrated.According to the results of the SCXRD for one of the crystals, the dynamics of the BGO structure in the temperature range of 140–480 K was characterized: the volumes of polyhedra (BiO6) and (GeO4) increase by 0.57 and 0.55%, correspondingly, and as a result, the BGO UCP increases by 0.19%. Using the original technique, the dependence of the BGO UCP on T was determined in the range of 100–500 K. It was shown that the results obtained for the two crystals coincide within the error. The temperature dynamics of the BGO thermal expansion tensor elements is:
| αij(i = j) = −4.369(1) × 10−11T2 + 3.067(1) × 10−8T + 1.121(1) × 10−6, αij(i ≠ j) = 0. |
On the example of the test determination of the UCPs of the Si and Ge single crystals certified by the Bond method on a single-crystal spectrometer, the effectiveness of using BGO as an external and internal X-ray diffraction standard in the study of mono- and polycrystals was shown. BGO diffraction patterns obtained on laboratory diffractometers during conventional sample preparation demonstrate quality, well-resolved doublets already at medium diffraction angles, as well as high intensity, including at high angles.
Author contributions
S. A. G.: conceptualization and methodology; V. N. S.: synthesis and chemical analysis; P. S. S.: X-ray diffraction experiments, data analysis and validation; P. S. S., V. N. S. and S. A. G.: original draft preparation; all authors contributed to writing and editing of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
Supplementary crystallographic data for Bi4Ge3O12 were deposited at the CCDC under numbers 2388565,45a 2428450–2428458.45b–jSupplementary information is available. See DOI: https://doi.org/10.1039/d5ce00563a.
Acknowledgements
This study was supported by the Russian Science Foundation and the Government of Novosibirsk Region (project no. 24-22-20017, https://rscf.ru/project/24-22-20017/, X-ray diffraction studies) and the Ministry of Science and Higher Education of the Russian Federation (N 121031700314-5, crystal growth).References
- F. H. Herbstein, Acta Crystallogr., Sect. B: Struct. Sci., 2000, 56, 547–557 CrossRef CAS.
- W. Wong-Ng, T. Siegrist, G. T. DeTitta, L. W. Finger, H. T. Evans, E. J. Gabe, G. D. Enright, J. T. Armstrong, M. Levenson, L. P. Cook and C. R. Hubbard, J. Res. Natl. Inst. Stand. Technol., 2001, 106, 1071–1094 CrossRef CAS PubMed.
- A. P. Dudka, E. S. Smirnova, I. A. Verin and N. B. Bolotina, Crystallogr. Rep., 2017, 62, 651–659 CrossRef CAS.
- P. S. Serebrennikova and S. A. Gromilov, J. Struct. Chem., 2022, 63, 1856–1871 CrossRef CAS.
- H. E. King and L. W. Finger, J. Appl. Crystallogr., 1979, 12, 374–378 CrossRef CAS.
- R. J. Angel and L. W. Finger, J. Appl. Crystallogr., 2011, 44, 247–251 CrossRef CAS.
- V. V. Lider, Phys.-Usp., 2020, 63, 907–928 CrossRef CAS.
- A. E. Blagov, M. V. Dekapoltsev, M. V. Kovalchuk, V. V. Lider, Y. V. Pisarevsky and P. A. Prosekov, Crystallogr. Rep., 2010, 55, 1074–1078 CrossRef CAS.
- P. S. Serebrennikova, S. I. Lobanov, A. S. Sukhikh, L. I. Isaenko and S. A. Gromilov, CrystEngComm, 2024, 26, 2207–2218 RSC.
- P. S. Serebrennikova, V. Y. Komarov, V. A. Trifonov, A. V. Panchenko and S. A. Gromilov, J. Struct. Chem., 2024, 65, 169–185 CrossRef CAS.
- S. A. Gromilov, J. Struct. Chem., 2022, 63, 976–982 CrossRef CAS.
- A. L. Kudryavtsev and S. A. Gromilov, J. Struct. Chem., 2024, 65, 2466–2477 CrossRef CAS.
- A. Durif, C. R. Seances Acad. Sci., Ser. C, 1982, 295, 555–556 CAS.
- T. I. Milenov, P. M. Rafailov, R. Petrova, Y. F. Kargin and M. M. Gospodinov, Mater. Sci. Eng., B, 2007, 138, 35–40 CrossRef CAS.
- H. Philipsborn, J. Cryst. Growth, 1971, 11, 348–350 CrossRef.
- G. M. Kuz'micheva, I. A. Kaurova, L. I. Ivleva, E. V. Khramov, P. A. Eistrikh-Geller, V. B. Rybakov, T. V. Chukhlovina and S. V. Firstov, Arabian J. Chem., 2018, 11, 1270–1280 CrossRef.
- M. C. Morris, H. F. McMurdie, E. H. Evans, B. Paretzkin, H. S. Parker, N. P. Pyrros and C. R. Hubbard, Standard X-Ray Diffraction Patterns, Natl. Bur. Stand., 1984, 25, 20 Search PubMed.
- S. F. Radaev, L. A. Muradyan, Yu. F. Kargin, V. A. Sarin, V. N. Kanepit and V. I. Simonov, Kristallografiya, 1990, 35, 361–364 CAS.
- P. Fischer and F. Waldner, Solid State Commun., 1982, 44, 657–661 CrossRef CAS.
- Powder Diffraction File, PDF-2, International Centre for Diffraction Data, Newtown, USA, 2021, https://www.icdd.com Search PubMed.
- V. I. Lysoivan, Izmerenie parametrov elementarnoi yacheyki na odnokristal'nom spektrometre (Measurement of Unit Cell Parameters on a Single-Crystal Spectrometer), Nauka, Novosibirsk, Russia, 1982 Search PubMed.
- A. V. Panchenko, P. S. Serebrennikova, V. Y. Komarov and S. A. Gromilov, J. Struct. Chem., 2023, 64, 1399–1411 CrossRef CAS.
- A. L. Kudryavtsev, P. S. Serebrennikova, N. G. Naumov and S. A. Gromilov, J. Struct. Chem., 2024, 65, 1932–1941 CrossRef CAS.
- Y. V. Vasiliev, R. R. Akhmetshin, Y. A. Borovliev, D. N. Grigoriev, V. A. Gusev, V. N. Shlegel and V. P. Smakhtin, Nucl. Instrum. Methods Phys. Res., Sect. A, 1996, 379, 533–535 CrossRef CAS.
- Y. A. Borovlev, N. V. Ivannikova, V. N. Shlegel, Y. V. Vasiliev and V. A. Gusev, J. Cryst. Growth, 2001, 229, 305–311 CrossRef CAS.
- N. Tsuchida, M. Ikeda, T. Kamae and M. Kokubun, Nucl. Instrum. Methods Phys. Res., Sect. A, 1997, 385, 290–298 CrossRef CAS.
- A. V. Firsov, PhD thesis, Karpov Institute of Physical Chemistry, Russia, 1994 Search PubMed.
- T. G. Xi, Y. Fei, W. P. Leung and C. L. Choy, J. Mater. Sci. Lett., 1989, 8, 1317–1319 CrossRef CAS.
- B. K. Rao, K. G. Subhadra and D. B. Sirdeshmuh, Indian J. Pure Appl. Phys., 1981, 19, 87–89 CAS.
- Bruker, APEX3 (Version 2019.1-0), SAINT (Version 8.40A) and SADABS (Version 2016/2), Bruker AXS Inc., Madison, Wisconsin, USA, 2019 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- G. M. Sheldrick, Acta Crystallogr., Sect. A: Found. Adv., 2015, 71, 3–8 CrossRef PubMed.
- G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- International Tables for Crystallography, Volume H: Powder Diffraction, ed. C. J. Gilmore, J. A. Kaduk and H. Schenk, Wiley, 1st online edn, 2019, ch. 2.1.6, p. 37 Search PubMed.
- OriginPro (Verdion), OriginLab Corporation, Northampton, MA, USA, 2022 Search PubMed.
- T. Langreiter and V. Kahlenberg, Crystals, 2015, 5, 143–153 CrossRef.
- P. S. Serebrennikova, A. L. Kudryavtsev, N. G. Naumov and S. A. Gromilov, J. Struct. Chem., 2024, 65, 2429–2437 CrossRef CAS.
- Y. Okada and Y. Tokumaru, J. Appl. Phys., 1984, 56, 314–320 CrossRef CAS.
- P. S. Serebrennikova, A. V. Panchenko, N. B. Egorov and S. A. Gromilov, Crystallogr. Rep., 2024, 69, 513–521 CrossRef CAS.
- B. V. Nonius, CAD4-Express Software, Ver. 5.1/1.2, Enraf Nonius, Delft, The Netherlands, 1994 Search PubMed.
- L. J. Farrugia, J. Appl. Crystallogr., 1999, 32, 837–838 CrossRef CAS.
- A. Savitzky and M. J. Golay, Anal. Chem., 1964, 36, 1627–1639 CrossRef CAS.
- M. Wojdyr, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- J. Kieffer and D. Karkoulis, J. Phys.:Conf. Ser., 2013, 425, 8–13 CrossRef.
- (a) CCDC 2388565: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2l5hhs; (b) CCDC 2428450: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj039; (c) CCDC 2428451: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj04b; (d) CCDC 2428452: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj05c; (e) CCDC 2428453: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj06d; (f) CCDC 2428454: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj07f; (g) CCDC 2428455: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj08g; (h) CCDC 2428456: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj09h; (i) CCDC 2428457: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj0bj; (j) CCDC 2428458: Experimental Crystal Structure Determination, 2025, DOI:10.25505/fiz.icsd.cc2mj0ck.
| This journal is © The Royal Society of Chemistry 2026 |