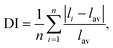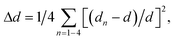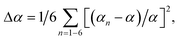β-Ca3(PO4)2-related structure and dielectric properties of Ca8CdLa(PO4)7
Elena V.
Sipina
a,
Evgeniya S.
Zhukovskaya
b,
Vladimir A.
Morozov
 b,
Sergey Yu.
Stefanovich
b,
Vadim V.
Grebenev
c,
Alexei A.
Belik
b,
Sergey Yu.
Stefanovich
b,
Vadim V.
Grebenev
c,
Alexei A.
Belik
 d,
Bogdan I.
Lazoryak
d,
Bogdan I.
Lazoryak
 b and
Dina V.
Deyneko
b and
Dina V.
Deyneko
 *b
*b
aPhysics Department, Moscow State University, 119991 Moscow, Russia
bChemistry Department, Moscow State University, 119991 Moscow, Russia. E-mail: deynekodv@my.msu.ru
cA.V. Shubnikov Institute of Crystallography of the Kurchatov Complex Crystallography and Photonics of the NRC “Kurchatov Institute”, 119333, Moscow, Russia
dResearch Center for Materials Nanoarchitectonics (MANA), Namiki 1-1, Tsukuba, Ibaraki, 305-0044, Japan
First published on 8th November 2025
Abstract
A Ca8CdLa(PO4)7 phase was prepared by a high-temperature solid-state reaction in air. The bulk and local cation composition was determined by inductively coupled plasma atomic emission spectroscopy and by energy-dispersive X-ray spectrometry. Second-harmonic generation, differential scanning calorimetry and dielectric measurements revealed the presence of a reversible ferroelectric first-order phase transition from a ferroelectric β-phase (space group (SG) R3c) to a paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c). The phase transition temperature, Tc, is 865 ± 10 K. The β-Ca3(PO4)2 (β-TCP) related structure was refined by the Rietveld method in the SG R3c using powder synchrotron X-ray diffraction data. The distribution of Ca2+, Cd2+ and La3+ cations among the sites of the β-TCP-type structure was found. According to crystal structure refinement, M5O6 octahedra are occupied by Ca2+ and Cd2+ (M5 = 0.307(6)Ca2+ + 0.693(6)Cd2+) while Ca2+ and La3+ cations occupy M1 and M3 sites of the β-TCP-type structure. Analysis of the difference electron density map [ρdif: (x; y; z)] revealed the presence of small residual electron density at the M4 site. The M4 position is partially occupied by Ca2+ cations (M4 = 0.131(6)Ca2+). The elemental composition after the Rietveld refinement is determined as Ca8.61Cd0.70La0.82(PO4)7. Conductivity measurements revealed that the calculated σbulk (σbulk = 4.01 × 10−6 S cm−1 at 900 K and σbulk = 1.49 × 10−4 S cm−1 at 1270 K) for Ca8.61Cd0.70La0.82(PO4)7 was lower than one for other β-TCP-type compounds.
c). The phase transition temperature, Tc, is 865 ± 10 K. The β-Ca3(PO4)2 (β-TCP) related structure was refined by the Rietveld method in the SG R3c using powder synchrotron X-ray diffraction data. The distribution of Ca2+, Cd2+ and La3+ cations among the sites of the β-TCP-type structure was found. According to crystal structure refinement, M5O6 octahedra are occupied by Ca2+ and Cd2+ (M5 = 0.307(6)Ca2+ + 0.693(6)Cd2+) while Ca2+ and La3+ cations occupy M1 and M3 sites of the β-TCP-type structure. Analysis of the difference electron density map [ρdif: (x; y; z)] revealed the presence of small residual electron density at the M4 site. The M4 position is partially occupied by Ca2+ cations (M4 = 0.131(6)Ca2+). The elemental composition after the Rietveld refinement is determined as Ca8.61Cd0.70La0.82(PO4)7. Conductivity measurements revealed that the calculated σbulk (σbulk = 4.01 × 10−6 S cm−1 at 900 K and σbulk = 1.49 × 10−4 S cm−1 at 1270 K) for Ca8.61Cd0.70La0.82(PO4)7 was lower than one for other β-TCP-type compounds.
1. Introduction
Ca8MLn(AO4)7 (M = Mg, Zn, Ca; Ln = rare-earth elements (REE); A = P, V) compounds with the β-Ca3(PO4)2-type (β-TCP) structure1 attract attention due to their applications as phosphors2 and lasers,3 nonlinear optical,4 bioactive,5 ferroelectric6 and antiferroelectric7 materials. Substitution of Ca2+ by various cations in the β-TCP-type structure allows obtaining materials with multifunctional properties and fine-tuning several of them. The introduction of some cations (Mg2+,8 Zn2+,9 Sr2+10) into the β-TCP-type structure reduces the ferroelectric transformation temperature or even suppresses the ferroelectric ordering. In particular, in the case of Ca9Ln(PO4)7 phosphates, the substitution of Ca2+ with Mg2+,11 Zn2+,12 or Cd2+ (ref. 13) leads to a change in the structure at room temperature (TR) from non-centrosymmetric (space group (SG) R3c) for Ca9Ln(PO4)7 phosphates to centrosymmetric (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) for Ca8MLn(AO4)7 (M = Mg, Zn, Cd; Ln = REE; A = P, V), and transformation of ferroelectrics14 to antiferroelectrics.15
c) for Ca8MLn(AO4)7 (M = Mg, Zn, Cd; Ln = REE; A = P, V), and transformation of ferroelectrics14 to antiferroelectrics.15
A similar change of ferroelectric to antiferroelectric phase was found in Ca9.5–1.5xMgEux(PO4)7 during step-by-step substitution of Ca2+ by Eu3+, which formed cation vacancies in the structure.16 The polar structure with SG R3c corresponds to compositions where 0 ≤ x < 1, while Ca8MgEu(PO4)7 exhibits an antiferroelectric phase. In Ca3−xSrx(PO4)2 solid solutions, increasing the Sr2+ content from x = 0 to x = 12/7 10 reduces the ferroelectric-to-paraelectric phase transition temperature from 920 K to 520 K. This change also decreases the second-harmonic generation response at TR from 3.2 to 0.04, with a maximum at x = 5/7. Further increasing the Sr2+ content from x = 12/7 to x = 13/7 changes the structure symmetry from R3c to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at the ferroelectric–paraelectric phase transition point (Tc).
m at the ferroelectric–paraelectric phase transition point (Tc).
A ferroelectric transition proceeds from a ferroelectric β-phase (SG R3c) to a paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) while an antiferroelectric transition happens from an antiferroelectric β-phase (SG R
c) while an antiferroelectric transition happens from an antiferroelectric β-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) to a paraelectric β′-phase (SG R
c) to a paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).8,9
m).8,9
In this work, we describe the structure and thermal, dielectric, nonlinear optical and ion-conducting properties of the β-TCP-related Ca8.61Cd0.70La0.82(PO4)7 phosphate.
2. Experimental
2.1. Materials and sample preparation
A Ca8CdLa(PO4)7 (CCLP) phase was prepared by a high-temperature solid-state reaction in air from stoichiometric amounts of CaCO3 (99.9%), CdO (99%), La2O3 (99.99%) and CaHPO4·2H2O (99.9%). All chemicals are commercial products from Sigma-Aldrich. The synthesis was performed in alumina crucibles at 1373 ± 10 K for 100 h. During the synthesis, the samples were ground every 24 hours of firing. After the final annealing, the samples were slowly cooled in a furnace from 1373 K to TR. An annealing temperature of 1373 K was used by analogy with previous studies.172.2. Characterization
The bulk cation composition of CCLP was determined by inductively coupled plasma atomic emission spectroscopy (ICP-AES) on an Agilent ICP-AES 5100 with an SPS4 autosampler device. Substances were previously dissolved in hydrochloric acid (37%, ISO grade). Calibration functions for elements were found using solutions of Ca, Cd and Eu. The collection of the emission was carried out at several wavelengths, and the obtained values were averaged. The local cation composition of CCLP was determined by energy-dispersive X-ray spectrometry (TEM-EDX) using a probe aberration corrected ThermoFisher Titan Themis Z transmission electron microscope at 200 kV equipped with a Super-X system for EDX analysis and an EDAX attachment. A sample for TEM was prepared by crushing powders in an agate mortar and dispersing them in methanol. A few drops of the dispersion were placed on copper grids with a holey carbon film. The EDX measurements of the Ca/Cd/La ratio were provided for probe diameters of 100–200 nm.A second-harmonic generation (SHG) powder technique similar to the one suggested by Kurtz and Perry18 was used for the center of symmetry test in CCLP. The SHG at the wavelength λω = 0.532 μm was excited by a Minilite-I YAG: Nd-laser operating in a Q-switched mode at λω = 1.064 μm and recorded in reflection geometry. Polycrystalline α-SiO2 with 3–5 μm size particles was used as a standard in order to calibrate the intensity of the SHG response I2ω according to the q = I2ω/I2ω(SiO2) relation. The sample was previously crushed into 3–5 μm powder for the sake of comparability with the α-SiO2 sample.
We used a NETZSCH STA Jupiter 449F1 simultaneous thermal analyzer to perform differential scanning calorimetric (DSC) measurement. DSC data were collected at 670–965 K with a heating/cooling rate of 10 K min−1 in Pt crucibles with pierced lids in air.
Dielectric properties at heating/cooling mode were measured on a Novocontrol Alpha-ANT impedance-analyzer in a ProboStat measuring cell using the four-wire two contact method in a frequency range of 10−1–1.4 × 107 Hz at 473–1273 K. The frequency dependence of the complex impedance Z*(ω) = Z′(ω) + iZ″(ω) was measured during step heating under temperature stabilization conditions (the average heating rate was 0.8 K min−1). Ceramic pellets were 40–50 mm2 in area and 1–2 mm in height. A Pt paste was placed on flat surfaces of pellets and heated at 1023 ± 10 K for 1 h to obtain Pt electrodes. The density of the ceramic samples was above 80% of the theoretical one. The bulk and grain boundary conductivities, σb and σgb, were calculated from the impedance spectra by means of equivalent electric circuits.
Powder X-ray diffraction (PXRD) data for phase analysis were obtained on a Thermo ARL X'TRA powder diffractometer (CuKα radiation, λ = 1.5418 Å, Bragg–Brentano geometry, scintillation detector) over the 5–65° 2θ range with a step of 0.02°. The phase analysis was performed using the JCPDS PDF-2 database. Lattice parameters were determined by Le Bail decomposition19 using JANA2006 software.20 To determine the structure of CCLP, we used experimental synchrotron XRD (SXRD) data obtained on the BL15XU beamline of SPring-8 (λ = 0.65298 Å)21,22 between 2.0° and 60.2° with a step of 0.003° in 2θ. Lindemann glass capillaries with an inner diameter of 0.1 mm were used as sample holders.
3. Results
3.1. Elemental analysis, SHG, DSC and dielectric measurements
Using ICP-AES, the Ca![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Cd
Cd![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) La ratio in CCLP was found to be 8.3 ± 0.2
La ratio in CCLP was found to be 8.3 ± 0.2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.90 ± 0.02
0.90 ± 0.02![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.90 ± 0.02, which differs from the expected bulk composition Ca8CdLa(PO4)7. Elemental contents were measured using TEM-EDX analysis at 10 points for each sample. The LaL, CdL and CaK lines in the EDX spectra were used. The oxygen and phosphorus contents were not quantified by EDX. TEM-EDX determined the composition to be Ca8.5Cd0.80La0.82(PO4)7 (83.9 ± 4 at% (Ca), 7.9 ± 0.3 at% (Cd), 8.1 ± 0.3 at% (La)).
0.90 ± 0.02, which differs from the expected bulk composition Ca8CdLa(PO4)7. Elemental contents were measured using TEM-EDX analysis at 10 points for each sample. The LaL, CdL and CaK lines in the EDX spectra were used. The oxygen and phosphorus contents were not quantified by EDX. TEM-EDX determined the composition to be Ca8.5Cd0.80La0.82(PO4)7 (83.9 ± 4 at% (Ca), 7.9 ± 0.3 at% (Cd), 8.1 ± 0.3 at% (La)).
Fig. 1a shows the temperature dependence of the SHG signal (I2ω/I2ω(SiO2)) during the heating/cooling of CCLP. The presence of SHG response (I2ω/I2ω(SiO2) > 1.5) at TR indicates the absence of a symmetry center in this structure, confirming a non-centrosymmetric structure with the SG R3c. Heating causes a sharp decline of the SHG signal to zero at 850 ± 10 K, while subsequent cooling results in signal recovery with a temperature hysteresis of several degrees. The disappearance/appearance of the SHG response upon heating/cooling indicates a reversible phase transition (PT) in CCLP. Substitution of Ca2+ by Cd2+ cations slightly increases the SHG signal magnitude from I2ω/I2ω(SiO2) = 0.87 in Ca9La(PO4)7 (ref. 23) to I2ω/I2ω(SiO2) = 1.8 in CCLP.
The reversible first-order PT in CCLP was studied using DSC analysis. Fragments of heating/cooling DSC curves for CCLP are shown in Fig. 1b. Reproducible endothermic/exothermic effects were observed. The DSC curves for CCLP reveal a single peak at 857 ± 5 K (at heating mode) and another at 839 ± 5 K (at cooling mode). This temperature hysteresis ΔT confirms the first-order PT found by SHG study. Although the endothermic effect is quite small (Fig. 1b), both the first-order PT and its temperature range are further confirmed by dielectric and conductivity measurements.
The reversible PT was detected by dielectric ε(T) anomalies appearing as slightly diffused maxima (Fig. 1c) in CCLP. The position of this maximum remains constant regardless of the applied field frequency. The transition temperature was found to be 863 ± 5 K during the heating. Temperature dependencies and dielectric loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) at different frequencies in CCLP are shown in Fig. 1d. The anomaly on the ε(T) curve can be associated with both ferroelectric (FE) and antiferroelectric (AFE) phase transitions. In FE compounds, the dielectric loss tangent tan δ(T) usually exhibits a maximum below the PT temperature – known as the Curie temperature Tc. This maximum is attributed to a change in the domain structure just below Tc. Antiferroelectrics, however, do not exhibit such a maximum on the tan δ(T) curve. The presence of a maximum in tan δ(T) at a temperature below Tc confirms the FE phase transition in CCLP.
δ) at different frequencies in CCLP are shown in Fig. 1d. The anomaly on the ε(T) curve can be associated with both ferroelectric (FE) and antiferroelectric (AFE) phase transitions. In FE compounds, the dielectric loss tangent tan δ(T) usually exhibits a maximum below the PT temperature – known as the Curie temperature Tc. This maximum is attributed to a change in the domain structure just below Tc. Antiferroelectrics, however, do not exhibit such a maximum on the tan δ(T) curve. The presence of a maximum in tan δ(T) at a temperature below Tc confirms the FE phase transition in CCLP.
3.2. Powder X-ray diffraction (PXRD) study
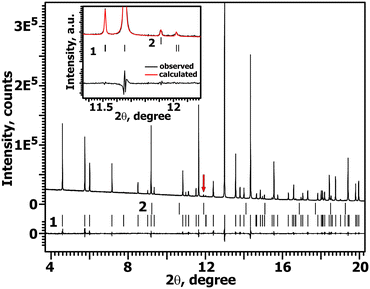
The PXRD pattern of CCLP is similar to previously studied Ca8MR(PO4)7 (M = Mg, Zn; R = REE)8,9 compounds and is related to the β-TCP-type structure1 with the unit cell parameters: a = 10.4590(4) Å, c = 37.422(2) Å and V = 3545.2(3) Å3. The absence of any impurity reflections on the PXRD patterns (Fig. 2) shows that La3+ and Cd2+ cations were completely incorporated into the β-TCP-type host.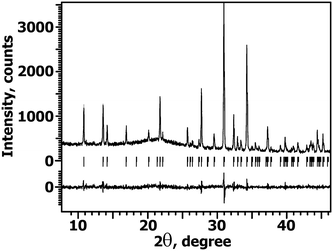 | ||
| Fig. 2 Parts of the PXRD patterns for CCLP in the 2θ range of 8–46°. Tick marks denote the peak positions of possible Bragg reflections. | ||
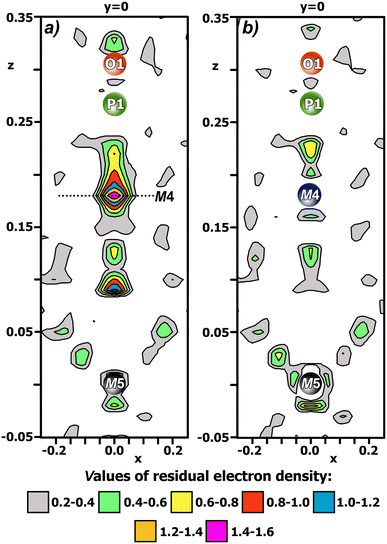
The SXPD data were used to refine the crystal structure. The structure was refined by the Rietveld method24 using the JANA2006 programme package.20 The main data under the SXPD data conditions and the results of the Rietveld refinement are presented in Table 1. The difference electron density maps in the (010) plane for the CCLP structure is shown in Fig. 3.
| Refined composition | 0.989(4)Ca8.61Cd0.70La0.82(PO4)7 + 0.011(4)Ca3La(PO4)3 |
|---|---|
| Composition after TEM-EDX | Ca8.5Cd0.8La0.82(PO4)7 |
| Composition after ICP-AES | Ca8.3Cd0.9La0.9(PO4)7 |
| Space group | R3c |
| Lattice parameters: a, Å | 10.46310(1) |
| c, Å | 37.42078(6) |
| Unit cell volume V, Å3 | 3547.842(7) |
| Calculated density, g cm−3 | 3.38(2) |
| Data collection | |
| Diffractometer | BL15XU beamline of SPring-8 |
| Radiation/wavelength (λ, Å) | Synchrotron/0.65298 |
| 2θ range (°) | 2.042–60.235 |
| Step scan (2θ) | 0.003 |
| Number of points | 19![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 394 394 |
| I max | 339![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 601 601 |
| Refinement | |
| Refinement | Rietveld |
| Background function | Legendre polynomials, 15 terms |
| No. of reflections (all/observed) | 2147/2123 |
| No. of refined parameters/refined atomic parameters | 89/65 |
| R and Rw (%) for Bragg reflections (Rall/Robs) | 3.58/3.51 and 4.35/4.34 |
| R P, RwP; Rexp (%) | 2.22, 3.63, 1.08 |
| Goodness of fit (ChiQ) | 3.37 |
| Max./min. residual density | 1.36/−2.50 |
| Selected crystal structure data | |
| n f-CaM1 | 1.115(7) |
| n f-CaM2 | ∼1.00(5) |
| n f-CaM3 | 1.521(6) |
| n f-CaM4 | 0.153(6) |
| n f-CaM5 | 2.170(9) |
| n f-CdM4 | 0.058(2) |
| n f-CdM5 | 0.817(3) |
| CCDC | 2473599 |
In contrast to laboratory PXRD patterns, the SXRD study of CCLP (Fig. 4) revealed the presence of a Ca3La(PO4)3 impurity (JCPDS, PDF-2, No. 29-0338) with the eulytite-type (Bi4(SiO4)3 (ref. 25) structure (SG I![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif) 3d, a = 9.9508 Å). According to the SHG data, the CCLP structure is noncentrosymmetric (Fig. 1a). The structural data for β-TCP (SG R3c (ref. 1)) were used as a starting model for the CCLP structure refinement. There are six cationic (M1–M6) sites in the β-TCP-related structures. The M1–M3 (18-fold) and M5 (6-fold) positions are always occupied, while the occupation of the M4 (6-fold) position can change from 0 to 1, and the M6 (6-fold) position is usually vacant. An overview of cation distributions among the M1–M5 sites of the β-TCP-type structure is given in ref. 26.
3d, a = 9.9508 Å). According to the SHG data, the CCLP structure is noncentrosymmetric (Fig. 1a). The structural data for β-TCP (SG R3c (ref. 1)) were used as a starting model for the CCLP structure refinement. There are six cationic (M1–M6) sites in the β-TCP-related structures. The M1–M3 (18-fold) and M5 (6-fold) positions are always occupied, while the occupation of the M4 (6-fold) position can change from 0 to 1, and the M6 (6-fold) position is usually vacant. An overview of cation distributions among the M1–M5 sites of the β-TCP-type structure is given in ref. 26.
At the second stage, the f curves for Cd2+ (M5 sites) were used, and all parameters of the chosen model were refined. The occupancy of the M5 position by Cd2+ is smaller than 1 (Table 1, nf-CdM5) indicating that a small amount of Ca2+ is located at the M5 site (M5 = nCd2+ + (1–n)Ca2+) as in the case of the previously studied Ca8.223Cd0.777Eu(PO4)7.17
In the final stage, the distribution of La3+ cations over the M1–M3 positions and Cd2+ across the M5 position was refined considering their multiplicities: (M1–M3) = nCa2+ + (1–n)Eu3+) and (M5) = nCa2+ + (1–n)Cd2+, without stoichiometric constraints on the global Eu/Ca and Cd/Ca ratios. The positional parameters (x; y; z) of La3+ and Ca2+ cations over the M3 position were refined without constraints. Analysis of the difference electron density map [ρdif: (x; y; z)] revealed a small residual electron density at the M4 site (Fig. 3a), indicating that this position is not empty but occupied by Ca2+ cations (Fig. 3b). The occupation of the M4 site by Ca2+ cations was chosen so that the composition from the structure refinement was close to the composition from TEM-EDX.
Atomic parameters of the Ca3Bi(PO4)3 structure27 were used as initial parameters for phase content refinement. The atomic parameters, site occupancies, and atomic displacement parameters for all atoms of the Ca3La(PO4)3 structure were not refined. Using the Ca3La(PO4)3 structural data enabled the determination of the sample's phase composition: 0.989(4)Ca8.61Cd0.70La0.82(PO4)7 + 0.011(4)Ca3La(PO4)3. The final results of the refinement are presented in Table 1. The fractional atomic coordinates, isotropic atomic displacement parameters, cation occupancies, the results of bond valence sum (BVS) calculations and main relevant interatomic distances for Ca8.61Cd0.70La0.82(PO4)7 are listed in Tables S1 and S2 of the SI. The CCDC deposition number is 2473599.
The differences in the determination of the elemental composition by the Rietveld refinement and ICP-AES method is due to the following reasons: firstly, the presence of a secondary Ca3La(PO4)3 phase revealed by SXRD study may explain the difference between ICP-AES and Rietveld refinement results. Secondly, perhaps Cd2+ cations are also located in the M1 and M3 positions of the Ca8.61Cd0.70La0.82(PO4)7 structure as the ionic radius of Cd2+ (rVIII(Cd2+) = 1.10 Å) is very close to that of Ca2+ (rVIII(Cd2+) = 1.12 Å); however, it is impossible to find the remaining 1.2 Cd2+ cations (the difference between the TEM-EDX and Rietveld refinement results is 0.2 × 6 for Z = 6) at 36 site positions (M1 (18-fold) and M3 (18-fold)), also containing much heavier La3+ cations.
3.3. Conductivity measurements
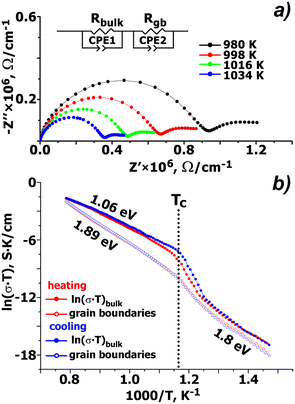
Fig. 5a shows complex electrical impedance diagrams for CCLP at 473–1273 K. Impedance spectra for CCLP are composed by parts of two semicircles at high and low frequencies (ω). The high-ω part of the complex impedance is known to characterize bulk transport properties of ionic conductors, whereas charge migration through the boundary interfaces is a lower-ω process.28Fig. 5b presents the temperature dependence at the heating/cooling mode of conductivity (σT) for bulk and grain boundary transport for CCLP at 473–1273 K. Different dependencies of ln(σT) vs. 1000/T as an Arrhenius plot are observed in a temperature range from 473 to 1273 K. In this temperature range, the dependence for bulk and grain boundary conductivity at heating/cooling can be divided into two approximately linear portions with different slopes. For example, at the heating mode, the activation energies (Ea) for these linear portions for the grain boundary are Ea ∼ 1.8 eV in a range from 473 to 800 K, and Ea ∼ 1.89 eV for a high-temperature region from 865 to 1273 K. The activation energy for the linear portion for bulk conductivity at 473–800 K is close to Ea for the grain boundary while approximated Ea ∼ 1.06 eV at 865–1273 K is lower than that for the grain boundary. A sharp increase of the conductivity above 800 K results in phase transition.
4. Discussion
The refinement of the Ca8.61Cd0.70La0.82(PO4)7 structure revealed that incorporating Cd2+ and La3+ ions into the β-TCP-type structure does not create an inversion center at TR or change the SG from R3c to R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c. This differs from previously studied phosphates containing Zn2+,9,23 Mg2+ (ref. 8) (Table 2) and Cd2+/Eu3+ ions.17 The changing of lattice cell parameters of Ca8MLa(PO4)7 (M = Mg, Zn, Cd, Ca) from the M2+ radius (CN = 6) is shown in Fig. S1 of the SI. Substituting Ca2+ (rVI = 1.00 Å (ref. 29)) with Mg2+ (rVI = 0.72 Å (ref. 29)) increases the lattice cell parameters while the maximum of the “a” parameter is observed for M = Cd.
c. This differs from previously studied phosphates containing Zn2+,9,23 Mg2+ (ref. 8) (Table 2) and Cd2+/Eu3+ ions.17 The changing of lattice cell parameters of Ca8MLa(PO4)7 (M = Mg, Zn, Cd, Ca) from the M2+ radius (CN = 6) is shown in Fig. S1 of the SI. Substituting Ca2+ (rVI = 1.00 Å (ref. 29)) with Mg2+ (rVI = 0.72 Å (ref. 29)) increases the lattice cell parameters while the maximum of the “a” parameter is observed for M = Cd.
| Mg | Zn | Cd | Ca | ||
|---|---|---|---|---|---|
| a Ref. 29. b Dielectric data. | |||||
| Space group |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c c |
R3c | R3c | |
| (rVI(M2+), Åa | 0.72 | 0.74 | 0.95 | 1.00 | |
| Lattice parameters: a, Å | 10.3859(1) | 10.387(8) | 10.46310(1) | 10.456(4)11 | |
| c, Å | 37.256(1) | 37.260(1) | 37.42078(6) | 37.476(4) | |
| Unit cell volume, Å3 | 3480.3(2) | 3481.7(4) | 3547.842(7) | 3648.6(2) | |
| I 2ω/I2ω(SiO2) | <0.1,8 0.03 (ref. 15) | 0.0,23 0.1,9 0.05 (ref. 15) | 1.8 | 0.87 (ref. 23) | |
| T c, Kb | 735 (ref. 8) | 782.2 (ref. 9) | 865 | 892 (ref. 14) | |
| P1O4 | <P1–O> | 1.536 | 1.540 | 1.57 | 1.46 |
| Δd | 0.0277 | 0.0270 | 0.0212 | 0.0432 | |
| Δα | 0.0001 | 0.0006 | 0.0006 | ||
| P2O4 | <P2–O> | 1.526 | 1.549 | 1.56 | 1.52 |
| Δd | 0.0293 | 0.0254 | 0.0233 | 0.0336 | |
| Δα | 0.0015 | 0.0012 | 0.0017 | ||
| P3O4 | <P3–O> | 1.54 | 1.55 | ||
| Δd | 0.0277 | 0.0267 | |||
| Δα | 0.0028 | ||||
| Occupancy M1 | 0.96Ca2+ + 0.04La3+ | 0.95Ca2+ + 0.05La3+ | 0.97Ca2+ + 0.03La3+ | 0.97Ca2+ + 0.03La3+ | |
| <M1–O> | 2.471 | 2.458 | 2.501 | 2.499 | |
| DI(M1–O) | 0.029 | 0.030 | 0.054 | 0.045 | |
| Occupancy M2 | 1Ca2+ | 0.97Ca2+ + 0.03La3+ | |||
| <M2–O> | 2.454 | 2.442 | |||
| DI(M2–O) | 0.041 | 0.022 | |||
| Occupancy M3 | 0.372Ca2+ + 0.128La3+ | 0.38Ca2+ + 0.12La3+ | 0.754Ca2+ 0.246La3+ | 0.74Ca2+ + 0.26La3+ | |
| <M3–O> | 2.541 | 2.586 | 2.629, 2.602 | 2.548 | |
| DI(M3–O) | 0.055 | 0.060 | 0.070, 0.054 | 0.089 | |
| Occupancy M4 | 0 | 0 | 0.128Ca2+ | 0 | |
| Occupancy M5 | 1Mg2+ | 1Zn2+ | 0.692Cd2+ 0.308Ca2+ | 1Ca2+ | |
| <M5–O> | 2.089 | 2.082 | 2.250, 2.252 | 2.305 | |
| DI(M5–O) | 0 | 0 | 0.029, 0.057 | 0.033 | |
| M3′–M3″ | 1.082(2) | 1.248(16) | 0.279(5) | 0 | |
| 0.213(17) | |||||
| 1.091(16) | |||||
| M5′–M5″ | 0 | 0 | 0.093(6) | 0 | |
The β-TCP-related structure of Ca8.61Cd0.70La0.82(PO4)7 consists of isolated PO4 tetrahedra that connect the MOn polyhedra into a 3D framework via common vertices. According to crystal structure refinement, M5O6 octahedra in Ca8CdLa(PO4)7 are occupied by Ca2+ and Cd2+ (M5 = 0.307(6)Ca2+ + 0.693(6)Cd2+), while Ca2+ and La3+ cations occupy the M1 and M3 sites of the β-TCP-type structure. Previously, similar occupation of the M5 position by Ca2+ and Cd2+ was observed in the Ca8.223Cd0.777Eu(PO4)7 structure (M5 = 0.223(4)Ca2++0.777(4)Cd2+ (ref. 17)).
The symmetry of the averaged crystal field of the ligands created near the M1–M3 and M5 sites of the R3c structure is higher for the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure. The average distances M1–O, M2–O, M3–O and M5–O are reducing with decreasing M2+ radius. Also, this was confirmed by the polyhedral distortion index (DI) for different coordination numbers calculated as:
c structure. The average distances M1–O, M2–O, M3–O and M5–O are reducing with decreasing M2+ radius. Also, this was confirmed by the polyhedral distortion index (DI) for different coordination numbers calculated as:
where dn is the individual P–O bond length, d is the average P–O bond length, αn is the individual O–P–O bond angle and α is the perfect tetrahedral angle.
The absence of a center of symmetry at TR was confirmed by the presence of SHG response (Fig. 1a). The disappearance/appearance of the SHG response during heating/cooling indicates a reversible PT in Ca8.61Cd0.70La0.82(PO4)7 from a non-centrosymmetric to centrosymmetric structure at 850 ± 10 K. DSC measurements show that this PT is first-order, with an endothermic effect at 857 ± 5 K when heated and an exothermic effect at 839 ± 5 K during cooling (Fig. 1b). The presence of an anomaly on the ε(T) curve (Fig. 1c) at Tc and a maximum in tan δ(T) at temperature below Tc (Fig. 1d) indicates the FE phase transition in Ca8.61Cd0.70La0.82(PO4)7 similar to that in Ca9La(PO4)7 (ref. 23) from a ferroelectric β-phase (SG R3c) to a paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c).
c).
In contrast to Ca8.61Cd0.70La0.82(PO4)7 and Ca9La(PO4)7, the PT for Ca8.223Cd0.777Eu(PO4)7 is AFE from a antiferroelectric β-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c) to a paraelectric β′-phase (SG R
c) to a paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m).17 The R
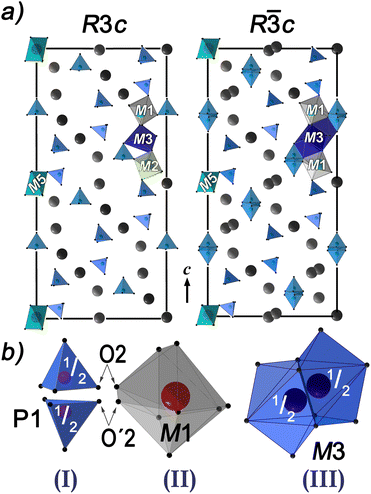
m).17 The R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure of the AFE phase is close to the R3c structure of the FE phase (Fig. 6a). The cation locations in M1–M3 positions in the R3c phase deviate only slightly from the centrosymmetric one. The anionic R
c structure of the AFE phase is close to the R3c structure of the FE phase (Fig. 6a). The cation locations in M1–M3 positions in the R3c phase deviate only slightly from the centrosymmetric one. The anionic R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c subcell becomes centrosymmetric as a result of half of the P1O4 tetrahedra turning over. Three disordered fragments exist in the R
c subcell becomes centrosymmetric as a result of half of the P1O4 tetrahedra turning over. Three disordered fragments exist in the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c structure in comparison to the R3c structure (Fig. 6b): I) disordering of P1O4 tetrahedra; II) two M1O8 polyhedra due to disordering of P1O4 tetrahedra and III) cation disordering at the M3 sites due to a displacement of the M3 positions from the center of symmetry (1/2, 0, 0).
c structure in comparison to the R3c structure (Fig. 6b): I) disordering of P1O4 tetrahedra; II) two M1O8 polyhedra due to disordering of P1O4 tetrahedra and III) cation disordering at the M3 sites due to a displacement of the M3 positions from the center of symmetry (1/2, 0, 0).
La3+ and Ca2+ occupy the M1–M3 positions of FE Ca8.61Cd0.70La0.82(PO4)7 and AFE Ca8.223Cd0.777Eu(PO4)7 β-TCP-related structures, while Cd3+ and Ca2+ occupy M5 sites. The occupancy of the M4 position by Ca2+ is close to 0, and M4 positions are free in Ca8.223Cd0.777Eu(PO4)7. In contrast to structures with the R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c space group, the M4 site occupancy differs from 0 in Ca8.61Cd0.70La0.82(PO4)7, and this position is partially occupied by Ca2+ cations (M4 = 0.131(6)Ca2+ (Table S1 of the SI)).
c space group, the M4 site occupancy differs from 0 in Ca8.61Cd0.70La0.82(PO4)7, and this position is partially occupied by Ca2+ cations (M4 = 0.131(6)Ca2+ (Table S1 of the SI)).
A transition from the FE to AFE phase was found for Ca9.5–1.5xMgEux(PO4)7 during progressive substitution Ca2+ → Eu3+.16 Dielectric loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) maxima were detected for all samples except when x = 1, while characteristic maxima in the temperature dependence of dielectric constant ε(T) were observed across all compositions. The R3c structure corresponds to compositions where 0 ≤ x < 1 in Ca9.5–1.5xMgEux(PO4)7, while Ca8MgEu(PO4)7 (x = 1) is AFE R
δ) maxima were detected for all samples except when x = 1, while characteristic maxima in the temperature dependence of dielectric constant ε(T) were observed across all compositions. The R3c structure corresponds to compositions where 0 ≤ x < 1 in Ca9.5–1.5xMgEux(PO4)7, while Ca8MgEu(PO4)7 (x = 1) is AFE R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c phase. Substitution of Ca2+ with Eu3+ leads to the cation vacancy formation in the M4 position in the structure up to x = 1. The occupancy of the M4 position by Ca2+ for x = 1 is 0 and M4 positions are fully free for Ca8MgEu(PO4)7. This allows rotations of P1O4 tetrahedra and a transformation from the FE to AFE phase. Thus, based on the dielectric loss tangent (tan
c phase. Substitution of Ca2+ with Eu3+ leads to the cation vacancy formation in the M4 position in the structure up to x = 1. The occupancy of the M4 position by Ca2+ for x = 1 is 0 and M4 positions are fully free for Ca8MgEu(PO4)7. This allows rotations of P1O4 tetrahedra and a transformation from the FE to AFE phase. Thus, based on the dielectric loss tangent (tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ) curve, we can give a conclusion about the relation between the occupancy of the M4 position and the FE or AFE nature of the phase transition.
δ) curve, we can give a conclusion about the relation between the occupancy of the M4 position and the FE or AFE nature of the phase transition.
The calculated σbulk for Ca8.61Cd0.70La0.82(PO4)7 (σbulk = 4.01 × 10−6 S cm−1 at 900 K and σbulk = 1.49 × 10−4 S cm−1 at 1270 K) is lower than that for other β-TCP-type compounds: σbulk = 0.8 × 10−2 S cm−1 at 1270 K for Ca7.5M1.5Gd(PO4)7 (M = Zn, Cd),15σbulk = 0.6 × 10−2 S cm−1 at 1270 K for β-TCP;10σbulk = 0.86 × 10−3 S cm−1 at 1200 K for Ca9Bi(VO4)7.30Ea for σbulk is approximated as ∼1.06 eV at 865–1273 K for Ca8.61Cd0.70La0.82(PO4)7 (Fig. 5) and is different than that for other β-TCP-type compounds: Ea ∼ 1.24 eV at 713–873 K for Ca9ZnLi(PO4)7;31Ea ∼ 1.00 eV at 865–1273 K for Ca9Bi(VO4)7.30
According to the bond valence energy landscape (BVEL) analysis,32 the β-TCP-type single crystals enclose a 3D migration network for cations and are characterized by the 3D character of ionic conductivity. In addition to I (… → M3 → M4 → M3′ → M6 → M3″ → …) and II (… → M4 → M2 → M4′→ …) pathways,33 the III pathway has been proposed (… → M2 → M4 → M2′ → M1 → M6 → M1′ → M2″ → …).34 Ca2+ cations can migrate along all pathways through the common faces of polyhedra or between faces of neighboring polyhedra. The M4 positions are involved in all pathways.
We compared the calculated σbulk for Ca8.61Cd0.70La0.82(PO4)7 with σbulk for other β-TCP-type compounds: Ca7.5M1.5Gd(PO4)7 (M = Zn, Cd), β-TCP and Ca9Bi(VO4)7. The M4 sites are free in Ca7.5M1.5Gd(PO4)7 (M = Zn, Cd) and Ca9Bi(VO4)7, while they are partially occupied by Ca2+ cations in the β-TCP and Ca8.61Cd0.70La0.82(PO4)7 structures. The filling of M3 positions with La3+ cations in Ca8.61Cd0.70La0.82(PO4)7 leads to the blocking of the I pathway for the Ca2+ ion migration. Probably the filling of M3 positions with La3+ cations and M4 site occupation by Ca2+ cations in the Ca8.61Cd0.70La0.82(PO4)7 structure are reasons for reducing σbulk.
Conclusions
The Ca8.61Cd0.70La0.82(PO4)7 phase with a β-TCP-related structure was prepared by a high-temperature solid-state reaction in air. Bulk and local cation compositions were determined by ICP-AES and TEM-EDX, respectively. The structure was refined by the Rietveld method in the space group R3c using powder synchrotron X-ray diffraction data. The distribution of Ca2+, Cd2+ and La3+ cations among the sites of the β-TCP-type structure was found. The phase transition temperature, Tc, is 865 ± 10 K. Dielectric measurements confirmed the ferroelectric nature of the phase transition. This reversible, first-order phase transition occurs between a polar ferroelectric β-phase (SG R3c) and a centrosymmetric paraelectric β′-phase (SG R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) c).
c).
Author contributions
The manuscript was prepared with contributions from all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
The data supporting this article have been included as part of the SI. Fractional atomic coordinates, site symmetry, isotropic displacement atomic parameters (Uiso) and site occupation for Ca8.61Cd0.70La0.82(PO4)7 samples from synchrotron SXRD data (Table S1). Selected distances (Å) in Ca8.61Cd0.70La0.82(PO4)7 samples from synchrotron SXRD data (Table S2). The lattice cell parameters of Ca8MLa(PO4)7 (M = Mg, Zn, Ca) and Ca8.61Cd0.70La0.82(PO4)7 (Fig. S1).Supplementary information: fractional atomic coordinates, site symmetry, isotropic displacement atomic parameters (Uiso), site occupation, and BVS values for Ca8.61Cd0.70La0.82(PO4)7 samples from synchrotron SXRD data (Table S1). Selected distances (Å), distortion indices (DIs), and, the tetrahedral distortion parameters Δd and Δα in Ca8.61Cd0.70La0.82(PO4)7 samples from synchrotron SXRD data (Table S2). The lattice cell parameters of Ca8MLa(PO4)7 (M = Mg, Zn, Ca) and Ca8.61Cd0.70La0.82(PO4)7 (Fig. S1). See DOI: https://doi.org/10.1039/d5ce00787a.
CCDC 2473599 contains the supplementary crystallographic data for this paper.35
Acknowledgements
This research was funded by the Russian Science Foundation (RSF Project 24-13-00148), https://rscf.ru/en/project/24-13-00148/. The synchrotron radiation experiments were conducted at the former NIMS beamline (BL15XU) of SPring-8 with the approval of the former NIMS Synchrotron X-ray Station (proposal numbers 2019A4501). We thank Dr. Y. Katsuya and Dr. M. Tanaka for their help at SPring-8.References
- B. Dickens, L. W. Schroeder and W. E. Brown, J. Solid State Chem., 1974, 10, 232–248 CrossRef CAS.
- Y. Huang, C. Jiang, Y. Cao, L. Shi and H. J. Seo, Mater. Res. Bull., 2009, 44, 793–798 CrossRef CAS.
- M. B. Kosmyna, P. V. Mateychenko, B. P. Nazarenko, A. N. Shekhovtsov, S. M. Aksenov, D. A. Spassky, A. V. Mosunov and S. Y. Stefanovich, J. Alloys Compd., 2017, 708, 285–293 CrossRef CAS.
- V. A. Morozov, A. A. Belik, S. Y. Stefanovich, V. V. Grebenev, O. I. Lebedev, G. Van Tendeloo and B. I. Lazoryak, J. Solid State Chem., 2002, 165, 278–288 CrossRef CAS.
- Q. Z. Liu, J. H. Kim, M. J. Cho, S. H. Kim, B. Xu, S. Amirthalingam, N. S. Hwang and J. H. Lee, Mater. Des., 2023, 229, 111914 CrossRef CAS.
- V. V. Titkov, S. Y. Stefanovich, D. V. Deyneko, Y. Y. Dikhtyar, S. M. Aksenov, O. V. Baryshnikova, A. A. Belik and B. I. Lazoryak, J. Solid State Chem., 2019, 279, 120966 CrossRef CAS.
- B. I. Lazoryak, E. S. Zhukovskaya, O. V. Baryshnikova, A. A. Belik, O. N. Leonidova, D. V. Deyneko, A. E. Savon, N. G. Dorbakov and V. A. Morozov, Mater. Res. Bull., 2018, 104, 20–26 CrossRef CAS.
- A. A. Belik, V. A. Morozov, D. V. Deyneko, A. E. Savon, O. V. Baryshnikova, E. S. Zhukovskaya, N. G. Dorbakov, Y. Katsuya, M. Tanaka, S. Y. Stefanovich, J. Hadermann and B. I. Lazoryak, J. Alloys Compd., 2017, 699, 928–937 CrossRef CAS.
- Y. Y. Dikhtyar, D. A. Spassky, V. A. Morozov, D. V. Deyneko, A. A. Belik, O. V. Baryshnikova, I. V. Nikiforov and B. I. Lazoryak, J. Alloys Compd., 2022, 908, 164521 CrossRef CAS.
- A. A. Belik, F. Izumi, S. Y. Stefanovich, A. P. Malakho, B. I. Lazoryak, I. A. Leonidov, O. N. Leonidova and S. A. Davydov, Chem. Mater., 2002, 14, 3197–3205 CrossRef CAS.
- A. El Khouri, M. Elaatmani, G. Della Ventura, A. Sodo, R. Rizzi, M. Rossi and F. Capitelli, Ceram. Int., 2017, 43, 15645–15653 CrossRef CAS.
- R. Rizzi, F. Capitelli, B. I. Lazoryak, V. A. Morozov, F. Piccinelli and A. Altomare, Cryst. Growth Des., 2021, 21, 2263–2276 CrossRef CAS.
- E. S. Zhukovskaya, D. V. Deyneko, O. V. Baryshnikova, A. A. Belik, I. I. Leonidov, A. V. Ishchenko, S. Y. Stefanovich, V. A. Morozov and B. I. Lazoryak, J. Alloys Compd., 2019, 787, 1301–1309 CrossRef CAS.
- A. V. Teterskii, V. A. Morozov, S. Y. Stefanovich and B. I. Lazoryak, Russ. J. Inorg. Chem., 2005, 50, 986–989 Search PubMed.
- A. V. Teterskii, S. Y. Stefanovich, B. I. Lazoryak and D. A. Rusakov, Russ. J. Inorg. Chem., 2007, 52, 308–314 CrossRef.
- D. V. Deyneko, D. A. Spassky, V. A. Morozov, S. M. Aksenov, S. P. Kubrin, M. S. Molokeev and B. I. Lazoryak, Inorg. Chem., 2021, 60, 3961–3971 CrossRef CAS PubMed.
- D. V. Deyneko, V. A. Morozov, E. S. Zhukovskaya, I. V. Nikiforov, D. A. Spassky, A. A. Belik and B. I. Lazoryak, J. Alloys Compd., 2020, 815, 152352 CrossRef CAS.
- S. K. Kurtz and T. T. Perry, J. Appl. Phys., 1968, 39, 3798–3813 CrossRef CAS.
- A. Le Bail, H. Duroy and J. L. Fourquet, Mater. Res. Bull., 1988, 23, 447–452 CrossRef CAS.
- V. Petricek, M. Dusek, L. Palatinus, V. Petrícek, M. Dušek and L. Palatinus, Z. Kristallogr. - Cryst. Mater., 2014, 229, 345–352 CrossRef CAS.
- M. Tanaka, Y. Katsuya and A. Yamamoto, Rev. Sci. Instrum., 2008, 79, 075106 CrossRef.
- M. Tanaka, Y. Katsuya, Y. Matsushita and O. Sakata, J. Ceram. Soc. Jpn., 2013, 121, 287–290 CrossRef CAS.
- Y. Y. Dikhtyar, D. V. Deyneko, K. N. Boldyrev, O. V. Baryshnikova, A. A. Belik, V. A. Morozov and B. I. Lazoryak, J. Lumin., 2021, 236, 118083 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef CAS.
- D. J. Segal, B. P. Santoro and R. E. Newnham, Z. Kristallogr. - Cryst. Mater., 2014, 123, 73–76 Search PubMed.
- D. V. Deyneko, V. A. Morozov, J. Hadermann, A. E. Savon, D. A. Spassky, S. Y. Stefanovich, A. A. Belik and B. I. Lazoryak, J. Alloys Compd., 2015, 647, 965–972 CrossRef CAS.
- P. P. Sahoo and T. N. Guru Row, Inorg. Chem., 2010, 49, 10013–10021 CrossRef CAS PubMed.
- B. Evgenij and M. J. Ross, Impedance Spectroscopy Theory, Experiment, and Applications, John Wiley & Sons, Inc, 2005 Search PubMed.
- R. D. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767 CrossRef.
- B. I. Lazoryak, O. V. Baryshnikova, S. Y. Stefanovich, A. P. Malakho, V. A. Morozov, A. A. Belik, I. A. Leonidov, O. N. Leonidova and G. Van Tendeloo, Chem. Mater., 2003, 15, 3003–3010 CrossRef CAS.
- D. Wei, Y. Huang, J. S. Kim, L. Shi and H. J. Seo, J. Electron. Mater., 2010, 39, 441–446 CrossRef CAS.
- D. V. Deyneko, D. A. Petrova, S. M. Aksenov, S. Y. Stefanovich, O. V. Baryshnikova, S. S. Fedotov, P. C. Burns, M. B. Kosmyna, A. N. Shekhovtsov and B. I. Lazoryak, CrystEngComm, 2019, 21, 1309–1319 RSC.
- I. A. Leonidov, A. A. Belik, O. N. Leonidova and B. I. Lazoryak, Russ. J. Inorg. Chem., 2002, 47, 305–312 Search PubMed.
- S. Y. Stefanovich, D. A. Petrova, V. A. Morozov, E. A. Fortalnova, D. A. Belov, D. V. Deyneko, O. V. Barishnikova, A. A. Belik, B. I. Lazoryak, B. I. Lazoryak, O. V. Barishnikova, A. A. Belik and B. I. Lazoryak, J. Alloys Compd., 2018, 735, 1826–1837 CrossRef CAS.
- CCDC 2473599: Experimental Crystal Structure Determination, 2025, DOI:10.5517/ccdc.csd.cc2p0zj7.
| This journal is © The Royal Society of Chemistry 2026 |