Length-dependent thermopower of self-assembled monolayers of alkanethiolates depends on direction of temperature gradient

Abstract

Self-assembled monolayers of alkanethiols on gold are often used as a benchmark for molecular junctions, particularly as a reference for length-dependence. However, their thermopower decreases with molecular length and is bifurcated. While the bifurcation can be explained by the presence of gateway states, the length-dependence directly contradicts theoretical predictions. We reproduced both experimentally using conical tips of eutectic Ga–In (EGaIn) to form junctions. We then show that this unusual length-dependence arrises from the direction of the applied thermal gradient; when the gold substrate is cooled instead of heated, thermopower increases with length monotonically as predicted by theory. This unprecedented relationship between length-dependence and direction of thermal gradient persists over a very large range of absolute temperature. We therefore ascribe it to shifts in level-alignment induced by the electric field in the leads, which is present experimentally, neglected in theoretical modeling and is determined by the direction of the thermal gradient.

---

Introduction

The thermoelectric effect enables the conversion of waste heat into electrical energy by generating a voltage across a temperature gradient.^1–9 Thermoelectrics based on organic molecules show promise in expanding this technology by enabling the integration and miniaturization of thermoelectric generators to harness low-grade waste heat such as that generated by the human body. The Seebeck coefficient S, measured in V K⁻¹, provides the most direct quantification of the thermoelectric effect, representing the magnitude of induced thermoelectric voltage V per unit temperature difference ΔT across a material.^10–15 Self-assembled monolayers (SAMs) of alkanethiolates provide access to highly insulating molecules by operating in the non-resonant tunneling regime when sandwiched between two electrodes.^16–18 The electrode-SAM-electrode structure in these measurements defines molecular ensemble junctions,¹⁹ in which S is heavily influenced by the energy offset between electrodes and molecular orbitals.²⁰ These offsets are nearly invariant for alkanes, meaning S should vary linearly across a series of alkanes due to the length-dependence of conductivity;^21–25 however, Yoon et al. observed two separate regimes of length-dependence.²⁶ They ascribed this observation to the presence of gateway states that vanish for longer alkane chains.^27–29

Despite serving as a common benchmark for conductance measurements in tunneling junctions due to their straightforward properties, alkanethiols exhibit surprisingly complex thermoelectric properties and a divergence between theory and experiment; theory predicts a uniformly increasing S with increasing molecular length,³⁰ while experimental studies show two different regimes of length-dependence²⁶ and all but two^31,32 show a monotonic decrease in S with increasing length.^33–37 Measurements are typically done in ambient conditions while heating the substrate to which the SAM is bound and holding the top-contact at room temperature because it is straightforward to insert a Peltier device under the substrate and heating avoids issues of condensation. We built an experimental platform, the Rick-9000,³⁸ capable of measuring thermoelectric voltages in SAMs using eutectic Ga–In (EGaIn) top-contacts over a large range of temperatures as illustrated in Fig. 1. Large-area molecular ensemble junctions are formed and measured in a N₂ atmosphere at 0% RH to prevent condensation, with 1% O₂, necessary for EGaIn to form stable tips.^39,40 The SAMs are grown on ultra-flat template-stripped⁴¹ Au (Au^TS) that also serves as the bottom electrode. We validated the Rick-9000 by measuring S of the two electrodes from −120 to 80 °C and then reproducing the unusual length-dependence reported by Yoon et al. near room temperature. We then measured S down to −80 °C, finding that the length-dependence and magnitude of S are both temperature-dependent and that S decreases with length when the substrate is the hot electrode, but increases when the substrate is the cold electrode.

Fig. 1 Schematic of the experimental setup summarizing its capabilities and the series of even-numbered alkanethiolates measured.

Results and discussion

Measuring thermopower with the Rick-9000

The Seebeck coefficient can be determined experimentally by measuring the voltage drop that develops along the applied temperature gradient as shown in eqn (1).

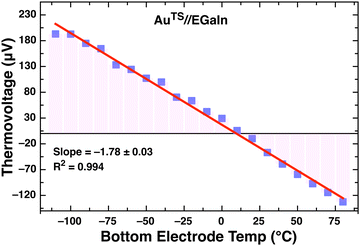
For molecular junctions, this gradient is applied out-of-plane by heating and/or cooling the top and/or bottom electrode(s). The Rick-9000 utilizes conical tips of EGaIn as top-contacts to form and measure junctions⁴² in a controlled atmosphere at 0% RH to prevent condensation; it is capable of operating at absolute temperatures far below the melting point of EGaIn (16 °C). While variable-temperature measurements using EGaIn have been reported, they use cylindrical molds to contain and shape it rather than free-standing tips.^40,43–47 Thus, to ensure that the determination of S over the full temperature range is not impacted by the use of free-standing EGaIn, we contacted Au^TS directly with conical tips of EGaIn and measured the thermovoltage (ΔV) at T_Au^TS = −110 to 80 °C and T_EGaIn = 15 °C. As shown in Fig. 2, 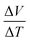is linear across the entire range of temperatures. The resulting value of S = (1.78 ± 0.03) μV K⁻¹ is very close to the literature value for Au of 1.94 μV K⁻¹.⁴⁸ Plots of the temperature and temperature-gradient stabilities are show in Fig. S1 (ESI†).

Fig. 2 Thermal voltage measurement of Au^TS//EGaIn contact across the entire range of 80 to −120 °C.

A large-area ensemble junction is created when a SAM is introduced between the EGaIn and Au^TS. We abbreviate the series of alkanethiolates SCn where n = 2 + 2(m − 1) and 1 ≤ m ≤ 9 for SAMs comprising S(CH₂)_n−1CH₃. Assembled junctions are denoted Au^TS/SCn//Ga₂O₃/Ga–In where “/” denotes a chemisorbed (covalent) interface and “//” denotes a physisorbed (van der Waals) interface. For simplicity we use EGaIn to represent the entire Ga₂O₃/Ga–In interface because the Ga₂O₃ does not play a significant role in charge-transport.⁴⁹ The Au^TS electrode is the bottom-contact (upon which the SAMs are formed) and EGaIn is the top-contact. Using the sign convention of ΔT = T_Au^TS − T_EGaIn, ΔV > 0 when ΔT < 0 and S is determined using eqn (2) where V_Contact is the thermovoltage that develops in the leads and electrodes (e.g.Fig. 2), which is subtracted from the measured voltage V_Meas to isolate the thermovoltage generated by the SAM, ΔV.

The length dependence of thermopower in Au^TS/SCn//EGaIn junctions can be explained using the semiempirical parametric equation eqn (3) proposed by Quek et al.⁵⁰ This equation implies that S_SAM linearly depends on the physical width of the energy barrier (number of carbons, n in SCn) and the slope β^S, which is the rate of thermopower change with n in units of μV Kn⁻¹. It is the thermopower analog to the tunneling decay coefficient β.^51,52 The term S_C is the thermopower of a hypothetical non-shorting junction, where n = 0, which captures the contributions to S that arise from everything other than S_SAM and may vary according to junction platform type and anchoring groups. In principle, β^S depends only on the shape of the energy barrier of the most insulating component in the junction, but as described below, the energy barrier manifests differently depending on the position of the Fermi level E_F. In practice, β^S is an experimentally accessible empirical parameter that captures the relationship between S and the effects n has on the energy barrier.

S_SAM = S_C + nβ^S (3)

Seebeck coefficients of SAMs of alkanethiolates

The thermopower of a molecular junction S can be further separated into the contribution of the anchor group and the molecule theoretically, similarly to the empirical parameters S_C and S_SAM. For example, ab initio modeling predicts that S < 0 for alkylisocyanates, but S > 0 for alkanethiols.³⁰ And it predicts that S hardly varies with length for alkylamines (β^S ≈ 0), varies inversely with length for alkylisocyanates (β^S < 0) and varies positively with length for alkanethiols (β^S > 0). The observed trends in β^S are ultimately determined by the total transmission probability of a junction, which in turn comprises the contributions from interfaces, anchor groups and molecular backbone. Fig. 3 is a single-level Lorentzian depiction of the zero-bias transmission probability⁵³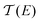 that illustrates how the level-alignment affects the magnitude and length dependence of S which, for non-resonant tunneling, is proportional to (e.g. eqn (S2), ESI†).⁵⁴ For π-conjugated molecules, the molecular orbital gap varies inversely with (conjugation) length, leading to a modest decrease in conductance with length (small β) and large increase in S (large β^S). The molecular orbital gap of alkanes, however, is nearly invariant with length and the transmission probability decreases mainly in the center of the gap with increasing length, resulting in a large drop in conductance (large β) and modest change in S (small β^S). Moreover, the trend in S is highly sensitive to the position of E_F and that the sign of S reverses at E = 0 in Fig. 3. Experimentally, ΔV also switches sign because the type of charge-carrier switches; holes when transport is facilitated by occupied states and electrons when it is facilitated by unoccupied states. This simple picture explains why the magnitudes of β^S and S increase as , while the opposite is true of β.⁵⁵ Selzer et al. applied this principle experimentally, using Bi instead of Au to eliminate gateway states and optimize the level-alignment to achieve large, positive values of S and β^S for alkanethiolates that agreed quantitatively with their model of .³²

Fig. 3 An idealized Lorentzian single-energy level zero-bias transmission probability versus E illustrating how conductance decreases across SCn with a fixed value of E.

While different trends in S have been observed for alkanes with different anchor groups and on different metals and the dependence of S on E_F is explained well by theory, the disagreement between theory and experiment for SAMs of alkanethiolates on Au persists; for alkanes, S ultimately depends on the combination of binding group and metal⁵⁶ and Au–S should produce S > 0 and β^S > 0.³⁰ A common feature of experimental determinations of S is that they are performed at T ≈ 300 K with small values of ΔT achieved by heating the bottom-contact (e.g. Au^TS) and keeping the top-contact equilibrated with ambient temperature. Theoretical modeling and single-molecule junction measurements are also almost always done using symmetrical chemisorbed contacts in which the direction of the temperature gradient does not matter. Measurements, however, are often performed on SAMs of monothiols with chemisorbed bottom-contacts and physisorbed top-contacts.^{26,34,36,37,57–61} The Rick-9000 is capable of both cooling and heating the bottom-contact while heating the top-contact, enabling not only a large range of absolute temperatures, but control over the direction of the thermal gradient (sign of ΔT) with respect to the disparate electrodes and interfaces. As can be seen in Fig. 2, the sign of the thermovoltage switches as the bottom electrode temperature crosses 0 °C, satisfying eqn (1); i.e. the sign of S is determined from the slope, not the sign of the thermovoltage with temperature.

We measured the Seebeck coefficient of Au^TS/SCn//EGaIn junction by computing the slope of −ΔV versus ΔT plots for each SCn SAM. The values of S for each combination of ΔT are summarized in Table S1 (ESI†). The accuracy of these measurements depends on the magnitude of ΔV and its distribution. Similar to previous methods, we obtained S_SAM by treating junctions as thermopower circuits.^20,57,62 In our case, we obtained the S_SAM by correcting for systematic bias, which eliminates all systematic voltage contributions V_Contact according to eqn (2). To validate S_SAM measurements, we measured Au^TS/SCn//EGaIn junctions at bottom-electrode temperatures (T_Au^TS) of 24, 28 and 32 °C while holding the top-contact (T_EGaIn) at 20 °C to reproduce the measurement conditions in ref. 26. The results shown in Fig. 4a perfectly reproduce the two values of β^S for n ≤ 10 and n ≥ 12 as well as the magnitudes of S.

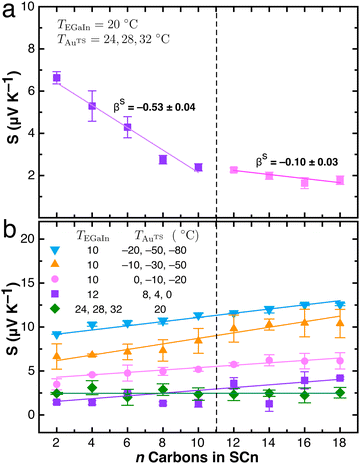Fig. 4 The Seebeck coefficients plotted against number of carbons n in the SAMs of SCn for Au^TS/SCn//EGaIn junctions. The slopes of these plots are the values of β^S that are plotted in Fig. 5. The dashed line between n ≤ 10 and n ≥ 12 is to guide the eye. When T_Au^TS > T_EGaIn, two different values of S < 0 are present for n = 2–10 and n = 12–18, reproducing the findings of ref. 26 (a). When T_Au^TS < T_EGaIn, there is one value of S ≥ 0 for n = 12–18 that increases with |ΔT| (b). The solid lines are linear fits of eqn (3).

Reversal of the length-dependence

As discussed above, theory predicts β^S > 0 for SCn, but β^S < 0 for Au^TS/SCn//EGaIn junctions has been reported previously and now reproduced in Fig. 4a.^26,63 For all alkanethiols and all values of ΔT, S > 1 and the sign of β^S is determined by whether S increases or decreases with increasing n in SCn. The explanation for the presence of two separate regimes of length-dependence is the presence of gap-states created by Au–S bonds that vanish with increasing length of SCn.^29,56 The presence and position of these “gateway” states depends on the binding chemistry as well as the electronic structure of the molecule. They create resonances in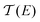 between the resonances associated with the frontier molecular orbitals, reducing the energy gap and affecting the length-dependence of thermopower, β^S, but they do not manifest clearly in the length-dependence of conductance, β.^64,65 The existence of gap-states accounts for the discontinuity in S between n = 10 and 12, but it does not explain why the sign of β^S differs from theoretical predictions. Importantly, Bi/SCn//EGaIn junctions do not exhibit two different regimes of length-dependence and β^S > 0,³² demonstrating that the presence of Au–S bonds leads to the aberrant length-dependence rather than something specific to SAMs, asymmetric contacts or EGaIn.

To probe the length-dependence of the thermopower of SCn further, we measured it at different values of T; specifically, we used the Rick-9000 to cool Au^TS instead of heating it, reversing ΔT. Surprisingly, the length-dependence collapsed into a single line that increases with length (β^S > 0) producing the plots shown in Fig. 4b, which are qualitatively indistinguishable from theoretical predictions.³⁰ The numbers in the legend show the temperatures of the EGaIn top-contacts and Au^TS bottom-contacts. In all cases, T_EGaIn > T_Au^TS and regardless of which electrode was held constant and which was varied, S > 0 and increases with length. There is a small discontinuity between n ≤ 10 and n ≥ 12 (indicated with a dashed line in Fig. 4), but it is within the uncertainty of S.

Linear fits to the data in Fig. 4 yielded the values of β^S shown in Fig. 5 (and Table S2, ESI†) plotted against the average temperature of the electrodes. The values at T = 26 °C show that S crosses zero when ΔT reverses. The magnitude of S then increases very slightly with decreasing temperature, meaning it is nearly constant with the increasing magnitude of ΔT. In general, the magnitude of S should increase with |ΔT|, as is the case in Fig. 4b, but there is no obvious physical reason that S_C (the Y-intercept) or β^S (the slope) should. From Fig. 5 we cannot conclude if β^S is dependent on |ΔT| or if the variation is due to uncertainty or error in the measurements, e.g. it becomes more difficult to control for fluctuating voltage and temperature drops in the leads as Au^TS is cooled far below ambient. As a strictly empirical observation, however, β^S passes through zero, which implies the presence of an underlying continuous variable driving the transition from β^S < 0 to β^S > 0. (Note that in all cases S remains positive, meaning transport is always HOMO-mediated.) Regardless, the restoration of the positive length-dependence at ΔT < 0 is unambiguous and well within the accuracy and precision of the Rick-9000.

Fig. 5 The rate of change of the Seebeck coefficients (β^S) for the SCn series plotted against the average temperature at which the Seebeck coefficients were measured. The dashed lines indicates where the direction of the thermal gradient switched. The red squares (inside dashed lines) show the separate values of β^S for the two different regimes of length-dependence (shown in Fig. 4a) when ΔT > 0; the blue squares (outside dashed lines) show the single value of β^S obtained for the entire SCn series (shown in Fig. 4b) when ΔT < 0.

The role of electric fields in Seebeck measurements

The room-temperature J/V curves of SCn in Au^TS/SCn//EGaIn junctions show a slight asymmetry that is tempting to ascribe to the different work functions of the two electrodes; however, it is an intrinsic property of molecules with asymmetric anchoring groups that is present even in Au/SCn//Au junctions.^66–69 The asymmetry arises because the electric field from the applied bias creates a Stark effect that shifts the positions of frontier molecular orbitals. Since transport is dominated by resonances in from on frontier orbital, this shift effectively pushes the transport level away from E_F at one bias and towards it at the other. This effect is shown schematically in Fig. 6a, where the sign of γ indicates the shift in the position of the frontier orbital that mediates transport E. (The distribution of the density of states should not be confused with the Lorentzian shown in Fig. 3.) While both are affected by Γ, depends on the difference between E_F and the transport level E. For example, if transport is mediated by the HOMO, then it depends on E_HOMO − E_F. can be described using a variety of different models (e.g.Fig. 3).

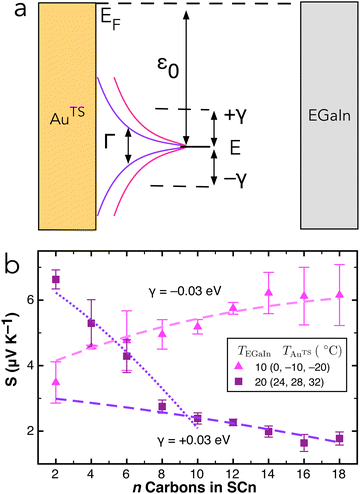Fig. 6 A simplified schematic of how the applied electric field induces a Stark shift in the transport level E (a). Experimental values of S from Fig. 4 plotted with computed values of n using the range of Γ values from ref. 68 at ε = −0.96 eV (dashed; −0.40 eV dotted) with shifts of ±0.03 eV (b).

As discussed above, the sign of the thermovoltage (which is different from thermopower) depends on the sign of ΔT. Fig. 2 shows the thermovoltage decreasing, crossing zero and then becoming negative as the bottom electrode temperature is raised while keeping the top electrode at a constant temperature, i.e. changing the sign of ΔT. Yet the thermopower (Seebeck coefficient) is positive at all values of ΔT. Thus, even though S is measured at zero applied bias, the applied temperature gradient creates an applied electric field that includes V_Contact from the leads that is subtracted when measuring S; i.e. the total bias can be larger the measured thermovoltage of the junction. We hypothesize that this electric field, which changes sign with ΔT (Fig. 2), leads to a shift in energy that is phenomenologically related to the Stark shift that causes current-rectification under applied bias. As noted above, β^S is influenced by the gap-states formed by Au–S bonds, which means they are involved in transport, but their effect on conductance is not resolvable from the tunneling decay coefficient β. We therefore further hypothesize that the Stark effect is more pronounced on the gap-states than the molecular orbitals such that are pushed out of the transport window when ΔT < 0. And because theoretical models do not consider gap-states, β^S comports to theoretical predictions only when ΔT < 0.

A single-level Lorentzian to describe can be combined with the Mott equation (eqn (S2), ESI†) to compute S using Γ to model the length-dependence of alkanes and π-conjugated molecules at different energy offsets.⁶³ Inserting a γ term into this equation yields the fits shown in Fig. 6b (see Section S2.1 for details, ESI†). These fits to experimental data from Fig. 4 account for both directions of ΔT using reasonable values of ε = −0.96 eV and γ = ±0.3 eV. Here, ε is the offset between E_F and the transport level (E in Fig. 3) and −0.96 eV is in good agreement with ref. 68. This model also accounts for the two different values of β^S at ΔT > 0 by treating the gap-states as smaller effective values of ε = −0.40 eV; i.e. the Stark effect acts primarily on the gap-states, pushing them in or out of the transport window. To convert n to Γ, we performed a linear fit to experimental values for Au/SCn//Au junctions.⁶⁸ These values predict larger values of S that our experimental observations. Thus, the computed values of S shown in Fig. 6b are only possible with either very small values of ε or larger values of Γ; we generated the fits using the latter strategy, adding an offset to the intercept of the linear fit of n to Γ. Furthermore, in order to reverse the length-dependence, the magnitude of the shift has to depend on n (see eqn (S3), ESI†), while for the γ parameter (Fig. 6a) for current-rectification is near-constant.⁶⁸ Nonetheless, data for both signs of β^S can be fit by reversing the sign of γ and the two length-dependences for ΔT > 0 can be fit by changing E_F − E; the dashed lines in Fig. 6b are from ε = −0.96 eV, while the dotted line is ε = −0.40 eV, which is compatible with the hypothesis that gateway states are pushed into the transport window and contribute strongly to the transport level for shorter chains. We also stress that the introduction of a γ parameter is only necessary to fit the data for β^S < 0; as is shown in Fig. 3, S increases with length at a fixed ε because 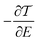increases with length. Therefore, if the gap-states are pushed out of the transport window when ΔT < 0, and transport becomes HOMO-mediated, there does not need to be any Stark effect on the HOMO to explain the behavior of β^S.

Conclusions

We have successfully reproduced the experimental observation that Au^TS/SCn//EGaIn junctions yield two different thermopower length-dependences, both of which exactly oppose theoretical predictions for alkanethiols. Using the Rick-9000, a custom-built experimental setup for measuring thermopower with EGaIn top-contacts, we determined that this unusual experimental observation only occurs when the bottom-contact is heated relative to the top-contact. When the bottom-contact is instead cooled, Au^TS/SCn//EGaIn junctions yield thermopower length-dependences that agree with theoretical predictions across a large range of temperatures.

The most significant finding in this study is that the thermopower of Au^TS/SCn//EGaIn junctions behaves as predicted without any modifications to existing theory. This is an important result because it simultaneously underscores the utility of EGaIn as a platform for studying thermoelectrics in large-area tunneling junctions and for providing fundamental insights into phenomenology that is not captured by theory. We hypothesize that the electric field created by the applied temperature gradient is not innocent and suggest that it should be considered together with the direction of the thermal gradient when modeling junctions with asymmetrical contacts, particularly at technologically-relevant magnitudes of thermal gradients, which are considerably larger than those typically used to study molecular junctions in laboratory settings. We were able to fit the experimental data for the aberrant length-dependence by assuming that the influence of this electric field is length-dependent. Future work is required to develop quantitative agreements between theory and experiment and a more detailed description of the direction of the thermal gradient in asymmetric junctions, but our results reconcile experiment with the unambiguous theoretical prediction that thermopower is positive and increases with lengths for alkanethiolates on gold.

Experimental

Molecules and materials

All reagents were used as supplied unless otherwise specified. All organic solvents were purchased from Sigma Aldrich and Acros Organics. n alkanenethiols (HSCn; n = 2, 4, 6, 8, 10, 12, 14, 16, 18) purity (95 to 99%) were purchased from Sigma Aldrich and Acros Organics (purity 97%). High – purity eutectic gallium indium (EGaIn; 99.99%) was obtained from Sigma Aldrich and used as supplied. All thiol derivatives were stored under N₂ atmosphere and at less 4 °C. Template stripped gold (200 nm) was thermally deposited onto silicon wafer (100 mm in diameter; 1 10 ohm per cm, 525 ± 50 μ per meter thick) by a custom built metal deposition evaporator. Optical adhesive was purchased from Norland(NOA81) and used as supplied.

Preparation and characterization of SAMs

Working in the glove-box (O₂ < 1 ppm, H₂O < 1 ppm), we prepared SAMs following the procedure reported previously.⁷⁰ A 3 mM ethanol anhydrous, 99.9% solution of CnSH was added to a vial. The solution was sealed and degassed by bubbling N₂ through the solution for 10 min. A freshly prepared Au^TS chip was rinsed with pure ethanol and placed in the solution with the exposed metal face up. The vial was then filled with N₂ from the glove-box environment. After 3 h incubation at room temperature, the SAM-bound Au^TS chip was removed from the solution and rinsed by repeatedly dipping the chip into pure ethanol (3 × 1 mL). The solvent on the SAM was then evaporated in air for a few seconds.

Junction preparation and thermopower measurements

A conical tip of EGaIn for use as a top contact was formed by extruding a small droplet of EGaIn from a 15 μL syringe onto the substrate and then raising the syringe. The resulting tip was then lowered onto the SAM to form a junction of approximately 20 μm in diameter. All junction formation and measurements in this work were carried out in an anhydrous 1% O₂ 99% N₂ environment. Thermal gradients were generated by heating the substrate or EGaIn tip and/or cooling the substrate. Voltages for molecular ensemble junctions were measured after allowing the temperature to equilibrate and stabilize (see Fig. S1, ESI†) and reported as V = V_meas − V₀ where V₀ is the thermovoltage measured for the EGaIn//Au^TS junction (without a SAM present). To analyze thermopower of junctions, we followed the previous method reported by Yoon, Segalman et al. Park2019,^20,57

Platform temperature conditions

Thermal voltage (ΔV) is created by holding the top electrode temperature and varying the bottom temperature and vise versa. At ambient conditions, the top electrode temperature (T_EGaIn) was fixed at 20 °C while the bottom electrode temperature (Au^TS) was increased to 24, 28, 32 °C to create ΔT of 4, 8, 12 (Table 1). The absolute temperature T_Abs is defined by taking the average of lowest and highest electrode temperatures i.e. at ambient, the lowest T_EGaIn = 20 + highest T_Au^TS = 32 therefore, (20 + 32 = 52 ÷ 2 = 26 °C ≈ 299 K). At Stage 1, T_Abs of 279 K was achieved using liquid nitrogen (N₂) to lower T_Au^TS to 8, 4, 0 °C while T_EGaIn remained fixed at 12 °C creating ΔT of −4, −8, −12. The stability of electrode temperatures is accounted for in Fig. S1 (ESI†).

Table 1 Description of temperature conditions

	Above 0 °C		Below 0 °C
	Ambient	Stage 1	Stage 2	Stage 3	Stage 4
Temp range	20–32	12–0	10–(−30)	10–(−60)	10–(−90)
T Abs (K)	299	279	263	248	233
Top T (°C)	20	12	10	10	10
Bottom T (°C)	24, 28, 32	8, 4, 0	0, −10, −20	−10, −30, −50	−20, −50, −80
ΔT (°C)	4, 8, 12	4, 8, 12	−10, −20, −30	−20, −40, −60	−30, −60, −90

---

At Stage 2 (T_Abs = 263 K), T_Au^TS was lowered to 0, −10, −20 °C while the T_EGaIn remained fixed at 10° creating ΔT of −10, −20, −30. T_Abs of 248 K at Stage 3, is a further lowering of T_Au^TS to −10, −30, −50 while T_EGaIn remained fixed at 10 °C which created a ΔT of −20, −40, −60 °C. The lowest T_Abs of 233 K at Stage 4, was a further lowering of T_Au^TS to −20, −50, −80 °C while T_EGaIn remained fixed at 10 °C creating a ΔT of −30, −60, −90. The sign + /or − of the gradient is determined from the standard calculation ΔT = T_Au^TS − T_EGaIn. A positive gradient is defined as 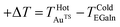and a negative is 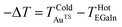. The minimum to maximum bottom electrode temperature is defined in Fig. 2 as temperature range.

Data availability

The data supporting this article have been included as part of the ESI.† The open-source software used to process raw I/V data can be downloaded via this DOI: https://doi.org/10.5281/zenodo.6422417.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge Rick van der Reijd for assistance in the design and construction of the Rick-9000. CLM acknowledges the National Research Foundation South Africa for financial support, grant UID 120208.

References

1. H. Park, Y. Eom, D. Lee, J. Kim, H. Kim, G. Park and W. Kim, High Power Output Based on Watch-Strap-Shaped Body Heat Harvester Using Bulk Thermoelectric Materials, Energy, 2019, 187, 115935.
2. N. Jaziri, A. Boughamoura, J. Müller, B. Mezghani, F. Tounsi and M. Ismail, A Comprehensive Review of Thermoelectric Generators: Technologies and Common Applications, Energy Rep., 2020, 6, 264–287.
3. Z. Tabaie and A. Omidvar, Human Body Heat-Driven Thermoelectric Generators as a Sustainable Power Supply for Wearable Electronic Devices: Recent Advances, Challenges, and Future Perspectives, Heliyon, 2023, 9, e14707.
4. D. Cotfas, A. Enesca and P. Cotfas, Enhancing the Performance of the Solar Thermoelectric Generator in Unconcentrated and Concentrated Light, Renewable Energy, 2024, 221, 119831.
5. D. Luo, Y. Yan, W.-H. Chen and B. Cao, Exploring the Dynamic Characteristics of Thermoelectric Generator Under Fluctuations of Exhaust Heat, Int. J. Heat Mass Transfer, 2024, 222, 125151.
6. W. Yang, C. Jin, W. Zhu, Y. Li, R. Zhang, L. Huang, C. Xie and Y. Shi, Taguchi Optimization and Thermoelectrical Analysis of a Pin Fin Annular Thermoelectric Generator for Automotive Waste Heat Recovery, Renewable Energy, 2024, 220, 119628.
7. D. Yousri, A. Fathy, H. E. Farag and E. F. El-Saadany, Optimal Dynamic Reconfiguration of Thermoelectric Generator Array Using RIME Optimizer to Maximize the Generated Power, Appl. Therm. Eng., 2024, 238, 122174.
8. P. Alegría, L. Catalán, M. Araiz, I. Erro and D. Astrain, Design and Optimization of Thermoelectric Generators for Harnessing Geothermal Anomalies: A Computational Model and Validation With Experimental Field Results, Appl. Therm. Eng., 2024, 236, 121364.
9. R.-E. Dong, A. M. Abed, P. K. Singh, N. Elboughdiri, F. S. Alharbi, S. Alkhalaf, S. M. Bouzgarrou, H. Al Garalleh, A. Elrashidi and S. Islam, Numerical Modeling of a Novel Hybrid System Composed of Tubiform Solid Oxide Fuel Cell and Segmented Annular Thermoelectric Generator (SOFC/SATEG), Appl. Therm. Eng., 2024, 243, 122706.
10. B. Yang, Y. Luo, C. Li, W. Li, C. Sun, Z. Ma, Y. Qian, X. Zeng, Y. Wei, H. Liu, D. Zhang, X. Li, Q. Jiang and J. Yang, Regulation of Electrical Properties via Ferroelectric Polarization for High Performance Sb₂Te₃ Thermoelectric Thin Films, Chem. Eng. J., 2023, 477, 147005.
11. F. Moshtaghi, M. Yousefpour and A. Habibolahzadeh, Electrodeposition and Characterization of Poly-Aniline-Bi-Te-Se-Sb Thin Films With Thermoelectric Properties, Mater. Sci. Eng. B, 2023, 296, 116712.
12. A. Ashfaq, R. S. Almufarij, I. Ragab, Y. Ali, L. G. Alharbe, E. A. Shokralla, S. Alghamdi, E. Alsubhe, O. Albeydani, R. R. Macadangdang and A. Ali, Post-Selenization Induced Structural Phase Transition and Enhanced Thermoelectric Properties in Ag-BiSe₂ Alloy Thin Films, Vacuum, 2024, 219, 112746.
13. Y. Thimont, P. Darnige and A. Barnabé, Development, Experimental and Simulated Performance of Copper Iodide (Gamma-CuI) Uni-Track Thin Film Thermoelectric Modules, Appl. Surf. Sci., 2024, 649, 159071.
14. A. Vora-ud, A. Tuan Thanh Pham, D. Cao Truong, S. Thoawankeaw, H. Thi Lai, T. Bao Nguyen Le, N. M. Q. Tran, M. Insawang, P. Muthitamongkol, M. Horprathum, M. Kumar, S. Park, G. Jeffrey Snyder, T. Seetawan and T. Bach Phan, Transparent-Flexible Thermoelectric Module From in/Ga Co-Doped ZnO Thin Films, Chem. Eng. J., 2023, 465, 142954.
15. M. Liu, F. Li, J. Gao and L. Bu, Study on the Electrodeposition of Bi₂Te₃ Thin Film Thermoelectric Material in Dimethyl Sulfoxide, Int. J. Electrochem. Sci., 2023, 18, 100306.
16. T. Wang and H. Jeng, Enhancements of Thermoelectric Performance Utilizing Self-Assembled Monolayers in Semiconductors, J. Phys. Chem. Solids, 2017, 104, 228–232.
17. A. Ismael, X. Wang, T. L. R. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Tuning the Thermoelectrical Properties of Anthracene-Based Self-Assembled Monolayers, Chem. Sci., 2020, 11, 6836–6841.
18. Z. Chen, S. Qin, J. Jin, Y. Wang, Z. Li, J. Luo, H. Huang, L. Wang and D. Liu, Manipulating Carrier Concentration by Self-Assembled Monolayers in Thermoelectric Polymer Thin Films, ACS Appl. Mater. Interfaces, 2021, 13, 32067–32074.
19. Y. Liu, X. Qiu, S. Soni and R. C. Chiechi, Charge Transport Through Molecular Ensembles: Recent Progress in Molecular Electronics, Chem. Phys. Rev., 2021, 2, 021303-1–021303-40.
20. P. Reddy, S.-Y. Jang, R. A. Segalman and A. Majumdar, Thermoelectricity in Molecular Junctions, Science, 2007, 315, 1568–1571.
21. N. Camillone, T. Y. B. Leung, P. Schwartz, P. Eisenberger and G. Scoles, Chain Length Dependence of the Striped Phases of Alkanethiol Monolayers Self-Assembled on Au(111): An Atomic Beam Diffraction Study, Langmuir, 1996, 12, 2737–2746.
22. V. B. Engelkes, J. M. Beebe and C. D. Frisbie, Length-Dependent Transport in Molecular Junctions Based on SAMs of Alkanethiols and Alkanedithiols: Effect of Metal Work Function and Applied Bias on Tunneling Effciency and Contact Resistance, J. Am. Chem. Soc., 2004, 126, 14287–14296.
23. Y. Zhang, C. Dou and Y. Wang, Single-Molecule Conductance Measurement of Self-Assembled Organic Monolayers Using Scanning Tunneling Spectroscopy in Combination With Statistics Analysis, Appl. Surf. Sci., 2011, 257, 6514–6517.
24. E. Mete, M. Yortanlı and M. F. Danışman, A van der Waals DFT Study of Chain Length Dependence of Alkanethiol Adsorption on Au(111): Physisorption vs. Chemisorption, Phys. Chem. Chem. Phys., 2017, 19, 13756–13766.
25. P. Bhadra and S. W. I. Siu, Effect of Concentration, Chain Length, Hydrophobicity, and an External Electric Field on the Growth of Mixed Alkanethiol Self-Assembled Monolayers: A Molecular Dynamics Study, Langmuir, 2021, 37, 1913–1924.
26. S. Park, N. Cho and H. J. Yoon, Two Different Length-Dependent Regimes in Thermoelectric Large-Area Junctions of N-Alkanethiolates, Chem. Mater., 2019, 31, 5973–5980.
27. C. Zeng, B. Li, B. Wang, H. Wang, K. Wang, J. Yang, J. G. Hou and Q. Zhu, What Can a Scanning Tunneling Microscope Image Do for the Insulating Alkanethiol Molecules on Au(111) Substrates?, J. Chem. Phys., 2002, 117, 851–856.
28. C.-C. Kaun and H. Guo, Resistance of Alkanethiol Molecular Wires, Nano Lett., 2003, 3, 1521–1525.
29. Y. X. Zhou, F. Jiang, H. Chen, R. Note, H. Mizuseki and Y. Kawazoe, First-Principles Study of Length Dependence of Conductance in Alkanedithiols, J. Chem. Phys., 2008, 128, 044704.
30. F. Hüser and G. C. Solomon, From Chemistry to Functionality: Trends for the Length Dependence of the Thermopower in Molecular Junctions, J. Phys. Chem. C, 2015, 119, 14056–14062.
31. S. Guo, G. Zhou and N. Tao, Single Molecule Conductance, Thermopower, and Transition Voltage, Nano Lett., 2013, 13, 4326–4332.
32. T. Frank, S. Shmueli, M. Cohen Jungerman, P. Shekhter and Y. Selzer, Large Seebeck Values in Metal-Molecule-Semimetal Junctions Attained by a Gateless Level-Alignment Method, Nano Lett., 2023, 23, 10473–10479.
33. J. A. Malen, P. Doak, K. Baheti, T. D. Tilley, R. A. Segalman and A. Majumdar, Identifying the Length Dependence of Orbital Alignment and Contact Coupling in Molecular Heterojunctions, Nano Lett., 2009, 9, 1164–1169.
34. J. Jang, P. He and H. J. Yoon, Molecular Thermoelectricity in EGaIn-Based Molecular Junctions, Acc. Chem. Res., 2023, 56, 1613–1622.
35. S. Park, H. R. Kim, J. Kim, B.-H. Hong and H. J. Yoon, Enhanced Thermopower of Saturated Molecules by Noncovalent Anchor Induced Electron Doping of Single Layer Graphene Electrode, Adv. Mater., 2021, 33, 2103177.
36. S. Park, E. Kim, Y. Choi, J. Jang, K. Kwak, M. Cho and H. J. Yoon, Thermoresponse of Odd-Even Effect in N-Alkanethiolate Self-Assembled Monolayers on Gold Substrates, Chem. – Eur. J., 2023, 29, 2203536.
37. P. He, A. H. S. Daaoub, S. Sangtarash, H. Sadeghi and H. J. Yoon, Thermopower in Underpotential Deposition-Based Molecular Junctions, Nano Lett., 2024, 24, 1988–1995.
38. C. L. Mthembu and R. C. Chiechi, Self-Assembly Determines Sign of Seebeck Coeffcient in Tunneling Junctions Comprising Monolayers and Bilayers of Fullerenes, Nano Lett., 2024, 35, 10921–10927.
39. J. R. Barber, H. J. Yoon, C. M. Bowers, M. M. Thuo, B. Breiten, D. M. Gooding and G. M. Whitesides, Influence of Environment on the Measurement of Rates of Charge Transport Across AgTS/SAM//Ga₂O₃/EGaIn Junctions, Chem. Mater., 2014, 26, 3938–3947.
40. M. Carlotti, M. Degen, Y. Zhang and R. C. Chiechi, Pronounced Environmental Effects on Injection Currents in EGaIn Tunneling Junctions Comprising Self-Assembled Monolayers, J. Phys. Chem. C, 2016, 120, 20437–20445.
41. E. A. Weiss, G. K. Kaufman, J. K. Kriebel, Z. Li, R. Schalek and G. M. Whitesides, SiO₂-Templated Formation of Ultraflat Metal Surfaces on Glass, Polymer, and Solder Supports: Their Use as Substrates for Self-Assembled Monolayers, Langmuir, 2007, 23, 9686–9694.
42. R. C. Chiechi, E. A. Weiss, M. D. Dickey and G. M. Whitesides, Eutectic Gallium-Indium (EGaIn): A Moldable Liquid Metal for Electrical Characterization of Self-Assembled Monolayers, Angew. Chem., Int. Ed., 2008, 47, 142–144.
43. M. D. Dickey, R. C. Chiechi, R. J. Larsen, E. A. Weiss, D. A. Weitz and G. M. Whitesides, Eutectic Gallium-Indium (EGaIn): A Liquid Metal Alloy for the Formation of Stable Structures in Microchannels at Room Temperature, Adv. Funct. Mater., 2008, 18, 1097–1104.
44. C. A. Nijhuis, W. F. Reus, J. R. Barber, M. D. Dickey and G. M. Whitesides, Charge Transport and Rectification in Arrays of SAM-Based Tunneling Junctions, Nano Lett., 2010, 10, 3611–3619.
45. C. A. Nijhuis, W. F. Reus, J. R. Barber and G. M. Whitesides, Comparison of SAMBased Junctions With Ga₂O₃/EGaIn Top Electrodes to Other Large-Area Tunneling Junctions, J. Phys. Chem. C, 2012, 116, 14139–14150.
46. S. K. Karuppannan, H. Hongting, C. Troadec, A. Vilan and C. A. Nijhuis, Ultrasmooth and Photoresist-Free Micropore-Based EGaIn Molecular Junctions: Fabrication and How Roughness Determines Voltage Response, Adv. Funct. Mater., 2019, 29, 1904452.
47. Z. Zhao, S. Soni, T. Lee, C. A. Nijhuis and D. Xiang, Smart Eutectic Gallium–Indium: From Properties to Applications, Adv. Mater., 2022, 35, 2203391.
48. A. V. da Rosa and J. C. Ordóñez, Fundamentals of Renewable Energy Processes, Elsevier, 2022.
49. W. F. Reus, M. M. Thuo, N. D. Shapiro, C. A. Nijhuis and G. M. Whitesides, The SAM, Not the Electrodes, Dominates Charge Transport in Metal-Monolayer//Ga₂O₃/Gallium–Indium Eutectic Junctions, ACS Nano, 2012, 6, 4806–4822.
50. S. Y. Quek, H. J. Choi, S. G. Louie and J. B. Neaton, Thermopower of Amine-Gold-Linked Aromatic Molecular Junctions From First Principles, ACS Nano, 2010, 5, 551–557.
51. J. G. Simmons, Electric Tunnel Effect Between Dissimilar Electrodes Separated by a Thin Insulating Film, J. Appl. Phys., 1963, 34, 2581–2590.
52. J. G. Simmons, Generalized Formula for the Electric Tunnel Effect Between Similar Electrodes Separated by a Thin Insulating Film, J. Appl. Phys., 1963, 34, 1793–1803.
53. J. A. Malen, S. K. Yee, A. Majumdar and R. A. Segalman, Fundamentals of Energy Transport, Energy Conversion, and Thermal Properties in Organic–inorganic Heterojunctions, Chem. Phys. Lett., 2010, 491, 109–122.
54. M. Paulsson and S. Datta, Thermoelectric Effect in Molecular Electronics, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 241403.
55. J. Jang, J. W. Jo, T. Ohto and H. J. Yoon, Seebeck Effect in Molecular Wires Facilitating Long-Range Transport, J. Am. Chem. Soc., 2024, 146, 4922–4929.
56. O. Karlström, M. Strange and G. C. Solomon, Understanding the Length Dependence of Molecular Junction Thermopower, J. Chem. Phys., 2014, 140, 044315.
57. S. Park and H. J. Yoon, New Approach for Large-Area Thermoelectric Junctions With a Liquid Eutectic Gallium–Indium Electrode, Nano Lett., 2018, 18, 7715–7718.
58. N. Cho, S. Kang, H. Lee, H. Kang, G. D. Kong and H. J. Yoon, Superexchange Coupling-Induced Enhancements of Thermoelectric Performance in Saturated Molecules, Nano Lett., 2020, 21, 360–366.
59. S. Park, J. Jang, H. Kim, D. I. Park, K. Kim and H. J. Yoon, Thermal Conductance in Single Molecules and Self-Assembled Monolayers: Physicochemical Insights, Progress, and Challenges, J. Mater. Chem. C, 2020, 8, 19746–19767.
60. S. Park, J. W. Jo, J. Jang, T. Ohto, H. Tada and H. J. Yoon, Thermopower in Transition From Tunneling to Hopping, Nano Lett., 2022, 22, 7682–7689.
61. S. Kang, S. Park, H. Kang, S. J. Cho, H. Song and H. J. Yoon, Tunneling and Thermoelectric Characteristics of N-Heterocyclic Carbene-Based Large-Area Molecular Junctions, Chem. Commun., 2019, 55, 8780–8783.
62. S. K. Yee, J. A. Malen, A. Majumdar and R. A. Segalman, Thermoelectricity in Fullerene–Metal Heterojunctions, Nano Lett., 2011, 11, 4089–4094.
63. S. Park, J. Jang and H. J. Yoon, Validating the Mott Formula With Self-Assembled Monolayer (SAM)-Based Large-Area Junctions: Effect of Length, Backbone, Spacer, Substituent, and Electrode on the Thermopower of SAMs, J. Phys. Chem. C, 2021, 125, 20035–20047.
64. J. R. Widawsky, W. Chen, H. Vázquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Length-Dependent Thermopower of Highly Conducting Au–C Bonded Single Molecule Junctions, Nano Lett., 2013, 13, 2889–2894.
65. F. C. Simeone, H. J. Yoon, M. M. Thuo, J. R. Barber, B. Smith and G. M. Whitesides, Defining the Value of Injection Current and Effective Electrical Contact Area for EGaIn-Based Molecular Tunneling Junctions, J. Am. Chem. Soc., 2013, 135, 18131–18144.
66. Y. Ai, A. Kovalchuk, X. Qiu, Y. Zhang, S. Kumar, X. Wang, M. Kühnel, K. Nørgaard and R. C. Chiechi, In-Place Modulation of Rectification in Tunneling Junctions Comprising Self-Assembled Monolayers, Nano Lett., 2018, 18, 7552–7559.
67. Z. Xie, I. Bâldea, Q. V. Nguyen and C. D. Frisbie, Quantitative Analysis of Weak Current Rectification in Molecular Tunnel Junctions Subject to Mechanical Deformation Reveals Two Different Rectification Mechanisms for Oligophenylene Thiolsversusalkane Thiols, Nanoscale, 2021, 13, 16755–16768.
68. Z. Xie, I. Bâldea and C. D. Frisbie, Why One Can Expect Large Rectification in Molecular Junctions Based on Alkane Monothiols and Why Rectification Is So Modest, Chem. Sci., 2018, 9, 4456–4467.
69. S. J. Cho, G. D. Kong, S. Park, J. Park, S. E. Byeon, T. Kim and H. J. Yoon, Molecularly Controlled Stark Effect Induces Significant Rectification in Polycyclic-Aromatic-Hydrocarbon-Terminated N-Alkanethiolates, Nano Lett., 2018, 19, 545–553.
70. G. D. Kong, M. Kim, S. J. Cho and H. J. Yoon, Gradients of Rectification: Tuning Molecular Electronic Devices by the Controlled Use of Different-Sized Diluents in Heterogeneous Self-Assembled Monolayers, Angew. Chem., Int. Ed., 2016, 55, 10307–10311.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03895a

---