Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Viscoplastic photoalignment modeling of asymmetric surface restructuring in azopolymer films by elliptically polarized light†
Nina
Tverdokhleb‡
 a,
Biagio
Audia
a,
Biagio
Audia
 b,
Pasquale
Pagliusi
b,
Pasquale
Pagliusi
 *bc and
Marina
Saphiannikova
*bc and
Marina
Saphiannikova
 *a
*a
aInstitute Theory of Polymers, Leibniz Institute of Polymer Research Dresden, Dresden 01069, Germany. E-mail: grenzer@ipfdd.de
bDepartment of Physics, University of Calabria, Ponte P. Bucci 31C, Rende 87036, CS, Italy. E-mail: pasquale.pagliusi@fis.unical.it
cCNR-Nanotec – Institute of Nanotechnology, S.S. Cosenza, Rende 87036, Italy
First published on 11th November 2024
Abstract
This study aims to test and validate the modern orientation approach of Saphiannikova et al. within the context of viscoplastic photoalignment (VPA) modeling. We focus on the formation of topographical structures under interference patterns featuring spatially varying elliptical polarization. By comparing our VPA modeling results with the asymmetric height profiles reported by Pagliusi et al., we observe a pronounced coupling effect between elliptically polarized light and the anisotropic orientation of azo-chromophores induced by this light. Our findings suggest that the photoinduced birefringent layer deviates the azimuth of elliptically polarized light, which in turn rotates the main axis of the anisotropic orientation in a chiral propagating structure. This self-induced rotation of light polarization influences the spatial dependence of interference profiles as a function of depth within the film. This research not only reinforces the importance of polymer backbone reorientation in azopolymer films but also enhances the predictive capabilities of VPA modeling in designing complex, light-driven topographical structures.
Introduction
Azobenzene (azo) chromophores are famous for their ability to transform the energy of light into the energy of mechanical switching and rotation.1,2 These molecules constitute a great variety of photosensitive materials widely applied in science and modern technologies. The structural changes, electronic properties and optical properties of molecular switches have been studied using density functional theory and molecular dynamics simulation to provide valuable insights into how their performance can be translated to macroscopic information of high interest in the fields of organic electronics, photonics and optomechanics.3–6 A system of small organic molecules with incorporated azo-chromophores can undergo a reversible order–disorder transition in response to the light of different wavelengths.7–10 Polarized visible light has been successfully applied to induce disorder–order transitions, often accompanied by noticeable surface and bulk deformations. Especially, in side-chain azopolymers, the direction of deformation can be precisely controlled by light polarization. For example, the linear polarization dictates deformation along the electric field vector, while circularly polarized light evokes deformations along the light propagation direction.11,12Projected on the thin azopolymer films, the interference pattern of laser light produces a unique periodically varying orientation state of azo-chromophores, which manifests itself as a birefringence grating. If the film is ultrathin (a few nanometers)13 or squeezed between two slides, a large variety of planar optical elements can be produced, depending on the polarization state of interfering beams.14–17 However, if the film is deposited on the substrate slide and has the other surface free, a peculiar phenomenon of periodic superficial restructuring is usually observed. The growth of these surface relief gratings (SRGs) has a strong temporal delay with respect to the birefringence grating. This is clearly seen when a glassy azopolymer film is irradiated with the SP interference pattern (i.e. orthogonal/parallel to the plane of incidence), which inscribes the SRG with a half-periodicity compared to that of the birefringence grating.18–20 The SRG continues to grow after 30 minutes of irradiation, while the amplitude of birefringence grating saturates after one minute.21
It seems that there is no limit nowadays in the variety of inscribed patterns. Inscription with a few different wavelengths of light can be done either simultaneously22 or in a multi-stage procedure,23–25 resulting in beat-like structures. This allows the encoding of structural colours and hierarchical Fourier topographies, with great potential for augmented/virtual reality displays,26 energy harvesting, bio-adhesion and bio-manipulation surfaces.27 Two-dimensional surface restructuring can be achieved by applying the interference pattern of multiple beams,15,28 spatial light modulators16,17,23,29–31 or computer-generated holography.32–34 The latter allows programming the complex irradiation patterns with the intensity and polarization of light varying in each point. Spectacular possibilities are provided when ordered arrays of micropillars are used instead of continuous azopolymer films.35–39
Irradiation of individual objects such as azopolymer micropillars and colloids not only opened the way to new practical applications but also advanced the scientific understanding of this peculiar phenomenon. This is because the effect of light-induced stresses in individual objects is not hindered by the boundary conditions that are always present in continuous films. Combined experimental and modeling studies40–43 on the photodeformation of individual objects helped to confirm that the local direction of optomechanical stresses follows the predictions of the modern orientation approach, as discussed in a recent theoretical review.44 The idea is quite simple: the unique orientation state of azo-chromophores, imposed by the interference pattern, is complemented by the reorientation of polymer backbones. Their mere tendency to reorient along the polarization of light creates a precisely defined field of light-induced stresses that plasticize the material and gradually bring it into its final shape. In this context, the temporal delay between birefringence grating and SRG can be explained by the extremely long rotational time of the polymer backbones compared to azo-chromophores.45
The orientation approach is a powerful tool to predict directional deformations induced by homogeneous irradiation with linearly and circularly polarized laser beams. The theoretical predictions are in excellent agreement with the experimental results, in which the linearly polarized light has been applied by spatially varying its intensity or polarization direction.42,46 On the other side, a vast pool of experiments exists, where the superficial restructuring of azopolymer films has been caused by irradiation with interference patterns of spatially varying elliptical polarization.9–12,28,47 A prominent example is the interference patterns produced by two beams with orthogonal linear (OL) polarization.48 The resulting polarization is characterized by an ellipse with constant orientation of principal axes. However, its ellipticity varies continuously between the two limiting states of linear and circular polarizations. To be able to predict the restructuring of azopolymer films under this and similar interference patterns, it is necessary to develop the orientation approach for the general case of elliptical polarization. This is the first theoretical part of our study. In the second part, we perform viscoplastic photoalignment (VPA) modeling of azopolymer films irradiated by the interference pattern of two beams with the OL polarization. Comparison with the experimental findings of Pagliusi et al.28,48 reveals the presence of additional asymmetry in the light patterns, which we ascribe to the effect of self-induced light polarization rotation. After correcting on this effect, we achieve rather good agreement between the modeling and experimental results. The paper is closed by a discussion on further perspective applications of the orientation approach and its implementation into the VPA modeling.
Theoretical approach
To predict the restructuring of azopolymer films under arbitrary interference patterns, we develop the orientation approach for the general case of elliptical polarization. Recently, we derived an expression for the effective orientation potential induced by the elliptically polarized light (EPL), presented as a superposition of two orthogonally polarized waves propagating along the same axis z:Ex(t) = Ex,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt and Ey(t) = Ey,0 ωt and Ey(t) = Ey,0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ωt ωt | (1) |
The amplitudes of the two waves, Ex,0 and Ey,0, are equal to the principal semi-axes of the polarization ellipse; ω is the angular frequency of the light. Since the trans–cis isomerization events generated by the two linearly polarized waves are independent processes, the effective potential ueff acting on azobenzenes can be presented as a superposition of the potentials produced by these two waves:
ueff = V0(px![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θx + py θx + py![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos2 cos2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θy) θy) | (2) |
Here, V0 is the strength of potential; the weight factors, px and py = 1 − px, are the relative contributions of the linearly polarized waves to the total light intensity. The angles, θx and θy, are formed by the long axis of azobenzenes with the x and y axes. The effective potential Ueff acting on the rigid segments in polymer backbones can be recalculated from ueff as follows:
Ueff = qmV0[px(u·![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) )2 + (1 − px)(u·ŷ)2] )2 + (1 − px)(u·ŷ)2] | (3) |
Here, we take explicitly into account the molecular architecture of azopolymers: the number m of azobenzenes in a rigid segment and their average orientation with respect to the long axis of the rigid segment, described by the shape factor q.41,49 The cosines of angles formed by the long axis of rigid segments with the x and y axes are presented in eqn (3) with the help of unit orientation vectors: u of the segment and ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) and ŷ of the corresponding axes.
and ŷ of the corresponding axes.
A general expression for the 2nd order orientation tensor a2 = 〈uu〉 of rigid segments in the presence of effective potential Ueff can be found in the textbook “Dynamics of Polymeric Liquids” by Bird:50
 | (4) |
Here, δ is the unit tensor and λR is the rotational time of backbone segments in the absence of light. First of all, it is necessary to transform the tensorial relationship (4) into a system of three equations for the diagonal components of a2 (non-diagonal components are equal to zero due to symmetry considerations). This can be done following the derivation steps, as documented in the supporting information of previous studies.41,42 An important intermediate result expresses the rate of change of the orientation state via the products of the polarization tensor ÊÊ with the 2nd and 4th order orientation tensors a2 and a4 = 〈uuuu〉:
 | (5) |
ÊÊ = px![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) ![[x with combining circumflex]](https://www.rsc.org/images/entities/b_char_0078_0302.gif) + (1 − px)ŷŷ + (1 − px)ŷŷ | (6) |
 | (7) |
This system can then be solved numerically using MATLAB or ANSYS software to obtain time evolution of the diagonal components of a2 for the light of changing ellipticity. The light-induced stress tensor is defined by the rate of change of these components:
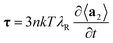 | (8) |
In the general case, the EPL produces a biaxial ordering of azobenzenes and polymer backbones.51 Such an ordering manifests itself through the inequality of three diagonal elements of the 2nd orientation tensor 〈ux2〉 ≠ 〈uy2〉 ≠ 〈uz2〉 and hence the light-induced stress tensor τxx ≠ τyy ≠ τzz.
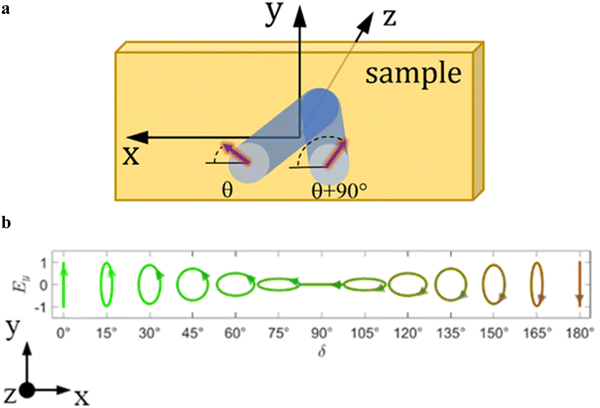
The regions of EPL are present in the interference pattern of two beams with the OL polarization.21,47,48 The orientation of the axes of the polarization ellipse is constant, while its azimuth (i.e., the angle of the major axis and the x axis) takes only two discrete values β0 = θ ± 45°, dependent on the angle θ made by the linear polarization of one of the interfering beams (the other's being at θ + 90°) with the x axis, coinciding with the grating vector direction (Fig. 1a).48 When θ = 45°, the Jones vector of the interference field is
 | (9) |
Fig. 1b shows the appearance of the polarization ellipse for θ = 45° at different positions x inside one period. The principal axes are oriented along x and y directions, whereas the weight factor px = sin2δ is modulated along the x axis. The tip of the electric field vector rotates anti-clockwise (left handed) for δ < 90° and clockwise (right handed) for δ > 90° when looking against the propagation direction z. Polarization patterns for other angles can be obtained by the appropriate rotation of the pattern for θ = 45°:
| ẼOL(θ) = R(θ − 45°)ẼOL(45°) | (10) |
All these patterns are symmetric around δ = 90° and, when implemented in the VPA modeling, produce symmetric gratings (see Fig. S1 in the ESI†). However, it is observed that the patterns for θ = 15° and θ = 30° inscribe highly asymmetric SRGs.28,48 Beside the photoanisotropic gradient force model proposed by Pagliusi et al.,48 a further explanation of the asymmetric SRGs is possible in the framework of the orientation approach, by taking into account the effect of the self-induced rotation of EPL, discovered by Nikolova et al. for thick azopolymer films.52 There, a significant rotation of the polarization azimuth β was observed as a function of the input ellipticity e of the recording beam which propagates through azopolymer films, while inducing a photobirefringence in it. Since the assignment of coordinate axes in ref. 52 is ambiguous and the sense of azimuth rotation controversial, we briefly repeat the calculations here (see the ESI†). The rotation Δβ ≡ β(z,δ) − β0 of the azimuth β with respect to the input value β0, as shown in Fig. 2a, has a common expression for all the polarization patterns of eqn (10):
Δβ = −Γ0,zsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2ε = Γ0,zsin 2ε = Γ0,zsin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2δ 2δ | (11) |
 | (12) |
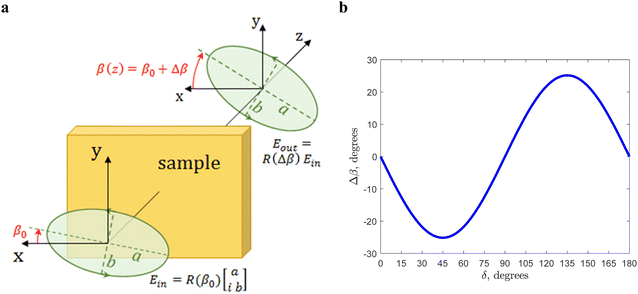 | ||
| Fig. 2 (a) Schematic diagram of an elliptically (right-handed) polarized beam, whose azimuth β rotates while passing through a photobirefringent film. (b) Azimuth rotation angle Δβ calculated at the exit of film versus the phase δ (see eqn (11)) for the OL interference fields (eqn (9) and (10)). A film thickness of h = 6.4 μm, a laser wavelength of λ = 458 nm and a linear birefringence of Δn0 = –0.01 have been considered. Note a change of sign at δ = 90°, when the rotation of the azimuth changes from negative (clockwise) to positive (anti-clockwise), while the polarization changes from left-handed to right-handed. | ||
Assuming that Δn0 < 0, as in most azopolymers and in ref. 48 as well, the positive and negative rotation Δβ occurs for right- (ε > 0) and left- (ε < 0) handed polarization, respectively. The azimuth of the polarization ellipse impinging on the film β0(θ,δ) is corrected by the rotation angle Δβ throughout the film thickness, see Fig. 2b.
Here, the rotation angle of azimuth is calculated with the same parameters as in the experiment:48 the film thickness h = 6.4 μm and the wavelength λ = 458 nm. The value of linear birefringence Δn0 = –0.01 is estimated from previous optical measurements on the same amorphous azopolymer.53 Accordingly, the coordinate system of each finite element is rotated on the angle θXY = θ − 45° + Δβ(z,δ) with respect to the GCS. The regions with linear polarization (i.e., δ = n·90°, n ∈ ![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) ) are not affected, since according to eqn (11) Δβ = 0° for ε = 0. The largest corrections are predicted for the regions with circular polarization (i.e., δ = (n + 1/2)·90°, n ∈
) are not affected, since according to eqn (11) Δβ = 0° for ε = 0. The largest corrections are predicted for the regions with circular polarization (i.e., δ = (n + 1/2)·90°, n ∈ ![[Doublestruck I]](https://www.rsc.org/images/entities/char_e16c.gif) ). At first glance, this appears counterintuitive. However, the azimuth of circularly polarized light is undefined54 and hence large correction angles for regions with the highest ellipticity do not affect the appearance of the pattern.
). At first glance, this appears counterintuitive. However, the azimuth of circularly polarized light is undefined54 and hence large correction angles for regions with the highest ellipticity do not affect the appearance of the pattern.
Since the sense of rotation of the azimuth angle depends on the sign of ellipticity of the input polarization, all the polarization patterns become asymmetric around δ = 90° as they propagate inside the photobirefringent film (see Fig. 3), except the polarization pattern for θ = 45°.
 | ||
| Fig. 3 Polarization patterns corrected by the effect of self-induced light polarization rotation. The angle θ describes the orientation of the interference pattern with respect to the grating vector in the absence of correction (see Fig. 1a). The horizontal axis represents the phase δ in degrees. The transparent lines correspond to the polarization at the film entrance, while the solid lines represent the polarization at the film exit. A film thickness of h = 6.4 μm, a laser wavelength of λ = 458 nm and a linear birefringence of Δn0 = − 0.01 have been considered. | ||
Viscoplastic photoalignment modeling
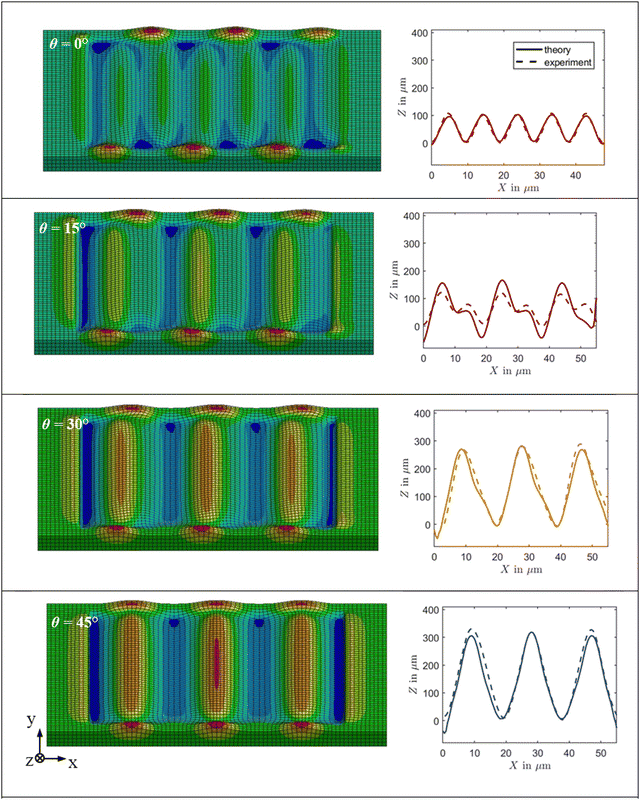
In the following, we present the results of viscoplastic photoalignment modeling of azopolymer films irradiated by the interference pattern of two beams with the OL polarization and compare these results with the experimental findings of Pagliusi et al.48 To ensure negligible intensity modulation and the confinement of the polarization ellipse in the xy plane, as described in eqn (9), the interference angle between the beams in the experiment48 was chosen to be quite small, yielding a period of the optical grating D of about 20 μm.48 Since modeling of the gratings with such a large periodicity is computationally expensive, a smaller optical period of 5 μm is implemented using ANSYS software. Several experimental studies show a significant increase in grating height with an increasing optical period for D < 4 μm.55,56 The viscoplastic modeling of grating growth supports this observation and predicts a saturation of grating growth for optical periods larger than D = 4 μm.46The modeled sample is 20 μm along the x axis, its width along the y axis is 15 μm and its height along the z axis is 1 μm. The illuminated spot contains three optical periods along the grating vector (here the x axis) and is 12.5 μm wide along the translational symmetry axis (here the y axis), see Fig. 4. The material parameters of azopolymers are close to those used in the previous studies: the Young's modulus of 1 GPa and the yield stress of 5 MPa. The light-induced stress is 12.5 MPa. The rotational time of backbone segments λR = 1000 s and the viscosity parameter γ = 0.01 s−1 in the viscoplastic material model (Perzyna) are chosen in such a way to speed up the process of inscription compared to its rate in the experiment. A description of the Perzyna model can be found elsewhere.42,44
Starting from the initial isotropic state, the time evolution of the backbone orientation and the light-induced stress is calculated for the interference patterns characterized by four different angles θ, similar as it was done in the real experiment.48 The modeling is stopped after 50 s, at which moment the gratings reach a significant height comparable to that observed in the experiment of Pagliusi et al.48 after 12 minutes of exposure with an intensity of 200 mW cm−2. A longer modeling of up to 100 s results in the appearance of non-sinusoidal features at the peak positions, also observed in some experiments at longer inscription times.56–59 The overall appearance of superficial deformations is seen in the screenshots on Fig. 4, left. Not only the illuminated spot becomes deformed but also the unilluminated area around. The interference pattern with θ = 0° creates a grating with half the optical period, in which the elongated protrusions (bright green) push the material alternatively along the positive and negative directions of the y axis. This leads to a growth of small peaks (red) in the unilluminated area at the sample borders. The surface deformations are symmetric with respect to the y axis only in the central area of the illuminated spot. The patterns with θ = 15° and 30° produce asymmetric gratings. The peaks in the unilluminated area move in the direction of the protrusion with the larger height. The interference pattern with θ = 45° inscribes a grating with a period equal to the optical one, with the peaks in the unilluminated area positioned symmetrically on each side of the elongated protrusions (orange).
The vertical deformations along the z axis are scanned along the central path of an illuminated area (at y = 7.5 μm) to obtain the modeled height profiles. They are stretched along the x axis by a factor of 3.8 to have the same periodicity D = 19 μm as in the experimentally measured profiles. Additionally, the same vertical rescaling of 0.65 is applied for all profiles to facilitate the comparison with the experimental data, as shown in Fig. 4, right. It is amazing how closely the VPA modeling reproduces the overall shape of experimental profiles, when the polarization patterns are only corrected for the effect of self-induced light polarization rotation (all gratings are symmetric in the absence of correction, see Fig. S1, ESI†). The best agreement is observed for the two sinusoidal gratings inscribed by the interference patterns with θ = 0° and θ = 45°. The symmetric shape of the grating with half the optical period is explained by the sinusoidal dependence of the light-induced strain along the x axis at θ = 0° (see Fig. S2, ESI†).
Also quite a good agreement is obtained for the asymmetric profile at θ = 30°. Here, the VPA modeling only slightly overpredicts an asymmetry of the profile that has a tiny shoulder on the right slope. A shoulder is also seen in the spatial dependence of light-induced strain (Fig. S2, ESI†), but on the left side of the peak. Finally, the results of VPA modelling reproduce rather well the positions of major and minor peaks in the asymmetric profile at θ = 15°. The discrepancy seen on the very right is explained by the edge effects caused by the unilluminated area. The height of major peaks and the depth of valleys are greater in the modeled profiles, which is probably explained by a shorter optical period D = 5 chosen for modeling.
In any case, the predictions of viscoplastic photoalignment modeling can be judged quite satisfactory, especially considering that no fitting parameters are used to reproduce the appearance of asymmetric profiles. To correct all the interference patterns, a common expression (11) is used, which accounts for the effect of self-induced light polarization rotation.
Conclusions
The orientation approach pursued by Saphiannikova et al. delivered recently a couple of decisive proofs41,42,46 that the reorientation of polymer backbones along the light polarization direction should be a main reason for photoinduced deformations in azopolymer films. Our intention in this study was to put this modern orientation approach to the test by applying it in the viscoplastic photoalignment modeling of topographical structures under the interference patterns with spatially varying elliptical polarization. Comparison with the asymmetric SRG profiles measured by Pagliusi et al.,48 reveals a strong coupling effect between the EPL and the anisotropic orientation state of the azo-chromophores. The photoinduced birefringent layer deviates the azimuth of EPL which in turn rotates the main axis of the anisotropic orientation in a supramolecular chiral structure. The described effect of self-induced light polarization rotation makes the interference profiles spatially dependent on the propagation depth within the film. To correct the profiles by this effect, we derive a rather elegant analytical expression that is a function of the wavelength and the linear birefringence value. Good agreement between modeled and experimentally measured profiles can only be achieved by incorporating the resulting 2D polarization state into the VPA modeling.After successful testing of the orientation approach on the asymmetric gratings inscribed by two orthogonally polarized beams, it would be interesting to apply it to even more complex interference patterns. A logical further development would be VPA modeling of two-dimensional topographical structures generated by multi-beam interference with constant resulting intensity.22,28 The challenge here lies in the correct implementation of the 3D polarization state in a sample with a large surface area.
Author contributions
Conceptualization: M. S. and P. P.; methodology: M. S., P. P., N. T. and B. A.; validation: P. P. and N. T.; resources: M. S. and P. P.; data curation: N. T. and B. A.; writing – original draft preparation: M. S. and P. P.; writing – review and editing: M. S., P. P., B. A. and N. T.; visualization: N. T. and P. P.; project administration: M. S. All authors have read and agreed to the published version of the manuscript.Data availability
Processed and published data for this article will be archived with a persistent URL by software DOXIS4 (archive and document management system) hosted at the Leibniz Institute of Polymer Research Dresden.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
M. S. acknowledges financial support from Deutsche Forschungsgemeinschaft under grant GR 3725/10-1. P. P. and B. A. acknowledge support of the microfabrication and characterization facility Beyond-Nano Polo di Cosenza (CNR PON project “Material and processes BEYOND the NANO scale – Beyond-Nano”, cod. PONa3-00362).References
- D. Bléger and S. Hecht, Visible-Light-Activated Molecular Switches, Angew. Chem., Int. Ed., 2015, 54(39), 11338–11349 CrossRef.
- D. Bléger, Orchestrating Molecular Motion with Light – From Single (macro)Molecules to Materials, Macromol. Chem. Phys., 2016, 217(2), 189–198 CrossRef.
- Y. Viero, G. Copie, D. Guérin, C. Krzeminski, D. Vuillaume, S. Lenfant and F. Cleri, High Conductance Ratio in Molecular Optical Switching of Functionalized Nanoparticle Self-Assembled Nanodevices, J. Phys. Chem. C, 2015, 119(36), 21173–21183 CrossRef CAS.
- U. Daswani, U. Singh, P. Sharma and A. Kumar, From Molecules to Devices: A DFT/TD-DFT Study of Dipole Moment and Internal Reorganization Energies in Optoelectronically Active Aryl Azo Chromophores, J. Phys. Chem. C, 2018, 122(26), 14390–14401 CrossRef CAS.
- V. Savchenko, M. Koch, A. S. Pavlov, M. Saphiannikova and O. Guskova, Stacks of Azobenzene Stars: Self-Assembly Scenario and Stabilising Forces Quantified in Computer Modelling, Molecules, 2019, 24(23), 4387 CrossRef.
- V. Savchenko, M. Hadjab, A. S. Pavlov and O. Guskova, Photo-Programmable Processes in Bithiophene-Azobenzene Monolayers on Gold Probed via Simulations, Processes, 2023, 11(9), 2657 CrossRef CAS.
- S. Lee, S. Oh, J. Lee, Y. Malpani, Y. S. Jung, B. Kang, J. Y. Lee, K. Ozasa, T. Isoshima, S. Y. Lee, M. Hara, D. Hashizume and J. M. Kim, Stimulus-Responsive Azobenzene Supramolecules: Fibers, Gels, and Hollow Spheres, Langmuir, 2013, 29(19), 5869–5877 CrossRef CAS.
- M. Koch, M. Saphiannikova and O. Guskova, Cyclic Photoisomerization of Azobenzene in Atomistic Simulations: Modeling the Effect of Light on Columnar Aggregates of Azo Stars, Molecules, 2021, 26(24), 7674 CrossRef CAS.
- S. Santer, Remote control of soft nano-objects by light using azobenzene containing surfactants, J. Phys. D: Appl. Phys., 2018, 51(1), 013002 CrossRef.
- M. Montagna and O. Guskova, Photosensitive Cationic Azobenzene Surfactants: Thermodynamics of Hydration and the Complex Formation with Poly(methacrylic acid), Langmuir, 2018, 34(1), 311–321 CrossRef CAS.
- H. S. Kang, H. T. Kim, J. K. Park and S. Lee, Light-Powered Healing of a Wearable Electrical Conductor, Adv. Funct. Mater., 2014, 24(46), 7273–7283 CrossRef CAS.
- F. Pirani, A. Angelini, F. Frascella, R. Rizzo, S. Ricciardi and E. Descrovi, Light-Driven Reversible Shaping of Individual Azopolymeric Micro-Pillars, Sci. Rep., 2016, 6, 31702 CrossRef CAS.
- N. V. Tabiryan, D. E. Roberts, Z. Liao, J.-Y. Hwang, M. Moran, O. Ouskova, A. Pshenichnyi, J. Sigley, A. Tabirian, R. Vergara, L. De Sio, B. R. Kimball, D. M. Steeves, J. Slagle, M. E. McConney and T. J. Bunning, Advances in Transparent Planar Optics: Enabling Large Aperture, Ultrathin Lenses, Adv. Opt. Mater., 2021, 9(5), 2001692 CrossRef CAS.
- C. Provenzano, P. Pagliusi, A. Mazzulla and G. Cipparrone, Method for artifact-free circular dichroism measurements based on polarization grating, Opt. Lett., 2010, 35(11), 1822–1824 CrossRef.
- U. Ruiz, P. Pagliusi, C. Provenzano, V. P. Shibaev and G. Cipparrone, Supramolecular Chiral Structures: Smart Polymer Organization Guided by 2D Polarization Light Patterns, Adv. Funct. Mater., 2012, 22(14), 2964–2970 CrossRef CAS.
- U. Ruiz, P. Pagliusi, C. Provenzano, K. Volke-Sepúlveda and G. Cipparrone, Polarization holograms allow highly efficient generation of complex light beams, Opt. Express, 2013, 21(6), 7505–7510 CrossRef CAS PubMed.
- U. Ruiz, P. Pagliusi, C. Provenzano, E. Lepera and G. Cipparrone, Liquid crystal microlens arrays recorded by polarization holography, Appl. Opt., 2015, 54(11), 3303–3307 CrossRef.
- T. G. Pedersen, P. M. Johansen, N. C. R. Holme, P. S. Ramanujam and S. Hvilsted, Mean-Field Theory of Photoinduced Formation of Surface Relief in Side-Chain Azobenzene Polymers, Phys. Rev. Lett., 1998, 80, 89–92 CrossRef CAS.
- D. Bublitz, B. Fleck and L. Wenke, A model for surface-relief formation in azobenzene polymers, Appl. Phys. B: Lasers Opt., 2001, 72, 931–936 CrossRef CAS.
- A. Sobolewska and A. Miniewicz, On the inscription of period and half-period surface relief gratings in azobenzene-functionalized polymers, J. Phys. Chem. B, 2008, 112(15), 4526–4535 CrossRef CAS PubMed.
- J. Jelken, C. Henkel and S. Santer, Formation of half-period surface relief gratings in azobenzene containing polymer films, Appl. Phys. B: Lasers Opt., 2020, 126(9), 149 CrossRef CAS.
- B. Audia, C. M. Tone, P. Pagliusi, A. Mazzulla and G. Cipparrone, Hierarchical Fourier Surfaces via Broadband Laser Vectorial Interferometry, ACS Photonics, 2023, 10(9), 3060–3069 CrossRef CAS.
- H. Rekola, A. Berdin, C. Fedele, M. Virkki and A. Priimagi, Digital holographic microscopy for real-time observation of surface-relief grating formation on azobenzene-containing films, Sci. Rep., 2020, 10(1), 19642 CrossRef CAS.
- A. Berdin, H. T. Rekola and A. Priimagi, Complex Fourier Surfaces by Superposition of Multiple Gratings on Azobenzene Thin Films, Adv. Opt. Mater., 2023, 2301597 Search PubMed.
- S. L. Oscurato, F. Reda, M. Salvatore, F. Borbone, P. Maddalena and A. Ambrosio, Large-Scale Multiplexed Azopolymer Gratings with Engineered Diffraction Behavior, Adv. Mater. Interfaces, 2021, 8(21), 2101375 CrossRef CAS.
- Y. Lim, S. J. Hong, Y. Cho, J. Bang and S. Lee, Fourier Surfaces Reaching Full-Color Diffraction Limits, Adv. Mater., 2024, 36(40), 2404540 CrossRef CAS PubMed.
- C. Rianna, A. Calabuig, M. Ventre, S. Cavalli, V. Pagliarulo, S. Grilli, P. Ferraro and P. A. Netti, Reversible Holographic Patterns on Azopolymers for Guiding Cell Adhesion and Orientation, ACS Appl. Mater. Interfaces, 2015, 7(31), 16984–16991 CrossRef CAS PubMed.
- B. Audia, P. Pagliusi, C. Provenzano, A. Roche, L. Oriol and G. Cipparrone, Influence of Photoanisotropies on Light-Controllable Structuration of Azopolymer Surface, ACS Appl. Polym. Mater., 2020, 2(4), 1597–1604 CrossRef CAS.
- A. K. Yetisen, H. Butt, T. Mikulchyk, R. Ahmed, Y. Montelongo, M. Humar, N. Jiang, S. Martin, I. Naydenova and S. H. Yun, Color-Selective 2.5D Holograms on Large-Area Flexible Substrates for Sensing and Multilevel Security, Adv. Opt. Mater., 2016, 4(10), 1589–1600 CrossRef CAS.
- J. Strobelt, D. Stolz, M. Leven, M. Van Soelen, L. Kurlandski, H. Abourahma and D. J. McGee, Optical microstructure fabrication using structured polarized illumination, Opt. Express, 2022, 30(5), 7308–7318 CrossRef CAS PubMed.
- J. Strobelt, M. Van Soelen, H. Abourahma and D. J. McGee, Supramolecular Azopolymers for Dynamic Surface Microstructures Using Digital Polarization Optics, Adv. Opt. Mater., 2023, 11(8), 2202245 CrossRef CAS.
- S. L. Oscurato, M. Salvatore, F. Borbone, P. Maddalena and A. Ambrosio, Computer-generated holograms for complex surface reliefs on azopolymer films, Sci. Rep., 2019, 9, 6775 CrossRef.
- S. L. Oscurato, F. Reda, M. Salvatore, F. Borbone, P. Maddalena and A. Ambrosio, Shapeshifting Diffractive Optical Devices, Laser Photonics Rev., 2022, 16(4), 2100514 CrossRef.
- F. Reda, M. Salvatore, M. Astarita, F. Borbone and S. L. Oscurato, Reprogrammable Holograms from Maskless Surface Photomorphing, Adv. Opt. Mater., 2023, 11(21), 2300823 CrossRef CAS.
- S. Lee, H. S. Kang, A. Ambrosio, J. K. Park and L. Marrucci, Directional Superficial Photofluidization for Deterministic Shaping of Complex 3D Architectures, ACS Appl. Mater. Interfaces, 2015, 7(15), 8209–8217 CrossRef CAS.
- S. L. Oscurato, F. Borbone, P. Maddalena and A. Ambrosio, Light-driven wettability tailoring of azopolymer surfaces with reconfigured three-dimensional posts, ACS Appl. Mater. Interfaces, 2017, 9(35), 30133–30142 CrossRef CAS.
- F. Pirani, A. Angelini, S. Ricciardi, F. Frascella and E. Descrovi, Laser-induced anisotropic wettability on azopolymeric micro-structures, Appl. Phys. Lett., 2017, 110(10), 101603 CrossRef.
- A. Puliafito, S. Ricciardi, F. Pirani, V. Čermochová, L. Boarino, N. De Leo, L. Primo and E. Descrovi, Driving Cells with Light-Controlled Topographies, Adv. Sci., 2019, 6(14), 1801826 CrossRef.
- I. K. Januariyasa, F. Borbone, M. Salvatore and S. L. Oscurato, Wavelength-Dependent Shaping of Azopolymer Micropillars for Three-Dimensional Structure Control, ACS Appl. Mater. Interfaces, 2023, 15(36), 43183–43192 CrossRef CAS PubMed.
- S. Loebner, N. Lomadze, A. Kopyshev, M. Koch, O. Guskova, M. Saphiannikova and S. Santer, Light-Induced Deformation of Azobenzene-Containing Colloidal Spheres: Calculation and Measurement of Opto-Mechanical Stresses, J. Phys. Chem. B, 2018, 122(6), 2001–2009 CrossRef CAS.
- B. Yadav, J. Domurath, K. Kim, S. Lee and M. Saphiannikova, Orientation Approach to Directional Photodeformations in Glassy Side-Chain Azopolymers. The, J. Phys. Chem. B, 2019, 123(15), 3337–3347 CrossRef CAS PubMed.
- S. Loebner, B. Yadav, N. Lomadze, N. Tverdokhleb, H. Donner, M. Saphiannikova and S. Santer, Local Direction of Optomechanical Stress in Azobenzene Containing Polymers During Surface Relief Grating Formation, Macromol. Mater. Eng., 2022, 31, 2100990 CrossRef.
- B. Yadav, Modeling optical inscription of complex surface patterns in azobenzene-containing materials, PhD thesis, TU Dresden, Dresden, 2023 Search PubMed.
- M. Saphiannikova, V. Toshchevikov and N. Tverdokhleb, Optical deformations of azobenzene polymers: orientation approach vs. other concepts, Soft Matter, 2024, 20, 2688–2710 RSC.
- J. M. Ilnytskyi, V. Toshchevikov and M. Saphiannikova, Modeling of the photo-induced stress in azobenzene polymers by combining theory and computer simulations, Soft Matter, 2019, 15(48), 9894–9908 RSC.
- N. Tverdokhleb, S. Loebner, B. Yadav, S. Santer and M. Saphiannikova, Viscoplastic Modeling of Surface Relief Grating Growth on Isotropic and Preoriented Azopolymer Films, Polymers, 2023, 15(2), 463 CrossRef CAS PubMed.
- G. Cipparrone, P. Pagliusi, C. Provenzano and V. P. Shibaev, Polarization Holographic Recording in Amorphous Polymer with Photoinduced Linear and Circular Birefringence, J. Phys. Chem. B, 2010, 114(27), 8900–8904 CrossRef CAS.
- P. Pagliusi, B. Audia, C. Provenzano, M. Piñol, L. Oriol and G. Cipparrone, Tunable Surface Patterning of Azopolymer by Vectorial Holography: The Role of Photoanisotropies in the Driving Force, ACS Appl. Mater. Interfaces, 2019, 11(37), 34471–34477 CrossRef CAS.
- V. Toshchevikov, M. Saphiannikova and G. Heinrich, Microscopic Theory of Light-Induced Deformation in Amorphous Side-Chain Azobenzene Polymers, J. Phys. Chem. B, 2009, 113(15), 5032–5045 CrossRef CAS PubMed.
- R. B. Bird; C. Curtiss; R. C. Armstrong and O. Hassager, Dynamics of polymeric liquids. Wiley-Interscience, New York, 1987 Search PubMed.
- V. Toshchevikov and M. Saphiannikova, Photo-Ordering and Deformation in Azobenzene-Containing Polymer Networks under Irradiation with Elliptically Polarized Light, Processes, 2023, 11(1), 129 CrossRef CAS.
- L. Nikolova, L. Nedelchev, T. Todorov, T. Petrova, N. Tomova, V. Dragostinova, P. S. Ramanujam and S. Hvilsted, Self-induced light polarization rotation in azobenzene-containing polymers, Appl. Phys. Lett., 2000, 77(5), 657–659 CrossRef CAS.
- J. Royes, C. Provenzano, P. Pagliusi, R. M. Tejedor, M. Piñol and L. Oriol, A Bifunctional Amorphous Polymer Exhibiting Equal Linear and Circular Photoinduced Birefringences, Macromol. Rapid Commun., 2014, 35(21), 1890–1895 CrossRef CAS.
- R. M. A. Azzam and N. M. Bashara, Ellipsometry and Polarized Light. North-Holland Publishing Company, New York, 1977 Search PubMed.
- Y. Lim, B. Kang, S. J. Hong, H. Son, E. Im, J. Bang and S. Lee, A Field Guide to Azopolymeric Optical Fourier Surfaces and Augmented Reality, Adv. Funct. Mater., 2021, 31(39), 2104105 CrossRef CAS.
- F. Reda, M. Salvatore, F. Borbone, P. Maddalena and S. L. Oscurato, Accurate Morphology-Related Diffraction Behavior of Light-Induced Surface Relief Gratings on Azopolymers. ACS, Mater. Lett., 2022, 4(5), 953–959 CAS.
- O. Kulikovska; K. Gharagozloo-Hubmann and J. Stumpe, In Polymer surface relief structures caused by light-driven diffusion, Conference on Organic Photorefractive and Photosensitive Materials for Holographic Applications, Seattle, Wa, Jul 09; Seattle, Wa, 2002; pp. 85–94.
- E. Schab-Balcerzak, M. Siwy, M. Kawalec, A. Sobolewska, A. Chamera and A. Miniewiez, Synthesis, Characterization, and Study of Photoinduced Optical Anisotropy in Polyimides Containing Side Azobenzene Units, J. Phys. Chem. A, 2009, 113(30), 8765–8780 CrossRef CAS.
- G. Pawlik, A. Miniewicz, A. Sobolewska and A. C. Mitus, Generic stochastic Monte Carlo model of the photoinduced mass transport in azo-polymers and fine structure of Surface Relief Gratings, Europhys. Lett., 2014, 105(2), 6 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available: The supporting information consists of two sections: I. Calculating the rotation of polarization azimuth. II. Details of ANSYS implementation. See DOI: https://doi.org/10.1039/d4tc04226c |
| ‡ Present address: Institute for Materials Science, TU Dresden, Dresden 01062, Germany. |
| This journal is © The Royal Society of Chemistry 2025 |