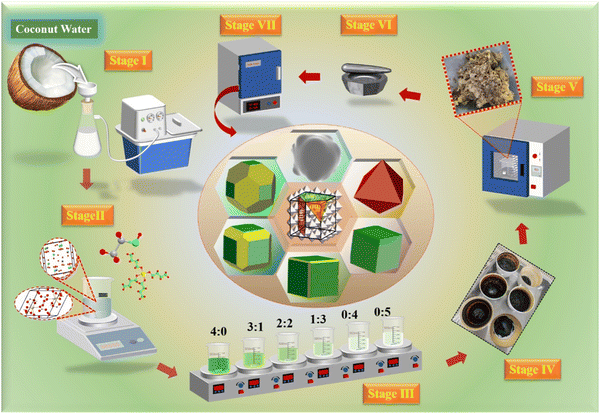
Crystal facet tailoring: a promising pathway toward high-performance Y2/3Cu3Ti4O12 thermosensitive ceramics†
Yaxin
Wei
ab,
Wenyuan
Li
ac,
Jia
Chen
ac,
Jianan
Xu
ac,
Kai
Li
d,
Hanao
Deng
a,
Ke
Zhao
b,
Yahong
Xie
 b,
Aimin
Chang
a and
Bo
Zhang
b,
Aimin
Chang
a and
Bo
Zhang
 *a
*a
aState Key Laboratory of Functional Materials and Devices for Special Environmental Conditions, Xinjiang Key Laboratory of Electronic Information Materials and Devices, Xinjiang Technical Institute of Physics & Chemistry of CAS, Urumqi, 830011, China. E-mail: zhangbocas@ms.xjb.ac.cn
bKey Laboratory of Oil & Gas Fine Chemicals, Ministry of Education and Xinjiang Uyghur Autonomous Region, State Key Laboratory of Chemistry and Utilization of Carbon Based Energy Resources, College of Chemical Engineering and Technology, Xinjiang University, Urumqi, 830017, P. R. China
cCenter of Materials Science and Optoelectronics Engineering, University of Chinese Academy of Sciences, Beijing, 100049, China
dChangchun Institute of Applied Chemistry of CAS, Changchun 130022, China
First published on 21st October 2024
Abstract
Y2/3Cu3Ti4O12 (YCTO) thermosensitive ceramics with high-sensitivity and fast-response characteristics have potential applications in the next generation of smart electronic devices. However, the narrow response temperature region and instability at high temperatures are problems that need to be urgently solved. Herein, we proposed a strategy of crystal facet tailoring using a bioprotein method. We utilized natural coconut water as a chelating agent to customize the {110} crystal facets of YCTO grains. The transformation of {hkl} crystal facets is the key to optimizing the thermosensitive properties of YCTO ceramics. This tailoring behavior can be understood as the result of the synergistic effect of the thermodynamic and kinetic mechanisms of crystal growth. Active ions in coconut water can compensate for cationic defects in the YCTO lattice and play a positive role in improving sintering activity, crystallinity and electrical properties. In addition, the dense microstructure and suppression of the double-exchange effect of ion pairs are important topics to prevent resistivity drift. This work can provide a reference for the modification of thermosensitive materials via crystal facet engineering.
1. Introduction
The shape customization and controllable synthesis of micro-/nanocrystals with different index crystal facets are interesting and challenging topics for basic science and potential applications.1–3 Many application techniques for polyoxides in the field of negative temperature coefficient (NTC) thermistors depend on the surface structure and characteristics of the material.4 Relying on surface/interface engineering (especially at the atomic level) to exploit their semiconducting properties may be an effective means and necessary tool in the future. Therefore, precisely customizing or adjusting the physico-chemical properties of semiconductor materials by controlling their morphology has become an important strategy in optimizing the reactivity and stability of sensitive devices.5,6In recent years, researchers have significantly intensified their investigations of metal oxide polyhedral micro-/nanostructures. Many novel high-performance micro-/nano materials have been developed by elucidating the relationship between crystal facets and properties.7,8 For example, Cu2O with exposed {110} facets demonstrates greater activity in the heterogeneous copper-catalyzed azide–alkyne cycloaddition (CuAAC) reaction than Cu2O with exposed {100} and {111} facets.9 SnO2 nanoflowers assembled by {102} and {113} facets with a high refractive index can be obtained after the hydrothermal treatment of a tin precursor with NaF, which can be an effective strategy to improve its sensitivity.10 In addition, ZnO nano-wires, ZnS nano-ribbons, WO3 octahedra, and Cu2O hexahedra exposed to specific crystal facets are highly sensitive to surface atomic structures. Remarkable results have been achieved in the application of photocatalysis, gas sensors, lithium-ion battery anode materials, supercapacitors, field emitters, and electrochromic devices by controlling and adjusting the exposed crystal facet of materials.11–14 These exciting optimizations are mainly attributed to the induced anisotropic growth of materials and subsequently suppressing defects by improving the preparation process and crystal quality. However, previous studies have predominantly focused on advancements related to simple oxides and noble metal nanocrystals.15–17 Unfortunately, except for natural ores, most studies have focused on the controlled growth of these oxide powders. A comprehensive understanding of facet transformations in ceramic grains remains less advanced compared to that of single crystal materials and simple oxides. Richer and more enigmatic structure–property relationships may exist for polyoxides with more complex bonding structures. However, no breakthroughs have been seen in this field, especially in rigid electronic ceramics.18
To meet the growing market and industry demand for NTC thermistors with a wide temperature range and high stability. For decades, doping and compositing have been considered as the most commonly used modification methods in the study of electronic ceramic materials.4 Subramanian et al. first reported ACu3Ti4O12 (ACTO, where A = Y2/3, La2/3, Sr, Ca, etc.) materials with a perovskite-like structure, which showed fascinating potential in thermistors due to a large B-value. It has shown broad application prospects for temperature measurement and control in household appliances, even in extreme environments such as space technology and deep-sea exploration.19–21 YCTO, with a large A-site ionic radius and flexible structure, is considered to be one of the most promising NTC thermistor materials. Its unique feature is that Y3+ occupies the A site, resulting in a natural 1/3 cation vacancy in the crystal lattice.22 Perovskite-like ceramics display various types of defects at grain boundaries and also contain randomly oriented domains within the grains.23,24 It is increasingly recognized that these imperfect structures (i.e., defects) may function as charge recombination centers that trap free charges, subsequently leading to diminished device performance. At the same time, defects located on the surface or within the grain typically result in rough and complex geometries.25,26 The significant difference in crystal quality and morphology indicates that YCTO ceramics are yet to reach their full potential.27 If YCTO ceramics have high-quality grains with well-defined crystal planes, their thermal stability and response temperature range could approach the theoretical limits. However, these types of work seem to have reached the ceiling of performance optimization. Also, no systematic evaluation has been found regarding the deterioration of the thermosensitive properties and thermal stability of the YCTO ceramics. The resistance drifts due to active variant-valence cation and copper-based oxide migration have also not been fully addressed.24,28,29 Therefore, it is difficult to evaluate their practicality. For NTC materials exposed to high-temperature and oxygen-rich environments for a long time, developing a highly chemically stable antioxidant material remains a huge challenge. Notably, conventional hydrocarbon organic precursors (e.g., ethylene glycol and pyrrolidone) are mostly based on petroleum-based polymers, which are often difficult to degrade. The use of low-toxicity coconut water during the experiment can reduce the volatilization of organic compounds produced by petroleum-based polymers at high temperatures. Coconut water is rich in metal minerals that are naturally present in the electrolyte solution in the form of inorganic salts. Therefore, coconut water has the conditions to create a stable complexation environment for metal ions.
In this study, a low-toxicity and eco-friendly bioprotein method was reported (Fig. 1). Its technical features were the use of bone glue as a polymer and natural coconut water as a chelating agent. The main challenge is to use coconut water as a variable to control the ordered growth of crystal planes, thereby achieving the adjustment of {110} crystal facets and crystal facet transformation between {110} and {100}. Finally, the cubic grains for YCTO were obtained, which seems to be a breakthrough for complex quaternary oxides. Additionally, we briefly discussed the identification of YCTO index crystal facets and the evolution of their geometric morphology. We also summarized the key factors influencing crystal plane tailoring and elucidated the underlying tailoring mechanisms. We found that the {hkl} crystal facet transformation can effectively adjust and enlarge the temperature response range (25–600 °C) of YCTO ceramics. In the aging test under repeated thermal shock, the aging coefficient of YCTO-50% ceramics was as low as 0.1%. We anticipate that crystal surface engineering can bring solutions and references to the challenges faced by NTC thermistors in terms of stability and temperature response range.
2. Results and discussion
2.1. Powder particle size and thermal analysis
YCTO samples with deionized water and coconut water proportions of 100%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0%, 75%
0%, 75%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 25%, 50%
25%, 50%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 50%, 25%
50%, 25%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 75%, 100%
75%, 100%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0% and 125%
0% and 125%![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
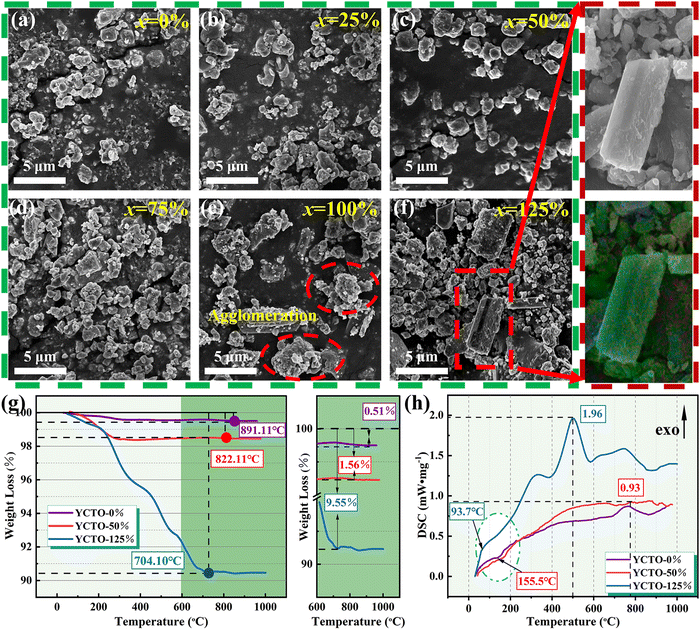
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0% were labeled as YCTO-x% (x = 0, 25, 50, 75, 100, 125). Fig. 2a–f shows the microstructure of YCTO powders synthesized by the bioprotein method in different proportions of coconut water. The particle size increases with increasing proportion of coconut water (Fig. S1a–f, ESI†). An increase in the concentration of reactants leads to an increase in the probability of collisions between atoms. As the temperature rises, the coalescence rate of particles is accelerated, which may lead to the formation of spontaneously aggregated particles (Fig. 2e).30,31 It is worth noting that particles with rod-shaped characteristics are scattered in the powder, which has never been found in previous studies (Fig. 2f). The results of elemental analysis were greater than the experimental design, which may be due to some soluble ions entering the YCTO powder after the evaporation of coconut water at high temperatures (Fig. S2, ESI†). As the proportion of coconut water increases, the TG curve shifts to the lower temperature region (Fig. 2g). The complexing environment provided by coconut water and bone glue reduces the active sites for cationic reactions, resulting in the TG curve of YCTO-125% powder stopping first at 704.10 °C, indicating that the increase in coconut water at high temperatures causes the powder exhibiting higher sintering activity.32 Notably, the slope of the DSC curves for the YCTO-125% powders around 93.7 °C is much larger than that of other samples, which confirms that coconut water is beneficial to promote the increase in reaction rate (Fig. 2h). These observations indicate a strong correlation between the proportion of coconut water and the solid solution and pyrolysis processes of YCTO materials. The active ions in coconut water are believed to be sintering aids that accelerate the collision and diffusion of ions, thereby lowering the reaction temperature. This is similar to the experimental phenomenon of ion doping in the solid-phase method.33,34
0% were labeled as YCTO-x% (x = 0, 25, 50, 75, 100, 125). Fig. 2a–f shows the microstructure of YCTO powders synthesized by the bioprotein method in different proportions of coconut water. The particle size increases with increasing proportion of coconut water (Fig. S1a–f, ESI†). An increase in the concentration of reactants leads to an increase in the probability of collisions between atoms. As the temperature rises, the coalescence rate of particles is accelerated, which may lead to the formation of spontaneously aggregated particles (Fig. 2e).30,31 It is worth noting that particles with rod-shaped characteristics are scattered in the powder, which has never been found in previous studies (Fig. 2f). The results of elemental analysis were greater than the experimental design, which may be due to some soluble ions entering the YCTO powder after the evaporation of coconut water at high temperatures (Fig. S2, ESI†). As the proportion of coconut water increases, the TG curve shifts to the lower temperature region (Fig. 2g). The complexing environment provided by coconut water and bone glue reduces the active sites for cationic reactions, resulting in the TG curve of YCTO-125% powder stopping first at 704.10 °C, indicating that the increase in coconut water at high temperatures causes the powder exhibiting higher sintering activity.32 Notably, the slope of the DSC curves for the YCTO-125% powders around 93.7 °C is much larger than that of other samples, which confirms that coconut water is beneficial to promote the increase in reaction rate (Fig. 2h). These observations indicate a strong correlation between the proportion of coconut water and the solid solution and pyrolysis processes of YCTO materials. The active ions in coconut water are believed to be sintering aids that accelerate the collision and diffusion of ions, thereby lowering the reaction temperature. This is similar to the experimental phenomenon of ion doping in the solid-phase method.33,34
2.2. XRD analysis
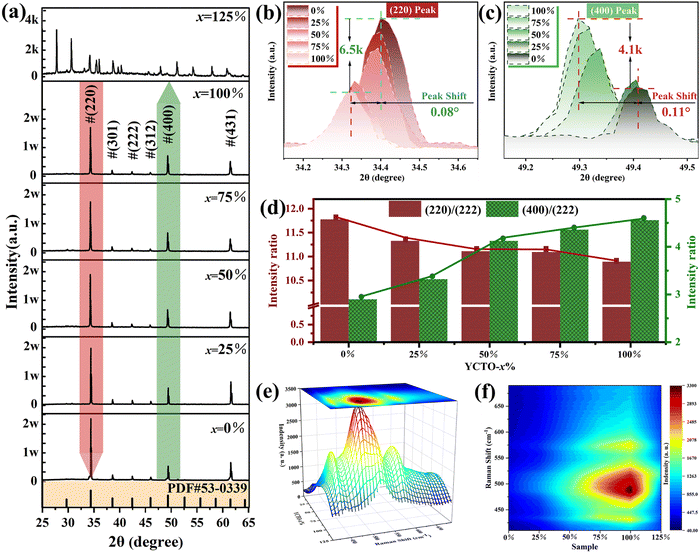
Fig. 3a shows the XRD patterns of ceramics sintered at 940 °C. The diffraction peaks of YCTO-x% (x ≤ 100) ceramics can be indexed as the body-centered cubic (BCC) YCTO phase (JCPDS no. 53-0339). This indicates that YCTO ceramics are successfully synthesized through the bioprotein method without the formation of an impurity phase, and trace active ions in coconut water (25 ≤ x ≤ 100) do not cause damage to the crystal structure. It is noteworthy that the XRD diffraction peaks show a significant deviation when x = 125, which does not match the standard spectrum (Fig. S4, ESI†). Interestingly, the positions of the (220) and (400) peaks are shifted towards lower angles with increasing coconut water (Fig. 3b and c). This confirms that perovskite-like crystals with greater structural flexibility provide sufficient host space for active ions in coconut water to enter the lattice and form solid solutions. Although active ions do not alter the structure of perovskite-like phases, they inevitably lead to the generation of lattice micro-strain. Similar phenomena have also been observed in previous studies.27,32In Fig. 3b and c, the (220) and (400) diffraction peaks located around 39.4° and 49.3°were magnified, respectively. It is worth noting that as coconut water increases, the diffraction intensity of the (220) peak gradually decreases (about 6500 counts), while the diffraction intensity of the (400) peak gradually increases (about 4100 counts). From the relative intensity shown in Fig. 3d, it is found that as the coconut water increases, (220)/(222) decreases while (400)/(222) increases, indicating that the changes in peak intensities (hk0) and (h00) are based on the results of the full XRD spectrum. However, the preferential growth of the crystal facet may cause a relative change in diffraction intensity.35 Coconut water promotes the contact of the metal nitrate with the active ions and preferentially arranges them along the preferred orientation, while the growth of the a (a = b = c) axis leads to the gradual expansion of the crystal structure.36 To obtain more convincing results, refinement of XRD was performed (Fig. S5a–e, ESI†). The results show that the lattice constant significantly increases with the increasing coconut water (Fig. S5f, ESI†). As shown in Fig. 3e, f and Fig. S6 (ESI†), the strong vibration mode at 491 cm−1 (Eg) with increasing coconut water indicates a strong interaction between Ti and O, leading to an increase in the local ordering of YCTO.37 Ultimately, the increase in atomic density leads to an increase in the percentage of {h00} crystal facets exposed in the body-centered cubic structure.36 The observation of its microstructure also confirms this change, and a more detailed analysis will be conducted in the following section.
2.3. Microstructure
As shown in Fig. 4a–f, the YCTO-x% ceramic is assembled from different polyhedral grains. Unlike other ceramics that exhibit multi-peak distributions, the distribution curve of the YCTO-50% sample tends to be a single peak with a Gaussian distribution, showing better consistency (Fig. S7a–f, ESI†). From the EDS elemental analysis in Fig. 4a–f, it is found that trace amounts of active ions are also found in the ceramics, which is consistent with the elemental analysis of the rod-shaped particles (Fig. S2, ESI†). The proportion of active ions in YCTO-x% ceramics increases with increasing coconut water while the density first increases and then decreases (Table S1, ESI†). This indicates that the presence of an appropriate number of active ions in the YCTO lattice may contribute to the densification of ceramics. The schematic in Fig. 4g depicts the solid solution process. It can be seen that active ions gradually enter the cationic vacancies or interstitial sites in the YCTO lattice with increasing coconut water.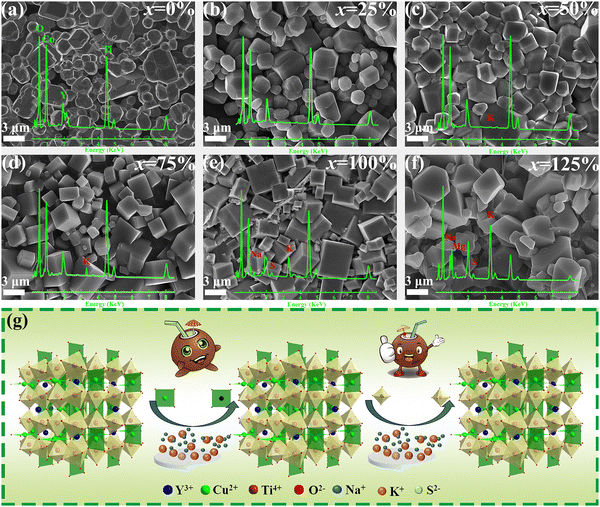 | ||
| Fig. 4 (a–f) SEM images of YCTO-x% ceramics and corresponding EDS element scanning images. (g) Schematic of the lattice variation of YCTO-x% ceramics with an increase in coconut water. | ||
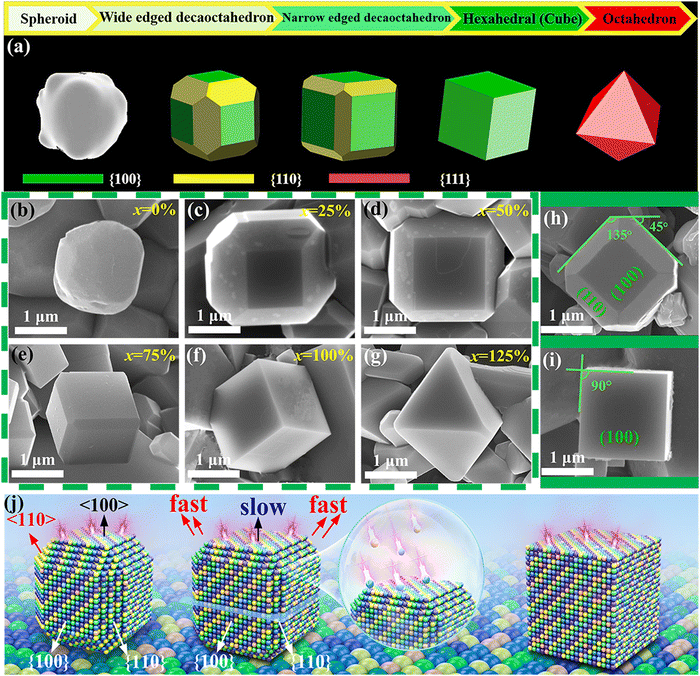
In order to better identify the details of YCTO grains, as shown in Fig. 5b–g, the morphology close-up of YCTO grains was sequentially captured by the high magnification lens of the SEM technique. Interestingly, the grains containing coconut water are surrounded by multiple regular crystal facets as opposed to the YCTO-0% grains, which show an amorphous smooth surface. By focusing on Fig. 5c–e, h and TEM (analyzed in the next section), it is found that samples with a lower proportion of coconut water can be identified as a decaoctahedron surrounded by {110} and {100} crystal facets according to perovskite-like cell and Bravais lattice. The decaoctahedron schematic diagram was used to estimate the proportion of the exposed area between the two crystal facets (Fig. S8, ESI†). It is found that as the coconut water increases, S{110} gradually decreases while S{100} gradually increases. Interestingly, when x = 100 (Fig. 5f), cubic grains surrounded by 6 facets, 8 vertices, and 12 edges were obtained. At this time, the {110} crystal facets of YCTO-100% completely disappear (S{110} = 0), and only the {100} crystal facets are exposed. This means that the growth rates of YCTO-100% grains are consistent with ideal BCC cells (a = b = c) in the a, b and c axes, respectively. The change in the relative intensity of XRD diffraction peaks indirectly records this evolution process (Fig. 3d). Surprisingly, when x = 125, the grains mutated from cubic to octahedral surrounded by {111} crystal facets (Fig. 5g). This answers the confusion about the phase structure abnormality of the YCTO-125% sample in XRD results.
We tried to summarize the entire tailoring process by the schematic diagram in Fig. 5j. The faster growth rate in the 〈110〉 direction leads to a gradual increase in the {100} crystal facets. Unfortunately, the slower growth rate in the 〈100〉 direction at this point leads to a gradual reduction or even disappearance of the {110} crystal facets. As the proportion of coconut water increases, the growth rate in the 〈110〉 direction becomes faster and faster. The tailoring direction is along 〈h00〉 while maintaining body center symmetry. This confirms that coconut water is an effective grain tailor. This would further explain that the emergence of the preferential orientation of the {h00} crystal facet mentioned in the XRD analyses is attributable to the rapid stacking of the {hk0} crystal facet, leading to the preferential growth of the (400) crystal facet. This result may also explain similar previous works on rutile structured materials.38,39 The evolution of YCTO crystal facets may have a revolutionary impact on the subsequent electrical performance.
2.4. TEM analysis
The whole “tailoring process” seems to have been processed by precision machine tools, consistently exposing the significant characteristics of the index crystal face, such as sharp corners, sharp edges and abnormally flat crystal facets. As with many other oxides, the crystal facet index of YCTO grains was identified using fast Fourier transform (FFT) patterns and selected area electron diffraction (SAED) patterns.40 The difference is that the FIB-TEM technology verifies the atomic level crystal phase of YCTO and confirms the periodicity of the crystal structure. Fig. 6a and h show the detailed cut positions and SEM of the slices for the YCTO-50% and YCTO-100% grains, respectively. HRTEM images show clear lattice fringes and good crystallinity (Fig. 6b and i). The periodic arrangement of atomic columns is consistent with the YCTO atomic model. After measurement, the lattice fringes on the YCTO-50% sample were formed by the arrangement of atoms on the {211} and {200} crystal planes (Fig. S9, ESI†). The lattice fringes on the YCTO-100% sample can be matched to the {200} and {110} crystal planes (Fig. S10, ESI†). The adjacent crystal facets of the grain obtained by the projection method follow the principle of constant crystal facet angles, which are 135° and 90°, respectively (Fig. 5h and i).41Fig. 6c and j show the SAED maps obtained from the vertical view. Its spot array can be represented by {0kl} and{00l} (i.e., [100] and [110] zone axis, conforming to the electron diffraction extinction rule of space groups: no. Im![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) ), respectively. Therefore, the zone axis along the vertical view surface is in the [100] and [110] directions, respectively. The incident direction of the accelerated electron beam is parallel to the zone axis of the surface vertical view. According to crystallographic theory and Steno's law, YCTO-50% grains can be identified as decaoctahedron grains with exposed {110} and {100} crystal facets, while YCTO-100% grains are cubic grains surrounded by {100} crystal facets.42,43
), respectively. Therefore, the zone axis along the vertical view surface is in the [100] and [110] directions, respectively. The incident direction of the accelerated electron beam is parallel to the zone axis of the surface vertical view. According to crystallographic theory and Steno's law, YCTO-50% grains can be identified as decaoctahedron grains with exposed {110} and {100} crystal facets, while YCTO-100% grains are cubic grains surrounded by {100} crystal facets.42,43
To better understand the effect of coconut water on the microstructure of YCTO, we obtained strain images of YCTO-50% and YCTO-100% ceramics along xx (compression) and yy (tension) directions by geometric phase analysis (GPA). Because cation vacancies usually affect only the nearest and next-nearest atoms, we observe a small amount of short-range strain fluctuations in the YCTO-50% sample (Fig. 6d and f). Inverse fast Fourier transform (IFFT) images along the (211) and (200) crystal planes show the distribution of structural defects within the YCTO-50% sample and clearly highlight the presence of lattice dislocations and distortions by white boxes (Fig. 6e and g). These dislocations are consistent with the distribution of local concentrated stresses, thus confirming the formation of local lattice distortions. However, with the increase of coconut water, the YCTO-100% sample shows uniform stress distribution and clear moiré fringes, which confirms that lattice dislocations and orthogonal distortions gradually disappear (Fig. 6k–n). The differential distribution of local strain fields across various directions can be traced back to lattice distortions arising from point defects. Active ions compensate for these defects, thereby facilitating the preferential growth of crystals. The localized stress surrounding dislocations effectively scatters mid-frequency phonons and restricts lattice conductivity within high-temperature regimes.44,45 With the increase of coconut water, dislocations and distortions may potentially affect carrier transport.
2.5. Kinetics of crystal facet tailoring
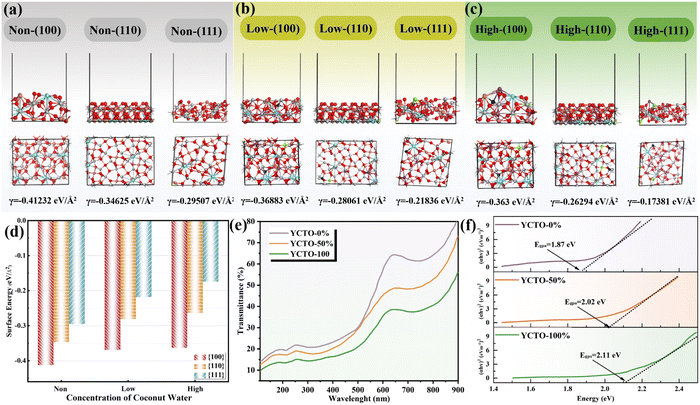
The surface stability and reactivity of inorganic crystals have been considered to be dominated by chemical energy and have an important impact on the synthesis of highly symmetrical crystals.46 Therefore, in addition to the experimental analysis, the surface energy of each facet was obtained by the first-principles calculation. As shown in Fig. 7, the surface energy of the {100} crystal facets decreases with increasing coconut water. The surface energy of each crystal facet follows the order γ{111} > γ{110} > γ{100}, which is consistent with the calculations that have been reported in the same perovskite crystal.47 The relative change in surface energy of the crystal facets is caused by the regulation of coconut water. The higher surface energy drives the gradual reduction or disappearance of the {111} and {110} crystal facets. As predicted by Curie and Woolf, polycrystals will choose a crystalline form to maintain the minimum surface energy in a solid solution.48,49 Therefore, the above analysis supports such a rule that YCTO grains have completed the evolution from decaoctahedron to platonic-polyhedron due to the gradual disappearance of {110} crystal facets (Fig. 5a). This can be interpreted as the crystal facet tailoring or shape customization of YCTO grains achieved by the bioprotein method with the assistance of coconut water. According to the Thomson–Gibbs equation, the surface energy of facets is proportional to the supersaturation of the crystal growth environment under a supersaturated condition (non-equilibrium condition).50 Therefore, the grain surface and the morphology of gains can be controlled by changing the degree of supersaturation of the crystal growth environment. Furthermore, the electronic structural information of YCTO-x% grains exposing different {hkl} facets was obtained by utilizing the reflection of light on the material surface (Fig. 7e). The bandgap energies of YCTO-x% were evaluated using the Tauc-plot analysis method (Fig. 7f). With the increase in {110} facets, the Egpa value rises from 1.87 eV to 2.11 eV. This orderly increase in bandgap energy may be correlated with the elimination of structural defects or localized states within the bandgap.51 The change in band gap indicates the difference in conductivity of ceramic materials. A wider bandgap typically signifies a decrease in the number of carriers thermally activated into the conduction band at room temperature, leading to a lower intrinsic carrier concentration and thus increasing the resistivity.522.6. Electrical property
The temperature dependence of the resistivity ρ was investigated by plotting the natural logarithm of the resistivity (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ρ) and the reciprocal of the absolute temperature (1000/T) of the ceramic samples. As shown in Fig. 8a–f, all samples exhibit good linearity, and the resistivity decreases with increasing temperature, showing the typical NTC characteristics. As shown in Fig. 8g, all samples except YCTO-125% show a good linear relationship. The Pearson's coefficient increases with increasing proportion of coconut water. Its linear correlation is a characteristic of the small polaron hopping transmission mechanism. This mechanism can be described by the Arrhenius equation:53
ρ) and the reciprocal of the absolute temperature (1000/T) of the ceramic samples. As shown in Fig. 8a–f, all samples exhibit good linearity, and the resistivity decreases with increasing temperature, showing the typical NTC characteristics. As shown in Fig. 8g, all samples except YCTO-125% show a good linear relationship. The Pearson's coefficient increases with increasing proportion of coconut water. Its linear correlation is a characteristic of the small polaron hopping transmission mechanism. This mechanism can be described by the Arrhenius equation:53where ρ is the resistivity of the material at infinite temperature, Ea is the activation energy, k is the Boltzmann constant, and T is the absolute temperature. Based on the small polaron hopping transport model, the electrical conductivity of these ceramics may be due to electron hopping between different oxidation states of the variant-valence cation in the lattice, explained as follows: During heating, the unstable Cu2+ is electronically reduced to Cu+ and Ti3+ in the lattice to maintain the charge balance. Therefore, the charge balance can be maintained by replacing Ti4+ at the Cu2+ position. The reaction is as follows:
 . During the cooling process, Cu+ is oxidized again to Cu2+, and the lost electrons enter the 3d conduction band of Ti. The reaction is as follows: Cu+ + Ti4+ → Cu2+ + Ti3+. Electron hopping between Cu2+/Cu+ ions as well as Ti4+/Ti3+ ions is the main carrier of YCTO ceramics.54 Therefore, the transition between different valence states of the variant-valence cation provides a transport channel for the electrical properties of the ceramics.
. During the cooling process, Cu+ is oxidized again to Cu2+, and the lost electrons enter the 3d conduction band of Ti. The reaction is as follows: Cu+ + Ti4+ → Cu2+ + Ti3+. Electron hopping between Cu2+/Cu+ ions as well as Ti4+/Ti3+ ions is the main carrier of YCTO ceramics.54 Therefore, the transition between different valence states of the variant-valence cation provides a transport channel for the electrical properties of the ceramics.
As shown in Fig. 8h and i, the upper limit resistance and B-value of YCTO gradually increase as the proportion of coconut water increases. Thus, the high resistivity exhibited by YCTO-100% ceramics provides enough room for resistivity degradation during high temperatures. Except for the YCTO-125% ceramics, the temperature response range gradually broadens with increasing coconut water from the initial 25–250 °C (YCTO-0%) to 25–600 °C (YCTO-100%), suggesting a strong correlation between the tailoring of the {110} crystal facets and the thermosensitive properties. This seems to be a breakthrough for the application of YCTO materials in the high-temperature range (over 300 °C). Firstly, based on the quantitative results of XPS, it seems that the cause has been identified (Fig. S11 and Table S2, ESI†). The concentration of Cu+ and Ti3+ decreases gradually with increasing coconut water. As is well known, the concentration of variable valence ions (Cu+ and Ti3+) in YCTO ceramics is closely related to the repeated thermal shock process. The redox reaction consumes additional electrons while active ions make up for the vacant A-site cations in the YCTO lattice, as shown in the following Kroger–Vink equation (ref. 55): 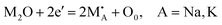 , 2O0 + 2Cu2+ + 2Ti4+ + 4e′ ↔ 2Cu2+ + 2Ti3+ + O2(g). The reduction in the number of charge carriers received or provided by YCTO-100% ceramics in an applied electric field simultaneously increases the energy barrier for polaron hopping, thus exhibiting a higher resistivity. Secondly, electronic ceramic materials consist of semiconductor grains and insulating grain boundaries.56 As S{100}/S{110} increases, the grain boundaries per unit volume of particles gradually increase (SCubes > SSpheroids), resulting in the increase of resistivity. In addition, Fig. 4e reveals that some gaps are inevitably formed in the ceramic body due to the disordered self-assembly of cubic grains in the geometric space. This leads to the obstruction of the transport channels for electron hopping between neighboring positions and further results in decreased mutual conductivity between semiconductor grains.57 Based on the above analysis, controlling the crystal facets can effectively regulate the resistivity of YCTO ceramics and broaden their response temperature range.
, 2O0 + 2Cu2+ + 2Ti4+ + 4e′ ↔ 2Cu2+ + 2Ti3+ + O2(g). The reduction in the number of charge carriers received or provided by YCTO-100% ceramics in an applied electric field simultaneously increases the energy barrier for polaron hopping, thus exhibiting a higher resistivity. Secondly, electronic ceramic materials consist of semiconductor grains and insulating grain boundaries.56 As S{100}/S{110} increases, the grain boundaries per unit volume of particles gradually increase (SCubes > SSpheroids), resulting in the increase of resistivity. In addition, Fig. 4e reveals that some gaps are inevitably formed in the ceramic body due to the disordered self-assembly of cubic grains in the geometric space. This leads to the obstruction of the transport channels for electron hopping between neighboring positions and further results in decreased mutual conductivity between semiconductor grains.57 Based on the above analysis, controlling the crystal facets can effectively regulate the resistivity of YCTO ceramics and broaden their response temperature range.
2.7. Aging property
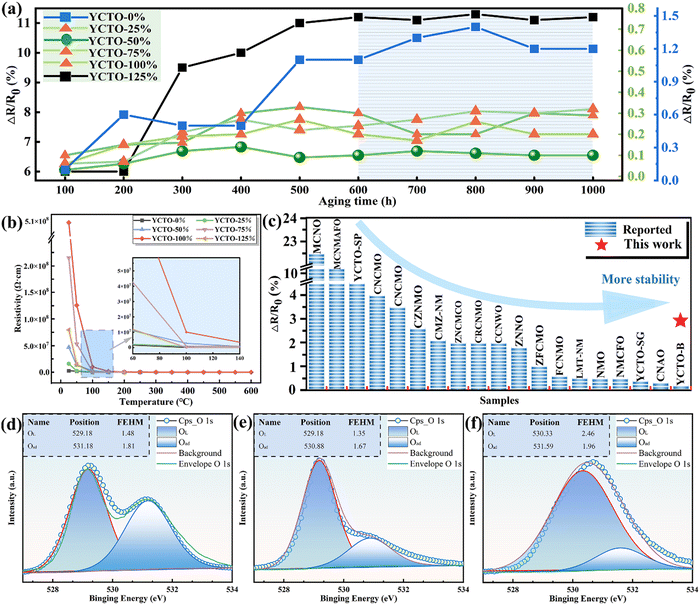
To evaluate the application prospects of YCTO ceramics in practical environments, their stability under sustained high temperatures was monitored. The curve in Fig. 9a shows the measurement results of the aging performance of YCTO ceramics at different stages during a continuous 1000 h aging. This interesting phenomenon can be divided into two phases. In the first phase (<600 h), the aging curves of all samples are found to rise in an undesirable manner as aging time increases. In the second stage, after 600 hours, the aging coefficient gradually stabilizes. This is because residual internal stress and internal defects are partially retained in the ceramic body in a metastable state with higher free energy after high-temperature annealing.58,59 With the fixation of the variable valence structure in the redox reaction, it eventually converges to a low-energy steady state. The impact of a sustained high-temperature environment will accelerate this process, thereby reducing the concentration of internal defects and stress in the material.60,61 Eventually, the aging coefficient tends to stabilize as the aging time increases.The aging coefficients and resistance-temperature curves of the ceramics after 1000 h are shown in Fig. 9a and b. Except for YCTO-125% ceramics, the performance loss of ceramics with coconut water (ΔR/R0 < 1.2%) was reduced by about an order of magnitude compared to ceramics without coconut water (ΔR/R0 ∼ 11%). It is worth noting that the lowest aging coefficient of the YCTO-50% ceramics with a mixed crystal facet is only 0.1%. More details of the high stability of the YCTO-50% ceramics seem to be verified by the O 1s XPS spectra of the samples (Fig. 9d–f). The results of the quantitative analysis show that YCTO-0% ceramics have the lowest lattice oxygen concentration (Table S2, ESI†). This indicates the presence of a higher concentration of oxygen vacancies, which leads to lattice mismatch. As is well known, the oxygen loss caused by high-temperature sintering of most titanium-based materials will reduce some Ti4+ to Ti3+ and further increase the loss in the alternating electric field.62 The increase in oxygen vacancies and ion concentrations (Cu+ and Ti3+) jointly exacerbates the resistance drift. The lower oxygen vacancy concentration and the stable variant-valence cation in YCTO-50% ceramics effectively inhibit the deterioration of electrical properties at high temperatures. At the same time, the moderate number of active ions compensates for the structural defects in YCTO-50%, and thus a more stable crystal structure is obtained. YCTO-50% ceramics exhibit more excellent densities and homogeneous particle sizes (Fig. 4c and Fig. S7c, ESI†). These have a positive effect on preventing oxygen absorption-oxidation of oxide materials under sustained thermal shock. The excellent thermal stability of YCTO-50% ceramics is rare compared to the reported NTC materials (Fig. 9c and Table S3, ESI†). This proves that the bioprotein method is beneficial for improving the thermal stability of thermistors.
3. Conclusion
In this study, YCTO-x% ceramics were successfully synthesized using the bioprotein method. With the increase of coconut water, YCTO grains with wide-edged decaoctahedron, narrow-edged decaoctahedron and cubic structures were obtained sequentially. However, excessive amounts of coconut water can lead to mutations in the phase structure and overall deterioration of the thermosensitive properties. The rapid stacking of the {110} crystal facets led to a preferred orientation of the {h00} crystal facets. The crystals follow the γ{111} > γ{110} > γ{100} rule, which is the kinetics reason for the gradual exposure of the {100} crystal facet. The insulating grain boundary per unit volume gradually increased with the increased coconut water. When x = 100, the responsive temperature range of YCTO reached 25–600 °C. The lower concentration of oxygen vacancies, stable variable-valence structure, and dense microstructure effectively inhibited the absorption oxidation of oxygen at high temperatures. After 1000 hours of high-temperature aging, the aging coefficient of YCTO-50% was 0.1%. This work not only provides a method for preparing grain-assembled ceramics but also lays the foundation for studying the effect of crystal facet transformation on improving the thermosensitive properties of ceramics.Data availability
Data will be made available on request.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
We would like to acknowledge financial support from the Natural Science Foundation of Xinjiang Uygur Autonomous Region (Grant No. 2024D01E32), the National Natural Science Foundation of China (Grant No. 62471468), the Youth Innovation Promotion Association of the Chinese Academy of Sciences (Grant No. Y2023117), the Xinjiang Tianshan Talent Training Program (Grant No. 2023TSYCCX0092), the Tianshan Innovation Team Plan of Xinjiang (Grant No. 2022TSYCTD0003), National Natural Science Foundation of China (52162035), Natural Science Foundation of Xinjiang Uygur Autonomous Region (2022D01C374), and Outstanding Doctoral Student Innovation Project of Xinjiang University (XJU2024BS079).References
- X. Zheng, H. Guo, Y. Xu, J. Zhang and L. Wang, J. Mater. Chem. C, 2020, 8, 13836–13842 RSC.
- H.-S. Kang, M.-Y. Long, T. Zhou, J.-C. Liu, Y.-T. Duan, L. Ma, X.-B. Chen, S.-J. Ding and L. Zhou, J. Mater. Chem. C, 2022, 10, 958–968 RSC.
- J. Xue, R. Wang and Y. Yang, Nat. Rev. Mater., 2020, 5, 809–827 CrossRef CAS.
- A. Feteira, J. Am. Ceram. Soc., 2009, 92, 967–983 CrossRef CAS.
- S. Dong, Z.-Y. Hu, P. Wei, J. Han, Z. Wang, J. Liu, B.-L. Su, D. Zhao and Y. Liu, Adv. Mater., 2022, 34, 37 Search PubMed.
- K. Huang, L. Yuan and S. Feng, Inorg. Chem. Front., 2015, 2, 965–981 RSC.
- H. Zhang, M. Jin and Y. Xia, Angew. Chem., Int. Ed., 2012, 51, 7656–7673 CrossRef CAS PubMed.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732–735 CrossRef CAS.
- K. Chanda, S. Rej and M. H. Huang, Chem. – Eur. J., 2013, 19, 16036–16043 CrossRef CAS PubMed.
- H. Wang, K. Dou, W. Y. Teoh, Y. Zhan, T. F. Hung, F. Zhang, J. Xu, R. Zhang and A. L. Rogach, Adv. Funct. Mater., 2013, 23, 4847–4853 CrossRef CAS.
- B. M. Klepser and B. M. Bartlett, J. Am. Chem. Soc., 2014, 136, 1694–1697 CrossRef CAS.
- M. Shibuya and M. Miyauchi, Chem. Phys. Lett., 2009, 473, 126–130 CrossRef CAS.
- J. Zhang, J.-p Tu, X.-h Xia, X.-l Wang and C.-d Gu, J. Mater. Chem., 2011, 21, 5492–5498 RSC.
- D. Xu, T. Jiang, D. Wang, L. Chen, L. Zhang, Z. Fu, L. Wang and T. Xie, ACS Appl. Mater. Interfaces, 2014, 6, 9321–9327 CrossRef CAS PubMed.
- H. Yang, Y. Zhou, Y. Yang, D. Yi, T. Ye, T. D. Lam, D. Golberg, B. Bao, J. Yao and X. Wang, J. Mater. Chem. C, 2018, 6, 11707–11713 RSC.
- Y. Yu, J. Du and C. Jing, J. Mater. Chem. C, 2019, 7, 14239–14244 RSC.
- M. Chen, B. Wu, J. Yang and N. Zheng, Adv. Mater., 2012, 24, 862–879 CrossRef CAS.
- S. Sun, X. Zhang, J. Cui, Q. Yang and S. Liang, Nanoscale, 2019, 11, 15739–15762 RSC.
- M. Subramanian, D. Li, N. Duan, B. Reisner and A. Sleight, J. Solid State Chem., 2000, 151, 323–325 CrossRef CAS.
- S. W. Ko, J. Li, N. J. Podraza, E. C. Dickey and S. Trolier-McKinstry, J. Am. Ceram. Soc., 2011, 94, 516–523 CrossRef CAS.
- M. Schubert, C. Muench, S. Schuurman, V. Poulain, J. Kita and R. Moos, J. Eur. Ceram. Soc., 2018, 38, 613–619 CrossRef CAS.
- M. Subramanian and A. Sleight, Solid State Sci., 2002, 4, 347–351 CrossRef CAS.
- J. Jumpatam, W. Somphan, J. Boonlakhorn, B. Putasaeng, P. Kidkhunthod, P. Thongbai and S. Maensiri, J. Am. Ceram. Soc., 2017, 100, 157–166 CrossRef CAS.
- P. Liang, F. Li, X. Chao and Z. Yang, Ceram. Int., 2015, 41, 11314–11322 CrossRef CAS.
- S. C. Baker-Finch and K. R. McIntosh, Prog. Photovoltaics, 2013, 21, 960–971 Search PubMed.
- Z. Peng, J. Li, P. Liang, Z. Yang and X. Chao, J. Eur. Ceram. Soc., 2017, 37, 4637–4644 CrossRef CAS.
- H. E. Kim, S.-d Yang, J.-W. Lee, H. M. Park and S.-I. Yoo, J. Cryst. Growth, 2014, 408, 60–63 CrossRef CAS.
- P. Liang, X. Chao and Z. Yang, J. Appl. Phys., 2014, 116, 4 Search PubMed.
- P. Mao, J. Wang, S. Liu, L. Zhang, Y. Zhao, K. Wu, Z. Wang and J. Li, Ceram. Int., 2019, 45, 15082–15090 CrossRef.
- D. Zhou, D. Zhao, Q. Fu, Y. Hu, G. Jian, X. Cheng and X. Shen, Ceram. Int., 2013, 39, 2457–2462 CrossRef CAS.
- L. Singh, I. W. Kim, B. C. Sin, K. D. Mandal, U. S. Rai, A. Ullah, H. Chung and Y. Lee, RSC Adv., 2014, 4, 52770–52784 RSC.
- J. Li, P. Liang, J. Yi, X. Chao and Z. Yang, J. Am. Ceram. Soc., 2015, 98, 795–803 CrossRef CAS.
- L. Singh, U. S. Rai and K. D. Mandal, Mater. Res. Bull., 2013, 48, 2117–2122 CrossRef CAS.
- S. Sharma, M. M. Singh, U. S. Rai and K. D. Mandal, Mater. Sci. Semicond. Process., 2015, 31, 720–727 CrossRef CAS.
- Y. P. Xie, G. Liu, L. Yin and H.-M. Cheng, J. Mater. Chem., 2012, 22, 6746–6751 RSC.
- C. Ma, M. Gratzel and N.-G. Park, ACS Energy Lett., 2022, 7, 3120–3128 CrossRef CAS.
- P. Mao, J. Wang, L. He, L. Zhang, A. Annadi, F. Kang, Q. Sun, Z. Wang and H. Gong, ACS Appl. Mater. Interfaces, 2020, 12, 48781–48793 CrossRef CAS.
- H. G. Yang, C. H. Sun, S. Z. Qiao, J. Zou, G. Liu, S. C. Smith, H. M. Cheng and G. Q. Lu, Nature, 2008, 453, 638–641 CrossRef CAS.
- J. Qu, Y. Wang, X. Mu, J. Hu, B. Zeng, Y. Lu, M. Sui, R. Li and C. Li, Adv. Mater., 2022, 34, 37 Search PubMed.
- N. Tian, Z.-Y. Zhou, S.-G. Sun, Y. Ding and Z. L. Wang, Science, 2007, 316, 732–735 CrossRef CAS PubMed.
- Y. Ma, Q. Kuang, Z. Jiang, Z. Xie, R. Huang and L. Zheng, Angew. Chem., Int. Ed., 2008, 47, 8901–8904 CrossRef CAS PubMed.
- T. Ming, W. Feng, Q. Tang, F. Wang, L. Sun, J. Wang and C. Yan, J. Am. Chem. Soc., 2009, 131, 16350 CrossRef CAS.
- K. Choi, N. Hwang and D. Kim, J. Am. Ceram. Soc., 2002, 85, 2313–2318 CrossRef CAS.
- Z. Shi, S. Tong, J. Wei, Y. Guo, Y. Zhang, L. Wang and J. Zhang, ACS Appl. Mater. Interfaces, 2022, 14, 32166–32175 CrossRef CAS PubMed.
- B. Zhao, Z. Yan, Y. Du, L. Rao, G. Chen, Y. Wu, L. Yang, J. Zhang, L. Wu, D. W. Zhang and R. Che, Adv. Mater., 2023, 35, 11 Search PubMed.
- Z. Sun, J. H. Kim, Y. Zhao, F. Bijarbooneh, V. Malgras, Y. Lee, Y.-M. Kang and S. X. Dou, J. Am. Chem. Soc., 2011, 133, 19314–19317 CrossRef CAS PubMed.
- W. Chen, Q. Kuang and Z. Xie, Sci. China Mater., 2015, 58, 281–288 CrossRef CAS.
- P. Curie, Bull. Mineral., 1885, 8, 145–150 Search PubMed.
- X. Yang, J. Fu, C. Jin, J. Chen, C. Liang, M. Wu and W. Zhou, J. Am. Chem. Soc., 2010, 132, 14279–14287 CrossRef CAS PubMed.
- H.-x Lin, Z.-c Lei, Z.-y Jiang, C.-p Hou, D.-y Liu, M.-m Xu, Z.-Q. Tian and Z.-x Xie, J. Am. Ceram. Soc., 2013, 135, 9311–9314 CrossRef CAS.
- F. Moura, A. Z. Simoes, R. C. Deus, M. R. Silva, J. A. Varela and E. Longo, Ceram. Int., 2013, 39, 3499–3506 CrossRef CAS.
- M. Xu, D. Wang, K. Fu, D. H. Mudiyanselage, H. Fu and Y. Zhao, Oxford Open Mater. Sci., 2022, 2, itac004 CrossRef CAS.
- P. R. Bueno, R. Tararan, R. Parra, E. Joanni, M. A. Ramirez, W. C. Ribeiro, E. Longo and J. A. Varela, J. Phys. D: Appl. Phys., 2009, 42, 5 CrossRef.
- T. B. Adams, D. C. Sinclair and A. R. West, J. Am. Ceram. Soc., 2006, 89, 3129–3135 CrossRef CAS.
- R. Das, S. Sharma and K. Mandal, J. Magn. Magn. Mater., 2016, 401, 129–137 CrossRef CAS.
- W. Z. Yang, M. M. Mao, X. Q. Liu and X. M. Chen, J. Appl. Phys., 2010, 107, 12 Search PubMed.
- B. Zhang, A. Chang, Q. Zhao, H. Ye and Y. Wu, J. Electron. Mater., 2014, 43, 4048–4055 CrossRef CAS.
- Q. Xu, M. Chen, W. Chen, H.-X. Liu, B.-H. Kim and B.-K. Ahn, Acta Mater., 2008, 56, 642–650 CrossRef CAS.
- B. Feng, I. Sugiyama, H. Hojo, H. Ohta, N. Shibata and Y. Ikuhara, Sci. Rep., 2016, 6, 20288 CrossRef CAS.
- X. Ma, J. Zhuang, P. Zhao, H. Zhang, H. Li, J. Xie, J. Rong, Y. Ding and G. Wang, J. Mater. Sci.: Mater. Electron., 2021, 32, 25201–25213 CrossRef CAS.
- H. Nesbitt and D. Banerjee, Am. Mineral., 1998, 83, 305–315 CrossRef CAS.
- S. Lei, H. Fan, W. Chen, Z. Liu and M. Li, J. Am. Ceram. Soc., 2017, 100, 235–246 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03724c |
| This journal is © The Royal Society of Chemistry 2025 |