Mn-doping method boosts Se doping concentration in Cu₂S towards high thermoelectric performance

Abstract

Copper chalcogenides have garnered attention as promising thermoelectric materials, owing to their environmental benignity, cost-effectiveness, and superior thermoelectric performance. Anionic doping within the same group is an effective method to improve the thermoelectric performance of copper chalcogenides, but Se-doped Cu₂S contains a large fraction of the secondary phase leading to poor thermoelectric properties. In this study, we refined the thermoelectric properties of Cu₂S by extending the concentration limit of Se-doping concentration. Our findings reveal that the incorporation of 2% Mn significantly elevates the concentration limit of Se from 1.5% to 5%. The increased Se doping effectively narrows the band gap, augmenting the carrier concentration to an optimal level. Furthermore, it also adjusts the electronic structure, enabling additional bands to contribute to electron transport, which results in elevated weighted mobility, and consequently, enhanced electrical conductivity performance. Additionally, the Se doping introduces dislocations and lattice distortions that bolster alloy scattering, thereby diminishing lattice thermal conductivity. As a result, the zT of Cu_1.96Mn_0.02S_0.95Se_0.05 reaches a peak of 0.97 at 723 K, which is 3.8 times that of Cu₂S, and at a high level compared with the reported Cu₂S-based materials. Hence, our research underscores the efficacy of co-doping as a strategy to expand the Se-doping concentration limit, and anionic doping within the same group can optimize the thermoelectric properties of Cu₂S-based materials.

---

1. Introduction

Thermoelectric (TE) materials represent a burgeoning class of energy conversion materials, capable of directly transforming thermal energy into electrical energy, and are poised for significant development in the face of dwindling natural resources.^1–3 The thermoelectric efficiency of TE materials hinges on a dimensionless figure of merit, zT, defined as zT = α²σT/κ, where α is the Seebeck coefficient, σ is the electrical conductivity, κ is the thermal conductivity, and T is the absolute temperature in Kelvin.^4–6 Researchers have discovered a variety of thermoelectric materials with excellent properties, such as PbTe,^7–9 GeTe,^10–12 SnTe,^13,14 BiTe^15,16 and so on. Copper chalcogenides, characterized by liquid-like properties, exhibit low lattice thermal conductivity and good thermoelectric performance, positioning them as promising candidates for thermoelectric applications.^17–20

Anionic doping within the same group in copper chalcogenide has been demonstrated to diminish lattice thermal conductivity and modulate carrier concentration, thereby effectively ameliorating the TE performance of these materials.^21–23 For instance, 8% S doping in Cu₂Se has been shown to optimize carrier concentration, augmenting the power factor (PF) to 11 μW cm⁻¹ K⁻² at 1000 K.²⁴ 30% Te doping in Cu₂Se has been reported to curtail lattice thermal conductivity, thereby elevating the zT value to 1.4 at 1000 K.²⁵ Se or S doping in Cu₂Te has similarly been observed to enhance TE performance.²⁶ However, Se-doping in Cu₂S is less effective due to a low doping concentration limit, leading to suboptimal TE performance. Wang et al. detected a substantial fraction of Se-rich secondary phases in the energy-dispersive spectroscopy (EDS) analysis of Cu_1.98S_0.985Se_0.015, alongside an additional phase transition peak in differential scanning calorimetry (DSC), suggesting that the doping concentration limit of Se less than 1.5%.²⁷ Recent studies have indicated that anionic and cationic co-doping methodologies can extend the anionic doping limit, exemplified by Cu_1.8Ag_0.2Se_0.9S_0.1²⁸ and Pb_0.9875Sb_0.0125Te_1−xS_x.²⁹ Thus, co-doping emerges as a promising avenue to escalate the doping concentration limit of Se in Cu₂S and to optimize its TE properties.

In this study, we optimized the TE properties of Cu₂S by increasing the Se-doping concentration limit. Mn doping weakens the Cu–S bond and stabilizes the high-temperature cubic phase, which increases the doping concentration limit of Se. Therefore, we involved 2% Mn in Cu₂S, successfully elevating the doping concentration limit of Se from 1.5% to 5%. Furthermore, Se doping was found to narrow the band gap, thereby increasing the carrier concentration to an optimal value. Additionally, it adjusted the electronic structure, facilitating the participation of an extra band in electron transport, which led to enhanced weighted mobility, and a consequent increase in the power factor to 7.74 μW cm⁻¹ K⁻² at 723 K. Moreover, the Se doping induced alloy scattering, which served to reduce lattice thermal conductivity, thereby suppressing it to its minimum value in the Cu_1.96Mn_0.02S_0.925Se_0.075. Ultimately, the zT value for Cu_1.96Mn_0.02S_0.95Se_0.05 achieved a peak of 0.97 at 723 K, marking a 3.8-fold improvement over that of pristine Cu₂S. Our experimental findings corroborate that co-doping is an efficacious strategy for augmenting the Se-doping concentration limit and further optimizing the TE properties of Cu₂S-based materials.

2. Experimental

2.1. Sample synthesis

A series of Cu₂S_1−xSe_x (0.015, 0.025, 0.05, 0.1) and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05, and 0.075) samples were fabricated via a high-temperature melting-annealing-hot pressing technique. High-purity elements, including copper (Cu, shots, 99.9999%, AlfaAesar), manganese (Mn, pieces, 99.8%, AlfaAesar), sulfur (S, pieces, 99.999%, AlfaAesar), and selenium (Se, shots, 99.9999%, AlfaAesar), were weighed according to the stoichiometric proportions, mixed, and loaded into a quartz tube. The tube was then sealed in a vacuum environment. The mixture was transferred to a muffle furnace, heated to 1373 K, and held for 12 hours to ensure a complete reaction of all elements. Subsequently, the samples were annealed at 873 K for 5 days to prevent the precipitation of copper. The resulting initial samples were manually milled into powders and loaded into a hot-pressing mold. Utilizing a hot press machine, the powders were compacted for 10 minutes under a program of 713 K and 60 MPa, yielding cylindrical samples with a diameter of 10 mm and a height of 12 mm.

2.2. Characterization

The phase purity and crystalline structure of Cu₂S and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05 and 0.075) samples were examined using room temperature X-ray diffraction (XRD, Cu Kα, Rint 2000, Rigaku, Japan) at a scanning speed of 10° min⁻¹ over a range of 5–80°. The surface microstructure of the polished samples was visualized using scanning electron microscopy (SEM, JEOL/JSM-7610FPlus), and elemental distribution was analyzed by energy dispersive spectroscopy (EDS, JED-2300T). The valence states of the Cu_1.96Mn_0.02S_0.975Se_0.025 sample were investigated using X-ray photoelectron spectroscopy (XPS, Thermo Scientific Nexsa). Diffuse reflectance measurements were performed on the powdered samples using a UV-vis-NIR spectrophotometer (Cary 5000, Varian, USA). The microstructure of the Cu_1.96Mn_0.02S_0.975Se_0.025 sample was elucidated using a transmission electron microscope (TEM, Philips Tecnai F20). The carrier concentration (n_H) and mobility (μ_H) at room temperature were determined using a Hall measurement system. Electrical conductivity (σ) and Seebeck coefficient (α) were measured in an argon atmosphere using the Ulvac ZEM-3 system over a temperature range from room temperature to 723 K. The total thermal conductivity κ was calculated as κ = C_p × ρ × D, where the thermal diffusion coefficient D was measured using the laser flash method (Netzsch, LFA-457), and the density ρ was determined. The heat capacity C_p was measured using the Archimedes method and calculated based on the Dulong–Petit law.

2.3. Calculations

The first-principles calculations were carried out using the Vienna ab initio Simulation Package (VASP).³⁰ Based on the density functional theory (DFT), the projector augmented-wave (PAW) approach with the generalized gradient approximation (GGA) method of Perdew–Burke–Ernzerhof (PBE) was introduced to calculate the electronic and phonon structures. The electron correlation and exchange of 3d orbitals of Cu are described by the Hubbard-type correction U_eff (U_eff = U − J) (4 eV).³¹ 520 eV is the plane-wave energy cutoff point, and 10⁻⁵ eV is the energy convergence criterion, calculated using the phonon spectrum and electric band structure, respectively.

3. Results and discussion

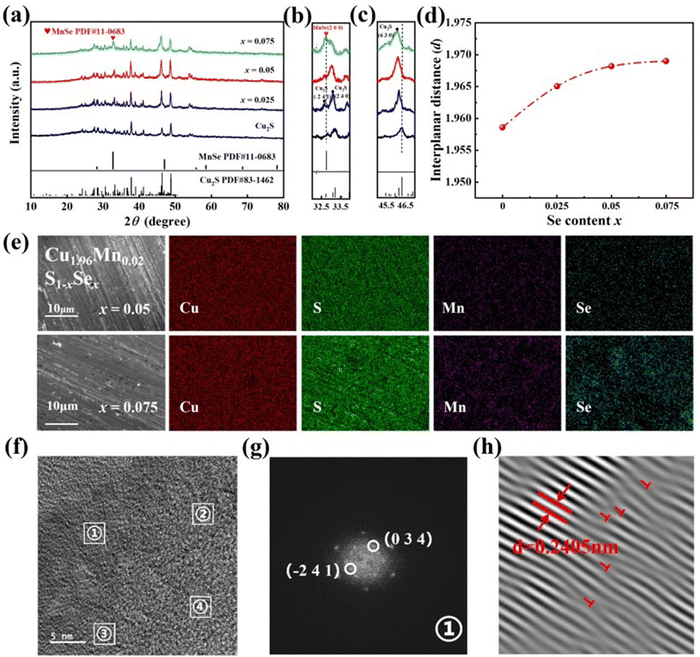
The phase composition of Cu₂S and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05, and 0.075) at room temperature was examined using X-ray diffraction (XRD), as presented in Fig. 1a. The diffraction pattern of the Cu₂S sample aligns with the monoclinic Cu₂S phase (PDF#83-1462). Upon slight Mn and Se co-doping, the XRD peak remains unaltered, with no discernible impurity phase peaks. The local amplification of the XRD pattern at 32–34° is shown in Fig. 4b. It reveals that the main peak of Cu₂S was at 33.02°, which suggests that it is the (2 4 0) peak of Cu₂S. When the doping concentration of Se reaches 0.25 and 0.05, the peak is consistent with that of Cu₂S. But a strong peak appears next to the (2 4 0) peak of Cu_1.96Mn_0.02S_0.925Se_0.075, which corresponds to the (2 0 0) characteristic peak of MnSe (PDF#11-0683), suggesting that Se has reached its doping concentration limit. Local amplification of the XRD pattern (Fig. 1c) indicates that the (6 3 0) characteristic peak of Cu_1.96Mn_0.02S_1−xSe_x near 2θ = 45.933° shifts towards a lower 2θ angle with Se doping, due to the larger ionic radius of Se compared to that of S.³² We calculated the interplanar spacing of the (6 3 0) plane, as shown in Fig. 1d, which increases and then exhibits minimal change with Se doping, implying a Se doping limit of less than 7.5%.

Fig. 1 Microstructure for Cu_1.96Mn_0.02S_1−xSe_x. XRD patterns of Cu₂S and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05 and 0.075) bulk samples at room temperature at (a) 2θ = 10–80°, and amplified X-ray diffraction patterns at (b) 2θ = 32–34°, and (c) 2θ = 45-47°. (d) Interplanar distance of Cu₂S and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05 and 0.075). (e) SEM images of Cu_1.96Mn_0.02S_1−xSe_x (x = 0.05 and 0.075) and its EDS mapping for Cu, S, Mn and Se. (f) High-magnification TEM image of Cu_1.96Mn_0.02S_0.975Se_0.025. (g) The fast Fourier transform (FFT) patterns for region 1 in the TEM image. (h) Inverse FFT (IFFT) patterns.

The impact of Mn doping on the solid solubility of Se was further investigated by energy-dispersive X-ray spectroscopy (EDS) mapping, as depicted in Fig. S1 (ESI†) and Fig. 1c. The Se enrichment in Cu₂S_0.985Se_0.015 (Fig. S1, ESI†), indicates that the doping limit of Se in Cu₂S is less than 1.5%. However, upon the introduction of 2% Mn, Cu, S, Mn, and Se are uniformly dispersed across the characterization region in Cu_1.96Mn_0.02S_0.95Se_0.05, without any element aggregation. This uniform distribution suggests that a 5% Se-doping can form a homogeneous solid solution. The Mn doping is inferred to enhance configurationally entropy and induce lattice distortion,³³ facilitating the incorporation of Se into the Cu₂S lattice. Consequently, co-doping is demonstrated to effectively elevate the doping limit of Se.

Further investigation of the microstructure of Cu_1.96Mn_0.02S_0.975Se_0.025 was performed using a high-magnification transmission electron microscope (TEM). EDS mapping confirms the uniform distribution of Cu, Mn, S, and Se (Fig. S2, ESI†). Fast Fourier transform (FFT) was performed on four distinct regions within the TEM image (Fig. 2d), with the results displayed in Fig. 2e. The four regions exhibit the same diffraction pattern, albeit with varying diffraction intensities. The marked diffraction points correspond to the (0 3 4) and (−2 4 1) planes of Cu₂S, with the lattice spacing of (0 3 4) being 0.2405 nm.³⁴ Inverse FFT (Fig. 2f) reveals that Mn and Se doping have induced lattice distortion and dislocations (marked with red “T”). The abundance of dislocations and the bending of lattice fringes contribute to phonon scattering,³⁵ which effectively reduces the lattice thermal conductivity of the co-doped samples.

Fig. 2 Electronic structure for Cu_1.96Mn_0.02S_1−xSe_x. (a)–(d) Plots of (F(R) × hv)^1/2vs. photon energy (hv) of Cu₂S and Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05 and 0.075), respectively. (e) The calculated electronic band structures for the Cu₂S and Cu_1.96S_0.925Se_0.075. (f) Schematic diagram of changes in the band structure of Cu₂S and Cu₂S_1-xSe_x.

Fig. S3a (ESI†) presents the X-ray photoelectron spectroscopy (XPS) analysis of Cu_1.96Mn_0.02S_0.975Se_0.025. The two spin-orbital peaks of Cu in Fig. S3b (ESI†) suggest that the Cu 2p peak predominantly corresponds to Cu⁺.³⁶ The binding energy observed in the XPS spectrum for S 2p in Fig. S3c (ESI†) indicates the presence of sulfur in the form of S²⁻. Due to the spin–orbit coupling, Mn exhibits two peaks in the binding energy spectrum (Fig. S3d, ESI†), with an additional satellite peak for Mn²⁺ at 2P_3/2 appearing at a binding energy of 647.18 eV.³⁷ The Mn 3s core state spectrum (Fig. S3e, ESI†) further corroborates that Mn ions are predominantly in the Mn²⁺ state.^38–40 The Se 3d spectrum consists of 3d_5/2 at 53.8 eV and 3d_3/2 at 54.5 eV, which are characteristic of Se²⁻.³⁵

According to previous studies, doping has a great influence on band structure, such as band degeneracy,^13,14,41,42 resonance level,^11,43,44 the Rashba effect,^45,46 classical and quantum size effect.⁴⁷ We conducted UV-visible diffuse reflectance studies and density functional theory (DFT) calculations to investigate the electronic structure. Utilizing the Tauc plot method (with the calculation formula detailed in the ESI†),^48,49Fig. 2a–d illustrate that the band gap of Cu₂S was 1.011 eV but gradually reduced to 0.884 eV with Se doping, signifying that Se doping narrows the band gap of Cu₂S. Furthermore, the DFT calculations, depicted in Fig. 2e and Fig. S4 (ESI†), and the schematic representation of the band structure in Fig. 2f, reveal that Se doping elevates the valence band and narrows the band gap, which is in agreement with the results from the UV-visible diffuse reflectance measurements. The valence band of Cu₂S is anti-bond, composed of the Cu 3d orbital and S 3p orbital,³⁵ and the energy of the Se 4p orbital is higher than that of the S 3p orbital.⁵⁰ Thus, Se doping increases the energy of the anti-bond. Additionally, Se doping weakens the Cu–S bond, leading to a narrower band gap (as shown in Fig. S5, ESI†). Moreover, the increase in the valence band at the M point is more pronounced than at the gamma point following Se doping, resulting in a gradual decrease in the energy difference between the M points and the gamma point (as illustrated in Fig. 2f), which is consistent with the pDOS in Fig. S6 (ESI†), After Se doping, the atomic orbital of Se is higher than that of S, so the energy of the anti-bond of Se is increased, leading to the increase in the energy of the M point in the band structure, and the electrical performance is improved. As a result, Se doping enhances the contribution of the band at the M point to electron transport, thereby increasing the effective mass and the Seebeck coefficient.

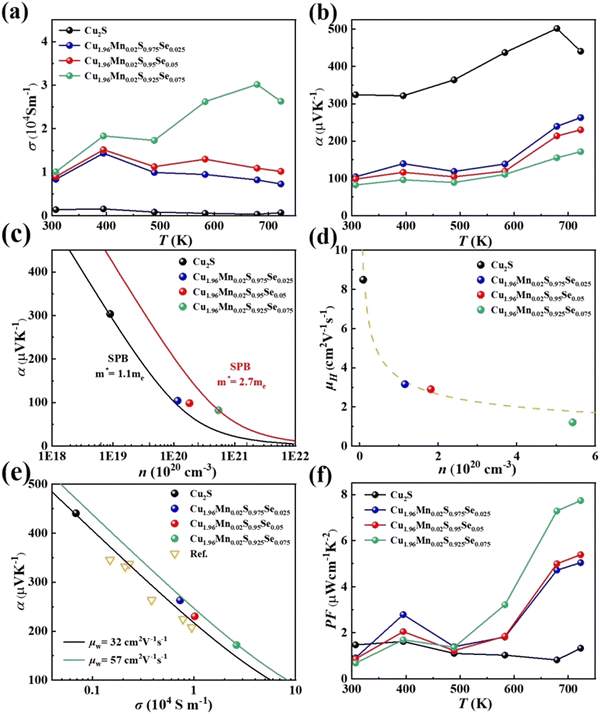
The temperature-dependent electrical transport properties of Cu_1.96Mn_0.02S_1-xSe_x are illustrated in Fig. 3. Se doping enhances electrical conductivity, but concurrently diminishes the Seebeck coefficient, as depicted in Fig. 3a and b.²⁷ This behavior is primarily attributed to the effects on carrier concentration (n) and effective mass (m*). The introduction of Se weakens Cu–S bonds and narrows the band gap, thereby increasing the carrier concentration, as shown in Fig. 3c. Given that Cu₂S typically exhibits a suboptimal carrier concentration, appropriate Se doping can optimize this parameter, thereby enhancing electrical performance.

Fig. 3 Electrical performance of Cu_1.96Mn_0.02S_1−xSe_x (x = 0.025, 0.05, 0.075). (a) Electrical conductivity σ, (b) Seebeck coefficient α depends on the temperature. (c) The relationship between the Seebeck coefficient and carrier concentration at room temperature. (d) Plot of carrier mobility (μ_H) versus carrier concentration (n) measured at room temperature. (e) The relationship between the Seebeck coefficient and electrical conductivity at 723 K. (f) Power factor PF depended on the temperature.

The effective mass (m*) was estimated using a single parabolic band (SPB) model, with detailed formulas provided in the ESI.†^51,52 The effective mass is initially 1.1m_e for pristine Cu₂S (black curve) and progressively increases to 2.7m_e (red curve) with Se doping (Fig. 3c). This increase in m* is due to Se doping, which encourages additional bands to participate in the electron transport, thereby improving the electrical transport properties.

Furthermore, Fig. 3d presents the carrier mobility (μ_H) for all samples. The reduced carrier mobility in Cu_1.96Mn_0.02S_0.925Se_0.075 is attributed to the Se-rich secondary phase, which induces alloy scattering and thus decreases mobility. However, for the carrier mobility of other samples, a decrease in mobility with an increase in carrier concentration aligns with the μ_H ∝ 1/n relationship, indicating that electron–phonon scattering is the predominant scattering mechanism.⁵³ Since Se and S are from the same group in the periodic table, Se doping in Cu₂S does not introduce significant additional scattering mechanisms such as alloy scattering,⁵⁴ or ionized impurity scattering,⁵⁵ which helps maintain carrier mobility.

As a result, due to the increased effective mass and reduced scattering, the weighted mobility (μ_w) increased from 32 cm² V⁻¹ S⁻¹ of Cu₂S to 57 cm² V⁻¹ S⁻¹ of Cu_1.96Mn_0.02S_0.925Se_0.075 with Se doping (Fig. 3e). This leads to a significant enhancement in the power factor (PF), with Cu_1.96Mn_0.02S_0.925Se_0.075 achieving a maximum PF of 7.74 μW cm⁻¹ K⁻² at 723 K, nearly four times greater than that of Cu₂S. Due to the phase transition, PF fluctuates significantly at 400 K. Thus, co-doping with elements from the same group is an effective approach to optimize the electrical transport properties of Cu₂S.

Se doping not only refines the electrical properties but also displays a significant impact on thermal conductivity, as illustrated in Fig. 4a. The total thermal conductivity (κ) escalates with Se doping, mirroring the trend observed in electrical conductivity. The total thermal conductivity (κ) is the sum of lattice thermal conductivity (κ_L) and electronic thermal conductivity (κ_e). The electronic thermal conductivity (κ_e) is estimated using the Wiedemann–Franz formula, κ_e = LσT, where L is the Lorentz constant, which can be approximated from the single parabolic band (SPB) model (as shown in Fig. S8, ESI†).⁵⁶ Sedoping engenders substantial lattice distortion and dislocations, which augment phonon scattering and consequently lead to a reduction in the lattice thermal conductivity of the doped samples (Fig. 4a). Comparative analysis with the lattice thermal conductivity of Te-doped in Cu₂S,⁵⁷ S doped in Cu₂Se,^24,58 Te doped in Cu₂Se and Se doped in Cu₂Te,^25,26 it reveals a consistent trend: the lattice thermal conductivity of the doped samples decreases with increasing doping concentration. This suggests that doping with elements from the same group not only boosts the power factor (PF) but also serves as an effective strategy to diminish the lattice thermal conductivity of copper chalcogenides. Consequently, if the Se-doping concentration limit could be further extended, the lattice thermal conductivity would be expected to continue to decrease.

Fig. 4 Thermal performance and zT value for Cu_1.96Mn_0.02S_1-xSe_x (x = 0.025, 0.05, and 0.075). (a) Temperature dependence of thermal conductivity κ and lattice thermal conductivity κ_L. (b) κ_L of the same-group doping in copper chalcogenide. (c) Figure of merit zT value. (d) Comparison of the figure of merit zT for Cu₂S-based materials in this work with other reported research.

The dimensionless figure of merit (zT) values for all doped samples are significantly higher than those of pristine Cu₂S (as depicted in Fig. 4c), due to the enhanced electrical and thermal transport properties following co-doping with Mn and Se. On the one hand, Se doping enhances the weighted mobility, thereby optimizing the electrical transport properties. On the other hand, Se doping diminishes the lattice's thermal conductivity, optimizing the thermal transport properties. Ultimately, the zT value for Cu_1.96Mn_0.02S_0.95Se_0.05 peaks at 0.97 at 723 K, and when juxtaposed with the reported Cu₂S-based materials and other class of performing copper-based materials containing multiple dopants, the zT value of Cu_1.96Mn_0.02S_0.95Se_0.05 is notably high (as shown in Fig. 4d and Fig. S10, ESI†).^{36,57,59–61}

4. Conclusions

In summary, we have demonstrated that the increased Se-doping concentration limit can optimize Cu₂S thermoelectric properties. The co-doping of 2% Mn and Se effectively raises the doping concentration limit of Se from 1.5% to 5%. This elevated level of Se-doping has not only solely increased the carrier concentration to an optimal range but also reconfigured the electronic structure. The inclusion of additional bands in electron transport engendered a heightened weighted mobility, thereby significantly enhancing the electrical transport properties. This enhancement propelled the power factor (PF) of the Cu_1.96Mn_0.02S_0.95Se_0.05 to reach 7.74 μW cm⁻¹ K⁻² at 723K. Moreover, extra alloy scattering generated by Se doping results in its lattice thermal conductance below Cu₂S. Finally, the zT value of the Cu_1.96Mn_0.02S_0.95Se_0.05 reaches 0.97 at 723 K, which is 3.8 times that of pristine Cu₂S. Therefore, it is an effective strategy to increase the concentration limit of Se through co-doping and optimize the thermoelectric properties with anionic doping within the same group, which has the potential for broad applications to other thermoelectric materials.

Author contributions

Chen Gong: investigation, methodology, writing – original draft preparation. Zhiwei Zeng: methodology. Xiaoling Sun: methodology. Chengran Luo: methodology. Hongyi Chen: supervision, project administration, conceptualization, writing – reviewing and editing.

Data availability

The data supporting this article have been included in the manuscript and ESI.†

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgements

This work was supported by Excellent Youth Funding of the Natural Science Foundation of Hunan Province (Grant No. 2022JJ20062), the National Natural Science Foundation of China (Grant No. 52002406), the National Natural Science Foundation of China-Hunan Joint Funds (Grant No. U20A20247). We are grateful to the High-Performance Computing Center of Central South University for partial support of this work.

Notes and references

1. J. Mao, Z. Liu, J. Zhou, H. Zhu, Q. Zhang, G. Chen and Z. Ren, Adv. Phys., 2018, 67, 69–147.
2. G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114.
3. Q. Yang, S. Yang, P. Qiu, L. Peng, T.-R. Wei, Z. Zhang, X. Shi and L. Chen, Science, 2022, 377, 854–858.
4. X. Li, Y. Lou, K. Jin, L. Fu, P. Xu, Z. Shi, T. Feng and B. Xu, Angew. Chem., Int. Ed., 2022, 61, e202212885.
5. P. Qiu, X. Shi and L. Chen, Energy Storage Mater., 2016, 3, 85–97.
6. Y. Yu, D. Yang, J. Li, M. Zhang, H. Luo, Q. Liang, H. Ye, Q. Zhang, X. Tang and J. Wu, Adv. Funct. Mater., 2022, 32, 2107284.
7. Z. Chen, Z. Jian, W. Li, Y. Chang, B. Ge, R. Hanus, J. Yang, Y. Chen, M. Huang, G. J. Snyder and Y. Pei, Adv. Mater., 2017, 29, 1606768.
8. R. Hanus, M. T. Agne, A. J. E. Rettie, Z. Chen, G. Tan, D. Y. Chung, M. G. Kanatzidis, Y. Pei, P. W. Voorhees and G. J. Snyder, Adv. Mater., 2019, 31, 1900108.
9. Y. Pei, N. A. Heinz, A. LaLonde and G. J. Snyder, Energy Environ. Sci., 2011, 4, 3640–3645.
10. X. Zhang, Z. Bu, S. Lin, Z. Chen and Y. Pei, Joule, 2020, 4, 986–1003.
11. U. S. Shenoy, G. K. D and D. K. Bhat, J. Alloys Compd., 2022, 921, 165965.
12. J. Li, X. Zhang, Z. Chen, S. Lin, W. Li, J. Shen, I. T. Witting, A. Faghaninia, Y. Chen, A. Jain, L. Chen, G. J. Snyder and Y. Pei, Joule, 2018, 2, 976–987.
13. U. S. Shenoy, G. K. D and D. K. Bhat, Mater. Adv., 2022, 3, 5941–5946.
14. U. S. Shenoy and D. K. Bhat, J. Alloys Compd. Commun., 2024, 1, 100001.
15. M. Samanta, K. Pal, U. V. Waghmare and K. Biswas, Angew. Chem., Int. Ed., 2020, 59, 4822–4829.
16. Y. Li, S. Bai, Y. Wen, Z. Zhao, L. Wang, S. Liu, J. Zheng, S. Wang, S. Liu, D. Gao, D. Liu, Y. Zhu, Q. Cao, X. Gao, H. Xie and L.-D. Zhao, Sci. Bull., 2024, 69, 1728–1737.
17. K. Zhao, P. Qiu, X. Shi and L. Chen, Adv. Funct. Mater., 2020, 30, 1903867.
18. Y. He, T. Day, T. Zhang, H. Liu, X. Shi, L. Chen and G. J. Snyder, Adv. Mater., 2014, 26, 3974–3978.
19. H. Liu, X. Shi, F. Xu, L. Zhang, W. Zhang, L. Chen, Q. Li, C. Uher, T. Day and G. J. Snyder, Nat. Mater., 2012, 11, 422–425.
20. H. Chen, Z. Yue, D. Ren, H. Zeng, T. Wei, K. Zhao, R. Yang, P. Qiu, L. Chen and X. Shi, Adv. Mater., 2019, 31, 1806518.
21. F. Shen, Y. Zheng, L. Miao, C. Liu, J. Gao, X. Wang, P. Liu, K. Yoshida and H. Cai, ACS Appl. Mater. Interfaces, 2020, 12, 8385–8391.
22. T. Xing, C. Zhu, Q. Song, H. Huang, J. Xiao, D. Ren, M. Shi, P. Qiu, X. Shi, F. Xu and L. Chen, Adv. Mater., 2021, 33, 2008773.
23. H. Xu, H. Wan, R. Xu, Z. Hu, X. Liang, Z. Li and J. Song, J. Mater. Chem. A, 2023, 11, 4310–4318.
24. K. Zhao, A. B. Blichfeld, H. Chen, Q. Song, T. Zhang, C. Zhu, D. Ren, R. Hanus, P. Qiu, B. B. Iversen, F. Xu, G. J. Snyder, X. Shi and L. Chen, Chem. Mater., 2017, 29, 6367–6377.
25. K. Zhao, M. Guan, P. Qiu, A. B. Blichfeld, E. Eikeland, C. Zhu, D. Ren, F. Xu, B. B. Iversen, X. Shi and L. Chen, J. Mater. Chem. A, 2018, 6, 6977–6986.
26. R. Rajkumar, J. Mani, S. Radha, M. Arivanandhan, R. Jayavel and G. Anbalagan, J. Mater. Sci.: Mater. Electron., 2023, 34, 1041.
27. Y. Wang, Z. Long, Y. Cheng, M. Zhou, H. Chen, K. Zhao and X. Shi, Mater. Today Phys., 2023, 32, 101028.
28. M. Guan, K. Zhao, P. Qiu, D. Ren, X. Shi and L. Chen, ACS Appl. Mater. Interfaces, 2019, 11, 13433–13440.
29. G. Tan, C. C. Stoumpos, S. Wang, T. P. Bailey, L.-D. Zhao, C. Uher and M. G. Kanatzidis, Adv. Energy Mater., 2017, 7, 1700099.
30. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
31. A. Jain, G. Hautier, S. P. Ong, C. J. Moore, C. C. Fischer, K. A. Persson and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 045115.
32. Y. Yao, B.-P. Zhang, J. Pei, Y.-C. Liu and J.-F. Li, J. Mater. Chem. C, 2017, 5, 7845–7852.
33. X. Zhang, M. Huang, H. Li, J. Chen, P. Xu, B. Xu, Y. Wang, G. Tang and S. Yang, J. Mater. Chem. A, 2023, 11, 8150–8161.
34. X. Lu, P. Lu, Y. Wei, C. Zhu, H. Su, X. Qiu, S. Feng, P. Qiu, X. Shi, L. Chen and F. Xu, Nano Lett., 2024, 24, 2853–2860.
35. Z. Long, Y. Wang, X. Sun, Y. Li, Z. Zeng, L. Zhang and H. Chen, Adv. Mater., 2023, 35, 2210345.
36. X. Liang, D. Jin and F. Dai, Adv. Electron. Mater., 2019, 5, 1900486.
37. J. Liu, M. P. Hanson, J. A. Peters and B. W. Wessels, ACS Appl. Mater. Interfaces, 2015, 7, 24159–24167.
38. G. C. Allen, S. J. Harris, J. A. Jutson and J. M. Dyke, Appl. Surf. Sci., 1989, 37, 111–134.
39. N. Andreu, D. Flahaut, R. Dedryvère, M. Minvielle, H. Martinez and D. Gonbeau, ACS Appl. Mater. Interfaces, 2015, 7, 6629–6636.
40. V. A. M. Brabers, F. M. van Setten and P. S. A. Knapen, J. Solid State Chem., 1983, 49, 93–98.
41. J. Li, X. Zhang, X. Wang, Z. Bu, L. Zheng, B. Zhou, F. Long, Y. Chen and Y. Pei, J. Am. Chem. Soc., 2018, 140, 16190–16197.
42. U. S. Shenoy, G. K. Ddd and D. K. Bhat, J. Alloys Compd., 2022, 905, 164146.
43. S. Perumal, M. Samanta, T. Ghosh, U. S. Shenoy, A. K. Bohra, S. Bhattacharya, A. Singh, U. V. Waghmare and K. Biswas, Joule, 2019, 3, 2565–2580.
44. U. S. Shenoy and D. K. Bhat, Mater. Adv., 2021, 2, 6267–6271.
45. U. S. Shenoy and D. K. Bhat, ACS Sustainable Chem. Eng., 2021, 9, 13033–13038.
46. M. Hong, W. Lyv, M. Li, S. Xu and Z. G. Chen, Joule, 2020, 4, 2030–2043.
47. J. He and T. M. Tritt, Science, 2017, 357, eaak9997.
48. Y. Li, W. Qi, Y. Li, E. Janssens and B. Huang, J. Phys. Chem. C, 2012, 116, 9800–9804.
49. R. Marshall and S. S. Mitra, J. Appl. Phys., 1965, 36, 3882–3883.
50. Y. Zhang, Y. Wang, L. Xi, R. Qiu, X. Shi, P. Zhang and W. Zhang, J. Chem. Phys., 2014, 140, 074702.
51. Y. Xiao, H. Wu, W. Li, M. Yin, Y. Pei, Y. Zhang, L. Fu, Y. Chen, S. J. Pennycook, L. Huang, J. He and L.-D. Zhao, J. Am. Chem. Soc., 2017, 139, 18732–18738.
52. A. F. May, E. S. Toberer, A. Saramat and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125205.
53. A. F. May, J. P. Fleurial and G. J. Snyder, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 125205.
54. R. Gurunathan, R. Hanus and G. J. Snyder, Mater. Horiz., 2020, 7, 1452–1456.
55. C. Hu, K. Xia, C. Fu, X. Zhao and T. Zhu, Energy Environ. Sci., 2022, 15, 1406–1422.
56. H. J. Goldsmid, Conversion Efficiency and Figure-of-Merit, CRC Handbook of Thermoelectrics, 1995.
57. Y. Yao, B.-P. Zhang, J. Pei, Q. Sun, G. Nie, W.-Z. Zhang, Z.-T. Zhuo and W. Zhou, ACS Appl. Mater. Interfaces, 2018, 10, 32201–32211.
58. K. Zhao, A. B. Blichfeld, E. Eikeland, P. Qiu, D. Ren, B. B. Iversen, X. Shi and L. Chen, J. Mater. Chem. A, 2017, 5, 18148–18156.
59. S. Zhao, H. Chen, X. Zhao, J. Luo, Z. Tang, G. Zeng, K. Yang, Z. Wei, W. Wen, X. Chen and Y. Sun, Mater. Today Phys., 2020, 15, 100271.
60. H. Kim, S. K. Kihoi, U. S. Shenoy, J. N. Kahiu, D. H. Shin, D. K. Bhat and H. S. Lee, J. Mater. Chem. A, 2023, 11, 8119–8130.
61. Y.-H. Zhao, Z.-H. Shan, W. Zhou, R. Zhang, J. Pei, H.-Z. Li, J.-F. Li, Z.-H. Ge, Y.-B. Wang and B.-P. Zhang, ACS Appl. Energy Mater., 2022, 5, 5076–5086.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc03056g

---