Understanding ionic transport in perovskite lithium-ion conductor Li_3/8Sr_7/16Ta_3/4Hf_1/4O₃: a neutron diffraction and molecular dynamics simulation study

Abstract

Solid-state Li-ion electrolytes (SSEs) are essential for the development of next-generation solid-state Li-metal batteries and new Li-extraction electrochemical cells. Among these, the perovskite-type SSE Li₃/₈Sr₇/₁₆Ta₃/₄Hf₁/₄O₃ (LSTH) has garnered attention for Li-extraction applications, owing to its outstanding chemical and thermal stability and high ionic conductivity. However, its precise crystal structure and Li-ion transport mechanisms remain insufficiently understood. This study addresses these gaps by employing neutron diffraction to resolve LSTH's crystallography and machine learning force field (MLFF) based MD simulations to elucidate ionic transport mechanisms. A single-phase LSTH, synthesized via the sol–gel method, exhibits a room-temperature bulk conductivity of 0.418 mS cm⁻¹ and a relative density of 98%. Neutron diffraction reveals 2.625 Li vacancies per unit cell, with the remaining 0.375 Li occupying the unconventional Wyckoff position (24k), different from the traditional A-site position (1a) of regular perovskites. This unique crystallography suggests a “zig–zag” Li-ion migration pathway via vacancies. However, MLFF based MD simulations suggest that Li ions at (24k), compared to (1a) occupancy, have limited mobility due to strong Li-vacancy ordering at low temperatures, leading to higher activation energy barriers and lower ionic conductivity. These findings underscore the critical influence of Li-site occupancy on ionic conductivity and provide structural insights for designing high-conductivity SSEs.

---

1. Introduction

To increase the energy density of lithium-ion batteries (LIBs), replacing the graphite anode with lithium metal is an attractive option, as lithium offers a much higher theoretical capacity of 3840 mA h/g.¹ However, the practical use of lithium anodes is hindered by substantial reactions with liquid electrolytes, forming resistive interfacial phases,² and attack of lithium dendrites, causing short circuiting.³ Solid-state electrolytes (SSEs) present a potential alternative to conventional liquid electrolytes to resist interfacial reactions and dendrite growth, thus mitigating cell failure.⁴ In addition, SSEs exhibit greater thermal and chemical stability, allowing batteries to operate over a wider temperature range and in harsher environments.^5,6 Among these, perovskite-type electrolytes attract attention due to their excellent chemical and structural stabilities in ambient environments and aqueous solutions over a broad pH range (1–13), making them also attractive as a membrane for Li extraction from brine and seawater.⁷ However, their synthesis, crystallography, ionic transport, and potential applications remain relatively underexplored.^8–11

Perovskite oxides exhibit a specific crystal structure, typically described by the formula ABO₃, where “A” and “B” are cations of different sizes. Li₃/₈Sr₇/₁₆Ta₃/₄Hf₁/₄O₃ (LSTH) has recently been identified as a promising perovskite-type Li-ion conductor.^8–10 In LSTH, lithium (Li) and strontium (Sr) are conventionally considered A cations occupying site (000), tantalum (Ta) and hafnium (Hf) are deemed B cations occupying the site (111) and O occupies the site (110).^10,11 However, whether Li in LSTH occupies the traditional A site is still in question due to its much smaller ionic radius and stronger interactions with O atoms than other A cations.¹⁰ Until now, there is no direct crystallographic evidence showing that Li indeed occupies the traditional A site. Furthermore, the crystal structure of LSTH is only explored by X-ray diffraction (XRD) so far, which cannot provide accurate crystallographic information on light Li atoms.^8,12,13 The small electron shell of Li (the 3rd element in the periodic table) interacts weakly with the charged X-ray, thus reducing the accuracy in determining the position of Li atoms. In contrast, neutrons interact with the nucleus of an atom, instead of electrons, thus capable of providing more accurate crystallographic information than XRD, especially for lighter atoms.¹⁴ Therefore, neutron diffraction is a technique better suited for determining the crystal structure of LSTH with high accuracy.

In this study, we employ the POWGEN neutron diffraction facility at Oak Ridge National Laboratory to determine the crystal structure of LSTH. With the high accuracy crystallographic data, we further conduct ab inito MD (AIMD) and MLFF based MD simulations to understand LSTH's ionic transport properties.¹⁵ MLFF based MD simulations are capable of revealing possible ionic pathways, analyzing the effect of the state of ordering on ion migration, and calculating ionic conductivity and energy barriers, thus making them a commonly used theoretical method to understand fundamentals of ion transport phenomena.^16–18

In addition, we also explore the synthesis of LSTH using a sol–gel method in this study, aiming to further lower the sintering temperature/time and achieve a better bulk density, ionic conductivity and homogeneity compared to conventional solid-state reactions (SSRs).^9,19–22 Previously, we have systematically investigated SSR conditions, e.g., excess Li, mother powder bed (MPB) protection and sintering temperature, to yield single-phase LSTH.⁹ We concluded from this early study that as long as MPB is used and the sintering temperature is ≥1450 °C, single-phase LSTH can be obtained without excess Li. Here we show how sol–gel derived LSTH powder lowers the sintering temperature and duration to achieve a single phase while increasing bulk density and ionic conductivity with the use of the MPB technique.

2. Results and discussion

2.1 Sol–gel synthesis of LSTH

For the first time, LSTH was synthesized using a sol–gel method to lower both the sintering temperature/time and increase bulk density and conductivity. Fig. 1(a) shows that a single phase LSTH can be achieved at 1400 °C for 6 hours, in comparison to 1450 °C for 10 hours with the SSR-derived sample.⁹Fig. 1(b) further shows the dense microstructure of the sol–gel derived LSTH, with 98% of theoretical density measured by Archimedes' method. The Arrhenius plot of bulk ionic conductivity in Fig. 1(c) indicates an activation energy of 0.350 eV, which is comparable to that of LSTH prepared with SSR, hot pressing and spark plasma sintering.^9,12,23,24Table 1 summarizes bulk conductivity and density as a function of sintering temperature for easy comparison.

Fig. 1 (a) XRD patterns of LSTH synthesized from sol–gel synthesis at different temperatures for 6 hours; (b) microstructure of LSTH sintered at 1400 °C; (c) Arrhenius plot of bulk ionic conductivity.

Table 1 RT bulk ionic conductivity, bulk density, and relative density of the synthesized LSTH

Sintering temperature (°C)	RT bulk conductivity (mS cm^−1)	Density (g cm^−3)	Relative density (%)
1100	0.269	6.58	93.2
1200	0.316	6.84	97.2
1300	0.383	6.77	96.1
1400	0.571	6.91	98.0

---

It is worth mentioning that there is no clear grain boundary (GB) contribution to the total resistance in LSTH, which is in stark contrast to La_0.56Li_0.33TiO₃ (LLTO) systems exhibiting significantly higher GB resistance.²⁵ Fig. S1† shows an example of the electrochemical impedance spectrum measured from the sol–gel derived LSTH. We have also observed the same grain-boundary free phenomenon in LSTH made by the SSR.⁹

The chemical composition of the synthesized LSTH was analyzed by ICP. The normalized data are shown in Table S1.† The actual composition of the synthesized sample is Li_0.34Sr_0.42Ta_0.75Hf_0.24O₃, which is very close to the nominal composition of Li₃/₈Sr₇/₁₆Ta₃/₄Hf₁/₄O₃.

2.2 Crystal structure of LSTH

The neutron diffraction pattern and Rietveld refinement of LSTH are shown in Fig. 2. During the refinement, the occupancies of Hf, Ta and O are fixed at 0.25, 0.75 and unity, respectively, whereas the occupancies of Sr and Li are allowed to vary. Positions with lower site symmetry are tested first, but they produce poor fitting quality and are therefore disregarded. Atomic displacement parameters (ADPs) are refined for all the positions, apart from Li, as the Li ADP shows a strong correlation with both the Li atomic positions and the Li site occupancy. Therefore, B_iso for Li was fixed at 1 Ų. The final atomic positions refined are listed in Table 2.

Fig. 2 Neutron diffraction pattern and Rietveld refinement of LSTH.

Table 2 Atomic positions and occupancies of each element in LSTH^a

	x	y	z	Occupancy	U 11 (Å^2)	U 22 (Å^2)	U 33 (Å^2)
a The value in parentheses represents the error value; for instance, the lattice parameter of the refinement has an uncertainty of 0.0001 Å. Temperature factors are the Unn.
Li	0	0	−0.396(5)	0.052(6)	0.13	=U11	=U11
Sr	0	0	0	0.425(3)	0.0031(1)	=U11	=U11
Ta	0	0	0	0.75	0.0033(1)	=U11	=U11
Hf	0	0	0	0.25	0.0033(1)	=U11	=U11
O	0	0.5	0.5	1	0.0039(2)	0.0215(2)	=U22

---

For LSTH, changing the atomic displacement factor of O from isotropic to anisotropic leads to an improvement in the fitting quality, with weighted profile R-factor (R_wp) reduced from 6.8% to 5.0%. For other atomic sites, isotropic ADPs are used, and the final refinement converges with R_wp = 4.6%. Table 3 lists the lattice parameters as well as refinement reliability.

Table 3 Lattice parameters and R factors for LSTH

Parameter	Value (error)
Temperature (K)	298 K
Space group	Pm3̄m
a (Å)	3.9892 (1)
b (Å)	3.9892 (1)
c (Å)	3.9892 (1)
α (°)	90 (0)
β (°)	90 (0)
γ (°)	90 (0)
V (Å^3)	63.4829 (1)
R p (%)	5.7
R wp (%)	4.6
R exp (%)	2.2
GOF	2.1

---

The refinement shown in Fig. 2 suggests that the sample is well-crystallized, single-phase, and indexable to the Pm3̄m space group. The refined crystallographic data are summarized in Table 2, based on which the crystal structure of LSTH is reconstructed using CrystalMaker and shown in Fig. 3(a). The refined lattice parameter of LSTH is 3.9892 (1) Å, which agrees well with the reported 3.991 Å in the literature.¹⁰ The refined displacement parameters of O are highly directional, pointing toward the nearest neighboring Li positions. This anisotropic atomic displacement is due to the strong local Li–O attraction, pulling O away from its high-symmetry position. These refinement results are also consistent with the expected chemical stoichiometry of LSTH.

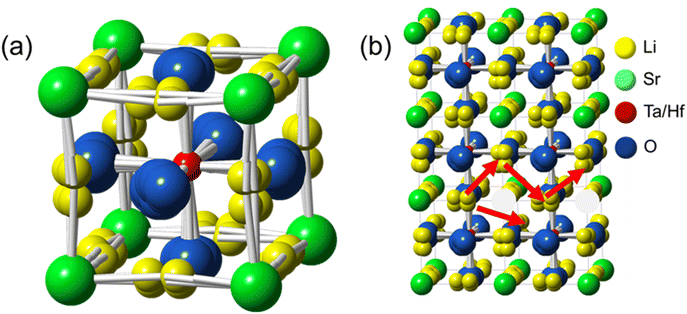Fig. 3 (a) Unit cell structure of LSTH (yellow ball represents Li); (b) a possible Li migration pathway in LSTH.

Notably, Li, instead of occupying the Sr position at site (1a), occupies the (24k) site between two oxygen atoms located at the edge of the unit cell. In addition, O atoms do not reside at the typical face center position (0, 1/2, 1/2) but at a different position, suggesting a locally distorted tetrahedral coordination due to the strong Li–O interactions. A displacement of the B-cation could occur due to the altered O coordination, but our refinement does not show any significant improvement with additional degrees of freedom, suggesting no clear evidence for this displacement. This new Li-occupancy suggests a Li migration pathway different from the conventional “linear pathway” through two O atoms in the perovskite structure. Instead, we think that Li migrates in a “zig–zag” pattern (see Fig. 3(b)). Within this ionic transport model, fast Li migration is likely favored when Li vacancies are present.

The occupancy of Li at the edge site (24k) offers more Li vacancies per unit cell than the conventional (1a) site since Li is no longer sharing sites with Sr (see Table 4). In such a perovskite structure, Li migrates by hopping over vacancies. However, as revealed by the following machine learning force field (MLFF) based MD simulations, the high concentration of Li-vacancies leads to ordering in the lower temperature regime, thus lowering conductivity.

Table 4 Composition of LSTH at different Li sites

Li site	Composition	Li occupancy per unit cell	Li vacancy per unit cell
1a	(Li3/8Sr7/16□3/16)Ta3/4Hf1/4O3	1 (8 × 1/8)	0.1875
24k	(Li3/8□21/8)Sr7/16Ta3/4Hf1/4O3	3 (12 × 1/4)	2.625

---

2.2.1 DeePMD simulations of LSTH. To understand the ionic conductivity observed in the experiment, we chose to investigate the influence of structural disorder and Li-site occupancy via MLFF based MD simulations. Two types of disorders were considered in the simulations: the electrostatic ground-state (ESGS) and the special quasi-random structure (SQS). The ESGS structure is generally regarded as a useful approximation for short-range order state in ionic compounds,^26–28 while the SQS structure approximates a fully random state (fully disordered).^27,29–31 The ESGS structures are generated by minimizing the Ewald summations of all ions. This can be done using packages such as pymatgen.³² The SQS structures²⁹ are generated by minimizing the difference between cluster probability with the random limit, which can be done using packages such as ATAT.³³ The two types of Li occupancies, e.g., Li occupying (1a) and (24k) sites, are considered in the simulations, which yield four types of structures shown in Fig. 4(a)–(d). AIMD simulations are performed to generate enough trajectories for training the MLFF using the DeePMD package. As is shown in Fig. 4(e)–(f), the MLFF based MD simulations yield a non-Arrhenius transition for all four types of structures.

Fig. 4 (a–d) LSTH perovskite structures based on four different Li occupancies; (e–f) the simulated Arrhenius plot of Li-ion conductivity in MLFF based MD simulations for ESGS (e) and SQS (f) LSTH. Black arrows mark the temperatures at transition points. The red pentagrams represent the predicted ionic conductivity at room temperature (298 K) through linear extrapolation.

For ease of comparison, the structures were grouped based on their disorder state while varying site occupancy. Fig. 4(e) illustrates the impact of Li occupancy for ESGS structures, whereas Fig. 4(f) highlights the impact of Li occupancy for SQS structures. In both cases, structures with (1a) occupancy exhibit higher conductivity at low temperatures but lower conductivity at high temperatures than those with the (24k) occupancy. The non-Arrhenius transition is observed for all four structures in the temperature range of 600–700 K; detailed activation barriers and ionic conductivities are summarized in Table 5.

Table 5 Room temperature ionic conductivities (σ_298K) and activation energies (E_a) of LSTH for four different Li occupancies obtained from MLFF based MD simulations

Li site	Li@1a (ESGS)	Li@24k (ESGS)	Li@1a (SQS)	Li@24k (SQS)
E a (eV)	0.22 (298–600 K)	0.55 (400–700 K)	0.23 (298–600 K)	0.43 (328–700 K)
	0.11 (600–1500 K)	0.11 (700–1500 K)	0.05 (600–1300 K)	0.15 (700–1500 K)
σ 298K,DeePMD (mS cm^−1)	3.73	—	3.24	—
σ 298K,predict (mS cm^−1)	4.05	0.0038	4.16	0.031

---

An interesting observation of conductivity in Fig. 4 is the “kink” behavior at 700 K for (24k) site occupancy and 600 K for (1a) site occupancy, respectively. This is likely caused by a potential disorder-to-order (2nd order) phase transition as the temperature decreases, i.e. the Li lattice becomes more ordered, due to high concentrations of Li-vacancies (see Table 4). Such an “order-disorder” transition is a common phenomenon for ionic conductors.^34–36 Additionally, the highest AIMD simulation and MLFF based MD simulation temperature is 1500 K. It can be inferred from our simulation that the system did not undergo amorphization even after 200 ps, implying reasonable thermodynamic stability at high temperature. To further identify the stability of LSTH, we have calculated the energy above hull of all configurations of LSTH based on a compositional phase diagram.³⁷ It is as low as 50 meV/atom, taking HfO₂, Sr₂Ta₂O₇, SrTa₂O₆, and SrLi₂Ta₂O₇ as the competing phases. Such energy above the hull value is comparable to many good oxide-based ionic conductors,^37,38 which also reveals the reasonable stability of our evaluated compounds.

The mean square displacement (MSD) of Li ions and Li probability density distributions are illustrated in Fig. S2–S5† and 5, respectively. The ESGS structure exhibits significant anisotropic diffusion, with diffusion along the ab-plane and c-axis dominating in Li@1a (Fig. S2†) and Li@24k (Fig. S3†), respectively. However, due to the more disordered structure, the SQS configuration exhibits isotropic diffusion, with similar contributions from all three directions in Li@1a (Fig. S4†) and Li@24k (Fig. S5†). Note that the diffusion pathway is relatively insensitive to temperature from the MSD component contributions between 500 K and 900 K. The possible Li migration pathways as Li probability density distributions of the four structures are further illustrated in Fig. 5, which depicts anisotropic Li diffusion in ESGS and isotropic Li diffusion in SQS. Overall, there is very little difference in overall ionic conductivity between ESGS and SQS. The major difference is that the Li diffusion in the ESGS structure is more anisotropic, whereas it is more isotropic in SQS.

Fig. 5 The visualized lithium probability density within the iso-surface (light yellow color) of LSTH obtained from MLFF based MD simulations for (a and e) Li@1a (ESGS), (b and f) Li@24k (ESGS), (c and g) Li@1a (SQS), and (d and h) Li@24k (SQS) at 500 K. Red dashed arrows represent the dominated diffusion direction of lithium ions.

It is important to point out that the extrapolated ionic conductivity at 298 K from MLFF based MD simulations is much higher for the (1a) site and lower for the (24k) site than the experimental value (0.571 mS cm⁻¹) (see Table 5). The closest match between the calculated and experimental values, i.e. 0.031 vs. 0.571 mS cm⁻¹, is observed for the (24k) site in the SQS structure (disordered). The activation energy derived from experiments (0.35 eV) is relatively close to the MLFF based MD predicted value for the (24k) site in the SQS structure (0.43 eV). The disagreement between theoretical and experimental data is common in the literature, particularly for oxides,^39,40 reflecting the need to further improve theoretical models.

3. Conclusion

Single-phase LSTH perovskite-type electrolytes with a high bulk ionic conductivity and relative density have been successfully synthesized via a sol–gel method. To facilitate the understanding of ion transport, we apply a combined experimental and theoretical approach, i.e. neutron diffraction for crystal structure analysis and MLFF based MD simulations for ion transport. Neutron diffraction, with its high sensitivity to Li, reveals that Li primarily occupies the Wycoff position (24k), rather than the commonly perceived conventional (1a) site, with abundant Li-vacancies within the lattice. The unique Li occupancy at the (24k) site creates a “zig–zag” pathway for Li-migration. MLFF based MD simulations further suggest that Li-occupancy at (1a) yields a higher conductivity than the (24k) occupancy in the low temperature regime. One plausible reason is that the high concentration of Li-vacancy in the (24k) model becomes easily ordered over long ranges at lower temperatures, thus significantly limiting the mobility of Li-ions.

4. Experimental section

4.1. Sol–gel synthesis of LSTH

LSTH was synthesized via a sol–gel method. Citric acid (Sigma-Aldrich, 99%) and acetylacetone (FisherScientific, 99%) were chosen as chelating agents. The molecular weight ratio of total metal ions, citric acid and acetyl acetone is 1 : 2 : 1. The stoichiometric amount of LiNO₃ (0% excess Li) (FisherScientific, 99%), Sr(NO₃)₂ (FisherScientific, 99%) and 0.4 M citric acid were dissolved in 50 ml DI water. The pH of the aqueous solution was adjusted to 2 with HNO₃ (Sigma-Aldrich, 70%) under vigorous stirring. Stoichiometric amounts of Hf(OEt)₄ (FisherScientific, 99.9%) and Ta(OEt)₅ (Sigma-Aldrich, 99.98%) were dissolved in ethanol (99.9%) and acetylacetone. A pure organic solution with low water content was necessary to avoid the hydrolysis of metal ethoxides. The ethanol solution was heated to 100 °C and stirred vigorously until the solution was clear. The organic solution was then added into the aqueous solution drop by drop at 200 °C and stirred vigorously. The resultant solution was then transferred to a zirconia crucible and heated at 120 °C in a furnace overnight. The dry gel was calcined at 400 °C for 6 hours in a muffle furnace. The resulting powder was finally mixed with 3 wt% of PVB, pelletized and sintered at various temperatures for 6 hours in a muffle furnace covered with 200 wt% of mother power bed. The ionic conductivity data were obtained by electrochemical impedance spectroscopy (EIS) with a Solartron 1255 frequency response analyzer within a frequency ranging from 1M Hz to 100 Hz and 10 mV AC perturbation. The density of LSTH was measured via Archimedes' method.

4.2. Neutron diffraction and Rietveld refinement

Neutron diffraction data were collected using a POWGEN diffractometer at the Spallation Neutron Source, Oak Ridge National Laboratory. Approximately 0.6 g of the sample was loaded into a 6 mm diameter cylindrical vanadium sample can. Data were collected for approximately 3 h in high-resolution mode, using a center wavelength of 0.8 Å covering the d space from 0.25 Å to 7.0 Å. For the Rietveld analysis, the peak profile was described using a convolution of a Gaussian peak shape and a GSAS back-to-back exponential peak shape accounting for asymmetry. The peak profile was obtained by refining a SRM Si 640d.²⁹ Refinement was carried out using TOPAS 6.³⁰

4.3. AIMD simulations

The diffusion behavior of Li-ions in LSTH is first investigated by DFT calculations implemented in the Vienna Ab initio Simulation Package (VASP). We employed the Perdew–Burke–Ernzerhof generalized gradient approximation (GGA-PBE) to approximate the exchange–correlation functional for LSTH, as it has been shown to provide reliable results for superionic conductors while balancing computational cost and accuracy. GGA-PBE has been widely used in various superionic conductors, including Li-thiophospate,^41–43 Na-thiophospate,⁴⁴ rocksalt-type oxides,³⁸ and NASICON.⁴⁵ Given its demonstrated effectiveness across these diverse superionic conductors, GGA-PBE was selected for LSTH structure calculations to ensure both calculation efficiency and accuracy. In addition, single k-points at the Γ point and a plane-wave kinetic energy cutoff of 520 eV were used for AIMD simulations. AIMD simulations with an NVT ensemble are performed for the unit cell of LSTH (154 atoms) with a timestep of 2 fs, and the Nosé–Hoover thermostat is used to control the temperature. All AIMD simulations were run for 160 ps to get sufficient diffusion behaviors. The AIMD simulation results are performed at five temperatures, e.g., 800 K, 900 K, 1000 K, 1200 K and 1500 K. These trajectories are also used for training the machine learning force fields.

4.4. Deep learning potential

The deep learning potential was developed using the deep neural network method implemented in DeePMD-kit (v2.2.7). The structures in the training dataset were provided by AIMD simulation, with 80% of structures randomly selected for training and the remaining 20% for validation. The neural network architecture consisted of an embedding network with {5, 10, 20} neurons and a fitting network with {240, 240, 240} neurons. A cutoff radius of 6 Å was chosen, and the total number of training steps was set to 10⁶, with all other parameters set to their default values. The se_e2_a descriptor was used for training the force field. To ensure the reliability of the ML potential, we included the training and validation models. Additionally, we tested a more complex descriptor, se_e3, and found that it did not significantly alter the observed trends, confirming the accuracy and robustness of the chosen descriptor.

4.5 Machine learning force field molecular dynamics (MLFF-MD) simulations

The molecular dynamics simulations were performed using LAMMPS software based on the machine learning force field. To ensure the convergence of diffusivity at different temperatures, the MLFF-MD simulations were run for 200 ps at 600 ≤ T ≤ 1500 K, 1 ns at 400 ≤ T < 600 K, and 10 ns at 298 ≤ T < 400 K.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

We acknowledge the South Carolina SmartState Center program for financial support. This research used resources at the Spallation Neutron Source (POWGEN, ITPS-31092), a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The Computational resources were provided by the Advanced Cyberinfrastructure Coordination Ecosystem: Services & Support (ACCESS), the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science and the U.S. Department of Energy under contract no. DE-AC02-05CH11231 and the Research Computing Center (RCC) at Florida State University. Computation and data processing were also supported by the supercomputing resources from the Department of Energy's Office of Energy Efficiency and Renewable Energy at the National Renewable Energy Laboratory.

References

1. Q. Wang, B. Liu, Y. Shen, J. Wu, Z. Zhao, C. Zhong and W. Hu, Confronting the Challenges in Lithium Anodes for Lithium Metal Batteries, Adv. Sci., 2021, 8, 2101111.
2. D. Aurbach, E. Zinigrad, Y. Cohen and H. Teller, A short review of failure mechanisms of lithium metal and lithiated graphite anodes in liquid electrolyte solutions, Solid State Ionics, 2002, 148, 405–416.
3. K. N. Wood, E. Kazyak, A. F. Chadwick, K.-H. Chen, J.-G. Zhang, K. Thornton and N. P. Dasgupta, Dendrites and Pits: Untangling the Complex Behavior of Lithium Metal Anodes through Operando Video Microscopy, ACS Cent. Sci., 2016, 2, 790–801.
4. H. Liu, X.-B. Cheng, J.-Q. Huang, H. Yuan, Y. Lu, C. Yan, G.-L. Zhu, R. Xu, C.-Z. Zhao, L.-P. Hou, C. He, S. Kaskel and Q. Zhang, Controlling Dendrite Growth in Solid-State Electrolytes, ACS Energy Lett., 2020, 5, 833–843.
5. R. Chen, A. M. Nolan, J. Lu, J. Wang, X. Yu, Y. Mo, L. Chen, X. Huang and H. Li, The Thermal Stability of Lithium Solid Electrolytes with Metallic Lithium, Joule, 2020, 4, 812–821.
6. D. Zhang, Y. Hao, L. Zheng, Y. Ma, H. Feng and H. Luo, Nitrogen and sulfur co-doped ordered mesoporous carbon with enhanced electrochemical capacitance performance, J. Mater. Chem. A, 2013, 1, 7584–7591.
7. R. Xie, D. Sun, J. Tang, X. Shen, P. Pishva, Y. Zhu, K. Huang and Z. Peng, Ecofriendly, Highly Selective Lithium Extraction by Redox-Mediated Electrodialysis, ACS Cent. Sci., 2024, 10, 2119–2124.
8. Y. Li, H. Xu, P.-H. Chien, N. Wu, S. Xin, L. Xue, K. Park, Y.-Y. Hu and J. B. Goodenough, A Perovskite Electrolyte That Is Stable in Moist Air for Lithium-Ion Batteries, Angew. Chem., Int. Ed., 2018, 57, 8587–8591.
9. D. Sun, N. Wu, C. Qin, R. White and K. Huang, Synthesis and Characterization of Impurity-Free Li_6/16Sr_7/16Ta_3/4Hf_1/4O₃ Perovskite as a Solid-State Lithium-Ion Conductor, Energy Technol., 2023, 11, 2201455.
10. B. Huang, B. Xu, Y. Li, W. Zhou, Y. You, S. Zhong, C.-A. Wang and J. B. Goodenough, Li-Ion Conduction and Stability of Perovskite Li_3/8Sr_7/16Hf_1/4Ta_3/4O₃, ACS Appl. Mater. Interfaces, 2016, 8, 14552–14557.
11. F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, Review on solid electrolytes for all-solid-state lithium-ion batteries, J. Power Sources, 2018, 389, 198–213.
12. B. Xu, B. Huang, H. Liu, H. Duan, S. Zhong and C.-A. Wang, Influence of sintering additives on Li+ conductivity and electrochemical property of perovskite-type Li_3/8Sr_7/16Hf_1/4Ta_3/4O₃, Electrochim. Acta, 2017, 234, 1–6.
13. Y. Kong, Y. Li, J. Lu, X. Wang and J. Li, Effect of doping (Al, La, Sm) on the conductivity of Li_0.375Sr_0.4375Hf_0.25Ta_0.75O3 ceramics, Mater. Res. Express, 2017, 4, 095504.
14. J. K. Burdett, T. Hughbanks, G. J. Miller, J. W. Richardson Jr. and J. V. Smith, Structural-electronic relationships in inorganic solids: powder neutron diffraction studies of the rutile and anatase polymorphs of titanium dioxide at 15 and 295 K, J. Am. Chem. Soc., 1987, 109, 3639–3646.
15. D. Marx and J. Hutter, Ab Initio Molecular Dynamics: Basic Theory and Advanced Methods, Cambridge University Press, 2009, ISBN: 9780511609633.
16. D. E. Galvez-Aranda and J. M. Seminario, Solid electrolyte interphase formation between the Li_0.29La_0.57TiO₃ solid-state electrolyte and a Li-metal anode: an ab initio molecular dynamics study, RSC Adv., 2020, 10, 9000–9015.
17. B. Andriyevsky, K. Doll and T. Jacob, Ab initio molecular dynamics study of lithium diffusion in tetragonal Li₇La₃Zr₂O₁₂, Mater. Chem. Phys., 2017, 185, 210–217.
18. R. Jalem, M. Nakayama, W. Manalastas Jr., J. A. Kilner, R. W. Grimes, T. Kasuga and K. Kanamura, Insights into the Lithium-Ion Conduction Mechanism of Garnet-Type Cubic Li₅La₃Ta₂O₁₂ by ab Initio Calculations, J. Phys. Chem. C., 2015, 119, 20783–20791.
19. R. Roy, Ceramics by the Solution-Sol-Gel Route, Science, 1987, 238, 1664–1669.
20. K. Kitaoka, H. Kozuka, T. Hashimoto and T. Yoko, Preparation of La_0.5Li_0.5TiO₃ perovskite thin films by the sol–gel method, J. Mater. Sci., 1997, 32, 2063–2070.
21. I. Kokal, M. Somer, P. H. L. Notten and H. T. Hintzen, Sol–gel synthesis and lithium ion conductivity of Li₇La₃Zr₂O₁₂ with garnet-related type structure, Solid State Ionics, 2011, 185, 42–46.
22. Z. Rahmati, D. Sun, N. Wu, C. Qin, X. Huang and K. Huang, A “rigid and flexible” multi-functional structure for solid-state Li-metal batteries, Solid State Ionics, 2024, 406, 116484.
23. J. Luo, S. Zhong, Z. Huang, B. Huang and C.-A. Wang, High Li+-conductive perovskite Li_3/8Sr_7/16Ta_3/4Zr_1/4O₃ electrolyte prepared by hot-pressing for all-solid-state Li-ion batteries, Solid State Ionics, 2019, 338, 1–4.
24. B. Huang, S. Zhong, J. Luo, Z. Huang and C. A. Wang, Highly dense perovskite electrolyte with a high Li+ conductivity for Li–ion batteries, J. Power Sources, 2019, 429, 75–79.
25. S. Peng, Y. Chen, X. Zhou, M. Tang, J. Wang, H. Wang, L. Guo, L. Huang, W. Yang and X. Gao, Atomistic origin of high grain boundary resistance in solid electrolyte lanthanum lithium titanate, J Materiomics., 2024, 10, 1214–1221.
26. L. Li, B. Ouyang, Z. Lun, H. Huo, D. Chen, Y. Yue, C. Ophus, W. Tong, G. Chen, G. Ceder and C. Wang, Atomic-scale probing of short-range order and its impact on electrochemical properties in cation-disordered oxide cathodes, Nat. Commun., 2023, 14, 7448.
27. L. Wang, T. He and O. Bin, The Impact of Domain Knowledge on Universal Machine Learning Models, ChemRxiv, 2024, August, Version 1.
28. L. Wang, N. Sunariwal, Y. He, D.-h. Kim, D.-h. Yeon, Y. Zeng, J. Cabana and B. Ouyang, Elemental Stability Rules for High Entropy Disordered Rocksalt Type Li-ion Battery Positive Electrodes, Adv. Energy Mater., 2025, 2404982.
29. A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Special quasirandom structures, Phys. Rev. Lett., 1990, 65, 353–356.
30. Z. Lun, B. Ouyang, D.-H. Kwon, Y. Ha, E. E. Foley, T.-Y. Huang, Z. Cai, H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. Kim, B. D. McCloskey, W. Yang, R. J. Clément, H. Ji and G. Ceder, Cation-disordered rocksalt-type high-entropy cathodes for Li-ion batteries, Nat. Mater., 2021, 20, 214–221.
31. L. Wang and B. Ouyang, Phase Selection Rules of Multi-Principal Element Alloys, Adv. Mater., 2024, 36, 2307860.
32. S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Python Materials Genomics (pymatgen): A robust, open-source python library for materials analysis, Comput. Mater. Sci., 2013, 68, 314–319.
33. https://brown.edu/Departments/Engineering/Labs/avdw/atat/ .
34. J. B. Boyce and B. A. Huberman, Superionic conductors: Transitions, structures, dynamics, Phys. Rep., 1979, 51, 189–265.
35. J. Qi, S. Banerjee, Y. Zuo, C. Chen, Z. Zhu, M. L. Holekevi Chandrappa, X. Li and S. P. Ong, Bridging the gap between simulated and experimental ionic conductivities in lithium superionic conductors, Mater. Today Phys., 2021, 21, 100463.
36. J. Huang, L. Zhang, H. Wang, J. Zhao, J. Cheng and W. E, Deep potential generation scheme and simulation protocol for the Li10GeP2S12-type superionic conductors, J. Chem. Phys., 2021, 154, 094703.
37. B. Ouyang, J. Wang, T. He, C. J. Bartel, H. Huo, Y. Wang, V. Lacivita, H. Kim and G. Ceder, Synthetic accessibility and stability rules of NASICONs, Nat. Commun., 2021, 12, 5752.
38. Y. Chen, Z. Lun, X. Zhao, K. P. Koirala, L. Li, Y. Sun, C. A. O'Keefe, X. Yang, Z. Cai, C. Wang, H. Ji, C. P. Grey, B. Ouyang and G. Ceder, Unlocking Li superionic conductivity in face-centred cubic oxides via face-sharing configurations, Nat. Mater., 2024, 23, 535–542.
39. K. Jun, Y. Sun, Y. Xiao, Y. Zeng, R. Kim, H. Kim, L. J. Miara, D. Im, Y. Wang and G. Ceder, Lithium superionic conductors with corner-sharing frameworks, Nat. Mater., 2022, 21, 924–931.
40. X. He, Y. Zhu, A. Epstein and Y. Mo, Statistical variances of diffusional properties from ab initio molecular dynamics simulations, npj Comput. Mater., 2018, 4, 18.
41. Y. Sun, B. Ouyang, Y. Wang, Y. Zhang, S. Sun, Z. Cai, V. Lacivita, Y. Guo and G. Ceder, Enhanced ionic conductivity and lack of paddle-wheel effect in pseudohalogen-substituted Li argyrodites, Matter, 2022, 5, 4379–4395.
42. P.-H. Chien, B. Ouyang, X. Feng, L. Dong, D. Mitlin, J. Nanda and J. Liu, Promoting Fast Ion Conduction in Li-Argyrodite through Lithium Sublattice Engineering, Chem. Mater., 2024, 36, 382–393.
43. B. Lee, K. Jun, B. Ouyang and G. Ceder, Weak Correlation between the Polyanion Environment and Ionic Conductivity in Amorphous Li–P–S Superionic Conductors, Chem. Mater., 2023, 35, 891–899.
44. B. Ouyang, Y. Wang, Y. Sun and G. Ceder, Computational Investigation of Halogen-Substituted Na Argyrodites as Solid-State Superionic Conductors, Chem. Mater., 2020, 32, 1896–1903.
45. J. Wang, T. He, X. Yang, Z. Cai, Y. Wang, V. Lacivita, H. Kim, B. Ouyang and G. Ceder, Design principles for NASICON super-ionic conductors, Nat. Commun., 2023, 14, 5210.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5ta01157d

---