 Open Access Article
Open Access ArticleCategory-specific topological learning of metal–organic frameworks†
Dong
Chen
a,
Chun-Long
Chen
 b and
Guo-Wei
Wei
b and
Guo-Wei
Wei
 *acd
*acd
aDepartment of Mathematics, Michigan State University, MI 48824, USA. E-mail: weig@msu.edu
bPhysical Sciences Division, Pacific Northwest National Laboratory, Richland, Washington 99354, USA. E-mail: chunlong.chen@pnnl.gov
cDepartment of Electrical and Computer Engineering, Michigan State University, MI 48824, USA
dDepartment of Biochemistry and Molecular Biology, Michigan State University, MI 48824, USA
First published on 24th February 2025
Abstract
Metal–organic frameworks (MOFs) are porous, crystalline materials with high surface area, adjustable porosity, and structural tunability, making them ideal for diverse applications. However, traditional experimental and computational methods have limited scalability and interpretability, hindering effective exploration of MOF structure–property relationships. To address these challenges, we introduce, for the first time, a category-specific topological learning (CSTL), which combines algebraic topology with chemical insights for robust property prediction. The model represents MOF structures as simplicial complexes and incorporates elemental categorizations to enable balanced, interpretable machine learning study. By integrating category-specific persistent homology, CSTL captures both global and local structural characteristics, rendering multi-dimensional, category-specific descriptors that support a predictive model with high accuracy and robustness across eight MOF datasets, outperforming all previous results. This alignment of topological and chemical features enhances the predictive power and interpretability of CSTL, advancing understanding of structure–property relationships of MOFs and promoting efficient material discovery.
1 Introduction
Metal–organic frameworks (MOFs) are a unique class of porous materials made up of metal ions or clusters connected to organic ligands, forming crystalline structures with remarkable tunability. Their customizable properties, including high surface area, adjustable porosity, and structural versatility, make MOFs highly suitable for a range of applications,1–4 such as gas storage,5 separation,6 catalysis,7,8 and sensing.9 Although the design possibilities for MOFs are vast, with potentially infinite structures that can be synthesized. A thorough understanding of the relationship between MOF structure and its properties is therefore crucial for designing MOFs tailored to specific applications.10,11 However, challenges remain. Traditional experimental methods, while valuable for providing insights into MOF behavior, can be labor-intensive, costly, and limited in scope, hindering the ability to explore the extensive chemical space that MOFs occupy. Computational methods, such as molecular dynamics (MD),12 enable the simulation of atomic motion over time and can be performed using either classical force fields13 or first-principles methods, i.e., density functional theory (DFT).14 As a first-principles approach, DFT provides a quantum mechanical description of material properties and can be used in MD simulations. However, both classical and DFT-based MD often face scalability challenges,15 making simulations computationally prohibitive, particularly for large or complex MOF systems, due to the extensive calculations required.16–19Given the limitations of traditional experimental and computational approaches in studying MOF structure–property relationships, advanced data-driven techniques have become essential. Machine learning (ML) than has become increasingly important in studying MOF structure–property relationships and offering a possible solutions to those limitations.20–23 And thanks to the high-throughput computational screening, in particular, has emerged as a valuable approach, has laid a solid foundation by generating extensive, high-quality MOF databases,24,25 such as the CoRE MOF26 and hMOF datasets,27 which enable ML applications in MOF research. Recently, ML models have leveraged geometric descriptors of MOF structures, such as void fraction and pore volume, to predict gas adsorption properties with notable accuracy.28,29 For instance, energy grid histograms have been used as descriptors in ML models to predict gas uptake,30 while other models utilize geometric, atom-type, and chemical feature descriptors to forecast N2/O2 selectivity and diffusivity.28 Despite these advances, prediction accuracy remains a challenge for certain properties. The deep learning (DL) models are introduced, including convolution neural networks, graph neural networks31,32 and transformer-based architectures,33–36 have further enhanced the predictive power for various MOF properties by harnessing large datasets. However, these models come with certain limitations: they can be computationally demanding, often require substantial amounts of data, and sometimes function as ‘black-box’ systems, presenting challenges for interpretability. Addressing these considerations through continued refinement will help enhance the accessibility and interpretability of ML, particularly in advancing MOF discovery.
To address challenges in MOF research, incorporating mathematically derived, explainable features is essential. These features enhance interpretability and contribute to more robust predictive models for MOF properties. Instead of relying solely on conventional descriptors,28,29 advanced mathematical tools from fields like geometry and topology can be employed to extract insightful, high-level features. Techniques such as algebraic graph theory,37,38 persistent homology,39 element-specific persistent homology,40 path topology,41 and topological Laplacians42 are increasingly used in molecular and materials science, offering new methods to capture the structural and functional nuances of complex materials. Mathematics-based methods have already shown success in fields such as drug discovery,38 biological sciences,43 and materials science,44 linking structural features to machine learning models for interpretable and detailed representations. For instance, persistent hyperdigraphs have enabled accurate predictions of protein–ligand interactions by capturing essential molecular details within a rigorous mathematical and transformer framework.45 Mathematical deep learning was a top winner for pose and binding affinity prediction and ranking in D3R Grand Challenges, a worldwide competition series in computer-aided drug design.46,47
In this work, we propose a category-specific topological leaning (CSTL) model for predicting the properties of MOFs. This model introduces a mathematically sound and chemically informed framework designed to analyze and predict MOF properties by integrating both structural complexity and elemental composition. Specifically, each MOF structure is represented as a simplicial complex, establishing a robust topological basis for capturing the unique geometric features of MOFs. To enhance structural analysis with chemical insights, the model incorporates category-specific representations by categorizing elements based on valence electron similarity and occurrence frequency. This categorization ensures a balanced representation across the diverse elemental distributions of MOFs. For each elemental category, the model constructs tailored topological representations and applies persistent homology analysis. This method captures both global and local structural features using topological invariants, while also preserving detailed geometric information—particularly beneficial for materials with complex pore networks and spatially organized atomic structures. The model generates multi-dimensional, category-specific descriptors to encapsulate these intricate structural characteristics, which then serve as input to a gradient boosting tree model for predictive analysis. This approach provides an interpretable, chemically informed framework for predicting a broad range of MOF properties, including eight gas selectivity datasets, with the state-of-the-art performance and improved robustness. By aligning topological features with elemental distributions, CSTL addresses the limitations of conventional approaches, advancing the understanding and prediction of structure–property relationships in MOF materials.
2 Results
2.1 Workflow and schematic of a category-specific topological model
Fig. 1a presents the workflow of our proposed category-specific topological model, designed to analyze and predict properties of MOF structures. In this workflow, the model begins by constructing a simplicial complex representation, which provides a robust topological framework tailored to capture the complex geometry of MOF materials. However, persistent homology itself is not enough for molecular modeling.40,43 To enhance the structural analysis of MOFs with chemical insights, we introduce category-specific topological representations, denoted as categories C0 through C7 and Call, where Call represents the full structure. The necessity of this categorization arises from the fact that different elements play distinct roles in MOF functionality, influencing stability, reactivity, and porosity. Grouping elements into categories facilitates a more systematic understanding of their contributions and interactions within the framework. To establish these categories, an elemental distribution analysis is first conducted across the dataset, as illustrated in Fig. 1b, highlighting the frequency of elements and grouping them based on valence electron similarity and occurrence frequency. Elements with comparable properties are analyzed collectively, while highly prevalent elements such as carbon (C) and hydrogen (H), which play fundamental roles in MOF structures, are assigned distinct categories. This structured approach enables a more insightful analysis of elemental contributions, ultimately improving our ability to interpret and predict MOF properties. Table 1 further specifies these element categories. Notably, the dataset exhibits a broad range of elements, with particular diversity among metallic elements, though specific metallic elements appear less frequently. The categorization process addresses these distribution variances, ensuring that infrequent elements are adequately considered within the predictive model to prevent overemphasis on particular elements' influence.| Element category | Notation |
|---|---|
| Alkali metals, alkaline metals, and other metals | C0 |
| Transition metals, lanthanoids, actinoids | C1 |
| Metalloids | C2 |
| Halogens | C3 |
| Hydrogen (H) | C4 |
| Carbon (C) | C5 |
| Nitrogen (N), phosphorus (P) | C6 |
| Oxygen (O), sulfur (S), selenium (Se) | C7 |
| All | Call |
Based on these elemental categories, category-specific topological representations are constructed for each MOF structure using alpha complexes, which provide a categorized-level topology for these materials. The alpha complex is a type of simplicial complex that generalizes the concept of a graph. Unlike graphs, which capture only pairwise interactions, alpha complexes can represent higher-order interactions, making them well-suited for describing the structural complexity of MOFs. As illustrated in Fig. 5, the simplicial complex (Fig. 5a) can be decomposed into different dimensional components. The 0-simplices (Fig. 5b) correspond to individual points (atoms) in the structure. The 1-simplices, representing edges, encode pairwise interactions, forming a molecular graph. The 2-simplices (Fig. 5c) capture three-body interactions, as they consist of triangles encompassing three points. Higher-order interactions are similarly represented by higher-dimensional simplices. To extract topological features from these complexes, we employ algebraic topology tools such as homology, which captures topological invariants of the structure. Specifically, in this work, we utilize rank of homology groups Hk for k = 0, 1, 2, corresponding to topological invariants in the first three dimensions, providing insights into connectivity, loops, and cavities within the MOF structures.
Subsequently, category-specific persistent homology analysis is applied, denoted as Hk(a,b), where k = 0, 1, 2 represents different topological dimensions, and a = 0 to b = 25 defines the distance interval, allowing a detailed examination of structure across multiple scales. Multi-dimensional category-specific barcodes are then computed to capture geometric and topological information specific to each elemental category. Following this, a featurization step was introduced. In a previous study, Krishnapriyan et al.48 proposed a method that used persistent homology to extract 1D and 2D topological features of MOF pores and channels by computing birth–death pairs across spatial scales. The resulting persistence diagram was then transformed into a 2D vectorized representation using Gaussian kernels and grid discretization. In contrast, instead of generating a 2D vectorized representation, we introduced a featurization step that bins barcodes into fixed intervals ranging from 0 to 25 Å with a resolution of 0.1 Å. This approach captures more geometric details while maintaining a manageable feature dimensionality, making the subsequent machine learning model more effective with limited data. Finally, these features are concatenated to create a comprehensive and category-specific topological descriptor, which is fed into a gradient boosting tree model for predictive modeling across various MOF properties. This approach ensures a balanced representation of elements within the model, enhancing predictive robustness and capturing the nuanced impacts of elemental distribution on MOF properties.
2.2 Properties prediction for MOFs
In this study, we validated the proposed category-specific topological models by predicting key properties of MOF materials, including the Henry's constant for N2 and O2 (mol kg−1 Pa−1), uptake values for N2 and O2 (mol kg−1), self-diffusivity of N2 and O2 at 1 bar (cm2 s−1), and self-diffusivity at infinite dilution (cm2 s−1). Table 3 and the datasets section provide detailed descriptions of these datasets. The prediction outcomes, shown in Fig. 2, demonstrate close alignment between predicted and actual values across all eight datasets, with an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 random split for training, validation, and testing, respectively.33,34 Performance metrics, specifically r2 and MAE, averaged over 100 repeated experiments, are presented in the top left corner of each dataset's plot, underscoring the model's accuracy and reliability.
10 random split for training, validation, and testing, respectively.33,34 Performance metrics, specifically r2 and MAE, averaged over 100 repeated experiments, are presented in the top left corner of each dataset's plot, underscoring the model's accuracy and reliability.
To benchmark the model's performance, we compared it with state-of-the-art models, including MOFTransformer33 and PMTransformer,34 both of which were trained on over a million structures for MOF property prediction. As shown in Table 2, the category-specific topological model consistently outperforms these models across all datasets, achieving superior r2, MAE, and RMSE metrics. It is noted that a universal set of hyperparameters was applied across all eight datasets to ensure robustness and prevent overfitting; validation data was not specifically used. In practical applications, incorporating the validation data into the training set could further enhance model accuracy.
| Datasets | CSTL | Descriptor-based28 | MOFTransformer33 | PMTransformer34 | ||||
|---|---|---|---|---|---|---|---|---|
| r 2 | MAE | RMSE | r 2 | RMSE | r 2 | MAE | MAE | |
| Henry's constant N2 | 0.80 | 4.90 × 10−7 | 7.25 × 10−7 | 0.70 | 8.94 × 10−7 | |||
| Henry's constant O2 | 0.83 | 4.98 × 10−7 | 7.63 × 10−7 | 0.74 | 9.60 × 10−7 | |||
| N2 uptake (mol kg−1) | 0.79 | 4.98 × 10−2 | 7.37 × 10−2 | 0.71 | 8.62 × 10−2 | 0.78 | 7.10 × 10−2 | 6.90 × 10−2 |
| O2 uptake (mol kg−1) | 0.85 | 4.50 × 10−2 | 6.82 × 10−2 | 0.74 | 9.28 × 10−2 | 0.83 | 5.10 × 10−2 | 5.30 × 10−2 |
| Self-diffusion of N2 at 1 bar (cm2 s−1) | 0.80 | 3.40 × 10−5 | 4.69 × 10−5 | 0.76 | 5.00 × 10−5 | 0.77 | 4.52 × 10−5 | 4.53 × 10−5 |
| Self-diffusion of N2 at infinite dilution (cm2 s−1) | 0.80 | 3.75 × 10−5 | 5.15 × 10−5 | 0.76 | 5.50 × 10−5 | |||
| Self-diffusion of O2 at 1 bar (cm2 s−1) | 0.82 | 3.21 × 10−5 | 4.45 × 10−5 | 0.78 | 4.98 × 10−5 | 0.78 | 4.04 × 10−5 | 3.99 × 10−5 |
| Self-diffusion of O2 at infinite dilution (cm2 s−1) | 0.79 | 3.34 × 10−5 | 4.53 × 10−5 | 0.74 | 4.95 × 10−5 | |||
Additionally, we evaluated model robustness by testing on a 20% holdout set across all datasets, with results shown in Fig. S1 and Table S1,† where the proposed model continued to outperform previous models. To ensure the validation stability, we trained 100 models using 10 different seeds, each repeated across 10 randomly initialized predictive models. Heatmaps in Fig. S2–S4† illustrate that variations in seed selection have minimal impact on model performance, confirming the robustness and stability of the predictive model across both fixed and variable data splits. Furthermore, to demonstrate the improvement of CSTL with the categorized features, we apply Call solely for the machine learning model. Under the same parameter settings, we found that CSTL outperforms the Call-only model across all datasets and metrics. The detailed results are provided in Table S3.† This comparison highlights the importance of incorporating additional chemical information through the categorized method.
2.3 Feature analysis for the category-specific topological models
In this work, we propose a category-specific topological model to capture the distinctive characteristics of MOF materials. The model encodes each component's inherent structural and functional attributes by categorizing elements based on their chemical roles and applying persistent homology to analyze each category separately. This approach allows us to represent both the inorganic and organic building blocks of MOFs through distinct topological features, providing a nuanced view that goes beyond treating all atoms as identical.MOFs are typically built from two primary types of components: inorganic metal nodes and organic linkers. Metal ions or clusters in the inorganic units serve as coordination centers and framework backbones, offering stability and structural rigidity while connecting to the organic linkers. Although metal nodes often appear in smaller quantities than organic atoms, they strongly influence the overall material properties.4,49 Because of the diversity among metal elements, it becomes challenging to systematically understand the effect of each metal across all samples—especially for rare metals like Rn, Bi, and Cs that appear infrequently. Organic linkers, composed mainly of carboxylates or nitrogen-containing ligands, bridge these metal nodes, defining the MOF's porosity and connectivity. These organic components typically make up the majority of the framework and play a critical role in establishing the intricate, symmetrical structures of MOFs.
To address these component-specific influences, we group metals into categorical types (C0, C1, C2, C3) while non-metals are clustered into single element or few elements set (C4, C5, C6, and C7) as shown in Table 1. This CSTL thus captures the functional contributions of distinct components within the MOF without overemphasizing elemental diversity, allowing each category to reveal its unique structural influence through topological embedding.
Visualizing the 2D t-SNE reduction in Fig. 3, each green point represents a different MOF material, with distinct clusters reflecting the influence of the CSTL features. Here, key properties such as N2 uptake, O2 uptake, and self-diffusivity values are mapped, where materials with the maximum and minimum values for each property are highlighted. Even without predictive modeling, CSTL features differentiate structures with significant property variations, suggesting that the model inherently captures critical structure–property relationships. For example, the MOF material labeled ELOZEK_clean, which has the lowest N2/O2 uptake values (8.64 × 10−3 mol kg−1 for both N2 and O2) and Henry's constants (8.64 × 10−3 mol kg−1 Pa−1 for both N2 and O2), reflects poor gas absorption. Similarly, COVPAG_clean demonstrates minimal self-diffusivity for N2 (4.15 × 10−7 cm2 s−1), underscoring its limited diffusion capabilities. Such distinctions underscore the power of the CSTL approach to reveal essential structural variations directly through category-specific topological embeddings, distinguishing materials with extreme property values across the MOF dataset.
To quantify the significance of each feature within the proposed CSTL model, we analyzed the tree-based feature importance derived from trained predictive models, as illustrated in Fig. 4. The features with higher importance scores correspond to those that play a significant role in model predictions. This analysis highlights several key trends across different homology dimensions (H0, H1, and H2) and categories, reflecting the structural and categorical influence on the model's predictions.
Generally, we observe that feature importance is concentrated at the beginning of each dimensional homology (H0, H1, and H2) across all categories. This is due to the intentionally large end value set for the intervals (25 Å), ensuring the model's robustness across a broader range of structures, including potential extreme cases beyond the current dataset. Consequently, topological features in the later portion of the interval largely default to zero, explaining the higher importance of features at the beginning of each homology dimension. For category C2, which includes metalloids like B, Si, Ge, As, Sb, Te, Po, and At, the feature importance appears limited. Since these elements have valence electron configurations similar to carbon, and their occurrence within the dataset is low (as shown in Fig. 1b), their influence is often overshadowed by the predominant presence of carbon. This results in carbon having a stronger impact within this category, affecting the overall model importance distribution.
Focusing on Henry's constant, shown in the green-highlighted section of Fig. 4a, we see distinct variations in feature importance between different gases (N2 in blue and O2 in orange). Categories C5 and C7, representing carbon and oxides respectively, exhibit substantial shifts in importance, indicating that carbon-based structures and strongly oxidizing elements influence the selectivity of MOF materials towards these gases. In particular, H2 in C5 suggests that carbon-based cavities strongly affect gas selectivity, while H0 in C7 highlights the role of oxidizing element spacing on selectivity. A similar trend is observed for N2 and O2 uptake properties, as shown in Fig. 4b. For self-diffusivity of N2/O2, whether at 1 bar or infinite dilution, Fig. 4c and d indicate that cycles and cavities within the overall MOF structure, particularly within H1 and H2 of the Call category, are the primary factors influencing diffusion properties. This suggests that the model effectively captures the topological elements critical to gas diffusion across MOF structures.
Furthermore, when comparing properties related to gas absorption (Fig. 4a and b) and diffusivity (Fig. 4c and d), we note that C1 shows significant variations in importance. This implies that metal atoms have a pronounced effect on gas absorptivity, in contrast to their relatively lower impact on diffusivity properties. In conclusion, this feature analysis demonstrates the versatility and precision of the proposed CSTL model, which adeptly balances generalization and prediction accuracy across diverse property predictions. By integrating both structural and elemental distinctions, the model captures the nuanced interactions within MOF materials, offering a robust framework for predicting many functional properties.
3 Conclusion
The unique properties of MOFs stem from the combination of metal clusters and organic linkers, which endow them with high surface area, adjustable porosity, and the ability to finely tune their structures. Despite these advantageous characteristics, traditional experimental and computational methods face significant challenges when scaling to the vast chemical and structural diversity of MOFs, as well as in interpreting the complex structure–property relationships.In this work, we introduce the Category-Specific Topological Learning (CSTL) model, a novel and efficient approach for predicting MOF properties. CSTL combines advanced topological techniques with chemically informed categorization to overcome the limitations of conventional methods. By representing MOF structures as topological objects, i.e., simplicial complexes, CSTL captures both global and local geometric features, while persistent homology facilitates the extraction of topological invariants that provide unique insights into the material's structural properties. Furthermore, the integration of category-specific representations-based on valence electron similarity and occurrence frequency ensures a more balanced and nuanced understanding of elemental distributions in various MOFs. This approach enhances the accuracy and interpretability of predictions related to gas selectivity, adsorption, and other key properties. The multi-dimensional, category-specific descriptors generated by CSTL serve as inputs to a gradient boosting tree model, which demonstrates state-of-the-art performance in predicting a broad range of MOF properties with increased robustness and accuracy.
Additionally, our analysis of the trained model reveals that specific categories, particularly those including transition metals, lanthanoids, and actinoids, exert a more significant influence on adsorption-related properties such as Henry's constant and gas uptake than on self-diffusivity properties. The proposed CSTL model offers a scalable, interpretable, and chemically informed framework that advances our understanding of MOF structure–property relationships. This method provides a powerful tool for the rational design of MOFs with targeted properties, accelerating the discovery of new materials for diverse applications, including energy storage, environmental remediation, and beyond. By bridging the gap between structural complexity and chemical composition, CSTL represents a significant advancement in the computational modeling of advanced materials.
4 Method
4.1 Datasets
All datasets used in this study originate from the CoRE MOFs 2019 database.26 The properties of interest, such as O2 and N2 selectivity, were simulated in earlier studies.26 Certain entries, identified as outliers, were found to lie at the extreme upper end of the distribution, significantly distant from the majority of data points.28 To enhance the robustness and reliability of the models, these outliers were excluded. Additionally, the data used for validating property predictions was further refined by applying upper-limit threshold values, as outlined in the work of Orhan et al.28 This filtering process removed the outliers, resulting in a more uniform and comprehensive distribution, ensuring a well-represented target-variable space. The filtering methodology follows that of Orhan et al.28 To ensure a clear and transparent comparison, we compiled the data information for all methods compared in this study, as summarized in Table S1† In this study, the input features were derived solely from MOF structural data stored in CIF files, without the use of any additional descriptors. Detailed information about the datasets, including the filtered properties and prediction performance, is provided in Table 3.| Datasets (properties) | Sizes | Train![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) valide valide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) test test |
Splitting method |
|---|---|---|---|
| Henry's constant of N2 (mol kg−1 Pa−1) | 4744 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| Henry's constant of O2 (mol kg−1 Pa−1) | 5036 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| N2 uptake (mol kg−1) | 5132 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| O2 uptake (mol kg−1) | 5241 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| Self-diffusivity of N2 at 1 bar (cm2 s−1) | 5056 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| Self-diffusivity of N2 at infinite dilution (cm2 s−1) | 5192 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| Self-diffusivity of O2 at 1 bar (cm2 s−1) | 5223 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
| Self-diffusivity of O2 at infinite dilution (cm2 s−1) | 5097 | 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 10 |
Random split |
4.2 Category-specific topology
 | (1) |
A simplicial complex K is a collection of simplices such that (1) every face of a simplex in K is also in K, and (2) the intersection of any two simplices is either empty or a common face.
In this work, we represent MOF structures using simplicial complexes, where atoms are 0-simplices (vertices), bonds are 1-simplices (edges), and higher-order interactions, such as atomic rings and cavities, are captured as higher-dimensional simplices. This approach allows us to model not only the pairwise connections but also the higher-order geometric and topological features essential for understanding the physical and chemical properties of MOFs. In the category-specific representation framework for MOF structures, all atoms are grouped into distinct sets based on the categories listed in Table 1, denoted as C0 to C7. Additionally, Call represents the set containing all atoms. For each category-specific set, topological representations are constructed to capture the interactions among atoms across different categories.
 . The boundary operator ∂k maps k-chains to (k – 1)-chains, defined as:
. The boundary operator ∂k maps k-chains to (k – 1)-chains, defined as: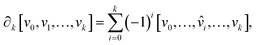 | (2) |
![[small nu, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e1dd.gif) i indicates the omission of vertex vi. This operation helps identify cycles (chains with no boundary) and boundaries (chains that are boundaries of higher-dimensional simplices). The k-th homology group Hk is then defined as:
i indicates the omission of vertex vi. This operation helps identify cycles (chains with no boundary) and boundaries (chains that are boundaries of higher-dimensional simplices). The k-th homology group Hk is then defined as:| Hk = ker(∂k)/im(∂k+1), | (3) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∂k means the kernel of the boundary ∂k, and the Bk = im
∂k means the kernel of the boundary ∂k, and the Bk = im![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∂k+1 represents the image of the boundary ∂k+1.
∂k+1 represents the image of the boundary ∂k+1.
To capture how these topological features vary with the spatial scale, persistent homology is introduced.39,50,51 It tracks the evolution of homological features as a parameter (e.g., bond length or distance threshold) changes. This is achieved through a filtration, a sequence of nested subcomplexes {Ki} where K0 ⊆ K1 ⊆…⊆ Kn. There are some common used filtration methods, such Vietoris–Rips complex,52 Cech complex,53 and alpha complex.54 In this work, we employ the alpha complex for analyzing MOF structures. The alpha complex is constructed based on the Delaunay triangulation of the atomic positions. For a given parameter α, a simplex (e.g., an edge, triangle, or tetrahedron) is included in the complex if the radius of the smallest empty circumsphere that encloses it is less than or equal to α. As α increases, the alpha complex grows, progressively capturing larger topological features in the MOF structure, such as rings, tunnels, and cavities, an example is shown Fig. 5f.
Persistent homology quantifies the persistence of these features across different scales, revealing stable patterns that correspond to critical geometric and chemical properties of the MOF. Each k-th homology group is tracked across the filtration, providing insights into how certain features (e.g., porosity or connectivity) appear, merge, and disappear as the structure evolves. These persistent patterns are typically visualized using barcodes,55 where the length of each bar represents the lifespan of a particular topological feature. An example of barcodes corresponding to the alpha complex is shown in Fig. 5g, and the loops represented in Fig. 5f are highlighted at filtration parameters α = 2 and 3.
Our method involves two main stages: (1) for a given MOF structure, category-specific topological representations are constructed based on the elemental types of atoms, categorized as C0 to C7, along with an additional set Call containing all atoms. (2) The persistent homology of each category from stage (1) is computed to capture global and category-level topological patterns, characterized by their Betti numbers in the H0, H1, and H2 homology spaces. This approach allows the topological analysis to incorporate both structural and chemical information. For each category and each homology dimension, we employ a grid-based method to generate the topological embeddings. Specifically, we construct a grid ranging from 0 to 25 Å with a step size of 0.1 Å and record the Betti numbers (i.e., the number of topological features that persist at each scale). This process yields a feature vector of length 750 (250 steps × 3 homology dimensions: H0, H1, and H2) for each element category. Here, each 250 features are denoted as one feature group. By concatenating these feature vectors across all eight categories, we obtain a 6000-dimensional representation. When combined with the features derived from the entire MOF structure, the final topological embedding results in a 6750-dimensional vector that integrates both global structural patterns and category-specific chemical information.
4.3 Predictive modeling
In this work, a Gradient Boosting Tree (GBT) model was constructed to perform regression analysis using the proposed category-specific topological embedding as input features. Gradient boosting is an ensemble learning method that builds multiple weak learners (typically decision trees) sequentially, where each tree is trained to correct the errors made by the previous ones, thereby producing a more accurate model. We implemented the gradient boosting regressor from Scikit-learn,56 optimizing the squared error loss function. The model parameters were set as follows: max_depth = 7, max_features = ‘sqrt’, min_samples_leaf = 1, min_samples_split = 2, n_estimators = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, and subsample = 0.5. These settings were not fine-tuned, as we aimed to demonstrate the robustness of the proposed predictive model with a single set of hyperparameters.
000, and subsample = 0.5. These settings were not fine-tuned, as we aimed to demonstrate the robustness of the proposed predictive model with a single set of hyperparameters.
All input features were normalized using standard scaling, and the target properties were standardized to facilitate regression analysis. For model evaluation, we split the dataset into train, validation, and test sets using an 80%, 10%, and 10% ratio, respectively.28,33 Since we used a universal set of hyperparameters, the validation set was not employed for model selection. Instead, 80% of the data was used for training to establish a fair comparison with previous works. The results for the test set (10%) and for both the test and validation sets combined (20%) are reported to assess the model's performance comprehensively.
To ensure robust evaluation, we repeated the random data split 10 times, and for each split, 10 models were trained with different random seeds, resulting in a total of 100 models per dataset. The performance metrics, including root mean square error (RMSE), mean absolute error (MAE), and r2 correlation, were averaged over these 100 models and reported as the final results (as seen in ESI Section †). This approach of using a single set of hyperparameters and a consistent evaluation protocol highlights the robustness of the predictive model, making the results reliable and comparable to existing methods in the literature.
Data availability
The datasets utilized in this work are derived from the structures available in the CoRE MOFs 2019 database.26 The properties for each dataset were obtained using the methods outlined in Orhan et al.28Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported in part by NIH grants R01GM126189, R01AI164266, and R35GM148196, National Science Foundation Grants DMS2052983 and IIS-1900473, Michigan State University Research Foundation, and Bristol-Myers Squibb 65109. D. C. was supported in part by the AMS-Simons Travel Grant. C.-L. C. gratefully acknowledges financial support from the Defense Threat Reduction Agency (Project CB11141), and the Department of Energy (DOE), Office of Science, Office of Basic Energy Sciences (BES) under an award FWP 80124 at Pacific Northwest National Laboratory (PNNL). PNNL is a multiprogram national laboratory operated for the Department of Energy by Battelle under Contract DE-AC05-76RL01830.References
- R. Freund, O. Zaremba, G. Arnauts, R. Ameloot, G. Skorupskii, M. Dincă, A. Bavykina, J. Gascon, A. Ejsmont and J. Goscianska, et al., The current status of mof and cof applications, Angew. Chem., Int. Ed., 2021, 60(45), 23975–24001 CrossRef CAS PubMed.
- S. Kumar, S. Jain, M. Nehra, N. Dilbaghi, G. Marrazza and Ki-H. Kim, Green synthesis of metal–organic frameworks: A state-of-the-art review of potential environmental and medical applications, Coord. Chem. Rev., 2020, 420, 213407 CrossRef CAS.
- C.-L. Chen and A. M. Beatty, Guest inclusion and structural dynamics in 2-d hydrogen-bonded metal- organic frameworks, J. Am. Chem. Soc., 2008, 130(51), 17222–17223 CrossRef CAS PubMed.
- C.-L. Chen, A. M. Goforth, M. D. Smith, C.-Y. Su and H.-C. z. Loye, [co2 (ppca) 2 (h2o)(v4o12) 0.5]: a framework material exhibiting reversible shrinkage and expansion through a single-crystal-to-single-crystal transformation involving a change in the cobalt coordination environment, Angew. Chem., Int. Ed., 2005, 44(41), 6673–6677 CrossRef CAS PubMed.
- S. Ma and H.-C. Zhou, Gas storage in porous metal–organic frameworks for clean energy applications, Chem. Commun., 2010, 46(1), 44–53 RSC.
- Q. Qian, P. A. Asinger, M. J. Lee, G. Han, K. Mizrahi Rodriguez, S. Lin, F. M. Benedetti, A. X. Wu, W. S. Chi and Z. P. Smith, Mof-based membranes for gas separations, Chem. Rev., 2020, 120(16), 8161–8266 CrossRef CAS PubMed.
- J. Y. Lee, O. K. Farha, J. Roberts, K. A. Scheidt, S. B. T. Nguyen and J. T. Hupp, Metal–organic framework materials as catalysts, Chem. Soc. Rev., 2009, 38(5), 1450–1459 RSC.
- K. O. Kirlikovali, Z. Chen, T. Islamoglu, J. T. Hupp and O. K. Farha, Zirconium-based metal–organic frameworks for the catalytic hydrolysis of organophosphorus nerve agents, ACS Appl. Mater. Interfaces, 2020, 12(13), 14702–14720 CrossRef CAS PubMed.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. V. Duyne and J. T. Hupp, Metal–organic framework materials as chemical sensors, Chem. Rev., 2012, 112(2), 1105–1125 CrossRef CAS PubMed.
- Y. J. Colón and R. Q. Snurr, High-throughput computational screening of metal–organic frameworks, Chem. Soc. Rev., 2014, 43(16), 5735–5749 RSC.
- S. Lee, B. Kim, H. Cho, H. Lee, S. Y. Lee, E. S. Cho and J. Kim, Computational screening of trillions of metal–organic frameworks for high-performance methane storage, ACS Appl. Mater. Interfaces, 2021, 13(20), 23647–23654 CrossRef CAS PubMed.
- M. Karplus and G. A. Petsko, Molecular dynamics simulations in biology, Nature, 1990, 347(6294), 631–639 CrossRef CAS PubMed.
- W. D. Cornell, P. Cieplak, C. I. Bayly, I. R. Gould, K. M. Merz, D. M. Ferguson, D. C. Spellmeyer, T. Fox, J. W. Caldwell and P. A. Kollman, A second generation force field for the simulation of proteins, nucleic acids, and organic molecules, J. Am. Chem. Soc., 1995, 117(19), 5179–5197 CrossRef CAS.
- W. Kohn, A. D. Becke and R. G. Parr, Density functional theory of electronic structure, J. Phys. Chem., 1996, 100(31), 12974–12980 CrossRef CAS.
- L. Shao, J. Ma, J. L. Prelesnik, Y. Zhou, M. Nguyen, M. Zhao, S. A. Jenekhe, S. V. Kalinin, A. L. Ferguson and J. Pfaendtner, et al., Hierarchical materials from high information content macromolecular building blocks: construction, dynamic interventions, and prediction, Chem. Rev., 2022, 122(24), 17397–17478 CrossRef CAS PubMed.
- H. Daglar and S. Keskin, Recent advances, opportunities, and challenges in high-throughput computational screening of mofs for gas separations, Coord. Chem. Rev., 2020, 422, 213470 CrossRef CAS.
- K. Torkelson, N. Y. Naser, X. Qi, Z. Li, W. Yang, K. Pushpavanam, C.-L. Chen, F. Baneyx and J. Pfaendtner, Rational design of novel biomimetic sequence-defined polymers for mineralization applications, Chem. Mater., 2024, 36(2), 786–794 CrossRef CAS.
- M. Zhao, S. Zhang, R. Zheng, S. Alamdari, C. J. Mundy, J. Pfaendtner, L. D. Pozzo, C.-L. Chen, J. J. De Yoreo and A. L. Ferguson, Computational and experimental determination of the properties, structure, and stability of peptoid nanosheets and nanotubes, Biomacromolecules, 2023, 24(6), 2618–2632 CrossRef CAS PubMed.
- S. Yadav Schmid, M. Xiang, J. A. Hammons, S. T. Mergelsberg, B. S. Harris, T. Ferron, W. Yang, W. Zhou, R. Zheng and S. Zhang, et al., Influence of peptoid sequence on the mechanisms and kinetics of 2d assembly, ACS Nano, 2024, 18(4), 3497–3508 CrossRef CAS PubMed.
- J. Wei, X. Chu, X.-Y. Sun, K. Xu, H.-X. Deng, J. Chen, Z. Wei and M. Lei, Machine learning in materials science, InfoMat, 2019, 1(3), 338–358 CrossRef CAS.
- Y. Luo, S. Bag, O. Zaremba, A. Cierpka, J. Andreo, S. Wuttke, P. Friederich and M. Tsotsalas, Mof synthesis prediction enabled by automatic data mining and machine learning, Angew. Chem., Int. Ed., 2022, 61(19), e202200242 CrossRef CAS PubMed.
- S. Chong, S. Lee, B. Kim and J. Kim, Applications of machine learning in metal-organic frameworks, Coord. Chem. Rev., 2020, 423, 213487 CrossRef CAS.
- Z. Han, Y. Yang, J. Rushlow, J. Huo, Z. Liu, Yu-C. Hsu, R. Yin, M. Wang, R. Liang and K.-Y. Wang, et al., Development of the design and synthesis of metal–organic frameworks (mofs)–from large scale attempts, functional oriented modifications, to artificial intelligence (ai) predictions, Chem. Soc. Rev., 2025, 54(1), 367–395 RSC.
- D. Banerjee, C. M. Simon, A. M. Plonka, R. K. Motkuri, J. Liu, X. Chen, B. Smit, J. B. Parise, M. Haranczyk and P. K. Thallapally, Metal–organic framework with optimally selective xenon adsorption and separation, Nat. Commun., 2016, 7(1), 1–7 Search PubMed.
- P. Z. Moghadam, Y. G. Chung and R. Q. Snurr, Progress toward the computational discovery of new metal–organic framework adsorbents for energy applications, Nat. Energy, 2024, 9(2), 121–133 CrossRef CAS.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling and J. S. Camp, et al., Advances, updates, and analytics for the computation-ready, experimental metal–organic framework database: Core mof 2019, J. Chem. Eng. Data, 2019, 64(12), 5985–5998 CrossRef CAS.
- C. E. Wilmer, M. Leaf, C. Y. Lee, K. F. Omar, B. G. Hauser, J. T. Hupp and R. Q. Snurr, Large-scale screening of hypothetical metal–organic frameworks, Nat. Chem., 2012, 4(2), 83–89 CrossRef CAS PubMed.
- I. B. Orhan, H. Daglar, S. Keskin, Tu C. Le and R. Babarao, Prediction of o2/n2 selectivity in metal–organic frameworks via high-throughput computational screening and machine learning, ACS Appl. Mater. Interfaces, 2021, 14(1), 736–749 CrossRef PubMed.
- A. Nandy, C. Duan and H. J. Kulik, Using machine learning and data mining to leverage community knowledge for the engineering of stable metal–organic frameworks, J. Am. Chem. Soc., 2021, 143(42), 17535–17547 CrossRef CAS PubMed.
- B. J. Bucior, N. Scott Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, K. F. Omar, N. Bagheri and R. Q. Snurr, Energy-based descriptors to rapidly predict hydrogen storage in metal–organic frameworks, Mol. Syst. Des. Eng., 2019, 4(1), 162–174 RSC.
- A. S. Rosen, S. M. Iyer, D. Ray, Z. Yao, A. Aspuru-Guzik, L. Gagliardi, J. M. Notestein and R. Q. Snurr, Machine learning the quantum-chemical properties of metal–organic frameworks for accelerated materials discovery, Matter, 2021, 4(5), 1578–1597 CrossRef CAS.
- T. Xie and J. C. Grossman, Crystal graph convolutional neural networks for an accurate and interpretable prediction of material properties, Phys. Rev. Lett., 2018, 120(14), 145301 CrossRef CAS PubMed.
- Y. Kang, H. Park, B. Smit and J. Kim, A multi-modal pre-training transformer for universal transfer learning in metal–organic frameworks, Nat. Mach. Intell., 2023, 5(3), 309–318 CrossRef.
- H. Park, Y. Kang and J. Kim, Enhancing structure–property relationships in porous materials through transfer learning and cross-material few-shot learning, ACS Appl. Mater. Interfaces, 2023, 15(48), 56375–56385 CrossRef CAS PubMed.
- Z. Cao, R. Magar, Y. Wang and A. B. Farimani, Moformer: self-supervised transformer model for metal–organic framework property prediction, J. Am. Chem. Soc., 2023, 145(5), 2958–2967 CrossRef CAS PubMed.
- P. Chen, R. Jiao, J. Liu, Y. Liu and Y. Lu, Interpretable graph transformer network for predicting adsorption isotherms of metal–organic frameworks, J. Chem. Inf. Model., 2022, 62(22), 5446–5456 CrossRef CAS PubMed.
- D. D. Nguyen and G.-W. Wei, Agl-score: algebraic graph learning score for protein–ligand binding scoring, ranking, docking, and screening, J. Chem. Inf. Model., 2019, 59(7), 3291–3304 CrossRef CAS PubMed.
- D. Chen, K. Gao, D. D. Nguyen, X. Chen, Y. Jiang, G.-W. Wei and F. Pan, Algebraic graph-assisted bidirectional transformers for molecular property prediction, Nat. Commun., 2021, 12(1), 3521 CrossRef CAS PubMed.
- A. Zomorodian and G. Carlsson, Computing persistent homology, in Proceedings of the Twentieth Annual Symposium on Computational Geometry, 2004, pp. 347–356 Search PubMed.
- Z. Cang and G.-W. Wei, Integration of element specific persistent homology and machine learning for protein-ligand binding affinity prediction, Int. J. Numer. Method. Biomed. Eng., 2018, 34(2), e2914 CrossRef PubMed.
- D. Chen, J. Liu, J. Wu, G.-W. Wei, F. Pan and S.-T. Yau, Path topology in molecular and materials sciences, J. Phys. Chem. Lett., 2023, 14(4), 954–964 CrossRef CAS PubMed.
- R. Wang, D. D. Nguyen and G.-W. Wei, Persistent spectral graph, Int. J. Numer. Method. Biomed. Eng., 2020, 36(9), e3376 CrossRef PubMed.
- Z. Cang and G.-W. Wei, Topologynet: Topology based deep convolutional and multi-task neural networks for biomolecular property predictions, PLoS Comput. Biol., 2017, 13(7), e1005690 CrossRef PubMed.
- Y. Jiang, D. Chen, X. Chen, T. Li, G.-W. Wei and F. Pan, Topological representations of crystalline compounds for the machine-learning prediction of materials properties, npj Comput. Mater., 2021, 7(1), 28 CrossRef CAS PubMed.
- D. Chen, J. Liu and G.-W. Wei, Multiscale topology-enabled structure-to-sequence transformer for protein–ligand interaction predictions, Nat. Mach. Intell., 2024, 6(7), 799–810 CrossRef.
- D. D. Nguyen, Z. Cang, K. Wu, M. Wang, Y. Cao and G.-W. Wei, Mathematical deep learning for pose and binding affinity prediction and ranking in d3r grand challenges, J. Comput.-Aided Mol. Des., 2019, 33, 71–82 CrossRef CAS PubMed.
- D. D. Nguyen, K. Gao, M. Wang and G.-W. Wei, Mathdl: mathematical deep learning for d3r grand challenge 4, J. Comput.-Aided Mol. Des., 2020, 34, 131–147 CrossRef CAS PubMed.
- A. S. Krishnapriyan, J. Montoya, M. Haranczyk, J. Hummelshøj and D. Morozov, Machine learning with persistent homology and chemical word embeddings improves prediction accuracy and interpretability in metal-organic frameworks, Sci. Rep., 2021, 11(1), 8888 CrossRef CAS PubMed.
- R. C. Rohde, K. M. Carsch, M. N. Dods, H. Z. H. Jiang, A. R. McIsaac, R. A. Klein, H. Kwon, S. L. Karstens, Y. Wang and A. J. Huang, et al., High-temperature carbon dioxide capture in a porous material with terminal zinc hydride sites, Science, 2024, 386(6723), 814–819 CrossRef CAS PubMed.
- H. Edelsbrunner, Geometry and Topology for Mesh Generation, Cambridge University Press, 2001 Search PubMed.
- J. Z. Afra, Topology for Computing, Cambridge University Press, 2005, vol. 16 Search PubMed.
- J.-C. Hausmann, et al., On the Vietoris-Rips complexes and a cohomology theory for metric spaces, Université de Genève-Section de Mathématiques, 1994 Search PubMed.
- R. W. Ghrist, Elementary Applied Topology, Createspace, Seattle, 2014, vol. 1 Search PubMed.
- H. Edelsbrunner, Smooth surfaces for multi-scale shape representation, in International Conference on Foundations of Software Technology and Theoretical Computer Science, Springer, 1995, pp. 391–412 Search PubMed.
- R. Ghrist, Barcodes: the persistent topology of data, Bull. Am. Math. Soc., 2008, 45(1), 61–75 CrossRef.
- F. Pedregosa, G. Varoquaux, A. Gramfort, M. Vincent, T. Bertrand, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss and D. Vincent, et al., Scikit-learn: Machine learning in python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta08877h |
| This journal is © The Royal Society of Chemistry 2025 |





