 Open Access Article
Open Access ArticleExistence of nonequilibrium glasses in the degenerate stealthy hyperuniform ground-state manifold
Salvatore
Torquato
 *abcd and
Jaeuk
Kim
cba
*abcd and
Jaeuk
Kim
cba
aDepartment of Chemistry, Princeton University, Princeton, New Jersey 08544, USA
bDepartment of Physics, Princeton University, Princeton, New Jersey 08544, USA
cPrinceton Materials Institute, Princeton University, Princeton, New Jersey 08544, USA
dProgram in Applied and Computational Mathematics, Princeton University, Princeton, New Jersey 08544, USA. E-mail: torquato@princeton.edu
First published on 2nd June 2025
Abstract
Stealthy interactions are an emerging class of nontrivial, bounded long-ranged oscillatory pair potentials with classical ground states that can be disordered, hyperuniform, and infinitely degenerate. Their hybrid crystal-liquid nature endows them with novel physical properties with advantages over their crystalline counterparts. Here, we show the existence of nonequilibrium hard-sphere glasses within this unusual ground-state manifold as the stealthiness parameter χ tends to zero that are remarkably configurationally extremely close to hyperuniform 3D maximally random jammed (MRJ) sphere packings. The latter are prototypical glasses since they are maximally disordered, perfectly rigid, and perfectly nonergodic. Our optimization procedure, which leverages the maximum cardinality of the infinite ground-state set, not only guarantees that our packings are hyperuniform with the same structure-factor scaling exponent as the MRJ state, but they share other salient structural attributes, including a packing fraction of 0.638, a mean contact number per particle of 6, gap exponent of 0.44(1), and pair correlation functions g2(r) and structures factors S(k) that are virtually identical to one another for all r and k, respectively. Moreover, we demonstrate that stealthy hyperuniform packings can be created within the disordered regime (0 < χ < 1/2) with heretofore unattained maximal packing fractions. As χ increases from zero, the particles in this family of disordered packings always form interparticle contacts, albeit with sparser contact networks as χ increases from zero, resulting in linear polymer-like chains of contacting particles with increasingly shorter chain lengths. The capacity to generate ultradense stealthy hyperuniform packings for all χ opens up new materials applications in optics and acoustics.
1. Introduction
Disordered hyperuniform many-particle systems1,2 are an emerging exotic class of amorphous states of matter that arise in a variety of contexts and fields, including the eigenvalues of random matrices,3 nontrivial zeros of the Riemann zeta function,4 maximally random jammed sphere packings,5,6 avian photoreceptor mosaics,7 antigen receptors in the immune system,8 fermionic ground states,9,10 nonequilibrium phase transitions,11–14 active matter,15 quasicrystals,16,17 distribution of prime numbers,18 the large-scale structure of the universe,19 soft polymeric materials,20 quantum spin liquids,21 and myriads of other examples (see ref. 2 and references therein). These correlated disordered systems are characterized by a “hidden order” due to the unusual combination of being statistically isotropic without any long-range order, like ordinary liquids, and yet anomalously suppress infinite-wavelength density fluctuations, like perfect crystals and quasicrystals.A disordered hyperuniform many-particle system in d-dimensional Euclidean space ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d is one in which the structure factor S(k) vanishes as the wavenumber k ≡ |k| tends to zero.1,2 An important subclass are disordered stealthy hyperuniform (SHU) systems in which S(k) = 0 within a spherical “exclusion” region of radius K centered at the origin, i.e., S(k) = 0 for 0 ≤ k < K. SHU many-particle systems are derived as classical ground states of many-particle systems of certain nontrivial, bounded long-ranged oscillatory pair potentials. Remarkably, these hyperuniform ground states can be disordered and infinitely degenerate in the thermodynamic limit.22–24 The fact that these singular isotropic amorphous states of matter have the character of crystals (S(k) = 0 from infinite wavelengths to intermediate wavelengths of order 2π/K)2,25–27 and liquids (statistical isotropy on small length scales)2 endow them with novel optical, transport, and mechanical properties with advantages over their crystalline counterparts.28–47
d is one in which the structure factor S(k) vanishes as the wavenumber k ≡ |k| tends to zero.1,2 An important subclass are disordered stealthy hyperuniform (SHU) systems in which S(k) = 0 within a spherical “exclusion” region of radius K centered at the origin, i.e., S(k) = 0 for 0 ≤ k < K. SHU many-particle systems are derived as classical ground states of many-particle systems of certain nontrivial, bounded long-ranged oscillatory pair potentials. Remarkably, these hyperuniform ground states can be disordered and infinitely degenerate in the thermodynamic limit.22–24 The fact that these singular isotropic amorphous states of matter have the character of crystals (S(k) = 0 from infinite wavelengths to intermediate wavelengths of order 2π/K)2,25–27 and liquids (statistical isotropy on small length scales)2 endow them with novel optical, transport, and mechanical properties with advantages over their crystalline counterparts.28–47
While it is commonplace for quantum-mechanical ground states to be disordered for a variety of typical Hamiltonians,9,10,48–54 it is unusual for classical many-particle systems to remain disordered down to absolute zero temperature with nontrivial interactions, as is the case for disordered SHU ground states. The standard collective-coordinate optimization scheme has been used to create disordered SHU ground states from random initial configurations of N particles within a simulation cell with pair potential v(r) under periodic boundary conditions.22,23,55–57 The total potential energy has the Fourier-space form
 | (1) |
 | ||
| Fig. 1 The three-dimensional direct-space long-ranged pair potential v(r) versus the dimensionless distance rK associated with the Fourier transform ṽ(k) that is unity for k < K and zero otherwise, i.e., ṽ(k) = v0Θ(K − k). We choose v0 = 1. This pair potential will be used in our subsequent computations; see eqn (3) with d = 3. | ||
SHU ground states have been numerically generated with ultrahigh accuracy.23,55,56 The disordered ground-state regime for d ≥ 2 occurs when 0 < χ < 1/2,24 where χ ≡ M(K)/d(N − 1) is a dimensionless stealthiness parameter† that specifies the number of independently constrained wavevectors, M(K), (within the exclusion sphere of radius K) relative to the total number of degrees of freedom of the system, d(N − 1).‡ Importantly, the dimensionality of the configuration space per particle, dc, decreases linearly with χ as dc = d(1 − 2χ) in the thermodynamic limit, explaining the transition from infinitely degenerate disordered phases (when χ < 1/2) to unique crystal structures when χ < 1/2;24 see Fig. 2. Thus, dc is a measure of the cardinality of the infinitely degenerate ground-state manifold set, which, importantly, is maximized in the limit χ → 0. We will see that this distinguished limit plays a central role in the primary results obtained in this paper.
 | ||
| Fig. 2 Phase diagram for d-dimensional SHU ground states (T = 0) as a function of χ for relatively low dimensions with d ≥ 2. The maximal value of χ, denoted by χmax, depends on the space dimension d. Adapted from ref. 24. | ||
In the disordered regime, the nature of the energy landscape allows one to find ground states with exquisite precision23,55,56 with a 100% success rate for relatively large N from random initial conditions. In the limit χ → 0, i.e., when the cardinality of the infinitely degenerate manifold is maximized, the ground states are ideal-gas-like (Poisson-like), and thus particle pairs can get arbitrarily close to one another. As χ increases from zero, the short-range order and minimum pair separation also increase due to an increase in the number of constrained degrees of freedom in a finite-N system.23,24,55 Such high-χ disordered ground states have been generated to create SHU sphere packings by circumscribing the points by identical nonoverlapping spheres.58 However, the success rate to find allowable packing configurations among all ground states obtained with even moderate values of the packing fraction ϕ (<0.25) falls off rapidly with N and vanishes in the thermodynamic limit.59
Is it possible to exploit the huge degeneracy of the energy landscape to obtain much denser stealthy ground-state packings by biasing the search in configuration space so that such atypical portions of the manifold are found? In this article, we show this possible and, by doing so, shed new light on the nature of the infinitely degenerate ground-state manifold under the action of a generalized stealthy long-ranged potential (defined in eqn (2)). We begin by demonstrating that this manifold, counterintuitively, in the zero-stealthy limit (χ → 0) when the cardinality is maximized, contains states that are remarkably configurationally extremely close to the hyperuniform nonequilibrium MRJ sphere packings that were recently reported by Maher et al.6 using the linear programming packing algorithm of Torquato and Jiao.60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) § The MRJ packing state is a prototypical nonequilibrium glass, since it is the most disordered packing subject to strict jamming,¶ resulting in packings that are perfectly nonergodic (i.e., permanently trapped in configuration space) and possess infinite elastic moduli.67,68 For this reason, it is remarkable the aforementioned special ground-state packings and MRJ packings share the following salient structural attributes: pair correlation functions g2(r) and structures factors S(k) that are virtually identical to one another for all r and k, respectively, a packing fraction of 0.638, a mean contact number per particle of 6 and a “gap” exponent of 0.44. Moreover, our 3D ground-state packings become hyperuniform, but appropriately no longer stealthy, in the thermodynamic (infinite-size) limit with the same structure-factor scaling exponent as the MRJ state. Figuratively, this is akin to finding a nonequilibrium “needle” in a “haystack.”
§ The MRJ packing state is a prototypical nonequilibrium glass, since it is the most disordered packing subject to strict jamming,¶ resulting in packings that are perfectly nonergodic (i.e., permanently trapped in configuration space) and possess infinite elastic moduli.67,68 For this reason, it is remarkable the aforementioned special ground-state packings and MRJ packings share the following salient structural attributes: pair correlation functions g2(r) and structures factors S(k) that are virtually identical to one another for all r and k, respectively, a packing fraction of 0.638, a mean contact number per particle of 6 and a “gap” exponent of 0.44. Moreover, our 3D ground-state packings become hyperuniform, but appropriately no longer stealthy, in the thermodynamic (infinite-size) limit with the same structure-factor scaling exponent as the MRJ state. Figuratively, this is akin to finding a nonequilibrium “needle” in a “haystack.”
We also show that a large family of other stealthy hyperuniform packings can be created as χ increases up to 1/2 with heretofore unattained maximal packing fractions. These packings also have interesting structural characteristics; the particles in this family of disordered packings always form interparticle contacts, albeit with sparser contact networks as χ increases from zero, resulting in linear polymer-like chains of contacting particles that progressively possess shorter mean chain lengths. (The reader is referred to ref. 59 for a comprehensive study of SHU packings with and without soft-core repulsions within the disordered regime for d = 1, 2, 3). This capacity to generate ultradense SHU packings opens up new applications in optics and acoustics relative to previous studies that used low-density SHU packings.29,34,36,43,69
The rest of the paper is organized as follows: in Section 2, we describe the modified collective-coordinate optimization scheme and how it is applied to determine the maximal packing fraction of SHU packings with a given value of χ. Here we also describe how to determine whether the corresponding contact networks percolate. In Section 3, we provide results for the ultradense SHU packings with χ tending to zero and select positive values of χ within the disordered regime, including their maximal packing fractions, pair statistics, and mean contact numbers. Finally, in Section 4, we provide concluding remarks and outlook for future work.
2. Simulation method
2.1. Generation of dense disordered SHU packings
To achieve the desired goal of creating ultradense disordered SHU packings, we modify the total potential energy function (1) by including an additional pairwise soft-core repulsive potential u(r) that is bounded, differentiable, and positive with support in the finite range 0 ≤ r < σ:36,57,69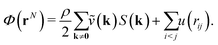 | (2) |
We choose ṽ(k) = v0Θ(K − k), where Θ(x) is the Heaviside step function, yielding the bounded long-ranged pair potential
 | (3) |
A general form of the soft-core repulsion u(r) in the potential energy (2) is
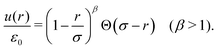 | (4) |
Importantly, the ground states of potential (2) are independent of the ratio of v0/ε0 if v0 and ε0 are positive and finite. We consider a cubic fundamental cell, and set the energy scales to be v0 = 1 and ε0 = 100v0, enabling us to generate valid packings that are ground states in a reasonable amount of computational time for N ≈ 400–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 and nc = 102–104, where nc is the number of configurations. Specifically, using an Intel(R) Xeon(R) CPU (E5-2680, 2.40 GHz), it takes approximately 15 core-hours to generate one 3D ground state with χ = 0.45, ϕ = 0.47, and N = 4000. It takes roughly 130 core-hours on the same CPU to generate one 3D ground state with χ = 9.28 × 10−5, N = 10
774 and nc = 102–104, where nc is the number of configurations. Specifically, using an Intel(R) Xeon(R) CPU (E5-2680, 2.40 GHz), it takes approximately 15 core-hours to generate one 3D ground state with χ = 0.45, ϕ = 0.47, and N = 4000. It takes roughly 130 core-hours on the same CPU to generate one 3D ground state with χ = 9.28 × 10−5, N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774, and ϕ = 0.638.
774, and ϕ = 0.638.
The algorithm to find ultradense SHU ground-state packings is performed as follows: For given parameters of system size N, χ(>0), and target packing fraction ϕ = ϕmax(χ), we begin with a random initial condition in a simple cubic fundamental cell and minimize its potential energy Φ given in eqn (3)via the low-storage Broyden–Fletcher–Goldfarb–Shanno (L-BFGS) algorithm.74,75 The minimization stops when (i) Φ < 5 × 10−20,|| (ii) the number of evaluations exceeds 5 × 106, or (iii) the mean particle displacements are less than 10−15ρ−1/d. After terminating the minimization, we retain the ground-state point pattern that satisfies condition (i) and discard it otherwise. The values of system size N, the number of configurations nc, and stealthiness parameter χ are listed in Table 3.
2.2. Determination of maximum packing fractions
We first determine the maximal target packing fraction of 3D SHU ground states with the smallest value of χ, denoted by χmin. For the simple cubic fundamental cell we consider, χmin is a function of particle number N: | (5) |
| Models | N | ϕ max (0+) | γ |
|---|---|---|---|
| SHU packings | 400 | 0.636 | 0.45(1) |
| SHU packings | 1198 | 0.637 | 0.44(1) |
| SHU packings | 3592 | 0.637 | 0.44(1) |
| SHU packings | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
0.638 | 0.44(1) |
| 3D MRJ packing | 5000 | 0.638 | 0.44(1) |
Using the same procedure, we also numerically determine ϕmax(χ) for χ = 0.10, 0.20, 0.30, 0.35, 0.40, and 0.45, but apply a slightly looser criterion than for χmin to save overall computation cost in both determination of ϕmax(χ) and generation of the ultradense SHU packings. At each χ value, we use either a given number of initial conditions ni(=50) or, at most, 840 core hours to obtain ground states. We consider the largest value of ϕ achieved at least 10% of success ratio as ϕmax(χ). This search is done by varying ϕ from 0.20 to the packing fraction of the densest lattice packing in increments of 0.01. The obtained values of ϕmax(χ) are tabulated in Table 2.
| χ | ϕ max(χ) | Z(D+) | p [%] |
|---|---|---|---|
| 0+ | 0.638 | 6.0(1) | 100.0 |
| 0.10 | 0.61 | 4.388(4) | 100.0 |
| 0.20 | 0.58 | 2.960(4) | 100.0 |
| 0.30 | 0.55 | 1.975(3) | 100.0 |
| 0.35 | 0.53 | 1.514(3) | 38.6 |
| 0.40 | 0.50 | 0.975(23) | 0.0 |
| 0.45 | 0.47 | 0.600(21) | 0.0 |
| N | χ | n c |
|---|---|---|
| 400 | χ min = 2.51 × 10−3 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
| 1198 | χ min = 8.35 × 10−4 | 5000 |
| 3592 | χ min = 2.78 × 10−4 | 1000 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 774 |
χ min = 9.28 × 10−5 | 100 |
| 4000 | 0.10 | 500 |
| 4000 | 0.20 | 500 |
| 4000 | 0.30 | 500 |
| 4000 | 0.35 | 500 |
| 4000 | 0.40 | 500 |
| 4000 | 0.45 | 500 |
2.3. Percolation of contact networks
For the contact networks explained in the caption of Fig. 4, we determine whether they percolate by a simplified version of the algorithm for general networks, explained in ref. 58 and 76. Specifically, we begin by creating a contact network of a configuration in which each vertex (or node) is a particle and an edge is formed between any two particles whose separation is less than σ + 10−3ρ−1/3. For such a network, we randomly choose an initial vertex and recursively search for all vertices connected to it. This search stops under two conditions: (i) when there are no further vertices to explore or (ii) when a newly searched vertex is a periodic copy of the initial vertex. When condition (ii) is met, we terminate the search for that configuration and consider the associated contact network to be percolated. Otherwise, we repeat this procedure up to 1000 different initial vertices for each configuration. Table 2 of the Results section provides the percentage of contact networks that percolate, i.e., topologically connected across the sample.3. Results
Employing our modified collective-coordinate optimization procedure described in Section 2, we demonstrate that our disordered packings, as χ tends to zero, become hyperuniform and non-stealthy in the thermodynamic limit with the same structure-factor scaling exponent as the MRJ state reported in ref. 6. Furthermore, they share other salient structural attributes, including a packing fraction of 0.638, a mean contact number per particle of 6 (isostaticity), a gap exponent γ = 0.44, and pair correlation functions g2(r) and structure factors S(k) that are virtually identical to one another for all r and k, respectively. We begin by showing that we can create other stealthy hyperuniform packings whose particles always form interparticle contacts for positive values of χ as it increases up to 1/2 with heretofore unattained high packing fractions and determine their maximal packing fractions as well as mean contact numbers per particle. Subsequently, we focus on the pair statistics of the hyperuniform packings in the limit χ → 0 and SHU packings with χ = 0.45. We determine the limit χ → 0 by applying χ = χmin(N) given by eqn (5) and the associated total potential Φ given in eqn (9) for a given N to a sequence of increasing system sizes with N = 400, 1198, 3592 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774, yielding χmin = 2.51 × 10−3, 8.35 × 10−4, 2.78 × 10−4 and 9.27 × 10−5, respectively, and then extrapolating to the limit χ = 0 by increasing N. Importantly, the potential (9) guarantees the obtained ground states are (stelathy) hyperuniform for any N, different from compression algorithms. Henceforth, we will refer to this limit simply as χ = 0+.
774, yielding χmin = 2.51 × 10−3, 8.35 × 10−4, 2.78 × 10−4 and 9.27 × 10−5, respectively, and then extrapolating to the limit χ = 0 by increasing N. Importantly, the potential (9) guarantees the obtained ground states are (stelathy) hyperuniform for any N, different from compression algorithms. Henceforth, we will refer to this limit simply as χ = 0+.
3.1. Maximal packing fractions and mean contact numbers
Application of our modified collective-coordinate optimization procedure (see Section 2 for details) within the disordered regime (0 < χ < 1/2) yields achievable packing fractions that are substantially larger than those that can be obtained from the standard collective-coordinate procedure without the soft-core repulsive potential. Importantly, the maximal packing fraction decreases (not increases) as χ increases and approaches χ = 1/2, as seen in Table 1 and Fig. 2(A). The fact that ϕmax is highest in the small-χ limit and then monotonically decreases with χ up to χ = 1/2 is consistent with the decrease in the relative degrees of freedom as χ increases. Such χ-dependence on ϕmax(χ) can be well approximated by the following [1,1] Padé approximant: | (6) |
 | ||
Fig. 3 Parameters of 3D disordered ultradense SHU sphere-packing ground states across stealthiness parameter χ. (A) Maximal packing fraction ϕmax(χ) as a function of χ. The filled circles are simulation data (with N up to 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774 and 102–104 configurations) and the solid curve is the [1,1] Padé approximant of the data given by eqn (6). (B) Mean contact number per particle Z(D+) as a function of χ. The solid line is the theoretical prediction (8). The data in both (A) and (B) are tabulated in Table 2 in the Results section. Note that the gray and orange regions in (A) and (B) correspond to the SAT and UNSAT phases70,71 of the ground state of eqn (2), respectively. The reader is referred to ref. 59 for details. 774 and 102–104 configurations) and the solid curve is the [1,1] Padé approximant of the data given by eqn (6). (B) Mean contact number per particle Z(D+) as a function of χ. The solid line is the theoretical prediction (8). The data in both (A) and (B) are tabulated in Table 2 in the Results section. Note that the gray and orange regions in (A) and (B) correspond to the SAT and UNSAT phases70,71 of the ground state of eqn (2), respectively. The reader is referred to ref. 59 for details. | ||
It is noteworthy that for all χ values within the disordered regime, particles in this family of packings always form interparticle contacts. The quantity
 | (7) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) d, 2χ × d(N − 1) degrees of freedom are already constrained among d(N − 1) total degrees of freedom by the stealthy hyperuniform condition. Thus, the remaining degrees of freedom determine the maximum number of constraints from effectively contacting particles:
d, 2χ × d(N − 1) degrees of freedom are already constrained among d(N − 1) total degrees of freedom by the stealthy hyperuniform condition. Thus, the remaining degrees of freedom determine the maximum number of constraints from effectively contacting particles:| Z(D+) = 2d(1 − 2χ). | (8) |
Fig. 4 shows representative contact networks of the ultradense SHU packings at selected values of χ between 0 to 1/2, some of which percolate across the entire system. At χ = 0+, shown in Fig. 4(A), the contact network percolates and effectively satisfies the isostatic condition Z(D+) ≈ 6.0, implying that these packings are effectively jammed. As χ increases from zero, the contact networks are always sub-isostatic, as predicted by eqn (8). For χ = 0.20, the contact network percolates, and almost all of the spheres are part of it, but the network becomes sparser (contact number decreases) from the isostatic value of 6 for χ → 0 with Z(D+) ≈ 3.0, as seen in Fig. 4(B) and Table 2. As χ increases from 0.20 to 1/2, Z(D+) continues to decrease, i.e., the contact networks become even sparser, resulting in linear polymer-like chains of contacting particles that progressively possess shorter mean chain lengths. This trend is evident in Fig. 4(C) for χ = 0.35 with Z(D+) ≈ 1.5, and in Fig. 4(D) for χ = 0.45 with Z(D+) ≈ 0.6. In addition, approximately 38.6% of the contact networks percolate when χ = 0.35, and they then cease to percolate for the higher values of χ; see Table 2 and Section 2.3 for details about how we estimate percolation behaviors. When χ = 0.45, the non-percolating contact network consists of dimer polymer-like chains. Here, about half of the particles in the packing are monomers. The reader is referred to ref. 59 for the details behind these results for all χ as well as corresponding findings concerning local spatial statistics (nearest-neighbor and minimal pair-distance distributions) for not only 3D cases, but 1D and 2D instances.
3.2. Structure factors
An isostatic value of Z(D+) = 6.0 and packing fraction ϕ = 0.638 are not sufficient to define an MRJ packing. Therefore, we now show that the ground-state packings in the limit χ → 0 (i.e., when the cardinality of the infinitely degenerate ground-state manifold) are configurationally extremely close to the MRJ state, as measured by structure factors S(k) that are virtually the same as one another for all k. While MRJ packings are hyperuniform, they are not perfectly stealthy,6 and hence the limit χ → 0 (corresponding to maximal cardinality of the infinite set of degenerate ground states) is a necessary condition to check if SHU packings have any correspondence to the MRJ state, since the stealthiness vanishes in this limit while being hyperuniform, which importantly implies the thermodynamic (infinite-N) limit. To approach the large-N limit, we study a sequence of increasing systems sizes with N = 400, 1198, 3592 and 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774, while taking χ = χmin(N) given by eqn (5) and then extrapolate to the limit N → ∞. We find that as χ becomes small, the already small stealthy region diminishes in size, and remarkably, the ground states become hyperuniform but not stealthy in the limit χ → 0. We also confirm that the ultradense SHU packings with χ = χmin exhibit the power-law scaling form S(k) ∼ k as k → 0 by extrapolating S(k) in the range of KD < kD ⪅ 1.3, which is consistent with those for MRJ state reported in ref. 6; see the inset of Fig. 5(A). Fig. 5(A) also compares the structure factor for a wide range of wavenumbers for the SHU packings at the largest value of N (=10
774, while taking χ = χmin(N) given by eqn (5) and then extrapolate to the limit N → ∞. We find that as χ becomes small, the already small stealthy region diminishes in size, and remarkably, the ground states become hyperuniform but not stealthy in the limit χ → 0. We also confirm that the ultradense SHU packings with χ = χmin exhibit the power-law scaling form S(k) ∼ k as k → 0 by extrapolating S(k) in the range of KD < kD ⪅ 1.3, which is consistent with those for MRJ state reported in ref. 6; see the inset of Fig. 5(A). Fig. 5(A) also compares the structure factor for a wide range of wavenumbers for the SHU packings at the largest value of N (=10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774) to the recent corresponding MRJ data,6 revealing that they are virtually identical to one another on the scale of this figure.
774) to the recent corresponding MRJ data,6 revealing that they are virtually identical to one another on the scale of this figure.
 | ||
Fig. 5 The structure factor S(k) versus dimensionless wavenumber kD of 3D SHU sphere-packing ground states. (A) Comparison of the data of 3D hyperuniform MRJ sphere packings from ref. 6 to the corresponding structure factor for our 3D hyperuniform sphere-packing ground states in the limit χ → 0, as extrapolated from the various system sizes studied, namely, N = 400, 1198, 3592, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774. Both models have the same packing fraction, ϕ = 0.638. The inset shows S(k) in the range of kD < 2 for SHU sphere-packing ground states with χ = χmin(N) as obtained for the aforementioned sizes and MRJ states. The black dashed line is a linear fit of the data, i.e., S(k) ∼ k in the limit k → 0. (B) 3D SHU sphere-packing ground states with χ = 0.45, N = 4000, ϕ = 0.47, and nc = 500 are shown. In both (A) and (B), D is the hard-sphere diameter. 774. Both models have the same packing fraction, ϕ = 0.638. The inset shows S(k) in the range of kD < 2 for SHU sphere-packing ground states with χ = χmin(N) as obtained for the aforementioned sizes and MRJ states. The black dashed line is a linear fit of the data, i.e., S(k) ∼ k in the limit k → 0. (B) 3D SHU sphere-packing ground states with χ = 0.45, N = 4000, ϕ = 0.47, and nc = 500 are shown. In both (A) and (B), D is the hard-sphere diameter. | ||
By contrast, the structure factors S(k) of the SHU sphere-packing ground states with the larger values of χ are quite distinct from those in the zero-χ limit; see Fig. 5(B) for the case χ = 0.45. When the ground states have large values of χ, S(k) clearly have a wide exclusion region in which S(k) = 0 for small k. Furthermore, the oscillations in S(k) decay more rapidly as wavenumber k increases, reflecting a decrease in the degree of order at short-range length scales due to the formation of dimer polymer-like chains.
3.3. Pair correlation functions and cumulative coordination number
To further confirm the striking correspondence to MRJ packings, we compare its pair correlation function g2(r) to that of our ground-state packings with χ = 0+ in Fig. 6(A) for the largest system size. Again, we see that the pair correlation functions are virtually identical to one another on the scale of this figure, including subtle small-scale structural features. Specifically, they share a Dirac-delta-like peak at r = D, the well-known split second peak seen in disordered jammed packings at and 2, as well as the power-law singularity for near contacts.66 For general dense packings, the exponent γ in the power-law singularity, i.e., g2(r) ∼ (r/D − 1)−γ for 0 < r/D − 1 < 0.2, is expected to increase with increasing short-range order.66 Specifically, γ → 0 means a constant g2 near contact, which is a signature of the ideal gas. In contrast, γ → 1 means that the first and second peaks are clearly separated with a wide range of gaps, which is typical of crystal packings. Thus, γ for the MRJ-like SHU ground states should lie between 0 and 1.
and 2, as well as the power-law singularity for near contacts.66 For general dense packings, the exponent γ in the power-law singularity, i.e., g2(r) ∼ (r/D − 1)−γ for 0 < r/D − 1 < 0.2, is expected to increase with increasing short-range order.66 Specifically, γ → 0 means a constant g2 near contact, which is a signature of the ideal gas. In contrast, γ → 1 means that the first and second peaks are clearly separated with a wide range of gaps, which is typical of crystal packings. Thus, γ for the MRJ-like SHU ground states should lie between 0 and 1.
 | ||
| Fig. 6 Comparisons of 3D hyperuniform sphere-packing ground states (χ = 0+) and 3D MRJ sphere packings in direct space. (A) The pair correlation function g2(r) versus dimensionless distance r/D of the two models. (B) The cumulative coordination number Z(r) versus dimensionless distance r/D of the two models. In both panels, we consider 3D MRJ packings taken from ref. 6 and D is the hard-sphere diameter. In both (A) and (B), two models have the same packing fraction, ϕ = 0.638. | ||
The excellent agreement of the near-contact divergence in the ground-state packings with χ = 0+ and MRJ packings is more apparent in the cumulative coordination number Z(r); see Fig. 6(B). Here, we find that both packings yield the same fit Z(x) ∼ Zfit + Cx1−γ, where x ≡ r/D − 1. In the near-contact region (i.e., 0.001 < x < 0.1), the fitted gap exponents are γ = 0.44(1) for largest ultradense SHU packings with χ = χmin and the MRJ state. Table 1 summarizes the values of γ at various system sizes N. Interestingly, by the same contact criterion stated in the caption of Fig. 4, we estimate the rattler concentration to be about 2%, which is close to the recently reported value for MRJ packings.6
For the SHU packings with the largest value of the stealthiness parameter examined, i.e., χ(=0.45), the pair correlation function g2(r) also possesses a sharp peak at r = D but does not exhibit either a power-law divergence for near contacts nor split second peaks; see Fig. 7. Furthermore, the small-scale oscillations in g2(r) for χ = 0.45 for large r decay slightly faster than those with χ = 0+. Such differences in g2(r) for the SHU ground states with χ = 0+ and 0.45 arise because those with χ = 0.45 form only a small number of dimers but lack additional short-range order.
4. Conclusions and discussion
In sum, we have shown that one can use the modified collective-coordinate optimization procedure [cf.eqn (2)] to create disordered SHU ground-state packings with packing fractions that far exceed those produced in our previous work within the disordered χ regime,36,69 thus advancing our understanding of the nature of this highly degenerate ground-state manifold. We revealed that in the small-χ limit, the ground-state packings associated with eqn (2) are hyperuniform, effectively jammed, and configurationally very near MRJ sphere packings, as measured by the same values of the packing fraction and mean contact number per particle, similar rattler concentrations, as well as pair statistics, both S(k) and g2(r), that are strikingly virtually identical to one another. The extraordinary existence of nonstealthy hyperuniform MRJ-like packings in the degenerate SHU ground-state manifold is possible because the cardinality of this infinite set is maximized as the stealthiness parameter χ tends to zero. On the other hand, while our ground-state packings have a Dirac-delta distribution in packing fraction for finite N, numerically created MRJ packings have a range of packing fractions for finite N, which becomes a Dirac-delta distribution only in the thermodynamic limit.We also showed that the modified optimization technique yields a large family of SHU packings for all values of χ < 1/2 that exhibit other novel structural features. The particles in these disordered packings always form interparticle contacts, albeit with sparser contact networks, and have heretofore unattained maximal packing fractions ϕmax(χ) compared to previous works on stealthy hyperuniform systems. In the χ–ϕmax plane, the regions below and above the function ϕmax(χ) are satisfiable and unsatisfiable phases, respectively; see Fig. 3(a). By increasing χ from 0 to 1/2, one can tune the contact networks of the SHU ground states from those that percolate with various degrees of connectivity for small to intermediate χ values to those that do not percolate at higher χ values characterized by dimer polymer-like chains. Detailed analyses of local structural statistics of these 3D SHU packings as a function of system size for χ > 0 and their lower-dimensional counterparts are reported in ref. 59.
The capability to attain ultradense SHU packings for all χ within the disordered regime opens up exploration of new applications in optics and acoustics using such exotic amorphous materials.33,35,36,38,42–44,47,69 Indeed, Vanoni et al.77 recently showed how certain dynamical physical properties (i.e., effective dynamic dielectric constant and time-dependent diffusion spreadability) of two-phase media derived from them are improved for a range of χ within the disordered regime and packing fractions ϕ.
Finally, we note that it has been a great computational challenge to generate the ideal MRJ state, which must be free of rattlers (defects).78 Rapid-compression algorithms have been used over the years to generate such packings,5,6,60,79 but they produce a small but significant fraction of rattlers that prevent the ideal MRJ state from truly forming due to a critical slowing down.80 In future work, it would be interesting to explore the use of our effectively jammed but hyperuniform packing states as improved initial conditions for the Torquato–Jiao linear programming packing algorithm, which is designed to find inherent structures efficiently,60 to possibly reduce the fraction of rattlers below 1.5%, thereby approaching the ideal state.
Author contributions
S. T.: conceptualization, investigation, data curation, writing, funding acquisition; J. K.: data curation, software, investigation, writing.Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Conflicts of interest
There are no conflicts to declare.Appendices
A. Simulation parameters
Here, we tabulate the simulation parameters for 3D ultradense SHU packings employed in this work.B. Total potential in the limit of χ → 0
We provide an explicit expression of the total potential (2) with χ = χmin(N) of N-particle systems (denoted by χ = 0+ in Section 3): | (9) |
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 3. Importantly, we approach the limit of χ → 0 by increasing N in eqn (9) as large as possible (i.e., N = 10
3. Importantly, we approach the limit of χ → 0 by increasing N in eqn (9) as large as possible (i.e., N = 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 774), ensuring that the obtained ground states are hyperuniform in this limit, which is challenging for conventional compression algorithms to achieve.
774), ensuring that the obtained ground states are hyperuniform in this limit, which is challenging for conventional compression algorithms to achieve.
Acknowledgements
We thank Peter Morse, Charles Maher, and Paul Steinhardt for their very helpful remarks. This research was sponsored by the Army Research Office, accomplished under Cooperative Agreement Number W911NF-22-2-0103 and the National Science Foundation under Award No. CBET-2133179.Notes and references
- S. Torquato and F. H. Stillinger, Phys. Rev. E, 2003, 68, 041113 CrossRef PubMed.
- S. Torquato, Phys. Rep., 2018, 745, 1–95 CrossRef CAS.
- F. J. Dyson, Commun. Math. Phys., 1970, 19, 235–250 CrossRef.
- H. L. Montgomery, Am. Math. Soc., 1973, 181–193 Search PubMed.
- A. Donev, F. H. Stillinger and S. Torquato, Phys. Rev. Lett., 2005, 95, 090604 CrossRef PubMed.
- C. E. Maher, Y. Jiao and S. Torquato, Phys. Rev. E, 2023, 108, 064602 CrossRef CAS PubMed.
- Y. Jiao, T. Lau, H. Hatzikirou, M. Meyer-Hermann, J. C. Corbo and S. Torquato, Phys. Rev. E, 2014, 89, 022721 CrossRef PubMed.
- A. Mayer, V. Balasubramanian, T. Mora and A. M. Walczak, Proc. Nat. Acad. Sci. U. S. A., 2015, 112, 5950–5955 CrossRef CAS PubMed.
- S. Torquato, A. Scardicchio and C. E. Zachary, J. Stat. Mech.: Theory Exp., 2008, P11019 CrossRef.
- H. Wang, R. Samajdar and S. Torquato, Phys. Rev. B, 2024, 110, 104201 CrossRef CAS.
- C. Reichhardt and C. J. O. Reichhardt, Soft Matter, 2014, 10, 7502–7510 RSC.
- D. Hexner and D. Levine, Phys. Rev. Lett., 2015, 114, 110602 CrossRef PubMed.
- D. Hexner, P. M. Chaikin and D. Levine, Proc. Nat. Acad. Sci. U. S. A., 2017, 114, 4294–4299 CrossRef CAS PubMed.
- H. Zhang, X. Wang, J. Zhang, H.-B. Yu and J. F. Douglas, Eur. Phys. J. E: Soft Matter Biol. Phys., 2023, 46, 50 CrossRef CAS PubMed.
- Q.-L. Lei and R. Ni, Proc. Nat. Acad. Sci. U. S. A., 2019, 116, 22983–22989 CrossRef CAS PubMed.
- C. E. Zachary and S. Torquato, J. Stat. Mech.:Theory Exp., 2009, P12015 CrossRef.
- E. C. Oğuz, J. E. S. Socolar, P. J. Steinhardt and S. Torquato, Phys. Rev. B, 2017, 95, 054119 CrossRef.
- S. Torquato, G. Zhang and M. de Courcy-Ireland, J. Phys. A: Math. Theor., 2019, 52, 135002 CrossRef.
- O. H. E. Philcox and S. Torquato, Phys. Rev. X, 2023, 13, 011038 CAS.
- A. Chremos and J. F. Douglas, Phys. Rev. Lett., 2018, 121, 258002 CrossRef PubMed.
- D. Chen, R. Samajdar, Y. Jiao and S. Torquato, Proc. Natl. Acad. Soc., 2025, 122, e2416111122 CrossRef CAS PubMed.
- O. U. Uche, F. H. Stillinger and S. Torquato, Phys. Rev. E, 2004, 70, 046122 CrossRef PubMed.
- R. D. Batten, F. H. Stillinger and S. Torquato, J. Appl. Phys., 2008, 104, 033504 CrossRef.
- S. Torquato, G. Zhang and F. H. Stillinger, Phys. Rev. X, 2015, 5, 021020 Search PubMed.
- G. Zhang, F. H. Stillinger and S. Torquato, Soft Matter, 2017, 13, 6197–6207 RSC.
- S. Ghosh and J. L. Lebowitz, Commun. Math. Phys., 2018, 363, 97–110 CrossRef.
- M. Salvalaglio, D. J. Skinner, J. Dunkel and A. Voigt, Phys. Rev. Res., 2024, 6, 023107 CrossRef CAS.
- M. Florescu, S. Torquato and P. J. Steinhardt, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 20658–20663 CrossRef CAS PubMed.
- G. Gkantzounis, T. Amoah and M. Florescu, Phys. Rev. B, 2017, 95, 094120 CrossRef.
- L. S. Froufe-Pérez, M. Engel, J. José Sáenz and F. Scheffold, Proc. Nat. Acad. Sci. U. S. A., 2017, 114, 9570–9574 CrossRef PubMed.
- M. Castro-Lopez, M. Gaio, S. Sellers, G. Gkantzounis, M. Florescu and R. Sapienza, APL Photonics, 2017, 2, 061302 CrossRef.
- S. Torquato and D. Chen, Multifunct. Mater., 2018, 1, 015001 CrossRef CAS.
- F. Bigourdan, R. Pierrat and R. Carminati, Opt. Express, 2019, 27, 8666–8682 CrossRef CAS PubMed.
- V. Romero-García, N. Lamothe, G. Theocharis, O. Richoux and L. M. García-Raffi, Phys. Rev. Appl., 2019, 11, 054076 CrossRef.
- A. Rohfritsch, J.-M. Conoir, T. Valier-Brasier and R. Marchiano, Phys. Rev. E, 2020, 102, 053001 CrossRef CAS PubMed.
- S. Torquato and J. Kim, Phys. Rev. X, 2021, 11, 021002 CAS.
- O. Christogeorgos, H. Zhang, Q. Cheng and Y. Hao, Phys. Rev. Appl., 2021, 15, 014062 CrossRef CAS.
- H. Zhang, Q. Cheng, H. Chu, O. Christogeorgos, W. Wu and Y. Hao, Appl. Phys. Lett., 2021, 118, 101601 CrossRef CAS.
- V. Romero-García, É. Chéron, S. Kuznetsova, J.-P. Groby, S. Félix, V. Pagneux and L. M. Garcia-Raffi, APL Mater., 2021, 9, 101101 CrossRef.
- M. A. Klatt, P. J. Steinhardt and S. Torquato, Proc. Nat. Acad. Sci. U. S. A., 2022, 119, e2213633119 CrossRef CAS PubMed.
- N. Tavakoli, R. Spalding, A. Lambertz, P. Koppejan, G. Gkantzounis, C. Wan, R. Rohrich, E. Kontoleta, A. F. Koenderink, R. Sapienza, M. Florescu and E. Alarcon-Llado, ACS Photonics, 2022, 9, 1206–1217 CrossRef CAS PubMed.
- K. Tang, Y. Wang, S. Wang, D. Gao, H. Li, X. Liang, P. Sebbah, Y. Li, J. Zhang and J. Shi, Phys. Rev. Appl., 2023, 19, 054035 CrossRef CAS.
- M. Merkel, M. Stappers, D. Ray, C. Denz and J. Imbrock, Adv. Photonics Res., 2023, 5, 2300256 CrossRef.
- L. Alhatz, J.-M. Conoir and T. Valier-Brasier, Phys. Rev. E, 2023, 108, 065001 CrossRef PubMed.
- N. Granchi, M. Lodde, K. Stokkereit, R. Spalding, P. J. Veldhoven, R. Sapienza, A. Fiore, M. Gurioli, M. Florescu and F. Intonti, Phys. Rev. B, 2023, 107, 064204 CrossRef CAS.
- H. Zhuang, D. Chen, L. Liu, D. Keeney, G. Zhang and Y. Jiao, J. Phys.: Condens. Matter, 2024, 36, 285703 CrossRef CAS PubMed.
- S. Kuznetsova, J. P. Groby, L. M. Garcia-Raffi and V. Romero-García, Waves Random Complex Media, 2024, 34, 1878–1896 Search PubMed.
- E. Wigner, Phys. Rev., 1934, 46, 1002 CrossRef CAS.
- R. P. Feynman and M. Cohen, Phys. Rev., 1956, 102, 1189–1204 CrossRef.
- R. B. Laughlin, The Quantum Hall Effect, Springer, 1987, pp. 233–301 Search PubMed.
- C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Science, 2020, 367, eaay0668 CrossRef CAS PubMed.
- G. Semeghini, H. Levine, A. Keesling, S. Ebadi, T. T. Wang, D. Bluvstein, R. Verresen, H. Pichler, M. Kalinowski, R. Samajdar, A. Omran, S. Sachdev, A. Vishwanath, M. Greiner, V. Vuletić and M. D. Lukin, Science, 2021, 374, 1242–1247 CrossRef CAS PubMed.
- R. Samajdar, W. W. Ho, H. Pichler, M. D. Lukin and S. Sachdev, Proc. Natl. Acad. Soc., 2021, 118, e2015785118 CrossRef CAS PubMed.
- S. Kivelson and S. Sondhi, Nat. Rev. Phys., 2023, 5, 368–369 CrossRef.
- G. Zhang, F. Stillinger and S. Torquato, Phys. Rev. E, 2015, 92, 022119 CrossRef CAS PubMed.
- P. K. Morse, J. Kim, P. J. Steinhardt and S. Torquato, Phys. Rev. Res., 2023, 5, 033190 CrossRef CAS.
- A. Shih, M. Casiulis and S. Martiniani, Phys. Rev. E, 2024, 110, 034122 CrossRef CAS PubMed.
- G. Zhang, F. H. Stillinger and S. Torquato, J. Chem. Phys., 2016, 145, 244109 CrossRef CAS PubMed.
- J. Kim and S. Torquato, J. Chem. Phys., 2025, in press; arXiv, 2025, preprint, arXiv:2504.16924, https://arxiv.org/abs/2504.16924 Search PubMed.
- S. Torquato and Y. Jiao, Phys. Rev. E, 2010, 82, 061302 CrossRef CAS PubMed.
- P. Charbonneau, E. I. Corwin, G. Parisi and F. Zamponi, Phys. Rev. Lett., 2012, 109, 205501 CrossRef PubMed.
- F. H. Stillinger, E. A. DiMarzio and R. L. Kornegay, J. Chem. Phys., 1964, 40, 1564–1576 CrossRef CAS.
- C. S. O'Hern, S. A. Langer, A. J. Liu and S. R. Nagel, Phys. Rev. Lett., 2002, 88, 075507 CrossRef PubMed.
- S. Wilken, R. E. Guerra, D. Levine and P. M. Chaikin, Phys. Rev. Lett., 2021, 127, 038002 CrossRef CAS PubMed.
- S. Atkinson, F. H. Stillinger and S. Torquato, Phys. Rev. E, 2013, 88, 062208 CrossRef PubMed.
- A. Donev, S. Torquato and F. H. Stillinger, Phys. Rev. E, 2005, 71(011105), 1–14 Search PubMed.
- S. Torquato, Int. J. Solids Structures, 2000, 37, 411–422 CrossRef.
- S. Torquato and F. H. Stillinger, Rev. Mod. Phys., 2010, 82, 2633 CrossRef.
- J. Kim and S. Torquato, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 8764–8774 Search PubMed.
- G. Matheron, Cahiers de Géostatistique, 1993, 107, 107–113 Search PubMed.
- S. Franz, G. Parisi, M. Sevelev, P. Urbani and F. Zamponi, Sci. Phys., 2017, 2, 019 CrossRef.
- C. S. O'Hern, L. E. Silbert, A. J. Liu and S. R. Nagel, Phys. Rev. E, 2003, 68, 011306 CrossRef PubMed.
- Y. Jin and H. Yoshino, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2021794118 CrossRef CAS PubMed.
- J. Nocedal, Math. Comput., 1980, 35, 773–782 CrossRef.
- D. C. Liu and J. Nocedal, Math. Program., 1989, 45, 503–528 CrossRef.
- M. E. J. Newman and R. M. Ziff, Phys. Rev. Lett., 2000, 85, 4104–4107 CrossRef CAS PubMed.
- C. Vanoni, J. Kim, P. J. Steinhardt and S. Torquato, Dynamical properties of particulate composites derived from ultradense stealthy hyperuniform sphere packings, 2025 Search PubMed.
- S. Torquato, Phys. Rev. E, 2021, 103, 052126 CrossRef CAS PubMed.
- S. Torquato, T. M. Truskett and P. G. Debenedetti, Phys. Rev. Lett., 2000, 84, 2064–2067 CrossRef CAS PubMed.
- S. Atkinson, G. Zhang, A. B. Hopkins and S. Torquato, Phys. Rev. E, 2016, 94, 012902 CrossRef PubMed.
Footnotes |
| † In the thermodynamic limit, χ is inversely proportional to ρ according to the exact relation24ρχ = ν1(K)/[2d(2π)d], where ν1(R) is the volume of a d-dimensional sphere of radius R. |
| ‡ Although there are 2M(K) + 1 wavevectors inside the spherical exclusion region of radius K centered at the origin, only M(K) of them are independently constrained because S(k) is inversion symmetric, i.e., S(k) = S(−k). |
| § Such MRJ-like disordered jammed states have been created by various protocols and systems under periodic boundary conditions, including rapid compression of hard spheres5,6,60,61 to their deep mechanically stable local “energy” (−ϕ) minima (inherent structures60,62), rapid quenching of soft spheres at high T to find inherent structures at T = 0 via conjugate gradient techniques,61,63 or as a dynamical phase transition via a biased random organization protocol.64 It is well-known that these current packing protocols lead to disordered jammed packings with similar but not exactly the same structural features, such as rattler concentrations, gap exponents, hyperuniformity, and force distributions. For example, the Torquato–Jiao linear programming algorithm60 produces 50% less rattlers65 than that of the modified Lubachevsky-Stillinger algorithm.66 Work on rapid quenching of soft spheres61,63 typically use only the soft-core potential in (2), i.e., without the stealthy contribution, and hence cannot guarantee hyperuniformity of the packing. |
| ¶ A packing is strictly jammed if there are no possible collective rearrangements of some finite subset of particles, and no volume-nonincreasing deformation that can be applied to the packing without violating the impenetrability constraints of the particles.68 |
| || This threshold is close to zero energy of the potential, given in eqn (3), within the double precision of the machine |
| This journal is © The Royal Society of Chemistry 2025 |


