Winding up dynamics for matched and unmatched elastic constants in chiral nematic liquid crystals

Abstract

Recently discovered materials have opened up the possibility of easily and repeatably altering the ratio among the elastic constants characterizing nematic liquid crystals. These ratios are crucial for defining the pathways for the relaxation process from the unwound state to the Grandjean (planar) state in chiral nematics. In this study, we use the Landau–de Gennes method in the Q-tensor formalism to investigate this textural transition for different bend-to-twist ratios representing nematic phases that are currently easily prepared. We also examine the effect of varying alignment conditions and strength on this transition and make qualitative comparisons with experimental data. This work demonstrates how the dynamics are entirely different under small changes in the material and the confinement and how one can use its results to design reflective chiral nematic displays.

---

1 Introduction

The field of liquid crystals (LCs) has experienced an expressive change in recent years. Before the 21st century, it was common, at least for small molecule materials, for nematic phases to have three main elastic distortions that follow the rule K₃₃ > K₁₁ > K₂₂, that is, the elastic constant of bend is larger than the elastic constant of splay, which is larger than that of twist,¹ at least for typical calamitic systems.² The role of these elastic constants and the fundamental deformation modes have been well established,^3–6 and the consequences of changing these ratios have been explored.^7–10 Although changing elastic constant values has long been possible through additives such as nanoparticles and other mesogens,^11–13 it often results in changes in all elastic constants at some level. However, high-level chemistry and materials engineering have produced new materials that changed this understanding. For example, dimer materials that form the so-called twist-bend nematic phase are known to present K₁₁ > K₂₂ > K₃₃, in the nematic phase.^14,15 In addition, the case K₃₃ > K₂₂ > K₁₁ has been reported for materials that present splay nematic phases.^16,17 This departure from the traditional nematic elasticity allows for new phenomena and opens up the possibility of revisiting old problems and applications that are no longer in the limelight. Among them are ferroelectric nematic phases with tremendous potential for applications.¹⁸ Furthermore, electrically color-tunable reflectors,^19,20 tunable spatial light modulators,²¹ switchable windows²² and many others are now being studied due to these new materials.

An interesting phenomenon that is entirely different depending on the type of material used is the transition from the unwound state (or homeotropic) to Grandjean (or planar) in chiral nematic materials (CLC).¹ This transition is typically studied by applying an electric field high enough to unwind the CLC's helix.^23–31 Upon removal of the field, it is expected that the material first relaxes to a transient planar structure (TP) whose pitch length is approximately K₃₃/K₂₂ times the natural pitch,³² so, for regular materials, the TP pitch (P_t) is roughly twice the natural pitch (P₀). A recent study theoretically described this transition in detail.³³ Recent experimental work has shown that if a regular LC (E7) is mixed with a dimer material (CB7CB), the value of K₃₃ can be lowered to the point where K₂₂ ∼ K₃₃.³⁴ The transition differs from regular materials in this case, with fewer defects observed and considerably faster relaxation. An even more recent work explored the transition but for a mixture where K₃₃ < K₂₂.³⁵ As expected, when light reflection is monitored, a peak is observed during the TP state, which occurs for wavelengths shorter than the reflection of the natural pitch. In addition, this case appears to take longer to relax to a uniform state than the case K₂₂ ∼ K₃₃.^34,35 Since CLCs reflect light if the pitch length is compared to the wavelength of visible light, it becomes essential to understand how these transitions take place and how to improve these processes for reflective displays.¹

In our study, we use the Landau–de Gennes Q tensor (LdG) simulation method with finite elements to study the homeotropic to planar transition under different alignment conditions and for K₃₃ = NK₂₂, with N = 0.067, 1.0 and 2.0 (where the first value represents the measured ratio for CB7CB,¹⁴ the second case represents matched elastic constants,³⁴ and the third case represents the usual materials¹) to understand how the transition and the relaxation time are affected. We use the same analysis used in ref. 33, showing the system's calculated textures, director orientation, and other parameters changing over time. We also make qualitative comparisons with experimental data.

2 Methods

The fundamental equations governing the CLC dynamics were numerically solved for the Q-tensor in the Landau–de Gennes (LdG) formalism. The free energy is formulated through the symmetric, traceless order parameter tensor Q_ij, written in the following manner:³⁶

Q_ij = 3/2S(n_in_j − 1/2δ_i,j) + 1/2P(l_il_j − m_im_j) (1)

In this context, (S) and (P) represent the uniaxial and biaxial order parameters. Here, n⃑ denotes the primary director, l⃑ signifies the secondary director, and the vector m⃑ is defined as n⃑ × l⃑. The system is governed by free energy density expressed as:where is the integral of the volume of the cell, Q_ij,k = ∂Q_ij/∂x_k represents the spatial derivative of Q_ij along the k-th direction, with T signifying the sample liquid crystal temperature and T* the hypothetical temperature for the nematic–isotropic phase transition. The parameters a, B, and C are thermodynamic parameters, and the constants L_i are elastic constants of the LdG formalism, which may be connected to the usual Frank elastic constants according to eqn (S3) (ESI†). For more details of the model, see the ESI.† We used finite element discretization implemented in Comsol Multiphysics, and the time evolution was controlled with a backward difference formula (BDF). In all simulations conducted in this work, we used a slab cell with dimensions 4.5 μm × 4.5 μm × 1.5 μm, in the directions x, y, and z, respectively, with periodic boundary conditions in x and y. The CLC sample used in all simulations was set with a natural pitch, so the material has 12π turns in the z direction in a perfectly aligned Grandjean texture. We apply a strong electric field in the z direction until the sample is completely unwound; all molecules are oriented parallel to the field. The field is then removed, and in t = 0 the CLC winding begins. See Fig. S1 (ESI†) for more details on the system studied here. To investigate the role played by the elastic constants, we kept the ratio of splay to twist fixed (K₁₁/K₂₂ = 1.82) and used three sets of elastic constants of bend to twist: set 1, with K₃₃/K₂₂ = 1.0, set 2 with K₃₃/K₂₂ = 2.0 and set 3 with K₃₃/K₂₂ = 0.067. Furthermore, we used several anchoring conditions to understand the role of anchoring type and strength in the transition dynamics. We used strong (W = 1 × 10⁻² J m⁻²) and weak (W = 1 × 10⁻⁵ J m⁻²) planar, homeotropic, and hybrid (planar on one side and homeotropic on the other). We shall use PS to refer to the strong anchoring planar cell, PW to the weak planar cell, HS to the strong homeotropic case, HW to the weak homeotropic case, Hyb when referring to the hybrid aligned cell, FG for a planar degenerate case, and NA when referring to the cell with free boundaries.

Regarding the thermal parameters used in the LdG formalism, we used A = a(T − T*) = −1.72 × 10⁵ J m⁻³, B = −2.12 × 10⁶ J m⁻³, and C = 1.73 × 10⁶ J m⁻³. Furthermore, the interaction of the LC molecules with the substrate was given in two ways: with the Fournier–Galatola³⁷ energy for the FG case or the Rapini–Papoular (RP)³⁶ anchoring energy for the planar and homeotropic cases (ESI†). The planar case with RP energy had a 1° pretilt in the x direction. The electric field was applied in the z direction, where a constant approximation was used to simulate the electric field since the purpose was to enforce a homeotropic state in the system, at which the electric field would be approximately constant. The electric field strength of E = 8.14 × 10⁷ V m⁻¹k̂ was applied for 1 ms to ensure perfect homeotropic alignment at the beginning of every simulation. All the polarizing optical microscopy textures were calculated with the Mueller method described in the ESI.† Short videos showing the time evolution of the textures for all the different samples studied here are also provided in the ESI.† See the ESI† for further details.

3 Results

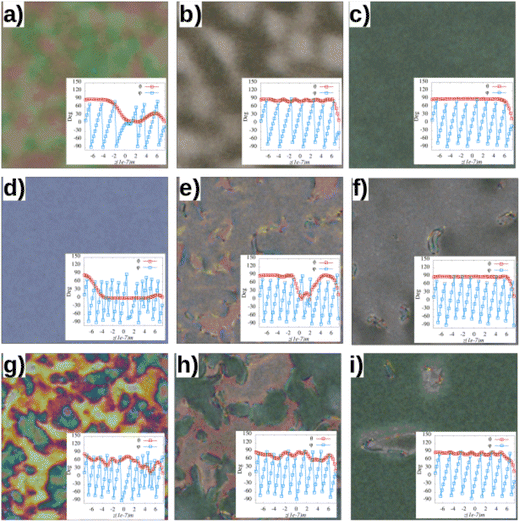
We previously reported on the relaxation of the strong planar (PS) and free boundaries (NA) for the case where K₃₃/K₂₂ = 2.0. For the planar case, the material starts to wind up from the substrates, and the transient-planar state, with pitch P_t = (K₃₃/K₂₂)P₀ occurring within the first millisecond. Then, the sample slowly relaxes to the natural pitch by bending the pseudolayers in a process with the annealing of coreless defect lines. The whole process takes nearly a second in this case. The results are described in detail in ref. 33, so here we only show the textures calculated during this transition at different moments in Fig. 1, where the insets show the polar angle (θ(z), shown as red squares) and the azimuthal angle (ϕ(z), shown as blue circles) across the cell. It is clear that in the initial moments, the TP state is formed and that the system relaxes by forming the fingerprint state and slowly annealing the coreless (λ) lines until the system is left with oily streaks (Lehman clusters). The insets show that the gain of new layers occurs by deviation of the polar angle from the planar orientation, which involves buckling and bending the CLC layers.

Fig. 1 Dynamics of the PS cell for K₃₃/K₂₂ = 2.0. (a) The director field at t = 0.066 ms, where the system is still relaxing from the homeotropic state. (b) At t = 1.69 ms the fully developed TP state is shown. (c) Calculated at t = 2.80 ms, showing the initial bend of the layers. In contrast, (d) at t = 4.33 ms and (e) at t = 6.54 ms show the development of the fingerprint texture as a way of developing new layers to meet the chirality requirement of the system. (f) t = 9.66 ms, demonstrating the start of the slow annealing that results in a new turn of the CLC structure. (g)–(i) The development of the planar structure at t = 14.0, t = 20.4, and t = 121.6 ms, respectively. The whole process is described in detail in ref. 33. The whole transition takes place in roughly 1 s.

The NA case relaxes by forming the transient pitch everywhere, and the dynamics consist of removing core defects that form across the sample. The total energies of splay, twist, and bend for the PS and NA samples are presented in S2(a)–(c) (ESI†), respectively, and they are discussed in detail in ref. 33.

Here, we start studying the case K₃₃/K₂₂ = 1.0 in the PS cell. In this case, as before, the material starts to twist off the substrates, but since P_t = P₀, the initial pitch is already the preferred one, which speeds up the process. Fig. 2(a) shows the director field for the winding process at t = 0.58 ms starting from the substrates with approximately the natural pitch P₀. Notice that the directors are coded by the perpendicular component of the page, which means that blue indicates in-plane orientation while red indicates out-of-plane orientation. This scheme is used in all the figures of this work. Once the two fronts meet, the mismatch results in defects such as λ lines in the layered structure that separate different twist domains. Fig. 2(b) shows a zoomed region at t = 1.05 ms to illustrate the mismatched region. The structure evolves by uniformly combining the layers at t = 2.7 ms, as shown in Fig. 2(c). Fig. 2(d) shows the λ⁺¹ (yellow) and λ⁻¹ (green) calculated from the SSB and STW parameters (see ref. 33), respectively, for the structure shown in Fig. 2(c). These defect lines tend to form closed loops that quickly shrink down so the uniform state is reached. Fig. 2(e), (g) and (i) show the calculated texture for t = 0.58 ms, t = 0.8 ms, and t = 4.3 ms, respectively. Fig. 2(f), (h) and (j) show the polar (θ(z)) and azimuthal (ϕ(z)) angles in the cell for each corresponding texture. Notice how ϕ(z) is nearly uniform from the beginning, reflecting the P_t = P₀ for this sample. Therefore, defects separating different twisting domains quickly anneal, which is faster than having to introduce new layers as in the case K₃₃/K₂₂ = 2.0.³³ Fig. S2(c)–(e) (ESI†) show the total splay, twist, and bend energies during the relaxation process. Splay and twist present a substantial decrease within the first millisecond, representing the transient-planar phase. A local maximum in the splay energy of around 1 ms corresponds to the first encounter of different twisting domains. This can also be seen in the bend energy, which simultaneously presents a maximum with the splay energy.

Fig. 2 Dynamics of the PS cell for K₃₃/K₂₂ = 1.0. (a) The director field at t = 0.58 ms, showing the twisting zones developing from the walls with P_t = P₀. (b) Dislocation defects that form once different twisting domains meet. (c) The evolution of the calculated texture at t = 2.7 ms, forming λ lines quickly that shrink down. The lines corresponding to the director field in (c) are shown in (d). (e), (g) and (i) The calculated textures, and (f), (h) and (j) the corresponding polar (red squares) and azimuthal (blue squares) angles across the cell for t = 0.58 ms, t = 0.80 ms and t = 4.3 ms, respectively. The whole transition takes place in roughly 9 ms.

Next, we simulated the case in which K₃₃/K₂₂ = 0.067, which means P_t ≪ P₀, for the PS cell. In this case, the winding starts from the surfaces with the natural pitch, but since the transient pitch is much smaller than the natural pitch, twist domains develop everywhere in the bulk from the moment the field is turned off, as shown in Fig. 3(a) for t = 0.13 ms. The twisting domains grow rapidly, forming dislocations where they meet. The dislocations climb and anneal each other, as shown by the sequence of snapshots in Fig. 3(b)–(d), at times t = 1.69 ms, t = 4.33 ms and t = 6.54 ms, respectively. Fig. 2(e) and (f) show θ(z) and ϕ(z) at t = 0.066 ms and t = 9.66 ms. From Fig. 3(e), looking at ϕ(z), it is possible to observe that in the initial moments, the pitch is shorter than the natural pitch, as expected. The whole transition takes roughly 10 ms. Fig. 3(g)–(i) show the calculated textures. Fig. 3(g) is calculated at t = 0.21 ms, where different colors demonstrate the initial formation of twist domains; Fig. 3(h) is calculated at t = 1.69 ms, where different twist domains can be seen, and Fig. 3(i) is calculated at t = 9.66 ms, where the homogeneous texture is almost completed. Fig. S2(g)–(i) (ESI†) show how the splay, twist, and bend energies are decreasing functions of time. Furthermore, Table 1 shows the time it takes to achieve the static texture after starting from the homeotropically aligned configuration for each case studied here.

Fig. 3 PS cell for K₃₃/K₂₂ = 0.067. (a) The directors at t = 0.14 ms. Twist grows from the walls and everywhere in the bulk (P_t < P₀). (b)–(d) The evolution of dislocation defects. (e) and (f) The polar and azimuthal angles across the cell for t = 0.07 ms and t = 9.66 ms, respectively. (g)–(i) The calculated texture at t = 0.21 ms, t = 1.69 ms and t = 9.66 ms.

Table 1 Summary of approximate relaxation times for each boundary condition and the different values of elastic constants studied

K33/K22	PS (ms)	PW (ms)	HS (ms)	FG (ms)	Hyb (ms)
a The cases PW and FG with K33/K22 = 0.067 and PW with K33/K22 = 1.0 the times are greater due to the defect formation while relaxing.
2.0	1000	120	30	15	10
1.0	9	1000^a	69	50	20
0.067	20	500^a	52	212^a	20

---

From the results so far, it is clear that the ratio K₃₃/K₂₂ greatly affects the homeotropic to planar transition in CLCs, changing the pathways from one texture to the other and, consequently, how long the transition takes. However, it is interesting to note that for the two cases studied here and the case in which K₃₃ = 2.0K₂₂,³³ the twisting process always begins from the substrates. Thus, it is natural to investigate other types of alignment. We first investigate the case in which the surface is treated to induce a planar anchoring just as before, but the anchoring strength is 100 times lower than before, with W = 1 × 10⁻⁵ J m⁻², called PW. As expected, this case is very similar to the NA (when K₃₃ = 2.0K₂₂) study,³³ which can also be seen from the energies, Fig. S2(a)–(c) (ESI†). For K₃₃ = 2.0K₂₂, the CLC layers appear everywhere instead of growing from the surfaces, and the process is described in ref. 33. The case K₃₃ = 2.0K₂₂ for the PW situation takes approximately 120 ms to reach the homogeneous state. If K₃₃ = 1.0K₂₂, twisting domains arise from every part of the sample instead of the surfaces. However, since P_t = P₀, the twisting domains have a smaller pitch compared to K₃₃ = 2.0K₂₂, and the mismatch between the domains creates several χ defects.³³ As a result, after 1 s of simulation, the homogeneous state has not yet been reached, and several defects are still observed. Fig. 4(a)–(c) show three calculated textures at times t = 0.58 ms, t = 2.79 ms and t = 1.0 s, respectively. Fig. 4(d) shows an example of a dissociated χ defect forming the λ^1/2 (yellow) and τ^−1/2 (green) lines and the director configuration around it. Thus, in contrast to the PS cell, where K₃₃ = 1.0K₂₂ is much faster to relax to a homogeneous state, the PW cell is slower due to the many twist domains formed, which take a very long time to anneal.

Fig. 4 PW sample for K₃₃/K₂₂ = 1.0. (a)–(c) Calculated textures at t = 0.58 ms, t = 2.79 ms and t = 1.0 s. (d) The director and the λ lines structure formed after a χ line dissociates forming λ^1/2 and τ^−1/2 lines. See ref. 33 for more details.

For K₃₃/K₂₂ = 0.067, a similar mismatch is observed between the twisted domains, as shown by the calculated texture in Fig. 5(a) at t = 0.38 ms. This mismatch forms everywhere a few moments after the field is turned off. However, the high value of K₂₂ compared to K₃₃ makes twist deformations too energetically costly, so layered defects are pushed toward the substrates to give rise to a uniform bulk configuration (where the natural pitch forms). Fig. 5(b) and (c) show the calculated textures at t = 2.78 ms and t = 496.12 ms, respectively. At the substrates, after the layered structure is formed in the bulk, several undulations are formed due to the low bend elastic constant as the dislocations glide, resulting in a mesh of λ lines, as shown in Fig. 5(d) and (e).

Fig. 5 PW sample for K₃₃/K₂₂ = 0.067. (a)–(c) Calculated textures at t = 0.38 ms, t = 2.78 ms, and t = 496.12 ms, respectively. (d) A mesh of λ lines near the substrates after the CLC structure is formed in the bulk. (e) The director configuration corresponding to (e).

Based on the findings provided up to this point, which also encompass those outlined in ref. 33, we notice that the textural transition is very slow for the weak anchoring situation for all K₃₃/K₂₂ ratios. This results from the limited impact of the substrates in determining a specific orientation for the helix. However, even in the strong anchoring situation, the transition is slow for K₃₃/K₂₂ = 2.0 due to the need to add more CLC layers (decrease the pitch) after the two wavefronts meet once the electric field is switched off. Next, we study the three K₃₃/K₂₂ ratios for the HS anchoring situation. In this case, the polar anchoring energy is strong, and the azimuthal energy is negligible, so we can understand which kind (polar or azimuthal) matters the most and how a boundary condition incompatible with the helix affects the transition.

Starting again with the sample K₃₃/K₂₂ = 2.0, we first notice that the strong anchoring causes the twist to start from the substrates and move into the bulk as before, as shown by the directors in Fig. 6(a). Since the boundary condition favors the initial state after the field is turned off, the polar angle across the sample does not drop to zero as fast as in the planar cases, which reduces the total splay and bend energies when compared to the PS case, for example (see Fig. S2(a)–(c), ESI†). As before, P_t = 2P₀ in this case, but since the azimuthal energy is zero, new layers continuously develop from the surfaces to the bulk. This process is shown in Fig. 6(b)–(d), where the lack of azimuthal energy allows the director to rotate on the substrates, which consequently leads to the addition of new layers to the bulk. Not surprisingly, this process is much faster than in the PS case. In fact, Fig. 6(a)–(d) were calculated at t = 0.13 ms, t = 0.21 ms, t = 1.69 ms and t = 29.3 ms, respectively. Within the first 10 ms, nearly all the layers have already formed into the bulk, but a few undulations are still present, which quickly die out. Fig. 6(e)–(h) show the calculated textures corresponding to the directors shown in Fig. 6(a)–(d). Notice that the directors are completely homeotropic near the substrates, and the CLC unwinds. An elastic boundary layer separates the Grandjean CLC material from the unwound material on the substrates. This fact can be seen from the insets in Fig. 6(e) and (h), which show θ(z) and ϕ(z) for the corresponding texture. Fig. 6(h) shows that θ = 0° on the substrates becomes 90° within an elastic boundary layer of roughly 0.1 μm.

Fig. 6 HS cell for the K₃₃/K₂₂ = 2.0 case. (a)–(d) The director field, and (e)–(h) the corresponding calculated textures at t = 0.13 ms, t = 0.21 ms, t = 1.69 ms, and t = 29.3 ms, respectively. The insets of (e) and (h) show the polar and azimuthal angles across the cell at the corresponding times.

Regarding the cases K₃₃/K₂₂ = 1.0 and K₃₃/K₂₂ = 0.067, the overall dynamics are similar to the PS case presented before. In other words, in both cases, twist grows from the substrates toward the bulk, but, as before, the transient pitch is not larger than the natural pitch; thus, there is no need to add new layers once the transient pitch is formed across the cell, and the homogeneous state is reached once the different twisting domains become uniform. It is also important to stress that for K₃₃/K₂₂ = 0.067, the transient pitch is smaller than the natural pitch and forms throughout the bulk, while the twisting zones move from the surfaces, as previously described. However, in our simulations, the azimuthal energy plays a minor role for the cases in which K₃₃/K₂₂ ≤ 1. Fig. 7(a)–(c) show the calculated textures for K₃₃/K₂₂ = 1, while Fig. 7(d)–(f) show the case K₃₃/K₂₂ = 0.067 for t = 0.57 ms, t = 1.69 ms and t = 29.3 ms, respectively. The sample with K₃₃/K₂₂ = 1 takes roughly 69 ms to achieve the final state, while the sample with K₃₃/K₂₂ = 0.067 relaxes in approximately 52 ms. If the anchoring is set to weak homeotropic, the dynamics for the three K₃₃/K₂₂ ratios are very similar to the PW case, and therefore we shall not discuss this here.

Fig. 7 (a)–(c) The calculated textures for the HS cell for K₃₃/K₂₂ = 1.0, and (d)–(f) the calculated textures for the HS cell for K₃₃/K₂₂ = 0.067. (a) and (d) are calculated for t = 0.57 ms, (b) and (e) for t = 1.69 ms and (c) and (f) for t = 29.3 ms.

From the results analyzed to this point, we observe that K₃₃/K₂₂ = 2.0 is slow in the strong planar case due to the large transient pitch and the fact that new CLC layers cannot be added by director rotation at the substrates due to the strong azimuthal energy. However, the same material presents the transition much faster if the azimuthal anchoring energy is low. To verify that azimuthal anchoring is the main reason for the speed of the transition, we studied a sample sandwiched between two strong planar degenerate substrates, the FG cell. Polar anchoring is strong (W_p = 1 × 10⁻² J m⁻²) while the azimuthal energy is zero. For K₃₃/K₂₂ = 2.0, as expected, once the transient pitch is formed, the continuous rotation of the director on the substrates adds more layers to the bulk. In this sense, no defects are observed, and hence, the transition is considerably fast in our simulations, reaching a homogeneous state in nearly 15 ms. For K₃₃/K₂₂ = 1.0 and K₃₃/K₂₂ = 0.067, as discussed above for the strong homeotropic case, the azimuthal energy does not play an important role, since the material does not need to relax from an initially unwound transient planar state. Instead, both cases only need to eliminate boundary domains and different twisting domains, and the dynamics are similar to what was discussed for the strong homeotropic case. The K₃₃/K₂₂ = 1.0 case relaxes in t_r ∼ 50 ms, faster than the HS case, as expected. However, t_r ∼ 212 ms for the K₃₃/K₂₂ = 0.067 sample, much longer than in the HS case. Fig. 8(a)–(d) show the calculated texture and the polar and azimuthal angles across the sample for t = 0.66 and t = 212 ms, respectively, for the K₃₃/K₂₂ = 0.067 sample. Since the transient pitch is smaller than the natural pitch, many twisting domains form across the sample. However, the dislocations separating the domains take much longer to anneal than in the HS and PS cases. Fig. 8(e) shows some dislocations (see Fig. 3 also) that slowly anneal for this sample.

Fig. 8 FG cell for K₃₃/K₂₂ = 0.067. (a) and (b) The calculated textures for t = 0.66 ms and t = 212 ms, respectively. (c) and (d) The polar and azimuthal angles across the cell corresponding to (a) and (b). (e) An example of dislocations that form during this transition.

The low azimuthal anchoring energy considerably reduces the transition time for conventional materials (K₃₃/K₂₂ = 2.0). Still, the use of homeotropic anchoring may reduce optical reflection for reflective CLC displays¹ due to the distortion near the substrates and the possible formation of domains where the helical axis points in a slightly different direction.¹ However, strong degenerate anchoring is not easily made, and the azimuthal energy is weak but, in practical applications, not zero. We thus simulated a hybrid cell in which the bottom substrate is fabricated with PS anchoring, and the top substrate is made with HS anchoring. For K₃₃/K₂₂ = 2.0, as for the HS case, new layers are added through the top substrate after the transient pitch is formed, and despite a few undulations, no defects are formed. Hence, the transition is fast, reaching the final state in about 10 ms, as shown in Fig. 9(a)–(c), taken at t = 0.067 ms, 0.38 ms, and 7.67 ms, respectively. Thus, the transition is faster than in the HS case. Because in the case of K₃₃/K₂₂ = 1 or K₃₃/K₂₂ = 0.067, all CLC layers are formed in the transient planar state. Different twisting zones have to connect (instead of new twisting zones having to form from the transient planar state); using hybrid alignment layers does not offer any advantage over the other anchoring situations tested here. The development is very similar to other cases described before. Fig. 9(d)–(f) show the cases of K₃₃/K₂₂ = 1.0 for t = 0.13 ms, 0.92 ms and 9.67 ms respectively, while Fig. 9(g)–(i) show the cases of K₃₃/K₂₂ = 0.067 for t = 0.067 ms, 0.92 ms and 9.67 ms.

Fig. 9 Calculated textures for the Hyb cell. (a)–(c) The K₃₃/K₂₂ = 2.0 case for t = 0.067 ms, t = 0.38 ms, and t = 7.67 ms. (d)–(f) The K₃₃/K₂₂ = 1.0 case for t = 0.13 ms, t = 0.92 ms, and t = 9.67. (g)–(i) The K₃₃/K₂₂ = 0.067 case for t = 0.067 ms, t = 0.92 ms, and t = 9.67 ms. The insets in all figures show the corresponding polar and azimuthal angles across the cell.

In general, looking at the evolution of total splay, twist, and bend energies also helps us to understand the global behavior of all the cells studied here. Starting from the case K₃₃/K₂₂ = 2.0, Fig. S2(a)–(c) (ESI†), it can be seen that the twist energy quickly decreases during initial moments as more turns are added to the sample, with the PS and FG samples slowly relaxing to F_T/F_T0 = 1 after this initial fast decrease. While in the FG case this slower process is related to constant rotation on the substrates, in the PS case this process is associated with the complex migration of defects and the formation of Lehman clusters (see ref. 33). Total splay and bend ((a) and (c)) also show these two distinct regimes of the PS sample, presenting a large initial drop during the transient planar state but presenting a secondary rise and drop for longer times.³³ The total splay follows a similar trend for all the samples, presenting an initial growth followed by a quick drop during the TP state. Notice that the HS case takes a bit longer to present the maxima since the boundary conditions reinforce the configuration set by the field.

For all alignments, the twist energy decreases with time, as expected from the unwounded initial configuration. Splay energy increases in the initial moments during the homeotropic to transient planar state for all the strong planar alignments and the weak energy samples. The strong energy cases quickly drop slightly lower than the final homogeneous state, probably because the final state has some oily streaks (PS) and slight undulations (FG). In weak anchoring cases, after the maximum distortion, samples slowly relax as the twist domains anneal. Interestingly, the HS case only peaks the distortion a few moments after the other samples because the initial configuration satisfies the boundary conditions. Also, notice how the Hyb cell never experiences any considerable variation in splay energy since the process occurs by director rotation at the homeotropic substrate. The bend energy follows a similar trend to the splay energy in all samples except for the PS case. In this case, the energy drops from the initial moments, resulting from the transient planar state forming faster than in the other cases before we printed our first result. Note that there is a maximum near log[t] ≈ 10, which represents the point where λ^1/2 lines form, as discussed in ref. 33. From Fig. S2(a)–(c) (ESI†), it is clear how similar the PS and NA samples are, and thus we do not show the NA energies for the other K₃₃/K₂₂ ratios. For K₃₃/K₂₂ = 1.0, Fig. S2(d)–(f) (ESI†), it is interesting to see that both the splay and bend energies form a peak around 1 ms for all the anchoring cases, except for the FG anchoring. This peak represents the moment when the two wavefronts of twisting zones developing from the walls meet at the center of the cell. Since the FG case has zero azimuthal energy and strong polar energy (not favoring the initial unwound state by the field), it does not develop from the walls but instead forms everywhere in the CLC layers. The total energies also show how the alignment kind does not change the dynamic significantly for K₃₃/K₂₂ = 0.067, Fig. S2(g)–(i) (ESI†), where all the cases are very similar.

4 Discussion and experimental data

To proceed, we can compare the simulations qualitatively with experimental data. Since most of the features of this texture transition take place within a few milliseconds, it is pretty challenging to observe most of the features reported here directly. However, we can indirectly compare some of our results with measurements performed in recent publications and new experiments conducted for this work. First, two recent publications^34,35 studied the electro-optical characteristics of a regular liquid crystal (E7 and BL038) mixed with a chiral dopant and the dimer CB7CB, which is known to reduce the bend elastic constant when added to regular liquid crystals. Among the many measurements, the authors measured the reflected spectra vs. time for the samples filled in a cell treated to provide strong planar anchoring after switching off an applied field high enough to unwind the CLC. The results are reproduced here in Fig. 10. Notice that, when comparing the simulations with the experimental data, the pitch length used in the experiments is much shorter than that used for the simulations. Furthermore, simulations do not consider the viscosity change associated with adding the dimer. For samples with ratio K₃₃/K₂₂ ∼ 1.7, Fig. 10(a), the time to go from homeotropic to planar is on the order of minutes. This is due to the many defects that form and slowly die out in the transition from the TP state to the planar state.³³ The reflectance vs. wavelength measurement clearly shows a peak in the infrared in the initial milliseconds (corresponding to the TP state), followed by a few seconds without any reflection (FP state) and then a reflection peak around 500 nm that slowly increases as defects anneal. If a sample with K₃₃/K₂₂ ∼ 1.0, Fig. 10(b), is used, no peak is associated with the TP state. In just a few milliseconds, a peak starts to develop around the 500 nm region, and the transition finishes in nearly 500 ms, much faster than in the other case. Our results agree well with these measurements, showing fewer defects under similar conditions and that the transition is considerably faster.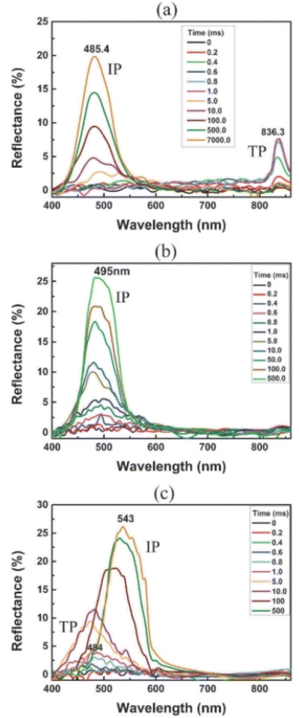

Fig. 10 Reflection spectra during the transition from homeotropic to planar. (a) The case for K₃₃ = 1.71K₂₂, (b) the case for K₃₃ = 1.0K₂₂ and (c) the case for K₃₃ = 0.89K₂₂. Figure reproduced from ref. 34.

Finally, when K₃₃/K₂₂ ∼ 0.9, Fig. 10(c), in the initial milliseconds, a peak forms around 485 nm, corresponding to the TP state with a pitch smaller than the natural pitch. Then, the peak shifts toward 550 nm (natural pitch). The transition occurs much faster than in the K₃₃/K₂₂ ∼ 1.7 case, in approximately 500 ms. Notice that all the experimental aspects follow the results reported here for the PS cell; that is, the TP state is different in each situation, directly affecting the transition time for each cell. A newer publication also observes the same phenomenon.³⁵

Next, we performed a simple experiment to demonstrate how important the anchoring condition is on the homeotropic to planar transition in CLCs. We prepared a mixture of E44 plus 2.9% of S1011 and 19.3% of S811 by weight. The mixture forms a green CLC with a center reflection wavelength of 550 nm. This mixture was filled into four different cells, all with roughly 5 μm thickness: cell 1 coated on both sides with PI-2555, cell 2 coated with polyvinyl alcohol (PVA), cell 3 coated with SE-1211 on one side and PI-2555 on the other side, and cell 4 without an alignment layer. PI-2555 provides strong planar anchoring, with a polar strength of 1.5 × 10⁻³ J m⁻² (ref. 34) and azimuthal strength of ∼1 × 10⁻⁴ J m⁻².³⁸ PVA also provides planar anchoring. However, the polar strength is on the order of 1 × 10⁻⁴ J m⁻² (ref. 39 and 40) while the azimuthal strength is approximately 1 × 10⁻⁵ J m⁻².⁴⁰ SE-1211 is commonly used for strong homeotropic anchoring, with a polar strength of ∼1 × 10⁻³ J m⁻².⁴¹ Lastly, rubbed bare glass also provides planar alignment; however, it is much weaker than PI-2555, with polar and azimuthal strengths of ∼1 × 10⁻⁵ J m⁻².³⁸ Thus, sample 1 has strong planar anchoring, sample 3 has strong hybrid alignment, and samples 2 and 4 have weaker planar anchoring. We then measured the response time of each sample by measuring the reflected light source from an ORIEL Argon lamp 66011 connected to a monochromator set to 550 nm. In the homeotropic state, reflection was utilized as the dark or background state. In contrast, the reflection at 0 V was the bright or reference state. This technique standardizes the reflection and evaluates the transition speed from dark to bright states per cell. It does not assess the reflection magnitudes across different cells. We tracked the optical signal after a 60 V pulse was applied for 50 ms and turned off suddenly until the initial or near the initial reflectance value was obtained. The results are presented in Fig. 11. The PI-2555 case has the slowest response time, 0% to 90%, on the order of seconds. Both samples with weaker planar anchoring have a response time of 100 ms, with the bare glass slightly faster. This result agrees well with what we observe in the simulations. The hybrid cell, on the other hand, has the fastest response time of nearly 10 ms. We notice a peak around 1 ms (clipped in the figure). We hypothesize that this peak occurs because the planar layers develop more rapidly than the focal-conic domains, which emerge close to the homeotropic region. After all, the CLC helix is incompatible with the homeotropic anchoring. Consequently, the reflection tends to increase once the voltage is turned off. After a short period, however, the focal-conic domains are established, scattering light and reducing the reflection.

Fig. 11 Reflection vs. log of time for a CLC mixture in a cell with four anchoring situations. The red squares represent a hybrid alignment cell; the black circles represent a rubbed bare glass cell, the green circles represent PVA, and the black line is the PI-2555 alignment layer.

5 Conclusions

In conclusion, we have studied the homeotropic to planar transition dynamics in chiral nematics with the Landau–de Gennes method in the Q-tensor formalism. We used three sets of elastic constants to emulate the nematic phases currently available to researchers and analyzed their behavior in several anchoring situations. Our results indicate that the elastic constants play an essential role in determining the pathway of this transition, with the matched bend and twist elastic constant case being the faster case because the transient pitch is equal to the natural pitch. Hence, fewer defects are formed.³⁴ Concerning the anchorings, we conclude that low azimuthal energy is best for allowing the CLC layers to grow, so even homeotropic anchoring becomes faster than the regular planar strong anchoring case. Remarkably, the hybrid cell appears quick for regular materials with a transient pitch roughly twice the natural pitch because of the lack of azimuthal anchoring on the homeotropic side. In contrast, the planar side imposes the desired configuration of the helix. With simple experiments previously published and a newer one, we qualitatively verified some of the results presented here. The results may be a starting point for designing reflective CLC displays, which are long-desired displays capable of fast response times to meet the demand for video rates.

Author contributions

Conception and design: E. K. O., R. F. S., R. T. S. and R. S. Z.; analysis and interpretation of the data: E. K. O., R. F. S., R. T. S. and R. S. Z.; drafting of the paper: E. K. O., R. F. S., R. T. S. and R. S. Z.; revision: E. K. O., R. F. S., R. T. S. and R. S. Z. All authors have read and agreed to the published version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

All data used in the paper are included within the paper.

Acknowledgements

This study was financed in part by the Coordenação de Aperfeiçoamento de Pessoal de Nível Superior – Brasil (CAPES) – Finance Code 001. R. S. Z. thanks the National Council for Scientific and Technological Development, CNPq, Process No. (304634/2020-4) and (465259/2014-6), the National Institute of Science and Technology Complex Fluids (INCT-FCx), and the São Paulo Research Foundation (FAPESP – 2014/50983-3).

Notes and references

1. D. Yang and S. Wu, Fundamentals of Liquid Crystal Devices, Wiley, 2014.
2. G. Heppke and D. Krüerke, in Encyclopedia of Materials: Science and Technology, ed. K. J. Buschow, R. W. Cahn, M. C. Flemings, B. Ilschner, E. J. Kramer, S. Mahajan and P. Veyssière, Elsevier, Oxford, 2001, pp. 6046–6051.
3. C. W. Oseen, Trans. Faraday Soc., 1933, 29, 883–899.
4. H. Zocher, Trans. Faraday Soc., 1933, 29, 945–957.
5. F. C. Frank, Discuss. Faraday Soc., 1958, 25, 19–28.
6. J. V. Selinger, Annu. Rev. Condens. Matter Phys., 2022, 13, 49–71.
7. I. Dozov, Europhys. Lett., 2001, 56, 247.
8. R. Hall, K. Miyachi, D. Newton, H. Takezoe and A. Fukuda, Jpn. J. Appl. Phys., 1992, 31, 329.
9. K. Schiele and S. Trimper, Phys. Status Solidi B, 1983, 118, 267–274.
10. L. Longa and W. Tomczyk, J. Phys. Chem. C, 2020, 124, 22761–22775.
11. H. Allinson and H. F. Gleeson, J. Mater. Chem., 1995, 5, 2139–2144.
12. P. Sathyanarayana, B. K. Sadashiva and S. Dhara, Soft Matter, 2011, 7, 8556–8560.
13. R. S. Zola, Y.-C. Yang and D.-K. Yang, J. Soc. Inf. Disp., 2011, 19, 410–416.
14. V. Borshch, Y.-K. Kim, J. Xiang, M. Gao, A. Jákli, V. P. Panov, J. K. Vij, C. T. Imrie, M.-G. Tamba and G. H. Mehl, et al., Nat. Commun., 2013, 4, 2635.
15. C.-J. Yun, M. R. Vengatesan, J. K. Vij and J.-K. Song, Appl. Phys. Lett., 2015, 106, 173102.
16. A. Mertelj, L. Cmok, N. Sebastián, R. J. Mandle, R. R. Parker, A. C. Whitwood, J. W. Goodby and M. Čopič, Phys. Rev. X, 2018, 8, 041025.
17. M. P. Rosseto and J. V. Selinger, Phys. Rev. E, 2020, 101, 052707.
18. N. Sebastián, M. Čopič and A. Mertelj, Phys. Rev. E, 2022, 106, 021001.
19. J. Xiang, Y. Li, Q. Li, D. A. Paterson, J. M. D. Storey, C. T. Imrie and O. D. Lavrentovich, Adv. Mater., 2015, 27, 3014–3018.
20. M. S. H. Himel, K. Perera, A. Adaka, P. Guragain, R. J. Twieg, S. Sprunt, J. T. Gleeson and A. Jákli, Adv. Funct. Mater., 2025, 35, 2413674.
21. C.-T. Xu, B.-H. Liu, C. Peng, Q.-M. Chen, P. Chen, P.-Z. Sun, Z.-G. Zheng, Y.-Q. Lu and W. Hu, Adv. Opt. Mater., 2022, 10, 2201088.
22. Z. Zhou, X. Zhang, S. Halder, L. Hu, Y. Shin and D.-K. Yang, Adv. Opt. Mater., 2024, 12, 2302851.
23. D. Yang, J. L. West, L. Chien and J. W. Doane, J. Appl. Phys., 1994, 76, 1331–1333.
24. P. Watson, V. Sergan, J. E. Anderson, J. Ruth and P. J. Bos, Liq. Cryst., 1999, 26, 731–736.
25. P. Watson, J. E. Anderson, V. Sergan and P. J. Bos, Liq. Cryst., 1999, 26, 1307–1314.
26. P. Watson, J. E. Anderson, V. Sergan and P. J. Bos, Liq. Cryst., 2001, 28, 1–15.
27. V. Sergan, Y. Reznikov, J. Anderson, P. Watson, J. Ruth and P. Bos, Mol. Cryst. Liq. Cryst. Sci. Technol., Sect. A, 1999, 330, 95–100.
28. M.-H. Lee, Y.-C. Yang, J.-E. Kim and H. Y. Park, Phys. Rev. E, 2003, 68, 051701.
29. M.-H. Lee, J.-E. Kim and H. Y. Park, Liq. Cryst., 2004, 31, 333–337.
30. I.-A. Yao, J.-J. Wu and S.-H. Chen, Jpn. J. Appl. Phys., 2004, 43, 1488–1491.
31. I.-A. Yao, J.-J. Wu and S.-H. Chen, Jpn. J. Appl. Phys., 2004, 43, 705–708.
32. D.-K. Yang and Z.-J. Lu, Dig. Tech. Pap. – Soc. Inf. Disp. Int. Symp., 1995, XXVI, 351.
33. E. K. Omori, R. F. de Souza, A. Jakli, R. T. de Souza and R. S. Zola, Phys. Rev. E, 2022, 106, 064701.
34. M. Yu, X. Zhou, J. Jiang, H. Yang and D.-K. Yang, Soft Matter, 2016, 12, 4483–4488.
35. X. Zhang, Z. Zhou, S. Halder, L. Hu and D.-K. Yang, Phys. Rev. Appl., 2024, 22, 044020.
36. R. de Souza, E. Omori and R. Zola, Comput. Phys. Commun., 2022, 277, 108379.
37. J.-B. Fournier and P. Galatola, Europhys. Lett., 2005, 72, 403.
38. Y. Cui, PhD thesis, Kent State University, 2014.
39. M. B. Feller, W. Chen and Y. R. Shen, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 6778–6792.
40. Y. Cui, R. S. Zola, Y.-C. Yang and D.-K. Yang, J. Appl. Phys., 2012, 111, 063520.
41. G. Carbone and C. Rosenblatt, Phys. Rev. Lett., 2005, 94, 057802.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00373c

---