Low-data machine learning models for predicting thermodynamic properties of solid–solid phase transformations in plastic crystals

Abstract

Plastic crystals, many of which are globular small molecules that exhibit transitions between rotationally ordered and rotationally disordered states, represent an important subclass of colossal barocaloric effect materials. The known set of plastic crystals is notably sparse, which presents a challenge to developing predictive thermodynamic models to describe new molecular structures. To predict the transformation entropy of plastic crystals, we developed a comprehensive database of tetrahedral plastic crystal molecules (neopentane analogs) and used several types of features, including chemical functional groups, molecular symmetry, DFT-calculated vibrational entropy, and energy decomposition analysis to train a machine learning model. To select the most relevant features, we used a correlation matrix to screen out highly correlated features and ran sure independence screening and sparsifying operator (SISSO) regression on the remaining features. The SISSO regression samples over combinatorial spaces, including operations and features, to find the relationship between material properties. Using a dataset of 49 plastic crystals and 37 non-plastic crystals based on a common tetrahedral geometry, we have demonstrated the effectiveness of this strategy. Furthermore, we applied this strategy to develop a regression model to predict transition entropy and enthalpy. The top 100 models from the operation space showed that the overall distribution of performance became narrower, sacrificing the top-performing model but avoiding the worst models. Using this approach, we identified the top-performing descriptors to further clarify the underlying mechanisms of the plastic crystal transformation.

---

1 Introduction

Modern refrigeration technologies rely largely on fluorinated vapor-phase refrigerants, which, when they escape into the atmosphere, can contribute significantly to climate change,¹ as well as other potential health and environmental effects associated with per- and poly-fluoroalkyl substances (PFAS). In contrast, solid state caloric effect materials offer an alternative strategy to eliminate the use of vapor phase refrigerants.² In ferroic caloric effect materials, the application of external fields such as magnetic fields,³ electric fields,⁴ and pressure,^5,6 can induce a phase transition, which results in a change in the internal state variable (entropy or temperature) of the material, forming the basis for a refrigeration cycle. Among these, plastic crystal phases^7–10 exhibit colossal barocaloric effects,^5,6,11–13 resulting in a comparatively larger entropy change during phase transition per unit mass for an attainable field change. The required “fields” for phase transformations are generally quite high for their domain: 2 T (for magnetocaloric materials), 1 kV m⁻¹ (for electrocaloric), or 700 MPa (for elastocaloric materials). In contrast, barocaloric materials usually only require about 200 MPa of pressure.⁵

The mechanism of plastic crystal transformations^14,15 in the model system neopentyl glycol (NPG) has been investigated using ab initio methods,¹⁶ demonstrating that intermolecular hydrogen bonds play a key role in regulating phase stability in NPG. Upon treatment with external pressure, these hydrogen bonds are further strengthened, influencing the thermodynamics of order-to-disorder transition. When the temperature increases, the rotational entropy contribution becomes larger, and the disordered cubic phase becomes more favorable in terms of ΔG. Other plastic crystals that lack hydrogen bonds (e.g., CCl₄) show a similar mechanism, but the interactions among molecules are not as strong as in neopentyl glycol (NPG). These molecules have been shown to exhibit many orientations.¹⁷ While some orientations are more energetically favored, many of the others are still accessible in the disordered phase.

The broader goal of developing barocaloric phases with specifically targeted properties (transformation temperature, enthalpy of transition, etc.) requires a strategy to map the effect of molecular chemistry onto the corresponding phase transition behavior. Due to the large combinatorial space consisting of a parent globular molecule (e.g., NPG) with chemically allowable substituted functional groups, sequential synthesis and characterization of individual molecules is practically infeasible. Thus, developing an accurate predictive strategy offers significant advantages. To achieve this aim, one could turn toward machine learning techniques to both predict the properties of future plastic crystals and understand the thermodynamics in existing systems. Since the 1960s, 27 plastic crystal molecular types have been reported.^10,18 Here, we seek to assess the predictive ability of trained models based on the sparse known set of tetrahedral plastic crystalline phases. A chief objective of this work is to determine whether this current data set is sufficient to predict whether a related unknown compound will exhibit a plastic crystalline state, as well as the magnitude of entropy and enthalpy changes and the equilibrium transformation temperature.

To address this question, we systematically assessed previously reported experimental data on tetrahedral carbon-centered small molecules, a class that includes a number of compounds (including methane analogs and neopentane analogs) known to exhibit plastic crystalline states, as well as compounds with similar geometries in which this state is not observed. To develop a machine learning model capable of predicting phase transition properties, we aim to use descriptors with high correlation to relevant properties. The descriptor design focuses on two key aspects: molecular shapes and interactions. Overall, we developed five descriptor calculation methods: group contribution analysis, molecular symmetry, hydrogen bond strength (both donors and acceptors), DFT-derived molecular properties, and intermolecular energy decomposition analysis terms.

Molecular symmetry has been shown to correlate strongly with the classification of plastic versus non-plastic crystals through interaction with environmental orientation.¹⁹ This symmetry also correlates with rotational entropy as described by the equation ΔS^rot_m = R ln σ.²⁰ Given the transformation's reliance on rotational degrees of freedom, sphericity—derived from the moment of inertia tensor²¹—is included as a molecular symmetry descriptor. To quantify molecular interactions, a previously calculated empirical table correlating hydrogen bond strength with functional groups²² was utilized. Furthermore, descriptors such as single-molecule vibrational entropy, intermolecular interaction energy, and single-molecule volume, all calculated using DFT, were incorporated as molecular properties.

Based on this training set, we evaluated the ability to quantitatively predict (1) the existence of solid–solid transitions into a plastic crystal state, and (2) the related thermodynamic properties of the solid–solid transition.²³ To tackle the problem of high dimensionality from the molecular descriptors where only limited data are available, we utilized the sure-independence screening and sparsifying operator (SISSO) approach to explore the large combinatorial spaces that use operators (addition, subtraction, and multiplication) and all available features. In this study, we applied a feature selection strategy to tackle this low-data problem.^24–27 The results show that the strategy of using a correlation matrix and SISSO is effective in extracting information from the original descriptors and in improving the predictive accuracy. Furthermore, interpreting the operation of the original descriptors could potentially guide us to the relationship between the descriptors.

2 Material and methods

In this work, the term descriptor is used when an individual parameter that is obtained from the chemical species or environment. The term feature is used when referring to the direct input to the machine learning model.

2.1 Dataset parameters

The possible chemical space investigated in this study consists of small globular carbon-centered tetrahedral molecules, only a small number of which are observed to exhibit a rotationally disordered plastic crystalline state. We conducted an extensive literature search to identify the appropriate training and test sets for these systems. The resulting database, TetraPlastC^{5,6,10–13,28–46} consists of globular and tetrahedral molecules wherein the enthalpy of the solid–solid plastic crystalline transition is either comparable to or larger than the latent heat of melting. While there are other globular molecules that are proven plastic crystals (e.g., adamantane), these do not exhibit tetrahedral configurations, and thus, are considered out of the scope of this study. Additionally, we only considered relatively small functional groups (shown in Table 1) in the tetrahedral structure to reduce the steric variability.

Table 1 Hydrogen bond donor and acceptor strength

Functional group	Donor element and strength	Acceptor element and strength
–CH3	C: 0.5	No acceptor
–C2H5	C: 0.5	No acceptor
–CH2OH	O: 4.1	O: 6.3
–COOH	O: 5.5	O: 6.3
–NH2	N: 2.0	N: 8.6
–CH2NH2	N: 2.0	N: 8.6
–NO2	No donor	O: 5.5
–X (X = F, Cl, Br, I)	No donor	F: 3.9, Cl: 3.10, Br: 2.90, I: 2.61
–CH2X (X = F, Cl, Br, I)	C: 1.3	F: 3.9, Cl: 3.10, Br: 2.90, I: 2.61
–SH	S: 2.0	S: 3.5
–CHO	O: 0.9	O: 5.5
–C4H9	C: 0.5	No acceptor
–CONH2	N: 4.5	O: 8.3

---

Reviewing the identified plastic crystalline compounds, it was observed that the dataset collected is biased toward compounds that contain hydroxyl, methoxy, and alkyl groups. This occurrence is likely due to the wide utilization of these compounds in synthesis, for their stability in ambient environments and their presence in the most well-studied plastic crystalline compounds such as NPG. 86 molecules with tetrahedral-like structures were collected from the literature, including compounds which had only a single type of functional group (e.g., neopentane), and increasingly complex compounds which had two different functional groups (e.g., NPG), and three or even four different functional groups (e.g., 2-methyl-2-butanethiol, which is observed to exhibit a plastic crystal transition⁴⁷).

The plastic crystals (49) in the dataset include (1) phases that have direct experimental evidence of rotational disorder (e.g., electrical impedance spectroscopy), as well as (2) phases that are calorimetrically determined to have large changes in configurational entropy at this solid–solid transformation relative to the melting transformation (as defined by dS_s–s − dS_s–l). In contrast, molecules that are determined to “not exhibit” a plastic crystal state (37) included (1) compounds that present data (e.g., temperature-dependent heat capacity data) which conclusively demonstrate the lack of an additional solid–solid phase transformation over the relevant temperature range of interest, (2) phases which exhibit low-entropy transitions from one solid crystalline state to another solid crystalline state, and (3) studies which present thermophysical data (e.g., enthalpies of fusion) that would have made it more likely than not to observe a solid–solid plastic crystal transition if one exist near the melting transition. Compounds with limited reported information e.g., only low-temperature single crystal structure determination, or room-temperature spectroscopy information) were labeled as “inconclusive” (14) and were not included as part of our known dataset. 84 molecules were identified to have no calorimetric data and thus, were not included into our dataset. The summary of the dataset, classification labels, and sources are provided in our GitHub repository (link provided in the ESI†).

2.2 Features

Five categories of descriptors of small molecules are considered, as follows:

2.2.1 Group contribution descriptors. This set of descriptors relies on the nature and quantity of the four chemical groups attached to the central carbon atom (Fig. 1). The number of occurrences of each-R group will be encoded into the features. In the compiled dataset, 26 distinct chemical groups are observed.

Fig. 1 (a) Illustration of an idealized tetrahedral-like molecule (b) database sparsity (c) calculation workflow.

Group contribution methods have been shown in other applications to predict the melting point and boiling point of aromatic compounds,⁴⁸ as well as enthalpies and entropies of fusion of broad sets of low molecular weight organic compounds.^49–51 They also form the basis for many cheminformatics-based models on organic molecule solubility, synthesizability, and other applications.^52,53

2.2.2 Molecular shape and symmetry descriptors. Descriptors of molecular shape included in this study are the average and standard deviation of the effective radius, the average and standard deviation of six internal angles, and the distance between the center of mass and the central carbon atom. The effective radius of a molecule is the distance between the central carbon atom and the furthest non-hydrogen atom in each leg of the tetrahedral molecule. The standard deviation of the effective radius (over the four functional groups that compose the tetrahedral molecule) reflects one aspect of the sphericity of the molecule. A lower standard deviation exhibits a more uniform molecular geometry. A second measure of sphericity is calculated based on the moment of inertia tensor, as described in ref. 21. We calculated the moment of inertia tensor and obtained the three principal components by diagonalizing the matrix. By ranking these three components, we have I₁, I₂ and I₃, where I₁ is the smallest and I₃ is the largest. Two factors are calculated: npr₁ = I₁/I₃, npr₂ = I₂/I₃ and these are used to compute sphericity = npr₁ + npr₂ − 1. The internal angles are calculated with all combinations of the first atom of four functional groups and the central carbon as the middle atom in that angle. 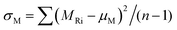Molecular symmetry values are the number of indistinguishable rotated positions of a molecule, which is also associated with the point group of the molecule, as described in Wei et al.⁵⁴ The effects of the mass distribution in a molecule are accounted for by two descriptors, average and standard deviation of mass of the four functional groups (, where M = mass and n = 4). All bonds and angles considered are described in Fig. 1(a).

2.2.3 Hydrogen bond strength. As hydrogen bond strength is understood to play a pivotal role in fixing the orientation of globular molecules in the rotationally ordered state,¹⁶ we include descriptors based on calculated hydrogen bond strength. The hydrogen bond acceptor/donor strength is determined by the functional group in the molecule (Table 1).²² After determining all the acceptor/donor strengths, the following values are calculated: (1) the average donor/acceptor strength, (2) the standard deviation of donor/acceptor strength, and (3) the maximum of donor/acceptor strength. For functional groups that were not previously published in the literature, such as Cl, Br, and I, we scaled the values proportionally to the electronegativity of the atom, using F as a reference. For example, the average acceptor strength of F is 3.90, Cl is 3.10, and Br is 2.90.

Table 2 Functional group model weights

Identifiers			Sampling
			ΔS	ΔH	T tr	T m
a	–H	Hydrogen	1.9	−0.5	10.9	19.4
b	–CH3	Methyl	6.7	1.0	44.6	64.0
c	–C2H5	Ethyl	0.3	−4.6	14.4	2.3
d	–CH2OH	Hydroxymethyl	19.1	7.6	100.9	117.9
e	–CHFOH	Hydroxyfluoromethyl	−0.7	−3.4	38.4	124.4
f	–CHClOH	Hydroxychloromethyl	11.8	0.4	31.4	56.1
g	–COOH	Carboxyl	20.3	10.8	153.2	162.6
h	–NH2	Amino	26.7	8.7	97.2	80.6
i	–CH2NH2	Methylamine	19.1	5.5	66.5	67.8
j	–NO2	Nitro	10.6	3.6	81.9	87.4
k	–F	Fluoro	5.1	0.4	19.1	22.4
l	–Cl	Chloro	7.2	1.6	56.9	59.3
m	–Br	Bromo	5.7	1.8	78.5	88.6
o	–CH2F	Fluoromethyl	11.1	2.4	58.8	89.8
p	–CH2Cl	Chloromethyl	6.1	1.7	61.1	69.9
r	–SH	Thiol	21.7	5.7	36.6	60.6
v	–CHO	Aldehyde	6.3	1.7	50.0	79.9
z	–C4H9	Butyl	113.2	2.9	70.8	133.0

---

2.2.4 DFT-calculated intermolecular interaction properties. Given that entropy change is linked to molecular degrees of freedom, we included several atomistic-scale features in our analysis to enhance predictive accuracy. Electronic structure calculations can give some insights into molecular interactions as well as molecular rotational entropy. We calculated vibrational entropies, dimer interaction energies, and molecular volumes, which are related to plastic crystal transformation. All calculations were performed using Gaussian16. The calculation workflow is described in Fig. 1(c). First, we obtained smiles string for all 49 molecules and generated random 3D structures using OpenBabel.⁵⁵ Second, a CREST conformer generation calculation⁵⁶ was performed to find the lowest energy conformer of the molecule. From here, the geometry was optimized using Gaussian 16⁵⁷ under ωB97X-D/def2-SV(P) level of theory on the lowest energy conformer and a frequency calculation to calculate the vibrational entropy. Using the optimized monomer, 100 volume calculations were performed to get the average molecular volume with a standard deviation of less than 5%. Additionally, the optimized monomer was used to generate dimer initial structures and CREST⁵⁶ conformer generation. The lowest energy conformer was further optimized, and the interaction energy of the dimer was obtained using the lowest-energy dimer configuration (more details are provided in the ESI†).

2.2.5 Energy decomposition analysis. An energy decomposition analysis (EDA) of the non-covalent interactions of dimers of the molecules was performed using Q-Chem 5.4.0.⁵⁸ The structures are obtained from the lowest-energy dimer configuration using CREST conformer search⁵⁶ and further optimized using Gaussian 16.⁵⁷ The methods used in the Absolutely Localized Molecular Orbitals ALMO-EDA scheme are described in ref. 59. The electrostatic, Pauli exclusion, dispersion, polarization, and charge transfer terms are considered as separate descriptors in the correlation matrix.

2.3 Downselection of features

Once all descriptors were evaluated for the molecules in this database, we wanted to investigate the limit of informative linear regressions with discrete descriptors. To achieve this, an F-test was conducted on two linear regression models to select the top five descriptors. The first model utilized the group contribution method as input to predict transformational entropy, while the second model relied on all other descriptors. The downselection in the group contribution model aimed to identify the functional groups most critical for prediction. Meanwhile, the other descriptors, being structure-related, were analyzed to determine the key factors influencing the transformation. Reducing the number of features to five in both models also helped to prevent overfitting of the training data.

3 Results and discussion

3.1 Classification of plastic crystals

We first consider the classification problem. Classifying whether a particular compound exhibits a plastic crystalline phase can help screen candidate molecules, and prioritize certain compounds over others. Therefore, we collected other non-plastic crystal tetrahedral-like molecules into our dataset for classification. The final set of tetrahedral molecules that do not contain a plastic crystal phase contains 37 molecules. Subsequently, we constructed a correlation matrix and then employed SISSO to obtain sets of two features from combinations of the descriptors. In order to avoid overfitting, we conducted tests using different numbers of allowed operators and descriptors. The results indicated that reducing the number of operations to three (seven was used in the regression) could be a sweet spot that balances between underfitting and overfitting (testing accuracy improves from 50% to 75%). Using a limited set of descriptors, we obtained a classification model with 70 percent accuracy (Fig. 2(b)–(e)). We also mapped the two features obtained from this model to see if a boundary exists (in feature space) that effectively separates molecules that do or do not exhibit plastic crystal states. From Fig. 2(b) and (c), it can be determined that plastic and non-plastic crystals can be separated using this set of features. The results above indicate that the SISSO-reducing technique helps with (1) identifying the key descriptors and (2) improving the performance compared to models that take all the descriptors as inputs. Within this low data regime, fewer inputs can avoid overfitting.

Fig. 2 (a) Distribution that shows descriptors that are obtained from SISSO for classification. The scores are plotted to show which descriptors tend to give better performance. Maximum hydrogen acceptor strength, charge transfer and dispersion are the top three descriptors. (b) and (c) By mapping the two features and labeled with types (blue for plastic crystal and red for non-plastic crystal). The overall mapping shows that there is a non-linear separation between two types of data. (d) and (e) One random seed train/test split classification result. The overall accuracy is around 0.7.

3.2 Multiple linear regression analysis

3.2.1 Group contribution approach. Group contribution methods use multiple linear regression analysis to derive thermodynamic properties from the numbers and types of chemical functional groups present in a particular molecule. This approach has previously been shown to provide reasonable predictive power for melting points and boiling points of organic compounds.⁴⁸ This is often applied to thousands of data, while we only have fewer than a hundred points. We applied multiple linear regression analysis to evaluate the overall correlation between the number of groups and the experimental thermodynamic properties. The resulting determination coefficient is above 0.7 for all key thermodynamic properties (R² (ΔS_tr): 0.77, MAD (ΔS_tr): 0.18 (Fig. 3(a)), R² (ΔH_tr): 0.86, MAD (ΔH_tr): 0.21, R² (T_tr): 0.93, MAD (T_tr): 0.07, R² (T_melt): 0.94, MAD (T_melt): 0.06). Although we obtain a high R² for the entire dataset, there is a risk that the linear regression model is an overfitted model since it was trained and tested on the same data. This means we cannot assess its performance using unseen data. Additionally, the ratio of descriptors to data points is approximately 1 : 2, which is quite high for most machine learning models. As previously mentioned, the data set is highly biased towards hydroxymethyl and methyl compounds.

Fig. 3 (a) Tailored group contribution model of the entropy of transition for the TetraPlastC database. (b) The results of linear regression with all descriptors in the database. (c) The results for the downselected descriptor linear regressions of the entropy of the transition.

Through consideration of the weighing strength of each functional group, this dataset is capable of determining functional groups that have a greater impact on the plastic crystal transition (Table 2). The larger the weighting factor, the more influential that specific functional group on that thermodynamic property. The more influential functional groups tend to be those that have strong hydrogen bonds. The results for using all 30 features (types of functional groups) from group contribution methods have high correlation factors. Additionally, the tailored group contribution method is inflexible for prediction as with this method, there are no ways to predict the properties of compounds containing functional groups that are not present or that are poorly sampled in the testing database. The present model provides reasonable predictions for key thermodynamic properties related to the functional groups tested, but cannot be extended to those outside the testing dataset, since the number of features is still considered too high compared to the size of the existing dataset.

3.2.2 Structural descriptor approach. Structural descriptor-based methods relate the impact of chemical functional groups on the resulting thermodynamic properties of plastic crystal molecules by correlating the impact of those functional regressions and provide insight into the underlying mechanisms that influence the plastic crystalline transition by applying multiple linear regression analysis to search for correlations between thermodynamic properties and structural descriptors, rather than the quantity and type of chemical functional groups (as in the previous section). The structural descriptor-based regressions provide insight into the underlying mechanisms that influence the plastic crystalline transition. These models apply multiple linear regression analysis to search for correlations between thermodynamic properties and structural descriptors rather than the quantity and type of chemical functional groups (as in the previous section). The regressions that take in only calculated descriptors resulted in high correlation coefficients (R² (ΔS_tr): 0.80, MAD (ΔS_tr): 0.17, R² (ΔH_tr): 0.84, MAD (ΔH_tr): 0.23, R² (T_tr): 0.89, MAD (T_tr): 0.09, R² (T_melt): 0.89, MAD (T_melt): 0.08). Similarly to the group contribution regressions, the correlation coefficients (see ESI,† Fig. S1 and S2) also imply that the linear regression models overfit because the ratio of features to data points is also high at about one descriptor for every two data points. The descriptors with the highest significance were the interaction-based descriptors, except for the average radius (as a proxy for size, see ESI,† S6). Having a direct correlation to the phenomena from a structural descriptor allows an intuitive connection between the impact of each descriptor and the influence on the observed phenomena. Using structural descriptors also allows modular predictions for compounds with functional groups not represented in the database. To deal with these potential over-fitting problems, the down-selected structural descriptors provide a guarantee against over-fitting while retaining the simple interpretations at the expense of accuracy. These models' correlation coefficients reflect the lower accuracy as the coefficients for melting temperature, transition temperature, enthalpy of transition, and entropy of transition are 0.82, 0.86, 0.77, and 0.67, respectively.

3.3 Low data machine learning techniques: employing SISSO

Based on the results presented in the previous sections, it remains difficult to accurately predict the classification and thermodynamic properties of unknown molecules. In the following section, we assess the performance using the distribution of 100 randomly generated train/test split sets to avoid the risk of obtaining a good performance from a “lucky” set. Additionally, due to the limited amount of available data, we employed two separate dimensionality reduction techniques: (1) removing high correlation descriptors within each group of descriptors and (2) applying sure-independence screening and sparsifying operator (SISSO) techniques. By limiting the number of descriptors in the machine learning model, we can avoid the overfitting problem for testing set molecules. In order to maintain an appropriate number for each group, we used different criteria to screen out unnecessary descriptors. The highly correlated descriptors were determined by a value of the correlation coefficient, r ≥ 0.5 (r ≥ 0.1 for group contribution method threshold of 0.5 (0.1 for group contribution method to ensure that not too many descriptors are included). After screening out the highly correlated descriptors, we combined these descriptors into the SISSO task and selected two features as our final inputs for the regression (or classification model). To evaluate the validity of this strategy, we examined a subset of 30 molecules out of the 49 plastic crystal molecules contained in the full data set and checked the testing score distribution. By choosing 30 data points, we are able to conduct “every-set” testing as the number of combinations of hypothetical train/test split is computationally feasible (30!/(24!6!) = 593 775). Plotting the testing score distribution can indicate the overall performance in case the sampled train/test split is occasionally the “easy” set to predict. We compared the testing score distribution between the original descriptors and the two features that were down-selected after the two screening steps (Fig. 4(a)–(e)). Additionally, the comparison is done on five groups of descriptors since these have been shown to have a high correlation with transformational entropy. The results of all five testing groups indicate that the dimensionality reduction strategy here improves the overall performance significantly (the peak shifts to the right for all five cases).

Fig. 4 To show the effectiveness of SISSO, we plotted testing distributions using the following categories of descriptors: (a) group contribution method, (b) molecular symmetry, (c) hydrogen bond strength, (d) Svib, volume, interaction energy, (e) energy decomposition analysis. The green bars use all descriptors, while the yellow bars are SISSO-reduced features. These are trained and tested on the sampled training and sets, and the distribution is based on every possible train/test split. (f) and (g) 70 000 scores obtained from 100 train per test splits sampled from the whole dataset. The scores are calculated among 100 × 7 (7-fold cross-validation) × 100 (top 100 models from SISSO) sets.

3.4 Predicting transformational entropy and enthalpy

As the subset of 30 sampled molecules described in the previous section demonstrated the validity of the strategy, we further applied this strategy to the complete dataset of 49 plastic crystal molecules. We excluded the division operation in the SISSO regression task, as the division operation could possibly lead to infinity if one of the descriptors in the data is 0, which will results in untrainable features. Since the number of potential train/test splits is very large, an every-set testing approach (where every possible train/test split is tested) is not feasible. We sampled 100 train per test splits to approximate the distribution of the scores over these possible splits. We performed a 7-fold cross-validation (because of the dataset size of 49). Furthermore, by using SISSO, we identified the top 100 combinations of descriptors from the original set. To summarize, we obtained 100 feature sets from one train/test split and an overall 70 000 scores from the sampling (Fig. 4(f) and (g)). Here we plotted the distribution for all 100 splits. The peak in the distribution is around R² 0.5, which is already an improvement within the data size we have. In Fig. 5(c)–(f), predictions on two different splits are shown to show some edge cases in the distribution. The selected descriptors are listed below each panel. This result demonstrates that the performance is strongly dependent on which specific train/test split is initially selected. This strategy highlights that examining the overall correlation across the dataset is insufficient to determine the model's suitability for future screening. The down-selection approach can help pinpoint key descriptors, but its predictive power remains uncertain since it relies solely on fitting the entire dataset. Furthermore, for small and sparse datasets, evaluating models across various data splits is crucial to assess their overall predictive performance.

Fig. 5 One train/test split prediction obtained from the regression task. Selected features are described below the plot. (a) and (b) Distribution that shows features that are obtained from SISSO for regression. The scores are plotted to show which descriptors tend to give better performance. Interaction energy, maximum hydrogen acceptor strength, dispersion, and average distances between central carbon and four functional groups are the top four descriptors. (c) and (d) Examples showing a good prediction of both entropy and enthalpy. (e) and (f) Examples showing a poor prediction of both entropy and enthalpy.

3.5 Chronological assessment

Over the past few decades, the total sum of knowledge on tetrahedral plastic crystal molecules has steadily increased. In this section, we considered this accumulation of knowledge and posed the question of, “How has our ability to accurately predict the properties of solid–solid phase transformations between rotationally ordered and disordered states evolved over time?” (if these models had existed throughout time). To answer this question, we re-trained the SISSO model at different points in time, including the cumulative body of knowledge that was known at that point in time, and evaluated the validity of that model on data that was collected after that point in time. This test evaluates whether certain periods of time introduced new functional groups that complicate the overall prediction or if the measured experimental values are relatively inaccurate. On the training side, we can observe the evolution of the relative performance of the model and whether a particular data set deteriorated the performance of the model. On the testing side, we can estimate the difficulty of a certain functional group not being within the training data, which we expect makes the overall training harder. We tested on both regression and classification tasks. For regression (Fig. 6(a) and (b)), the molecules associated with higher prediction losses in 1999 are highlighted above the plot. Specifically, 1,3-dichloro-2,2-dimethylpropane and 2,2-dichloropropane are identified as problematic molecules for these models. For classification, a significant drop in accuracy occurred in 2008, coinciding with the addition of two molecules containing carbonyl groups. In 2019, the accuracy declined again, primarily due to the very small size of the test set. The trends in entropy and enthalpy predictions indicate that the discovery of new plastic crystals and corresponding experimental data generally improved the models predictive performance. From Fig. 6, we can tell that predictions after 1994 and 2005 started to show a decreasing trend in the prediction loss, which corresponds to a training data size of 20 and 34. Additionally, after the chloro-containing compounds are added to the training set, the prediction loss decreases.

Fig. 6 Chronological plots for regression (a) and (b) and classification (c) that the data before a certain year was trained and tested on all the other. The molecules labeled are the ones that were added in that year, which decreased the overall performance. The yellow triangle, square, and circle dots correspond to training, testing, and total dataset size.

3.6 Correlation between selected features and model performance

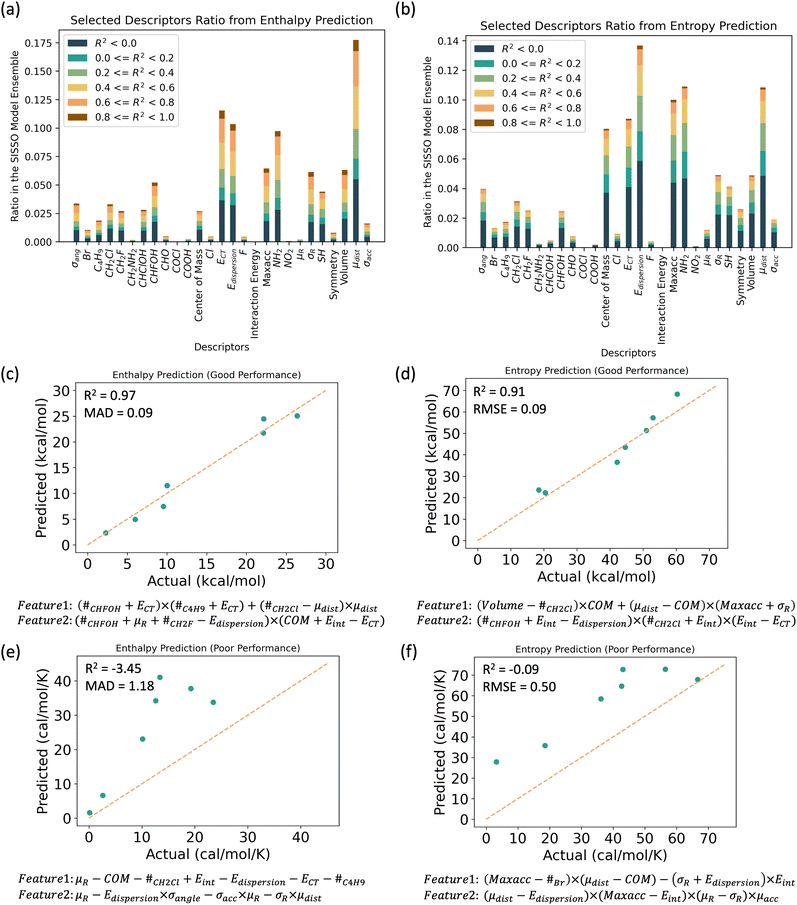
From the top 100 models and 100 sampled train/test splits, we generated 10 000 combinations of features selected using SISSO. We then counted the occurrences of certain descriptors and color-coded them based on the corresponding model scores. The results are shown in the Fig. 5(a) and (b). Among these descriptors, maximum acceptor strength, charge transfer, and dispersion energies are the top-performing descriptors. All these terms are related to either hydrogen bond strength or molecular interactions between two molecules. As secondary ranking descriptors, geometry-related descriptors are also commonly selected, particularly those used for understanding the shape of the molecule.

We conclude that electronic interactions and molecular shapes are the top descriptors that correlate with transformational enthalpy and entropy, aligning with our observations using an f-test down-selection method. For commonly seen operating correlations, we identified two frequently observed feature operations:

(1) Maximum acceptor strength – center of mass and

(2) Center of mass × E_dispersion

Based on these observations, we can conclude both molecular rotation and interaction between molecules are important to transformational entropy. Although the relationship between mass and dispersion energy is not entirely clear, their contribution to transformational entropy is significant enough to warrant inclusion in future training. Overall, by running 100 models, we identified the top candidates for future model applications. Compared to other thermodynamic property models, such as a predictive model for T_g,^60–65 our model demonstrates several advantages. First, we present the performance distribution across multiple train/test splits, ensuring that the results are not biased by datasets that are easier to learn. Additionally, our model achieves moderate performance without incorporating melting temperature as a descriptor. According to the literature, melting points are highly correlated with the glass transition temperature, yet they are not easily accessible features. In contrast, our model benefits from using descriptors that can be computed theoretically, making it more suitable for candidate screening. Finally, while some previous models achieve R² > 0.8^63,65 (with melting point as one of their features), our model shows a peak performance around 0.7 (70% accuracy), which is an improvement over earlier T_g prediction models.^60–65

4 Conclusions

In conclusion, we have aggregated previously reported experimental ΔS data for all previously reported carbon-centered tetrahedral-like plastic crystal molecules. Using five types of molecular descriptors, including DFT calculations, we have demonstrated that both correlation matrix and SISSO approaches can effectively reduce feature dimensions and improve overall model performance. To show the effectiveness of this approach, with sampled set testing, the performance distribution is consistently right-shifted, regardless of which descriptors are used. We used the same strategy for classification, which resulted in an average of 0.7 accuracy. By plotting the score and selecting features from each model, we were able to obtain top performance descriptors. We have quantified the impact of structural descriptors that are essential for developing predictive models and identified key mechanisms underlying the plastic crystalline transition: (1) hydrogen bond strength and center of mass, and (2) center of mass and dispersion energy in the dimer configuration. These descriptors can be categorized into molecular interactions and molecular shape. Both hydrogen bonding and dispersion forces contribute to intermolecular interactions and are the dominant forces in plastic crystalline materials, as demonstrated in previous studies.^16,17 Regarding the center of mass, previous research has explored how variations in the moment of inertia influence plastic crystal transitions, and our findings align with these studies. These simple regression models provide valuable insights for designing new plastic crystalline compounds with tailored thermal properties, expanding the scope of materials suitable for practical applications.

Conflicts of interest

There are no conflicts to declare.

Data availability

All code and data are available in the following Github repository: https://github.com/Tabor-Research-Group/TetraPlastiC.

Acknowledgements

T.-H. Chao and D. P. Tabor acknowledge support from the Robert A. Welch Foundation, grant no. A-2049-20230405. P. J. Shamberger and A. Foncerrada acknowledge support from the Department of the Navy, Office of Naval Research under award no. N00014-22-1-2050. Portions of this research were conducted with high-performance research computing resources provided by Texas A&M University HPRC. The authors thank Chase Somodi for feedback and helpful discussions on the manuscript.

Notes and references

1. E. Molenbroek, M. Smith, N. Surmeli, S. Schimschar, P. Waide, J. Tait and C. McAllister, Saving and benefits of global regulations for energy efficient products. A “cost of non-world” study, European Commission, Directorate-General for Energy, 2015. Accessed 2025-06-14, https://energy.ec.europa.eu/publications/savings-and-benefits-global-regulations-energy-efficient-products-cost-non-world-study_en.
2. S. Fähler and V. K. Pecharsky, MRS Bull., 2018, 43, 264–268.
3. B. Shen, J. Sun, F. Hu, H. Zhang and Z. Cheng, Adv. Mater., 2009, 21, 4545–4564.
4. X. Moya, S. Kar-Narayan and N. D. Mathur, Nat. Mater., 2014, 13, 439–450.
5. B. Li, Y. Kawakita, S. Ohira-Kawamura, T. Sugahara, H. Wang, J. Wang, Y. Chen, S. I. Kawaguchi, S. Kawaguchi and K. Ohara, et al. , Nature, 2019, 567, 506–510.
6. P. Lloveras, A. Aznar, M. Barrio, P. Negrier, C. Popescu, A. Planes, L. Mañosa, E. Stern-Taulats, A. Avramenko and N. D. Mathur, et al. , Nat. Commun., 2019, 10, 1803.
7. W. Press, Science, 1980, 207, 880–881.
8. L. Staveley, Annu. Rev. Phys. Chem., 1962, 13, 351–368.
9. D. Bansal, J. Hong, C. W. Li, A. F. May, W. Porter, M. Y. Hu, D. L. Abernathy and O. Delaire, Phys. Rev. B, 2016, 94, 054307.
10. E. F. Westrum Jr, Pure Appl. Chem., 1961, 2, 241–250.
11. J. Font, J. Muntasell and E. Cesari, Mater. Res. Bull., 1995, 30, 839–844.
12. J. Li, D. Dunstan, X. Lou, A. Planes, L. Mañosa, M. Barrio, J.-L. Tamarit and P. Lloveras, J. Mater. Chem. A, 2020, 8, 20354–20362.
13. Q. Ren, J. Qi, D. Yu, Z. Zhang, R. Song, W. Song, B. Yuan, T. Wang, W. Ren and Z. Zhang, et al. , Nat. Commun., 2022, 13, 2293.
14. C. Escorihuela-Sayalero, L. C. Pardo, M. Romanini, N. Obrecht, S. Loehlé, P. Lloveras, J.-L. Tamarit and C. Cazorla, npj Comput. Mater., 2024, 10, 13.
15. L. Schmidt, D. Van der Spoel and M.-M. Walz, ACS Phys. Chem. Au, 2022, 3, 84–93.
16. F. Li, M. Li, X. Xu, Z. Yang, H. Xu, C. Jia, K. Li, J. He, B. Li and H. Wang, Nat. Commun., 2020, 11, 4190.
17. A. H.-T. Li, S.-C. Huang and S. D. Chao, J. Chem. Phys., 2010, 132, 024506.
18. S. Das, A. Mondal and C. M. Reddy, Chem. Soc. Rev., 2020, 49, 8878–8896.
19. W. Shen, J. Antonaglia, J. A. Anderson, M. Engel, G. van Anders and S. C. Glotzer, Soft Matter, 2019, 15, 2571–2579.
20. R.-M. Dannenfelser and S. H. Yalkowsky, Ind. Eng. Chem. Res., 1996, 35, 1483–1486.
21. M. Wirth, A. Volkamer, V. Zoete, F. Rippmann, O. Michielin, M. Rarey and W. H. Sauer, J. Comput.-Aided Mol. Des., 2013, 27, 511–524.
22. D. Santos-Martins and S. Forli, J. Chem. Theory Comput., 2020, 16, 2846–2856.
23. F. Musil, S. De, J. Yang, J. E. Campbell, G. M. Day and M. Ceriotti, Chem. Sci., 2018, 9, 1289–1300.
24. Y. Zhang and C. Ling, npj Comput. Mater., 2018, 4, 25.
25. P. Xu, X. Ji, M. Li and W. Lu, npj Comput. Mater., 2023, 9, 42.
26. R. Ouyang, E. Ahmetcik, C. Carbogno, M. Scheffler and L. M. Ghiringhelli, J. Phys.: Mater., 2019, 2, 024002.
27. A. L. Liu, R. Venkatesh, M. McBride, E. Reichmanis, J. C. Meredith and M. A. Grover, ACS Appl. Polym. Mater., 2020, 2, 5592–5601.
28. N. I. of Standards and Technology, NIST Computational Chemistry Comparison and Benchmark Databases, U.S. Department of Commerce Technical Report NIST Standard Reference Database Number 101 Release 22, May 2022, 2022.
29. A. Aznar, P. Lloveras, M. Barrio and J. L. Tamarit, Eur. Phys. J.-Spec. Top., 2017, 226, 1017–1029.
30. A. Aznar, P. Lloveras, M. Barrio, P. Negrier, A. Planes, L. Mañosa, N. D. Mathur, X. Moya and J.-L. Tamarit, J. Mater. Chem. A, 2020, 8, 639–647.
31. D. Chandra, W. Ding, R. A. Lynch and J. J. Tomilinson, J. Less-Common Met., 1991, 168, 159–167.
32. K. Kobashi and M. Oguni, J. Phys. Chem. B, 1999, 103, 7687–7694.
33. H. Enokido, T. Shinoda and Y.-i Mashiko, Bull. Chem. Soc. Jpn., 1969, 42, 84–91.
34. J. Hicks, J. Hooley and C. Stephenson, J. Am. Chem. Soc., 1944, 66, 1064–1067.
35. R. Andon, J. Counsell, D. Lee and J. Martin, J. Chem. Soc., Faraday Trans. 1, 1973, 69, 1721–1726.
36. F. Meersman, B. Geukens, M. Wübbenhorst, J. Leys, S. Napolitano, Y. Filinchuk, G. Van Assche, B. Van Mele and E. Nies, J. Phys. Chem. B, 2010, 114, 13944–13949.
37. S. Hore, R. Dinnebier, W. Wen, J. Hanson and J. Maier, Z. Anorg. Allg. Chem., 2009, 635, 88–93.
38. A. B. Bazyleva, G. J. Kabo and A. V. Blokhin, Phys. B, 2006, 383, 243–252.
39. J. Font and J. Muntasell, J. Mater. Chem., 1995, 5, 1137–1140.
40. D. Sake Gowda and R. Rudman, J. Chem. Phys., 1982, 77, 4666–4670.
41. D. Sake Gowda and R. Rudman, J. Chem. Phys., 1982, 77, 4671–4677.
42. D. Sake Gowda, N. Federlein and R. Rudman, J. Chem. Phys., 1982, 77, 4659–4665.
43. N. Doshi, M. Furman and R. Rudman, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 1973, 29, 143–144.
44. P. Hall, Trans. Faraday Soc., 1971, 67, 556–562.
45. J. N. Sherwood, The Plastically crystalline state: orientationally disordered crystals, John Wiley & Sons, 1979.
46. L. Silver and R. Rudman, J. Phys. Chem., 1970, 74, 3134–3139.
47. S. Kondo, Bull. Chem. Soc. Jpn., 1965, 38, 527–529.
48. P. Simamora and S. H. Yalkowsky, Ind. Eng. Chem. Res., 1994, 33, 1405–1409.
49. J. S. Chickos, C. M. Braton, D. G. Hesse and J. F. Liebman, J. Org. Chem., 1991, 56, 927–938.
50. F. Gharagheizi and G. R. Salehi, Thermochim. Acta, 2011, 521, 37–40.
51. K. Mansour and M. Korichi, Computer Aided Chemical Engineering, Elsevier, 2023, vol. 52, pp. 661–666.
52. F. Gharagheizi, A. Eslamimanesh, A. H. Mohammadi and D. Richon, Ind. Eng. Chem. Res., 2011, 50, 10344–10349.
53. E. Stefanis and C. Panayiotou, Int. J. Thermophys., 2008, 29, 568–585.
54. J. Wei, Ind. Eng. Chem. Res., 1999, 38, 5019–5027.
55. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 1–14.
56. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
57. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision C.01, Gaussian Inc., Wallingford CT, 2016.
58. Y. Shao, Z. Gan, E. Epifanovsky, A. T. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng and X. Feng, et al. , Mol. Phys., 2015, 113, 184–215.
59. P. R. Horn and M. Head-Gordon, J. Chem. Phys., 2015, 143, 114111.
60. J. McDonagh, T. van Mourik and J. B. Mitchell, Mol. Inf., 2015, 34, 715–724.
61. J. Zhang, M. Zhao, C. Zhong, J. Liu, K. Hu and X. Lin, Nanoscale, 2023, 15, 18511–18522.
62. L. Tao, V. Varshney and Y. Li, J. Chem. Inf. Model., 2021, 61, 5395–5413.
63. T. Galeazzo and M. Shiraiwa, Environ. Sci.: Atmos., 2022, 2, 362–374.
64. G. M. Casanola-Martin, A. Karuth, H. Pham-The, H. González-Daz, D. C. Webster and B. Rasulev, Commun. Chem., 2024, 7, 226.
65. G. Armeli, J.-H. Peters and T. Koop, ACS Omega, 2023, 8, 12298–12309.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00353a

---