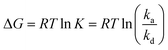Co-assembly of nanometer- and submicrometer-sized colloidal particles into multi-component ordered superstructures

Abstract

Despite advances in computational chemistry and modeling, the discovery of new materials still remains largely empirical, often resembling an art rather than a precise science. A promising approach is to prepare superstructures from building blocks with intrinsic useful properties. Monodisperse nanometer- and submicrometer-sized colloidal particles, in particular, serve as versatile building blocks for this purpose. Their assembly has become a popular “bottom-up” method for creating superstructures. When two or more types of colloidal particles co-assemble, they form multi-component superstructures—often referred to as metamaterials—with diverse ordered arrangements and new properties emerging from synergistic interactions between the different particles. This review aims to systematically explore the co-assembly of two or more types of uniform nanometer- and submicrometer-sized colloidal particles into these multi-component superstructures. We also cover the fundamentals of particle assembly, including the development of uniform particles, maintaining their colloidal stability, and controlling the interparticle forces. Additionally, we discuss the kinetics of particle assembly, summarize the methods used to prepare particle superstructures, address defects that may occur, and provide an overview of their characterization techniques. Finally, we outline the challenges and opportunities in designing multi-component superstructures with ordered arrangements.

---

1. Introduction

Advancements in colloidal synthesis enable the precise control of particle size and shape.^1–4 Given the versatile chemical and physical properties of nanometer- and submicrometer-sized colloidal particles, they form a rich material library. This variety holds promise for innovative applications across biological sciences,^5–8 computing and data storage,^9,10 photovoltaics,¹¹ and thermoelectrics.¹²

Colloidal particles at the nanometer and submicrometer scales can serve as “building blocks” for constructing two- and three-dimensional superstructures, which exhibit both fascinating fundamental properties and practical applications.^2,13–15 The “bottom-up” assembly approach—as discussed in this review for colloidal particles—is a common principle across chemistry, biology, and materials science. Various systems, including DNA,¹⁶ proteins,¹⁷ bacteria,¹⁸ macromolecules,¹⁹ or colloidal particles,²⁰ can self-assemble into highly ordered superstructures with precision.

The co-assembly of various colloidal particles into multi-component superstructures, superlattices, or supercrystals provides a versatile method for advancing metamaterial development.^21–26 To help the reader navigate this review and ensure clarity, we use only the term superstructures, which refer to the arrangement of building blocks into well-defined, often complex architectures. As such, this term includes both superlattices—periodic arrangement of colloidal particles with long-range order—and supercrystals—ordered assemblies where the individual particles act like artificial atoms in a macroscopic crystal lattice. Co-assembly allows precise control over particle arrangement, enabling the design of superstructures with tailored physical and chemical properties. These properties can arise from the particle arrangement, the inherent characteristics of individual particles, or new behaviors emerging from particle synergy. For example, arranging particles into superstructures can alter their Raman scattering properties;²⁷ co-assembling two types of magnetic particles can result in magnets with higher energy density;^10,28 co-assembling magnetic and semiconductor particles can produce advanced magneto-optic materials;²⁹ co-assembling semiconductor particles may lead to optoelectronic materials;³⁰ multi-component films made from different particles can serve as multifunctional catalysts or photocatalysts;²⁹ and co-assembled superstructures can achieve conductivities up to 100 times greater than those made from the constituent particles.¹²

Designing and engineering multi-component superstructures rely on a thorough understanding of particle co-assembly. When different types of particles co-assemble, they can form superstructures with intricate phase diagrams, exhibiting close-packed, non-close-packed, and even quasicrystalline arrangements.^31–33 Close-packed superstructures arise purely from entropy, where particles optimize space without needing specific energetic interactions.^34–40 However, many multi-component superstructures deviate from close packing, indicating that specific energetic interactions, such as van der Waals forces,^41–44 ligand–ligand interactions,^45–47 capillary forces,⁴⁸ electrostatic interactions,^49–51 or depletion forces,⁵² play a role in their formation. Therefore, the formation of multi-component superstructures is a complex balance of entropy and specific energetic interactions. This complexity is further compounded by the variable influence of each driving force, which can change depending on the particle type and size, substrate properties, ligands, solvents, and synthesis methods.

Numerous reviews have examined the self-assembly of colloidal particles,^53,54 discussing fundamental principles,^55–57 particle types capable of self-assembling,^1,21,58 and the characterization, properties, and applications of the resulting superstructures.^14,59–61 We refer interested readers to these comprehensive references. In contrast, this review explores the co-assembly of two or more types of uniform particles into multi-component superstructures with ordered arrangements. While we briefly mention theoretical work for context, our primary aim is to highlight experimental progress in the field. Specifically, we focus on the co-assembly of nanometer-sized particles (∼1 to ∼100 nm) and submicrometer-sized particles (∼0.1 to ∼1 μm). Larger colloidal particles are less suited for binary superstructures due to gravitational effects and slower assembly rates.^62,63 We detail various synthetic methods for preparing these superstructures, including adjusting solvent conditions (e.g., solvent evaporation), air–liquid interface techniques, electrostatic and DNA-guided approaches, and external force-assisted and emulsion-assisted methods. The fundamentals of particle assembly are also discussed, including the importance of producing uniform particles, maintaining their colloidal stability, and controlling interparticle forces. Additionally, the kinetic factors driving particle assembly are presented, the potential defects on superstructures (e.g., vacancies, dislocations, stacking faults, or cracks) are examined, and the techniques used for characterizing the superstructures are briefly addressed. This review concludes by discussing the challenges and future opportunities in developing multi-component superstructures with ordered arrangements.

2. Fundamentals of colloidal particle assembly

The assembly of nanometer- and submicrometer-sized colloidal particles allows for the preparation of ordered superstructures.^64,65 To study these superstructures, it is important to understand the fundamentals of particle assembly, including preparing uniform particles, ensuring their colloidal stability, and controlling the interparticle forces that drive their assembly.⁶⁶ These principles apply universally, whether assembling a single type of particle or co-assembling multiple types.

2.1. Developing uniform colloidal particles

Nanometer- and submicrometer-sized colloidal particles are fundamental building blocks for assembling superstructures.^67–70 To successfully assemble these colloidal particles in an ordered manner, it is important to prepare particles that are uniform in size and shape. Researchers are continually working to increase the variety of uniform particles.^1,71–73 Achieving precise control over their synthesis requires careful balance of synthetic parameters, including precursors, modulators, reaction time, and temperature.^74–76

Nanometer- and submicrometer-sized colloidal particles possess various degrees of freedom, including shape, size, chemical composition, and capping ligands.^21,53 For example, the shape of particles affects their interactions, leading to directional or anisotropic interactions.⁷⁷ These particles can be engineered into various shapes such as octahedra, cubes, rhombic dodecahedra, tetrahedra, nanorods, nanoplates, bitetrahedra, decahedra, and icosahedra.^78–90 More complex shapes can also be designed by growing branches or pods of controlled sizes;^21,91–95 patterning surfaces to create valence^96,97 and Janus particles;⁹⁸ etching core@shell particles to create convex, pod-like shapes;^99,100 using chiral molecules to influence growth;^101–104 and selectively etching certain crystallographic directions to form nanoframes and nanocages (Fig. 1).^105–108

Fig. 1 Colloidal nanoparticles or submicrometer-sized particles with various shapes. SEM images of (a) Au octahedra, (b) Ag cubes, (c) Ag decahedron, (d) Ag tetrahedron, (e) Au icosahedron with some truncated corners, (f) Au nanorods, (g) Au nanoplates, (h) chiral Au cubes, and (i) Pt octahedral nanoframes. (j) 3D reconstruction of a single branched CdSe/CdS octapod from STEM projections. Scale bars: (a) 100 nm; (b) 50 nm; (c) 300 nm; (d) 500 nm; (e) 400 nm; (f) 500 nm; (g) 200 nm; (h) 200 nm; (i) 100 nm; and (j) 20 nm. (a) Adapted with permission from ref. 86. Copyright 2017 The Royal Society of Chemistry. (b) Adapted with permission from ref. 87. Copyright 2006 American Chemical Society. (c)–(e) Adapted with permission from ref. 88. Copyright 2012 The Royal Society of Chemistry. (f) Adapted with permission from ref. 89. Copyright 2017 John Wiley and Sons. (g) Adapted with permission from ref. 90. Copyright 2022 Springer Nature. (h) Adapted with permission from ref. 104. Copyright 2018 Springer Nature. (i) Adapted with permission from ref. 108. Copyright 2022 Springer Nature. (j) Adapted with permission from ref. 95. Copyright 2011 Springer Nature.

For readers interested in a more in-depth understanding of uniform particle preparation, we refer them to the following specialized literature: ref. 1, 21, 58, 75, 109, and 110

2.2. Ensuring colloidal stability

The colloidal stability of nanometer- and submicrometer-sized colloidal particles in a solution is essential for their subsequent assembly into ordered superstructures. In a colloidal dispersion, particles remain stable when repulsive forces dominate their interactions. However, this stability can be disrupted by attractive forces. For example, van der Waals interactions, which arise from temporary fluctuations in the distribution of electrons, can lead to uncontrolled aggregation of the particles.^76,111 To enhance colloidal stability, two main approaches are commonly used: steric stabilization and electrostatic stabilization (Fig. 2).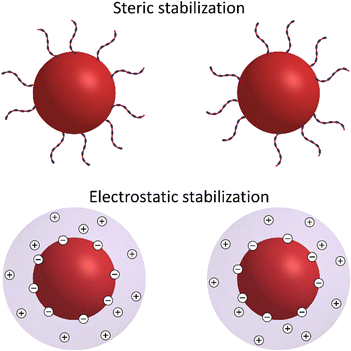

Fig. 2 Schematic representation of sterically and electrostatically stabilized nanometer- and submicrometer-sized particles.

Steric stabilization is based on attaching ligands to the surfaces of particles, thereby forming a steric barrier that prevents the particles from approaching each other too closely.^112,113 This barrier is established by osmotic and elastic repulsions among the ligand coronas. When the ligand chains of two particles begin to overlap, solvent molecules are excluded, generating osmotic pressure that pushes the particles apart. This repulsion occurs when the distance between particles (d) is less than twice the thickness (L) of the ligand layer (d < 2L). As the particles get even closer, the ligand chains compress, resulting in elastic repulsion. This elastic repulsion rapidly overcomes thermal energy. Therefore, the most common scenario during Brownian motion is a moderate overlap (L < d < 2L).¹¹⁴ It is worth noting that the total steric interaction between two particles is the sum of the repulsive potentials associated with each pair of ligands on the particles.

Electrostatic stabilization refers to the process of controlling the surface charge on particles by adsorbing charged species onto them, allowing management of electrostatic interactions.^112,115,116 Surface-charged particles become neutralized by counterions with opposite charge in the surrounding solution, forming an electrical double-layer around each particle. In polar solutions, the overlapping of the electrical clouds around particles causes osmotic repulsion among them, thereby screening their van der Waals interaction. However, when less polar liquids are added to the solvent, the dielectric screening is reduced, causing the counterion clouds to collapse. This collapse allows the particles to approach each other more closely, which can result in aggregation.

For a more detailed overview of the fundamental principles governing colloidal stability, we refer the readers to the following references: ref. 117–121.

2.3. Controlling the interparticle forces

The assembly of nanometer- and submicrometer-sized colloidal particles is guided by thermodynamic principles. At equilibrium, particles assemble into ordered superstructures where the Helmholtz (F) or Gibbs (G) free energy of the system reaches a minimum.¹²² For example, at constant volume and temperature, the equilibrium superstructure minimizes the Helmholtz free energy of the system, defined as:

F = U − TS (1)

where U is the internal energy, T is the temperature and S is the entropy. The assembly process is driven by changes in Helmholtz free energy (dF), which result from variations in internal energy (dU) and/or entropy (dS):

dF = dU − TdS (2)

The entropy of a system of particles can be divided into configurational entropy and the free volume entropy.^36,123,124 Configurational entropy relates to the spatial arrangement of particles, while free volume entropy refers to the available space for particles to move locally. Entropy-driven assembly occurs when the increase in free volume entropy outweighs the decrease in configurational entropy. This balance of entropy drives the formation of superstructures in systems of hard particles.^36,125 Superstructures with higher packing densities provide more free volume entropy, resulting in lower free energy of the system. As a result, hard particles tend to form ordered superstructures that maximize packing density.^126–128

Changes in internal energy are associated with potential energy variations of particle–particle interactions, expressed as:

dU(r) = (F_rep + F_att + F_ext)dr (3)

Here, F_rep, F_att, and F_ext are the repulsive (e.g., electrostatic or steric), attractive (e.g., van der Waals or π–π stacking), and external forces (e.g., electric or magnetic), respectively, with r being the interparticle distance.

Accurately calculating the total free energy of the system is extremely complex due to the numerous terms affecting interparticle potential, the unknown contributions of each term, and the dynamic nature of the assembly process.¹²⁹ Therefore, theoretical and simulation approaches often simplify assumptions about particle shape and interactions. The geometry of particles, in particular, plays a dominant role in determining the final superstructures, allowing models to reasonably predict many assemblies.

For further details on controlling interparticle interactions in colloidal systems, see ref. 53, 55–57, 122, and 129–132.

3. Kinetics of particle assembly

The assembly of nanometer- and submicrometer-sized colloidal particles into superstructures at or near equilibrium is a phase transition similar to crystallization, involving superstructure nucleation^133,134 and growth steps.^135,136 In other words, an ordered phase forms within a disordered phase (nucleation) and grows until it reaches thermodynamic equilibrium.

Nucleation usually involves multiple steps and can be either homogeneous, in a solution, or heterogeneous, near an interface.¹³⁴ Homogeneous nucleation requires overcoming a high free energy barrier, known as the nucleation barrier. Therefore, nucleation is typically the rate-limiting step at low driving forces. Nucleation barrier can be lowered, increasing the nucleation rate, by increasing the particle concentration through evaporation or reducing solvent quality. However, if the solvent evaporates or destabilizes too rapidly, particles may aggregate chaotically (barrierless aggregation), leading to a disordered superstructure.

Heterogeneous nucleation is generally faster because the interface helps to arrange the particles. The surfaces where particles assemble are as important as the properties of the particles themselves.¹³⁷ For instance, capillary forces can trap particles within lithographically patterned templates, directing their arrangement.^138–140 These patterns can control the placement, quantity, and interactions of the particles.^141,142 Similarly, the confinement of particles within three-dimensional (3D) surfaces (e.g., emulsion droplets or microfluidic capillaries) can guide their assembly into ordered superstructures.^143–149

A low barrier to nucleation causes many nuclei to form, which results in multiple clusters or superstructure domains. In solution, larger clusters move more slowly than smaller ones or individual particles, which hinders the merging of these domains. As a result, multiple nucleation sites often lead to the formation of zero-dimensional (0D) superstructures, such as platelets, polyhedra, or spheres.⁵³

Once nucleation happens, growth proceeds as more particles are added to the initial growing seed. During growth, the size, shape, and surface characteristics of the final superstructure are established. The growth rate depends on the availability of particles and the energy required to form surface defects. Strain accumulation can significantly alter the dynamics of particle assemblies,^150,151 often resulting in grain boundaries, dislocations, voids, and vacancies.

Understanding the kinetics, free energies, and mechanism of nucleation is essential for identifying the kinetic pathways available for creating specific superstructures. This knowledge can also help devise pathways to create thermodynamically metastable superstructures with superior properties. The kinetic accessibility of superstructures is mainly explored computationally, and accurately describing heterogeneous nucleation, often the dominant pathway for superstructure formation, remains challenging.¹⁵²

For additional insights into particle assembly kinetics, see ref. 137, 143, 144, 146, and 152–155.

4. Defects in ordered particle superstructures

In perfectly ordered superstructures, particles are arranged at precise and predictable distances from one another. Thermal motion and defects introduce disorder into superstructures.¹⁵⁰ Defects raise the enthalpy of the superstructures due to the energy required to break bonds and accommodate strain, but they also increase configurational entropy, which lowers the total Gibbs free energy of the systems. Defects in a superstructure are classified by their dimensionality: point defects (0D), line defects (one-dimensional (1D)), planar defects (two-dimensional (2D)), and volume defects (3D) (Fig. 3).⁵³

Fig. 3 Schematic representation of defects in a superstructure, including point defects (0D), line defects (1D), planar defects (2D), and volume defects (3D).

Point defects, including vacancies, interstitial, and substitutional defects, occur at a single point within a superstructure and are the most common defects in binary superstructures. Vacancies occur when a particle is missing from its expected position. Interstitial defects arise when a particle occupies a normally empty site. Substitutional defects occur when a different type of particle replaces another in the superstructure.

Line defects include dislocations and disclinations. Dislocations, including edge dislocations and screw dislocations, disrupt the translational symmetry of superstructures. Edge dislocations occur when an extra half-plane of particles is inserted into the superstructure, while screw dislocations appear as an additional layer embedded into a smooth surface. Disclinations disrupt the rotational symmetry of superstructures.

2D defects include both internal and external surfaces. Since superstructures are not infinitely large, they all have surface terminations. This discussion focusses on internal surfaces, such as stacking faults and various boundaries. A stacking fault occurs when the regular sequence of particle planes is disrupted by the insertion or removal of a plane within the superstructure. When this disruption creates an interface between two mirror-image domains, it forms a twin boundary. In binary superstructures, a unique planar defect known as antiphase boundary can occur, where the positions of the two types of particles on either sides of the defect plane are swapped. Stacking faults, twin boundaries, and antiphase boundaries are low-energy defects, characterized by a high lattice fit and minimal broken bonds. They typically form due to minor disturbances during the growth of a single superstructure domain.⁵³

Additionally, two domains might nucleate and grow separately until they meet. In such cases, it is unlikely for the superstructure domains to reorient themselves to form an optimal interface. Instead, the domains often remain in random orientations, with individual particles adjusting locally to reduce interfacial energy. Tilt boundaries occur when two domains meet at an angle that prevents the formation of a low-energy interface, resulting in a small amorphous layer between them. A related defect, the twist boundary, arises when there is an axis of rotation passing through the boundary plane. This can happen due to an abrupt change in crystallographic orientation during growth or the gradual alignment of two domains by the collective motion of dislocations in later stages of superstructure formation.⁵³

In particle superstructures, especially in binary ones, different phases often nucleate and grow at the same time on the same substrate. A phase boundary appears when these phases come into contact. These boundaries can form by coalescence or epitaxial phase change during superstructure growth. The latter is a low-energy defect, as it involves a good lattice match on both sides of the defect plane.⁵³

Bulk defects, such as voids, cracks, and precipitates, are the most energetically costly defects since they involve numerous broken bonds. Voids are 3D gaps within an otherwise continuous superstructure and can form due to impurities or nucleation of vapor bubbles, preventing particles from filling these spaces during growth.⁵³ Cracks are voids that extend in one direction. They often form as a strain release mechanism in particle assemblies,¹⁵⁶ especially when superstructure contraction due to solvent loss is resisted by the substrate surface. Precipitates occur when an ordered or a disordered superstructure forms within another superstructure. This happens when a superstructure grows around particles that have already arranged into an ordered or a disordered arrangement.

For more detailed information on defects in ordered particle assemblies, see ref. 53, 157, and 158.

5. Characterization of ordered superstructures

To precisely characterize ordered particle superstructures, including their defects, scientists use imaging (real-space) and scattering (reciprocal-space) techniques. These complementary methods provide detailed information about the position and orientation of individual nanometer- and submicrometer-sized particles within a superstructure, the size and orientation of superstructure domains, and the presence of defects. Advanced technologies, such as electron microscopies and synchrotron facilities, are often necessary for these characterizations.

Transmission electron microscopy (TEM) is a widely used technique for imaging superstructures. It generates 2D images of 3D structures. By tilting the sample holder at various angles relative to the electron beam, TEM captures images from various crystallographic perspectives.³⁹ These images can be combined using tomographic reconstruction software to create 3D models of the superstructures.^159–163 TEM analysis requires samples to be in a vacuum chamber, which limits the technique to dry specimens. While this traditional TEM characterization is effective for studying particle superstructures once they are dry, it does not reveal the assembly process. Recent advances in liquid-cell TEM¹⁶⁴ have allowed the visualization of the movements of individual particles in solution and their real-time assembly into superstructures.^165–168

While TEM is best suited for thin samples, scanning electron microscopy (SEM) excels at surface imaging of thicker superstructures. Focused ion beam SEM (FIB-SEM) tomography, in particular, offers robust 3D reconstruction capabilities.^169,170 Atomic force microscopy (AFM) is another useful technique that provides detailed quantitative information about the surface topography of particle superstructures.

In reciprocal space, scientists obtain an averaged view of overall particle superstructures. One method involves applying a fast Fourier transform (FFT) to real-space images, converting them into plots of spatial frequencies.⁵³ Each point in these plots corresponds to a lattice spacing in the real-space image. Another approach is capturing an electron diffraction (ED) pattern of the superstructure using a TEM. This helps distinguish between similar arrangements in real space. Low-angle data from these techniques reveal the position of particles, while high-angle FFT or ED data provide insights into their arrangement and orientation.⁵³

Small-angle X-ray scattering (SAXS) is another technique used to analyze particles in solution and their arrangements into superstructures.¹⁷¹ It provides information on the average size, shape, and distribution of particles.^172,173 When particles form an ordered superstructure, the SAXS pattern displays off-center spots corresponding to Bragg reflections from the superstructure planes.⁵³ Similar to FFT or ED, high-angle reflections in SAXS reveal the orientation of particles within superstructures.^174–179 Notably, time-resolved SAXS enables in situ monitoring of superstructure formation kinetics, capturing the dynamic evolution of ordering processes.¹⁷⁰

Grazing-incidence SAXS (GISAXS) is a valuable technique for measuring scattering patterns from ordered particle superstructures. With high intensity synchrotron radiation sources, GISAXS provides strong in-plane and out-of-plane X-ray scattering signals with low background noise and in situ capabilities, allowing researchers to observe assembly kinetics in real time.^180–183 However, the limited accessibility of synchrotron facilities has restricted GISAXS from becoming a routine tool for structural analysis.

For readers seeking a more detailed understanding of the characterization of ordered superstructures, we refer to the following studies: ref. 53, 159, 164, and 171.

6. Methods to co-assemble particles into multi-component ordered superstructures

To co-assemble particles into desired superstructures, their interactions need to be adjusted, shifting from repulsion to attraction. The interactions must be carefully balanced—if they are too weak, the particles may not assemble properly, leading to disordered systems, while excessively strong interactions can cause the particles to irreversibly aggregate.

There are various strategies to promote particles to co-assemble: adjusting the solvent conditions, air–liquid interface approaches, electrostatic-based co-assembly, DNA-guided co-assembly, and external force-assisted and emulsion-assisted methods.

6.1. Co-assembly of nanoparticles

In this review, we separately discuss the co-assembly of nanoparticles and submicrometer-sized colloidal particles, although most strategies to promote co-assembly are generally similar across these scales. We chose to make this distinction because, for micrometer-sized particles, co-assembly is typically regarded as an entropy-driven process governed by the space-filling principle, unless particle surface charges are carefully adjusted or an external field is applied. In contrast, the co-assembly of colloidal nanoparticles can result in a diverse array of superstructures where multiple forces—including entropic effects, coulombic forces, dipole–dipole interactions, and van der Waals forces—may or may not contribute.

6.1.1. Co-assembly of nanoparticles by evaporation-induced self-assembly (EISA). The most common methods for guiding the co-assembly process involve modifying the interactions between nanoparticles by solvent evaporation (Table S1, ESI†). Initially, the nanoparticles are dispersed in a solvent. As the solvent evaporates, the available free volume decreases. When the average distance between nanoparticles becomes comparable to their sizes, the system may transition from a disordered to an ordered state. During this transition, the configurational entropy of the system decreases, but the free volume entropy increases as the nanoparticles gain more space to move. If the gain in free volume entropy outweighs the loss in configurational entropy, the overall entropy of the system increases, driving the phase transition and stabilizing the ordered state—entropic force. Additionally, interactions between the nanoparticles—such as coulombic, dipole–dipole, and van der Waals forces—also play a significant role. Thus, the assembly of nanoparticles is governed by a complex interplay of these forces.

In an early example, Redl et al. reported the co-assembly of 6 nm spherical PbSe semiconductor quantum dots and 11 nm spherical γ-Fe₂O₃ magnetic nanoparticles (a size ratio (γ) of 0.55) into ordered 3D binary superstructures by evaporating a dibutyl ether solution containing both nanoparticles.¹⁸⁴ Two distinct superstructures, having LS₁₃ and LS₂ stoichiometries, were prepared, corresponding to the crystal structures of the intermetallic compounds NaZn₁₃ (SG 226, Fm3̄c) and AlB₂ (SG 191, P6/mmm), respectively. It should be noted that “L” refers to the large nanoparticles and “S” to the small ones. The concentrations of the nanoparticles were adjusted to achieve specific structural compositions, such as a 1 : 13 ratio for the LS₁₃ superstructure. In the NaZn₁₃-type superstructure, the large nanoparticles form a cubic framework, with small nanoparticles arranged in an icosahedron pattern within this framework and an additional small nanoparticle at the center of each icosahedron. Adjacent icosahedra are twisted by 90°, resulting in a unit cell composed of eight cubes. The AlB₂-type superstructure features parallel layers of hexagonally ordered large nanoparticles, with small nanoparticles positioned in the trigonal prismatic gaps. The small nanoparticles form a second layer above the hexagonal layer of large nanoparticles. Additionally, in this study, a third superstructure, isostructural with CaCu₅ (SG 191, P6/mmm), was similarly formed by co-assembling 11 nm spherical γ-Fe₂O₃ nanoparticles and 6.3 nm spherical PbSe quantum dots. In this superstructure, large nanoparticles are arranged in a hexagonal pattern, with small nanoparticles occupying the trigonal interstices. These hexagonally arranged layers are separated by a network of small nanoparticles arranged in a Kagomé-like pattern.¹⁸⁴

In a subsequent study, Shevchenko et al. demonstrated that spherical PbSe semiconductor quantum dots and spherical Pd nanoparticles could co-assemble into two different polymorphic superstructures with LS₁₃ stoichiometry by evaporating a toluene dispersion containing these nanoparticles (Fig. 4).²⁹ Initially, 5.8 nm PbSe and 3.0 nm Pd nanoparticles (γ = 0.627) were stabilized using oleic acid (OA) and dodecanethiol (DDT), respectively. The dispersion, with a 1 : 20 PbSe to Pd nanoparticle ratio, was then evaporated to form the superstructures. In one polymorph, the small nanoparticles occupied the vertices of icosahedra, forming the ico-LS₁₃ structure, which is isostructural with NaZn₁₃. The second, unexpected polymorph had small nanoparticles at the vertices of cuboctahedra, resulting in a cub-LS₁₃ superstructure with lower packing density. The ico-LS₁₃ superstructure was expected to be favored due to its higher calculated packing density (0.738) compared to cub-LS₁₃ (0.7). Theoretical calculations confirmed the stability of the ico-LS₁₃ superstructure in hard sphere mixtures.^36,124,185 Monte Carlo simulations demonstrated that entropic effects alone, without specific energetic interactions, are sufficient to stabilize the ico-LS₁₃ superstructure. The entropy of ico-LS₁₃ at a specific size ratio is higher than that of a mixture of face-centered cubic (fcc) single-component superstructures.³⁶ Despite its lower maximum packing density, cub-LS₁₃ coexisted with ico-LS₁₃. The formation of the less dense cub-LS₁₃ superstructure was likely driven by van der Waals forces and other “non-hard-sphere” interactions.^34,35 This finding highlights the limitations of relying solely on simple space-filling principles to understand nanoparticle assembly and emphasizes the need for models that account for van der Waals, dipolar, and hydrophobic forces. Additionally, it was observed that the ico-LS₁₃ superstructures tended to orient with the [110] planes parallel to the substrate, while only small fragments of [110] planes of cub-LS₁₃ were observed on the substrates. In contrast, the [100] orientation dominated for the cub-LS₁₃ regions. The preferential growth of cub-LS₁₃ and ico-LS₁₃ with [100] and [110] orientations, respectively, could result from the alignment of the facets of the icosahedron and cuboctahedron of the small nanoparticles with the substrate plane.²⁹

Fig. 4 TEM images of the (a) [100] and (b) [110] projections of ico-LS₁₃ superstructures, which match with the (c) [100] and (e) [110] planes of the modeled ico-LS₁₃. The minimum number of layers in (d) [100] and (f) [110] planes of ico-LS₁₃ required to form structures equivalent to the observed ones. TEM images of the (g) [100] and (h) [110] projections of cub-LS₁₃ superstructures, which match with the (i) [100] and (k) [110] planes of the modeled cub-LS₁₃. The minimum number of layers in (j) [100] and (l) [110] planes of cub-LS₁₃ required to form structures equivalent to the observed ones. Adapted with permission from ref. 29. Copyright 2005 American Chemical Society.

Chen et al. systematically studied the formation of binary superstructures by co-assembling spherical CdSe quantum dots (4.4 nm in diameter) with spherical CdTe quantum dots of various sizes: 9.1, 8.1, 7.0, or 5.9 nm.^37,38 The superstructures were formed on TEM grids after the slow evaporation of a tetrachloroethylene (TCE) solution containing the nanoparticles. 9.1 nm CdTe and 4.4 nm CdSe nanoparticles (γ ≈ 0.57) co-assembled into cub-LS₁₃-, NaZn₁₃-, and AlB₂-type binary superstructures. These superstructures were observed across all tested CdTe to CdSe concentration ratios. However, samples with a 1 : 13 and 1 : 16 ratio favored the presence of cub-LS₁₃ and NaZn₁₃ superstructures, while a 1 : 3 ratio led to more AlB₂ domains. In the case of 8.1 nm CdTe and 4.4 nm CdSe nanoparticles (γ ≈ 0.63), cub-LS₁₃-, NaZn₁₃-, and CaCu₅-type binary superstructures were formed. Cub-LS₁₃- and NaZn₁₃-type superstructures dominated when the concentration ratio was approximately 1 : 13 and 1 : 16, while CaCu₅-type superstructures appeared more prominently as the ratio shifted to 1 : 6 and 1 : 9. In contrast, when the concentration ratios were ∼1 : 1, 1 : 2, or 1 : 3, almost no ordered superstructures were observed. The 7.0 nm CdTe and 4.4 nm CdSe nanoparticles (γ ≈ 0.71) uniquely co-assembled into CaCu₅-type binary superstructures across different concentration ratios. For the 5.9 nm CdTe and 4.4 nm CdSe nanoparticles (γ ≈ 0.81), MgZn₂-type Laves phases were exclusively formed, regardless of the concentration ratios. These MgZn₂-type superstructures (SG 194, P6₃/mmc) contain four formula units per unit cell. In this arrangement, small nanoparticles form tetrahedral units, which are alternately connected base-to-base and point-to-point, while larger nanoparticles occupy the voids between tetrahedra. Such Laves phases are commonly seen in intermetallic compounds and solid van der Waals compounds, like CH₄(H₂)₂¹⁸⁶ and Ar(H₂)₂.¹⁸⁷ The observed superstructures, based on their size ratios, closely resembled those found in binary colloidal systems composed of submicrometer-sized particles. Yoshimura and Hachisu observed the co-assembly of submicrometer-sized latex particles into AlB₂-, NaZn₁₃-, LS₄-, CaCu₅-, and MgCu₂-type binary superstructures at 0.5 ≤ γ ≤ 0.56, 0.61 ≤ γ ≤ 0.63, γ ≈ 0.62, 0.72 ≤ γ ≤ 0.75, and 0.77 ≤ γ ≤ 0.84, respectively.^35,188 This similarity underscored entropy as a major driving force in forming binary superstructures across different scales.^37,38

Through solvent evaporation, Shevchenko et al. formed various binary nanoparticle superstructures by co-assembling different types and sizes of spherical nanoparticles.^31,32 These included semiconducting (e.g., PbSe: 7.6 nm, 7.2 nm, 6.7 nm, 6.3 nm, 6.2 nm, and 5.8 nm; PbS: 6.7 nm), metallic (e.g., Au: 5.5 nm and 5.0 nm; Ag: 4.2 nm, 3.7 nm, and 3.4 nm; Pd: 3.0 nm; CoPt₃: 6.2 nm, 4.5 nm, and 2.6 nm; Bi: 14.4 nm), and magnetic (e.g., γ-Fe₂O₃: 13.4 nm) nanoparticles. The nanoparticles were first coated with ligands such as DDT, primary amines (e.g., dodecylamine and hexadecylamine), carboxylic acids (e.g., OA and 1-adamantanecarboxylic acid), or tri-n-alkylphosphine oxides (e.g., tri-n-octylphosphine oxide (TOPO)), and then dispersed in toluene or a toluene mixture with TCE or chloroform. Superstructures were finally formed by solvent evaporation. The resulting superstructures included: NaCl-type, CuAu-type, orthorhombic LS-type, AlB₂-type, MgZn₂-type, MgNi₂-type, Cu₃Au-type, Fe₄C-type, CaCu₅-type, CaB₆-type, NaZn₁₃-type, and cub-LS₁₃-type structures.

NaCl-type superstructures were formed from various nanoparticle combinations, including 13.4 nm γ-Fe₂O₃–5.0 nm Au (γ = 0.43), 7.2 nm PbSe–3.0 nm Pd (γ = 0.528), 6.2 nm PbSe–3.0 nm Pd (γ = 0.59), and 5.8 nm PbSe–3.0 nm Pd (γ = 0.62) (Fig. 5).^31,32 In NaCl-type binary superstructures (SG 225, Fm3̄m), both types of particles are arranged in a fcc structure. The smaller particles occupy the octahedral voids within the fcc lattice of the larger particles. NaCl-type superstructure exhibits the highest packing density (0.793 at a size ratio of 0.414) among binary lattices with LS stoichiometry. This packing density surpasses that of fcc close-packed spheres for all size ratios below 0.458.^34,35 Therefore, the size ratios observed in these nanoparticle combinations exceed the stability range predicted for NaCl composed of hard, noninteracting spheres.¹²⁴ In the γ-Fe₂O₃–Au and 7.2 nm PbSe–3.0 nm Pd systems, NaCl-type superstructures were typically observed with (111) projections. For 5.8 nm PbSe–3.0 nm Pd systems, the (100) oriented NaCl-type superstructures dominated.^31,32 Kiely et al. also reported the formation of NaCl-type superstructures co-assembling spherical Au and Ag nanoparticles.¹⁸⁹ Similarly, Saunders et al. observed the co-assembly of spherical Fe and Au nanoparticles into NaCl-type superstructures.¹⁹⁰

Fig. 5 (a) NaCl unit cell. (b) (100) planes and the minimum number of layers in the (100) projections required to form patterns identical to the observed ones. (c) (111) planes and the minimum number of layers in the (111) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with NaCl: (d) (111) projection formed by 13.4 nm γ-Fe₂O₃ and 5.0 nm Au nanoparticles and (e) 7.2 nm PbSe and 3.0 nm Pd nanoparticles; (f) (100) projection formed by 5.8 nm PbSe and 3.0 nm Pd nanoparticles. Upper insets: (d) and (e) (100) projections of the superstructure. Bottom insets: (d)–(f) small-angle ED patterns. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

CuAu-type superstructures were assembled from various nanoparticle combinations, including 6.7 nm PbSe–3 nm Ag (γ = 0.56), 6.2 nm PbSe–3 nm Pd (γ = 0.59), 5.8 nm PbSe – 3.4 nm Ag (γ = 0.68), 7.6 nm PbSe–5 nm Au (γ = 0.70), and 6.2 nm PbSe–5 nm Au (γ = 0.82) (Fig. 6).^31,32 This CuAu-type lattice (SG 123, P4/mmm) has been observed in many intermetallic compounds.¹⁸⁹ In this superstructure, each particle is surrounded by four particles of the same type and eight particles of the other component. Particles that form CuAu-type superstructures typically had an effective size ratio between 0.55 and 0.70. This range was significantly smaller than the size ratios reported for intermetallic compounds with a CuAu lattice. These superstructures typically showed two orientations, (001) and (100). In PbSe–Au superstructures, the (001) orientation was the most common, while the (100) orientation dominated in PbSe–Ag superstructures. Additionally, antiphase boundaries were observed in CuAu superstructures assembled from 6.7 nm PbS and 3.0 nm Pd nanoparticles. CuAu-type superstructures often coexisted with Cu₃Au-type superstructures.^31,32

Fig. 6 (a) CuAu unit cell. (b) (001) planes and the minimum number of layers in the (001) projections required to form patterns identical to the observed ones. (c) (100) planes and the minimum number of layers in the (100) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with CuAu: (d) and (e) (001) and (f) (100) projections formed by 7.6 nm PbSe and 5.0 nm Au nanoparticles; (g) (001) projections formed by 6.2 nm PbSe and 5.0 nm Au nanoparticles; (h) (100) projection formed by 5.8 nm PbSe and 3.4 nm Ag nanoparticles; and (i) (100) projection containing nanoparticle “antiphases”. Insets: (d) and (h) small-angle ED patterns. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

Superstructures with an orthorhombic symmetry class (SG 51, Pmma) were prepared by the assembly of various nanoparticle combinations, including 6.2 nm PbSe–3 nm Pd (γ = 0.59), 5.8 nm PbSe–3 nm Pd (γ = 0.63), and 7.2 nm PbSe–4.2 nm Ag (γ = 0.66) (Fig. 7).^31,32

Fig. 7 (a) Orthorhombic lattice. (b) (100) planes and the minimum number of layers in the (100) projections required to form patterns identical to the observed ones. (c) (010) planes and the minimum number of layers in the (010) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with orthorhombic lattices: (d) and (e) (100) and (f) (010) projections formed by 5.8 nm PbSe and 3.0 nm Pd nanoparticles; and (g) (100) and (h) (010) projections formed by 7.2 nm PbSe and 4.2 nm Pd nanoparticles. Insets: (d) and (g) small-angle ED patterns. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

Various nanoparticle combinations were reported to co-assemble into AlB₂-type superstructures, including 13.4 nm γ-Fe₂O₃–5.8 nm PbSe (γ = 0.5), 13.4 nm γ-Fe₂O₃–6.2 nm CoPt₃ (γ = 0.54), 6.7 nm PbSe–3.0 nm Pd (γ = 0.56), 6.2 nm PbSe–3 nm Pd (γ = 0.59), 5.8 nm PbSe–3.0 nm Pd (γ = 0.63), 5.8 nm PbSe–3.7 nm Ag (γ = 0.71), and 7.2 nm PbSe–5.5 nm Au (γ = 0.787) (Fig. 8).^31,32 Murray and Sanders predicted that the AlB₂-type superstructures would be stable when the size ratio is between 0.482 and 0.624.^34,35 However, size ratio values of 0.71 and 0.787, as observed in some of these combinations, exceed this predicted range. It was suggested that the flexibility of the organic ligand shells around the nanoparticles may allow the superstructure to tolerate a broader range of size ratio values. Smith et al. also prepared AlB₂-type superstructures by co-assembling OA-coated 11.5 nm spherical γ-Fe₂O₃ nanoparticles and DDT-coated 6.1 nm spherical Au nanoparticles (γ = 0.53).¹⁸¹ These superstructures were formed by slowly evaporating colloidal toluene dispersions containing the nanoparticles. They formed only when excess OA was added, likely due to depletion attraction forces that helped overcome kinetic barriers. Variations were noted in the size of the crystalline superstructure grains and their orientations relative to the substrate. Initially, the superstructure formed on the substrate, followed by 8–12% uniaxial shrinkage perpendicular to the substrate. This shrinkage, observed in other evaporated films (e.g., block copolymers,¹⁹¹ mesoporous metal oxides,¹⁹² and Au nanoparticle superstructures¹⁹³), occurred due to the evaporation of trapped residual solvent after superstructure formation. As the solvent evaporated, the superstructure contracted, but the nanoparticles remained fixed to the substrate, preventing lateral movement and causing superstructure to undergo uniaxial compression. Smaller grains showed more shrinkage than larger ones. Nearly periodic dislocations were also observed in the superstructures, where half-planes of Au nanoparticles were inserted. Additionally, another type of binary superstructure was identified, similar to a cub-LS₁₃ superstructure (space group 226, Fm3̄c). In this structure, γ-Fe₂O₃ nanoparticles replaced Au nanoparticles at the 8a Wyckoff positions in the unit cell (of space group 226). This superstructure was found only in thin layers of nanoparticles.¹⁸¹

Fig. 8 (a) AlB₂ unit cell. (b) (001) planes and minimum number of layers in the (001) projections required to form patterns identical to the observed ones. (c) (110) planes and minimum number of layers in the (110) projections required to form patterns identical to the observed ones. (d) (011) planes and minimum number of layers in the (011) projections required to form patterns identical to the observed ones. (e) (111) planes and minimum number of layers in the (111) projections required to form patterns identical to the observed ones. (f) (1−11) planes and minimum number of layers in the (1−11) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with AlB₂: (g)–(k) (001) projections formed by (g) 6.7 nm PbSe and 3.0 nm Pd nanoparticles, (h) 13.4 nm γ-Fe₂O₃ and 6.2 nm CoPt₃ nanoparticles, (i) 5.8 nm PbSe and 3.7 nm Ag nanoparticles, (j) 13.4 nm γ-Fe₂O₃ and 5.8 nm PbSe nanoparticles, and (k) 7.2 nm PbSe and 5.5 nm Au nanoparticles; and (l) (110), (m) (011), and (n) (111) projections formed by 5.8 nm PbSe and 3.0 nm Pd nanoparticles and (o) grain boundaries between (010) and (110) and (001) oriented planes. Top insets: (g)–(i) and (k) TEM images of superstructures. Bottom insets: (g),(i)–(l) small-angle ED patterns. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

6.2 nm PbSe and 3.0 nm Pd nanoparticles (γ = 0.59) were observed to assemble into superstructures isostructural with MgZn₂-type superstructures (Fig. 9a–d).^31,32 A key factor in the formation of these phases is the size ratio, with a maximum packing density of 0.71 corresponding to a size ratio of approximately 0.813.^6,193 For intermetallic compounds, this ratio typically ranges from 0.606 to 0.952. In this case, the Pd to PbSe nanoparticle size ratio of 0.59 approached the lower boundary for MgZn₂-type phases. In these Pd–PbSe nanoparticle superstructures, the MgZn₂-type phase frequently coexisted with other Laves phases, such as the MgNi₂-type superstructures. The MgNi₂ structure shares the same space group as MgZn₂ but differs in stacking sequences: ABABAB… for MgZn₂ and ABACABAC… for MgNi₂. The MgNi₂-type structure contains eight formula units per unit cell.

Fig. 9 (a) MgZn₂ unit cell. (b) (001) planes and the minimum number of layers in the (001) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with MgZn₂: (c) and (d) (001) projection formed by 6.2 nm PbSe and 3.0 nm Pd nanoparticles. (e) Cu₃Au unit cell. (f) (001) planes and minimum number of layers in the (001) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with Cu₃Au: (g) and (h) (001) projection formed by 5.8 nm PbSe and 3.4 nm Ag nanoparticles. Inset: (c) and (g) small-angle ED pattern. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

Superstructures isostructural with cubic Cu₃Au intermetallic compounds (SG 221, Pm3̄m) were reported to be formed by assembling mixtures of 6.2 nm PbSe–3.0 nm Pd nanoparticles (γ = 0.59), 7.2 nm PbSe–4.2 nm Ag nanoparticles (γ = 0.66), and 5.8 nm PbSe–3.4 nm Ag nanoparticles (γ = 0.68) (Fig. 9e and f).^31,32 In this arrangement, large particles are positioned at the corners of the cubic cell, while small particles occupy the face-centered positions. Each large particle at the corners is surrounded by twelve small particles, and each small particle at the faces is adjacent to four large particles and eight small particles.

Binary nanoparticle superstructures isostructural with Fe₄C (SG 215, P4̄3m) were formed by assembling 6.2 nm PbSe with 3.0 nm Pd nanoparticles (γ = 0.59), 5.8 nm PbSe with 3.0 nm Pd nanoparticles (γ = 0.63), and 7.2 nm PbSe with 4.2 nm Ag nanoparticles (γ = 0.66) (Fig. 10a–e).^31,32 In this superstructure, each large particle is surrounded by four small particles arranged in a tetrahedral pattern. In some samples, the Fe₄C-like superstructures coexisted with orthorhombic LS superstructures.

Fig. 10 (a) Fe₄C unit cell. (b) (100) planes and the minimum number of layers in the (100) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with Fe₄C: (c) and (d) (100) projection formed by 5.8 nm PbSe and 3.0 nm Pd nanoparticles; and (e) (100) projection formed by 7.2 nm PbSe and 4.2 nm Ag nanoparticles. (f) CaCu₅ unit cell. (g) (001) planes and the minimum number of layers in the (001) projections required to form patterns identical to the observed ones. TEM images of superstructures isostructural with CaCu₅: (001) projection formed by (h) 6.3 nm PbSe and 3.6 nm Ag nanoparticles, (i) 7.2 nm PbSe and 5.0 nm Au nanoparticles, and (j) 6.2 nm PbSe and 5.0 nm Au nanoparticles. Top insets: (i) and (j) TEM images of superstructures. Bottom insets: (c), (h), (i) and (j) small-angle ED patterns. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

Binary nanoparticle superstructures with a CaCu₅-type lattice were reported to be assembled using 3.6 nm Ag–6.3 nm PbSe nanoparticles (γ = 0.66), 2.6 nm–4.5 nm CoPt₃ nanoparticles (γ = 0.71), and 5.0 nm Au–7.2 nm PbSe nanoparticles (γ = 0.73) (Fig. 10f–j).^31,32

6.2 nm PbSe and 3.0 nm Pd nanoparticles (γ = 0.59), 13.4 nm γ-Fe₂O₃ and 5.0 nm Au nanoparticles (γ = 0.43), as well as 5.8 nm PbSe and 3 nm Pd nanoparticles (γ = 0.63) co-assembled into binary nanoparticle superstructures isostructural with CaB₆ (SG 221, Pm3̄m).^31,32 In this structure, four large particles form a simple cubic lattice, while six small particles form an octahedron at the center of each cube. Ye, Chen, and coworkers co-assembled 4.6 nm spherical Au nanoparticles and 14.0 nm spherical Fe₃O₄ nanoparticles (γ ≈ 0.40) into two different polymorphs: CaB₆-type superstructures and LS₆ superstructures with body-centered cubic (bcc) symmetry (Fig. 11).¹⁹⁴ The assembly was achieved by slowly evaporating a trichloroethylene solution containing a Fe₃O₄-to-Au nanoparticle ratio of about 1 : 8. Before assembly, Au and Fe₃O₄ nanoparticles were functionalized with OA and DDT, respectively. In the bcc-LS₆ superstructure, large nanoparticles form a bcc lattice, with small nanoparticles placed in squares on the six cube faces. This arrangement is isomorphic to certain alkali-metal intercalation compounds of fullerene C₆₀ (e.g., K₆C₆₀, Cs₆C₆₀ etc.).¹⁹⁵ The size ratio (γ ≈ 0.40) fell within the range required for high packing densities in both structures, indicating that the polymorphism was likely driven by entropy. When the size of the Au nanoparticle increased to 5.8 nm, with Fe₃O₄ nanoparticles unchanged (γ ≈ 0.48), only bcc-LS₆ superstructures formed, without the coexistence of the CaB₆ phase. This 20% increase in Au nanoparticle size created a 25% difference in packing density between the two polymorphs, leading to a phase-pure bcc-LS₆ structure. In LS₆ superstructures formed from 4.6 nm Au and 14.0 nm Fe₃O₄ nanoparticles, [100]-oriented domains were observed for CaB₆ superstructures, while bcc-LS₆ superstructures exhibited [110]-oriented domains. However, for bcc-LS₆ superstructures formed with 5.8 nm Au and 14.0 nm Fe₃O₄ nanoparticles, [100]-oriented domains were also found. The preferred orientations were likely due to the lowest-energy crystallographic planes in each phase. Given the size ratio γ ≈ 0.40, which is close to that seen in quasicrystalline ordering in binary nanoparticle superstructures, the possibility of Archimedean tiling-based aperiodic ordering was also explored by adjusting the relative concentration of Au and Fe₃O₄ nanoparticles. When the Fe₃O₄-to-Au nanoparticle ratio was about 1 : 5, large-area (3².4.3.4) tiling appeared, along with some bcc-LS₆ domains.¹⁹⁴

Fig. 11 Unit cells of (a) CaB₆ and (c) bcc-LS₆ binary nanoparticle superstructures. TEM images and structural models (inset) of the (b) [001] projection of CaB₆ superstructures and (d) the [110] projection of bcc-LS₆ superstructures. (e) and (f) TEM images of binary nanoparticle superstructures exhibiting the periodic (3².4.3.4) Archimedean tiling (AT). The inset in (e) shows the corresponding FFT pattern of the superstructures. (g) TEM image showing the coexistence of both Archimedean tiling and bcc-LS₆ binary nanoparticle superstructures. Adapted with permission from ref. 194. Copyright 2011 American Chemical Society.

5.8 nm PbSe–3.0 nm Pd (γ = 0.63) and 7.2 nm PbSe – 4.2 nm Ag (γ = 0.66) nanoparticle pairs co-assembled into NaZn₁₃-type superstructures (Fig. 12a–c).^31,32 Interestingly, these effective particle size ratios exceeded the upper stability limit calculated for NaZn₁₃ structures. Theoretically, a NaZn₁₃ lattice made of hard spheres remains stable for size ratios between 0.54 and 0.61. Frenkel et al. showed through simulations that NaZn₁₃-type superstructures can form solely due to entropy, without the need for specific energetic interactions.³⁶ Cub-LS₁₃-type superstructures were also assembled using both nanoparticle combinations (Fig. 12d–f).^31,32

Fig. 12 (a) NaZn₁₃ unit cell. TEM images of superstructures isostructural with NaZn₁₃ formed by (b) 5.8 nm PbSe and 3.0 nm Pd nanoparticles and (c) 7.2 nm PbSe and 4.2 nm Ag nanoparticles. (d) Cub-LS₁₃ unit cell. TEM images of superstructures isostructural with cub-LS₁₃ formed by (e) 5.8 nm PbSe and 3.0 nm Pd nanoparticles and (f) 7.2 nm PbSe and 4.2 nm Ag nanoparticles. Inset: (e) and (f) small-angle ED pattern. Adapted with permission from ref. 32. Copyright 2006 American Chemical Society.

Shevchenko et al. reported the formation of multiple superstructures on the same substrate, usually in separate regions, under the same experimental conditions.^31,32 Occasionally, a smooth transition between these phases is observed. For example, 11 different superstructures were assembled from a combination of 6.2 nm PbSe and 3.0 nm Pd nanoparticles. The same type of superstructure could also be prepared from different nanoparticle combinations over a wide range of ratios. For example, the AlB₂-type superstructure was assembled from 9 different combinations of nanoparticles.^31,32

By adjusting the charge state of nanoparticles, the solvent evaporation-driven co-assembly process could be controlled. The introduction of ligands like carboxylic acids, TOPO, or dodecylamine allowed for reproducible switching between different superstructures. For example, co-assembling 6.2 nm PbSe and 3.0 nm Pd nanoparticles at a concentration ratio of around 1 : 5 led to the formation of several binary nanoparticle superstructures, with MgZn₂ and cub-LS₁₃ lattices being the most common. However, adding OA shifted the assembly toward orthorhombic LS- and AlB₂-type superstructures, while adding dodecylamine or TOPO resulted in NaZn₁₃- or cub-LS₁₃-type superstructures, respectively (Fig. 13).^31,32

Fig. 13 (a)–(f) TEM images of binary superstructures assembled in the presence of 4 mM OA or 6 mM TOPO. 6.2 nm PbSe and 3.0 nm Pd nanoparticles co-assembled into (a) orthorhombic LS- and AlB₂-type superstructures or into (b) NaZn₁₃-type superstructures. 7.2 nm PbSe and 4.2 nm Ag nanoparticles co-assembled into (c) orthorhombic LS or (d) cub-LS₁₃ superstructures. 6.2 nm PbSe and 5.0 nmAu nanoparticles co-assembled into (e) CuAu-type or (f) CaCu₅-type superstructures. Adapted with permission from ref. 31. Copyright 2006 Springer Nature.

For hard spheres, a binary superstructure forms if its entropy is higher than the combined entropies of large and small spheres packed separately in an fcc-structure. Typically, stable binary lattices have a packing density higher than that of the fcc lattice (∼0.74). This follows a simple principle: higher packing density leads to more excluded volume, which in turn increases the entropy of the system during superstructure crystallization.^34,35 A preliminary prediction of stability for hard-sphere binary superstructures can be made by comparing their packing density with that of the fcc phase.

The formation of binary superstructures with packing densities lower than those of single-component fcc superstructures suggested that entropy was not the primary driver of ordering. It was initially suggested that the co-assembly of those binary nanoparticle superstructures was driven by Coulomb attraction between oppositely charged nanoparticles, which arose from slight deviations in composition or ligand adsorption/desorption.³¹ The interplay between space-filling principles and soft Coulomb interparticle interactions can lead to a complex phase diagram, as seen in binary superstructures of charged polymethylmethacrylate (PMMA) beads.¹⁹⁶ However, Coulomb forces alone could not account for the variety of binary nanoparticle superstructures observed in the studies of Shevchenko et al.^31,32 Therefore, the phase diagram of these co-assembled binary nanoparticles superstructures was reported to arise from a combination of interactions among sterically stabilized nanoparticles, including not only Coulomb forces but also van der Waals forces. Additionally, surfactants were also shown to influence nanoparticle assembly.⁴⁵ Another factor affecting packing symmetry was the deviation of nanoparticles from a spherical shape, which is often determined by nanoparticle faceting.^34,35,197 Faceted nanoparticles achieve their highest packing density and strongest van der Waals attraction when the packing symmetry aligns with the shape of the nanoparticle building blocks. The energetic factors discussed above influenced the relative stability of binary superstructures. Moreover, the kinetics of nucleation and growth of superstructures could contribute to the preferential formation of certain superstructures over others. For example, the relatively simple and highly symmetric cub-LS₁₃ superstructure may nucleate more readily, potentially explaining its prevalence over the denser and, in theory, more stable NaZn₁₃-type superstructure.²⁹

6.1.1.1. Quasicrystalline superstructures. The discovery of quasicrystals in 1984 transformed our understanding of ordered solids.^198,199 Unlike traditional crystals, quasicrystals have long-range order without translational symmetry, allowing for rotational symmetries—such as five-, eight-, ten-, and twelve-fold—that are forbidden in classical crystallography.^200,201 Despite this difference, quasicrystals still produce sharp diffraction patterns. Talapin et al. demonstrated that colloidal inorganic nanoparticles can co-assemble through solvent evaporation into binary aperiodic quasicrystalline superstructures, which exhibited long-range order without translational symmetry (Fig. 14).³³ Combinations of 13.4 nm γ-Fe₂O₃ with 5 nm Au nanoparticles, 12.6 nm Fe₃O₄ with 4.7 nm Au nanoparticles, and 9 nm PbS with 3 nm Pd nanoparticles were reported to assemble into quasicrystals that displayed dodecagonal (12-fold) rotational symmetry (dodecagonal quasicrystals, DDQCs). The size ratios for all three nanoparticle combinations were similar, γ ≈ 0.43. These DDQCs showed an approximate stoichiometry of LS_3.84. The nanoparticles formed these structures through slow evaporation of TCE dispersions. Before their co-assembly, the nanoparticles were coated with OA or DDT, creating short-range steric repulsion. Since DDQC phases were formed from various nanoparticle combinations with consistent size ratios, it was suggested that quasicrystal formation was driven by entropy and simple interparticle interactions, rather than specific interparticle forces.³⁸ In other words, the quasi-periodic ordering could result from the optimal packing of square and triangular “tiles”, making the quasicrystalline state more stable than crystalline superstructures.^201–203 Under similar synthesis conditions, assemblies of 13.4 nm γ-Fe₂O₃ and 5 nm Au nanoparticles exhibited (3².4.3.4) Archimedean tiling. Archimedean tilings, first studied by Kepler in 1619,²⁰⁴ are regular patterns made from regular polygons. In each pattern, only one type of vertex arrangement is allowed, meaning the same combination of polygons meets at every vertex. These tilings are described by a sequence of integers (n₁.n₂.n₃…), where each number represents the number of sides of the polygons meeting at a vertex.²⁰⁵ In this study, each γ-Fe₂O₃ nanoparticle was surrounded by five equally spaced γ-Fe₂O₃ nanoparticles. Au nanoparticles and (Au)₆ octahedral clusters followed a regular pattern around each Fe₂O₃ nanoparticle, following a consistent clockwise sequence: (Au)₆, Au, (Au)₆, Au, Au. Connecting the centers of adjacent γ-Fe₂O₃ nanoparticles formed a pattern of equilateral triangles and squares, known in topology as (3².4.3.4) Archimedean tiling. Small fragments of (3³.4²) Archimedean tiling were also observed. Both (3².4.3.4) and (3³.4²) superstructures showed an LS₄ stoichiometry. Additionally, it was found that 13.4 nm γ-Fe₂O₃ and 5.0 nm Au nanoparticles formed different binary nanoparticle superstructures when modifying the nanoparticle ratio in the dispersion. A large (∼10-fold) excess of Au nanoparticles resulted in a CaB₆-type superstructure, while an AlB₂-type superstructure formed with a Fe₂O₃-to-Au ratio of about 1 : 2. It should be noted that the 2D [001] projections of AlB₂- and CaB₆-type structures corresponded to (3⁶) and (4⁴) Archimedean tiling patterns, respectively. Overall, periodic binary superstructures were formed when the size ratio was either above or below 0.43 or when nanoparticle concentrations were unsuitable for forming the DDQC phase.³³

Fig. 14 (a) and (b) TEM images of a dodecagonal quasicrystalline superstructure assembled from 13.4 nm γ-Fe₂O₃ and 5 nm Au nanoparticles. Inset of (a) ED pattern with non-crystallographic 12-fold rotational symmetry. (c) TEM images of a dodecagonal quasicrystalline superstructure assembled from 9 nm PbS and 3 nm Pd nanoparticles. Inset of (c), FFT pattern of the quasicrystalline superstructure. (d) TEM image of a (3².4.3.4) Archimedean tiling with LS₄ stoichiometry assembled from 13.4 nm γ-Fe₂O₃ and 5 nm Au nanoparticles. Inset of (d), ED pattern measured from the (3².4.3.4) Archimedean tiling. (e) TEM image of a (3³.4²) Archimedean tiling with LS₄ stoichiometry assembled from 13.4 nm γ-Fe₂O₃ and 5 nm Au nanoparticles. TEM images of (f) AlB₂-type and (g) CaB₆-type superstructures assembled from 13.4 nm γ-Fe₂O₃ and 5 nm Au nanoparticles. Adapted with permission from ref. 33. Copyright 2009 Springer Nature.

Bodnarchuk et al. demonstrated that DDQCs can form via the co-assembly of spherical polyoxometalate (POM) clusters with oleate-capped, spherical, semiconductor nanoparticles (PbS, CdSe or PbS/CdS).²⁰⁶ Before co-assembly, the POM clusters were coated with dodecyldimethylammonium (DDA) cations,²⁰⁷ enhancing their solubility in nonpolar solvents such as toluene or chlorobenzene. The POM clusters and semiconductor nanoparticles were initially dispersed in these solvents, and co-assembly subsequently occurred through crystallization driven by solvent evaporation. When 2.9 nm polyoxomolybdate {Mo₁₃₂} clusters co-assembled with PbS nanoparticles at a size ratio of 0.51, small regions of DDQCs were found. Similar quasicrystals appeared when {Mo₁₃₂} clusters co-assembled with CdSe nanoparticles at a size ratio of 0.49. At size ratios of 0.51 and 0.58, and a {Mo₁₃₂}-to-PbS concentration ratio of 10 or less, AlB₂-type superstructures appeared. At a size ratio of 0.58, NaZn₁₃-type superstructures coexisted with the AlB₂ superstructures. It should be mentioned that a 15–20 fold excess of {Mo₁₃₂} clusters favored the formation of NaZn₁₃-type superstructures. At a size ratio of 0.41, a small fraction of bcc-LS₆-type superstructures was observed. At a size ratio of 0.74, CaCu₅-type superstructures dominated. No binary superstructures formed when smaller PbS nanoparticles (γ > 0.74) were used.²⁰⁶

The role of magnetic interactions in the co-assembly of mixtures into quasicrystalline superstructures has been explored.²⁰⁸ In brief, Co and Ag spherical nanoparticles in toluene solutions could co-assemble on carbon-coated copper TEM grids through solvent evaporation. At 25 °C, 9 nm amorphous-phase Co and 4 nm Ag nanoparticles (γ = 0.49) formed NaCl-type binary superstructures, driven primarily by entropic forces. This resulting superstructure, with a packing density of about 0.71, matched the predictions of the hard-sphere model. However, 9 nm ferromagnetic hexagonal close-packed (hcp)-phase Co and 4 nm Ag nanoparticles co-assembled into DDQCs, as well as NaZn₁₃-, CuAu-, and Cu₃Au-type superstructures. The more densely packed NaCl-type superstructure (0.71) did not form. When the temperature was raised to 65 °C, the 9 nm hcp Co nanoparticles became superparamagnetic, leading to the formation of Cu₃Au- and AlB₂-type superstructures, similar to those seen with 9 nm amorphous Co nanoparticles. Reducing the size of Co nanoparticles to 7 nm (γ = 0.59), where both amorphous and hcp-phase Co nanoparticles are superparamagnetic, resulted in the assembly of AlB₂-type superstructures, independent of the Co nanoparticle crystallinity. This AlB₂-type superstructure, with a packing density of 0.76, was particularly favorable due to its higher density compared to the dense packing of single-component particles (0.74). In summary, these findings highlight the role of strong magnetic interactions between ferromagnetic Co nanoparticles in stabilizing quasicrystals and non-densely packed superstructures. These interactions played a dominant role in the co-assembly when ferromagnetic nanoparticles were present, while superparamagnetic nanoparticles were governed by hard-sphere interactions.²⁰⁸

6.1.1.2. Role of nanoparticles. The type of nanoparticles used influences the formation of different co-assembled superstructures, even when assembled under the same conditions.⁴⁰ For example, colloidal superstructures were reported to be formed by evaporating hexane from binary mixtures of PbSe and CdSe nanoparticles with a size ratio between 0.53 and 0.83, or from binary mixtures of PbSe and Au nanoparticles with a size ratio between 0.47 and 0.86. For 0.45 ≤ γ ≤ 0.54, PbSe and Au nanoparticles tended to form single-component superstructures, while PbSe and CdSe nanoparticles (γ = 0.53) formed both AlB₂-type binary superstructures and single-component phases. This aligned with the theoretical phase diagrams, where AlB₂-type superstructures are the stable structures at a size ratio of 0.53.^36,123,209

For 0.54 ≤ γ ≤ 0.61, co-assembling PbSe and CdSe (γ = 0.56) produced four different superstructures: two fcc superstructures and AlB₂- and NaZn₁₃-type binary superstructures. When the ratio of CdSe to PbSe nanoparticles was below 4, the AlB₂-type superstructures were predominant, reaching a maximum at a particle ratio of around 5. As the concentration of small CdSe nanoparticles increased, the NaZn₁₃-type superstructures became more common. At a size ratio of 0.59, although some AlB₂-type superstructures remained, NaZn₁₃-type superstructures became the dominant structure. These findings aligned with theoretical predictions for binary hard-sphere mixtures.^36,123,209 In contrast, solvent evaporation from binary suspensions of PbSe and Au nanoparticles predominantly produced single-component fcc superstructures. This suggested that in systems with metallic nanoparticles, enhanced van der Waals attractions play a significant role, and entropy alone does not drive superstructure formation.

For 0.64 ≤ γ ≤ 0.75, PbSe and CdSe nanoparticles (γ = 0.65 and 0.72) primarily co-assembled into single-component superstructures, although small amounts of CaCu₅- and MgZn₂-type binary superstructures were observed. At a size ratio of 0.73, however, MgZn₂-type binary superstructures became dominant, coexisting with the single-component fcc superstructures and traces of CaCu₅-type superstructures. Increasing the concentration of small CdSe nanoparticles relative to larger PbSe ones led to a rise in MgZn₂-type superstructures, reaching a maximum at a CdSe-to-PbSe ratio of 7. Beyond this relative concentration, the CdSe single-component superstructure became dominant. It was concluded that the MgZn₂-type binary superstructure was thermodynamically stable at a size ratio of 0.73, at a slightly smaller size ratio than the predicted value of 0.76.¹²⁷ This conclusion also applied to a size ratio of 0.75. As predicted by theory, PbSe and CdSe nanoparticles co-assembled into MgZn₂-type binary superstructures at size ratios of 0.79 and 0.80, although these superstructures appeared only in trace amounts compared to the dominant single-component superstructures. When PbSe nanoparticles were co-assembled with Au nanoparticles, CsCl-type binary superstructures (SG 211, Pm3̄m) formed alongside single-component superstructures. In this binary superstructure, particles form a simple cubic lattice, with large particles located at the unit cell centers and small particles positioned at the corners. These CsCl-type binary superstructures can only be stabilized when interparticle interactions are considered. Therefore, entropy was the primary driving force for co-assembly, but small changes in the assembly conditions—such as using metallic nanoparticles—enhanced van der Waals attractions. This resulted in the formation of superstructures that are typically unstable in binary hard-sphere mixtures.⁴⁰

Nanoparticle samples always exhibit a range of particle sizes, which can significantly affect both the thermodynamics and kinetics of forming binary nanoparticle superstructures. Murray and Sanders demonstrated that even a slight variation in the size of small particles can increase the packing density of the NaZn₁₃-type superstructure from 0.738 to 0.760.^34,35 Shevchenko et al. found that mixtures with a broad size distribution (greater than ∼14% standard deviation) suppressed co-assembly. Small fragments of binary superstructures occasionally formed in solutions with a polydispersity of ∼10–12% standard deviation.^31,32 These observations are consistent with numerical models predicting that nucleation is suppressed in mixtures of polydisperse hard spheres.²¹⁰

6.1.1.3. Role of solvent. The formation of nanoparticle superstructures was found to be highly dependent on the solvent used in dispersion and to be subsequently destabilized.²¹¹ For example, when 3.4 nm spherical CdSe nanoparticles and 7.3 nm spherical PbSe nanoparticles (γ = 0.56) were dispersed in TCE and allowed to evaporate on TEM grids, they formed AlB₂- and cub-LS₁₃-type binary superstructures. In contrast, dispersions in toluene or chloroform generally led to single-component PbSe or CdSe superstructures with hexagonal order, along with some disordered regions. The AlB₂-type superstructure preferentially oriented with its (0001) plane parallel to the substrate. The cub-LS₁₃ structure primarily oriented with the (100) plane parallel to the substrate, although some lattices displayed the (110) plane parallel to the substrate. At low CdSe-to-PbSe concentration ratios (<2), only disordered structures or single-component CdSe superstructures formed. As the ratio increases (from 2 to 9), AlB₂-type binary superstructures appeared. Between ratios of 7 and 20, cub-LS₁₃-type binary superstructures became dominant. At ratios above 20, single-component CdSe superstructures gradually replaced the cub-LS₁₃-type binary superstructures. According to the hard-sphere model, both the single-component superstructure (a filling factor of 0.74) and the AlB₂-type binary superstructure (a filling factor of 0.74) are more likely to form than the cub-LS₁₃-type binary superstructure (a filling factor of 0.65). This aligned with experimental observations for CdSe-to-PbSe concentration ratios between 1 and 9. However, when the concentration ratio increased to between 7 and 20, the cub-LS₁₃-type superstructure became the dominant structure. This deviation from the hard-sphere model suggested that interparticle interactions, particularly van der Waals forces, played a significant role in the co-assembly process.²¹¹
6.1.1.4. Role of temperature. Temperature—which drives co-assembly by adjusting solvent conditions—affects the balance between internal energy (U) and entropy (S) in the Helmholtz free energy equation (F = U − TS), allowing guiding of nanoparticle assembly into desired structures. In this context, Bodnarchuk et al. demonstrated that temperature can be used to control co-assembly of nanoparticles into various binary superstructures.⁴¹ At 85 °C, TDPA-HDA-TOPO-TOP-capped 8.0 nm spherical CdSe nanoparticles and OA-capped 3.1 nm spherical PbS nanoparticles (γ = 0.47, CdSe-to-PbS concentration ratio ∼1 : 8) co-assembled into NaCl-type superstructures (Fig. 15a). At 65 °C, NaCl-type superstructures were the most common, although AlB₂-type superstructures were also present. At temperatures of 0, 25, or 40 °C, only AlB₂-type superstructures were observed. Both superstructures represent the densest phases, with a nearly identical packing density of about 0.73 at a size ratio of 0.47. When the temperature was further reduced to −20 °C, NaZn₁₃-type superstructures formed, exhibiting a significantly lower packing density of approximately 0.66. The temperature-induced transition from low-density NaZn₁₃-type superstructures to the denser AlB₂- and NaCl-type superstructures followed expected trends.¹²³ However, the absence of other superstructures at low temperatures was not fully explained. It was proposed that NaZn₁₃-type superstructures had a higher cohesive energy compared to AlB₂- and NaCl-type superstructures. At low temperatures, this internal energy competed with free volume entropy, but it was insufficient to overcome the TdS term as temperature increased.

Fig. 15 (a) Binary superstructures co-assembled by 8 nm CdSe and 3.1 nm PbS nanoparticles (γ = 0.47, CdSe : PbS ∼1 : 8) at different temperatures. (b) Binary superstructures co-assembled by 7.7 nm PbSe and 3.4 nm Pd nanoparticles (γ = 0.53, PbSe : Pd ∼1 : 9) at different temperatures. (c) Binary superstructures co-assembled by 7.7 nm PbSe and 3.4 nm Pd nanoparticles (γ = 0.53, PbSe : Pd ∼1 : 18) at different temperatures. (d) Binary superstructures co-assembled by 7.7 nm PbSe and 3.4 nm Pd nanoparticles (γ = 0.53, PbSe : Pd ∼1 : 4.5) at different temperatures. Adapted with permission from ref. 41. Copyright 2010 American Chemical Society.

At a size ratio of around 0.54, the formation of AlB₂- and NaZn₁₃-type superstructures was predicted and experimentally confirmed by Hunt et al.²¹² However, the predominant binary nanoparticle superstructures formed from OA-capped 7.7 nm spherical PbSe nanoparticles and DDT-capped 3.4 nm spherical Pd nanoparticles (γ ≈ 0.53, PbSe-to-Pd concentration ratio ∼1 : 9) were found to be CuAu- and Cu₃Au-type superstructures (a packing density of approximately 0.60) at −20, 40, 85, and 100 °C (Fig. 15b).⁴¹ This co-assembly was not governed by entropy-driven crystallization but rather by interparticle interactions. At the low temperature of −20 °C, these binary nanoparticle superstructures co-existed with NaZn₁₃ and AlB₂-type superstructures. Near room temperature, the high-density AlB₂ phase became dominant across all examined PbSe-to-Pd nanoparticle ratios (∼1 : 9, ∼1 : 18, and ∼1 : 4.5). At 65 and 85 °C, Fe₄C-type superstructures were identified.³¹ At 100 °C, only CuAu- and Cu₃Au-type superstructures were observed.

Increasing the PbSe-to-Pd nanoparticle ratio to ∼1 : 18, a similar sequence of binary superstructures co-assembled at different temperatures was found (Fig. 15c).⁴¹ The major difference at this concentration compared to the 1 : 9 concentration ratio was the enhanced probability to form NaZn₁₃-type superstructures, which were the only superstructures presented at −20 °C. NaZn₁₃-type superstructures also appeared at 25 °C, coexisting with AlB₂-type and other superstructures. At elevated temperatures, only CuAu- and Cu₃Au-type superstructures were detected. Conversely, when the PbSe-to-Pd nanoparticle concentration ratio was reduced to ∼1 : 4.5, NaZn₁₃-type superstructures were not observed (Fig. 15d). Instead, NaCl-type superstructures formed at low temperatures, AlB₂-type emerged at intermediate temperatures, and CuAu- and Cu₃Au-type superstructures formed at high temperatures.⁴¹

The simultaneous formation of multiple superstructures may occur when various binary superstructures have comparable chemical potentials or when there are inhomogeneities in the nanoparticle samples. Depending on the temperature, mixtures of identical nanoparticles can lead to either a single superstructure or multiple superstructures, indicating a degeneracy in superstructure formation at specific temperatures.

In hard-sphere calculations, it was found that at a size ratio of 0.74, no thermodynamically stable binary superstructures could form,^127,212 a result supported by experiments on PMMA particles.²¹² However, PbSe and Pd nanoparticles (γ = 0.74) demonstrated different behaviors, assembling into six different binary superstructures.⁴¹ This was attributed to the significant difference in interaction energies between the large and small nanoparticles. At low temperatures, OA-capped 7.7 nm PbSe and OA-capped 4.9 nm Pd nanoparticles (PbSe-to-Pd concentration ratio ∼1 : 8) also formed NaZn₁₃-type superstructures, despite having a relatively low packing density of ∼0.61. NaZn₁₃-type superstructures formed only at low temperatures, likely due to two reasons. First, their assembly was probably driven by the potential energy, rather than by the free volume entropy. Second, the kinetics of nanoparticle assembly could play a role. The assembly could involve the pre-formation of icosahedral clusters of Pd nanoparticles, driven by van der Waals and electrostatic forces, which then transformed into the NaZn₁₃-type superstructure. When the concentration ratio of PbSe-to-Pd was reduced, these superstructures disappeared, and CaCu₅-type superstructures with a higher packing density (∼0.67) emerged. MgZn₂-type Laves-phase superstructures formed at 65 °C, exhibiting a significantly higher packing density compared to the system at a size ratio of 0.53. At higher temperatures, CuAu- and CsCl-type superstructures dominated, consistent with their highest packing density for this size ratio.⁴¹

Summarizing, low-temperature binary superstructures (NaZn₁₃ and CaCu₅) consist of large nanoparticles forming a sub-lattice, separated by clusters of small nanoparticles. In the NaZn₁₃-type superstructure, these clusters contain 13 nanoparticles. The CaCu₅-type superstructure features a hexagonal packing of large spheres with close-packed trigonal bipyramidal clusters of five small spheres. The AlB₂-type binary superstructure, typically found at intermediate temperatures, exhibits clusters of two small nanoparticles. High-temperature binary superstructures (NaCl, CuAu, CsCl, and Cu₃Au) lack contact between small spheres. When small nanoparticles have stronger attractive forces than large ones, binary superstructures with clusters of small nanoparticles gain extra stability from short-range attractions between tightly packed small nanoparticles. This effect is especially pronounced in the PbSe–Pd system due to strong van der Waals interactions between Pd nanoparticles. The formation of many binary superstructures within a narrow temperature range requires that the magnitudes of |dU| and |TdS| be similar. For CdSe–PbS nanoparticles, |dU| < |TdS| during assembly, while for PbSe–Pd nanoparticles, |dU| > |TdS|. As temperature increases, the main driving force for nanoparticle co-assembly gradually shifts from interparticle interactions (dominant at low temperatures) to free-volume entropy (dominant at high temperatures).⁴¹

As discussed in the previous section, selecting appropriate solvents can make the electrostatic and van der Waals forces between nanoparticles nearly temperature-independent. However, the interactions among ligands can still vary with temperature, as shown by atomistic molecular dynamics (MD) simulations conducted by Vlugt et al.²¹³ In a good solvent like n-alkane, direct interactions among ligands are efficiently screened, resulting in purely repulsive forces that provide steric stabilization for nanoparticles.²¹³ However, when the solvent evaporates, this screening decreases, transforming ligand–ligand interactions from repulsive to strongly attractive.^47,213

6.1.1.5. Role of ligands. To effectively guide the co-assembly process by tuning nanoparticle interactions—through adjusting solvent conditions and other strategies—it is important to understand the key role that ligands play in these interactions. A set of packing rules for soft materials (e.g., nanoparticles with surface ligands) have been established, which shed light on how entropy influences the co-assembly of materials capable of adjusting their shape based on local interactions.²¹⁴ These rules were built on principles of sphere packing.^34,35

Rule (1): the “softness” of capped nanoparticles (λ), defined as the ratio of the capping ligand length (L) to the core radius (R), influences their ability to adjust to specific coordination environments. Nanoparticles with low softness tend to follow sphere-packing principles during co-assembly. In contrast, for those with higher softness relying more on the redistribution of ligands away from contact points during co-assembly becomes important. As the solvent evaporates, nanoparticles come closer together, causing the ligand chains to concentrate along the central axis between neighboring nanoparticles. This accumulation of ligands creates osmotic pressure, which pushes the solvated ligands outward. Each nanoparticle in a densely packed array experiences nearly uniform pressure from all directions, whereas a nanoparticle with low coordination does not have this uniform pressure. In a densely packed array, each nanoparticle experiences nearly uniform pressure from all sides, while a nanoparticle with low coordination does not. Consequently, the entropic tendency of ligands to distribute evenly in the space between nanoparticles compels coordinatively unsaturated nanoparticles to shift their ligands away from contact points, enabling them to position themselves closer to their neighbors.^215,216

Rule (2): in low-coordination sites, soft nanoparticles pack more efficiently than hard ones, as they can reshape to fit the surrounding geometry. When the symmetry of their spherical outer layer is distorted, these nanoparticles adopt shapes similar to the Voronoi cell of the lattice site. This geometric adaptation transforms poorly packing units into softer versions of perfectly fitting Voronoi polyhedra.

Rule (3): softness promotes co-assembly. Deformable particles can effectively “glue” together, leading to the formation of dense binary superstructures.

Rule (4): soft nanoparticles tend to favor low-coordination structures, as these arrangements enable the most efficient packing of ligands.

Wei et al. studied the influence of ligands on the co-assembly of nanoparticles into binary superstructures. They prepared a series of superstructures by evaporating mixed colloidal solutions of spherical nanoparticles onto a TEM grid.²¹⁷ When Ag nanoparticles were coated with oleylamine (OAM) and the small-to-large nanoparticle ratio was fixed to 4, 2.9 nm and 11.9 nm Ag nanoparticles (γ = 0.42) co-assembled into NaCl-type superstructures.¹⁷² Replacing the small Ag nanoparticles with 3.7 nm Ag nanoparticles, while maintaining the large ones at 11.9 nm (γ = 0.44), still resulted in the formation of NaCl-type superstructures. When the large Ag nanoparticles were reduced to 9.6 nm while keeping the small ones at 3.7 nm (γ = 0.52), AlB₂-type superstructures formed.³¹ Similarly, co-assembling 2.9 nm or 3.7 nm small Ag nanoparticles with large 8.2 nm ones (γ = 0.55 and 0.58, respectively) also produced AlB₂-type superstructures. For a size ratio of 0.58, a NaZn₁₃-type superstructure was additionally observed. A size ratio of 0.64, achieved by co-assembling 3.7 nm and 7.5 nm Ag nanoparticles, led to NaZn₁₃-type superstructures. Further increasing the size ratio to 0.79 (co-assembling 5.5 nm and 3.7 nm Ag nanoparticles) and 0.81 (co-assembling 7.5 nm and 5.5 nm Ag nanoparticles) resulted in MgZn₂-type superstructures. By using small-to-large nanoparticle ratios of 2 and 10 and keeping the same coating agent (OAM), similar binary superstructures were obtained across the various size ratios. The observed sequence of binary nanoparticle superstructures—ranging from NaCl- to AlB₂- to NaZn₁₃- to MgZn₂-type superstructures—aligned with the phase diagrams of binary mixtures of hard spheres driven solely by entropic forces. According to these diagrams, NaCl-, AlB₂-, and NaZn₁₃-type superstructures are stable within the size ratio range of 0.414 ≤ γ ≤ 0.45, 0.45 ≤ γ ≤ 0.61, and 0.54 ≤ γ ≤ 0.625, respectively.^40,218 Laves phases (MgZn₂-, MgCu₂- and MgNi₂-type superstructures) are stable in the range of 0.76 ≤ γ ≤ 0.84.^40,218 These findings confirmed that the hard-sphere model is applicable to binary nanoparticle mixtures with identical surface coatings.²¹⁷

Spherical nanoparticles with different coatings were co-assembled under identical conditions to investigate how these coatings influence the formation of binary superstructures.²¹⁷ The results revealed that binary superstructures formed by nanoparticles with different coatings significantly deviate from the hard-sphere model. For example, 11.9 nm Ag nanoparticles coated with OAM and 4.0 nm Ag nanoparticles coated with DDT (γ ≈ 0.42) co-assembled into CaB₆-type superstructures. Additionally, DDQCs were observed for small-to-large nanoparticle ratios ranging from 2 to 4. Notably, at the size ratio γ ≈ 0.42, these superstructures differed from the NaCl-type superstructure predicted by the hard-sphere model and formed when both nanoparticles were coated with the same ligand. When 11.9 nm Ag nanoparticles coated with OAM and 4.0 nm Ag nanoparticles coated with DDT were dispersed in hexane (instead of toluene, as in previous experiments) and co-assembled using the air–liquid interface method,¹⁷⁶ NaCl-type superstructures formed. The resulting superstructures were the same as those previously observed with nanoparticles carrying the same ligands. Notably, the solvent evaporation time was significantly reduced from 4 hours (in toluene) to just 5 minutes when using hexane. Therefore, the co-assembly of binary mixtures may also be kinetically controlled by the ligands. It has been suggested that ligand exchange can occur as the solvent evaporates during the assembly process. In this drying phase, ligands adsorb and desorb from the nanoparticle surfaces in the colloidal solution. This bonding among nanoparticles and ligands is described by the equilibrium constant (K). According to the Arrhenius equation,

where k_a and k_d are the kinetic constants for adsorption and desorption, respectively. In binary systems where nanoparticles have the same ligand, it is assumed that the adsorption and desorption rates of ligands remain constant and do not depend on the nanoparticle size.²¹⁹ As a result, the co-assembly of nanoparticles with identical ligands is primarily determined by their effective size ratios. In contrast, in binary systems with two different ligands, the thermodynamic constant (K) differs for each type of nanoparticle. The evaporation of the solvent provides time for ligand exchange to occur. As nanoparticle superstructures form, the system incurs an energetic penalty to facilitate this ligand exchange, which influences the thermodynamics of co-assembly. Consequently, the formation of superstructures with lower packing densities may be kinetically favored because the energetic penalty for achieving these superstructures is less than that required for denser arrangements.²²⁰ Supporting this idea, a thorough review of the literature indicates that the formation of either CaB₆-type superstructures or quasicrystalline superstructures occurs when nanoparticles are coated with two different ligands (Fig. 16).^33,194,206

Fig. 16 (a) Schematic illustration of the ligand exchange between nanoparticles with different ligands. (b) Schematic illustration of multiple ligand systems: 11.9 nm Ag nanoparticles coated with OAM and 4.0 nm Ag nanoparticles coated with DDT. (c) TEM image of a CaB₆-type superstructure formed with 11.9 nm Ag nanoparticles coated with OAM and 4.0 nm Ag nanoparticles coated with DDT. Inset: CaB₆ model. (d) TEM image of a DDQC formed with 11.9 nm Ag nanoparticles coated with OAM and 4.0 nm Ag nanoparticles coated with DDT. (e) Schematic illustration of multiple ligand systems: 12 nm CoFe₂O₄ nanoparticles coated with OA and 3.7 nm Ag nanoparticles coated with OAM. (f) and (g) TEM images of binary superstructures formed with 12 nm CoFe₂O₄ nanoparticles coated with OA and 3.7 nm Ag nanoparticles coated with OAM: (3².4.3.4) Archimedean tiling, DDQCs, and AlB₂-type superstructures. (h) Schematic illustration of multiple ligand systems: 12 nm CoFe₂O₄ nanoparticles coated with OA and 4 nm Ag nanoparticles coated with OAM. (i) and (j) TEM images of binary superstructures formed with 12 nm CoFe₂O₄ nanoparticles coated with OA and 4 nm Ag nanoparticles coated with OAM: CaB₆-type superstructures and DDQCs. Adapted with permission from ref. 217. Copyright 2015 American Chemical Society.

Coropceanu et al. further explored how different capping ligands affect this nanoparticle co-assembly process.²²¹ In their study, 5.1 nm Au nanoparticles were capped with hexanethiol (C₆), nonanethiol (C₉), DDT (C₁₂), or pentadecanethiol (C₁₅), while 7.5 nm PbS nanoparticles were capped with OA (C₁₈), nonanoic acid (C₉), myristic acid (C₁₄), or erucic acid (C₂₂). As the ligand lengths varied, different superstructures formed, even when the size ratio between Au and PbS nanoparticles remained constant. For example, when PbS–C₉ and Au–C₆ nanoparticles (γ = 0.68, λ_PbS = 0.32, and λ_Au = 0.33) were co-assembled on a TEM grid by solvent (octane) evaporation, only single-component superstructures formed. However, co-assembling PbS–C₁₄ and Au–C₉ (γ = 0.68, λ_PbS = 0.48, and λ_Au = 0.47) led to irregularly shaped, highly intermixed domains. Co-assembly of PbS–C₁₈ and Au–C₁₂ (γ = 0.69, λ_PbS = 0.55, and λ_Au = 0.61) produced MgZn₂- and CaCu₅-type binary superstructures. Finally, the softest pair, PbS–C₂₂ and Au–C₁₅ (γ = 0.70, λ_PbS = 0.67, and λ_Au = 0.75), resulted in disordered binary films. This behavior was consistent across other Au and PbS nanoparticle pairs. Short ligands led to rapid assembly of single-component phases. On the other hand, long ligands caused the particles to jam during assembly, preventing them from organizing into ordered superstructures. However, ligands of intermediate length balanced these effects, allowing the formation of binary superstructures, regardless of the size ratio of the nanoparticles.

The study also investigated why some combinations of nanoparticles promote co-assembly into superstructures, while others result in phase separation.²²¹ To explore this, 70 assembly experiments were conducted using different combinations of Au and PbS nanoparticle sizes and ligand lengths. The results revealed that size asymmetry played a key role in binary superstructure formation. When PbS particles were significantly larger than Au particles, binary superstructures consistently formed. However, when the sizes were similar, the systems tended to exhibit disorder or phase separation. Some binary superstructures were successfully modeled using hard sphere approximations. In these cases, the predicted and experimental packing fractions were either above or just slightly below the fcc limit. However, in other cases, the hard sphere model did not accurately describe the experimentally observed lattice constants or packing fractions. This discrepancy was attributed to the flexible nature of ligand shell around the particles. Using the orbifold topological model (OTM), developed by Travesset,^222,223 it became possible to predict how particles deviate from the hard sphere model and pack more densely. A key aspect of the OTM is that ligands are not restricted to maintain the same orientation as they do in isolated particles. Instead, they can compress at the contact point between neighboring particles and collectively bend away from the contact axis. One superstructure, the CuAu-type, could not be accurately described by any of the models. The observed small lattice constants suggested that the original ligand density could not be maintained during assembly, indicating potential ligand loss or rearrangement during the process.

To understand why some superstructures are more favored than others, factors beyond density were considered. It was proposed that certain superstructures can form more easily because they have a lower nucleation barrier.²²¹ This hypothesis was supported by the analysis of various samples, which revealed a significant number of distinct fragments with the same superstructure (specifically, CaCu₅-, NaZn₁₃-, or AlB₂-type superstructures). The presence of these many disconnected fragments suggests that the co-assembly process involved multiple independent nucleation events. This observation implies that these binary superstructures may have a more favorable pathway for nucleation. It was noted that many of these superstructures show local structural characteristics resembling a generalized form of icosahedral symmetry. This observation suggested a potential relationship between the level of icosahedral order in a binary superstructure and the ease of nucleating such superstructure. Such a relationship was found in the structure of the fluid before nucleation occurs. Both experimental and theoretical studies indicate that in many systems, from colloids to metallic glasses, nucleation does not initiate directly from a homogeneous liquid. Instead, the liquid often develops a degree of short- or medium-range order before nucleation occurs.²²⁴ This local structure is frequently dominated by icosahedral or polytetrahedral order.^225–229 This icosahedral arrangement is energetically favorable because it allows a central particle to interact with 12 neighboring particles. In the context of binary nanoparticle superstructure formation during solvent evaporation, the initial state consists of nanoparticles that are well-dispersed in the solution, exhibiting only weak structural correlations (Fig. 17). As the solvent evaporates and the system contracts, local order begins to emerge. Particles form either transient or more stable tetrahedral and icosahedral clusters, or fragments of these clusters. Over time, binary superstructures start to nucleate within this structured liquid. Those superstructures with unit cells that closely resemble the liquid structure tend to nucleate more readily. This phenomenon explains the relatively easy nucleation of superstructures like NaZn₁₃ or CaCu₅, as their unit cells share common structural motifs with the proposed local structure of the prenucleation liquid. A similar rationale applies to the formation of various quasicrystalline binary superstructures.^200,202 The hypothesis also accounts for the relative scarcity of superstructures such as NaCl, where nucleation necessitates significant rearrangement.

Fig. 17 Evolution of a binary solution of nanoparticles: (t₀) isotropic solution; (t_i) the solution becomes denser and develops units or fragments with icosahedral or polytetrahedral arrangements; (t_f) these fragments can nucleate into a solid phase, exhibiting a unit cell that shares similarities with the structure of the original liquid, as demonstrated by the coordination of B particles in NaZn₁₃- and CaCu₅-type binary superstructures. Adapted with permission from ref. 221. Copyright 2019 American Chemical Society.

6.1.1.6. Anisotropic nanoparticles. As reviewed, a variety of periodic and quasicrystalline multi-component superstructures have been prepared by co-assembling isotropic, spherical particles through adjusting solvent conditions and other assembly methods. Additionally, anisotropic particles can co-assemble into multi-component superstructures as well (Table S2, ESI†). The use of anisotropic particles expands the range of possible superstructures, resulting in a more extensive phase diagram compared to that of isotropic particles. Importantly, anisotropic particles may offer shape-dependent physical and chemical properties, adding a new degree of freedom to tailor the collective properties of superstructures.²³⁰

In an early study, Kiely et al. prepared ordered 2D superstructures by co-assembling anisotropic gold nanoparticles coated with alkanethiol (C₁₀-thiol).²⁴ These nanoparticles were of two distinct sizes: small particles with a diameter of 4.5 nm and larger ones measuring 7.8 nm (γ = 0.58). The larger nanoparticles were primarily icosahedral or decahedral, while the small ones were truncated cuboctahedra. The colloidal crystals were formed by slowly evaporating a toluene solution containing the gold nanoparticles onto a carbon-coated copper mesh grid. In the resulting assembly, the large particles arranged into a hexagonal lattice, with the small particles occupying the trigonal spaces between them, resulting in an LS₂ stoichiometry. Comparable patterns have been observed in materials such as Brazilian gem opals,²³¹ charge-stabilized polystyrene (PS) spheres,¹⁸⁸ latex,²³² and PMMA spheres.²³³ When the size ratio was 0.47 (with particle sizes of 4.5 and 9.6 nm), the particles separated into distinct domains of small and large spheres, each domain displaying 2D hexagonal packing. This behavior aligned with Murray and Sanders' findings, which suggested that such segregation occurs when size ratio is between 0.458 and 0.482.^34,35 In contrast, when the size ratio was 0.87, the structure resembled a random alloy, with particles of different sizes occupying random positions.²⁴

LaF₃ triangular nanoplates and spherical Au or PbSe nanoparticles have been reported to co-assemble into binary superstructures (Fig. 18).³¹ In the LaF₃-Au assembly, the LaF₃ nanoplates laid flat on silicon oxide surface but stood upright when assembled on amorphous carbon. Therefore, space-filling (entropic) effects, Coulomb forces, and particle–substrate interactions combined to determine the final structure of the superstructures.³¹

Fig. 18 TEM images of assemblies formed from LaF₃ triangular nanoplates (9.0 nm side) and 5.0 nm Au nanoparticles on (a) silicon oxide surfaces or (b) on amorphous carbon substrates. (c) TEM image of an assembly formed from LaF₃ triangular nanoplates (9.0 nm side) and 6.2 nm Au nanoparticles on amorphous carbon substrates. Insets: (a) magnified image; (b) and (c) proposed unit cells of the corresponding superstructures. Adapted with permission from ref. 31. Copyright 2006 Springer Nature.

Cherniukh et al. explored the co-assembly of oleate-coated LaF₃ nanodisks of different sizes with CsPbBr₃ nanocubes (5.3 nm and 8.6 nm) coated with didodecyldimethylammonium bromide (DDAB).²³⁴ This co-assembly was achieved by slowly evaporating a solvent, either octane or toluene, from a mixture of the nanoparticles on a substrate. The 5.3 nm CsPbBr₃ nanocubes and LaF₃ nanodisks with sizes of 12.5, 13.3, 16.6, and 18.5 nm (γ = 0.430, 0.408, 0.337, and 0.306) co-assembled into columnar LS(I)-type superstructures. In this structure, vertically stacked nanodisks created a simple square columnar lattice with p4mm plane group symmetry, while nanocube pillars filled the space between disk columns (Fig. 19a and b). The 8.6 nm CsPbBr₃ nanocubes and 26.5 nm LaF₃ nanodisks (γ = 0.335) also formed columnar LS(I)-type superstructures. The 5.3 nm CsPbBr₃ nanocubes and 26.5 nm LaF₃ nanodisks (γ = 0.221) co-assembled into columnar centered rectangular LS₂(I)-type binary superstructures with c2mm symmetry (Fig. 19c and d). In this arrangement, two nanocube pillars filled the spaces between every four nanodisk columns. Similar to other LS₂(I)-type superstructures made of disks and rods,²³⁵ two possible configurations were possible due to varying alignments of the four nanocube sets around each nanodisk column. In one, all four sets aligned in the same directions (D_2h point group symmetry); in the other, there was a 79° angle between two nanocube sets (C_2v symmetry). The coexistence of these configurations within a single domain led to twin boundaries, suggesting minimal differences in their formation energies.^235,236 When 5.3 nm CsPbBr₃ nanocubes and 12.5 nm LaF₃ nanodisks co-assembled (γ = 0.430), they formed another columnar LS₂(II)-type superstructure: a centered rectangular lattice with LS₂ stoichiometry and c2mm symmetry (Fig. 19e and f). In this structure, the original hcp arrangement of nanodisks expanded in one direction, as the nanocubes filled the interstitial spaces. Each column of disks was surrounded by two disk pillars and six cube pillars, with each cube orienting two faces and one edge toward three neighboring disks. The positioning of eight neighboring nanocubes around each disk created twin boundaries between two configurations. The dominant configuration (D_2h symmetry) had three cubes separating adjacent disks on both sides. In the second configuration, disks were separated by four cubes on one side and two cubes on the other, with an angle of about 140° (C_2v symmetry, with a mirror plane intersecting the disks). The arrangement of nine adjacent nanodisk columns with C_2v symmetry led to a nonagonal flower-like assembly (Fig. 19g). When the concentration of CsPbBr₃ nanocubes increased, while maintaining the size of both nanoparticles (γ = 0.430), columnar LS₄-type superstructures formed (Fig. 19h). Columns of nanodisks arranged in a simple hexagonal lattice were uniformly surrounded by nanocubes. However, the arrangement of the nanocubes within columns was not clearly resolved, preventing the precise determination of their vertical stacking. A plausible model suggests that the LS₄ layers were stacked with a 60° shift relative to one another (Fig. 19i). Columnar hexagonal LS₆-type superstructures, consisting of 12 distinct pillars of nanocubes arranged in a dodecagonal pattern around columns of nanodisks, were prepared by co-assembling 5.3 nm CsPbBr₃ nanocubes with 21.0 or 28.4 nm LaF₃ nanoparticles (γ = 0.273 or 0.207, respectively) (Fig. 19j and k). LaF₃ nanodisks of 9.2 nm and 5.3 nm CsPbBr₃ nanocubes (γ = 0.555) arranged into a columnar centered rectangular LS(II)-type superstructure. In this structure, pairs of nanocube columns occupied interstitial sites created by six columns of adjacent disks (Fig. 19l and m). The translational order was distorted due to varying alignment of the nanocube sets, which were either parallel or angled at ∼102°. The 8.6 nm CsPbBr₃ nanocubes and 18.5 nm LaF₃ nanodisks (γ = 0.463) did not form columnar superstructures; instead, they exhibited lamellar ordering (Fig. 19n and o). This behavior is similar to the layered structures found in other systems, such as rhombic and tripodal nanoplates,²³⁷ nanoplates and nanospheres,²³⁸ and nanodisks and nanorods.²³⁵ The lamellar superstructures consisted of alternating 1D strings of nanodisks and nanocubes stacked face-to-face on the substrate. In this arrangement, the strings of nanodisks in the upper layer were positioned directly above the strings of nanocubes in the lower layer, resembling a columnar LS(I)-type superstructure. The co-assembly of 5.3 nm CsPbBr₃ nanocubes and 6.5 nm LaF₃ nanodisks resulted in lamellar L₂S-type superstructures, where each chain of nanocubes was surrounded by six chains of nanodisks (Fig. 19p and q).

Fig. 19 (a) Low and (b) high magnification TEM images of columnar LS(I)-type superstructures co-assembled from 5.3 nm CsPbBr₃ nanocubes and LaF₃ nanodisks with a size of 16.6 nm. Inset in (a): structural model. (c) Low and (d) high magnification TEM images of columnar LS₂(I)-type superstructures co-assembled from 5.3 nm CsPbBr₃ nanoparticles and 26.5 nm LaF₃ nanodisks. Inset in (c): structural model. (e) TEM image of columnar LS₂(II)-type superstructures co-assembled from 5.3 nm CsPbBr₃ nanoparticles and 12.5 nm LaF₃ nanodisks. (f) Structural models (showing D_2h and C_2v configurations). (g) TEM image of nonagonal superstructure domains. (h) TEM image of columnar LS₄-type superstructures co-assembled from 5.3 nm CsPbBr₃ and 12.5 nm LaF₃ nanodisks. (i) Structural models of LS₄-type superstructures. Inset in (h): small-angle ED pattern. (j) High-magnification TEM image of columnar LS₆-type superstructures co-assembled from 5.3 nm CsPbBr₃ and 21.0 nm LaF₃ nanodisks. (k) Structural models of LS₆-type binary superstructures. Inset in (j): small-angle ED pattern. (l) and (m) TEM images at different magnifications of centered rectangular columnar LS(IIII)-type superstructures co-assembled from 5.3 nm CsPbBr₃ nanocubes and 9.2 nm LaF₃ nanodisks. Inset in (l): structural model of LS(II)-type superstructures. (n) TEM images at different magnifications of lamellar LS(I)-type superstructures co-assembled from 8.6 nm CsPbBr₃ nanocubes and 18.5 nm LaF₃ nanodisks. Inset in (n): small-angle ED pattern. (o) Structural model of lamellar LS(I)-type superstructures. (p) HAADF-STEM image of lamellar L₂S-type superstructures co-assembled from 5.3 nm CsPbBr₃ nanocubes and 6.5 nm LaF₃ nanodisks. Inset in (p): image obtained by template-matching analysis of the HAADF-STEM image. (q) Structural model of L₂S-type superstructures. (r) TEM image of NaCl-type superstructures co-assembled from 8.6 nm CsPbBr₃ nanocubes and 12.5 nm LaF₃ nanodisks. Inset in (r): small-angle ED pattern. (s) HAADF-STEM image of NaCl-type superstructures co-assembled from 8.6 nm CsPbBr₃ nanocubes and 12.5 nm LaF₃ nanodisks. Inset in (s): structural model of NaCl-type superstructures. (t) TEM image of ReO₃-type superstructures co-assembled from 8.6 nm CsPbBr₃ nanocubes and 9 nm LaF₃ nanodisks. Inset in (t): structural model of ReO₃-type superstructures. (u) TEM images of disrupted ReO₃-type superstructures co-assembled from 8.6 nm CsPbBr₃ nanocubes and 6.5 nm LaF₃ nanodisks. Lower inset in (u): structural model of the disrupted ReO₃-type superstructures. (v) TEM images taken at different magnifications of a columnar binary superstructure domain co-assembled from 8.6 nm CsPbBr₃ nanocubes and 6.5 nm LaF₃ nanodisks. Lower inset in (v): structural model of the columnar binary superstructure. Adapted with permission from ref. 234. Copyright 2021 American Chemical Society.

Combining disks and cubes of similar size produced 3D, non-columnar superstructures.²³⁴ For example, 8.6 nm CsPbBr₃ nanocubes and 12.5 nm LaF₃ nanodisks formed NaCl-type superstructures, with clusters of three disks occupying individual lattice sites in the fcc sublattice (Fig. 19r and s). ReO₃-type superstructures (SG 221, Fm3̄m) were formed by co-assembling 8.6 nm CsPbBr₃ nanocubes and 9 nm LaF₃ nanodisks (Fig. 19t). The nanocubes occupied the primitive positions of the unit cell, forming a simple cubic arrangement, while the nanodisks were positioned between the nanocubes, aligned face-to-face. A similar arrangement, driven by strong face-to-face interactions, was observed in systems where LaF₃ triangular plates were positioned between PbTe cubes.²³⁹ When 8.6 nm CsPbBr₃ nanocubes were combined with 6.5 nm LaF₃ nanodisks, ReO₃-type superstructures became disrupted. This led to the formation of additional voids in the structure, which were filled by extra nanodisks (Fig. 19u). Alternatively, another 3D structure appeared (Fig. 19v). In this arrangement, CsPbBr₃ nanocubes formed columns, with individual nanodisks interlayered vertically. Paired nanodisks occupied single lattice sites, forming columns with alternating in-plane orientations. Lamellar and ReO₃-type superstructures, made from large 8.6 nm CsPbBr₃ nanocubes, showed distinct signs of collective ultrafast light emission—superfluorescence. This effect resulted from the coherent coupling of emission dipoles in the excited state.²³⁴

The same research group presented the structural variety of multi-component superstructures formed by co-assembling CsPbBr₃ nanocubes with spherical, truncated cuboid, and disk-shaped nanoparticles (Fig. 20).²⁴⁰ These superstructures were prepared by evaporating a small volume of a nanoparticle mixture (in toluene) onto hydrophobic substrates. The co-assembly of cubic CsPbBr₃ nanoparticles with spherical Fe₃O₄ and NaGdF₄ nanoparticles was first examined. When 8.6 nm CsPbBr₃ nanocubes were co-assembled with 18.6 nm spherical NaGdF₄ nanoparticles (γ = 0.439) at a low cube-to-sphere ratio (∼1.2 : 1), NaCl-type superstructures formed, where each CsPbBr₃ cube interacted with six NaGdF₄ spheres via flat facets. At a higher cube to sphere ratio (∼4.2 : 1), co-assembly of 8.6 nm CsPbBr₃ nanocubes with either 16.5 nm spherical NaGdF₄ nanoparticles or 19.8 nm spherical Fe₃O₄ nanoparticles resulted in perovskite-type (ABO₃-type) binary superstructures (SG 221, Pm3̄m), isostructural with a cubic CaTiO₃ perovskite, where the spherical nanoparticles occupied the A site (1a position of a Pm3̄m perovskite structure), and nanocubes occupied the B site (1b position) and O sites (3c position). When 8.6 nm CsPbBr₃ nanocubes were co-assembled with 21.5 or 25.1 nm spherical Fe₃O₄ nanoparticles and 11.7 nm truncated cuboidal PbS nanoparticles, they formed ABO₃-type ternary superstructures, with the PbS nanoparticles positioned at the B-sites. At intermediate cube-to-sphere ratios (∼2.2 : 1), co-assembly of 8.6 nm CsPbBr₃ nanocubes with 19.8 nm Fe₃O₄ or 16.5 nm spherical β-NaGdF₄ nanoparticles led to AlB₂-type binary superstructures. In these superstructures, the nanocubes filled trigonal prismatic voids within a simple hexagonal lattice of spheres, interacting with three spheres on one side of the trigonal prismatic void through their facets, and with three spheres on another side through their edges. For smaller 5.3 nm CsPbBr₃ nanocubes, co-assembly with spherical Fe₃O₄ nanoparticles (11.2–15.6 nm, γ = 0.443 to 0.336) also led to AlB₂-type binary superstructures. Additionally, an LS₂-type superstructure, belonging to the tetragonal crystal system (P4₂/mmc), was observed, where spherical nanoparticles formed alternating trigonal prisms and the cubic nanoparticles filled the voids. At a size ratio of 0.315 and a high cube-to-sphere ratio (∼12 : 1), co-assembly of 5.3 nm CsPbBr₃ nanocubes and 16.9 nm spherical Fe₃O₄ nanoparticles produced ABO₆-type binary superstructures (SG 221, Pm3̄m), with cubic nanoparticles occupying the B-site (1b Wyckoff position) and six O-sites (6f Wyckoff position). Co-assembly of 5.3 nm CsPbBr₃ nanocubes and 15.2 nm spherical NaGdF₄ nanoparticles (γ = 0.344) resulted in a mixture of NaCl-, AlB₂-, and LS₂-type superstructures, with ABO₃-type binary superstructures forming at high cube-to-sphere ratios.²⁴⁰

Fig. 20 Diversity of binary and ternary superstructures obtained from 5.3 and 8.6 nm cubic CsPbBr₃ nanoparticles combined with 11.2–25.1 nm spherical Fe₃O₄ and NaGdF₄ nanoparticles, 10.7–11.7 nm truncated cuboid PbS nanoparticles, and NaGdF₄ disks (31.5 nm in diameter and 18.5 nm thick). Adapted with permission from ref. 240. Copyright 2022 American Chemical Society.

The study also explored the co-assembly of cubic CsPbBr₃ nanoparticles with truncated cuboid PbS nanoparticles.²⁴⁰ PbS nanoparticles, despite their cuboid shape, behaved similarly to spheres, occupying A-sites in binary ABO₃- and NaCl-type superstructures, though they lost some orientational freedom. 8.6 nm cubic CsPbBr₃ nanoparticles and 10.7–11.7 nm truncated cubic PbS nanoparticles (γ = 0.72–0.78) co-assembled into ABO₃-type binary superstructures. At lower CsPbBr₃ concentrations, NaCl-type became the dominant phase. 8.6 nm cubic CsPbBr₃ nanoparticles and 10.7 nm truncated cuboid PbS nanoparticles also formed CuAu-type superstructures. Smaller cubic CsPbBr₃ nanoparticles (5.3 nm) with 10.7 nm PbS nanoparticles produced AlB₂-type superstructures.²⁴⁰

The co-assembly of cubic CsPbBr₃ nanoparticles and disk-shaped NaGdF₄ nanoparticles (31.5 nm in diameter and 18.5 nm thick) was finally investigated.²⁴⁰ 8.6 nm CsPbBr₃ nanocubes and NaGdF₄ nanodisks co-assembled into CaC₂-type superstructures (SG 139, I4/mmm), characterized by the periodic clustering of two CsPbBr₃ nanocubes. In each layer, the nanocubes are surrounded by four vertically oriented disks—two aligned with their flat faces and two with their rims. In the next layer, nanodisks align directly above the nanocubes from the previous layer.²⁴⁰

Hybrid organic–inorganic perovskite nanoparticles, specifically formamidinium lead bromide (FAPbBr₃) nanoparticles, have also been shown to act as building blocks for superstructure formation.²⁴⁰ For example, 9 nm FAPbBr₃ nanocubes and 15.1–19.5 nm spherical NaGdF₄ nanoparticles co-assembled into ABO₃-, AlB₂-, and LS₂-type binary superstructures. The 5.7 nm FAPbBr₃ nanocubes formed the NaCl-type binary superstructure when co-assembled with 15.1 nm NaGdF₄ spheres. In contrast, when co-assembled with 12.5 nm LaF₃ nanodisks, they produced columnar LS-type or lamellar (which is the dominant product) superstructures.²⁴⁰

These superstructures lead to collective electronic states in perovskite nanoparticles at low temperatures.²⁴⁰ This phenomenon is evidenced by the presence of sharp red-shifted bands in the photoluminescence and absorption spectra, which are observed at 6 K and continue to persist up to 200 K. The dense, periodic arrangement of the nanoparticles facilitates these collective states.

6.1.1.7. Ternary superstructures. As reviewed, many binary superstructures have been successfully prepared by co-assembling colloidal nanoparticles through adjusting solvent conditions. In contrast, only a few ternary superstructures have been achieved using analogous co-assembly techniques with colloidal nanoparticles (Table S3, ESI†). In an early example, Shevchenko et al. prepared quasi-ternary nanoparticle superstructures by co-assembling two types of spherical nanoparticles: 11.7 nm hollow core–shell iron/iron oxide and 4.5 nm Au nanoparticles, through evaporation of toluene–TCE mixtures.²⁴¹ When these nanoparticles were mixed in a 1 : 2 ratio, NaCl-type quasi-tertiary superstructures formed. When extra DDT was added to the 1 : 2 mixture, a hexagonal NiAs-type superstructure (SG 194, P6₃/mmc) emerged. The structure features alternating ABAC stacking, where Ni occupies the A sites and As occupies the B and C sites. The Ni atoms adopt a fcc configuration, while As atoms form a hcp arrangement. The NiAs-type superstructure coexisted with an AlB₂-type superstructure when the nanoparticles were mixed in a 1 : 4 ratio with extra DDT. In a 1 : 4–5 ratio without extra capping agents, or a 1 : 3 ratio with extra OA, the nanoparticles assembled into an AlB₂-type superstructure. When mixed in a 1 : 6–8 ratio, either without extra capping agents or with OAM, NaZn₁₃- and cub-LS₁₃-type superstructures appeared, with characteristic (001) and (110) projections, respectively.²⁴¹

Evers et al. reported the preparation of AlMgB₄-type ternary colloidal crystals by assembling spherical PbSe nanoparticles of two different diameters (12.1 and 7.9 nm) and spherical CdSe nanoparticles (5.8 nm).¹⁶⁰ A mixed suspension was first prepared with concentration ratios of approximately [M]/[L] = 1.3 and [S]/[L] = 10.9, where L refers to large PbSe, M to small PbSe, and S to CdSe. The nanoparticles were assembled into colloidal crystals on a TEM grid by solvent evaporation. In addition to a few single-component superstructures, LS₂ (isostructural with AlB₂) and MS₂ (isostructural with MgZn₂) binary superstructures, as well as LMS₄ (isostructural with AlMgB₄) ternary superstructures were formed. The ternary domains were epitaxially connected to binary LS₂ domains.¹⁶⁰

Cherniukh et al. co-assembled cubic and spherical sterically stabilized nanoparticles into binary and ternary ABO₃-type superstructures (Fig. 21).²⁴² This was achieved through solvent evaporation from a mixture of nanoparticles in toluene on various substrates. For example, CsPbBr₃ nanocubes (8.6 nm) coated with DDAB were co-assembled with oleate-capped spherical Fe₃O₄ nanoparticles (9.6–25.1 nm). When the Fe₃O₄ nanoparticles ranged from 9.6 to 14 nm, NaCl-type superstructures, single-component superstructures or disordered mixtures formed. For Fe₃O₄ nanoparticles sized between 14.5 and 20.7 nm, ABO₃-type superstructures emerged. In these superstructures, large spherical Fe₃O₄ nanoparticles occupied the A sites, while small cubic CsPbBr₃ nanoparticles occupied two Wyckoff positions: 1b and 3c. At 1b, (B site), the 〈100〉 crystallographic directions of the nanocubes aligned along the 〈100〉 direction of the superstructure. At 3c (O site), two 〈110〉 directions of the nanocubes aligned with the 〈100〉 direction of the superstructure. These ABO₃-type superstructures coexisted with AlB₂- and NaCl-type superstructures, with NaCl-type becoming more prominent as the fraction of CsPbBr₃ nanocubes decreased. When the Fe₃O₄ nanoparticles reached 25.1 nm, NaCl-type superstructures became dominant. ABO₃-type superstructures were also formed by 8.6 nm CsPbBr₃ nanocubes co-assembled with spherical NaGdF₄ nanoparticles ranging from 15.2 to 19.5 nm. Ternary ABO₃-type superstructures were formed by co-assembling 8.6 nm cubic CsPbBr₃ nanoparticles, 19.8 nm spherical Fe₃O₄ nanoparticles, and 10.7 nm truncated-cuboid PbS nanoparticles (γ_O/A = 0.414, γ_B/A = 0.533). Here, PbS nanoparticles substituted CsPbBr₃ at the B sites, with the degree of substitution increasing with the PbS to CsPbBr₃ ratio. Complete B-site substitution was observed when co-assembling 8.6 nm CsPbBr₃ nanoparticles, 25.1 nm Fe₃O₄ nanoparticles, and 11.7 nm PbS nanoparticles (γ_O/A = 0.327, γ_B/A = 0.460). These perovskite-based superstructures exhibited superfluorescence—an intense burst of light produced through collective emission, with an ultrafast radiative decay (22 ps). This characteristic makes them promising candidates for ultrabright (quantum) light sources. By further refining the perovskite nanoparticles and engineering their superstructures, new possibilities arise for studying many-body light–matter interactions, such as Dicke quantum phase transitions.^243,244 This research could lead to brighter perovskite superstructures or enable the development of highly entangled multiphoton quantum light sources,²⁴⁵ with potential applications in optical quantum computing²⁴⁶ or quantum imaging.²⁴⁷

Fig. 21 (a) TEM image of a binary ABO₃-type superstructure assembled from 8.6 nm CsPbBr₃ and 19.5 nm Fe₃O₄ nanoparticles (γ = 0.420). Top inset: High magnification TEM image. Bottom inset: ABO₃ unit cell, Fe₃O₄ = grey spheres; CsPbBr₃ = blue cubes. (b) HAADF-STEM image of a ternary ABO₃-type superstructure assembled from 8.6 nm CsPbBr₃, 10.7 nm PbS and 19.8 nm Fe₃O₄ nanoparticles (γ_O/A = 0.414, γ_B/A = 0.533). Top inset: ABO₃ unit cell, Fe₃O₄ = grey spheres; CsPbBr₃ = blue cubes; PbS = red truncated cubes. Bottom inset: TEM image. (c) TEM image of a ternary ABO₃-type superstructure assembled from 8.6 nm CsPbBr₃, 11.7 nm PbS and 25.1 nm Fe₃O₄ nanoparticles (γ_O/A = 0.327, γ_B/A = 0.46). Top inset: ABO₃ unit cell, Fe₃O₄ = grey spheres; CsPbBr₃ = blue cubes; PbS = red truncated cubes. Bottom inset: HAADF-STEM image. Adapted with permission from ref. 242. Copyright 2021 Springer Nature.

6.1.2. Co-assembly of nanoparticles at the air–liquid interface. Rather than adjusting solvent conditions through evaporation on a substrate, solvent evaporation can be performed on another liquid of higher boiling point—air–liquid interface co-assembly. In doing so, the superstructures formed without the limitations of a solid substrate, as the nanoparticles co-assembled on the surface of an immiscible liquid during solvent evaporation (Table S1, ESI†). This co-assembly often results in the formation of 2D superstructures.²⁴⁸ The thickness of these superstructures, which can be several nanoparticles, depends on the initial concentration of the nanoparticle solution and the area it covers. During drying, the interactions between nanoparticles can change. For example, as the solvent dries and the salt concentration increases, the electrostatic interactions become less significant.²⁴⁹ If the evaporation occurs sufficiently slow, the process can be considered quasi-static, progressing through a series of equilibrium states at each solvent concentration. In mixtures of different nanoparticles, these changing interactions can lead to either the formation of binary superstructures or phase separation.²⁵⁰ Compared to solvent destabilization co-assembly, this approach reduces local variations in nanoparticle concentration, resulting in fewer simultaneous formations of different superstructures.^31,32,248

Precise atomistic MD simulations at various air–liquid interfaces revealed that diethylene glycol (DEG), when used as the liquid phase, significantly influences co-assembly processes.^251–253 First, the interaction energies between DEG and the nanoparticles are much stronger than those among the nanoparticles themselves, making the nanoparticles cover the DEG surface. Second, nanoparticles coated with DDT, oleate or similar ligands immerse into the DEG by about half their diameter. This partial immersion allows DEG to organize the bottom layer of nanoparticles more effectively than in bulk solution. Lastly, when the interaction energies between DEG and different types of nanoparticles are nearly identical, the nanoparticles have similar affinities for the DEG surface, enabling them to displace one another during co-assembly. Together, these factors allow DEG to facilitate the formation of binary superstructures that would not form otherwise.

In an early example, Dong et al. reported the co-assembly of spherical FePt and Fe₃O₄ nanoparticles into binary nanoparticle superstructures at an air–liquid interface.²⁴⁸ Specifically, a hexane solution containing FePt (6 nm) and Fe₃O₄ (15 nm) nanoparticles (∼3 : 1 FePt/Fe₃O₄ particle ratio) was spread on a DEG surface (Fig. 22). As the hexane evaporated, a solid membrane formed on the liquid surface, which was then transferred to a substrate and vacuum-dried to remove residual DEG. The nanoparticles arranged into AlB₂-type superstructures, along with minor domains of Cu₃Au- and NaZn₁₃-type superstructures. By adjusting the nanoparticle size or concentration ratio, the structure of assemblies could be tailored. For example, NaCl-type superstructures formed when the ratio of 4 nm FePt to 15 nm Fe₃O₄ nanoparticles was ∼2 : 1, while increasing this particle ratio produced CaB₆-type superstructures. This approach was also generalizable to other nanoparticle combinations, such as Fe₃O₄–Fe₃O₄ and Fe₃O₄–CoPt₃. This air–liquid interface assembly process was found to depend on the solvent evaporation rates and the choice of immiscible liquid surface. Faster-evaporating solvents like hexane resulted in well-ordered superstructures, while slower solvents such as toluene led to random mixtures. DEG or tetraethylene glycol were particularly effective as immiscible liquid surfaces due to their chemical stability and slow evaporation, enabling continuous binary superstructure film growth. In contrast, ethylene glycol produced only islands of binary superstructures. The liquid-surface assembly process proved useful for creating nanoparticle-based devices. For example, to fabricate magnetoresistive devices, 15 nm Fe₃O₄ and 7 nm Fe₃O₄ nanoparticles were co-assembled and transferred onto a sapphire substrate with prepatterned gold electrodes. After annealing at 500 °C, the binary superstructure was preserved, while interparticle spacing was reduced. Precise control over superstructures enabled fine-tuning of the magnetoresistance properties of the devices. Additionally, the binary nanoparticle superstructures could also be fabricated as free-standing membranes.²⁴⁸

Fig. 22 (a) Schematic illustration of the preparation of binary nanoparticle superstructures at the air–liquid interface. AlB₂-type superstructures co-assembled from 15 nm Fe₃O₄ and 6 nm FePt nanoparticles: (b) TEM image of the (001) lattice projection (insets: upper, magnified view; lower, small-angle ED pattern); (c) crystallographic model of the (001) lattice projection; (d) high-resolution SEM of the (001) lattice projection; (e) TEM image of the (100) lattice projection (insets: upper, magnified view; lower, small-angle ED pattern); (f) crystallographic model of the (100) lattice projection; and (g) high-resolution SEM of the (001) lattice projection. Adapted with permission from ref. 248. Copyright 2010 Springer Nature.

In a similar study, Ye et al. reported the formation of 2D and 3D binary nanoparticle superstructures by co-assembling spherical PS-grafted Au and Fe₃O₄ nanoparticles using an air–liquid interface (Fig. 23).²⁵⁴ These superstructures were formed by evaporating a toluene solution of nanoparticles over an immiscible DEG subphase.²⁴⁸ 13.4 nm Fe₃O₄ nanoparticles grafted with PS (M_n = 5.3k) co-assembled with 3.8 nm Au nanoparticles (M_n = 3.0k, γ = 0.49). This co-assembly resulted in the formation of NaZn₁₃-type superstructures. Similar superstructures have been seen in nanoparticles capped with short alkyl chains.^{31,39,41,176,214,248} Reducing the concentration ratio from ∼15 : 1 (used for NaZn₁₃-type superstructures) to ∼7 : 1 resulted in the formation of bcc-LS₆-type superstructures.^255–257 Further reducing the nanoparticle concentration ratio produced phase-pure binary nanoparticle superstructures with lower stoichiometries, such as Cu₃Au, AlB₂ and NaCl. It is important to note that all five superstructures were achieved using nanoparticles with a single size ratio (γ = 0.49), which highlights the sensitivity of these PS-grafted nanoparticles to changes in the nanoparticle mixing ratio. The size ratio of nanoparticles also affected the superstructure. NaCl-type superstructures formed when co-assembling 4.2 nm (1.1k) Au and 13.4 nm (5.3k) Fe₃O₄ nanoparticles (γ = 0.40). This structure preference was favored by its high theoretical packing density of 0.793, which surpasses other superstructures at this ratio. However, when the smaller nanoparticles were 6.1 nm (5.3k) Au, resulting in a size ratio of 0.69, MgZn₂-type and CaCu₅-type superstructures became favored due to their improved packing densities at this size ratio. The CaCu₅-type superstructure also formed using larger Au nanoparticles (7.6 nm) grafted with shorter PS chains (γ = 0.68), demonstrating the adaptability of spherical polymer-grafted nanoparticles in constructing complex assemblies. Reducing the total nanoparticle concentration in the spreading solution by 10–15 times led to the formation of 2D binary superstructures. 2D LS-type binary superstructures formed from 3.8 nm (3.0k) Au and 13.4 nm (5.3k) Fe₃O₄ nanoparticles. The large Fe₃O₄ nanoparticles formed a square lattice, with the small Au nanoparticles positioned at the centre of each square.²⁵³ Without PS ligands, the nanoparticles would either phase-separate or form disordered films. Increasing the concentration ratio resulted in the formation of 2D L₂S₃-type and LS₈-type superstructures.²⁵⁴ It should be noted that polymeric ligands, unlike alkyl-chain ligands, offer more flexibility. In particular, in the concentrated polymer brush regime, they strongly influence interactions among nanoparticles.^258,259 In good solvents, extended polymer chains shield the van der Waals forces between the nanoparticle cores and introduce longer-range steric interactions compared to short alkyl ligands. As assembly progresses and drying occurs, the polymer brushes compress and interpenetrate, softening repulsive forces and optimizing system entropy during superstructure formation.

Fig. 23 Binary superstructures co-assembled from 3.8 nm (3.0k) Au and 13.4 nm (5.3k) Fe₃O₄ nanoparticles. (a) and (c) TEM images of NaZn₁₃-type superstructures. (b) Structural model of the [001] projection of NaZn₁₃-type binary superstructures. (d) and (f) TEM images of bcc-LS₆-type superstructures. (e) Structural model of the [001] projection of bcc-LS₆-type binary superstructures. (g) and (i) TEM images of Cu₃Au-type superstructures. (h) Structural model of the [001] projection of Cu₃Au-type binary superstructures. (j) and (l) TEM images of AlB₂-type superstructures. (k) Structural model of the [1−10] projection of AlB₂-type binary superstructures. (m) and (o) TEM images of NaCl-type superstructures. (n) Structural model of the [001] projection of NaCl-type binary superstructures. Scale bars: (a) 100 nm; (c) 20 nm; (d) 100 nm; (f) 20 nm; (g) 100 nm; (i) 20 nm; (j) 50 nm; (l) 20 nm; (m) 100 nm; (o) 20 nm. Adapted with permission from ref. 254. Copyright 2015 Springer Nature.

Udayabhaskararao et al. prepared non-close-packed nanoparticle arrays by selectively removing one component from binary nanoparticle superstructures, which were formed at the air–liquid interface.^248,251 The superstructures, after transferring them onto a substrate, underwent thermal desorption to remove ligands from the nanoparticles.²⁶⁰ The samples were then treated with an etchant that selectively dissolved one type of nanoparticle. This process resulted in distinct “nanoallotropes”—nanoporous materials with the same composition but different nanoscale structures. For example, a mixture of DDT-coated Au nanoparticles (5.2 nm) and oleate-coated Fe₃O₄ nanoparticles (10.6 nm) in a ∼1 : 1 ratio formed an LS-type binary monolayer.²⁴⁸ In an aqueous HCl solution, the Fe₃O₄ nanoparticles were etched away, leaving the Au nanoparticles in place, creating a non-close-packed array of Au nanoparticles, known as vac₁Au₁. Alternatively, treating the monolayer with cyanide removed the Au nanoparticles, resulting in a square array of Fe₃O₄ nanoparticles. By increasing the Au:Fe₃O₄ nanoparticle ratio to ∼5, an LS₆-type binary superstructure (lacking the top layer of Au nanoparticles) formed. Etching away Fe₃O₄ nanoparticles led to clusters of five Au nanoparticles in a tetrahedral arrangement, referred to as vac₁Au₅. When the Au:Fe₃O₄ nanoparticle ratio was raised to ∼10, an LS₁₁-type binary superstructure emerged. After Fe₃O₄ removal, alternating layers of Au quartets and septets, [(–Au₄–Au₇–)_n pattern], were observed, resulting in vac₁Au₁₁. Reducing the Au:Fe₃O₄ nanoparticle ratio to ∼4 and using polydisperse Au nanoparticles (4.9 nm) led to binary superstructures formed with Au nanoparticles arranging in a zigzag-like pattern. These superstructures consisted of stacked layers with an LS₄ stoichiometry, where “L” represents Fe₃O₄ nanoparticles, and “S” refers to large (6.2 nm), medium (5.3 nm), and small (4.1 nm) Au nanoparticles in a 1 : 2 : 1 ratio. The formation of such ordered superstructures, despite the polydispersity, highlights the ability of nanoparticles to optimize packing efficiency at the air–liquid interface. Etching these superstructures produced non-close-packed vac₁Au₁Au₂′Au₁′′ arrays, where Au, Au′, and Au′′ denote differently sized Au nanoparticles. An ∼5 : 1 mixture of polydisperse Au nanoparticles (4.9 nm) and monodisperse Fe₃O₄ nanoparticles formed a quasi-ternary superstructure with an LSM₄ stoichiometry. In this structure, “S” corresponds to small Au nanoparticles (∼4.0 nm), and “M” corresponds to large Au nanoparticles (∼5.5 nm). Upon etching this superstructure, non-close-packed vac₁Au₁Au₄′ arrays were produced, where Au and Au′ refer to the small and large Au nanoparticles, respectively. Etching was also applied to multilayered systems, such as LS₄-type binary superstructures. These superstructures were created by co-assembling 5.2 nm Au and 10.6 nm Fe₃O₄ nanoparticles, premixed in a ∼4 : 1 ratio. Different superstructure thickness was achieved based on nanoparticle concentrations at the air–liquid interface. Prolonged heating of these superstructures transformed them into exotic, yet unidentified patterns. The etching was also extended to nanoparticles of other sizes. For example, by increasing the size of Fe₃O₄ nanoparticles from 10.6 to 13.0 nm, the distance between 5.2 nm Au nanoparticles in vac₁Au₁ arrays extended from 12.5 to 15.3 nm.²⁵¹

In a related study on using the air–liquid interface for co-assembling nanoparticles, Rupich et al. first self-assembled PbS nanoparticle (7.3 or 8.8 nm) into monolayers at the air–liquid interface and then explored the epitaxial growth of Au nanoparticles (8.3 nm) on these monolayers, which acted as the substrate.²⁶¹ Once formed, the PbS monolayers were transferred onto a silicon wafer, where they adhered firmly through van der Waals forces, remaining stable even when exposed to solvents like toluene or hexane. The monolayers exhibited a long-range hexagonal arrangement. Au nanoparticles were deposited onto PbS nanoparticle monolayers using a solvent mixture of hexane and octane (9 : 1 by volume). As the solvent evaporated, the surface potentials of the PbS nanoparticle monolayers guided the arrangement of the Au nanoparticles. Annealing the samples in toluene vapor further enhanced the stability and ordering of the Au nanoparticle layers. Due to the softness of the interparticle forces, the epitaxial assembly was minimally disrupted compared to assembly on a flat surface. This softness allowed the epitaxial layers to form coherently, even with variations in lattice mismatches and surface curvatures. It is worth noting that the softness of the interactions can be tuned by adjusting the length of the ligands: shorter ligands lead to stiffer interactions, while longer ligands result in more flexible ones. The epitaxial growth exhibited a strain-driven transition from Frank van der Merwe (layer-by-layer growth) to Stranski–Krastanov (layer-plus-island growth). A kinetic bottleneck was observed during the transition from monolayer to multilayer coverage, underscoring the importance of solvent annealing. This bottleneck might arise from the different critical island sizes needed for the formation of the first and second nanoparticle adlayers.²⁶² While the first adlayer of Au nanoparticles occurred on the PbS nanoparticle monolayer, the second adlayer of Au nanoparticles grew on the initial Au adlayer. The interactions between the nanoparticles in the second adlayer and the underlying first adlayer were stronger than those between the first adlayer and the substrate. This energy barrier limited nanoparticle movement in the second adlayer, possibly leading to a more disordered structure. As a result, the activation energy required for the diffusion of Au nanoparticles was higher in the second adlayer than in the first. This energy barrier limited the diffusion of Au nanoparticles in the second adlayer, possibly leading to a more disordered structure. However, solvent annealing at elevated temperatures enhanced nanoparticle diffusion, resulting in well-ordered monolayers. Additionally, the epitaxial growth of CdSe nanorods (55 nm × 8 nm) was also explored. When these nanorods were deposited on a hexagonally packed PbS nanoparticle monolayer, the substrate guided their alignment along one of three equivalent directions, forming small, unidirectionally aligned domains. The substrate negatively impacted the organization of the adlayer for nanorods, suppressing the formation of the larger, smectic domains typically seen on smoother substrates.²⁶³ Colloidal binary superstructures, consisting of 15.5 nm Fe₃O₄ and 6.0 or 8.3 nm Au nanoparticles arranged in AlB₂-, CaB₆-, and bcc-LS₆-type superstructures, were also used as substrates for the epitaxial assembly of Au and PbS nanoparticles. For example, 8.3 nm Au nanoparticles were deposited onto these binary superstructures, occupying the interstitial sites between the Fe₃O₄ nanoparticles. These results demonstrate the potential of binary nanoparticle superstructures to support the epitaxial assembly of nanoparticles, paving the way for designing more complex nanoparticle superstructures.²⁶¹

6.1.2.1. Anisotropic nanoparticles. Anisotropic particles were also co-assembled into ordered superstructures at air–liquid interfaces (Table S2, ESI†). For example, in an early study, Paik et al. co-assembled GdF₃ nanoplates—either ellipsoidal (16 nm by 10 nm) or rhombic (35 nm by 25 nm)—with spherical 9 nm β-NaGdF₄ nanoparticles at an air–liquid interface. The nanoplates stacked face-to-face and edge-on, forming an ordered lamellar structure with their long axes aligned parallel to the substrate. The β-NaGdF4 nanoparticles filled the gaps between the stacked nanoplates.²³⁸

Nanorods and nanospheres have also been co-assembled into binary nanoparticle superstructures at air–liquid interfaces, overcoming their natural entropic tendency to phase-separate.²⁶⁴ Specifically, Fe₃O₄ nanospheres (11.0 nm in diameter) and NaYF₄ nanorods (38.5 nm in length, and 19.5 nm in diameter) were assembled at an air–liquid interface by slowly evaporating a hexane suspension of the nanoparticles over ethylene glycol.^44,248,265 Three distinct phases were observed: phase separation (Fig. 24a and d), a lamellar phase (Fig. 24b and e) and an LS₂ binary superstructure (Fig. 24c and f). The LS₂ superstructure was co-assembled using specific concentrations of NaYF₄ nanorods and Fe₃O₄ nanospheres. In these superstructures, the nanorods displayed both positional and orientational order, optimizing their packing. Phase separation occurred when the concentration of nanospheres was either much lower or higher than that of nanorods. Additionally, the total concentration of nanoparticles also influenced the assembly process. At low concentrations, random mixtures formed due to entropic effects. As concentrations increased, microphase separation into alternating layers appeared, as well as LS₂ superstructures forming stripes or filament-like assemblies. Other nanospheres (e.g., UO₂, Au, and Pd) and nanorods (e.g., CdSe) were also explored to understand how size ratios affect assembly. For example, 7.4 nm UO₂ nanospheres co-assembled with NaYF₄ nanorods into ordered arrays. However, the small UO₂ nanospheres remained disordered, stabilizing the lamellar phase. Large nanospheres, too large to fit between nanorod layers, led to phase separation into single-component superstructures. Monte Carlo simulations were used to explore how particle shape and interactions affect co-assembly. The simulations indicated that while LS₂ superstructures were entropically stable at high packing fractions, demixing was preferred at experimental densities. Therefore, short-ranged interactions, such as those induced by ligand stabilizers or depletion effects, were crucial in overcoming entropic demixing tendencies and stabilizing the LS₂ superstructures.²⁶⁴

Fig. 24 Co-assembled superstructures of Fe₃O₄ nanospheres and NaYF₄ nanorods exhibited three distinct phases based on the size ratio and concentration of the nanoparticles: (a) and (d) bulk demixing, (b) and (e) a lamellar phase with disordered (mobile) nanospheres, and (c) and (f) an LS₂ binary superstructure. TEM images (a)–(c) are shown alongside theoretical reconstructions (d)–(f). Scale bars: 25 nm. Adapted with permission from ref. 264. Copyright 2013 American Chemical Society.

Two types of anisotropic nanoplates—rhombic GdF₃ nanoplates (24 nm base, 20 nm height, and 34 nm long axis) and tripodal Gd₂O₃ nanoplates (23 nm arm length, 7 nm width, and 2 nm thick)—have also been co-assembled into binary superstructures at an air–liquid interface, with DEG as the subphase (Fig. 25).^237,248 The shapes of the anisotropic nanoplates guided their positions within the superstructures, resulting in long-range orientational and positional order of each nanoplate. The rhombic nanoplates stood upright between the tripodal ones. Within each 1D string of rhombic and tripodal nanoplates, the nanoplates self-assembled into separate, single-component 1D arrays through shape-specific face-to-face interactions, without binding between rhombic and tripodal nanoplates. Therefore, interactions between identical nanoplates played a key role in the co-assembly of these binary superstructures. The design of anisotropic nanoparticles with complementary shapes enables their predictable co-assembly into binary superstructures with well-defined structures.²³⁷

Fig. 25 (a) Schematic illustration of rhombic, tripodal nanoplates, and binary assembly. TEM images of (b) a binary co-assembly of tripodal and rhombic nanoplates formed via complementary-shape interaction, (c) a binary superstructure domain bordering a single-component superstructure domain of rhombic nanoplates, and (d) a fractured binary superstructure consisting of co-assembled tripodal and rhombic nanoplates. Adapted with permission from ref. 237. Copyright 2013 American Chemical Society.

LaF₃ nanodisks (13.2 or 22.3 nm diameter, 1.6 nm thickness) and CdSe/CdS nanorods (15.1 nm length, 3.8 nm diameter) have been co-assembled into binary superstructures using air–liquid interfacial assembly (Fig. 26).^235,248 Hexane solutions containing the nanoparticles were deposited onto DEG subphases, leading to the formation of superstructures. In one assembly, 22.3 nm LaF₃ nanodisks and CdSe/CdS nanorods co-assembled into LS₂-type binary superstructures with C2mm symmetry (Fig. 26d–f).²⁶⁶ The nanodisks stacked in columns perpendicular to the plane, while two vertically aligned nanorods filled the spaces between the columns. Although the lattice appeared 2D, the structure was 3D, with nanodisk columns containing 5 to 6 disks, matching the height of the nanorods. When the LaF₃ nanodisk diameter was decreased to 13.2 nm, the assembly shifted to LS-type binary superstructures with P4mm symmetry (Fig. 26a–c).²⁶⁶ In this structure, the vertically aligned nanorods filled the gaps between arrays of nanodisks. Increasing the concentration of nanorods while using 22.3 nm nanodisks led to LS₆-type binary superstructures with P6mm symmetry, where the nanodisks formed hexagonal columns surrounded by a dodecagonal array of vertically aligned nanorods (Fig. 26g–i). The orientation of the superstructures could be adjusted by changing the liquid subphases. For example, replacing DEG with ethylene glycol resulted in lamellar liquid crystalline structures with a small presence of LS₂-type binary superstructures. The co-assembled structures maximized the packing of their building blocks, increasing free-volume entropy and reducing Helmholtz free energy. Space-filling models explained the formation of these binary superstructures.^43,267–269 Stability for LS-type binary arrangements was predicted when the size ratio was between 0.155 and 0.414.²⁶⁹ For the LS-type superstructure formed from nanodisks and nanorods with diameters of 13.2 nm and 3.8 nm, respectively, the size ratio was about 0.40, within the stable range. It is important to note that the effective size of the colloidal nanoparticles depended on the thickness of their alkyl ligand shells. When the nanodisk size increased to 22.3 nm, the size ratio dropped to 0.25, consistent with the predicted stability of LS₂-type arrangements (0.155 < γ < 0.281).²⁶⁹ Increasing the nanorod concentration while maintaining the size ratio led to the formation of LS₆-type binary superstructures, stable within the range of 0.101 < γ < 0.349.^235,269

Fig. 26 Binary superstructures assembled from LaF₃ nanodisks and CdSe/CdS nanorods. TEM images of (a) a superstructure self-assembled from 13.2 nm LaF₃ nanodisks, (b) an LS-type binary superstructure, (d) a superstructure self-assembled from 22.3 nm LaF₃ nanodisks, (e) an LS₂-type binary superstructure, and (g) and (h) an LS₆-type binary superstructure. Structural models of (c) the LS-type binary superstructure, (f) the LS₂-type binary superstructure, and (i) the LS₆-type binary superstructure. Adapted with permission from ref. 235. Copyright 2015 American Chemical Society.

Similarly, at the air–liquid interface, using DEG as the subphase, spherical Fe₃O₄ particles and branched nanoparticles, known as octapods, have been co-assembled into binary superstructures resembling a “tic-tac-toe” pattern (Fig. 27).²⁷⁰ Each octapod consisted of a CdSe core with eight CdS arms, rested on four of its arms, creating a cross-like shape from above. Two types of octapods were used: one with a length to diameter ratio (L/D) of 4 (L = 48 nm, D = 12.0 nm) and another with L/D = 7 (L = 73 nm, D = 10.4 nm). The octapods were thiol-stabilized. OA-coated Fe₃O₄ spheres had radii of either 7 nm or 12.5 nm. As the hexane suspension containing both types of particles slowly evaporated on a DEG liquid substrate, superstructures formed through interfacial co-assembly.²⁴⁸ The octapods aligned tip-to-tip, while Fe₃O₄ spheres filled the square gaps between them, resulting in the tic-tac-toe arrangement. The fit of the spheres between the octapods depended on the ratio of sphere diameter to octapod length (2R/L). The tic-tac-toe arrangement occurred only when octapods had an L/D of 4 and were combined with spheres of 12.5 nm radius, yielding a 2R/L ratio of 0.52. Numerical simulations and theoretical analysis revealed that the formation of these superstructures was driven purely by entropic factors.²⁷⁰

Fig. 27 Defects observed in tic-tac-toe arrangements formed by thiol-stabilized octapods combined with Fe₃O₄ spheres (2R/L = 0.52). SEM images showing: (a) a vacancy where an octapod was missing; (b) a substitutional defect where an octapod occupied a position meant for a sphere; (c) a local perturbation in the superstructure caused by octapods of varying sizes; (d) a gradual change in orientation; (e) a section of the superstructure that resulted in octapods aligning pod-to-pod. Scale bars: 50 nm. Adapted with permission from ref. 270. Copyright 2016 American Chemical Society.

Co-assembly of perovskite nanoparticles has also been achieved at the air–liquid interface.²⁴⁰ This process took place as the solvent containing a mixture of nanoparticles evaporated on glyceryl triacetate, resulting in the formation of ordered binary mono- and multilayers. The structures of these layers varied based on the concentration, number of particles, and size ratios of the nanoparticles. For instance, 8.6 nm cubic CsPbBr₃ nanoparticles and 19.8 nm spherical Fe₃O₄ nanoparticles co-assembled into LS-type monolayers when using dodecane as a solvent, and into NaCl- and AlB₂-type superstructures when using decane. Notably, the co-assembly on glyceryl triacetate occurs over minutes to hours, depending on the rate of solvent evaporation (hexane, octane, decane, or dodecane).²⁴⁰

6.1.2.2. Ternary superstructures. Ternary superstructures have also been successfully co-assembled from nanoparticles at air–liquid interfaces (Table S3, ESI†). For example, in an early example, Dong et al. reported the formation of ternary nanoparticle superstructure bilayers using the air–liquid interfacial assembly approach.²⁵³ By co-assembling three types of nanoparticles—16.5 nm Fe₃O₄ (L), 7.0 nm Fe₃O₄ (M), and 5.0 nm FePt (S)—a bilayered LMS₂-type ternary superstructure was formed. In this structure, two small FePt nanoparticles coordinated with one large Fe₃O₄ nanoparticle, while the medium-sized Fe₃O₄ nanoparticle occupied the gaps between two adjacent large Fe₃O₄ nanoparticles. This ternary structure was stable only in bilayer form.²⁵³

LMS-type ternary superstructures were co-assembled from small and large LaF₃ nanodisks along with CdSe/CdS nanorods (Fig. 28).²³⁵ Hexane solutions containing the nanoparticles were deposited onto DEG subphases, leading to the formation of superstructures. In this structure, stacked columns of small and large nanodisks co-assembled into centered rectangular lattices, with vertically aligned nanorods positioned in the gaps between the small LaF₃ nanodisk columns.²³⁵

Fig. 28 (a) and (b) TEM images and (c) the structural model of an LMS-type superstructure co-assembled from small and large LaF₃ nanodisks and CdSe/CdS nanorods. Adapted with permission from ref. 235. Copyright 2015 American Chemical Society.

6.1.3. Electrostatic co-assembly of nanoparticles. Electrostatic interactions among nanoparticles have been used to direct their co-assembly into ordered superstructures (Table S1, ESI†). In an early example, Kalsin et al. reported the electrostatic co-assembly of spherical, oppositely charged Au and Ag nanoparticles into diamond-like (or sphalerite-like) superstructures (Fig. 29).⁴⁹ Au nanoparticles with a diameter of 5.1 nm and Ag nanoparticles with a diameter of 4.8 nm were functionalized with HS(CH₂)₁₁NMe₃⁺Cl⁻ (TMA) and HS(CH₂)₁₀COOH (MUA), respectively.²⁷¹ Both types of nanoparticles remained stable and unaggregated in separate aqueous solutions. However, when mixed, the positively charged AgTMA nanoparticles interacted with the negatively charged AuMUA nanoparticles. Aggregation occurred rapidly when their molar ratio was close to 1 : 1, neutralizing their overall charge and leading to precipitation. Colloidal crystals formed from the nanoparticle precipitate, where the nanoparticles arranged into a diamond lattice. In this structure, each nanoparticle was surrounded by four oppositely charged neighbors at the vertices of a tetrahedron. The resulting crystal morphologies were identical to those found in macroscopic diamond or sphalerite structures. The crystallization of nanoparticles into a diamond-like structure was driven by screened electrostatic interactions. This screening occurred because the metallic nanoparticle cores were surrounded by counterions, which led to short-range electrostatic forces between the nanoparticles. The screening length was about 2.7 nm, meaning that the electrostatic energy was mainly influenced by interactions between neighboring nanoparticles with opposite and like charges.²⁷² The total crystal energy was the sum of favorable attractive interactions of opposite charges and unfavorable repulsive interactions of like charges. In the case of the diamond structure, the attractive interactions dominated, making the crystal energy favorable (negative). In contrast, structures like NaCl and CsCl experienced stronger repulsive interactions between like charges, reducing their energetic stability compared to the diamond lattice. This explains why the nanoparticles formed a diamond structure rather than the more closely packed NaCl or CsCl lattices.⁴⁹ Theoretical models that exclude screening effects, even when accounting for entropy and/or van der Waals interactions, cannot explain the formation of the diamond lattice.^273–275

Fig. 29 Different morphologies of colloidal crystals formed from AuMUA and AgTMA nanoparticles (left column) and their macroscopic sphalerite (a) to (d) and diamond (e) counterparts (right column). (a) An octahedron, with insets showing the {111} and {100} crystal facets. (b) A cut tetrahedron, with insets showing the {111} and {100} crystal facets. (c) An octahedron with two triangular facets cut, with the inset showing the {111} crystal facet. (d) A twinned octahedron, with insets showing the {111} crystal facets at the twinning point and the {100} crystal facet of a neighboring broken crystal. (e) A truncated tetrahedron, with the inset showing the {111} crystal facet. Adapted with permission from ref. 49. Copyright 2006 The American Association for the Advancement of Science.

Nanoparticles with opposite charges—positively charged octahedral cubic-phase In₂O₃ (c-In₂O₃) nanoparticles, with a diagonal length of 15.9 nm, and negatively charged spherical Pd nanoparticles, with a diameter of 5.8 nm—have been reported to co-assemble into 2D binary nanoparticle superstructures.⁵⁰ Prior to co-assembly, the c-In₂O₃ nanoparticles were stabilized with OA and OAM, while the Pd nanoparticles were coated with DDT. These nanoparticles were then suspended in toluene at a c-In₂O₃-to-Pd molar ratio of 4.8 : 1. Superstructures formed by simply dropping the nanoparticle suspension onto copper TEM grids. They depended on the arrangement of the octahedral c-In₂O₃ nanoparticles, which acted as a “skeleton pattern”. Two distinct packing configurations were observed to coexist. In one configuration, the octahedral c-In₂O₃ nanoparticles were oriented along the 〈001〉 direction and positioned on their vertices, allowing the Pd nanoparticles to settle near the four vertices, close to the four nearest neighboring octahedral c-In₂O₃ nanoparticles. Alternatively, when the c-In₂O₃ nanoparticles were oriented along the 〈001〉 direction but positioned on their edges, the Pd nanoparticles were located between the vertices of any two adjacent c-In₂O₃ nanoparticles in a row, rather than in the gaps between the rows. The primary driving force behind this co-assembly was attributed to Coulomb forces between the oppositely charged nanoparticles, rather than van der Waals, steric, or dipolar interactions.⁵⁰

6.1.4. DNA-guided co-assembly of nanoparticles. Using ligands with tether groups allows precise directional interactions that steric, ionic, or van der Waals interactions cannot achieve. These tether interactions typically occur through hydrogen bonding at specific sites, which are geometrically arranged to create strong bonds with their complementary tethers. Noncomplementary tethers, on the other hand, dissociate reversibly, allowing the structure to self-heal. These interactions facilitate the robust assembly of nanoparticles through preprogrammed heterogeneous nucleation and cooperative binding, guaranteeing that each building block binds correctly (Table S1, ESI†).

Deoxyribonucleic acid (DNA) is the prime example of a ligand that favors the robust assembly of nanoparticles into superstructures. Sequences of the four nucleobases—adenine (A), cytosine (C), guanine (G), and thymine (T)—direct the interactions by bonding with their complementary bases. Single- and double-stranded DNA (ssDNA and dsDNA) chains are commonly used to guide the assembly of nanoparticles and control their interactions.^276–284 The unpaired nucleobases at the ends of DNA strands seek out complementary partners, resulting in hybridization and attractive interactions between the nanoparticles. Interactions between nanoparticles depend not only on the DNA strands themselves but also on their location on the nanoparticle surfaces, such as at edges or facets. This positioning affects how the DNA strands hybridize, aiming to maximize the hybridization area while satisfying entropic effects. These combined factors result in complex interactions.^{107,285–291} While other ligands can also provide specific molecular-level instructions for nanoparticle binding, DNA ligands are particularly attractive in nanoparticle assembly due to their chemical stability, ability to be functionalized with different chemical groups, predictable sequence-based interactions, control over mechanical properties through their single- and double-stranded forms, and structural plasticity.^279,280

The assembly of nanoparticles into superstructures could be precisely controlled using DNA-grafted nanoparticles combined with DNA frames.^292–295 By enclosing nanoparticles within DNA polyhedral wireframes, specific directional interactions are achieved. These nanoparticles act as a cargo within these DNA frames.²⁹⁶ In doing so, the assembly is primarily driven by directional hybridization interactions between DNA strands at specific points, like the edges of the frames. This method partially reduces the entropic constraints that affect nanoparticles when not encapsulated within the DNA frames.

In an early study, Nykypanchuk et al. reported the assembly of DNA-functionalized gold nanoparticles into CsCl-type superstructures.²⁷⁸ Gold nanoparticles, either 11.4 nm or 12.5 nm in size, were functionalized with thiol-modified ssDNA. Two types of DNA-capped nanoparticles were assembled through DNA hybridization, driven by the complementary sequences on their DNA strands. When longer, more flexible DNA linkers were used, the nanoparticles formed CsCl-type superstructures with long-range order. In contrast, shorter or more rigid linkers led to amorphous structures. The formation of the ordered superstructures required melting the assemblies and then cooling, suggesting that assembly at lower temperatures was kinetically hindered. At low temperatures, nanoparticles could be trapped in non-equilibrium positions, leading to disordered assemblies. Heating reduced DNA-induced attraction, allowing the system to anneal into equilibrium, improving their spacing and structural order. These superstructures were reversible, forming and dissolving with heating–cooling cycles.²⁷⁸

Macfarlane et al. proposed six design rules to guide the assembly of nanoparticles into specific superstructures through programmable interactions between DNA strands.²⁵⁶ These rules were derived from a study on the assembly of spherical gold nanoparticles functionalized with DNA linkers. Due to the polyvalent nature of DNA-functionalized nanoparticles, each nanoparticle binds to multiple linker strands, forming hundreds of sticky-end duplexes with neighboring nanoparticles, resulting in superstructures. Through thermal annealing, the nanoparticles were able to rearrange into well-ordered lattices.²⁹⁷ A total of 41 assemblies were produced, yielding nine different crystal structures, including fcc, bcc, and hcp arrangements, as well as LS lattices isostructural with CsCl, LS₂ lattices isostructural with AlB₂, LS₃ lattices isostructural with Cr₃Si, LS₆ lattices isostructural with the alkali-fullerene complex Cs₆C₆₀, LS lattices isostructural with NaCl; and simple cubic lattices. It was found that when all DNA-functionalized nanoparticles have the same hydrodynamic radius, each nanoparticle in the thermodynamic product maximizes the number of DNA-based connections to its nearest neighbors (rule (1)). For example, when linkers with self-complementary sticky ends were used, allowing all gold nanoparticles to bind to one another in solution, the resulting thermodynamic product consistently formed an fcc lattice, as predicted by theory.²⁹⁸ However, when two sets of gold nanoparticles were functionalized with linkers containing different but complementary sticky ends, binding occurred only between particles of opposite types, resulting in a bcc lattice as the most stable structure for these binary systems. When two superstructures have comparable stability, the kinetic structure can form by slowing down the dehybridization and rehybridization of DNA linkers (rule (2)). For example, stable hcp superstructures can be achieved by annealing at low temperatures and reducing the local DNA density around nanoparticles. Hcp superstructures are considered kinetic structures because they are slightly less stable than fcc superstructures.²⁹⁹ The hydrodynamic radius of a DNA-functionalized nanoparticle, which includes the size of the nanoparticle and the attached DNA, primarily determines its assembly and packing behavior, rather than the size of its individual nanoparticle or DNA components (rule (3)). For example, colloidal crystals with CsCl-type superstructure showed the same arrangement and connectivity of DNA-functionalized nanoparticles as a bcc lattice but used two different sizes of nanoparticle cores. The thermodynamically preferred superstructure in a binary system depends on the size ratio and DNA linker ratio between the two types of nanoparticles (rule 4). For example, adjusting the size ratio (γ = 0.64) of DNA-functionalized nanoparticles resulted in AlB₂-type superstructures. By altering both the size ratio (γ = 0.37) and DNA linker ratio (∼2), Cr₃Si-type superstructures (SG 223, Pm3̄n) were formed. In this superstructure, a large particle is positioned at the 2a Wyckoff site and is symmetrically surrounded by small particles located at the 6c Wyckoff sites. Additionally, bcc-LS₆-type superstructures were synthesized with a DNA linker ratio of ∼3 and a size ratio of ∼0.35. Two systems with the same size ratio and DNA linker ratio form the same thermodynamically favored superstructure, regardless of the size of the nanoparticles or the number of DNA linkers per nanoparticle (rule (5)). The most stable superstructure achieves the highest level of DNA sequence-specific hybridization interactions (rule (6)). By attaching various DNA sequences to a nanoparticle, multiple sequence-specific duplexes can form. For example, gold nanoparticles were co-functionalized with two different DNA linkers: one with a self-complementary sticky end and another with a sequence that could bind to the sticky end of a different gold nanoparticle. The co-functionalized nanoparticle could interact with all nanoparticles in the system, while the second nanoparticle only interacted with the first. A NaCl-type superstructure was formed when the size ratio between the two nanoparticles was approximately 0.3 to 0.4. Both self-complementary and non-self-complementary linkers were arranged to form duplexes within the superstructure.²⁵⁶

6.1.4.1. Anisotropic nanoparticles. DNA ligands have also been shown to direct the co-assembly of anisotropic nanoparticles into ordered superstructures (Table S2, ESI†). Nanoparticles functionalized with dsDNA can be considered “programmable atom equivalents”.²⁸⁹ In this analogy, the nanoparticle core acts as the “atom,” while the DNA strands are the “bonds” that connect nanoparticles through complementary DNA hybridization.^280,300,301 The DNA sequence can be precisely programmed to control both the chemical complementarity between particles and the distance between them, with subnanometer accuracy determined by the number of base pairs in each DNA strand.^256,302,303 The nanoparticle serves as a scaffold; organizing the DNA into a shell may reflect the shape of the nanoparticle. Consequently, the shape of the nanoparticle can influence the symmetry of DNA interactions within superstructures.³⁰²

In an early example, O’Brien et al. co-assembled different anisotropic nanoparticles using DNA as a surface ligand.²⁸⁹ The programmability of the DNA sequences on the nanoparticle surfaces was used to direct the co-crystallization of various anisotropic nanoparticles. First, DNA-functionalized cubic gold nanoparticles of different sizes were co-assembled in a 1 : 1 ratio. One cube had a fixed length of 47 nm, while the other varied from 47 to 85 nm, resulting in size differences of up to 38 nm (or 81%). Despite these differences, all samples formed NaCl-type superstructures with the cubes aligned face-to-face. However, the long-range order decreased as the size differences between the cubes increased. It was observed that as the size difference between cubes increased, the ‘melting’ temperatures—referring to the particle–particle dissociation, which reflects the DNA bond strength^304,305 —also increased. When the size difference was small, DNA strands near the edges and corners of the cubes were less likely to hybridize. However, a larger size difference allowed more DNA strands at these regions of the smaller cube to hybridize. 1 : 1 mixtures of DNA-functionalized cubic gold nanoparticles, all the same size (L = 65 nm), but with different degrees of concavity or convexity, were assembled to study shape complementarity in DNA-mediated assembly (Fig. 30). The maximum depth of these concave or convex features was around 10 nm. The DNA shell adapted to the shape of each nanoparticle.³⁰² Five nanoparticle combinations formed NaCl-type superstructures with different levels of long-range order, ranked from highest to lowest: cube–cube (a packing efficiency of 0.99), concave cube–convex cube (a packing efficiency of 0.99), cube–concave cube (a packing efficiency of 0.85), cube–convex cube (a packing efficiency of 0.75), and concave cube–concave cube (a packing efficiency of 0.69). When the packing efficiency further decreased, as in the convex cube–convex cube combination (packing efficiency of 0.58), shape complementarity between nanoparticles diminished, resulting in a disordered superstructure. Thus, better shape complementarity led to more DNA shell overlap between adjacent nanoparticles, enhancing the number of DNA connections and improving the co-assembly process, as shown by the higher long-range order in these superstructures.²⁸⁹

Fig. 30 (a) Concave cubes (left), cubes (middle) and convex cubes (right) functionalized with complementary DNA. (b) Six combinations were examined, ranging from low shape complementarity (blue, low packing efficiency) to high shape complementarity (red, high packing efficiency): convex cube–convex cube, concave cube–concave cube, convex cube–cube, concave cube–cube, concave cube–convex cube, and cube–cube. SAXS data (solid lines) and simulated SAXS data (dashed lines) are plotted in a log–log format, with I(q) normalized to the intensity of the first peak. Note that no simulated data are available for the convex cube–convex cube mixture due to its amorphous nature. (c) A packing model based on nanoparticle shape. (d) SAXS and EM data were used to estimate the locations of DNA connections between particles (indicated in grey). (e) High-magnification SEM images of silica-encapsulated superstructures confirm the orientation and lattice symmetry of the particles. Scale bars, 50 nm. (f) Low-magnification STEM images of silica-encapsulated superstructures reveal larger, faceted crystals with enhanced long-range order for higher shape complementarity. Adapted with permission from ref. 289. Copyright 2015 Springer Nature.

Gold nanocubes (L = 52 nm) and disk-shaped gold nanoparticles were co-assembled using three different lengths of DNA to guide the process.²⁸⁹ For disk-shaped nanoparticles, two types of interactions were possible: between their flat circular faces or along their edges. When assembled with the nanocubes, it was expected that the flat face of the disks would align with the faces of the cubes, creating a shape-complementary interaction, while the edge-based interaction could potentially disrupt this complementarity. To explore this, the disk diameter (D) was systematically varied (from 35 to 120 nm) while keeping the thickness constant (8 nm). If D < L, 3D structures were predicted, where cubes arranged in a face-to-face cubic pattern with disks occupying the interstitial spaces between the cube faces. If D > L, 1D structures were expected, with alternating cubes and disks, where the disks blocked access to the remaining cube faces. For the shortest DNA lengths, the results matched these predictions: 3D structures formed when D/L < 1, a mix of 3D and 1D structures when D/L ∼ 1, and mostly 1D structures when D/L > 1. However, as the DNA length increased, the range of D/L values where 3D structures formed expanded significantly, reducing the occurrence of 1D structures.²⁸⁹

DNA ligands attached to polyhedral nanoparticles enable precise control over their interactions, guiding their thermodynamic assembly. However, long DNA ligands can hinder the formation of space-filling superstructures by altering the shape of the nanoparticles, which negatively affects their assembly. Therefore, it is important to separate the influence of DNA ligands from the core shape of the nanoparticles to successfully design space-filling superstructures. To address this, Zhou, Li and coworkers incorporated oligoethylene glycol (OEG) into DNA strands to introduce flexibility.³⁰⁶ These strands were designed with sticky ends to hybridize with others in the system. As a proof of concept, using these modified DNA strands, three types of polyhedral Au nanoparticles—cubes, truncated octahedra, and rhombic dodecahedra—were assembled into space-filling colloidal crystals: simple cubic, bcc, and fcc superstructures, respectively. Increasing the OEG length resulted in larger superstructure domains, while polyhedral nanoparticles with DNA linkers lacking OEG formed defective superstructures. The OEG-modified DNA allowed polyhedral nanoparticles to assemble into superstructures resembling the Voronoi polyhedron that closely matches their shape. For example, truncated bitetrahedron Au nanoparticles, which resemble the Voronoi cell shape of the interlocked honeycomb (ih) lattice, co-assembled into ih colloidal superstructures with hexagonal prismatic structures. Similarly, the flexible DNA approach helped match the shapes of polyhedron pairs to form space-filling, multi-component colloidal crystals. For example, cuboctahedral and octahedral Au nanoparticles with matching edge lengths co-assembled into CsCl-type superstructures with rectified cubic honeycomb (rch) packing symmetry.³⁰⁷ Tetrahedral and octahedral Au nanoparticles formed the tetra-octa honeycomb (toh) structure, exhibiting an octahedral crystal habit. Octahedral and bitetrahedral Au nanoparticles co-assembled into a gyrated tetra-octa honeycomb (gtoh) structure, forming a hexagonal prismatic crystal habit. Decahedral and octahedral Au nanoparticles also co-assembled: ten octahedra surrounded a central decahedron, forming a structure that extended periodically along its polar axis, creating an infinite pillar with aligned decahedral tips. Two pillars connected at their equatorial regions by a row of shared octahedra. As these connections extend, the pillars formed a superstructure pattern, resembling Penrose P1 tiling. Due to the quasi-space-filling nature of the decahedral and octahedral nanoparticles, gaps appeared between neighboring octahedra within pillars. Without sufficient flexibility in the linker molecules, these gaps would generate structural strain in the 3D superstructure. This strain was relieved by increasing the OEG flexor region, which allowed nanoparticles to assemble into superstructures with smaller aspect ratios and fewer structural defects.³⁰⁶

6.1.5. External force-assisted co-assembly of nanoparticles. Although only a few examples have been reported, external fields—such as light, electric and magnetic fields, or shear forces—may guide the co-assembly of nanoparticles into multi-component superstructures (Table S1, ESI†).
6.1.5.1. Spin-coating-assisted co-assembly of nanoparticles. Spin-coating has been applied to co-assemble nanoparticles into colloidal crystals, allowing for large-area coverage within minutes. However, achieving a highly ordered crystal structure can be challenging due to the strong lateral shear forces and rapid solvent evaporation inherent to this technique.

Wang et al. reported a kinetically controlled assembly of polymer-grafted nanoparticles into binary superstructures by using spin-coating, followed by solvent annealing (Fig. 31).³⁰⁸ In their study, Fe₃O₄ nanoparticles of 5.4 and 13.5 nm were functionalized with pentaethylenehexamine-terminated PS and diethylenetriamine-terminated PS, respectively. These nanoparticles were initially deposited as disordered mixtures on silicon substrates via spin-coating and then exposed to solvent annealing under CHCl₃ vapor. The annealing process led to a disorder-to-order transition. After 2 minutes, a phase separation resembling spinodal decomposition occurred, with regions enriched in either small or large nanoparticles, likely driven by the faster ordering of the small particles. At 3 minutes, nuclei of NaZn₁₃-type superstructures formed, marking the nucleation stage, which progressed until 5 minutes. Between 5 and 10 minutes, these NaZn₁₃-type domains coarsened, reducing grain boundaries and consolidating nucleated regions. By 15 minutes, highly crystalline NaZn₁₃-type superstructures with minimal defects and preferred [001] orientation were obtained. Therefore, the formation of these NaZn₁₃-type superstructures followed a multistep crystallization pathway, beginning with a spinodal-like preordering of nanoparticles, followed by nucleation and growth of the NaZn₁₃-type superstructures.³⁰⁸ Similar multistep pathways are common in various colloidal systems, as observed in both experiments and simulations.^168,309,310 Solvent vapor pressure, nanoparticle concentration, and the softness of the nanoparticles were key factors influencing the assembly kinetics, as supported by computer simulations.^311,312

Fig. 31 Evolution of the assembly of nanoparticles from a disordered state to NaZn₁₃-type superstructures under CHCl₃ vapor. (a)–(f) Low-magnification SEM images, FFT patterns (top insets), high-magnification SEM images (bottom insets), and schematic illustrations of nanoparticle films: (a) before solvent vapor annealing and after solvent vapor annealing for (b) 2 minutes, (c) 3 minutes, (d) 5 minutes, (e) 10 minutes, and (f) 15 minutes. Scale bars: SEM images: 200 nm; inset SEM images: 50 nm; FFT patterns: 0.05 nm⁻¹. Adapted with permission from ref. 308. Copyright 2021 American Chemical Society.

6.1.6. Emulsion-assisted co-assembly of nanoparticles. Colloidal particles can co-assemble inside emulsion droplets dispersed within another immiscible liquid (Table S1, ESI†). In this approach, the emulsion droplets served as confined space to facilitate the formation of superstructures.^240,313,314 Once assembled, these particles can lock together through electrostatic or van der Waals forces. In an early study, Kister et al. prepared three different types of binary supraparticles—NaZn₁₃-type superstructures, Janus supraparticles, and core–shell supraparticles—by evaporating oil-in-water emulsions.²⁵⁰ 4 nm and 8 nm Au nanoparticles coated with 1-hexadecanethiol were first dispersed in hexane (the oil phase) and then emulsified with an aqueous phase containing non-ionic surfactants, through stirring. As the hexane droplets evaporated, the spherical nanoparticles assembled into supraparticles. The type of surfactant used determined which supraparticle structure formed. Triton X-100 resulted in NaZn₁₃-type superstructures, longer-chain surfactants (Triton X-102 and X-165) led to Janus supraparticles, and the longest-chain surfactants (Triton X-305, X-405, and X-705) produced core–shell supraparticles, where large nanoparticles formed a core surrounded by a disordered shell of small nanoparticles. The different surfactants affected the Laplace pressures inside the emulsion droplets, which in turn influenced interparticle interactions and the timing of nucleation, guiding the assembly of nanoparticles into specific structures. For emulsions stabilized by Triton X-100 (which has 9–10 ethoxylate units as the hydrophilic chain), nucleation began after 150 minutes, with NaZn₁₃-type superstructures forming by 180 minutes. In contrast, with Triton X-165 (16 ethoxylate units), large nanoparticles started agglomerating at 240 minutes, and small nanoparticles did not begin until 420 minutes. The earlier agglomeration of large nanoparticles was due to their stronger mutual attraction. Later, small nanoparticles aggregated separately and were ultimately combined into a Janus supraparticle as the emulsion droplet shrank. In emulsions stabilized by Triton X-705 (55 ethoxylate units), large nanoparticles began agglomerating at 270 minutes, but small nanoparticles only began at 660 minutes. At that time, the limited free volume led to the formation of core–shell supraparticles, with small nanoparticles forming a shell around the large nanoparticle core.²⁵⁰

Similarly, Wang et al. co-assembled spherical Au and Fe₃O₄ nanoparticles into colloidal binary crystals using an oil-in-water emulsion.³¹⁵ Initially, oil-in-water droplets were formed, with the oil phase containing 10 nm superparamagnetic Fe₃O₄ and 5 nm plasmonic Au nanoparticles (γ = 0.5). The nanoparticles were stabilized by long-chain alkyl molecules (OA or DDT). Without this surface treatment, the nanoparticles formed amorphous structures instead of organized assemblies. As the organic solvent evaporated, interactions among the nanoparticles drove them to assemble into superstructures. By varying the concentration ratio of Fe₃O₄ to Au nanoparticles, different binary colloidal crystals were observed to be formed. When the ratio was around 1 : 15, the nanoparticles assembled into an NaZn₁₃-type colloidal crystal.^29,184 This co-assembly was not driven solely by hard sphere packing. Instead, short-range interactions involving surface ligands appeared to influence the formation of the NaZn₁₃-type colloidal crystals.^{214,222,316–318} At a higher Fe₃O₄-to-Au ratio (∼10 : 1), the Fe₃O₄ nanoparticles formed an ordered fcc lattice, while the Au nanoparticles occupied interstitial sites randomly.¹⁶³ As the concentration of Au nanoparticles increased, more ordered domains appeared during the assembly, leading to the formation of AlB₂- and Cu₃Au-type colloidal crystals. This assembly process also allowed for size control of the final colloidal crystals by adjusting factors such as surfactant concentration in the water phase or the shear rate during emulsification. Lower surfactant concentrations or shear rates generally produced larger colloidal crystals.³¹⁵

A gram-scale synthesis of phase-pure binary nanoparticle superstructures has been accomplished using an emulsion-based co-assembly process (Fig. 32).³¹⁹ In brief, hexane solutions containing 8.0 nm CoFe₂O₄ and 17.0 nm Fe₃O₄ nanoparticles, along with aqueous solutions of surfactant stabilizers (e.g., dodecyltrimethylammonium bromide, DTAB), were emulsified to form hexane-in-water emulsions. When these emulsions were heated under a nitrogen flow, the hexane gradually evaporated from the droplets, triggering the confined co-assembly of the nanoparticles into binary superstructures. This process consistently yielded gram-scale quantities of binary superstructures in the form of discrete spheres or quasi-spheres. When the ratio of Fe₃O₄-to-CoFe₂O₄ nanoparticles was approximately 1 : 13, the nanoparticles formed NaZn₁₃-type superstructures. Unlike other assembly methods, which often produced multiple superstructure types to coexist,^32,40,248 this approach produced exclusively NaZn₁₃-type binary superstructures. The simultaneous formation of different superstructure types was attributed to variations in local nanoparticle concentrations during solvent evaporation.^31,32,248 Here, the phase purity was attributed to the controlled assembly process, where each emulsion droplet acted as a microreactor, maintaining uniform nanoparticle concentrations. This ensured the formation of a single binary phase. The same NaZn₁₃-type superstructures were also achieved by co-assembling 17.0 and 8.5 nm Fe₃O₄ nanoparticles at an ∼1 : 13 ratio. Other types of binary superstructures were also prepared using this emulsion-based co-assembly process. For example, AlB₂-, MgZn₂-, CaCu₅-, and NaCl-type superstructures were formed by co-assembling 4.5 nm CoFe₂O₄ with 11.0 nm Fe₃O₄, nanoparticles, 6.5 with 9.0 nm Fe₃O₄ nanoparticles, 4.5 nm CoFe₂O₄ with 7.0 nm Fe₃O₄ nanoparticles, and 4.5 nm CoFe₂O₄ with 15.0 nm Fe₃O₄ nanoparticles, respectively. The NaZn₁₃-type superstructures, co-assembled from CoFe₂O₄ and Fe₃O₄ nanoparticles, exhibited single-phase magnetic switching due to strong dipolar coupling between the magnetically hard CoFe₂O₄ and soft Fe₃O₄ components. These superstructures also demonstrated enhanced lithium storage performance compared to their individual components when used as anode materials for lithium-ion batteries. They retained a stable capacity of around 800 mA h g⁻¹ after 500 cycles at 2 A g⁻¹. The non-close packing of NaZn₁₃-type superstructures played a key role in improving lithiation/delithiation kinetics and maintaining structural integrity during repeated cycling.³¹⁹

Fig. 32 (a) TEM image of a NaZn₁₃-type superstructure co-assembled from 8.0 nm CoFe₂O₄ and 17.0 nm Fe₃O₄ nanoparticles. Inset: FFT of the TEM image shown in (a). (b) and (c) TEM images of NaZn₁₃-type superstructures co-assembled from 8.5 and 17.0 nm Fe₃O₄ nanoparticles. Inset: FFT of the TEM image shown in (b). (d) TEM image of an AlB₂-type superstructure co-assembled from 4.5 nm CoFe₂O₄ and 11.0 nm Fe₃O₄ nanoparticles. Inset: FFT of the TEM image shown in (d). (e) TEM image of an MgZn₂-type superstructure co-assembled from 6.5 and 9.0 nm Fe₃O₄ nanoparticles. (f) TEM image of a CaCu₅-type superstructure co-assembled from 4.5 nm CoFe₂O₄ and 7.0 nm Fe₃O₄ nanoparticles. (g) TEM image of a NaCl-type superstructure co-assembled from 4.5 nm CoFe₂O₄ and 15.0 nm Fe₃O₄ nanoparticles. Adapted with permission from ref. 319. Copyright 2018 American Chemical Society.

Due to variations in droplet sizes, the resulting product contains a range of sizes. A more uniform size distribution of clusters or supraparticles can be achieved by co-assembling nanoparticles within emulsion droplets in microfluidic devices. In other words, microfluidic methods allow precise control over the dimensionality of the resulting supraparticles. For example, Bodnarchuk et al. reported the use of a microfluidic platform to co-assemble 20 nm CoFe₂O₄ nanoparticles with either 8 nm CdSe or 10 nm PbS nanoparticles, forming AlB₂-type superstructures.¹⁴⁹ In this process, a mixture of nanoparticles in TCE was injected into an immiscible carrier fluid, either perfluoro-tri-n-butylamine and perfluoro-di-n-butylmethylamine (FC-40) or perfluorotripentylamine (FC-70). The flow rate of the carrier fluid controlled the spacing between droplets. Binary superstructures formed through evaporation-driven co-assembly, as TCE gradually diffused into the carrier fluid and evaporated through the capillary walls, shrinking the droplet volume until the solvent fully evaporated.

Anisotropic nanoparticles have also been reported to co-assemble within emulsion droplets. For example, in a toluene droplet containing 8.6 nm cubic CsPbBr₃ nanoparticles and 18.6 nm spherical NaGdF₄ nanoparticles, dispersed in solvents like FC-40 or HFE-750 (with surfactant 008-FS), the nanoparticles co-assembled into ABO₃-type binary superstructures as the toluene evaporated.²⁴⁰

6.2. Co-assembly of submicrometer-sized particles

The co-assembly of submicrometer-sized colloidal particles (∼0.1 to ∼1 μm) is primarily driven by entropy, following the space-filling principle. However, this process can be modified by precisely adjusting the surface charge of the particles or by applying an external field.^320–326

6.2.1. Co-assembly of submicrometer-sized particles by adjusting solvent conditions. A common method for guiding the co-assembly process of submicrometer-sized colloidal particles is solvent destabilization (e.g., solvent evaporation) (Table S4, ESI†). Assembly driven by solvent changes has been successfully demonstrated in various submicrometer-sized particles, allowing precise control over their assembly and disassembly, and sometimes even enabling reversibility.

In an early study, Bartlett and coworkers co-assembled binary mixtures of spherical submicrometer-sized PMMA particles into superstructures by a slow solvent destabilization process.²³³ It should be noted that rapid destabilization can lead to disordered particle aggregates. The particles had diameters of 642 and 372 nm, resulting in a size ratio of 0.58. These particles were sterically stabilized with poly-12-hydroxystearic acid and suspended in a mixture of decalin and carbon disulphide.³²⁷ Depending on the ratio of the two particle types, two 2D superstructures, LS₂ and LS₁₃, were observed. The LS₂ superstructure was seen in suspensions with small-to-large particle number ratios of 4 and 6. LS₂ co-assembly occurred after about five weeks, resulting in a lower solid phase with nucleated superstructure crystallites and an upper colloidal fluid phase. In this superstructure, the small spheres occupied trigonal prismatic cavities between the large spheres. However, when the number ratio was 2, no crystalline LS₂ formed, and the suspension remained amorphous even after several months. The LS₁₃ superstructure formed in suspensions with a higher proportion of small particles, with a number ratio ranging from 9 to 30. The LS₁₃ superstructure crystallized rapidly, within days of sample preparation. A similar study with a slightly larger size ratio (γ = 0.62) showed different results.³²⁸ The slight increase in the size ratio prevented LS₂ crystallization; suspensions with a number ratio between 2 and 10 remained amorphous for months. The LS₁₃ superstructure formed at a number ratio of 13, but it was metastable, forming more slowly and eventually dissolving after months, often mixed with pure small superstructures. Computer simulations by Eldridge and Madden supported these findings, demonstrating that the LS₁₃ superstructure was stable at a size ratio of 0.58 but became unstable at size ratios above 0.62.²³³

Sonication has been used for solvent destabilization and thus organizing non-Brownian particles up to 0.1 mm in size.^320,322 For example, a mixture of PS and/or soda lime glass particles (0.6–100 μm) in deionized water was sonicated on a hydrophilic glass substrate, leading to predictable superstructure formation. The assembly process was influenced by changes to the bath medium, substrate, or solvent.³²² For a size ratio below 0.1, large particles formed closely packed structures, with small particles filling gaps, but no clear ordered superstructures formed due to geometric limitations. When the size ratios approached unity, the particles behaved like a single, non-uniform population, leading to disorder. However, short-range order emerged for size ratios between 0.10 and 0.28. The likelihood of achieving ordered superstructures decreased as the size ratio increased.³²⁹

Solvent evaporation is the most common method to guide the co-assembly of submicrometer-sized particles. In an early example, Mukhopadhyay et al. demonstrated that spherical PS submicrometer-sized particles can co-assemble into 2D, hexagonally ordered, binary superstructures by solvent evaporation.³³⁰ The study reported successful co-assembly of the following particle pairs: 368 nm SO₄-PS with 60 nm NH₂–PS, 497.1 nm NH₂–PS with 70.8 nm SO₄-PS, 519.8 nm SO₄-PS with 152.1 nm NH₂–PS, 368 nm SO₄-PS with 59.5 nm COOH–PS, and 368 nm SO₄-PS with 70.8 nm SO₄-PS. While some ordering was observed on hydrophilic surfaces, it was less pronounced compared to hydrophobic ones. In these assemblies, large particles formed a hexagonal pattern, with small particles occupying the spaces between them. The surface chemistry—whether sulfated, carboxylated, or aminated, all with negative zeta potential—did not affect the formation of these ordered superstructures. Co-assembly was successful across a wide pH range (4–10) and with both concentrated and dilute suspensions. However, at pH 2, the assembly became highly disordered, likely due to the aggregation of smaller particles with lower zeta potentials before they could properly assemble. This indicated that within the pH range of 4–10, surface charge did not affect superstructure formation. The formation of these superstructures was suggested to be driven by entropy, optimizing space. A capillary flow mechanism was also proposed to be cause of superstructure formation.³³¹ In brief, the convex shape of the droplet on hydrophobic surfaces leads to a stronger evaporative flux. This process drives large particles to the perimeter of the droplet, resulting in hierarchical co-assembly, with small particles filling the gaps. As the solvent evaporates, ionic strength increases, and surface double layers diminish, allowing particles of any charge to come closer and assemble.³³⁰

The same research group reported the co-assembly of submicrometer-sized particles into 2D, hexagonally ordered, binary superstructures through solvent evaporation within confined spaces.³³² Various particles were dispersed in water at appropriate concentrations, ensuring uniform distribution. Specifically, SO₄-PS (1 μm or 3.1 μm) or COOH–PS (2 μm) was mixed with NH₂–PS (200 nm), and NH₂–PS (200 nm) with COOH–Si (50 nm). These mixtures were drop-cast within a rubber O-ring placed on a hydrophilic surface. The confined space provided by the O-ring allowed precise control over capillary forces, leading to the formation of highly ordered binary superstructures. Electrostatic repulsion, due to the negative zeta potentials on the particle surfaces, was essential in maintaining particle separation until entropic forces drove co-assembly, resulting in the superstructures. After drop-casting, the substrate was placed in a vacuum desiccator for solvent evaporation, resulting in the binary superstructures. The arrangement of these superstructures was determined by the size ratios of the particles. When the size ratio was less than 0.1, many small particles surrounded the hexagonally packed large particles. As the size ratio increased, fewer small particles surrounded the larger ones, until the size ratio exceeded 0.20, where only one layer of small particles surrounded the larger ones. These binary superstructures were used to create highly ordered protein and antibody patterns with precise spacing control. To do so, before co-assembly, one or both types of particles were coated with proteins such as human lysozyme (LZM) and human serum albumin (HSA) or bovine serum albumin (BSA). Antibodies were also adsorbed onto one type of particle. The spacing between proteins was finely tuned by adjusting the size ratios of the particles during co-assembly. These resulting patterns are potentially valuable for protein and cell biosensor applications.³³² These 2D, hexagonally ordered, binary superstructures also served as masks to develop chemical patterns.³³³ These masks enabled the deposition of an amino-functionalized ultrathin film via plasma polymerization. Small particles allowed plasma to reach the substrate, forming a plasma-polymer film underneath, while large particles blocked deposition, leaving those areas uncoated. The amine groups on the patterned surface were then used to covalently bond poly(ethylene glycol) propionaldehyde (PEG-PALD), resulting in a surface for selective protein adsorption. Proteins preferentially attached to regions without PEG-PALD, aligning with the nanoscale pattern. By adjusting the mask morphology and plasma-polymer deposition time, precise patterns with specific features can be created, useful for applications like cell adhesion studies, cell patterning, and biological sensing.³³³

When the suspension of colloidal particles is spread on a hydrophilic substrate within a confined area, the height of the liquid layer inside the area (h) is much greater than the diameter of the large particles (d_L), i.e., h ≫ d_L. This allows electrostatic forces and Brownian motion to maintain the colloidal stability of the particles, preventing them from aggregating. As the liquid evaporates, it does more rapidly from the center than from the edges, reducing the liquid height (h ∼ d_L) and forming a concave meniscus. The meniscus forms around the larger particles, causing a flow of particle-containing liquid, to replenish the evaporated liquid, from high-pressure regions away from the center to the low-pressure nucleated region.³³⁴ This movement is driven by convective or hydrodynamic forces.³³⁵ With continued evaporation, capillary forces overcome electrostatic barriers, bringing particles closer and leading to the nucleation of a superstructure.³³⁴ In this nucleated region, loosely packed large particles are surrounded by smaller ones. As drying progresses, the concentration of particles increases, leading to an entropy-driven phase transition. Once a critical concentration is reached, the particles begin to assemble and grow.³³⁶ The small particles assemble on the template layer of larger particles, resulting in the growth of multi-component ordered superstructures. Further evaporation stabilizes the superstructure by minimizing the free energy of the system. Therefore, the assembly within the confined area during evaporation is controlled by electrostatic forces, capillary forces, convective flow, entropic forces, and the minimization of surface energy.^{233,336–338}

In a subsequent study, this research group further explored how 2D binary ordered superstructures, prepared using evaporation within confined spaces, could influence interactions between cells and surfaces.³³⁹ A library of these superstructures was generated by systematically screening 24 different colloidal particles, including 11 large particles (≥1 μm) and 13 submicrometer-sized particles (<1 μm), made of PS, silica and PMMA. These particles ranged in size from 24 nm to 5 μm and had various surface functionalities, including unmodified, hydroxyl-, carboxylic acid-, amine-, and sulphate-modified. This screening produced 143 binary combinations, with at least 44 forming high-quality 2D binary ordered superstructures, particularly when the size ratios were between 0.02 and 0.1. Formation of these superstructures required both particles to be negatively charged, with zeta potentials below −30 mV. The particle density determined whether the superstructures formed first in 3D and then transitioned to 2D, or directly as a 2D array. For example, large silica particles mixed with smaller polymer particles formed a loosely packed 2D layer initially, with the smaller particles filling in gaps to create a close-packed 2D superstructure. Conversely, when two polymer particles were mixed, 3D superstructures formed in suspension and later settled to create 2D superstructures on the surface. In this case, the 2D superstructures were randomly distributed on the surface, leading to lower surface coverage. In contrast, mixing large polymer particles with small silica particles did not result in 2D binary ordered superstructures due to early sedimentation of the small particles. Hydrophilic surfaces, with a water contact angle below 20°, were found to be more effective for particle assembly, leading to larger areas of 2D binary ordered superstructures. These 2D superstructures were tested with three cell types: L929 fibroblasts, MG63 osteoblasts, and primary human adipose-derived mesenchymal stem cells (hADSCs). The cells responded differently to the superstructured surfaces compared to flat controls, with cell spreading generally inhibited on the superstructures due to their topography. However, the chemical compositions of the superstructures could modify this effect, depending on the specific particle combinations used. Therefore, the surface properties, influenced by both topography and chemical composition, show potential for controlling biointerface interactions.³³⁹

Velikov et al. demonstrated the preparation of binary colloidal crystals by sequentially drying colloidal solutions layer-by-layer on a vertical substrate.³³⁷ The process began with a layer of silica spheres (406 nm) forming a 2D hcp structure on a glass surface. This layer served as a template for small spherical particles—silica (220 or 202 nm) or PS (194 nm)—with size ratios of 0.54, 0.50, and 0.48, respectively. During drying, the arrangement of the small particles was influenced by their volume fraction (ϕ), size, and the arrangement of the first large-particle layer (Fig. 33). When the volume fraction was high (ϕ₄), the small particles formed a second hexagonal layer on top of the large particles. Though this second layer was not perfectly flat, the size ratio near 0.5 enabled it to adopt a hexagonal arrangement. For example, a complete close-packed layer of small particles on top of the large ones was achieved with a size ratio of 0.54 and a volume fraction of 4.3 × 10⁻⁴. Similarly, with a size ratio of 0.48 and a volume fraction of 4.1 × 10⁻⁴, the small particles completely covered the large particles. At a lower volume fraction (ϕ₃) the second layer could not completely cover the first, causing the protruded particles to detach first. For instance, at a size ratio of 0.48 and a volume fraction of 2.1 × 10⁻⁴, three small particles filled the gaps between large spheres, forming a triangular arrangement and creating an open kagomé lattice structure. This lattice coexisted with either the LS₂ structure or a full layer of small particles. Adding a second layer of large particles led to the formation of an LS₃ binary colloidal crystal. It should be mentioned that LS₃ arrangement was not achieved at a size ratio of 0.54. At an even lower volume fraction (ϕ₂), fewer particles were present at the drying front. For example, at a size ratio of 0.54 and a volume fraction of 2.1 × 10⁻⁴, the smaller particles formed a hexagonal but more open packing, filling the hexagonal gaps created by the first layer of large particles. The next layer of large particles was deposited directly on top of the first layer, forming LS₂ binary colloidal crystals. Repeating this layer-by-layer deposition produced an LS₂ binary colloidal crystal with the desired thickness. The transition from ϕ₃ to ϕ₂ was subtle, often resulting in LS₃ structures coexisting with LS₂ and defects in the transition zone. At ϕ₁, with even fewer particles, the smallest particles filled the lowest points in the drying film, creating the LS structure. Although the small particles did not touch, they maintained a long-range hexagonal arrangement. The next layer of large particles could stack directly above the first layer (AA stacking) or in the gaps left by the small particles in the initial hexagonal layer (AB stacking). At a size ratio of 0.48, AB stacking was preferred, though this preference might diminish at higher size ratio values. In the fourth layer of small particles, no specific alignment relative to the second layer was observed, adding uncertainty to the final 3D structure. To produce non-close-packed crystals, an LS₂ binary crystal composed of alternating layers of inorganic silica and organic PS particles was first formed. Afterward, the organic layer was removed by heating. This process resulted in a hexagonal non-close-packed (hncp) crystal with a low packing fraction (0.60) compared to a close-packed structure (0.74).³³⁷

Fig. 33 Schematic illustration of the arrangement of small spheres onto a hexagonal layer of large spheres (γ ≈ 0.5), depending on the volume fraction. Adapted with permission from ref. 337. Copyright 2002 The American Association for the Advancement of Science.

In vertical deposition, the solution wets the substrate, forming a meniscus.³⁴⁰ As the solvent evaporates from the meniscus, capillary flow (Marangoni flow) transports colloidal particles from the suspension to the meniscus. There, interparticle capillary forces drive the co-assembly of these particles into close-packed structures. The success of this process relies on having an optimal evaporation rate and a uniform particle distribution in the suspension. A challenge in co-assembling colloidal particles of different sizes through vertical deposition is that the small particles can jam the spaces between the large particles. This blockage disrupts liquid flow before the particles reach the meniscus, reducing capillary flow and leading to disordered structures. This prevents the colloids from settling into their optimal positions, leading to disordered structures. The problem worsens with increasing size differences between the particles.

Zheng et al. developed an infrared (IR)-assisted vertical deposition method to improve the co-assembly of colloidal particles of different sizes.³⁴⁰ The IR-assisted method irradiates the meniscus with a characteristic infrared light while simultaneously controlling the temperature and vapor pressure. This IR irradiation regulates the local evaporation rate without affecting the overall environment, enhancing capillary flow. As a result, the jamming effect is mitigated, allowing for smoother particle transport and more ordered assembly.

Kitaev et al. introduced a modification to the evaporation process on vertical substrates.³⁴¹ They prepared binary ordered superstructures through confined convective vertical deposition co-assembly of monodisperse spherical colloidal particles. In their process, large PS (1.28 μm) and small PS or silica particles (from 145 to 290 nm) were dispersed in anhydrous ethanol. All particles carried a negative charge, causing them to repel each other in solution, which prevented self-assembly or aggregation at the low concentrations used. Glass slides served as substrates, placed vertically in the dispersion of spheres. A challenge in the vertical deposition approach is the sedimentation of colloids, which typically restricts the size of spheres to 450–500 nm for silica and 1–1.1 μm for PS.³⁴² This limitation was overcome by using low pressure to accelerate ethanol evaporation, allowing it to counteract sedimentation. As ethanol evaporated under low pressure, convective mass flow and capillary forces drove the co-assembly of the spheres at the air–ethanol–glass interface.^159,342,343 This process resulted in an ordered hcp monolayer of large PS spheres, with small spheres forming regular arrays in the cavities between them. The arrangement of small spheres was found to depend on the size ratio and the concentration of small spheres. At low concentration of small spheres, different ordered superstructures formed, depending on the size ratio. For example, at a size ratio of 0.225, small spheres mainly formed triangular triplets, while at a size ratio of 0.20, both triangular triplets and some tetrahedral clusters appeared. When the size ratio reached 0.175, small spheres exclusively formed tetrahedral clusters. As the concentration of small spheres increased, at a size ratio of 0.225, more small spheres began to cover the large ones. At a size ratio of 0.20, the small spheres packed more densely around the large ones, although the arrangement was irregular. At a size ratio of 0.175, the small spheres filled the channels between the tetrahedral clusters. At a size ratio of around 0.16, small spheres formed hexagonal septuplets at the spaces between large particles. Increasing the concentration of small spheres caused more small spheres to fill the bridging channels, forming close-packed doublet lines, but the resulting binary lattice remained disordered.^337,342 For size ratio values above 0.225, small spheres did not organize well in the interstitial sites, and only local ordering was observed at a size ratio of 0.26. When the size ratio exceeded 0.3, the small spheres disrupted the packing of large spheres, leading to completely disordered superstructures.³⁴¹

Mun Ho Kim et al. modified the confined convective vertical deposition co-assembly by controlling the position of the substrates.^344,345 In brief, an aqueous solution containing 460 nm PS colloidal particles was placed between two glass substrates. Capillary forces held the colloidal suspension in place within this gap. The back glass substrate was connected to a dipping machine to control its lifting speed, while the front substrate remained stationary. As the back substrate was lifted, hot air was directed at the meniscus formed between the glass and the suspension, evaporating the water and causing the particles to assemble into a monolayer on the back substrate. This arrangement was driven by capillary forces acting on the particles as they protruded through the drying meniscus. The procedure was repeated with aqueous suspensions of small PS colloidal particles (260, 230, 180, or 140 nm). The back substrate, now coated with the particle monolayer, was reattached to the dipping machine, and the suspension containing small particles was added to the gap. As the back substrate was lifted again with hot air directed at the meniscus, the small particles were deposited onto the existing monolayer. Therefore, the monolayer of large colloidal particles served as a template for precisely localizing the small particles. By adjusting the size ratio of the particles and the concentration of the small particles, LS₂, LS₃, LS₄ or LS₅ binary ordered superstructures were prepared. When PS particles with a diameter of 260 nm (γ = 0.57) were used as small particles, binary ordered superstructures with LS₂ stoichiometry formed. In this superstructure, each small particle settled into the gaps between the hcp large particles. When smaller particles, 230 nm in diameter (γ = 0.5), were used, two types of binary ordered superstructures formed depending on the concentration of small particles in the suspension. At a concentration of about 0.12 wt%, each gap in the large particle template was filled by one small particle, forming a binary ordered superstructure with LS₂ stoichiometry. At a higher concentration of approximately 0.16 wt%, three small particles occupied each gap connecting with each other, forming a binary ordered superstructure with LS₃ stoichiometry, When PS particles with a diameter of 180 nm (γ = 0.39) were deposited on the large particle template, a different arrangement emerged. One small particle settled in the gaps of the large particles, with a periodic vacancy similar to the LS superstructure, and an additional group of three small particles were embedded in this vacancy, resulting in a binary ordered superstructure with LS₄ stoichiometry. For even smaller particles with a diameter of 140 nm (γ = 0.39), a binary ordered superstructure with LS₅ stoichiometry was formed. In this case, one small particle occupied a gap in the large particle template, similar to the LS₂ superstructure, while additional small particles filled the gaps formed between two small and two large particles.³⁴⁴

The meniscus shape was found to determine whether a mono- or a multilayer colloidal superstructure formed.^345,346 A steep meniscus favored monolayer formation, while a gentler slope resulted in multilayer formation. This meniscus shape was influenced by the lifting speed of the substrate. A slow lifting speed led to multilayers, while a fast speed produced a monolayer or sparser superstructures. The concentration of colloidal suspensions also played a role; higher concentrations required a faster lifting speed to achieve a monolayer. Additionally, the rate of water evaporation, controlled by blowing hot air, affected the superstructure. Hot air accelerated evaporation, leading to an ordered monolayer of colloidal crystals. Without hot air, slower evaporation resulted in sparser superstructures due to fewer particles assembling at the meniscus.³⁴⁵

6.2.1.1. Anisotropic submicrometer-sized particles. Anisotropic submicrometer-sized colloidal particles can also co-assemble into multi-component superstructures by solvent destabilization (Table S4, ESI†). For example, Adams et al. reported the co-assembly of rod-like and sphere-like particles within rectangular glass capillaries.³⁴⁷ Polyethylene oxide (PEO), polyethylene glycol (PEG) or PS spheres were added to water suspensions of the filamentous fd virus (6.6 nm diameter, 880 nm contour length, and 2.2 μm persistence length). The fd virus was either in the isotropic or nematic phase. When 100 nm PS spheres were introduced into a dilute fd nematic sample, they assembled into columns about 300 nm in diameter and up to 5 μm long. These columns were oriented perpendicular to the virus rods and formed a 2D lattice, with columns spaced two rod lengths apart, without disrupting the alignment of the rods. This structure was termed “columnar” phase. As more spheres were added, the columns became smaller in diameter, and the spheres began to fill the space between columns. At even higher concentrations, the columns disappeared, resulting in a “lamellar” phase, where alternating layers of rods and spheres formed. Both the lamellar and columnar phases were found to be equilibrium structures. PS spheres larger than 250 nm did not form the lamellar phase. When 300 nm PS spheres were added at low concentrations, they grouped into chain-like structures. At higher concentrations, the spheres arranged into a cubic array with a lattice spacing equal to the length of one fd rod.³⁴⁷ These co-assemblies, driven by entropy, were consistent with previous theories and simulations.³⁴⁸

Recently, Meng et al. demonstrated the co-assembly of polyhedral metal–organic framework (MOF) particles into binary superstructures.³⁴⁹ They reported the formation of 2D LS₂ superstructures, where large PS spheres (600 nm) formed hcp monolayers, with cubic ZIF-8 particles (135 or 196 nm in edge length) filling the gaps between them. This arrangement was achieved by solvent evaporation of aqueous dispersions containing both oppositely charged ZIF-8 and PS particles. Using a similar approach, they co-assembled cubic ZIF-8 particles (196 nm) with shape-complementary, oppositely charged, truncated rhombic dodecahedral ZIF-8 particles (414 nm, with a truncation of 0.68) into NaCl-type superstructures. Although both types of ZIF-8 particles initially had a positive surface charge, the truncated rhombic dodecahedral particles were functionalized with Pluronic F127-COOH, imparting a negative surface charge that enabled their orderly assembly.³⁴⁹ Wu et al. have also used MOF particles as building blocks to prepare 2D binary superstructures via air–liquid co-assembly.³⁵⁰ To enable dispersion in nonpolar solvents and ensure colloidal stability, the MOF particles were hydrophobized using oleyl phosphate (OP) ligands. Spherical MOF-801 particles (∼120 nm) co-assembled with either truncated octahedral MOF-801 particles (∼40 nm) or octahedral UiO-66-NH₂ particles (∼35 nm) into LS₂-type binary superstructures. Similar LS₂-type superstructures were also obtained by co-assembling MOF-801 particles (∼100 nm) with NaYF₄ nanocrystals (∼32 nm). Additionally, LS-type binary superstructures were achieved by co-assembling MOF-801 particles (∼40 nm) with Fe₃O₄ nanocrystals (∼21 nm). The transition from LS₂- to LS-type arrangements was attributed to the higher packing density of the latter at γ ≈ 0.53.³⁵⁰

6.2.1.2. Ternary and quaternary superstructures. Ternary and quaternary superstructures have also been prepared by co-assembly of submicrometer-sized colloidal particles through solvent destabilization (Table S5, ESI†). In an early example, Wang et al. prepared ternary colloidal superstructures through vertical lifting deposition on glass substrates at a controlled speed.³⁵¹ The large, medium and small particles used were PS microspheres, PMMA nanospheres and silica particles with diameters of 465, 84 and 6 nm, respectively. The size ratios were γ_M/L = d_Medium/d_Large = 0.18 and γ_S/M = d_Small/d_Medium = 0.071. In the superstructures, the large PS particles formed a fcc structure, the medium PMMA particles filled the interstitial spaces, and the small silica particles filled the remaining voids. The co-assembly of the particles was driven by capillary forces and liquid flux. After pyrolysis of the PS and PMMA particles, a granular silica matrix remained, which could be described as a binary inverse opal with meso- and macroporosity. Vis-NIR spectroscopy confirmed the highly ordered crystal superstructures.³⁵¹

The co-assembly of submicrometer colloidal particles into multi-component superstructures has also been successfully achieved through solvent evaporation in confined spaces. Singh et al. used evaporation-induced layer-by-layer assembly on hydrophilic surfaces to create multi-component ordered superstructures composed of up to four different types of functionalized PS and silica particles (Fig. 34).^352,353 This technique allows for the preparation of large-area, highly ordered 2D and 3D superstructures with a controlled number of layers, using particles of different sizes. The multi-component superstructures were formed by using binary superstructures as templates, with a third type of particle filling the gaps according to the space-filling principle. Therefore, the formation of multi-component superstructures followed similar principles to binary ones, with larger particles guiding the assembly of smaller ones. For example, in ternary superstructures composed of 50 nm COOH–Si, 200 nm NH₂–PS and 2 μm COOH–PS (γ_S/M = 0.25, γ_M/L = 0.10), and 50 nm COOH–Si, 200 nm NH₂–PS and 3.1 μm SO₄-PS (γ_S/M = 0.25, γ_M/L = 0.064), the arrangement resembled binary superstructures with γ = 0.10 and γ = 0.064. Similarly, quaternary ordered superstructures formed when the smallest nanoparticles filled interstitial sites generated by three larger particles. For example, in a superstructure with 5 μm plain Si, 50 nm COOH–Si, 200 nm NH₂–PS and 1 μm plain Si, the 5 μm particles were surrounded by a ring of 50 nm, 200 nm, and 1 μm particles, with each size progressively surrounding the next.³⁵³

Fig. 34 Schematic illustration of the formation of ordered colloidal superstructures through confined-area evaporation-induced layer-by-layer assembly. (a) A suspension of large colloidal particles is placed inside the rubber ring. (b) As the liquid evaporates, a concave meniscus forms, creating capillary forces that bring the particles together, initiating crystal nucleation. (c) After complete evaporation, a monolayer of large colloidal particles is formed. (d) A second suspension of small particles is added inside the rubber ring. (e) Upon evaporation, the small particles settle in the gaps of the hexagonal pattern formed by the large particles, creating a binary colloidal superstructure. (f) A third suspension is added, leading to the formation of a ternary colloidal superstructure after evaporation. Adapted with permission from ref. 352. Copyright 2011 John Wiley and Sons.

6.2.2. Co-assembly of submicrometer-sized particles at the air–liquid interface. Submicrometer-sized particles have also been co-assembled into ordered binary superstructures at air–liquid interfaces (Table S4, ESI†). For example, monodisperse PS spheres of different sizes have been co-assembled into binary colloidal monolayers at an air–water interface (Fig. 35).³⁵⁴ When a mixture of PS sphere suspended in 1 : 1 water–ethanol solution was injected onto a water film, the spheres initially sank into the water. Ethanol rapidly diffused and evaporated, generating convective flow. This flow carried both large and small PS spheres to the water surface. Once at the surface, the PS spheres remained afloat due to their hydrophobic nature and the surface tension of the water.³⁵⁵ Capillary forces between adjacent spheres caused them to co-assemble into colloidal crystals.^189,356 As the large and small spheres spread uniformly on the water surface, the large spheres formed an hcp structure, while the small spheres settled into the gaps. The large spheres provided two sites for the smaller ones: 3-fold voids among three adjacent large spheres (site 1) and bridge sites connecting these voids (site 2). To minimize energy, the small spheres arranged themselves in a regular pattern, preferring to occupy the 3-fold voids first and then the bridge sites, rather than moving freely.^357–359 Binary colloidal monolayers with various arrangements were prepared by precisely controlling the size ratio and volume ratio of the particles. For example, when the size ratio was 0.175 (with particle sizes of 350 nm and 2 μm) and volume ratio was 0.048, the resulting crystal formed an LS₉ pattern. With the same size ratio of 0.175, varying volume ratio to 0.032, 0.064, and 0.091 led to the formation of crystals with LS₆, LS₁₂, and LS₁₇ patterns, respectively. When the size ratio was reduced to 0.1 (200 nm and 2 μm particles), volume ratio values of 0.020 and 0.026 produced crystals with LS₂₀ and LS₂₆ patterns, respectively. At specific volume ratio values, mixed-phase structures appeared. For example, with a size ratio of 0.175 and volume ratio of 0.056, a combination of LS₉ and LS₁₂ phases was observed. A number ratio of small-to-large spheres of 20 at a size ratio of 0.175 produced an unstable structure, but stability was achieved at a number ratio of 17, corresponding to the LS₁₇ pattern. Increasing the size ratio to 0.25 lowered the maximum stable number ratio to 6, corresponding to the LS₆ pattern.³⁵⁴

Fig. 35 (a) Schematic of the preparation of 2D binary colloidal crystals at the air–liquid interface. (b) Photograph and (c) and (d) SEM images of the binary colloidal crystal prepared by ethanol-assisted co-assembly with a size ratio of 0.175 (particle sizes of 350 nm and 2 μm) and volume ratio of 0.048. Inset: Magnified image of (c), showing the LS₉ pattern. (e)–(g) SEM images of the binary colloidal crystal prepared by ethanol-assisted co-assembly with a size ratio of 0.175 (particle sizes of 350 nm and 2 μm) and volume ratio of 0.032, 0.064, and 0.09, respectively. (h) and (i) SEM images of the binary colloidal crystal prepared by ethanol-assisted co-assembly with a size ratio of 0.1 (particle sizes of 200 nm and 2 μm) and volume ratio of 0.02 and 0.027, respectively. (j) SEM image of the binary colloidal crystal prepared by ethanol-assisted co-assembly with a size ratio of 0.25 (particle sizes of 500 nm and 2 μm) and volume ratio of 0.094, respectively. Adapted with permission from ref. 354. Copyright 2012 American Chemical Society.

With some modifications from the previous study, Yu et al. also co-assembled PS nanospheres into 2D binary colloidal crystals at the air–water interface (Fig. 36).³⁶⁰ In brief, ethanolic colloidal suspensions of PS nanospheres, of two different sizes, were dropped onto hydrophilic glass slides surrounded by water containing the sodium dodecyl sulfate (SDS) surfactant. The ethanolic colloidal suspensions spread across the glass slide, reaching the edges and contacting the surrounding water. This caused the PS nanospheres to spread onto the water surface and assembled into organized arrays due to attractive capillary forces and repulsive electrostatic forces.^189,361 The large spheres assembled into ordered arrays, while the small spheres settled into the spaces between them, forming a monolayer of binary colloidal crystals. The small spheres could occupy either the 3-fold voids formed by three neighboring large spheres or the channels between two large spheres. The resulting binary crystal structure depended on the size ratio and the number ratio of the two PS nanospheres. For example, when 130 nm small spheres and 887 nm large spheres (γ = 0.147) were co-assembled at a number ratio of 2, they formed an LS₂ binary colloidal crystal, where each 3-fold void was occupied by a single small sphere. Increasing the number ratio to 4 led to three small spheres filling each void, surrounding each large sphere with about six small spheres, resulting in an LS₆ binary colloidal crystal. At a number ratio of 8, more small spheres filled both the voids and channels, and at number ratio of 12, the spheres remained highly ordered, but with tighter packing. When 173 nm small spheres and 887 nm large spheres (γ = 0.195) were co-assembled, they also formed binary colloidal crystals with different structures depending on the concentration of small spheres. At a number ratio of 12, the system formed a disordered structure, unlike the ordered arrangement observed with a smaller size ratio (γ = 0.147). This indicates that for a given size ratio, when the number of small spheres exceeds a certain threshold, they can no longer fit into the available spaces around the large spheres, leading to disorder.³⁶⁰

Fig. 36 SEM images of binary colloidal crystals of PS nanospheres: (a) a size ratio of 0.147, a number ratio of 2; (b) a size ratio of 0.147, number ratio of 4; (c) a size ratio of 0.147, a number ratio of 8; (d) a size ratio of 0.147, a number ratio of 12; (e) a size ratio of 0.195, a number ratio of 2; (f) a size ratio of 0.195, a number ratio of 4; (g) a size ratio of 0.195, a number ratio of 8; and (h) a size ratio of 0.195, a number ratio of 12. The insets are the corresponding 2D FFT images. Adapted with permission from ref. 360. Copyright 2010 American Chemical Society.

PS-based binary colloidal monolayers have also been prepared at the air–water interface using the Langmuir–Blodgett technique.³²⁹ First, colloidal particles were deposited on the air–water interface. After the particles settled and the system reached equilibrium, the floating layer was compressed to form the monolayer. The water beneath the monolayer was then drained, transferring the formed monolayer onto a substrate placed below the interface. PS particles with a diameter of 1.063 μm were co-assembled with small PS particles—either 202 nm (γ = 0.19) or 225 nm (γ = 0.21)—to form binary colloidal monolayers. The ratio of small to large particles was set to 2, 6, and 9, resulting in structures with LS₂, LS₆, and LS₉ stoichiometries, respectively. In these assemblies, the large particles formed a close-packed hexagonal layer, while the small particles occupied the interstitial spaces. When the small PS particles were 303 nm in diameter (γ = 0.29), they were too large to form the LS₉ structure. Therefore, a particle ratio higher than 6 led to a loss of order in the monolayers. When the small PS particles were 336 nm (γ = 0.32), they became too large to fit into the LS₆ structure. Adding more small particles disrupted the structure, leading to an amorphous arrangement. Further increasing the size of the small particles to 408 nm (γ = 0.40) introduced significant disorder, as the small particles interfered with the arrangement of the large ones. Although the overall monolayer became disordered, some small co-assembled regions with lower symmetry appeared, where the small particles in the interstitial sites formed touching dimers. The pH of the subphase played an important role in the co-assembly process.^362,363 As the particles were functionalized with carboxylic acids, an increase in pH led to greater deprotonation, resulting in a higher charge density on their surfaces. This increased electrostatic repulsion enhanced the long-range order of the monolayers by counteracting attractive van der Waals and capillary forces.³⁶² As a result, the particles had more time to reach energetically favorable positions.³⁶⁴ Moreover, the higher charge density increased the hydrophilicity of the particles, causing large particles to sink deeper into the water subphase and creating a larger interstitial volume at the interface. Additionally, the contact angle of the particles at the air–water interface could be adjusted by changing the pH. A decrease in the contact angle (or increased particle immersion in the water subphase) increased the volume of interstitial spaces at the air–water interface. The resulting binary colloidal monolayers were utilized as evaporation masks to produce Au nanostructure arrays through colloidal lithography.³²⁹

The co-assembly of PS particles into binary colloidal monolayers has also been achieved at the air–water interface within a confined area (Fig. 37).³⁶⁵ These crystals formed three different patterns based on the ratio of small-to-large nanoparticles: LS₂, with one small nanoparticle in each interstice; LS₃, with three small nanoparticles per interstice; and LS₇, which alternated between three and four nanoparticles in the six interstices. To achieve these crystals, aqueous suspensions containing particles of 200 and 1 μm in diameter (γ = 0.2) were mixed at different ratios and combined with ethanol. This mixture was then added to the air–water interface within a confined ring. The particles were left to assemble at the interface. To promote orderly crystallization, a suitable amount of surfactant (SDS) was added to the water bath. The resulting binary colloidal monolayers were transferred onto substrates by draining the water from the glass container.³⁶⁵

Fig. 37 (a) Schematic illustration of co-assembling at the air–water interface by surface confinement and water discharge: (i) sample placement and water filling, (ii) particle addition and co-assembly, and (iii) monolayer transfer to a substrate as the water is discharged. SEM images of binary colloidal monolayers of PS particles (γ = 0.2, 200 and 1 μm in diameter): (b) LS₂ stoichiometry, (c) LS₆ stoichiometry, and (d) LS₇ stoichiometry. Scale bar: 2 μm. Adapted with permission from ref. 365. Copyright 2016 American Chemical Society.

6.2.3. Electrostatic co-assembly of submicrometer-sized particles. Electrostatic interactions among submicrometer-sized particles have also been used to direct their co-assembly into ordered superstructures (Table S4, ESI†). Leunissen et al. showed that electrostatic interactions between oppositely charged submicrometer-sized particles can be tuned to promote the formation of ionic colloidal crystals.¹⁹⁶ In their study, PMMA colloidal particles were dispersed in a solution of cyclohexyl bromide and cis-decalin. By adding the tetrabutylammonium bromide (TBAB) salt, the particle charges were adjusted, even reversing them from positive to negative at moderate salt concentrations, which allowed precise tuning of the electrostatic interactions.²²⁸ Individual suspensions of fluorescently labeled spherical particles were left to equilibrate for several hours before being mixed. When combined, particles with opposite charges formed binary colloidal systems. Suspensions of positively charged PMMA particles (2.16 μm) and negatively charged PMMA particles (1.98 μm, γ = 0.92) formed CsCl-type superstructures when the particle number ratio was 1 : 1; the total volume fraction was about 0.12 and the suspensions contained around 60 μM TBAB. The positive and negative particles carried charges of Z₁ = +110 and Z₂ = −75, respectively. At much higher particle charges, only irreversible aggregation was observed. When the total volume fraction reached approximately 0.30 and the mixture contained around 190 μM TBAB, a close-packed lattice formed with randomly distributed positive and negative particles. This structure, known as a ‘solid solution’, had a lattice spacing about 6% larger than the densest possible packing (with a packing fraction of 0.74). It was suggested that this structure, predicted in simulations,³⁶⁶ was caused by lower particle charges. Suspensions of positively charged PMMA particles (1.16 μm) and negatively charged silica particles (1.04 μm, γ = 0.90) formed CsCl-type superstructures when the total volume fraction was 0.13–0.20, with the suspensions containing about 160 μM TBAB. Despite the density difference between PMMA (∼1.2 g cm⁻³) and silica (∼2.0 g cm⁻³), the electrostatic attractions were strong enough to counterbalance the effects of sedimentation. It has been shown that PMMA can be burned away from colloidal crystals, maintaining silica spheres.³³⁷ This method allows the transformation of CsCl-type crystals into a simple cubic lattice. Colloidal crystals with an LS₆ stoichiometry were formed by decreasing the size ratio between large negatively charged PMMA spheres (2.32 μm) and small positively charged PMMA spheres (720 nm, γ = 0.31). The particle number ratio was set at 1 : 8 (large-to-small), with a total volume fraction of approximately 0.11, and the suspensions contained about 120 μM TBAB. The resulting structure exhibited a face-centered orthorhombic lattice formed by large spheres. Each tetrahedral hole was filled with a small sphere, and each octahedral hole contained four small spheres. These colloidal crystals closely resembled the crystal structures found in certain alkali-metal intercalation compounds of fullerene C₆₀, which share the same stoichiometry. At a slightly lower ionic strength, an LS₈ structure was observed. In this arrangement, each large colloid was surrounded by six small spheres, which filled the triangular gaps in the hexagonal planes. Above and below this ‘mixed’ layer, the small spheres formed planes arranged in a Kagomé pattern. When the particle number ratio was set to 1 : 8, with a total volume fraction of approximately 0.23, and no TBAB salt was added, two different colloidal crystal structures with LS stoichiometry were observed to coexist: NaCl- and NiAs-type. In these ionic systems, the potential energy is strongly influenced by Coulomb interactions.¹⁹⁶

Bartlett reported the co-assembly of oppositely charged colloidal microspheres into colloidal crystals.³⁶⁷ PMMA particles, with diameters of 777 nm and 720 nm (γ = 0.93), were suspended in a mixture of cycloheptyl bromide and cis-decalin. The large particles were dyed with the orange–red fluorescent dye DiIC₁₈, while the small ones were labeled with the green fluorescent dye DiOC₁₈. In the low-polarity solvent, PMMA particles gained a slight positive surface charge. The DiIC₁₈-tagged particles, being more polar, acquired a higher charge than the DiOC₁₈-labeled particles. By adjusting the concentration of Br⁻ ions in the solution, the charge of the particles could be tuned. At low or high Br⁻ concentrations, both types of particles carried the same charge, either positive or negative, and repulsive interactions dominated, leading to a behavior modeled by hard-sphere interactions. However, at intermediate Br⁻ concentrations, the two types of particles carried opposite charges, resulting in attractive interactions. Introducing a small piece of ferromagnetic wire into the suspensions further induced partial charge inversion. At low particle concentrations (volume fraction), these suspensions behaved like fluids. When the volume fraction exceeded 0.494, the particles crystallized into a random hexagonal close-packed (rhcp) structure. Crystallization occurred until the volume fraction reached about 0.58, at which point a glass transition happened, preventing further nucleation and growth. In this range of 0.494 < volume fraction < 0.58, three distinct ordered structures emerged depending on particle charge. Weakly charged particles formed a twelve-fold coordinated substitutionally disordered rhcp lattice (Fig. 38a). As the opposite charges on the particles increased, they organized into CsCl-type superstructures (Fig. 38b). Further increases in particle charge resulted in the formation of NaCl-type superstructures (Fig. 38c). These co-assemblies resulted from a balance between entropy, which drives the formation of close-packed structures, and electrostatic forces, which favor the formation of more open, non-close-packed arrangements.³⁶⁷

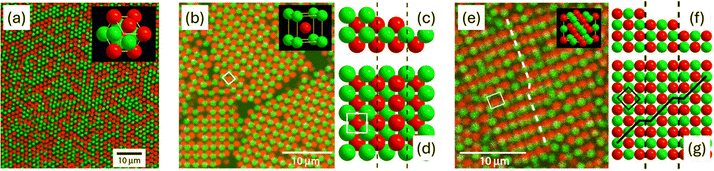Fig. 38 (a) Confocal image of a substitutionally-disordered rhcp crystal formed in a suspension with a volume fraction of 0.507. Inset: an fcc unit cell. (b) Confocal image of the CsCl-type superstructure formed in suspension with a volume fraction of 0.528. Inset: CsCl unit cell. (c) and (d) Crystallographic model of the CsCl-type superstructure. (e) Confocal image of the NaCl-type superstructure formed in suspension with a volume fraction of 0.528. Inset: NaCl unit cell. (f) and (g) Crystallographic model of the NaCl-type superstructure. Adapted with permission from ref. 367. Copyright 2005 American Physical Society.

Hueckel et al. developed a method, referred to as polymer-attenuated coulombic self-assembly, to grow ionic binary colloidal crystals by using the surface charge of particles in water.³⁶⁸ The attraction between these charged particles was driven by the interaction of their surrounding electrical double layers—clouds of oppositely charged ions. The strength of this electrostatic attraction depended on the Debye screening length (λ_D) and the distance between particles, which was determined by the thickness of a polymer spacer (L). Therefore, the polymer brush played two roles: maintaining particles at precise distances and controlling the overlap of their electrical double layers. When λ_D was much smaller than L, the polymer brush prevented the double layers from overlapping, eliminating electrostatic attraction and stabilizing the particles sterically. When λ_D was much larger than L, the polymer brush had little effect, allowing full overlap of the double layers and leading to particle aggregation. When λ_D and L were similar, the repulsion from the polymer brush balanced the electrostatic attraction, resulting in stable ionic bonding between the particles. Various oppositely charged particles, including silica, 3-(trimethoxysilyl) propyl methacrylate (TPM) and PS, ranging from 200 nm to 2 μm, were tested to explore this co-assembly approach. The particles were first coated with polymers, then equilibrated in NaCl solutions and finally mixed in water. Left undisturbed, the particles formed binary colloidal crystals. It should be noted that there was a narrow range of salt concentrations where the particles behaved like ions, co-assembling into ordered ionic solids. Polymers with different brush lengths—F108, F127, F68, and F38 (from longest to shortest)—were tested, with shorter polymers requiring higher salt concentrations to reduce λ_D and mimic the co-assembly behavior of longer polymers. F38, the shortest polymer, could not form colloidal crystals, likely due to weak surface attachment. Once the particles were co-assembled into binary colloidal crystals, the removal of salt through dilution or dialysis fixed their structure, allowing the crystals to retain their order when handled in solution or dried. This process was irreversible, with the crystals remaining intact even if the salt was reintroduced, suggesting strong van der Waals interactions. The pH of the mixture significantly affected the charge of the particles and their co-assembly. As pH shifted from neutral, particles lost charge—positive ones under basic conditions and negative ones under acidic conditions. This weakened electrostatic attraction leads to disassembly of the colloidal crystals. However, increasing λ_D could maintain crystallization even with reduced electrostatic forces. Using the polymer-attenuated coulombic self-assembly method, different binary superstructures formed depending on the size ratio of the particles. CsCl-type superstructures appeared when the size ratio ranged from 0.95 to 0.81, AlB₂-type formed at a ratio of 0.61, K₄C₆₀-type at 0.53, and NaCl-type at 0.47. Besides forming through homogeneous nucleation in bulk suspensions, binary colloidal crystals were also co-assembled via heterogeneous nucleation on charged substrates. This approach enabled control over the crystal growth direction, allowing the crystals to grow with specific shapes.³⁶⁸

6.2.4. DNA-guided co-assembly of submicrometer-sized particles. DNA ligands have also been reported to direct the assembly of isotropic and anisotropic submicrometer-sized particles (Table S4, ESI†). For example, DNA-functionalized Au triangular bipyramids (∼250 nm long edge and 177 nm short edge) have been reported to self-assemble into superstructures with clathrate-like structures.²⁸⁸ The use of long, flexible DNA strands was crucial in minimizing strain during the assembly process. It should be noted that when the DNA coating on colloidal particles is much thinner than the particles themselves, they tend to form random aggregates.

Wang and Wang et al. reported the co-assembly of micrometer-sized DNA-coated colloids.²⁵⁷ First, micrometer-sized colloidal PS, PMMA, silica, and TPM particles were coated with ssDNA. The ssDNA featured a 61-base poly-T sequence, which served as a flexible spacer, and a short sticky end at the 3’ terminus to enable specific binding through DNA hybridization. The DNA was covalently grafted to the particle surfaces at the 5’ terminus using a strain-promoted alkyne-azide cycloaddition reaction.³⁶⁹ The method significantly increased the DNA coverage on the particles, up to an order of magnitude higher than that previously reported.^370–372 Different sets of DNA-functionalized particles were created, varying in size and sticky ends. Particles with a 4-base GCAG sticky end and green Cy3 dye were labelled ‘A’. Particles with a complementary 4-base CTGC sticky end and a red Cy5 dye were labeled ‘B’. Particles with a self-complementary 4-base CGCG sticky end and a red Cy5 dye were labeled ‘P’. Then, the DNA-coated particles underwent assembly and disassembly processes when cooled below and heated above a specific melting temperature (T_m). For example, 1.0 μm P particles (T_m = 46.5 °C) spontaneously nucleated within 5 minutes and grew within 60 minutes after being cooled from above T_m to 45 °C. Different types of superstructures formed depending on the size ratio between the particles. When 1.0 μm A and 1.0 μm B particles (γ = ∼1) co-assembled, CsCl-type superstructures were formed. With 1.0 μm A and 540 nm B particles (γ = ∼0.54), AlB₂-type superstructures emerged. When 1.5 μm A and 540 nm B particles (γ = ∼0.36) were combined, bcc-LS₆-type superstructures appeared.²⁵⁷ These structures were consistent with those observed in systems with similar size ratios, such as oppositely charged spheres^194,196,255 and dsDNA-coated Au nanoparticles, where the DNA strand is comparable in length to the nanoparticle diameters.²⁵⁶

The assembly of micrometer-sized colloids allowed real-time observation of co-assembly kinetics through optical microscopy.²⁵⁷ The kinetics of different superstructures followed a similar temperature-dependent trend but progressed at different rates. In the lowest quenches, co-assembly proceeded via nucleation and growth. As the quench depth increased, the process remained similar but accelerated due to a faster nucleation rate. This aligns with classical nucleation theory, where both the free energy barrier and critical nucleus size decrease with deeper quenches.³⁷³ While nuclei formed more quickly, crystal growth was slower compared to lower quenches, as particles took longer to move and settle into their lattice positions. Faster nucleation resulted in more, but smaller, colloidal crystals. In the deepest quenches, colloidal crystal formation occurred in two stages: first, a dense, metastable amorphous aggregate formed rapidly, followed by slower crystallization through local particle rearrangements via diffusion. Although the time for aggregates to form decreased with quench depth, colloidal crystal growth became progressively slower. As a result, the fastest overall colloidal crystal formation happened at intermediate quench depths. Additionally, larger particles and longer DNA sticky ends both slowed down the co-assembly process.²⁵⁷

6.2.5. External force-assisted co-assembly of submicrometer-sized particles. External fields can also guide the co-assembly of submicrometer-sized particles into multi-component superstructures (Table S4, ESI†).
6.2.5.1. Spin-coating-assisted co-assembly of submicrometer-sized particles. Binary colloidal crystals have been prepared by co-assembling submicrometer-sized particles under non-equilibrium conditions using a stepwise spin-coating technique (Fig. 39).³⁷⁴ The process began with the formation of a 2D colloidal crystal of large silica spheres on a substrate using spin-coating. The resulting hcp monolayer served as a template for the subsequent deposition of small silica spheres. As the small spheres were spread centrifugally over the template, they sequentially settled into the gaps formed by the large spheres. First, they occupied the lowest interstices, then the recesses, and finally, they formed an hcp monolayer on top. This stepwise layering led to the formation of binary colloidal crystals. For example, binary colloidal crystals made of 442 nm and 222 nm silica spheres (with a size ratio of 0.5) were prepared using stepwise spin-coating at 3000 rpm. The small 222 nm spheres predominantly occupied the interstitial sites between the large 442 nm spheres, forming an LS₂ structure, where each small sphere is surrounded by three neighbors. When the spin speed was increased to 10 000 rpm, binary colloidal crystals with LS₃ structures were observed, suggesting that higher centrifugal forces could induce rotation in the small spheres, promoting the formation of these structures. LS structures were not achieved, likely due to this induced rotation.³⁷⁴

Fig. 39 (a) Schematic illustration of the stepwise spin-coating technique used to prepare binary colloidal crystals. SEM images of the binary colloidal crystals prepared by stepwise spin-coating: (b) 519 nm and 891 nm silica spheres (γ = 0.58), (c) 442 nm and 891 nm silica spheres (γ = 0.50), and (d) 222 nm and 891 nm silica spheres (γ = 0.25). Solid and empty circles indicate the positions of small spheres, while polygon frames outline their arrangement patterns. Adapted with permission from ref. 374. Copyright 2004 John Wiley and Sons.

The size ratio also influenced the resulting binary colloidal crystals at a fixed spin speed. Binary colloidal crystals formed from 891 nm and 442 nm spheres (γ = 0.50) exhibited the LS₂ structure, while those made from 891 nm and 519 nm spheres (γ = 0.58) displayed a transitional phase between LS₂ and LS₃ structures, characterized by a mix of six- and five-sphere coordination around the larger spheres. When using 891 nm and 222 nm spheres (γ = 0.25), the resulting binary colloidal crystals exclusively exhibited LS₂ structure, with the small 222 nm spheres entirely occupying the interstices of the large spheres. No triangular or tetrahedral clusters of the small spheres were observed, likely because the number of 222 nm spheres was roughly equal to the number of available interstices, each of which could accommodate more than one small sphere.³⁷⁴

6.2.5.2. Electric field-assisted co-assembly of submicrometer-sized particles. Electric fields can direct the assembly of submicrometer-sized particles by aligning their permanent electric or magnetic dipole moments with the field.³⁷⁵ For example, electrophoretic deposition uses electric fields to guide the arrangement of charge-stabilized submicrometer-sized particles onto solid substrates. In an early study, Huang et al. prepared binary monolayers of PS particles using electrophoretic deposition (Fig. 40).³⁷⁶ First, PS particles, either 700 nm or 1.8 μm in diameter, were self-assembled into hcp monolayers on a glass substrate coated with indium tin oxide (ITO). These particles were then lightly sintered to bond them together and fix them to the substrate, ensuring the stability of the monolayer for further processing. The prepared template was placed in an electrophoretic deposition cell as the anode, with a platinum sheet as the cathode. An aqueous suspension of small colloidal particles (150, 180, 240, 400 or 640 nm) was introduced between the electrodes, and an electric field was applied. Due to the dielectric mismatch between PS particles (ε_r ∼ 2.15–2.65) and water (ε_r ∼80), the electric field near the ITO substrate became slightly distorted. This caused the electric field strength at the interstitial sites between the larger PS particles to be higher than that in the surrounding areas. These interstices acted as traps, attracting and localizing small particles by minimizing their electrostatic potential energy. As a result, an ordered binary colloidal monolayer formed. Finally, a strong voltage was applied to stabilize the particles on the template. When 1.8 μm and 180 nm PS particles were used (γ = 0.10), an ordered structure did not form due to the large size difference. Instead, the small particles filled the gaps in the ordered template, resulting in a colloidal crystal with a complex stoichiometry. Using 400 nm PS particles (γ = 0.22), the small particles occupied the interstitial sites between the 1.8 μm PS particles. Each interstitial site accommodated four small particles arranged in an inverse pyramid, with each large particle surrounded by 24 small ones. This arrangement resulted in a structure with LS₈ stoichiometry. A similar structure was observed when 150 nm PS particles occupied the interstitial sites of a template made of 700 nm PS particles (γ = 0.2). For 400 nm and 700 nm PS particles (γ = 0.57), binary colloidal monolayers with LS₂ stoichiometry were formed. When 700 nm and 640 nm PS particles (γ = 0.91) were used, the small particles tended to occupy three separated interstitial sites, resulting in binary colloidal monolayers with LS stoichiometry. These LS monolayers exhibited structural defects, leaving the monolayer of small particles incomplete. To investigate the influence of volume fraction on binary colloidal monolayer formation, suspensions of 240 nm PS particles at 0.5‰ and 1% were used on a monolayer made of 700 nm PS particles (γ = 0.34). The lower volume fraction resulted in a binary monolayer with LS₂ stoichiometry, while the higher volume fraction produced a binary monolayer with LS₄ stoichiometry. The method was also extended to the preparation of ternary colloidal monolayers by depositing 150 nm PS particles onto a binary monolayer of 240 nm and 700 nm PS particles (γ_SM = 0.625, γ_ML = 0.34). In this arrangement, five 150 nm PS particles filled each secondary interstitial site between two 240 nm PS particles, with one particle positioned in the middle and four others forming a layer above it. This arrangement resulted in a structure with LM₂S₁₅ stoichiometry.³⁷⁶

Fig. 40 Schematic illustration of the preparation of binary colloidal monolayers using the electrophoretic deposition. Adapted with permission from ref. 376. Copyright 2007 American Chemical Society.

For micrometer-sized colloids, gravity and slow crystallization rates can limit the formation of binary superstructures. For example, when a binary mixture of 1.37 μm and 410 nm silica spheres (γ = 0.3) in DMSO was compressed by gravity, small domains of NaCl- and NiAs-type superstructures formed. To increase the size and control the structure of these domains, a horizontal electric field has been applied perpendicular to gravity during the co-assembly process.³⁷⁷ This field induced dipole moments in the large colloids, promoting homogeneous co-assembly within 10 minutes. As gravity further compressed the system, heterogeneous co-assembly began at the bottom wall. However, the different sedimentation rates of the particles resulted in a non-stoichiometric superstructure, with fewer small particles than required for a perfect NaCl-type superstructure. Colloidal epitaxy, where particles sediment onto a structured surface, was also applied to control the orientation of colloidal superstructures.^378,379 By employing a 2D hole array made with soft lithography, NaCl-type superstructures formed, having the size of the template. The NiAs-type superstructure, however, could not grow on this template. A glycerol–water solvent mixture was used instead of DMSO for this experiment. To further improve co-assembly, dielectrophoretic forces were applied using electric field gradients, a technique called the “electric bottle”.^380,381 This method compressed the binary dispersion horizontally, preventing gravitational separation of particles. The electric field gradients concentrated the colloids into a field-free zone, resulting in high-quality, large NaCl-type superstructures that matched the size of the template without lattice distortions. Glycerol–water solvent was again used, as in the sedimentation experiments.³⁷⁷

7. Outlook

Since the initial reports on nanometer- and submicrometer-sized colloidal particle superstructures in the 1980s,^188,382 the variety of particle shapes, sizes, and chemical compositions has greatly expanded, enabling significant progress in their assembly into ordered superstructures. Currently, research focuses on co-assembling various types of these colloidal particles into complex, multi-component ordered superstructures with practical applications.

These multi-component superstructures are promising as templates for planarized microphotonic crystal chips, near-field photolithography, nanosphere optics, and nanosphere cluster formation.^251,341,383 They hold potential as photonic band gap devices,^{330,353,367,384–386} microelectronic systems,^{12,179,262,387–389} thermoelectric devices,^12,390 chemical and biological sensors,^391–394 superhydrophobic surfaces,^395–397 and capillary columns for chromatography³⁹⁸ and for applications in surface-enhanced Raman scattering (SERS),^399–401 catalysis,^402–405 data storage,^{9,10,406–408} nano-lithography,^{355,409–414} and surface patterning.^415,416 Furthermore, they serve as valuable models for crystallographic studies.^196,377

Experimental methods for producing, characterizing, and manipulating nanometer- and submicrometer-sized colloidal particles have led to a wide range of multi-component superstructures. However, several challenges must be overcome before these superstructures can reach their full potential.^417,418

To develop multi-component superstructures with revolutionary properties, it is essential to connect their structure to their properties. Future progress will rely on advancing both experimental and theoretical understanding beyond current boundaries to fully establish this connection. In particular, theoretical approaches are expected to play an increasingly important role in this effort.

A comprehensive understanding of how particle properties—such as composition, shape, size, or surface ligands—interact with environmental factors—such as temperature, solvent, substrate, or external fields—to affect the assembly process is still lacking. For example, predicting the behavior of grafted nanometer- and submicrometer-sized colloidal particles becomes increasingly difficult as ligand complexity increases.^419,420 Particles often have facets with different crystallographic orientations, each interacting differently with ligands, which leads to varying ligand densities on each facet, even when the same ligand is used.⁴²¹ The complexity further increases when mixtures of ligands with different binding groups and molecular structures are involved.¹⁵² Developing a precise model to predict how nanometer- and submicrometer-sized colloidal particles assemble, based on their properties and environmental factors, remains a challenging goal that still requires further experimental, theoretical, and computational efforts.

Another challenge is to characterize equilibrium and metastability. Determining whether these multi-component superstructures reach thermodynamic equilibrium or remain kinetically trapped in metastable states is particularly difficult. Thermodynamic equilibrium and kinetically trapped superstructures can have similar free energy. Though still largely unexplored, nonequilibrium effects offer opportunities to control both equilibrium and metastable superstructures, paving the way for active systems with various functions. Understanding these effects could lead to the design of superstructures with a wide range of capabilities.¹⁵²

A key challenge is creating superstructures that can perform multiple functions simultaneously and adapt their structure as needed, mimicking the complex functions of living systems. Achieving this requires assembly processes that are robust, accurate, adaptable, and programmable. Dynamic nanometer- and submicrometer-sized particles, which can respond to external stimuli, offer exciting opportunities in this area. These stimuli can be chemical, such as solvents, pH, metal ions, gases, and biomolecules, or physical, such as temperature, magnetic fields, and electrical fields.^422–424 The challenge is to design these particles to store information and perform programmed tasks, assembling only when the stimulus is present and disassembling when it is removed.^422,425,426 The potential applications of these stimuli-responsive particle superstructures are extensive. They could be used in drug delivery systems that respond to environmental signals for targeted and controlled release, as well as in bioimaging where superstructures change in response to specific biological signals. They could be also valuable in theragnostics, combination therapy and diagnostics. These superstructures could create responsive coatings with self-healing capabilities and smart textiles that adapt to environmental conditions. Additionally, they could be used in environmental sensing, water treatment, and as soft actuators.^427–430

Another growing focus in nanometer- and submicrometer-sized particle co-assembly is the creation of ordered low-dimensional superstructures, including colloidosomes, strings, sheets, or vesicles. To achieve this, researchers are increasingly exploring complex ligand chemistry.¹⁵²

New methods are emerging to address these challenges and build complex, multi-component ordered superstructures, moving beyond traditional approaches like solvent destabilization. For example, recent research has explored using particles as inks for 3D printing, merging bottom-up assembly with top-down techniques.⁴³¹

In summary, the future of co-assembling nanometer- and submicrometer-sized colloidal particles into complex, multi-component superstructures is promising and full of potential. For example, we are close to achieving electronic devices and components entirely constructed from nanoparticles, a breakthrough that could revolutionize numerous fields. Progress in superstructure preparation methods, environmental control, surface chemistry, and theoretical models, will bridge the gap between foundational research and real-world applications, leading to a new generation of functional materials with unprecedented capabilities. These are exciting times ahead.

Author contributions

Javier Fonseca: writing – original draft, writing – reviewing and editing, project administration, funding acquisition, visualization, conceptualization, data curation, methodology; Li Jiao: writing – reviewing and editing; Anna Broto-Ribas: writing – reviewing and editing; Gurvinder Singh: writing – reviewing and editing; Angang Dong: writing – reviewing and editing,

Conflicts of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Abbreviations

3D	Three-dimensional
0D	Zero-dimensional
1D	One-dimensional
2D	Two-dimensional
TEM	Transmission electron microscopy
SEM	Scanning electron microscopy
AFM	Atomic force microscopy
FFT	Fast Fourier transform
ED	Electron diffraction
SAXS	Small-angle X-ray scattering
GISAXS	Grazing-incidence SAXS
γ	Size ratio
OA	Oleic acid
DDT	Dodecanethiol
fcc	Face-centered cubic
TCE	Tetrachloroethylene
TOPO	Tri-n-octylphosphine oxide
bcc	Body-centered cubic
AT	Archimedean tiling
PMMA	Polymethylmethacrylate
DDQC	Dodecagonal quasicrystal
POM	Polyoxometalate
DDA	Dodecyldimethylammonium
hcp	Hexagonal close-packed
MD	Molecular dynamics
OAM	Oleylamine
OTM	Orbifold topological model
PS	Polystyrene
DDAB	Didodecyldimethylammonium bromide
DEG	Diethylene glycol
TMA	HS(CH2)11NMe3^+Cl^−
MUA	HS(CH2)10COOH
DNA	Deoxyribonucleic acid
ssDNA	Single-stranded DNA
dsDNA	Double-stranded DNA
OEG	Oligoethylene glycol
ih	Interlocked honeycomb
rch	Cubic honeycomb
toh	Tetra-octa honeycomb
gtoh	Gyrated tetra-octa honeycomb
FC-40	Perfluoro-di-n-butylmethylamine
FC-70	Perfluorotripentylamine
LZM	Human lysozyme
HAS	Human serum albumin
BSA	Bovine serum albumin
PEG-PALD	Poly(ethylene glycol) propionaldehyde
hADSCs	Human adipose-derived mesenchymal stem cells
DTAB	Dodecyltrimethylammonium bromide
ϕ	Volume fraction
hncp	Hexagonal non-close-packed
IR	Infrared
PEO	Polyethylene oxide
PEG	Polyethylene glycol
MOF	Metal–organic framework
SDS	Sodium dodecyl sulfate
TBAB	Tetrabutylammonium bromide
TPM	3-(Trimethoxysilyl) propyl methacrylate
ITO	Indium tin oxide
SERS	Surface-enhanced Raman scattering

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Acknowledgements

The Chemical Engineering Department at Northeastern University supported this work.

References

1. T. Hueckel, G. M. Hocky and S. Sacanna, Total synthesis of colloidal matter, Nat. Rev. Mater., 2021, 6, 1053–1069,  DOI:10.1038/s41578-021-00323-x.
2. W. Li, H. Palis, R. Mérindol, J. Majimel, S. Ravaine and E. Duguet, Colloidal molecules and patchy particles: complementary concepts, synthesis and self-assembly, Chem. Soc. Rev., 2020, 49, 1955–1976,  10.1039/C9CS00804G.
3. A. P. Alivisatos, Semiconductor clusters, nanocrystals, and quantum dots, Science, 1996, 271, 933–937,  DOI:10.1126/science.271.5251.933.
4. Y. Xia, P. Yang, Y. Sun, Y. Wu, B. Mayers, B. Gates, Y. Yin, F. Kim and H. Yan, One-dimensional nanostructures: Synthesis, characterization, and applications, Adv. Mater., 2003, 15, 353–389,  DOI:10.1002/adma.200390087.
5. A. P. Alivisatos, The use of nanocrystals in biological detection, Nat. Biotechnol., 2004, 22, 47–52,  DOI:10.1038/nbt927.
6. N. J. Durr, T. Larson, D. K. Smith, B. A. Korgel, K. Sokolov and A. Ben-Yakar, Two-photon luminescence imaging of cancer cells using molecularly targeted gold nanorods, Nano Lett., 2007, 7, 941–945,  DOI:10.1021/nl062962v.
7. J. H. Lee, Y. M. Huh, Y. Jun, J. Seo, J. Jang, H. T. Song, S. Kim, E. J. Cho, H. G. Yoon, J. S. Suh and J. Cheon, Artificially engineered magnetic nanoparticles for ultra-sensitive molecular imaging, Nat. Med., 2007, 13, 95–99,  DOI:10.1038/nm1467.
8. X. Michalet, F. F. Pinaud, L. A. Bentolila, J. M. Tsay, S. Doose, J. J. Li, G. Sundaresan, A. M. Wu, S. S. Gambhir and S. Weiss, Quantum dots for live cells, in vivo imaging, and diagnostics, Science, 2005, 307, 538–544,  DOI:10.1126/science.1104274.
9. D. C. Lee, D. K. Smith, A. T. Heitsch and B. A. Korgel, Colloidal magnetic nanocrystals: synthesis, properties and applications, Annu. Rep. Prog. Chem., Sect. C:Phys. Chem., 2007, 103, 351–402,  10.1039/B605630J.
10. H. Zeng, J. Li, J. P. Liu, Z. L. Wang and S. Sun, Exchange-coupled nanocomposite magnets by nanoparticle self-assembly, Nature, 2002, 420, 395–398,  DOI:10.1038/nature01208.
11. I. Gur, N. A. Fromer, M. L. Geier and A. P. Alivisatos, Air-stable all-inorganic nanocrystal solar cells processed from solution, Science, 2005, 310, 462–465,  DOI:10.1126/science.1117908.
12. J. J. Urban, D. V. Talapin, E. V. Shevchenko, C. R. Kagan and C. B. Murray, Synergism in binary nanocrystal superlattices leads to enhanced p-type conductivity in self-assembled PbTe/Ag2Te thin films, Nat. Mater., 2007, 6, 115–121,  DOI:10.1038/nmat1826.
13. M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Colloidal diamond, Nature, 2020, 585, 524–529,  DOI:10.1038/s41586-020-2718-6.
14. Z. Cai, Z. Li, S. Ravaine, M. He, Y. Song, Y. Yin, H. Zheng, J. Teng and A. Zhang, From colloidal particles to photonic crystals: advances in self-assembly and their emerging applications, Chem. Soc. Rev., 2021, 50, 5898–5951,  10.1039/D0CS00706D.
15. Z. Li, Q. Fan and Y. Yin, Colloidal self-assembly approaches to smart nanostructured materials, Chem. Rev., 2022, 122, 4976–5067,  DOI:10.1021/acs.chemrev.1c00482.
16. A. V. Pinheiro, D. Han, W. M. Shih and H. Yan, Challenges and opportunities for structural DNA nanotechnology, Nat. Nanotechnol., 2011, 6, 763–772,  DOI:10.1038/nnano.2011.187.
17. K. A. Dill and J. L. MacCallum, The protein-folding problem, 50 years on, Science, 2012, 338, 1042–1046,  DOI:10.1126/science.1219021.
18. W. Shenton, D. Pum, U. B. Sleytr and S. Mann, Synthesis of cadmium sulphide superlattices using self-assembled bacterial S-layers, Nature, 1997, 389, 585–587,  DOI:10.1038/39287.
19. K. W. Guarini, C. T. Black and S. H. I. Yeung, Optimization of diblock copolymer thin film self assembly, Adv. Mater., 2002, 14, 1290–1294,  DOI:10.1002/1521-4095(20020916)14:18<1290::AID-ADMA1290>3.0.CO;2-N.
20. X. Li, X. Liu and X. Liu, Self-assembly of colloidal inorganic nanocrystals: nanoscale forces, emergent properties and applications, Chem. Soc. Rev., 2021, 50, 2074–2101,  10.1039/D0CS00436G.
21. S. C. Glotzer and M. J. Solomon, Anisotropy of building blocks and their assembly into complex structures, Nat. Mater., 2007, 6, 557–562,  DOI:10.1038/nmat1949.
22. Y. Zhao, K. Thorkelsson, A. J. Mastroianni, T. Schilling, J. M. Luther, B. J. Rancatore, K. Matsunaga, H. Jinnai, Y. Wu, D. Poulsen, J. M. J. Fréchet, A. P. Alivisatos and T. Xu, Small-molecule-directed nanoparticle assembly towards stimuli-responsive nanocomposites, Nat. Mater., 2009, 8, 979–985,  DOI:10.1038/nmat2565.
23. W. Cheng, M. J. Campolongo, J. J. Cha, S. J. Tan, C. C. Umbach, D. A. Muller and D. Luo, Free-standing nanoparticle superlattice sheets controlled by DNA, Nat. Mater., 2009, 8, 519–525,  DOI:10.1038/nmat2440.
24. C. J. Kiely, J. Fink, M. Brust, D. Bethell and D. J. Schiffrin, Spontaneous ordering of bimodal ensembles of nanoscopic gold clusters, Nature, 1998, 396, 444–446,  DOI:10.1038/24808.
25. C. B. Murray, C. R. Kagan and M. G. Bawendi, Synthesis and characterization of monodisperse nanocrystals and close-packed nanocrystal assemblies, Annu. Rev. Mater. Sci., 2000, 30, 545–610,  DOI:10.1146/annurev.matsci.30.1.545.
26. M. Grzelczak, J. Vermant, E. M. Furst and L. M. Liz-Marzán, Directed self-assembly of nanoparticles, ACS Nano, 2010, 4, 3591–3605,  DOI:10.1021/nn100869j.
27. A. Courty, A. Mermet, P. A. Albouy, E. Duval and M. P. Pileni, Vibrational coherence of self-organized silver nanocrystals in f.c.c. supra-crystals, Nat. Mater., 2005, 4, 395–398,  DOI:10.1038/nmat1366.
28. J. Cheon, J. I. Park, J. Choi, Y. Jun, S. Kim, M. G. Kim, Y. M. Kim and Y. J. Kim, Magnetic superlattices and their nanoscale phase transition effects, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 3023–3027,  DOI:10.1073/pnas.0508877103.
29. E. V. Shevchenko, D. V. Talapin, S. O'Brien and C. B. Murray, Polymorphism in AB13 nanoparticle superlattices:  An example of semiconductor-metal metamaterials, J. Am. Chem. Soc., 2005, 127, 8741–8747,  DOI:10.1021/ja050510z.
30. C. P. Collier, T. Vossmeyer and J. R. Heath, Nanocrystal superlattices, Annu. Rev. Phys. Chem., 1998, 49, 371–404,  DOI:10.1146/annurev.physchem.49.1.371.
31. E. V. Shevchenko, D. V. Talapin, N. A. Kotov, S. O'Brien and C. B. Murray, Structural diversity in binary nanoparticle superlattices, Nature, 2006, 439, 55–59,  DOI:10.1038/nature04414.
32. E. V. Shevchenko, D. V. Talapin, C. B. Murray and S. O'Brien, Structural characterization of self-assembled multifunctional binary nanoparticle superlattices, J. Am. Chem. Soc., 2006, 128, 3620–3637,  DOI:10.1021/ja0564261.
33. D. V. Talapin, E. V. Shevchenko, M. I. Bodnarchuk, X. Ye, J. Chen and C. B. Murray, Quasicrystalline order in self-assembled binary nanoparticle superlattices, Nature, 2009, 461, 964–967,  DOI:10.1038/nature08439.
34. J. V. Sanders, Close-packed structures of spheres of two different sizes I. Observations on natural opal, Philos. Mag. A, 1980, 42, 705–720,  DOI:10.1080/01418618008239379.
35. M. J. Murray and J. V. Sanders, Close-packed structures of spheres of two different sizes II. The packing densities of likely arrangements, Philos. Mag. A, 1980, 42, 721–740,  DOI:10.1080/01418618008239380.
36. M. D. Eldridge, P. A. Madden and D. Frenkel, Entropy-driven formation of a superlattice in a hard-sphere binary mixture, Nature, 1993, 365, 35–37,  DOI:10.1038/365035a0.
37. Z. Chen, J. Moore, G. Radtke, H. Sirringhaus and S. O'Brien, Binary nanoparticle superlattices in the semiconductor-semiconductor system: CdTe and CdSe, J. Am. Chem. Soc., 2007, 129, 15702–15709,  DOI:10.1021/ja076698z.
38. Z. Chen and S. O'Brien, Structure direction of II–VI semiconductor quantum dot binary nanoparticle superlattices by tuning radius ratio, ACS Nano, 2008, 2, 1219–1229,  DOI:10.1021/nn800129s.
39. J. Chen, X. Ye and C. B. Murray, Systematic electron crystallographic studies of self-assembled binary nanocrystal superlattices, ACS Nano, 2010, 4, 2374–2381,  DOI:10.1021/nn1003259.
40. W. H. Evers, B. D. Nijs, L. Filion, S. Castillo, M. Dijkstra and D. Vanmaekelbergh, Entropy-driven formation of binary semiconductor-nanocrystal superlattices, Nano Lett., 2010, 10, 4235–4241,  DOI:10.1021/nl102705p.
41. M. I. Bodnarchuk, M. V. Kovalenko, W. Heiss and D. V. Talapin, Energetic and entropic contributions to self-assembly of binary nanocrystal superlattices: Temperature as the structure-directing factor, J. Am. Chem. Soc., 2010, 132, 11967–11977,  DOI:10.1021/ja103083q.
42. A. V. Titov and P. Král, Modeling the self-assembly of colloidal nanorod superlattices, Nano Lett., 2008, 8, 3605–3612,  DOI:10.1021/nl801530x.
43. A. D. Law, D. M. A. Buzza and T. S. Horozov, Two-dimensional colloidal alloys, Phys. Rev. Lett., 2011, 106, 128302,  DOI:10.1103/PhysRevLett.106.128302.
44. X. Ye, J. Chen, M. Engel, J. A. Millan, W. Li, L. Qi, G. Xing, J. E. Collins, C. R. Kagan, J. Li, S. C. Glotzer and C. B. Murray, Competition of shape and interaction patchiness for self-assembling nanoplates, Nat. Chem., 2013, 5, 466–473,  DOI:10.1038/nchem.1651.
45. W. D. Luedtke and U. Landman, Structure, dynamics, and thermodynamics of passivated gold nanocrystallites and their assemblies, J. Phys. Chem., 1996, 100, 13323–13329,  DOI:10.1021/jp961721g.
46. U. Landman and W. D. Luedtke, Small is different: energetic, structural, thermal, and mechanical properties of passivated nanocluster assemblies, Faraday Discuss., 2004, 125, 1–22,  10.1039/B312640B.
47. K. E. Mueggenburg, X.-M. Lin, R. H. Goldsmith and H. M. Jaeger, Elastic membranes of close-packed nanoparticle arrays, Nat. Mater., 2007, 6, 656–660,  DOI:10.1038/nmat1965.
48. B. D. Rabideau and R. T. Bonnecaze, Computational study of the self-organization of bidisperse nanoparticles, Langmuir, 2004, 20, 9408–9414,  DOI:10.1021/la049100z.
49. A. M. Kalsin, M. Fialkowski, M. Paszewski, S. K. Smoukov, K. J. M. Bishop and B. A. Grzybowski, Electrostatic self-assembly of binary nanoparticle crystals with a diamond-like lattice, Science, 2006, 312, 420–424,  DOI:10.1126/science.1125124.
50. Z. Sun, Z. Luo and J. Fang, Assembling nonspherical 2D binary nanoparticle superlattices by opposite electrical charges: The role of Coulomb forces, ACS Nano, 2010, 4, 1821–1828,  DOI:10.1021/nn100302v.
51. H. Chan, A. Demortière, L. Vukovic, P. Král and C. Petit, Colloidal nanocube supercrystals stabilized by multipolar Coulombic coupling, ACS Nano, 2012, 6, 4203–4213,  DOI:10.1021/nn3007338.
52. D. Baranov, A. Fiore, M. van Huis, C. Giannini, A. Falqui, U. Lafont, H. Zandbergen, M. Zanella, R. Cingolani and L. Manna, Assembly of colloidal semiconductor nanorods in solution by depletion attraction, Nano Lett., 2010, 10, 743–749,  DOI:10.1021/nl903946n.
53. M. A. Boles, M. Engel and D. V. Talapin, Self-assembly of colloidal nanocrystals: From intricate structures to functional materials, Chem. Rev., 2016, 116, 11220–11289,  DOI:10.1021/acs.chemrev.6b00196.
54. B. Li, D. Zhou and Y. Han, Assembly and phase transitions of colloidal crystals, Nat. Rev. Mater., 2016, 1, 15011,  DOI:10.1038/natrevmats.2015.11.
55. E. Guzmán, F. Ortega and R. G. Rubio, Forces controlling the assembly of particles at fluid interfaces, Langmuir, 2022, 38, 13313–13321,  DOI:10.1021/acs.Langmuir.2c02038.
56. F. Cui, S. Marbach, J. A. Zheng, M. Holmes-Cerfon and D. J. Pine, Comprehensive view of microscopic interactions between DNA-coated colloids, Nat. Commun., 2022, 13, 2304,  DOI:10.1038/s41467-022-29853-w.
57. M. Dijkstra and E. Luijten, From predictive modelling to machine learning and reverse engineering of colloidal self-assembly, Nat. Mater., 2021, 20, 762–773,  DOI:10.1038/s41563-021-01014-2.
58. E. Matijevic, Preparation and properties of uniform size colloids, Chem. Mater., 1993, 5, 412–426,  DOI:10.1021/cm00028a004.
59. K. Thorkelsson, P. Bai and T. Xu, Self-assembly and applications of anisotropic nanomaterials: A review, Nano Today, 2015, 10, 48–66,  DOI:10.1016/j.nantod.2014.12.005.
60. P. Liu, L. Bai, J. Yang, H. Gu, Q. Zhong, Z. Xie and Z. Gu, Self-assembled colloidal arrays for structural color, Nanoscale Adv., 2019, 1, 1672–1685,  10.1039/C8NA00328A.
61. F. Qi, Z. Meng, M. Xue and L. Qiu, Recent advances in self-assemblies and sensing applications of colloidal photonic crystals, Anal. Chim. Acta, 2020, 1123, 91–112,  DOI:10.1016/j.aca.2020.02.026.
62. P. Bartlett, P. N. Pusey and R. H. Ottewill, Colloidal crystallization under time-averaged zero gravity, Langmuir, 1991, 7, 213–215,  DOI:10.1021/la00050a001.
63. P. Bartlett and R. H. Ottewill, Gravitational effects on the phase behaviour of dispersions, Adv. Colloid Interface Sci., 1994, 50, 39–50,  DOI:10.1016/0001-8686(94)80024-3.
64. C. Avci, I. Imaz, A. Carné-Sánchez, J. A. Pariente, N. Tasios, J. Pérez-Carvajal, M. I. Alonso, A. Blanco, M. Dijkstra, C. López and D. Maspoch, Self-assembly of polyhedral metal-organic framework particles into three-dimensional ordered superstructures, Nat. Chem., 2018, 10, 78–84,  DOI:10.1038/nchem.2875.
65. J. Fonseca, L. Meng, P. Moronta, I. Imaz, C. López and D. Maspoch, Assembly of covalent organic frameworks into colloidal photonic crystals, J. Am. Chem. Soc., 2023, 145, 20163–20168,  DOI:10.1021/jacs.3c06265.
66. J. Fonseca, L. Meng, I. Imaz and D. Maspoch, Self-assembly of colloidal metal–organic framework (MOF) particles, Chem. Soc. Rev., 2023, 52, 2528–2543,  10.1039/D2CS00858K.
67. A. J. Nozik, Photoelectrochemistry: Applications to solar energy conversion, Annu. Rev. Phys. Chem., 1978, 29, 189–222,  DOI:10.1146/annurev.pc.29.100178.001201.
68. A. L. Efros and A. L. Efros, Interband absorption of light in a semiconductor sphere, Sov. Phys. Semicond, 1982, 16, 772–775.
69. L. E. Brus, Electron–electron and electron-hole interactions in small semiconductor crystallites: The size dependence of the lowest excited electronic state, J. Chem. Phys., 1984, 80, 4403–4409,  DOI:10.1063/1.447218.
70. C. B. Murray, D. J. Norris and M. G. Bawendi, Synthesis and characterization of nearly monodisperse CdE (E = sulfur, selenium, tellurium) semiconductor nanocrystallites, J. Am. Chem. Soc., 1993, 115, 8706–8715,  DOI:10.1021/ja00072a025.
71. F. Yang, H. Mu, C. Wang, L. Xiang, K. X. Yao, L. Liu, Y. Yang, Y. Han, Y. Li and Y. Pan, Morphological map of ZIF-8 crystals with five distinctive shapes: Feature of filler in mixed-matrix membranes on C3H6/C3H8 separation, Chem. Mater., 2018, 30, 3467–3473,  DOI:10.1021/acs.chemmater.8b01073.
72. J. Cravillon, R. Nayuk, S. Springer, A. Feldhoff, K. Huber and M. Wiebcke, Controlling zeolitic imidazolate framework nano- and microcrystal formation: Insight into crystal growth by time-resolved in situ static light scattering, Chem. Mater., 2011, 23, 2130–2141,  DOI:10.1021/cm103571y.
73. M. Kamp, S. Sacanna and R. P. A. Dullens, Spearheading a new era in complex colloid synthesis with TPM and other silanes, Nat. Rev. Chem., 2024, 8, 433–453,  DOI:10.1038/s41570-024-00603-4.
74. N. Yanai and S. Granick, Directional self-assembly of a colloidal metal-organic framework, Angew. Chem., Int. Ed., 2012, 51, 5638–5641,  DOI:10.1002/anie.201109132.
75. J. Troyano, A. Carné-Sánchez, C. Avci, I. Imaz and D. Maspoch, Colloidal metal-organic framework particles: the pioneering case of ZIF-8, Chem. Soc. Rev., 2019, 48, 5534–5546,  10.1039/C9CS00472F.
76. M. Sindoro, N. Yanai, A.-Y. Jee and S. Granick, Colloidal-sized metal-organic frameworks: Synthesis and applications, Acc. Chem. Res., 2014, 47, 459–469,  DOI:10.1021/ar400151n.
77. Y. Liu, M. Klement, Y. Wang, Y. Zhong, B. Zhu, J. Chen, M. Engel and X. Ye, Macromolecular ligand engineering for programmable nanoprism assembly, J. Am. Chem. Soc., 2021, 143, 16163–16172,  DOI:10.1021/jacs.1c07281.
78. X. Xia, J. Zeng, Q. Zhang, C. H. Moran and Y. Xia, Recent developments in shape-controlled synthesis of silver nanocrystals, J. Phys. Chem. C, 2012, 116, 21647–21656,  DOI:10.1021/jp306063p.
79. H.-Y. Ahn, H.-E. Lee, K. Jin and K. T. Nam, Extended gold nano-morphology diagram: synthesis of rhombic dodecahedra using CTAB and ascorbic acid, J. Mater. Chem. C, 2013, 1, 6861–6868,  10.1039/C3TC31135J.
80. M. Sun, Z. Cheng, W. Chen and M. Jones, Understanding symmetry breaking at the single-particle level via the growth of tetrahedron-shaped nanocrystals from higher-symmetry precursors, ACS Nano, 2021, 15, 15953–15961,  DOI:10.1021/acsnano.1c04056.
81. M. R. Langille, J. Zhang, M. L. Personick, S. Li and C. A. Mirkin, Stepwise evolution of spherical seeds into 20-fold twinned icosahedra, Science, 2012, 337, 954–957,  DOI:10.1126/science.1225653.
82. X. Ye, C. Zheng, J. Chen, Y. Gao and C. B. Murray, Using binary surfactant mixtures to simultaneously improve the dimensional tunability and monodispersity in the seeded growth of gold nanorods, Nano Lett., 2013, 13, 765–771,  DOI:10.1021/nl304478h.
83. X. Ye, L. Jin, H. Caglayan, J. Chen, G. Xing, C. Zheng, V. Doan-Nguyen, Y. Kang, N. Engheta, C. R. Kagan and C. B. Murray, Improved size-tunable synthesis of monodisperse gold nanorods through the use of aromatic additives, ACS Nano, 2012, 6, 2804–2817,  DOI:10.1021/nn300315j.
84. D. Wang, Y. Kang, X. Kang and C. B. Murray, Mineralizer-assisted shape-control of rare earth oxide nanoplates, Chem. Mater., 2014, 26, 6328–6332,  DOI:10.1021/cm502301u.
85. B. K. Choi, J. Kim, Z. Luo, J. Kim, J. H. Kim, T. Hyeon, S. Mehraeen, S. Park and J. Park, Shape transformation mechanism of gold nanoplates, ACS Nano, 2023, 17, 2007–2018,  DOI:10.1021/acsnano.2c07256.
86. Y. Lu, H. Zhang, F. Wu, H. Liu and J. Fang, Size-tunable uniform gold octahedra: fast synthesis, characterization, and plasmonic properties, RSC Adv., 2017, 7, 18601–18608,  10.1039/C7RA01223C.
87. B. J. Wiley, S. H. Im, Z.-Y. Li, J. McLellan, A. Siekkinen and Y. Xia, Maneuvering the surface plasmon resonance of silver nanostructures through shape-controlled synthesis, J. Phys. Chem. B, 2006, 110, 15666–15675,  DOI:10.1021/jp0608628.
88. M. M. Mariscal, J. J. Velázquez-Salazar and M. J. Yacaman, Growth mechanism of nanoparticles: theoretical calculations and experimental results, CrystEngComm, 2012, 14, 544–549,  10.1039/C1CE05602F.
89. K. Liu, Y. Bu, Y. Zheng, X. Jiang, A. Yu and H. Wang, Seedless synthesis of monodispersed gold nanorods with remarkably high yield: Synergistic effect of template modification and growth kinetics regulation, Chem. – Eur. J., 2017, 23, 3291–3299,  DOI:10.1002/chem.201781463.
90. B. Huang, L. Miao, J. Li, Z. Xie, Y. Wang, J. Chai and Y. Zhai, Identification of plasmon-driven nanoparticle-coalescence-dominated growth of gold nanoplates through nanopore sensing, Nat. Commun., 2022, 13, 1402,  DOI:10.1038/s41467-022-29123-9.
91. L. Manna, D. J. Milliron, A. Meisel, E. C. Scher and A. P. Alivisatos, Controlled growth of tetrapod-branched inorganic nanocrystals, Nat. Mater., 2003, 2, 382–385,  DOI:10.1038/nmat902.
92. S. Chen, Z. L. Wang, J. Ballato, S. H. Foulger and D. L. Carroll, Monopod, bipod, tripod, and tetrapod gold nanocrystals, J. Am. Chem. Soc., 2003, 125, 16186–16187,  DOI:10.1021/ja038927x.
93. K. Chandra, K. S. B. Culver, S. E. Werner, R. C. Lee and T. W. Odom, Manipulating the anisotropic structure of gold nanostars using good's buffers, Chem. Mater., 2016, 28, 6763–6769,  DOI:10.1021/acs.chemmater.6b03242.
94. S. Deka, K. Miszta, D. Dorfs, A. Genovese, G. Bertoni and L. Manna, Octapod-shaped colloidal nanocrystals of cadmium chalcogenides via “one-pot” cation exchange and seeded growth, Nano Lett., 2010, 10, 3770–3776,  DOI:10.1021/nl102539a.
95. K. Miszta, J. de Graaf, G. Bertoni, D. Dorfs, R. Brescia, S. Marras, L. Ceseracciu, R. Cingolani, R. van Roij, M. Dijkstra and L. Manna, Hierarchical self-assembly of suspended branched colloidal nanocrystals into superlattice structures, Nat. Mater., 2011, 10, 872–876,  DOI:10.1038/nmat3121.
96. G. Zhang, D. Wang and H. Möhwald, Decoration of microspheres with gold nanodots—Giving colloidal spheres valences, Angew. Chem., Int. Ed., 2005, 44, 7767–7770,  DOI:10.1002/anie.200502117.
97. S. Sun, S. Yang, H. L. Xin, D. Nykypanchuk, M. Liu, H. Zhang and O. Gang, Valence-programmable nanoparticle architectures, Nat. Commun., 2020, 11, 2279,  DOI:10.1038/s41467-020-16157-0.
98. K. H. Roh, D. C. Martin and J. Lahann, Biphasic Janus particles with nanoscale anisotropy, Nat. Mater., 2005, 4, 759–763,  DOI:10.1038/nmat1486.
99. A. Leonardi and M. Engel, Particle shape control via etching of core@shell nanocrystals, ACS Nano, 2018, 12, 9186–9195,  DOI:10.1021/acsnano.8b03759.
100. L. Chen, A. Leonardi, J. Chen, M. Cao, N. Li, D. Su, Q. Zhang, M. Engel and X. Ye, Imaging the kinetics of anisotropic dissolution of bimetallic core-shell nanocubes using graphene liquid cells, Nat. Commun., 2020, 11, 3041,  DOI:10.1038/s41467-020-16645-3.
101. N. Suzuki, Y. Wang, P. Elvati, Z.-B. Qu, K. Kim, S. Jiang, E. Baumeister, J. Lee, B. Yeom, J. H. Bahng, J. Lee, A. Violi and N. A. Kotov, Chiral graphene quantum dots, ACS Nano, 2016, 10, 1744–1755,  DOI:10.1021/acsnano.5b06369.
102. W. Ma, L. Xu, A. F. de Moura, X. Wu, H. Kuang, C. Xu and N. A. Kotov, Chiral inorganic nanostructures, Chem. Rev., 2017, 117, 8041–8093,  DOI:10.1021/acs.chemrev.6b00755.
103. J. S. Googasian, G. R. Lewis, Z. J. Woessner, E. Ringe and S. E. Skrabalak, Seed-directed synthesis of chiroptically active Au nanocrystals of varied symmetries, Chem. Commun., 2022, 58, 11575–11578,  10.1039/D2CC04126J.
104. H.-E. Lee, H.-Y. Ahn, J. Mun, Y. Y. Lee, M. Kim, N. H. Cho, K. Chang, W. S. Kim, J. Rho and K. T. Nam, Amino-acid- and peptide-directed synthesis of chiral plasmonic gold nanoparticles, Nature, 2018, 556, 360–365,  DOI:10.1038/s41586-018-0034-1.
105. E. González, J. Arbiol and V. F. Puntes, Carving at the nanoscale: Sequential galvanic exchange and Kirkendall growth at room temperature, Science, 2011, 334, 1377–1380,  DOI:10.1126/science.1212822.
106. S. Ham, H. J. Jang, Y. Song, K. L. Shuford and S. Park, Octahedral and cubic gold nanoframes with platinum framework, Angew. Chem., Int. Ed., 2015, 54, 9025–9028,  DOI:10.1002/anie.201503996.
107. Y. Li, W. Zhou, I. Tanriover, W. Hadibrata, B. E. Partridge, H. Lin, X. Hu, B. Lee, J. Liu, V. P. Dravid, K. Aydin and C. A. Mirkin, Open-channel metal particle superlattices, Nature, 2022, 611, 695–701,  DOI:10.1038/s41586-022-05291-y.
108. H. Hilal, Q. Zhao, J. Kim, S. Lee, M. N. Haddadnezhad, S. Yoo, S. Lee, W. Park, W. Park, J. Lee, J. W. Lee, I. Jung and S. Park, Three-dimensional nanoframes with dual rims as nanoprobes for biosensing, Nat. Commun., 2022, 13, 4813,  DOI:10.1038/s41467-022-32549-w.
109. T. Sugimoto, Preparation of monodispersed colloidal particles, Adv. Colloid Interface Sci., 1987, 28, 65–108,  DOI:10.1016/0001-8686(87)80009-X.
110. E. Matijevic, Production of monodispersed colloidal particles, Annu. Rev. Mater. Res., 1985, 15, 483–516,  DOI:10.1146/annurev.ms.15.080185.002411.
111. X. Chen, Y. Zhuang, N. Rampal, R. Hewitt, G. Divitini, C. A. O'Keefe, X. Liu, D. J. Whitaker, J. W. Wills, R. Jugdaohsingh, J. J. Powell, H. Yu, C. P. Grey, O. A. Scherman and D. Fairen-Jimenez, Formulation of metal-organic framework-based drug carriers by controlled coordination of methoxy PEG phosphate: Boosting colloidal stability and redispersibility, J. Am. Chem. Soc., 2021, 143, 13557–13572,  DOI:10.1021/jacs.1c03943.
112. E. P. K. Currie, W. Norde and M. A. C. Stuart, Tethered polymer chains: surface chemistry and their impact on colloidal and surface properties, Adv. Colloid Interface Sci., 2003, 100–102, 205–265,  DOI:10.1016/S0001-8686(02)00061-1.
113. K. M. L. Taylor, W. J. Rieter and W. Lin, Manganese-based nanoscale metal-organic frameworks for magnetic resonance imaging, J. Am. Chem. Soc., 2008, 130, 14358–14359,  DOI:10.1021/ja803777x.
114. B. Vincent, J. Edwards, S. Emmett and A. Jones, Depletion flocculation in dispersions of sterically-stabilised particles (“soft spheres”), Colloids Surf., 1986, 18, 261–281,  DOI:10.1016/0166-6622(86)80317-1.
115. E. Alonso-Redondo, M. Schmitt, Z. Urbach, C. M. Hui, R. Sainidou, P. Rembert, K. Matyjaszewski, M. R. Bockstaller and G. Fytas, A new class of tunable hypersonic phononic crystals based on polymer-tethered colloids, Nat. Commun., 2015, 6, 8309,  DOI:10.1038/ncomms9309.
116. S. Ding, Y. Zhang, F. Lou, M. K. Aslam, Y. Sun, M. Li, J. Duan, Y. Li and S. Chen, “Uncapped” metal–organic framework (MOF) dispersions driven by O2 plasma towards superior oxygen evolution electrocatalysis, J. Mater. Chem. A, 2022, 10, 20813–20818,  10.1039/D2TA05387J.
117. Y. Liang, N. Hilal, P. Langston and V. Starov, Interaction forces between colloidal particles in liquid: Theory and experiment, Adv. Colloid Interface Sci., 2007, 134–135, 151–166,  DOI:10.1016/j.cis.2007.04.003.
118. R. B. Grubbs, Roles of polymer ligands in nanoparticle stabilization, Polym. Rev., 2007, 47, 197–215,  DOI:10.1080/15583720701271245.
119. J.-M. Nam, J. S. Owen and D. V. Talapin, The ligand-surface interface and its influence on nanoparticle properties, Acc. Chem. Res., 2023, 56, 2265–2266,  DOI:10.1021/acs.accounts.3c00416.
120. C. Femina Carolin and T. Kamalesh, Advances in stabilization of metallic nanoparticle with biosurfactants- a review on current trends, Heliyon, 2024, 10, e29773,  DOI:10.1016/j.heliyon.2024.e29773.
121. C. Wang and H. Zhao, Polymer brushes and surface nanostructures: Molecular design, precise synthesis, and self-assembly, Langmuir, 2024, 40, 2439–2464,  DOI:10.1021/acs.Langmuir.3c02813.
122. B. A. Grzybowski, C. E. Wilmer, J. Kim, K. P. Browne and K. J. M. Bishop, Self-assembly: from crystals to cells, Soft Matter, 2009, 5, 1110–1128,  10.1039/B819321P.
123. E. Trizac, M. D. Eldridge and P. A. Madden, Stability of the AB crystal for asymmetric binary hard sphere mixtures, Mol. Phys., 1997, 90, 675–678,  DOI:10.1080/002689797172408.
124. X. Cottin and P. A. Monson, Substitutionally ordered solid solutions of hard spheres, J. Chem. Phys., 1995, 102, 3354–3360,  DOI:10.1063/1.469209.
125. P. G. Bolhuis, D. Frenkel, S. C. Mau and D. A. Huse, Entropy difference between crystal phases, Nature, 1997, 388, 235–236,  DOI:10.1038/40779.
126. A. B. Schofield, P. N. Pusey and P. Radcliffe, Stability of the binary colloidal crystals AB2 and AB13, Phys. Rev. E, 2005, 72, 031407,  DOI:10.1103/PhysRevE.72.031407.
127. A.-P. Hynninen, L. Filion and M. Dijkstra, Stability of LS and LS2 crystal structures in binary mixtures of hard and charged spheres, J. Chem. Phys., 2009, 131, 064902,  DOI:10.1063/1.3182724.
128. D. Frenkel, Plenty of room at the top, Nat. Mater., 2006, 5, 85–86,  DOI:10.1038/nmat1572.
129. C. A. Silvera Batista, R. G. Larson and N. A. Kotov, Nonadditivity of nanoparticle interactions, Science, 2015, 350, 1242477,  DOI:10.1126/science.1242477.
130. Q. Li, U. Jonas, X. S. Zhao and M. Kappl, The forces at work in colloidal self-assembly: a review on fundamental interactions between colloidal particles, Asia-Pac. J. Chem. Eng., 2008, 3, 255–268,  DOI:10.1002/apj.144.
131. A. Yethiraj, Tunable colloids: control of colloidal phase transitions with tunable interactions, Soft Matter, 2007, 3, 1099–1115,  10.1039/B704251P.
132. S. Jambhulkar, D. Ravichandran, Y. Zhu, V. Thippanna, A. Ramanathan, D. Patil, N. Fonseca, S. Vaishnavi Thummalapalli, B. Sundaravadivelan, A. Sun, W. Xu, S. Yang, A. Mada Kannan, Y. Golan, J. Lancaster, L. Chen, E. B. Joyee and K. Song, Nanoparticle assembly: From self-organization to controlled micropatterning for enhanced functionalities, Small, 2024, 20, 2306394,  DOI:10.1002/smll.202306394.
133. T. K. Haxton, L. O. Hedges and S. Whitelam, Crystallization and arrest mechanisms of model colloids, Soft Matter, 2015, 11, 9307–9320,  10.1039/C5SM01833A.
134. I. Coropceanu, E. M. Janke, J. Portner, D. Haubold, T. D. Nguyen, A. Das, C. P. N. Tanner, J. K. Utterback, S. W. Teitelbaum, M. H. Hudson, N. A. Sarma, A. M. Hinkle, C. J. Tassone, A. Eychmüller, D. T. Limmer, M. Olvera de la Cruz, N. S. Ginsberg and D. V. Talapin, Self-assembly of nanocrystals into strongly electronically coupled all-inorganic supercrystals, Science, 2022, 375, 1422–1426,  DOI:10.1126/science.abm6753.
135. E. Auyeung, T. Li, A. J. Senesi, A. L. Schmucker, B. C. Pals, M. Olvera de la Cruz and C. A. Mirkin, DNA-mediated nanoparticle crystallization into Wulff polyhedra, Nature, 2014, 505, 73–77,  DOI:10.1038/nature12739.
136. S. E. Seo, M. Girard, M. Olvera de la Cruz and C. A. Mirkin, Non-equilibrium anisotropic colloidal single crystal growth with DNA, Nat. Commun., 2018, 9, 4558,  DOI:10.1038/s41467-018-06982-9.
137. M. R. Jones, K. D. Osberg, R. J. Macfarlane, M. R. Langille and C. A. Mirkin, Templated techniques for the synthesis and assembly of plasmonic nanostructures, Chem. Rev., 2011, 111, 3736–3827,  DOI:10.1021/cr1004452.
138. Y. Cui, M. T. Björk, J. A. Liddle, C. Sönnichsen, B. Boussert and A. P. Alivisatos, Integration of colloidal nanocrystals into lithographically patterned devices, Nano Lett., 2004, 4, 1093–1098,  DOI:10.1021/nl049488i.
139. Y. Zhou, X. Zhou, D. J. Park, K. Torabi, K. A. Brown, M. R. Jones, C. Zhang, G. C. Schatz and C. A. Mirkin, Shape-selective deposition and assembly of anisotropic nanoparticles, Nano Lett., 2014, 14, 2157–2161,  DOI:10.1021/nl500471g.
140. L. Jiang, X. Chen, N. Lu and L. Chi, Spatially confined assembly of nanoparticles, Acc. Chem. Res., 2014, 47, 3009–3017,  DOI:10.1021/ar500196r.
141. J. A. Fan, K. Bao, L. Sun, J. Bao, V. N. Manoharan, P. Nordlander and F. Capasso, Plasmonic mode engineering with templated self-assembled nanoclusters, Nano Lett., 2012, 12, 5318–5324,  DOI:10.1021/nl302650t.
142. N. J. Greybush, M. Saboktakin, X. Ye, C. Della Giovampaola, S. J. Oh, N. E. Berry, N. Engheta, C. B. Murray and C. R. Kagan, Plasmon-enhanced upconversion luminescence in single nanophosphor-nanorod heterodimers formed through template-assisted self-assembly, ACS Nano, 2014, 8, 9482–9491,  DOI:10.1021/nn503675a.
143. Z. Lu and Y. Yin, Colloidal nanoparticle clusters: functional materials by design, Chem. Soc. Rev., 2012, 41, 6874–6887,  10.1039/C2CS35197H.
144. T. Wang, D. LaMontagne, J. Lynch, J. Zhuang and Y. C. Cao, Colloidal superparticles from nanoparticle assembly, Chem. Soc. Rev., 2013, 42, 2804–2823,  10.1039/C2CS35318K.
145. X. Wang, J. Feng, Y. Bai, Q. Zhang and Y. Yin, Synthesis, properties, and applications of hollow micro-/nanostructures, Chem. Rev., 2016, 116, 10983–11060,  DOI:10.1021/acs.chemrev.5b00731.
146. A. Böker, J. He, T. Emrick and T. P. Russell, Self-assembly of nanoparticles at interfaces, Soft Matter, 2007, 3, 1231–1248,  10.1039/B706609K.
147. J. W. J. de Folter, E. M. Hutter, S. I. R. Castillo, K. E. Klop, A. P. Philipse and W. K. Kegel, Particle shape anisotropy in Pickering emulsions: Cubes and peanuts, Langmuir, 2014, 30, 955–964,  DOI:10.1021/la402427q.
148. F. Bai, D. Wang, Z. Huo, W. Chen, L. Liu, X. Liang, C. Chen, X. Wang, Q. Peng and Y. Li, A versatile bottom-up assembly approach to colloidal spheres from nanocrystals, Angew. Chem., Int. Ed., 2007, 46, 6650–6653,  DOI:10.1002/anie.200701355.
149. M. I. Bodnarchuk, L. Li, A. Fok, S. Nachtergaele, R. F. Ismagilov and D. V. Talapin, Three-dimensional nanocrystal superlattices grown in nanoliter microfluidic plugs, J. Am. Chem. Soc., 2011, 133, 8956–8960,  DOI:10.1021/ja201129n.
150. J. C. Ondry and A. P. Alivisatos, Application of dislocation theory to minimize defects in artificial solids built with nanocrystal building blocks, Acc. Chem. Res., 2021, 54, 1419–1429,  DOI:10.1021/acs.accounts.0c00719.
151. Y. Zhong, V. R. Allen, J. Chen, Y. Wang and X. Ye, Multistep crystallization of dynamic nanoparticle superlattices in nonaqueous solutions, J. Am. Chem. Soc., 2022, 144, 14915–14922,  DOI:10.1021/jacs.2c06535.
152. C. L. Bassani, G. van Anders, U. Banin, D. Baranov, Q. Chen, M. Dijkstra, M. S. Dimitriyev, E. Efrati, J. Faraudo, O. Gang, N. Gaston, R. Golestanian, G. I. Guerrero-Garcia, M. Gruenwald, A. Haji-Akbari, M. Ibáñez, M. Karg, T. Kraus, B. Lee, R. C. Van Lehn, R. J. Macfarlane, B. M. Mognetti, A. Nikoubashman, S. Osat, O. V. Prezhdo, G. M. Rotskoff, L. Saiz, A.-C. Shi, S. Skrabalak, I. I. Smalyukh, M. Tagliazucchi, D. V. Talapin, A. V. Tkachenko, S. Tretiak, D. Vaknin, A. Widmer-Cooper, G. C. L. Wong, X. Ye, S. Zhou, E. Rabani, M. Engel and A. Travesset, Nanocrystal assemblies: Current advances and open problems, ACS Nano, 2024, 18, 14791–14840,  DOI:10.1021/acsnano.3c10201.
153. F. Gambinossi, S. E. Mylon and J. K. Ferri, Aggregation kinetics and colloidal stability of functionalized nanoparticles, Adv. Colloid Interface Sci., 2015, 222, 332–349,  DOI:10.1016/j.cis.2014.07.015.
154. Y. Fu, S. Zhao, W. Chen, Q. Zhang and Y. Chai, Self-assembly of nanoparticles with stimulated responses at liquid interfaces, Nano Today, 2024, 54, 102073,  DOI:10.1016/j.nantod.2023.102073.
155. K. Zhang, M. Jiang and D. Chen, Self-assembly of particles—The regulatory role of particle flexibility, Prog. Polym. Sci., 2012, 37, 445–486,  DOI:10.1016/j.progpolymsci.2011.09.003.
156. M. P. Pileni, Supracrystals of inorganic nanocrystals: An open challenge for new physical properties, Acc. Chem. Res., 2008, 41, 1799–1809,  DOI:10.1021/ar800082q.
157. Y. Wang, H. Wan, L. Gao, Y. Wu and L.-T. Yan, Self-assembly in curved space: Ordering, defect and entropy, Processes, 2024, 12, 119,  DOI:10.3390/pr12010119.
158. W. Li and M. Müller, Defects in the self-assembly of block copolymers and their relevance for directed self-assembly, Annu. Rev. Chem. Biomol. Eng., 2015, 6, 187–216,  DOI:10.1146/annurev-chembioeng-061114-123209.
159. P. A. Midgley and M. Weyland, 3D electron microscopy in the physical sciences: the development of Z-contrast and EFTEM tomography, Ultramicroscopy, 2003, 96, 413–431,  DOI:10.1016/S0304-3991(03)00105-0.
160. W. H. Evers, H. Friedrich, L. Filion, M. Dijkstra and D. Vanmaekelbergh, Observation of a ternary nanocrystal superlattice and its structural characterization by electron tomography, Angew. Chem., Int. Ed., 2009, 48, 9655–9657,  DOI:10.1002/anie.200904821.
161. H. Friedrich, C. J. Gommes, K. Overgaag, J. D. Meeldijk, W. H. Evers, B. de Nijs, M. P. Boneschanscher, P. E. de Jongh, A. J. Verkleij, K. P. de Jong, A. van Blaaderen and D. Vanmaekelbergh, Quantitative structural analysis of binary nanocrystal superlattices by electron tomography, Nano Lett., 2009, 9, 2719–2724,  DOI:10.1021/nl901212m.
162. M. P. Boneschanscher, W. H. Evers, W. Qi, J. D. Meeldijk, M. Dijkstra and D. Vanmaekelbergh, Electron tomography resolves a novel crystal structure in a binary nanocrystal superlattice, Nano Lett., 2013, 13, 1312–1316,  DOI:10.1021/nl400100c.
163. M. Cargnello, A. C. Johnston-Peck, B. T. Diroll, E. Wong, B. Datta, D. Damodhar, V. V. T. Doan-Nguyen, A. A. Herzing, C. R. Kagan and C. B. Murray, Substitutional doping in nanocrystal superlattices, Nature, 2015, 524, 450–453,  DOI:10.1038/nature14872.
164. F. M. Ross, Opportunities and challenges in liquid cell electron microscopy, Science, 2015, 350, aaa9886,  DOI:10.1126/science.aaa9886.
165. J. Park, H. Zheng, W. C. Lee, P. L. Geissler, E. Rabani and A. P. Alivisatos, Direct observation of nanoparticle superlattice formation by using liquid cell transmission electron microscopy, ACS Nano, 2012, 6, 2078–2085,  DOI:10.1021/nn203837m.
166. Y. Liu, X.-M. Lin, Y. Sun and T. Rajh, In situ visualization of self-assembly of charged gold nanoparticles, J. Am. Chem. Soc., 2013, 135, 3764–3767,  DOI:10.1021/ja312620e.
167. E. Sutter, P. Sutter, A. V. Tkachenko, R. Krahne, J. de Graaf, M. Arciniegas and L. Manna, In situ microscopy of the self-assembly of branched nanocrystals in solution, Nat. Commun., 2016, 7, 11213,  DOI:10.1038/ncomms11213.
168. Z. Ou, Z. Wang, B. Luo, E. Luijten and Q. Chen, Kinetic pathways of crystallization at the nanoscale, Nat. Mater., 2020, 19, 450–455,  DOI:10.1038/s41563-019-0514-1.
169. D. García-Lojo, S. Gómez-Graña, V. F. Martín, D. M. Solís, J. M. Taboada, J. Pérez-Juste and I. Pastoriza-Santos, Integrating plasmonic supercrystals in microfluidics for ultrasensitive, label-free, and selective surface-enhanced Raman spectroscopy detection, ACS Appl. Mater. Interfaces, 2020, 12, 46557–46564,  DOI:10.1021/acsami.0c13940.
170. D. García-Lojo, E. Modin, S. Gómez-Graña, M. Impéror-Clerc, A. Chuvilin, I. Pastoriza-Santos, J. Pérez-Juste, D. Constantin and C. Hamon, Structure and formation kinetics of millimeter-size single domain supercrystals, Adv. Funct. Mater., 2021, 31, 2101869,  DOI:10.1002/adfm.202101869.
171. T. Li, A. J. Senesi and B. Lee, Small angle X-ray scattering for nanoparticle research, Chem. Rev., 2016, 116, 11128–11180,  DOI:10.1021/acs.chemrev.5b00690.
172. A. J. Senesi and B. Lee, Small-angle scattering of particle assemblies, J. Appl. Cryst., 2015, 48, 1172–1182,  DOI:10.1107/S1600576715011474.
173. K. G. Yager, Y. Zhang, F. Lu and O. Gang, Periodic lattices of arbitrary nano-objects: modeling and applications for self-assembled systems, J. Appl. Cryst., 2014, 47, 118–129,  DOI:10.1107/S160057671302832X.
174. K. Bian, J. J. Choi, A. Kaushik, P. Clancy, D.-M. Smilgies and T. Hanrath, Shape-anisotropy driven symmetry transformations in nanocrystal superlattice polymorphs, ACS Nano, 2011, 5, 2815–2823,  DOI:10.1021/nn103303q.
175. M. C. Weidman, D.-M. Smilgies and W. A. Tisdale, Kinetics of the self-assembly of nanocrystal superlattices measured by real-time in situ X-ray scattering, Nat. Mater., 2016, 15, 775–781,  DOI:10.1038/nmat4600.
176. J. Chen, A. Dong, J. Cai, X. Ye, Y. Kang, J. M. Kikkawa and C. B. Murray, Collective dipolar interactions in self-assembled magnetic binary nanocrystal superlattice membranes, Nano Lett., 2010, 10, 5103–5108,  DOI:10.1021/nl103568q.
177. B. Sun and H. Sirringhaus, Surface tension and fluid flow driven self-assembly of ordered ZnO nanorod films for high-performance field effect transistors, J. Am. Chem. Soc., 2006, 128, 16231–16237,  DOI:10.1021/ja065242z.
178. G. I. Koleilat, L. Levina, H. Shukla, S. H. Myrskog, S. Hinds, A. G. Pattantyus-Abraham and E. H. Sargent, Efficient, stable infrared photovoltaics based on solution-cast colloidal quantum dots, ACS Nano, 2008, 2, 833–840,  DOI:10.1021/nn800093v.
179. D. V. Talapin and C. B. Murray, PbSe nanocrystal solids for n- and p-channel thin film field-effect transistors, Science, 2005, 310, 86–89,  DOI:10.1126/science.1116703.
180. A. T. Heitsch, R. N. Patel, B. W. Goodfellow, D. M. Smilgies and B. A. Korgel, GISAXS characterization of order in hexagonal monolayers of FePt nanocrystals, J. Phys. Chem. C, 2010, 114, 14427–14432,  DOI:10.1021/jp1047979.
181. D. K. Smith, B. Goodfellow, D. M. Smilgies and B. A. Korgel, Self-assembled simple hexagonal AB2 binary nanocrystal superlattices: SEM, GISAXS, and defects, J. Am. Chem. Soc., 2009, 131, 3281–3290,  DOI:10.1021/ja8085438.
182. B. Lee, P. Podsiadlo, S. Rupich, D. V. Talapin, T. Rajh and E. V. Shevchenko, Comparison of structural behavior of nanocrystals in randomly packed films and long-range ordered superlattices by time-resolved small angle X-ray scattering, J. Am. Chem. Soc., 2009, 131, 16386–16388,  DOI:10.1021/ja906632b.
183. S. Narayanan, J. Wang and X.-M. Lin, Dynamical self-assembly of nanocrystal superlattices during colloidal droplet evaporation by in situ small angle X-ray scattering, Phys. Rev. Lett., 2004, 93, 135503,  DOI:10.1103/PhysRevLett.93.135503.
184. F. X. Redl, K. S. Cho, C. B. Murray and S. O'Brien, Three-dimensional binary superlattices of magnetic nanocrystals and semiconductor quantum dots, Nature, 2003, 423, 968–971,  DOI:10.1038/nature01702.
185. M. D. Eldridge, P. A. Madden and D. Frenkel, The stability of the AB13 crystal in a binary hard sphere system, Mol. Phys., 1993, 79, 105–120,  DOI:10.1080/00268979300101101.
186. M. S. Somayazulu, L. W. Finger, R. J. Hemley and H. K. Mao, High-pressure compounds in methane-hydrogen mixtures, Science, 1996, 271, 1400–1402,  DOI:10.1126/science.271.5254.1400.
187. P. Loubeyre, R. LeToullec and J.-P. Pinceaux, Compression of Ar(H2)2 up to 175 GPa: A new path for the dissociation of molecular hydrogen?, Phys. Rev. Lett., 1994, 72, 1360–1363,  DOI:10.1103/PhysRevLett.72.1360.
188. S. Yoshimura and S. Hachisu, Order formation in binary mixtures of monodisperse latices, Prog. Colloid Polym. Sci., 1983, 68, 59–70,  DOI:10.1007/BFb0114141.
189. C. J. Kiely, J. Fink, J. G. Zheng, M. Brust, D. Bethell and D. J. Schiffrin, Ordered colloidal nanoalloys, Adv. Mater., 2000, 12, 640–643,  DOI:10.1002/(SICI)1521-4095(200005)12:9<640::AID-ADMA640>3.0.CO;2-J.
190. A. E. Saunders and B. A. Korgel, Observation of an AB phase in bidisperse nanocrystal superlattices, ChemPhysChem, 2005, 6, 61–65,  DOI:10.1002/cphc.200400382.
191. J. K. Bosworth, M. Y. Paik, R. Ruiz, E. L. Schwartz, J. Q. Huang, A. W. Ko, D.-M. Smilgies, C. T. Black and C. K. Ober, Control of self-assembly of lithographically patternable block copolymer films, ACS Nano, 2008, 2, 1396–1402,  DOI:10.1021/nn8001505.
192. W. Ruland and B. M. Smarsly, Two-dimensional small-angle X-ray scattering of self-assembled nanocomposite films with oriented arrays of spheres: determination of lattice type, preferred orientation, deformation and imperfection, J. Appl. Crystallogr., 2007, 40, 409–417,  DOI:10.1107/S0021889807010503.
193. D. Dunphy, H. Fan, X. Li, J. Wang and C. J. Brinker, Dynamic investigation of gold nanocrystal assembly using in situ grazing-incidence small-angle X-ray scattering, Langmuir, 2008, 24, 10575–10578,  DOI:10.1021/la802120n.
194. X. Ye, J. Chen and C. B. Murray, Polymorphism in self-assembled AB6 binary nanocrystal superlattices, J. Am. Chem. Soc., 2011, 133, 2613–2620,  DOI:10.1021/ja108708v.
195. O. Zhou, J. E. Fischer, N. Coustel, S. Kycia, Q. Zhu, A. R. McGhie, W. J. Romanow, J. P. McCauley, A. B. Smith and D. E. Cox, Structure and bonding in alkali-metal-doped C60, Nature, 1991, 351, 462–464,  DOI:10.1038/351462a0.
196. M. E. Leunissen, C. G. Christova, A.-P. Hynninen, C. P. Royall, A. I. Campbell, A. Imhof, M. Dijkstra, R. van Roij and A. van Blaaderen, Ionic colloidal crystals of oppositely charged particles, Nature, 2005, 437, 235–240,  DOI:10.1038/nature03946.
197. Z. L. Wang, Structural analysis of self-assembling nanocrystal superlattices, Adv. Mater., 1998, 10, 13–30,  DOI:10.1002/(SICI)1521-4095(199801)10:1<13::AID-ADMA13>3.0.CO;2-W.
198. D. Shechtman, I. Blech, D. Gratias and J. W. Cahn, Metallic phase with long-range orientational order and no translational symmetry, Phys. Rev. Lett., 1984, 53, 1951–1953,  DOI:10.1103/PhysRevLett.53.1951.
199. D. Levine and P. J. Steinhardt, Quasicrystals: A new class of ordered structures, Phys. Rev. Lett., 1984, 53, 2477–2480,  DOI:10.1103/PhysRevLett.53.2477.
200. A. S. Keys and S. C. Glotzer, How do quasicrystals grow, Phys. Rev. Lett., 2007, 99, 235503,  DOI:10.1103/PhysRevLett.99.235503.
201. E. Abe, Y. Yan and S. J. Pennycook, Quasicrystals as cluster aggregates, Nat. Mater., 2004, 3, 759–767,  DOI:10.1038/nmat1244.
202. M. Widom, Bethe ansatz solution of the square-triangle random tiling model, Phys. Rev. Lett., 1993, 70, 2094–2097,  DOI:10.1103/PhysRevLett.70.2094.
203. M. Oxborrow and C. L. Henley, Random square-triangle tilings: A model for twelvefold-symmetric quasicrystals, Phys. Rev. B, 1993, 48, 6966–6998,  DOI:10.1103/PhysRevB.48.6966.
204. N. Peyerimhoff and M. Täufer, Eigenfunctions and the integrated density of states on Archimedean tilings, J. Spectr. Theory, 2021, 11, 461–488,  DOI:10.4171/JST/347.
205. K. Ueda, T. Dotera and T. Gemma, Photonic band structure calculations of two-dimensional Archimedean tiling patterns, Phys. Rev. B, 2007, 75, 195122,  DOI:10.1103/PhysRevB.75.195122.
206. M. I. Bodnarchuk, R. Erni, F. Krumeich and M. V. Kovalenko, Binary superlattices from colloidal nanocrystals and giant polyoxometalate clusters, Nano Lett., 2013, 13, 1699–1705,  DOI:10.1021/nl4002475.
207. D. Volkmer, A. Du Chesne, D. G. Kurth, H. Schnablegger, P. Lehmann, M. J. Koop and A. Müller, Toward nanodevices:  Synthesis and characterization of the nanoporous surfactant-encapsulated Keplerate (DODA)40(NH₄)2[(H₂O)_n⊂Mo132O372(CH₃COO)30(H₂O)72], J. Am. Chem. Soc., 2000, 122, 1995–1998,  DOI:10.1021/ja992350v.
208. Z. Yang, J. Wei, P. Bonville and M.-P. Pileni, Beyond Entropy: Magnetic forces induce formation of quasicrystalline structure in binary nanocrystal superlattices, J. Am. Chem. Soc., 2015, 137, 4487–4493,  DOI:10.1021/jacs.5b00332.
209. M. D. Eldridge, P. A. Madden, P. N. Pusey and P. Bartlett, Binary hard-sphere mixtures: a comparison between computer simulation and experiment, Mol. Phys., 1995, 84, 395–420,  DOI:10.1080/00268979500100271.
210. S. Auer and D. Frenkel, Suppression of crystal nucleation in polydisperse colloids due to increase of the surface free energy, Nature, 2001, 413, 711–713,  DOI:10.1038/35099513.
211. K. Overgaag, W. Evers, B. de Nijs, R. Koole, J. Meeldijk and D. Vanmaekelbergh, Binary superlattices of PbSe and CdSe nanocrystals, J. Am. Chem. Soc., 2008, 130, 7833–7835,  DOI:10.1021/ja802932m.
212. N. Hunt, R. Jardine and P. Bartlett, Superlattice formation in mixtures of hard-sphere colloids, Phys. Rev. E, 2000, 62, 900–913,  DOI:10.1103/PhysRevE.62.900.
213. P. Schapotschnikow, R. Pool and T. J. H. Vlugt, Molecular simulations of interacting nanocrystals, Nano Lett., 2008, 8, 2930–2934,  DOI:10.1021/nl8017862.
214. M. A. Boles and D. V. Talapin, Many-body effects in nanocrystal superlattices: Departure from sphere packing explains stability of binary phases, J. Am. Chem. Soc., 2015, 137, 4494–4502,  DOI:10.1021/jacs.5b00839.
215. P. Schapotschnikow and T. J. H. Vlugt, Understanding interactions between capped nanocrystals: Three-body and chain packing effects, J. Chem. Phys., 2009, 131, 124705,  DOI:10.1063/1.3227043.
216. M. W. Matsen, Effect of chain tilt on the interaction between brush-coated colloids, Macromolecules, 2005, 38, 4525–4530,  DOI:10.1021/ma050362x.
217. J. Wei, N. Schaeffer and M.-P. Pileni, Ligand exchange governs the crystal structures in binary nanocrystal superlattices, J. Am. Chem. Soc., 2015, 137, 14773–14784,  DOI:10.1021/jacs.5b09959.
218. L. Filion and M. Dijkstra, Prediction of binary hard-sphere crystal structures, Phys. Rev. E, 2009, 79, 046714,  DOI:10.1103/PhysRevE.79.046714.
219. X. Ji, D. Copenhaver, C. Sichmeller and X. Peng, Ligand bonding and dynamics on colloidal nanocrystals at room temperature: The case of alkylamines on CdSe nanocrystals, J. Am. Chem. Soc., 2008, 130, 5726–5735,  DOI:10.1021/ja710909f.
220. Y. Nagaoka, O. Chen, Z. Wang and Y. C. Cao, Structural control of nanocrystal superlattices using organic guest molecules, J. Am. Chem. Soc., 2012, 134, 2868–2871,  DOI:10.1021/ja209062d.
221. I. Coropceanu, M. A. Boles and D. V. Talapin, Systematic mapping of binary nanocrystal superlattices: The role of topology in phase selection, J. Am. Chem. Soc., 2019, 141, 5728–5740,  DOI:10.1021/jacs.8b12539.
222. A. Travesset, Soft skyrmions, spontaneous valence and selection rules in nanoparticle superlattices, ACS Nano, 2017, 11, 5375–5382,  DOI:10.1021/acsnano.7b02219.
223. A. Travesset, Topological structure prediction in binary nanoparticle superlattices, Soft Matter, 2017, 13, 147–157,  10.1039/C6SM00713A.
224. T. Kawasaki and H. Tanaka, Formation of a crystal nucleus from liquid, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 14036–14041,  DOI:10.1073/pnas.1001040107.
225. H. Jónsson and H. C. Andersen, Icosahedral ordering in the Lennard-Jones liquid and glass, Phys. Rev. Lett., 1988, 60, 2295–2298,  DOI:10.1103/PhysRevLett.60.2295.
226. H. Reichert, O. Klein, H. Dosch, M. Denk, V. Honkimäki, T. Lippmann and G. Reiter, Observation of five-fold local symmetry in liquid lead, Nature, 2000, 408, 839–841,  DOI:10.1038/35048537.
227. J. P. K. Doye and D. J. Wales, Structural consequences of the range of the interatomic potential A menagerie of clusters, J. Chem. Soc., Faraday Trans., 1997, 93, 4233–4243,  10.1039/A706221D.
228. U. Gasser, A. Schofield and D. A. Weitz, Local order in a supercooled colloidal fluid observed by confocal microscopy, J. Phys.:Condens. Matter, 2003, 15, S375–S380,  DOI:10.1088/0953-8984/15/1/351.
229. F. C. Frank, Supercooling of liquids, Proc. R. Soc. London, Ser. A, 1952, 215, 43–46,  DOI:10.1098/rspa.1952.0194.
230. T. Wang, J. Zhuang, J. Lynch, O. Chen, Z. Wang, X. Wang, D. LaMontagne, H. Wu, Z. Wang and Y. C. Cao, Long-range ordered carbon clusters: A crystalline material with amorphous building blocks, Science, 2012, 338, 358–363,  DOI:10.1126/science.1220522.
231. J. V. Sanders and M. J. Murray, Ordered arrangements of spheres of two different sizes in opal, Nature, 1978, 275, 201–203,  DOI:10.1038/275201a0.
232. S. Hachisu and S. Yoshimura, Optical demonstration of crystalline superstructures in binary mixtures of latex globules, Nature, 1980, 283, 188–189,  DOI:10.1038/283188a0.
233. P. Bartlett, R. H. Ottewill and P. N. Pusey, Superlattice formation in binary mixtures of hard-sphere colloids, Phys. Rev. Lett., 1992, 68, 3801–3804,  DOI:10.1103/PhysRevLett.68.3801.
234. I. Cherniukh, G. Rainò, T. V. Sekh, C. Zhu, Y. Shynkarenko, R. A. John, E. Kobiyama, R. F. Mahrt, T. Stöferle, R. Erni, M. V. Kovalenko and M. I. Bodnarchuk, Shape-directed co-assembly of lead halide perovskite nanocubes with dielectric nanodisks into binary nanocrystal superlattices, ACS Nano, 2021, 15, 16488–16500,  DOI:10.1021/acsnano.1c06047.
235. T. Paik, B. T. Diroll, C. R. Kagan and C. B. Murray, Binary and ternary superlattices self-assembled from colloidal nanodisks and nanorods, J. Am. Chem. Soc., 2015, 137, 6662–6669,  DOI:10.1021/jacs.5b03234.
236. J. L. Elechiguerra, J. Reyes-Gasga and M. J. Yacaman, The role of twinning in shape evolution of anisotropic noble metal nanostructures, J. Mater. Chem., 2006, 16, 3906–3919,  10.1039/B607128G.
237. T. Paik and C. B. Murray, Shape-directed binary assembly of anisotropic nanoplates: A nanocrystal puzzle with shape-complementary building blocks, Nano Lett., 2013, 13, 2952–2956,  DOI:10.1021/nl401370n.
238. T. Paik, D.-K. Ko, T. R. Gordon, V. Doan-Nguyen and C. B. Murray, Studies of liquid crystalline self-assembly of GdF3 nanoplates by in-plane, out-of-plane SAXS, ACS Nano, 2011, 5, 8322–8330,  DOI:10.1021/nn203049t.
239. K. C. Elbert, W. Zygmunt, T. Vo, C. M. Vara, D. J. Rosen, N. M. Krook, S. C. Glotzer and C. B. Murray, Anisotropic nanocrystal shape and ligand design for co-assembly, Sci. Adv., 2021, 7, eabf9402,  DOI:10.1126/sciadv.abf9402.
240. I. Cherniukh, T. V. Sekh, G. Rainò, O. J. Ashton, M. Burian, A. Travesset, M. Athanasiou, A. Manoli, R. A. John, M. Svyrydenko, V. Morad, Y. Shynkarenko, F. Montanarella, D. Naumenko, H. Amenitsch, G. Itskos, R. F. Mahrt, T. Stöferle, R. Erni, M. V. Kovalenko and M. I. Bodnarchuk, Structural diversity in multicomponent nanocrystal superlattices comprising lead halide perovskite nanocubes, ACS Nano, 2022, 16, 7210–7232,  DOI:10.1021/acsnano.1c10702.
241. E. V. Shevchenko, J. B. Kortright, D. V. Talapin, S. Aloni and A. P. Alivisatos, Quasi-ternary nanoparticle superlattices through nanoparticle design, Adv. Mater., 2007, 19, 4183–4187,  DOI:10.1002/adma.200701470.
242. I. Cherniukh, G. Rainò, T. Stöferle, M. Burian, A. Travesset, D. Naumenko, H. Amenitsch, R. Erni, R. F. Mahrt, M. I. Bodnarchuk and M. V. Kovalenko, Perovskite-type superlattices from lead halide perovskite nanocubes, Nature, 2021, 593, 535–542,  DOI:10.1038/s41586-021-03492-5.
243. K. Baumann, C. Guerlin, F. Brennecke and T. Esslinger, Dicke quantum phase transition with a superfluid gas in an optical cavity, Nature, 2010, 464, 1301–1306,  DOI:10.1038/nature09009.
244. P. Strack and S. Sachdev, Dicke quantum spin glass of atoms and photons, Phys. Rev. Lett., 2011, 107, 277202,  DOI:10.1103/PhysRevLett.107.277202.
245. C. Sánchez Muñoz, E. del Valle, A. González Tudela, K. Müller, S. Lichtmannecker, M. Kaniber, C. Tejedor, J. J. Finley and F. P. Laussy, Emitters of N-photon bundles, Nat. Photonics, 2014, 8, 550–555,  DOI:10.1038/nphoton.2014.114.
246. H. Wang, J. Qin, X. Ding, M.-C. Chen, S. Chen, X. You, Y.-M. He, X. Jiang, L. You, Z. Wang, C. Schneider, J. J. Renema, S. Höfling, C.-Y. Lu and J.-W. Pan, Boson sampling with 20 input photons and a 60-mode interferometer in a 1014-dimensional Hilbert space, Phys. Rev. Lett., 2019, 123, 250503,  DOI:10.1103/PhysRevLett.123.250503.
247. R. Tenne, U. Rossman, B. Rephael, Y. Israel, A. Krupinski-Ptaszek, R. Lapkiewicz, Y. Silberberg and D. Oron, Super-resolution enhancement by quantum image scanning microscopy, Nat. Photonics, 2019, 13, 116–122,  DOI:10.1038/s41566-018-0324-z.
248. A. Dong, J. Chen, P. M. Vora, J. M. Kikkawa and C. B. Murray, Binary nanocrystal superlattice membranes self-assembled at the liquid-air interface, Nature, 2010, 466, 474–477,  DOI:10.1038/nature09188.
249. W. Liu, M. Kappl, W. Steffen and H.-J. Butt, Controlling supraparticle shape and structure by tuning colloidal interactions, J. Colloid Interface Sci., 2022, 607, 1661–1670,  DOI:10.1016/j.jcis.2021.09.035.
250. T. Kister, M. Mravlak, T. Schilling and T. Kraus, Pressure-controlled formation of crystalline, Janus, and core–shell supraparticles, Nanoscale, 2016, 8, 13377–13384,  10.1039/C6NR01940D.
251. T. Udayabhaskararao, T. Altantzis, L. Houben, M. Coronado-Puchau, J. Langer, R. Popovitz-Biro, L. M. Liz-Marzán, L. Vuković, P. Král, S. Bals and R. Klajn, Tunable porous nanoallotropes prepared by post-assembly etching of binary nanoparticle superlattices, Science, 2017, 358, 514–518,  DOI:10.1126/science.aan6046.
252. V. Aleksandrovic, D. Greshnykh, I. Randjelovic, A. Frömsdorf, A. Kornowski, S. V. Roth, C. Klinke and H. Weller, Preparation and electrical properties of cobalt-platinum nanoparticle monolayers deposited by the Langmuir–Blodgett technique, ACS Nano, 2008, 2, 1123–1130,  DOI:10.1021/nn800147a.
253. A. Dong, X. Ye, J. Chen and C. B. Murray, Two-dimensional binary and ternary nanocrystal superlattices: The case of monolayers and bilayers, Nano Lett., 2011, 11, 1804–1809,  DOI:10.1021/nl200468p.
254. X. Ye, C. Zhu, P. Ercius, S. N. Raja, B. He, M. R. Jones, M. R. Hauwiller, Y. Liu, T. Xu and A. P. Alivisatos, Structural diversity in binary superlattices self-assembled from polymer-grafted nanocrystals, Nat. Commun., 2015, 6, 10052,  DOI:10.1038/ncomms10052.
255. A.-P. Hynninen, C. G. Christova, R. van Roij, A. van Blaaderen and M. Dijkstra, Prediction and observation of crystal structures of oppositely charged colloids, Phys. Rev. Lett., 2006, 96, 138308,  DOI:10.1103/PhysRevLett.96.138308.
256. R. J. Macfarlane, B. Lee, M. R. Jones, N. Harris, G. C. Schatz and C. A. Mirkin, Nanoparticle superlattice engineering with DNA, Science, 2011, 334, 204–208,  DOI:10.1126/science.1210493.
257. Y. Wang, Y. Wang, X. Zheng, É. Ducrot, J. S. Yodh, M. Weck and D. J. Pine, Crystallization of DNA-coated colloids, Nat. Commun., 2015, 6, 7253,  DOI:10.1038/ncomms8253.
258. H. J. Taunton, C. Toprakcioglu, L. J. Fetters and J. Klein, Interactions between surfaces bearing end-adsorbed chains in a good solvent, Macromolecules, 1990, 23, 571–580,  DOI:10.1021/ma00204a033.
259. J. U. Kim and M. W. Matsen, Interaction between polymer-grafted particles, Macromolecules, 2008, 41, 4435–4443,  DOI:10.1021/ma8002856.
260. Y. Yu, C. A. Bosoy, D. M. Smilgies and B. A. Korgel, Self-assembly and thermal stability of binary superlattices of gold and silicon nanocrystals, J. Phys. Chem. Lett., 2013, 4, 3677–3682,  DOI:10.1021/jz401964s.
261. S. M. Rupich, F. C. Castro, W. T. M. Irvine and D. V. Talapin, Soft epitaxy of nanocrystal superlattices, Nat. Commun., 2014, 5, 5045,  DOI:10.1038/ncomms6045.
262. S. Coe, W.-K. Woo, M. Bawendi and V. Bulović, Electroluminescence from single monolayers of nanocrystals in molecular organic devices, Nature, 2002, 420, 800–803,  DOI:10.1038/nature01217.
263. H. Maeda and Y. Maeda, Liquid crystal formation in suspensions of hard rodlike colloidal particles: Direct observation of particle arrangement and self-ordering behavior, Phys. Rev. Lett., 2003, 90, 018303,  DOI:10.1103/PhysRevLett.90.018303.
264. X. Ye, J. A. Millan, M. Engel, J. Chen, B. T. Diroll, S. C. Glotzer and C. B. Murray, Shape alloys of nanorods and nanospheres from self-assembly, Nano Lett, 2013, 13, 4980–4988,  DOI:10.1021/nl403149u.
265. X. Ye, J. E. Collins, Y. Kang, J. Chen, D. T. N. Chen, A. G. Yodh and C. B. Murray, Morphologically controlled synthesis of colloidal upconversion nanophosphors and their shape-directed self-assembly, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 22430–22435,  DOI:10.1073/pnas.1008958107.
266. C. Tschierske, Liquid crystal engineering – new complex mesophase structures and their relations to polymer morphologies, nanoscale patterning and crystal engineering, Chem. Soc. Rev., 2007, 36, 1930–1970,  10.1039/B615517K.
267. L. Assoud, R. Messina and H. Löwen, Stable crystalline lattices in two-dimensional binary mixtures of dipolar particles, Europhys. Lett., 2007, 80, 48001,  DOI:10.1209/0295-5075/80/48001.
268. O. U. Uche, F. H. Stillinger and S. Torquato, Concerning maximal packing arrangements of binary disk mixtures, Phys. A, 2004, 342, 428–446,  DOI:10.1016/j.physa.2004.05.082.
269. C. N. Likos and C. L. Henley, Complex alloy phases for binary hard-disc mixtures, Philos. Mag. B, 1993, 68, 85–113,  DOI:10.1080/13642819308215284.
270. A. Castelli, J. de Graaf, M. Prato, L. Manna and M. P. Arciniegas, Tic-tac-toe binary lattices from the interfacial self-assembly of branched and spherical nanocrystals, ACS Nano, 2016, 10, 4345–4353,  DOI:10.1021/acsnano.5b08018.
271. D. Witt, R. Klajn, P. Barski and B. A. Grzybowski, Applications, Properties and Synthesis of ω-Functionalized n-Alkanethiols and Disulfides - the Building Blocks of Self-Assembled Monolayers, Curr. Org. Chem., 2004, 8, 1763–1797,  DOI:10.2174/1385272043369421.
272. J. Z. Wu, D. Bratko, H. W. Blanch and J. M. Prausnitz, Monte Carlo simulation for the potential of mean force between ionic colloids in solutions of asymmetric salts, J. Chem. Phys., 1999, 111, 7084–7094,  DOI:10.1063/1.480000.
273. P. Ziherl and R. D. Kamien, Maximizing entropy by minimizing area: Towards a new principle of self-organization, J. Phys. Chem. B, 2001, 105, 10147–10158,  DOI:10.1021/jp010944q.
274. L. Salem, Attractive forces between long saturated chains at short distances, J. Chem. Phys., 1962, 37, 2100–2113,  DOI:10.1063/1.1733431.
275. P. Ziherl and R. D. Kamien, Soap froths and crystal structures, Phys. Rev. Lett., 2000, 85, 3528–3531,  DOI:10.1103/PhysRevLett.85.3528.
276. A. P. Alivisatos, K. P. Johnsson, X. Peng, T. E. Wilson, C. J. Loweth, M. P. Bruchez and P. G. Schultz, Organization of 'nanocrystal molecules' using DNA, Nature, 1996, 382, 609–611,  DOI:10.1038/382609a0.
277. S. Y. Park, A. K. R. Lytton-Jean, B. Lee, S. Weigand, G. C. Schatz and C. A. Mirkin, DNA-programmable nanoparticle crystallization, Nature, 2008, 451, 553–556,  DOI:10.1038/nature06508.
278. D. Nykypanchuk, M. M. Maye, D. Van Der Lelie and O. Gang, DNA-guided crystallization of colloidal nanoparticles, Nature, 2008, 451, 549–552,  DOI:10.1038/nature06560.
279. N. C. Seeman and O. Gang, Three-dimensional molecular and nanoparticle crystallization by DNA nanotechnology, MRS Bull., 2017, 42, 904–912,  DOI:10.1557/mrs.2017.280.
280. M. R. Jones, N. C. Seeman and C. A. Mirkin, Programmable materials and the nature of the DNA bond, Science, 2015, 347, 1260901,  DOI:10.1126/science.1260901.
281. J. S. Kahn and O. Gang, Designer nanomaterials through programmable assembly, Angew. Chem., Int. Ed., 2022, 61, e202105678,  DOI:10.1002/anie.202105678.
282. F. Hong, F. Zhang, Y. Liu and H. Yan, DNA origami: Scaffolds for creating higher order structures, Chem. Rev., 2017, 117, 12584–12640,  DOI:10.1021/acs.chemrev.6b00825.
283. W. B. Rogers, W. M. Shih and V. N. Manoharan, Using DNA to program the self-assembly of colloidal nanoparticles and microparticles, Nat. Rev. Mater., 2016, 1, 16008,  DOI:10.1038/natrevmats.2016.8.
284. Y. Ke, L. L. Ong, W. M. Shih and P. Yin, Three-dimensional structures self-assembled from DNA bricks, Science, 2012, 338, 1177–1183,  DOI:10.1126/science.1227268.
285. C. Knorowski and A. Travesset, Self-assembly and crystallization of hairy (f-star) and DNA-grafted nanocubes, J. Am. Chem. Soc., 2014, 136, 653–659,  DOI:10.1021/ja406241n.
286. C. Knorowski and A. Travesset, Materials design by DNA programmed self-assembly, Curr. Opin. Solid State Mater. Sci., 2011, 15, 262–270,  DOI:10.1016/j.cossms.2011.07.002.
287. R. Sknepnek, G. Vernizzi and M. O. De La Cruz, Buckling of multicomponent elastic shells with line tension, Soft Matter, 2012, 8, 636–644,  10.1039/C1SM06325A.
288. H. Lin, S. Lee, L. Sun, M. Spellings, M. Engel, S. C. Glotzer and C. A. Mirkin, Clathrate colloidal crystals, Science, 2017, 355, 931–935,  DOI:10.1126/science.aal3919.
289. M. N. O’Brien, M. R. Jones, B. Lee and C. A. Mirkin, Anisotropic nanoparticle complementarity in DNA-mediated co-crystallization, Nat. Mater., 2015, 14, 833–839,  DOI:10.1038/nmat4293.
290. F. Lu, T. Vo, Y. Zhang, A. Frenkel, K. G. Yager, S. Kumar and O. Gang, Unusual packing of soft-shelled nanocubes, Sci. Adv., 2019, 5, eaaw2399,  DOI:10.1126/sciadv.aaw2399.
291. F. Lu, K. G. Yager, Y. Zhang, H. Xin and O. Gang, Superlattices assembled through shape-induced directional binding, Nat. Commun., 2015, 6, 6912,  DOI:10.1038/ncomms7912.
292. W. Liu, M. Tagawa, H. L. Xin, T. Wang, H. Emamy, H. Li, K. G. Yager, F. W. Starr, A. V. Tkachenko and O. Gang, Diamond family of nanoparticle superlattices, Science, 2016, 351, 582–586,  DOI:10.1126/science.aad2080.
293. Y. Tian, Y. Zhang, T. Wang, H. L. Xin, H. Li and O. Gang, Lattice engineering through nanoparticle–DNA frameworks, Nat. Mater., 2016, 15, 654–661,  DOI:10.1038/nmat4571.
294. M. Y. Ben Zion, X. He, C. C. Maass, R. Sha, N. C. Seeman and P. M. Chaikin, Self-assembled three-dimensional chiral colloidal architecture, Science, 2017, 358, 633–636,  DOI:10.1126/science.aan5404.
295. T. Zhang, C. Hartl, K. Frank, A. Heuer-Jungemann, S. Fischer, P. C. Nickels, B. Nickel and T. Liedl, 3D DNA origami crystals, Adv. Mater., 2018, 30, 1800273,  DOI:10.1002/adma.201800273.
296. Y. Tian, J. R. Lhermitte, L. Bai, T. Vo, H. L. Xin, H. Li, R. Li, M. Fukuto, K. G. Yager, J. S. Kahn, Y. Xiong, B. Minevich, S. K. Kumar and O. Gang, Ordered three-dimensional nanomaterials using DNA-prescribed and valence-controlled material voxels, Nat. Mater., 2020, 19, 789–796,  DOI:10.1038/s41563-019-0550-x.
297. R. J. Macfarlane, B. Lee, H. D. Hill, A. J. Senesi, S. Seifert and C. A. Mirkin, Assembly and organization processes in DNA-directed colloidal crystallization, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 10493–10498,  DOI:10.1073/pnas.0900630106.
298. S. J. Park, A. A. Lazarides, J. J. Storhoff, L. Pesce and C. A. Mirkin, The structural characterization of oligonucleotide-modified gold nanoparticle networks formed by DNA hybridization, J. Phys. Chem. B, 2004, 108, 12375–12380,  DOI:10.1021/jp040242b.
299. L. V. Woodcock, Entropy difference between the face-centred cubic and hexagonal close-packed crystal structures, Nature, 1997, 385, 141–143,  DOI:10.1038/385141a0.
300. R. J. Macfarlane, M. N. O'Brien, S. H. Petrosko and C. A. Mirkin, Nucleic acid-modified nanostructures as programmable atom equivalents: Forging a new “table of elements, Angew. Chem., Int. Ed., 2013, 52, 5688–5698,  DOI:10.1002/anie.201209336.
301. R. J. Macfarlane, R. V. Thaner, K. A. Brown, J. Zhang, B. Lee, S. B. T. Nguyen and C. A. Mirkin, Importance of the DNA “bond” in programmable nanoparticle crystallization, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 14995–15000,  DOI:10.1073/pnas.1416489111.
302. M. R. Jones, R. J. Macfarlane, B. Lee, J. Zhang, K. L. Young, A. J. Senesi and C. A. Mirkin, DNA-nanoparticle superlattices formed from anisotropic building blocks, Nat. Mater., 2010, 9, 913–917,  DOI:10.1038/nmat2870.
303. R. J. Macfarlane, M. R. Jones, A. J. Senesi, K. L. Young, B. Lee, J. Wu and C. A. Mirkin, Establishing the design rules for DNA-mediated programmable colloidal crystallization, Angew. Chem., Int. Ed., 2010, 49, 4589–4592,  DOI:10.1002/anie.201000633.
304. M. N. O'Brien, B. Radha, K. A. Brown, M. R. Jones and C. A. Mirkin, Langmuir analysis of nanoparticle polyvalency in DNA-mediated adsorption, Angew. Chem., Int. Ed., 2014, 53, 9532–9538,  DOI:10.1002/anie.201405317.
305. R. Jin, G. Wu, Z. Li, C. A. Mirkin and G. C. Schatz, What controls the melting properties of DNA-linked gold nanoparticle assemblies?, J. Am. Chem. Soc., 2003, 125, 1643–1654,  DOI:10.1021/ja021096v.
306. W. Zhou, Y. Li, K. Je, T. Vo, H. Lin, B. E. Partridge, Z. Huang, S. C. Glotzer and C. A. Mirkin, Space-tiled colloidal crystals from DNA-forced shape-complementary polyhedra pairing, Science, 2024, 383, 312–319,  DOI:10.1126/science.adj1021.
307. M. R. Khadilkar and F. A. Escobedo, Self-assembly of binary space-tessellating compounds, J. Chem. Phys., 2012, 137, 194907,  DOI:10.1063/1.4765699.
308. Y. Wang, J. Chen, C. Zhu, B. Zhu, S. Jeong, Y. Yi, Y. Liu, J. Fiadorwu, P. He and X. Ye, Kinetically controlled self-assembly of binary polymer-grafted nanocrystals into ordered superstructures via solvent vapor annealing, Nano Lett., 2021, 21, 5053–5059,  DOI:10.1021/acs.nanolett.1c00890.
309. J. Russo and H. Tanaka, Nonclassical pathways of crystallization in colloidal systems, MRS Bull., 2016, 41, 369–374,  DOI:10.1557/mrs.2016.84.
310. J. J. De Yoreo, P. Gilbert, N. Sommerdijk, R. L. Penn, S. Whitelam, D. Joester, H. Zhang, J. D. Rimer, A. Navrotsky, J. F. Banfield, A. F. Wallace, F. M. Michel, F. C. Meldrum, H. Cölfen and P. M. Dove, Crystallization by particle attachment in synthetic, biogenic, and geologic environments, Science, 2015, 349, aaa6760,  DOI:10.1126/science.aaa6760.
311. R. A. LaCour, C. S. Adorf, J. Dshemuchadse and S. C. Glotzer, Influence of softness on the stability of binary colloidal crystals, ACS Nano, 2019, 13, 13829–13842,  DOI:10.1021/acsnano.9b04274.
312. T. Dasgupta, G. M. Coli and M. Dijkstra, Tuning the glass transition: Enhanced crystallization of the laves phases in nearly hard spheres, ACS Nano, 2020, 14, 3957–3968,  DOI:10.1021/acsnano.9b07090.
313. J. Zhuang, H. Wu, Y. Yang and Y. C. Cao, Supercrystalline colloidal particles from artificial atoms, J. Am. Chem. Soc., 2007, 129, 14166–14167,  DOI:10.1021/ja076494i.
314. J. Zhuang, H. Wu, Y. Yang and Y. C. Cao, Controlling colloidal superparticle growth through solvophobic interactions, Angew. Chem., Int. Ed., 2008, 47, 2208–2212,  DOI:10.1002/anie.200705049.
315. P.-P. Wang, Q. Qiao, Y. Zhu and M. Ouyang, Colloidal binary supracrystals with tunable structural lattices, J. Am. Chem. Soc., 2018, 140, 9095–9098,  DOI:10.1021/jacs.8b05643.
316. A. Travesset, Binary nanoparticle superlattices of soft-particle systems, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 9563–9567,  DOI:10.1073/pnas.1504677112.
317. A. V. Tkachenko, Generic phase diagram of binary superlattices, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 10269–10274,  DOI:10.1073/pnas.1525358113.
318. D. Luo, C. Yan and T. Wang, Interparticle forces underlying nanoparticle self-assemblies, Small, 2015, 11, 5984–6008,  DOI:10.1002/smll.201501783.
319. Y. Yang, B. Wang, X. Shen, L. Yao, L. Wang, X. Chen, S. Xie, T. Li, J. Hu, D. Yang and A. Dong, Scalable assembly of crystalline binary nanocrystal superparticles and their enhanced magnetic and electrochemical properties, J. Am. Chem. Soc., 2018, 140, 15038–15047,  DOI:10.1021/jacs.8b09779.
320. M. H. Lash, J. C. Jordan, L. C. Blevins, M. V. Fedorchak, S. R. Little and J. J. McCarthy, Non-brownian particle-based materials with microscale and nanoscale hierarchy, Angew. Chem., Int. Ed., 2015, 54, 5854–5858,  DOI:10.1002/anie.201500273.
321. E. R. Nowak, J. B. Knight, E. Ben-Naim, H. M. Jaeger and S. R. Nagel, Density fluctuations in vibrated granular materials, Phys. Rev. E, 1998, 57, 1971–1982,  DOI:10.1103/PhysRevE.57.1971.
322. M. H. Lash, M. V. Fedorchak, S. R. Little and J. J. McCarthy, Fabrication and characterization of non-brownian particle-based crystals, Langmuir, 2015, 31, 898–905,  DOI:10.1021/la501511s.
323. A. Jain, M. J. Metzger and B. J. Glasser, Effect of particle size distribution on segregation in vibrated systems, Powder Technol., 2013, 237, 543–553,  DOI:10.1016/j.powtec.2012.12.044.
324. M. J. Metzger, B. Remy and B. J. Glasser, All the Brazil nuts are not on top: Vibration induced granular size segregation of binary, ternary and multi-sized mixtures, Powder Technol., 2011, 205, 42–51,  DOI:10.1016/j.powtec.2010.08.062.
325. R. Brito and R. Soto, Competition of Brazil nut effect, buoyancy, and inelasticity induced segregation in a granular mixture, Eur. Phys. J.:Spec. Top., 2009, 179, 207–219,  DOI:10.1140/epjst/e2010-01204-5.
326. Z. Xie, P. Wu, S. Wang, Y. Huang, S. Zhang, S. Chen, C. Jia, C. Liu and L. Wang, Behaviour of a binary particle system under the effects of simultaneous vertical vibration and rotation, Soft Matter, 2013, 9, 5074–5086,  10.1039/C3SM26982E.
327. L. Antl, J. W. Goodwin, R. D. Hill, R. H. Ottewill, S. M. Owens, S. Papworth and J. A. Waters, The preparation of poly(methyl methacrylate) latices in non-aqueous media, Colloids Surf., 1986, 17, 67–78,  DOI:10.1016/0166-6622(86)80187-1.
328. P. Bartlett, R. H. Ottewill and P. N. Pusey, Freezing of binary mixtures of colloidal hard spheres, J. Chem. Phys., 1990, 93, 1299–1312,  DOI:10.1063/1.459142.
329. N. Vogel, L. de Viguerie, U. Jonas, C. K. Weiss and K. Landfester, Wafer-scale fabrication of ordered binary colloidal monolayers with adjustable stoichiometries, Adv. Funct. Mater., 2011, 21, 3064–3073,  DOI:10.1002/adfm.201100414.
330. R. Mukhopadhyay, O. Al-Hanbali, S. Pillai, A. G. Hemmersam, R. L. Meyer, A. C. Hunter, K. J. Rutt, F. Besenbacher, S. M. Moghimi and P. Kingshott, Ordering of binary polymeric nanoparticles on hydrophobic surfaces assembled from low volume fraction dispersions, J. Am. Chem. Soc., 2007, 129, 13390–13391,  DOI:10.1021/ja075988c.
331. R. D. Deegan, O. Bakajin, T. F. Dupont, G. Huber, S. R. Nagel and T. A. Witten, Capillary flow as the cause of ring stains from dried liquid drops, Nature, 1997, 389, 827–829,  DOI:10.1038/39827.
332. G. Singh, S. Pillai, A. Arpanaei and P. Kingshott, Highly ordered mixed protein patterns over large areas from self-assembly of binary colloids, Adv. Mater., 2011, 23, 1519–1523,  DOI:10.1002/adma.201004657.
333. G. Singh, H. J. Griesser, K. Bremmell and P. Kingshott, Highly ordered nanometer-scale chemical and protein patterns by binary colloidal crystal lithography combined with plasma polymerization, Adv. Funct. Mater., 2011, 21, 540–546,  DOI:10.1002/adfm.201001340.
334. P. A. Kralchevsky and K. Nagayama, Capillary forces between colloidal particles, Langmuir, 1994, 10, 23–36,  DOI:10.1021/la00013a004.
335. N. D. Denkov, O. D. Velev, P. A. Kralchevsky, I. B. Ivanov, H. Yoshimura and K. Nagayama, Two-dimensional crystallization, Nature, 1993, 361, 26,  DOI:10.1038/361026a0.
336. K. J. M. Bishop, C. E. Wilmer, S. Soh and B. A. Grzybowski, Nanoscale forces and their uses in self-assembly, Small, 2009, 5, 1600–1630,  DOI:10.1002/smll.200900358.
337. K. P. Velikov, C. G. Christova, R. P. A. Dullens and A. van Blaaderen, Layer-by-layer growth of binary colloidal crystals, Science, 2002, 296, 106–109,  DOI:10.1126/science.1067141.
338. N. D. Denkov, O. D. Velev, P. A. Kralchevsky, I. B. Ivanov, H. Yoshimura and K. Nagayama, Mechanism of formation of two-dimensional crystals from latex particles on substrates, Langmuir, 1992, 8, 3183–3190,  DOI:10.1021/la00048a054.
339. P.-Y. Wang, H. Pingle, P. Koegler, H. Thissen and P. Kingshott, Self-assembled binary colloidal crystal monolayers as cell culture substrates, J. Mater. Chem. B, 2015, 3, 2545–2552,  10.1039/C4TB02006E.
340. Z. Zheng, K. Gao, Y. Luo, D. Li, Q. Meng, Y. Wang and D. Zhang, Rapidly infrared-assisted cooperatively self-assembled highly ordered multiscale porous materials, J. Am. Chem. Soc., 2008, 130, 9785–9789,  DOI:10.1021/ja800327n.
341. V. Kitaev and G. A. Ozin, Self-assembled surface patterns of binary colloidal crystals, Adv. Mater., 2003, 15, 75–78,  DOI:10.1002/adma.200390016.
342. P. Jiang, J. F. Bertone, K. S. Hwang and V. L. Colvin, Single-crystal colloidal multilayers of controlled thickness, Chem. Mater., 1999, 11, 2132–2140,  DOI:10.1021/cm990080.
343. A. S. Dimitrov and K. Nagayama, Continuous convective assembling of fine particles into two-dimensional arrays on solid surfaces, Langmuir, 1996, 12, 1303–1311,  DOI:10.1021/la9502251.
344. M. H. Kim, S. H. Im and O. O. Park, Fabrication and structural analysis of binary colloidal crystals with two-dimensional superlattices, Adv. Mater., 2005, 17, 2501–2505,  DOI:10.1002/adma.200501080.
345. M. H. Kim, S. H. Im and O. O. Park, Rapid fabrication of two- and three-dimensional colloidal crystal films via confined convective assembly, Adv. Funct. Mater., 2005, 15, 1329–1335,  DOI:10.1002/adfm.200400602.
346. S. H. Im, M. H. Kim and O. O. Park, Thickness control of colloidal crystals with a substrate dipped at a tilted angle into a colloidal suspension, Chem. Mater., 2003, 15, 1797–1802,  DOI:10.1021/cm021793m.
347. M. Adams, Z. Dogic, S. L. Keller and S. Fraden, Entropically driven microphase transitions in mixtures of colloidal rods and spheres, Nature, 1998, 393, 349–352,  DOI:10.1038/30700.
348. T. Koda, M. Numajiri and S. Ikeda, Smectic-A phase of a bidisperse system of parallel hard rods and hard spheres, J. Phys. Soc. Jpn., 1996, 65, 3551–3556,  DOI:10.1143/JPSJ.65.3551.
349. L. Meng, J. Fonseca, R. Sánchez-Naya, A. M. Ghadiri, I. Imaz and D. Maspoch, Coassembly of complementary polyhedral metal-organic framework particles into binary ordered superstructures, J. Am. Chem. Soc., 2024, 146, 21225–21230,  DOI:10.1021/jacs.4c07194.
350. X. Wu, Y. Gao, H. Wang, Z. Zhang, X. Xi, D. Yang, T. Li and A. Dong, Hydrophobized metal-organic frameworks as versatile building blocks for tailored nanocrystal superlattices, J. Am. Chem. Soc., 2025, 147, 6361–6366,  DOI:10.1021/jacs.4c17724.
351. J. Wang, Q. Li, W. Knoll and U. Jonas, Preparation of multilayered trimodal colloid crystals and binary inverse opals, J. Am. Chem. Soc., 2006, 128, 15606–15607,  DOI:10.1021/ja067221a.
352. G. Singh, S. Pillai, A. Arpanaei and P. Kingshott, Layer-by-layer growth of multicomponent colloidal crystals over large areas, Adv. Funct. Mater., 2011, 21, 2556–2563,  DOI:10.1002/adfm.201002716.
353. G. Singh, S. Pillai, A. Arpanaei and P. Kingshott, Multicomponent colloidal crystals that are tunable over large areas, Soft Matter, 2011, 7, 3290–3294,  10.1039/C0SM01360A.
354. Z. Dai, Y. Li, G. Duan, L. Jia and W. Cai, Phase diagram, design of monolayer binary colloidal crystals, and their fabrication based on ethanol-assisted self-assembly at the air/water interface, ACS Nano, 2012, 6, 6706–6716,  DOI:10.1021/nn3013178.
355. F. Burmeister, C. Schäfle, B. Keilhofer, C. Bechinger, J. Boneberg and P. Leiderer, From mesoscopic to nanoscopic surface structures: Lithography with colloid monolayers, Adv. Mater., 1998, 10, 495–497,  DOI:10.1002/(SICI)1521-4095(199804)10:6<495::AID-ADMA495>3.0.CO;2-A.
356. H. H. Wickman and J. N. Korley, Colloid crystal self-organization and dynamics at the air/water interface, Nature, 1998, 393, 445–447,  DOI:10.1038/30930.
357. P. C. Ohara, D. V. Leff, J. R. Heath and W. M. Gelbart, Crystallization of opals from polydisperse nanoparticles, Phys. Rev. Lett., 1995, 75, 3466–3469,  DOI:10.1103/PhysRevLett.75.3466.
358. S.-H. Han, Y.-H. Choi and S.-H. Kim, Co-Assembly of colloids and eumelanin nanoparticles in droplets for structural pigments with high saturation, Small, 2022, 18, 2106048,  DOI:10.1002/smll.202106048.
359. D. Y. Wang and H. Möhwald, Template-directed colloidal self-assembly – the route to ‘top-down’ nanochemical engineering, J. Mater. Chem., 2004, 14, 459–468,  10.1039/B311283G.
360. J. Yu, Q. Yan and D. Shen, Co-self-assembly of binary colloidal crystals at the air-water interface, ACS Appl. Mater. Interfaces, 2010, 2, 1922–1926,  DOI:10.1021/am100250c.
361. M. Retsch, Z. Zhou, S. Rivera, M. Kappl, X. S. Zhao, U. Jonas and Q. Li, Fabrication of large-area, transferable colloidal monolayers utilizing self-assembly at the air/water interface, Macromol. Chem. Phys., 2009, 210, 230–241,  DOI:10.1002/macp.200800484.
362. E. Sirotkin, J. D. Apweiler and F. Y. Ogrin, Macroscopic ordering of polystyrene carboxylate-modified nanospheres self-assembled at the water-air interface, Langmuir, 2010, 26, 10677–10683,  DOI:10.1021/la1009658.
363. P. D. Garcia, R. Sapienza and C. López, Photonic glasses: A step beyond white paint, Adv. Mater., 2010, 22, 12–19,  DOI:10.1002/adma.200900827.
364. F. S. Diba, A. Boden, H. Thissen, M. Bhave, P. Kingshott and P.-Y. Wang, Binary colloidal crystals (BCCs): Interactions, fabrication, and applications, Adv. Colloid Interface Sci., 2018, 261, 102–127,  DOI:10.1016/j.cis.2018.08.005.
365. V. Lotito and T. Zambelli, Self-assembly of single-sized and binary colloidal particles at air/water interface by surface confinement and water discharge, Langmuir, 2016, 32, 9582–9590,  DOI:10.1021/acs.Langmuir.6b02157.
366. F. Bresme, C. Vega and J. L. F. Abascal, Order-disorder transition in the solid phase of a charged hard sphere model, Phys. Rev. Lett., 2000, 85, 3217–3220,  DOI:10.1103/PhysRevLett.85.3217.
367. P. Bartlett and A. I. Campbell, Three-dimensional binary superlattices of oppositely charged colloids, Phys. Rev. Lett., 2005, 95, 128302,  DOI:10.1103/PhysRevLett.95.128302.
368. T. Hueckel, G. M. Hocky, J. Palacci and S. Sacanna, Ionic solids from common colloids, Nature, 2020, 580, 487–490,  DOI:10.1038/s41586-020-2205-0.
369. N. J. Agard, J. A. Prescher and C. R. Bertozzi, A strain-promoted [3+2] azide-alkyne cycloaddition for covalent modification of biomolecules in living systems, J. Am. Chem. Soc., 2004, 126, 15046–15047,  DOI:10.1021/ja044996f.
370. R. Dreyfus, M. E. Leunissen, R. Sha, A. Tkachenko, N. C. Seeman, D. J. Pine and P. M. Chaikin, Aggregation-disaggregation transition of DNA-coated colloids: Experiments and theory, Phys. Rev. E, 2010, 81, 041404,  DOI:10.1103/PhysRevE.81.041404.
371. K.-T. Wu, L. Feng, R. Sha, R. Dreyfus, A. Y. Grosberg, N. C. Seeman and P. M. Chaikin, Kinetics of DNA-coated sticky particles, Phys. Rev. E, 2013, 88, 022304,  DOI:10.1103/PhysRevE.88.022304.
372. A. J. Kim, V. N. Manoharan and J. C. Crocker, Swelling-based method for preparing stable, functionalized polymer colloids, J. Am. Chem. Soc., 2005, 127, 1592–1593,  DOI:10.1021/ja0450051.
373. S. Auer and D. Frenkel, Prediction of absolute crystal-nucleation rate in hard-sphere colloids, Nature, 2001, 409, 1020–1023,  DOI:10.1038/35059035.
374. D. Wang and H. Möhwald, Rapid fabrication of binary colloidal crystals by stepwise spin-coating, Adv. Mater., 2004, 16, 244–247,  DOI:10.1002/adma.200305565.
375. Y. Lalatonne, J. Richardi and M. P. Pileni, van der Waals versus dipolar forces controlling mesoscopic organizations of magnetic nanocrystals, Nat. Mater., 2004, 3, 121–125,  DOI:10.1038/nmat1054.
376. X. Huang, J. Zhou, M. Fu, B. Li, Y. Wang, Q. Zhao, Z. Yang, Q. Xie and L. Li, Binary colloidal crystals with a wide range of size ratios via template-assisted electric-field-induced assembly, Langmuir, 2007, 23, 8695–8698,  DOI:10.1021/la700512j.
377. E. C. M. Vermolen, A. Kuijk, L. C. Filion, M. Hermes, J. H. J. Thijssen, M. Dijkstra and A. van Blaaderen, Fabrication of large binary colloidal crystals with a NaCl structure, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 16063–16067,  DOI:10.1073/pnas.0900605106.
378. A. van Blaaderen, R. Ruel and P. Wiltzius, Template-directed colloidal crystallization, Nature, 1997, 385, 321–324,  DOI:10.1038/385321a0.
379. J. P. Hoogenboom, A. K. van Langen-Suurling, J. Romijn and A. van Blaaderen, Hard-sphere crystals with hcp and non-close-packed structure grown by colloidal epitaxy, Phys. Rev. Lett., 2003, 90, 138301,  DOI:10.1103/PhysRevLett.90.138301.
380. M. E. Leunissen, M. T. Sullivan, P. M. Chaikin and A. van Blaaderen, Concentrating colloids with electric field gradients. I. Particle transport and growth mechanism of hard-sphere-like crystals in an electric bottle, J. Chem. Phys., 2008, 128, 164508,  DOI:10.1063/1.2909198.
381. M. T. Sullivan, K. Zhao, A. D. Hollingsworth, R. H. Austin, W. B. Russel and P. M. Chaikin, An electric bottle for colloids, Phys. Rev. Lett., 2006, 96, 015703,  DOI:10.1103/PhysRevLett.96.015703.
382. M. D. Bentzon, J. van Wonterghem, S. Mørup, A. Thölén and C. J. W. Koch, Ordered aggregates of ultrafine iron oxide particles: ‘Super crystals’, Philos. Mag. B, 1989, 60, 169–178,  DOI:10.1080/13642818908211188.
383. S. M. Yang, H. Miguez and G. A. Ozin, Opal circuits of light—Planarized microphotonic crystal chips, Adv. Funct. Mater., 2002, 12, 425–431,  DOI:10.1002/1616-3028(20020618)12:6/7<425::AID-ADFM425>3.0.CO;2-U.
384. I. I. Tarhan and G. H. Watson, Photonic band structure of fcc colloidal crystals, Phys. Rev. Lett., 1996, 76, 315–318,  DOI:10.1103/PhysRevLett.76.315.
385. Y. A. Vlasov, X.-Z. Bo, J. C. Sturm and D. J. Norris, On-chip natural assembly of silicon photonic bandgap crystals, Nature, 2001, 414, 289–293,  DOI:10.1038/35104529.
386. A. Blanco, E. Chomski, S. Grabtchak, M. Ibisate, S. John, S. W. Leonard, C. López, F. Meseguer, H. Míguez, J. P. Mondia, G. A. Ozin, O. Toader and H. M. van Driel, Large-scale synthesis of a silicon photonic crystal with a complete three-dimensional bandgap near 1.5 micrometres, Nature, 2000, 405, 437–440,  DOI:10.1038/35013024.
387. D. V. Talapin, J. S. Lee, M. V. Kovalenko and E. V. Shevchenko, Prospects of colloidal nanocrystals for electronic and optoelectronic applications, Chem. Rev., 2010, 110, 389–458,  DOI:10.1021/cr900137k.
388. E. H. Sargent, Colloidal quantum dot solar cells, Nat. Photonics, 2012, 6, 133–135,  DOI:10.1038/nphoton.2012.33.
389. S. Choi, I. Park, Z. Hao, H.-Y. N. Holman, A. P. Pisano and T. I. Zohdi, Ultrafast self-assembly of microscale particles by open-channel flow, Langmuir, 2010, 26, 4661–4667,  DOI:10.1021/la903492w.
390. T. C. Harman, P. J. Taylor, M. P. Walsh and B. E. LaForge, Quantum dot superlattice thermoelectric materials and devices, Science, 2002, 297, 2229–2232,  DOI:10.1126/science.1072886.
391. J. H. Holtz and S. A. Asher, Polymerized colloidal crystal hydrogel films as intelligent chemical sensing materials, Nature, 1997, 389, 829–832,  DOI:10.1038/39834.
392. F. Sun, W. Cai, Y. Li, L. Jia and F. Lu, Direct growth of mono- and multilayer nanostructured porous films on curved surfaces and their application as gas sensors, Adv. Mater., 2005, 17, 2872–2877,  DOI:10.1002/adma.200500936.
393. T. Waitz, T. Wagner, T. Sauerwald, C. D. Kohl and M. Tiemann, Ordered mesoporous In2O3: Synthesis by structure replication and application as a methane gas sensor, Adv. Funct. Mater., 2009, 19, 653–661,  DOI:10.1002/adfm.200801458.
394. M. Zayats, A. B. Kharitonov, S. P. Pogorelova, O. Lioubashevski, E. Katz and I. Willner, Probing photoelectrochemical processes in Au–CdS nanoparticle arrays by surface plasmon resonance:  Application for the detection of acetylcholine esterase inhibitors, J. Am. Chem. Soc., 2003, 125, 16006–16014,  DOI:10.1021/ja0379215.
395. Y. Li, X. J. Huang, S. H. Heo, C. C. Li, Y. K. Choi, W. P. Cai and S. O. Cho, Superhydrophobic bionic surfaces with hierarchical microsphere/SWCNT composite arrays, Langmuir, 2007, 23, 2169–2174,  DOI:10.1021/la0620758.
396. J. Y. Shiu, C. W. Kuo, P. Chen and C. Y. Mou, Fabrication of tunable superhydrophobic surfaces by nanosphere lithography, Chem. Mater., 2004, 16, 561–564,  DOI:10.1021/cm034696h.
397. H. Yang and P. Jiang, Scalable fabrication of superhydrophobic hierarchical colloidal arrays, J. Colloid Interface Sci., 2010, 352, 558–565,  DOI:10.1016/j.jcis.2010.08.070.
398. U. Kamp, V. Kitaev, G. von Freymann, G. A. Ozin and S. A. Mabury, Colloidal crystal capillary columns—Towards optical chromatography, Adv. Mater., 2005, 17, 438–443,  DOI:10.1002/adma.200400020.
399. K. L. Kelly, E. Coronado, L. L. Zhao and G. C. Schatz, The optical properties of metal nanoparticles:  The influence of size, shape, and dielectric environment, J. Phys. Chem. B, 2003, 107, 668–677,  DOI:10.1021/jp026731y.
400. G. Duan, W. Cai, Y. Luo, Z. Li and Y. Li, Electrochemically induced flowerlike gold nanoarchitectures and their strong surface-enhanced Raman scattering effect, Appl. Phys. Lett, 2006, 89, 211905,  DOI:10.1063/1.2392822.
401. G. Liu, W. Cai, L. Kong, G. Duan and F. Lü, Vertically cross-linking silver nanoplate arrays with controllable density based on seed-assisted electrochemical growth and their structurally enhanced SERS activity, J. Mater. Chem., 2010, 20, 767–772,  10.1039/B917167C.
402. J. Grunes, J. Zhu, E. A. Anderson and G. A. Somorjai, Ethylene hydrogenation over platinum nanoparticle array model catalysts fabricated by electron beam lithography:  Determination of active metal surface area, J. Phys. Chem. B, 2002, 106, 11463–11468,  DOI:10.1021/jp021641e.
403. J. Wang, S. Ahl, Q. Li, M. Kreiter, T. Neumann, K. Burkert, W. Knoll and U. Jonas, Structural and optical characterization of 3D binary colloidal crystal and inverse opal films prepared by direct co-deposition, J. Mater. Chem., 2008, 18, 981–988,  10.1039/B715329E.
404. S. Zhao, J. Zhao, L.-L. Lou and S. Liu, Amino-functionalized SBA-15 immobilized NiBr2(PPh3)2 as a highly effective catalyst for ATRP of MMA, Microporous Mesoporous Mater., 2011, 137, 36–42,  DOI:10.1016/j.micromeso.2010.08.018.
405. Y. Kang, X. Ye, J. Chen, Y. Cai, R. E. Diaz, R. R. Adzic, E. A. Stach and C. B. Murray, Design of Pt-Pd binary superlattices exploiting shape effects and synergistic effects for oxygen reduction reactions, J. Am. Chem. Soc., 2013, 135, 42–45,  DOI:10.1021/ja3097527.
406. E. V. Shevchenko, D. V. Talapin, A. L. Rogach, A. Kornowski, M. Haase and H. Weller, Colloidal synthesis and self-assembly of CoPt3 nanocrystals, J. Am. Chem. Soc., 2002, 124, 11480–11485,  DOI:10.1021/ja025976l.
407. I. Gourevich, H. Pham, J. E. N. Jonkman and E. Kumacheva, Multidye nanostructured material for optical data storage and security labeling, Chem. Mater., 2004, 16, 1472–1479,  DOI:10.1021/cm030070f.
408. J. Hoinville, A. Bewick, D. Gleeson, R. Jones, O. Kasyutich, E. Mayes, A. Nartowski, B. Warne, J. Wiggins and K. Wong, High density magnetic recording on protein-derived nanoparticles, J. Appl. Phys., 2003, 93, 7187–7189,  DOI:10.1063/1.1555896.
409. G. Singh, V. Gohri, S. Pillai, A. Arpanaei, M. Foss and P. Kingshott, Large-area protein patterns generated by ordered binary colloidal assemblies as templates, ACS Nano, 2011, 5, 3542–3551,  DOI:10.1021/nn102867z.
410. J. C. Hulteen, D. A. Treichel, M. T. Smith, M. L. Duval, T. R. Jensen and R. P. Van Duyne, Nanosphere lithography: Size-tunable silver nanoparticle and surface cluster arrays, J. Phys. Chem. B, 1999, 103, 3854–3863,  DOI:10.1021/jp9904771.
411. Y. Li, E. J. Lee, W. Cai, K. Y. Kim and S. O. Cho, Unconventional method for morphology-controlled carbonaceous nanoarrays based on electron irradiation of a polystyrene colloidal monolayer, ACS Nano, 2008, 2, 1108–1112,  DOI:10.1021/nn8001483.
412. G. Duan, W. Cai, Y. Luo, F. Lv, J. Yang and Y. Li, Design and electrochemical fabrication of gold binary ordered micro/nanostructured porous arrays via step-by-step colloidal lithography, Langmuir, 2009, 25, 2558–2562,  DOI:10.1021/la803794s.
413. J. C. Hulteen and R. P. Van Duyne, Nanosphere lithography: A materials general fabrication process for periodic particle array surfaces, J. Vac. Sci. Technol., A, 1995, 13, 1553–1558,  DOI:10.1116/1.579726.
414. J. Zhang, Y. Li, X. Zhang and B. Yang, Colloidal self-assembly meets nanofabrication: From two-dimensional colloidal crystals to nanostructure arrays, Adv. Mater., 2010, 22, 4249–4269,  DOI:10.1002/adma.201000755.
415. N. Vogel, M. Jung, M. Retsch, W. Knoll, U. Jonas and I. Köper, Laterally Patterned Ultraflat Surfaces, Small, 2009, 5, 821–825,  DOI:10.1002/smll.200801583.
416. M. Retsch, K.-H. Dostert, S. K. Nett, N. Vogel, J. S. Gutmann and U. Jonas, Template-free structuring of colloidal hetero-monolayers by inkjet printing and particle floating, Soft Matter, 2010, 6, 2403–2412,  10.1039/C001306D.
417. M. V. Kovalenko, L. Manna, A. Cabot, Z. Hens, D. V. Talapin, C. R. Kagan, V. I. Klimov, A. L. Rogach, P. Reiss, D. J. Milliron, P. Guyot-Sionnest, G. Konstantatos, W. J. Parak, T. Hyeon, B. A. Korgel, C. B. Murray and W. Heiss, Prospects of nanoscience with nanocrystals, ACS Nano, 2015, 9, 1012–1057,  DOI:10.1021/nn506223h.
418. B. Pelaz, S. Jaber, D. Jimenez de Aberasturi, V. Wulf, T. Aida, J. M. de la Fuente, J. Feldmann, H. E. Gaub, L. Josephson, C. R. Kagan, N. A. Kotov, L. M. Liz-Marzán, H. Mattoussi, P. Mulvaney, C. B. Murray, A. L. Rogach, P. S. Weiss, I. Willner and W. J. Parak, The state of nanoparticle-based nanoscience and biotechnology: Progress, promises, and challenges, ACS Nano, 2012, 6, 8468–8483,  DOI:10.1021/nn303929a.
419. A. K. Chew and R. C. Van Lehn, Effect of core morphology on the structural asymmetry of alkanethiol monolayer-protected gold nanoparticles, J. Phys. Chem. C, 2018, 122, 26288–26297,  DOI:10.1021/acs.jpcc.8b09323.
420. Y. Yang, H. Qin, M. Jiang, L. Lin, T. Fu, X. Dai, Z. Zhang, Y. Niu, H. Cao, Y. Jin, F. Zhao and X. Peng, Entropic Ligands for Nanocrystals: From Unexpected Solution Properties to Outstanding Processability, Nano Lett., 2016, 16, 2133–2138,  DOI:10.1021/acs.nanolett.6b00730.
421. B.-K. Pong, J.-Y. Lee and B. L. Trout, First principles computational study for understanding the interactions between ssDNA and gold nanoparticles: Adsorption of methylamine on gold nanoparticulate surfaces, Langmuir, 2005, 21, 11599–11603,  DOI:10.1021/la052116k.
422. M. Grzelczak, L. M. Liz-Marzán and R. Klajn, Stimuli-responsive self-assembly of nanoparticles, Chem. Soc. Rev., 2019, 48, 1342–1361,  10.1039/C8CS00787J.
423. Q. Fu, Z. Li, F. Fu, X. Chen, J. Song and H. Yang, Stimuli-responsive plasmonic assemblies and their biomedical applications, Nano Today, 2021, 36, 101014,  DOI:10.1016/j.nantod.2020.101014.
424. X. Wu, C. Hao, J. Kumar, H. Kuang, N. A. Kotov, L. M. Liz-Marzán and C. Xu, Environmentally responsive plasmonic nanoassemblies for biosensing, Chem. Soc. Rev., 2018, 47, 4677–4696,  10.1039/C7CS00894E.
425. C. Pigliacelli, R. Sánchez-Fernández, M. D. García, C. Peinador and E. Pazos, Self-assembled peptide–inorganic nanoparticle superstructures: from component design to applications, Chem. Commun., 2020, 56, 8000–8014,  10.1039/D0CC02914A.
426. X. An, A. Zhu, H. Luo, H. Ke, H. Chen and Y. Zhao, Rational design of multi-stimuli-responsive nanoparticles for precise cancer therapy, ACS Nano, 2016, 10, 5947–5958,  DOI:10.1021/acsnano.6b01296.
427. F. Li, J. Lu, X. Kong, T. Hyeon and D. Ling, Dynamic nanoparticle assemblies for biomedical applications, Adv. Mater., 2017, 29, 1605897,  DOI:10.1002/adma.201605897.
428. J. V. Vaghasiya, C. C. Mayorga-Martinez, S. Matějková and M. Pumera, Pick up and dispose of pollutants from water via temperature-responsive micellar copolymers on magnetite nanorobots, Nat. Commun., 2022, 13, 1026,  DOI:10.1038/s41467-022-28406-5.
429. Z. Li, F. Yang and Y. Yin, Smart materials by nanoscale magnetic assembly, Adv. Funct. Mater., 2020, 30, 1903467,  DOI:10.1002/adfm.201903467.
430. L. He, M. Wang, J. Ge and Y. Yin, Magnetic assembly route to colloidal responsive photonic nanostructures, Acc. Chem. Res., 2012, 45, 1431–1440,  DOI:10.1021/ar200276t.
431. B. P. Isaacoff and K. A. Brown, Progress in top-down control of bottom-up assembly, Nano Lett., 2017, 17, 6508–6510,  DOI:10.1021/acs.nanolett.7b04479.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sm00247h

---