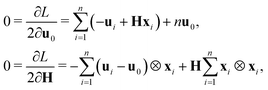DOI:
10.1039/D5SM00035A
(Paper)
Soft Matter, 2025,
21, 5655-5668
Statistical mechanics of cell aggregates: explaining the phase transition and paradoxical piezoelectric behavior of soft biological tissues
Received
14th January 2025
, Accepted 19th March 2025
First published on 28th March 2025
Abstract
Piezoelectricity in biological soft tissues is a controversial issue with differing opinions. While there is compelling experimental evidence to suggest a piezoelectric-like response in tissues such as the aortic wall (among others), there are equally compelling experiments that argue against this notion. In addition, the lack of a polar structure in the underlying components of most soft biological tissues supports the latter. In this paper, we address the collective behavior of cells within a two-dimensional cell aggregate from the viewpoint of statistical mechanics. Our starting point is the simplest form of energy for cell behavior that only includes known observable facts e.g., the electrical Maxwell stress or electrostriction, resting potential across cell membranes, elasticity, and we explicitly exclude any possibility of electromechanical coupling reminiscent of piezoelectricity at the cellular level. We coarse-grain our cellular aggregate to obtain its emergent mechanical, physical, and electromechanical properties. Our findings indicate that the fluctuation of cellular strain (E) plays a similar role as the absolute temperature in a conventional atomistic-level statistical model. The coarse-grained effective free energy reveals several intriguing features of the collective behavior of cell aggregates, such as solid–fluid phase transitions and a distinct piezoelectric-like coupling, even though it is completely absent at the microscale. Closed-form formulas are obtained for key electromechanical properties, including stiffness, effective resting potential, critical E2-temperature (or fluctuation) for solid–fluid phase transitions, and apparent piezoelectric coupling in terms of fluctuation and electric potential regulated by active cellular processes.
1. Introduction
Cell aggregates or tissues are composed of individual cells, intricately organized with notable variability in their shapes, sizes, and spatial arrangements. Each constituent cell is structurally complex, featuring a bilipid membrane interspersed with ion channels and molecular pumps. Enclosed within this membrane are cytoskeleton, cytoplasm, and various organelles. The hierarchical structures and complex interplay of biophysical processes within cells give rise to intriguing electromechanical properties of single cells and cell aggregates. In particular, the bilipid membrane and cytoskeleton provide shear resistance and maintain the structural integrity of a cell;1 the combined activities of numerous ion channels and molecular pumps induce a long-term, steady-state electric potential difference across the cell membrane.2 The propagation of changes in transmembrane potentials mediates cellular signaling and regulates critical biophysical processes.3 Conversely, mechanical deformations can regulate ion channels and pumps, inducing cellular bioelectricity within cell aggregates. These electromechanical couplings provide the fundamental physical mechanism underlying biological functions, including cellular adhesion, migration, differentiation, and mechanosensing.4–9
Cells in an aggregate interact with each other both mechanically and electrically. The resulting electromechanical properties of cell aggregates or tissues are derived from the collective behavior of individual cells, leading to properties and functionalities that are significantly richer than those of a single cell. For example, cell aggregates reversibly transition between a rigid solid-like phase and a floppy fluid-like phase referred to as a solid–fluid phase transition, which plays a critical role in the biological function of living tissues.10–17 This phase transition can be actively regulated by transmembrane potential.18–21
Currently, several mechanisms have been proposed to explain the solid–fluid phase transition in cell aggregates. These include a topological transition which promotes tissue fluidization by relaxing elastic stresses over longer time scales;10,22,23 the sliding of coherent cells within the aggregate, where external forces induce gradual rearrangements of cell conformations;21 and transitions driven by the density of multicellular vertices (rosettes) and intracellular tensions.11 Within a tissue, cellular deformation and electric potential exhibit considerable fluctuation and variability. The fluctuation in cellular shape and size can be readily quantified, providing valuable insight into the physiological stage of the tissue.24
The true nature of the electromechanical behavior of soft biological tissues has attracted repeated controversy. Claims have been made regarding the piezoelectricity of these tissues cf. Fukada and reference therein25 and even the presence of ferroelectricity.26 Convincing counter-arguments have been made against this by Lenz et al.,27 who argue that the observable electromechanical coupling is due to Maxwell stress or electrostriction. In an interesting turn of events, in a more recent work, we turn full circle where Ikushima et al.28 highlight ultrasound experiments that do appear to indicate the presence of piezoelectricity in aortic wall tissue.
Existing approaches to modeling cells and their aggregates can be broadly divided into three categories: agent-based models, continuum models, and statistical models. The agent-based approach treats a single cell as a homogeneous, isotropic, elastic, and spherical body.29–32 While this approach is valuable for studying the interaction of individual cells with each other and with their environment,33–35 its applicability to the macroscopic behavior of cell aggregates remains limited. Continuum models for cell aggregates,36–41 by contrast, are well-suited for modeling large-scale phenomena where aggregate properties vary smoothly over length scales spanning several cell diameters. These models effectively capture the macroscopic response of cell aggregates and can be extended to incorporate additional physical phenomena such as intercellular interactions and formation of cell aggregates.42 For instance, a continuum description of cell motility, driven by cell–cell and cell–ECM (extracellular matrix) interactions, was developed using a non-local interaction term to account for adhesion between cells and between cells and the ECM.43–45 Despite these successes, continuum approaches fall short in capturing the inherent variability in cellular deformation and electric potential within tissues. In contrast, statistical models provide a robust framework for addressing these limitations.46–49 By applying the framework of statistical mechanics to cell aggregates, we can effectively describe the mechanical and electrical fluctuations observed in tissues, bridging the gap between microscopic cellular properties and macroscopic tissue behavior. As discussed below, this approach also allows for a quantitative analysis of deformation and electric potential fluctuation, offering deeper insights into the emergent electromechanical properties of cell aggregates.
The method of statistical mechanics has been employed in a number of studies on cells and their aggregates. A recently developed theory50,51 addressed the active processes in cells to provide insights into cell size distribution. They extended that work to include electrical fields to establish the threshold electrical fields that can be sensed by a cell.52 The work10 based on non-equilibrium statistical mechanics and a 2D vertex model was able to capture mechanical instabilities in cell aggregates. The study in ref. 53 for active matter (living cells) focused on steric and aligning interactions and interactions driven by shape changes. The impact of thermal fluctuations in polarization on the renormalization of the flexoelectric coupling coefficient of cell membranes has also been studied using statistical mechanics.54 However, none of the existing models incorporate both the mechanical and electrical fluctuations and inter-cellular interactions for cell aggregates.
In this work, we propose an electromechanical model to describe both single cells and cell aggregates based on structural symmetries and derive its macroscopic continuum limit. Notably, our starting point for the microscopic model (at the cell level) does not include any piezoelectric behavior and simply takes cognizance of the fact that there is a resting potential across the cell and the presence of electrostriction (which is exhibited by all materials). Fluctuations in geometric parameters, such as cell area and aspect ratio, can be effectively quantified through the analysis of tissue micrographs. Notably, the fluctuation in strain—later referred to as the E2-temperature due to its analogous role to absolute temperature in classical thermal physics—serves as a quantitative measure of the inherent system variability.55 Our resulting coarse-grained electromechanical model for cell aggregates is particularly well-suited for applications to epithelial tissues, which consist of flattened, tightly packed cell layers. However, our insights are broader and transferrable to other tissue configurations. Based on the coarse-grained model, we investigate the macroscopic electromechanical behavior of cell aggregates, demonstrating that effective electromechanical coupling and solid–fluid phase transitions arise from the collective cellular interactions. These resolve the existing paradox in the literature. The emergent properties depend on the E2-temperature. The quantitative dependence of effective resting potential, tissue stiffness, T1-transition rate, viscosity, and critical point for solid–fluid phase transition on the E2-temperature could be validated by experimental observations. Such comparisons open the door to understanding how fluctuation and variability contribute to tissue behavior in different biological contexts, making the E2-temperature an experimentally testable concept for linking microscopic fluctuations with macroscopic emergent properties.
1.1. Central premise
Following the paradigm of statistical mechanics, we treat a cell aggregate as a canonical ensemble of many cells. We borrow the terminologies and methodology from statistical mechanics with the caveat that the fluctuation or variability of the system mainly arise from biological active processes (e.g. growing, diffusion, etc.), defects, inhomogeneities, among others, instead of the actual thermal agitations. Therefore, the benchmark energy scale (![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β) used in this work is a phenomenological constant; the fluctuation or variability in cellular states arises not only from thermal agitations but also from many other passive and active processes that entail “equilibrium” of the system at the observation time-scale. The collection of cellular strains and electric potentials in a cell aggregate are assumed to describe the microstates of the system. For their collective properties in a cell aggregates, we first propose a single-cell Hamiltonian based on the underlying structural symmetries and experimental observations of their electromechanical responses. We employ the mean-field approximation, which allows for an analytical solution of the model and yields a closed-form expression for the effective free energy of cell aggregates. Based on this effective free energy, we present several experimentally testable predictions, including the macroscopic electromechanical properties, the solid–fluid phase transitions observed in cell aggregates, and their dependence on the E2-temperature and average electric potential regulated by active processes.
BT = 1/β) used in this work is a phenomenological constant; the fluctuation or variability in cellular states arises not only from thermal agitations but also from many other passive and active processes that entail “equilibrium” of the system at the observation time-scale. The collection of cellular strains and electric potentials in a cell aggregate are assumed to describe the microstates of the system. For their collective properties in a cell aggregates, we first propose a single-cell Hamiltonian based on the underlying structural symmetries and experimental observations of their electromechanical responses. We employ the mean-field approximation, which allows for an analytical solution of the model and yields a closed-form expression for the effective free energy of cell aggregates. Based on this effective free energy, we present several experimentally testable predictions, including the macroscopic electromechanical properties, the solid–fluid phase transitions observed in cell aggregates, and their dependence on the E2-temperature and average electric potential regulated by active processes.
2. An electromechanical model for cell aggregates
We are interested in the macroscopic electromechanical response of a cell aggregate as illustrated in Fig. 1(a). We first introduce independent state variables for describing physical and geometrical configurations of cells and their aggregates. Fig. 1(a) shows a schematic of a typical amorphous cell aggregate. We idealize the cell aggregate as a tessellation of a plane by equal-area polygons as illustrated in Fig. 1(b). Denote by Ci⊂![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 the polygon/domain occupied by the ith cell, A the area of the polygon Ci, and ci the spatial positions of the centroids of cells. For simplicity, we assume that each cell precisely occupies the Voronoi cell associated with {ci: i = 1, …, N}.56 Though it is tempting to employ the centroids of cells as the fundamental state variables, a reasonable physical model or Hamiltonian for the tessellation in terms of {ci: i = 1, …, N} must be interacting and permutation invariant, and hence not amenable to systematic perturbation methods. On the other hand, for cell aggregates illustrated in Fig. 1(a), we see that the shapes of cells and statistical properties of aspect ratios are good indicator of different physiological stages of cell aggregates (or tissues) which, presumably, dictate the physical properties of cell aggregates as well.55,57,58 Therefore, we choose the deformation or strain as one of the independent state variables for the cell aggregate.
2 the polygon/domain occupied by the ith cell, A the area of the polygon Ci, and ci the spatial positions of the centroids of cells. For simplicity, we assume that each cell precisely occupies the Voronoi cell associated with {ci: i = 1, …, N}.56 Though it is tempting to employ the centroids of cells as the fundamental state variables, a reasonable physical model or Hamiltonian for the tessellation in terms of {ci: i = 1, …, N} must be interacting and permutation invariant, and hence not amenable to systematic perturbation methods. On the other hand, for cell aggregates illustrated in Fig. 1(a), we see that the shapes of cells and statistical properties of aspect ratios are good indicator of different physiological stages of cell aggregates (or tissues) which, presumably, dictate the physical properties of cell aggregates as well.55,57,58 Therefore, we choose the deformation or strain as one of the independent state variables for the cell aggregate.
 |
| | Fig. 1 Cell aggregate and single cell. (a) A typical cell aggregate (plated Madin-Darby Canine Kidney cells, Courtesy of K. Irvine). (b) Geometrically, a cell aggregate is regarded as a tessellation of a plane by polygons. (c) Schematic of a single cell occupying a regular hexagonal domain (n = 6) and (d) a deformed hexagon, where c, xj, yj is the position of the centroid of the cell, the jth vertex of the cell in undeformed and deformed configuration, respectively. | |
Unlike crystalline solids for which there exists a natural reference configuration (i.e., crystalline lattice), at least locally, for defining the deformation and strain, a cell aggregate is amorphous whose deformation or strain, strictly speaking, cannot be defined for a single current configuration. Nevertheless, neglecting the compatibility requirement for neighboring cells, “strain” could be defined for each individual cell by a few alternative procedures. The essence of these procedures is such that the introduced strain tensor E ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym is a measure of orientation and aspect ratio of individual cells and the underlying arrangement of cells. In particular, we require that the strain tensor E ∈
2×2sym is a measure of orientation and aspect ratio of individual cells and the underlying arrangement of cells. In particular, we require that the strain tensor E ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym satisfy the following.
2×2sym satisfy the following.
(R1) The strain E = 0 if the cell is a regular polygon.
(R2) For small strains with |E| ≪ 1, the ratio of eigenvalues of strain tensor E ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym measures the “aspect ratio” of the cell.
2×2sym measures the “aspect ratio” of the cell.
(R3) For small strains with |E| ≪ 1, the eigenvectors of strain tensor E ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym defines the “orientation” of the cell.
2×2sym defines the “orientation” of the cell.
As a tessellation of a plane, cells in aggregates occupy polygonal domain  with n vertices yj (j = 1,…,n). As illustrated in Fig. 1(a), typically n = 4, 5, 6, 7 from experiments. Suppose a cell occupies an irregular hexagon as in Fig. 1(d). We choose the regular hexagon of the same area in Fig. 1(c) as the reference undeformed configuration.
with n vertices yj (j = 1,…,n). As illustrated in Fig. 1(a), typically n = 4, 5, 6, 7 from experiments. Suppose a cell occupies an irregular hexagon as in Fig. 1(d). We choose the regular hexagon of the same area in Fig. 1(c) as the reference undeformed configuration.
Below we introduce two procedures to identify the strain tensor E associated with a single cell in the regime of small strain (|E| ≪ 1).
(i) Let xj (j = 1,…,n) be vertices of the regular n-gon centered at the origin:
| |  | (1) |
where

is such that the area of the regular
n-gon equals the area of the cell. By the method of least square, we can in general define a deformation gradient
F ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2
2×2 and a translational vector
u0 ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2
2 for the cell:
Let
uj =
yi −
xi be the displacement of the
ith vertex and
H =
F −
I the unsymmetrized strain (
I ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2
2×2 is the identity matrix). We write
L(
F,
u0) as
By the first-order necessary conditions we have
which imply that
From classical continuum mechanics, the linearized symmetric strain for the cell can be written as
| |  | (2) |
(ii) A second procedure to determine the strain tensor is through the normalized second moment of the current position vector. For a polygon

illustrated in
Fig. 1(d), without loss of generality we assume the centroid is at the origin:

Then the normalized second moment tensor is given by
| |  | (3) |
where

is the second moment tensor of a regular
n-gon of the same area (
cf.Fig. 1(c)). Suppose that the current shape

is obtained by deforming the regular
n-gon

with vertices given by
xj in
(1),
i.e.,
yj =
Fxj. The second normalized moment tensor is given by
Then the strain tensor may be defined as
which clearly fulfills the previously mentioned requirements (R1)–(R3).
We remark that strains defined by (2) and (4) coincide to the leading order for small strains with |E| ≪ 1 and both of them have been used to quantify experimental and numerical results.55,57 Also, for hexagons the shape index57 or perimeter (p)-to-sqrt of area  ratio can be expressed as a function of strain E:
ratio can be expressed as a function of strain E:
| | 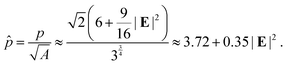 | (5) |
2.1. Strain from rearrangement of cells
As for crystalline solids, significant strain can be generated by structural rearrangement of cells from the viewpoint of centroid positions. Such a transformation strain cannot be characterized by the two definitions ((2) and (4)) of strain tensor. As illustrated in Fig. 2, in a rearrangement process called T1-transition commonly observed in the development of epithelial tissues, neighboring cells exchange their positions through a reorganization of intercellular junctions without significant changes in the shape of individual cells. Though the final configuration in Fig. 2(c) in T1-transition is a deformed configuration relative to the initial configuration in Fig. 2(a), the strain calculated by either (2) or (4) vanishes for every cell. To remedy this issue, we observe that, as a cluster of cells, the final configuration in Fig. 2(c) can be obtained by compressing (and stretching) the initial configuration in Fig. 2(a) in y-direction (in x-direction). The strain associated with this deformation process may be identified as| |  | (6) |
where the T1-transition strain γ* ∼ 1 is beyond the regime of small strains and will be determined later from empirical data.
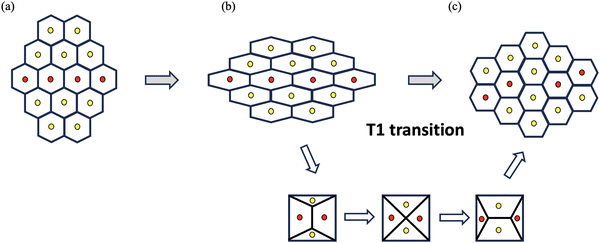 |
| | Fig. 2 T1-transition in cell aggregates. Cell aggregates undergo rearrangement in which neighboring cells exchange their positions through a reorganization of intercellular junctions without significant changes in the shape of individual cells and transition from (a) initial configuration to (b) intermediate configuration to (c) final configuration. | |
To summarize, we note that both definitions of the strain tensor, (2) and (4), encounter difficulty in consistently capturing the local structural rearrangements of cells. This limitation arises from the inherent complexity of cellular configurations. In this work, we take a pragmatic approach and treat the strain tensor E as an “order parameter” as in the framework of Landau's phenomenological theory.59,60 In this context, the precise mathematical definition of strain tensor E beyond the regime of small strain is secondary, as long as it qualitatively reflects the key geometric characteristics—namely, the shape changes and structural arrangement of the underlying cells. By adopting this perspective, the strain tensor serves as a convenient and effective state variable for quantifying the geometry and arrangement of cells in a cell aggregate and can be confidently computed by either (2) or (4) in the regime of small strain.
In addition to elasticity, we will consider electric interactions between cells. Cell aggregates, in spite of adhesion between them, in general, are immersed in an extracellular matrix (ECM) whose electric potential may be assigned as the ground potential. Ionic channels, i.e., specialized protein structures embedded in the cell membrane, allow selective passage of ions (e.g., Na+, K+, Ca2+, Cl−, etc.) across the membrane. This selective transport ensures and maintains a resting membrane potential ξ*, which is essential for numerous biological functions.2 For simplicity, we assume the interior of each cell is of equipotential. The actual potential of the ith-cell, denoted by ξi, could be significantly different from the resting potential ξ* due to electromechanical coupling and other passive or active transport processes in cell aggregates.
In summary, for a phenomenological model of cell aggregates we assume that the state of the cell aggregates are completely described by the strain tensor and electric potential of cells:
| |  | (7) |
where the constraint Tr
E = 0 arises from the incompressibility of cells. For brevity and future convenience, denote by
s,
![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif)
,
s′ the collection of state variables of
N-cells, the average, and their deviations:
| | 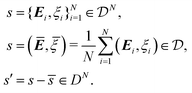 | (8) |
2.2. Energetics
In line with standard practices in physical modeling, we formulate the electromechanical model for cell aggregates via an energy function. As illustrated in Fig. 1(d), we consider a single cell from the aggregate with strain-electric potential  and propose that the cellular energy is given by
and propose that the cellular energy is given by| |  | (9) |
where A is the area of the cell, and μ, γ* (∼1), ε, λ > 0 and ξ*, K are constant model parameters. Physically, the energy terms in (9) are motivated from the following consideration. The first term characterizes the strain energy; the specific expression is the minimal form that is isotropic, thermodynamically stable, and admits the regular hexagonal tessellation (cf.Fig. 2(a)) and its equivalent configuration after T1-transition (cf.Fig. 2(c)) as the strain-energy minimizing states. In particular, the constant μ may be recognized as the shear modulus (for small strain). The second term 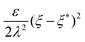 is the electric field energy with ξ* being the resting potential (at the absence of electromechanical coupling, i.e., K = 0), ε the dielectric constant, and λ a length scale comparable to the thickness of cell membrane. The electric field energy penalizes the deviation of interior cellular potential from the resting potential. The last term K(ξ − ξ*)|E|2 is for capturing the coupling between electrical field and mechanical strain. We remark that the proposed single-cell energy (9) represents the minimal isotropic electromechanical model that achieves the following: (i) it effectively reproduces the observed T1-transitions in cell aggregates, featuring with the characteristic rearrangements during tissue remodeling, and (ii) it incorporates nontrivial electromechanical coupling, allowing for a meaningful interplay between mechanical deformations and electrical responses. This balance of simplicity and functionality makes the proposed model (9) a robust foundation for exploring the electromechanical properties of tissues.
is the electric field energy with ξ* being the resting potential (at the absence of electromechanical coupling, i.e., K = 0), ε the dielectric constant, and λ a length scale comparable to the thickness of cell membrane. The electric field energy penalizes the deviation of interior cellular potential from the resting potential. The last term K(ξ − ξ*)|E|2 is for capturing the coupling between electrical field and mechanical strain. We remark that the proposed single-cell energy (9) represents the minimal isotropic electromechanical model that achieves the following: (i) it effectively reproduces the observed T1-transitions in cell aggregates, featuring with the characteristic rearrangements during tissue remodeling, and (ii) it incorporates nontrivial electromechanical coupling, allowing for a meaningful interplay between mechanical deformations and electrical responses. This balance of simplicity and functionality makes the proposed model (9) a robust foundation for exploring the electromechanical properties of tissues.
We next consider cell aggregates that are nonuniformly deformed or charged. Let  be the index set that contains all neighboring cells in contact with the ith cell. In account of nonuniformity, we postulate that the interaction energy for the ith cell is:
be the index set that contains all neighboring cells in contact with the ith cell. In account of nonuniformity, we postulate that the interaction energy for the ith cell is:
| |  | (10) |
where the length scale
l is comparable to the overall size of a cell, and constant
Jelast > 0 (resp.
Jelect > 0) measures the increase of energy when the strain (resp. electric potential) of a cell is different from that of neighboring cells. In the context of the Ising model,
Jelast and
Jelect are referred to as the exchange constants. Combining
(9) with
(10), we identify the Hamiltonian of an
N-cell system as
| |  | (11) |
which serves as the foundation for our statistical mechanics model.
We will follow the standard procedure of statistical mechanics to analyze the cell aggregate. In the classical statistical and thermal physics, the critical concept of (absolute) temperature reflects the fluctuation of energy associated with microstates of the system, whereas entropy measures the number of accessible microstates of the system. In thermal equilibrium, the probability distribution over all admissible microstates of the system is dictated by the Second Law, which can then be used to determine macroscopic properties and thermodynamic relations of the system. To apply this approach to the electromechanical model (11) of a cell aggregate, we start from the following hypotheses.61
(H1) The variability or fluctuations in state variables (E, ξ) are macroscopically homogeneous within the system (a cell aggregate) and can still be characterized by a single benchmark energy scale ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β.
BT = 1/β.
We remark that unlike the classical systems such as ideal gases, the stochasticity in cell aggregates has many contributions including but not limited to thermal agitations, passive and active biological processes (e.g., growing, diffusion, etc.), among others. Therefore, the benchmark energy scale ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β should be understood as a phenomenological parameter instead of the actual thermal energy scale that originates from the oscillations of constituent molecules or atoms. Nevertheless, for physiological relevance we can still interpret T as the absolute temperature of the system. Meanwhile,
BT = 1/β should be understood as a phenomenological parameter instead of the actual thermal energy scale that originates from the oscillations of constituent molecules or atoms. Nevertheless, for physiological relevance we can still interpret T as the absolute temperature of the system. Meanwhile, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) B should be regarded as an empirical constant in parallel to the classical Boltzmann's constant. Similar ideas have been used in the literature to describe novel phenomena in a range of physical systems, including granular media62 and plasticity in polycrystalline materials.61
B should be regarded as an empirical constant in parallel to the classical Boltzmann's constant. Similar ideas have been used in the literature to describe novel phenomena in a range of physical systems, including granular media62 and plasticity in polycrystalline materials.61
(H2) In quasi-static processes, the cell aggregate may exchange energy with the environment and stay in instantaneous equilibrium with a constant and uniform temperature T, and hence follows the Boltzmann distribution:
where

represents an admissible microstate of the cell aggregate and
p(
s) is the probability of the aggregate in the microstate
s.
Based on these hypotheses, we consider a canonical ensemble of the system at a constant temperature T and upscale from the microscopic model described by the Hamiltonian (11) to a macroscopic coarse-grained model. Denote the collection of all microstates with prescribed average (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) by
) by
| |  | (13) |
For a coarse-grained macroscopic model, we aim to calculate the effective free energy (per cell) with a prescribed average:
| |  | (14) |
where, by
(12), the partition function with prescribed average is identified as
| |  | (15) |
We remark that the effective free energy defined in
(14) is such that the partition function without prescribed average is given by
| | 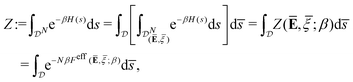 | (16) |
where the last equality justifies the terminology of “effective” free energy that governs the macroscopic coarse-grained properties of cell aggregates.
3. Effective free energy by mean-field approximation
For an N-cell aggregate in equilibrium, presumably cells would stay at the resting potential ξ* and tessellate the plane by regular hexagons to minimize the total energy. However, the presence of passive and active noises, size dispersion, topological defects, and thermal agitations give rise to variability and randomness in cell aggregates. From the postulated Boltzmann distribution (12), we can (i) identify the temperature or energy scale 1/β = ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT from the fluctuations of states of cell aggregates, and (ii) predict the macroscopic measurable effective material properties (e.g., shear modulus and electromechanical coupling coefficients) and how they depend on the fluctuations or, equivalently, the energy scale
BT from the fluctuations of states of cell aggregates, and (ii) predict the macroscopic measurable effective material properties (e.g., shear modulus and electromechanical coupling coefficients) and how they depend on the fluctuations or, equivalently, the energy scale ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT. For these purposes, we need to evaluate the partition function (15) and the effective free energy (14) for some prescribed average/macroscopic strain and potential (Ē,
BT. For these purposes, we need to evaluate the partition function (15) and the effective free energy (14) for some prescribed average/macroscopic strain and potential (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ).
).
3.1. Mean-field approximation
As for a standard Ising model, an exact solution to (15) is still an open problem for nontrivial interactions (encoded by the index set  ). A widely accepted approximation method is the so-called the mean-field theory, which simplifies the problem by neglecting the contribution of interaction energy from fluctuations. More precisely, we rewrite the interaction energy of cell aggregates in (11) as
). A widely accepted approximation method is the so-called the mean-field theory, which simplifies the problem by neglecting the contribution of interaction energy from fluctuations. More precisely, we rewrite the interaction energy of cell aggregates in (11) as| |  | (17) |
where q is the number of neighboring cells (i.e. the size of the index set  ) which is assumed to be independent of i. Denote by
) which is assumed to be independent of i. Denote by
the deviation from the average strain and average electric potential, respectively. In general, a Hamiltonian can be decomposed into three parts: the first depends only on the averaged or coarse-grained state variables, the second only on the deviations or high-frequency microscopic fluctuations, and the third on both. For instance, within the mean-field approximation (17) the Hamiltonian (11) of the cell aggregate can be written as| | H(s) = H0(![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) + H1(s′) + H2(s′; ) + H1(s′) + H2(s′; ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ), ), | (18) |
where, by direct calculation, we find that| |  | (19) |
We remark that the Hamiltonian (18), albeit anharmonic, is non-interacting because of the mean-field approximation. The associated partition function (15) and free energy (14) can be approximately evaluated by perturbation methods. To this end, we insert (18) and (19) into (14) and obtain| |  | (20) |
Further, upon neglecting the constraint in the integration domain, i.e., replacing  by
by  , we can write
, we can write ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) defined above as
defined above as| |  | (21) |
Two remarks are worth noting here. First, the replacement of  by
by  can be justified a posteriori. As will be shown shortly, the expected value of the deviations in our subsequent calculations does satisfy 〈E′〉 = 〈ξ′〉 = 0. Second, the reduction of the integral over the high-dimensional space
can be justified a posteriori. As will be shown shortly, the expected value of the deviations in our subsequent calculations does satisfy 〈E′〉 = 〈ξ′〉 = 0. Second, the reduction of the integral over the high-dimensional space  to
to  is possible due to the mean-field approximation (18), which accounts for interactions between neighboring cells by mean-fields.
is possible due to the mean-field approximation (18), which accounts for interactions between neighboring cells by mean-fields.
3.2. Variational perturbation method
We now evaluate the effective free energy (Feff), i.e., the integral (21), using the variational perturbation method. However, the presence of anharmonic terms like |E′|4 and |E′|6 in Ψ (cf. (9)) defies an exact closed-form solution to (21). One approach to making progress is through the standard perturbation method. To this end, we choose a comparison energy function Ψc = Ψc(E′, ξ′) and denote by| |  | (22) |
the probability distribution function (PDF) associated with the comparison energy function Ψc. The statistical average using PDF (22) is defined as| |  | (23) |
Then the Bogoliubov inequality63 asserts that for any energy function of E′ and ξ′, e.g., the function ![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (E′, ξ′; Ē,
(E′, ξ′; Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) defined in (21), we have
) defined in (21), we have
| | ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (Ē, (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) ≲ ; β) ≲ ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) U(Ē, U(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) = Fc + 〈 ; β) = Fc + 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (E′, ξ′; Ē, (E′, ξ′; Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) − ψc(E′, ξ′)〉c, ) − ψc(E′, ξ′)〉c, | (24) |
where
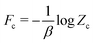
is a constant independent of coarse-grained state variables (
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
).
We now analytically evaluate the right-hand-side of (24) by choosing a quadratic comparison energy function:
| |  | (25) |
where
μc,
ηc > 0 and
κc ∈
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif)
are some constants that guarantee positivity of
(25) and will be fixed later. For the best upper-bound estimate of
Feff, by
(20) we may set
| | Feff(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) = Ψ(Ē, ; β) = Ψ(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) + min{ ) + min{![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) U(Ē, U(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) ; β)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μc,ηc > 0, κc ∈ μc,ηc > 0, κc ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) }, }, | (26) |
where the minimization problem is over all reasonable Gaussian distribution
(22) or positive harmonic comparison energy function
ψc(
E′,
ξ′).
In this work, we consider a planar model in which the fluctuating strain E′, average strain Ē can be written as
| |  | (27) |
The quadratic nature of the comparison energy turns integrals in
(23) into Gaussian-type integrals which can be analytically evaluated. In particular, we are interested in evaluating the (
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
)-dependent terms on the right-hand side of
(24),
i.e., 〈
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
(
E′,
ξ′;
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
)〉
c. From
(9) and (21)
2, we find that
| |  | (28) |
where OT(
E′,
ξ′;
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
) represents terms that are odd in (
E′,
ξ′), and hence will not contribute to 〈
![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif)
〉
c. By tedious but straightforward calculations, we find that
| |  | (29) |
where
μ0 includes all terms that are independent of (
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
), and
| | 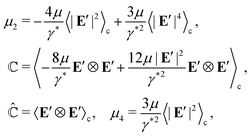 | (30) |
and
| |  | (31) |
Further, we find that the fourth-ordetensor  satisfies that
satisfies that
meaning that the fourth-order tensor

is isotropic and such that
| |  | (32) |
Inserting
(30)–(32) into
(29), we obtain the closed-form upper bound estimate for the effective free energy
Feff(
Ē,
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
;
β) defined in
(26) as
| |  | (33) |
where higher-order terms beyond

and immaterial constants are neglected, and the relevant effective properties are given by
| |  | (34) |
We remark that the effective free energy function, as defined in
(33), governs the macroscopic electromechanical properties of cell aggregates.
4. Results and discussion
In this section, we explore biophysical implications of the coarse-grained model (33), with a particular focus on understanding how fluctuations impact the electromechanical behavior of cell aggregates. To facilitate meaningful comparisons with experimental results and numerical simulations, we select relevant model parameters in (9) such that their values lie within the physiological range. Specifically, the resting potential is chosen as ξ* = −60 mV,12,64 the range of change in electric potential of a single cell as (![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) − ξ*) ∈ [−200 mV, 200 mV],13,16,17,64 the thickness of cell membrane as λ = 5 nm,65 shear modulus as μ = 200 Pa,66–69 the relative permittivity of a single cell as εr = 20,65 and the electromechanical coupling constant for a single cell is chosen as
− ξ*) ∈ [−200 mV, 200 mV],13,16,17,64 the thickness of cell membrane as λ = 5 nm,65 shear modulus as μ = 200 Pa,66–69 the relative permittivity of a single cell as εr = 20,65 and the electromechanical coupling constant for a single cell is chosen as  . For simplicity, we focus on scenarios of simple shear with
. For simplicity, we focus on scenarios of simple shear with
Upon neglecting an (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) )-independent constant, we rewrite the effective free energy function (33) as
)-independent constant, we rewrite the effective free energy function (33) as| |  | (35) |
4.1. Characterization of relevant energy scale
As demonstrated in ref. 55 and 57, the fluctuation 〈|E′|2〉c can be directly obtained from experimental and numerical images of tissues. By (31), we see that the relevant energy scale| |  | (36) |
Aside from a proportionality constant, the fluctuation 〈|E′|2〉c plays exactly the same role as the temperature in the classical statistical mechanics and is referred to as the E2-temperature in ref. 55. E2-temperature characterizes stochasticity (or fluctuations) in cellular strains contributed by complex active and passive biological processes. Therefore, E2-temperature should be understood as some kind of empirical parameter or effective temperature61,70–72 instead of the actual thermal temperature that originates from the vibration of atoms in classical thermodynamics. Subsequently, we study how macroscopic electromechanical properties of the cell aggregate depend on the E2-temperature (or fluctuation).
4.2. Renormalized resting potential
At the absence of external mechanical loading, the equilibrium state of the cell aggregate is determined by the principle of minimum free energy:| |  | (37) |
It is easy to see that a local small-strain minimizer is given by| |  | (38) |
Depending on the sign of K in the single-cell Hamiltonian (9), the E2-temperature 〈|E′|2〉c effectively lowers (if K > 0) or increases (if K < 0) the resting potential. We remark that this effective resting potential ξ*eff does not account for active processes of living cells. Biological processes, including ionic transport through channels and pumps, metabolic activities, and other cellular interactions, can significantly alter the electrical state of the cell.
4.3. Solid-to-fluid phase transition
It has been widely shown that cell aggregates may undergo a phase transition from a rigid solid-like phase to a floppy fluid-like phase, depending on the degree of “deviations” from the regular hexagonal tessellation.16,17,55,57 In the current setting, we interpret this transition as the critical point such that the small strain local minimizer (38) loses its stability, meaning that†| |  | (39) |
By (34) and (38), we find the critical E2-temperature to be the one at which the cell aggregate at resting condition (i.e., no external shear stress), transits from a solid-like phase to a fluid-like phase as| |  | (40) |
Bi et al. (201673) show that the solid–fluid phase transition occurs at the critical shape index ![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) cr = 3.81 at the absence of electromechanical coupling. By (5) we may fix γ* ≈ 2.0 for consistency.
cr = 3.81 at the absence of electromechanical coupling. By (5) we may fix γ* ≈ 2.0 for consistency.
Moreover, living cells are capable of regulating their transmembrane potentials. At the presence of electromechanical coupling, tissues can actively regulate their stiffness and solid-to-fluid transition by manipulating their electric potentials. This capability allows them to adaptively respond to varying environmental conditions and physiological demands. Suppose that the average electric potential of a cell aggregate is fixed at ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) via certain active biophysical processes. By (35) we find that the apparent shear modulus as
via certain active biophysical processes. By (35) we find that the apparent shear modulus as
| |  | (41) |
The critical
E2-temperature (or fluctuation) for solid–fluid phase transition at this prescribed potential
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif)
is identified as that at which the apparent shear modulus
μapparent of the cell aggregate vanishes:
| |  | (42) |
Fig. 3 shows the phase diagram for solid-to-fluid phase transition governed by the coarse-grained model (35). The black solid line shows the phase boundary. The region below and above the phase boundary corresponds to the rigid solid-like phase and floppy fluid-like phase, respectively. At a fixed applied electric potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) , an increase in E2-temperature 〈|E′|2〉c would transform the cell aggregate from a rigid solid-like phase to a floppy fluid-like phase. Similarly, at a prescribed E2-temperature, an increase in electric potential
, an increase in E2-temperature 〈|E′|2〉c would transform the cell aggregate from a rigid solid-like phase to a floppy fluid-like phase. Similarly, at a prescribed E2-temperature, an increase in electric potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) would transform the cell aggregate from a fluid-like phase to a solid-like phase.
would transform the cell aggregate from a fluid-like phase to a solid-like phase.
 |
| | Fig. 3 Phase diagram for solid-to-fluid phase transition in cell aggregates. For chosen numerical values in this work, the range of non-dimensional x-axis corresponds to the range of change in electric potential as (![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) − ξ*) ∈ [−200 mV, 200 mV] consistent with the physiological range; the y-axis represents the E2-temperature 〈|E′|2〉c. − ξ*) ∈ [−200 mV, 200 mV] consistent with the physiological range; the y-axis represents the E2-temperature 〈|E′|2〉c. | |
4.4. Energy barrier
The effective free energy function (35) is anharmonic and admits multiple critical points in γ for a prescribed average potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) . Graphically, as γ increases from 0, we observe that the first critical point (γ = 0) and the third critical point (γT1) are locally stable while the second critical point is unstable, reflecting the T1-transition illustrated in Fig. 2. To find the energy barrier between the two stable equilibria, we consider the equations for critical points:
. Graphically, as γ increases from 0, we observe that the first critical point (γ = 0) and the third critical point (γT1) are locally stable while the second critical point is unstable, reflecting the T1-transition illustrated in Fig. 2. To find the energy barrier between the two stable equilibria, we consider the equations for critical points:
By (35) we find that the unstable small-strain solution to the above equation is approximately given by
Therefore, by (35) the energy barrier between the stable equilibria γ = 0 and γ = γT1 is given by
The energy barrier can be used to quantitatively assess the rate of T1-transition. Following the classical Kramer's model,74 we may postulate the rate k of T1-transition per unit volume as| |  | (43) |
where the positive dimensionless constant 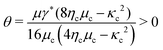 follows from the last equality in (31). We remark that (43) is consistent with the physical interpretation of solid-to-fluid phase transitions determined by (41). In particular, the transition rate k ≪ 1 if the fluctuation 〈|E′|2〉c ≪ 1 whereas k ∼ 1 if μapparent = 0. Moreover, the rate of transition may be identified as the self-diffusivity which, by the Stokes–Einstein's relation, implies that the viscosity η of the cell aggregates should satisfy
follows from the last equality in (31). We remark that (43) is consistent with the physical interpretation of solid-to-fluid phase transitions determined by (41). In particular, the transition rate k ≪ 1 if the fluctuation 〈|E′|2〉c ≪ 1 whereas k ∼ 1 if μapparent = 0. Moreover, the rate of transition may be identified as the self-diffusivity which, by the Stokes–Einstein's relation, implies that the viscosity η of the cell aggregates should satisfy
4.5. Electromechanical responses
Finally, we consider the electromechanical properties of the cell aggregate in the solid phase. Suppose that the cell aggregate is under the application of external shear stress σe. By (35), we observe that the external shear stress can alter the average cross-membrane potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) . Conversely, changes of the average transmembrane potential
. Conversely, changes of the average transmembrane potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) can influence the overall shear strain of the cell aggregate. These interactions highlight a two-way coupling between mechanical and electrical responses within the system. Furthermore, both responses are significantly modulated by E2-temperature (or fluctuations) of the system. For a fixed applied shear stress σe, average potential
can influence the overall shear strain of the cell aggregate. These interactions highlight a two-way coupling between mechanical and electrical responses within the system. Furthermore, both responses are significantly modulated by E2-temperature (or fluctuations) of the system. For a fixed applied shear stress σe, average potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) , and E2-temperature, we obtain the equilibrium shear strain γeq by the principle of minimum free energy:
, and E2-temperature, we obtain the equilibrium shear strain γeq by the principle of minimum free energy:| | 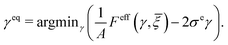 | (44) |
That is, γeq is the solution of the following nonlinear algebraic equation (cf.(35)):| |  | (45) |
In general, the above nonlinear equation admits multiple solutions. We are only interested in the “small-strain” solution, which we numerically compute using MATLAB.
We first consider the dependence of strain on the external stress under different E2-temperature 〈|E′|2〉c. As an example, we set the average electric potential the same as the effective resting potential ξ*eff in (38): ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ*eff. Fig. 4 shows the stress–strain relation of cell aggregate at different E2-temperatures (or fluctuations) below the critical E2-temperature in (40). We observe that the macroscopic elastic response of the cell aggregate is generally nonlinear and matches the typical range for cell aggregates.68 We also notice that an increase in E2-temperature (or fluctuation) softens the macroscopic elastic response, consistent with the effect of thermal temperature for classical crystalline solids.
= ξ*eff. Fig. 4 shows the stress–strain relation of cell aggregate at different E2-temperatures (or fluctuations) below the critical E2-temperature in (40). We observe that the macroscopic elastic response of the cell aggregate is generally nonlinear and matches the typical range for cell aggregates.68 We also notice that an increase in E2-temperature (or fluctuation) softens the macroscopic elastic response, consistent with the effect of thermal temperature for classical crystalline solids.
 |
| | Fig. 4 Macroscopic non-linear elastic response of cell aggregate for known fluctuation and applied electric potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ*eff. = ξ*eff. | |
Next, we consider the dependence of strain on the average cellular potential. Fig. 5 shows the equilibrium shear strain γeq plotted against normalized applied electric potential  for σe = 0.02μ and different E2 -temperatures 〈|E′|2〉c. We observe that as the average electric potential increases, the equilibrium shear strain decreases nonlinearly, showing a nonlinear piezoelectric response for cell aggregates. For a given average electric potential, the equilibrium shear strain is higher for higher E2-temperature. We also observe that the changes in equilibrium shear strain due to changes in average electric potential are more significant at higher E2-temperature. Physically, this implies that a softer cell aggregate possesses an enhanced electro-mechanical response, making its shape changes more significant and more sensitive to the changes in transmembrane electric potential. This observation is consistent with the solid-to-fluid phase transition for cell aggregate (cf.Fig. 3) that for a given average electric potential, an increase in E2-temperature (or fluctuation) brings a solid cell aggregate closer to the solid-to-fluid phase transition point.
for σe = 0.02μ and different E2 -temperatures 〈|E′|2〉c. We observe that as the average electric potential increases, the equilibrium shear strain decreases nonlinearly, showing a nonlinear piezoelectric response for cell aggregates. For a given average electric potential, the equilibrium shear strain is higher for higher E2-temperature. We also observe that the changes in equilibrium shear strain due to changes in average electric potential are more significant at higher E2-temperature. Physically, this implies that a softer cell aggregate possesses an enhanced electro-mechanical response, making its shape changes more significant and more sensitive to the changes in transmembrane electric potential. This observation is consistent with the solid-to-fluid phase transition for cell aggregate (cf.Fig. 3) that for a given average electric potential, an increase in E2-temperature (or fluctuation) brings a solid cell aggregate closer to the solid-to-fluid phase transition point.
 |
| | Fig. 5 Macroscopic inverse piezoelectric-like response of cell aggregate. Equilibrium shear strain γeq is plotted against normalized applied electric potential along x-axis. For chosen numerical values in this work, the range of non-dimensional x-axis in the plot corresponds to the range of change in electric potential as (![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) − ξ*) ∈ [−200 mV, 200 mV] consistent with the physiological range. − ξ*) ∈ [−200 mV, 200 mV] consistent with the physiological range. | |
5. Concluding remarks
In this work we first established the concept of strain tensor that characterizes the shape and orientation of individual cells and local arrangement of cells in amorphous cell aggregates. Based on the underlying structural symmetry and T1-transition experimentally observed in tissues, we proposed an electromechanical model for single cells and their interactions. For collective behavior of cell aggregates, we employed the approach of statistical mechanics and achieved a coarse-grained model for macroscopic electromechanical properties of cell aggregates. Fluctuation in cellular strains can be precisely quantified, which is referred as the E2-temperature for its analogous role as the absolute temperature in a conventional statistical model. The closed-form expression of the effective free energy enabled us to predict the macroscopic electromechanical properties of the cell aggregate. In particular, we derived the renormalized mechanical and electromechanical coupling coefficients and highlight how the average electric potential and E2-temperature can independently regulate the electromechanical properties and solid–fluid phase transitions in cell aggregates. Our work resolves the controversy of whether soft biological tissues are piezoelectric. The answer is simple. They are not intrinsically piezoelectric since they lack an underlying polar structure however, due to the electrostriction (or Maxwell stress) behavior of a single cell, and the resting potential, the aggregate or collective behavior of cells can mimic piezoelectric-like behavior.
There are several possible future directions: (i) the developed theory for living cell aggregates could be extended to explicitly account for the active processes (e.g., effects of active protein forces) by using the principles of non-equilibrium statistical mechanics.50,75,76 (ii) The derived effective free-energy may be used to explore the rich instability and bifurcation behavior in soft tissues cf. ref. 77 and 78 (iii) We have ignored the electromechanical coupling mechanism of flexoelectricity6 or rather its possible emergence at the tissue scale. Prior work appears to indicate that flexoelectricity, at least at the cellular level, is implicated in a variety of biophysical phenomena such as the hearing mechanism cf. ref. 79–81, and may also have consequences for energy extraction at the coarser level cf. ref. 82. An approach similar to outlined in this work may be used to address this mechanism. (iv) The developed theory can be augmented to include the non-local inter-cellular interactions83–87 by going beyond the nearest-neighbor interaction assumption used in this work.
Data availability
All data used in the paper is included within the paper.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
L. L. gratefully acknowledges the support of NSF DMS-2306254 and Simons travel grant. P. S. gratefully acknowledges the support of the Hugh Roy and Lillie Cranz Cullen Distinguished University Chair from the University of Houston.
References
- S. Safran, N. Gov, A. Nicolas, U. S. Schwarz and T. Tlusty, Physics of cell elasticity, shape and adhesion, Phys. A, 2005, 352(1), 171–201 CrossRef CAS.
-
B. Hille, Ion Channels of Excitable Membranes, Sinauer Associates, Sunderland, MA, 3rd edn, 2001 Search PubMed.
- M. Levin, Molecular bioelectricity: how endogenous voltage potentials control cell behavior and instruct pattern regulation in vivo, Mol. Biol. Cell, 2014, 25(24), 3835–3850 CrossRef PubMed.
- I. Nitsan, S. Drori, Y. E. Lewis, S. Cohen and S. Tzlil, Mechanical communication in cardiac cell synchronized beating, Nat. Phys., 2016, 12(5), 472–477 Search PubMed.
- A. D. Bershadsky, N. Q. Balaban and B. Geiger, Adhesion-dependent cell mechanosensitivity, Annu. Rev. Cell Dev. Biol., 2003, 19(1), 677–695 CAS.
- M. Torbati, K. Mozaffari, L. Liu and P. Sharma, Coupling of mechanical deformation and electromagnetic fields in biological cells, Rev. Mod. Phys., 2022, 94(2), 025003 CrossRef.
- T. E. Angelini, E. Hannezo, X. Trepat, J. J. Fredberg and D. A. Weitz, Cell migration driven by cooperative substrate deformation patterns, Phys. Rev. Lett., 2010, 104(16), 168104 CrossRef PubMed.
- X. Tang, P. Bajaj, R. Bashir and T. A. Saif, How far cardiac cells can see each other mechanically, Soft Matter., 2011, 7(13), 6151–6158 RSC.
- S. Tzlil and D. A. Tirrell, Strain propagation in artificial extracellular matrix proteins can accelerate cell spreading and polarization, Soft Matter., 2013, 9(23), 5602–5608 RSC.
- D. Grossman and J. F. Joanny, Instabilities and geometry of growing tissues, Phys. Rev. Lett., 2022, 129(4), 048102 CrossRef CAS PubMed.
- L. Yan and D. Bi, Multicellular rosettes drive fluid-solid transition in epithelial tissues, Phys. Rev. X, 2019, 9(1), 011029 CAS.
- T. Heimburg and A. D. Jackson, On soliton propagation in biomembranes and nerves, Proc. Natl. Acad. Sci. U. S. A., 2005, 102(28), 9790–9795 CrossRef CAS PubMed.
- V. Antonov, E. Y. Smirnova and E. Shevchenko, Electric field increases the phase transition temperature in the bilayer membrane of phosphatidic acid, Chem. Phys. Lipids, 1990, 52(3–4), 251–257 CrossRef CAS PubMed.
- R. Cotterill, Field effects on lipid membrane melting, Phys. Scr., 1978, 18(3), 191 CrossRef CAS.
- T. Mužić, F. Tounsi, S. B. Madsen, D. Pollakowski, M. Konrad and T. Heimburg, Melting transitions in biomembranes, Biochim. Biophys. Acta, Biomembr., 2019, 1861(11), 183026 CrossRef PubMed.
- T. Heimburg, The capacitance and electromechanical coupling of lipid membranes close to transitions: the effect of electrostriction, Biophys. J., 2012, 103(5), 918–929 CrossRef CAS PubMed.
- L. D. Mosgaard, K. A. Zecchi and T. Heimburg, Mechano-capacitive properties of polarized membranes, Soft Matter., 2015, 11(40), 7899–7910 RSC.
- D. A. Beysens, G. Forgacs and J. A. Glazier, Cell sorting is analogous to phase ordering in fluids, Proc. Natl. Acad. Sci., 2000, 97(17), 9467–9471 CrossRef CAS PubMed.
-
M. Steinberg, Cell Behaviour, Cambridge University Press, 1982 Search PubMed.
- G. Forgacs, R. A. Foty, Y. Shafrir and M. S. Steinberg, Viscoelastic properties of living embryonic tissues: a quantitative study, Biophys. J., 1998, 74(5), 2227–2234 CrossRef CAS PubMed.
- H. Phillips, M. Steinberg and B. Lipton, Embryonic tissues as elasticoviscous liquids, Dev. Biol., 1977, 59(2), 124–134 CAS.
- E. Hannezo, J. Prost and J. F. Joanny, Theory of epithelial sheet morphology in three dimensions, Proc. Natl. Acad. Sci., 2014, 111(1), 27–32 CrossRef CAS PubMed.
- N. Murisic, V. Hakim, I. G. Kevrekidis, S. Y. Shvartsman and B. Audoly, From discrete to continuum models of three-dimensional deformations in epithelial sheets, Biophys. J., 2015, 109(1), 154–163 CrossRef CAS PubMed.
- J. Cervera, J. A. Manzanares, S. Mafe and M. Levin, Synchronization of bioelectric oscillations in networks of nonexcitable cells: from single-cell to multicellular states, J. Phys. Chem. B, 2019, 123(18), 3924–3934 CrossRef CAS PubMed.
- E. Fukada, Piezoelectricity of biopolymers, Biorheology, 1995, 32(6), 593–609 CAS.
- Y. Liu, H. L. Cai, M. Zelisko, Y. Wang, J. Sun and F. Yan,
et al., Ferroelectric switching of elastin, Proc. Natl. Acad. Sci., 2014, 111(27), E2780–E2786 CrossRef CAS PubMed.
- T. Lenz, R. Hummel, I. Katsouras, W. A. Groen, M. Nijemeisland and R. Ruemmler,
et al., Ferroelectricity and piezoelectricity in soft biological tissue: Porcine aortic walls revisited, Appl. Phys. Lett., 2017, 111(13), 133701 CrossRef.
- K. Ikushima, T. Kumamoto, K. Ito and Y. Anzai, Electric polarization of soft biological tissues induced by ultrasound waves, Phys. Rev. Lett., 2019, 123(23), 238101 CrossRef CAS PubMed.
- D. Drasdo and S. Höhme, A single-cell-based model of tumor growth in vitro: monolayers and spheroids, Phys. Biol., 2005, 2(3), 133 CrossRef CAS PubMed.
- J. Griffié, R. Peters and D. M. Owen, An agent-based model of molecular aggregation at the cell membrane, PLoS One, 2020, 15(2), e0226825 CrossRef PubMed.
- A. R. Anderson, M. A. Chaplain, E. L. Newman, R. J. Steele and A. M. Thompson, Mathematical modelling of tumour invasion and metastasis, Comput. Math. Methods Med., 2000, 2(2), 129–154 CrossRef.
- M. Block, E. Schöll and D. Drasdo, Classifying the expansion kinetics and critical surface dynamics of growing cell populations, Phys. Rev. Lett., 2007, 99(24), 248101 CrossRef CAS PubMed.
- J. Moreira and A. Deutsch, Cellular automaton models of tumor development: a critical review, Adv. Complex Syst., 2002, 5(02n03), 247–267 Search PubMed.
-
M. S. Alber, M. A. Kiskowski, J. A. Glazier and Y. Jiang, On cellular automaton approaches to modeling biological cells. Mathematical systems theory in biology, communications, computation, and finance. Springer, 2003, pp. 1–39 Search PubMed.
- T. Alarcón, H. M. Byrne and P. K. Maini, A mathematical model of the effects of hypoxia on the cell-cycle of normal and cancer cells, J. Theor. Biol., 2004, 229(3), 395–411 CrossRef PubMed.
- A. C. Callan-Jones and F. Jülicher, Hydrodynamics of active permeating gels, New J. Phys., 2011, 13(9), 093027 CrossRef.
- J. Ranft, M. Basan, J. Elgeti, J. F. Joanny, J. Prost and F. Jülicher, Fluidization of tissues by cell division and apoptosis, Proc. Natl. Acad. Sci., 2010, 107(49), 20863–20868 CrossRef CAS PubMed.
- J. Prost, F. Jülicher and J. F. Joanny, Active gel physics, Nat. Phys., 2015, 11(2), 111–117 Search PubMed.
- M. H. Köpf and L. M. Pismen, A continuum model of epithelial spreading, Soft Matter, 2013, 9(14), 3727–3734 Search PubMed.
- J. C. Arciero, Q. Mi, M. F. Branca, D. J. Hackam and D. Swigon, Continuum model of collective cell migration in wound healing and colony expansion, Biophys. J., 2011, 100(3), 535–543 CrossRef CAS PubMed.
- S. Ishihara, P. Marcq and K. Sugimura, From cells to tissue: A continuum model of epithelial mechanics, Phys. Rev. E, 2017, 96(2), 022418 CrossRef PubMed.
- S. Firooz, S. Kaessmair, V. Zaburdaev, A. Javili and P. Steinmann, On continuum modeling of cell aggregation phenomena, J. Mech. Phys. Solids, 2022, 167, 105004 Search PubMed.
- N. J. Armstrong, K. J. Painter and J. A. Sherratt, A continuum approach to modelling cell-cell adhesion, J. Theor. Biol., 2006, 243(1), 98–113 CAS.
- A. Gerisch and M. A. Chaplain, Mathematical modelling of cancer cell invasion of tissue: local and non-local models and the effect of adhesion, J. Theor. Biol., 2008, 250(4), 684–704 CrossRef CAS PubMed.
- I. Ramis-Conde, M. A. Chaplain and A. R. Anderson, Mathematical modelling of cancer cell invasion of tissue, Math. Comput. Modell., 2008, 47(5–6), 533–545 CrossRef.
- F. W. Wiegel and A. S. Perelson, Statistical mechanics of red blood cell aggregation: the distribution of rouleaux in thermal equilibrium, J. Stat. Phys., 1982, 29, 813–848 Search PubMed.
- A. E. Teschendorff and A. P. Feinberg, Statistical mechanics meets single-cell biology, Nat. Rev. Genet., 2021, 22(7), 459–476 CrossRef CAS PubMed.
- N. Loy and L. Preziosi, A Statistical Mechanics Approach to Describe Cell Reorientation Under Stretch, Bull. Math. Biol., 2023, 85(7), 60 CrossRef CAS PubMed.
- C. Åberg, J. A. Varela, L. W. Fitzpatrick and K. A. Dawson, Spatial and structural metrics for living cells inspired by statistical mechanics, Sci. Rep., 2016, 6(1), 34457 CrossRef PubMed.
- Y. Kulkarni, Fluctuations of active membranes with nonlinear curvature elasticity, J. Mech. Phys. Solids, 2023, 173, 105240 CrossRef.
- S. Ramesh and Y. Kulkarni, Statistical mechanics of active vesicles and the size distribution paradox, J. Mech. Phys. Solids, 2024, 191, 105749 CrossRef.
- A. Mathew and Y. Kulkarni, Active matter as the underpinning agency for extraordinary sensitivity of biological membranes to electric fields, Proc. Natl. Acad. Sci. U. S. A., 2025, 122(12), e2427255122 CrossRef PubMed.
- É. Fodor and M. C. Marchetti, The statistical physics of active matter: From self-catalytic colloids to living cells, Phys. A, 2018, 504, 106–120 CrossRef.
- L. Liu and P. Sharma, Flexoelectricity and thermal fluctuations of lipid bilayer membranes: Renormalization of flexoelectric, dielectric, and elastic properties, Phys. Rev. E, 2013, 87(3), 032715 CrossRef.
- R. Li, C. Ibar, Z. Zhou, S. Moazzeni, A. Norris and K. Irvine,
et al., E2 and Gamma Distributions in Polygonal Networks, Phy. Rev. Res., 2021, 3(4), L042001 CrossRef CAS PubMed.
- M. Bock, A. K. Tyagi, J. U. Kreft and W. Alt, Generalized Voronoi Tessellation as a Model of Two-dimensional Cell Tissue Dynamics, Bull. Math. Biol., 2010, 72, 1696–1731 CrossRef PubMed.
- L. Atia, D. Bi, Y. Sharma, J. Mitchel, B. Gweon and S. Koehler,
et al., Geometrical constraints during epithelial jamming, Nat. Phys., 2018, 14, 613 Search PubMed.
- R. Li, S. Moazzeni, L. Liu and H. Lin, Micro and Macroscopic Stress-Strain Relations in Disordered Tessellated Networks, Phys. Rev. Lett., 2023, 130(18), 188201 CrossRef CAS PubMed.
- L. D. Landau, On the Theory of Phase Transitions, Phy Z Sow., 1937, 11, 26 CAS.
-
L. D. Landau and E. M. Lifshitz, Statistical Physics, Pergamon Press, 3rd edn, 1999 Search PubMed.
- P. Khandagale, L. Liu and P. Sharma, Statistical mechanics of plasticity: Elucidating anomalous size-effects and emergent fractional nonlocal continuum behavior, J. Mech. Phys. Solids, 2024, 191, 105747 CrossRef CAS.
- S. Ogawa, A. Umemura and N. Oshima, On the equations of fully fluidized granular materials, J. Appl. Math. Phys., 1980, 31, 483–493 Search PubMed.
- N. N. J. Bogolyubov, On model dynamical systems in statistical mechanics, Physica, 1966, 32, 933–944 CrossRef.
- A. Beyder and F. Sachs, Electromechanical coupling in the membranes of Shaker-transfected HEK cells, Proc. Natl. Acad. Sci., 2009, 106(16), 6626–6631 CrossRef CAS PubMed.
- S. Krichen, L. Liu and P. Sharma, Biological cell as a soft magnetoelectric material: Elucidating the physical mechanisms underpinning the detection of magnetic fields by animals, Phys. Rev. E, 2017, 96(4), 042404 CrossRef CAS PubMed.
- I. Levental, P. C. Georges and P. A. Janmey, Soft biological materials and their impact on cell function, Soft Matter, 2007, 3(3), 299–306 RSC.
- S. Hiratsuka, Y. Mizutani, M. Tsuchiya, K. Kawahara, H. Tokumoto and T. Okajima, The number distribution of complex shear modulus of single cells measured by atomic force microscopy, Ultramicroscopy, 2009, 109(8), 937–941 CrossRef CAS PubMed.
- J. Huang, J. O. Cochran, S. M. Fielding, M. C. Marchetti and D. Bi, Shear-driven solidification and nonlinear elasticity in epithelial tissues, Phys. Rev. Lett., 2022, 128(17), 178001 CrossRef CAS PubMed.
- D. Bi, J. Lopez, J. M. Schwarz and M. L. Manning, A density-independent rigidity transition in biological tissues, Nat. Phys., 2015, 11(12), 1074–1079 Search PubMed.
- E. T. Jaynes, Information theory and statistical mechanics, Phys. Rev., 1957, 106(4), 620 CrossRef.
- S. F. Edwards and R. Oakeshott, Theory of powders, Phys. A, 1989, 157(3), 1080–1090 CrossRef.
- A. S. Balankin and L. Flores-Cano, Edwards's statistical mechanics of crumpling networks in crushed self-avoiding sheets with finite bending rigidity, Phys. Rev. E, 2015, 91(3), 032109 CrossRef PubMed.
- D. Bi, X. Yang, M. C. Marchetti and M. L. Manning, Motility-driven glass and jamming transitions in biological tissues, Phys. Rev. X, 2016, 6(2), 021011 Search PubMed.
- H. A. Kramers, Brownian motion in a field of force and the diffusion model of chemical reactions, Physica, 1940, 7, 284–304 CrossRef CAS.
- T. Leadbetter, P. K. Purohit and C. Reina, A statistical mechanics framework for constructing nonequilibrium thermodynamic models, Proc. Natl. Acad. Sci., 2023, 2(12), pgad417 Search PubMed.
- S. Huang, I. R. Graham, R. A. Riggleman, P. E. Arratia, S. Fitzgerald and C. Reina, Predicting the unobserved: A statistical mechanics framework for non-equilibrium material response with quantified uncertainty, J. Mech. Phys. Solids, 2022, 161, 104779 CrossRef CAS.
- S. Yang and P. Sharma, A tutorial on the stability and bifurcation analysis of the electromechanical behaviour of soft materials, Appl. Mech. Rev., 2023, 75(4), 044801 CrossRef.
- S. Yang, X. Zhao and P. Sharma, Revisiting the instability and bifurcation behavior of soft dielectrics, J. Appl. Mech., 2017, 84(3), 031008 CrossRef.
- K. D. Breneman, W. E. Brownell and R. D. Rabbitt, Hair cell bundles: flexoelectric motors of the inner ear, PLoS One, 2009, 4(4), e5201 CrossRef PubMed.
- K. Mozaffari, F. Ahmadpoor, Q. Deng and P. Sharma, A minimal physics-based model for musical perception, Proc. Natl. Acad. Sci., 2023, 120(5), e2216146120 CrossRef CAS.
- Q. Deng, F. Ahmadpoor, W. E. Brownell and P. Sharma, The collusion of flexoelectricity and Hopf bifurcation in the hearing mechanism, J. Mech. Phys. Solids, 2019, 130, 245–261 CrossRef CAS.
- B. Wang, S. Yang and P. Sharma, Flexoelectricity as a universal mechanism for energy harvesting from crumpling of thin sheets, Phys. Rev. B, 2019, 100(3), 035438 CrossRef CAS.
- J. Marshall and K. Dayal, Atomistic-to-continuum multiscale modeling with long-range electrostatic interactions in ionic solids, J. Mech. Phys. Solids, 2014, 62, 137–162 CrossRef CAS.
- P. Khandagale, T. Breitzman, C. Majidi and K. Dayal, Statistical field theory for nonlinear elasticity of polymer networks with excluded volume interactions, Phys. Rev. E, 2023, 107(6), 064501 CrossRef CAS PubMed.
- V. Abkevich, A. Gutin and E. Shakhnovich, Impact of local and non-local interactions on thermodynamics and kinetics of protein folding, J. Mol. Biol., 1995, 252(4), 460–471 CrossRef CAS PubMed.
- R. H. French, V. A. Parsegian, R. Podgornik, R. F. Rajter, A. Jagota and J. Luo,
et al., Long range interactions in nanoscale science, Rev. Mod. Phys., 2010, 82(2), 1887 CrossRef.
- A. Campa, T. Dauxois and S. Ruffo, Statistical mechanics and dynamics of solvable models with long-range interactions, Phys. Rep., 2009, 480(3–6), 57–159 CrossRef CAS.
Footnote |
| † We assume that the phase-transition is of the 2nd order type. Some evidence supports a first-order type transition. Our framework may be extended to address the latter scenario if desired. |
|
| This journal is © The Royal Society of Chemistry 2025 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Hao
Lin
a,
Hao
Lin
 b,
Liping
Liu
b,
Liping
Liu
 *bc and
Pradeep
Sharma
*bc and
Pradeep
Sharma
 *d
*d
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β) used in this work is a phenomenological constant; the fluctuation or variability in cellular states arises not only from thermal agitations but also from many other passive and active processes that entail “equilibrium” of the system at the observation time-scale. The collection of cellular strains and electric potentials in a cell aggregate are assumed to describe the microstates of the system. For their collective properties in a cell aggregates, we first propose a single-cell Hamiltonian based on the underlying structural symmetries and experimental observations of their electromechanical responses. We employ the mean-field approximation, which allows for an analytical solution of the model and yields a closed-form expression for the effective free energy of cell aggregates. Based on this effective free energy, we present several experimentally testable predictions, including the macroscopic electromechanical properties, the solid–fluid phase transitions observed in cell aggregates, and their dependence on the E2-temperature and average electric potential regulated by active processes.
BT = 1/β) used in this work is a phenomenological constant; the fluctuation or variability in cellular states arises not only from thermal agitations but also from many other passive and active processes that entail “equilibrium” of the system at the observation time-scale. The collection of cellular strains and electric potentials in a cell aggregate are assumed to describe the microstates of the system. For their collective properties in a cell aggregates, we first propose a single-cell Hamiltonian based on the underlying structural symmetries and experimental observations of their electromechanical responses. We employ the mean-field approximation, which allows for an analytical solution of the model and yields a closed-form expression for the effective free energy of cell aggregates. Based on this effective free energy, we present several experimentally testable predictions, including the macroscopic electromechanical properties, the solid–fluid phase transitions observed in cell aggregates, and their dependence on the E2-temperature and average electric potential regulated by active processes.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 the polygon/domain occupied by the ith cell, A the area of the polygon Ci, and ci the spatial positions of the centroids of cells. For simplicity, we assume that each cell precisely occupies the Voronoi cell associated with {ci: i = 1, …, N}.56 Though it is tempting to employ the centroids of cells as the fundamental state variables, a reasonable physical model or Hamiltonian for the tessellation in terms of {ci: i = 1, …, N} must be interacting and permutation invariant, and hence not amenable to systematic perturbation methods. On the other hand, for cell aggregates illustrated in Fig. 1(a), we see that the shapes of cells and statistical properties of aspect ratios are good indicator of different physiological stages of cell aggregates (or tissues) which, presumably, dictate the physical properties of cell aggregates as well.55,57,58 Therefore, we choose the deformation or strain as one of the independent state variables for the cell aggregate.
2 the polygon/domain occupied by the ith cell, A the area of the polygon Ci, and ci the spatial positions of the centroids of cells. For simplicity, we assume that each cell precisely occupies the Voronoi cell associated with {ci: i = 1, …, N}.56 Though it is tempting to employ the centroids of cells as the fundamental state variables, a reasonable physical model or Hamiltonian for the tessellation in terms of {ci: i = 1, …, N} must be interacting and permutation invariant, and hence not amenable to systematic perturbation methods. On the other hand, for cell aggregates illustrated in Fig. 1(a), we see that the shapes of cells and statistical properties of aspect ratios are good indicator of different physiological stages of cell aggregates (or tissues) which, presumably, dictate the physical properties of cell aggregates as well.55,57,58 Therefore, we choose the deformation or strain as one of the independent state variables for the cell aggregate.
![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym is a measure of orientation and aspect ratio of individual cells and the underlying arrangement of cells. In particular, we require that the strain tensor E ∈
2×2sym is a measure of orientation and aspect ratio of individual cells and the underlying arrangement of cells. In particular, we require that the strain tensor E ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym satisfy the following.
2×2sym satisfy the following.![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym measures the “aspect ratio” of the cell.
2×2sym measures the “aspect ratio” of the cell.![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2sym defines the “orientation” of the cell.
2×2sym defines the “orientation” of the cell. with n vertices yj (j = 1,…,n). As illustrated in Fig. 1(a), typically n = 4, 5, 6, 7 from experiments. Suppose a cell occupies an irregular hexagon as in Fig. 1(d). We choose the regular hexagon of the same area in Fig. 1(c) as the reference undeformed configuration.
with n vertices yj (j = 1,…,n). As illustrated in Fig. 1(a), typically n = 4, 5, 6, 7 from experiments. Suppose a cell occupies an irregular hexagon as in Fig. 1(d). We choose the regular hexagon of the same area in Fig. 1(c) as the reference undeformed configuration.
 is such that the area of the regular n-gon equals the area of the cell. By the method of least square, we can in general define a deformation gradient F ∈
is such that the area of the regular n-gon equals the area of the cell. By the method of least square, we can in general define a deformation gradient F ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2 and a translational vector u0 ∈
2×2 and a translational vector u0 ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2 for the cell:
2 for the cell:![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) 2×2 is the identity matrix). We write L(F, u0) as
2×2 is the identity matrix). We write L(F, u0) as
 illustrated in Fig. 1(d), without loss of generality we assume the centroid is at the origin:
illustrated in Fig. 1(d), without loss of generality we assume the centroid is at the origin:  Then the normalized second moment tensor is given by
Then the normalized second moment tensor is given by
 is the second moment tensor of a regular n-gon of the same area (cf.Fig. 1(c)). Suppose that the current shape
is the second moment tensor of a regular n-gon of the same area (cf.Fig. 1(c)). Suppose that the current shape  is obtained by deforming the regular n-gon
is obtained by deforming the regular n-gon  with vertices given by xj in (1), i.e., yj = Fxj. The second normalized moment tensor is given by
with vertices given by xj in (1), i.e., yj = Fxj. The second normalized moment tensor is given by ratio can be expressed as a function of strain E:
ratio can be expressed as a function of strain E: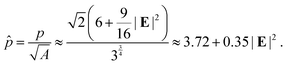


![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) , s′ the collection of state variables of N-cells, the average, and their deviations:
, s′ the collection of state variables of N-cells, the average, and their deviations: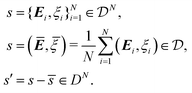
 and propose that the cellular energy is given by
and propose that the cellular energy is given by
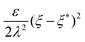 is the electric field energy with ξ* being the resting potential (at the absence of electromechanical coupling, i.e., K = 0), ε the dielectric constant, and λ a length scale comparable to the thickness of cell membrane. The electric field energy penalizes the deviation of interior cellular potential from the resting potential. The last term K(ξ − ξ*)|E|2 is for capturing the coupling between electrical field and mechanical strain. We remark that the proposed single-cell energy (9) represents the minimal isotropic electromechanical model that achieves the following: (i) it effectively reproduces the observed T1-transitions in cell aggregates, featuring with the characteristic rearrangements during tissue remodeling, and (ii) it incorporates nontrivial electromechanical coupling, allowing for a meaningful interplay between mechanical deformations and electrical responses. This balance of simplicity and functionality makes the proposed model (9) a robust foundation for exploring the electromechanical properties of tissues.
is the electric field energy with ξ* being the resting potential (at the absence of electromechanical coupling, i.e., K = 0), ε the dielectric constant, and λ a length scale comparable to the thickness of cell membrane. The electric field energy penalizes the deviation of interior cellular potential from the resting potential. The last term K(ξ − ξ*)|E|2 is for capturing the coupling between electrical field and mechanical strain. We remark that the proposed single-cell energy (9) represents the minimal isotropic electromechanical model that achieves the following: (i) it effectively reproduces the observed T1-transitions in cell aggregates, featuring with the characteristic rearrangements during tissue remodeling, and (ii) it incorporates nontrivial electromechanical coupling, allowing for a meaningful interplay between mechanical deformations and electrical responses. This balance of simplicity and functionality makes the proposed model (9) a robust foundation for exploring the electromechanical properties of tissues.
 be the index set that contains all neighboring cells in contact with the ith cell. In account of nonuniformity, we postulate that the interaction energy for the ith cell is:
be the index set that contains all neighboring cells in contact with the ith cell. In account of nonuniformity, we postulate that the interaction energy for the ith cell is:

![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β.
BT = 1/β.![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT = 1/β should be understood as a phenomenological parameter instead of the actual thermal energy scale that originates from the oscillations of constituent molecules or atoms. Nevertheless, for physiological relevance we can still interpret T as the absolute temperature of the system. Meanwhile,
BT = 1/β should be understood as a phenomenological parameter instead of the actual thermal energy scale that originates from the oscillations of constituent molecules or atoms. Nevertheless, for physiological relevance we can still interpret T as the absolute temperature of the system. Meanwhile, ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) B should be regarded as an empirical constant in parallel to the classical Boltzmann's constant. Similar ideas have been used in the literature to describe novel phenomena in a range of physical systems, including granular media62 and plasticity in polycrystalline materials.61
B should be regarded as an empirical constant in parallel to the classical Boltzmann's constant. Similar ideas have been used in the literature to describe novel phenomena in a range of physical systems, including granular media62 and plasticity in polycrystalline materials.61 represents an admissible microstate of the cell aggregate and p(s) is the probability of the aggregate in the microstate s.
represents an admissible microstate of the cell aggregate and p(s) is the probability of the aggregate in the microstate s.
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) by
) by


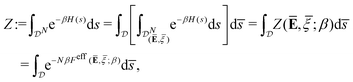
![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT from the fluctuations of states of cell aggregates, and (ii) predict the macroscopic measurable effective material properties (e.g., shear modulus and electromechanical coupling coefficients) and how they depend on the fluctuations or, equivalently, the energy scale
BT from the fluctuations of states of cell aggregates, and (ii) predict the macroscopic measurable effective material properties (e.g., shear modulus and electromechanical coupling coefficients) and how they depend on the fluctuations or, equivalently, the energy scale ![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) BT. For these purposes, we need to evaluate the partition function (15) and the effective free energy (14) for some prescribed average/macroscopic strain and potential (Ē,
BT. For these purposes, we need to evaluate the partition function (15) and the effective free energy (14) for some prescribed average/macroscopic strain and potential (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ).
).
 ). A widely accepted approximation method is the so-called the mean-field theory, which simplifies the problem by neglecting the contribution of interaction energy from fluctuations. More precisely, we rewrite the interaction energy of cell aggregates in (11) as
). A widely accepted approximation method is the so-called the mean-field theory, which simplifies the problem by neglecting the contribution of interaction energy from fluctuations. More precisely, we rewrite the interaction energy of cell aggregates in (11) as
 ) which is assumed to be independent of i. Denote by
) which is assumed to be independent of i. Denote by![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ) + H1(s′) + H2(s′;
) + H1(s′) + H2(s′; ![[s with combining macron]](https://www.rsc.org/images/entities/i_char_0073_0304.gif) ),
),

 by
by  , we can write
, we can write ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) defined above as
defined above as
 by
by  can be justified a posteriori. As will be shown shortly, the expected value of the deviations in our subsequent calculations does satisfy 〈E′〉 = 〈ξ′〉 = 0. Second, the reduction of the integral over the high-dimensional space
can be justified a posteriori. As will be shown shortly, the expected value of the deviations in our subsequent calculations does satisfy 〈E′〉 = 〈ξ′〉 = 0. Second, the reduction of the integral over the high-dimensional space  to
to  is possible due to the mean-field approximation (18), which accounts for interactions between neighboring cells by mean-fields.
is possible due to the mean-field approximation (18), which accounts for interactions between neighboring cells by mean-fields.

![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (E′, ξ′; Ē,
(E′, ξ′; Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) defined in (21), we have
) defined in (21), we have![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) (Ē,
(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) ≲
; β) ≲ ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) U(Ē,
U(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) = Fc + 〈
; β) = Fc + 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (E′, ξ′; Ē,
(E′, ξ′; Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) − ψc(E′, ξ′)〉c,
) − ψc(E′, ξ′)〉c,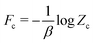 is a constant independent of coarse-grained state variables (Ē,
is a constant independent of coarse-grained state variables (Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ).
).

![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) are some constants that guarantee positivity of (25) and will be fixed later. For the best upper-bound estimate of Feff, by (20) we may set
are some constants that guarantee positivity of (25) and will be fixed later. For the best upper-bound estimate of Feff, by (20) we may set![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) = Ψ(Ē,
; β) = Ψ(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) + min{
) + min{![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) U(Ē,
U(Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β)
; β)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) μc,ηc > 0, κc ∈
μc,ηc > 0, κc ∈ ![[Doublestruck R]](https://www.rsc.org/images/entities/char_e175.gif) },
},
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) )-dependent terms on the right-hand side of (24), i.e., 〈
)-dependent terms on the right-hand side of (24), i.e., 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) (E′, ξ′; Ē,
(E′, ξ′; Ē, ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) )〉c. From (9) and (21)2, we find that
)〉c. From (9) and (21)2, we find that
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ) represents terms that are odd in (E′, ξ′), and hence will not contribute to 〈
) represents terms that are odd in (E′, ξ′), and hence will not contribute to 〈![[small psi, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e3.gif) 〉c. By tedious but straightforward calculations, we find that
〉c. By tedious but straightforward calculations, we find that
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ), and
), and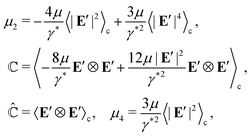

 satisfies that
satisfies that is isotropic and such that
is isotropic and such that
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) ; β) defined in (26) as
; β) defined in (26) as
 and immaterial constants are neglected, and the relevant effective properties are given by
and immaterial constants are neglected, and the relevant effective properties are given by
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) − ξ*) ∈ [−200 mV, 200 mV],13,16,17,64 the thickness of cell membrane as λ = 5 nm,65 shear modulus as μ = 200 Pa,66–69 the relative permittivity of a single cell as εr = 20,65 and the electromechanical coupling constant for a single cell is chosen as
− ξ*) ∈ [−200 mV, 200 mV],13,16,17,64 the thickness of cell membrane as λ = 5 nm,65 shear modulus as μ = 200 Pa,66–69 the relative permittivity of a single cell as εr = 20,65 and the electromechanical coupling constant for a single cell is chosen as  . For simplicity, we focus on scenarios of simple shear with
. For simplicity, we focus on scenarios of simple shear with![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) )-independent constant, we rewrite the effective free energy function (33) as
)-independent constant, we rewrite the effective free energy function (33) as





![[p with combining circumflex]](https://www.rsc.org/images/entities/i_char_0070_0302.gif) cr = 3.81 at the absence of electromechanical coupling. By (5) we may fix γ* ≈ 2.0 for consistency.
cr = 3.81 at the absence of electromechanical coupling. By (5) we may fix γ* ≈ 2.0 for consistency.
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) via certain active biophysical processes. By (35) we find that the apparent shear modulus as
via certain active biophysical processes. By (35) we find that the apparent shear modulus as
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) is identified as that at which the apparent shear modulus μapparent of the cell aggregate vanishes:
is identified as that at which the apparent shear modulus μapparent of the cell aggregate vanishes:
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) , an increase in E2-temperature 〈|E′|2〉c would transform the cell aggregate from a rigid solid-like phase to a floppy fluid-like phase. Similarly, at a prescribed E2-temperature, an increase in electric potential
, an increase in E2-temperature 〈|E′|2〉c would transform the cell aggregate from a rigid solid-like phase to a floppy fluid-like phase. Similarly, at a prescribed E2-temperature, an increase in electric potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) would transform the cell aggregate from a fluid-like phase to a solid-like phase.
would transform the cell aggregate from a fluid-like phase to a solid-like phase.![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) . Graphically, as γ increases from 0, we observe that the first critical point (γ = 0) and the third critical point (γT1) are locally stable while the second critical point is unstable, reflecting the T1-transition illustrated in Fig. 2. To find the energy barrier between the two stable equilibria, we consider the equations for critical points:
. Graphically, as γ increases from 0, we observe that the first critical point (γ = 0) and the third critical point (γT1) are locally stable while the second critical point is unstable, reflecting the T1-transition illustrated in Fig. 2. To find the energy barrier between the two stable equilibria, we consider the equations for critical points:
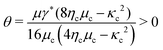 follows from the last equality in (31). We remark that (43) is consistent with the physical interpretation of solid-to-fluid phase transitions determined by (41). In particular, the transition rate k ≪ 1 if the fluctuation 〈|E′|2〉c ≪ 1 whereas k ∼ 1 if μapparent = 0. Moreover, the rate of transition may be identified as the self-diffusivity which, by the Stokes–Einstein's relation, implies that the viscosity η of the cell aggregates should satisfy
follows from the last equality in (31). We remark that (43) is consistent with the physical interpretation of solid-to-fluid phase transitions determined by (41). In particular, the transition rate k ≪ 1 if the fluctuation 〈|E′|2〉c ≪ 1 whereas k ∼ 1 if μapparent = 0. Moreover, the rate of transition may be identified as the self-diffusivity which, by the Stokes–Einstein's relation, implies that the viscosity η of the cell aggregates should satisfy![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) . Conversely, changes of the average transmembrane potential
. Conversely, changes of the average transmembrane potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) can influence the overall shear strain of the cell aggregate. These interactions highlight a two-way coupling between mechanical and electrical responses within the system. Furthermore, both responses are significantly modulated by E2-temperature (or fluctuations) of the system. For a fixed applied shear stress σe, average potential
can influence the overall shear strain of the cell aggregate. These interactions highlight a two-way coupling between mechanical and electrical responses within the system. Furthermore, both responses are significantly modulated by E2-temperature (or fluctuations) of the system. For a fixed applied shear stress σe, average potential ![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) , and E2-temperature, we obtain the equilibrium shear strain γeq by the principle of minimum free energy:
, and E2-temperature, we obtain the equilibrium shear strain γeq by the principle of minimum free energy: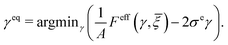

![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ*eff. Fig. 4 shows the stress–strain relation of cell aggregate at different E2-temperatures (or fluctuations) below the critical E2-temperature in (40). We observe that the macroscopic elastic response of the cell aggregate is generally nonlinear and matches the typical range for cell aggregates.68 We also notice that an increase in E2-temperature (or fluctuation) softens the macroscopic elastic response, consistent with the effect of thermal temperature for classical crystalline solids.
= ξ*eff. Fig. 4 shows the stress–strain relation of cell aggregate at different E2-temperatures (or fluctuations) below the critical E2-temperature in (40). We observe that the macroscopic elastic response of the cell aggregate is generally nonlinear and matches the typical range for cell aggregates.68 We also notice that an increase in E2-temperature (or fluctuation) softens the macroscopic elastic response, consistent with the effect of thermal temperature for classical crystalline solids.
![[small xi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0cf.gif) = ξ*eff.
= ξ*eff. for σe = 0.02μ and different E2 -temperatures 〈|E′|2〉c. We observe that as the average electric potential increases, the equilibrium shear strain decreases nonlinearly, showing a nonlinear piezoelectric response for cell aggregates. For a given average electric potential, the equilibrium shear strain is higher for higher E2-temperature. We also observe that the changes in equilibrium shear strain due to changes in average electric potential are more significant at higher E2-temperature. Physically, this implies that a softer cell aggregate possesses an enhanced electro-mechanical response, making its shape changes more significant and more sensitive to the changes in transmembrane electric potential. This observation is consistent with the solid-to-fluid phase transition for cell aggregate (cf.Fig. 3) that for a given average electric potential, an increase in E2-temperature (or fluctuation) brings a solid cell aggregate closer to the solid-to-fluid phase transition point.
for σe = 0.02μ and different E2 -temperatures 〈|E′|2〉c. We observe that as the average electric potential increases, the equilibrium shear strain decreases nonlinearly, showing a nonlinear piezoelectric response for cell aggregates. For a given average electric potential, the equilibrium shear strain is higher for higher E2-temperature. We also observe that the changes in equilibrium shear strain due to changes in average electric potential are more significant at higher E2-temperature. Physically, this implies that a softer cell aggregate possesses an enhanced electro-mechanical response, making its shape changes more significant and more sensitive to the changes in transmembrane electric potential. This observation is consistent with the solid-to-fluid phase transition for cell aggregate (cf.Fig. 3) that for a given average electric potential, an increase in E2-temperature (or fluctuation) brings a solid cell aggregate closer to the solid-to-fluid phase transition point.