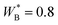Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the existence of prewetting in supracritical fluid mixtures
Jan
Forsman
 *a and
Clifford E.
Woodward
b
*a and
Clifford E.
Woodward
b
aComputational Chemistry, Lund University, P.O.Box 124, S-221 00 Lund, Sweden. E-mail: jan.forsmancompchem.lu.se
bSchool of Physical, Environmental and Mathematical Sciences University College, University of New South Wales, ADFA, Canberra, ACT 2600, Australia
First published on 20th March 2025
Abstract
We demonstrate the existence of a first-order prewetting transition of a supracritical model polymer solution adjacent to an attractive surface. The model fluid we use mimics (qualitatively) an aqueous polyethylene oxide solution and, like the actual solution, displays a closed loop 2-phase region with an upper and lower critical solution temperature. The model fluid is shown to undergo a prewetting transition at an adjacent attractive surface. For sufficiently strong surface affinities, the prewetting transition may occur even at temperatures below the lower critical solution temperature (supracriticality). This phenomenon follows from non-local thermodynamics when the length-scale of the relevant fluid structures of surface films are commensurate or smaller than the range of intermolecular interactions.
1. Introduction
Many binary fluid mixtures or solutions display a demixing phase diagram with both an upper and a lower critical solution temperature (U/LCST), which bracket the 2-phase region. Above the UCST and below the LCST, in what we will refer to as the supracritical regions, the mixture exists as a single phase. In this article, we will be primarily concerned with the supracritical region below the LCST.1.1. Background
The presence of an LCST is not common in mixtures of simple fluids (examples include nicotine-water and triethylamine-water), but in polymer solutions it is more the rule rather than the exception.1–7 One example is an aqueous solution of poly(ethylene oxide) (PEO) which has an LCST that approaches 100 °C at high molecular weights.8 Using classical polymer density functional theory (cDFT), we have generalised a successful theoretical model for such solutions,4 that can be used to model these solutions in heterogeneous environments.9–11 In this model, monomers are assumed to be in either of two classes of states, labelled A and B, where B is more solvophobic than A. Thus A states become preferred as the temperature is lowered, which promotes complete dissolution. On the other hand, the degeneracy of the B class exceeds that of A, which means the relative probability of B (solvophobic) monomers increases with temperature. This creates the possibility of demixing with increasing temperature, leading to an LCST. At a high enough temperature, the mixing entropy dominates interactions, giving rise to an UCST. We do not resort to temperature-dependent interactions per se, but instead make explicit the intrinsic enthalpic and entropic contributions of A and B species within an aqueous environment.Consider a bulk mixture which is able to diffuse freely into and out of a pore. If the pore surfaces interact directly with the confined fluid, they may cause a phase change relative to the bulk fluid, so-called capillary induced phase separation (CIPS).12 If we make the assumption that the fluid–fluid interactions are short-ranged compared to the size of the pore then the pore will only contribute surface terms to the free energy and CIPS can only occur if the bulk fluid is not supracritical. In pores which are narrow compared to the range of fluid–fluid interactions, there may be a significant shift along the temperature axis of the 2-phase region of the confined fluid. This is because surfaces will truncate intermolecular interactions between fluid particles.12–15 As these interactions are generally attractive at long range (at least for non-ionic fluids) this causes a decrease in the cohesive forces within the fluid. To illustrate, consider a single-component fluid displaying a critical temperature. Reduction in the cohesive forces, due to truncation, will mean the confined fluid behaves similarly to that of the bulk fluid, but at a higher temperature. Thus the overall phase diagram of the confined fluid is shifted to lower temperatures, compared to that of the bulk.14 Such a situation is still consistent with the requirement above, i.e., CIPS can only occur if the temperature of the bulk fluid is below the critical temperature. However, the scenario is more complex for mixtures that display an LCST in the bulk. In previous work, we have shown that confining the mixture in a pore reduces the LCST.9–11 Thus, in this case, the confined fluid may undergo CIPS, even though the bulk solution is supra-critical. Such transitions may occur also with inert surfaces.11
Some fluids may undergo first-order phase transitions at a single surface via so-called “thin-thick” (prewetting) transitions. These are surface transitions, as the prewetting phases involve structural changes of the fluid that are intrinsically confined to narrow films adjacent to the adsorbing surface. Thus, the truncation of fluid–fluid interactions discussed above will plausibly also affect prewetting transitions. In particular, according to the discussion above, one expects that the UCST of the prewetting transition is lower than that of the bulk phase transition. On the other hand, the role of these mechanisms in the vicinity of an LCST has hitherto not attracted significant attention in the literature, as far as we are aware.
1.2. Qualitative considerations
Consider a bulk 2-component solution, at some fixed pressure and temperature, T. This mixture possesses a demixing regime wherein the fluid separates into a concentrated, C, and dilute, D, phase with respect to one of the components (the “solute” species). For the moment, we will assume that this solution displays only a UCST. The prewetting behaviour of such systems are well established,16–21 but it is useful to recapitulate the main concepts. Suppose such a solution in its undersaturated D phase, T < UCST, is adjacent to a single surface, W, which is attractive to the solute species. A positive adsorption of solute at the surface gives rise to what we will label a “thin” surface film of excess solute. The surface tension at the surface–fluid interface is denoted as, γWD. Making the bulk fluid more concentrated will cause an increase in the excess solute adsorption. Above the so-called wetting temperature, TW, this increasing adsorption will grow by way of a thickening film, with width L. The fluid in this film will have a character similar to the metastable C phase and the surface–fluid interfacial tension will approach γWC. This occurs because γWC < γWD and the free energy is lowered accordingly. However, the film also establishes a C–D interface with the bulk and the ensuing positive surface tension contribution, γCD, will act to counter the free energy lowering at the adsorbing surface. At saturation (i.e., on the bulk coexistence curve), the free energy penalty for growing a film (L → ∞) approaches Δγ (= γWC + γCD − γWD), from above, where the surface tensions are defined with respect to the coexisting C and D phases. For T > TW, γCD is sufficiently small so that, Δγ < 0, and the film grows to infinity spontaneously. This gives rise to a divergence in the excess adsorption of solute and complete wetting. For T < TW, γCD is large enough that Δγ > 0: the thin film persists and no wetting layer forms (partial wetting).As stated earlier, in some cases, the film thickness may grow discontinuously, undergoing a first-order, so-called “thin-thick” (or prewetting) transition, at some undersaturated value of D. The locus of concentrations (versus T) where this transition occurs, is called the prewetting line. This line intercepts the bulk coexistence line at, TW, and terminates at some upper, prewetting critical temperature, UCSTpw < UCST. This last inequality occurs due to the truncation mechanism described earlier, which applies here because of the finite width of the fluid films that coexist on the prewetting line. The free energy (per unit area) cost for film formation at T > TW in an undersaturated bulk solution can be written as Δγ + ΔFCD(L). Here, ΔFCD(L) > 0 is essentially the intrinsic free energy of the thick fluid film, without the contributions from the wall–fluid and fluid–fluid surface terms. If ΔfCD denotes the difference in free energy per unit volume of the metastable bulk C phase relative to the stable bulk D phase (at the same temperature and pressure), then we have ΔFCD(L) ≈ ΔfCDL for large enough L. The prewetting transition occurs because the system admits two stable film phases on the prewetting line. For T = TW we have ΔFCD(L) = Δγ = 0.
In particular, according to the discussion above, one expects that the UCST of the prewetting transition is lower than that of the bulk phase transition. We should note that this phenomenon is not universal, e.g., type I superconductors (SC) can display a prewetting like transition above the critical temperature. This is due to the enhancement of the SC transition at surfaces, leading to nucleation of finite width layers that merge with the prewetting line.22
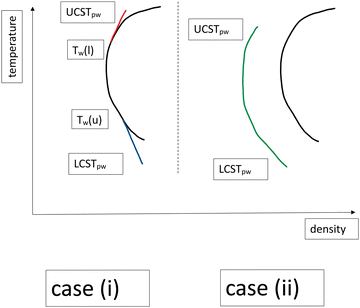
So what happens for a mixture which also possesses an LCST as well? As argued above for the case of a UCST only, TW, primarily arises due to the increase in γCD as the temperature decreases. This is correlated with the increasing compositional differences between coexisting bulk C and D phases, as the temperature decreases. When an LCST is present, the 2-phase region becomes a closed loop, which causes γCD to decrease again as T decreases toward the LCST. This gives rise to the possibility that both an upper and lower wetting temperature exist, giving rise to two prewetting lines, respectively terminating above at UCSTpw and below at LCSTpw (“case (i)”). Within the case (i) scenario, we also include systems which possess either an upper or lower prewetting line alone. On the other hand, it is possible that one or both prewetting lines will detach from the coexistence line. This would result in at least one prewetting line of finite length, as shown in Fig. 1 (“case (ii)”), and complete wetting as one approaches the bulk coexistence line.
Furthermore, due to truncation of intermolecular forces in the finite films of prewetting phases, as described above, we also anticipate a possibility that LCSTpw < LCST, see Fig. 1. This suggests the fascinating option of thin-thick transitions under supracritical conditions (supracritical prewetting). That is, at some temperatures, lower than LCST, prewetting transitions occur but don't signal the onset of film growth on the surface as the bulk solution concentration increases. Thus the excess solute adsorption always remains finite at all bulk concentrations. In this sense, the term “prewetting transition” becomes something of a misnomer. That is, while the system can undergo a thin-thick transition it does not lead to complete wetting as the composition increases. This underlines the fact that the prewetting transition is essentially a surface transition and is not intrinsically dependent on complete wetting in any fundamental sense.
2. Model and theory
Following this qualitative discussion, we will now turn to quantitative predictions. In particular, we will use the aqueous PEO solution model described earlier. This will require some model details, and definitions. We let N(R) denote the density distribution of monodisperse PEO polymers with r monomers. Here, R = r1, r2,…,rr, where ri is the coordinate of monomer i. The polymers are assumed linear with monomers joined by freely rotating bonds, described by a potential Vb. This potential is chosen to ensure a constant bond length b, i.e. e−βVb(R) ∝ Πδ(|ri+1 − ri| − b), where δ(x) is the Dirac delta function, and β = 1/(kT) is the inverse thermal energy. We will assume that the total mixture (polymer and solvent) is incompressible. This is ensured by constraining the total density of monomers + solvent particles to a fixed value, nt, i.e. nt = n(r) + nS(r), where n(r) and nS(r) are the monomer and solvent densities at position r. Specifically, we have set ntσ3 = 1, where σ is the Lennard-Jones length parameter, common to all species, as defined below. According to our description above, we introduce the monomer state probabilities PA and PB, and defining state densities nA(r) ≡ n(r)PA(r) and nB(r) ≡ n(r)(1 − PA(r)), we write the fluid free energy density functional, F, as: | (1) |
All particles (monomers and solvent) particles have a hard core with diameter, σ, and interact with each other via a Lennard-Jones (L-J) potential, ϕ(a)αβ(r):
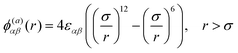 | (2) |
Defining a reference energy parameter, εref, we obtain reduced parameters 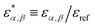 , as well as a reduced temperature T* = kT/εref. We will use the same energy parameters as in our previous studies.9–11 In that model, the parameters are shifted so that all long-range AA, AS and SS interactions vanish, i.e.,
, as well as a reduced temperature T* = kT/εref. We will use the same energy parameters as in our previous studies.9–11 In that model, the parameters are shifted so that all long-range AA, AS and SS interactions vanish, i.e.,  , while
, while 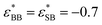 , and
, and  . We have previously shown that for gA/gB = 13, one obtains a bulk fluid with both a UCST and an LCST, for long enough chains.10 Note that this means that we are employing spherically symmetric interactions, which obviously differ from (say) the PEO/water system. Directional interactions may often be relevant but in this generic work we show that such properties are not requied to produce the behaviours we seeek to elucidate.
. We have previously shown that for gA/gB = 13, one obtains a bulk fluid with both a UCST and an LCST, for long enough chains.10 Note that this means that we are employing spherically symmetric interactions, which obviously differ from (say) the PEO/water system. Directional interactions may often be relevant but in this generic work we show that such properties are not requied to produce the behaviours we seeek to elucidate.
The potential function, Vαex(r), defines the nature of the surface, which is modelled as a hard flat wall parallel to the (x, y) plane (with z normal). We set:
 | (3) |
 , that determines the affinity to B. The adsorption potential is illustrated in Fig. 2, under conditions that are typical to this work. We note that, although the wall potential is formally limited by zc, it actually decays quite fast, and becomes almost insignificant beyond 3σ or so. We emphasise that in the present generic work the specific functional form of this short-ranged adsorption potential is qualitatively irrelevant, and we could instead have chosen (say) a square well potential.
, that determines the affinity to B. The adsorption potential is illustrated in Fig. 2, under conditions that are typical to this work. We note that, although the wall potential is formally limited by zc, it actually decays quite fast, and becomes almost insignificant beyond 3σ or so. We emphasise that in the present generic work the specific functional form of this short-ranged adsorption potential is qualitatively irrelevant, and we could instead have chosen (say) a square well potential.
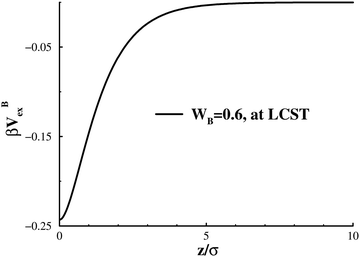 | ||
| Fig. 2 An illustration of the surface adsorption potential, normalised by thermal energy, with WB = 0.6, at the LCST. | ||
The grand potential is defined as,  , where μp is the polymer chemical potential and A is the surface area of the walls, which we assume is infinite. The functional, Ω, is then minimised with respect to both n(z) and Pα(z) to obtain the equilibrium density profiles of the different monomer species and the incompressibility constraint allows us to infer the solvent density profile. The net reduced monomer adsorption, Γ*, is obtained as
, where μp is the polymer chemical potential and A is the surface area of the walls, which we assume is infinite. The functional, Ω, is then minimised with respect to both n(z) and Pα(z) to obtain the equilibrium density profiles of the different monomer species and the incompressibility constraint allows us to infer the solvent density profile. The net reduced monomer adsorption, Γ*, is obtained as  , where nb is the bulk monomer density. Integrals are solved on a grid (along z), up to some large distance (H = 50σ or 100σ, depending on conditions), beyond which bulk conditions are assumed. Test calculations were performed to verify convergence, i.e. that we have used a fine enough grid, and a large enough value of H.
, where nb is the bulk monomer density. Integrals are solved on a grid (along z), up to some large distance (H = 50σ or 100σ, depending on conditions), beyond which bulk conditions are assumed. Test calculations were performed to verify convergence, i.e. that we have used a fine enough grid, and a large enough value of H.
3. Results
Using this type of surface model, we have established that a prewetting transition can occur in a 300-mer polymer solution. In Fig. 3 we show the prewetting phase diagram, Γ* vs. T, for surface attractions (WB) that are strong enough to result in “case (ii)” behaviour. The temperature is scaled with respect to the the bulk LCST. The prewetting transition describes a closed loop over the range, UCSTpw to LCSTpw, which indicates that the prewetting line is completely detached from the bulk 2-phase line and there are no wetting temperatures. Furthermore, we see that both prewetting critical temperatures are below their bulk counterparts. This confirms that prewetting transitions can occur in supracritical regions of the bulk fluid. | ||
| Fig. 3 Thin-thick coexistence curves, for a 300-mer polymer solution that displays an LCST. Crosses, plus signs, and circles denote various strengths of a short-ranged B-specific adsorption potential (see eqn (3)), with circles denoting the strongest attraction. Note that in the latter case, the lower critical surface temperature is about 8% below the LCST. For PEO/water this would correspond to about 30 °C. All these systems are of “case (ii)” type, i.e. there is no upper wetting temperature. Instead, the thin and thick phases merge at some upper critical temperature. | ||
In Fig. 4 we show the prewetting line together with the dilute part of the bulk coexistence region, for a range of surface potential strengths. Here, we also include results with quite weak adsorption, whereby “case (i)” scenarios emerge (dashed lines), i.e. prewetting lines that terminate at bulk coexistence conditions, thereby defining an upper wetting temperature. In those cases, the prewetting line does not proceed below the LCST. It is not immediately obvious that one could not find “case (i)” systems for which the lower critical prewetting temperature is lower than the LCST. Nevertheless, we were unable to establish such a scenario for the systems that we have investigated in this work. We also note that it is at least possible that thin-thick transitions may take place at an inert surface, without preferential attraction to any fluid species. This is because of the unequal mutual interactions between species, i.e., the system can minimise the wall–fluid interfacial tension by preferential adsorption of species with weaker interactions. For example, such a mechanism gives rise to CIPS in narrow inert pores.9,11 We have so far only established thin-thick coexistence for surfaces that are somewhat more attractive to the solvophobic B monomers for the current model. On the other hand, the surface attractions required are short-ranged, and quite weak, so we do not rule out that one might observe prewetting transitions for non-adsorbing surfaces with other interaction models. We also note, in Fig. 4, that the “case (i)” systems lack an upper prewetting line, for the systems that we have investigated here.
In Fig. 5, we give an example of density profiles for coexisting thin and thick phases; in this case at a temperature corresponding to the bulk LCST. These merge together at LCSTpw. The two phases are quite similar, since we are relatively close to the lower prewetting temperature, LCSTpw. Nevertheless, it is quite clear that two phases remain discernable, despite critical conditions in the bulk.
 | ||
Fig. 5 Density profiles, for coexisting thin (black) and thick (red) phases, for a 300-mer solution, at the bulk LCST, with  . Separate profiles for A (dashed) and B (solid) type are displayed. . Separate profiles for A (dashed) and B (solid) type are displayed. | ||
In Fig. 6 we illustrate a fundamental difference between “ordinary” prewetting (above LCST) and supracritical prewetting (below LCST). In the former case, the net adsorption diverges as we increase the bulk phase concentration towards the bulk coexistence line. For supracritical adsorption, the thickness remains finite for all bulk concentrations and, indeed, the net adsorption decreases at some point, as the bulk concentration increases, due to polymer depletion and the lower energy per monomer in the bulk.
The transitions will also depend upon the length of the polymer chains. In Fig. 7, we compare our results for 300-mer mixtures, with a corresponding phase diagram for a 100-mer mixture. Adsorption of polymers is a cooperative process, and with shorter polymers a stronger surface affinity of B-type monomers is required, in order to push the lower critical surface temperature below the bulk LCST. In this case, we have set  for the 100-mers, which leads to a similar T/LCST ratio at the lower surface critical temperature, as for 300-mers, with
for the 100-mers, which leads to a similar T/LCST ratio at the lower surface critical temperature, as for 300-mers, with  . We also note a smaller overall difference between thin and thick phases, for shorter polymers, throughout the demixing regime.
. We also note a smaller overall difference between thin and thick phases, for shorter polymers, throughout the demixing regime.
 | ||
Fig. 7 Thin-thick coexistence curves, 300-mer polymer solutions, as well as a 100-mer polymer solution, below their respective bulk LCST. The notation for the 300-mer cases is the same as in Fig. 3, whereas 100-mer coexistence, with 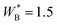 is indicated by diamond symbols and dashed lines (the latter to guide the eye). is indicated by diamond symbols and dashed lines (the latter to guide the eye). | ||
4. Conclusions
This work thus demonstrates that first-order prewetting surface transitions can occur even in situations where the adjacent bulk fluid is outside its 2-phase region (supracritical). In this case, it has been shown to occur for mixtures that exhibit an LCST. However, our results imply that coexisting surface phases don't rely on the existence of a “corresponding” metastable bulk phase. This latter type of description is often used in conjunction with the assumption of localised thermodynamics in the inhomogeneous surface phase, which is clearly not justified when the spatial extent of the relevant fluid structures are of the same order or smaller than the range of interactions. One signature of this supracritical prewetting is that, as the bulk phase increases in concentration, there is no divergence in the net adsorption of the thick phase, as occurs in complete wetting.In this work, we have only established supracritical prewetting for systems where the surface affinity is so strong that the prewetting line is detached from the bulk coexistence line. This fact does not exclude the possibility that prewetting below the LCST also might be found for systems where there is an upper wetting temperature, i.e. with a prewetting line that terminates at bulk coexistence.
Finally, it is of interest to note that all interactions in our model are isotropic. In many “real” solution mixtures, there are also anisotropic interactions and, as argued by Karlström and co-workers,4,23 the difference in solvophilicity between monomers in different structural states may be a result of a shift in polarity or hydrogen-bonding ability to the solute species. These are orientation-dependent pair interactions. The intrinsic degeneracies that distinguishes the A and B may then be viewed as a coarse-grained description of such differences. Moreover, our treatment here demonstrates that there are no formal requirements of anisotropicity, in order achieve the behaviours that we have investigated.
Data availability
All generated data, as well as all codes used to generate these data, are freely available upon reasonable request. Moreover, the code, as well as a significant part of the calculated data, can be found on GitHub: https://github.com/janneforsman/LCST_thinthickConflicts of interest
There are no conflicts to declare.Acknowledgements
J. F. acknowledges financial support by the Swedish Research Council, grant number VR2021-04041.References
- L. A. Kleintjens and R. Koningsveld, Coll. Polym. Sci., 1980, 258, 711–718 CAS.
- P. H. van Koynenburg and R. L. Scott, Phil. Trans. R. Soc. Lond. A, 1980, 298, 495 Search PubMed.
- H. Nakanishi and M. E. Fisher, Phys. Rev. Lett., 1982, 49, 1565–1568 CAS.
- G. Karlström, J. Phys. Chem., 1985, 89, 4962–4964 CrossRef.
- G. Jackson, Mol. Phys., 1991, 72, 1365–1385 CrossRef CAS.
- K. Morishige, H. Fujii, M. Uga and D. Kinukawa, Langmuir, 1997, 13, 3494–3498 CrossRef CAS.
- E. E. Dormidontova, Macromolecules, 2002, 35, 987 CrossRef CAS.
- S. Saeki, N. Kuwahara, S. Konno and M. Kaneko’, Macromolecules, 1973, 6, 246–250 CrossRef CAS.
- F. Xie, C. E. Woodward and J. Forsman, Langmuir, 2013, 29, 2659–2666 CrossRef CAS PubMed.
- F. Xie, C. E. Woodward and J. Forsman, Soft Matter, 2016, 12, 658–663 RSC.
- S. Haddadi, C. E. Woodward and J. Forsman, Fluid Phase Equilib., 2021, 540, 112983 CrossRef CAS.
- H. Wennerström, K. Thuresson, P. Linse and E. Freyssingeas, Langmuir, 1998, 14, 5664 CrossRef.
- J. E. Lane and T. H. Spurling, Aust. J. Chem., 1981, 34, 1529 CrossRef CAS.
- C. G. V. Burgess, D. H. Everett and S. Nutall, Pure Appl. Chem., 1989, 61, 1845–1852 CrossRef CAS.
- M. Kotelyanskii and S. K. Kumar, Phys. Rev. Lett., 1998, 80, 1252–1255 CrossRef CAS.
- J. W. Cahn, J. Chem. Phys., 1977, 66, 3667 CrossRef CAS.
- C. Ebner and W. F. Saam, Phys. Rev. Lett., 1977, 38, 1486–1489 CrossRef CAS.
- P. G. deGennes, Rev. Mod. Phys., 1985, 57, 827 CrossRef CAS.
- D. Beysens and D. Esteve, Phys. Rev. Lett., 1985, 54, 2123–2126 CrossRef CAS PubMed.
- R. Evans, U. M. B. Marconi and P. Tarazona, J. Chem. Phys., 1986, 84, 2376–2399 CrossRef CAS.
- A. Drzewiński, A. Maciołek, A. Barasiński and S. Dietrich, Phys. Rev. E, 2009, 79, 041145 CrossRef PubMed.
- J. Indekeu and J. van Leeuwen, Phys. C: Superconductivity, 1995, 251, 290–306 CrossRef CAS.
- M. Andersson and G. Karlstrom, J. Phys. Chem., 1985, 89, 4957–4962 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2025 |