Topological sorting of magnetic colloidal bipeds

Aneena Rinu Perayil; Piotr Kuświk; Maciej Urbaniak; Feliks Stobiecki; Sapida Akhundzada; Arno Ehresmann; Daniel de las Heras; Thomas M. Fischer

doi:10.1039/D4SM01480D

View PDF VersionPrevious ArticleNext Article

Open Access Article

This Open Access Article is licensed under a
Creative Commons Attribution 3.0 Unported Licence

DOI: 10.1039/D4SM01480D (Paper) Soft Matter, 2025, 21, 2716-2722

Topological sorting of magnetic colloidal bipeds†

Aneena Rinu Perayil ^a, Piotr Kuświk ^b, Maciej Urbaniak ^b, Feliks Stobiecki ^b, Sapida Akhundzada ^c, Arno Ehresmann ^c, Daniel de las Heras ^d and Thomas M. Fischer *^a
^aExperimentalphysik X, Physikalisches Institut, Universität Bayreuth, D-95440 Bayreuth, Germany. E-mail: thomas.fischer@uni-bayreuth.de
^bInstitute of Molecular Physics, Polish Academy of Sciences, 60-179 Poznań, Poland
^cInstitute of Physics and Center for Interdisciplinary Nanostructure Science and Technology (CINSaT), Universität Kassel, D-34132 Kassel, Germany
^dTheoretische Physik II, Physikalisches Institut, Universität Bayreuth, D-95440 Bayreuth, Germany

Received 13th December 2024 , Accepted 8th March 2025

First published on 10th March 2025

Abstract

Topologically nontrivial adiabatic loops of the orientation of a homogeneous external magnetic field drive the walking of paramagnetic colloidal bipeds above a deformed quasi-periodic magnetic square pattern. Depending on the topological properties of the loop we can simultaneously control the walking directions of colloidal bipeds as a function of their size and as a function of the size of a deformed unit cell of the pattern. The bipeds walk performing steps with their two feet alternatingly grounding one foot and lifting the other. The step width of the bipeds is given by a set of winding numbers (w_x, w_y) ∈ [Doublestruck Z] ² – a set of topological invariants – that can only change by integers as we continuously increase the length of the bipeds. We experimentally use this discrete size dependence for the robust sorting of bipeds according to their length.

1. Introduction

In a first step, sorting classifies a set of objects into disjunct categories that are determined by the properties of the objects. In a second step, subsets of objects falling into one category are transported to a region in space reserved for one category thereby being separated in space from objects belonging to other categories. The properties of the objects can be discrete. For example, in the Golgi apparatus different proteins are sorted and packed into vesicles for transport to various destinations within the cell.¹ On the cellular scale, during the embryo genesis the cells differentiate and move toward their correct location.^2,3 The objects properties can also be continuous such as the length,⁴ the width,⁵ and the size^6–11 among others.^11–14 In the continuous case, categories are intervals and the interval boundaries are bifurcation points between different discrete categories. Sorting objects with a computer algorithm is a serial or weakly parallel process, while the separation of chemicals via electrophoresis is a massive parallel process. Massive parallel processes allow for high-throughput sorting.¹⁵ Active sorting^16–19 occurs when self propelled objects sort themselves. Active sorting is usually more robust than passive sorting.^20,21 Microfluidic sorting devices often rely on optical,²² steric²³ patterns that guide specific particles along different conduits. In biology one tries to understand sorting mechanisms – originally developed via evolution – by analyzing whether the sorting persists or not after applying all kinds of perturbations.^24–27

Analytical^24–27 as well as machine learning^28,29 approaches try to identify and exploit how a preexisting sorting mechanism works. Synthetic approaches are used to construct a sorting process by having understood a priori how it works. Here we follow a synthetic path to generate a sorting device for colloidal bipeds of different length from first principles. Knowing the mathematical laws that govern the transport of colloidal bipeds^30–32 we design a magnetic pattern and a modulation that forces the sorting of colloidal bipeds according to their length using external commands.

The mathematical principles that govern the transport are of topological nature, that is, the transport is fully controlled by a set of topological invariants. We have used those topological laws to robustly transport paramagnetic and diamagnetic colloids on periodic patterns,^33–35 to independently transport them into different directions,^33,34 to simultaneously write different letters,³⁰ or to walk in a time reversal or non-time reversal way.³⁶ We have induced skipping orbits at the edge of topologically distinct³⁷ and topologically equivalent³⁸ lattices. We have generalized this topological concept to non-periodic metamorphic patterns that are locally but not globally periodic³⁹ and used the concept to synthesize colloidal assemblies called bipeds of a desired length on a hexagonal pattern with constant lattice constant but varying symmetry phase³² and to cloak certain regions against colloidal trespassers.⁴⁰ In this work we show that a metamorphic square pattern with varying lattice constant and a magnetic driving loop with a mirror symmetry different from ref. 32 can force the colloids to automatically fulfill a new task compared to those reported in ref. 30–40: different length colloidal bipeds sort themselves. This requires them not only to separate but additionally to walk to predefined attractor locations differing for each different biped length.

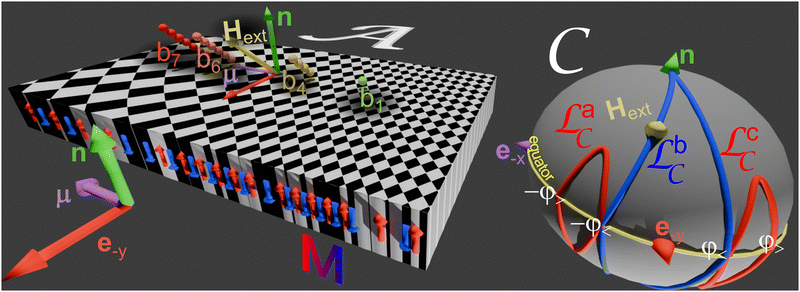
2. Setup

Paramagnetic colloidal particles (diameter d = 2.8 μm) immersed in water are placed on top of a two-dimensional magnetic pattern. The pattern is a deformed square lattice of alternating regions with positive and negative magnetization relative to the direction normal to the pattern, see Fig. 1. For our thin film we choose a pattern with magnetization


	(1)

where r is the two dimensional vector in action space [scr A, script letter A]

, which is the plane parallel to the pattern where the colloids move. The modulus of the saturation magnetization is denoted by M_s, h is the thickness of the film, n is the vector normal to the film, the z coordinate runs in direction of n. The vectors q_i = qRⁱ_π/2·e_x, (i = 0, 1), are two coplanar primitive reciprocal unit vectors of common modulus q, and R_π/2 is an anticlockwise rotation matrix around the normal vector n by π/2. In previous work^30,34–36 we have fixed the modulus (∇q = 0) and the pattern was a periodic square pattern of fixed period a = 2π/q.


	Fig. 1 Schematics of the setup. The pattern is a square pattern with alternating black and white domains that vary in the size of their lattice constant along the direction μ. The pattern is covered with a photoresist spacer layer of 1.3 μm thickness (not shown). Paramagnetic bipeds of length b_n orient along the external magnetic field H_ext and sediment with one foot on the spacer layer above the pattern. The external field adiabatically varies in control space along a sorting loop ^sort = ^a × ^b × ^c that crosses the equatorial plane at the characteristic loop angles −φ_>, −φ_<, φ_<, and −φ_<. The sorting loop is a concatenation of three loops, the red loops ^a and ^c winding in the mathematical negative sense and the blue loop ^b winding in the positive sense. The sorting loop lets the bipeds walk toward attractor lines perpendicular to the μ-direction that depends on the length of the biped.

Rendering the modulus, q(r), a function of action space (r ∈ [scr A, script letter A] ) breaks the discrete translational symmetry. Here we use a modulus


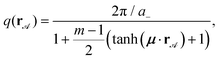	(2)

with a small and fixed morphing reciprocal vector μ = −e_x/ξ. This continuously morphs the pattern within a transition region of width 2ξ from a periodic square pattern of period a₋ = a₊/m toward a periodic square pattern of a larger period a₊ (see Fig. 2). In eqn (2)m is the magnification factor between the asymptotic unit cell sizes. In the transition region, the distortion also breaks the periodicity of the pattern along the e_y-direction (perpendicular to the morphing direction μ). In the e_y-direction the unit cells are sheared with the amount of shearing increasing as one moves away form the central symmetry line located at y = 0.


	Fig. 2 Magnetic pattern (top view). The magnetization of the pattern follows eqn (1) with the modulus given by eqn (2). The larger lattice constant is a₊ = 21 μm, the magnification factor is m = 3 (a₋ = 7 μm), and the transition length is ξ = 75 μm.

A uniform time-dependent external field H_ext of constant magnitude H_ext = 3.5 kA m⁻¹ is superimposed to the non-uniform time-independent magnetic field generated by the pattern. The strong external field induces strong dipolar interactions between the colloidal particles which respond by self-assembling into rods of n = 2–10 particles with length b_n = nd. The two ends of the rod are called the feet and when the rods start to walk we call them bipeds.

The orientation of the external field changes adiabatically along a closed loop [script L] ^sort (Fig. 1). We call the set of possible external field orientations the control space [capital script C] , represented by a sphere in Fig. 1.

3. Periodic pattern

On top of a periodic pattern, where ∇q = 0, despite the field returning to its initial direction, single colloidal particles and bipeds can be topologically transported by one unit cell after completion of one loop.^30,33,35 The current section summarizes our previous work on the transport on periodic patterns^30,33,35 that already allowed us to separate bipeds by moving them into different directions but did not allow us to sort them to a final destination.

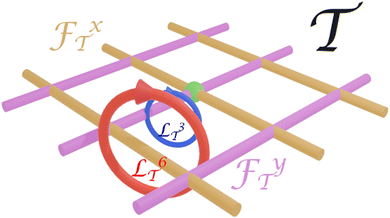
The orientation of the biped is locked to that of the external field with the northern foot being a magnetic north pole and the southern foot being a south pole. Let b_n denote the vector from the northern foot to the southern foot of a biped of length b_n. We call the three-dimensional vector space spanned by the end to end vectors b_n of the bipeds the transcription space [scr T, script letter T] . While the control space [capital script C] has units of a magnetic field, transcription space has units of a length. The loop is a transcription of the control loop [script L] onto a sphere of radius b_n in transcription space . The transport occurs provided that the transcribed loop ⁿ winds around specific fences [scr F, script letter F] ^x and ^y in transcription space.³⁰ These fences are parallel lines along the e_y and e_x directions equally spaced in [scr T, script letter T] by the lattice period a of the periodic pattern in action space [scr A, script letter A] . The central fence lines pass through the origin of transcription space . If the transcribed loop [script L] ⁿ winds around the [scr F, script letter F] ^x and ^y lines with winding numbers wⁿ_x(ⁿ) ∈ [Doublestruck Z] and wⁿ_y(ⁿ) ∈ the biped is topologically transported by


Δr = a(wⁿ_xe_x + wⁿ_ye_y).	(3)

Fig. 3 shows two transcriptions [script L] ³ and ⁶ of the same loop with different winding numbers around the fences [scr F, script letter F] ^x and ^y in transcription space [scr T, script letter T] . The winding number w_x³ = 0 and hence a biped of length b₃ will not be transported by the loop , while the winding number w_x⁶ = 1 and therefore a biped of length b₆ will be transported by the displacement Δr = ae_x.


	Fig. 3 Transcriptions of the same loop in control space to the loops ³ and ⁶ in transcription space corresponding to the biped sizes b₃ and b₆ with different winding numbers wⁿ_x around the fences ^x. The green sphere marks the origin of transcription space and the loops ³ and ⁶ lie on corresponding spheres centered at the origin.

4. Non-periodic pattern

Due to the topological nature of the transport, eqn (3) remains valid for small deformations of the periodic pattern. We have shown that eqn (3) is invariant under rotations³⁹ and under conformal transformations⁴⁰ of the pattern and invariant under modulations of the symmetry phase of patterns with three fold symmetry.³² We therefore expect the displacement on top of a deformed non-periodic four fold pattern with varying lattice constant ∇q ≠ 0 to be expressed by the same eqn (3), provided that the deformation is locally small. That is:


Δr = a(r)(wⁿ_x(r)e_x + wⁿ_y(r)e_y),	(4)

with a(r) the local value of the lattice constant at the position r, and with local fences lines in transcription space [scr F, script letter F]

^x(r) and

^y(r) now being parallel lines along the e_y and e_x direction equally spaced by the local lattice constant a(r) of the non-periodic pattern in action space [scr A, script letter A]

. The loop [script L]

ⁿ is independent of the location r of the biped on the pattern. However the fences change with the biped location r and so do the winding numbers of the fixed loop around the varying fences. It is for this reason that the winding numbers and thus the displacement of a fixed loop [script L]

causes different transport for different biped length b_n as well as for different locations r.

5. Sorting loop

We test the validity of eqn (4) using a sorting loop [script L]

^sort =

^a ×

^b ×

^c being the concatenation of three fundamental loops [script L]

^a,

^b, and

^c. We present [script L]

^sort in Fig. 1. We call a fundamental loop a loop that crosses the equator of control space twice: once at time t_↑ up from the southern hemisphere to the northern hemisphere at an external field H_ext(t_↑) and once at time t_↓ down from the northern hemisphere to the southern hemisphere at an external field H_ext(t_↓). The angle of the crossing field direction to the reciprocal unit vector q₁ is given by qH_ext [thin space (1/6-em)]

sin(ψ_↑↓) = (q₁ × H_ext(t_↑↓))·n. We choose a loop [script L]

^sort with the three pairs of equator crossing angles ψ^a_↑,ψ^a_↓,ψ^b_↓,ψ^b_↑,ψ^c_↑, and ψ^c_↓ that may be described by the two angles φ_< and φ_> as indicated in Table 1 (see also Fig. 1). Due to the symmetric choice of the angles, the winding number around the [scr F, script letter F]

^y-fences vanishes irrespective of the length of the biped wⁿ_y( [script L]

^sort) = 0 and we expect no topological transport along the y-direction.

Table 1 Properties of the sorting loop

^a		^b		^c
ψ ^a_↑	ψ ^a_↓	ψ ^b_↓	ψ^b_↑	ψ ^c_↑	ψ ^c_↓
−φ_>	−φ_<		φ _<		φ _>

6. Experimental results

We define a parameter λ to characterize the sorting loop as λ( [script L]

^sort) = sin [thin space (1/6-em)]

φ_>/(2

sin

φ_<). Due to the symmetric choice of the sorting loop, λ is the only relevant loop parameter determining the winding numbers. We have performed experiments using sorting loops with λ = 0.67, 0.76, 0.84, and 1.17 that sort bipeds of size b₃−b₈ with single particle diameter d = 2.8 μm on top of the pattern depicted in Fig. 2. Fig. 4 shows an overlay of microscopy images of the pattern covered with bipeds subject to a sorting loop with λ = 0.84 at different times together with trajectories of those bipeds obtained via particle tracking. Single particles, n = 1 (red), and doublets n = 2, are traveling one unit cell per loop in the positive x-direction, i.e., toward the unit cells of smaller size a₋. The travel direction of larger bipeds (n > 2) depends on the location on the pattern. For each biped size b_n there is a set of attractor lines

along the y-direction separated by separatrixes r^s,n. For initial positions r in the region between two adjacent separatrixes all bipeds of size b_n are attracted toward the attractor line

between both seperatrixes. On either side of the attractor line after each application of the sorting loop the bipeds perform a step by one, two or more unit cells closer to the attractor line. At the attractor line after each application of the sorting loop, bipeds step from one side of the attractor line toward the other side of the line. This essentially makes the bipeds stop to move after reaching the attractor line.


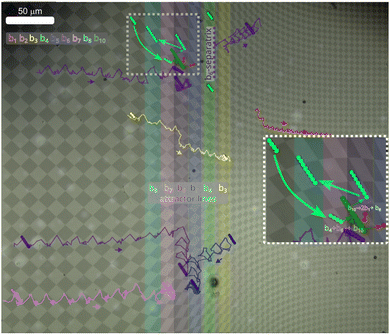	Fig. 4 Sorting experiments. Overlay of several microscopy images of bipeds at different times above the sorting pattern, together with trajectories of bipeds of different length b_n subject to the repeated sorting loop with sorting parameter λ = 0.84. The trajectories are colored according to the biped length as indicated in the image. The magnified dotted square region shows a biped reaction b₄ + b₆ → b₁₀ → b₈ + 2b₁ and the resorting of the resulting b₈-biped. Supplementary movie 1 (ESI†) provides a dynamic impression of the sorting process. Supplementary movie 2 (ESI†) shows the sorting of a b₇-biped that is missing in the experiment shown in this figure.

Far away from the symmetry line, y = 0, the unit cells of the pattern are sheared. A shear is a superposition of an extension and a rotation. The rotation of cells in action space also rotates the direction of the fence lines in transcription space. This also causes transport into the y-direction, of bipeds residing in the transition region further away from the symmetry line (see e.g. the b₅- and the b₆-trajectories in the lower part of Fig. 4).

Because the attractor line depends on the length b_n of the biped, all bipeds are essentially sorted to their individual attractor line. In Fig. 4 we also see a non-sorted b₆-biped to the right of the b₆-separatrix walking away from the separatrix toward a second b₆-attractor line, with , that does not exist on the current pattern since the lattice constant does not shrink below the minimum lattice constant of a₋.

Eventually a walking biped of length b_m, can collide with a sorted and therefore no longer walking biped of larger length b_n with n > m to form a longer biped of length b_n+m. The attractor line for the b_n+m-biped is different from both attractor lengths of the bipeds prior to the collision. Hence, they are sorted to their new attractor line after the collision. The inset of Fig. 4 is a magnification of the dotted squared region of the main figure. There we see a b₆-biped already sorted to its attractor line. A not yet sorted b₄-biped while walking to its attractor line collides with the sorted b₆ biped an initiates an addition reaction b₄ + b₆ → b₁₀. The resulting b₁₀-biped loses two single colloidal particles, i.e. b₁₀ → b₈ + 2b₁ leaving a non-sorted b₈ behind that is then sorted toward its attractor line by moving into the −x direction. Supplementary movie 1 (ESI†) shows the sorting of bipeds of length b₃, b₄, b₅, b₆ and b₈ and the resorting after a biped addition reaction of Fig. 4. Supplementary movie 2 (ESI†) shows the sorting of bipeds of length b₇ toward its attractor line. Note that Supplementary movie 1 and 2 (ESI†) are speeded up by a factor of 50 and 70, respectively.

7. Winding number

The winding number around the family of [scr F, script letter F]

^x fence lines depends on the sorting loop parameter λ and the biped length measured in units of the local lattice constant β(r) = b_n [thin space (1/6-em)]

sin

φ_</a(r). The winding number can be computed using the construction of Fig. 3 to our sorting loop [script L]

^sort and it reads:


wⁿ_x(λ, β) = 1 + 4[β(r)] − 2[2λβ(r)]	(5)

where the square brackets [x] denote the floor- (ceiling-) function for

. The winding number wⁿ_x(λ, β) around the [scr F, script letter F]

^x fence lines is an odd integer that can be smaller or larger than zero. In Fig. 5 we plot the signum of the winding number as a function of β(r) and λ. The border between positive (wⁿ_x = 1) and negative (wⁿ_x = −1) winding number is a line given by


	(6)

that oscillates around the (dashed white) line λ = 1. The walking direction is toward the positive x-direction in the bright gray regime and toward the negative x-direction in the dark gray regime. Small bipeds always walk toward the right. If the gradient of the lattice constant points in the negative x-direction ∇a(r)·e_x<0, as in our pattern, the parameter β(r) will increase with each walking step to the right. The walking direction changes at the position

when the bipeds cross from the bright gray (w_x < 0) to the line between the dark (w_x > 0) and the bright gray region at a negative slope of the line λ^c(β). Negative slopes of the line λ^c(β) between positive and negative winding numbers are attractors of bipeds that are classified by the integer [β]. Sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. For λ = 1 there are an infinite number of attractor sections while for λ ≠ 1 the number of attractor sections is finite.


	Fig. 5 The winding number wⁿ_x, eqn (5), as a function of β(r) = b_nsinφ_</a(r) and λ. If the gradient of the lattice constant points in the negative x-direction ∇a(r)·e_x<0 negative slopes of the line, eqn (6), between positive and negative winding numbers are attractors for bipeds, while sections with positive slopes are separatrices between regions where bipeds are attracted toward different sections with negative slope. The star symbols correspond to final experimental positions of the bipeds, the circles are initial experimental positions beyond the first separatrix with bipeds walking toward the [β] = 1 attractor line. The solid circle is most left initial position observed among all those initial positions.

We check our sorting experiments by measuring the biped length b_n, the attractor positions and the local unit cell size 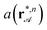of the attractor line for all different biped sizes and loop parameters λ. From these measurements we compute . Experimental pairs of and λ are then plotted as star symbols into Fig. 5. For all different lengths of bipeds b_n, n = 3,…,8 the experimental attractor points fit well on the theoretical prediction of eqn (6). Bipeds attracted to the second attractor line with [β] = 1 start walking from initial locations r^i,n, i = 1,…,k in the direction opposite to the separatrix location r^s,n. In Fig. 5 we plot the corresponding pairs λ, and min^k_i=1β(r^i,n), that lie closest to the separatrix for each value of λ (solid circle). These points are upper bounds for the separatrix location. All initial locations of bipeds approaching the [β] = 1 attractor line (open circles) lie in the bright gray region of negative winding number wⁿ_x<0 consistent with the theoretical prediction. Their very different separations from the theoretical separatrix is due to the random initial placements of the set of bipeds on the pattern.

8. Discussion and conclusion

Our experimental data is in good agreement with the predictions of eqn (6). Therefore by choosing a specific sorting loop, bipeds walk to their attractor position without any need to enforce their proper walk using a feedback mechanism. The decision to walk to the proper place under the periodic external driving is made internally by the bipeds. This is particularly prominent when an addition reaction b_n + b_m → b_n+m changes the length of two colliding bipeds toward a third length and the longer length biped is automatically resorted. For an attractor line family with the same integer classification [β], the attractor line position evolves continuously with the length b_n of the bipeds. Using attractor lines with family classification [β] > 0 it is possible to separate larger length bipeds from shorter biped attractor destinations even further, when choosing a driving loop with parameter λ ≠ 1 such that the larger biped is part of the family with classification [β] > 0, while the shorter is not.

We have sorted bipeds of length b₃–b₈. One may ask what happens to bipeds of shorter and longer length. Single colloidal particles and b₂ bipeds are both shorter than the smallest unit cell on the pattern. Therefore the transcription of control space into transcription space for these two biped lengths are spheres of radius 2.8 μm and 5.6 μm. Both transcription spheres are smaller than the smallest unit cell (the spacing of the fences in Fig. 3). The winding number of the transcribed side loops w_x( [script L] ^na) = 0 = w_x(^nc) vanish anywhere on the pattern, and the winding number of the transcribed central loops w_x(^nb) = 1 is constant and positive anywhere on the pattern. Single colloidal particles and b₂ bipeds therefore walk toward the right searching for putative attractor lines smaller than the smallest unit cell size a₋, which they can never find on this pattern. Single colloidal particles and b₂ bipeds are thus never sorted.

In the experiments there are no bipeds of size b₁₀ or larger before starting the loops. Such long bipeds only occur due to irreversible additions of smaller bipeds to the longer biped. For an addition reaction to occur, smaller bipeds must collide with each other. This happens predominantly in the attractor regions of the b₃–b₈ bipeds because it is in this region that smaller bipeds of different length counter propagate. Long bipeds are therefore found mostly on the right half of the pattern, which is a location already to the right of the first separatrices of these bipeds. Like the single colloidal particles and b₂ bipeds, they start to search for an attractor line smaller than 7 μm that does not exist on the pattern. Ultimately they are not sorted for the very same reason as the single colloidal particles and b₂ bipeds.

The probability of collisions in the attractor regions of the b₃–b₈ bipeds is also the reason one cannot increase the concentration of colloids. Colloids will collide in this region to form large bipeds that leave the pattern and only a small amount of sorted bipeds similar to what we see in our experiments presented remain sorted on the pattern.

We define the efficiency of sorting as the probability that a biped b_n is transported to the correct attractor line λ^c(β) without colliding with another biped to form a biped of a different length prior to the sorting. At our low concentration of particles the efficiency of the sorting is roughly 90%. Note that sorting is not the same as separation. Attractor lines for bipeds of different lengths b_n and b_n+dn are separated by a distance that is the larger the smaller is the morphing reciprocal vector μ. If we define the efficiency of separation as the differential of separation of attractor lines with respect to the variation biped length , then the efficiency of separation is proportional to the correlation length ξ of the pattern. A third efficiency is the time efficiency, i.e. the time we need to sort the bipeds. The deeper the colloidal potential, the faster we can modulate and still be in the adiabatic regime. The colloidal potential is deeper the farther we are separated with the loop in transcription space from the fence lines. This is best done amongst the family of topologically equivalent loops by choosing loops that avoid spending significant arclength of their path near the equator. In our experiments we use a period of T = 20 s per fundamental loop. The pattern and the loop are optimized with respect to the task of sorting bipeds to different predefined locations given the constraints of also being able to simultaneously observe all bipeds.

In conclusion we placed paramagnetic colloidal particles on top of a square-like magnetization pattern with alternating domains of magnetization with a locally varying unit cell size and apply a sorting loop [script L] ^sort that lets bipeds assembled via dipolar attraction automatically sort themselves to attractor lines that depend on the length of the bipeds. In contrast to separation techniques like electrophoresis, the biped length do not separate as a function of time but all bipeds walk simultaneously to their attractor final destination that varies with the length of the bipeds.

Author contributions

ARP, DdlH, & TMF designed and performed the experiment and wrote the manuscript with input from all the other authors. PK, MU & FS produced the magnetic film. SA, & ArE performed the fabrication of the micromagnetic patterns within the magnetic thin film.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is funded by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project number 531559581. DdlH acknowledges support via the Heisenberg program of the DFG via project number HE 7360/7-1. P. K., F. S., and M. U. acknowledge financial support from the National Science Centre Poland through the OPUS funding (Grant No. 2019/33/B/ST5/02013). S. A. acknowledges funding by a PhD scholarship of Kassel University. A. E., S. A. acknowledges support by the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation) under project numbers 514858524, INST 159/139-1 FUGG, INST 159/94-1 FUGG, and INST 159/95-1 FUGG.

Notes and references

E. Rodriguez-Boulan and A. Müsch, Biochim. Biophys. Acta, Mol. Cell Res., 2005, 1744, 455–464 CrossRef PubMed.
P. Haffter, M. Granato, M. Brand, M. C. Mullins, M. Hammerschmidt, D. A. Kane, J. Odenthal, F. J. M. van Eeden, Y.-J. Jiang, C.-P. Heisenberg, R. N. Kelsh, M. Furutani-Seiki, E. Vogelsang, D. Beuchle, U. Schach, C. Fabian and C. Nüsslein-Volhard, Development, 1996, 123, 1–36 CAS.
S. F. Krens and C.-P. Heisenberg, in Forces and Tension in Development, ed. M. Labouesse, Current Topics in Developmental Biology, Academic Press, 2011, pp. 189–213, vol. 95 Search PubMed.
Y. Zhang, Y. Li, H. Wen, L. Cao, W. Xiao, J. Zhao, Z. Nan, S. Zhang, S. Qiu and Q. Li, Carbon, 2023, 215, 118468 CAS.
M. S. Arnold, A. A. Green, J. F. Hulvat, S. I. Stupp and M. C. Hersam, Nat. Nanotechnol., 2006, 1, 60–65 CAS.
L. R. Huang, E. C. Cox, R. H. Austin and J. C. Sturm, Science, 2004, 304, 987–990 CAS.
P. Zhou, J. He, Y.-M. Zha, G.-P. Zhang, G.-Y. Jiang and Y.-X. Huang, Chem. Eng. Sci., 2023, 282, 119319 CAS.
X. Wang and I. Papautsky, Lab Chip, 2015, 15, 1350–1359 CAS.
F. Nan and Z. Yan, Nano Lett., 2018, 18, 4500–4505 CAS.
Y.-C. Tan, Y. L. Ho and A. P. Lee, Microfluid. Nanofluid., 2008, 4, 343–348 CrossRef CAS.
M. P. MacDonald, G. C. Spalding and K. Dholakia, Nature, 2003, 426, 421–424 CrossRef CAS PubMed.
H. Jung, M.-S. Chun and M.-S. Chang, Analyst, 2015, 140, 1265–1274 RSC.
A. Dalili, E. Samiei and M. Hoorfar, Analyst, 2019, 144, 87–113 RSC.
H.-D. Xi, H. Zheng, W. Guo, A. M. Gañán-Calvo, Y. Ai, C.-W. Tsao, J. Zhou, W. Li, Y. Huang, N.-T. Nguyen and S. H. Tan, Lab Chip, 2017, 17, 751–771 RSC.
P. Sajeesh and A. K. Sen, Microfluid. Nanofluid., 2014, 17, 1–52 CrossRef.
S. Goh, R. G. Winkler and G. Gompper, New J. Phys., 2022, 24, 093039 CrossRef.
J. Rozman and J. M. Yeomans, Phys. Rev. Lett., 2024, 133, 248401 CrossRef CAS PubMed.
S. Bhattacharyya and J. M. Yeomans, Phys. Rev. Lett., 2023, 130, 238201 CrossRef CAS PubMed.
J. N. Graham, G. Zhang and J. M. Yeomans, Soft Matter, 2024, 20, 2955–2960 CAS.
C. Dobson, C. Zielke, C. W. Pan, C. Feit and P. Abbyad, Micromachines, 2020, 11, 964 Search PubMed.
Y. Zhang, T. Zheng, L. Wang, L. Feng, M. Wang, Z. Zhang and H. Feng, Rev. Adv. Mater. Sci., 2021, 60, 313–324 Search PubMed.
R. L. Smith, G. C. Spalding, K. Dholakia and M. P. MacDonald, J. Opt. A: Pure Appl. Opt., 2007, 9, S134 Search PubMed.
N. P. Vizarim, C. Reichhardt, C. J. O. Reichhardt and P. A. Venegas, New J. Phys., 2020, 22, 053025 CAS.
P. L. Townes and J. Holtfreter, J. Exp. Zool., 1955, 128, 53–120 Search PubMed.
C. Carlberg and F. Molnár, Embryogenesis and Cellular Differentiation, Springer Singapore, Singapore, 2018, pp. 123–140 Search PubMed.
M. E. Rula, K. Q. Cai, R. Moore, D.-H. Yang, C. M. Staub, C. D. Capo-chichi, S. A. Jablonski, P. H. Howe, E. R. Smith and X.-X. Xu, Genesis, 2007, 45, 327–338 CAS.
O. Cochet-Escartin, T. T. Locke, W. H. Shi, R. E. Steele and E.-M. S. Collins, Biophys. J., 2017, 113, 2827–2841 CAS.
A. Torrik and M. Zarif, J. Chem. Phys., 2024, 161, 094907 CAS.
Z. Zhou, J. Shang and Y. Li, Electronics, 2023, 12, 3700 Search PubMed.
M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, J. Gördes, M. Reginka, A. Ehresmann and T. M. Fischer, Nat. Commun., 2020, 11, 4670 CAS.
M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2021, 17, 1663–1674 CAS.
J. Elschner, F. Farrokhzad, P. Kuświk, M. Urbaniak, F. Stobiecki, S. Akhundzada, A. Ehresmann, D. de las Heras and T. M. Fischer, Nat. Commun., 2024, 15, 5735 CAS.
J. Loehr, M. Loenne, A. Ernst, D. de las Heras and T. M. Fischer, Nat. Commun., 2016, 7, 11745 CAS.
J. Loehr, D. de las Heras, M. Loenne, J. Bugase, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2017, 13, 5044–5075 RSC.
D. de las Heras, J. Loehr, M. Loenne and T. M. Fischer, New. J. Phys., 2016, 18, 105009 Search PubMed.
M. Mirzaee-Kakhki, A. Ernst, D. de las Heras, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, J. Gördes, A. Ehresmann, D. Holzinger, M. Reginka and T. M. Fischer, Soft Matter, 2020, 16, 1594–1598 RSC.
J. Loehr, D. de las Heras, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Commun. Phys., 2018, 1, 4 CrossRef.
H. Massana-Cid, A. Ernst, D. de las Heras, A. Jarosz, M. Urbaniak, F. Stobiecki, A. Tomita, R. Huhnstock, I. Koch, A. Ehresmann, D. Holzinger and T. M. Fischer, Soft Matter, 2019, 15, 1539–1550 RSC.
N. C. X. Stuhlmüller, F. Farrokhzad, P. Kuświk, F. Stobiecki, M. Urbaniak, S. Akhundzada, A. Ehresmann, T. M. Fischer and D. de las Heras, Nat. Commun., 2023, 14, 7517 CrossRef PubMed.
A. M. E. B. Rossi, T. Märker, N. C. X. Stuhlmüller, P. Kuświk, F. Stobiecki, M. Urbaniak, S. Akhundzada, A. J. Vereijken, A. Ehresmann, D. de las Heras and T. M. Fischer, Nat. Commun., 2025, 16, 1828 CrossRef CAS PubMed.

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01480d

Click here to see how this site uses Cookies. View our privacy policy here.