Open Access Article
Open Access ArticleUltra-slow self-similar coarsening of physical fibrillar gels formed by semiflexible polymers†
Martin
Kröger
 *ab,
Clarisse
Luap
*c and
Patrick
Ilg
*ab,
Clarisse
Luap
*c and
Patrick
Ilg
 *d
*d
aComputational Polymer Physics, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland. E-mail: mk@mat.ethz.ch
bMagnetism and Interface Physics, Department of Materials, ETH Zurich, 8093 Zurich, Switzerland
cIndependent researcher, 8049 Zurich, Switzerland. E-mail: clarisse.luap@alumni.ethz.ch
dSchool of Mathematical, Physical, and Computational Sciences, University of Reading, Reading, RG6 6AX, UK. E-mail: p.ilg@reading.ac.uk
First published on 26th February 2025
Abstract
Biopolymers tend to form fibrils that self-assemble into open network structures. While permanently crosslinked flexible polymers are relatively well understood, structure–property relationships of open networks and pseudo-gels formed by bundles of biopolymers are still controversial. Here we employ a generic coarse-grained bead-spring chain model incorporating semiflexibility and cohesive nonbonded interactions, that forms physical instead of chemical crosslinks. For flexible chains, the cohesive forces lead to the formation of a droplet phase while, at the same concentration, stiffer chains form bundles that self-assemble into percolated networks. From comprehensive molecular dynamics simulations we find that the reversible crosslinks allow for permanent relaxation processes. However, the associated reorganization of the filamentous network is severely hindered, leading to aging of its topology. Based on morphometric analyses, the ultra-slow coarsening in these systems is proven to be self-similar, which implies a number of scaling relations between structural quantities as the networks age. The percolated structures are characterized by different dynamic regimes of slow, anomalous diffusion with highly non-Gaussian displacements. Relaxation dynamics is found to become extremely slow already on moderate length scales and further slowing down as coarsening proceeds. Using a minimal model supported by observations on filament rupture and rearrangement, our study helps to shed light on various interrelated structural and dynamical aspects of coarsening nonergodic systems relevant for fibrous networks, pseudo-gels, and physical fibrillar gels.
1 Introduction
Semiflexible macromolecules are ubiquitous in nature.1 A prominent example is cellulose, a semiflexible glucose polymer. As the main constituent of plant fiber, it is the most abundant organic compound on earth. DNA and proteins are other examples of important semiflexible biopolymers. Under typical conditions, many of these monofilaments form bundles2 or fibrillar structures that assemble into transient networks with physical, i.e. reversible crosslinks.3–5 These networks show remarkable properties such as strain stiffening and negative normal stresses,6 which are rather different from networks of permanently crosslinked flexible chains that have been intensively studied using traditional network theories and simulation. For example, structure–property relationships were investigated for cellulose hydrogels, with mechanical properties found to depend on fibril length instead of concentration as expected from traditional network theories.7 The network structure formed by physically crosslinked semiflexible polymers has an important influence on their mechanical properties.8–10For a better understanding of these structures, it is helpful to note that they are prepared experimentally e.g. using a change of temperature, ionic strength, or pH.1,11 Theoretically, the resulting gelation via bundling and network formation from suspensions of semiflexible polymers is interpreted as emerging from spinodal decomposition and kinetic arrest.3,12–15 The associated reorganizations of the network can be extremely slow, in some cases exceeding several days.16 The corresponding phenomena of slow coarsening dynamics with very long correlation lengths are known as “anomalous aging” since the time evolution and relaxation dynamics differs markedly from the more intensively studied glassy systems.17 Nonergodicity and anomalous aging has been observed in a broad range of different systems such as amyloid fibrils,1,18 methylcellulose,16 alginate gels19 and colloidal gels.17 Considerable work is ongoing to extend traditional theoretical approaches to capture such biological soft matter systems.9,20
Here, we focus on reversible networks of semiflexible chains without permanent crosslinks for which classical theories can not readily be applied.5 Although such transient structures are theoretically fascinating and highly relevant e.g. for food systems or protein-based filaments, they remain underexplored.9 Several fundamental questions on the structure and dynamics of these networks stay unclear.8 For cellulose derivatives often used in food systems, for example, fibrillar structures with a characteristic mean diameter of about 5 to 30 nm are observed experimentally.11,21,22 From cryo-TEM imaging and small-angle neutron scattering (SANS), the fibril mean diameter was found to be rather independent of molecular weight, temperature and concentration, but increasing with increasing bending stiffness.11,21 From detailed molecular simulation, these fibrils were either explained as stacked ring structures23 or length-wise aggregation of chain molecules.24 Different X-ray scattering experiments and cryo-TEM images seem to be more consistent with the latter scenario, suggesting axially oriented semi-crystalline chains forming the core of the fibril, interspersed with less dense regions.25,26 Small angle X-ray scattering experiments (SAXS) experiments were used to study fibrils formed from short peptides. The change in the characteristic slope in the scattering functions was consistent with a model of thick cylinders.27 While scattering experiments on dilute solutions of semiflexible chains are well understood,28,29 corresponding results for networks of semiflexible chains provide valuable structural information that, however, is sometimes difficult to interpret. One difficulty is that experimentally prepared networks are often found to be spatially inhomogeneous. Mesh sizes estimated from permanent networks of rodlike particles give the right order of magnitude measured for the more compact regions, whereas much larger values are found for the more open regions.30
Networks of semiflexible chains show intriguing dynamics that is challenging to study not least because of their non-ergodic nature.1,9 For example, non-diffusive compressed exponential relaxation was observed in amyloid fibrils from dynamic light scattering experiments.31 These findings hint at structural heterogeneities of the network, but the origin of the relaxation remains unclear. Additionally, uncertainties persist regarding the different dynamic regimes and anomalous diffusion in transient networks of semiflexible chains,32 their underlying microscopic origins, and their connection to resulting mechanical properties.9
In general, computer simulations can help to address these questions as they offer detailed insight into structural as well as dynamical properties. They allow to detect microscopic mechanisms accompanying the coarsening process. The majority of simulations in this field seem to employ detailed atomistic or moderately coarse-grained models to investigate specific systems.23,24,27,33,34 Because of the computational complexity of these systems only few computational studies appeared to date on the self-assembly process of semiflexible filaments and the dynamics of their networks.34 To overcome these limitations, several coarse-grained models have been proposed that differ considerably in the level of detail retained.33 Recently, promising multi-scale simulations have appeared that address the mechanisms of self-assembly in methylcellulose.24 Rather than targeting such a specific chemistry, we aim at exploring universal properties of transient networks of semiflexible chains. As has been noted,5,15 (i) the bundling of semiflexible chains into fibrils, (ii) the characteristic and rather uniform fibril diameters, and (iii) network topologies appear to be rather similar for different types of polymers. Effective attractions arise in many biopolymeric systems as a result of depletion forces.
With this in mind, we here employ a generic model of semiflexible polymers in terms of multibead-spring chains with bending stiffness and short-range attraction, building on the so-called Kremer–Grest35 and FENE-CB36–38 models. Models with qualitative similarities have been used in the past to study microphase separation in fibrillar gels,39 the phase behavior of semiflexible attractive chains, showing a liquid–vapor coexistence region for low enough temperatures or strong enough cohesive energies,40 and the formation of fibrous bundles,41,42 which then assemble to form a temporary network.15 For a two-dimensional version of the model, network structures were investigated in detail, distinguishing percolated from disintegrated networks.43 Other recent studies used a similar model to investigate the network structure and their tensile properties, finding that high strength networks have high densities and that the cohesive energy is the most important parameter for their mechanical response.44,45 While bead-spring models are an extremely versatile model for various polymeric systems,46 we note in passing that other coarse-grained models have sporadically been used to study aspects of semiflexible polymer networks, such as an extended fluid particle model for the evolution and stability of networks,47 and a discrete element method for the study of gelation, bundles, and pore size distributions.48
Studying the aging model system requires special care not only due to the loss of ergodicity1 which introduces a dependence on the preparation conditions, but also due to the additional effect of the waiting time since system preparation.49 Several simulation studies on semiflexible polymer networks artificially arrested aging by introducing sticky beads or permanent crosslinks or quenching the temperature to zero.44,45,48 Here, we avoid such drastic interventions and study the structure, dynamics, and aging of a self-assembling, physically crosslinked semiflexible polymer system. We pay special attention to carefully prepare the systems to follow the aging process as far as possible.12,50 To address the lack of ergodicity, we typically investigate 10 statistically independent samples, and we investigate the influence of waiting time (tw) and bending stiffness (κ) on static and dynamic properties.
2 Model system
The model studied here is a semiflexible, anharmonic multibead-spring model that differs from the celebrated KG model35 for linear polymer chains in melts only with respect to bending energy and interaction cutoff, and is conveniently implemented using LAMMPS51 (LAMMPS script available in Section S8, ESI†).2.1 Model equations and parameters
The usually Nc = 1000 linear, monodisperse bead-spring chains, each consisting of N = 30 identical beads, Nb = NcN beads in total, are contained in a periodic simulation box with volume V, at bead number density ρ = Nb/V and temperature T. All permanently bonded beads along the linear chains interact via the radially symmetric finitely extendable nonlinear elastic (FENE) potential,52 | (1) |
| ULJ(r) = 4εb(r−12 − r−6 − rc−12 + rc−6), r ≤ rc, | (2) |
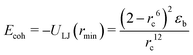 | (3) |
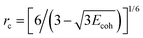 .
.
Finally, each triplet of adjacent permanently bonded beads interacts via the cosine bending potential36–38
| Ubend = κ(1 − ui·ui+1) | (4) |
Polymer chains are assumed to be embedded in a solvent which is modeled implicitly. The quality of the solvent is related to the cohesive energy Ecoh, while dynamic effects are captured in the free-draining approximation by friction forces acting on all beads. To this end, a Langevin thermostat is applied to ensure a constant temperature T. We choose T = 1 and set kB = 1, so that κ/kBT = κ in our case, and we write κ/kBT only if it serves to highlight a dependency on temperature. Otherwise, LJ units are used throughout.
2.2 Preparation of model systems
Systems are generated by placing Nc semiflexible chains with initial bond length binit = 1 and with persistence length involving the Langevin function
involving the Langevin function ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) (x) = coth(x) − x−1, but without overlap (minimum bead–bead distance 0.85)54 into a periodic simulation box whose volume is determined by either (i) an initial bead number density ρinit = 0.02 for the NPT ensemble, or (ii) ρinit = 0.05 for the NVT ensemble simulations. The equations of motion resulting from the mentioned potentials are then integrated using classical thermo- and barostats (NPT only) using an integration time step Δt = 0.005. For case (i) the system is equilibrated within the NPT ensemble until its pressure is fluctuating about zero; at this time the system has reached a number density ρ that may largely deviate from ρinit, and is moreover insensitive to ρinit due to the relatively low εb = 3 that we have chosen. The simulations within the NPT ensemble suggest to use ρ = 0.05 for the NVT ensemble simulation. Here, for case (ii), the short relaxation stage (duration 103) is followed by a measurement stage of duration 105. Long runs up to tw = 2.1 × 106 were performed for κ ∈ {10, 50, 75}. The begin of the measurement stage defines waiting time tw = 0. During these stages, we keep ρ fixed and integrate the equations of motion using a Langevin thermostat with friction coefficient ζ = 0.5, following previous works.35,55 Movies E to G and E+ to G+ (ESI†) show show selected systems during the short relaxation and early measurement stage, and during the coarsening stage, respectively.
(x) = coth(x) − x−1, but without overlap (minimum bead–bead distance 0.85)54 into a periodic simulation box whose volume is determined by either (i) an initial bead number density ρinit = 0.02 for the NPT ensemble, or (ii) ρinit = 0.05 for the NVT ensemble simulations. The equations of motion resulting from the mentioned potentials are then integrated using classical thermo- and barostats (NPT only) using an integration time step Δt = 0.005. For case (i) the system is equilibrated within the NPT ensemble until its pressure is fluctuating about zero; at this time the system has reached a number density ρ that may largely deviate from ρinit, and is moreover insensitive to ρinit due to the relatively low εb = 3 that we have chosen. The simulations within the NPT ensemble suggest to use ρ = 0.05 for the NVT ensemble simulation. Here, for case (ii), the short relaxation stage (duration 103) is followed by a measurement stage of duration 105. Long runs up to tw = 2.1 × 106 were performed for κ ∈ {10, 50, 75}. The begin of the measurement stage defines waiting time tw = 0. During these stages, we keep ρ fixed and integrate the equations of motion using a Langevin thermostat with friction coefficient ζ = 0.5, following previous works.35,55 Movies E to G and E+ to G+ (ESI†) show show selected systems during the short relaxation and early measurement stage, and during the coarsening stage, respectively.
3 Results and discussion
We study in detail structural characteristics as well as dynamic properties of cohesive semiflexible polymers using the model described in Section 2. Fig. 2 serves to demonstrate the richness of structures that our simple model is able to capture at a single temperature, using chains of identical length. It shows projections of snapshots of various systems at a bead number density of ρ = 0.05. This density we determined from a series of NPT simulations for pressure P = 0 for intermediate values of bending stiffness κ. For better comparison we then fixed ρ = 0.05 in NVT simulations for all systems and κ values investigated. The systems shown in Fig. 2 were simulated for a relatively short time, up to time tw = 104 since system preparation. Varying the cohesive energy Ecoh (horizontally) and bending stiffness κ (vertically) is found to lead to different structures. For small Ecoh ≲ T, isolated chains are found that become more straight with increasing bending stiffness. Increasing Ecoh leads to cluster and structure formation. For low κ, these clusters tend to be more compact, while larger κ together with cohesive attractions leads to open, network-like structures.To carefully study these structures and resulting properties, from now on we fix a representative value of the cohesive energy (Ecoh = 1.4) and focus on the influence of the bending stiffness κ on static and dynamic properties. With the chosen value of Ecoh, we make sure to include compact as well as open structures in our study (green framed regime in Fig. 2).
3.1 Initial observations
Snapshots of representative system configurations with Nc = 1000 chains, polymerization degree N = 30, thus Nb = NcN = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads in total are shown at a late stage of a typical run in Fig. 3. Different panels in the figure correspond to different values of bending stiffness κ. These figures are thus not only close-up three-dimensional versions of the corresponding panels of Fig. 2, but show those systems after considerable longer times tw. For rather flexible chains, κ ≲ 5, droplets are formed by several coiled chains. For more rigid chains, κ ≳ 5, strongly bent configurations are energetically too unfavorable: droplets mixed with short, near-cylindrical bundles (κ = 5) as well as system-spanning networks of long, fibrillar bundles (κ ≳ 10) are formed. Thus, the snapshots suggest both an ordering and a percolation transition as the bending stiffness increases. These observations are in agreement with Monte–Carlo simulation of very small systems that found a transition from amorphous aggregates to polymer bundles at κ ≈ 6.41 For a few (2 out of 10 in each case) samples within the transition regime we also observed thick filaments percolated in one dimension for κ = 5, and networks for κ = 10 percolated in two dimensions (Fig. S14, ESI†). We will come back to these points later.
000 beads in total are shown at a late stage of a typical run in Fig. 3. Different panels in the figure correspond to different values of bending stiffness κ. These figures are thus not only close-up three-dimensional versions of the corresponding panels of Fig. 2, but show those systems after considerable longer times tw. For rather flexible chains, κ ≲ 5, droplets are formed by several coiled chains. For more rigid chains, κ ≳ 5, strongly bent configurations are energetically too unfavorable: droplets mixed with short, near-cylindrical bundles (κ = 5) as well as system-spanning networks of long, fibrillar bundles (κ ≳ 10) are formed. Thus, the snapshots suggest both an ordering and a percolation transition as the bending stiffness increases. These observations are in agreement with Monte–Carlo simulation of very small systems that found a transition from amorphous aggregates to polymer bundles at κ ≈ 6.41 For a few (2 out of 10 in each case) samples within the transition regime we also observed thick filaments percolated in one dimension for κ = 5, and networks for κ = 10 percolated in two dimensions (Fig. S14, ESI†). We will come back to these points later.
As a first proxy for structure evolution, we monitor the mean pair energy (epair) and mean bending energy per particle (ea) as a function of tw. The pair energy epair is defined as the mean LJ energy (2) per bead. As can be seen from Fig. 4, epair and ea both decrease with time as expected for equilibration. As a decreasing ea reflects local bending stiffening, chains tend to straighten out in the course of tw. The decrease of epair suggests an increase in local ordering and decrease in surface area. When plotting these two quantities on a linear time scale, Fig. 4(a) and (b), one might be inclined to conclude that equilibration is mainly achieved. However, closer inspection and using a logarithmic time scale (Fig. 4(c) and Fig. S7, ESI†) reveals a very slow ongoing relaxation with a relaxation time that increases significantly with system age.
 | ||
Fig. 4 Energies during aging. Panel (a) shows the pair energy per bead, epair, as a function of waiting time tw since system preparation for various values of the bending stiffness κ > 0 shown in the legend of panel (d). Panel (b) shows the bending energy per bead, ea, versus tw, while panel (c) shows the same data on a semilogarithmic scale. Panel (d) shows a parametric plot of ea(t) versus epair(t). Time thus increases from right to left in (d). From ea we extract a local persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p, shown in Fig. 6. While all percolated networks (κ ≥ 10) follow a similar trend, the energetics of the unordered spherical (κ ≤ 2) and little cylindrical bundles (κ = 5, Movie H, ESI†) phases is markedly different. Plots extending to later times tw = 2.1 × 106 are available in Fig. S7 (ESI†). p, shown in Fig. 6. While all percolated networks (κ ≥ 10) follow a similar trend, the energetics of the unordered spherical (κ ≤ 2) and little cylindrical bundles (κ = 5, Movie H, ESI†) phases is markedly different. Plots extending to later times tw = 2.1 × 106 are available in Fig. S7 (ESI†). | ||
Recall that aging and ultra-slow coarsening have been observed in several network-forming soft matter systems.12–14,16–19,47,49,50,56,57 The essential absence of complete relaxation in these systems has been attributed to phase separation and quasi-arrested spinodal decomposition, explaining the similar phenomenology observed in rather different systems.12,57,58 In particular, spinodal decomposition has been identified as the driving force for bundling and network formation in polymeric systems similar to the one studied here.3,14,15 In the following, we study and discuss the aging and coarsening behavior. As an interesting first observation, Fig. 4(d) shows a linear relation between the pair and bending energy during relaxation, indicating that coarsening proceeds along certain rules.
3.2 Structure analysis and static properties
We begin by analyzing the structures that are formed for different values of κ and the corresponding static properties. In view of the ultra-slow ongoing relaxation, we perform all structural analysis at different tw.We first present results for the isotropic single-chain structure factor, Ssc(q), as function of wave number q. Experimentally, Ssc can be measured through small-angle neutron scattering (SANS) on samples where a small fraction of polymer chains have been selectively labeled. In simulations, the static structure factor can conveniently be extracted from bead positions. See Section 5.1 for details and in particular eqn (8) for a definition of Ssc(q). Fig. 3(a) shows Ssc obtained for various values of the bending stiffness κ. Data averaged over two different ranges of waiting times tw are quasi indistinguishable. As κ increases we see a transition from a near-random walk behavior (Ssc ∼ q−2) to an extended range of q values where Ssc ∼ q−1 shows the typical scaling of rod-like objects. It is remarkable that despite chain–chain interactions, Ssc can still be described very well by the scattering function of the discrete wormlike chain (WLC) model (for details see Section 5.1). However, the required values of persistence lengths differ from the local persistence lengths ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p that are inferred from the bending energy ea (Section 5.2).
p that are inferred from the bending energy ea (Section 5.2).
To confirm this observation, we analysed directly two single-chain properties: the mean-square end-to-end distance 〈R2〉 and the gyration radius Rg. For the WLC model, these quantities are given in terms of the number of beads per chain N and the global persistence length Lp (see Section 5.2 and Fig. S10, ESI†). Values for Lp extracted from the ratio 〈R2〉/R2g are shown in Fig. 6 (time series in Fig. S7, ESI†) together with those extracted from the fits of the single chain structure factor. The latter are systematically smaller but follow the same trend: the effective global persistence length initially increases approximately linearly with κ, before crossing over to a much slower increase for κ ≳ 20. The local effective persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p evaluated from the bending energy agree with those from Rg for κ ≳ 2, but clear differences are seen for stiffer chains where bending energies imply larger values of
p evaluated from the bending energy agree with those from Rg for κ ≳ 2, but clear differences are seen for stiffer chains where bending energies imply larger values of ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p compared to Lp's from the gyration radius. For our systems, we suspect that the scale-dependency of the persistence length of chains within the fibrous networks may be caused by the formation of junctions connected by strands whose lengths do not exceed Lp by far.
p compared to Lp's from the gyration radius. For our systems, we suspect that the scale-dependency of the persistence length of chains within the fibrous networks may be caused by the formation of junctions connected by strands whose lengths do not exceed Lp by far.
 as defined in eqn (7) accounts for all beads in the system, regardless of bond topology. Fig. 5(b) presents S(q) for the same range of bending stiffness κ as in Fig. 5(a). At first glance, two different families of curves can be distinguished in Fig. 5(b): (i) the one for rather flexible chains (κ ≤ 5) forming droplet phases and (ii) the one for stiffer chains κ ≥ 10 forming percolated fibrous networks. These findings corroborate earlier observations from the snapshots in Fig. 3 which indicate a transition from a droplet- to a network-forming phase as κ increases from κ = 5 to κ = 10.
as defined in eqn (7) accounts for all beads in the system, regardless of bond topology. Fig. 5(b) presents S(q) for the same range of bending stiffness κ as in Fig. 5(a). At first glance, two different families of curves can be distinguished in Fig. 5(b): (i) the one for rather flexible chains (κ ≤ 5) forming droplet phases and (ii) the one for stiffer chains κ ≥ 10 forming percolated fibrous networks. These findings corroborate earlier observations from the snapshots in Fig. 3 which indicate a transition from a droplet- to a network-forming phase as κ increases from κ = 5 to κ = 10.
At large scattering vectors (q ≥ 7), both systems exhibit the usual diffuse scattering peaks reminiscent of the bead-bead intra and inter-chain correlations.
For droplet systems, the S(q) curves show no distinct peaks or fringes, indicating that the dense globular droplets are quite irregular in shape and/or polydisperse. However, fringes of small amplitudes are detectable in individual samples if averaged over the last 100 time units only (data not shown). Due to the limited size of our systems, the Guinier regime (qRg < 1) is not reached and no correlation peaks corresponding to a characteristic droplet–droplet distance are observed. In the probed (intermediate) q range, the scattering curves follow a Porod-like behavior S(q) = Kp/q4, and are therefore dominated by the scattering arising from the sharp density change at the droplet interfaces. For spherical droplets of radius R, this regime appears for q > qc where qc ∝ 1/R. The proportionality constant Kp, setting the level of S(q) in the Porod regime, is given in our case by Kp = 2πρf2Af/Nb, where ρf is the bead number density in the dense polymer phase and Af its total surface area.59
 | ||
Fig. 6 Persistence lengths versus κ at two different waiting times tw. (a) Global Lp extracted from the ratio 〈R2〉/R2g (black squares), using the discrete WLC expression (10), local ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p obtained from the specific bending energy ea (red diamonds), and Lp estimated upon fitting the Ssc by the WLC model (green pentagons). Dot-dashed green line p obtained from the specific bending energy ea (red diamonds), and Lp estimated upon fitting the Ssc by the WLC model (green pentagons). Dot-dashed green line  for the ideal WLC has been added to guide the eye. (b) Same data as shown in (a), here relative to the the ideal WLC. Global Lp's obtained using the bond length b and R2g, or alternatively 〈R2〉 alone are basically identical to those obtained from the ratio. The single chain structure factor Ssc(q) (Fig. 5) is very well approximated by the WLC structure factor, using Lp values that are slightly below the ones obtained from the ratio. for the ideal WLC has been added to guide the eye. (b) Same data as shown in (a), here relative to the the ideal WLC. Global Lp's obtained using the bond length b and R2g, or alternatively 〈R2〉 alone are basically identical to those obtained from the ratio. The single chain structure factor Ssc(q) (Fig. 5) is very well approximated by the WLC structure factor, using Lp values that are slightly below the ones obtained from the ratio. | ||
For the percolated network structures, the shape of scattering curves is consistent with that expected for polydisperse cylindrical objects. A narrower Porod regime is observed (qc ∝ 1/d with d denoting a cylinder diameter) whose onset slightly shifts to higher q with increasing stiffness, indicating a slight decrease in fiber diameters which saturates at large κ. The levels of S(q) in the Porod regime are significantly higher than those for the droplet systems, in agreement with the higher interfacial area of the fibrous network structures. In Fig. 5, the structure factors averaged over two different ranges of waiting times tw since system preparation are nearly undistinguishable. Yet a slight increase in the Porod constant over time is hinted. Overall, the structure factors data allow to clearly classify our systems into two types of structures: globular and cylindrical. However, the limited low-q range and the absence of prominent features in the curves make it challenging to extract precise quantitative structural information.
First, our cluster analysis (Section 5.4.1) confirms a percolation transition where a single, system-spanning infinite cluster (C = 1) is formed for semiflexible chains with κ ≥ 10 (Fig. 22). For more flexible chains with κ ≤ 5, several droplets of isolated smaller clusters of coiled chains are seen. Those clusters tend to coagulate with time for κ ≤ 2, while short bundles of aligned chains tend to be more stable for κ = 5. Note that the precise location of the percolation transition also depends on the value of the cohesive energy Ecoh and moves to larger κ as Ecoh decreases. While there are no critical (load-bearing) bonds60 (Section 5.4.1) for the droplet systems, the number of critical bonds in the percolated networks (κ ≥ 10) is quite insensitive to κ. The system at κ = 30 attains the largest number (roughly 600) of critical bonds and may thus be envisioned as the most mechanically stable system under study (this prediction could be scrutinized e.g. by mechanical tests).
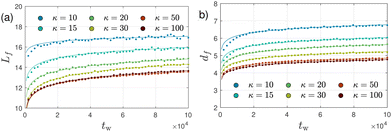
Fig. 7(a)–(f) show the ensemble-averaged strand length Lf and thickness df (Section 5.4.4), number of edges E, junctions J, and loops L∘ (Section 5.4.3), and the mean pore size rpore introduced by Gelb and Gubbins61 (Section 5.4.5), respectively, as a function of the bending stiffness κ ≥ 10 for percolated systems at two selected values of the waiting time, tw = 5 × 104 and tw = 105. All but the pore size have been obtained with the help of skeletons (Section 5.4.2, Fig. S3, ESI†), whose flexible multibead strands (of mean contour length Lf) follow the centerlines of the filamentous bundles, until they terminate at one- (dangling ends) or higher-functional junctions (see Fig. 1(b) for a sketch). Each skeleton bead is easily characterized by its functionality, and from the knowledge of the number nf of skeleton beads with given functionality f, and the number C of clusters, one has direct access to the number of edges, junctions, vertices, and loops without inspecting the network further. We observe that Lf, strand diameter df (≃mean thickness of the polymeric strands centered at the skeleton) and pore radius rpore decrease monotonically with increasing bending stiffness (at given tw) until reaching a plateau for large κ. The number of edges, junctions, and loops exhibit the opposite trend. The stiff systems therefore exhibit more junctions, thinner filaments, and a smaller pore radius compared with the flexible systems at comparable age, but upon aging the stiffer systems much further, their topological characteristics tend to become similar to those of the more flexible, younger systems.
For an ideal network free of dangling ends and solely composed of three-functional junctions the number of junctions equals the number of vertices, the number of edges is 3/2 times the number of junctions, E/J = 3/2, and the number of loops is L∘ = C + E/3. As mentioned, our coarsed percolated networks all exhibit a single infinite cluster, C = 1. From the quantities displayed in Fig. 7(c), (d) and (f) one can infer the number of dangling ends, n1 = C + E − J − L∘, which is relatively small, and a mean functionality of junctions, ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) J = (2E − n1)/J, close to three. To be specific, we find at tw = 105 that the ratio of dangling ends to three-fold junctions, n1/n3, monotonically decreases from about 0.07 at κ = 10 to 0.04 at κ = 100, while the ratio of four-fold to three-fold junctions, n4/n3, monotonically and weakly increases with κ from about 0.01 to 0.03 over the same κ range and there is a negligible amount of higher-functional junctions. In more quantitative terms, for the ratio E/J we obtain a nearly constant value of ≈1.535 over the whole range of κ values, while L∘/(1 + E/3) moderately increases from 0.93 to 0.97 between κ = 10 and κ = 100. For this reason, our networks are near-ideal three-functional at tw = 105, and they approach this stage in a manner that is captured by the time series of functionalities (Fig. S4, ESI†). Even though systems with different κ age at different rates, the mentioned trends are unaffected by the choice of tw.
J = (2E − n1)/J, close to three. To be specific, we find at tw = 105 that the ratio of dangling ends to three-fold junctions, n1/n3, monotonically decreases from about 0.07 at κ = 10 to 0.04 at κ = 100, while the ratio of four-fold to three-fold junctions, n4/n3, monotonically and weakly increases with κ from about 0.01 to 0.03 over the same κ range and there is a negligible amount of higher-functional junctions. In more quantitative terms, for the ratio E/J we obtain a nearly constant value of ≈1.535 over the whole range of κ values, while L∘/(1 + E/3) moderately increases from 0.93 to 0.97 between κ = 10 and κ = 100. For this reason, our networks are near-ideal three-functional at tw = 105, and they approach this stage in a manner that is captured by the time series of functionalities (Fig. S4, ESI†). Even though systems with different κ age at different rates, the mentioned trends are unaffected by the choice of tw.
Our results concerning df are in qualitative agreement with earlier simulations of a similar model system.45 In comparison to the static structure factor shown in Fig. 5, the quantities Lf, df, L∘ and also rpore show more clear differences for the two values of tw. Mass conservation arguments can be used, as shown in Section 5.5.4, to heuristically derive a scaling relation between the mean filament diameter df and the mean pore size,
| df ∼ rpore. | (5) |
The values shown in Fig. 7 provide descriptions of the network structure in terms of mean quantities, and thus do not allow us to draw conclusions about possible heterogeneities. Therefore, we show in Fig. 8(a) and (b) the weighted distribution of filament lengths Lf and diameters df, respectively, for selected values of the bending stiffness κ. We find that not only the mean value of Lf remains approximately constant for κ ≳ 40 (see Fig. 8(a)), but the whole distribution, positively skewed, hardly changes in this regime as κ increases. For the filament diameter df on the other hand, the probability distribution is more Gaussian and moves to lower values as κ increases, approaching a limiting distribution only at higher values. Both distributions are relatively broad.
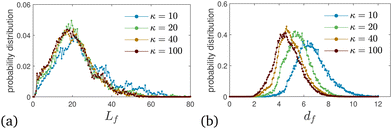 | ||
| Fig. 8 Polydispersity of filamentous bundles. Probability distribution of filament lengths Lf and diameters df, for selected κ, collected within the time frame tw ∈ [5 × 104,105]. | ||
Within the same spirit, in Fig. 9, we show the pore size distribution G-Pcumpore(r), i.e. the cumulative probability that the largest sphere, containing a randomly chosen point within the void space, and not overlapping with any of the beads, has a radius smaller or equal than r. For more information on this quantity see Section 5.4.5. For small values of κ, the system is unpercolated and the distributions have to be interpreted with care. For larger κ, the vast majority of pores have a radius between around 10 and 20. Together with the smooth increase of G-Pcumpore(r) we conclude that the networks formed do not show pronounced heterogeneities. We also observe that the mean pore radii rpore very slightly get larger with increasing waiting time (Fig. S7, ESI†), in agreement with Fig. 7(f). For comparison, Torquato's63 cumulative T-Pcumpore(r), defined in Section S4 (ESI†), is shown in Fig. S9 (ESI†). The T-Pcumpore(r) is known to underestimate the pore radius,64 but is much less time-consuming to extract with high accuracy. While the pore size distributions do not reveal any qualitative peculiarities, they will help us to demonstrate self-similarity during ultra-slow coarsening.
Another important, convenient measure of the characteristic length scales of a network is given by the so-called chord length distribution (Section 5.4.6).65 Roughly speaking, the chord length s is the distance between two consecutive network-pore interfaces along a virtual line through the system.50,57,66Fig. 10(a) shows the weighted chord length distribution  of the dense polymeric phase for several values of the bending stiffness κ. The corresponding weighted chord length distribution of the void space
of the dense polymeric phase for several values of the bending stiffness κ. The corresponding weighted chord length distribution of the void space  has been extracted and analyzed as well (Fig. 23). In the droplet phase for κ ≤ 5,
has been extracted and analyzed as well (Fig. 23). In the droplet phase for κ ≤ 5,  shows a pronounced peak at small s (s ≈ 2), a weaker and broader peak at larger s (s ≈ 10…20), followed by a relatively long tail (data not shown). The broad peak can be related to the typical size of droplets (Fig. 3). In the network-forming phase for κ > 10, the shape of the chord length distribution
shows a pronounced peak at small s (s ≈ 2), a weaker and broader peak at larger s (s ≈ 10…20), followed by a relatively long tail (data not shown). The broad peak can be related to the typical size of droplets (Fig. 3). In the network-forming phase for κ > 10, the shape of the chord length distribution  changes to a unimodal shape. The location and height of the peak are found to be rather insensitive to the precise value of κ in this regime. We note that the most probable chord length decreases weakly with increasing κ from about s ≈ 7 (κ = 10) to s ≈ 4.5 (κ = 100) and is, within numerical uncertainties, identical with the mean filament thickness df (Fig. 7b). This finding perfectly supports the conclusion that our percolated systems contain mainly near-cylindrical filaments with Lf > df.65 We note that Fig. 10(a) corresponds to a particular time tw = 105. The time-dependence and remaining panels of Fig. 10 will be discussed next.
changes to a unimodal shape. The location and height of the peak are found to be rather insensitive to the precise value of κ in this regime. We note that the most probable chord length decreases weakly with increasing κ from about s ≈ 7 (κ = 10) to s ≈ 4.5 (κ = 100) and is, within numerical uncertainties, identical with the mean filament thickness df (Fig. 7b). This finding perfectly supports the conclusion that our percolated systems contain mainly near-cylindrical filaments with Lf > df.65 We note that Fig. 10(a) corresponds to a particular time tw = 105. The time-dependence and remaining panels of Fig. 10 will be discussed next.
 | ||
Fig. 10 Chord lengths and self-similarity. (a) Weighted distribution  of chord lengths are shown at tw = 105 for various values of bending stiffness κ as indicated in the legend. (b) Mean weighted chord length of chord lengths are shown at tw = 105 for various values of bending stiffness κ as indicated in the legend. (b) Mean weighted chord length  as a function of time tw since system preparation. Panel (c) shows the weighted chord length distribution as a function of time tw since system preparation. Panel (c) shows the weighted chord length distribution  for κ = 50. Distributions are recorded at various times tw, increasing from blue to red as indicated by selected tw in the legend. Panel (d) shows the same data as (c) but rescaled as for κ = 50. Distributions are recorded at various times tw, increasing from blue to red as indicated by selected tw in the legend. Panel (d) shows the same data as (c) but rescaled as 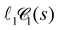 versus s/ versus s/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1. The corresponding plots for the distribution 1. The corresponding plots for the distribution  are shown in Fig. S23 (ESI†). are shown in Fig. S23 (ESI†). | ||
3.3 Ultra-slow coarsening and self-similarity
As we have seen in Section 3.2, various structural quantities show a weak dependence on the waiting time tw since system preparation and do not seem to have fully reached steady state during the simulation time window. In this section we study this relaxation and the associated aging phenomenon more closely.
Fig. 11 shows a sequence of snapshots for a typical system with κ = 50 (see Fig. S2 for corresponding snapshots for κ = 10, ESI†). The snapshots already suggest a coarsening of the network structure with increasing waiting time tw. To study the ongoing coarsening more quantitatively, we monitor the polymer surfaces and skeletons, as illustrated in Fig. 12. We note that our polymer surfaces look rather similar to SEM or AFM images of biopolymers.7,31,56,67,68Fig. 13(a), (b) and 10(b) show the time evolution of the skeleton and surface-based characteristics, including the mean filament length Lf and diameter df and mean weighted chord length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 since system preparation, respectively. The very slow relaxation seen in Fig. 4 can thus be attributed to an ultra-slow coarsening process of the network structure, as suggested by Fig. 11 and 12. Indeed, mass conservation arguments detailed in Section 5.5.4 suggest the scaling relation (5) to hold during late stages of coarsening, which we find to be satisfied to a good degree. Therefore, we conclude that coarsening mainly consists of filaments very slowly becoming thicker with pores very slowly getting larger.
1 since system preparation, respectively. The very slow relaxation seen in Fig. 4 can thus be attributed to an ultra-slow coarsening process of the network structure, as suggested by Fig. 11 and 12. Indeed, mass conservation arguments detailed in Section 5.5.4 suggest the scaling relation (5) to hold during late stages of coarsening, which we find to be satisfied to a good degree. Therefore, we conclude that coarsening mainly consists of filaments very slowly becoming thicker with pores very slowly getting larger.
 | ||
| Fig. 12 Accessible polymer surfaces and skeletons, morphometric analysis. Orthographic projections of (a)–(c) polymer surface and corresponding (α-γ) skeletons (purple lines) for the three configurations shown in Fig. 11. In (a)–(c) the polymer surfaces are obtained using Ovito's69 “construct surface mesh” modifier with probe sphere radius 1.5 and smoothing level 4. In (α-γ) the system beads are rendered as semi-transparent gray spheres. | ||
We can monitor the ultra-slow coarsening also via the weighted chord length distribution of the dense phase, 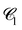 . As seen in Fig. 10(c) and (d), coarsening in the droplet and network-forming phase is associated with a slow shift of
. As seen in Fig. 10(c) and (d), coarsening in the droplet and network-forming phase is associated with a slow shift of  to larger chord lengths, in agreement with the ultra-slow increase of the mean weighted chord length
to larger chord lengths, in agreement with the ultra-slow increase of the mean weighted chord length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 over time seen in Fig. 10(b). The curves for κ > 10 in Fig. 10(b) are well reproduced (up to within 2%) by a logarithmic growth law (see Section 5.5.2). Extrapolating this law to a hypothetical final state of a single droplet or cylindrical filament would mean that
1 over time seen in Fig. 10(b). The curves for κ > 10 in Fig. 10(b) are well reproduced (up to within 2%) by a logarithmic growth law (see Section 5.5.2). Extrapolating this law to a hypothetical final state of a single droplet or cylindrical filament would mean that ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 keeps rising significantly up to times of the order of t = 1015 to 1020! In other words, the mean
1 keeps rising significantly up to times of the order of t = 1015 to 1020! In other words, the mean ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1, if averaged over all times up to time tend, increases by about 15% if tend is increased by one order of magnitude. Using
1, if averaged over all times up to time tend, increases by about 15% if tend is increased by one order of magnitude. Using ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1(t) as a time-dependent characteristic length scale of the network, we can rescale
1(t) as a time-dependent characteristic length scale of the network, we can rescale  at different times t onto a single master curve,
at different times t onto a single master curve,  (for details see Section 5.5.3, ESI†). Fig. 10(d) shows the rescaled curves for different times tw. A very good collapse of all data shown in Fig. 10(c) onto a single master curve f1(x) is observed. The functional form of the universal master curve f1(x) for the network-forming phase is well represented by the analytical expression given in eqn (29). Similar observations are made based on the weighted chord length distributions of the void space
(for details see Section 5.5.3, ESI†). Fig. 10(d) shows the rescaled curves for different times tw. A very good collapse of all data shown in Fig. 10(c) onto a single master curve f1(x) is observed. The functional form of the universal master curve f1(x) for the network-forming phase is well represented by the analytical expression given in eqn (29). Similar observations are made based on the weighted chord length distributions of the void space  (Fig. 23). When scaled with the corresponding mean chord length of the void space
(Fig. 23). When scaled with the corresponding mean chord length of the void space ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0(t), its master curve f0(x) is captured by the analytical expression (27). We can use the functional form of f0(x) to extrapolate
0(t), its master curve f0(x) is captured by the analytical expression (27). We can use the functional form of f0(x) to extrapolate  beyond the box size. This procedure allows us to estimate the moments of the distribution including the mean weighted and unweighted chord lengths,
beyond the box size. This procedure allows us to estimate the moments of the distribution including the mean weighted and unweighted chord lengths, ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 and l0, free of finite-size effects.
0 and l0, free of finite-size effects.
Furthermore, we find that the scaled filament length Lf/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 and thickness df/
1 and thickness df/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 as well as the scaled mean pore size rpore/
1 as well as the scaled mean pore size rpore/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 are essentially time-independent when early stages of coarsening are discarded. Therefore, we conclude that the ultra-slow coarsening observed here is self-similar. A corresponding conclusion has recently been reached for a network-forming colloidal suspension based on the weighted chord length distribution
1 are essentially time-independent when early stages of coarsening are discarded. Therefore, we conclude that the ultra-slow coarsening observed here is self-similar. A corresponding conclusion has recently been reached for a network-forming colloidal suspension based on the weighted chord length distribution 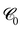 of the void spaces.12
of the void spaces.12
3.4 Coarsening mechanism
In an effort to better understand the ultra-slow coarsening mechanism, we propose a minimal model of fibril breaking and rearrangement. See Fig. 14 for a sketch. In this model, a representative fibril between two network junctions is modeled as a bundle of parallel chains that can diffuse longitudinally and independently of each other. The number c of chains in the bundle is proportional to the fibril cross section. When all chain ends meet, the bundle breaks into two parts that each join a different fibril, leading to a corresponding increase in fibril cross sections. For fibrils with larger cross sections and correspondingly more chains, the probability that all chain ends meet is reduced and so is bundle breakage, leading to an increase in rupture time τrup ∝ Nc−1. Employing a simple rate equation dc/dtw ∝ c/tw, this model predicts c(tw) ≈ a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(tw), i.e. a logarithmic growth for the mean number of chains in the cross-section of a fibril, eqn (20), derived in Section 5.5.1. Therefore, the minimal model motivates the use of logarithmic growth laws to describe our data on coarsening. We find that logarithmic growth laws describe well not only the coarsening of the mean filament length and diameter as shown in Fig. 13, but also other structural quantities such as the mean pore size, chord lengths, as well as pair and bending energies, with relative deviations of only a few percent. Some of these other quantities are shown together with fits to logarithmic growth laws in Fig. S5–S7 (ESI†).
ln(tw), i.e. a logarithmic growth for the mean number of chains in the cross-section of a fibril, eqn (20), derived in Section 5.5.1. Therefore, the minimal model motivates the use of logarithmic growth laws to describe our data on coarsening. We find that logarithmic growth laws describe well not only the coarsening of the mean filament length and diameter as shown in Fig. 13, but also other structural quantities such as the mean pore size, chord lengths, as well as pair and bending energies, with relative deviations of only a few percent. Some of these other quantities are shown together with fits to logarithmic growth laws in Fig. S5–S7 (ESI†).
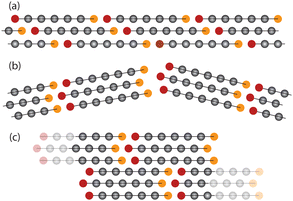 | ||
| Fig. 14 Minimal model. (a) Filamentous strand composed of three bead-spring chains within its cross-section. Chain ends are marked in red and orange. (b) The strand tends to preferably break when chain ends are aligned, giving rise to two dangling bundles. (c) These bundles join existing strands and thus help to increase their cross-sections (Movie A, ESI†). | ||
Coarsening of network structures has been observed in similar systems and described as either power-law12 or logarithmic growth.50 Power law and logarithmic behavior have been associated with two different universality classes of growth kinetics of activated processes, depending on whether the activation barriers grow (logarithmic) or do not grow (power law) with the domain size.70 While the above arguments seem to favor logarithmic growth, we actually find that both families of fit functions provide equally good descriptions of our data. This indicates that our data do not allow to distinguish between the two universality classes of domain growth advocated in ref. 70. Furthermore, our systems do not exhibit the exponent 0.5 found in the power-law growth of characteristic pore sizes reported for the gas–liquid demixing of colloidal suspensions and simple fluids.12 Instead, we observe a much weaker exponent of around 0.1 when fitting to power-law behavior. This finding might be taken as a further hint of non-universality of the ultra-slow coarsening kinetics and is in line with recent reports on non-universal aspects regarding the role of elasticity in polymer and colloidal gels.58 Further investigations on universality classes in ultra-slow coarsening and limits thereof are left for future research.
3.5 Anomalous diffusion and relaxational dynamics
The enduring ultra-slow coarsening of these networks poses some challenges for the investigation of their dynamical properties. First and foremost, the lack of time-translational invariance since a stationary state has not been reached implies that we need to carefully distinguish dynamical properties at different waiting times tw since preparation of the system.As a first dynamic quantity we study the mean-square displacement (MSD) of bead positions  as a function of time t since starting at a given waiting time tw. Fig. 15(a) shows the exemplary case of Δ(t,0) for κ = 50 and all 10 independent realizations of the system. For the corresponding Δ(t,105) up to t = 106 see Fig. S1 (ESI†). Even though each system contains Nb = 30
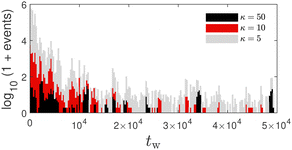
as a function of time t since starting at a given waiting time tw. Fig. 15(a) shows the exemplary case of Δ(t,0) for κ = 50 and all 10 independent realizations of the system. For the corresponding Δ(t,105) up to t = 106 see Fig. S1 (ESI†). Even though each system contains Nb = 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 beads, due to the absence of time-averaging, considerable sample-to-sample fluctuations are seen in Fig. 15(a), Fig. S1 (ESI†) and for other values of κ (not shown). Closer inspection of trajectories reveals that, except for the relatively early stage (tw ≲ 104), filament fluctuations are rather small with correspondingly small bead displacements. At certain times, however, large reorganizations of the filament networks occur via filament breakage and subsequent re-attachment to another strand, leading to very large displacements in some parts of the network over a short time period. Fig. 16 illustrates such a filament breaking event and the corresponding evolution of the MSD for an individual sample in the late stage of coarsening. Similar dynamic heterogeneities occur in a number of different systems, e.g. in glass-forming liquids57 and aging colloidal gels.17
000 beads, due to the absence of time-averaging, considerable sample-to-sample fluctuations are seen in Fig. 15(a), Fig. S1 (ESI†) and for other values of κ (not shown). Closer inspection of trajectories reveals that, except for the relatively early stage (tw ≲ 104), filament fluctuations are rather small with correspondingly small bead displacements. At certain times, however, large reorganizations of the filament networks occur via filament breakage and subsequent re-attachment to another strand, leading to very large displacements in some parts of the network over a short time period. Fig. 16 illustrates such a filament breaking event and the corresponding evolution of the MSD for an individual sample in the late stage of coarsening. Similar dynamic heterogeneities occur in a number of different systems, e.g. in glass-forming liquids57 and aging colloidal gels.17
 | ||
| Fig. 15 Mean square bead displacement. (a) MSD Δ(t,0) up to t = 105 for κ = 50 and individual realizations (each sample has its own color). The ensemble average is shown by the black solid line. (b) Ensemble-averaged MSD 〈Δ(t, tw)〉 at three different values for tw on a double-logarithmic scale (same data on a linear scale are shown in the inset). (c) MSD averaged over two different waiting time intervals: (i) tw ∈ [0,105] for all κ and (ii) tw ∈ [105,106] for κ ∈ {10,50,75}. All systems, including the unpercolated, flexible system (κ = 2 shown) seem to approach a diffusive regime only in (A). (d) The non-Gaussian parameter α2(15) is shown on a semi-logarithmic scale for case (i). For case (ii), the peak of the non-Gaussian parameter α2 grows and occurs at later times. | ||
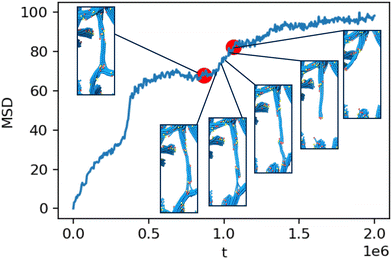 | ||
| Fig. 16 Filament rupture event. Zoom into a single filament rupture event responsible for the 2nd significant jump in the MSD (t = 0 corresponds to tw = 105) of an individual sample (κ = 50, realization 1), recorded at about t = 1 × 106 (Movies A–D, ESI†). End beads are colored in red and yellow, as in Fig. 14, all remaining beads are colored in blue. | ||
We will henceforth focus mostly on the ensemble-averaged MSD 〈Δ(t, tw)〉. Fig. 15(b) shows 〈Δ(t, tw) 〉 for κ = 50 and three different values of tw. We note that the short-time ballistic regime is not visible on the scale shown in Fig. 15(b). Instead, on a double-logarithmic scale, different diffusive regimes can be distinguished in Fig. 15(b), all of them sub-diffusive on the time scale investigated. Moreover, the dynamics is found to be very slow with beads moving only a fraction of their diameter up to times t ≈ 103 except for the case tw = 0. In the regime t = 5 × 104 up to 5 × 105, data seem to follow 〈Δ(t, tw)〉 ∼ t0.5. In addition, a very significant dynamic slowing down is seen from Fig. 15(b) as the MSD decreases with increasing tw. Similar observations of waiting-time dependence and dynamic slowing down have been made for aging in colloidal gels.17 At least on a qualitative level, the observed slowing down can in our case be linked to the coarsening network structure investigated above. Before investigating this relation further, we want to point out that ignoring the non-stationary nature of the networks and naively averaging over tw can lead to wrong conclusions on the diffusive behavior of the system. As an example, Fig. 15(c) shows 〈Δ(t, tw)〉 for various values of bending stiffness κ, averaged over rather large time intervals at an early tw ∈ [0, 105] and later stage tw ∈ [105, 106]. In this case, the apparent MSD depends strongly on the chosen averaging interval. Moreover, with such averaging, significantly larger values of diffusion exponents are obtained that in some cases may even suggest normal diffusion. Similar artifacts due to inappropriate temporal averages in nonergodic systems are known and have been analyzed within continuous time random walk models with power-law distributed waiting times.71
We note that the dynamics observed here bears some similarities to the subdiffusive regime with MSD(t) ∼ t3/4 found in dilute and entangled solutions of semiflexible polymers.72,73 For those systems, subdiffusive behavior occurs due to preferential fluctuations perpendicular to the chain contour for inner monomers at short times, before the MSD crosses over to normal diffusion at longer times when the MSD becomes comparable to the polymer size, MSD(t) ≈ 〈R2〉. For our systems, however, almost all chains are part of the temporary network, which leads to a severe hindrance of their mobility. As a consequence, the maximal values of MSD(t) achieved over the duration of the simulations reported in Fig. 15(c) remain an order of magnitude lower than 〈R2〉. Also for the unpercolated system with κ = 2, we observe a subdiffusive behavior MSD(t) ∼ t2/3, probably due to chain confinement within droplets as discussed in Section 3.2. Some of our observations may support the wormlike bundle model which predicts different dynamic regimes with the MSD perpendicular to the chain contour scaling first as t3/4 then t1/2 and again t3/4, before ultimately approaching a plateau, as this model disregards filament rupture.74
To further characterize bead mobility, we refer to the non-Gaussian parameter α2 defined in eqn (15). This quantity (Fig. 15d) characterizes deviations of bead displacements from a Gaussian distribution. For unpercolated systems (κ = 2), α2 remains small and approaches zero relatively quickly. For percolated systems on the other hand, α2 reaches peak values between 4 and 5 for κ ≥ 30 over an extended period of time around t ≈ 102…103 before the system enters a different diffusive regime. For larger tw, the peak height of the non-Gaussian parameter grows and moves to later times. Similar peaks in the non-Gaussian parameter have been observed in other systems such as supercooled liquids and glass-forming flexible polymers. In those systems, the peaks in α2 occur near the end of the plateau region of the MSD and have been associated with dynamic heterogeneities due to collective relaxation phenomena such as “cage breaking”.75 Here, however, the peak values observed in α2 are much larger, indicating much stronger deviations from a Gaussian distribution. In addition, although Fig. 15(b) indicates very slow, sub-diffusive dynamics, the MSD is still increasing and does not really plateau at intermediate times. These results are more similar to those found in network liquids76 and suggest that there are different relaxation mechanisms at work in these percolated networks compared to glassy dynamics, in agreement with recent conclusions.58 For intermediate values of the bending stiffness at the onset of a percolated network (κ = 10), an additional peak in α2 is seen from Fig. 15(d). In polymer melts composed of rather rigid chains, the onset of a second peak was seen in computer simulation studies of a model system similar to the one considered here.77 These authors assumed slow relaxation of nematic domains as the underlying mechanisms of the second peak at late times. Such explanations probably do not carry over to the present case where we observe an additional peak in α2 at earlier times. A double peak in α2 was also seen in computer simulations for a particular choice of parameters in a model for microemulsions, and related to the difference between local cage-breaking versus bond relaxation events.78
The self part of the intermediate scattering function, Fs(q, t), defined in eqn (14) provides more information on the length-scale dependent relaxational dynamics. See Section 5.3 for more details on this quantity, and Section S1 (ESI†) for a visualization of contributions to Fs(q, t). Fig. 17 shows Fs(q, t) for several (color coded) values of the wave number q over a similar range to those investigated for the static structure factor Ssc(q) in Fig. 5. For better visibility, only a tiny fraction of the simulation data are shown as circles in this plot (full datasets available in Fig. S13, ESI†). On small length scales below the bead diameter, i.e. q ≳ 6, relaxation occurs relatively fast and is not much affected by the bending stiffness κ. On the length scales of the end-to-end distances R of the polymers, corresponding to qee = 2π/R, the relaxation of Fs(qee, t) is generally faster than the orientational end-to-end vector relaxation (see Fig. S8, ESI†), indicating the importance of cooperative effects on these length scales (including the formation locally aligned chains in droplets and bundles). For all systems investigated, relaxation is slowing down by orders of magnitude with decreasing q corresponding to larger length scales. Except for κ = 0, each panel in Fig. 17 shows two sets of data corresponding to waiting times tw = 0 and tw = 105. Relaxation slows down with increasing waiting time, consistent with our observation of dynamic slowing down of the MSD. Such behavior is typical for aging, especially in glassy systems.79,80 The slowing with increasing tw is particularly strong for small q values (q < 1), where the intermediate scattering function does not relax to zero on the time scale of the simulations (and would not do so for q ≪ 1 even if we were to increase the simulation time window by many orders or magnitude). Therefore, we deal with an effective aging and non-ergodic system. This non-ergodic behavior is not only common in colloidal systems with infinite lifetime of bonds,78 but also reported for real transient networks of semiflexible polymers.1
 | ||
| Fig. 17 Incoherent scattering. The time decay of the self part of the intermediate scattering function, Fs(q, t), eqn (14) is shown on a semi-logarithmic scale for selected q-values as indicated in the colorbar. Different panels correspond to different values of the bending stiffness κ (mentioned in the panel title). In each panel, open and closed circles correspond to Fs(q, t) data for tw = 0 and tw = 105, respectively. All lines are fits to the power-ML function (6). The chosen set of q values is not identical for the two tw's, but they are uniquely color-coded (full data sets available in Fig. S13, ESI†). | ||
To discuss the relaxation dynamics more quantitatively, we fit the Fs(q, t) simulation data using the “power-ML” function
 | (6) |
 denotes the Mittag-Leffler function and Γ(x) the Gamma function. For the special case α = β, eqn (6) reduces to the standard Mittag–Leffler function
denotes the Mittag-Leffler function and Γ(x) the Gamma function. For the special case α = β, eqn (6) reduces to the standard Mittag–Leffler function  which is discussed in the literature as the solution to a linear fractional differential equation.81 By construction, we impose non-negative Eβ, i.e. we restrict the fits to β ∈ [0,1]. With two exponents α, β and an effective relaxation time τq, our simulation data for tw = 0 and all values of κ and q investigated and over seven orders of magnitude in t can be fitted very well by the power-ML function (6), as shown by the close agreement between the lines and open symbols in Fig. 17. For the tw = 105 data (filled symbols) eqn (6) does not capture all details in the intermediate time and q (q ≈ 1) regime.
which is discussed in the literature as the solution to a linear fractional differential equation.81 By construction, we impose non-negative Eβ, i.e. we restrict the fits to β ∈ [0,1]. With two exponents α, β and an effective relaxation time τq, our simulation data for tw = 0 and all values of κ and q investigated and over seven orders of magnitude in t can be fitted very well by the power-ML function (6), as shown by the close agreement between the lines and open symbols in Fig. 17. For the tw = 105 data (filled symbols) eqn (6) does not capture all details in the intermediate time and q (q ≈ 1) regime.
For relatively early times,  the power-ML function
the power-ML function ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) s describes a stretched exponential decay exp[−(t/τq)β], frequently employed to fit relaxation in gels and glasses.17,78 The corresponding values of the stretching exponents β are shown for tw = 0 in Fig. 18(b). A stretching exponent β = 3/4 was theoretically predicted for solutions of semiflexible polymers.82 Here we observe a rather large range of β ∈ [0.6,1] values that moreover vary non-monotonically with the wave number q. Note that similar values of β but in a smaller range [0.6, 0.75] are found if a stretched exponential function is used to fit Fs(q, t) for all times. Those results are not shown since the quality of the corresponding fits is generally inferior to those by the power-ML function. For our model system we can rule out compressed exponential relaxation17 not only because the power-ML (6) does not allow to capture the β > 1 regime, but also since t(d/dt)[ln(−ln
s describes a stretched exponential decay exp[−(t/τq)β], frequently employed to fit relaxation in gels and glasses.17,78 The corresponding values of the stretching exponents β are shown for tw = 0 in Fig. 18(b). A stretching exponent β = 3/4 was theoretically predicted for solutions of semiflexible polymers.82 Here we observe a rather large range of β ∈ [0.6,1] values that moreover vary non-monotonically with the wave number q. Note that similar values of β but in a smaller range [0.6, 0.75] are found if a stretched exponential function is used to fit Fs(q, t) for all times. Those results are not shown since the quality of the corresponding fits is generally inferior to those by the power-ML function. For our model system we can rule out compressed exponential relaxation17 not only because the power-ML (6) does not allow to capture the β > 1 regime, but also since t(d/dt)[ln(−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Fs(q, t))] does not exceed unity for our measured data, for both tw = 0 and tw = 105. From a second-order cumulant expansion,
Fs(q, t))] does not exceed unity for our measured data, for both tw = 0 and tw = 105. From a second-order cumulant expansion,  the short-time, small wave vector limit is related to the mean-square diffusion studied above. Our numerical data satisfy this relation (not shown). For times
the short-time, small wave vector limit is related to the mean-square diffusion studied above. Our numerical data satisfy this relation (not shown). For times  the power-ML function (6) smoothly interpolates to a power-law behavior,
the power-ML function (6) smoothly interpolates to a power-law behavior, ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) s ∼ t−α, with α ≠ β in general. Such pronounced power-law behavior is seen in Fig. 17, in particular for small q values. The power-law exponent α obtained from fits to eqn (6) is shown in Fig. 18(a). While for q ≳ 5, Fs(q, t) decays relatively rapidly so that the behavior is dominated by a stretched-exponential relaxation, relaxation slows down significantly for q ≲ 1 and the power-law regime becomes more and more dominant. Most strikingly, we find that in this regime the α decreases towards zero with decreasing q. While the values of α vary significantly with κ for tw = 0, only small variations are seen for tw = 105, where approximately α ∼ q6/5 for q < 1 (Fig. S11b, ESI†). Therefore, the long-time relaxation becomes slower and slower on larger scales as the exponent decreases towards zero.
s ∼ t−α, with α ≠ β in general. Such pronounced power-law behavior is seen in Fig. 17, in particular for small q values. The power-law exponent α obtained from fits to eqn (6) is shown in Fig. 18(a). While for q ≳ 5, Fs(q, t) decays relatively rapidly so that the behavior is dominated by a stretched-exponential relaxation, relaxation slows down significantly for q ≲ 1 and the power-law regime becomes more and more dominant. Most strikingly, we find that in this regime the α decreases towards zero with decreasing q. While the values of α vary significantly with κ for tw = 0, only small variations are seen for tw = 105, where approximately α ∼ q6/5 for q < 1 (Fig. S11b, ESI†). Therefore, the long-time relaxation becomes slower and slower on larger scales as the exponent decreases towards zero.
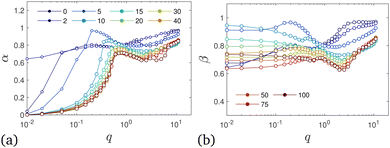 | ||
Fig. 18 Power-Mittag–Leffler parameters. (a) Exponent α characterizing the power-law regime at  and (b) exponent β characterizing the stretched exponential regime at and (b) exponent β characterizing the stretched exponential regime at 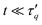 of the power-ML function (6)versus the wave number q extracted from Fs(q, t) (data symbols in Fig. 17), with additional values of q and κ as indicated in the legend. The range of κ values shown (legend distributed over both panels) covers the droplet and network phase. Shown are the exponents for tw = 0. For additional details see Fig. S11 and S12 (ESI†). of the power-ML function (6)versus the wave number q extracted from Fs(q, t) (data symbols in Fig. 17), with additional values of q and κ as indicated in the legend. The range of κ values shown (legend distributed over both panels) covers the droplet and network phase. Shown are the exponents for tw = 0. For additional details see Fig. S11 and S12 (ESI†). | ||
Having clarified short and long-time relaxation regimes, we now turn to a discussion of the characteristic relaxation times. Fig. 19(a) shows the relaxation time τq of the power-ML function (6) governing the time scale of the stretched exponential relaxation. In addition, Fig. 19(b) shows an alternative definition of a relaxation time ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q which characterizes the decay of Fs(q, t) to a prescribed level. For convenience we here choose Fs(q,
q which characterizes the decay of Fs(q, t) to a prescribed level. For convenience we here choose Fs(q, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q) = 1/2. For those cases where the simulation data of Fs(q, t) do not decay below 1/2, we use extrapolations from eqn (6) to determine
q) = 1/2. For those cases where the simulation data of Fs(q, t) do not decay below 1/2, we use extrapolations from eqn (6) to determine ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q. While the numerical values of τq and
q. While the numerical values of τq and ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q are different, both characteristic relaxation times show qualitative similar behavior at large q. First, for tw = 0 (open symbols in Fig. 19), the relaxation times show approximately a scaling q−2 for q ≳ 10−1 and the relaxation times are increasing with increasing bending stiffness κ. Aged systems with tw = 105, however, show a rather abrupt increase of τq,
q are different, both characteristic relaxation times show qualitative similar behavior at large q. First, for tw = 0 (open symbols in Fig. 19), the relaxation times show approximately a scaling q−2 for q ≳ 10−1 and the relaxation times are increasing with increasing bending stiffness κ. Aged systems with tw = 105, however, show a rather abrupt increase of τq, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q by about three orders of magnitude when q decreases from q ≈ 3 to q ≈ 2. Interestingly, τq,
q by about three orders of magnitude when q decreases from q ≈ 3 to q ≈ 2. Interestingly, τq, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q are rather insensitive to the precise value of κ in the network-forming regime over a relatively large interval of q values. Fig. 19 demonstrates a very rich relaxation behavior of the system that moreover changes significantly between initial (tw = 0) and aged (tw = 105) samples. Not only do large structures relax more slowly in these systems, they do so in a particular manner with a κ-independent onset at a characteristic wave number qc. With qc ≈ 2…3, this length scale roughly corresponds to the filament radius df/2. With relaxation times exceeding 106…108 for q < 10−1 by far, these systems show ultra-slow relaxation alongside the coarsening behavior established above.
q are rather insensitive to the precise value of κ in the network-forming regime over a relatively large interval of q values. Fig. 19 demonstrates a very rich relaxation behavior of the system that moreover changes significantly between initial (tw = 0) and aged (tw = 105) samples. Not only do large structures relax more slowly in these systems, they do so in a particular manner with a κ-independent onset at a characteristic wave number qc. With qc ≈ 2…3, this length scale roughly corresponds to the filament radius df/2. With relaxation times exceeding 106…108 for q < 10−1 by far, these systems show ultra-slow relaxation alongside the coarsening behavior established above.
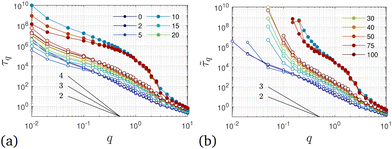 | ||
Fig. 19 Effective relaxation times. (a) Characteristic relaxation times τq, eqn (6), in the droplet and network phase versus the wave number q extracted from the incoherent scattering function (symbols in Fig. 17), with additional values of q and κ as indicated in the legend (distributed over both panels). (b) Same as (a) but for the alternative definition of relaxation time ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q defined as Fs(q, q defined as Fs(q, ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q) = 1/2. To highlight the dependency of relaxation times on the waiting time, we here display results using tw = 0 (open circles) and tw = 105 (filled circles). Not directly measurable q) = 1/2. To highlight the dependency of relaxation times on the waiting time, we here display results using tw = 0 (open circles) and tw = 105 (filled circles). Not directly measurable ![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif) q values had been extrapolated using the q values had been extrapolated using the ![[F with combining tilde]](https://www.rsc.org/images/entities/i_char_0046_0303.gif) s(q, t) fits (lines in Fig. 17). s(q, t) fits (lines in Fig. 17). | ||
4 Conclusions
We study systems of semiflexible polymers where cohesive interactions lead to physical, reversible crosslinks. From comprehensive molecular simulations of a generic coarse-grained model, we find polymers to self-assemble into droplets for weak bending stiffness, i.e. for relatively flexible chains. For more rigid chains, on the other hand, the interplay between attractive interactions with periodic boundary conditions results in the formation of percolated networks of filaments – a typical behavior observed in many biopolymers.The self-assembled structures possess well-defined interfaces as evidenced from a pronounced q−4 Porod regime of the static structure factor at intermediate scattering values q. From a skeleton analysis, we find that the network is dominated by three-fold junctions, with four- or higher-order junctions and dangling ends accounting for a tiny fraction only. We identify the links between junctions as filaments and observe that their mean thickness decreases monotonically with increasing persistence length, in agreement with previous simulation studies,45 but in contrast with results from scattering experiments on PEG-grafted methylcellulose chains.22 The resolution of this conundrum is left for future research. We determine the pore size and chord length distribution used to define typical mesh sizes. We find characteristic scaling laws for these systems so that e.g. the mean pore radius and the mean filament thickness are proportional to one another.
The systems investigated here show different dynamic regimes of slow, sub-diffusive dynamics with strongly non-Gaussian displacements over a broad time window. In addition, dynamic slowing down is observed as the system ages. The underlying reason for the anomalous diffusion are dynamical heterogeneities due to rare reorganizations of the filament networks with large cooperative displacements of a significant number of beads. The relaxation dynamics is therefore intermittent and dominated by individual events of filament breaking and recombining that become more rare as the system coarsens (Fig. 20). These dynamical heterogeneities are also reflected by stretched exponential and power-law relaxation of the incoherent scattering function, with substantial dynamical slowing down as the system relaxes further. It is important to remark that the incoherent scattering function in the small wave number regime does not decay to zero on the time scale of our simulations. The corresponding lack of ergodicity since large-scale structure are not fully equilibrated has been pointed out also in experiments on gels of amyloid fibers.1
We observe a logarithmic dependence on waiting time since system preparation for structural and thermodynamic quantities. This weak logarithmic dependence is easily overlooked when monitoring these quantities on linear scales as is usually done to check for stationarity. Also some quantities like the static structure factor and gyration radius are less sensitive to the ultra-slow relaxation (see Fig. 4 and Fig. S7, ESI†). For other, in particular dynamic, quantities, however, the waiting-time dependence is more significant and naive averaging can lead to incorrect conclusions, e.g. regarding the diffusive behavior.
The ultra-slow logarithmic relaxation prevents us from reaching a (approximate) stationary state even with a massive increase in computational resources. The enduring relaxation can be interpreted as an aging process as encountered in many complex and amorphous materials, where the system explores lower and lower potential (bond and bending) energy minima. Structurally, for our system this aging phenomenon involves an ultra-slow coarsening process of network structures where filaments very slowly become thicker while pores become larger. Since both length scales are intimately linked, the ultra-slow coarsening is self-similar in the course of time as evidenced by the very good data collapse onto master curves of the chord length and pore size distributions. It would be interesting to compare these findings with experimental results on aging in comparable biopolymer networks. Exploring the interplay of aging and coarsening with viscoelastic properties of these networks is left for future research.
5 Materials and methods
5.1 Static structure factors
The static structure factor S(q) is defined by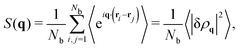 | (7) |
 are the Fourier modes of the fluctuating density field. The angular brackets denote ensemble averaging. For isotropic systems, S depends only on the modulus q = |q| of the wave vector, and can be used to calculate the pair correlation function
are the Fourier modes of the fluctuating density field. The angular brackets denote ensemble averaging. For isotropic systems, S depends only on the modulus q = |q| of the wave vector, and can be used to calculate the pair correlation function  . We efficiently evaluate S(q) via numerical Fourier transform on a 212 × 212 grid to prevent evaluating a double sum or the pair correlation function at large distances (we find that smaller grids lead to inaccurate results in the vicinity of the first minimum of S(q) at about q = π). The smallest wave vector qmin = 2π/Lx that we can meaningfully study corresponds to the largest length scale of our system which is the linear size Lx = V1/3 of the cubic simulation box. The largest qmax = 4096qmin is determined by the chosen grid.
. We efficiently evaluate S(q) via numerical Fourier transform on a 212 × 212 grid to prevent evaluating a double sum or the pair correlation function at large distances (we find that smaller grids lead to inaccurate results in the vicinity of the first minimum of S(q) at about q = π). The smallest wave vector qmin = 2π/Lx that we can meaningfully study corresponds to the largest length scale of our system which is the linear size Lx = V1/3 of the cubic simulation box. The largest qmax = 4096qmin is determined by the chosen grid.
We also evaluate the isotropic scattering function of an individual chain, defined by the Fourier-transformed intra-molecular radial pair correlation function83
 | (8) |
For discrete WLCs in the absence of excluded volume effects, Ssc can be calculated (i) recursively via the Laplace-transformed moments of the end-to-end distribution function,86,87 or (ii) numerically upon generating an ensemble of discrete WLCs, or (iii) analytically using one of the existing approximations for the radially symmetric distribution function f(L, Lp; R) for the end-to-end distance R of a discrete WLC with contour length L and persistence length Lp. We here employed the two latter approaches: (ii) to generate an ensemble of Nc discrete WLC with given N, b and κ/kBT or  we grow each chain bond by bond, choose bond vector
we grow each chain bond by bond, choose bond vector  with z = −1 + ln(1 + cξ)kBT/κ, ξ a random number equally distributed on the interval [0,1], u a random unit vector, and c = e2κ/kBT − 1. This algorithm follows from the known distribution of bond angles for the discrete WLC. For huge κ/kBT > 100, to prevent numerical precision problems, z = max(−1, 1 + ln(ξ)kBT/κ) can be employed instead of the above exact expression. The bead positions, given by ri = ri−1 + bi, are then directly used to evaluate eqn (8). For approach (iii), we start from the highly accurate analytic expression for f(L, Lp; R) proposed by Becker et al.,88 subsequently normalized so that
with z = −1 + ln(1 + cξ)kBT/κ, ξ a random number equally distributed on the interval [0,1], u a random unit vector, and c = e2κ/kBT − 1. This algorithm follows from the known distribution of bond angles for the discrete WLC. For huge κ/kBT > 100, to prevent numerical precision problems, z = max(−1, 1 + ln(ξ)kBT/κ) can be employed instead of the above exact expression. The bead positions, given by ri = ri−1 + bi, are then directly used to evaluate eqn (8). For approach (iii), we start from the highly accurate analytic expression for f(L, Lp; R) proposed by Becker et al.,88 subsequently normalized so that  and then evaluate the intramolecular pair correlation function gsc(r) by summing over all partial contour distances, i.e.,
and then evaluate the intramolecular pair correlation function gsc(r) by summing over all partial contour distances, i.e.,  . With gsc(r) at hand, we evaluate
. With gsc(r) at hand, we evaluate  with L = (N − 1)b. For the large Lp > Nb, approach (iii) runs into numerical problems and we rely on (ii). Both approaches (ii) and (iii) allow us to consider variable bond lengths b, but we find that our measured Ssc(q) is already well captured over the whole q range including the peaks for q ≫ b−1, by using a fixed value b = 1. As a side-result, we have access to gsc(r) without having to measure this quantity directly.
with L = (N − 1)b. For the large Lp > Nb, approach (iii) runs into numerical problems and we rely on (ii). Both approaches (ii) and (iii) allow us to consider variable bond lengths b, but we find that our measured Ssc(q) is already well captured over the whole q range including the peaks for q ≫ b−1, by using a fixed value b = 1. As a side-result, we have access to gsc(r) without having to measure this quantity directly.
5.2 Effective persistence lengths
We implemented two approaches to extract effective persistence lengths![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p and Lp from chain configurations. In the “local” approach, we use the mean bending energy per atom ea, usually reported by LAMMPS (eangle). The corresponding
p and Lp from chain configurations. In the “local” approach, we use the mean bending energy per atom ea, usually reported by LAMMPS (eangle). The corresponding ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p is then given by
p is then given by ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p = −b/ln〈ui·ui+1〉 with 〈ui·ui+1〉 = 1 − Nea/[(N − 2)κ]. In the second “global” approach we use the ratio between mean squared end-to-end distance 〈R2〉 and squared radius of gyration R2g of the N-chains (Fig. S10, ESI†) and estimate an effective persistence length Lp assuming that the individual chains exhibit the statistics of a discrete WLC (Fig. 21). To this end let us recall the exact analytic expressions for a discrete WLC with N − 1 bonds and contour length L = (N − 1)b,54
p = −b/ln〈ui·ui+1〉 with 〈ui·ui+1〉 = 1 − Nea/[(N − 2)κ]. In the second “global” approach we use the ratio between mean squared end-to-end distance 〈R2〉 and squared radius of gyration R2g of the N-chains (Fig. S10, ESI†) and estimate an effective persistence length Lp assuming that the individual chains exhibit the statistics of a discrete WLC (Fig. 21). To this end let us recall the exact analytic expressions for a discrete WLC with N − 1 bonds and contour length L = (N − 1)b,54 | (9) |
 | (10) |
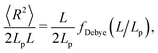 | (11) |
 | (12) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p (obtained from ea) and global Lp (obtained from 〈R2〉, R2g, or their ratio) are identical, and
p (obtained from ea) and global Lp (obtained from 〈R2〉, R2g, or their ratio) are identical, and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p = Lp = LWLCp with
p = Lp = LWLCp with  .
.
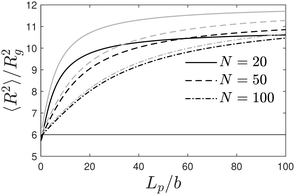 | ||
| Fig. 21 WLC model prediction. Ratio 〈R2〉/R2gversus Lp/b for three different N according to eqn (9) and (10) (black) and eqn (11) and (12) (light gray) for comparison. We extract an effective persistence length Lp from this ratio, instead of monitoring the bond–bond correlation function. Alternatively, we extract an effective persistence length Lp by fitting the measured Ssc(q) to the discrete WLC model, as described in Section 5.1. | ||
Note that expressions (9) and (10) were written differently, but equivalently, in the mentioned ref. 54. With the nonzero components A13 = −(π/2)I1(Lp/b)/sinh(Lp/b) and A33 = z of a 3 × 3 matrix A, involving the modified Bessel function I1 of the first kind, the mean squared end-to-end distance was left un-evaluated in terms of A as 〈R2〉/bL = C∞ − [2/(N − 1)][A·(1 −AN−1)·(1 − A)−2]33, where C∞ = [(1 + A)·(1 − A)−1]33.
5.3 Intermediate scattering function F(q, t)
Letting rj(t) denote the coordinates of the jth bead at time t, the intermediate scattering function (also known as dynamic structure factor) is defined by | (13) |
 the instantaneous density fluctuation at wave vector q. For t = 0, eqn (13) reduces to the static structure factor F(q, 0) = S(q) introduced in eqn (7).
the instantaneous density fluctuation at wave vector q. For t = 0, eqn (13) reduces to the static structure factor F(q, 0) = S(q) introduced in eqn (7).
We evaluate the radially symmetric self-part of F(q, t),90Fs(q, t) = 〈exp[iq·(rj(t + tw) − rj(tw))]〉, for a selected number of q values. The average is taken over trajectories of 10 statistically independent starting configurations, and all q-vectors with length q = |q|. Such integrals over the unit sphere of orientations of q vectors amounts to evaluating
 | (14) |
For small q, eqn (14) can be expanded to give90 which depends only on the displacements and the non-Gaussian parameter defined by
which depends only on the displacements and the non-Gaussian parameter defined by
 | (15) |
For percolated networks the Fs(q, t), evaluated for tw = 0, exhibits power-law behavior at small q ≲ qc, and stretched exponential behavior at q ≳ qc, where 2π/qc is comparable with the filament diameter df. A class of functions providing the required asymptotic behaviors are the three-parametric Mittag–Leffler functions 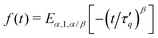 .91 Another class, involving the simpler one-parametric Mittag–Leffler function, are the power-ML functions
.91 Another class, involving the simpler one-parametric Mittag–Leffler function, are the power-ML functions  with q-dependent β ∈ (0,1), α > 0,
with q-dependent β ∈ (0,1), α > 0,  , which we are using in this work, as they better capture the data. Both versions are characterized by f(t) = exp[−(t/τq)β] at
, which we are using in this work, as they better capture the data. Both versions are characterized by f(t) = exp[−(t/τq)β] at  , and
, and  at
at  , while the ratios
, while the ratios  and
and  are both uniquely determined by α and β. For the power-ML one has
are both uniquely determined by α and β. For the power-ML one has  and
and  as stated in eqn (6) already. Due to the existing relationship between τq and
as stated in eqn (6) already. Due to the existing relationship between τq and  it is generally not possible to fit both terminal (early/late) regimes of a measured Fs(q, t) perfectly, and the fitted exponents α and β may not coincide exactly with the exponents one would obtain when fitting the asymptotic regimes separately (Section S5, ESI†). This fact must be taken into account when interpreting the exponents.
it is generally not possible to fit both terminal (early/late) regimes of a measured Fs(q, t) perfectly, and the fitted exponents α and β may not coincide exactly with the exponents one would obtain when fitting the asymptotic regimes separately (Section S5, ESI†). This fact must be taken into account when interpreting the exponents.
5.4 Network analysis algorithms
 | ||
| Fig. 22 Clusters and critical bonds. (a) Amount of clusters versus waiting time based on graph constructed from the reversible and permanent bonds. (b) Amount of critical bonds. The visible blue line at the figure bottom is for κ = 5, while there are no critical bonds for κ ≤ 2. The finite number of critical bonds for κ = 5 stems from the few 1D percolated configurations (Fig. S14, ESI†). | ||
The thinning algorithm operates on the bead positions and their permanent and temporary bond information and produces a reduced configuration, the skeleton, upon deleting beads from the original configuration that are identified to not being part of it. The remaining skeleton is free from unattached beads, and made of linear strands connecting junctions. In our implementation, directly connected junctions in the reduced configuration are merged to form a single, higher-functional junction, to prevent the artificial occurrence of filaments with a single bond. The linear strands follow the centerline of the thick filaments and the minimum number of beads that form a loop is the single parameter of the algorithm. While this parameter was chosen as low as 3 in the original work on colloidal gels, and iteratively larger in subsequent works,94 we use a value of 25. We find that results for the systems under study are basically unaffected by the choice as long as the parameter exceeds 20. Since this skeleton algorithm does not alter the coordinates, and because beads deep inside filaments reside on crystal-like lattices, the linear strands making the skeleton eventually exhibit zig–zag regions. To be able to estimate strand lengths Lf at high precision, as well as their amount E, and the total filament length Ltotal = ELf, we smooth the contour of linear skeleton strands by walking, starting from each junction, along all chains emanating from it up to the next junction (or the chain end), and place each skeleton bead halfway between preceding and next skeleton bead. The adjusted bead positions are then constituting the skeleton, representing the centerlines of the bundles and their junctions (Fig. 12 and Fig. S3, ESI†).
 junctions is given by
junctions is given by  , where nf denotes the number of skeleton beads with f neighbors and the summation
, where nf denotes the number of skeleton beads with f neighbors and the summation 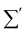 runs over all vertices f with f ≠ 2. For a general network consisting of C disconnected clusters, the total number of independent cycles “loops” L∘ (also known as circuit rank, cyclomatic number, or nullity of a graph) is determined by the number of edges and vertices as95,96
runs over all vertices f with f ≠ 2. For a general network consisting of C disconnected clusters, the total number of independent cycles “loops” L∘ (also known as circuit rank, cyclomatic number, or nullity of a graph) is determined by the number of edges and vertices as95,96 | (16) |
 . The mean junction functionality
. The mean junction functionality 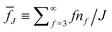 can alternatively be written as
can alternatively be written as ![[f with combining macron]](https://www.rsc.org/images/entities/i_char_0066_0304.gif) J = (2E − n1)/J.
J = (2E − n1)/J.
For the calculation of the total polymeric volume Vf and corresponding bead number density ρf = Nb/Vf, we use a basic Monte Carlo scheme, where we shoot randomly into the simulation box volume V. The Vf is then the fraction of shots that hit any of the bead volumes (unchanged radius r∘), multiplied by V. Generally, results for Vf and df are sensitive to the choice of r∘, but at fixed radius we can still evaluate the effect of κ and time on the Vf(t) and df(t) trajectories.
A rigorous bead number density ![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) f deep inside the filamentous bundles we identify with the mean inverse Voronoi volume of skeleton beads, while the Voronoi construction is performed using all beads. The corresponding polymeric volume, assuming that there is no density gradient inside bundles, is then Ṽf = Nb/
f deep inside the filamentous bundles we identify with the mean inverse Voronoi volume of skeleton beads, while the Voronoi construction is performed using all beads. The corresponding polymeric volume, assuming that there is no density gradient inside bundles, is then Ṽf = Nb/![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) f.
f.
 approaches unity for r → ∞. This G-Ppore(r)dr is the probability that the largest sphere, containing a randomly chosen point within the void space and not overlapping with the material spheres, has a radius between r and r + dr. The corresponding cumulative pore size distribution is shown in Fig. 9. The mean pore radius is evaluated as
approaches unity for r → ∞. This G-Ppore(r)dr is the probability that the largest sphere, containing a randomly chosen point within the void space and not overlapping with the material spheres, has a radius between r and r + dr. The corresponding cumulative pore size distribution is shown in Fig. 9. The mean pore radius is evaluated as  .
.
A simpler and only marginally related quantity T-Ppore(r) is known as Scheidegger or Torquato-PSD.63,98 We interpret T-Ppore(r) as the probability of the largest sphere with radius r that can be fitted at a random position within the system without overlapping any material sphere. For comparison, we show in Fig. S9 (ESI†) the cumulative pore size distribution based on T-Ppore. By construction, both cumulative pore size distributions are increasing functions. However, clear differences between Fig. 9 and Fig. S9 (ESI†) can be seen, emphasizing the different definitions of both quantities.
 chord length distributions for both the void (x = 0) and dense (x = 1) phases. Periodic boundaries are taken into account. To define the surface, we consider points in the void space to have a distance exceeding 2r∘ = 1.5 from any of the beads. The value 1.5 is large enough to ensure that we do not greatly overestimate the surface area (due to increased roughness at smaller values).
chord length distributions for both the void (x = 0) and dense (x = 1) phases. Periodic boundaries are taken into account. To define the surface, we consider points in the void space to have a distance exceeding 2r∘ = 1.5 from any of the beads. The value 1.5 is large enough to ensure that we do not greatly overestimate the surface area (due to increased roughness at smaller values).
Since the probability to choose a point on a chord of length s is proportional to s, the weighted and unweighted distributions for the x-phase are interrelated by  with
with 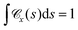 . The mean unweighted and weighted chord lengths are then denoted by
. The mean unweighted and weighted chord lengths are then denoted by  and
and  respectively. The unweighted Cx(s) had been employed in many theoretical works,57 where one considers all possible chords, while the weighted
respectively. The unweighted Cx(s) had been employed in many theoretical works,57 where one considers all possible chords, while the weighted  is usually extracted by randomly choosing many points inside the x-phase, and determining their chord lengths.12 Analytic expressions exist for some simple geometries like spheres and cylinders.65 For an ideal cylinder of diameter df and length Lf one has l1 = dfLf/(Lf + df/2) and
is usually extracted by randomly choosing many points inside the x-phase, and determining their chord lengths.12 Analytic expressions exist for some simple geometries like spheres and cylinders.65 For an ideal cylinder of diameter df and length Lf one has l1 = dfLf/(Lf + df/2) and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1 ≈ 1.27 × l1.
1 ≈ 1.27 × l1.
We extract the chord length distributions with high resolution based on the Cauchy–Crofton formula.66,99 To this end we generate an ensemble of X lines equally distributed in a large sphere of radius  and surface area AL = 4πrL2 enclosing the cubic simulation box. Each of the lines connects two random points residing on the surface of the large sphere. This procedure ensures a homogeneous density of an ensemble of X lines within the simulation box volume. For each line, we calculate the number of its intersections with the surface of our filamentous network (including periodic images). Denoting the total number of intersections by Xf, the resulting accessible polymer surface area is Af = XfAL/2X. The factor 2 accounts for the number of intersections of each line with the surface of the large sphere. As an immediate, but most important by-result one obtains the unweighted distribution of chord lengths, Cx(s), and the weighted distribution
and surface area AL = 4πrL2 enclosing the cubic simulation box. Each of the lines connects two random points residing on the surface of the large sphere. This procedure ensures a homogeneous density of an ensemble of X lines within the simulation box volume. For each line, we calculate the number of its intersections with the surface of our filamentous network (including periodic images). Denoting the total number of intersections by Xf, the resulting accessible polymer surface area is Af = XfAL/2X. The factor 2 accounts for the number of intersections of each line with the surface of the large sphere. As an immediate, but most important by-result one obtains the unweighted distribution of chord lengths, Cx(s), and the weighted distribution  (s) herefrom.
(s) herefrom.
If one were interested in Af only, it is sufficient to employ a Monte Carlo scheme where one shoots randomly into the surfaces of the Nb beads defining the void space, and counts the fraction of shots that do not reside inside any of the remaining spheres. This fraction, multiplied by the total surface area of Nb individual spheres equals Af. We checked that the so-obtained Af coincides with the Af from the Cauchy–Crofton approach.
5.5 Self-similar coarsening
 | (17) |
In a first approximation, let us assume that the total length of all filaments, Ltotal, and the mean filament length, Lf, are unaffected by c. The equation of change for c then reads
 | (18) |
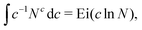 by
by | (19) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(y), so that the explicit expression for c(tw) can be written as
ln(y), so that the explicit expression for c(tw) can be written as | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(tw) that we used to fit the data (Section 5.5.2). Inserting eqn (20) into the expression for τrup suggests that τrup increases quasi-linearly with tw.
ln(tw) that we used to fit the data (Section 5.5.2). Inserting eqn (20) into the expression for τrup suggests that τrup increases quasi-linearly with tw.
This minimal model can be extended to filaments with a length Lf = mN that is a multiple of N, i.e., to filaments of diameter  that contain mc chains, and mc unpaired bonds. A motivation for this extension is that we know that Lf is roughly proportional to df,
that contain mc chains, and mc unpaired bonds. A motivation for this extension is that we know that Lf is roughly proportional to df,  . The probability that c unpaired bonds are located, for the first time, at the same position after s ≫ 1 steps is [1 − pc−1]m(s−1)pc−1[1 − pc−1]m−1 = [1 − pc−1]ms−1pc−1 with p = 1/N, implying τrup(c, Lf) = [1 − (1 − Nc−1)Lf/N]−1 − 1, keeping in mind that
. The probability that c unpaired bonds are located, for the first time, at the same position after s ≫ 1 steps is [1 − pc−1]m(s−1)pc−1[1 − pc−1]m−1 = [1 − pc−1]ms−1pc−1 with p = 1/N, implying τrup(c, Lf) = [1 − (1 − Nc−1)Lf/N]−1 − 1, keeping in mind that  . For Lf = N (m = 1) this reduces to the earlier expression. For large N ≫ 1, τrup(c, Lf) ≈ m−1Nc−1 is thus by a factor
. For Lf = N (m = 1) this reduces to the earlier expression. For large N ≫ 1, τrup(c, Lf) ≈ m−1Nc−1 is thus by a factor  smaller than τrup(c). Putting this together
smaller than τrup(c). Putting this together
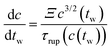 | (21) |
While the minimal model gives rise to logarithmic growth of the number of chains in the cross-section of filaments, it completely ignores length or thickness distributions of filaments, and any variation of the total length of filaments with c. It can thus be improved further to the expense that the corresponding ODE can be solved only numerically.
f(tw) = aκ + bκ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(tw) (tw ≥ 104), ln(tw) (tw ≥ 104), | (22) |
 | (23) |
 | (24) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(tw/τκ) with τk = exp(−aκ/bκ). For large κ ≫ 1, one has
ln(tw/τκ) with τk = exp(−aκ/bκ). For large κ ≫ 1, one has | (25) |
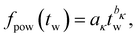 where aκ and bκ are again given by eqn (23) but with different values for A0,1 and B0,1. As a matter of fact, a power-law dependency cannot be ruled out completely. We moreover tested if we can find simple fit functions that capture the various averages much better than the unbounded eqn (22), since most of the measured quantities have an upper or lower bound. We find that the three-parametric rational function f(tw) = c1(1 + c2x)/(1 + c3x) with x = ln(tw) or x = ln2(x) serves this purpose, and then allows to estimate a stationary
where aκ and bκ are again given by eqn (23) but with different values for A0,1 and B0,1. As a matter of fact, a power-law dependency cannot be ruled out completely. We moreover tested if we can find simple fit functions that capture the various averages much better than the unbounded eqn (22), since most of the measured quantities have an upper or lower bound. We find that the three-parametric rational function f(tw) = c1(1 + c2x)/(1 + c3x) with x = ln(tw) or x = ln2(x) serves this purpose, and then allows to estimate a stationary  as well as the time where f(tw) has reached a certain fraction of its final value. However, such extrapolations to very long times carry a large amount of uncertainty.
as well as the time where f(tw) has reached a certain fraction of its final value. However, such extrapolations to very long times carry a large amount of uncertainty.
 and
and  .
We find that all time-dependent, weighted chord length distributions
.
We find that all time-dependent, weighted chord length distributions  , multiplied by the characteristic length scale
, multiplied by the characteristic length scale ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) x(t), fall onto a master curve, if plotted versus s/
x(t), fall onto a master curve, if plotted versus s/![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) x(t). This finding is in the same spirit as observations made for other model gels.12 The multiplication with
x(t). This finding is in the same spirit as observations made for other model gels.12 The multiplication with ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) x(t) is necessary to keep the normalization intact.
x(t) is necessary to keep the normalization intact.
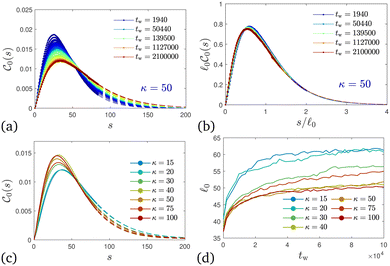 | ||
Fig. 23 Distribution and self-similarity of weighted chord lengths. Same as Fig. 10(c)–(f) for the distribution  operating on the void space. The extrapolated lines at s > Lx (dashed) were obtained assuming the form (27) obtained upon studying larger systems with Nc = 50 operating on the void space. The extrapolated lines at s > Lx (dashed) were obtained assuming the form (27) obtained upon studying larger systems with Nc = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains. 000 chains. | ||
For our small systems,  as opposed to
as opposed to  , does not drop to zero when s reaches the box size Lx ≈ 84.3. As for
, does not drop to zero when s reaches the box size Lx ≈ 84.3. As for 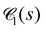 however, the rescaled, measured part of
however, the rescaled, measured part of  falls onto a master curve. We use this finding to estimate the full
falls onto a master curve. We use this finding to estimate the full 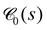 for all percolated systems by studying a number of large systems with Nc = 50
for all percolated systems by studying a number of large systems with Nc = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains (Fig. 19) at unchanged number density for selected κ up to relatively small times tw = 5 × 104. For these systems, the box size Lx ≈ 310.7 is sufficiently large to observe the full
000 chains (Fig. 19) at unchanged number density for selected κ up to relatively small times tw = 5 × 104. For these systems, the box size Lx ≈ 310.7 is sufficiently large to observe the full  curve. We find that
curve. We find that  is (within 2% relative deviation) described by the master curve
is (within 2% relative deviation) described by the master curve
 | (26) |
 | (27) |
 and time-dependent first moment
and time-dependent first moment  by construction. This
by construction. This  has its maximum at smax0 = (ν0 − 1)
has its maximum at smax0 = (ν0 − 1)![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0/ν0. For the exponent we find ν0 ≈ 2.3 ± 0.1 for κ = 50 (large system with Nc = 50
0/ν0. For the exponent we find ν0 ≈ 2.3 ± 0.1 for κ = 50 (large system with Nc = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains) and ν0 = 2.4 ± 0.15 independent on κ for all small systems. For ν0 = 2.3, smax0 ≈ 0.63
000 chains) and ν0 = 2.4 ± 0.15 independent on κ for all small systems. For ν0 = 2.3, smax0 ≈ 0.63![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0.
0.
For the smaller systems with Nc = 1000 chains, we have measured the un-normalized 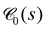 up to smax0 ≤ s ≤ Lx, so that we have already determined smax0. We then fit the available data to the form (27) to extract ν0, and herefrom obtain
up to smax0 ≤ s ≤ Lx, so that we have already determined smax0. We then fit the available data to the form (27) to extract ν0, and herefrom obtain ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 0 = ν0smax0/(ν0 − 1).
0 = ν0smax0/(ν0 − 1).
For  we find the following analytic expression to capture the master curve,
we find the following analytic expression to capture the master curve,
 | (28) |
 | (29) |
 | (30) |
 . The maximum of
. The maximum of  is achieved at s = smax1, and the maximum amplitude is
is achieved at s = smax1, and the maximum amplitude is 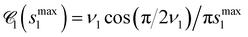 so that we can use the measured smax1 and
so that we can use the measured smax1 and  to determine both ν1 and
to determine both ν1 and ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1. For the exponent we find ν1 ≈ 2.9 ± 0.1 for κ = 50 (large system with Nc = 50
1. For the exponent we find ν1 ≈ 2.9 ± 0.1 for κ = 50 (large system with Nc = 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 chains) and the same range of value for all κ (smaller systems with Nc = 1000 chains). For ν1 = 2.9, smax1 ≈ 0.6
000 chains) and the same range of value for all κ (smaller systems with Nc = 1000 chains). For ν1 = 2.9, smax1 ≈ 0.6 ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1.
1.
Just note the identity  implying that Cx(s) does not fall onto a master curve except if
implying that Cx(s) does not fall onto a master curve except if ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) x/lx is a constant at all times. Using the analytic expressions
x/lx is a constant at all times. Using the analytic expressions  allows to (i) write lx as an integral, which we can be evaluated analytically as well (Fig. 24), and (ii) to estimate the scattering intensity, under certain assumptions like convexity,101,102 which do not strictly apply for our system.
allows to (i) write lx as an integral, which we can be evaluated analytically as well (Fig. 24), and (ii) to estimate the scattering intensity, under certain assumptions like convexity,101,102 which do not strictly apply for our system.
 | ||
Fig. 24 Mean chord lengths. Ratio between mean weighted and mean unweighted chord lengths versus exponent νx with x ∈ {0, 1}, predicted by the analytical expressions (27) and (29). The measured ratios range in the regimes marked by the red rectangles. In every case the ratio is larger than the ratio one obtains for cylinders whose height exceeds their radius (dashed). For a sphere C1(s) ∝ s and thus ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) 1/l1 = 9/8 = 1.125. 1/l1 = 9/8 = 1.125. | ||
From the skeleton analysis we know the total length of filaments Ltotal as well as the mean filament diameter df. Assuming cylindrical filaments where chains are densely packed with cross sectional area fraction ϕ (with ϕ = π/4 for the 100-plane of fcc packing), filaments contain on average c = 4ϕ(df/σ)2 different chains within each cross-section, with σ an effective bead diameter. Therefore, the total number of chains can be estimated by Nc ≈ cLtotal/L1 where L1 = (N − 1)b the contour length of a single chain. The simulations confirm that this ratio is indeed constant, independent of κ. For simplicity of the argument, let us approximate the network structure as a cubic grid with mesh size equal to the mean pore radius rpore. In this case, the total filament length is given by Ltotal ≈ 3V/r2pore, rather close to Ltotal ≈ 2V/r2pore found in the simulations. Inserting into the above relation we find that filament diameter and mean pore size are proportional to each other,
| df = m1rpore, | (31) |
In a similar spirit, we can estimate the pair energy per particle from interactions within filaments as
 | (32) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) denotes the average coordination number within a filament. For the bending energy per bond, ea, we assume filaments are approximately straight and bent only at the junctions with an average angle corresponding to 〈cos
denotes the average coordination number within a filament. For the bending energy per bond, ea, we assume filaments are approximately straight and bent only at the junctions with an average angle corresponding to 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb〉. Estimating the number of junctions from the number of filaments E = Ltotal/Lf we find
θb〉. Estimating the number of junctions from the number of filaments E = Ltotal/Lf we find | (33) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p accounts for the bending energy of an individual chain in terms of the effective persistence length
p accounts for the bending energy of an individual chain in terms of the effective persistence length ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) p introduced in Section 5.2. Thus, we find that the mean bending energy varies linearly with the pair energy,
p introduced in Section 5.2. Thus, we find that the mean bending energy varies linearly with the pair energy,| ea ≈ ea,1 + m2epair | (34) |
 | (35) |
![[z with combining macron]](https://www.rsc.org/images/entities/i_char_007a_0304.gif) and average bending angle between filaments 〈cos
and average bending angle between filaments 〈cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θb〉 to be approximately constant for late stages of coarsening, eqn (35) suggests that the ratio of pair and bend energy is dictated by the dimensionless parameter (Lf/b)(Ecoh/κ). Note that a similar parameter was found to govern two-dimensional network structures formed by attractive semiflexible chains.43 The approximate linear relation (34) between pair and bend energy is in agreement with our observations in Fig. 4(d).
θb〉 to be approximately constant for late stages of coarsening, eqn (35) suggests that the ratio of pair and bend energy is dictated by the dimensionless parameter (Lf/b)(Ecoh/κ). Note that a similar parameter was found to govern two-dimensional network structures formed by attractive semiflexible chains.43 The approximate linear relation (34) between pair and bend energy is in agreement with our observations in Fig. 4(d).
Author contributions
C. L.: conceptualization, methodology, software, formal analysis, validation, movies, Fig. 11, 12, 16 and Fig. S2, S3 (ESI†), writing – review & editing; P. I.: conceptualization, formal analysis, validation, writing original draft, writing – review & editing; M. K.: conceptualization, methodology, software, formal analysis, resources, remaining figures, writing – review & editing.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
P. I. was supported by EPSRC via grant EP/X014738/1 and gratefully acknowledges hospitality of ETH Zürich where part of this research was undertaken.Notes and references
- M. Usuelli, Y. Cao, M. Bagnani, S. Handschin, G. Nystrom and R. Mezzenga, Probing the structure of filamentous nonergodic gels by dynamic light scattering, Macromolecules, 2020, 53, 5950–5956 CrossRef.
- J. Schnauß, T. Händler and J. Käs, Semiflexible Biopolymers in Bundled Arrangements, Polymers, 2016, 8, 274 CrossRef.
- K. Tohyama and W. G. Miller, Network structure in gels of rod-like polypeptides, Nature, 1981, 289, 813–814 CrossRef PubMed.
- A. D. Augst, H. J. Kong and D. J. Mooney, Alginate Hydrogels as Biomaterials, Macromol. Biosci., 2006, 6, 623–633 CrossRef.
- S. R. Raghavan and J. F. Douglas, The conundrum of gel formation by molecular nanofibers, wormlike micelles, and filamentous proteins: gelation without cross-links?, Soft Matter, 2012, 8, 8539 RSC.
- A. S. G. Van Oosten, M. Vahabi, A. J. Licup, A. Sharma, P. A. Galie, F. C. MacKintosh and P. A. Janmey, Uncoupling shear and uniaxial elastic moduli of semiflexible biopolymer networks: compression-softening and stretch-stiffening, Sci. Rep., 2016, 6, 19270 CrossRef.
- M. Arcari, R. Axelrod, J. Adamcik, S. Handschin, A. Sánchez-Ferrer, R. Mezzenga and G. Nyström, Structure–property relationships of cellulose nanofibril hydro- and aerogels and their building blocks, Nanoscale, 2020, 12, 11638–11646 RSC.
- R. C. Picu, Mechanics of random fiber networks–a review, Soft Matter, 2011, 7, 6768 RSC.
- F. Meng and E. Terentjev, Theory of Semiflexible Filaments and Networks, Polymers, 2017, 9, 52 CrossRef PubMed.
- A. G. Zilman and S. A. Safran, Thermodynamics and structure of self-assembled networks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2002, 66, 051107 CrossRef PubMed.
- M. L. Coughlin, L. Liberman, S. P. Ertem, J. Edmund, F. S. Bates and T. P. Lodge, Methyl cellulose solutions and gels: fibril formation and gelation properties, Prog. Polym. Sci., 2021, 112, 101324 CrossRef.
- M. Tateno and H. Tanaka, Power-law coarsening in network-forming phase separation governed by mechanical relaxation, Nat. Commun., 2021, 12, 912 CrossRef PubMed.
- J. Yuan, M. Tateno and H. Tanaka, Mechanical slowing down of network-forming phase separation of polymer solutions, ACS Nano, 2023, 17, 18025–18036 CrossRef PubMed.
- V. Padmanabhan and S. K. Kumar, Gelation in semiflexible polymers, J. Chem. Phys., 2011, 134, 174902 CrossRef PubMed.
- F. Vargas-Lara and J. Douglas, Fiber Network Formation in Semi-Flexible Polymer Solutions: An Exploratory Computational Study, Gels, 2018, 4, 27 CrossRef PubMed.
- N. Schupper, Y. Rabin and M. Rosenbluh, Multiple Stages in the Aging of a Physical Polymer Gel, Macromolecules, 2008, 41, 3983–3994 CrossRef.
- P. Chaudhuri and L. Berthier, Ultra-long-range dynamic correlations in a microscopic model for aging gels, Phys. Rev. E, 2017, 95, 060601 CrossRef PubMed.
- M. Manno, D. Giacomazza, J. Newman, V. Martorana and P. L. San Biagio, Amyloid Gels: Precocious Appearance of Elastic Properties during the Formation of an Insulin Fibrillar Network, Langmuir, 2010, 26, 1424–1426 CrossRef PubMed.
- R. Pastore, C. Siviello and D. Larobina, Elastic and Dynamic Heterogeneity in Aging Alginate Gels, Polymers, 2021, 13, 3618 CrossRef PubMed.
- C. P. Broedersz and F. C. MacKintosh, Modeling semiflexible polymer networks, Rev. Mod. Phys., 2014, 86, 995–1036 CrossRef CAS.
- J. R. Lott, J. W. McAllister, M. Wasbrough, R. L. Sammler, F. S. Bates and T. P. Lodge, Fibrillar Structure in Aqueous Methylcellulose Solutions and Gels, Macromolecules, 2013, 46, 9760–9771 CrossRef CAS.
- S. Morozova, P. W. Schmidt, F. S. Bates and T. P. Lodge, Effect of Poly(ethylene glycol) Grafting Density on Methylcellulose Fibril Formation, Macromolecules, 2018, 51, 9413–9421 CrossRef CAS.
- W. Huang, R. Ramesh, P. K. Jha and R. G. Larson, A Systematic Coarse-Grained Model for Methylcellulose Polymers: Spontaneous Ring Formation at Elevated Temperature, Macromolecules, 2016, 49, 1490–1503 CrossRef CAS.
- Z. Wu, A. M. Collins and A. Jayaraman, Understanding Self-Assembly and Molecular Packing in Methylcellulose Aqueous Solutions Using Multiscale Modeling and Simulations, Biomacromolecules, 2024, 25, 1682–1695 CrossRef CAS.
- P. W. Schmidt, S. Morozova, P. M. Owens, R. Adden, Y. Li, F. S. Bates and T. P. Lodge, Molecular Weight Dependence of Methylcellulose Fibrillar Networks, Macromolecules, 2018, 51, 7767–7775 CrossRef CAS.
- P. W. Schmidt, S. Morozova, S. P. Ertem, M. L. Coughlin, I. Davidovich, Y. Talmon, T. M. Reineke, F. S. Bates and T. P. Lodge, Internal Structure of Methylcellulose Fibrils, Macromolecules, 2020, 53, 398–405 CrossRef CAS.
- C. L. P. Oliveira, M. A. Behrens, J. S. Pedersen, K. Erlacher, D. Otzen and J. S. Pedersen, A SAXS study of glucagon fibrillation, J. Mol. Biol., 2009, 387, 147–161 CrossRef CAS PubMed.
- J. S. Pedersen and P. Schurtenberger, Scattering functions of semiflexible polymers with and without excluded volume effects, Macromolecules, 1996, 29, 7602–7612 CrossRef CAS.
- X. Bu and X. Zhang, Scattering and Gaussian Fluctuation Theory for Semiflexible Polymers, Polymers, 2016, 8, 301 CrossRef PubMed.
- L. Jowkarderis and T. G. M. Van De Ven, Mesh size analysis of cellulose nanofibril hydrogels using solute exclusion and PFG-NMR spectroscopy, Soft Matter, 2015, 11, 9201–9210 RSC.
- V. Martorana, S. Raccosta, D. Giacomazza, L. A. Ditta, R. Noto, P. L. San Biagio and M. Manno, Amyloid jams: Mechanical and dynamical properties of an amyloid fibrillar network, Biophys. Chem., 2019, 253, 106231 CrossRef.
- A. Rao, H. Yao and B. D. Olsen, Bridging dynamic regimes of segmental relaxation and center-of-mass diffusion in associative protein hydrogels, Phys. Rev. Res., 2020, 2, 043369 CrossRef.
- A. Y. Mehandzhiyski and I. Zozoulenko, A Review of Cellulose Coarse-Grained Models and Their Applications, Polysaccharides, 2021, 2, 257–270 CrossRef.
- B. Strodel, Amyloid aggregation simulations: challenges, advances and perspectives, Curr. Opin. Struct. Biol., 2021, 67, 145–152 CrossRef.
- K. Kremer and G. S. Grest, Dynamics of entangled linear polymer melts – A molecular dynamics simulation, J. Chem. Phys., 1990, 92, 5057–5086 CrossRef.
- M. Kröger and A. Ben-Shaul, On the presence of loops in linear self-assembling systems, Cah. Rheol., 1997, 16, 1–6 Search PubMed.
- M. Kröger, Micro/mesoscopic approaches to the ring formation in linear wormlike micellar systems, Macromol. Symp., 1998, 133, 101–112 CrossRef.
- R. Faller, A. Kolb and F. Müller-Plathe, Local chain ordering inamorphous polymer melts: influence of chain stiffness, Phys. Chem. Chem. Phys., 1999, 1, 2071 RSC.
- O. Peleg, M. Kröger, I. Hecht and Y. Rabin, Filamentous networks in phase-separating two-dimensional gels, Europhys. Lett., 2007, 77, 58007 CrossRef.
- J. Midya, S. A. Egorov, K. Binder and A. Nikoubashman, Phase behavior of flexible and semiflexible polymers in solvents of varying quality, J. Chem. Phys., 2019, 151, 034902 CrossRef PubMed.
- J. Zierenberg, M. Marenz and W. Janke, Dilute Semiflexible Polymers with Attraction: Collapse, Folding and Aggregation, Polymers, 2016, 8, 333 CrossRef.
- T. Arcangeli, T. Skrbic, S. Azote, D. Marcato, A. Rosa, J. R. Banavar, R. Piazza, A. Maritan and A. Giacometti, Phase Behavior and Self-Assembly of Semiflexible Polymers in Poor-Solvent Solutions, Macromolecules, 2024, 57, 8940–8955 Search PubMed.
- R. C. Picu and A. Sengab, Structural evolution and stability of non-crosslinked fiber networks with inter-fiber adhesion, Soft Matter, 2018, 14, 2254–2266 RSC.
- Y. Zhang, E. P. DeBenedictis and S. Keten, Cohesive and adhesive properties of crosslinked semiflexible biopolymer networks, Soft Matter, 2019, 15, 3807–3816 RSC.
- E. P. DeBenedictis, Y. Zhang and S. Keten, Structure and Mechanics of Bundled Semiflexible Polymer Networks, Macromolecules, 2020, 53, 6123–6134 CrossRef.
- A. Jüngel, Polymer Chains and Networks: Statistical Foundations and Computer Simulations, Oxford University Press, UK, 2005 Search PubMed.
- R. D. Groot, Mesoscale simulation of semiflexible chains. II. Evolution dynamics and stability of fiber bundle networks, J. Chem. Phys., 2013, 138, 224904 CrossRef PubMed.
- P. N. Depta, P. Gurikov, B. Schroeter, A. Forgács, J. Kalmár, G. Paul, L. Marchese, S. Heinrich and M. Dosta, DEM-Based Approach for the Modeling of Gelation and Its Application to Alginate, J. Chem. Inf. Model., 2022, 62, 49–70 CrossRef PubMed.
- R. Bandyopadhyay, D. Liang, J. L. Harden and R. L. Leheny, Slow dynamics, aging, and glassy rheology in soft and living matter, Solid State Commun., 2006, 139, 589–598 CrossRef.
- S. C. Volpe, D. Leporini and F. Puosi, Structure and Mechanical Properties of a Porous Polymer Material via Molecular Dynamics Simulations, Polymers, 2023, 15, 358 CrossRef PubMed.
- S. Plimpton and B. Hendrickson, A new parallel method for molecular dynamics simulation of macromolecular systems, J. Comput. Chem., 1996, 17, 326–337 CrossRef.
- H. R. Warner, Kinetic theory and rheology of dilute suspensions of finitely extendible dumbbells, Ind. Eng. Chem. Fundam., 1972, 11, 379–387 CrossRef.
- M. Kröger, Simple, admissible, and accurate approximants of the inverse Langevin and Brillouin functions, relevant for strong polymer deformations and flows, J. Non-Newt. Fluid Mech., 2015, 223, 77–87 CrossRef.
- O. Weismantel, A. A. Galata, M. Sadeghi, A. Kröger and M. Kröger, Efficient generation of self-avoiding, semiflexible rotational isomeric chain ensembles in bulk, in confined geometries, and on surfaces, Comput. Phys. Commun., 2022, 270, 108176 CrossRef.
- Y. Xu, Y. Hamada and T. Taniguchi, Multiscale simulations for polymer melt spinning process using Kremer–Grest CG model and continuous fluid mechanics model, J. Non-Newt. Fluid Mech., 2024, 325, 105195 CrossRef.
- O. Lieleg, J. Kayser, G. Brambilla, L. Cipelletti and A. R. Bausch, Slow dynamics and internal stress relaxation in bundled cytoskeletal networks, Nat. Mater., 2011, 10, 236–242 CrossRef PubMed.
- V. Testard, L. Berthier and W. Kob, Intermittent dynamics and logarithmic domain growth during the spinodal decomposition of a glass-forming liquid, J. Chem. Phys., 2014, 140, 164502 CrossRef PubMed.
- Y. Wang, M. Tateno and H. Tanaka, Distinct elastic properties and their origins in glasses and gels, Nat. Phys., 2024, 20, 1171–1179 Search PubMed.
- S. Ciccariello and J. Brumberger, On the Porod law, J. Appl. Crystallogr., 1988, 21, 117 CrossRef.
- S. Agrawal, S. Galmarini and M. Kröger, Energy formulation for infinite structures: order parameter for percolation, critical bonds and power-law scaling of contact-based transport, Phys. Rev. Lett., 2024, 132, 196101 CrossRef.
- L. D. Gelb and K. Gubbins, Pore Size Distributions in Porous Glasses: A Computer Simulation Study, Langmuir, 1999, 15, 305–308 CrossRef.
- Y. Masubuchi, Phantom chain simulations for fracture of end-linking networks, Polymer, 2024, 297, 126880 CrossRef.
- S. Torquato, B. Lu and J. Rubinstein, Nearest-neighbor distribution functions in many-body systems, Phys. Rev. A: At., Mol., Opt. Phys., 1990, 41, 2059 CrossRef.
- M. Kröger, S. Agrawal and S. Galmarini, Generalized geometric pore size distribution code GPSD-3D for periodic systems composed of monodisperse spheres, Comput. Phys. Commun., 2024, 301, 109212 CrossRef.
- W. Gille, Particle and particle systems characterization: small-angle scattering (SAS) applications, CRC Press, 2013 Search PubMed.
- L. D. Gelb and K. Gubbins, Characterization of porous glasses: simulation models, adsorption isotherms, and the Brunauer–Emmett–Teller analysis method, Langmuir, 1998, 14, 2097–2111 CrossRef.
- G. Ruben, Intraneuronal Neurofibrillary Tangles Isolated from AlzheimerDisease Affected Brains Visualized by Vertical Platinum-Carbon Replication for TEM, Microsc. Microanal., 1997, 3, 47–48 CrossRef.
- M. Usuelli, T. Germerdonk, Y. Cao, M. Peydayesh, M. Bagnani, S. Handschin, G. Nyström and R. Mezzenga, Polysaccharide-reinforced amyloid fibril hydrogels and aerogels, Nanoscale, 2021, 13, 12534–12545 RSC.
- A. Stukowski, Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- Z. W. Lai, G. F. Mazenko and O. T. Valls, Classes for growth kinetics problems at low temperatures, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 9481–9494 CrossRef PubMed.
- A. Lubelski, I. M. Sokolov and J. Klafter, Nonergodicity mimics inhomogeneity in single particle tracking, Phys. Rev. Lett., 2008, 100, 250602 CrossRef PubMed.
- A. Nikoubashman, A. Milchev and K. Binder, Dynamics of single semiflexible polymers in dilute solution, J. Chem. Phys., 2016, 145, 234903 CrossRef PubMed.
- P. Lang and E. Frey, Disentangling entanglements in biopolymer solutions, Nat. Commun., 2018, 9, 494 CrossRef PubMed.
- C. Heussinger, F. Schüller and E. Frey, Statics and dynamics of the wormlike bundle model, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 81, 021904 CrossRef PubMed.
- W.-S. Xu, J. F. Douglas and K. F. Freed, Influence of Cohesive Energy on Relaxation in a Model Glass-Forming Polymer Melt, Macromolecules, 2016, 49, 8355–8370 CrossRef.
- S. Roldán-Vargas, L. Rovigatti and F. Sciortino, Connectivity, dynamics, and structure in a tetrahedral network liquid, Soft Matter, 2017, 13, 514–530 RSC.
- H. T. Nguyen and R. S. Hoy, Effect of chain stiffness and temperature on the dynamics and microstructure of crystallizable bead-spring polymer melts, Phys. Rev. E, 2016, 94, 052502 CrossRef PubMed.
- P. Chaudhuri, P. I. Hurtado, L. Berthier and W. Kob, Relaxation dynamics in a transient network fluid with competing gel and glass phases, J. Chem. Phys., 2015, 142, 174503 CrossRef PubMed.
- W. Kob and J.-L. Barrat, Fluctuations, response and aging dynamics in a simple glass-forming liquid out of equilibrium, Eur. Phys. J. B, 2000, 13, 319–333 CrossRef CAS.
- W. Kob and J.-L. Barrat, Aging Effects in a Lennard-Jones Glass, Phys. Rev. Lett., 1997, 78, 4581–4584 CrossRef CAS.
- F. Mainardi, On some properties of the Mittag-Leffler function Eα(−tα), Discr. Contin. Dyn. Syst. B, 2013, 19, 2267–2278 Search PubMed.
- K. Kroy and E. Frey, Dynamic scattering from solutions of semiflexible polymers, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1997, 55, 3092–3101 CrossRef.
- J. Higgins, H. Benot and H. Benot, Polymers and Neutron Scattering, Clarendon Press, New York, 1996 Search PubMed.
- J. des Cloizeaux, Form Factor of an Infinite Kratky-Porod Chain, Macromolecules, 1973, 6, 403–407 CrossRef.
- Y. Nakamura and T. Norisuye, Scattering function for wormlike chains with finite thickness, J. Polym. Sci., Part B:Polym. Phys., 2004, 42, 1398–1407 CrossRef.
- A. J. Spakowitz and Z.-G. Wang, Exact Results for a Semiflexible Polymer Chain in an Aligning Field, Macromolecules, 2004, 37, 5814–5823 CrossRef.
- A. J. Spakowitz, PhD thesis, California Institute of Technology, 2005 Search PubMed.
- N. Becker, A. Rosa and R. Everaers, The radial distribution function of worm-like chains, Eur. Phys. J. E:Soft Matter Biol. Phys., 2010, 32, 53–69 CrossRef PubMed.
- O. Kratky and G. Porod, Röntgenuntersuchung gelöster fadenmoleküle, Recl. Trav. Chim. Pays-Bas, 1949, 68, 1106–1122 CrossRef.
- W. Van Megen, T. C. Mortensen, S. R. Williams and J. Müller, Measurement of the self-intermediate scattering function of suspensions of hard spherical particles near the glass transition, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1998, 58, 6073–6085 CrossRef.
- K. Górska, A. Horzela and K. A. Penson, Non-Debye Relaxations: The Ups and Downs of the Stretched Exponential vs. Mittag-Lefflers Matchings, Fract. Fractional, 2021, 5, 265 CrossRef.
- M. Gimperlein and M. Schmiedeberg, Structural and dynamical properties of dilute gel networks in colloid–polymer mixtures, J. Chem. Phys., 2021, 154, 244903 CrossRef PubMed.
- P. Kollmannsberger, M. Kerschnitzki, F. Repp, W. Wagermaier, R. Weinkamer and P. Fratzl, The small world of osteocytes: connectomics of the lacuno-canalicular network in bone, New J. Phys., 2017, 19, 073019 CrossRef.
- K. Hirata and T. Araki, Formation dynamics of branching structure in the slippery DLCA model, J. Chem. Phys., 2024, 160, 234901 CrossRef PubMed.
- R. J. Trudeau, Dots and Lines, Kent State University Press, United States, 1976 Search PubMed.
- C. Berge, Cyclomatic number, The Theory of Graphs, Courier Dover Publications, 2001, pp. 27–30 Search PubMed.
- M. M. Tomadakis and T. J. Robertson, Pore size distribution, survival probability, and relaxation time in random and ordered arrays of fibers, J. Chem. Phys., 2003, 119, 1741–1749 CrossRef.
- A. E. Scheidegger, The Physics of Flow Through Porous Media, University of Toronto Press, Toronto, Canada, 1957, p. 7 Search PubMed.
- Y.-S. Liu, J. Yi, H. Zhang, G.-Q. Zheng and J.-C. Paul, Surface area estimation of digitized 3D objects using quasi-Monte Carlo methods, Pattern Recogn., 2010, 43, 3900–3909 CrossRef.
- M. Abramowitz and I. A. Stegun, Handbook of Mathematical Functions, Dover Publ., New York, 1970 Search PubMed.
- P. Levitz and D. Tchoubar, Disordered porous solids: from chord distributions to small angle scattering, J. Phys. I, 1992, 2, 771–790 CrossRef.
- C. J. Gommes, Y. Jiao, A. P. Roberts and D. Jeulin, Chord-length distributions cannot generally be obtained from small-angle scattering, J. Appl. Crystallogr., 2020, 53, 127–132 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Displacements, aging and ultra-slow coarsening, end-to-end vector correlation, Torquato's pore size distribution, intermediate scattering function, additional snapshots, movies, Github repository. See DOI: https://doi.org/10.1039/d4sm01479k |
| This journal is © The Royal Society of Chemistry 2025 |