Scalability of a graph neural network in accurate prediction of frictional contact networks in suspensions

Abstract

Dense suspensions often exhibit shear thickening, characterized by a dramatic increase in viscosity under large external forcing. This behavior has recently been linked to the formation of a system-spanning frictional contact network (FCN), which contributes to increased resistance during deformation. However, identifying these frictional contacts poses experimental challenges and is computationally expensive. This study introduces a graph neural network (GNN) model designed to accurately predict FCNs by two dimensional simulations of dense shear thickening suspensions. The results demonstrate the robustness and scalability of the GNN model across various stress levels (σ), packing fractions (ϕ), system sizes, particle size ratios (Δ), and amounts of smaller particles. The model is further able to predict both the occurrence and structure of a FCN. The presented model is accurate and interpolates and extrapolates to conditions far from its control parameters. This machine learning approach provides an accurate, lower cost, and faster predictions of suspension properties compared to conventional methods, while it is trained using only small systems. Ultimately, the findings in this study pave the way for predicting frictional contact networks in real-life large-scale polydisperse suspensions, for which theoretical models are largely limited owing to computational challenges.

---

1 Introduction

Dense particulate suspensions are ubiquitous in natural, human health, and industrial settings, with examples ranging from mud to blood to paint and cement.^1–4 Under external deformation, they exhibit diverse non-Newtonian complex rheological behaviors, such as yielding, normal stress differences, shear-thinning, shear-thickening, and jamming.^5–7 Shear-thickening (ST) is a non-linear phenomenon where viscosity η increases continuously (CST) or discontinuously (DST) with increasing shear rate [small gamma, Greek, dot above] at a given volume fraction ϕ.⁸ A vast body of research has linked non-Newtonian rheology in dense suspensions to constraints on the relative motion that stabilizes the force and contact network under applied deformation.^5,9–18 As such, many recent studies have used network science techniques to characterize and analyze the properties of these networks in suspensions^{14,15,19–24} as well as in colloidal gels^25–29 and correlate them with the resultant rheology. Historically, the mesoscale network features have been linked to the emergence of rigidity,³⁰ sound propagation,³¹ and non-locality³² for both frictionless and frictional particle packings in dry granular materials. Therefore, accurate and easy identification of contact networks in amorphous materials, specifically in flowing dense suspensions, is highly beneficial for understanding and developing a statistical physics framework for rheological responses.

However, identifying frictional contact networks (FCNs) in most particulate suspensions remains challenging owing to the limitations of the experimental methods and the complex nature of particulate systems. State-of-the-art experimental efforts are limited by the protocol to freeze the sheared microstructure, along with the cost and toxicity of the chemicals used to generate a model suspension system.^12,29,33 These frictional contacts are readily accessible in discrete particle simulations; however, traditional methods remain computationally expensive, making large system sizes computationally intractable, despite recent advances in computational power. The two fundamental questions that remain unanswered are: (i) how can frictional contacts under applied stress be predicted, i.e., is it possible to predict which particles will be in contact? (ii) Can the structure of the frictional contact network for various solid concentrations, system sizes, particle size dispersities, and applied stresses be predicted?

Recently, a more promising avenue has been the use of machine-learning (ML) techniques.^34–42 In soft matter systems, ML has been used to predict wall penetration by particles in coarse-grained simulations using the random forest method,⁴³ prediction of drag forces,⁴⁴ particle stress development using the physics-informed neural network,⁴⁵ and detection of hidden correlation in particle size distribution and mechanical behavior.⁴⁶ Among the diverse ML techniques, graph neural networks (GNNs) have exhibited superior performance compared to traditional methods, mainly owing to their more expressive and adeptness in handling unstructured data, making them an ideal candidate for predicting the frictional contact network. Traditional methods such as graph-theoretical approaches or force/distance criteria rely on predefined rules to identify particle contacts and are unable to capture the underlying nonlinear and multi-scale interactions. By contrast, the GNN learns these relationships directly from the data, capturing hidden features and complex patterns without manual thresholds or rules. This adaptability makes GNNs highly effective for modeling complex systems with interactions that are difficult to parametrize. Most studies on particulate suspensions have focused only on the dilute limit,^37,38 not of interest here. In the dense limit, recently Mandal et al.³⁴ employed a GNN in dry granular matter, demonstrating the network prediction in both frictionless and frictional materials from the undeformed structure. However, the simulations were performed for relatively high volume fractions close to or above jamming, which is not feasible for rigid particles, and when tasked with an extrapolation setting, the accuracy drops sharply.

This study addresses the previously mentioned challenges in predicting the structure of FCNs in dense suspensions only with the knowledge of the relative distance between particles by employing a robust GNN approach to a well-established simulation approach for dense suspensions.^9,10,47–51 By comparing the predictions from the ML technique with the simulation results, it is demonstrated that the GNN model can accurately predict the frictional contacts under applied stress. In addition, the aforementioned capabilities hold for many values of applied stress σ, system size N, and particle sizes, even when the machine has not seen these conditions. Finally, this work can help make meaningful predictions about suspension properties for computationally and experimentally challenging cases (large system sizes, bidisperse packings, etc.) while being trained on less challenging conditions within reasonable computational cost and time.

2 Methodology

Simulating dense suspensions

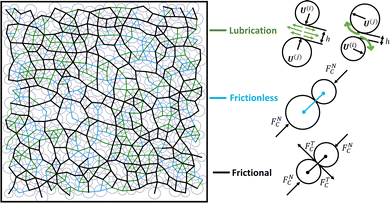
Although the real-world dense suspensions are three-dimensional, related prior works have shown the flow behavior for 2D and 3D to be similar if the volume fraction ϕ is appropriately scaled.^20,22 Thus, two-dimensional simulations (a monolayer of spheres) are performed for clarity, simplicity, computational efficiency, and as a first demonstration of the application of the GNN to predict the FCN. The simulation scheme (LF-DEM) integrates two modeling approaches: lubrication flow (LF) and the discrete element DEM method from dry granular materials.^5,9,10,52 The particle motion is considered to be inertialess, that is, particles obey the overdamped equation of motion

0 = F_H(X,U) + F_C(X), (1)

where X and U refer to the particle position and velocities, respectively. Here, F_H, F_C denote hydrodynamic and contact forces, respectively. The hydrodynamic force includes one body Stokes drag and two body lubrication forces. The lubrication force is regularized allowing the particles to make contact as the overlap (δ^(i,j) = a_i + a_j − |r_i − r_j|) becomes positive.^10,53 Here, a_i and a_j refer to particle radii, and r_i and r_j represent the position vectors of the center of particles i and j, respectively. The contact forces include both normal and tangential frictional forces, i.e., F_C = F^N_C + F^T_C. The contact force is modeled using traditional Cundall & Strack⁵⁴ and following the algorithm described by Luding.⁵⁵ We employ linear springs in normal k_n and tangential k_t directions to model contacts between particles, which are tuned such that the maximum scaled particle overlap does not exceed 3% and the rigid particle approximation is satisfied.⁵⁶ In our simulations, we do not employ the dashpot; instead, the hydrodynamic resistance provides energy dissipation.⁴⁷ The tangential component of the contact force satisfies Coulomb's friction law |F^t_C ≤ μ|Fⁿ_C| with μ = 0.5 being the static friction coefficient. The critical load model (CLM) is used to introduce rate dependence, where the normal force F^N_C ≥ F₀ is needed to activate interparticle friction, giving a characteristic stress scale σ₀ = F₀/a². This implies that a solely negative gap (or positive overlap δ) between particles is not representative of the frictional contact between them. A series of stress-controlled simple shear flows are simulated for N = 400 to 5000 non-Brownian bidisperse particles with Lees–Edwards periodic boundary condition in a unit cell with particle size ratio Δ = R_L/R_S ∈ [1.4, 6] and different volumetric mixing ratios α = V_S/(V_L + V_S) ∈ [0.1, 0.9]. Here, R_S (R_L) and V_S (V_L) are the radii and volume of small (and large) particles, respectively. This work focuses on the frictional contact network, which is the dominant contribution to viscosity at high packing fractions and is the primary driver for DST and SJ.^9,10,52,57Fig. 1 represents a typical contact network resulting from the simulations. The colors represent different types of interactions with green, blue, and red lines representing lubrication, frictionless, and frictional forces, respectively.

Fig. 1 Contact network inferring all forces. Snapshot of the contact network for ϕ = 0.76 and σ/σ₀ = 1. Green, blue, and black lines depict lubrication, frictionless, and frictional interactions, respectively.

Machine learning methodology

In this work, the concept is adapted from Li et al., which made very deep training of graphs based on the graph convolutional neural network (GCN) possible by incorporating residual and dense connections, along with the use of dilated convolutions to remedy the vanishing gradient problem.^58,59 Their technique called deep graph convolutional neural network (DeepGCN) is used, and then the models are optimized by training them at different hyperparameters. Compared to the traditional GCN, this deep learning method provides more reliable and deeper training and an interpretable representation of large graphs and node property prediction tasks in dense particulate systems.⁵⁸ This node classification approach identifies particles in frictional contacts that participate in FCNs.

Fig. 2 illustrates the process and architecture of the DeepGCN. Initially, configurations are generated through our simulation scheme, which contains details regarding all the particles involved. These data include information that relates to all the particles irrespective of their participation in the FCN. To train the model, first, the dynamic simulation dataset consisting of all particles is transformed into graphs by treating particles as nodes (h_v and h_u are node features for a specific particle and neighborhood particles, respectively) and drawing edges (e_vu, edge attributes) between them to represent their interactions (both frictionless and frictional). The node features include the particle radius, and the edges representing interactions called edge attributes contain information about the distance between particles (r_ij), x and y components of vector r_ij, and the Sine and Cosine of the angle r_ij makes with the x-axis (flow direction). The DeepGCN model consists of N_l layers that incorporate the residual connections. A node's feature vector is updated in each residual layer through a message-passing process, aggregating information from its neighbors, including nodes and connected edges within the graph. A nonlinear activation function, ReLU, followed by a linear classification function (for node or particle classification), is applied to the output to predict the probability of each particle being a part of the FCN. The detailed equation for DeepGCN is:

Fig. 2 Schematic detailing simulation snapshot and the graph neural network (GNN) for predicting frictional contact networks (FCNs). Initially, necessary snapshots for ML consisting of information of all particles (whether the particles participate in the FCN or not) are driven through LF-DEM simulation technique which then is transformed into a graph comprising its constituent particles and the frictional contact network. These particles and the chain network, analogous to nodes and edges in the graph, undergo processing through residual convolutional layers. The message-passing process is done in these layers, employing an aggregation function to update information across nodes and edges. Subsequently, a non-linear activation function (ReLU) is applied to enhance the model's prediction capabilities, particularly in capturing complex relationships. A linear function is applied to assign each node to a specific class for classification. To mitigate overfitting, regularization techniques such as dropout are employed at the final stage of the model.

Here, h^(l)_v is the updated node feature or the hidden state for node v at layer l, [scr N, script letter N](v) denotes the neighborhood of node v, that is, the set of nodes connected to v, f is a function that takes as input the features of neighboring nodes, i.e., h^(l−1)_v and h^(l−1)_u and their edge features e_uv, concatenating the features and applying a non-linear aggregation function, and h^(l−1)_v is the original node feature that is added to the output of the GCN. More details regarding the mechanism and architecture of DeepGCN are provided in the ESI.†⁶⁰

Fig. 3 illustrates the loss function and accuracy as a function of the epochs during model training. During training, the model's parameters are adjusted iteratively to align the predicted outputs more closely with the actual targets through the loss function (details about binary cross entropy (BCE) are available at https://pytorch.org/docs/master/generated/torch.nn.BCEWithLogitsLoss.html#torch.nn.BCEWithLogitsLosshere). We employed the Adam optimizer with a learning rate of 0.005 to minimize the loss function on the training set. The accuracy is the ratio of correctly classified nodes (particles) to the total number of nodes in the evaluation set. Subsequently, we assess the network's performance on a separate and independent test sets. Our training dataset comprised 320 configurations (80% of our overall dataset), whereas a set of 80 configurations (20% of the dataset) was reserved for testing performance of the model. We stop the training process when the loss value does not improve after 15 epochs by saving the last iteration parameters at which the loss is minimum. Subsequently, we employed 400 previously unseen configurations for validation purposes well beyond the initially seen training conditions. These predictions derived the reported average prediction accuracy of the FCN. In addition to the average accuracy, we measured average precision measure, recall, F1 score, AUC, and specificity, which are presented and discussed in Table S1 in the ESI.†⁶⁰

Fig. 3 An example of prediction accuracy and loss function (binary cross entropy) for training the model. The model is trained at ϕ = 0.80 and σ/σ₀ = 10 with 320 graphs and a set of 80 graphs for testing using the early stop technique that prevents overfitting.

3 Results

Evolution of the frictional contact network under shear stress

Before turning to the results on the accuracy of the model, Fig. 4 shows the evolution of the contact network obtained from the simulations at packing fractions of ϕ = 0.76 and 0.80 with increasing stress σ/σ₀ from left to right. Line segments connect the centers of two contacting particles and are color-coded according to the type of force they experience; we show frictionless contacts (blue line) and frictional (black line). At the lowest stress considered here σ/σ₀ = 0.1, only frictionless contacts (blue bonds) are observed. At higher stresses σ/σ₀ = 5,10, both frictionless (blue) and frictional (black) contacts are observed. Eventually, at the highest stress σ/σ₀ = 100, the suspension is fully frictional (only black lines are present). This visual observation is consistent with the literature¹⁰ and our results on the coordination number (Fig. S1, ESI†). Note that for a given, constant packing fraction ϕ, frictional coordination number Z_μ in a fully frictional state is larger than the frictionless contacts at a low stress, non-thickened state. This suggests that with an increase in stress, as particle contacts become frictional, the suspension rearranges into a distinct microstructure. Hence, it is non-trivial to predict the FCN even knowing particle overlap without the critical load force F₀.

Fig. 4 Development of frictional contacts with increasing shear stress. Snapshots of the contact network for both frictionless (normal force below the critical threshold F₀) shown as blue lines and frictional contacts (normal force above the critical threshold F₀) as black lines. Snapshots corresponding to simulations with σ/σ₀ = 0.1, 5, 10, and 50 (from left to right) are presented for ϕ = 0.76 (top) and ϕ = 0.8 (bottom).

The following describes two striking features of the DeepGCN scheme for predicting frictional contacts: robustness and scalability.

Robustness of the DeepGCN model

First, the DeepGCN method is shown to be highly robust in predicting the frictional contacts in a dynamical system, where the network continuously forms and breaks due to the bulk shearing motion (Fig. 5). N = 400 particles are used at packing fractions ϕ = 0.76,0.78,0.8 with Δ = 1.4 and α = 0.5. The full rheological flowcurves (η_r(ϕ,σ/σ₀)) and the frictional coordination number (Z_μ(ϕ,σ/σ₀)) are presented in Fig. S1 (ESI†).⁶⁰ In short, the suspension undergoes CST for ϕ = 0.76,0.78 and DST into a nearly jammed state for ϕ = 0.8. The presented two-dimensional rheological flowcurves are also compared with the literature results in the ESI.† We show qualitative agreement with previous three-dimensional simulations (Fig. S4, ESI†) and experimental data on the silica colloids (Fig. S5, ESI†), once the packing fraction is properly scaled with respect to ϕ^μ_J.

Fig. 5 Robustness in the prediction of the FCN for a prototypical shear thickening suspension. The GNN models are trained separately on the simulation data set at a fixed stress σ/σ₀ = 10 and at different packing fractions ϕ for N = 400 and bidispersity (Δ,α = 1.4,0.5). (a) Prediction accuracy for the FCN for different values of ϕ,σ/σ₀, with the GNN conditioned at σ/σ₀ = 10 for each ϕ. (b) Frictional coordination number 〈Z_μ〉 as a function of stress for various values of ϕ. For the sake of simplicity, here, only the visualization consisting of particles participating in the FCN are provided where (c) and (d) visualise the training condition with ϕ = 0.76, showing (c) sheared packing at σ/σ₀ = 10 with particles participating in the FCN along with (d) the black lines showing the frictional network. (e) and (f) Predicted configuration at σ/σ₀ = 100 with (e) particles participating in the FCN along with the misclassified particles by the model shown in lattice-patterned blue and (f) the predicted FCN. Misidentified particles are shown in lattice-patterned blue. (g) and (h) Same as (c) and (d) but for ϕ = 0.8 and σ/σ₀ = 10. (i) and (j) The corresponding network based on (g) and (h).

The model is trained at σ/σ₀ = 10 for each ϕ, and predictions are made for other applied stresses. Remarkably, despite the sensitivity of the FCN to both the stress and packing fractions, the model is capable of accurate predictions (>90%) for all values of (σ/σ₀, ϕ) (Fig. 5a). In Fig. 5e, f and i, j, the predictions with numerical simulation results at σ/σ₀ = 100 are visualized where the models are trained at σ/σ₀ = 10 (Fig. 5c, d and g, h) for the corresponding ϕ = 0.76 and 0.8, respectively. For simplicity, only the particles that have at least one frictional contact (Fig. 5c, e, g and i) together with their FCN (Fig. 5d, f, h and j) are shown, and the configurations do not depict all particles (N = 400). The predictions depict ground truth for direct simulations, where the misclassified particles by the model are highlighted in red. Besides that, larger (smaller) particles are represented in darker (lighter) colors. As can be seen, only a few particles evade the predictions of the model. Especially for ϕ = 0.8, the training stress (σ/σ₀ = 10) is in an unjammed flowing state, while the prediction stress (σ/σ₀ = 100) is nearly in the shear-jammed state, yet an accuracy of 95% is achieved, highlighting the strength of the model. This accuracy at ϕ = 0.80 is expected since the model has “seen” the complex structure; hence, it can accurately predict the complex features. Fig. 5b shows Z_μ for the values of σ/σ₀ of interest here (results for all stress values in ref. 60 (Fig. S1, ESI†)). With increasing stress, the FCN becomes increasingly interconnected, spanning both compressive and tensile directions (Fig. 3). The decrease in prediction accuracy at higher stresses suggests the difficulty of predicting the FCN, highlighting the increase in complexity at higher stresses. The results of these rigorous checks demonstrate that the model maintains a highly accurate performance, with extrapolated predictions for unseen conditions, without prior knowledge of interparticle forces, and with only information on relative distance solely at a fixed stress value.

A natural question arises regarding the choice of σ/σ₀ = 10 to train the model on. Fig. 6 illustrates the test accuracy results when the model is trained at different values of σ/σ₀ for a fixed ϕ = 0.76. Although the predictions of the model trained at σ/σ₀ = 5 are unsatisfactory, the predictions improve significantly when the model is trained at σ/σ₀ = 10 and 50. These results align with the fact that the number of frictional contacts increases with increasing stress. Hence, at higher stresses, it is easier for the model to predict whether a given particle is in frictional contact. It is important to note that this is an extrapolation task, which is inherently more challenging for the model, particularly given that the rheological properties of suspensions vary with σ/σ₀ (Fig. S1b, ESI†). To explore the physical rationale behind this observation, Fig. S3 (ESI†) illustrates the evolution of the contact network and the corresponding structure factor with increasing stress. As shown already in Fig. 3 and Fig. S1a (ESI†), the number (or fraction) of frictional contacts begins to saturate (frictionless contacts diminish) in the limit of σ/σ₀ ≥ 50, which implies that the physics is fully dominated by frictional contacts in that regime. Although the evolution trend appears similar, a larger number of contacts (denser FCN) are observed for a higher packing fraction ϕ = 0.8.

Fig. 6 Comparison of prediction accuracy of the GNN when trained at different stresses. Prediction accuracy as a function of σ/σ₀ while the models have been trained separately at ϕ = 0.76 and different fixed σ/σ₀ = 5, 10, and 50.

Experimental and simulation studies have shown that bidispersity significantly affects the rheology and microstructure of dense particulate systems and colloidal gels.^61–66 The dependence of viscosity (η_r(α)) and frictional coordination number (Z_μ(α)) on α are presented in Fig. S2 (ESI†).⁶⁰ Hence, it is tempting to ask whether the presented GNN model can predict the FCN for different values of α for a constant Δ. Fig. 7a demonstrates the robustness of the GNN model in predicting the FCN at various values of α for a fixed size ratio Δ = 1.4 with an accuracy exceeding 98%. Fig. 7b shows an example of the training set consisting of particles in frictional contact, and Fig. 7c shows the corresponding FCN. This visualization shows only particles with at least one frictional contact. Fig. 7d and e show examples for visualization of the model predictions (only particles in contact and the misidentified particles depicted in lattice-patterned blue) for α = 0.1 and 0.9 (on previously unseen configurations) with remarkable accuracies along with their FCN (Fig. 7e and g). Visualizations for all particles, the predicted structure factor of the exact frictional contacts, and the absolute error of the prediction and direct simulation results are analyzed and shown in Fig. S4 (ESI†). This consistent accuracy is achieved (Fig. 7a) for all values of α even though the contact network has a distinct structure (dominated by small or large particles for the two values of α). The accuracy is robust to the choice of the training value of α (0.1, 0.5, or 0.9). This implies that the presented GNN model can predict the FCN for a distinct system despite having information from only a limited number of particles, mostly of one type.

Fig. 7 Robustness in FCN predictions for various volumetric mixing ratios α. All the configurations are generated for ϕ = 0.76, Δ = 1.4, and sheared at fixed stress of σ/σ₀ = 50. The GNN model is trained separately with the configurations consisting of 400 particles at different α = 0.1, 0.5, and 0.9 and can also robustly predict the FCN at other values of α. (a) Test accuracy results, (b) and (c) the configuration on which the training is conditioned with (b) showing sheared packing with particles participating in the FCN where the dark (and light) blue depicts larger (and smaller) particles, and (c) frictional network. (d) and (e) The predictions for α = 0.1: (d) showing the configuration with particles in contact and the misclassified particles in lattice-patterned blue, (e) black lines showing the corresponding FCN. (f) and (g) Same as (d) and (e) but for the configuration with α = 0.9. Note that (b), (d), and (f) only show particles with at least one frictional contact.

Scalability of the DeepGCN model

Next, the scalability of the ML model is demonstrated to make predictions for larger system sizes and complexities, such as different particle size ratios, despite the distinct rheology and microstructure. The relative viscosity η_r and frictional coordination number Z_μ as a function of Δ for suspensions with different particle numbers are shown in Fig. S3 (ESI†).⁶⁰ This ability of the model is tested by training it on a rather small system size (N = 400) at σ/σ₀ = 50 and ϕ = 0.76 (Fig. 7b and c) and then testing the predictions with not only a larger N but also a larger size ratio Δ. Fig. 8 demonstrates the scalability, showing no substantial decrease in accuracy even at 10 times the system size across very different particle size ratios (from 1.4 to 6). Fig. 8b to e depict examples of the predictions of particles participating in the FCN for different systems, with {N,Δ} = {400,4}, {N,Δ} = {800,6}, {N,Δ} = {2000,6}, and {N,Δ} = {5000,5}, respectively, and (f)–(i) display the corresponding frictional chain network for (b)–(e). Here, darker particles represent particles with larger radii, and misclassified particles are highlighted in lattice-patterned blue to show the difference between predictions and ground truth. Interestingly, larger particles are less prone to errors as they can make more contacts than smaller particles, given a larger surface area. The results show that the model can capture the relationship between particles and adapt it to large-scale systems, given only local neighborhood information.

Fig. 8 Scalability in predicting the FCN across different system sizes and varying particle size ratios Δ. All configurations sheared at a constant scaled stress σ/σ₀ = 50, and packing fraction ϕ = 0.76 and volumetric mixing ratio α = 0.5. The model is trained on configurations with N = 400 for Δ = 1.4 (Fig. 7b and c). (b)–(e) The prediction of particles participating in the FCN along with misclassified particles highlighted in lattice-patterned blue at different systems, with (b) {N,Δ} = {400,4}, (c) {N,Δ} = {800,6}, (d) {N,Δ} = {2000,6}, and (e) {N,Δ} = {5000,5}. (f)–(i) The corresponding frictional contact network for (b)–(e).

Before we close, it is important to discuss the role of dimensionality and possible extension to experimental systems. For the sake of simplicity and demonstration of application of the GNN method to frictional contact networks (FCNs) in dense suspensions, we simulated a two-dimensional monolayer of spheres. Our results in predicting the unseen FCNs by the GNN are promising and point towards extending the formalism to three-dimensional systems, given that the only information needed are particle positions, radii of particles and interparticle gaps. Nonetheless, a previous study reported by Gameiro et al.²⁰ had demonstrated that the correlation between frictional network topological features and the bulk rheology is very similar in two- and three-dimensional systems. We also show that the two-dimensional results presented here can qualitatively reproduce the literature results based on three-dimensional simulations and experiments (ESI†). This similarity is primarily because, in the shear thickening suspensions, the structural and kinematic features appear in the velocity and velocity gradient directions with minimal variation across the vorticity direction. Thus, the structural interrogations concerning the velocity and gradient directions are sufficient to describe the main structural/rheological features of the system. This assumption might not hold in some cases in real-world flow, as an example, when orthogonal flows are superposed in the vorticity direction.⁶⁷

4 Concluding remarks

This study demonstrated the application of DeepGNN in predicting the frictional contact network (FCN) structure in dense suspensions by utilizing fixed configurations under simple shear. The obtained DeepGNN model exhibits remarkable generalization capabilities, accurately predicting FCNs across a wide range of unseen configurations, even under conditions significantly different from the original training environment. This highlights its scalability and robustness in predicting the FCN across varying system sizes N, bidispersity (Δ and α), and applied stress σ. This DeepGNN model offers valuable insights into the particle information and frictional contact structure of the simulated suspensions, without the need for explicit knowledge of interparticle interactions.

The presented GNN model is particularly appealing because of the computational expense of tracking system dynamics with many-body interactions and boundary conditions. Its scalability and versatility suggest its potential for predicting various physical and rheological properties in more complex real-world flows of experimental relevance. Although the frictional force chain concept originated in a two-dimensional granular system,⁶⁸ recent experimental efforts have extended to not only three-dimensional granular systems but also to dense suspensions^12,33 as well.

Although the current study focused only on lubrication and frictional interactions, in principle, the model can be extended to incorporate van der Waals, depletion, and electrostatic forces, as well as more complete hydrodynamic interactions. Such models have potential applications in diverse particulate systems such as colloidal gels, polymer composites, foams, and granular materials where network physics is critical towards understanding the bulk response.^25–29 This capability will enable the exploration of large-scale, real-life systems in natural and industrial contexts with reduced computational costs and resources.

Author contributions

Armin Aminimajd: conceptualization (equal); data curation (lead); formal analysis (lead); and writing – original draft (lead). Joao Maia: conceptualization (lead); data curation (equal); formal analysis (equal); and writing – original draft (equal). Abhinendra Singh: conceptualization (lead); data curation (equal); formal analysis (equal); and writing – original draft (lead).

Data availability

Data for this article, including the LF-DEM simulation dataset used for the prediction of FCN employing GNN, are available at OSF home at https://doi.org/10.17605/OSF.IO/E9PYV. Further data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors have no conflicts to disclose.

Acknowledgements

This work used the High-Performance Computing Resource in the Core Facility for Advanced Research Computing at Case Western Reserve University. A. S. acknowledges the Case Western Reserve University for start-up funding. S. Rogers, M. Ramaswamy, V. Sharma, S. Root, and S. Pradeep are acknowledged for their fruitful discussions.

References

1. P. Coussot, Mudflow Rheology and Dynamics, CRC Press, 1997.
2. D. J. Jerolmack and K. E. Daniels, Viewing Earth's surface as a soft-matter landscape, Nat. Rev. Phys., 2019, 1(12), 716–730.
3. G. P. Galdi, R. Rannacher, A. M. Robertson and S. Turek, Hemodynamical flows. Delhi Book Store, 2008, pp. 8–10.
4. J. Benbow and J. Bridgewater, Paste flow and extrusion, Oxford University Press, UK, 1993.
5. J. F. Morris, Shear thickening of concentrated suspensions: Recent developments and relation to other phenomena, Annu. Rev. Fluid Mech., 2020, 52, 121–144.
6. M. M. Denn, J. F. Morris and D. Bonn, Shear thickening in concentrated suspensions of smooth spheres in Newtonian suspending fluids, Soft Matter, 2018, 14(2), 170–184.
7. A. Singh, Hidden hierarchy in the rheology of dense suspensions, MRS Commun., 2023, 13(6), 971–979.
8. J. Mewis and N. J. Wagner, Colloidal Suspension Rheology, Cambridge University Press, 2011.
9. A. Singh, C. Ness, R. Seto, J. J. de Pablo and H. M. Jaeger, Shear Thickening and Jamming of Dense Suspensions: The “Roll” of Friction, Phys. Rev. Lett., 2020, 124, 248005.
10. R. Mari, R. Seto, J. F. Morris and M. M. Denn, Shear thickening, frictionless and frictional rheologies in non-Brownian suspensions, J. Rheol., 2014, 58(6), 1693–1724.
11. A. Boromand, S. Jamali, B. Grove and J. M. Maia, A generalized frictional and hydrodynamic model of the dynamics and structure of dense colloidal suspensions, J. Rheol., 2018, 62(4), 905–918.
12. S. Pradeep, M. Nabizadeh, A. R. Jacob, S. Jamali and L. C. Hsiao, Jamming distance dictates colloidal shear thickening, Phys. Rev. Lett., 2021, 127(15), 158002.
13. O. Sedes, A. Singh and J. F. Morris, Fluctuations at the onset of discontinuous shear thickening in a suspension, J. Rheol., 2020, 64(2), 309–319.
14. O. Sedes, H. A. Makse, B. Chakraborty and J. F. Morris, K-core analysis of shear-thickening suspensions, Phys. Rev. Fluids, 2022, 7(2), 024304.
15. M. van der Naald, A. Singh, T. T. Eid, K. Tang, J. J. de Pablo and H. M. Jaeger, Minimally rigid clusters in dense suspension flow, Nat. Phys., 2024, 1–7.
16. C. Chen, M. van der Naald, A. Singh, N. D. Dolinski, G. L. Jackson and H. M. Jaeger, et al., Leveraging the Polymer Glass Transition to Access Thermally Switchable Shear Jamming Suspensions. ACS Central, Science, 2023, 9(4), 639–647.
17. V. Rathee, A. Monti, M. E. Rosti and A. Q. Shen, Shear thickening behavior in dense repulsive and attractive suspensions of hard spheres, Soft Matter, 2021, 17(35), 8047–8058.
18. A. D’Amico, S. Tu and A. Singh, Topological insights into dense frictional suspension rheology: Third order loops drive discontinuous shear thickening, arXiv, 2025, preprint, arXiv:250102062 DOI:10.48550/arXiv.2501.02062.
19. J. E. Thomas, K. Ramola, A. Singh, R. Mari, J. F. Morris and B. Chakraborty, Microscopic origin of frictional rheology in dense suspensions: correlations in force space, Phys. Rev. Lett., 2018, 121(12), 128002.
20. M. Gameiro, A. Singh, L. Kondic, K. Mischaikow and J. F. Morris, Interaction network analysis in shear thickening suspensions, Phys. Rev. Fluids, 2020, 5(3), 034307.
21. J. E. Thomas, A. Goyal, D. Singh Bedi, A. Singh, E. Del Gado and B. Chakraborty, Investigating the nature of discontinuous shear thickening: Beyond a mean-field description, J. Rheol., 2020, 64(2), 329–341.
22. M. Nabizadeh, A. Singh and S. Jamali, Structure and dynamics of force clusters and networks in shear thickening suspensions, Phys. Rev. Lett., 2022, 129(6), 068001.
23. L. E. Edens, S. Pednekar, J. F. Morris, G. K. Schenter, A. E. Clark and J. Chun, Global topology of contact force networks: Insight into shear thickening suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2019, 99(1), 012607.
24. L. E. Edens, E. G. Alvarado, A. Singh, J. F. Morris, G. K. Schenter and J. Chun, et al., Shear stress dependence of force networks in 3D dense suspensions, Soft Matter, 2021, 17(32), 7476–7486.
25. A. D. Smith, G. J. Donley, E. Del Gado and V. M. Zavala, Topological data analysis for particulate gels, ACS Nano, 2024, 18(42), 28622–28635.
26. A. Gupta, C. Barone, E. Quijano, A. S. Piotrowski-Daspit, J. D. Perera and A. Riccardi, et al., Next generation triplex-forming PNAs for site-specific genome editing of the F508del CFTR mutation, J. Cystic Fibrosis, 2024, 142–148.
27. K. A. Whitaker, Z. Varga, L. C. Hsiao, M. J. Solomon, J. W. Swan and E. M. Furst, Colloidal gel elasticity arises from the packing of locally glassy clusters, Nat. Commun., 2019, 10(1), 2237.
28. S. Bindgen, F. Bossler, J. Allard and E. Koos, Connecting particle clustering and rheology in attractive particle networks, Soft Matter, 2020, 16(36), 8380–8393.
29. M. Nabizadeh, F. Nasirian, X. Li, Y. Saraswat, R. Waheibi and L. C. Hsiao, et al., Network physics of attractive colloidal gels: Resilience, rigidity, and phase diagram, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(3), e2316394121.
30. S. Henkes, D. A. Quint, Y. Fily and J. M. Schwarz, Rigid Cluster Decomposition Reveals Criticality in Frictional Jamming, Phys. Rev. Lett., 2016, 116, 028301.
31. E. T. Owens and K. E. Daniels, Sound propagation and force chains in granular materials, Europhys. Lett., 2011, 94(5), 54005.
32. A. Thomas, Z. Tang, K. E. Daniels and N. Vriend, Force fluctuations at the transition from quasi-static to inertial granular flow, Soft Matter, 2019, 15(42), 8532–8542.
33. S. Pradeep and L. C. Hsiao, Contact criterion for suspensions of smooth and rough colloids, Soft Matter, 2020, 16(21), 4980–4989.
34. R. Mandal, C. Casert and P. Sollich, Robust prediction of force chains in jammed solids using graph neural networks, Nat. Commun., 2022, 13(1), 1–7.
35. Z. Li, X. Li, H. Zhang, D. Huang and L. Zhang, The Prediction of Contact Force Networks in Granular Materials Based On Graph Neural Networks, J. Chem. Phys., 2023, 158, 054905.
36. N. R. Ashwin, Z. Cao, N. Muralidhar, D. Tafti and A. Karpatne, Deep learning methods for predicting fluid forces in dense particle suspensions, Powder Technol., 2022, 401, 117303.
37. A. Rossi, F. Alberini and E. Brunazzi, Identification of suspension state using passive acoustic emission and machine learning in a solid-liquid mixing system, Chem. Eng. Res. Des., 2022, 177, 273–282.
38. P. Binel, A. Jain, A. Jaeggi, D. Biri, A. K. Rajagopalan and A. J. DeMello, et al., Online 3D Characterization of Micrometer-Sized Cuboidal Particles in Suspension, Small Methods, 2023, 7(1), 2201018.
39. K. Galloway, E. Teich, X. Ma, C. Kammer, I. Graham and N. Keim, et al., Relationships between structure, memory and flow in sheared disordered materials, Nat. Phys., 2022, 18(5), 565–570.
40. A. L. Ferguson, Machine learning and data science in soft materials engineering, J. Phys.: Condens. Matter, 2017, 30(4), 043002.
41. E. D. Cubuk, S. S. Schoenholz, J. M. Rieser, B. D. Malone, J. Rottler and D. J. Durian, et al., Identifying structural flow defects in disordered solids using machine-learning methods, Phys. Rev. Lett., 2015, 114(10), 108001.
42. G. Carleo, I. Cirac, K. Cranmer, L. Daudet, M. Schuld and N. Tishby, et al., Machine learning and the physical sciences, Rev. Mod. Phys., 2019, 91(4), 045002.
43. E. I. Barcelos, S. Khani, M. F. Naccache and J. Maia, Supervised learning for accurate mesoscale simulations of suspension flow in wall-bounded geometries, Phys. Fluids, 2022, 34(5) DOI:10.1063/5.0086759.
44. L. He and D. K. Tafti, A supervised machine learning approach for predicting variable drag forces on spherical particles in suspension, Powder Technol., 2019, 345, 379–389.
45. A. A. Howard, J. Dong, R. Patel, M. D’Elia, M. R. Maxey and P. Stinis, Machine learning methods for particle stress development in suspension Poiseuille flows, Rheol. Acta, 2023, 62(10), 507–534.
46. I. Gonzalez Tejada and P. Antolin, Use of machine learning for unraveling hidden correlations between particle size distributions and the mechanical behavior of granular materials, Acta Geotech., 2022, 17(4), 1443–1461.
47. R. Mari, R. Seto, J. F. Morris and M. M. Denn, Nonmonotonic flow curves of shear thickening suspensions, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2015, 91(5), 052302.
48. R. Mari, R. Seto, J. F. Morris and M. M. Denn, Discontinuous shear thickening in Brownian suspensions by dynamic simulation, Proc. Natl. Acad. Sci. U. S. A., 2015, 112(50), 15326–15330.
49. A. Singh, R. Mari, M. M. Denn and J. F. Morris, A constitutive model for simple shear of dense frictional suspensions, J. Rheol., 2018, 62(2), 457–468.
50. A. Singh, S. Pednekar, J. Chun, M. M. Denn and J. F. Morris, From yielding to shear jamming in a cohesive frictional suspension, Phys. Rev. Lett., 2019, 122(9), 098004.
51. A. Singh, G. L. Jackson, M. van der Naald, J. J. de Pablo and H. M. Jaeger, Stress-activated constraints in dense suspension rheology, Phys. Rev. Fluids, 2022, 7(5), 054302.
52. R. Seto, R. Botet, M. Meireles, G. K. Auernhammer and B. Cabane, Compressive consolidation of strongly aggregated particle gels, J. Rheol., 2013, 57(5), 1347–1366.
53. R. C. Ball and J. R. Melrose, Lubrication breakdown in hydrodynamic simulations of concentrated colloids, Adv. Colloid Interface Sci., 1995, 59, 19–30.
54. P. A. Cundall and O. D. L. Strack, A discrete numerical model for granular assemblies, Geotechnique, 1979, 29, 47–65.
55. S. Luding, Cohesive, frictional powders: contact models for tension, Granular Matter, 2008, 10, 235–246.
56. A. Singh, V. Magnanimo, K. Saitoh and S. Luding, The role of gravity or pressure and contact stiffness in granular rheology, New J. Phys., 2015, 17(4), 043028.
57. C. Ness and J. Sun, Shear thickening regimes of dense non-Brownian suspensions, Soft Matter, 2016, 12(3), 914–924.
58. G. Li, C. Xiong, A. K. Thabet and B. Ghanem, DeeperGCN: All You Need to Train Deeper GCNs. CoRR, arXiv, 2020, preprint, arXiv:abs/2006.07739 DOI:10.48550/arXiv.2006.07739.
59. G. Li, M. Muller, A. Thabet and B. Ghanem, Deepgcns: Can gcns go as deep as cnns? in Proceedings of the IEEE/CVF international conference on computer vision, 2019, pp. 9267–9276.
60. See ESI† for details, which includes ref. 44 and 45.
61. B. J. Maranzano and N. J. Wagner, The effects of particle size on reversible shear thickening of concentrated colloidal dispersions, J. Chem. Phys., 2001, 114, 10514–10527.
62. S. Pednekar, J. Chun and J. F. Morris, Bidisperse and polydisperse suspension rheology at large solid fraction, J. Rheol., 2018, 62(2), 513–526.
63. J. C. Petit, N. Kumar, S. Luding and M. Sperl, Additional transition line in jammed asymmetric bidisperse granular packings, Phys. Rev. Lett., 2020, 125(21), 215501.
64. B. M. Guy, C. Ness, M. Hermes, L. J. Sawiak, J. Sun and W. C. Poon, Testing the Wyart-Cates model for non-Brownian shear thickening using bidisperse suspensions, Soft Matter, 2020, 16(1), 229–237.
65. A. Singh, C. Ness, A. K. Sharma, J. J. de Pablo and H. M. Jaeger, Rheology of bidisperse non-Brownian suspensions, Phys. Rev. E, 2024, 110(3), 034901.
66. R. A. Waheibi and L. C. Hsiao, Pairing-specific microstructure in depletion gels of bidisperse colloids, Soft Matter, 2024, 9083–9094.
67. P. Sehgal, M. Ramaswamy, I. Cohen and B. J. Kirby, Using acoustic perturbations to dynamically tune shear thickening in colloidal suspensions, Phys. Rev. Lett., 2019, 123(12), 128001.
68. T. S. Majmudar and R. P. Behringer, Contact force measurements and stress-induced anisotropy in granular materials, Nature, 2005, 435(7045), 1079–1082.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01391c

---