 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The role of substrate mechanics in osmotic biofilm spreading†
Anthony
Pietz
a,
Karin
John
 b and
Uwe
Thiele
b and
Uwe
Thiele
 *ac
*ac
aInstitut für Theoretische Physik, Universität Münster, Wilhelm-Klemm-Str. 9, 48149 Münster, Germany. E-mail: u.thiele@uni-muenster.de
bUniversité Grenoble Alpes, CNRS, LIPhy, 38000 Grenoble, France. E-mail: karin.john@univ-grenoble-alpes.fr
cCenter for Nonlinear Science (CeNoS), Universität Münster, Corrensstr. 2, 48149 Münster, Germany
First published on 27th March 2025
Abstract
Bacteria invade surfaces by forming dense colonies encased in a polymer matrix. Successful settlement of founder bacteria, early microcolony development and later macroscopic spreading of these biofilms on surfaces rely on complex physical mechanisms. Recent data show that on soft hydrogels, substrate rigidity is an important determinant for biofilm initiation and spreading, through mostly unknown mechanisms. Using a thermodynamically consistent thin-film approach for suspensions on soft elastic surfaces supplemented with biomass production we investigate in silico the role of substrate softness in the osmotic spreading of biofilms. We show that on soft substrates with an imposed osmotic pressure spreading is considerably slowed down and may be completely halted depending on the biomass production rate. We find that the critical slowing down of biofilm spreading on soft surfaces is caused by a reduced osmotic influx of solvent into the biofilm at the edges, which results from the thermodynamic coupling between substrate deformation and interfacial forces. By linking substrate osmotic pressure and mechanical softness through scaling laws, our simple model semi-quantitatively captures a range of experimentally observed biofilm spreading dynamics on hydrogels with different architectures, underscoring the importance of inherent substrate properties in the spreading process.
1 Introduction
Bacteria spend most of their life attached to surfaces in structured colonies encased in a self-produced polymeric matrix, called biofilms, which are the prevalent form of life on earth.1 The organisation in biofilms confers bacteria a selective advantage over the individual, e.g. by increasing resistance to mechanical damage and antibiotic agents. Biofilm formation requires bacteria to transition from a free-swimming, individual lifestyle, to a sessile cooperative one. Since the discovery of the multicellular tissue-like behaviour of bacteria about 100 years ago, research has focused on dissecting the environmental cues and biological pathways driving bacterial adhesion and biofilm formation: genetic changes, intracellular signalling, and cell–cell communication.2 However, bacteria in their natural environments are continuously exposed to physical and physico-chemical forces, including mechanical stresses,3–8 osmotic pressure gradients,9–16 capillary17–19 and wetting forces20,21 and it remains often unclear how individuals or colonies integrate such physical cues. However, it is becoming increasingly known that many bacterial communities control and use the mechanical and physico-chemical properties of their surrounding habitat to maximise their chances of survival and dissemination.22 It is now well understood that auto-produced matrix molecules act as osmolytes for biofilms grown on hydrogel substrates. The resulting flux of water with nutrients from the substrate into the biofilm can act as a driving force for lateral biofilm expansion. It has also been demonstrated that capillary, wetting and adhesion forces play a major role in the dynamics of the advancing edge of biofilms,20,23,24 and swarming colonies.17–19,25,26 Bacteria-produced surfactants allow the biofilm to overcome wetting-induced stalling of the biofilm edge20,27 and accelerate spreading in swarming colonies through Marangoni-flows, that may also trigger a fingering instability at the spreading front.19,27The influence of other material properties on biofilm spreading is less well explored. An example is the role of the mechanical substrate stiffness that represents an important parameter for the growth of biofilms on and in soft tissues. Over the past decade, only a few studies have specifically focused on the role of substrate rigidity on bacterial dynamics, both at the single cell and community level.5,7,28–40 Their results show that the rigidity of the underlying substrate does impact bacterial attachment and motility as well as colony morphology and dynamics. However, the observed trends are not consistent between different bacterial strains (e.g. Pseudomonas aeruginosa, Escherichia coli), different types of soft substrates (hydrogels, elastomers, layer-by-layer polymeric substrates) and different explored stiffness ranges (kPa–MPa). Thereby, one of the main experimental difficulties is the independent variation of physico-chemical properties (e.g. osmotic pressure) and mechanical rigidity of the substrate, which might explain opposing trends observed on different hydrogel architectures with identical mechanical properties (shear modulus). Within this context, the osmotic spreading of biofilms has been studied on various substrate architectures and chemical compositions.7 There it has been shown that at constant osmotic pressure, spreading is slower on soft than on rigid substrates, raising the question about the underlying coupling mechanism between the dynamics of the biofilm edge and the substrate rigidity.
Motivated by the aforementioned observations, here, we numerically study the effect of the rigidity of a soft elastic substrate on osmotic biofilm spreading. To that end we employ a minimal thin-film model which naturally captures the effect of interfacial forces and elastic substrate deformations on the motion of the advancing biofilm edge. Briefly, we consider the biofilm as a shallow drop of viscous suspension whose lateral spreading is driven by bioactive growth and ensuing osmotic fluxes. The relevant evolution equations for the biofilm components and the substrate deformation are derived from a gradient dynamics approach41,42 supplemented by a bioactive growth term that mimics biological growth processes (cell division and matrix production).
Within this framework we investigate how substrate rigidity and biomass production rate affect the lateral spreading speed at the biofilm edge. We recover the experimentally observed behaviour of a slowing down of spreading with increasing substrate softness, i.e. with decreasing rigidity, at constant substrate osmotic pressure. Furthermore, we identify a growth regime, where the substrate softness leads to a complete arrest of the biofilm edge. We find that the reduced biofilm spreading speed on soft surfaces is not directly related to the visco-elastic braking observed for the spreading of droplets of passive liquid on soft solid surfaces42–45 but is rather caused by a reduced osmotic influx of solvent into the biofilm at its edges, which results from the thermodynamic coupling between substrate deformation and interfacial forces.
The manuscript is structured as follows. In Section 2 we introduce a minimal dynamic model for osmotic spreading on a soft elastic substrate and discuss the relevant parameters. In Sections 3–5 the model behaviour is analysed using full numerical simulations. First, in Section 3 we investigate equilibrium biofilm shapes and substrate deformations for model biofilms with an imposed amount of biomass. Then, in Section 4 we analyse the dependence of the spreading dynamics of active model biofilms on the substrate softness and biomass growth rate. Finally, in Section 5, we establish a link between our theoretical results and the experiments of Asp et al.,7 and thereby propose a unifying description of the qualitatively different dependencies of the spreading velocity on the substrate stiffness on hydrogels of various architectures. We conclude in Section 6 by a thorough discussion of our theoretical results.
2 Model
We consider osmotic biofilm growth and spreading on a soft solid substrate within a mesoscopic modelling framework (Fig. 1) as previously introduced for rigid solid substrates.20,46 Here, we incorporate an underlying viscoelastic substrate in analogy to the approach introduced by Henkel et al.,42,47 namely, by considering a strain energy related to the vertical displacement of the solid–liquid interface in the fully compressible case. The biofilm itself is modelled as a thin liquid film of a suspension of biomass (bacteria and extracellular matrix) in a solvent (nutrient-rich water). The relevant field variables are the film thickness h(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t), the biomass Ψ(
,t), the biomass Ψ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) and the vertical substrate displacement ξ(
,t) and the vertical substrate displacement ξ(![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) ,t) where
,t) where ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) = (x,y)T are planar Cartesian coordinates. The biomass variable Ψ represents the effective biomass height, i.e. any spatial variations in the vertical direction within the biofilm are neglected. In addition, for convenience, we introduce the biomass volume fraction ϕ which is related to the effective biomass thickness Ψ by
= (x,y)T are planar Cartesian coordinates. The biomass variable Ψ represents the effective biomass height, i.e. any spatial variations in the vertical direction within the biofilm are neglected. In addition, for convenience, we introduce the biomass volume fraction ϕ which is related to the effective biomass thickness Ψ by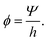 | (1) |
For a thorough discussion of the usage of Ψ and ϕ see Trinschek et al.46 The free energy functional ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) (expressed in h, ξ, and ϕ) that determines the physico-chemical driving forces for all transport processes for the passive (non-bioactive) suspension is
(expressed in h, ξ, and ϕ) that determines the physico-chemical driving forces for all transport processes for the passive (non-bioactive) suspension is
 | (2) |
 | (3) |
 | (4) |
 | (5) |
The entropy of mixing in the bulk of the liquid film is given by
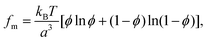 | (6) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ), which breaks the variational structure and renders the suspension bioactive. The resulting evolution equations for the thermodynamic variables h, Ψ, ξ are given by
ϕ), which breaks the variational structure and renders the suspension bioactive. The resulting evolution equations for the thermodynamic variables h, Ψ, ξ are given by | (7) |
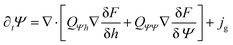 | (8) |
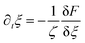 | (9) |
Note, that here we employ the variation of the free energy F[h,ξ,Ψ] which relates to the free energy ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) [h,ξ,ϕ] in (2) as
[h,ξ,ϕ] in (2) as ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) [h,ξ,ϕ] =
[h,ξ,ϕ] = ![[F with combining macron]](https://www.rsc.org/images/entities/i_char_0046_0304.gif) [h,ξ,Ψ/h] = F[h,ξ,Ψ]. In the following ϕ should only be seen as a convenient short-hand notation for Ψ/h. The mobilities Qij form the symmetric and positive definite mobility matrix
[h,ξ,Ψ/h] = F[h,ξ,Ψ]. In the following ϕ should only be seen as a convenient short-hand notation for Ψ/h. The mobilities Qij form the symmetric and positive definite mobility matrix
 | (10) |
Here, η denotes the composition-dependent biofilm viscosity
| η = η0[(1 − ϕ) + μϕ], | (11) |
 of the viscosities of the pure biomass ηb and the pure solvent η0. Further, D = a2/(6πη) denotes the biomass diffusivity consistent with the diffusion constant Ddiff = kBT/(6πηa) with a being the typical biomass length scale as introduced in eqn (6). Finally, ζ denotes the viscosity of the solid viscoelastic substrate.
of the viscosities of the pure biomass ηb and the pure solvent η0. Further, D = a2/(6πη) denotes the biomass diffusivity consistent with the diffusion constant Ddiff = kBT/(6πηa) with a being the typical biomass length scale as introduced in eqn (6). Finally, ζ denotes the viscosity of the solid viscoelastic substrate.
The non-conserved fluxes jo and jg correspond to the osmotic flux of solvent between the moist substrate and the biofilm and the active growth of biomass in the biofilm, respectively. Thereby, the osmotic flux is thermodynamically driven by the difference between the osmotic pressures in the biofilm Π and in the substrate Πs, i.e.
| jo = Qo(Π − Πs), | (12) |
 | (13) |
 | (14) |
Eqn (14) implies that a thick biofilm of uniform height h ≫ ha and biomass concentration ϕeq is in thermodynamic equilibrium with the substrate. Note, that we treat the substrate as an infinite solvent reservoir at fixed uniform osmotic pressure Πs (i.e. a chemostat). In other words, we neglect any effect a substrate deformation might have on Πs. Finally, Qo denotes a mobility.
The active biomass growth jg is modelled as logistic growth with limited resources
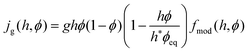 | (15) |
 | (16) |
A core feature of the employed simple gradient dynamics-based modelling for thin films of mixtures is the approximation that vertical concentration gradients are small.41,46 Note that another class of models takes vertical concentration gradients into account.24,58 However, Tam et al.24 also show that such vertical dependencies are small for biologically realistic parameters further confirming our chosen modelling approach.
To facilitate the model analysis we introduce the vertical length scale
![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = ha, = ha, | (17) |
 | (18) |
 | (19) |
The scaling of space and time results in a nondimensional parameter, the substrate softness s ∼ 1/κv (i.e. the inverse of the substrate rigidity)
 | (20) |
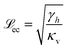 enters naturally, which characterises the typical elastic deformation induced by surface tension.
enters naturally, which characterises the typical elastic deformation induced by surface tension.
In the remainder of the manuscript all dimensional quantities will be expressed tacitly in the scales ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) ,
, ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) and
and ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , e.g. the biomass growth rate constant g in units of 1/
, e.g. the biomass growth rate constant g in units of 1/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) , the biofilm height h and biomass layer thickness Ψ in units of
, the biofilm height h and biomass layer thickness Ψ in units of ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) , the horizontal distance x in units of
, the horizontal distance x in units of ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , etc. The nondimensional model equations and nondimensional parameters are summarised in Table S1 in Section S1 of the ESI.† The above system of eqn (2)–(16) is numerically integrated using the finite element method (FEM) implemented in the software package oomph-lib.59,60 This package enables efficient direct time simulations, incorporating adaptive time stepping based on a second-order backward differentiation method. The software's spatial adaptivity makes it suitable for handling large-scale systems and sharp geometric features like wetting ridges. Simulations of eqn (2)–(16) were performed on one-dimensional domains of size L = 2000 with Neumann boundary conditions.
, etc. The nondimensional model equations and nondimensional parameters are summarised in Table S1 in Section S1 of the ESI.† The above system of eqn (2)–(16) is numerically integrated using the finite element method (FEM) implemented in the software package oomph-lib.59,60 This package enables efficient direct time simulations, incorporating adaptive time stepping based on a second-order backward differentiation method. The software's spatial adaptivity makes it suitable for handling large-scale systems and sharp geometric features like wetting ridges. Simulations of eqn (2)–(16) were performed on one-dimensional domains of size L = 2000 with Neumann boundary conditions.
3 Passive behaviour of a biofilm on a soft elastic substrate
In a first set of simulations, we characterise the passive spreading dynamics of biofilm droplets of fixed constant biomass , i.e. without biomass growth (g = 0), depending on the substrate softness s. In this scenario droplets may exchange solvent with the substrate which acts as an osmotic chemostat. The equilibrium state is characterised by a vanishing of all fluxes, a stationary droplet shape and a stationary substrate deformation.
, i.e. without biomass growth (g = 0), depending on the substrate softness s. In this scenario droplets may exchange solvent with the substrate which acts as an osmotic chemostat. The equilibrium state is characterised by a vanishing of all fluxes, a stationary droplet shape and a stationary substrate deformation.
We initialise all droplets with the identical parabolic film profile h0(x) with the Young–Dupré contact angle42,61 on an undeformed substrate and an initial profile for the biomass height Ψ0(x) = h0(x)ϕeq (for more details refer to Section S2 of the ESI†). Droplets then evolve towards their equilibrium shapes according to eqn (2)–(16). Fig. 2(a)–(c) illustrates the resulting equilibrium drop shapes and substrate deformations as a function of substrate softness s. On a rigid substrate the droplet does not deform the substrate (Fig. 2(a)). As softness increases, wetting and capillary forces increasingly deform the substrate, impacting in turn the drop shape. The first apparent signature of elastocapillary forces is the deformation of the substrate in the contact line region: with increasing softness a so-called wetting ridge is increasingly pulled out of the substrate in the vertical direction (Fig. 2(b)). For very soft substrates, the distinguished wetting ridge shrinks again as the droplet rather sinks into the substrate forming a liquid lens (Fig. 2(c)). Note that the resulting equilibrium droplet volume V only depends very weakly on the substrate softness s (see Fig. S1 in Section S3 of the ESI†).
As characterised for drops of simple passive liquids on soft elastic substrates,42,45 three different regimes of elastocapillarity can be identified. The three regimes can formally be distinguished by the scaling of the height of the wetting ridge‡ Δξmax with the substrate softness42 (Fig. 2(d)). The transitions between the three regimes are associated with the interplay of three length scales, namely, the elastocapillary length ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ec, the mesoscopic scale
ec, the mesoscopic scale ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , i.e. the interface width which is governed by capillarity and wetting forces, and the macroscopic scale, i.e. the typical drop size r.42,45,62
, i.e. the interface width which is governed by capillarity and wetting forces, and the macroscopic scale, i.e. the typical drop size r.42,45,62
Briefly, we identify a nearly rigid regime  , where the drop barely ‘feels’ the substrate softness as elastic forces completely dominate. In consequence, the substrate barely deforms in the mesoscopic contact line region, and the droplet shape is governed by the Young–Dupré equation (Fig. 2(a)). The wetting ridge height scales linearly with softness, i.e. Δξmax ∼ s. This can be intuitively understood by expressing the vertical force balance at the contact line as κvξr
, where the drop barely ‘feels’ the substrate softness as elastic forces completely dominate. In consequence, the substrate barely deforms in the mesoscopic contact line region, and the droplet shape is governed by the Young–Dupré equation (Fig. 2(a)). The wetting ridge height scales linearly with softness, i.e. Δξmax ∼ s. This can be intuitively understood by expressing the vertical force balance at the contact line as κvξr![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = γh
= γh![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θh where ξr denotes the substrate displacement at the contact line. This results in the scaling Δξmax = ξr ∼ κv−1 ∼ s (using κv ∼ s−1 from eqn (20)).
θh where ξr denotes the substrate displacement at the contact line. This results in the scaling Δξmax = ξr ∼ κv−1 ∼ s (using κv ∼ s−1 from eqn (20)).
In the moderately soft regime (10 < s < 105; ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) <
< ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ec < r) a wetting ridge with a height smaller but comparable to the drop size is pulled out (Fig. 2(b)). Its height scales with softness as Δξmax ∼ s1/2.
ec < r) a wetting ridge with a height smaller but comparable to the drop size is pulled out (Fig. 2(b)). Its height scales with softness as Δξmax ∼ s1/2.
In the very soft regime, where the droplet sinks into the substrate the wetting ridge height decreases as Δξmax ∼ s−1 (Fig. 2(c)). In this regime ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ec > r, capillarity and wetting forces dominate while elastic forces can be neglected. The scaling in the moderately and very soft regimes can be understood by considering the macroscopic vertical force balance at the contact line for a liquid ridge in the small slope approximation, i.e.
ec > r, capillarity and wetting forces dominate while elastic forces can be neglected. The scaling in the moderately and very soft regimes can be understood by considering the macroscopic vertical force balance at the contact line for a liquid ridge in the small slope approximation, i.e. and
and  . In this case the vertical force balance reads (see Section S4 of the ESI† for details)
. In this case the vertical force balance reads (see Section S4 of the ESI† for details)
| 0 = [γh∂x(h + ξ) + γs∂xξ]x=r− − [γsv∂xξ]x=r+, | (21) |
In the moderately soft regime (![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ec < r) eqn (21) reads
ec < r) eqn (21) reads
 | (22) |
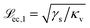 and
and 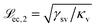 to the left and the right of the contact line, respectively. This results in the scaling
to the left and the right of the contact line, respectively. This results in the scaling  .
.
In the very soft regime (![[script L]](https://www.rsc.org/images/entities/char_e144.gif) ec > r) the liquid–vapour surface tension drives the droplet into the substrate via the curvature of the liquid–vapour interface
ec > r) the liquid–vapour surface tension drives the droplet into the substrate via the curvature of the liquid–vapour interface  and exerts an upward directed point force on the surface at the contact line (pr). The force balance (eqn (21)) can be rewritten in the intuitive formulation
and exerts an upward directed point force on the surface at the contact line (pr). The force balance (eqn (21)) can be rewritten in the intuitive formulation
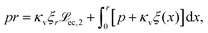 | (23) |
 | (24) |
 (see Section S4 of the ESI† for the detailed calculation) and
(see Section S4 of the ESI† for the detailed calculation) and  . Note, that the slow decay of the displacement of the bare substrate contributes to the scaling of Δξmax. Note also, that we assume here that the Laplace pressure and radius of the droplet are constant and correspond to the liquid regime with vanishing κv, where the wetting ridge vanishes and the droplet floats with a lens-like shape at the substrate–vapour interface.
. Note, that the slow decay of the displacement of the bare substrate contributes to the scaling of Δξmax. Note also, that we assume here that the Laplace pressure and radius of the droplet are constant and correspond to the liquid regime with vanishing κv, where the wetting ridge vanishes and the droplet floats with a lens-like shape at the substrate–vapour interface.
In the examples of Fig. 2, the droplet size r is of order 100![[script L]](https://www.rsc.org/images/entities/char_e144.gif) , situating the transition from the moderately soft to the very soft regime at s ≈ 104, which well agrees with our simulations. Having studied the case of passive drops as a reference case, next we consider the bioactive case.
, situating the transition from the moderately soft to the very soft regime at s ≈ 104, which well agrees with our simulations. Having studied the case of passive drops as a reference case, next we consider the bioactive case.
4 Spreading of active biofilms on soft substrates
Here we focus on an investigation of the spreading behaviour of bioactive films on moderately soft and very soft substrates (i.e. s > 10, g > 0). Note that the osmotic spreading of biofilms on rigid solid substrates has been extensively characterised by Trinschek et al.20,46 Simulations of biofilm growth are started from a small biofilm droplet (parabolic film profile h0 with biomass profile Ψ0 = h0ϕeq, see Section S2 of the ESI† for details), which then develops according to eqn (2)–(16) with a biomass growth rate constant g > 0. Fig. 3 exemplarily characterises the spreading behaviour at fixed substrate softness s = 104 for two different biomass growth rates (for numerical details see Section S5 of the ESI†). | ||
| Fig. 3 Spreading of active biofilms on soft substrates. (a) and (b) Snapshots of biofilm profiles (blue shading) and substrate deformation profiles (brown shading) at (a) low biomass growth rate constant (g = 1.3 × 10−6) and (b) high biomass growth rate constant (g = 5.3 × 10−6). The colour gradient in the biofilm profile indicates the progression of time: darker colours represent initial evolution steps and lighter colours indicate later stages. The profiles correspond to times t ∈ {0, 5.49 × 106, 1.37 × 107, 3.16 × 107, 4.44 × 108} in (a) and t ∈ {0, 1.3 × 106, 3.1 × 106, 1 × 107, 3 × 107, 5 × 107, 7 × 107, 9 × 107} in (b). Note that the colour scale is logarithmic in (a) and linear in (b). In (a) the film, biomass and substrate deformation profile evolve towards a stationary state (arrest of spreading). In (b), after an initial swelling phase, the biofilm edge advances at constant shape and speed (continuous spreading). (c) and (d) Time evolution of biofilm and biomass volume (V, blue and green, respectively), maximal biofilm (hmax, blue) and wetting ridge (Δξ, red) heights, macroscopic contact angle θh (for details of measurement see Section S5 of ESI†) and biofilm extension (r). The dashed vertical line in (d) denotes the onset of the continuous spreading regime. The substrate softness is s = 104 and remaining parameters are as given in Table S1 in the ESI.† | ||
At low biomass growth rate (g = 1.3 × 10−6, Fig. 3(a)) the biofilm swells until reaching a stationary state where drop, biomass and substrate deformation profiles do not change any more. This parallels the state of arrested growth already described in Trinschek et al.,20 with the addition, that the substrate is deformed and a stationary wetting ridge develops at the biofilm edge. Strikingly, at an increased biomass growth rate constant (g = 5.3 × 10−6, Fig. 3(b)), the spreading behaviour dramatically changes. After a transient phase of combined vertical and horizontal swelling, similar to the transient in the arrested case, the biofilm enters a continuous lateral spreading regime. Then the biofilm edge advances with a constant shape and speed. This behaviour mirrors the continuous growth state described in Trinschek et al.20 with the additional feature that the biofilm edge deforms the substrate and a wetting ridge continuously advances with the biofilm edge.
Fig. 3(c) and (d) further characterise the arrested and continuous spreading regimes at long times in terms of the evolution of the biofilm volume and total biomass (V, blue and green curves, respectively), the maximal film height hmax and wetting ridge height Δξ, the contact angle of the biofilm edge θh, and the lateral biofilm extension r. The short-time behaviour is shown in more detail in Fig. S2 in Section S6 of the ESI.† In the arrested case, at large times, the film volume, biomass and lateral biofilm extension reach plateau values whereas in the continuous growth case they increase linearly with time. In both cases, the maximal value of the film height reaches a constant value close to the imposed maximal film height h*, where the net biomass increase stops [eqn (15)]. In the case of continuous spreading the growth restriction leads to a pronounced pancake-like shape of the biofilm, whereas in the arrested case, the biofilm adopts a spherical cap-like shape. Furthermore, in both cases, the wetting ridge height converges to the value found in the passive limiting case (for a detailed analysis see Fig. 4). Also, the contact angle is evolving in both cases in a similar manner.
We next investigate the robustness of the above described transition between arrested and continuous biofilm growth by varying the substrate softness s. Fig. 4(a)–(f) show exemplary biofilm profiles for various growth rate constants and substrate softnesses s while Fig. 4(g) presents a nonequilibrium phase diagram that gives the spreading speed in the parameter plane spanned by the biomass-growth rate g and the substrate softness s. For completeness the effect of the biomass growth on the wetting ridge height is shown in Fig. S3 of Section S7 of the ESI.† In general, biofilm spreading is favoured on rigid substrates. In contrast, soft substrates are unfavourable for biofilm spreading and may completely stop biofilm evolution. At very low growth rates, continuous spreading can not be achieved, independent of the substrate softness. Importantly, in the intermediate regime, spanning one order of magnitude for the growth rate constant g (5 × 10−7 < g < 5 × 10−6), the biofilm spreading velocity is controlled by substrate softness in a parameter region spanning nearly 3 orders of magnitude, i.e. 102 < s < 105 (Fig. 4(g) and (h)). At large growth rates (g > 5 × 10−6), continuous spreading occurs across all three softness regimes such that even on very soft substrates spreading is continuous, albeit with a low velocity (blue curve in Fig. 4(h)). Note, that at high growth rates the velocity does not drop monotonically with increasing substrate softness, but slightly increases with increasing softness before dropping sharply (blue and red curves in Fig. 4(h)). For rigid substrates Trinschek et al.20 find that the transition from arrested to continuous spreading occurs when reducing the influence of surface forces as compared to entropic forces. Here, a similar transition is observed when varying the substrate elasticity. This shows that substrate softness represents another important passive material property, which fundamentally alters biofilm spreading behaviour.
To gain a better understanding of the physical mechanism underlying the arrest of spreading on very soft substrates we next investigate the hypothesis, that the osmotic solvent exchange between the substrate and the biofilm is altered in spreading biofilms as compared to arrested biofilms. Fig. 4(i) shows exemplary spatial profiles of the osmotic exchange flux jo(x) between the substrate and the biofilm for a spreading (s = 300) and an arrested (s = 9000) biofilm. In the spreading biofilm, the flux vanishes in the central region of the biofilm (x ≈ 0). Close to the biofilm edge, where biomass is produced, the osmotic flux is directed from the substrate into the biofilm. Interestingly, in a region between the biofilm edge and the biofilm centre, the osmotic flux is directed from the biofilm into the substrate. However, the osmotic outflow in this region is weak compared to the massive osmotic influx at the advancing biofilm edge. In the arrested case, osmotic fluxes are still present. Although the spatial profiles (film height h, biomass Ψ, substrate deformation ξ) are stationary, and conserved and nonconserved fluxes are balanced, they do not vanish. This is a signature of active, i.e., out-of-equilibrium, behaviour and is a direct result of the gradient dynamics structure being broken by biomass growth jg in eqn (8). The osmotic flux is directed into the substrate at the centre of the biofilm and into the biofilm close to the edge of the biofilm, where it drops to zero as the wetting ridge is approached. From the inspection of the osmotic flux profiles on the macroscale it does not yet become clear, what feature causes the spreading arrest, since the observed osmotic influx close to the biofilm edge should favour spreading in both cases.
However, a close inspection of the osmotic pressure profile in the biofilm on the mesoscopic scale in the contact line region reveals important differences between arrested and spreading biofilms. Fig. 5(a) shows the spatial profile of the osmotic pressure difference ΔΠ between the biofilm and the substrate in the contact line region for spreading and arrested biofilms. All profiles were laterally shifted such that the wetting ridge is located at x = 0. The osmotic pressure difference ΔΠ for the advancing biofilm fronts (s < 9000) is positive and shows a local maximum in the contact line region x ≈ 0 indicating solvent influx into the biofilm. However, for the arrested biofilm front at s = 9000 the osmotic pressure difference ΔΠ ≈ 0. The osmotic pressure difference contains two contributions: one results from the entropy of mixing of biomass ΔΠentropic and another one results from interfacial forces (capillarity and wettability) ΔΠinterface. Using expression (14) for the constant osmotic pressure  in the substrate, the two contributions can be expressed as (see eqn (12) and (13))
in the substrate, the two contributions can be expressed as (see eqn (12) and (13))
 | (25) |
 | (26) |
 | ||
| Fig. 5 Role of the osmotic flux between the substrate and the biofilm in spreading on soft substrates. (a) Osmotic pressure difference ΔΠ between biofilm and substrate in the contact line region for various agar softnesses s as indicated in the legend. The growth rate constant is g = 1.3 × 10−6. At a softness of s = 9000 the contact line is stationary. All other curves (s < 9000) belong to spreading biofilm fronts. (b) Entropic ΔΠentropic, see eqn (25), and (c) interfacial ΔΠinterface, see eqn (26), contributions to the osmotic pressure difference. The legends are as in (a). The grey dashed lines in (a)–(c) indicate the location of the wetting ridge for all profiles. Remaining parameters are given in Table S1 in the ESI.† | ||
The decomposition of the osmotic pressure difference ΔΠ into entropic and interfacial contributions (Fig. 5(b) and (c)) reveals that for advancing biofilm edges (s ≤ 3000) at the contact line the entropic contribution favours osmotic outflux (ΔΠentropic < 0) since the biomass concentration is below the equilibrium value (ϕ < ϕeq). However, the interfacial contribution favours osmotic influx (ΔΠinterface > 0). The resulting net flux is small (10−4, compared to the magnitude of 10−2 for each individual flux) but positive, driving the advancement of the biofilm edge. In contrast, for arrested fronts (s = 9000 in Fig. 5(b) and (c)) the biomass concentration in the biofilm ϕ favours solvent influx, whereas the interfacial forces are inducing a negative osmotic pressure difference, such that outflux is favoured. Importantly, the net solvent flux between substrate and biofilm vanishes at the contact line. Note, that a fully developed advancing biofilm front (that has developed on a rigid substrate) will initially recede until the biofilm adopts the stationary droplet shape on a soft substrate.
In conclusion, arrested and spreading case differ qualitatively w.r.t. the forces which drive osmotic fluxes. The transition between the two regimes results from a subtle equilibration of these forces in the contact line region. It emerges that direction and magnitude of osmotic solvent fluxes are decisive for biofilm spreading. Viscoelastic braking observed in droplet spreading of passive fluids is certainly present in biofilms as well, but not the major determinant for a decreased spreading speed on moderately soft to very soft substrates.
5 Comparison with experiments
Up to now, we have treated the osmotic pressure in the substrate (determined by the hydrogel concentration ϕeq) and the substrate softness s as independent parameters, and have obtained results as discussed at Fig. 3 and 4 at fixed ϕeq. This ideal assumption of independent parameters only approximately holds for specific experimental protocols of substrate fabrication. Typically, the hydrogel substrate rigidity is varied, e.g. by increasing the cross-linker concentration at constant hydrogel concentration or by changing the hydrogel concentration at constant cross-linker concentration. When the latter method is used both parameters, osmotic pressure and elastic modulus of the substrate, are impacted in a way specific for each hydrogel. To be able to discuss such scenarios, we study the influence of the osmotic pressure of the substrate (via the equilibrium biomass concentration ϕeq63,64). Fig. 6(a) shows the resulting morphological phase diagram in the plane spanned by s and ϕeq at fixed biomass growth rate g = 5.3 × 10−6. Generally speaking, rigid substrates and a low substrate osmotic pressure favour a rapid biofilm expansion. An increase in the biofilm osmotic pressure reduces the propagation speed of the biofilm edge, since a larger amount of biomass has to be produced in the biofilm to draw water from the substrate into the biofilm. | ||
| Fig. 6 (a) and (b) Phase diagrams characterising the biofilm spreading velocity in the plane spanned by the equilibrium biomass concentration ϕeq and (a) on the one hand the softness s and (b) on the other hand the elastic shear modulus G′. Thereby, the colour (scales given on the right of each panel) indicates the lateral (adimensional (a), dimensional (b)) spreading velocity within the continuous spreading regime. (c)–(e) Biofilm spreading velocity depending on the substrate shear modulus G′ for three exemplary scenarios G′(ϕeq) as indicated by matching coloured lines in (b), see main text. Lines represent theoretically calculated spreading velocities; symbols correspond to the experimental data of Asp et al.7 on three different substrate architectures, namely, (c) PAA substrate with fixed PAA concentration and varying cross-linker (bis-acrylamide) concentration, (d) PAA substrate with varying PAA concentration and constant cross-linker (bis-acrylamide) concentration, and (e) Agar substrate with varying agar concentration. The (nondimensional) growth rate constant is g = 5.3 × 10−6. The dimensional velocity and the shear modulus are determined as described in the main text. | ||
To establish at least a semi-quantitive link between theory and experiment based on the obtained phase diagram, we introduce (i) appropriate scales to relate the nondimensional softness and the elastic modulus as well as the nondimensional spreading speed to the dimensional one and (ii) we relate substrate osmotic pressure and elastic modulus for a given experimentally employed substrate architecture.
Regarding (i), the shear modulus G′ scales as G′ ∼ κvd, with κv denoting the model elastic constant of the substrate and d denoting the substrate thickness.42 Using the definitions of softness s(20) and elastocapillary length 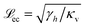 we find a scaling between the linear shear modulus G′ and the softness s
we find a scaling between the linear shear modulus G′ and the softness s
 | (27) |
The velocity scale is given by ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) /
/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) with the length scale
with the length scale ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) and time scale
and time scale ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) defined in eqn (18) and (19).
defined in eqn (18) and (19).
With this scaling we now compare our results with the experimental observations reported by Asp et al.7 (see their Fig. 4). They investigate biofilm spreading on hydrogel substrates of various chemical compositions and architectures (agar substrate, bis-acrylamide (Bis) cross-linked polyacrylamide (PAA)). Thereby, they influence the elastic modulus by varying either the polymer concentration (agar, PAA) or the cross-linker concentration (Bis). Osmotic spreading on agar substrates with varying concentrations has also been studied, e.g. by Ziege et al.,36 Kochanowski et al.,63 with similar observed trends as reported in Asp et al.7
To proceed we assume a (nondimensional) growth rate constant g = 5.3 × 10−6 and visually compare our Fig. 4(h) with Fig. 4 of Asp et al.7 In this way, we are able to establish the relation sG′ = γhd/![[script L]](https://www.rsc.org/images/entities/char_e144.gif) 2 = 2 × 107 Pa between s and G′ and to determine the velocity scale to be
2 = 2 × 107 Pa between s and G′ and to determine the velocity scale to be ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) /
/![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 2.8 mm s−1. Using the gel thickness d = 1 mm7 and the surface tension and viscosity of water (γh = 70 × 10−3 N m−1, η0 = 10−3 Pa s), we obtain the lateral length scale
= 2.8 mm s−1. Using the gel thickness d = 1 mm7 and the surface tension and viscosity of water (γh = 70 × 10−3 N m−1, η0 = 10−3 Pa s), we obtain the lateral length scale ![[script L]](https://www.rsc.org/images/entities/char_e144.gif) = 1.9 μm, the vertical length scale
= 1.9 μm, the vertical length scale ![[script letter H]](https://www.rsc.org/images/entities/char_e142.gif) = 0.1 μm, and the time scale
= 0.1 μm, and the time scale ![[scr T, script letter T]](https://www.rsc.org/images/entities/char_e533.gif) = 7 × 10−4 s. These scales are consistent with a Hamaker constant A = 10−18 N m and a dimensional biomass (extracellular matrix, bacteria) growth rate constant g = 0.5 min−1. The scaling procedure above results in Fig. 6(b) that gives the rescaled representation of the biofilm spreading speed in the plane spanned by the equilibrium biomass concentration ϕeq and the elastic shear modulus G′. Also here we see that more rigid substrates with low osmotic pressure favour a rapid biofilm expansion.
= 7 × 10−4 s. These scales are consistent with a Hamaker constant A = 10−18 N m and a dimensional biomass (extracellular matrix, bacteria) growth rate constant g = 0.5 min−1. The scaling procedure above results in Fig. 6(b) that gives the rescaled representation of the biofilm spreading speed in the plane spanned by the equilibrium biomass concentration ϕeq and the elastic shear modulus G′. Also here we see that more rigid substrates with low osmotic pressure favour a rapid biofilm expansion.
Finally, we come back to point (ii) from above, regarding the relation between parameters that we have treated as independent up to now. Identifying the experimental parameter of hydrogel concentration with our ϕeq, we consider three example scenarios for the dependence of hydrogel stiffness G′ on ϕeq that correspond to the experimental conditions reported by Asp et al.7 in their Fig. 4: in scenario one, G′ is increased via an increase of the cross-linker concentration at fixed PAA concentration (i.e. ϕeq remains constant, red solid line in Fig. 6(b) and (c)). In scenario two, G′ ∼ ϕeq scales linearly with the hydrogel concentration (PAA, constant cross-linker concentration, measured by Asp et al.,7 blue dot-dashed line in Fig. 6(b) and (d)). In scenario three, G′ ∼ ϕνeq scales with an exponent ν ≥ 2 (agarose,65,66 green dashed line in Fig. 6(b) and (e)).
The mentioned Fig. 6(c)–(e) compare the resulting dependence of spreading velocity on shear modulus G′ as experimentally measured by Asp et al.7 and as obtained here when following the three trajectories in the (ϕeq,G′)-plane (Fig. 6(b)). Interestingly, depending on the hydrogel substrate and the implied specific functional dependence G′(ϕeq), biofilm spreading can be enhanced with increasing substrate stiffness (Fig. 6(c)), can show a nonmonotonic behaviour (Fig. 6(d)), or can be slowed down with increasing substrate stiffness (Fig. 6(e)). The obtained coherent explanation of seemingly contradictory results for the dependencies on G′ underscores the importance of understanding the relation between the hydrogel parameters elasticity and osmotic pressure.
6 Conclusion
We have demonstrated that biofilm spreading on soft substrates is critically slowed down compared to rigid substrates and that substrate softness can even lead to the complete arrest of the biofilm edge. This result holds for the case where mechanical (rigidity) and physico-chemical (osmotic pressure) substrate properties can be independently controlled. Furthermore, we find that the reduction of the biofilm spreading speed on soft substrates is not directly related to the viscoelastic braking observed for the hydrodynamic spreading of liquid droplets on soft solid substrates42–45 but is rather caused by a reduced osmotic influx of solvent into the biofilm at its edges, which results from the thermodynamic coupling between substrate deformation and interfacial forces. However, for practically used hydrogel substrates often the mechanical softness and the osmotic pressure cannot be independently controlled, i.e. they cannot be treated as independent parameters. Typically, an increase in substrate softness which slows down spreading is also associated with a reduced osmotic pressure in the substrate, which in turn accelerates spreading. This effect is clearly illustrated by Asp et al.7 where they show that the biofilm spreading velocity on hydrogels strongly depends on substrate architecture. The spreading velocity may increase or decrease with increasing substrate rigidity or may even show nonmonotonic behaviour. Coupling substrate rigidity and substrate osmotic pressure via scaling laws, our minimal theory coherently captures these seemingly contradictory experimental results and clearly underscores the importance of substrate deformations and osmotic fluxes in the dynamics of the advancing biofilm edge.While the here proposed minimalistic model applies to biofilm growth on abiotic surfaces under air, other more physiological settings may be considered within a slightly modified modelling framework: biofilm growth on biotic surfaces (e.g. airway epithelia, airway mucus; relevant for biofilm development in cystic fibrosis patients due to Pseudomonas aeruginosa67,68) or growth of immersed biofilms on soft abiotic and biotic surfaces.5,69 In the latter case, the coupling between osmotic substrate pressure and substrate rheology is a less important feature, since osmotic fluxes between biofilm and the surrounding medium will dominate over the solvent exchange between biofilm and substrate. Furthermore, more complex situations may be investigated in parallel with experiments, e.g. biofilm spreading on soft substrates with spatially varying stiffness or the coupling between matrix/surfactant production and softness.
While our model cannot capture important (species-dependent) biological factors of biofilm initiation and development (e.g. quorum sensing), it constitutes nevertheless a useful tool to understand how the physico-chemical and mechanical environmental parameters impact the dynamics of the advancing biofilm edge and may help e.g. to develop alternative therapeutic strategies in a targeted manner that do not rely on antibiotic drugs.
Author contributions
AP, KJ, and UT designed research. AP performed all numerical calculations. AP, KJ, and UT wrote the manuscript.Data availability
All data necessary to plot Fig. 2–6 and the Fig. S1–S3 (ESI†) are available in the zenodo repository under the URL https://zenodo.org/records/14235001.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge support by the Studienstiftung des Deutschen Volkes (AP), the doctoral school “Active living fluids” funded by the German French University (Grant No. CDFA-01-14); the Deutsche Forschungsgemeinschaft (DFG, Grant No. TH781/12-2 within SPP 2171). The authors thank Sigolène Lecuyer, Delphine Débarre and Lionel Bureau for fruitful discussions.References
- H.-C. Flemming, J. Wingender, U. Szewzyk, P. Steinberg, S. A. Rice and S. Kjelleberg, Nat. Rev. Microbiol., 2016, 14, 563–575 CrossRef CAS.
- B. I. Kazmierczak, M. Schniederberend and R. Jain, Curr. Opin. Microbiol., 2015, 28, 78–82 CrossRef CAS.
- A. Persat, Y. F. Inclan, J. N. Engel, H. A. Stone and Z. Gitai, Proc. Natl. Acad. Sci. U. S. A., 2015, 112, 7563–7568 CrossRef CAS.
- J. Yan, C. Fei, S. Mao, A. Moreau, N. S. Wingreen, A. Košmrlj, H. A. Stone and B. L. Bassler, eLife, 2019, 8, e43920 CrossRef PubMed.
- A. Cont, T. Rossy, Z. Al-Mayyah and A. Persat, eLife, 2020, 9, e56533 CrossRef CAS.
- Y. F. Dufrêne and A. Persat, Nat. Rev. Microbiol., 2020, 18, 227–240 Search PubMed.
- M. E. Asp, M.-T. Ho Thanh, D. A. Germann, R. J. Carroll, A. Franceski, R. D. Welch, A. Gopinath and A. E. Patteson, PNAS Nexus, 2022, 1, 1 CrossRef CAS PubMed.
- S. Geisel, E. Secchi and J. Vermant, eLife, 2022, 11, e76027 CrossRef CAS.
- S. M. Rubinstein, I. Kolodkin-Gal, A. Mcloon, L. Chai, R. Kolter, R. Losick and D. A. Weitz, Mol. Microbiol., 2012, 86, 426–436 CrossRef CAS.
- A. Seminara, T. E. Angelini, J. N. Wilking, H. Vlamakis, S. Ebrahim, R. Kolter, D. A. Weitz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 1116–1121 CrossRef CAS PubMed.
- J. Yan, C. D. Nadell, H. A. Stone, N. S. Wingreen and B. L. Bassler, Nat. Commun., 2017, 8, 327 CrossRef PubMed.
- W. Zhang, A. Seminara, M. Suaris, M. P. Brenner, D. A. Weitz and T. E. Angelini, New J. Phys., 2014, 16, 015028 CrossRef.
- W. Zhang, W. Dai, S.-M. Tsai, S. Zehnder, M. Sarntinoranont and T. Angelini, Soft Matter, 2015, 11, 3612–3617 RSC.
- S. Srinivasan, C. N. Kaplan and L. Mahadevan, eLife, 2019, 8, e42697 CrossRef.
- R. Paul, T. Ghosh, T. Tang and A. Kumar, Soft Matter, 2019, 15, 5400–5411 RSC.
- U. Kumar and S. Pushpavanam, Phys. Fluids, 2024, 36, 021906 CrossRef CAS.
- M. Fauvart, P. Phillips, D. Bachaspatimayum, N. Verstraeten, J. Fransaer, J. Michiels and J. Vermant, Soft Matter, 2012, 8, 70–76 RSC.
- R. De Dier, M. Fauvart, J. Michiels and J. Vermant, The Physical Basis of Bacterial Quorum Communication, Springer, 2015, pp. 189–204 Search PubMed.
- S. Trinschek, K. John and U. Thiele, Soft Matter, 2018, 14, 4464–4476 RSC.
- S. Trinschek, K. John, S. Lecuyer and U. Thiele, Phys. Rev. Lett., 2017, 119, 078003 CrossRef PubMed.
- Z. C. Kampouraki, M. Petala, A. Boumpakis, G. Skordaris, N. Michailidis, E. Deliyanni, M. Kostoglou and T. D. Karapantsios, Langmuir, 2022, 38, 9810–9821 CrossRef CAS PubMed.
- B. Maier, Annu. Rev. Biophys., 2021, 50, 401–417 CrossRef CAS.
- T. Si, Z. Ma and J. X. Tang, Soft Matter, 2018, 14, 301–311 RSC.
- A. K. Tam, B. Harding, J. E. F. Green, S. Balasuriya and B. J. Binder, Phys. Rev. E, 2022, 105, 014408 CrossRef CAS PubMed.
- H. S. Kotian, A. Z. Abdulla, K. Hithysini, S. Harkar, S. Joge, A. Mishra, V. Singh and M. M. Varma, Phys. Rev. E, 2020, 101, 012407 CrossRef CAS PubMed.
- H. Ma, J. Bell, W. Chen, S. Mani and J. X. Tang, Soft Matter, 2021, 17, 2315–2326 RSC.
- U. Kumar and P. Subramaniam, Soft Matter, 2024, 21, 226–240 RSC.
- N. Saha, C. Monge, V. Dulong, C. Picart and K. Glinel, Biomacromolecules, 2013, 14, 520–528 CrossRef CAS PubMed.
- F. Song and D. Ren, Langmuir, 2014, 30, 10354–10362 CrossRef CAS PubMed.
- C. Guégan, J. Garderes, G. Le Pennec, F. Gaillard, F. Fay, I. Linossier, J.-M. Herry, M.-N. B. Fontaine and K. V. Réhel, Colloids Surf., B, 2014, 114, 193–200 CrossRef PubMed.
- A. Siryaporn, S. L. Kuchma, G. A. O’Toole and Z. Gitai, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 16860–16865 CrossRef CAS PubMed.
- R. Zhang, L. Ni, Z. Jin, J. Li and F. Jin, Nat. Commun., 2014, 5, 5541 CrossRef CAS PubMed.
- S. L. Arias, J. Devorkin, A. Civantos and J. P. Allain, Langmuir, 2020, 37, 16–25 CrossRef.
- J. Blacutt, Z. Lan, E. M. Cosgriff-Hernandez and V. D. Gordon, R. Soc. Open Sci., 2021, 8, 201453 CrossRef CAS PubMed.
- S. Gomez, L. Bureau, K. John, E.-N. Chêne, D. Débarre and S. Lecuyer, eLife, 2023, 12, e81112 CrossRef CAS PubMed.
- R. Ziege, A.-M. Tsirigoni, B. Large, D. O. Serra, K. G. Blank, R. Hengge, P. Fratzl and C. M. Bidan, ACS Biomater. Sci. Eng., 2021, 7, 5315–5325 CrossRef CAS PubMed.
- M. D. Koch, M. E. Black, E. Han, J. W. Shaevitz and Z. Gitai, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2119434119 CrossRef CAS PubMed.
- P. Rashtchi, D. Sudmalis, E. van der Linden, T. Abee and M. Habibi, Microbiol. Res., 2024, 283, 127674 CrossRef CAS.
- N. Faiza, R. Welch and A. Patteson, APL Bioeng., 2025, 9, 016104 CrossRef PubMed.
- M. Techakasikornpanich, K. Jangpatarapongsa, D. Polpanich and A. Elaissari, Polym. Adv. Technol., 2024, 35, e6311 CrossRef CAS.
- U. Thiele, Colloids Surf., A, 2018, 553, 487–495 CrossRef CAS.
- C. Henkel, J. H. Snoeijer and U. Thiele, Soft Matter, 2021, 17, 10359–10375 RSC.
- S. Karpitschka, S. Das, M. van Gorcum, H. Perrin, B. Andreotti and J. H. Snoeijer, Nat. Commun., 2015, 6, 7891 CrossRef CAS.
- A. Carré and M. E. R. Shanahan, Langmuir, 2001, 17, 2982–2985 CrossRef.
- B. Andreotti and J. H. Snoeijer, Annu. Rev. Fluid Mech., 2020, 52, 285–308 CrossRef.
- S. Trinschek, K. John and U. Thiele, AIMS Mater. Sci., 2016, 3, 1138–1159 Search PubMed.
- C. Henkel, M. H. Essink, T. Hoang, G. J. van Zwieten, E. H. van Brummelen, U. Thiele and J. H. Snoeijer, Proc. R. Soc. A, 2022, 478, 20220132 CrossRef CAS PubMed.
- D. Bonn, J. Eggers, J. Indekeu, J. Meunier and E. Rolley, Rev. Mod. Phys., 2009, 81, 739 CrossRef CAS.
- U. Thiele, Structure Formation in Thin Liquid Films, in Thin Films of Soft Matter, ed. S. Kalliadasis and U. Thiele, Springer Vienna, Vienna, 2007, pp. 25–93 Search PubMed.
- M. N. Popescu, G. Oshanin, S. Dietrich and A. Cazabat, J. Phys.: Condens. Matter, 2012, 24, 243102 CrossRef CAS PubMed.
- K. John and U. Thiele, Phys. Rev. Lett., 2010, 104, 107801 CrossRef PubMed.
- F. Stegemerten, K. John and U. Thiele, Soft Matter, 2022, 18, 5823–5832 RSC.
- F. Voss and U. Thiele, J. Eng. Math., 2024, 149, 2 CrossRef.
- U. Thiele, Eur. Phys. J.:Spec. Top., 2011, 197, 213–220 CAS.
- U. Thiele, D. V. Todorova and H. Lopez, Phys. Rev. Lett., 2013, 111, 117801 CrossRef PubMed.
- X. Xu, U. Thiele and T. Qian, J. Phys.: Condens. Matter, 2015, 27, 085005 CrossRef CAS PubMed.
- S. Hartmann, J. Diekmann, D. Greve and U. Thiele, Langmuir, 2024, 40, 4001–4021 CAS.
- J. P. Ward and J. R. King, J. Eng. Math., 2011, 73, 71–92 Search PubMed.
- M. Heil and A. L. Hazel, oomph-lib – An Object-Oriented Multi-Physics Finite-Element Library, Springer, Berlin, Heidelberg, 2006, pp. 19–49 Search PubMed.
- M. Heil, A. Hazel and P. Matharu, oomph-lib, 2022, https://github.com/oomph-lib/oomph-lib.
- U. Thiele, J. H. Snoeijer, S. Trinschek and K. John, Langmuir, 2018, 34, 7210–7221 CAS.
- L. A. Lubbers, J. H. Weijs, L. Botto, S. Das, B. Andreotti and J. H. Snoeijer, J. Fluid Mech., 2014, 747, R1 CrossRef CAS.
- J. A. Kochanowski, B. Carroll, M. E. Asp, E. C. Kaputa and A. E. Patteson, ACS Appl. Bio Mater., 2024, 7, 7809–7817 CAS.
- S. G. V. Charlton, D. L. Kurz, S. Geisel, J. Jimenez-Martinez and E. Secchi, Interface Focus, 2022, 12, 20220035 Search PubMed.
- T. Fujii, T. Yano, H. Kumagai and O. Miyawaki, Biosci., Biotechnol., Biochem., 2000, 64, 1618–1622 CAS.
- M. Tokita and K. Hikichi, Phys. Rev. A:At., Mol., Opt. Phys., 1987, 35, 4329–4333 CAS.
- H. Matsui, V. E. Wagner, D. B. Hill, U. E. Schwab, T. D. Rogers, B. Button, R. M. Taylor, R. Superfine, M. Rubinstein, B. H. Iglewski and R. C. Boucher, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 18131–18136 Search PubMed.
- S. Moreau-Marquis, B. A. Stanton and G. A. O’Toole, Pulm. Pharmacol. Ther., 2008, 21, 595–599 CrossRef CAS PubMed.
- E. G. Di Domenico, A. Oliva and M. Guembe, Microorganisms, 2022, 10, 1259 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01463d |
| ‡ Here we define the wetting ridge height as the difference Δξmax = ξmax − ξ(L), where ξmax denotes the maximal vertical substrate displacement in the contact line region and ξ(L) indicates the substrate displacement in the adhesion layer far away from the biofilm edge. |
| This journal is © The Royal Society of Chemistry 2025 |




