Dynamic control of self-assembly of quasicrystalline structures through reinforcement learning

Abstract

We propose reinforcement learning to control the dynamical self-assembly of a dodecagonal quasicrystal (DDQC) from patchy particles. Patchy particles undergo anisotropic interactions with other particles and form DDQCs. However, their structures in steady states are significantly influenced by the kinetic pathways of their structural formation. We estimate the best temperature control policy using the Q-learning method and demonstrate its effectiveness in generating DDQCs with few defects. It is found that reinforcement learning autonomously discovers a characteristic temperature at which structural fluctuations enhance the chance of forming a globally stable state. The estimated policy guides the system toward the characteristic temperature to assist the formation of DDQCs. We also illustrate the performance of RL when the target is metastable or unstable.

---

1. Introduction

Nano- and colloidal self-assembly is promising due to its high potential in creating complex structures with emergent photonic,^1,2 magnetic,³ and electronic⁴ properties. To make various self-assembly structures, several particles have been proposed, such as patchy particles,^5–7 non-spherical particles,⁸ and particles with non-monotonic interactions.⁹ Among them, patchy particles, which undergo anisotropic interactions, are good candidates due to their high flexibility in designing the interactions and the capability to form complex structures.^6,10 In fact, complex structures, such as diamonds and quasicrystals, are reproduced by using patchy particles. Still, designing a desired structure remains a formidable task and relies on trial and error.

Recently, there has been growing interest in the inverse design of desired self-assembly structures. In the conventional forward-type approach, we start from a given model with a specific type of interaction between particles and tune its parameters to analyse the obtained structure. In contrast, the inverse design estimates the model from the desired structure. This approach has been successfully applied to several complex structures, such as quasicrystals.^11–14 However, so far, most of the methods of the inverse design rely on static control, such as optimisation of parameters in the potential interactions, and do not take into account the kinetic process of self-assemblies. It is well-known that the steady-state structure is largely affected by dynamic control, such as the change in temperature and external mechanical forces. For example, ref. 15 demonstrates the temperature protocol that can select a desired structure from two competing ones in a multicomponent self-assembly.

To design self-assembly structures by dynamic control, we need to access their kinetic pathways, which are unknown from the static interactions. Systems may often have many metastable states even with the same parameters. As a result, once the structure gets trapped in the metastable state at a low temperature, the system hardly escapes from it to reach the global minimum. Let us take an example of the two-dimensional dodecagonal quasicrystal (DDQC) self-assembled from five-fold symmetrical patchy particles. The DDQC can be attained by linearly slowly decreasing the temperature in the system (annealing).⁷ The obtained structures are not always ideal as the assemblies may have defects. This is particularly the case when the speed of temperature change is too fast. In this case, the DDQC structure no longer appears. In a Monte Carlo simulation of five-patch patchy particles,¹⁶ the temperature is quickly cooled down to zero, and then subsequently it is fixed at a specific value. This two-step temperature protocol was developed empirically. The challenge is to find a method that can learn and find suitable temperature settings to facilitate the formation of DDQCs with few defects, with no or little prior knowledge. In this study, we will show that reinforcement learning is useful for this purpose.

Reinforcement learning (RL) is a branch of machine learning that aims to learn an optimal policy and protocol to interact with the environment through experience. From the viewpoint of physical science, RL can estimate an external force or parameter change as a function of the state of the system. Therefore, RL shares many aspects with adaptive optimal control theory.¹⁷ RL can be versatilely applied in strategy games,^18,19 robotics,²⁰ and physical problems. Applying RL in dynamical physical problems, such as fluid mechanics^21,22 and navigation of a single self-propelled particle,²³ is promising because of its capability of finding the best control policy by iterating (experiencing) the dynamical processes without any prior knowledge. RL has been applied in optimising the best operational parameters for a system^24,25 or tuning the operational parameter during a dynamical process.²³ In ref. 25, the Q-learning algorithm²⁶ is used to remove grain boundaries from a crystalline cluster of colloids. Few studies have focused on many-body particles and their collective behaviours of active matter systems^27–29 or self-assemblies.^25,30 In ref. 30, the evolutionary optimisation method has been used to learn temperature and chemical potential changes for self-assembly of complex structures, such as Archimedean tilings. Despite the high performance of this black-box approach, the mechanism of success remains to be elucidated. We will discuss a more detailed comparison between this approach and our method in Section 4.

In this study, our main objective is to understand how and why RL works in a self-assembly process. Therefore, we employ a theoretically well-founded algorithm based on Markov decision processes, such as Q-learning, and demonstrate that RL can learn to control the temperature during the self-assembly of patchy particles into DDQC structures. Aside from that, different targets and different models are considered to demonstrate the generality of the proposed RL and to gain physical insights into these systems (see Section 4).

The paper is organised as follows: In Section 2, we explain our system and the simulations of the self-assembly, the basics of RL and the Q-learning approach, and the setting of the assembly problem into Q-learning. In Section 3, we show how the policy is estimated during training, and how the estimated policy works during tests to evaluate its optimality for the DDQC target. The generality of the current approach is demonstrated by using different targets whose structures are unknown. In Section 4, we discuss several issues, such as how the estimated policy avoids metastable states, training costs and the discreteness of states in Q-learning. We also discuss physical insights that we obtain from the RL results and a comparison of different RL approaches. Finally, we summarise the main findings of this work.

2 Methods

2.1 Reinforcement learning for dynamic self-assembly

Fig. 1 shows the schematic of reinforcement learning (RL) for the dynamical process of self-assembly. In RL, an agent learns how to interact with environments through actions, so as to maximise reward signals.^31–33 In the context of self-assemblies, RL aims to control the external force or the parameters on-the-fly so that the desired structure is organised from a random particle configuration. In this study, we control the temperature; our action is whether the temperature increases, decreases, or remains at the current value. The environment is the configuration of the particles under certain conditions, such as temperature and density. In principle, the dimension of the particle configuration is huge. It consists of all the degrees of freedom of the particles, their positions and orientations, which are, respectively, 2N and 3N for the system in this study. Our purpose is to make the desired structure, which is the DDQC. Therefore, we use statistical quantities (or feature values) to characterise the particle configurations. This is the number of σ particles, denoted as N_σ; we will discuss this issue in detail in Section 2.3. We consider two observed states from the environment: the temperature T and the ratio of σ particles of the DDQC, which is extracted from the particle configuration, to the total particles. We denote the ratio by σ = N_σ/N. From the observed states, we take an action a updating the current temperature to the next one. We also get a reward r_t from the measured state. From the reward, the next action is decided at each step and the procedure continues to update all different states. Within each step, the configuration of particles is updated by BD simulations. The control algorithm to be used is Q-learning. The details of RL and Q-learning are found in Section S1 in the ESI.†

Fig. 1 Schematic of reinforcement learning for dynamic self-assembly. The agent observes the state s from the environment and decides to take an action a based on the policy π. The agent learns the policy π by a training process to optimise the rewards r. In this study, the environment is the particle configuration under a given temperature. The observed states s are the ratio of the sigma particle σ and the temperature T. The action a is to decrease, maintain, or increase the current temperature.

The schematic for training with Q-learning in this study is given in Fig. 2. Initially, Q-table is set to zero for all a and s. The RL includes N_e epochs or episodes in which the ε-greedy method is applied. In each epoch, the initial state, i.e. the initial particle configuration, and the initial temperature (σ₀,T₀) are assigned. Next, the action a₀ (either decrease, maintain, or increase T) for the temperature is decided based on the current policy and the ε-greedy strategy, resulting in the new temperature T₁. The Brownian dynamics simulation for the current particle configuration at T₁ is conducted. Details of the Brownian dynamics simulation can be found in Section 2.2. The new particle configuration is obtained after a predetermined time t = N_BDΔt. Then one can determine the state σ₁, the reward r₁, and eventually update the Q-value Q(σ₀,T₀,a₀). This concludes the Q-learning of the first step. The next step can be conducted analogically from the current state (σ₁,T₁). The Q-table is updated at every action step and every epoch, until the training process ends.

Fig. 2 Schematic of Q-learning at each epoch with the ε-greedy method. The action a is chosen based on the current policy π and ε. Q is updated according to eqn (S2) (ESI†). The Brownian dynamics (BD) simulation is conducted for every action step in N_step of each epoch.

From the trained Q-table, we can estimate the policy for controlling the temperature with respect to the current state. In order to evaluate the estimated policy, 20 independent tests are conducted. Each test starts with an assigned initial particle configuration and temperature (initial states), followed by consecutive steps of deciding the next action based on the estimated policy, observing the new states, and so on. Unless otherwise stated, we set the parameters the same as the parameters used during training, except that ε = 0 is fixed in every test.

Table 1 shows the parameters of a training set for the target DDQC from patchy particles. The two observed states are the ratio of the sigma particle σ and the temperature T. Initially, the configuration of the particle is random (corresponding to σ₀ ≈ 0.1) and T₀ values are chosen randomly in the investigated range. The initial positions are obtained by inflation of randomly distributed points under repulsive forces to prevent overlapping. During RL, while the fraction of sigma particle never reaches out of the range [0,1], the temperature T_k+1 after the action a_k may exceed the investigated range. In this case, the updating is carried out as usual except that we treat T_k+1 = T_k. The policy after training is used for the test at the same conditions as training (except ε).

Table 1 Parameters for the training set of DDQC patchy particles

Parameter	Value
–States of the sigma fraction, σ	[0,1] With an interval of 0.1
–States of temperature, T	[0.2,1.3] With an interval of 0.1
–Actions on the temperature, a	{−0.05,0,0.05}
–Number of epochs, Ne	101
–ε-Greedy	Linearly decrease in each epoch from 1 to 0
–Initial temperature at each epoch, T0	Random, T0 ∈ [0.2,1.3]
–Initial structure at each epoch, σ0	Random configuration (σ0 ≈ 0.1)
–Number of action steps (RL steps) in each epoch, Nstep	200
–Number of BD steps in each RL step, NBD	100 000 Steps
–Time step in the BD simulation, Δt	10^−4
–Target, σ*	0.91
–Rewards, r	−(σ−σ*)^2
–Learning rate, α	0.7
–Discount factor, γ	0.9
–Number of particles, N	256
–Area fraction, A = πa^2N/(LxLy)	0.75

---

2.2. Self-assembly of patchy particles through Brownian dynamics simulations

Our system consists of N patchy particles. Each particle stochastically moves and rotates following eqn (1) and (2) at temperature T and time t (see Fig. 1). The patchy particle undergoes anisotropic interactions with other particles. Depending on the anisotropy, the particles may form an ordered self-assembled structure. Because the thermal fluctuation of the particles is dependent on the temperature, the self-assembled structure varies as the temperature changes.

The Brownian dynamics (BD) simulation is employed to simulate the assembly of five-fold-symmetric patchy particles.^7,13 The patchiness on the spherical particle is described by the spherical harmonic of Y₅₅. There are 5 positive patches and 5 negative patches arranged alternatively around the particle's equator (see Fig. 1). We set that the same sign patches are attractive while opposite patches are repulsive. The particles are confined to a flat plane, meaning that the particles can translate on the plane while they can rotate freely in three dimensions. We use the NVT ensemble under periodic boundary conditions applied in the x and y directions of a simulation box of size L_x × L_y × 2a, where a is the particle radius. In the Brownian dynamics, the position r and orientation Ω of the particle are updated according to the following equations:

where D^T and D^R are the translational and rotational diffusion coefficients, respectively, k_B is the Boltzmann constant, F and T are the force and torque, and the Gaussian noise terms δr and δΩ are with zero mean and satisfying 〈δrδr^T〉 = 2D^TΔt and 〈δΩδΩ^T〉 = 2D^RΔt, respectively. The characteristic length, energy, time, and temperature for the nondimensionalisation are the particle radius a, the potential well-depth ε_V, the Brownian diffusion time τ_B = a²/D^T, and ε_V/k_B, respectively.

The interaction potential of a pair of particles i and j is V_ij = V_WCA(r_ij) + V_M(r_ij)Ξ(Ω_ij). The isotropic Week-Chandler–Anderson term V_WCA prevents the overlapping of particles. The interaction of the patchiness is given by the Morse potential V_M and the mutual orientation dependent term Ξ(Ω_ij) as follows:

where r is the center–particle distance and the Morse potential equilibrium position, depth and range are respectively r_eq = 1.878a, M_d = 2.294a, and M_r = a.³⁴

The orientation of particle i is determined by the orthogonal local bases n̂⁽ⁱ⁾_m, m = 1,2,3 (see Fig. S7, ESI†). Let r̂ be the unit distance vector of particles i and j. The interaction of a pair of particle Y_lm is Ξ_lm ∝ {n̂^l–m₀n̂^m₊}_(i)⊙{r̂^2l}⊙{n̂^l–m₀n̂^m₊}_(j), where n̂₀ = n̂₃, , and {} indicates the irreducible tensor. For a pair of Y₅₅ particles Ξ₅₅ ∝ {n̂⁵₊}_(i)⊙{r̂¹⁰}⊙{n̂⁵₊}_(j), Ξ is normalised to be in the range of [−1,1].

2.3 Characterisation of DDQC structures

One method to characterise two-dimensional DDQCs is to determine local structures around each particle according to its nearest neighbours^7,16,35 (Fig. 3). Given the particle positions, the σ, hexagonal Z, and H local structures are estimated. A DDQC structure usually contains a few Z dispersed in many σ particles and a few H particles. In detail, a dodecagonal motif, which is made from one centred Z and 18 σ particles (Fig. 3d), is observed in the DDQC. The motifs can be packed in different ways, e.g. the centres form triangles and squares.^7,16 The ratios of the σ, Z, and H particles to the total particles in the packed motifs are found to be 0.8 ≤ σ ≤ 0.93, 0.07 ≤ Z ≤ 0.14, and 0 ≤ H ≤ 0.13, respectively. Such ratios are found comparable to those in square-triangle tiling³⁶ or the simulated DDQC.^7,16

Fig. 3 Characterisation of DDQCs. (a) Demonstration of local structures. (b) and (c) Examples of DDQCs with few and many defects, and the corresponding Fourier transformations. The particles are coloured grey, yellow, and orange according to the local structures σ, Z, and H in (a). The undefined particles (U) are marked purple. The fraction of sigma in (b) and (c) are 0.84 and 0.67, respectively. (d) Dodecagonal motif made from one Z particle centred in 18 σ particles.

In our previous study,⁷ we found that the DDQC consists of several different motifs, each of which can form an approximate. In this view, the ratio of the number of sigma particles to the total number of particles in DDQCs is expected to be 0.8 ≤ σ ≤ 0.93, as mentioned earlier. However, at finite temperatures, defects can always appear during the self-assembled process, and therefore, σ can be smaller than those values, which we consider 0.7 ≲ σ ≲ 0.93. Besides this, when the structure is frozen with many defects and forms metastable states, σ becomes much smaller. We should note that in our simulations, the out-of-plane rotation is allowed. Therefore, the plane of five patches may deviate from the xy plane. We check that this rotation rarely occurs for DDQC structures, while the deviation occurs for the Z-rich phase (see Fig. S7, ESI†).

In order to clarify equilibrium and metastable structures, RL is supplemented by three additional simulation methods under the same conditions of RL with an area fraction A = πa²N/(L_xL_y) = 0.75, and the investigated temperature is T ∈ [0.2,1.3]. The three methods are (i) replica exchange Monte Carlo^37,38 (REMC, or called parallel tempering) described in Section S3 in the ESI,† (ii) BD simulations under quenching to a fixed temperature (Section S4 in the ESI†), and (iii) BD simulations under annealing temperature (Fig. 7). In (ii), we prepare an initial configuration at a random position and orientation, and then, set the temperature at a lower value.

In REMC, we found that the equilibrium phases are fluid at high temperatures T ≳ 1.8, the Z-phase at intermediate temperatures T ≳ 0.9, the DDQC (σ = 0.84 ± 0.023) at low temperatures T ≲ 0.89. We should note that the σ-phase appears when the area fraction is smaller than the current value. Details of the calculation of the phases in REMC are found in Fig. 12 and Section S3 (ESI†).

The DDQC with defects can typically be seen in the self-assemblies under quenching to a fixed temperature from a random initial configuration (Fig. S6, ESI†). At intermediate temperature T ∈ [0.7,0.85], there is a DDQC with σ ∈ [0.7,0.9]. At a lower temperature T ∈ [0.35,0.7], σ decreases within σ ∈ [0.5,0.7] as T decreases. This lower value of σ is different from that of the equilibrium state, as shown in Fig. 12 (see also Table S3, ESI†). Therefore, we refer to these structures as metastable because many particles are kinetically trapped during the growth of the DDQC. At much lower T, σ keeps decreasing to 0.2.

During the training of RL, the value of σ is used to evaluate the DDQC structures (Fig. 3). As discussed in this section, we consider that structures with 0.7 ≲ σ ≲ 0.93 are DDQCs with a few defects. We take this range from the value of the equilibrium DDQC obtained from REMC (see Fig. 12 and Table S3, ESI†). These values of σ are comparable with the ideal value of the DDQC. The finite range of σ of the DDQC arises from the appearance of defects at finite temperatures in which structural fluctuations effectively reduce σ. On the other hand, when 0.5 ≤ σ ≤ 0.7, there are many defects in the structures and we refer to them as metastable states. This argument confirms that the DDQC and metastable structures can be distinguished by the value of σ. In fact, their Fourier transformation is distinguishable. The DDQC has clear twelve-fold symmetric spots separated from the background, whereas the metastable structure has blurred twelve-fold symmetry (Fig. 3).

2.4 Target structures for RL

In RL, we choose σ as one of the RL states with 0 ≤ σ ≤ 1. The value σ* of the target DDQC is set as σ* = 0.91. At the density used in this study, using σ alone is adequate to identify different states formed during the assembly process (see Section 2.3 and Table S3 for the details of other local structures, ESI†). In other cases where the system has more complex structures, other quantities, such as Z and H, may be needed. However, as we demonstrate, using σ not only works for the DDQC target σ* = 0.91 (Section 3.1), but also for other targets such as σ* = 0.65 and σ* = 0.35 (Section 3.2). We will demonstrate that RL is capable of stabilising a metastable structure (σ* = 0.65) and even finding a policy to control the structure dynamically to realise the unstable target structure (σ* = 0.35). To do this, we use the value iteration method for the two targets (see Section S2 in the ESI†).

Another state used in RL is the temperature T. The range of the temperature is chosen as 0.2 ≤ T ≤ 1.3 so that the particle interaction dominates the noise at T_min and the noise dominates the interaction at T_max.

We also demonstrate the generality of proposed RL by estimating the policy for DDQC formation from particles interacting through a two-length scale isotropic potential in Section S7 (ESI†). This model is known to exhibit DDQC structures.³⁹ Details of the isotropic potential are found in ref. 7 and the references therein.

3 Results

3.1 Optimal temperature change to generate DDQCs from patchy particles

3.1.1 Training process. First, we demonstrate the capability of Q-learning to find the best temperature schedule to create DDQCs of patchy particles from random configurations. Fig. 4 shows the training result under the condition in Table 1, where the policy is trained with N_e = 101 epochs and the initial temperature T₀ at each epoch is randomly assigned within the investigated range. During each epoch, the action changes according to the current policy and ε, hence the states of temperature T and ratio σ change at each step, as shown in Fig. 4(a and b). In the first epoch in which ε = 1, T fluctuates around T ≈ 1.0. Accordingly, σ is low σ < 0.2 and far from the target value σ*. As the training continues, the Q-table is updated. In the next epoch, we repeat the process with a new initial random configuration and random temperature. However, we use smaller ε and the updated Q-table. In the mid epoch n = 51 at which ε = 0.5, T fluctuates around T ≈ 0.7, whereas in the last epoch n = 101 at which ε = 0, T shows less fluctuation around T ≲ 0.7. After the epoch n = 51, σ approaches closer to σ*.

Fig. 4 Training data under the conditions of random T₀ and number of epochs N_e = 101 in Table 1. (a) and (b) The progression of the states T and σ at selected epochs: first, middle and last epoch (equivalent ε = 0, 0.5, and 1, respectively). (c) The policy after training, the dashed line indicates the target at σ* = 0.91. (d) The change of the ratio of the number of accessed states to total states and (e) the ratio of flipped-policy states to accessed states after each epoch during training, the horizontal axis on the top of the graph is the corresponding value of ε. The inset shows the number of flips at each state from epoch 81 to epoch 101.

Fig. 4(c) demonstrates the policy after training, which is the action for the maximum of Q, namely, argmax_aQ(σ,T,a). This state-space roughly consists of two regions divided by a characteristic temperature T* = 0.7. The estimated policy is to decrease the temperature above T* and to increase the temperature below T*. When σ ≥ 0.8, the temperature can be decreased further to T ≈ 0.5. Such a behaviour is expressed by the blue and grey cells, defined by the lower left corner, at (σ,T) = (0.8,0.5), (0.8,0.6) and (0.7,0.6). We will evaluate this policy by performing tests in Section 3.1.2. The action of ‘maintaining temperature’ can be seen scattered in the policy, but no clear correlation to the states is observed. The policy has states that are not accessed during training. The action for these inaccessible states is random. Fig. 4(d) presents the ratio of the number of accessed states to total states during training (the total number of states is 10 × 11). We also measure whether the policy converges to its optimal in Fig. 4(e), by defining the ratio of the number of flipped states to accessed states. The flipped state is counted when the policy at the current epoch π⁽ⁱ⁾(s,a) changes compared to the policy at the previous epoch π⁽ⁱ⁻¹⁾(s,a). The ratio decays to ≲ 0.1, but the decay is slow. Even after the epoch of ε ≲ 0.4 after which the number of accessed states reaches a plateau, the ratio is still decaying slowly, meaning that there is still uncertainty in policy. The number of flipped states of each (σ,T) during epoch 81 to 101 is shown. Majority of the flips comes from the states with σ ∈ [0.5,0.8] and T ∈ [0.7,0.8]. This result suggests that many epochs are required to reach an optimal policy.

3.1.2. Testing evaluation. After training, the estimated policy is tested. The results of the test are presented in Fig. 5. The time evolution of temperature and σ during the test with initial configurations of random particle positions and orientations and with random T₀ is shown in Fig. 5(a and b). First, T quickly reaches the characteristic temperature T* = 0.7 and then fluctuates around that value until σ reaches the target value. Finally, T decreases to T ≈ 0.6. The final temperature is dependent on each realisation. The snapshots at the final steps have dodecagonal motifs consisting of one Z particle centred in 18 σ particles (see Fig. 3(d)). The intensities in the Fourier space show clear twelve-fold symmetry, although some defects are present in the real space.

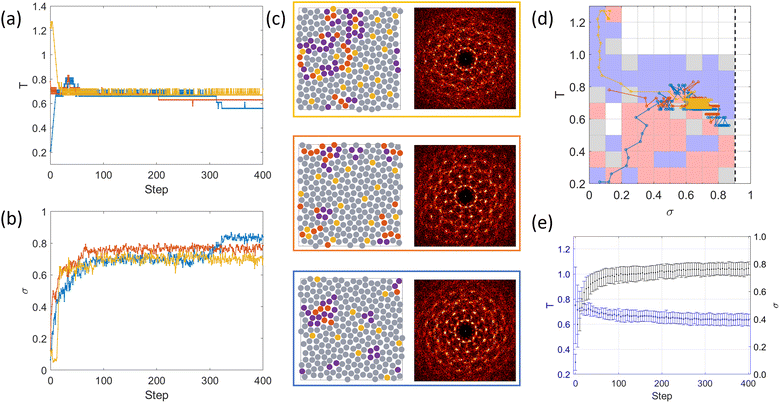Fig. 5 Testing data of the policy obtained under the conditions of random T₀ and number of epochs N_e = 101 in Fig. 4. Samples starting with low (blue), intermediate (red), and high (yellow) initial temperatures are shown with (a) the temperature schedule, (b) corresponding σ, and (c) snapshots at the last step of the corresponding trajectories. Particles are coloured by the local structures defined in Fig. 3. (d) The trajectories of (a,b) on the policy plane obtained from Fig. 4(c), in which the starting points are from the left side. Changes of temperatures of the trajectories follow the policy shown in the background. The vertical dashed line indicates σ = σ*. (e) Error bars of temperature (blue) and σ (black) showing the mean and standard deviation from 40 independent samples.

Fig. 5(d) shows trajectories of the states (T and σ) during the test together with the estimated policy. We show the three trajectories with different initial temperatures: high T₀, intermediate T₀, and low T₀. In the case of high T₀, the temperature decreases to T ≈ 0.8 but σ does not increase. Once the temperature becomes T ≈ 0.7, dodecagonal structures start to appear and σ increases and fluctuates around σ ≈ 0.7.

In the case of low T₀, some dodecagonal structures appear from the beginning because the temperature is low. As the temperature is increased to T ≈ 0.7, σ is also increased and reaches σ ≈ 0.7. The temperature is found to decrease at a point of σ ≈ 0.8.

When the initial temperature T₀ is intermediate, σ increased, then fluctuates, and finally, it is increased more when T is decreased slightly. Note that in all cases, the initial σ is small because the initial configuration of particles is random in position. Using this policy, the DDQC structure can be obtained in tests at any value of the initial temperature, as depicted as σ = 0.77 ± 0.05 in the last step in Fig. 5(e). In this figure, in the first 10 RL steps, the variance of temperature is large because the initial temperature is random in the investigated range. After 50 steps, the temperature reaches the characteristic temperature. Then, the mean temperature statistically decreases from 0.7 to 0.63 as the mean σ increases from 0.68 to 0.77. The result suggests that RL has learned the importance of maintaining the temperature at T*, which then further decreases when σ ≥ 0.8. We would note that although the policy still flips, such a behaviour is observed, e.g. the tests following the policy obtained at epoch 81 and epoch 101 are statistically similar (see Section S9, ESI†). The tests seem independent of the number of epochs when the number of epochs is large enough.

We also check the test in which the initial configurations are not random but chosen from the state with σ = 0.56 and σ = 0.87 (see Section S6, ESI†).

In short, the RL agent has found out the role of the characteristic temperature T* in facilitating the formation of the DDQC structure. As a result, when the DDQC is not formed (low σ), the RL policy suggests to drive the temperature to T* until a DDQC (high σ) is formed and then decrease T to stabilise the structure. We discuss T* in comparison with the temperature where the transition of the DDQC and Z-state is observed in Section 3.3.

The RL has discovered the characteristic temperature by itself. We do not feed any information about the role of T* nor its value. The role of T* is in contrast with the results for the system with the isotropic interactions (see Section S7, ESI†). The policy in the isotropic system is simple; that is, quenching the temperature to 0.4 results in the DDQC after 50 RL steps. For example, when the initial temperature is high, e.g. T₀ = 1.2, then during the decrease of temperature, the DDQC is created from the Z-phase at T ≈ 0.8. A further decrease of the temperature to T = 0.5 brings almost no change in the DDQC structure. We rarely observe the metastable state (σ ∈ [0.5,0.7]) in the isotropic system. The RL learns that in the isotropic particle system, the transition temperature between the DDQC and the Z-phase is not important in the formation of the DDQC.

We further check the stability of the optimised structures, by extending the simulations at fixed temperatures in the last RL step. The results of the stability test are shown in Fig. 6 along with the statistics of the local environments. Compared with the RL test, we found no significant difference in the statistics of the local environments, which implies that optimised structures are inherently stable.

Fig. 6 Stability of the RL tests under the conditions of random T₀ and the number of epochs N_e = 101 in Fig. 5. (a) Continuation of the optimised structures from the step 400 in Fig. 5(a) at a fixed temperature. The number of BD steps is 20 × 10⁶ steps, equivalent to 200 RL steps. (b) Statistics of the local structure for 20 independent samples in Fig. 5(e).

3.1.3. Comparison of RL with conventional approaches. Next, we compare the formation of a DDQC using the estimated policy with the self-assembly using the conventional annealing and quenching methods.⁷Fig. 7 shows the trajectories of T and σ for different realisations. In the annealing simulations, we have used the linear temperature decrease during BD steps. In this case, the time step for each BD step was also decreased for numerical stability. In annealing and RL methods, σ values reach σ ≈ 0.8, in which the dodecagonal structures appear clearly with a few defects. The ratios of Z and H are also comparable between the two methods (see Table S3, ESI†). To evaluate the speed of DDQC formation, we fit each trajectory of σ(t) by a sigmoid function and estimate its time. In the case of annealing, we have used a pre-fixed temperature schedule, and therefore, t ≳ 1600 is required for the dodecagonal structures. Before the temperature reaches T ≈ 0.8, no structural changes occur. In contrast, with the RL policy, σ increases quickly and then levels off. The estimated timescale is t ≈ 150, which is much faster than that of annealing. We should emphasize that when RL is used, the temperature is controlled according to the measured states. To check its importance, we try fast annealing in which the temperature is decreased until t = 150 and then fixed at the low temperature (see purple lines in Fig. 7). In this case, the DDQC starts appearing at the comparable time τ_sigmoid ≈ 90 with the RL case (τ_sigmoid ≈ 150). However, the final structure under the fast annealing is σ < 0.6 and contains many defects in the DDQC. This result demonstrates that the fast annealing schedule using a speed comparable to RL does not make a clear DDQC as our RL can do.

Fig. 7 Comparing DDQC assemblies by the RL temperature policy and annealing. The thin lines are the temporal changes of the temperature and σ ratio of samples from RL testing (grey), annealing (blue), fast annealing (purple), and fixed temperature at T = 0.6 (quenching) (red). The bold lines of σ are the mean values. Simulation parameters are N = 256, A = 0.75, and random initial configurations are used. The vertical dashed lines τ_sigmoid indicate the average onset time of DDQC formation for RL (grey) and annealing (blue and purple) tests fitted by sigmoid functions. The corresponding temperatures at τ_sigmoid of the annealing settings are 0.8 (blue) and 0.74 (purple).

We also compare RL and rapid quenching at a fixed temperature. The temperatures in RL change, but their values finally become in the range of [0.6, 0.7]. Therefore, the quenching temperature we chose is T = 0.6. As depicted in Fig. 7, the obtained assemblies have σ ≈ 0.6, meaning that they are trapped in the metastable states and contain more defects than that of RL or annealing. Readers may refer to Fig. S6 (ESI†) for quenching at other temperatures.

In the training steps, we use a small system size, N = 256. It is important to check whether the estimated policy using RL can work upscale. We perform tests at larger system sizes N = 512 and N = 1024 using the estimated policy with N = 256 (Fig. 4(c)). Fig. 8 demonstrates the obtained structures of different system sizes. The estimated policy for the smaller systems size works even for the tests with all investigated system sizes, namely, we obtain σ ≳ 0.7. The mean value of σ seems to slightly decrease with the system size. This is because the larger system size requires more time to stabilise. If more steps are conducted for a larger system size, there is no significant difference between the three groups. In fact, the snapshots both in the real and Fourier spaces for the larger system sizes show dodecagonal structures.

Fig. 8 Performance of the testing on different system sizes, where the policy is trained with the system of N = 256 particles. The means and standard deviations are calculated from 20 independent samples after 400 RL steps (black) and 1000 RL steps (blue). The snapshots and Fourier transformations are demonstrated for N = 512 (upper) and N = 1024 (lower) tests.

3.2 Reinforcement learning for unknown targets of patchy particles

In Section 3.1, we use the target σ* = 0.91 to obtain the DDQC structure. This structure is at an equilibrium state under a certain temperature (see Section 3.3). In this section, we demonstrate that RL also works for the unknown target structures, which are not equilibrium states. To do this, we perform RL for different targets: σ* = 0.65 and σ* = 0.35 in patchy particle systems. The estimation of the policy is conducted by the value iteration method (Section S2, ESI†) instead of training the Q-table through numerous episodes because of the availability of sufficient data (see Table S4, ESI†). As shown in Fig. 9, RL estimates different policies for different targets.

Fig. 9 Reinforcement learning for other assemblies of patchy particles with the targets (a)–(c) σ* = 0.65 and (d)–(f) σ* = 0.35. (a)–(c) The policy with selected trajectories during the tests and the corresponding temperature and σ of the tests for σ* = 0.65. The mean and standard deviation of σ from 20 independent samples are 0.63 and 0.03, respectively. The snapshot at the last point of the blue trajectory is given. (e) and (f) The temperature schedule and σ of selected trajectories for σ* = 0.35. Three snapshots of the orange trajectory are given. (d) The trajectories of the tests on the policy plane in which only part of the data (darker points) is used. The mean and standard deviation of σ from 20 independent samples are 0.42 and 0.14. The vertical dashed line in (a) and (d) indicates σ = σ*.

For σ* = 0.65, the structure obtained from the estimated policy has σ ≈ σ*, which is close to the DDQC but with many defects. The policy in Fig. 9(a) shows a border at the characteristic temperature at T* = 0.7 when σ is small σ < 0.6. The policy is similar to the case of the DDQC target in Fig. 4 and 5. It suggests to drive the temperature to T* so that σ increases, that is to decrease T if T₀ is high (orange trajectory) and to increase T if T₀ is low (blue trajectory). Then, when σ ≳ 0.6, we decrease the temperature and maintain it around T ∈ [0.4,0.5] to trap the particles kinetically. As a result, the structures remains metastable with σ ≈ σ* = 0.65.

Moreover, the structures obtained at the end of RL undergo stabilisation at the corresponding temperatures (Fig. 10). The continuation of the two trajectories in Fig. 9(c) is shown in Fig. 10(a). Here, the temperature is fixed at the last temperature of RL tests, which is T ≈ 0.5. No significant change of σ is observed. Fig. 10(b) indicates that σ is statistically maintained around σ* = 0.65 before and after stabilisation. When σ > 0.8, the DDQC is the undesired structure as we set σ* = 0.65. Fig. 9(a) also shows how the policy prevents the DDQC by increasing T whenever σ > 0.8. It can be inferred that the system will be brought to the state of high T and low σ, which locates on the upper left of the policy in Fig. 9(a). Then the state-action is operated somewhat similar to the trajectory in orange. This kind of behaviour when σ deviates from the target is observed more clearly when the target structure is σ* = 0.35.

Fig. 10 Stability of the RL tests for σ* = 0.65. (a) Continuation of the optimised structures from the step 200 in Fig. 9(a)–(c) at the fixed temperature. The number of BD steps is 20 × 10⁶ steps, equivalent to 200 RL steps. (b) Statistics of the local structure for 20 independent samples.

In Fig. 9(d–f), the policy and tests for the target σ* = 0.35 are demonstrated. The policy can be divided into three regimes, represented by the snapshots 1, 2, and 3. First, a large σ structure (σ > 0.5) is avoided by increasing the temperature (see snapshot 1 of Fig. 9(d–f)). When T ≈ 0.85, the structure strongly fluctuates with 0 < σ < 0.65, for example, between snapshots 1 and 2. When σ becomes small, the blue region in the policy around snapshot 2 suggests decreasing the temperature, and the system attempts to reach a state such as snapshot 3. The structure near snapshot 3 is not stable, and after a long time, the structure deviates from the target, i.e. σ > 0.5. Then, a new cycle of snapshots 3 → 1 → 2 occurs.

We check the stability of the obtained structure from the RL test, similar to the case of σ* = 0.91 and σ* = 0.65. We fix the temperature after the RL tests at the corresponding temperature after 1000 RL steps (Fig. 11). The samples before fixing the temperature have σ close to σ*. Fig. 11(b) illustrates structural changes after the stability test. The results show that the obtained structure is not stable for the target σ* = 0.35. After fixing the temperature, some tests at T < 0.5 still have their σ fluctuate around σ*, while others deviate from the target. In order to drive these tests to the target, the temperature should follow the policy. The result reveals that RL can learn even when the target is unstable, and we can obtain the target structure dynamically by changing the temperature.

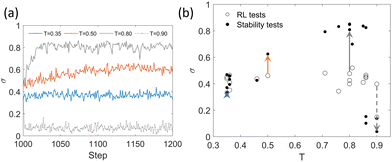Fig. 11 Stability of the RL tests for σ* = 0.35. (a) Continuation of the structures from the step 1000 in Fig. 9(d)–(f) at the corresponding temperature. Two more tests (grey) are given. The number of BD steps is 20 × 10⁶ steps, equivalent to 200 RL steps. (b) Comparison of the structures in the first and last points in (a) for 20 independent tests. The arrows connect the first and last points of the tests in (a).

3.3 RL, equilibrium phases, and metastability

We have investigated how the RL agent learns and proposes policies for temperature control of patchy particles to form a DDQC. Our results suggest that the best policy for making the DDQC is to change the temperature quickly to a characteristic temperature T* = 0.7, maintain the temperature until the system is dominated by the dodecagonal structures, and then decrease the temperature further to get the DDQC stabilised. It is noted that the characteristic temperature T* is autonomously found out by RL. At this temperature, the structural fluctuations are enhanced. As a result, there is more chance of getting the dodecagonal structure. In the estimated policy by RL, if the temperature is high, the particles are too mobile to make an order structure. Hence, a decrease in temperature is suggested. When we start from low T₀, the policy suggests increasing temperature so that the system may escape from the metastable state.

Our RL suggests that the policy changes at the characteristic temperature T* = 0.7. Fig. 12 shows an equilibrium local structure at each temperature computed by REMC. The phase change between the Z-phase and the DDQC occurs at T ≈ 0.89 (see Section S3, ESI†). Simulations of random initial configurations with finite cooling rate methods such as quenching (rapid temperature change) and annealing (slow temperature change) show the transition at lower temperatures. In quenching (Fig. S6, ESI†), the DDQC is formed when T ≈ [0.7,0.85]. If T < 0.7, the patchy particles cannot form DDQCs because the system gets trapped in the metastable states, and it is unlikely to remove the defects at the fixed temperature. In this sense, the characteristic temperature T* = 0.7 coincides with the lower limit of fixed T setting for the DDQC. On the other hand, during annealing (Fig. 7, blue lines), the system has more chance to escape from the metastable states. The onset of the DDQC is observed at T ≈ 0.8. In our study, the action space for temperature is a = {−0.05,0,0.05}, meaning that the cooling rate is at most −0.05 per RL step. At this rate, the onset of the DDQC occurs at T ≈ 0.74 (Fig. 7, purple lines). A faster cooling rate generally lowers the effective transition temperature, because the particles do not have sufficient time to settle in the stable configuration. They remain at the disordered state even when the temperature decreases and passes the transition temperature. Therefore, the system needs a further drop in temperature for the transition to occur. At a result, the observed transition temperature becomes effectively lower in RL than that by REMC. We should note that in the policy of RL, the temperature is discretised in a mesh size of 0.1. The characteristic temperature T* may exhibit deviations dependent on the mesh size. Another point to be noted is that T* in the policy exists when the current structure is not a DDQC, in particular σ < 0.7. When a DDQC structure is obtained, the temperature should be kept around 0.5.

Fig. 12 Dependence of the local structure on temperature, and the dominant phase by REMC. The mean (dot) and standard deviation (bar) are calculated from RE step 200 to 1000 in Fig. S2 (ESI†).

We should emphasise that our RL does not optimise the distribution of σ as a function of temperature, nor the phase diagram. The RL policy suggests the most rewarding pathway to reach the target. RL can learn that the characteristic temperature T* plays an important role in enhancing the probability of QC structural formation. The RL method automatically finds them during the training steps without being provided with the existence or the value of this temperature.

4 Discussion and conclusions

Before summarising our study, we discuss several issues to clarify the mechanism and generalisation of RL and compare our RL with other studies.

We focus on the estimation of the policy for the DDQC, which is stable in a certain range of temperature. The optimal policy includes maintaining the temperature around a characteristic temperature T* = 0.7 and then decreasing the temperature when the structure reaches the DDQC target. However, our RL method is not limited to such a stable target structure. In fact, we demonstrate that RL can estimate the temperature protocol for metastable and even transiently stable structures. To obtain the metastable structure as a target (σ* = 0.65), we may maintain the system near the characteristic temperature T* = 0.7 in which structural fluctuation is large. Then, the temperature is rapidly decreased so that the structure is frozen at the desired metastable state. When the target is not even at the metastable state (σ* = 0.35), starting from a random configuration, the policy suggests to wait at a certain low temperature to obtain the target structure. In this case, the structure is transient, and after some time, it escapes from the target. Then, the temperature changes so that the system returns to the target structure.

RL can work for different types of particle interactions. We demonstrate it by studying particles forming DDQCs with the isotropic two-length-scale interaction. The result also highlights different properties of self-assembly in the two systems. Compared to the policy for the DDQC by patchy particles, the policy in the isotropic interaction system is much simpler, as no characteristic temperature is found.

These results, including the temperature protocol for the DDQC, may be reached from a sophisticated guess, but we think that this is not the case for many people. For example, a simple feedback control (that is to keep T constant if σ < σ* and decrease T if σ ≥ σ*) works only when the initial temperature is T*. From a higher temperature, T > T*, the system remains in the Z state, whereas from a lower temperature, T < T*, the system gets trapped in the metastable states σ < 0.6. Since we do not have prior information of T*, we cannot obtain the DDQC by the simple control. We believe that RL, like any machine learning method, can assist our finding mechanisms of unknown phenomena and making decisions more efficiently. To tackle more complex, highly non-linear, and high dimensional problems, the combination of machine learning with expertise in decision making may help to understand the problem better.

The choice of statistical quantities that characterise the structures is crucial for designing a successful RL system. This includes the choice of the relevant states and how finely to discretise the states (for Q-table). In the case of DDQC, the continuous state we choose is the ratio of the σ particles because σ can span over a wide range in [0,1] under the investigated temperature. Therefore, the states can distinguish the DDQC from metastable and disordered structures. The Z particles can be considered to evaluate the DDQC structure. However, under the same conditions, the performance of Q-learning with Z is not as good as Q-learning with σ because the ratio of Z spans over a much narrower range. Methodologically, there is no limit of number of states in RL. For example, one may include two microscopic states, e.g. σ and Z. When the dimension of states is much higher, the computational cost using a Q-table is too high. Approximation of the Q-function by the small number of continuous basis functions is promising in this direction.⁴⁰

One general concern in RL is the training cost. In our study, the total number of discretised states in Q(σ,T,a) is not so huge; therefore, we propose to use 101 epochs for training. Considering the dimension of the Q-table, this choice of the number of epochs is consistent with previous studies. For example, Nasiri and Liebchen²³ employed RL with a neural network to optimise the path of a self-propelled particle on a two-dimensional space. They performed 200 000 episodes for a total state-action space of 50 × 50 × 60. Sankaewtong et al.⁴¹ trained their neural network for smart microswimmers in three-dimensional flow fields with 1000 episodes. Their system has 19 states and 7 actions.

The number of particles in self-assembly is an important factor as it directly affects the computational cost. In our study, we consider N = 256 during training. The cost for training increases with the system size in two ways: (i) cost per simulation step scales as N² if the forces of all pairs in the Brownian dynamics simulation are included. It can cost less depending on the range of the potential and the use of neighbour list methods. (ii) The simulation time increases because the relaxation time increases with the system size. It means that in each RL step in training where the action is applied, the number of Brownian dynamics steps should be increased so that the structure is sufficiently relaxed. We should emphasise that our estimated policy using N = 256 can be used for the tests of the larger system sizes without extra training efforts (Fig. 8).

The periodic boundary conditions implicitly impose artificial periodicity on quasicrystals. Therefore, our DDQC is, strictly speaking, not quasicrystal but periodic (higher-order approximants), though its unit cell is very large. Still, the structures found in our system exhibit similar characteristics to a true DDQC,⁷e.g. the Fourier transform has twelve-fold symmetry. Despite the limitation in system size, our results demonstrate that RL can learn to create structures with specific symmetries.

In this study, we use the states of T and σ, the action space of change in temperature ΔT, and the reward function of −(σ − σ*)². However, we still need to consider many hyperparameters, such as the number of epochs N_e during training and the effect of discretisation. We discuss some general issues: how prior knowledge can help reduce the calculation cost, the effect of discretisation of Q-table, and the effect of ε-greedy, in the ESI.†

There are many ways of doing reinforcement learning.^32,33 In their study on RL for self-assembly,³⁰ Whitelam and Tamblyn have shown that the evolutionary optimisation to train the neural network can learn actions on the control parameters, such as temperature and chemical potential, for the self-assembly of a target structure. Evolutionary optimisation uses a black-box approach to learn the action as a function of the state (or time), which is expressed by the weights in the neural network.⁴² On the other hand, Q-learning relies on the maximisation of future reward, which is expressed by Bellman's equation. The sampling during training is also different in the two methods. The evolutionary optimisation requires the final outcome of the trajectory of the self-assembly process, while Q-learning updates the policy iteratively by observing the state-action pair during the dynamical process. As a result, Q-learning works on-the-fly and requires a less computational cost compared to evolutionary optimisation. We should emphasize that regardless of the differences, both evolution-type optimisation and Q-learning based on the Markov decision process estimate the policy that can produce the target faster than a conventional cooling scheme. More studies are necessary to clarify generic guidelines on how to choose a suitable RL model.

Although RL can estimate the best temperature protocol, it has to be related to the physical properties of the system. The work in ref. 15 proposed a temperature protocol based on free energy calculations of the nucleation barrier and metastability of the free energy minima. Although it is treated as a toy model, relating the physical properties of QC formation and performance of RL would be an interesting future direction.

To summarise, we employ RL to estimate the best policy for temperature control during the self-assembly of patchy particles into DDQC structures. Using the estimated policy, we successfully obtain the DDQCs even for the system size larger than the size we use for training. The key to the success is that RL finds the characteristic temperature of the DDQC self-assembly during training. The estimated policy suggests that, first, we change the temperature to the characteristic temperature so that the larger fluctuations enhance the probability of forming DDQCs, and then decrease the temperature slightly to remove defects. In order to avoid metastable states, the optimal policy suggests increasing the temperature if we start from a low temperature. The RL is capable of giving insights into different self-assembled systems, and dynamically adapting the policy in response to the unstable target. We should emphasize that our method can be applied to other parameters that we may control. Therefore, we believe that the method presented in this work can be applied to other self-assembly problems.

Author contributions

U. L. performed the simulations and analysed the data. N. Y. designed the research. All the authors developed the method and were involved in the evaluation of the data and the preparation of the manuscript.

Data availability

The data supporting this article have been included in the ESI.† The codes of RL for the self-assembly of patchy particles can be found at https://github.com/ULieu/RL_patchy.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge the support from the JSPS KAKENHI Grant number JP20K14437, JP23K13078 to U. L., and JP20K03874 to N. Y. This work is also supported by the JST FOREST Program Grant Number JPMJFR2140 to N. Y. The authors would like to thank Rafael A. Monteiro for bringing the idea of reinforcement learning to our attention.

References

1. A.-P. Hynninen, J. H. J. Thijssen, E. C. M. Vermolen, M. Dijkstra and A. van Blaaderen, Nat. Mater., 2007, 6, 202–205.
2. M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529.
3. R. Tamura, A. Ishikawa, S. Suzuki, T. Kotajima, Y. Tanaka, T. Seki, N. Shibata, T. Yamada, T. Fujii, C.-W. Wang, M. Avdeev, K. Nawa, D. Okuyama and T. J. Sato, J. Am. Chem. Soc., 2021, 143, 19938–19944.
4. K. Deguchi, S. Matsukawa, N. K. Sato, T. Hattori, K. Ishida, H. Takakura and T. Ishimasa, Nat. Mater., 2012, 11, 1013–1016.
5. Q. Chen, S. C. Bae and S. Granick, Nature, 2011, 469, 381–384.
6. I. E. Ventura Rosales, L. Rovigatti, E. Bianchi, C. N. Likos and E. Locatelli, Nanoscale, 2020, 12, 21188–21197.
7. U. T. Lieu and N. Yoshinaga, Soft Matter, 2022, 18, 7497–7509.
8. S. C. Glotzer and M. J. Solomon, Nat. Mater., 2007, 6, 557–562.
9. M. Engel, P. F. Damasceno, C. L. Phillips and S. C. Glotzer, Nat. Mater., 2015, 14, 109–116.
10. Y. Geng, G. Van Anders and S. C. Glotzer, Nanoscale, 2021, 13, 13301–13309.
11. R. Kumar, G. M. Coli, M. Dijkstra and S. Sastry, J. Chem. Phys., 2019, 151, 084109.
12. Y. Ma and A. L. Ferguson, Soft Matter, 2019, 15, 8808–8826.
13. U. T. Lieu and N. Yoshinaga, J. Chem. Phys., 2022, 156, 054901.
14. N. Yoshinaga and S. Tokuda, Phys. Rev. E, 2022, 106, 065301.
15. A. Bupathy, D. Frenkel and S. Sastry, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2119315119.
16. M. N. van der Linden, J. P. K. Doye and A. A. Louis, J. Chem. Phys., 2012, 136, 054904.
17. J. Bechhoefer, Control theory for physicists, Cambridge University Press, 2021.
18. D. Silver, T. Hubert, J. Schrittwieser, I. Antonoglou, M. Lai, A. Guez, M. Lanctot, L. Sifre, D. Kumaran, T. Graepel, T. Lillicrap, K. Simonyan and D. Hassabis, Science, 2018, 362, 1140–1144.
19. OpenAI Five Defeats Dota 2 World Champions, https://openai.com/research/openai-five-defeats-dota-2-world-champions.
20. T. Zhang and H. Mo, Int. J. Adv. Robot. Syst., 2021, 18, 172988142110073.
21. S. Verma, G. Novati and P. Koumoutsakos, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 5849–5854.
22. P. Garnier, J. Viquerat, J. Rabault, A. Larcher, A. Kuhnle and E. Hachem, Comput. Fluids, 2021, 225, 104973.
23. M. Nasiri and B. Liebchen, New J. Phys., 2022, 24, 073042.
24. Z. Huang, X. Liu and J. Zang, Nanoscale, 2019, 11, 21748–21758.
25. J. Zhang, J. Yang, Y. Zhang and M. A. Bevan, Sci. Adv., 2020, 6, eabd6716.
26. Q. Wei, F. L. Lewis, Q. Sun, P. Yan and R. Song, IEEE Trans. Cybern., 2017, 47, 1224–1237.
27. M. M. Norton, P. Grover, M. F. Hagan and S. Fraden, Phys. Rev. Lett., 2020, 125, 178005.
28. M. J. Falk, V. Alizadehyazdi, H. Jaeger and A. Murugan, Phys. Rev. Res., 2021, 3, 033291.
29. M. Durve, F. Peruani and A. Celani, Phys. Rev. E, 2020, 102, 012601.
30. S. Whitelam and I. Tamblyn, Phys. Rev. E, 2020, 101, 052604.
31. R. S. Sutton and A. G. Barto, Reinforcement Learning: An Introduction, MIT Press, Cambridge, Mass, 1998.
32. S. L. Brunton and J. N. Kutz, Data-Driven Science and Engineering: Machine Learning, Dynamical Systems, and Control, Cambridge University Press, 2nd edn, 2022.
33. S. Ravichandiran, Deep Reinforcement Learning with Python: Master Classic RL, Deep RL, Distributional RL, Inverse RL, and More with OpenAI Gym and TensorFlow, Packt Publishing Limited, Birmingham, 2nd edn, 2020.
34. R. A. DeLaCruz-Araujo, D. J. Beltran-Villegas, R. G. Larson and U. M. Córdova-Figueroa, Soft Matter, 2016, 12, 4071–4081.
35. A. Reinhardt, F. Romano and J. P. K. Doye, Phys. Rev. Lett., 2013, 110, 255503.
36. P. W. Leung, C. L. Henley and G. V. Chester, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 39, 446–458.
37. Y. Sugita, A. Kitao and Y. Okamoto, J. Chem. Phys., 2000, 113, 6042–6051.
38. Y. Iba, Int. J. Mod. Phys. C, 2001, 12, 623–656.
39. M. Engel and H.-R. Trebin, Phys. Rev. Lett., 2007, 98, 225505.
40. S. Lobel, S. Rammohan, B. He, S. Yu and G. Konidaris, Proceedings of the AAAI Conference on Artificial Intelligence, 2023, vol. 37, pp. 8932–8939.
41. K. Sankaewtong, J. J. Molina and R. Yamamoto, Phys. Fluids, 2024, 36, 041902.
42. T. Salimans, J. Ho, X. Chen, S. Sidor and I. Sutskever, arXiv, 2017, preprint, arXiv:1703.03864,  DOI:10.48550/arXiv.1703.03864.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sm01038h

---