 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A process simulation study on the impact of electrochemical discharge on the circularity of lithium-ion batteries using new multi-dimensional indicators†
Minerva
Vierunketo
 a,
Anna
Klemettinen
a,
Annukka
Santasalo-Aarnio
b and
Rodrigo
Serna-Guerrero
*a
a,
Anna
Klemettinen
a,
Annukka
Santasalo-Aarnio
b and
Rodrigo
Serna-Guerrero
*a
aDepartment of Chemical and Metallurgical Engineering, School of Chemical Engineering, Aalto University, P. O. Box 16200, Aalto, 00076, Finland. E-mail: rodrigo.serna@aalto.fi
bDepartment of Mechanical Engineering, School of Engineering, Aalto University, P. O. Box 14400, FI-00076 Aalto, Finland
First published on 4th July 2025
Abstract
Spent lithium-ion batteries (LIBs) contain residual energy, which might be hazardous during storage, transportation, and recycling. Therefore, it is essential to either deactivate or discharge LIBs prior to any mechanical processing step. As recycling is a key activity to transform from a linear economy into a circular one, the evaluation of a discharge step from the perspective of circular economy (CE) is essential but remains largely unexplored. In this work, battery discharge systems using three different Na+-based aqueous solutions (i.e., NaCl, Na2SO4, and Na2CO3) were modelled with HSC® process simulation software. The resulting mass and energy flows were interpreted using a novel methodology involving multidimensional circularity parameters (i.e., statistical entropy, exergy, and exentropy). Statistical entropy only evaluates the concentrating action of different components in a system, without discriminating whether the produced streams are in a usable chemical form or irreversibly changed. Thus, a weighting factor for irreversible transformations was implemented for statistical entropy analysis. Exergy analysis revealed that the discharge systems do not significantly destroy energy, although it was unexpectedly revealed that corrosion aids in exergy preservation by producing highly concentrated hydrogen from the water splitting reaction. To further reconcile the preservation of energy and materials, the recently developed exentropy (χ) analysis was used. Na2CO3 was identified as the most promising electrolyte (χ = 0.066) compared to NaCl (χ = −0.055) and Na2SO4 (χ = −0.106), providing for the first time a parametrized basis to the idea that electrochemical discharge systems with strong corrosion are inefficient from the perspective of circularity.
1 Introduction
Lithium-ion batteries (LIBs) are one of the preferred options for energy storage supporting the decarbonization effects of the energy and transportation sectors.1 By some estimates, LIB production will have an expected annual growth rate of 22% in this decade,2 and there are already more than 2 million LIBs discarded each year.3 The recycling of spent LIBs thus grows in importance as their disposal in landfills causes several issues, from environmental pollution to loss of valuable natural resources.4 The need to develop efficient recycling technologies for battery materials is reflected by the large number of articles published in the scientific literature in recent years.5–7There is however one important aspect to be considered before the recycling of batteries, especially with direct recycling methods. When spent LIBs have reached their end-of-life (EoL), they are often discarded with residual energy.8 This represents an explosion and fire risk during subsequent processing, as the cathode and anode could come into contact with each other during dismantling or crushing. In such cases, the result is a short circuit current flow leading to the uncontrolled release of heat, the ignition of volatile and flammable solvents, and the subsequent inflammation or explosion of batteries.9 Neglecting the elimination of residual energy in battery recycling processes represents a potential security risk, particularly considering the increasing volumes of EoL LIBs. Hence, more attention should be given to spent LIB discharge.10 Therefore, it is necessary to set a discharging step at the start of any LIB recycling process.11
Some authors have recently proposed the deactivation of LIBs during crushing using cryogenic methods, an inert atmosphere, or thermal treatment, but these methods do not discharge the batteries in a strict sense and have no means to recover the remanent energy.12 The typical approaches for battery discharge can be broadly classified as physical or chemical methods.13 Physical discharging refers to those in which an external short circuit is created to discharge the batteries by using a resistor or a discharge cabinet, which are connected to the cathodic and anodic poles of a battery.13,14 Physical methods also include the use of conductive particles (e.g., metal or graphite powder),12 which convert the residual charge of batteries into thermal energy by closing the circuit between the positive and negative poles.11 On the other hand, chemical discharge methods utilize salt, acid, or alkaline solutions in which the batteries are immersed for a sufficiently long time.13 The discharge mechanisms in this case are electrochemical reactions that consume the remaining power of the battery.15
All the above-mentioned methods have both advantages and disadvantages. The use of a resistor or discharge cabinet is fast and consumes no chemicals, but it is impractical, and installing many discharge cabinets increases the recovery costs.13 Also, the precise details for a resistor discharge are usually not explained in detail in the published literature.16 Metal powder discharge is efficient but usually unstable and difficult to control, generating a sharp increase in the temperature of the powder,12 which might further lead to dust explosions.17 Chemical discharging is simpler since no specialized equipment is required, and it can be applied for larger battery streams independent of their geometrical design. However, the electrochemical discharge rate is reportedly slow when using some electrolytes, and there exists the risk of battery corrosion leading to electrolyte leakage and pollution.13 Nonetheless, the chemical discharging method has gained a lot of attention due to the aforementioned advantages and might become the preferable solution in industrial applications.11 Also, the released heat from the batteries during discharging can be absorbed by the solution, which makes the method less risky compared to e.g., powder discharge.10 The use of solutions for battery discharge is already a widely researched topic, with a growing number of articles with exploration of different discharge media published recently, such as the studies by Wu et al. (2023),15 Shaw-Stewart et al. (2019),18 and Nazarov et al. (2023).19
In electrochemical solution discharge, NaCl is likely the most widely applied salt due to its cost-effectiveness, availability, and low toxicity.20 The use of different concentrations of NaCl in battery discharging has been studied by several researchers, such as Xiao et al. (2020),10 Nazarov et al. (2023),19 Yao et al., (2020),21 and Torabian et al. (2022).22 However, the use of NaCl also has some drawbacks, such as serious metal corrosion.10 It has been concluded that galvanic corrosion and organic leakage might be caused by Cl− ions when the anode is destroyed.12 Therefore, other options have been explored, and the discharging of spent LIBs has been reported with various aqueous solutions of sulfites (e.g., Na2SO4, MnSO4, and FeSO4), carbonates (e.g., Na2CO3, K2CO3, and (NH4)2CO3), and phosphates (e.g., Na2HPO4 and K2HPO4). For example, Shaw-Stewart et al. (2019)18 studied pole corrosion and the rate of discharge by using 26 different liquid Na+, K+, or NH4+-based solutions, e.g., different sulfides, carbonates and phosphates. Ojanen et al. (2018)23 studied the use of FeSO4, ZnSO4, and Na2SO4, Wu et al. (2022)13 combined two different sulfate salts (Na2SO4 with FeSO4 and Na2SO4), Wang et al. (2022)24 used Na2SO4, Na2CO3, and MnSO4, Xiao et al. (2020)10 used MnSO4 and MgSO4, Rouhi et al. (2021)25 studied the use of K2CO3 and Na2CO3, and Rouhi et al. (2022)26 studied the use of (NH4)2CO3. From all the different salts explored, Na2SO4 is a commonly used electrolyte in addition to NaCl.15,27 Also, it has been considered that low corrosion is obtained with carbonate salts, therefore being a promising discharging media.18,23,24
All the studies described above focus either on the corrosion of battery materials or their discharge time. As the discharge step is part of a battery recycling process, and recycling is one of the key activities to shift from a linear economy into a circular one, it becomes relevant to evaluate the impact of discharging strategies from the perspective of circular economy (CE). Presently, the proper manner to measure the circularity of a system remains an open question. The use of scientific, quantitative circularity indicators is a relatively new field, and the application of new evolution methods is necessary.
To the best of the authors' knowledge, the battery discharge systems have not been evaluated before using circularity indicators. To evaluate the circularity of different battery discharge systems, a simulation of three different salt solution discharge systems was conducted using HSC Chemistry® 10-software.28 The salts and the data needed for the discharge simulation were obtained from existing research conducted by others.20,24,29 As sufficient data are needed to conduct the simulation, the three different salts chosen were (i) NaCl, as it is the most widely used electrolyte due to its low cost;20 (ii) Na2SO4, as sulfate forms of Na have been explored as an alternative electrolyte recently;15,27 and (iii) Na2CO3, since the use of carbonates reportedly result in low battery corrosion.18,23,24 The data obtained from the simulation were used to calculate the necessary data of materials and energy flows for their evaluation through statistical entropy analysis (SEA) and exergy analysis (ExA), respectively. SEA is applied to study the preservation of materials through concentration or dilution action and ExA to study the irreversible energy losses. As both perspectives are important in terms of CE, multidimensional analysis through exentropy, which evaluates both materials and energy preservation in the system simultaneously, was also performed to provide a thorough evaluation of the system's circularity. As has been concluded in the proof-of-concept of exentropy,30 one-dimensional indicators may have contradicting results, so multidimensional indicators are needed.
2 Methodology
2.1 Multidimensional circularity analysis using the exentropy methodology
The exentropy (χ) analysis is a novel approach aimed at simultaneously accounting for materials and energy preservation in transformative systems. A detailed description of the methodology to calculate χ can be found in previously published work.30 However, in consideration to the reader, a brief description of the SEA, ExA, and χ is provided next.| s1: spent LIBs | s2: discharge residues | s3: off-gas |
| s4: discharged LIBs | s5: water for water splitting | s6: salt used for discharge |
The aim in recycling systems is to separate substances from different mixtures, i.e., to concentrate them and consequently reduce their statistical entropy (h). Statistical entropy is calculated using eqn (1):
 | (1) |
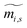 [dimensionless] is the standardized mass fraction, and ci,s [fractional] is the concentration of a component i in the stream s. The calculation of the standardized mass fraction requires the use of eqn (2) and eqn (3):
[dimensionless] is the standardized mass fraction, and ci,s [fractional] is the concentration of a component i in the stream s. The calculation of the standardized mass fraction requires the use of eqn (2) and eqn (3): | (2) |
| Ẋi = ṁsci,s | (3) |
Eqn (4) describes the sum of statistical entropies  in the streams of a certain stage, which is the total statistical entropy of a stage (Hi,q). In recycling processes, the value of the statistical entropy at the first stage is typically the maximum statistical entropy (Hi,qmax) of the process and for simplicity, it is used as a benchmark value to calculate the relative statistical entropy (RSE) as described in eqn (5). With the use of RSE, it is possible to compare elements with different concentrations in the system.
in the streams of a certain stage, which is the total statistical entropy of a stage (Hi,q). In recycling processes, the value of the statistical entropy at the first stage is typically the maximum statistical entropy (Hi,qmax) of the process and for simplicity, it is used as a benchmark value to calculate the relative statistical entropy (RSE) as described in eqn (5). With the use of RSE, it is possible to compare elements with different concentrations in the system.
 | (4) |
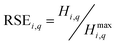 | (5) |
However, there may be a limitation with this definition of SEA as it does not consider whether elements or compounds obtained after transformative units are recovered in a potentially useful form. This becomes particularly relevant in the case of electrochemical battery discharge. As corrosion results in the extraction of metals, they are leached into the discharge solution, and eventually into the residue phase, which can be misinterpreted by SEA as an effective concentration of materials. Evidently, corrosion is undesired when discharging batteries. To properly account for this negative effect, the losses of battery materials into the stream “residues” were interpreted as emissions (i.e., losses to the environment) which are irreversibly diluted in the receiving media (i.e., air, water, or ground).32
The Practical Handbook of Material Flow Analysis32 proposes a method to include the emissions in the calculation of RSE if all of the component i is directed to the emission stream. However, in our study, only a part of the component i is directed to the emission stream, while the rest is directed to the desired product stream. Therefore, another solution is required to consider both unwanted and useful concentration simultaneously. The approach hereby used was the use of a weighting factor named “transfer coefficient (TC)”.32 The TC describes the partitioning of a substance in a process,32 so in this case it could be used to consider different kinds of concentrations at the same time. The value of the TC for battery materials ending up in the “residue” can be calculated according to eqn (6):
 | (6) |
As the concentration of battery materials into residues contributes to an increase in the value of RSE, the use of the TC as a weighting factor should cause the new RSE value  to be higher than the original RSE. Thus, the RSE′ can be calculated as follows (eqn (7)):
to be higher than the original RSE. Thus, the RSE′ can be calculated as follows (eqn (7)):
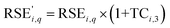 | (7) |
 | (8) |
| Exheat = q × (1 − T0/Theat) | (9) |
The only required inputs from the user to calculate the exergy content of the streams are nk (a mass flow or stoichiometric amount of an element or a compound in a stream) and the temperature of each stream. This temperature is used by the software to obtain enthalpies (N) and thermodynamical entropies (S) of species at the given temperature. Thermodynamic entropies in the standard state (25 °C, 1 bar), a standard Gibbs free energy of formation (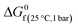 ) and elemental exergies of elements (bkref) are also obtained from the software database. The calculation of heat flow (q) requires the temperature of the standard state (T0 = 25 °C), and the temperature of the heat source (Theat(°C)).
) and elemental exergies of elements (bkref) are also obtained from the software database. The calculation of heat flow (q) requires the temperature of the standard state (T0 = 25 °C), and the temperature of the heat source (Theat(°C)).
Unlike energy, exergy does not follow the laws of conservation, and the input exergy might not be equal to the output exergy. A term called exergy destruction (ExD) is introduced to write the exergy balance in a conservative form. ExD quantifies the energy degradation during a process, being zero only in theoretical cases of fully reversible processes. However, in reality, all transformative stages destroy exergy as a result of thermodynamic entropy generation, making ExD a good tool to evaluate the preservation of energy in a system.35 The exergy balance of a process is presented in eqn (10):
| Exfeed + Exenergy = Exproducts + Exwaste + ExQ + ExD | (10) |
The input exergy on the left side consists of exergy of the materials in the feed (Exfeed) and input energy (Exenergy). The output exergy consists of exergy of the materials in the products (Exproducts), materials in waste (Exwaste), heat losses (ExQ), and ExD.
For comparative purposes, relative exergy content (REX) reflects the preservation of exergy relative to the total exergy input, making it a normalized parameter useful to compare systems with different flows of input material. In other words, REX describes the ability of a process to conserve energy, and it is defined for each stage by dividing the exergy content at any given stage by the exergy content at the first stage (Exmax), as in eqn (11).
 | (11) |
 is the sum of the exergies of all streams in stage q.
is the sum of the exergies of all streams in stage q.
When evaluating battery recycling processes, the value of RSE should tend to zero, as the aim is to produce highly concentrated elements or compounds.30 It should be noted that this is not the case in electrochemical discharging systems since this is a pre-processing step that is not aimed at recovering battery materials. While RSE is not expected to approach a value of zero, it should still decrease below one since the input stream is divided into three output streams, as shown in Fig. 1.
Furthermore, the value of REX should remain as high as possible in any system to avoid the loss of useful energy. Thus, the value of RSE should be lower than the value of REX, which indicates that the value of χ should be positive for optimum systems. As was stated earlier, the calculation of RSE′ required the TC as a weighting factor to include the loss of materials into the residues (i.e., waste), so this RSE′ should be applied to evaluate systems where corrosion is present. Thus, for the specific case where irreversible losses of materials are known and quantifiable, exentropy can be calculated using eqn (12).
 | (12) |
2.2 The simulation of a battery discharging step
The data used for simulation in this paper were taken from the work by Wang et al. (2022),24 who carried out studies of discharge using e.g., NaCl, Na2SO4, and Na2CO3. According to their report, they submerged the batteries in different concentrations of these saline solutions and conducted measurements of voltages with time using a digital multimeter. They also determined the concentration of the battery elements in the filtrate and the composition of the off-gas by using inductively coupled plasma-mass spectrometry (ICP-MS) and gas chromatography-mass spectrometry (GC-MS), respectively. In addition, we used the work published by Shepard (2022)31 to calculate the energy flows and the work by Punt et al. (2022)20 to estimate the metal fractions lost from the batteries into the discharge solution.HSC Chemistry® 10 -software28 was used to simulate the battery discharge process, as it is an appropriate software used to simulate unit operations involving solid particles and metallurgical refining, which usually are the processing stages in LIB recycling, and our research team has used the software in our previous studies.30,36 HSC Chemistry® is also the industrial standard in mineral processing simulation software. Although HSC® does not count with an electrolyte discharge module, this was programmed using an empty reaction unit with two input and three output streams. To have a properly functioning unit, the input streams, stream distributions, reactions and reaction rates, energy input and output of the batteries, and off-gas compositions needed to be defined. All these setups are described in this chapter and summarized later in Table 3.
The battery discharge process is a semi-batch process, but for the purposes of HCS, it was modelled as a continuous process. To that aim, the battery discharge kinetics were estimated from the published experimental data on discharge rates and corrosion byproducts obtained with the electrolyte solutions hereby explored.20,24,29 In the simulation, the capacity of the discharge tank was fixed to treat 100 kg of batteries. Thus, the different times required for discharge with each specific electrolyte solution were considered. According to several studies,24–26 the safety threshold prior to disassembling and shredding the batteries is a residual voltage of 2 V or below.
The time to reach the voltage limit of 2 V was estimated for each selected electrolyte based on the discharging curves reported by Wang et al. (2022).24 Since the aforementioned reference reported 2.2 V as the minimum voltage reached with Na2SO4, this was chosen as the target voltage. Therefore, the feed flow rate of EoL batteries was obtained by dividing the tank capacity (kg) with the discharge time (h). To conduct a fair comparison of different systems, their productivity can be used as the benchmark. Productivity is hereby defined as the number of batches handled per day, and it is calculated by dividing the daily LIB mass input by the fixed tank capacity.
The first input stream to the process consisted of spent LIBs with the composition presented in Table 2. The LIB composition was adopted from the previous work published by our research team,5 which describes this composition to be typical for LIBs. The battery cathodes were assumed to be LiCoO2 (LCO), as it has been a dominant cathode chemistry in LIBs and is expected to represent the battery type that will reach EoL in the subsequent years.37,38 The anode was assumed to be graphite, as it is the most widely used cathode material. Current collectors were assumed to be Cu and Al, separator polypropylene (PP), binder polyvinylidene fluoride (PVDF), electrolyte a mixture of lithium hexafluorophosphate (LiPF6) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethylene carbonate (EC)/dimethyl carbonate (DMC) solution, and casing steel.
1 ethylene carbonate (EC)/dimethyl carbonate (DMC) solution, and casing steel.
| Battery component | Composition (%) |
|---|---|
| Cathode: LiCoO2 | 27 |
| Anode: graphite | 17 |
| Current collectors: Cu and Al | 13 |
| Separator: polypropylene (PP) | 4 |
| Binder: polyvinylidene fluoride (PVDF) | 4 |
Electrolyte: lithium hexafluorophosphate (LiPF6) in a 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ethylene carbonate (EC)/dimethyl carbonate (DMC) mixture 1 ethylene carbonate (EC)/dimethyl carbonate (DMC) mixture |
10 |
| Casing: steel | 25 |
To estimate the energy content of the battery feed, the specific power of LIBs with an LCO cathode was assumed to be 600 W kg−1.29 This was multiplied with the mass of batteries in the feed to obtain the total input energies (i.e., 15 kW for NaCl, 2.5 kW for Na2SO4, and 6 kW for Na2CO3). The batteries were assumed to have an initial voltage of 3.7 V24 and the residual voltage after discharge was assumed to be either 2 V or 2.2 V, as explained earlier. The energy remaining in the batteries (%) was calculated by dividing the residual voltage by the initial voltage and multiplying that with 100%.
The second input stream to the process corresponds to the salt hereby studied (i.e., NaCl, Na2SO4, or Na2CO3) and the water required to replace the losses associated with water splitting during the discharge reaction. It is thus assumed that the tank contains a constant volume of excess water to fix the concentration of the studied salt at 1 M.24 No output of liquid water is considered, as the amount of it is assumed to be minor in the “residue” stream, which consists of the corrosion products from the batteries and traces of the applied salt. Also, an off-gas stream is included that accounts for the H2 and O2 gases evolving from the water splitting. The outline of the simulation model is presented in the ESI in Fig. S1.†
For simplicity, all the corrosion byproducts and some traces of the used salt were assumed to precipitate together into a single stream defined as “residues”. As will be discussed later, the “residue” stream contains species that are not considered recuperable in any practical form. According to multiple studies,15,20,23,24,39 both NaCl and Na2SO4 cause corrosion during discharge, which may lead to loss of Fe, Al, and Cu, and the leakage of electrolyte into the discharge solution. The corrosion is severe especially with chlorine-containing salts, due to the presence of the Cl− ions in the solution, which leads to the loss of the casing shell and connector poles according to eqn (13) and (14), respectively.39 Also, some of the Cu might be lost according to eqn (15).
| Fe + 2H2O → Fe(OH)2 + H2 | (13) |
| Al + 3H2O → Al(OH)3 + ¾H2 | (14) |
| Cu + 2H2O → Cu(OH)2 + H2 | (15) |
The values in Table 3 show the fraction of materials lost into the discharge solutions. These values were used as reaction rates with the reactions presented above (eqn (13)–(15)) in HSC® to define the mass flow of corroded materials in the “residue” stream. Based on the study by Punt et al. (2022),20 it was assumed that during the NaCl discharge, 89.4 wt%, 1.9 wt%, and 3.0 wt% of Fe, Al, and Cu in the batteries were lost in the discharge solution. With Na2SO4, the loss rates were slightly reduced, being 64.2 wt%, 1.4 wt%, and 0.3 wt% of Fe, Al, and Cu, respectively.20,24 The electrolyte leakage was modelled based on the study by Wang et al. (2022)24 with reported values of 2.36 wt% for NaCl and 0.29 wt% for Na2SO4. With Na2CO3, it was assumed that no corrosion occurred24 and hence no mass losses were considered in this case. Whenever leakage of LiPF6 occurred, a reaction with water was assumed, forming LiF, POF3, and HF20,40 (eqn (16)). Accordingly, the leaked carbonates (i.e., DMC and EC) from the electrolyte decomposed into methanol (CH3OH), ethylene glycol (C2H6O2), and CO2 (eqn (17) and (18)).
| LiPF6 + H2O → LiF + POF3 + 2HF | (16) |
| C3H6O3 + H2O → 2CH3OH + CO2 | (17) |
| C3H4O3 + H2O → CO2 + C2H6O2 | (18) |
| NaCl | Na2SO4 | Na2CO3 | Ref. | |
|---|---|---|---|---|
| Concentration of salt (mol L−1) | 1 | 1 | 1 | 24 |
| Discharge time to reach 2 V (h) | 4 | 24 | 10 | 24 |
| Tank capacity for batteries (kg) | 100 | 100 | 100 | This study |
| Feed (kg h−1) | 25 | 4.2 | 10 | This study |
| Starting voltage (V) | 3.7 | 3.7 | 3.7 | 24 |
| Final voltage in the simulation (V) | 2.0 | 2.2 | 2.0 | This study |
| Energy content (W kg−1) | 600 | 600 | 600 | 29 |
| Energy input in LIBs (kW) | 15 | 2.5 | 6 | This study |
| Energy output in LIBs (kW) | 8.1 | 1.5 | 3.2 | This study |
| Losses of Fe, Cu, and Al from the batteries into the discharge solution due to corrosion (%) | Fe: 89.4 | Fe: 64.2 | Fe: — | 20, 24 |
| Al: 1.9 | Al: 1.4 | Al: — | ||
| Cu: 3.0 | Cu: 0.3 | Cu: — | ||
| Electrolyte leakage (%) | 2.36 | 0.29 | — | 24 |
| Off-gas composition (vol%) | H2: 94.2 | H2: 62.6 | H2: 61.7 | 24, 39 |
| O2: 5.8 | O2: 37.4 | O2: 38.3 | ||
| Cl2: 0.01 |
As with the corrosion of metals (eqn (13)–(15)), a rate of the electrolyte loss based on the work by Punt et al. (2022)20 was defined in the HSC® simulation to estimate its mass contribution into the “residue” stream.
Another output stream in the process contains the off-gases from the water splitting reaction, where water splits into H2 and O2 gases in the negative and positive electrode, respectively.25 The energy of batteries is consumed by the water splitting reaction, and the reaction rate is defined by HSC®. The program calculates it as a function of the energy being drained during the process. The water splitting half reactions for the anode and cathode are presented in eqn (19) and (20), respectively.
| 2H2O → O2 + 4H+ + 4e− | (19) |
| 2H2O + 2e− → H2 + OH− | (20) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. However, since the corrosion of Fe (eqn (13)) is a competitive reaction competing with the formation of O2 in the anode (eqn (19)), the off-gas composition ratio of H2 to O2 becomes higher than 2
1. However, since the corrosion of Fe (eqn (13)) is a competitive reaction competing with the formation of O2 in the anode (eqn (19)), the off-gas composition ratio of H2 to O2 becomes higher than 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 in corrosive systems.24 In other words, as more severe corrosion of Fe in the electrolyte leads to higher consumption of O2−, it inhibits the formation of O2 gas, leading to a higher purity of H2 in the gaseous byproducts. Since each electrolyte solution has different electrochemical potentials, the resulting extent of Fe corrosion and water splitting will vary depending on the composition of the discharging system.
1 in corrosive systems.24 In other words, as more severe corrosion of Fe in the electrolyte leads to higher consumption of O2−, it inhibits the formation of O2 gas, leading to a higher purity of H2 in the gaseous byproducts. Since each electrolyte solution has different electrochemical potentials, the resulting extent of Fe corrosion and water splitting will vary depending on the composition of the discharging system.
Thus, according to the study by Wang et al. (2022),24 the off-gas compositions were assumed to be (i) 94.2 vol% and 5.8 vol% of H2 and O2, respectively, for NaCl; (ii) 62.6 vol% and 37.4 vol% of H2 and O2, respectively, for Na2SO4; and (iii) 61.7 vol% and 38.3 vol% H2 and O2, respectively, for Na2CO3. A special case is that of NaCl, as in addition to the release of H2 and O2, it was assumed that approximately 24 L of Cl2 gas was released for every 1 ton of spent batteries.39 Thus, in the system with NaCl, the off-gas was assumed to include 0.01 vol% of Cl2 in addition to H2 and O2. All the data presented earlier in this chapter, either obtained or calculated from the literature and required for the simulation, are summarized in Table 3.
3 Results and discussion
3.1 Statistical entropy analysis (SEA)
SEA was conducted to study the concentration of materials in an electrochemical battery discharge system. As explained in the Methodology section, SEA does not consider whether elements or compounds obtained after transformative units are recovered in a potentially useful form and thus, TCloss was used to consider both unwanted and useful concentration simultaneously.The battery metals represented in the systems (i.e., Cu, Fe, Al, Li, and Co), as well as H and O, which were present in the battery components but also in the water needed for the discharge and off-gas being produced, were traced in all discharging systems studied here. “Others” contain the rest of the battery elements (i.e., Na, Cl, S, and C), which were not traced in more detail, and the elements of salts (i.e., Na, Cl, S, or C) depending on the system studied. The TCloss for each element and the total system, and the increased RSE′ according to the TCloss value were calculated for each element and for the total system as shown in Fig. 2. The exact values of TCloss and RSE′ for different systems can be found in ESI, Table S1 and S2,† respectively.
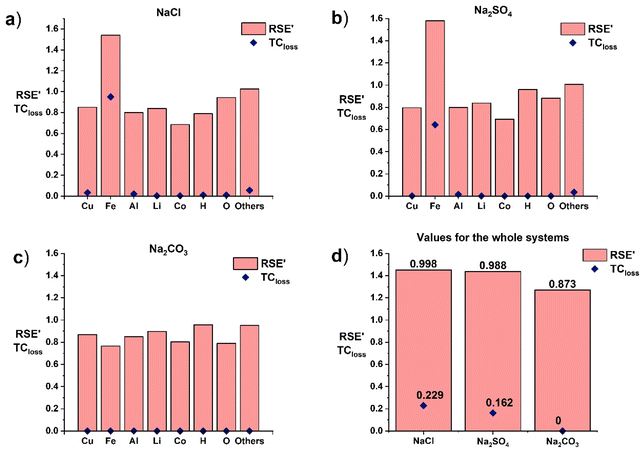 | ||
| Fig. 2 TCloss, and RSE′ of different discharging systems: (a) NaCl, (b) Na2SO4, (c) Na2CO3, and (d) the whole systems. | ||
As seen in Fig. 2, the TCloss of Fe was the highest for the system with NaCl (Fig. 2a), as the corrosion of battery materials was the most severe with this discharging system. As was mentioned before, chloride ions in discharging solutions react with other ions in the solution causing severe corrosion of the battery metals. The TCloss value for Fe is also high in the system with Na2SO4 (Fig. 2b). However, the TCloss for other metals affected by corrosion (i.e., Al and Cu) appears to be nearly zero (Fig. 2a and b), as the corrosion rate for these metals was much lower than that for Fe. The system total TCloss for these two systems was also relatively low, as the overall mass loss remained low. For Na2CO3 (Fig. 2c), TCloss was zero for each component, and thus for the whole system, as no corrosion of battery materials was assumed.
From Fig. 2b, it is also observed that RSE′ of Fe is the highest for the system with Na2SO4. Because the system with NaCl contained more water in the input compared to the system with Na2SO4, all the elements appear to be more diluted in the feed stream. As the RSE values are dependent on the concentration of the components at Stage 1, lower concentrations at Stage 1 have more effect on the value of RSE at Stage 2. Thus, the value of RSE for NaCl decreased more between Stage 1 and Stage 2, also affecting the value of RSE′. However, the system-level values of RSE′ remained close to unity, which demonstrates in a quantitative manner that more corrosion negatively affects the recovery of materials in the system. This is visualized in Fig. 3.
The RSE′ value for the system with Na2SO4 was indeed slightly smaller than that for the system with NaCl. As was already discussed, some of the higher RSE′ values for some elements in the Na2SO4 system are caused by the difference in the amount of water fed into the process, but the total RSE′ for NaCl is higher due to the more severe corrosion. The higher amount of corrosion leads to higher TC values for the whole battery system, causing the RSE′ value to be higher compared to the RSE value. However, the difference between the RSE′ values of the NaCl and Na2SO4 systems was minor, even though the difference between material losses due to corrosion is more visible. These results corroborate how SEA can be used to identify the best systems in terms of material preservation, favouring those without any corrosion.
3.2 Exergy analysis (ExA)
As energy preservation is also a relevant dimension to be considered in CE, exergy analysis of the electrochemical discharge process was conducted to observe the irreversible losses of energy in the process. A schematic representation of the input (LIB feed, discharge solution, and energy content of batteries) and output (discharged LIBs, residues, off-gas, and ExD) exergy streams is presented in Fig. 4. | ||
| Fig. 4 The exergy content of each stream, with the input rate of spent LIBs in kg h−1, for the three different discharge solutions: (a) NaCl, (b) Na2SO4 and (c) Na2CO3. | ||
Fig. 4 visualizes that, when more batteries are fed into the process, there is also more exergy flowing into the process, both associated with the materials and the total remaining charge in the batteries. In a day, the total mass of batteries that can be treated is 600 kg, 100 kg, and 240 kg with NaCl, Na2SO4, and Na2CO3, respectively. According to productivity, these correspond to approximately six, one, and two batches per day. A higher productivity also means that more energy needs to be discharged to reach the safe voltage level of batteries prior to dismantling. In turn, this influences the off-gas production, as more energy is available for the water splitting reaction.
An interesting observation is that the exergy content of the off-gas stream for the system with NaCl is comparatively higher than that obtained with Na2SO4 or Na2CO3 (Fig. 4). A reasonable explanation is that the dissolution of Fe from the casing competes with the half reaction forming O2 during the water splitting, so in the corroded systems less gaseous oxygen is being produced.24 In such cases, the “off-gas” stream is composed of highly concentrated H2, which has a significantly higher bkref (236 kJ mol−1) than O2 (4 kJ mol−1). Indeed, the off-gas stream produced using NaCl solution consists mainly of H2 (94.2 vol%), whereas with Na2SO4 the H2 content in off gas is only 62.6 vol% and with Na2CO3 61.7 vol%.
It is also seen that discharge with NaCl solution resulted in the highest ExD, but since the input rate of spent batteries is not equal in the different discharge systems hereby studied, the values of ExD cannot be directly compared. Consequently, a normalized parameter such as REX is needed. The REX values for all three electrolyte systems, calculated using eqn (19), are shown in Fig. 5.
The REX values in Fig. 5 reflect the two main effects contributing to exergy preservation explained above: (i) the generation of a highly concentrated H2 stream in the case of NaCl, and (ii) the preservation of the intrinsic exergy of materials in the absence of corrosion for Na2CO3. As Na2SO4 solution is neither an extremely corrosive environment nor one that fully prevents corrosion, it results in the most exergy destructive option.
Overall, all the systems had high REX values, which implies that the loss of useful energy was not significant in any of the discharging systems. As discussed earlier, the mass losses are not substantial in any system, and at the same time the discharged energy is transferred to species with high exergy values, such as H2. If only this dimension is considered one could argue that corrosion might not be a negative phenomenon, as the exergy content of highly concentrated off-gas appears to be an efficient means for exergy preservation. These seemingly contradictory results to those obtained from the SEA support the need for a multidimensional analysis of these systems to reconcile the effects of materials and energy preservation.
3.3 Exentropy (χ) analysis
From the individual analyses alone, SEA implied that corrosion is harmful in terms of RSE, while ExA implied that corrosion might be beneficial for the production of H2, which contains high intrinsic energy. To obtain a more robust comparison, exentropy analysis considers both RSE and REX values simultaneously. In the context of battery discharging systems, exentropy analysis considers both material losses due to corrosion and the preservation of useful energy. The results of the exentropy analysis are presented in Fig. 6.As already explained in the Methodology section, positive exentropy values should be obtained for systems where materials and energy are sufficiently preserved. As shown in Fig. 6, negative exentropy values were obtained when using either NaCl or Na2SO4 solutions as the discharging medium, implying that these systems are not efficient. Exentropy is thus a parameter capable of identifying the negative impact of irreversible material losses into the corrosion product stream (i.e., residues) even when highly concentrated H2 is obtained as a byproduct. Therefore, studying the exentropy of different battery compositions might not be efficient, if the corrosion rates would remain the same.
Thus, to obtain high exentropy values, the focus should be on avoiding corrosion as much possible. A relevant question is how to obtain the high productivity possible with NaCl solutions while minimizing the corrosion of battery materials in the discharging system. To approach this issue, one could study either different electrolytes, that would cause no corrosion in the system, or study alternative battery materials, which would not be affected by corrosion in the discharging media used in this study. In any case, this could be a promising study in the future and a way to optimize the battery discharging process using exentropy.
Based on the results of this work, it is important to monitor the composition of side streams (i.e., off-gas and residues) of electrochemical discharge processes in more detail. As seen in Fig. 4, the high H2 content in off-gas increases its exergy content, so e.g., inhibiting the O2 production during the discharge process could increase the exergy content of the off-gas making its utilization more profitable. Also, Punt et al. (2022)20 reported that the discharge slurry could provide a secondary source for Fe and Al after drying. In this case, the slurry byproduct may not be treated as a waste stream, thus not affecting the original value of RSE, but finding the means to recover the metals in this stream both efficiently and profitably would remain a challenge.
4 Conclusions
Safe and efficient discharging methods are required for the proper handling of EoL LIBs. Among the various available options, electrochemical discharge is a promising method due to its simplicity, flexibility, and desirability in industrial applications. Hereby, electrochemical discharge with different media was evaluated for the first time using a multi-dimensional indicator (i.e., exentropy) relevant for the CE.Statistical entropy evaluated the concentrating action of different elements inside the discharge system. However, to reflect that the produced “residue”-stream represents materials that are irreversibly lost, a weighting factor (TCloss) for RSE was implemented for the first time in this context, revealing that corrosion in discharging systems led towards more unfavourable values of RSE′. On the other hand, exergy analysis disclosed that exergy was not destroyed significantly in any of the systems. Unexpectedly, it also suggested that corrosion leads to exergy preservation by producing highly concentrated hydrogen from the water splitting reaction. Therefore, exentropy analysis is particularly interesting since it considers both the concentrating action of materials and loss of useful energy simultaneously and was able to identify the negative effects of corrosion on the circularity of battery materials.
Accordingly, only systems without corrosion can be considered sufficiently efficient, as positive exentropy values were only obtained in the case of Na2CO3 discharge. Ideally, both the discharge time and rate of corrosion should be optimized: systems with fast discharge times with zero corrosion are considered as optimal. This study showed that exentropy analysis can be used to evaluate the circularity of battery discharge systems. However, as the indicator studies material and energy flows, it can be universally applied on any system with those kind of flows within it.
Admittedly, a limitation of this study is that it is based on process simulation models using the modest amount of data available in the scientific literature. To create as realistic a simulation model as possible, the data obtained for it must be accurate. Even in a simple discharging unit like the one analysed in this study, the simulation model requires complex parameters to function properly. The models used would thus benefit from more extensive experimental results, potentially including other discharge media. Also, the so-called voltage rebound effect was not considered in this study, so it is uncertain whether the batteries would be safe to disassemble after the time considered in this study. In addition, as exentropy considers only the material and energy side of the process, adding more dimensions, such as economic or environmental factors, could enhance the results further. These are all interesting aspects to be considered in future studies.
Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Minerva Vierunketo: conceptualization, methodology, investigation, writing – original draft, visualization. Anna Klemettinen: conceptualization, methodology, writing – review & editing. Annukka Santasalo-Aarnio: conceptualization, writing – review & editing. Rodrigo Serna-Guerrero: conceptualization, methodology, writing – review & editing, supervision, funding acquisition.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is part of the HYPER-SPHERE project (Grant No. 341628) supported by the Research Council of Finland.References
- D. Latini, Chem. Eng. Trans., 2022, 96, 25–30 Search PubMed.
- H. Ali, H. A. Khan and M. G. Pecht, J. Energy Storage, 2021, 40, 102690 CrossRef.
- B. Niu, J. Xiao and Z. Xu, J. Hazard. Mater., 2022, 439, 129678 CrossRef CAS.
- E. Asadi Dalini, G. Karimi, S. Zandevakili and M. Goodarzi, Miner. Process. Extr. Metall. Rev., 2020, 42(7), 451–472 CrossRef.
- O. Velázquez-Martínez, J. Valio, A. Santasalo-Aarnio, M. Reuter and R. Serna-Guerrero, Batteries, 2019, 5(4), 68 CrossRef.
- R. E. Ciez and J. F. Whitacre, Nat. Sustain., 2019, 2(2), 148–156 CrossRef.
- R. Sommerville, P. Zhu, M. A. Rajaeifar, O. Heidrich, V. Goodship and E. Kendrick, Resour., Conserv. Recycl., 2021, 165, 105219 CrossRef CAS.
- R. Wang, Y. Zhang, K. Sun, C. Qian and W. Bao, J. Mater. Chem. A, 2022, 10(33), 17053–17076 RSC.
- S. Kim, J. Bang, J. Yoo, Y. Shin, J. Bae, J. Jeong, K. Kim, P. Dong and K. Kwon, J. Cleaner Prod., 2021, 294, 126329 CrossRef CAS.
- J. Xiao, J. Guo, L. Zhan and Z. Xu, J. Cleaner Prod., 2020, 255, 120064 CrossRef CAS.
- Z. Fang, Q. Duan, Q. Peng, Z. Wei, H. Cao, J. Sun and Q. Wang, J. Cleaner Prod., 2022, 359, 132116 CrossRef CAS.
- T. Gao, T. Dai, N. Fan, Z. Han and X. Gao, J. Environ. Manage., 2024, 363, 121314 CrossRef CAS.
- L. Wu, F. S. Zhang, K. He, Z. Y. Zhang and C. C. Zhang, J. Cleaner Prod., 2022, 380, 135045 CrossRef CAS.
- G. Shi, J. Cheng, J. Wang, S. Zhang, X. Shao, X. Chen, X. Li and B. Xin, J. Energy Storage, 2023, 72(C), 108486 CrossRef.
- L. Wu, Z. Y. Zhang and C. C. Zhang, Sep. Purif. Technol., 2023, 306(B), 122640 CrossRef CAS.
- R. Sommerville, J. Shaw-Stewart, V. Goodship, N. Rowson and E. Kendrick, Sustainable Mater. Technol., 2020, 25, e00197 CrossRef CAS.
- J. Li, G. Wang and Z. Xu, Waste Manage., 2016, 52, 221–227 CrossRef CAS.
- J. Shaw-Stewart, A. Alvarez-Reguera, A. Greszta, J. Marco, M. Masood, R. Sommerville and E. Kendrick, Sustainable Mater. Technol., 2019, 22, e00110 CrossRef CAS.
- V. I. Nazarov, V. M. Retivov, D. A. Makarenkov, A. P. Popov, G. R. Aflyatunova and N. A. Kuznetsova, Coke Chem., 2023, 65(11), 564–571 CrossRef.
- T. Punt, S. M. Bradshaw, P. van Wyk and G. Akdogan, Minerals, 2022, 12(6), 753 CrossRef CAS.
- L. P. Yao, Q. Zeng, T. Qi and J. Li, J. Cleaner Prod., 2020, 245, 118820 CrossRef CAS.
- M. M. Torabian, M. Jafari and A. Bazargan, Waste Manag. Res., 2022, 40(4), 402–409 CrossRef CAS.
- S. Ojanen, M. Lundström, A. Santasalo-Aarnio and R. Serna-Guerrero, Waste Manage., 2018, 76, 242–249 CrossRef CAS.
- H. Wang, G. Qu, J. Yang, S. Zhou, B. Li and Y. Wei, J. Energy Storage, 2022, 54, 105383 CrossRef.
- H. Rouhi, E. Karola, R. Serna-Guerrero and A. Santasalo-Aarnio, J. Energy Storage, 2021, 25, 102323 CrossRef.
- H. Rouhi, R. Serna-Guerrero and A. Santasalo-Aarnio, J. Energy Storage, 2022, 55, 105734 CrossRef.
- A. Amato, A. Becci, M. Villen-Guzman, C. Vereda-Alonso and F. Beolchini, J. Cleaner Prod., 2021, 300, 126954 CrossRef.
- Metso, HSC Chemistry™ Software, https://www.mogroup.com/portfolio/hsc-chemistry/, accessed 27 March 2025.
- Battery Power Tips, What are six key considerations when choosing a Li-ion battery chemistry?, https://www.batterypowertips.com/what-are-six-key-considerations-when-choosing-a-li-on-battery-chemistry/, accessed 27 March 2025.
- M. Vierunketo, A. Klemettinen, M. A. Reuter, A. Santasalo-Aarnio and R. Serna-Guerrero, iScience, 2023, 26(11), 108237 CrossRef CAS.
- H. Rechberger and P. H. Brunner, Environ. Sci. Technol., 2002, 36(4), 809–816 CrossRef CAS.
- P. H. Brunner and H. Rechberger, Practical Handbook of Material Flow Analysis, A CRC Press Company, Boca Raton FL, 2005 Search PubMed.
- R. Serna-Guerrero, S. Ikonen, O. Kallela and E. Hakanen, J. Cleaner Prod., 2022, 374, 133984 CrossRef.
- I. B. Fernandes, A. Abadías Llamas and M. A. Reuter, Jom, 2020, 72(7), 2754–2769 CrossRef CAS.
- M. A. Reuter, A. van Schaik, J. Gutzmer, N. Bartie and A. Abadías Llamas, Annu. Rev. Mater. Res., 2019, 49(1), 253–274 CrossRef CAS.
- M. Vierunketo, A. Klemettinen, M. A. Reuter, A. Santasalo-Aarnio and R. Serna-Guerrero, J. Cleaner Prod., 2024, 471, 143435 CrossRef CAS.
- N. Vieceli, C. A. Nogueira, M. F. C. Pereira, F. O. Durao, C. Guimaraes and F. Margarido, J. Environ. Manage., 2018, 228, 140–148 CrossRef CAS.
- B. Zhang, Y. Xu, B. Makuza, F. Zhu, H. Wang, N. Hong, Z. Long, W. Deng, G. Zou, H. Hou and X. Ji, Chem. Eng. J., 2023, 452, 139258 CrossRef CAS.
- Z. Huang, J. Zhu, X. Wu, P. Wang, Y. Fu and J. Ruan, ACS Sustainable Chem. Eng., 2023, 11(6), 2089–2101 CrossRef CAS.
- X. Zhong, W. Liu, J. Han, F. Jiao, W. Qin and T. Liu, J. Cleaner Prod., 2020, 263, 121439 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Fig. S1: the lithium-ion battery (LIB) discharge simulation model; Table S1: TCloss values in different discharge systems. See DOI: https://doi.org/10.1039/d5se00439j |
| This journal is © The Royal Society of Chemistry 2025 |




