Open Access Article
Open Access ArticlePhysically interpretable descriptors drive the materials design of metal hydrides for hydrogen storage
Seong-Hoon
Jang
 *a,
Di
Zhang
*a,
Di
Zhang
 a,
Hung Ba
Tran
a,
Hung Ba
Tran
 a,
Xue
Jia
a,
Xue
Jia
 a,
Kiyoe
Konno
a,
Kiyoe
Konno
 ab,
Ryuhei
Sato
ab,
Ryuhei
Sato
 c,
Shin-ichi
Orimo
c,
Shin-ichi
Orimo
 *ad and
Hao
Li
*ad and
Hao
Li
 *a
*a
aAdvanced Institute for Materials Research (WPI-AIMR), Tohoku University, Sendai 980-8577, Japan. E-mail: jang.seonghoon.b4@tohoku.ac.jp; shin-ichi.orimo.a6@tohoku.ac.jp; li.hao.b8@tohoku.ac.jp
bInstitute of Fluid Science, Tohoku University, Sendai, 980-8577, Japan
cDepartment of Materials Engineering, The University of Tokyo, Tokyo 113-8656, Japan
dInstitute for Materials Research (IMR), Tohoku University, Sendai, 980-8577, Japan
First published on 23rd October 2025
Abstract
Designing metal hydrides for hydrogen storage remains a longstanding challenge due to the vast compositional space and complex structure–property relationships. Herein, for the first time, we present physically interpretable models for predicting two key performance metrics, gravimetric hydrogen density w and equilibrium pressure Peq,RT at room temperature, based on a minimal set of chemically meaningful descriptors. Using a rigorously curated dataset of 5089 metal hydride compositions from our recently developed Digital Hydrogen Platform (DigHyd) based on large-scale data mining from available experimental literature of solid-state hydrogen storage materials, we systematically constructed over 1.6 million candidate models using combinations of scalar transformations and nonlinear link functions. The final closed-form models, derived from 2–3 descriptors each (e.g., atomic mass, electronegativity, molar density, and ionic filling factor), achieve predictive accuracies on par with state-of-the-art machine learning methods, while maintaining full physical transparency. Strikingly, descriptor-based design maps generated from these models reveal a fundamental trade-off between w and Peq,RT: saline-type hydrides, composed of light electropositive elements, offer high w but low Peq,RT, whereas interstitial-type hydrides based on heavier electronegative transition metals show the opposite trend. Notably, beryllium (Be)-based systems, such as Be–Na alloys, emerge as rare candidates that simultaneously satisfy both performance metrics, attributed to the unique combination of light mass and high molar density for Be. Our models indicate that, while there remains room for improvement between the current state of solid-state hydrogen storage materials and the US-DOE targets, Be-based systems may offer renewed prospects for approaching these benchmarks. These results provide chemically intuitive guidelines for materials design and establish a scalable framework for the rational discovery of materials in complex chemical spaces. The methodology is broadly applicable and could serve as a template for data-driven exploration across other energy-relevant materials domains.
Introduction
Hydrogen is a leading candidate for enabling carbon-neutral energy technologies due to its high specific energy and clean combustion profile.1,2 However, its practical deployment in fuel cells and energy systems is constrained by the lack of compact, safe, and reversible storage solutions.3 Among various strategies, solid-state hydrogen storage using metal hydrides has received significant attention owing to their high volumetric density, cyclability, and integrability into engineered systems.4–6Metal hydrides, such as MgH2, Mg2NiH4, FeTiH2, PdH0.6, and LaNi5H6, have long served as prototypical systems.7–15 These materials span a wide thermodynamic range: saline hydrides, based on light metal atoms (e.g., MgH2) provide high gravimetric capacities but suffer from high decomposition temperatures,13 while interstitial hydrides, based on transition or heavy metal atoms (e.g., LaNi5H6) offer excellent kinetics and hydrogen equilibrium pressures but limited capacity.11 Significant efforts have focused on modifying these systems through compositional tuning, nanostructuring, and catalysis to improve hydrogenation performance for the target metrics.4–6
Yet despite decades of study, the compositional landscape of hydride-forming alloys remains largely underexplored. Thousands of binary and multinary combinations are theoretically possible, yet only a small subset has been synthesized and evaluated. This data sparsity is compounded by the lack of predictive, physically grounded frameworks that can guide rational materials discovery. While recent machine learning (ML) efforts have shown potential in accelerating property prediction,16,17 they often rely on relatively small scale of data, poorly curated datasets, and opaque modeling strategies that limit interpretability and chemical insight.
To address these challenges, herein, we present a data-driven but physically interpretable approach to the design of metal hydrides. Using a rigorously curated dataset, our recently developed Digital Hydrogen Platform (DigHyd: https://www.dighyd.org) via large-scale data mining from available experimental literature on solid-state hydrogen storage materials, we construct regression models that accurately predict two key metrics: gravimetric hydrogen density (w) and equilibrium pressure (Peq,RT) at room temperature (298.15 K). Our models utilize a minimal set of intuitive descriptors (i.e., atomic mass (M), electronegativity (χ), molar density (ρmol), and ionic filling factor (ηf)) and achieve predictive accuracy comparable to modern black-box ML algorithms. Importantly, these models enable the generation of compositional design maps, which reveal fundamental structure–property relationships and identify promising candidate systems—particularly beryllium (Be)-based alloys—for high-performance hydrogen storage. In doing so, they also highlight the challenges that remain in bridging the difference between the current performance of solid-state hydrogen storage materials and the ambitious targets set by the US-DOE, while indicating that Be-based systems may offer a viable pathway toward bridging this divide. This work provides a transparent and scalable framework for accelerating the rational discovery of solid-state hydrogen storage materials.
Results and discussion
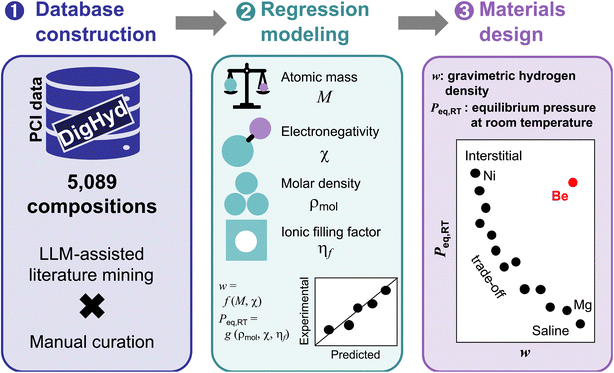
A schematic overview of our descriptor-based approach to hydrogen storage materials discovery is presented in Fig. 1. The workflow begins with the construction of a curated database, followed by regression modeling using physically meaningful descriptors, and culminates in compositional mapping for rational materials design. The database component is based on the DigHyd platform, which consolidates 5089 pressure-composition isotherm (PCI) data points specifically for metal hydrides. These entries were initially identified from 910 literature sources using large language model assisted mining and then subjected to rigorous manual review. During this curation process, entries lacking clearly defined chemical formulae were excluded to ensure compositional consistency. For Peq,RT, we included values either directly reported in the literature or indirectly estimated using the van't Hoff equation when thermodynamic parameters, namely enthalpy (ΔH) and entropy (ΔS), were available from multi-temperature PCI data. After removing duplicate compositions, the final dataset comprised 1967 and 1078 unique entries for w and Peq,RT, respectively, spanning a broad range of metal hydride chemistries.While both DigHyd database and the previously developed ML_Hydpark16 database represent valuable data resources for hydrogen storage research, DigHyd, which serves as a superset of ML_Hydpark, offers several distinct advantages for data-driven modeling. Most importantly, DigHyd includes an order of magnitude more PCI entries for metal hydrides (DigHyd: 5089 vs. ML_Hydpark: 430)16 and additionally encompasses covalent organic frameworks (COFs) and metal–organic frameworks (MOFs), which were not used in the present study but are available within the platform. Furthermore, DigHyd is structured in JavaScript Object Notation (JSON) format and includes full reference traceability via Digital Object Identifiers (DOIs), significantly improving data transparency and reproducibility. By contrast, ML_Hydpark is distributed in flat CSV format and lacks consistent bibliographic metadata, which limits its utility for model interpretation and downstream analysis. These attributes made DigHyd a more scalable and reliable foundation for building physically interpretable models in this work.
To develop low-cost, transparent predictive models, we found a set of effective descriptors that capture essential physical and chemical characteristics of metal hydride systems among the candidate features: M, χ, ρmol, and ηf. These variables serve as proxies for key mechanisms influencing hydrogen storage capacity and thermodynamic behavior: lattice weight, bond polarity, structural density, and steric occupancy. Closed-form regression models constructed from these descriptors were able to predict w and Peq,RT with high accuracy, while maintaining physical transparency, an essential attribute for guiding materials design beyond black-box ML prediction.
Finally, the model outputs were used to generate materials design maps that visualize hydrogen storage performance across a wide compositional space. Strikingly, these maps highlight an intrinsic trade-off between w and Peq,RT: saline-type hydrides, such as Mg-based systems, tend to exhibit high w but low Peq,RT, whereas interstitial-type hydrides, such as Ni-based systems, display the opposite trend. Notably, Be-based systems emerge as rare candidates that potentially circumvent this trade-off, achieving high w and high Peq,RT. While the broader implications of this trend are explored in detail later, the present figure serves to frame the conceptual structure of this study: from curated data to interpretable modeling, to chemically meaningful design guidance (Fig. 1).
To gain insights into the composition and diversity of the curated dataset, we analyzed the distribution of elements and key performance metrics within the DigHyd database. As shown in Fig. 2a, certain metal elements appear more frequently than others, reflecting historical research focus and experimental accessibility. Ni (2588 entries) and Mg (2263 entries) dominate the dataset, consistent with the prevalence of interstitial- and saline-type hydrides, respectively. Ti, Cr, Mn, La, V, Zr, Fe, and Al also appear prominently, representing a range of compositional classes, which ensures that the dataset captures both conventional and less-explored regions of the hydride design space.
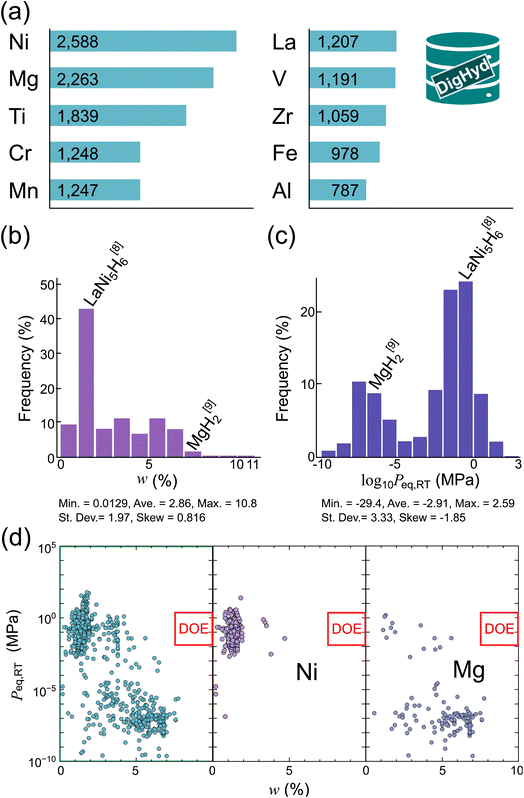 | ||
| Fig. 2 Data profile of metal hydrides in the DigHyd database. (a) Frequency of metal elements appearing in the dataset, with Ni and Mg being most prevalent. Histograms of (b) gravimetric hydrogen density (w) and (c) logarithm-scaled equilibrium pressure (Peq,RT) at room temperature, highlighting MgH2 (saline-type) and LaNi5H6 (interstitial-type) as representative cases.8,9 For both (b) and (c), the minimum (Min.), average (Ave.), maximum (Max.), standard deviation (St. Dev.), and skewness (Skew) are provided, illustrating the broad spread and asymmetry in the dataset. (d) Scatter plots of w versus Peq,RT: all compositions (left), Ni-containing but Mg-free systems (middle), and Mg-containing but Ni-free systems (right). The ultimate target region of U.S. Department of Energy (US-DOE) target region is indicated by red boxes. | ||
The distributions of the two target properties, w and Peq,RT, are shown in Fig. 2b and c, respectively. The histogram of w exhibits a right-skewed distribution, with most compositions clustering below 5%, and a long tail extending toward higher-capacity systems. While MgH2, a classic saline-type hydride, lies on the higher-capacity end, LaNi5H6, a representative interstitial-type compound, sits near the modal value. Meanwhile, the distribution of Peq,RT spans a wide range, highlighting the vast thermodynamic diversity of metal hydrides. Notably, MgH2 and LaNi5H6 again serve as instructive references, occupying opposite extremes of the pressure-capacity landscape. The statistical summaries are also annotated beneath each plot, including the minimum, average, maximum, standard deviation, and skewness.
In addition to the elemental distributions and property histograms, Fig. 2d provides a direct visualization of the relationship between w and Peq,RT. For the full dataset (Fig. 2d, left), a weak trade-off relationship between w and Peq,RT can be discerned. When focusing on Ni-containing but Mg-free systems, which are representative of interstitial-type hydrides (Fig. 2d, middle), the trend shifts toward high Peq,RT but low w. In contrast, Mg-containing but Ni-free systems, corresponding to saline-type hydrides (Fig. 2d, right), display the opposite behavior, namely low Peq,RT and high w. Notably, in all cases, the data points have not yet reached the US-DOE target region, outlined by red boxes, underscoring the substantial performance gap that persists in the current hydride landscape.
As represented in Fig. 3a, to enable physically interpretable modeling with low computational cost, we selected seven primary elemental features: the average atomic mass 〈M〉, the average electronegativity respect to hydrogen's 〈χ − χH〉, the average density 〈ρ〉,18 the average molar density 〈ρmol〉, the average valence 〈C〉, the average Shannon ionic radius assuming sixfold coordination 〈rVI〉,19 and the average ionic filling factor 〈ηf〉, of metal atoms (excluding hydrogen). More details can be found in the Methods section, SI. The interrelationships among the 7 features are illustrated by a Pearson correlation heatmap (Fig. S2). Furthermore, to capture the distributional characteristics of each feature, we included both the standard deviation σ(x) and the skewness r(x) for each descriptor, where x represents any of the following properties: x = M, χ − χH, ρ, ρmol, C, rVI, and ηf.
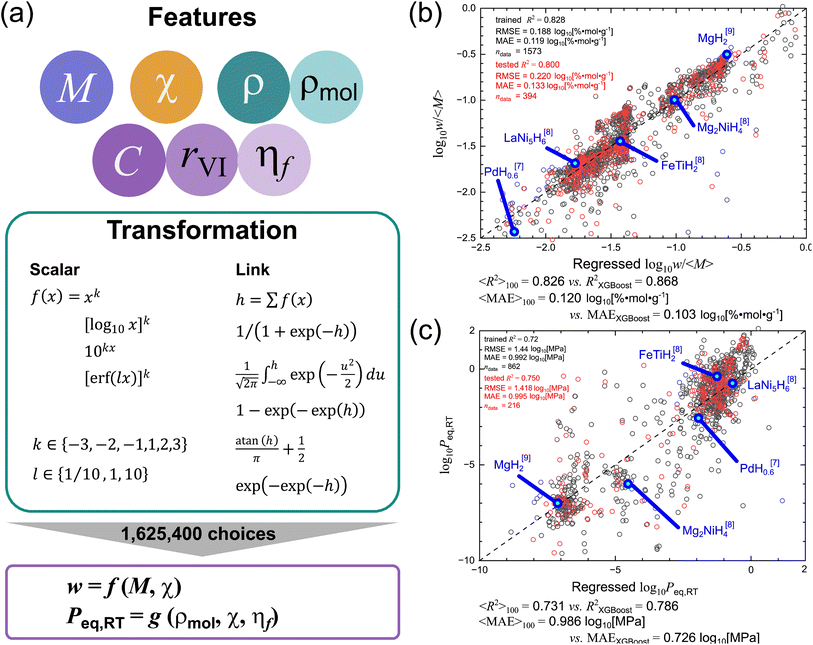 | ||
Fig. 3 Physically interpretable regression models for hydrogen storage properties. (a) Seven elemental descriptors were combined with scalar transformations and (non)linear link functions to generate 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625 625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 candidate models. Final models for (b) gravimetric hydrogen density (w) [based on 〈M〉 and 〈χ − χH〉; defined in eqn (1)] and (c) equilibrium pressure (Peq,RT) at room temperature [〈ρmol〉, 〈χ − χH〉, and 〈ηf〉; eqn (2)], wherein training and test datasets follow an 80 400 candidate models. Final models for (b) gravimetric hydrogen density (w) [based on 〈M〉 and 〈χ − χH〉; defined in eqn (1)] and (c) equilibrium pressure (Peq,RT) at room temperature [〈ρmol〉, 〈χ − χH〉, and 〈ηf〉; eqn (2)], wherein training and test datasets follow an 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20 split and are denoted by black and red open circles, respectively. For both (b) and (c), 5 representative cases (i.e., MgH2, Mg2NiH4, FeTiH2, PdH0.6, and LaNi5H6),7–9 the coefficient of determination (R2) and mean absolute error (MAE) for the test datasets are provided, comparing with the ML benchmarks.17 20 split and are denoted by black and red open circles, respectively. For both (b) and (c), 5 representative cases (i.e., MgH2, Mg2NiH4, FeTiH2, PdH0.6, and LaNi5H6),7–9 the coefficient of determination (R2) and mean absolute error (MAE) for the test datasets are provided, comparing with the ML benchmarks.17 | ||
To comprehensively explore possible regression models from the pool of 21 candidate descriptors, 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625
625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 regression models in total were constructed and assessed by using multivariate linear regression modeling and multivariate beta regression modeling, which also enables nonlinear fitting.20–24 More details can be found in the Methods section, SI. The final models for w (in the unit of %) and Peq,RT (MPa) were selected based on those exhibiting the highest coefficient-of-determination R2 values on test datasets, which were randomly sampled to comprise approximately 20% of the total data: 394 data points for w and 216 for Peq,RT. Among the 1
400 regression models in total were constructed and assessed by using multivariate linear regression modeling and multivariate beta regression modeling, which also enables nonlinear fitting.20–24 More details can be found in the Methods section, SI. The final models for w (in the unit of %) and Peq,RT (MPa) were selected based on those exhibiting the highest coefficient-of-determination R2 values on test datasets, which were randomly sampled to comprise approximately 20% of the total data: 394 data points for w and 216 for Peq,RT. Among the 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 625
625![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 candidate models evaluated, the optimal regression model for predicting w was identified as a two-descriptor expression involving 〈M〉 and 〈χ − χH〉 (Fig. 3b). The final expression takes the following form:
400 candidate models evaluated, the optimal regression model for predicting w was identified as a two-descriptor expression involving 〈M〉 and 〈χ − χH〉 (Fig. 3b). The final expression takes the following form:
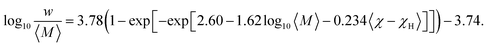 | (1) |
The regression model achieved R2 = 0.828, root mean squared error RMSE = 0.188![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1], and mean absolute error MAE = 0.119
log10[% mol g−1], and mean absolute error MAE = 0.119![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1] for the training dataset (wherein the size of the dataset was given as ndata = 1573) and R2 = 0.800, RMSE = 0.220
log10[% mol g−1] for the training dataset (wherein the size of the dataset was given as ndata = 1573) and R2 = 0.800, RMSE = 0.220![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1], and MAE = 0.133
log10[% mol g−1], and MAE = 0.133![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1] for the test dataset (ndata = 394). To further evaluate the model's robustness, we performed 100 random resamplings independently, each selecting ndata = 394 for testing. The resulting performance metrics were averaged to yield 〈R2〉100 = 0.826 ± 0.00101, 〈RMSE〉100 = 0.191 ± 0.000374 log10[% mol g−1], and 〈MAE〉100 = 0.120 ± 0.0000483
log10[% mol g−1] for the test dataset (ndata = 394). To further evaluate the model's robustness, we performed 100 random resamplings independently, each selecting ndata = 394 for testing. The resulting performance metrics were averaged to yield 〈R2〉100 = 0.826 ± 0.00101, 〈RMSE〉100 = 0.191 ± 0.000374 log10[% mol g−1], and 〈MAE〉100 = 0.120 ± 0.0000483![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1]. For reference, our own XGBoost analysis on the same dataset, refined using 10-fold cross-validation (see XGBoost regression section, SI), yielded R2 = 0.868, RMSE = 0.164
log10[% mol g−1]. For reference, our own XGBoost analysis on the same dataset, refined using 10-fold cross-validation (see XGBoost regression section, SI), yielded R2 = 0.868, RMSE = 0.164![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1], and MAE = 0.103
log10[% mol g−1], and MAE = 0.103![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[% mol g−1] for the test data points, confirming that proposed descriptor-based model achieves accuracy on par with state-of-the-art ML approaches. Importantly, the model generalizes well across chemical space: 5 representative compounds (i.e., MgH2, Mg2NiH4, FeTiH2, PdH0.6, and LaNi5H6)7–9 lie close to the “experimental = regressed” parity line, demonstrating both accuracy and practical utility in capturing real-world behavior.
log10[% mol g−1] for the test data points, confirming that proposed descriptor-based model achieves accuracy on par with state-of-the-art ML approaches. Importantly, the model generalizes well across chemical space: 5 representative compounds (i.e., MgH2, Mg2NiH4, FeTiH2, PdH0.6, and LaNi5H6)7–9 lie close to the “experimental = regressed” parity line, demonstrating both accuracy and practical utility in capturing real-world behavior.
We also provide detailed statistics of the regression model in Table S1, including standard errors, 95% confidence intervals, standardized coefficients, t-values, and variance inflation factors (VIF) for each term. All t-tests yield p-values <10−15, confirming that no term is redundant. The VIF value is suppressed (1.47), indicating the absence of multicollinearity. In addition, Fig. S3 presents histograms of the residuals for both training and test datasets, showing zero-centered distributions. This result demonstrates that the model errors are random rather than systematic, with no apparent bias or pattern.
The optimal regression model for predicting Peq,RT was derived using three physically meaningful descriptors: 〈ρmol〉, 〈χ − χH〉, and 〈ηf〉 (Fig. 3c). The resulting model is expressed as:
log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Peq,RT = 12.2(1 − exp[−exp[−1.37 + 21.0〈ρmol〉 − 0.163 × 10−〈χ−χH〉 − 0.878[erf(10〈ηf〉)]2]]) − 9.52. Peq,RT = 12.2(1 − exp[−exp[−1.37 + 21.0〈ρmol〉 − 0.163 × 10−〈χ−χH〉 − 0.878[erf(10〈ηf〉)]2]]) − 9.52. | (2) |
The regression model achieved R2 = 0.728, RMSE = 1.44![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa], and MAE = 0.992
log10[MPa], and MAE = 0.992![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa] for the training dataset (ndata = 862) and R2 = 0.750, RMSE = 1.418
log10[MPa] for the training dataset (ndata = 862) and R2 = 0.750, RMSE = 1.418![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa], and MAE = 0.995
log10[MPa], and MAE = 0.995![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa] for the test dataset (ndata = 216). To further evaluate the model's robustness, we performed 100 random resamplings independently, each selecting ndata = 216 for testing. The resulting performance metrics were averaged to yield 〈R2〉100 = 0.731 ± 0.00200, 〈RMSE〉100 = 1.42 ± 0.0136
log10[MPa] for the test dataset (ndata = 216). To further evaluate the model's robustness, we performed 100 random resamplings independently, each selecting ndata = 216 for testing. The resulting performance metrics were averaged to yield 〈R2〉100 = 0.731 ± 0.00200, 〈RMSE〉100 = 1.42 ± 0.0136![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa], and 〈MAE〉100 = 0.986 ± 0.00290
log10[MPa], and 〈MAE〉100 = 0.986 ± 0.00290![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa]. For reference, our own XGBoost analysis on the same dataset, refined using 10-fold cross-validation (see XGBoost regression section, SI), yielded R2 = 0.786, RMSE = 1.281
log10[MPa]. For reference, our own XGBoost analysis on the same dataset, refined using 10-fold cross-validation (see XGBoost regression section, SI), yielded R2 = 0.786, RMSE = 1.281![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa], and MAE = 0.726
log10[MPa], and MAE = 0.726![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log10[MPa] for the test data points, further confirming that the descriptor-based model performs on par with advanced ML methods again. Notably, the same 5 reference compounds remain well-aligned with the “experimental = regressed” trend, reinforcing the robustness of the models across both thermodynamic and capacity domains.
log10[MPa] for the test data points, further confirming that the descriptor-based model performs on par with advanced ML methods again. Notably, the same 5 reference compounds remain well-aligned with the “experimental = regressed” trend, reinforcing the robustness of the models across both thermodynamic and capacity domains.
Detailed regression statistics are provided in Table S2. All terms are significant (p < 10−11), and VIF values below 3 indicate no multicollinearity. Residual histograms in Fig. S4 show zero-centered distributions, confirming that model errors are random rather than systematic. The use of simple, physically grounded descriptors thus enables predictive, interpretable modeling of hydrogen storage performance with broad chemical applicability. A complete listing of the feature vales χ − χH, M, ρmol, and ηf is available in Table S3.
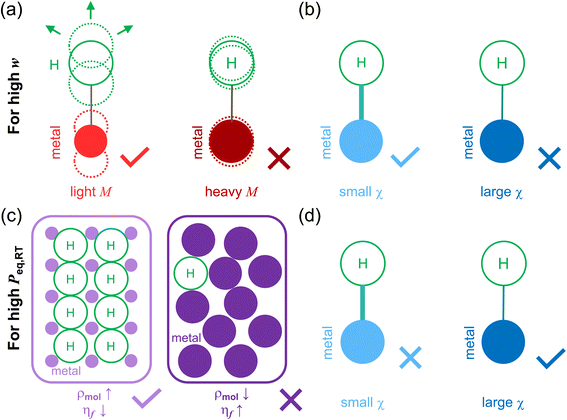
To elucidate the physical basis of the regression models, we provide schematic illustrations of how each key descriptor influences hydrogen storage behaviors (Fig. 4). For achieving high w, two primary factors are beneficial: a low M and a large |〈χ − χH〉| (given by small χ; χ < χH). As shown in Fig. 4a and b, lighter host metals not only reduce the overall system mass, directly contributing to higher weight-specific capacity, but also may facilitate more dynamic lattice vibrations, potentially enhancing hydrogen diffusion into the bulk. A larger |〈χ − χH〉| promotes stronger metal–hydrogen bond polarity, which is advantageous for maximizing hydrogen uptake under non-equilibrium or storage-focused conditions. Together, these descriptors encode essential atomic-scale design principles, providing both predictive power and chemical insights into the governing factors that enhance w in metal hydrides.
For Peq,RT, the relevant descriptors reflect a different physical regime, rooted in thermodynamic stability. As illustrated in Fig. 4c and d, high ρmol increases the number of reactive sites per volume, while a low ηf implies reduced steric hindrance, allowing hydrogen to occupy interstitial positions more readily. Furthermore, smaller |〈χ − χH〉|, implying weaker bond polarity, lead to higher hydrogen chemical potential in the solid phase. This destabilizes the metal–hydrogen bond and shifts the equilibrium toward desorption, resulting in higher Peq,RT. Collectively, these effects enhance lattice accessibility and reduce hydrogen binding strength under equilibrium conditions, providing a chemically intuitive explanation for the model's predictive trends.
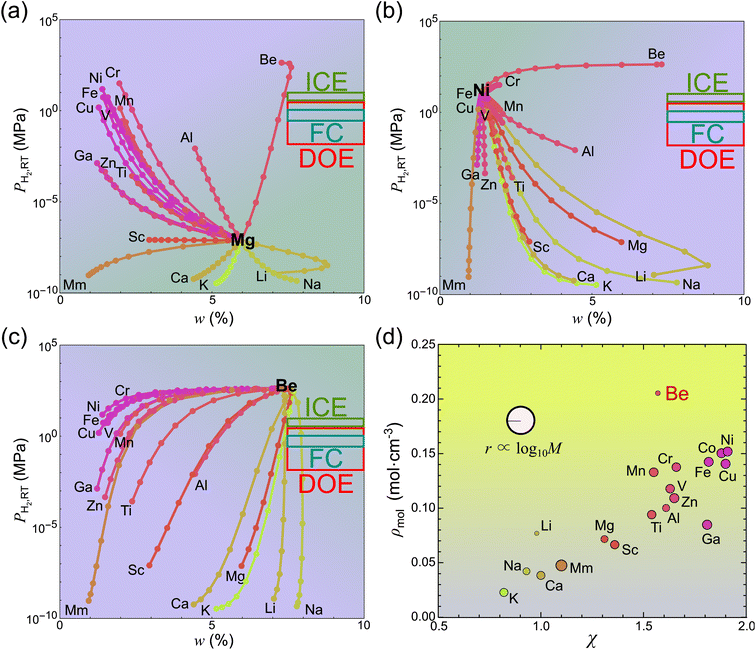
To further explore how the regression models guide rational compositional design, we constructed descriptor-based design maps by selecting three representative elemental anchors (i.e., Mg, Ni, and Be) and simulating compositional substitution trajectories with other metallic elements; additional compositional pathways originating from Li, Na, Al, K, Ca, Ce, Sc, Ti, V, Cr, Mn, Fe, Co, Cu, Zn, Ga, and Mm (mischmetal) are presented in Fig. S5. Also, a user-interactive Excel file is provided in the SI for predicting w and Peq,RT based on any input composition. As shown in Fig. 5a, Mg, a prototypical saline-type hydride former, lies near the high-w, low-Peq,RT corner of the map. Substituting Mg with other metals generally leads to increased Peq,RT but reduced w, reflecting a shift away from the saline regime. Conversely, Ni-based pathways in Fig. 5b, representing interstitial-type hydrides, exhibit the opposite trend: most substitutions lower Peq,RT while increasing w. These two maps together highlight the w–Peq,RT trade-off that characterizes conventional hydride systems.
In contrast, Be forms a unique trajectory on the design map, as represented in Fig. 5c, with compositions such as BebNa1−b. Three composition ranges, b = 0.622–0.717, 0.720–0.743, and 0.673–0.698 yield w = 7.92–7.97%, 7.89–7.91%, and 7.93–7.95%, together with Peq,RT = 0.016–3.1 MPa, 3.5–10 MPa, and 0.3–1.2 MPa, respectively. These ranges correspond to the ultimate US-DOE targets converted from operating ambient temperature via the van't Hoff relationship (see Ultimate US-DOE Targets of Peq,RTvia Van't Hoff conversion section, SI), the targets for internal combustion engine (ICE) applications, and the targets for fuel cell (FC) applications, respectively.25 No experimental reports on Be–Na hydrides are available to date. Be itself combines several rare and favorable features: low atomic mass (M = 9.01 g mol−1), moderately high electronegativity (χ − χH = −0.63), and the highest molar density (ρmol = 0.205 mol cm−3) among the studied elements. These attributes together enable the balancing of w and Peq,RT that few other systems can offer.
To better understand the physical origin of the w–Peq,RT trade-off, we analyze the elemental descriptor space in Fig. 5d, where each metal is plotted by its χ and ρmol, with M encoded in circle size. A clear positive correlation is observed between χ and ρmol, which may reflect that elements with stronger electron-attracting character favor shorter bond lengths and more compact lattice structures. This trend provides insight into the trade-off observed in Fig. 5a and b; metals with low χ (e.g., Mg, Li, Na) favor high w due to comparably low M and strong bond polarity to hydrogen (large |〈χ − χH〉|), but result in loose packing (low ρmol) and low Peq,RT. In contrast, transition metals (e.g., Ni, Fe, Cr), with high χ, exhibit tight packing (high ρmol) and high Peq,RT but reduced w due to heavy M and weaker polarity-driven uptake (small |〈χ − χH〉|).
Beryllium (Be), however, emerges as a distinct outlier in this landscape. Despite its relatively moderate electronegativity, Be possesses an unusually high ρmol and low M, positioning it in a sparsely populated upper-left region of the design space in Fig. 5d. This anomaly may be attributed to its unique electronic structure: the low principal quantum number (2) of its valence electrons facilitates tight orbital overlap and strong core-valence attraction, enabling a compact atomic arrangement. This high packing efficiency enhances Peq,RT, while the light M supports high w. As such, Be sits at a rare convergence point of design principles, suggesting that its alloys, particularly when judiciously combined with more electropositive elements, may serve as promising leads for next-generation hydrogen storage materials.26–29 However, the use of Be raises important safety concerns due to its known toxicity, particularly in powder or nanoparticle form,30 as well as its considerable cost. While the target metrics for hydrogen storage performance are favorable, any application of Be-based materials would require stringent handling protocols and careful risk-benefit evaluation.
Interestingly, the promising behavior of Be-based hydrides, particularly Be2Ti, is supported by experimental and computational findings that align closely with our model predictions. Mealand and Libowitz assumed that 0.1 MPa < Peq,RT < 15 MPa for Be2TiH3 with w = 4.4%.26 Our regression models predict w = 5.6% and Peq,RT = 171 MPa, reasonably capturing both the high w and a tendency toward elevated Peq,RT. More recently, Kim, Iwakiri, and Nakamichi conducted PCI measurements on Be2Ti and assumed Peq,RT ≫ 13 MPa, exceeding the upper limit of their apparatus.27 Although the experimentally observed w under 13 MPa was limited to 0.57% (not reaching equilibrium), this was attributed to surface BeO formation, which impedes hydrogen uptake. Importantly, their first-principles calculations, which estimated accessible stable hydrogen sites in the lattice, yielded w = 5.4%, closely corroborating both our prediction and earlier empirical data.26 Taken together, both studies appear to have failed to achieve clear equilibrium conditions, most plausibly due to the intrinsically high Peq,RT of the investigated Be-based hydride, which exceeded experimental constraints. In addition to Be2Ti, Maeland and Libowitz also studied Be2Zr, reporting the formation of a Be2ZrH2.3 phase with w = 2.1% at Peq,RT = 13 MPa.26 Our model forecasts w = 3.5% and Peq,RT = 40 MPa, again indicating good semi-quantitative agreement. These converging observations reinforce the notion that Be-based systems reside in a favorable region of the design space, offering a rare combination of high w and moderate-to-high Peq,RT, despite known practical challenges such as Be toxicity and oxide passivation. These real-world cases provide compelling validation for our model and emphasize the potential of Be-centered hydride chemistries.
Summary
In this work, we have developed and validated physically interpretable regression models for predicting two key performance metrics of metal hydrides: w and Peq,RT. Leveraging a rigorously curated dataset (DigHyd) and a minimal set of chemically meaningful descriptors, we constructed explicit analytic models that match the predictive accuracy of state-of-the-art ML methods, while preserving full physical transparency. Design maps generated from these models revealed a fundamental trade-off between w and Peq,RT performances, rooted in opposing trends in elemental properties, particularly χ. Saline-type hydrides, composed of light and more electropositive elements, tend to exhibit high w due to strong metal–hydrogen bond polarity but suffer from low Peq,RT. In contrast, interstitial-type hydrides based on heavier, more electronegative transition metals show the opposite behavior. Amid this trade-off landscape, Be-based systems, such as Be–Na alloys, emerge as rare candidates capable of balancing both metrics, owing to its unique combination of low M and high ρmol (possibly owing to the compact electronic structure). These findings offer chemically intuitive insights into the design principles governing hydrogen storage materials.Beyond binary hydrides, the regression framework established here is readily extensible to more complex compositional spaces, including ternary and high-entropy alloy systems, as well as porous materials such as MOFs and COFs. The incorporation of additional physically motivated descriptors, or integration with first-principles methods, may further enhance the scope and fidelity of the models. Importantly, identifying chemically benign analogs to high-performing but toxic systems like Be-based compounds remains an urgent priority. More broadly, this descriptor-driven modeling strategy offers a scalable and interpretable platform for data-guided materials discovery, with potential applicability across diverse energy-relevant domains where structure–property relationships remain poorly understood. We also note that the present models are limited to equilibrium and gravimetric metrics; dynamic stability and cycling durability remain unaddressed and will be explored in future extensions of the framework.
Author contributions
H. Li and S. Orimo conceived the idea and supervised the project. S.-H. Jang and H. Li wrote the manuscript. S.-H. Jang curated and manually examined the database, and constructed and interpreted the symbolic models. D. Zhang, H. B. Tran, X. Jia, and K. Konno developed the database using an AI model, with D. Zhang taking the lead. X. Jia also constructed the XGBoost model. R. Sato revised the manuscript and contributed conceptual insights. All authors discussed and analyzed the results during manuscript preparation.Conflicts of interest
There are no conflicts to declare.Data availability
The supporting user-interactive Excel file (wherein w and Peq,RT can be predicted for any user-defined composition) is openly available in GitHub at https://github.com/gtex-project/dighyd-MLmodel. The data for ML modeling are stored in our DigHyd database (https://www.dighyd.org).Supplementary information: methods, XGBoost regressions, ultimate US-DOE targets of Peq,RTvia Van't Hoff conversion, details of regression models, descriptor tables, and descriptor-based design map. Supporting Excel file: simulation wherein w and Peq,RT can be predicted for any user-defined composition. See DOI: https://doi.org/10.1039/d5sc07296d.
Acknowledgements
This work was supported by The Green Technologies of Excellence (GteX) Program, Japan (Grant No. JPMJGX23H1).References
- N. Johnson, M. Liebreich, D. M. Kammen, P. Ekins, R. McKenna and I. Staffell, Realistic roles for hydrogen in the future energy transition, Nat. Rev. Clean Technol., 2025, 1, 351–371, DOI:10.1038/s44359-025-00050-4.
- A. P. Zhao, S. Li, D. Xie, Y. Wang, Z. Li, P. J.-H. Hu and Q. Zhang, Hydrogen as the nexus of future sustainable transport and energy system, Nat. Rev. Electr. Eng., 2025, 2, 447–446, DOI:10.1038/s44287-025-00178-2.
- A. G. Gebretatios, F. Banat and C. K. Cheng, A critical review of hydrogen storage: Toward the nanoconfinement of complex hydrides from the synthesis and characterization perspectives, Sustain. Energy Fuels, 2024, 8(22), 5091–5130, 10.1039/d4se00353e.
- A. Züttel, Materials for hydrogen storage, Mater. Today, 2003, 6(9), 24–33, DOI:10.1016/S1369-7021(03)00922-2.
- J. Bellosta von Colbe, J.-R. Ares, J. Barale, M. Baricco, C. Buckley, G. Capurso, N. Gallandat, D. M. Grant, M. N. Guzik, I. Jacob, E. H. Jensen, T. Jensen, J. Jepsen, T. Klassen, M. V. Lototskyy, K. Manickam, A. Montone, J. Puszkiel, S. Sartori, D. A. Sheppard, A. Stuart, G. Walker, C. J. Webb, H. Yang, V. Yartys, A. Züttel and M. Dornheim, Application of hydrides in hydrogen storage and compression: Achievements, outlook and perspectives, Int. J. Hydrogen Energy, 2019, 44(15), 7780–7808, DOI:10.1016/j.ijhydene.2019.01.104.
- M. Hirscher, V. A. Yartys, M. Baricco, J. Bellosta von Colbe, D. Blanchard, R. C. Bowman, D. P. Broom, C. E. Buckley, F. Chang, P. Chen, Y. W. Cho, J.-C. Crivello, F. Cuevas, W. I. F. David, P. E. de Jongh, R. V. Denys, M. Dornheim, M. Felderhoff, Y. Filinchuk, G. E. Froudakis, D. M. Grant, E. M. Gray, B. C. Hauback, T. He, T. D. Humphries, T. R. Jensen, S. Kim, Y. Kojima, M. Latroche, H.-W. Li, M. V. Lototskyy, J. W. Makepeace, K. T. Møller, L. Naheed, P. Ngen, D. Noréus, M. M. Nygård, S. Orimo, M. Paskevicius, L. Pasquini, D. B. Ravnsbæk, M. V. Sofianos, T. J. Udovic, T. Vegge, G. S. Walker, C. J. Webb, C. Weidenthaler and C. Zlotea, Materials for hydrogen-based energy storage - Past, recent progress and future outlook, J. Alloys Compd., 2020, 827, 153548, DOI:10.1016/j.jallcom.2019.153548.
- E. Wicke, H. Brodowsky and H. Züchner, Hydrogen in palladium and palladium alloys, Hydrogen in Metals II, Topics in Applied Physics, ed. Alefeld, G. and Völkl, J., Springer, 1978, vol. 29, pp. 73–155, DOI:10.1007/3-540-08883-0_19.
- G. Sandrock, A panoramic overview of hydrogen storage alloys from a gas reaction point of view, J. Alloys Compd., 1999, 293–295, 877–888, DOI:10.1016/S0925-8388(99)00384-9.
- R. C. Bowman Jr and B. Fultz, Metallic hydrides I: Hydrogen storage and other gas-phase applications, MRS Bull., 2002, 27, 688–693, DOI:10.1557/mrs2002.223.
- S. Orimo, Y. Nakamori, J. R. Eliseo, A. Züttel and C. M. Jensen, Complex hydrides for hydrogen storage, Chem. Rev., 2007, 107, 4111–4132, DOI:10.1021/cr0501846.
- B. Sakintuna, F. Lamari-Darkrim and M. Hirscher, Metal hydride materials for solid hydrogen storage: A review, Int. J. Hydrogen Energy, 2007, 32(9), 1121–1140, DOI:10.1016/j.ijhydene.2006.11.022.
- I. P. Jain, P. Jain and A. Jain, Novel hydrogen storage materials: A review of lightweight complex hydrides, J. Alloys Compd., 2010, 503(2), 303–339, DOI:10.1016/j.jallcom.2010.04.250.
- I. P. Jain, C. Lal and A. Jain, Hydrogen storage in Mg: A most promising material, Int. J. Hydrogen Energy, 2010, 35(10), 5133–5144, DOI:10.1016/j.ijhydene.2009.08.088.
- G. Scarpati, E. Frasci, G. Di Ilio and E. Jannelli, A comprehensive review on metal hydrides-based hydrogen storage systems for mobile applications, J. Energy Storage, 2024, 102, 113934, DOI:10.1016/j.est.2024.113934.
- E. Nemukula, C. B. Mtshali and F. Nemangwele, Metal hydrides for sustainable hydrogen storage: A review, Int. J. Energy Res., 2025, 6302225, DOI:10.1155/er/6300225.
- M. Witman, S. Ling, D. M. Grant, G. S. Walker, S. Agarwal, V. Stavila and M. D. Allendorf, Extracting an empirical intermetallic hydride design principle from limited data via interpretable machine learning, J. Phys. Chem. Lett., 2019, 11(1), 40–47, DOI:10.1021/acs.jpclett.9b02971.
- M. D. Witman, S. Ling, M. Wadge, A. Bouzidi, N. Pineda-Romero, R. Clulow, G. Ek, J. M. Chames, E. J. Allendorf, S. Agarwal, M. D. Allendorf, G. S. Walker, D. M. Grant, M. Sahlberg, C. Zlotea and V. Stavila, Towards Pareto optimal high entropy hydrides via data-driven materials discovery, J. Mater. Chem. A, 2023, 11(29), 15878–15888, 10.1039/d3ta02323k.
- Density in the Periodic Table of Elements, https://pubchem.ncbi.nlm.nih.gov/ptable/density/.
- R. D. Shannon, Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides, Acta Crystallogr., Sect. A, 1976, 32(5), 751–767, DOI:10.1107/s0567739476001551.
- R. Kieschnick and B. D. McCullough, Regression analysis of variates observed on (0, 1): Percentages, proportions and fractions, Stat. Model., 2003, 3(3), 193–213, DOI:10.1191/1471082x03st053oa.
- S. Ferrari and F. Cribari-Neto, Beta regression for modelling rates and proportions, J. Appl. Stat., 2004, 31(7), 799–815, DOI:10.1080/0266476042000214501.
- M. Smithson and J. Verkuilen, A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables, Psychol. Methods, 2006, 11(1), 54–71, DOI:10.1037/1082-989x.11.1.54.
- F. Cribari-Neto and A. Zeileis, Beta regression in R, J. Stat. Softw., 2010, 34(2), 1–24, DOI:10.18637/jss.v034.i02.
- S. Jang, R. Jalem and Y. Tateyama, Predicting room-temperature conductivity of Na-ion super ionic conductors with the minimal number of easily-accessible descriptors, Adv. Energy Sustainability Res., 2024, 5(12), 2400158, DOI:10.1002/aesr.202400158.
- Targets for Onboard Hydrogen Storage Systems for Light-Duty Vehicles. US Department of Energy, Office of Energy Efficiency and Renewable Energy and The FreedomCAR and Fuel Partnership, https://www1.eere.energy.gov/hydrogenandfuelcells/storage/pdfs/targets_onboard_hydro_storage_explanation.pdf.
- A. J. Maeland and G. G. Libowitz, Hydrides of beryllium-based intermetallic compounds, J. Less-Common Met., 1983, 89(1), 197–200, DOI:10.1016/0022-5088(83)90266-7.
- J.-H. Kim, H. Iwakiri and M. Nakamichi, Reactivity with water vapor and hydrogen storage capacity of Be2Ti compound, Int. J. Hydrogen Energy, 2016, 41(21), 8893–8899, DOI:10.1016/j.ijhydene.2016.02.131.
- Y. Kenzhin, I. Kenzhina, T. Kulsartov, Z. Zaurbekova, S. Askerbekov, Y. Ponkratov, Y. Gordienko, A. Yelishenkov and S. Udartsev, Study of hydrogen sorption and desorption processes of zirconium beryllide ZrBe2, Nucl. Mater. Energy, 2024, 39, 101634, DOI:10.1016/j.nme.2024.101634.
- M. Ali, Z. Bibi, M. Awais, M. W. Younis and N. Sfina, Effective hydrogen storage in Na2(Be/Mg)H4 hydrides: Perspective from density functional theory, Int. J. Hydrogen Energy, 2024, 64, 329–338, DOI:10.1016/j.ijhydene.2024.03.234.
- World Health Organization & International Programme on Chemical Safety, Beryllium: Health and Safety Guide, World Health Organization, 1990, https://iris.who.int/handle/10665/40004 Search PubMed.
| This journal is © The Royal Society of Chemistry 2025 |