 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Designing and synthesizing perovskites with targeted bandgaps via tailored descriptors
Kenshin
Shibata
 a,
Fernando
Garcia-Escobar
a,
Fernando
Garcia-Escobar
 *a,
Tomoya
Tashiro
*a,
Tomoya
Tashiro
 a,
Lauren
Takahashi
a,
Lauren
Takahashi
 a and
Keisuke
Takahashi
a and
Keisuke
Takahashi
 *ab
*ab
aDepartment of Chemistry, Hokkaido University, North 10, West 8, Sapporo 060-0810, Japan. E-mail: fgares@sci.hokudai.ac.jp; keisuke.takahashi@sci.hokudai.ac.jp
bList Sustainable Digital Transformation Catalyst Collaboration Research Platform, Institute for Chemical Reaction Design and Discovery, Hokkaido University, Sapporo 001-0021, Japan
First published on 19th August 2025
Abstract
Descriptors that govern the bandgaps of perovskite-type oxides are identified by analyzing experimentally reported materials, focusing on compositional, structural, and electronic features relevant to solar energy conversion. These descriptors form the basis of a machine learning model that predicts bandgaps across a wide chemical space. Several compositions with targeted optical properties are predicted and subsequently synthesized. Structural and optical characterization studies confirm the formation of the predicted phases and the bandgap. Thus, this work demonstrates that the descriptor-driven, data-guided workflow accelerates the discovery of photoactive perovskites for solar energy conversion and visible-light-driven applications.
Introduction
Designing materials with targeted properties presents a fundamental challenge due to the vast compositional space and the complex interplay between atomic structure, crystal symmetry, and synthesis conditions.1–3 Material properties such as bandgap are highly sensitive to subtle variations in atomic arrangement and processing methods, making rational design nontrivial. Trial-and-error searches of materials often struggle to efficiently navigate this multidimensional design space. The rise of materials informatics addresses this complexity, where machine learning and data mining are utilized to uncover the hidden patterns and trends for predicting materials properties.4–7 Such methodologies are particularly effective in perovskite materials, a class known for their tunable optoelectronic and catalytic properties.8–12 Here, machine learning is employed to predict the bandgaps based on a dataset compiled from experimental literature, where predicted perovskite materials are synthesized experimentally.Perovskite materials are widely recognized for possessing near-ideal bandgaps for efficient solar light absorption, making them strong candidates for photovoltaic and photocatalytic applications.13–16 However, the bandgap in perovskites is highly sensitive to variations in atomic arrangement, including compositional tuning. If machine learning can unveil the hidden relationship between bandgap and atomic arrangement as well as descriptors for representing bandgap, one can consider that machine learning can be utilized to design the desired perovskite material.9,17,18 In this work, machine learning models are constructed using curated literature data to identify key material descriptors that govern bandgap behavior in perovskite materials. In addition, this work aims to link data, machine learning, experimental synthesis, and characterization in a unified discovery process. This approach provides insight into the underlying factors that control bandgap variation and offers a pathway for designing perovskites with tailored properties through informatics-guided screening.
Methods
Dataset collection and curation
The dataset used in this work is compiled from previous research on photocatalytic water splitting and contains multiple entries for the same material measured under different experimental conditions. It contains 540 data points from 151 papers.19 To focus on the relationship between the composition of materials and their bandgap, entries of perovskites with identical compositions but tested under different experimental conditions are removed to keep only one data point per unique perovskite composition. Therefore, 282 data entries are retained for further analysis.This compiled dataset comprises the following variables: Ref, the reference number of the original publication; A, B, and X, the host elements in the perovskite lattice; A1, A2, B1, B2, and X1, the dopant elements at the corresponding sites; A mole through X1 mole, the weight fractions of these elements; Prep Meth, the synthesis method; CalcT, the calcination temperature (°C); Calc, the calcination time (hour); Prom Meth, the promoter loading method; Promoter, the elements used as the promoter; Prom, the weight percent of the promoter; Crystal, the crystal structure; BandGap, the optical bandgap energy (eV).
To uniquely identify each perovskite composition, a custom standardized label in the form of “ABX1.0_1.0_3.0” is used, where the numbers represent the normalized mole fractions of the A-site, B-site, and X-site elements, respectively. This label is not chemically meaningful but serves solely for data deduplication and analysis. To generate these labels, the molar amount (ni) is calculated as presented in eqn (1), where wi is the weight fraction of element i, and Mi is the atomic mass of element i:
 | (1) |
Next, the mole fraction for each site is calculated using eqn (2), where nA, nB, and nX are the total molar amounts of elements at the A-, B-, and X-sites, respectively.
 | (2) |
Descriptor engineering
To construct machine learning descriptors from the perovskite composition data, a set of 754 base compositional descriptors is derived from elemental properties (e.g., atomic volume) and the mole fractions of the constituent elements. These descriptors are generated by integrating site-specific compositions with 58 elemental property reference values obtained from the XenonPy library,20 and their types and calculation methods are summarized in Table 1. These descriptors aim to capture structure–property relationships in multi-site crystalline materials by incorporating both atomic-scale features and compositional heterogeneity.To enhance the predictive performance of the machine learning model, additional descriptors are engineered by applying various mathematical transformations to the 754 base compositional descriptors. The applied transformations include power functions of degrees two to six, their corresponding roots, the natural logarithm, exponential functions, and reciprocals of all these transformations. As a result, a total of 9678 descriptors are generated.
Descriptor selection and hyperparameter optimization
Support-Vector Regression (SVR) is implemented using the scikit-learn library21 to predict the bandgap of materials based on compositional descriptors, where SVR is chosen for its good performance on medium-sized datasets and its suitability for predicting continuous variables. Prior to descriptor selection, an initial tuning of the SVR hyperparameters is performed to determine appropriate values for the regularization parameter C and the kernel coefficient γ, with ε fixed at 0.1. For this purpose, 30 descriptors are randomly sampled from the set of engineered base compositional descriptors, and this process is repeated five times with different random seeds. For each trial, γ is first optimized by grid search over discrete candidates {2−20, 2−19, …, 210}, selecting the value that maximizes the variance induced by a Gaussian kernel. Using the optimized γ, C is then selected from the same range by cross-validation as proposed by Kaneko et al.22 To further improve the model performance, the candidate ranges of C and γ are further refined through iterative grid searches around the initially selected values. Among the five trials, the best test r2 score of 0.61 is achieved with C = 3.86 and γ = 0.06, which are used in the subsequent descriptor selection step.Descriptor selection is conducted using the MonteCat method proposed by Garcia-Escobar et al.,23 which is a Monte Carlo-based approach for identifying an optimal subset of descriptors that maximizes cross-validated prediction performance. The algorithm performs multiple optimization runs at different temperature settings, and the descriptor set yielding the highest cross-validation score across all runs is ultimately selected. In particular, the optimization process is repeated for 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 iterations in each run. A total of 35 independent runs are conducted, each using a different random seed and a distinct MonteCat temperature parameter value selected from the range 5, 10, 20, 50, 100, 200, and 500.
000 iterations in each run. A total of 35 independent runs are conducted, each using a different random seed and a distinct MonteCat temperature parameter value selected from the range 5, 10, 20, 50, 100, 200, and 500.
After identifying the optimal descriptor set with the Montecat algorithm, a final round of SVR hyperparameter tuning is performed using only the selected descriptors. This results in updated values of C = 4.25 and γ = 0.06, leading to an improved average test r2 score of 0.87. These values are employed in the final prediction model. All descriptor values are standardized using the StandardScaler module in scikit-learn, which centers each feature to zero mean and scales it to unit variance.
Experimental synthesis
LaCrO3, LaFeO3, YFeO3, and YCrO3 are synthesized via a conventional solid-state reaction method using high-purity oxide precursors. For LaFeO3, 0.67 g of La2O3 (99.5% purity, Guaranteed Reagent, Junsei Chemical Co., Ltd.) and 0.33 g of Fe2O3 (Wako 1st Grade, FUJIFILM Wako Pure Chemical Corporation) are mixed and ball-milled at 400 rpm for 8 h using 20 g of zirconia balls in a planetary ball mill (ITO SEISAKUSHO, LP-M2). The milled powder is then transferred to an alumina crucible and calcined in air in a muffle furnace (KDF, 300 Plus). The calcination is performed by heating to 800 °C at a rate of 10 °C min−1, holding at 800 °C for 6 h, followed by cooling to room temperature over 4 h. YFeO3 is prepared under the same conditions as LaFeO3, using 0.59 g of Y2O3 (99.99% purity, FUJIFILM Wako Pure Chemical Corporation) and 0.33 g of Fe2O3 (Wako 1st Grade, FUJIFILM Wako Pure Chemical Corporation). For LaCrO3, 0.32 g of La2O3 (99.5% purity, Guaranteed Reagent, Junsei Chemical Co., Ltd.) and 0.15 g of Cr2O3 (Wako 1st Grade, FUJIFILM Wako Pure Chemical Corporation) are ball-milled for 16 h at 400 rpm using 20 g of zirconia balls. The milled powder is then calcined at 1100 °C at 10 °C min−1, held for 6 h, and cooled to room temperature over 4 h. YCrO3 is synthesized in the same manner as LaCrO3, using 0.22 g of Y2O3 (99.99% purity, FUJIFILM Wako Pure Chemical Corporation) and 0.15 g of Cr2O3 (Wako 1st Grade, FUJIFILM Wako Pure Chemical Corporation) as starting materials.Characterization methods
After synthesis, the phase composition, structural characteristics, and optical properties of the samples are analyzed using X-ray diffraction (XRD), scanning electron microscopy with energy-dispersive X-ray spectroscopy (SEM-EDS), and ultraviolet-visible-near-infrared (UV-vis-NIR) spectroscopy. X-ray diffraction (XRD) measurements are carried out using a diffractometer (MiniFlex600-C, Rigaku) equipped with Cu Kα radiation (λ = 1.5406 Å), operated at 40 kV and 15 mA. The scan is performed in 1D mode over a 2θ range of 10–90° with a scan speed of 10.00° min−1 and a step width of 0.01°. These measurements are conducted to identify crystalline phases and to evaluate the phase purity and crystallinity of the synthesized materials. Elemental distributions are examined using scanning electron microscopy equipped with energy-dispersive X-ray spectroscopy (JCM-7000 NeoScope, JEOL). The powder samples are mounted on carbon tape without any conductive coating. Measurement conditions are as follows: accelerating voltage of 15.0 kV, working distance (WD) of 15.0 mm, magnification of ×1000, and high probe current (High-PC) mode under charge-reduction vacuum (CR Vac.) conditions. SEM-EDS elemental mapping is performed using a backscattered electron detector (BED-S) to assess the spatial distribution of constituent elements, focusing on the localization of A-site and B-site cations (e.g., La/Fe, Y/Fe, La/Cr, and Y/Cr). Diffuse reflectance spectra in the UV-vis-NIR region are recorded using a spectrophotometer (V-770, JASCO). Measurements are performed over three wavelength ranges: 200–800 nm, 200–1000 nm, and 200–2700 nm. Optical bandgaps are estimated from Tauc plots derived from the reflectance data, assuming indirect allowed transitions.Materials prediction and candidate selection
Prediction of bandgap energies is conducted for 1852 perovskite-type compounds with the general formula ABO3, where the A- and B-site cations are selected from 60 candidate elements. The tolerance factor for each composition is calculated according to the method originally proposed by Goldschmidt, as described in ref. 24, using eqn (3), where rA, rB, and rO denote the ionic radii of the A-site cation, B-site cation, and oxygen anion, respectively. Only compositions with tolerance factors between 0.7 and 1.0 are retained as geometrically feasible candidates.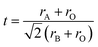 | (3) |
Using the optimized SVR model and selected descriptors, the bandgaps of these 1852 compounds are predicted. An inverse screening is conducted to identify candidates with chemically plausible structures and optical properties suitable for visible-light-driven solar energy applications, as detailed in the Results and discussion section. This screening yields 86 potential materials. Among these, four compounds LaCrO3, LaFeO3, YFeO3, and YCrO3 are selected for experimental validation.
Result and discussion
Data analysis and machine learning
The workflow for designing perovskite materials in this work is illustrated in Fig. 1. First, a literature dataset is collected, followed by data curation and preprocessing to generate a consistent and reliable dataset for further analysis. A machine learning model is then developed, incorporating feature engineering and descriptor selection using the MonteCat method to predict the bandgap in perovskite materials. Based on the predictions, perovskite materials with suitable bandgaps are identified. Among them, candidates are synthesized via solid-state reactions. The synthesized perovskite materials are characterized using XRD for structural analysis, SEM with EDS for morphology and elemental distribution, and UV-vis spectroscopy for bandgap estimation. | ||
| Fig. 1 Proposed workflow for materials design. (a) Data collection and curation. (b) Machine learning and descriptor search. (c) Materials synthesis in the experiment. (d) Materials characterization. | ||
Data analysis is performed in order to understand the statistical information. Pairwise correlation analysis is performed to examine the linear relationships among variables, as shown in Fig. 2. The chemical elements at the A and B sites are encoded using one-hot encoding. Categorical variables are thus transformed into binary features. The Calc prefix relates to variables in the calcination process: namely, calcination temperature (Calc_Temp in °C) and calcination time (Calc_time in h).
Fig. 2 indicates that the bandgap tends to decrease when the B-site element is one of the following: Cd, Co, Cr, Fe, or Ti. In contrast, it tends to increase when the B-site element is Ce or Ta. These tendencies suggest a notable influence of B-site elemental selection on the electronic structure of the materials. It is also noteworthy that bandgap tends to increase as the calcination temperature (CalcT) increases.
SVR with MonteCat is employed to identify the optimal set of descriptors for predicting the bandgap as a function of the elemental composition. As a result, 24 compositional descriptors are selected, as summarized in Table 2, along with their elemental property sources, descriptor construction types, and corresponding mathematical operations. Note that the descriptors identified in this work might, at least indirectly, reflect underlying physical properties such as the bandgap.
| Property (P) | Descriptor (D) | Operation |
|---|---|---|
| num_p_unfilled | P WtB | e−D |
| covalent_radius_pyykko | P A−B | e−D |
| num_d_unfilled | P A−B | e−D |
| atomic_weight | P WtA | D 6 |
| lattice_constant | P B+X | e−D |
| dipole_polarizability | P WtB | D 2 |
| atomic_radius_rahm | P B−X | eD |
| atomic_radius | P WtX | D 5 |
| atomic_volume | P A+X | D 4 |
| electron_negativity | P B−X | D −3 |
| fusion_enthalpy | P A−B | eD |
| covalent_radius_cordero | P A−X | D 3 |
| Density | P WtABX | D −6 |
| hhi_r | P A−B | D 5 |
| gs_bandgap | P WtABX | D 2 |
| num_d_valence | P A−B | eD |
| specific_heat | P A | D 6 |
| num_p_valence | P WtB | D 6 |
| melting_point | P B | D |
| covalent_radius_pyykko | P A−B | D 3 |
| en_ghosh | P WtA | D 4 |
| thermal_conductivity | P A−X | D 6 |
| num_s_unfilled | P WtB | D 5 |
| heat_of_formation | P WtABX | D 2 |
With these descriptors, an SVR model resulted in an average test r2 score of 0.87, as shown in Fig. 3, where the r2 score is obtained by averaging the r2 scores over 10 random train-test splits (80% training and 20% testing).
Bandgap predictions are then conducted for 1852 hypothetical perovskite-type compounds with the general formula ABO3, where the A and B cations are selected from 60 elements including Li, Be, Na, Mg, Al, K, Ca, Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn, Ga, Ge, Rb, Sr, Y, Zr, Nb, Mo, Tc, Ru, Rh, Pd, Ag, Cd, In, Sn, Sb, Cs, Ba, La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Lu, Hf, Ta, W, Re, Os, Ir, Pt, Au, Hg, Tl, Pb, and Bi. The geometric feasibility of each composition is evaluated using the tolerance factor, calculated by eqn (3). Only combinations with tolerance factors in the range of 0.7 to 1.0 are retained for subsequent prediction analysis.
These 1852 compositions are then given to the trained SVR model to predict their corresponding bandgaps. Based on the predicted results, 86 candidates are selected according to the following two criteria: (i) the predicted bandgap lies between 0.45 eV and 2.2 eV, and (ii) the sum of the oxidation states of the A and B cations equals +6, assuming a perovskite-type ABO3 structure with charge neutrality. Among the 86 filtered candidates, four compounds LaCrO3, LaFeO3, YFeO3, and YCrO3 are selected for experimental synthesis based on their predicted bandgaps.
Experimental results
In all cases, the experimental XRD patterns closely match the simulated reference patterns of the target perovskite phases, with sharp and well-resolved peaks confirming the successful formation of the desired crystal structures. Notably, the peaks of LaCrO3 are slightly shifted to lower 2θ values compared to the simulated pattern. Note that the minor peaks observed in Fig. 4(c) and (d) are attributed to residual Cr2O3, indicating incomplete reaction during the formation of LaCrO3. These XRD results collectively confirm that the dominant crystalline phases in all samples are the intended perovskite structures, with no detectable secondary phases.
 | ||
| Fig. 5 SEM image and elemental maps of LaFeO3 obtained by SEM-EDS. (a) SEM image, (b) O (K-line), (c) La (L-line), and (d) Fe (K-line). | ||
Similar elemental distribution patterns are observed for the other synthesized compositions (YFeO3, LaCrO3, and YCrO3), confirming that the A-site and B-site cations are homogeneously incorporated in each case without observable segregation. These results, in conjunction with the XRD analysis, provide strong evidence for the formation of single-phase perovskite structures with well-dispersed constituent elements. The full set of elemental maps for all samples is provided in the SI (Fig. S1–S3).
 | ||
| Fig. 6 UV-vis-NIR absorption spectra of synthesized samples measured in the range of 200–2700 nm: (a) LaFeO3, (b) YFeO3, (c) LaCrO3, and (d) YCrO3. | ||
Optical bandgaps are estimated using Tauc plots, assuming indirect allowed transitions. Values obtained over the full spectral range (200–2700 nm) are 1.00 eV (LaFeO3), 1.04 eV (YFeO3), 1.71 eV (LaCrO3), and 1.64 eV (YCrO3). Reanalysis using narrower spectral windows (200–800 nm and 200–1000 nm) reveals notable shifts in estimated bandgaps (Table 3), particularly for samples exhibiting multiple overlapping absorption bands. The predicted bandgaps show good agreement with experimental values measured in the 200–800 nm range. Specifically, the synthesized LaFeO3, YFeO3, LaCrO3, and YCrO3 samples exhibited bandgaps of 2.16 eV, 2.13 eV, 1.90 eV, and 1.93 eV, respectively. These values closely match the model predictions of 2.09 eV, 1.95 eV, 2.15 eV, and 2.05 eV, with deviations within 0.2 eV. This agreement demonstrates that the model successfully captures patterns in the training data and is effective for guiding the synthesis of perovskite materials with target bandgaps. It must be noted that deviations appear when experimental data are extended beyond 1000 nm, where the model tends to overestimate the bandgaps. This discrepancy likely arises from the model's limited capacity to capture low-energy transitions, as such spectral regions are not well represented in the training data. These findings emphasize the importance of measurement range in evaluating optical properties and confirm the reliability of the model within the spectral window covered by the training data.
| Sample | Training data bandgap (eV) | Predicted bandgap (eV) | Experimental bandgap (eV) | ||
|---|---|---|---|---|---|
| 200–800 | 200–1000 | 200–2700 nm | |||
| LaFeO3 | 2.10 | 2.09 | 2.16 | 1.79 | 1.00 |
| YFeO3 | N/A | 1.95 | 2.13 | 1.73 | 1.04 |
| LaCrO3 | N/A | 2.15 | 1.90 | 1.79 | 1.71 |
| YCrO3 | N/A | 2.05 | 1.93 | 1.86 | 1.64 |
Conclusion
A machine learning approach utilizing previously collected experimental data is employed to identify key descriptors governing the bandgaps of perovskite-type oxides and to predict their bandgaps. Based on the prediction results, several promising compositions are identified as potential photoactive materials for solar energy conversion and visible light driven applications. To validate the prediction, selected candidate materials are synthesized and subjected to structural and optical characterization. XRD analysis confirms the formation of the target perovskite phases, and UV-vis spectroscopy reveals that the experimentally measured bandgaps are in good agreement with the predicted values. These results highlight the effectiveness of combining descriptor-driven, data-guided prediction with experimental validation to accelerate the discovery of functional materials. The approach demonstrated here provides a practical framework for designing novel photoactive materials with targeted electronic properties, particularly in the context of solar energy conversion and visible-light-driven applications.Author contributions
K. T. conceived the central project idea. K. S., F. E., L. T., and K. T. performed data analysis and machine learning. K. S., T. T., and K. T. carried out experimental synthesis and characterization. K. T. and L. T. funded the project. All authors contributed to preparing the manuscript.Conflicts of interest
There are no conflicts to declare.Data availability
This study was carried out using the SI from E. Can and R. Yildirim, Appl. Catal., B, 2019, 242, 267–283 at https://doi.org/10.1016/j.apcatb.2018.09.104.The supporting information provides a list of the descriptors used, the predicted materials, SEM images, and the data analysis and visualization. See DOI: https://doi.org/10.1039/d5sc04813c.
Acknowledgements
This work was funded by the Japan Science and Technology Agency (JST) ERATO Grant Number JPMJER1903, PRESTO Grant Number JPMJPR24T5, JST Mirai Program Grant Number JP-MJMI25G1, and JSPS KAKENHI Grant-in-Aid for Scientific Research (B) Grant Numbers JP23H01762 and 24K01241.References
- S. Curtarolo, W. Setyawan, G. L. Hart, M. Jahnatek, R. V. Chepulskii, R. H. Taylor, S. Wang, J. Xue, K. Yang and O. Levy, et al., AFLOW: An automatic framework for high-throughput materials discovery, Comput. Mater. Sci., 2012, 58, 218–226 CrossRef.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner and G. Ceder, et al., Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
- S. Kirklin, J. E. Saal, B. Meredig, A. Thompson, J. W. Doak, M. Aykol, S. Rühl and C. Wolverton, The Open Quantum Materials Database (OQMD): assessing the accuracy of DFT formation energies, npj Comput. Mater., 2015, 1, 1–15 Search PubMed.
- K. Takahashi and Y. Tanaka, Materials informatics: a journey towards material design and synthesis, Dalton Trans., 2016, 45, 10497–10499 RSC.
- R. Ramprasad, R. Batra, G. Pilania, A. Mannodi-Kanakkithodi and C. Kim, Machine learning in materials informatics: recent applications and prospects, npj Comput. Mater., 2017, 3, 54 CrossRef.
- K. T. Butler, D. W. Davies, H. Cartwright, O. Isayev and A. Walsh, Machine learning for molecular and materials science, Nature, 2018, 559, 547–555 CrossRef.
- L. Ward, A. Dunn, A. Faghaninia, N. E. Zimmermann, S. Bajaj, Q. Wang, J. Montoya, J. Chen, K. Bystrom and M. Dylla, et al., Matminer: An open source toolkit for materials data mining, Comput. Mater. Sci., 2018, 152, 60–69 CrossRef.
- P. Dey, J. Bible, S. Datta, S. Broderick, J. Jasinski, M. Sunkara, M. Menon and K. Rajan, Informatics-aided bandgap engineering for solar materials, Comput. Mater. Sci., 2014, 83, 185–195 CrossRef.
- K. Takahashi, L. Takahashi, I. Miyazato and Y. Tanaka, Searching for hidden perovskite materials for photovoltaic systems by combining data science and first principle calculations, ACS Photonics, 2018, 5, 771–775 CrossRef.
- M. N. Mattur, N. Nagappan, S. Rath and T. Thomas, et al., Prediction of nature of band gap of perovskite oxides (ABO3) using a machine learning approach, J. Materiomics, 2022, 8, 937–948 CrossRef.
- S. Rath, G. S. Priyanga, N. Nagappan and T. Thomas, Discovery of direct band gap perovskites for light harvesting by using machine learning, Comput. Mater. Sci., 2022, 210, 111476 CrossRef.
- A. Talapatra, B. P. Uberuaga, C. R. Stanek and G. Pilania, Band gap predictions of double perovskite oxides using machine learning, Commun. Mater., 2023, 4, 46 CrossRef.
- H. S. Jung and N.-G. Park, Perovskite solar cells: from materials to devices, Small, 2015, 11, 10–25 CrossRef CAS PubMed.
- N.-G. Park, Perovskite solar cells: an emerging photovoltaic technology, Mater. Today, 2015, 18, 65–72 CrossRef CAS.
- J.-P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Promises and challenges of perovskite solar cells, Science, 2017, 358, 739–744 CrossRef CAS PubMed.
- R. Wang, M. Mujahid, Y. Duan, Z.-K. Wang, J. Xue and Y. Yang, A review of perovskites solar cell stability, Adv. Funct. Mater., 2019, 29, 1808843 CrossRef CAS.
- L. M. Ghiringhelli, J. Vybiral, S. V. Levchenko, C. Draxl and M. Scheffler, Big data of materials science: critical role of the descriptor, Phys. Rev. Lett., 2015, 114, 105503 CrossRef.
- R. Prasanna, A. Gold-Parker, T. Leijtens, B. Conings, A. Babayigit, H.-G. Boyen, M. F. Toney and M. D. McGehee, Band gap tuning via lattice contraction and octahedral tilting in perovskite materials for photovoltaics, J. Am. Chem. Soc., 2017, 139, 11117–11124 CrossRef CAS.
- E. Can and R. Yildirim, Data mining in photocatalytic water splitting over perovskites literature for higher hydrogen production, Appl. Catal., B, 2019, 242, 267–283 CrossRef CAS.
- D. Yamashita, T. Sato, A. Seko, K. Takahashi and I. Tanaka, XenonPy: An open-source platform for materials informatics, Comput. Mater. Sci., 2019, 161, 57–69 Search PubMed.
- F. Pedregosa, et al., Scikit-learn: Machine Learning in Python, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- H. Kaneko and K. Funatsu, Fast Optimization of Hyperparameters for Support Vector Regression Models with Highly Predictive Ability, Chemom. Intell. Lab. Syst., 2015, 142, 64–69 CrossRef CAS.
- F. Garcia-Escobar, T. Taniike and K. Takahashi, MonteCat: A Basin-Hopping-Inspired Catalyst Descriptor Search Algorithm for Machine Learning Models, J. Chem. Inf. Model., 2024, 64, 1512–1521 CrossRef CAS PubMed.
- V. M. Goldschmidt, Die Gesetze der Krystallochemie, Naturwissenschaften, 1926, 14, 477–485 CrossRef CAS.
- K. Momma and F. Izumi, VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, Commentary: The Materials Project: A materials genome approach to accelerating materials innovation, APL Mater., 2013, 1, 011002 CrossRef.
| This journal is © The Royal Society of Chemistry 2025 |





