Bayesian molecular optimization for accelerating reverse intersystem crossing

Abstract

Spin conversion in molecular excited states is crucial for the development of next-generation optoelectronic devices. However, optimizing molecular structures for rapid spin conversion has relied on time-consuming experimental trial-and-error, which limits the elucidation of the structure–property relationships. Here, we report a Bayesian molecular optimization approach that accelerates virtual screening for rapid triplet-to-singlet reverse intersystem crossing (RISC). One of the molecules identified through this virtual screening exhibits a fast RISC rate constant of 1.3 × 10⁸ s⁻¹ and a high external electroluminescence quantum efficiency of 25.7%, which remains as high as 22.8% even at a practical luminance of 5000 cd m⁻² in organic light-emitting diodes. Post-hoc analysis of the trained machine learning model reveals the impact of molecular structural features on spin conversion, paving the way for informed and precise materials development.

---

Introduction

Excitonic spin conversion is a key process driving innovation in various optoelectronic applications.^1–5 In the case of organic light-emitting diodes (OLEDs), the internal quantum efficiency is limited by inherent spin statistics that dictate a 1 : 3 ratio of singlet to triplet excitons from electron–hole recombination, resulting in a maximum efficiency of 25%. This limitation is due to the fact that triplet excitons in most organic molecules are dark states, which are spin-forbidden from decaying radiatively to the ground states. Researchers have explored the use of reverse intersystem crossing (RISC), where triplet excitons are converted into emissive singlet excitons to overcome this issue.^6–18 RISC is driven by ambient thermal energy, resulting in thermally activated delayed fluorescence (TADF) and allowing OLEDs to achieve internal quantum efficiencies approaching 100%.

The time constants of RISC are generally in the order of microseconds,^19–22 which presents a challenge in the form of competing bimolecular recombination processes, such as triplet–triplet annihilation. Such detrimental processes become increasingly dominant at higher current densities in OLEDs, resulting in an appreciable decrease in device efficiency, a phenomenon known as efficiency roll-off.²³ Thus, accelerating RISC and reducing efficiency roll-off are important hurdles to overcome for the practical use of TADF molecules in high-performance OLEDs.

Traditionally, TADF materials have been discovered through time-intensive experimental approaches; however, the advent of high-throughput virtual screening has offered a significant change in the materials design process.^24–29 By employing computationally inexpensive density functional theory (DFT) and machine learning techniques, researchers can extensively explore the relevant molecular space for potential TADF materials with a small singlet–triplet energy gap (ΔE_ST). However, despite these advances, calculating ΔE_ST alone remains an inefficient way to estimate the rate constant of RISC (k_RISC) and narrow down the most promising candidate molecules.

In the simplest physical picture, RISC is driven by a spin–orbit coupling at the crossing seam between the potential energy surfaces of singlet and triplet excited states. In cases of weak spin–orbit coupling in organic molecules, k_RISC is expected to follow the Marcus-type non-adiabatic rate expression:

where ℏ is the reduced Planck constant, H_SO is the spin–orbit coupling matrix element, k_B is the Boltzmann constant, T is the temperature, λ is the reorganization energy, and E_A is the activation energy required to reach the singlet–triplet crossing seam³⁰ (Fig. 1A). Accurately calculating these parameters is challenging, in part because the singlet–triplet crossing seam often involves a higher-lying triplet excited state (T₂), giving rise to the spin-vibronic mechanism for rapid RISC.^31–36 Explicitly computing the singlet–triplet crossing seam reproduced experimental k_RISC ranging over five orders of magnitude in various TADF molecules, although it requires additional computational time for the high-fidelity excited-state calculations.³⁰

Fig. 1 (A) Schematic potential energy surfaces of excited states associated with RISC. (B) Binary molecular fingerprints F_P for classifying candidate molecules in a six-dimensional space. (C) Comparison of Bayesian molecular optimization using different descriptor combinations and uniform random sampling for identifying the molecule with the highest k_RISC among 200 candidates for pre-training. Each line shows the probability of successful identification after a given number of iterations. (D) Beeswarm plots of the SHAP values for each descriptor, showing their impact on the model output (log₁₀ k_RISC). A high F_p (Sub. Pos.) value corresponds to substitutions at the 2,7-positions (meta-positions) of thioxanthone, while a low F_p (Sub. Pos.) value corresponds to substitution at the 3,6-positions (para-positions).

Here we implement a machine learning technique called Bayesian optimization to computationally screen for TADF molecules with high k_RISC. While conventional machine learning models for virtual screening require large number of training datasets, Bayesian optimization iteratively trains a probabilistic surrogate model with a limited number of datasets, strategically selecting the next data points to evaluate based on both exploration of uncertain space and exploitation of known space.^37–42 This dual focus allows Bayesian optimization to rapidly identify the optimal molecules with a minimized number of high-fidelity excited-state calculations.

In the following section, we describe the development of our Bayesian optimization-based virtual screening that identified a TADF molecule with experimentally determined k_RISC of 1.3 × 10⁸ s⁻¹. The external electroluminescence quantum efficiencies of the identified molecule reached 25.7%, which remained as high as 22.8% even at a practical luminance of 5000 cd m⁻².

Results and discussion

Search space generation

Typical TADF molecules contain donor and acceptor units that mediate low-lying singlet and triplet charge-transfer excited states (¹CT and ³CT) between the spatially separated highest occupied and lowest unoccupied molecular orbitals (HOMO and LUMO); such CT states result in a low singlet–triplet exchange energy, enabling RISC with ambient thermal energy. Spin flipping in RISC is driven by spin–orbit coupling at the singlet–triplet crossing seam, where an orbital transition between ¹CT and a triplet local excitation state (³LE) induces a relativistic interaction capable of spin flipping. To further enhance spin–orbit coupling and accelerate RISC, one can advantageously exploit the heavy atom effect of the group 16 and 17 atoms such as S, Se, Br, and I.^43–51 With these principles in mind, we generated a search space of 1.4 thousand molecules, all sharing a common thioxanthone acceptor unit with vastly different donor units. To ensure synthetic feasibility, we employed a donor–acceptor structural design (D_n–A, n = 1 or 2) that adheres to a set pattern dictating the substitution positions and symmetry (Fig. 1B). Each molecule incorporates a single type of donor unit, classifiable into four categories: carbazole (Cz), 1,8-dimethylcarbazole (MCz), 9,9-dimethylacridane (Acr), and phenoxazine (Pxz). The molecular weight of the candidates was limited to less than 1200 g mol⁻¹ due to the need for thermal evaporation in OLED fabrication. All molecular structures in the search space are listed in ‘ESI†’.

For each molecule, four quantum chemical properties were represented as descriptors for a vector search space: E_HOMO, E_LUMO, ΔE_ST, and H_SO, derived from low-cost DFT calculations with the 6-31G basis set without diffuse and polarization functions, as detailed in ‘Methods’. We also used in-house binary molecular fingerprints F_P as descriptors, which explicitly represent the number, positions, and categories of donor units (i.e., Cz, MCz, Acr, or Pxz) to classify candidate molecules in a six-dimensional space (Fig. 1B).

Pre-training

To identify the most effective combinations of descriptors for search performance, we tested Bayesian optimization with different descriptor sets on a search space consisting of 200 molecules; the k_RISC values of these molecules were pre-computed and stored in a database, using high-fidelity excited-state calculations including geometry optimization of the singlet–triplet crossing seam described in ‘Methods’. Beginning with a randomly selected molecule, the corresponding k_RISC value was retrieved from the database to train a Gaussian process surrogate model;⁵² an acquisition function was then used to select a molecule in the search space based on the expected improvement criterion for the next evaluation. This procedure continued iteratively until the molecule with the highest k_RISC in the 200 molecules was found.

Fig. 1C compares the search performance of the Bayesian molecular optimization with different descriptor sets to that of uniform random sampling. This comparison evaluates the cumulative probability of finding the molecule with the highest k_RISC as a function of the number of iterations, derived from 100 independent trials of the Bayesian optimization procedures, each with a different starting molecule. Essentially, Bayesian optimization outperforms uniform random sampling; however, its performance is highly dependent on the descriptor sets. In all 100 independent Bayesian optimization trials, the descriptor set (ΔE_ST, H_SO) consistently found the highest k_RISC within 82 iterations, whereas (E_HOMO, E_LUMO) required up to 148 iterations. Superficially, the superior performance of (ΔE_ST, H_SO) is not surprising, given their physical relationship to k_RISC. What is surprising, however, is that the DFT calculations of these descriptors rely on overly broad approximations to remain cost-effective, whose results may not even qualitatively align with those of the high-fidelity calculations for k_RISC. Such circumstances suggest that the surrogate model captures the complex correlation between the descriptors and k_RISC.

Combining F_P with the descriptors further improves the performance of Bayesian optimization, locating the maximum point within only 55 iterations using (ΔE_ST, H_SO, F_P). Incorporating F_P offers an additional advantage of chemical interpretability, allowing us to quantify the impact of molecular features on k_RISC based on the trained surrogate model, as will be discussed later.

Shortlisting and analysis

Having established the effective descriptor set (ΔE_ST, H_SO, F_P), we proceeded to examine the full search space of 1.4 thousand candidate molecules. Starting with the pre-trained data for the 200 molecules, 100 additional iterations of Bayesian optimization led to the identification of 78 candidate molecules with quantum-chemically calculated k_RISC over 10⁷ s⁻¹, an order of magnitude higher than that of the seminal TADF molecule 2,4,5,6-tetra(carbazol-9-yl)isophthalonitrile (4CzIPN).⁶ At the end of the optimization, the trained surrogate model achieved a coefficient of determination (R²) of 0.91 and a root mean squared error (RMSE) of 0.88 in predicting log₁₀ k_RISC, as verified through tenfold cross-validation. The trained model suggests 129 molecules with predicted k_RISC exceeding 10⁸ s⁻¹, corresponding to 9% of all the candidate molecules. We then assessed the synthetic feasibility of these molecules and selected MCz-p2 for further experimental evaluation, as will be discussed later. We note that the model was able to reidentify 3,6-bis(1,3,6,8-tetramethylcarbazol-9-yl)thioxanthone (MCz-TXT),⁴⁶ previously reported with an exceptionally high k_RISC of 1.1 × 10⁸ s⁻¹.

To extract chemical knowledge from the trained machine learning model, we assessed the descriptor importance using Shapley additive explanations (SHAP). This method assigns a SHAP value to each descriptor, quantifying its contribution to the model output by fairly distributing the difference between a given output and the average across all descriptors.⁵³ Fig. 1D presents a series of beeswarm plots of the SHAP values for each descriptor in the trained model. A positive SHAP value indicates that a specific descriptor value, represented by the color, increases the model output (i.e., log₁₀ k_RISC) above the average, whereas a negative SHAP value indicates that it decreases the output below the average. A wider spread of the SHAP values for ΔE_ST and H_SO in Fig. 1D suggests that these two descriptors are the most influential. However, the relationship between the descriptor values and the SHAP values appears to be nonlinear, implying that a smaller ΔE_ST and a larger H_SO do not necessarily equate to a higher k_RISC. These results highlight the limitations of the low-cost DFT outputs, and the importance of accounting for the spin-vibronic effects through the high-fidelity calculations of singlet–triplet crossing seams in predicting k_RISC. For F_P, a simpler pattern emerges in the SHAP plots: the presence of MCz positively correlates with the output, whereas the other descriptors (Cz, Pxz, and Acr) tend to correlate negatively with the output. The SHAP plots for F_P also indicate that two substitutions, especially at the 3,6-positions (para-positions) of thioxanthone, are more beneficial for enhancing k_RISC than one substitution or those at the 2,7-positions (meta-positions).

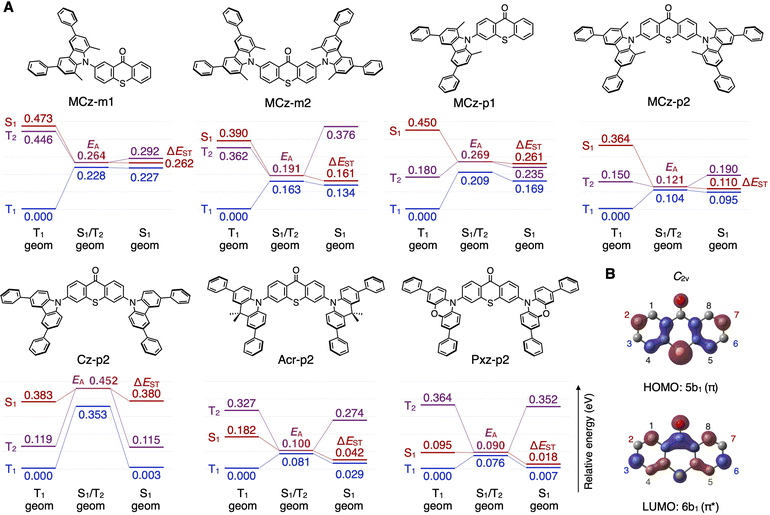
To understand the mechanism responsible for the trends in the importance of F_P for k_RISC, excited-state energy landscapes were established for seven model molecules by the high-fidelity TD-DFT calculations (Fig. 2A and S1† for relevant F_P). Four molecules, MCz-m1, MCz-m2, MCz-p1, and MCz-p2, share common MCz donor units, but possess different substitution numbers and positions. The calculated adiabatic ΔE_ST of MCz-p1 is smaller than that of MCz-m1 by increasing the substitution number from one to two and changing the meta-substitution to para-substitution, resulting in a lower E_A (the activation energy to reach the minimum-energy singlet–triplet crossing seam from equilibrium T₁) and thus a higher k_RISC of MCz-p2 (Table 1). Furthermore, the singlet–triplet crossing seam of MCz-p2 comprises more distinct orbital characters (¹CT and ³LE) compared to MCz-m2 (¹CT and ³CT + ³LE) (Fig. S2†), which is responsible for a higher H_SO of MCz-p2, consistent with El-Sayed's rule.⁵⁴ Additional calculations reveal that the 3,6-positions of thioxanthone are located at the nodes of its HOMO (Fig. 2B), leading us to interpret that the para-substitution of donor units suppresses π-conjugation and thus maintain a relatively pure ³LE on the thioxanthone unit, as in MCz-p2, resulting in higher k_RISC.

Fig. 2 (A) Molecular structures of seven thioxanthone derivatives with their relative excitation energies of S₁, T₁, and T₂ calculated at the optimized S₁ geometry, T₁ geometry, and S₁/T₂ crossing seam where the two states are equal in energy and relativistically coupled by a weak H_SO. (B) HOMO and LUMO of thioxanthone at C_2v symmetry.

Table 1 Quantum chemically calculated excited-state properties

Molecule	ES1^a (eV)	ET1^b (eV)	ΔEST^c (eV)	EA^d (eV)	λ^e (eV)	HSO^f (cm^−1)	kRISC^g (s^−1)
a Vertical S0–S1 excitation energy at the optimized S1 geometry.b Vertical S0–T1 excitation energy at the optimized T1 geometry.c Adiabatic energy gap between S1 and T1 at their respective optimized geometries.d Activation energy from the optimized T1 state to the minimum-energy singlet–triplet crossing seam.e Reorganization energy from the optimized T1 state to the optimized S1 state.f Spin–orbit coupling matrix element between S1 and T2 at the minimum-energy singlet–triplet crossing seam.g Rate constant of RISC calculated by using eqn (1).
MCz-m1	2.550	2.341	0.262	0.264	0.227	2.32	1.10 × 10^5
MCz-m2	2.334	2.254	0.161	0.191	0.134	1.44	9.20 × 10^5
MCz-p1	2.724	2.518	0.261	0.269	0.169	3.96	3.05 × 10^5
MCz-p2	2.524	2.257	0.110	0.121	0.0953	6.11	2.94 × 10^8
Cz-p2	2.614	2.305	0.380	0.452	0.235	3.74	1.96 × 10^2
Acr-p2	2.374	2.308	0.0424	0.100	0.0292	0.599	1.13 × 10^7
Pxz-p2	1.993	1.994	0.0181	0.0896	0.00669	0.385	1.47 × 10^7

---

The effect of the structural modification of the donor units is also evaluated in MCz-p2, Cz-p2, Acr-p2, and Pxz-p2 with the same substitution numbers and positions (Fig. 2A). Removal of the electron-donating methyl groups from MCz-p2 results in a blue-shifted S₁ of Cz-p2, which explain its larger ΔE_ST between S₁ (¹CT) and T₁ (³LE) and lower k_RISC (Table 1, Fig. 2A and 3 ESI†). In contrast, Acr-p2 and Pxz-p2, with more electron-rich donor units, possess a red-shifted S₁ (¹CT) and T₁ (³CT) with a smaller ΔE_ST, due to weak electron exchange coupling associated with the spatially separated orbitals comprising these CT excited states. However, as the ¹CT and ³CT undergo a red shift, their energy separation with the higher-lying ³LE increases, and thus the minimum-energy singlet–triplet crossing seam comprises CT characters, rather than LE, for both singlet and triplet states (Fig. S2†). The resultant lack of orbital change at the crossing seam suppresses spin–orbit coupling, as corroborated by the lower H_SO and k_RISC of Acr-p2 and Pxz-p2 than that of MCz-p2 (Table 1). These quantum chemical interpretations of the seven model molecules are in good agreement with the general trends in the F_P importance shown in Fig. 1D.

Experimental validation

To experimentally validate the virtual screening results, MCz-p2 with a quantum-chemically calculated k_RISC of 2.94 × 10⁸ s⁻¹ and a model-predicted k_RISC of 1.11 × 10⁸ s⁻¹ was synthesized. The photophysical properties of MCz-p2 were evaluated in a N₂-purged toluene solution. Under a steady-state photoexcitation condition, MCz-p2 exhibited a sky-blue emission with a maximum peak wavelength of 485 nm (2.56 eV) (Fig. 3A and Table 2), as consistent with the S₁ excitation energy (E_S1 = 2.52 eV) calculated by TD-DFT. The emission is characterized by a broad, unstructured spectrum originating from the predominantly ¹CT state. The photoluminescence (PL) quantum yield was measured to be 82%, which was reduced to 63% when measured in air. This reduction indicates the contribution of triplet excited states to the emission since the triplet states can be at least partially quenched by atmospheric O₂.

Fig. 3 (A) Steady-state absorption and PL spectra of MCz-p2 in a toluene solution (10⁻⁵ M). The inset in (A) is a photograph of the MCz-p2 solution exposed to UV light. (B) Transient PL decays of MCz-p2 measured with picosecond pulsed excitation at 375 nm. The blue line in (B) shows the fit of the transient PL decay to eqn (2) in ‘Methods’. The inset in (B) is the log–log representation. (C) Transient PL decays of MCz-p2 measured at varying temperatures. The inset in (C) represents the temperature-dependence of k_ISC and k_RISC with their fits to the Arrhenius equation. (D–F) Current density–voltage–luminance characteristics (D), EL spectra (E), and external quantum efficiency-luminance characteristics (F) of the fabricated OLEDs. The inset in (F) is a photograph of an OLED using MCz-p2 working at high luminance (>5000 cd m⁻²).

Table 2 Experimental excited-state properties of MCz-p2

λPL^a (nm)	ΦPL^b (%)	τPF^c (ns)	τDF^d (ns)	kr^e (s^−1)	knr^f (s^−1)	kISC^g (s^−1)	kRISC^h (s^−1)	ΔEST (eV)
a Photoluminescence (PL) peak wavelength.b PL quantum yield.c Time constant of prompt fluorescence.d Time constant of delayed fluorescence.e Rate constant of radiative decay of the S1 state to the S0 state.f Rate constant of non-radiative decay of the S1 state to the S0 state.g Rate constant of intersystem crossing (ISC) of the S1 state to the T1 state.h Rate constant of reverse intersystem crossing (RISC) of the T1 state to the S1 state.i Energy gap between the S1 and T1 states, estimated from the kRISC/kISC ratio, assuming the equilibrium between the S1 state and the three T1 sublevels.j Energy gap between the S1 and T1 states, estimated as the difference between activation energies of RISC and ISC.
485	82	1.4	852	5.3 × 10^6	1.2 × 10^6	5.8 × 10^8	1.3 × 10^8	0.010^i/0.050^j

---

Transient PL decay measurements of MCz-p2 confirmed both prompt and delayed fluorescence components, with time constants (τ_PF and τ_DF) of 1.4 ns and 852 ns, respectively (Fig. 3B and Table 2). In comparison to this sub-microsecond τ_DF of MCz-p2, typical TADF materials exhibit τ_DF in the microsecond to millisecond time range, e.g. 2.8 μs for the seminal TADF molecule 4CzIPN.⁶ Further kinetic analysis of the transient PL decay (described in ‘Methods’) revealed that the RISC of MCz-p2 is indeed on the order of nanoseconds with an exceptionally high k_RISC of 1.3 × 10⁸ s⁻¹, in good quantitative agreement with the model-predicted k_RISC of 1.11 × 10⁸ s⁻¹. We note that the rapid RISC of MCz-p2 can be retained in a solid-state host matrix 3,3′-bis(carbazol-9-yl)biphenyl (mCBP) (Table S1 and Fig. S4†), though the emission is slightly red-shifted to a maximum peak wavelength of 495 nm, indicating a stabilization of a ¹CT state in a higher dielectric environment of mCBP than toluene.

We measured the temperature-dependent transient PL decays of MCz-p2 in toluene (Fig. 3C). The decay kinetics suggest that the delayed fluorescence is attributed to a thermally activated process, as evidenced by the increase of τ_DF with decreasing temperature. Using the Arrhenius equation, the corresponding activation energies of ISC and RISC were estimated to be 0.001 eV and 0.051 eV, respectively. The difference between these activation energies gives ΔE_ST of 0.050 eV. An estimate of ΔE_ST was also obtained from the k_RISC/k_ISC ratio, yielding a value of 0.010 eV (Table 2). We note that the former estimate is reasonably closer to the calculated value of 0.110 eV (Table 1).

The electroluminescence properties of MCz-p2 were also evaluated to demonstrate the practical implications of high k_RISC in OLED performance (Fig. 3D–F). The details of the OLED structures and fabrication procedures are described in ‘Methods’. The fabricated OLEDs were confirmed to have MCz-p2 as the only source of electroluminescence with a maximum peak wavelength of 495 nm (Fig. 3E). The measured external quantum efficiency reached a maximum of 25.7% (Fig. 3F), corresponding to an internal quantum efficiency of 85.7%, assuming a light-outcoupling efficiency of 30% for a bottom-emission OLED. Crucially, a high external quantum efficiency of 22.8% was retained even at a practically high luminance of 5000 cd m⁻². The suppression of efficiency roll-off was further quantified by the critical current density (J_80%) at which the external quantum efficiency decreases to 80% of its maximum. A J_80% of 19 mA cm⁻² was recorded for the MCz-p2 device, indeed higher than 8.2 mA cm⁻² observed for a device using 4CzIPN as an emitter. These results are attributed to the higher k_RISC of MCz-p2, which maintains a comparatively low triplet exciton concentration and thus suppresses bimolecular recombination processes at high luminance.

Conclusions

We have shown that the coupling of Bayesian optimization and quantum chemical calculations provides a promising tool for identifying novel TADF molecules capable of rapid triplet-to-singlet conversion. A relevant molecule has been experimentally demonstrated to exhibit a high k_RISC of 1.3 × 10⁸ s⁻¹. Furthermore, the post-hoc interpretation of the machine-learning model reveals how the molecular structures influence excited-state energies, spin–orbit couplings, and ultimately k_RISC, offering valuable chemical insights for future materials design.

Bayesian optimization is poised to become an empowering tool for materials scientists in both academic and industrial settings by mitigating costly evaluations. Its efficient and scalable nature can further expedite the development of spin-conversion materials for organic optoelectronics, as demonstrated in this study, as well as in broader applications such as photocatalysis, fluorescent bioimaging, and photodynamic therapy.

Methods

Quantum chemical calculations

All of the quantum chemical calculations were performed in vacuum. For the low-cost calculations of the descriptors, the geometries of T₁ were optimized for each molecule using spin-unrestricted DFT with the LC-BLYP functional and the 6-31G basis set, as implemented in the Gaussian16 program.⁵⁵ Using the optimized T₁ geometries, single-point TD-DFT calculations were performed with the LC-BLYP functional and the 6-31G basis set within the Tamm–Dancoff approximation to obtain descriptors: E_HOMO, E_LUMO, and ΔE_ST. Based on these low-cost TD-DFT calculations, a descriptor H_SO was obtained using the Breit–Pauli spin–orbit Hamiltonian with an effective charge approximation, as implemented in the PySOC program.⁵⁶ The range-separation parameter of the LC-BLYP functional was set to 0.15 bohr⁻¹ to balance the Hartree–Fock exchange with the DFT exchange for the CT states in the donor–acceptor systems.

For the high-fidelity calculations of k_RISC using eqn (1), the geometries of the S₁, T₁, and singlet–triplet crossing seam were optimized for each molecule using the TD-DFT with the LC-BLYP functional and the 6-31+G(d) basis set within the Tamm–Dancoff approximation, as implemented in the GRRM17 program,⁵⁷ which refers to the energies and gradients calculated by the Gaussian16 program. The minimum-energy singlet–triplet crossing seam was calculated between S₁ and T₂ for all molecules except for mol-00003 (its molecular structure is given in ‘ESI†’), where the calculations converged between S₁ and T₃. The range-separation parameter of the LC-BLYP functional was non-empirically optimized for each molecule to minimize the differences between the HOMO energies and the ionization potentials in both the neutral and radical anion systems.⁵⁸ Geometry optimization calculations for the seven model molecules were carried out, considering relevant conformers.

Machine learning

The logarithmic scale values of the calculated k_RISC were used for the training data to facilitate balanced learning from the entire dataset, including both low and high k_RISC values. A Gaussian process surrogate model was used for Bayesian optimization, as implemented in the COMBO library.³⁸ Hyperparameters of the Gaussian kernels were optimized by maximizing the type-II likelihood, allowing the model to adapt to the data at each iteration of Bayesian optimization. Expected improvement was used as the acquisition function for balanced exploration and exploitation to select the next molecule for evaluation. SHAP values were calculated by the SHAP version 0.34.0 ⁵³ for the Gaussian process model trained on the dataset obtained through the Bayesian optimization procedures.

Synthesis

MCz-p2 was synthesized by palladium-catalyzed Buchwald–Hartwig amination of 3,6-dibromothioxanthone with 1,8-dimethyl-3,6-diphenyl-9H-carbazole. The detailed synthetic procedure and characterization data are given in ‘ESI†’.

Photophysical evaluation

Steady-state PL spectra were recorded on an Edinburgh Instruments FS5 spectrofluorometer with 375 nm photoexcitation from a Xe arc lamp. The absolute PL quantum yields were determined using a Hamamatsu Photonics C9920 integrated sphere system with 375 nm excitation from a Xe arc lamp. Transient PL decay measurements were performed by time-correlated single photon counting using an Edinburgh Instruments FS5 spectrofluorometer equipped with a 375 nm pulsed diode laser (pulse width 60 ps).

The differential rate equation of the S₁ and T₁ populations (eqn (2)) was employed in the numerical fitting of the transient PL decays to obtain the rate constants of each excited-state transition, assuming negligible radiative and non-radiative decays from T₁ to S₀.

where k_r, k_nr, k_ISC, and k_RISC represent the rate constants of radiative decay from S₁ to S₀, non-radiative decay from S₁ to S₀, ISC from S₁ to T₁, and RISC from T₁ to S₁, respectively. k_r + k_nr was resolved into individual rate constant using the PL quantum yield.

OLED fabrication and evaluation

OLEDs were fabricated on glass substrates covered with indium tin oxide (ITO) (sheet resistance = 15 Ω sq⁻¹). The substrates were sequentially cleaned by sonication in detergent, deionized water, acetone, and 2-propanol, followed by UV-ozone treatment. Phosphomolybdic acid (PMA) in acetonitrile (0.25 g L⁻¹) was spin-coated on the substrates and annealed at 120 °C on a hot plate for 10 min in ambient conditions. The organic layers and a LiF/Al cathode were sequentially deposited on the substrates under vacuum (<8 × 10⁻⁴ Pa) at a deposition rate of <0.9 nm s⁻¹ through a shadow mask defining a pixel size of 4.0 mm². The deposition rate and layer thicknesses of each layer were monitored using a quartz crystal microbalance. The fabricated OLEDs consist of the following layer sequences: glass/ITO (50 nm)/PMA (5 nm)/TAPC (70 nm)/CCP (10 nm)/12 wt% Emitter:mCBP (30 nm)/PPF (10 nm)/B3PyPB (40 nm)/LiF (1 nm)/Al (100 nm). EL spectra were recorded using a Hamamatsu Photonics PMA-12 photonic multichannel analyzer. Current density–voltage–luminance characteristics were measured using a Konica Minolta CS-200 luminance meter and a Keithley 2400 source meter. The viewing-angle dependence of luminance was confirmed to follow the Lambertian distribution.

Data availability

All data including the input and output data used with the machine learning model are present in the paper and/or the ESI.†

Author contributions

N. A. and Y. H. conceived the project and performed the computational work. T. W., R. K., and N. A. synthesized the compound and characterized the photophysical properties. M. S., S. M., Y.-J. P., and K. N. supervised the research. T. W. and N. A. wrote the paper. All authors contributed to the discussion and the preparation of the paper.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported in part by JST FOREST (JPMJFR221J for N. A. and JPMJFR2221 for Y. H.), JSPS KAKENHI (21H05413, 22H02051, and 23H03958 for N. A.), and NEDO (JPNP20004 for N. A.). T. W. thanks Sumitomo Electric Group CSR Foundation for their financial support.

Notes and references

1. M. R. Wasielewski, et al., Nat. Rev. Chem, 2020, 4, 490–504.
2. M. Einzinger, et al., Nature, 2019, 571, 90–94.
3. A. Rao, Nature, 2013, 500, 435–439.
4. S. L. Bayliss, et al., Science, 2020, 370, 1309–1312.
5. S. Izawa, et al., Nat. Commun., 2023, 14, 5494.
6. H. Uoyama, K. Goushi, K. Shizu, H. Nomura and C. Adachi, Nature, 2012, 492, 234–238.
7. H. Wang, L. Xie, Q. Peng, L. Meng, Y. Wang, Y. Yi and P. Wang, Adv. Mater., 2014, 26, 5198–5204.
8. Y. Liu, C. Li, Z. Ren, S. Yan and M. R. Bryce, Nat. Rev. Mater., 2018, 3, 18020.
9. T. L. Wu, et al., Nat. Photonics, 2018, 12, 235–240.
10. L.-S. Cui, et al., Nat. Photonics, 2020, 14, 636–642.
11. Z. Tu, G. Han, T. Hu, R. Duan and Y. Yi, Chem. Mater., 2019, 31, 6665–6671.
12. S. Dey, et al., J. Phys. Chem. C, 2022, 126, 5649–5657.
13. J. Bian, et al., Adv. Mater., 2022, 34, 2110547.
14. X.-C. Fan, et al., Nat. Photonics, 2023, 17, 280–285.
15. X. Li, et al., J. Phys. Chem. C, 2024, 128, 6612–6620.
16. L. Zhu, et al., J. Phys. Chem. C, 2024, 128, 15763–15777.
17. A. Sevilla-Pym, W. L. Primrose, B. T. Luppi, K. Bergmann and Z. M. Hudson, ACS Appl. Mater. Interfaces, 2024, 16, 46133–46144.
18. T. Huang, Q. Wang, H. Zhang, Y. Xin, Y. Zhang, X. Chen, D. Zhang and L. Duan, Nat. Mater., 2024, 23, 1523–1530.
19. W. Whitaker, I. V. Sazanovich, Y. Kwon, W. Jeon, M. S. Kwon and A. J. Orr-Ewing, J. Phys. Chem. A, 2023, 127, 10775–10788.
20. W. Qiu, et al., Nat. Commun., 2023, 14, 2564.
21. L. Wan, Z. Cheng, F. Liu and P. Lu, Mater. Chem. Front., 2023, 7, 4420–4444.
22. A. N. Stuart, K. Bergmann, I. Cho, W. J. Kendrick, Z. M. Hudson, W. W. Wong and G. Lakhwani, Chem. Sci., 2024, 15, 14027–14036.
23. C. Murawski, K. Leo and M. C. Gather, Adv. Mater., 2013, 25, 6801–6827.
24. R. Gómez-Bombarelli, et al., Nat. Mater., 2016, 15, 1120–1127.
25. R. Pollice, et al., Acc. Chem. Res., 2021, 54, 849–860.
26. K. Zhao, Ö. H. Omar, T. Nematiaram, D. Padula and A. Troisi, J. Mater. Chem. C, 2021, 9, 3324–3333.
27. K. H. Lin, G. J. A. Wetzelaer, P. W. Blom and D. Andrienko, Front. Chem., 2021, 9, 800027.
28. P. Li, Z. Wang, W. Li, J. Yuan and R. Chen, J. Phys. Chem. Lett., 2022, 13, 9910–9918.
29. Y. Bu and Q. Peng, J. Phys. Chem. C, 2023, 127, 23845–23851.
30. N. Aizawa, Y. Harabuchi, S. Maeda and Y. J. Pu, Nat. Commun., 2020, 11, 3909.
31. M. K. Etherington, J. Gibson, H. F. Higginbotham, T. J. Penfold and A. P. Monkman, Nat. Commun., 2016, 7, 13680.
32. C. M. Marian, J. Phys. Chem. C, 2016, 120, 3715–3721.
33. T. J. Penfold, F. B. Dias and A. P. Monkman, Chem. Commun., 2018, 54, 3926–3935.
34. H. Imahori, Y. Kobori and H. Kaji, Acc. Mater. Res., 2021, 2, 501–514.
35. K. Shizu and H. Kaji, Nat. Commun., 2024, 15, 4723.
36. F. Coppola, M. Hussain, J. Zhao, A. M. El-Zohry and M. Pastore, J. Phys. Chem. C, 2024, 128, 11998–12009.
37. K. Terayama, M. Sumita, R. Tamura and K. Tsuda, Acc. Chem. Res., 2021, 54, 1334–1346.
38. T. Ueno, T. D. Rhone, Z. Hou, T. Mizoguchi and K. Tsuda, Mater. Discovery, 2016, 4, 18–21.
39. D. M. Packwood and T. Hitosugi, Appl. Phys. Express, 2017, 10, 065502.
40. B. J. Shields, et al., Nature, 2021, 590, 89–96.
41. X. Li, et al., Nat. Chem., 2024, 16, 1286–1294.
42. N. H. Angello, et al., Nature, 2024, 633, 351–358.
43. I. S. Park, K. Matsuo, N. Aizawa and T. Yasuda, Adv. Funct. Mater., 2018, 28, 1802031.
44. B. H. Drummond, et al., J. Phys. Chem. C, 2020, 124, 6364–6370.
45. N. Aizawa, A. Matsumoto and T. Yasuda, Sci. Adv., 2021, 7, 5769.
46. Y. Ren, Y. Wada, K. Suzuki, Y. Kusakabe, J. Geldsetzer and H. Kaji, Appl. Phys. Express, 2021, 14, 071003.
47. S. Goto, et al., J. Mater. Chem. C, 2021, 9, 13942–13953.
48. Y. Hu, et al., Angew. Chem., Int. Ed., 2023, 62, 202302478.
49. K. Shizu, Y. Ren and H. Kaji, J. Phys. Chem. A, 2023, 127, 439–449.
50. X. Lv, J. Song, X. Fu, S. Guo, J. Gu, L. Meng and C. Z. Lu, J. Phys. Chem. A, 2024, 128, 1611–1619.
51. H. Miranda-Salinas, J. Wang, A. Danos, T. Matulaitis, K. Stavrou, A. P. Monkman and E. Zysman-Colman, J. Mater. Chem. C, 2024, 12, 1996–2006.
52. C. E. Rasmussen and H. Nickisch, J. Mach. Learn. Res., 2010, 11, 3011–3015.
53. S. M. Lundberg and S.-I. Lee, Adv. Neural Inf. Process. Syst., 2017, 30, 4765–4774.
54. M. El-Sayed, J. Chem. Phys., 1963, 38, 2834–2838.
55. M. J. Frisch, et al., Gaussian 16, Rev. C.01, Wallingford, CT, 2016.
56. X. Gao, et al., J. Chem. Theory Comput., 2017, 13, 515–524.
57. S. Maeda, et al., J. Comput. Chem., 2018, 39, 233–251.
58. R. Baer, E. Livshits and U. Salzner, Annu. Rev. Phys. Chem., 2010, 61, 85–109.

---

Footnote

† Electronic supplementary information (ESI) available: Fig. S1–S6 and Table S1, ESI method, materials, synthesis, note, and data for machine learning. See DOI: https://doi.org/10.1039/d5sc01903f

---