A mechanistic continuum of nucleophilic aromatic substitution reactions with azole nucleophiles

Abstract

Nucleophilic aromatic substitution (S_NAr) is a broadly used method for generating structural complexity in pharmaceuticals. Although S_NAr reactions were long assumed to be stepwise, recent kinetic isotope effect (KIE) studies have shown that many S_NAr reactions are actually concerted. However, it remains unclear how variations in substrate structure affect whether a reaction is stepwise, concerted, or borderline. In this paper, we show that reactions between indole and moderately electron-deficient aryl fluorides proceed by a borderline mechanism and are subject to general base catalysis. These findings are consistent with density functional theory (DFT) calculations, which also predict that borderline mechanisms are operative for a broad range of industrially relevant S_NAr reactions involving azole nucleophiles. The predicted transition structures vary smoothly independent of the mechanism, suggesting that these S_NAr reactions exist on a mechanistic continuum. The findings of widespread general base catalysis and a mechanistic continuum will guide future efforts to devise general models of S_NAr reactivity.

---

Introduction

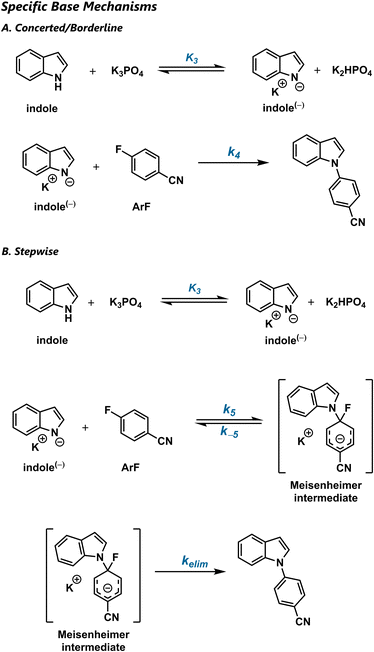
Nucleophilic aromatic substitution (S_NAr) reactions are a crucial synthetic tool for the amination of electron-deficient arenes.^1,2 Classically, S_NAr reactions were presumed to be stepwise, due to early mechanistic studies that focused on electrophiles capable of generating stable anionic σ-complexes, such as polynitroarenes and aza-aromatics.³ The highly electron-deficient nature of these substrates makes them easy to study, but also renders their σ-complexes (“Meisenheimer complexes”) unusually stable.⁴ Because these substrates are not representative, the conventional picture of most S_NAr reactions as stepwise processes is an overgeneralization (Scheme 1a).

Scheme 1 (a) A representative stepwise S_NAr reaction with a highly activated electrophile and poor leaving group. (b) A representative concerted S_NAr reaction with a less activated electrophile and better leaving group. (c) A qualitative Marcus analysis applied to S_NAr mechanisms.

Indeed, mechanistic studies of S_NAr reactions have recognized the possibility of concerted pathways (Scheme 1b),^5–8 with many such proposals arising from density functional theory (DFT) predictions.⁹ The value of DFT for predicting whether a given S_NAr reaction will be stepwise or concerted was recently confirmed by both coupled-cluster-quality benchmark calculations and kinetic isotope effect (KIE) measurements on a series of halogen-exchange reactions.¹⁰ In general, concerted pathways are predicted to be broadly operative in S_NAr reactions with typical, modestly activated electrophiles.

The stepwise and concerted mechanisms for S_NAr represent limiting topographies of the free energy surface. Stepwise reactions involve distinct addition and elimination transition states that are connected by a Meisenheimer intermediate, which lies in an energetic minimum and has an appreciable lifetime. In contrast, concerted reactions proceed via a single transition state that avoids an inaccessible Meisenheimer region that is high in both energy and energetic gradient.

As these previous studies make clear, the topography of a given S_NAr reaction depends on the structure of the starting materials. One way to conceptualize this influence is to consider the relative barriers of addition and elimination. When the arene is very electron-deficient, it is highly reactive and the addition step is fast. However, once the σ-complex is formed, the leaving group is tightly held and the elimination step is slow. As a result, the reaction occurs in two steps.

Concerted mechanisms can appear when the Meisenheimer intermediate is less stable. For example, when the leaving group is changed from fluoride (σ_m = 0.34) to bromide (σ_m = 0.39),¹¹ the electron demand of the arene increases such that addition is modestly accelerated. However, because bromide (pK_a = −9)¹² is a much better leaving group than fluoride (pK_a = −3), the elimination step becomes barrierless. Accordingly, the reaction proceeds through a single transition state. While the foregoing analysis might suggest that there are two distinct clusters of S_NAr mechanisms, it is also possible that the mechanism changes smoothly between the stepwise and concerted extremes. Such a mechanistic continuum is familiar in the context of aliphatic substitution reactions,^13,14 and distinct clusters are generally proposed for acyl substitution.¹⁵

In fact, a simple Marcus analysis^16,17 predicts that the transition between the stepwise and concerted regimes will be smooth. In this Marcus view, the minimum energy path for an S_NAr reaction results from the intersection of diabatic curves for the reactants, Meisenheimer intermediate, and products (Scheme 1c). When the intermediate is relatively stable, its diabatic curve forms part of the minimum energy path, and the reaction is stepwise with a clear intermediate and two transition states. As the curve corresponding to the Meisenheimer intermediate is destabilized, its diabatic curve rises above the starting material and product curves. Correspondingly, the rate of elimination increases, resulting in a concerted mechanism with a single transition state. When the Meisenheimer curve is moderately stable, it barely touches the minimum energy path, and a “borderline” mechanism results. Thus, the stepwise and concerted mechanisms can be considered as the extremes of a mechanistic continuum, connected by the “borderline” region.

Crucially, the borderline S_NAr mechanism does not represent a competition between stepwise and concerted reactions with similar rate constants. Rather, it is a reaction path that shares features of the stepwise and concerted mechanisms. In the borderline mechanism, the Meisenheimer region is stable enough to influence the minimum energy path as an energetic shoulder,¹⁸ but not stable enough to create a true intermediate. When the energy is plotted as a function of the forming and breaking bond lengths, this shoulder appears as a shallow trough. Accordingly, reactive trajectories may linger there for several bond vibrations before proceeding to product. Therefore, borderline reactions can be considered to be formally concerted on the potential energy surface, but stepwise on the free energy surface.

Although Marcus theory readily predicts the influence of electrophile structure on mechanism, the effect of nucleophile structure is less clear. Furthermore, many mechanistic studies have only considered anionic nucleophiles, despite the fact that many S_NAr reactions are carried out with protonated nucleophiles. The prior studies of protic amine nucleophiles that do exist have largely examined highly activated arenes and found stepwise mechanisms with rate-limiting addition,¹⁹ elimination,^20,21 and proton transfer^22–28 with different modes of acid and base catalysis. In the specific case of S_NAr with indoles, the only studies reported have focused on highly electrophilic species.^29–31

It is difficult to predict whether protic nucleophiles favour the stepwise or concerted mechanism. One possibility is that the increased positive charge on the nucleophile reduces the charge transferred to the arene in the addition step, increasing the stability of the Meisenheimer intermediate, and thus favouring the stepwise regime. However, this picture either requires a zwitterionic intermediate or partial deprotonation of the nucleophile in a general-base-catalysed addition step. General base catalysis is known to occur in both the addition³² and deprotonation³³ steps in S_NAr mechanisms with highly activated electrophiles. However, the effect of the proton on the stability of the Meisenheimer intermediate could not be elucidated under these conditions, because the highly activated electrophiles used already strongly favour the stepwise pathway. Alternatively, protic species, being inherently weak nucleophiles, might simply prefer to react in anionic form via specific base catalysis. Subsequently, the conjugate acid might then decrease the elimination barrier through hydrogen bonding, thus favouring a concerted mechanism.^34,35

In this study, we elucidate the effect of the proton on the mechanism of S_NAr reactions between aryl fluorides and indole nucleophiles. We show that this reaction proceeds with general base catalysis, and that the mechanism is neither stepwise nor concerted, but actually borderline (Scheme 2). DFT studies of related azole nucleophiles predict that borderline mechanisms are commonplace and confirm the Marcus picture of a mechanistic continuum in which the transition state geometries vary continuously across all three mechanisms. Because these transition structures can be viewed as linear interpolations, various reaction parameters exhibit straightforward correlations with ground state properties. This phenomenon provides a convenient basis for the future development of a general model for S_NAr reactivity.

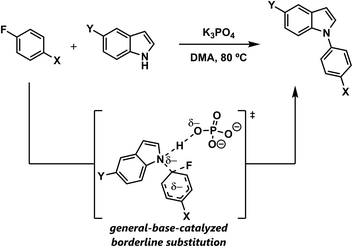Scheme 2 Prototypical S_NAr reaction between indoles and aryl fluorides, examined in this study and shown to proceed through a borderline mechanism that is subject to general base catalysis.

Absolute rates do not distinguish between mechanisms

A kinetic analysis of the K₃PO₄-promoted reaction between indole and 4-fluorobenzonitrile was carried out using initial rates. The reaction was studied using DMA, a polar aprotic solvent, due to the elevated temperatures and relative insolubility of the base.‡ At low concentrations, the process is first-order in both the aryl fluoride and indole. At higher concentrations, the rate plateaus, presumably due to due to rate-limiting phase transfer of the base in this heterogeneous reaction (Fig. 1). While the pK_a of K₃PO₄ in DMA is unknown, phosphate anion is likely the only sufficiently basic species in the reaction mixture, as experiments with K₂HPO₄ result in no reaction.

Fig. 1 Plots of initial rates vs. initial concentrations of starting materials, indicating that both starting materials affect reaction rate at low concentrations. (a) A plot of k_obs as [ArF]₀ is varied (0.5–0.025 M, [indole]₀ = 0.25 M). (b) A plot of k_obs as [indole]₀ is varied (0.175–0.01 M, [ArF]₀ = 0.25 M).

While these data show that single equivalents of the aryl fluoride and indole are both present in the rate-limiting transition state, they cannot distinguish between concerted, borderline, or stepwise processes. This limitation becomes clear when the corresponding rate laws for the potential mechanisms are examined, considering both general and specific base catalysis.

If S_NAr occurs in a single elementary step, the rate will depend on the concentrations of both the indole and the aryl fluoride (Scheme 3a). Because the concerted and borderline mechanisms both involve high-barrier addition and low-barrier elimination, they are kinetically indistinguishable. If general base catalysis is involved, the rate law will be first-order in base:

Rate = k_obs[ArF][indole][K₃PO₄] (1)

where the macroscopic rate constant k_obs is identical to the single microscopic rate constant k₁, and the rate is dependent on both starting materials (ArF = aryl fluoride).

Scheme 3 Mechanisms for general-base-catalysed concerted/borderline and stepwise S_NAr.

Stepwise addition–elimination results in the same rate law, although the microscopic composition of the macroscopic rate constant becomes more complex. Applying the steady-state approximation to the general-base-catalysed scenario (Scheme 3b) gives:

If k_elim ≫ k₋₂, addition is slow relative to elimination, and k_obs = k₂. Conversely, if k₋₂ ≫ k_elim, addition occurs in a fast pre-equilibrium step and k_obs ≃ k₂k_elim/k₋₂. Because the microscopic composition of k_obs is unobservable, these mechanistic scenarios are indistinguishable by absolute rates.§

However, if addition becomes so fast that it is essentially instantaneous, then elimination can no longer consume the intermediate quickly enough for the steady state approximation to hold. In this case, most of the reaction time course will be dominated by zero-order decay of the intermediate. While such behaviour would unambiguously implicate a stepwise process, this possibility is clearly ruled out by our data, which show that the rate does depend on starting material concentration when phase transfer is not rate-limiting.

The expected kinetic behaviour is analogous for specific-base-catalysed reactions. However, the rate law now depends on the pK_a of the base rather than its concentration:

Rate = k_obs[ArF][indole] (3)

Once again, the various mechanistic scenarios are indistinguishable (Scheme 4). For a concerted or borderline reaction, k_obs = k₃k₄/k_a. In the stepwise mechanism:

Scheme 4 Mechanisms for specific-base-catalysed concerted/borderline and stepwise S_NAr.

Thus, the absolute rates analysis shown in Fig. 1 is compatible with any of these mechanistic possibilities. Furthermore, it cannot determine the mode of base catalysis.

Moderate negative charge buildup

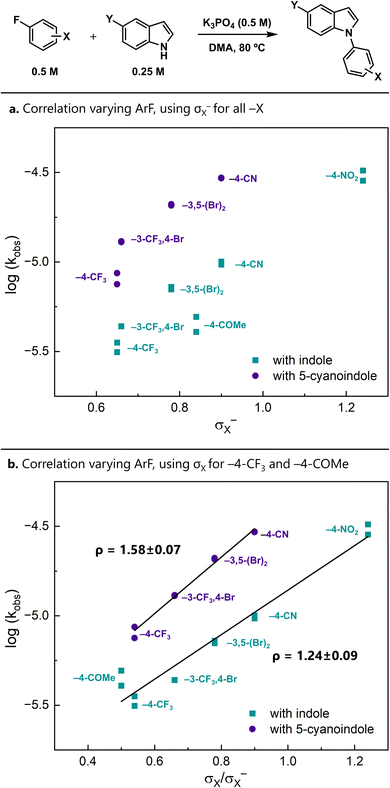
Relative rates offer a different approach for distinguishing the possible mechanisms. In particular, the modularity of the aryl fluoride and indole starting materials allowed us to conduct Brønsted and Hammett linear free energy relationship (LFER) studies. When substituents on the aryl fluoride were varied, we found that the reaction was moderately accelerated by electron-withdrawing substituents (Fig. 2).

Fig. 2 (a) LFER analysis varying the aryl fluoride, correlated with σ_X⁻. (b) A different analysis of the same data, using σ_X for −4–CF₃ and −4–COMe. In both plots, σ values were used for substituents with either no σ⁻ value or a nearly identical σ⁻ value. Indole (Y = H) and 5-cyanoindole (Y = CN) were used as the nucleophiles.

When σ⁻ is used for all substituents, the resulting Hammett correlation is relatively scattered (Fig. 2a).¶ An alternative approach to analysing the data uses σ for less electron-withdrawing substituents (−4–CF₃ and −4–COMe) and σ⁻ for the more electron-withdrawing substituents (−4–CN and −4–NO₂). The intervening substituents have nearly identical σ and σ⁻ values. The resulting correlations are linear and give moderate ρ values of 1.24(9) and 1.58(7) with indole and 5-cyanoindole as the nucleophile, respectively (Fig. 2b). Importantly, these ρ values are much smaller than those that are expected for S_NAr reactions proceeding through a Meisenheimer intermediate (ρ = 7–8)^36,37 and are more consistent with those observed in concerted reactions.^38–40

The observation that less electron-withdrawing substituents are best described by σ (as opposed to σ⁻) may reflect a difference in charge delocalization in the transition states. Stepwise-like reactions place more delocalized negative charge in the transition state. Therefore, σ⁻ parameters, which have been determined in model systems involving significant resonance,⁴¹ better represent substituent effects in such cases. In contrast, concerted-like mechanisms localize charge at the ipso position, and thus the substituent effects are better represented by σ. Correspondingly, one interpretation is that this plot is consistent with a changing transition state over the series of substituents, from a stepwise-like transition state to a concerted-like one.

Using 4-fluorobenzonitrile as the electrophile, we also examined the effects of the indole electronics and observed a ρ value of 1.06(12) using σ_m (Fig. 3a). This also indicates negative charge buildup on the indole nitrogen in the rate-limiting transition state. This diminished sensitivity compared to that observed on the arene could be due to the increased distance between the substituent and the indole nitrogen.

Fig. 3 (a) LFER analysis varying the indole, correlated with σ_Y(m), indicating a moderate degree of negative charge on the indole in the rate-limiting transition state. (b) A pseudo-Brønsted analysis of the same data, showing partial deprotonation of the indole in the rate-limiting transition state.

An alternative analysis treats these indole electronic effects as a pseudo-Brønsted⁴² correlation between k_obs and the pK_a of the indole.⁴³ This view provides additional insight into the degree of proton transfer between the nucleophile and base in the transition state (Fig. 3b). For a reaction with complete deprotonation in the rate-limiting transition state, the pK_a differences in the nucleophiles should be fully reflected in the reaction rate and thus the slope of the plot would be −1.|| Similarly, rate-limiting transition states with no proton transfer at all would result in a slope of 0. In this reaction, the slope of the pseudo-Brønsted plot is −0.38(4), which is consistent with partial deprotonation of the indole in the transition state in a general-base-catalysed mechanism.

General base catalysis is operative

While these LFER data indicate a modest degree of negative charge buildup in the transition state that is inconsistent with a stepwise mechanism, further experiments were needed to distinguish between the concerted or borderline mechanisms. Thus, we sought additional evidence in the form of a ¹²C/¹³C kinetic isotope effect (KIE) at the ipso carbon because this measurement is sensitive to both the forming and breaking bond lengths. Since DFT calculations have been shown to reproduce both ab initio benchmarks and experimental KIEs in other S_NAr reactions,¹⁰ the experimental KIEs can be directly compared to those predicted across the mechanistic continuum.

We measured a KIE of 1.035(4) via nuclear magnetic resonance (NMR) at natural abundance for the reaction between indole and 4-fluorobenzonitrile.^44,45 In contrast, the predicted KIE is much larger at 1.047 for a concerted mechanism involving indole anion as a nucleophile (Fig. 4a). Similarly large KIEs were obtained when modelling a specific base mechanism, and were unaffected by the presence or absence of a counterion.

Fig. 4 Predicted transition structures for the S_NAr reaction between indole and 4-fluorobenzonitrile. (a) Anionic transition state (TS_anionic) with no base. (b) Specific base transition state (TS_SB) with dihydrogenphosphate (H₂PO₄⁻) base. (c) General base transition state (TS_GB) with dihydrogenphosphate (H₂PO₄⁻) base. All calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMF).

We also considered the general-base-catalysed mechanism, but were unable to locate one using phosphate as the base. However, DFT does predict both general- and specific-base mechanisms (Fig. 4b and c) for weaker bases (DFT pK_a < 13)** such as dihydrogenphosphate (DFT pK_a = 3.4), chloride (DFT pK_a = −3.6), tetrazole (DFT pK_a = 4.6), and cyanide (DFT pK_a = 12.8). While the specific-base-catalysed transition states are similar in structure to the anionic transition state, the general-base catalysed transition states are later, with more advanced C–N bond formation. Accordingly, the predicted KIEs are reduced.

Remarkably, the predicted geometries and KIEs are largely independent of base structure and primarily depend on whether the general base or specific base mechanism is operative (Fig. 5). Each mode of base catalysis exhibits a characteristic KIE prediction: specific base transition states give predicted KIEs of 1.05, whereas general base transition states give predicted KIEs of 1.03, which is consistent with our experimental value.

Fig. 5 DFT-predicted KIEs plotted against predicted transition state geometries, defined by the length of the forming C–N bond. Transition states are calculated for the reaction between 4-fluorobenzonitrile and indole, using a series of bases. Calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMF).

Despite the very different geometries and charge distributions of the two base-catalysed transition states, they are predicted to have very similar energies. This prediction is implausible and highlights the limitations of implicitly solvated DFT calculations. Nonetheless, the insensitivity of the KIEs to base structure, coupled with the consistency between the predicted and experimental KIEs, allows us to reasonably conclude that general base catalysis is operative in this S_NAr reaction.

Partial deprotonation results in a borderline mechanism

This KIE analysis also reveals the influence of the proton on the mechanism. When the KIEs for the anionic reaction are plotted as a function of geometry, the concerted regime is seen to give the largest KIEs (Fig. 6). The transition states for the anionic (TS_anionic) and specific base (TS_SB) reactions lie on the verge of the concerted, high KIE region. In contrast, the general base transition state (TS_GB) is shifted later along the addition coordinate, and out of the high KIE region.

Fig. 6 DFT-predicted KIEs for the anionic reaction as a function of geometry. The predicted geometries for the anionic transition state, TS_SB, and TS_GB are marked, showing that TS_GB lies outside of the high KIE regime. Calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMF).

This shift of TS_GB lands it squarely in the “Meisenheimer region,” which encompasses structures with advanced C–N bond formation and little C–F bond cleavage. In contrast, TS_anionic and TS_SB lie earlier on the addition coordinate. The potential energy surface for the anionic reaction (Fig. 7) further shows that only a single transition state is expected along the addition coordinate, with no subsequent intermediate or elimination transition states being predicted.

Fig. 7 Calculated potential energy surface for the anionic reaction, showing a borderline mechanism. The predicted geometries for the anionic transition state, TS_SB, and TS_GB are marked. Calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMF).

Given the structural similarities between TS_GB and a hypothetical Meisenheimer intermediate, we might expect that TS_GB should bear significant negative charge on the arene. However, because a proton is now present, coordinates beyond the forming C–N and breaking C–F bond distances must be considered. While one might also consider a deprotonation coordinate, multi-dimensional representations are challenging to interpret.

Instead, we chose to conduct a Hirsheld population analysis⁴⁶ of the Meisenheimer intermediate and different transition structures (Table 1). At one extreme, the highly nucleophilic indole anion generates an early transition state. Correspondingly, there is only a minor degree of negative charge buildup on the arene (entry 2). Interestingly, the late structure TS_GB experiences a similarly small degree of negative charge buildup (entry 3) because some of the charge is absorbed by the proton. This diminished degree of negative charge in TS_GB is also consistent with the modest ρ values observed in the LFER experiments. At the other extreme, TS_SB (entry 4), which does not have a proton available, has a degree of charge buildup more comparable to that of the Meisenheimer intermediate (entry 5), despite falling earlier on the addition coordinate relative to TS_GB.

Table 1 Hirshfeld population analysis of arene charges^a

Entry	Structure	Arene charge^b	C–F (Å)	C–N (Å)	Base–H (Å)	KIE^c
a Calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMF).b Sum of charges at the positions ortho and para to the leaving group.c DFT-predicted KIE.d TS for the reaction between indole anion and 4-fluorobenzonitrile.e Calculated using tetrazole anion as the base.f Optimised structure constraining C–N and C–F at 1.4 Å.
1	4-Fluorobenzonitrile	−0.171	n/a	n/a	n/a	n/a
2	Anionic TS^d	−0.317	1.39	2.00	n/a	1.047
3	General base TS^e	−0.340	1.51	1.62	1.62	1.031
4	Specific base TS^e	−0.379	1.41	1.89	1.06	1.052
5	Meisenheimer intermediate^e^,^f	−0.429	1.40	1.40	1.00	n/a

---

Thus, although a concerted mechanism might be expected for this reaction based solely on the structure of the electrophile, the presence of the proton sufficiently stabilizes the Meisenheimer region to create a borderline mechanism. Still, the stabilization is insufficient to render the reaction fully stepwise.⁴⁷ Importantly, the poor leaving group ability of fluoride anion is the key factor that allows for observation of this mechanistic transition from concerted to borderline. For starting materials bearing better leaving groups, the reaction would almost certainly remain in the concerted regime.

Further, the stabilization conferred by general base catalysis is likely what allows this reaction to occur at all and is reflected in the smaller ρ value observed in the Hammett plot. General base catalysis decreases the negative charge transferred to the arene and makes strongly electron-withdrawing substituents unnecessary. Consequently, ρ decreases and the reaction scope becomes more general.⁴⁸

Visualizing the mechanistic continuum

We were interested to learn how the insights we gained into this S_NAr reaction with indole would relate to a broader range of azole nucleophiles and aryl fluoride electrophiles. To study this, we calculated the potential energy surfaces for 72 reactions spanning a range of azole nucleophiles and aryl fluoride electrophiles. Across this set of reactions, we observe a smooth transition from stepwise to concerted mechanisms, through the borderline regime. A subset of these calculations is shared here (Fig. 8a), and the full set is shared in the ESI.†

Fig. 8 (a) Ensemble of potential energy surfaces calculated for 20 anionic S_NAr reactions involving aryl fluoride electrophiles and azole nucleophiles. Electrophile range from highly activated (left) to deactivated (right); nucleophiles range from weakly acidic (top) to strongly acidic (bottom). The colour scale represents the relative energy for each individual potential energy surface. The complete set of 72 reactions can be found in the ESI.† (b) Transition structure geometries for all 72 S_NAr reactions. Inset plot: locations of transition states plotted on the same addition–elimination coordinate, showing clustering around the addition arm. The same points are shown in the larger plot, which has been zoomed-in. Points of the same colour represent transition states involving the same electrophile. Calculations carried out at B3LYP-D3(BJ)/6-31+g*/CPCM(DMA).

As electrophilicity decreases across the grid from left to right, the Meisenheimer region (short C–N and C–F distances, bottom left corner) becomes progressively less stable and the addition transition state shifts earlier. For stepwise reactions with very reactive electrophiles, the local minimum corresponding to the Meisenheimer intermediate can be observed, flanked by discrete addition and elimination transition states. Concerted reactions, on the right side of the grid, show a minimum energy path involving only a single transition state, and the Meisenheimer region is very unstable. In between, the minimum energy path for borderline reactions proceeds through the Meisenheimer region, with a gradual decrease in energy from the transition state to the products. Remarkably, the electrophile solely determines whether the mechanism is predicted to be stepwise, borderline, or concerted, as seen when considering any individual column in the grid of potential energy surfaces. Changes in nucleophilicity simply shift the location of the transition state along the addition coordinate.

Across the mechanistic continuum for this reaction, the transition structures are similar and vary smoothly (Fig. 8b). In the inset plot for Fig. 8b, the locations of the DFT-predicted transition structures for each reaction in Fig. 8a are plotted on the same addition–elimination coordinate. All of the transition structures are located along the addition arm of the reaction coordinate, with some variation in C–N distance but very little in C–F distance. Thus, regardless of whether the mechanism is stepwise, borderline, or concerted, the rate-limiting step involves predominantly addition and essentially no elimination. The mechanisms are instead distinguished only by the relative energies of the addition, elimination, and Meisenheimer structural regimes. The smooth changes in transition state geometry are also predicted by Marcus theory and are consistent with the gradually changing charge character as observed in the Hammett plot described above. In contrast, many reactions that can proceed through competing mechanisms exhibit clear delineations between those mechanisms.^13,15

This theoretical prediction is also mirrored by literature measurements of Eyring parameters for S_NAr reactions. When these values are aggregated, we see that the entropies of activation do not neatly separate into negative and positive groups for associative and dissociative rate-limiting steps, respectively.⁴⁹ Rather, there is significant enthalpy-entropy compensation and the entropy values vary smoothly from −60 e.u. to +60 e.u. across a wide range of substrates that likely span a mechanistic range from stepwise to concerted. This experimental observation is consistent with our DFT prediction that the S_NAr transition structures located in our computational grid also vary smoothly in geometry, irrespective of mechanism. We measured the entropy of activation for the indole/4-fluorobenzonitrile reaction and obtained ΔS‡ = −44(1) e.u., consistent with a highly organized rate-determining transition structure. It also falls within the previously reported range for S_NAr. In the context of S_NAr, this finding could be consistent with the associative step in any of the stepwise, borderline, or concerted regimes, but is inconsistent with rate-determining elimination in a stepwise mechanism.

Color-coding the transition states according to electrophile reveals sets of linear correlations between the C–N and C–F distances within homologous series of electrophiles (Fig. 8b). This suggests that the ensemble of DFT-predicted potential energy surfaces has a simple structure that lends itself to straightforward modelling. A linear regression analysis of the constituent transition state geometries shows that both the C– N and C–F distances can be linearly correlated with the pK_a of the nucleophile, the σ value of the electrophile substituent, and an intercept. That is, these distances can be predicted with high accuracy based only on these two ground-state parameters. Similarly, the energies of the Meisenheimer complexes and transition states can be modelled using the same parameters.

Given the importance of S_NAr as a method for functionalizing aromatic rings, there has been considerable interest in general methods for estimating the feasibility of unknown substitutions. An appealing strategy for prediction of S_NAr feasibility thus far has been to generate machine learning surrogates for DFT surfaces,^50–52 and the simple structures of the DFT surfaces generated here do lend themselves to this approach. However, future work in this area will need to account for the possibility of competing modes of base catalysis, given that DFT cannot accurately estimate the relative energies of these pathways. Failure to account for general base catalysis could lead to erroneous predictions of some S_NAr reactions as infeasible, when in fact the general base pathway would enable the reaction due to the stabilization and generality conferred by partial deprotonation. Future experimental studies across a broader range of chemical space will be required before a general model of S_NAr reactivity can be constructed.

Conclusions

We have demonstrated here that S_NAr reactions between indoles and aryl fluorides proceed through a general-base catalysed borderline mechanism and that these reactions broadly appear to lie on a mechanistic continuum. The Meisenheimer region is stabilized by partial deprotonation of the nucleophile, but not to a degree that allows for a stepwise process. As a result, elimination is fast, and the rate-determining step involves primarily addition. Our conclusions are supported by LFER studies, which find moderate degrees of negative charge on both the electrophile and nucleophile, and are reinforced by DFT predictions. A computational survey of 72 S_NAr reactions further reveals the mechanistic continuum, as transition structure geometries change smoothly between the stepwise and concerted extremes. The changing charge delocalization observed in the experimentally obtained LFER plot further corroborates the existence of this mechanistic continuum. It remains to be seen whether the existence of general-base catalysis is widespread, and whether the mechanistic continuum observed here translates to a broader scope of nucleophiles and electrophiles.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

A. K. T. conceived of and initiated the study. H. W. T., T. G., J. J. L., and A. K. T. performed and analysed kinetics experiments. K. J. Y. participated in the early development of the project. G. D. P., M. R., and E. E. K. performed NMR analysis of the KIE experiments. X. Z. and E. E. K. carried out the DFT calculations. A. K. T. supervised the project. The manuscript was written by A. K. T., including discussions with E. E. K.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We gratefully acknowledge Dr Nathan Cook and Dr Silas Brown (Williams College) and Dr Robert Samples (Smith College) for assistance with instrumentation, and Professor Joseph Gair (Michigan State University) for guidance and assistance with computations. This work was partially supported by the donors of the ACS Petroleum Research Fund under Undergraduate New Investigator Grant 65288-UNI4.

Notes and references

1. S. D. Roughley and A. M. Jordan, The Medicinal Chemist's Toolbox: An Analysis of Reactions Used in the Pursuit of Drug Candidates, J. Med. Chem., 2011, 54, 3451.
2. D. G. Brown and J. Boström, Analysis of Past and Present Synthetic Methodologies on Medicinal Chemistry: Where Have All the New Reactions Gone?, J. Med. Chem., 2016, 59, 4443.
3. F. Terrier, Modern Nucleophilic Aromatic Substitution, Wiley-VCH, Weinheim, 2013, and references therein.
4. W.-L. Zeng, Q. Xia, C.-Q. Li, M.-Y. Wang, W.-Y. Jin, H. Ding and W. Li, Bench-Stable Meisenheimer Complexes: Synthesis, Characterization, and Divergent Reactivity for Dearomatization, J. Am. Chem. Soc., 2024, 146, 30764.
5. A. Hunter, M. Renfrew, J. A. Taylor, J. M. J. Whitmore and A. Williams, A single transition state in nucleophilic aromatic substitution: reaction of phenolate ions with 2-(4-nitrophenoxy)-4,6-dimethoxy-1,3,5-triazine in aqueous solution, J. Chem. Soc., Perkin Trans. 2, 1993, 1703.
6. A. Hunter, M. Renfrew, D. Rettura, J. A. Taylor, J. M. J. Whitmore and A. Williams, Stepwise versus Concerted Mechanisms at Trigonal Carbon: Transfer of the 1,3,5-Triazinyl Group between Aryl Oxide Ions in Aqueous Solution, J. Am. Chem. Soc., 1995, 117, 5484.
7. J. Shakes, C. Raymond, D. Rettura and A. Williams, Concerted displacement mechanisms at trigonal carbon: the aminolysis of 4-aryloxy-2,6-dimethoxy-1,3,5-triazines, J. Chem. Soc., Perkin Trans. 2, 1996, 1553.
8. N. R. Cullum, D. Rettura, J. M. J. Whitmore and A. Williams, The aminolysis and hydrolysis of N-(4,6-diphenoxy-1,3,5-triazin-2-yl) substituted pyridinium salts: concerted displacement mechanism, J. Chem. Soc., Perkin Trans. 2, 1996, 1559.
9. S. Rohrbach, A. J. Smith, J. H. Pang, D. L. Poole, T. Tuttle, S. Chiba and J. A. Murphy, Concerted Nucleophilic Aromatic Substitution Reactions, Angew. Chem., Int. Ed., 2019, 58, 16368.
10. E. E. Kwan, Y. Zeng, H. A. Besser and E. N. Jacobsen, Concerted nucleophilic aromatic substitutions, Nat. Chem., 2018, 10, 917.
11. C. Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91, 165.
12. A. V. Levanov, U. D. Gurbanova, O. Y. Isaikina and V. V. Lunin, Dissociation Constants of Hydrohalic Acids HCl, HBr, and HI in Aqueous Solutions, Russ. J. Phys. Chem. A, 2019, 93, 93.
13. A. R. Katritzky and B. E. Brycki, The Mechanisms of Nucleophilic Substitution in Aliphatic Compounds, Chem. Soc. Rev., 1990, 19, 83.
14. Some aliphatic substitution pathways involve competing S_N1 and S_N2 mechanisms, T. B. Phan, C. Nolte, S. Kobayashi, A. R. Ofial and H. Mayr, Can One Predict Changes from S_N1 to S_N2 Mechanisms?, J. Am. Chem. Soc., 2009, 131, 11392.
15. M. L. Bender, Mechanisms of Catalysis of Nucleophilic Reactions of Carboxylic Acid Derivatives, Chem. Rev., 1960, 60, 1.
16. R. A. Marcus and N. Sutin, Electron transfers in chemistry and biology, Biochim. Biophys. Acta, 1985, 811, 265.
17. T. P. Silverstein, Marcus theory: thermodynamics can control the kinetics of electron transfer reactions, J. Chem. Educ., 2012, 89, 1159–1167.
18. J. F. Bunnett and C. Bernasconi, Kinetics of Reactions of Piperidine with Ethers of 2,4-Dinitrophenol in 10% Dioxane-90% Water. Dependence of Base Catalysis on the Group Displaced, J. Am. Chem. Soc., 1965, 87, 5209.
19. H. Raissi, I. Jamaoui, R. Goumont and T. Boubaker, Kinetic Studies on SNAr Reactions of Substituted Benzofurazan Derivatives: Quantification of the Electrophilic Reactivities and Effect of Amine Nature on Reaction Mechanism, Int. J. Chem. Kinet., 2017, 49, 837.
20. J. A. Orvik and J. F. Bunnett, Kinetics of the Separately Observable Formation and Decomposition of the Intermediate Complex in Aromatic Nucleophilic Substitution. Reactions of 2,4-Dinitro-1-naphthyl Ethyl Ether with n-Butyl- and t-Butylamine in Dimethyl Sulfoxide Solution, J. Am. Chem. Soc., 1970, 92, 2417.
21. I.-H. Um, M.-Y. Kim, T.-A. Kang and J. M. Dust, Kinetic Study on SNAr Reaction of 1-(Y-Substituted-phenoxy)-2,4-dinitrobenzenes with Cyclic Secondary Amines in Acetonitrile: Evidence for Cyclic Transition-State Structure, J. Org. Chem., 2014, 79, 7025.
22. C. F. Bernasconi, Kinetic Behavior of Short-Lived Anionic σ Complexes, Acc. Chem. Res., 1978, 11, 147.
23. I.-H. Um, S.-W. Min and J. M. Dust, Choice of Solvent (MeCN vs. H₂O) Decides Rate-Limiting Step in SNAr Aminolysis of 1-Fluoro-2,4-dinitrobenzene with Secondary Amines: Importance of Brønsted-Type Analysis in Acetonitrile, J. Org. Chem., 2007, 72, 8797.
24. I.-H. Um, L.-R. Im, J.-S. Kang, S. S. Bursey and J. M. Dust, Mechanistic Assessment of SNAr Displacement of Halides from 1-Halo-2,4-dinitrobenzenes by Selected Primary and Secondary Amines: Brønsted and Mayr Analyses, J. Org. Chem., 2012, 77, 9738.
25. C. F. Bernasconi and C. L. Gehriger, Intermediates in Nucleophilic Aromatic Substitution. XI. Spiro Meisenheimer Complex of N,N’-Dimethyl-N-picrylethylenediamine. Partially Rate-Limiting Proton Transfer of Complex Formation. A Temperature-Jump Study, J. Am. Chem. Soc., 1974, 96, 1092.
26. C. F. Bernasconi and F. Terrier, Intermediates in Nucleophilic Aromatic Substitution. XIV. Spiro Meisenheimer Complexes Derived from N,N’-Dimethylethylenediamine. Kinetics in Aqueous Dimethyl Sulfoxide, J. Am. Chem. Soc., 1975, 97, 7458.
27. E. Buncel and W. Eggimann, Base Catalysis of σ-Complex Formation between 1,3,5-Trinitrobenzene and Aniline in Dimethyl Sulfoxide. Rate Limiting Proton Transfer, J. Am. Chem. Soc., 1977, 99, 5958.
28. C. F. Bernasconi, M. C. Muller and P. Schmid, Rate-Limiting Proton Transfer in the Formation of Meisenheimer Complexes between 1,3,5-Trinitrobenzene and Amines. The Effect of Dimethyl Sulfoxide on Proton-Transfer Rates. Relative Leaving-Group Abilities of Amines and Alkoxide Ions, J. Org. Chem., 1979, 44, 3189.
29. F. Terrier, M.-J. Pouet, J.-C. Halle, S. Hunt, J. R. Jones and E. Buncel, Electrophilic Heteroaromatic Substitutions: Reactions of 5-X-Substituted Indoles with 4,6-Dinitrobenzofuroxan, J. Chem. Soc., Perkin Trans. 2, 1993, 1665.
30. F. Terrier, S. Lakhdar, T. Boubaker and R. Goumont, Ranking the Reactivity of Superelectrophilic Heteroaromatics on the Electrophilicity Scale, J. Org. Chem., 2005, 70, 6242.
31. S. Lakhdar, M. Westermaier, F. Terrier, R. Goumont, T. Boubaker, A. R. Ofial and H. Mayr, Nucleophilic Reactivities of Indoles, J. Org. Chem., 2006, 71, 9088.
32. R. H. de Rossi and A. Veglia, General-Base Catalysis in the Reaction of Water with Activated Aromatic Substrates. The Hydrolysis of 3-Methyl-1-picylimidazolum Ion, J. Org. Chem., 1983, 48, 1879.
33. C. F. Bernasconi, R. H. de Rossi and P. Schmid, Changing Views on the Mechanism of Base Catalysis in Nucleophilic Aromatic Substitution. Kinetics of Reactions of Nitroaryl Ethers with Piperidine and with n-Butylamine in Aqueous Dioxane, J. Am. Chem. Soc., 1977, 99, 4090.
34. J. Kim, Y. Hayashi, S. Badr, K. Okamoto, T. Hakogi, H. Furukawa, S. Yoshikawa, H. Nakanishi and H. Sugiyama, Mechanistic Insights into Amination via Nucleophilic Aromatic Substitution, React. Chem. Eng., 2023, 8, 2060.
35. C. F. Bernasconi and J. R. Gandler, Multiple Structure-Reactivity Relationships in the Acid-Catalyzed Breakdown of Meisenheimer Complexes, J. Am. Chem. Soc., 1978, 100, 8117.
36. J. Miller, Electrophilic and nucleophilic substitution in the Benzene ring and the Hammett equation, Aust. J. Chem., 1956, 9, 61.
37. J. Miller and W. Kai-Yan, The SN Mechanism in Aromatic Compounds. Part XXIX. Some para-Substituted Chlorobenzenes, J. Chem. Soc., 1963, 3492.
38. S. E. Fry and N. J. Pienta, Effects of Molten Salts on Reactions. Nucleophilic Aromatic Substitution by Halide Ions in Molten Dodecyltributylphosphonium Salts, J. Am. Chem. Soc., 1985, 107, 6399.
39. C. N. Neumann, J. M. Hooker and T. Ritter, Concerted nucleophilic aromatic substitution with 19F⁻ and 18F⁻, Nature, 2016, 534, 369.
40. D. J. Leonard, J. W. Ward and J. Clayden, Asymmetric α-arylation of amino acids, Nature, 2018, 562, 105.
41. A. I. Biggs and R. A. Robinson, The ionisation constants of some substituted anilines and phenols: a test of the Hammett relation, J. Chem. Soc., 1961, 388.
42. E. W. Lewis, Rate-Equilibrium LFER Characterization of Transition States: The Interpretation of α, J. Phys. Org. Chem., 1990, 3, 1.
43. M. A. Muñoz, P. Guardado, J. Hidalgo, C. Carmona and M. Balón, An Experimental and Theoretical Study of the Acid-base Properties of Substituted Indoles, Tetrahedron, 1992, 48, 5901.
44. G. Dal Poggetto, J. V. Soares and C. F. Tormena, Selective Nuclear Magnetic Resonance Experiments for Sign Sensitive Determination of Heteronuclear Couplings: Expanding the Analysis of Crude Reaction Mixtures, Anal. Chem., 2020, 92, 14047.
45. C. Mycroft, G. Dal Poggetto, T. M. Barbosa, C. F. Tormena, M. Nilsson, G. A. Morris and L. Castañar, Rapid Measurement of Heteronuclear Coupling Constants in Complex NMR Spectra, J. Am. Chem. Soc., 2023, 145, 19824.
46. A. V. Marenich, S. V. Jerome, C. J. Cramer and D. G. Truhlar, Charge Model 5: An Extension of Hirshfeld Population Analysis for the Accurate Description of Molecular Interactions in Gaseous and Condensed Phases, J. Chem. Theory Comput., 2012, 8, 527.
47. W. P. Jencks, When Is an Intermediate Not an Intermediate? Enforced Mechanisms of General Acid-Base Catalyzed, Carbocation, Carbanion, and Ligand Exchange Reactions, Acc. Chem. Res., 1980, 13, 161.
48. M. G. Kung, P. Onnuch and R. Y. Liu, Rapid and General Amination of Aryl Boronic Acids and Esters Using O-(Diphenylphosphinyl)hydroxylamine (DPPH), Org. Lett., 2024, 26, 9847.
49. V. M. Vlasov, Energetics of bimolecular nucleophilic reactions in solution, Russ. Chem. Rev., 2006, 75, 765.
50. K. Jorner, T. Brinck, P.-O. Norrby and D. Buttar, Machine learning meets mechanistic modelling for accurate prediction of experimental activation energies, Chem. Sci., 2021, 12, 1163.
51. T. Stuyver and S. Shaik, Promotion Energy Analysis Predicts Reaction Modes: Nucleophilic and Electrophilic Aromatic Substitution Reactions, J. Am. Chem. Soc., 2021, 143, 4367.
52. J. Lu, I. Paci and D. C. Leitch, A broadly applicable quantitative relative reactivity model for nucleophilic aromatic substitution (SNAr) using simple descriptors, Chem. Sci., 2022, 13, 12681.

---

Footnotes

† Electronic supplementary information (ESI) available: Full experimental details and initial rates plots, kinetic isotope effect methods, computational methods and coordinates, characterization of reaction products, NMR spectra, and raw data files (ZIP). See DOI: https://doi.org/10.1039/d5sc01856k

‡ The reaction can also be carried out in DMF and DMSO.

§ General base catalysis likely also would proceed through a mechanism involving pre-association of the base and the indole, and not through a termolecular elementary step. However, this microscopic pre-association step would also only lead to a change in the composition of k_obs, and is therefore also indistinguishable from the other scenarios.

¶ We chose to use σ⁻ as a reference, recognizing that resonance delocalization might play an important role. Using Hammett σ as a reference gave a scattered correlation (see ESI section II-E†).

|| This is a “pseudo-Brønsted” analysis because we examined the pK_a of the nucleophile rather than the pK_a of the base. This results in a slope of −1 for a mechanism involving full deprotonation; if the rate were correlated with the pK_a of the base, the maximum slope would be 1.

** These pK_a values are DFT-predicted and linearly scaled according to the experimental pK_a values in DMSO (see ESI section IV-C†).

---