External electric fields drive the formation of P → C dative bonds

Abstract

Chemical interactions driven by external electric fields (EFs) can serve as a catalytic force for molecular machines and linkers for smart materials. In this context, the EF-driven dative bond is demonstrated through the study of interactions between PH₃ and curved carbon-based nanostructures. The P → C dative bonds emerge only in the presence of EFs, whereas the interactions in the absence of EFs lead to van der Waals (vdW) complexes. The formation of EF-driven dative bonds can be verified with distinctive signals in vibrational, carbon-13 NMR, and UV/vis spectra. The nature of EF-driven dative bonds was theoretically analyzed with the block-localized wavefunction (BLW) method and the associated energy decomposition (BLW-ED) approach. It was found that the charge transfer interaction plays a dominating role and that even in the presence of EFs, complexes dissociate to monomers once the charge transfer interaction is “turned off”. Notably, the inter-fragment orbital mixing stabilizes the complexes and alters their multipoles, leading to additional stability through field–multipole interactions. This conclusion was supported by further decomposition of the charge transfer energy component, clarifying the precise role of orbital mixing. The inter-fragment orbital mixing, which occurs exclusively in the presence of EFs, was elucidated using “in situ” orbital correlation diagrams. Specifically, both external EFs and intermolecular perturbations remarkably reduce the energy gap between the frontier orbitals of the monomers, thereby facilitating inter-fragment orbital interactions. Significant covalency was confirmed through ab initio valence bond (VB) theory calculations of the EF-driven dative bonds, aligning with the crucial role of the charge transfer interaction. This pronounced covalency emerges as a key feature of EF-driven interactions, setting them apart from traditional dative bonds studied in parallel throughout this work.

---

1 Introduction

External electric fields (EFs) exert forces on both electrons and nuclei, leading to alterations in the electron density and nuclear framework, and subsequent changes in the potential energy surface.^1,2 EFs have been successfully employed to regulate molecular structures,^3–6 spectroscopy,^7,8 and chemical reactions.^9–14 Moreover, phase transitions,^15,16 magnetism,¹⁷ and self-assembly processes in larger-scale systems^18,19 can be influenced by EFs. Notably, EFs can serve as an elementary force in the operation of molecular machines,^20–33 enabling the miniaturization of devices to the nanoscale. For instance, EFs can drive ion@C₆₀ to pump water through a carbon nanotube³² and modulate the rotational process of a dipolar molecule encapsulated within C₇₀, resulting in a novel two-state molecular switch.³³ In general, the physical interactions between EFs and net charges or multipoles act as direct and efficient driving forces for molecular machines, as evidenced in the above examples.^{21–25,27–29,32,33} However, chemical bonding driven solely by external electric fields is indispensable for the rational design of EF-driven molecular machines, as the bond formation can result in significant geometric variations. Such structural responses to EFs fulfill the fundamental requirement for piezoelectric properties,³⁴ underscoring their potential in the development of smart materials. In addition, clarifying the distinctions between EF-driven chemical bonds and their conventional counterparts can enrich chemical bonding theory and attract broad interest.

The diverse family of chemical bonds^35–43 offers a rich array of options for exploring EF-driven chemical interactions. In this regard, the dative bond,^44–52 which can be regarded as a donor–acceptor interaction with unequally shared electrons, emerges as an ideal choice, due to its considerable covalency and ionic character. The ionic feature indicates oppositely charged fragments and a considerable dipole moment, which interacts strongly with EFs. Meanwhile, the covalent characteristic ensures the stability. In this regard, the N → B bond in ammonia borane (BH₃NH₃) is an illustrative example of traditional dative bonds,⁵³ and a series of novel patterns have been explored in recent years.^54–61 Particularly, dative bonds on the concave side of curved carbon nanostructures have been highlighted by Hobza et al.,^54–58 for their ability to functionalize carbon nanomaterials. Structural selectivity has been highlighted in these dative bonds. For example, piperidine forms a dative bond with C₆₀, but its interactions with single-walled carbon nanotubes or buckybowls result in van der Waals (vdW) complexes.⁵⁴ This structural selectivity suggests that these dative bonds could be used as driving forces for molecular machines, provided that the vdW interactions can be converted into dative bonds under the action of external electric fields.

There are three basic reasons why the EF-driven dative bonds are possible on nanostructures. First, EFs can shift the electron density within a curved carbon nanostructure from one side to the other, creating electrophilic carbon atoms for interacting with Lewis bases. It is necessary to note that these nanostructures typically exhibit high polarizability^62–64 and can respond sensitively to EFs. Second, EFs can direct the lone pair electrons of the Lewis base towards the electron-deficient center on the carbon nanostructure, facilitating the intermolecular charge transfer interaction. Finally, the dative bonds can be further stabilized by EFs due to their ionic character. The partially charge separated feature of dative bonds formed on the curved carbon nanostructures has already been evidenced in previous studies.⁵⁸ Besides, compared with vdW complexes, dative bonds exhibit unique and distinctive vibrational frequencies and chemical shifts in the carbon-13 NMR spectrum,^54,55 offering clear output signals for the design of molecular switches.

To theoretically explore the EF-driven dative bonds, ab initio valence bond (VB) theory^65–69 is an ideal approach due to its chemically meaningful characteristics. Specifically, VB theory defines the many-electron wavefunction as a linear combination of VB (resonance) structures constructed from strictly localized orbitals, and fundamental concepts in chemistry, such as the Lewis structure, resonance, and orbital overlap, are intrinsically incorporated. VB theory has been effectively utilized to elucidate the intriguing role of EFs as invisible and selective catalysts in a variety of reactions.^1,2,70 In this work, a dative bonding complex is described with two Lewis (resonance) structures similar to the well-known two-state electron transfer (ET) theory, as shown in Scheme 1a. In the neutral (prior-ET) state (Φ_neu), electrons are strictly localized on the nanomolecule and the Lewis base respectively. In contrast, the lone pair electrons of the Lewis base are shared with the bonding carbon atom in the ionic (post-ET) state (Φ_ion), which exhibits oppositely charged fragments and a notable dipole moment.^71,72 Here the positive direction of EFs is defined as the direction energetically favored by electrons, consistent with the convention preferred by chemists who focus on electron behaviors (Scheme 1b).

Scheme 1 (a) Illustration of the complete VB wavefunction with two Lewis (resonance) structures; (b) definition of the electric field direction in this work.

As the simplest variant of ab initio VB theory, the block-localized wavefunction (BLW) method^73–76 retains the localized orbitals but simplifies the wavefunction to a single determinant for each VB electron-localized (diabatic) state, achieving the computational efficiency of molecular orbital (MO) theory. In the BLW method, electrons and orbitals are partitioned into blocks (subgroups), with each orbital block-localized and solely expanded within its corresponding subgroup and self-consistently optimized. Thus, the BLW method fully incorporates the perturbations between monomers, providing a unique “in situ” orbital picture to interpret the subsequent orbital mixing.^77–79 Additionally, the charge transfer interaction can be precisely characterized by comparing the BLW and MO/DFT results. The BLW method has been extended to the DFT level and is capable of geometry optimization and vibrational frequency analysis for the diabatic state.⁷⁶ Moreover, the energy decomposition (BLW-ED) approach based on the BLW method can decompose the binding energy into physically meaningful components.^80–82 Schemes for BLW-ED in EFs have been further developed to elucidate the impact of EFs on the strength of non-covalent interactions and on the rotational potential energy surface of dipolar molecules encapsulated within C₇₀.^83,84 Notably, the response of different interactions to EFs can be governed by distinct physical factors. For example, the strength of hydrogen bonds is mainly regulated by the response of electrostatic interactions to the EFs, whereas the variation in the strength of halogen bonds results from the change in covalency due to EFs.⁸⁴ Hence, it is necessary and of broad interest to systematically explore the response of novel interactions to external electric fields using state-of-the-art theoretical methods. We note that numerous energy decomposition approaches^85–99 have been developed and served extensively as advanced theoretical tools to elucidate the nature of chemical bonds.^{84,89,90,98,100–103} Bonding analysis has also been developed from the perspective of electron density, orbital interactions and the bond force constant. Notable examples include the quantum theory of atoms in molecules (QTAIM),^104,105 reduced density gradient (RDG),¹⁰⁶ natural bond orbital (NBO) theory,^107–111 conceptual DFT,^112–115 and the local vibrational modes (LVMs).^116,117

This work focused on EF-driven dative bonds given their potential applications in the design of molecular machines. Curved carbon-based nanostructures, including C₃₀H₁₀ buckybowls, C₆₀ fullerene, and C₄₀H₂₀ nanohoops were selected as the electron-acceptors, with phosphine chosen as the universal electron-donor. The formation of dative bonds was confirmed from multiple perspectives. Distinctive spectroscopic features associated with the EF-driven formation of dative bonds were also elucidated. Finally, ab initio VB theory and the BLW method were employed to provide a chemically intuitive interpretation for the nature of EF-driven dative bonds. The prototypical dative bond in H₃P-BH₃ and the conventional P → C bond in H₃P-C₆₀ were also studied in the absence of EFs, serving as references to highlight the distinguishable features of the EF-driven cases.

2 Methods and computational details

2.1 BLW-ED approach in the absence and presence of EFs

The binding energy (ΔE_b) is the overall stability gained upon the formation of a complex from isolated and optimal monomers and comprises the deformation and interaction energy terms (eqn (1)). The deformation energy stands for the energy cost to deform the optimal monomers to their geometries in the complex. The interaction energy is the energy difference between the complex and isolated and deformed monomers (eqn (2)). In the absence of EFs, the interaction energy can be decomposed by employing the BLW-ED approach as expressed in eqn (2). Specifically, the frozen energy (ΔE_F) refers to the energy variation resulting from the construction of the complex using deformed monomers without adjusting their orbitals (electron densities). Subsequently, polarization energy (ΔE_pol) measures the energy lowering caused by orbital mixing within individual monomers (i.e., relaxations of electron densities) due to the electric field and Pauli exchange repulsion imposed on each other. Eventually, the complex is further stabilized by permitting electrons to move throughout the entire system. This stabilization is denoted as the charge transfer energy (ΔE_CT) and evaluated by using the energy difference between the MO or DFT wavefunction and BLW (eqn (3)) with the basis set superposition error (BSSE) correction. Additionally, Grimme's dispersion correction between the complex and distorted monomers is defined as the dispersion correction term (ΔE_D3).

ΔE_b = ΔE_def + ΔE_int (1)

ΔE_int = ΔE_F + ΔE_pol + ΔE_CT + ΔE_D3 (2)

ΔE_CT = E(Ψ^DFT) − E(Ψ^BLW) + BSSE (3)

External electric fields can alter the molecular electron density and interact with the perturbed multipoles, resulting in variations in energy, geometry and bond strength. Consequently, the structures of the complex and monomers need to be re-optimized in the presence of EFs for subsequent bonding analysis. The BLW-ED method under EFs adheres to the same scheme outlined in eqn (1)–(3). However, energies of all intermediate states are evaluated in the presence of EFs, with the complete BLW-ED scheme in EFs expressed in eqn (4).

ΔE_b = ΔE_def + ΔE_F + ΔE_pol + ΔE_CT + ΔE_D3 = ΔE_def + ΔE_int (4)

The charge transfer interaction was further subdivided, given its pivotal role in the EF-driven dative bonds, as elucidated in the following section. For each intermediate state, the total energy includes the intrinsic energy (E⁰) of the wavefunction perturbed by the external EF, and the field–molecule interaction (V), as expressed in eqn (5). Accordingly, the charge transfer interaction can be decomposed following eqn (6), where the intrinsic charge transfer energy (ΔE^I_CT) describes the energy lowering due to the orbital mixing between blocks, while the induced potential energy (ΔV_CT) measures the variation in electrostatic potential energy due to the inter-fragment orbital interactions. Note that the BSSE is fully incorporated in the intrinsic charge transfer energy.

E = E⁰ + V (5)

ΔE_CT = [E⁰(Ψ^DFT) + V(Ψ^DFT)] − [E⁰(Ψ^BLW) + V(Ψ^BLW)] + BSSE = [E⁰(Ψ^DFT) − E⁰(Ψ^BLW) + BSSE] + [V(Ψ^DFT) − V(Ψ^BLW)] = ΔE^I_CT +ΔV_CT (6)

2.2 Computational details

The EF was applied along the P → C direction with the field strength selected based on its effect on the interaction in the H₃P–C₆₀ complex, which is the most EF-sensitive case in this work. The EF-driven dative bond weakens approximately linearly with the decreasing field strength, showing positive binding energies below 0.01 a.u. (Fig. S1†). Interestingly, the repulsive interaction under an EF of 0.009 a.u. corresponds to a P–C bond length of 1.873 Å, suggesting potential metastability. Notably, a field strength of 0.018 a.u. was chosen because, at this value, the strongest EF-driven dative bond in this study (−22.82 kcal mol⁻¹) matches the binding energy of the prototypical H₃P–BH₃ dative bond,¹¹⁸ which is an ideal reference for highlighting the distinctive characteristics of EF-driven dative bonding. Geometrical optimizations of all complexes were conducted with and without external EFs at various theoretical levels. The PBE0-D3,^119,120 M062X-D3,^120,121 and ωB97XD¹²² functionals were employed in conjunction with def2-SVP, def2-TZVP, and def2-TZVPP basis sets.^123,124 The vdW complexes were observed without EFs, according to the binding energy and key geometrical parameters (Table S1†), while EF-driven formation of P → C dative bonds was confirmed across all theoretical levels examined (Table S2†). Importantly, the lengths and binding energies of EF-driven dative bonds exhibit insignificant variation with the changes in theoretical levels (Table S2†). Furthermore, the global geometrical differences of dative bonding complexes derived from different theoretical levels were measured through the minimized root mean square deviation (RMSD) of atom coordinates. Structures obtained from the PBE0-D3/def2-TZVPP theoretical level were utilized as the references for the RMSD calculations. As listed in Table S3,† the RMSD values are all less than 0.040 Å. In summary, the EF-driven formation of dative bonds is consistently supported across all theoretical levels examined. At the M06-2X-D3/def2-SVP level, the binding energy (−24.10 kcal mol⁻¹) closely aligns with the CCSD(T)/cc-pVTZ result (−21.10 kcal mol⁻¹) for the well-studied H₃P–BH₃ molecule. Besides, the length of the conventional P → C bond in H₃P–C₂₀ is 1.814 Å, within the reported range of 1.808–1.862 Å.⁵⁶ Ultimately, M06-2X-D3/def2-SVP was chosen for its balance of reliability and computational efficiency.

The reliability of the M06-2X-D3/def2-SVP level has been further validated by assessing its performance in a water dimer, a system systemically studied using the gold-standard coupled cluster method.¹²⁵ Specifically, the strengthening of hydrogen bonds (Fig. S2a†), and the elongation of O-H bonds (Fig. S2b†) caused by the increasing field strength along the direction of the hydrogen bond have been observed at the M062x-D3/def2-SVP theoretical level, in line with the benchmark results.¹²⁶ Notably, the M062x and ωB97X functionals have been proved to be good choices for studying the response of hydrogen bonds in a water dimer to EFs compared with other functionals, despite the overestimation of bond strengthening¹²⁶ using all DFTs tested.¹²⁶ BLW-ED has been employed to specify the factor determining the variation in bond strength under external EFs. As shown in Fig. S2a,† the enhancement in bond strength is governed by the frozen energy, in which the electrostatic interaction is included, in agreement with the SAPT results obtained using the coupled cluster method.¹²⁵

Two blocks, namely the electron donor and acceptor, were defined in the BLW calculations. The wavefunction shown in Scheme 1 was used for the VB description of dative bonds. Each active VB orbital was expanded using the basis functions of either the bonding carbon or phosphorus atoms, while the inactive orbitals were localized on the corresponding fragment. Due to the extensive computational cost for ab initio VB methods, the STO-6G basis set was employed for VBSCF calculations for the VB description of nanomolecules. Single point VBSCF calculations were performed with and without an external EF on the DFT optimized geometries of dative bonding cases. The relative deviations between VBSCF and DFT in the interaction energies of the EF-driven dative bonds range from −12.68% to −0.96% (Table S4†). Moreover, repulsive interaction energies were observed in the VB calculations for dative bonds when the external EF was turned off (Table S4†). Therefore, the EF-driven formation of dative bonds can be described in our VB calculations, despite the use of a small basis set for the sake of computational costs. The resonance energy was defined as the energy difference between the full VB wavefunction and the primary Lewis structure.

The DFT, BLW, and BLW-ED calculations were conducted using an in-house version of the GAMESS(US) software.¹²⁷ The RMSD of atom coordinates was calculated using the Visual Molecular Dynamics (VMD) program.¹²⁸ Post-SCF analyses, including QTAIM, Mayer bond order^129,130 and the natural population analysis (NPA),¹³¹ were performed employing Multiwfn.^132,133 Bond force constants¹³⁴ were derived from the localization of normal modes using the Localized Vibrational Model (LVM) theory. The CP2K package¹³⁵ was chosen for ab initio molecular dynamics (AIMD) simulations in the presence of an EF at 298.15 K, and the DZVP-MOLOPT-SR-GTH basis set¹³⁶ was employed in the AIMD simulations. Optimal structures of dative bonding complexes were selected as the initial structures, with the EF (0.018 a.u.) oriented along the P → C bond. The velocities of atoms were initialized randomly based on the Boltzmann–Maxwell distribution,¹³⁷ and the Berendsen thermostat¹³⁸ was adopted. A time step of 1.0 fs was chosen. After an equilibration period of 2000–10000 fs, productive simulations of 10 000 fs were conducted with data collected for further analyses. TD-DFT theory¹³⁹ was employed to calculate the ultraviolet-visible (UV/vis) absorption spectra representing the excitations from S₀ to S_1–6. Subsequently, the hole–electron analysis was conducted for each excitation through inspecting the charge density difference (CDD) between the ground state and each excited state using the Multiwfn and VMD programs. The GIAO method^140–142 was employed for NMR calculations.

3 Results and discussion

Optimal geometries of vdW complexes formed in the absence of EFs are depicted in Fig. 1a–c with the binding energies and shortest P⋯C distances denoted. Similar bonding patterns were observed in all vdW complexes. Two hydrogen atoms in phosphine are tilted toward nanostructures and slightly closer to them compared to the phosphorus atom, which is 3.49–3.31 Å away from the nearest carbon atom in all cases. In these structures, the π-cloud on the convex side of nanostructures can loosely attract both the positively charged hydrogens and the σ-hole on the phosphorus atom according to the electrostatic potentials (ESPs) of monomers (Fig. S3†). In the presence of an EF, however, P → C dative bonds are formed as evidenced by the bond lengths and binding energies (Fig. 1d–f). The carbon atoms at the bonding sites are pulled away from the convex surfaces of the nanostructures towards the phosphorus atom across all dative bonding cases. Additionally, the cross-sectional plane of the C₄₀H₂₀ nanotube turns elliptical upon the formation of the dative bond, showing remarkable structural deformation. The strongest EF-driven dative bond was observed in H₃P-C₆₀, exhibiting a binding energy of −22.8 kcal mol⁻¹, comparable to that of the prototypical P → B bond in H₃P-BH₃. Dative bonds formed with buckybowls and carbon nanotubes are relatively weaker, with the binding energies ranging from −12.4 to −3.8 kcal mol⁻¹. These data align with previous studies demonstrating that fullerenes are better electron-acceptors than buckybowls and carbon nanotubes, with which P → C dative bonds have not been observed previously. The stability of the present EF-driven dative bonds was confirmed by AIMD simulations, where the length of the EF-driven dative bond deviated insignificantly from the average value (R̄), showing few signs of dissociation. Moreover, the lengths of the C–H and P–H bonds were also inspected in the AIMD simulations under external EFs, with no bond breaking observed. For instance, the lengths of P–H bonds barely vary in all AIMD simulations (Fig S4†). It is necessary to note that these almost constant bond lengths may be caused by the absence of the quantum effect of nuclear motion, which may lead to bond fluctuations.¹⁴³

Fig. 1 Optimal structures of the vdW complexes (a–c) in the absence of EFs and the dative bonding (DB) complexes (d–f) in the presence of EFs, with the shortest P⋯C distances (R in Å) and binding energy (ΔE_b in kcal mol⁻¹) denoted, and the fluctuations of the P → C distances over time in the AIMD simulations of dative bonding complexes in the presence of EFs (g–i).

The EF-driven dative bonds shown in Fig. 1d–f can be evidenced by bond force constants, Mayer bond order, and bond critical points (BCPs), which are compiled in Table 1. They are comparable to traditional dative bonds such as H₃P → BH₃, indicating similar intrinsic bond strengths. Each EF-driven dative bond features a BCP with appropriate electron density and negative Laplacian values, consistent with the characteristics of a covalent bond. The amount of charge transferred between monomers during the formation of the complex was calculated based on the natural population analysis (NPA).¹³¹ The covalency of P → C bonds is in line with the amount of electrons transferred from PH₃ to the nanostructure (ΔQ) in the EF-driven cases. These EF-driven systems show similar bond force constants, bond orders, AIM results, and amounts of charge transfer as observed in the conventional P → C bond in H₃P-C₂₀. Notably, positive Laplacian values and a minimal amount of transferred charge were found at the BCP of the prototypical P → B bond, indicating a closed-shell interaction.

Table 1 Bond force constants (k in mDyn per Å), Mayer bond order (BO), amount of charge transferred between monomers (ΔQ), electron density (ρ in eÅ⁻³), and its Laplacian value (∇²ρ in a.u.) at the BCPs of dative bonds

Complexes	k	BO	ρ	∇^2ρ	ΔQ
H3P-C30H10	2.061	0.922	0.157	−0.116	1.128
H3P-C60	2.006	0.919	0.153	−0.108	1.084
H3P-C40H20	2.060	0.959	0.157	−0.118	1.083
H3P-C20	2.287	0.932	0.173	−0.091	1.012
H3P-BH3	1.489	0.830	0.098	0.158	0.552

---

Fig. 2 displays the computed spectra for both the vdW and dative bonding complexes, with distinctive signals for the dative bonding complexes highlighted with gray dashed lines. In vibrational spectra, the dative bond manifests a characteristic P → C stretching vibrational frequency at 627–636 cm⁻¹, which is absent in the vdW complex (Fig. 2a–c). It is important to note that the P → C stretching vibration participates in several normal modes, among which only the one with the frequency closest to the localized P → C frequency was denoted. Moreover, the formation of the dative bond changes the environment of the bonding carbon atom, giving rise to a distinctive signal in the carbon-13 NMR spectrum (Fig. 2d–f). In the UV absorption spectrum, the EF-driven dative bond also triggers characteristic absorption peaks which are absent in the corresponding vdW complex. In H₃P-C₃₀H₁₀ (Fig. 2g), the S₀ → S₂ excitation is responsible for the distinct visible absorption, and exhibits charge transfer (CT) characteristics. Specifically, the S₀ → S₂ excitation shifts electron density from the lone pair region of H₃P toward the left side of the buckybowl in the dative bonding complex (Fig. S5†). For the remaining vdW and dative bonding complexes, the UV absorption spectra and the CDD plots are shown in Fig. S5.† The characteristic absorption peaks at 665–880 nm were observed exclusively in the dative bonding cases, all of which originate from the excitation displaying charge transfer characteristics. From vdW interactions to the EF-driven dative bonds, notable variations in the P⋯C distance (Fig. 1) and spectral changes (Fig. 2) satisfy the fundamental requirements for the design of molecular machines and piezoelectric materials.

Fig. 2 Calculated IR spectra (a–c), carbon-13 NMR spectra (d–f) and UV absorption spectra (g–i) of the vdW (blue line) and dative bonding (red line) complexes.

BLW-ED analyses of the EF-driven dative bonds are summarized in Table 2. Remarkably, the charge transfer interactions are significant (−151.60 to −158.48 kcal mol⁻¹) across all EF-driven cases, primarily dominating the binding energy. The pivotal role of the charge transfer interactions aligns with the covalency suggested by the QTAIM results and amount of transferred charges (Table 1). Furthermore, geometrical optimizations of the electron-localized states were conducted in the presence of EFs. In each case, the P⋯C distance is stretched to longer than 3.5 Å after turning off the charge transfer interactions (Fig. S6†). Polarization interactions emerge as the second most stabilizing factor, while Grimme's D3 dispersion correction negligibly contributes to the overall stability. The significant polarization can be attributed to the substantial polarizabilities of the carbon nanomolecules (Table S5†). The high stabilizing charge transfer and polarization energies are offset by the repulsive frozen energy. The latter is dominated by Pauli exchange repulsion, which is the sole destabilizing factor within the frozen energy component. The key role of charge transfer interactions is also supported by the GKS-ED^94,95 computations. As summarized in Table S6,† the polarization energy, which accounts for the energy lowering caused by orbital mixing within (polarization in BLW-ED) and between (charge transfer) monomers, dominates the binding energies in all EF-driven cases, aligning with the BLW-ED results. Similarly, the reference cases are also dominated by the charge transfer interaction and further enhanced by the polarization effect, with a repulsive frozen interaction observed. It is necessary to note that the charge transfer interaction in the conventional P → B bond is much weaker than the P → C cases studied, suggesting that nanostructures are better electron-acceptors than BH₃.

Table 2 BLW-ED analyses (in kcal mol⁻¹) of the EF-driven dative bonding complexes and reference dative bonds

Complexes	ΔEdef	ΔEF	ΔEpol	ΔECT	ΔED3	ΔEint	ΔEb
H3P-C30H10	33.90	162.08	−55.12	−152.85	−0.45	−46.34	−12.44
H3P-C60	35.67	156.20	−55.68	−158.48	−0.53	−58.49	−22.82
H3P-C40H20	53.42	157.27	−62.54	−151.60	−0.40	−57.27	−3.85
H3P-C20	26.92	173.02	−60.84	−140.41	−0.28	−28.51	−1.59
H3P-BH3	12.12	41.31	−20.12	−57.39	−0.02	−36.22	−24.10

---

To gain deep insights into the details regarding the bonding nature, here we employed “in situ” orbital correlation diagrams to elucidate how the orbital interactions between monomers evolve in the presence of external EFs. In Fig. 3, A and B stand for the nanomolecule and PH₃, respectively, with the superscript “F” indicating perturbation from external EFs. The effects of both the external EF and intermolecular polarization are integrated into the “in situ” orbitals of the BLW, with the prefix “BL-” denoting the corresponding state. The highest occupied molecular orbital (HOMO) of the electron donor and lowest unoccupied molecular orbital (LUMO) of the acceptor were focused on. As shown in Fig. 3a–c, the HOMO of PH₃ corresponds to the lone pair orbital of the phosphorus atom, while the π-symmetric hybrid orbital on the bonding carbon atom is the LUMO of the acceptor. Notably, the LUMO energy of the nanostructure is reduced by the external EF, and further decreased by the molecular field including the electrostatic interactions and Pauli exchange repulsion imposed by PH₃. Simultaneously, the HOMO energy of PH₃ is increased by both the external EF and intermolecular perturbations. Thus, both the external EF and inter-fragment field effect tend to reduce the HOMO–LUMO gap, promoting the charge transfer interaction that is significantly strengthened in the presence of EFs. Specifically, the energy gap is decreased by 0.82–1.40 eV due to the external EF and further reduced by 0.84–2.42 eV through molecular perturbations. The H₃P–C₆₀ complex is a notable example, where the energy gap is 4.28 eV in the deformed monomers and reduces to 0.46 eV when monomers H₃P and C₆₀ are put together under the EF. In the absence of EFs, intermolecular polarization also increases the HOMO energy of the Lewis base and lowers the LUMO energy of the nanostructures, thereby reducing the HOMO–LUMO gap, which is significantly larger than the value observed in the presence of EFs (Fig. S7†).

Fig. 3 “In situ” orbital correlation diagrams upon the formation of EF-driven dative bonds. The superscript “F” denotes fragments perturbed by the external EF, while block-localized monomers in the presence of EFs are prefixed with “BL-”.

The lowering of the LUMO energy under an EF may serve as a necessary condition for the EF-driven formation of dative bonds, as the HOMO energy of a Lewis base is relatively insensitive to EFs. Therefore, a variety of EF-driven dative bonds could be anticipated between Lewis acids and bases with substantial polarizabilities, beyond the prototypical cases we have discussed. EF-driven dative bonds can also be realized by modulating the barrier in a Lewis acid–base reaction, where the vdW complex typically serves as a fleeting intermediate.¹⁴⁴ Particularly, the barrier height reaches approximately 15 kcal mol⁻¹ for the transition from vdW interaction to a dative bond in specific cases,⁵⁶ where external electric fields could lower the barrier by promoting the orbital interactions, thereby facilitating the formation of EF-driven dative bonds.

The charge transfer interaction was further scrutinized using the decomposition scheme outlined in eqn (6). As presented in Fig. 4a, the charge transfer energy is predominantly contributed by the intrinsic component, which describes the stability gained from orbital mixing between perturbed fragments. The induced potential energy is also stabilizing, consistent with the increase in dipole moment caused by intermolecular orbital interactions (Fig. 4b). We estimated the induced potential energy by calculating the product of the field strength and the increment of the dipole moment. The estimated values are almost identical to the decomposition results (Fig. 4c). Hence, the induced potential energy can be attributed to the field–dipole interaction, without accounting for contributions from higher-order multipoles. In summary, the inter-fragment orbital mixing lowers the intrinsic energy of the complex and enlarges its dipole moment, leading to additional stability arising from the field–dipole interaction.

Fig. 4 Decomposition results of the charge transfer interaction energy (a), correlation between the dipole moments of the electron localized and delocalized states (b) and the relationship between the induced potential energies and the corresponding estimated values (c).

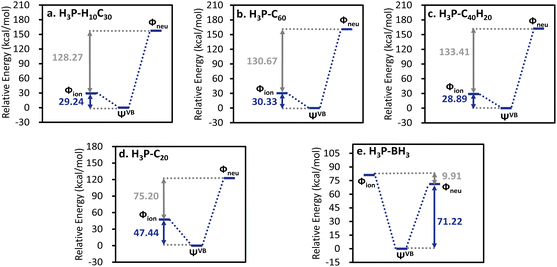
As mentioned above, ab initio VB theory can provide complementary information which is unavailable in MO theory. Here ab initio VB computations were performed to provide a chemically intuitive understanding for the EF-driven dative bonds. As shown in Fig. 5, the ionic structure (post-ET), in which lone pair electrons of phosphorus are shared between fragments, is significantly lower in energy than the neutral state (prior-ET) in all EF-driven cases. Similarly, the ionic state is the primary VB structure in H₃P-C₂₀. However, the energy difference between the neutral and ionic structures gets smaller in the H₃P-C₂₀ complex compared to the EF-driven cases. In the latter, the interaction between the significant dipole moment of the ionic state and the external EF further stabilizes the system. This primary role of the ionic structure is consistent with the positive Laplace values at BCPs, amount of charge transfer, and the significant charge transfer energies. Conversely, the neutral state is slightly lower in energy than the ionic structure in the prototypical P → B bond. Moreover, the insignificant energy difference between VB structures in H₃P-BH₃ leads to the highest resonance energy among all cases studied. In each EF-driven case, the active orbital of the electron acceptor is the hybrid orbital of the carbon atom at the bonding site, pointing towards the phosphorus atom and exhibits one nodal surface tangential to the curved surface formed by the molecular framework (Fig. S8†). Meanwhile, the active orbital of the H₃P molecule is its lone pair orbital. In summary, the active VB orbitals of the EF-driven dative bonds are strikingly similar to those of the reference systems.

Fig. 5 VB mixing diagram for the EF-driven dative bonds (a–c) and the reference H₃P-C₂₀ (d) and H₃P-BH₃ complexes (e), with the resonance energies (in blue) and the energy differences between VB structures (in grey) denoted.

4 Conclusion

The EF-driven P → C dative bonds on the concave surface of carbon-based nanostructures were proposed for their potential applications in the design of molecular machines. To this end, interactions between H₃P and nanostructures, including C₃₀H₁₀ buckybowls, C₆₀ fullerene, and C₄₀H₂₀ nanohoops, were studied theoretically. For comparison, conventional P → C and P → B bonds were also examined in the absence of EFs to identify the distinguishable characteristics of the EF-driven chemical bonds. In the absence of EFs, H₃P and nanostructures form vdW complexes. In contrast, P → C dative bonds were forged in the presence of EFs, as evidenced by the bond lengths, bond orders, bond force constants, and BCP points. Notably, negative Laplacian values at the BCPs of the EF-driven dative bonds indicated covalent characteristics, whereas positive values were found in the conventional P → B bond in H₃P-BH₃. The covalency was further supported by the amount of charges transferred from PH₃ to the nanostructure during the formation of the EF-driven dative bonds. These EF-driven dative bonds remained stable with no sign of dissociation in the AIMD simulations. All computed vibrational, carbon-13 NMR, and UV/vis spectra exhibited distinctive signals for the EF-driven dative bonds and these signals were absent in their vdW complexes. In summary, the external EF facilitates the formation of dative bonds with considerable covalency, deformations and distinctive spectral properties, indicating the potential of this interaction for designing molecular machines and smart materials.

BLW-ED analyses revealed that EF-driven dative bonds and the reference cases were all dominated by charge transfer interactions and further stabilized by polarization interaction. These stabilizing forces were offset by the repulsive frozen interaction ruled by the Pauli repulsion. Notably, the EF-driven dative bonds exhibited stronger charge transfer interactions than the conventional P → C bond in H₃P-C₂₀ and the prototypical P → B bond in H₃P-BH₃. The crucial charge transfer was further decomposed to distinguish the contributions from the intrinsic orbital mixing and the field–multipole interactions. Importantly, the inter-fragment orbital mixing dramatically lowers the intrinsic energy and governs the charge transfer interaction. Furthermore, orbital mixing also increases the dipole moment of the complex, leading to the strengthened field–dipole interaction. The “in situ” orbital correlation diagram was used to rationalize orbital interactions that solely occur in the presence of EFs. Both the external EF and the intermolecular field effect reduce the energy gap between the LUMO of the acceptor and the HOMO of the donor, facilitating intermolecular orbital mixings.

The covalency of the EF-driven dative bonds was further evidenced by ab initio VB calculations, where the primary VB structure was the ionic state, which depicts the electron sharing between interacting monomers. Similarly, the primary Lewis structure for the conventional P → C bond was also the ionic state. However, the energy difference between the ionic and neutral states was significantly lower in the H₃P–C₂₀ complex compared to the EF-driven cases, where the ionic states gained additional stabilization from the field–dipole interaction. The key distinction between the prototypical P → B bond and EF-driven cases, however, lies in their covalency. Interestingly, the neutral structure is more stable than the ionic form in H₃P-BH₃, indicating a close–shell interaction.

Data availability

The data that support the findings of this study are available in the ESI† of this article.

Author contributions

T. M.: visualization, investigation, and review and editing. X. W.: visualization and investigation. X. P.: resources. J. L.: resources. S. Y.: resources. Y. M.: supervision, methodology, review and editing. C. W.: supervision, conceptualization, writing of the original draft, review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

C. W. acknowledges the support from the Natural Science Foundation of China (grant 22073060). S. Y. acknowledges the support from the Natural Science Foundation of China (grant 22273054). This work was performed in part at the Joint School of Nanoscience and Nanoengineering, a member of the National Nanotechnology Coordinated Infrastructure (NNCI), which is supported by the National Science Foundation (grant ECCS2025462).

Notes and references

1. S. Shaik, D. Mandal and R. Ramanan, Oriented electric fields as future smart reagents in chemistry, Nat. Chem., 2016, 8, 1091–1098.
2. S. Shaik, My Vision of Electric-Field-Aided Chemistry in 2050, ACS Phys. Chem. Au, 2024, 4, 191–201.
3. M. Calvaresi, R. V. Martinez, N. S. Losilla, J. Martinez, R. Garcia and F. Zerbetto, Splitting CO₂ with Electric Fields: A Computational Investigation, J. Phys. Chem. Lett., 2010, 1, 3256–3260.
4. P. Papanikolaou and P. Karafiloglou, Investigating sigma bonds in an electric field from the Pauling's perspective: the behavior of Cl–X and H–X (X=C, Si) bonds, Theor. Chem. Acc., 2010, 126, 213–222.
5. L. Rincón, J. R. Mora, F. J. Torres and R. Almeida, On the activation of σ-bonds by electric fields: A Valence Bond perspective, Chem. Phys., 2016, 477, 1–7.
6. S. Sowlati-Hashjin and C. Matta, The chemical bond in external electric fields: energies, geometries, and vibrational Stark shifts of diatomic molecules, J. Chem. Phys., 2013, 139, 144101.
7. J. Stark, Observation of the Separation of Spectral Lines by an Electric Field, Nature, 1913, 92, 401.
8. J. Lu, Y. Song, F. Lei, X. Du, Y. Huo, S. Xu, C. Li, T. Ning, J. Yu and C. Zhang, Electric Field-Modulated Surface Enhanced Raman Spectroscopy by PVDF/Ag Hybrid, Sci. Rep., 2020, 10, 5269.
9. A. C. Aragonès, N. L. Haworth, N. Darwish, S. Ciampi, E. J. Mannix, G. G. Wallace, I. Diez-Perez and M. L. Coote, Electrostatic catalysis of a Diels–Alder reaction, Nature, 2016, 531, 88–91.
10. P. M. De Biase, F. Doctorovich, D. H. Murgida and D. A. Estrin, Electric field effects on the reactivity of heme model systems, Chem. Phys. Lett., 2007, 434, 121–126.
11. M. D. Esrafili, Electric field assisted activation of CO₂ over P-doped graphene: A DFT study, J. Mol. Graphics Modell., 2019, 90, 192–198.
12. C. Geng, J. Li, M. Schlangen, S. Shaik, X. Sun, N. Wang, T. Weiske, L. Yue, S. Zhou and H. Schwarz, Oriented external electric fields as mimics for probing the role of metal ions and ligands in the thermal gas-phase activation of methane, Dalton Trans., 2018, 47, 15271–15277.
13. C. Zhang, K. Ueno, A. Yamazaki, K. Yoshida, H. Moon, T. Mandai, Y. Umebayashi, K. Dokko and M. Watanabe, Chelate Effects in Glyme/Lithium Bis(trifluoromethanesulfonyl)amide Solvate Ionic Liquids. I. Stability of Solvate Cations and Correlation with Electrolyte Properties, J. Phys. Chem. B, 2014, 118, 5144–5153.
14. T. Stuyver, D. Danovich, J. Joy and S. Shaik, External electric field effects on chemical structure and reactivity, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1438.
15. H. R. Rasouli, J. Kim, N. Mehmood, A. Sheraz, M.-k. Jo, S. Song, K. Kang and T. S. Kasirga, Electric-Field-Induced Reversible Phase Transitions in a Spontaneously Ion-Intercalated 2D Metal Oxide, Nano Lett., 2021, 21, 3997–4005.
16. G. Cassone and F. Martelli, Electrofreezing of liquid water at ambient conditions, Nat. Commun., 2024, 15, 1856.
17. Z. Wang, T. Zhang, M. Ding, B. Dong, Y. Li, M. Chen, X. Li, J. Huang, H. Wang, X. Zhao, Y. Li, D. Li, C. Jia, L. Sun, H. Guo, Y. Ye, D. Sun, Y. Chen, T. Yang, J. Zhang, S. Ono, Z. Han and Z. Zhang, Electric-field control of magnetism in a few-layered van der Waals ferromagnetic semiconductor, Nat. Nanotechnol., 2018, 13, 554–559.
18. Y. Su, J. Liu, D. Yang, W. Hu, X. Jiang, Z. L. Wang and R. Yang, Electric Field-Assisted Self-Assembly of Diphenylalanine Peptides for High-Performance Energy Conversion, ACS Mater. Lett., 2023, 5, 2317–2323.
19. R. Francke, Self-assembly of molecules triggered by electricity, Nature, 2022, 603, 229–230.
20. R. Zhao, H. Zhang, R. Zhao, W. Liu, Q. Liu and H. Hu, Dynamic Cu(I)/Cu(II) Redox Shuttle for Maltose and Lactose Isomerization under Pulsed Electric Field, ACS Sustainable Chem. Eng., 2024, 12, 6232–6241.
21. B. Hu and J. Wen, Electric Field-Driven Dual-Rotation in Molecular Motors: Insights from Molecular Dynamics Simulations, Chem. Commun., 2025 10.1039/D4CC01408A , advance article.
22. Y. Han, C. Nickle, Z. Zhang, H. P. A. G. Astier, T. J. Duffin, D. Qi, Z. Wang, E. del Barco, D. Thompson and C. A. Nijhuis, Electric-field-driven dual-functional molecular switches in tunnel junctions, Nat. Mater., 2020, 19, 843–848.
23. Y. Xu, J. Xu, H. Liu and C. Yang, Electropumping of water in nanochannels using non-uniform electric fields, Chem. Eng. Sci., 2023, 267, 118325.
24. Z. Siwy and A. Fuliński, Fabrication of a Synthetic Nanopore Ion Pump, Phys. Rev. Lett., 2002, 89, 198103.
25. R. D. Astumian, How molecular motors work – insights from the molecular machinist's toolbox: the Nobel prize in Chemistry 2016, Chem. Sci., 2017, 8, 840–845.
26. G. Sun, T. Yang, J. Duan, Y. Zhang, M. Wang, R. Wang and C. Wang, Layer-by-layer N, P co-doped carbon materials with gradient electric field to suppress the shuttle effect for lithium sulfur batteries, J. Alloys Compd., 2021, 870, 159543.
27. H. J. Chandler, M. Stefanou, E. E. B. Campbell and R. Schaub, Li@C₆₀ as a multi-state molecular switch, Nat. Commun., 2019, 10, 2283.
28. J. Průša and M. Cifra, Molecular dynamics simulation of the nanosecond pulsed electric field effect on kinesin nanomotor, Sci. Rep., 2019, 9, 19721.
29. M. R. Hossan, D. Dutta, N. Islam and P. Dutta, Review: Electric field driven pumping in microfluidic device, Electrophoresis, 2018, 39, 702–731.
30. I. C.-Y. Hou, L. Li, H. Zhang and P. Naumov, Smart molecular crystal switches, Smart Mol., 2024, 2, e20230031.
31. Y. Lv, L. Bai, Q. Jin, S. Deng, X. Ma, F. Han, J. Wang, L. Zhang, L. Wu and X. Zhang, VSe₂/V₂C heterocatalyst with built-in electric field for efficient lithium-sulfur batteries: Remedies polysulfide shuttle and conversion kinetics, J. Energy Chem., 2024, 89, 397–409.
32. A. B. Farimani, M. Heiranian and N. R. Aluru, Nano-electro-mechanical pump: Giant pumping of water in carbon nanotubes, Sci. Rep., 2016, 6, 26211.
33. C. Foroutan-Nejad, V. Andrushchenko and M. Straka, Dipolar molecules inside C₇₀: an electric field-driven room-temperature single-molecule switch, Phys. Chem. Chem. Phys., 2016, 18, 32673–32677.
34. G. Cassone, J. Sponer, J. E. Sponer and F. Saija, Electrofreezing of Liquid Ammonia, J. Phys. Chem. Lett., 2022, 13, 9889–9894.
35. M. Juanes, R. T. Saragi, W. Caminati and A. Lesarri, The Hydrogen Bond and Beyond: Perspectives for Rotational Investigations of Non-Covalent Interactions, Chem.–Eur. J., 2019, 25, 11402–11411.
36. G. Cavallo, P. Metrangolo, R. Milani, T. Pilati, A. Priimagi, G. Resnati and G. Terraneo, The Halogen Bond, Chem. Rev., 2016, 116, 2478–2601.
37. A. Bauzá, T. J. Mooibroek and A. Frontera, Tetrel-Bonding Interaction: Rediscovered Supramolecular Force?, Angew. Chem., Int. Ed., 2013, 52, 12317–12321.
38. H. Sharma, B. C. Deka and P. K. Bhattacharyya, Behavior of potential energy surface of C–X bonds in presence of solvent and external electric field: A DFT study, J. Theor. Comput. Chem., 2016, 15, 1650051.
39. A. Das and E. Arunan, Unified classification of non-covalent bonds formed by main group elements: a bridge to chemical bonding, Phys. Chem. Chem. Phys., 2023, 25, 22583–22594.
40. S. Shaik, D. Danovich, J. M. Galbraith, B. Braïda, W. Wu and P. C. Hiberty, Charge-Shift Bonding: A New and Unique Form of Bonding, Angew. Chem., Int. Ed., 2020, 59, 984–1001.
41. S. Shaik, D. Danovich, B. Silvi, D. L. Lauvergnat and P. C. Hiberty, Charge-Shift Bonding—A Class of Electron-Pair Bonds That Emerges from Valence Bond Theory and Is Supported by the Electron Localization Function Approach, Chem.–Eur. J., 2005, 11, 6358–6371.
42. P. C. Hiberty, D. Danovich and S. Shaik, A Conversation on New Types of Chemical Bonds, Isr. J. Chem., 2022, 62, e202000114.
43. M. Kishimoto and T. Kubo, Long carbon–carbon bonds and beyond, Chem. Phys. Rev., 2024, 5, 031302.
44. A. Nandi and S. Kozuch, History and Future of Dative Bonds, Chem.–Eur. J., 2020, 26, 759–772.
45. A. Haaland, Covalent versus Dative Bonds to Main Group Metals, a Useful Distinction, Angew. Chem., Int. Ed., 1989, 28, 992–1007.
46. V. Jonas, G. Frenking and M. T. Reetz, Comparative Theoretical Study of Lewis Acid-Base Complexes of BH₃, BF₃, BCl₃, AlCl₃, and SO₂, J. Am. Chem. Soc., 1994, 116, 8741–8753.
47. D. Zhong and A. H. Zewail, Femtosecond dynamics of dative bonding: Concepts of reversible and dissociative electron transfer reactions, Proc. Natl. Acad. Sci. U. S. A., 1999, 96, 2602–2607.
48. J. Dillen and P. Verhoeven, The End of a 30-Year-Old Controversy? A Computational Study of the B−N Stretching Frequency of BH3−NH3 in the Solid State, J. Phys. Chem. A, 2003, 107, 2570–2577.
49. J. A. Plumley and J. D. Evanseck, Covalent and Ionic Nature of the Dative Bond and Account of Accurate Ammonia Borane Binding Enthalpies, J. Phys. Chem. A, 2007, 111, 13472–13483.
50. C. Lepetit, V. Maraval, Y. Canac and R. Chauvin, On the nature of the dative bond: Coordination to metals and beyond. The carbon case, Coord. Chem. Rev., 2016, 308, 59–75.
51. C. F. Pupim, A. J. L. Catão and A. López-Castillo, Boron–nitrogen dative bond, J. Mol. Model., 2018, 24, 283.
52. B. A. Smith and K. D. Vogiatzis, σ-Donation and π-Backdonation Effects in Dative Bonds of Main-Group Elements, J. Phys. Chem. A, 2021, 125, 7956–7966.
53. S. G. Shore and R. W. Parry, The crystalline compound ammonia-borane,¹H₃NBH₃, J. Am. Chem. Soc., 1955, 77, 6084–6085.
54. M. Lamanec, R. Lo, D. Nachtigallová, A. Bakandritsos, E. Mohammadi, M. Dračínský, R. Zbořil, P. Hobza and W. Wang, The Existence of a N → C Dative Bond in the C₆₀–Piperidine Complex, Angew. Chem., Int. Ed., 2021, 60, 1942–1950.
55. R. Lo, M. Lamanec, W. Wang, D. Manna, A. Bakandritsos, M. Dračínský, R. Zbořil, D. Nachtigallová and P. Hobza, Structure-directed formation of the dative/covalent bonds in complexes with C₇₀⋯piperidine, Phys. Chem. Chem. Phys., 2021, 23, 4365–4375.
56. R. Lo, D. Manna and P. Hobza, Tuning the P–C dative/covalent bond formation in R₃P–C₆₀ complexes by changing the R group, Chem. Commun., 2021, 57, 3363–3366.
57. R. Lo, D. Manna, M. Lamanec, W. Wang, A. Bakandritsos, M. Dračínský, R. Zbořil, D. Nachtigallová and P. Hobza, Addition Reaction between Piperidine and C₆₀ to Form 1,4-Disubstituted C₆₀ Proceeds through van der Waals and Dative Bond Complexes: Theoretical and Experimental Study, J. Am. Chem. Soc., 2021, 143, 10930–10939.
58. R. Lo, D. Manna and P. Hobza, P-Doped graphene–C₆₀ nanocomposite: a donor–acceptor complex with a P–C dative bond, Chem. Commun., 2022, 58, 1045–1048.
59. R. Tonner, F. Öxler, B. Neumüller, W. Petz and G. Frenking, Carbodiphosphoranes: The Chemistry of Divalent Carbon(0), Angew. Chem., Int. Ed., 2006, 45, 8038–8042.
60. F. Ramirez, N. B. Desai, B. Hansen and N. McKelvie, Hexaphenylcarbodiphosphorane, (C₆H₅)₃PCP(C₆H₅)₃, J. Am. Chem. Soc., 1961, 83, 3539–3540.
61. L. Zhao, M. Hermann, N. Holzmann and G. Frenking, Dative bonding in main group compounds, Coord. Chem. Rev., 2017, 344, 163–204.
62. E. N. Brothers, A. F. Izmaylov, G. E. Scuseria and K. N. Kudin, Analytically Calculated Polarizability of Carbon Nanotubes: Single Wall, Coaxial, and Bundled Systems, J. Phys. Chem. C, 2008, 112, 1396–1400.
63. D. S. Sabirov, Polarizability of C60 fullerene dimer and oligomers: the unexpected enhancement and its use for rational design of fullerene-based nanostructures with adjustable properties, RSC Adv., 2013, 3, 19430–19439.
64. E. Nestoros and M. C. Stuparu, Corannulene: a molecular bowl of carbon with multifaceted properties and diverse applications, Chem. Commun., 2018, 54, 6503–6519.
65. D. L. Cooper, P. B. Karadakov and T. Thorsteinsson, in Theor. Comput. Chem., ed. D. L. Cooper, Elsevier, Amsterdam, 2002, vol. 10.
66. G. A. Gallup, Valence Bond Methods: Theory and Applications, Cambridge University Press, Cambridge, 2002.
67. S. S. Shaik, P. C. Hiberty, A. Nemirowski and P. R. Schreiner, A Chemist's Guide to Valence Bond Theory, Wiley, Hoboken, New Jersey, 2008.
68. W. Wu, P. Su, S. Shaik and P. C. Hiberty, Classical Valence Bond Approach by Modern Methods, Chem. Rev., 2011, 111, 7557–7593.
69. Z. Chen and W. Wu, Ab initio valence bond theory: A brief history, recent developments, and near future, J. Chem. Phys., 2020, 153, 090902.
70. S. Shaik, R. Ramanan, D. Danovich and D. Mandal, Structure and reactivity/selectivity control by oriented-external electric fields, Chem. Soc. Rev., 2018, 47, 5125–5145.
71. A. A. Fiorillo and J. M. Galbraith, A Valence Bond Description of Coordinate Covalent Bonding, J. Phys. Chem. A, 2004, 108, 5126–5130.
72. Y. Mo, L. Song, W. Wu and Q. Zhang, Charge Transfer in the Electron Donor−Acceptor Complex BH3NH3, J. Am. Chem. Soc., 2004, 126, 3974–3982.
73. Y. Mo and S. D. Peyerimhoff, Theoretical analysis of electronic delocalization, J. Chem. Phys., 1998, 109, 1687–1697.
74. Y. Mo, L. Song, W. Wu, Z. Cao and Q. Zhang, Electronic delocalization: A quantitative study from modern ab initio valence bond theory, J. Theor. Comput. Chem., 2002, 01, 137–151.
75. Y. Mo, Geometrical optimization for strictly localized structures, J. Chem. Phys., 2003, 119, 1300–1306.
76. Y. Mo, L. Song and Y. Lin, Block-Localized Wavefunction (BLW) Method at the Density Functional Theory (DFT) Level, J. Phys. Chem. A, 2007, 111, 8291–8301.
77. H. Zhang, Z. Cao, W. Wu and Y. Mo, The Transition-Metal-Like Behavior of B₂(NHC)₂ in the Activation of CO: HOMO–LUMO Swap Without Photoinduction, Angew. Chem., Int. Ed., 2018, 57, 13076–13081.
78. C. Wang and Y. Mo, Classical Electrostatic Interaction Is the Origin for Blue-Shifting Halogen Bonds, Inorg. Chem., 2019, 58, 8577–8586.
79. X. Lin and Y. Mo, On the Bonding Nature in the Crystalline Tri-Thorium Cluster: Core-Shell Syngenetic σ-Aromaticity, Angew. Chem., Int. Ed., 2022, 61, e202209658.
80. Y. Mo, J. Gao and S. D. Peyerimhoff, Energy decomposition analysis of intermolecular interactions using a block-localized wave function approach, J. Chem. Phys., 2000, 112, 5530–5538.
81. Y. Mo, P. Bao and J. Gao, Energy decomposition analysis based on a block-localized wavefunction and multistate density functional theory, Phys. Chem. Chem. Phys., 2011, 13, 6760–6775.
82. Y. Mo, in The Chemical Bond: Fundamental Aspects of Chemical Bonding, Wiley-VCH Verlag GmbH & Co. KGaA, 2014, pp. 199–232,  DOI:10.1002/9783527664696.ch6.
83. X. Peng, L. Chen, J. Dang, C. Wang and Y. Mo, How External Electric Field Modulates the Rotation Energy Profiles of Dipolar Dopants Inside C₇₀: A Theoretical Interpretation with Electrostatic Shielding Effect Incorporated, ChemNanoMat, 2022, 8, e202200405.
84. L. Chen, Q. Feng, C. Wang, S. Yin and Y. Mo, Classical Electrostatics Remains the Driving Force for Interanion Hydrogen and Halogen Bonding, J. Phys. Chem. A, 2021, 125, 10428–10438.
85. K. Kitaura and K. Morokuma, A new energy decomposition scheme for molecular interactions within the Hartree-Fock approximation, Int. J. Quantum Chem., 1976, 10, 325–340.
86. T. Ziegler and A. Rauk, On the calculation of bonding energies by the Hartree Fock Slater method, Theor. Chim. Acta, 1977, 46, 1–10.
87. K. Morokuma and K. Kitaura, in Chemical Applications of Atomic and Molecular Electrostatic Potentials: Reactivity, Structure, Scattering, and Energetics of Organic, Inorganic, and Biological Systems, ed. P. Politzer and D. G. Truhlar, Springer US, Boston, MA, 1981,  DOI:10.1007/978-1-4757-9634-6_10, pp. 215–242.
88. B. Jeziorski, R. Moszynski and K. Szalewicz, Perturbation Theory Approach to Intermolecular Potential Energy Surfaces of van der Waals Complexes, Chem. Rev., 1994, 94, 1887–1930.
89. W. Chen and M. S. Gordon, Energy Decomposition Analyses for Many-Body Interaction and Applications to Water Complexes, J. Phys. Chem., 1996, 100, 14316–14328.
90. M. P. Mitoraj, A. Michalak and T. Ziegler, A Combined Charge and Energy Decomposition Scheme for Bond Analysis, J. Chem. Theory Comput., 2009, 5, 962–975.
91. P. Su and H. Li, Energy decomposition analysis of covalent bonds and intermolecular interactions, J. Chem. Phys., 2009, 131, 014102.
92. K. Szalewicz, Symmetry-adapted perturbation theory of intermolecular forces, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254–272.
93. P. Su, H. Liu and W. Wu, Free energy decomposition analysis of bonding and nonbonding interactions in solution, J. Chem. Phys., 2012, 137, 034111.
94. P. Su, Z. Jiang, Z. Chen and W. Wu, Energy Decomposition Scheme Based on the Generalized Kohn–Sham Scheme, J. Phys. Chem. A, 2014, 118, 2531–2542.
95. P. Su, Z. Tang and W. Wu, Generalized Kohn-Sham energy decomposition analysis and its applications, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2020, 10, e1460.
96. Y. Mao, M. Loipersberger, K. J. Kron, J. S. Derrick, C. J. Chang, S. M. Sharada and M. Head-Gordon, Consistent inclusion of continuum solvation in energy decomposition analysis: theory and application to molecular CO₂ reduction catalysts, Chem. Sci., 2021, 12, 1398–1414.
97. P. Su, in Exploring Chemical Concepts Through Theory and Computation, ed. S. Liu, 2024, pp. 433–454,  DOI:10.1002/9783527843435.ch17.
98. E. Miller, B. K. Mai, J. A. Read, W. C. Bell, J. S. Derrick, P. Liu and F. D. Toste, A Combined DFT, Energy Decomposition, and Data Analysis Approach to Investigate the Relationship Between Noncovalent Interactions and Selectivity in a Flexible DABCOnium/Chiral Anion Catalyst System, ACS Catal., 2022, 12, 12369–12385.
99. Y. Mao, P. R. Horn and M. Head-Gordon, Energy decomposition analysis in an adiabatic picture, Phys. Chem. Chem. Phys., 2017, 19, 5944–5958.
100. L. Chen, J. Dang, J. Du, C. Wang and Y. Mo, Hydrogen and Halogen Bonding in Homogeneous External Electric Fields: Modulating the Bond Strengths, Chem.–Eur. J., 2021, 27, 14042–14050.
101. M. O. Sinnokrot and C. D. Sherrill, Substituent Effects in π−π Interactions: Sandwich and T-Shaped Configurations, J. Am. Chem. Soc., 2004, 126, 7690–7697.
102. Y. Geng, T. Takatani, E. G. Hohenstein and C. D. Sherrill, Accurately Characterizing the π−π Interaction Energies of Indole−Benzene Complexes, J. Phys. Chem. A, 2010, 114, 3576–3582.
103. C. D. Sherrill, Energy component analysis of π interactions, Acc. Chem. Res., 2013, 46, 1020–1028.
104. I. Mata, E. Molins, I. Alkorta and E. Espinosa, Effect of an external electric field on the dissociation energy and the electron density properties: The case of the hydrogen bonded dimer HF⋯HF_a), J. Chem. Phys., 2009, 130, 044104.
105. Atoms in Molecules: A Quantum Theory, ed. R. F. W. Bader, Oxford University Press, 1990.
106. P. Wu, R. Chaudret, X. Hu and W. Yang, Noncovalent Interaction Analysis in Fluctuating Environments, J. Chem. Theory Comput., 2013, 9, 2226–2234.
107. E. D. Glendening, C. R. Landis and F. Weinhold, NBO 7.0: New vistas in localized and delocalized chemical bonding theory, J. Comput. Chem., 2019, 40, 2234–2241.
108. F. Weinhold, C. R. Landis and E. D. Glendening, What is NBO analysis and how is it useful?, Int. Rev. Phys. Chem., 2016, 35, 399–440.
109. E. D. Glendening, C. R. Landis and F. Weinhold, Natural bond orbital methods, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2012, 2, 1–42.
110. F. Weinhold and C. R. Landis, Natural bond orbitals and extensions of localizend bonding concepts, Chem. Educ. Res. Pract., 2001, 2, 91–104.
111. A. E. Reed, L. A. Curtiss and F. Weinhold, Intermolecular interactions from a natural bond orbital, donor-acceptor viewpoint, Chem. Rev., 1988, 88, 899–926.
112. P. Geerlings, F. De Proft and W. Langenaeker, Conceptual Density Functional Theory, Chem. Rev., 2003, 103, 1793–1874.
113. D. Chakraborty and P. K. Chattaraj, Conceptual density functional theory based electronic structure principles, Chem. Sci., 2021, 12, 6264–6279.
114. Conceptual Density Functional Theory: Towards a New Chemical Reactivity Theory, ed. S. Liu, Wiley-VCH, Weinheim, Germany, 2022.
115. P. Geerlings, E. Chamorro, P. K. Chattaraj, F. De Proft, J. L. Gázquez, S. Liu, C. Morell, A. Toro-Labbé, A. Vela and P. Ayers, Conceptual density functional theory: status, prospects, issues, Theor. Chem. Acc., 2020, 139, 36.
116. E. Kraka, M. Quintano, H. W. La Force, J. J. Antonio and M. Freindorf, The Local Vibrational Mode Theory and Its Place in the Vibrational Spectroscopy Arena, J. Phys. Chem. A, 2022, 126, 8781–8798.
117. E. Kraka, W. Zou and Y. Tao, Decoding chemical information from vibrational spectroscopy data: Local vibrational mode theory, Wiley Interdiscip. Rev. Comput. Mol. Sci., 2020, 10, e1480.
118. F. Wang and D. P. Chong, Electronic structure study of H₃BXH₃ (X=B, N and P) as hydrogen storage materials using calculated NMR and XPS spectra, Aust. J. Chem., 2023, 76, 854–863.
119. C. Adamo and V. Barone, Toward reliable density functional methods without adjustable parameters: The PBE0 model, J. Chem. Phys., 1999, 110, 6158–6170.
120. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
121. Y. Zhao and D. G. Truhlar, The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals, Theor. Chem. Acc., 2008, 120, 215–241.
122. J.-D. Chai and M. Head-Gordon, Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections, Phys. Chem. Chem. Phys., 2008, 10, 6615–6620.
123. F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: Design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
124. F. Weigend, Hartree–Fock exchange fitting basis sets for H to Rn, J. Comput. Chem., 2008, 29, 167–175.
125. A. Alessandro, M. F. Torre, K. Mràzikovà, F. Saija, S. Trusso, J. Xie, M. Tommasini and G. Cassone, Hydrogen Bonds under Electric Fields with Quantum Accuracy, ChemRxiv., 2025, preprint,  DOI:10.26434/chemrxiv-2025-v69sh.
126. M. F. Torre, A. Amadeo, G. Cassone, M. Tommasini, K. Mráziková and F. Saija, Water Dimer under Electric Fields: An Ab Initio Investigation up to Quantum Accuracy, J. Phys. Chem. A, 2024, 128, 5490–5499.
127. M. W. Schmidt, K. K. Baldridge, J. A. Boatz, S. T. Elbert, M. S. Gordon, J. H. Jensen, S. Koseki, N. Matsunaga, K. A. Nguyen, S. Su, T. L. Windus, M. Dupuis and J. A. Montgomery Jr, General atomic and molecular electronic structure system, J. Comput. Chem., 1993, 14, 1347–1363.
128. W. Humphrey, A. Dalke and K. Schulten, VMD: Visual molecular dynamics, J. Mol. Graphics, 1996, 14, 33–38.
129. I. Mayer, Charge, bond order and valence in the AB initio SCF theory, Chem. Phys. Lett., 1983, 97, 270–274.
130. I. Mayer, Bond order and valence: Relations to Mulliken's population analysis, Int. J. Quantum Chem., 1984, 26, 151–154.
131. A. E. Reed, R. B. Weinstock and F. Weinhold, Natural population analysis, J. Chem. Phys., 1985, 83, 735–746.
132. T. Lu and F. Chen, Multiwfn: A multifunctional wavefunction analyzer, J. Comput. Chem., 2012, 33, 580–592.
133. T. Lu and Q. Chen, Independent gradient model based on Hirshfeld partition: A new method for visual study of interactions in chemical systems, J. Comput. Chem., 2022, 43, 539–555.
134. D. Cremer, A. Wu, A. Larsson and E. Kraka, Some Thoughts about Bond Energies, Bond Lengths, and Force Constants, J. Mol. Model., 2000, 6, 396–412.
135. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An electronic structure and molecular dynamics software package – Quickstep: Efficient and accurate electronic structure calculations, J. Chem. Phys., 2020, 152, 194103.
136. J. VandeVondele and J. Hutter, Gaussian basis sets for accurate calculations on molecular systems in gas and condensed phases, J. Chem. Phys., 2007, 127, 114105.
137. J. S. Rowlinson, The Maxwell–Boltzmann distribution, Mol. Phys., 2005, 103, 2821–2828.
138. K. Zhou and B. Liu, in Molecular Dynamics Simulation, ed. K. Zhou and B. Liu, Elsevier, 2022, pp. 67–96,  DOI:10.1016/B978-0-12-816419-8.00008-8.
139. E. Runge and E. K. U. Gross, Density-Functional Theory for Time-Dependent Systems, Phys. Rev. Lett., 1984, 52, 997–1000.
140. G. Barone, D. Duca, A. Silvestri, L. Gomez-Paloma, R. Riccio and G. Bifulco, Determination of the Relative Stereochemistry of Flexible Organic Compounds by Ab Initio Methods: Conformational Analysis and Boltzmann-Averaged GIAO 13C NMR Chemical Shifts, Chem.–Eur. J., 2002, 8, 3240–3245.
141. G. Barone, L. Gomez-Paloma, D. Duca, A. Silvestri, R. Riccio and G. Bifulco, Structure Validation of Natural Products by Quantum-Mechanical GIAO Calculations of 13C NMR Chemical Shifts, Chem.–Eur. J., 2002, 8, 3233–3239.
142. S. G. Smith and J. M. Goodman, Assigning Stereochemistry to Single Diastereoisomers by GIAO NMR Calculation: The DP4 Probability, J. Am. Chem. Soc., 2010, 132, 12946–12959.
143. G. Cassone, Nuclear Quantum Effects Largely Influence Molecular Dissociation and Proton Transfer in Liquid Water under an Electric Field, J. Phys. Chem. Lett., 2020, 11, 8983–8988.
144. W.-C. Liu and F. P. Gabbaï, Characterization of a Lewis adduct in its inner and outer forms, Science, 2024, 385, 1184–1188.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc01701g

---