Machine learning workflows beyond linear models in low-data regimes

Abstract

Data-driven methodologies are transforming chemical research by providing chemists with digital tools that accelerate discovery and promote sustainability. In this context, non-linear machine learning algorithms are among the most disruptive technologies in the field and have proven effective for handling large datasets. However, in data-limited scenarios, linear regression has traditionally prevailed due to its simplicity and robustness, while non-linear models have been met with skepticism over concerns related to interpretability and overfitting. In this study, we introduce ready-to-use, automated workflows designed to overcome these challenges. These frameworks mitigate overfitting through Bayesian hyperparameter optimization by incorporating an objective function that accounts for overfitting in both interpolation and extrapolation. Benchmarking on eight diverse chemical datasets, ranging from 18 to 44 data points, demonstrates that when properly tuned and regularized, non-linear models can perform on par with or outperform linear regression. Furthermore, interpretability assessments and de novo predictions reveal that non-linear models capture underlying chemical relationships similarly to their linear counterparts. Ultimately, the automated non-linear workflows presented have the potential to become valuable tools in a chemist's toolbox for studying problems in low-data regimes alongside traditional linear models.

---

Introduction

Data-driven approaches have become increasingly popular due to their ability to save time, effort, and resources, all while promoting sustainability through digitalization.¹ In the field of chemistry, machine learning (ML) has significantly impacted the exploration of chemical spaces and the prediction of molecular properties and reaction outcomes.² These advancements have led to substantial progress in various areas,³ including drug discovery,^4,5 materials science,^6,7 chemical synthesis,^8–11 and catalyst development.^12,13

However, modeling small datasets in chemical research presents inherent challenges. Such datasets are particularly susceptible to underfitting, where models fail to capture underlying relationships, and overfitting, where models overly adapt to data by capturing noise or irrelevant patterns.¹⁴ These issues stem from the limited number of data points, the complexity of algorithms relative to dataset size, and the presence of noise, all of which hinder a model's ability to generalize effectively.¹⁵

Multivariate linear regression (MVL) is arguably the most used method in low-data scenarios due to its simplicity, robustness, and consistent performance with small datasets.¹⁶ MVL models often present a bias-variance tradeoff that helps mitigate overfitting while providing intuitive interpretability.¹⁴ Although more advanced ML algorithms like random forests (RF), gradient boosting (GB), and neural networks (NN) can achieve higher predictive accuracy,^17,18 their effectiveness in low-data scenarios is often limited by their sensitivity to overfitting and difficult interpretation.¹⁹ These models also require careful hyperparameter tuning and regularization techniques to generalize effectively.^20–22

To fully harness the capabilities of non-linear ML algorithms in low-data scenarios, it is essential to address these challenges. To this end, we have developed a fully automated workflow integrated into the ROBERT software. The approach is specifically designed to mitigate overfitting, reduce human intervention, eliminate biases in model selection, and enhance the interpretability of complex models. Our goal is to demonstrate that, even in low-data regimes, non-linear algorithms can be as effective as MVL when properly tuned and regularized. This new workflow not only broadens the scope of ML applications in chemistry but also aims to incorporate non-linear algorithms as part of the chemists' toolbox for studying low-data scenarios (Fig. 1).

Fig. 1 Traditional conceptions of linear and non-linear regression models for low-data regimes.

Discussion

Adapting non-linear ML workflows for small datasets

Recently, we developed ROBERT, a program that enables users to develop ML models automatically from a CSV database by performing data curation, hyperparameter optimization, model selection, and evaluation. It generates a comprehensive PDF report that includes key information such as performance metrics, cross-validation results, feature importance, and outlier detection, along with detailed guidelines to ensure reproducibility and transparency.

In line with previous studies,²³ we observed that the most limiting factor in applying non-linear models to low-data regimes is overfitting. Even though we aimed to maximize validation performance across multiple train-validation splits during hyperparameter optimization, we often observed a significant degree of overfitting in databases with fewer than 50 data points when using non-linear algorithms.

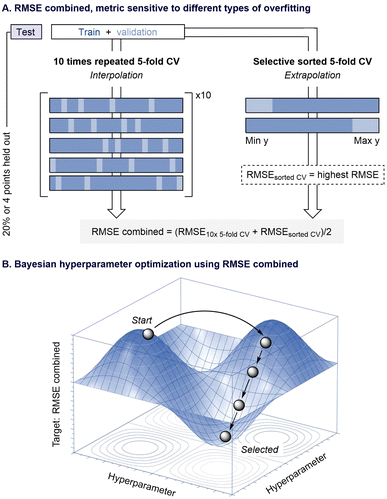
A wide array of techniques has been designed to measure overfitting, with CV being one of the most widely used.²⁴ In this context, introducing similar techniques during hyperparameter optimization should help reduce overfitting in the selected model. To test this hypothesis, we redesigned the program's hyperparameter optimization to use a combined Root Mean Squared Error (RMSE) calculated from different CV methods (Fig. 2A). This metric evaluates a model's generalization capability by averaging both interpolation and extrapolation CV performance. Interpolation is tested using a 10-times repeated 5-fold CV (10× 5-fold CV) process on the training and validation data, while extrapolation is assessed via a selective sorted 5-fold CV approach. This method sorts and partitions the data based on the target value (y) and considers the highest RMSE between the top and bottom partitions, a common practice for evaluating extrapolative performance.^25,26 In principle, this dual approach should not only identify models that perform well during training but also filter out those models that struggle with unseen data.

Fig. 2 (A) RMSE combined as a metric to detect different types of overfitting through 10× 5-fold CV and sorted CV schemes. (B) Bayesian optimization workflow using RMSE combined for hyperparameter tuning.

Using Bayesian optimization,^27,28 the new version of ROBERT systematically tunes hyperparameters using the combined RMSE metric as its objective function. As illustrated in Fig. 2B, this iterative exploration of the hyperparameter space consistently reduces the combined RMSE score, ensuring that the resulting model minimizes overfitting as much as possible. One optimization is performed for each selected algorithm, and the model with the best combined RMSE is used in the subsequent step of the workflow. Additionally, to prevent data leakage,²⁹ the methodology reserves 20% of the initial data (or a minimum of four data points) as an external test set, which is evaluated after hyperparameter optimization. The choice of the test set split is set to an “even” distribution by default, ensuring balanced representation of the target values. This approach helps maintain model generalizability, especially in cases of imbalanced datasets, while preventing overrepresentation of certain data ranges in the test set.

Benchmarking the workflows

The effectiveness of these new workflows in preventing overfitting in low-data scenarios was assessed using eight datasets ranging from 18 to 44 data points. The selected examples include datasets from Liu (A),³⁰ Milo (B),³¹ Doyle (F),³² Sigman (C, E, H),^33–35 and Paton (D),³⁶ where originally only MVL algorithms were tested (Fig. 3). For A, F, and H, we employed the same descriptors as those used in the original publications to ensure consistency with previous studies. For B, C, D, E, and G, we utilized the steric and electronic descriptors introduced by Cavallo et al. in their study,²⁶ where they reanalyzed previous datasets using MVL with new descriptors. In all cases (A–H), the same set of descriptors was used to train both linear and non-linear models, and the results are obtained through a single command line (Table S2†).

Fig. 3 (A–H) Overview of the chemical reactions and datasets explored, showing the number of data points and descriptors used. Bottom panels: scaled RMSE values across models for (left) 10× 5-fold CV and (right) external test sets, highlighting the top-performing models for each dataset. Bar order: RF, GB NN, and MVL.

The performance of three non-linear algorithms, RF, GB, and NN, was evaluated against MVL using scaled RMSE, which is expressed as a percentage of the target value range and helps interpret model performance relative to the range of predictions. To ensure fair comparisons while evaluating the train and validation set results, no specific train-validation splits were considered, as metrics can heavily depend on the selected split.³⁷ Instead, we used 10× 5-fold CV, which mitigates splitting effects and human bias. To further avoid bias, the external test sets were selected using a systematic method that evenly distributes y values across the prediction range.

Promisingly, the 10× 5-fold CV results show that the non-linear NN algorithm produces competitive results compared to the classic MVL model (Fig. 3, bottom-left). The NN model performs as well as or better than MVL for half of the examples (D, E, F and H), which range from 21 to 44 data points. Similarly, the best results for predicting external test sets are achieved using non-linear algorithms in five examples (A, C, F, G and H), with dataset sizes between 19 and 44 points (Fig. 3, bottom-right). Overall, these results support the inclusion of non-linear algorithms alongside MVL in data-driven approaches for small datasets.

Considering the widespread use of RF in chemistry,³⁸ it is noteworthy that this algorithm yielded the best results in only one case. This may be a consequence of introducing an extrapolation term during hyperoptimization, as tree-based models are known to have limitations for extrapolating beyond the training data range.³⁹ However, further analysis revealed that including this term leads to better models, as it prevents the occurrence of large errors in some of the examples (Fig. S1–9†). Based on the results, the higher errors observed for RF in examples A–H are mitigated and no longer represent a serious limitation when larger databases are used (Fig. S10 and S11†). See also the Evaluating combined metric for BO and dataset size section of the ESI† for additional discussion.

To further enhance algorithm evaluation, a new scoring system was developed on a scale of ten (Fig. 4A). The score is provided with the PDF report that ROBERT generates after each analysis and is based on three key aspects: predictive ability and overfitting, prediction uncertainty, and detection of spurious predictions.

Fig. 4 (A) Calculation of the updated ROBERT score. (B) Scores for examples A–H.

The first component is the most important, accounting for up to eight points. It includes (1 and 2) evaluating predictions from the 10× 5-fold CV and external test set using scaled RMSE, (3) assessing the difference between the two scaled RMSE values to detect overfitting, and (5) measuring the model's extrapolation ability using the lowest and highest folds in a sorted CV (Fig. 4A, top). The second component assesses prediction uncertainty by analyzing the average standard deviation (SD) of the predicted values obtained in the different CV repetitions (4). The final component identifies potentially flawed models by evaluating RMSE differences in the 10× 5-fold CV after applying data modifications such as y-shuffling⁴⁰ and one-hot encoding,⁴¹ and using a baseline error based on the y-mean test (6). A comprehensive explanation of the score is included in the ROBERT score section of the ESI† and in the ROBERT documentation.⁴² This scoring framework ensures that models are evaluated based on their predictive ability, level of overfitting, consistency of predictions, and robustness against flawed models.

Fig. 4B presents the ROBERT scores for the eight datasets from Fig. 3. Even under this more critical and restrictive evaluation method, non-linear algorithms perform as well as or better than MVL in five examples (C, D, E, F and G). These results align with previous findings and further support the inclusion of non-linear workflows alongside MVL in model selection.

Interpretability and de novo predictions of non-linear models

Next, we evaluated the interpretability and de novo prediction accuracy of linear and non-linear algorithms using example H.³³ In the original study, the authors used an MVL model to estimate reaction rate constants, ln(k) (Fig. 5). The most influential descriptor was the electronic parameter NBO_(C) on the carboxylate carbon with a coefficient of −1.37, followed by the Sterimol parameter B₁ of the amine reagent (−0.85), the buried volume V_bur around the carboxylate carbon (−0.71), and the frequency of the C=O bond in the intermediate product (ν_(C=O), +0.63). The first three descriptors have negative coefficients and an inverse relationship with ln(k), while ν_(C=O) has a positive coefficient and a direct correlation.

Fig. 5 Comparison of the original MVL equation with the SHAP analysis of the new NN model.

First, to evaluate the interpretability of the NN algorithm, we assessed whether it captures the same underlying relationships as the MVL model using SHAP analysis.⁴³ On the left side of the SHAP summary plot for the NN model, the descriptors are ordered from most important at the top to least important at the bottom, exactly mirroring the MVL model's findings. Similarly, pink and blue dots on the left side of the plot indicate that both MVL and NN identified the same inverse and direct correlations with the target value (+ and − symbols in the dashed line box, Fig. 5). These findings suggest that both linear and non-linear models capture similar data trends. It is important to note that SHAP uses local linear models to approximate the decision-making process of the NN and therefore does not directly provide information on the NN's internal structure.⁴⁴

Additionally, we compared the predictive accuracy of MVL and NN algorithms on the de novo molecule targets used in case H, using the values reported in the original study as the MVL baseline (Fig. 6). The RMSE values obtained for both models are nearly identical (5.32 and 5.31 M⁻¹ min⁻¹), demonstrating that a non-linear model can perform as well as the original MVL model.

Fig. 6 Predictive accuracy of MVL and NN models for de novo targets.

Conclusions

This work presents ready-to-use nonlinear ML workflows designed to mitigate overfitting through Bayesian hyperparameter optimization by incorporating an objective function that accounts for overfitting in both interpolation and extrapolation. Benchmarking on eight chemical datasets, ranging from 18 to 44 data points, suggests that when properly tuned and regularized, non-linear models perform on par with or outperform MVL models.

A scoring system was developed to evaluate models beyond traditional metrics, assigning a score out of 10. This score accounts for various factors, including overfitting, predictive ability, uncertainty, and the detection of spurious results.

Interpretability assessments using SHAP analysis reveal that non-linear models capture underlying chemical relationships similarly to their linear counterparts. Furthermore, both model types lead to analogous de novo predictions, suggesting their potential utility in chemical discovery when using small databases.

Overall, the automated non-linear workflows presented have the potential to become part of a chemist's toolbox for studying problems in low-data regimes. These techniques provide alternative algorithms that can be used alongside traditional linear models in data-driven studies.

Data availability

All protocols followed in this work are detailed in the ESI.† For each representation shown in the manuscript, we have included tables with their raw values. The input databases used and PDF reports from ROBERT, containing comprehensive information about the workflows, are also available in Zenodo (https://doi.org/10.5281/zenodo.14834558).

Author contributions

D. D. G. executed code, analyzed data, created the figures and wrote the manuscript. M. S. S. provided data, conceptualized ideas, and wrote the manuscript. J. V. A.-R. conceived the idea, supervised the study, generated code, and wrote the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

J. V. A.-R. and D. D. acknowledge Gobierno de Aragón-Fondo Social Europeo (Research Group E07_23R), the State Research Agency of Spain (MCIN/AEI/10.13039/501100011033/FEDER, UE) for financial support (PID2022-140159NA-I00) and the European Union's Recovery and Resilience Facility-Next Generation (MMT24-ISQCH-01) in the framework of the General Invitation of the Spanish Government's public business entity Red.es to participate in talent attraction and retention programmes within Investment 4 of Component 19 of the Recovery, Transformation and Resilience Plan (MOMENTUM, MMT24-ISQCH-01).

References

1. V. Zuin Zeidler, Science, 2024, 384, eadq3537.
2. E. M. Williamson and R. L. Brutchey, Inorg. Chem., 2023, 62, 16251–16262.
3. D. Dalmau and J. V. Alegre-Requena, Trends Chem., 2024, 6, 459–469.
4. J. Peña-Guerrero, P. A. Nguewa and A. T. García-Sosa, WIREs Comput. Mol. Sci., 2021, 11, e1513.
5. K. Batra, K. M. Zorn, D. H. Foil, E. Minerali, V. O. Gawriljuk, T. R. Lane and S. Ekins, J. Chem. Inf. Model., 2021, 61, 2641–2647.
6. C. M. Collins, L. M. Daniels, Q. Gibson, M. W. Gaultois, M. Moran, R. Feetham, M. J. Pitcher, M. S. Dyer, C. Delacotte, M. Zanella, C. A. Murray, G. Glodan, O. Pérez, D. Pelloquin, T. D. Manning, J. Alaria, G. R. Darling, J. B. Claridge and M. J. Rosseinsky, Angew. Chem., Int. Ed., 2021, 60, 16457–16465.
7. P. Karande, B. Gallagher and T. Y.-J. Han, Chem. Mater., 2022, 34, 7650–7665.
8. Y. Xie, C. Zhang, X. Hu, C. Zhang, S. P. Kelley, J. L. Atwood and J. Lin, J. Am. Chem. Soc., 2020, 142, 1475–1481.
9. P. M. Pflüger and F. Glorius, Angew. Chem., Int. Ed., 2020, 59, 18860–18865.
10. J. C. A. Oliveira, J. Frey, S.-Q. Zhang, L.-C. Xu, X. Li, S.-W. Li, X. Hong and L. Ackermann, Trends Chem., 2022, 4, 863–885.
11. J. J. Dotson, L. van Dijk, J. C. Timmerman, S. Grosslight, R. C. Walroth, F. Gosselin, K. Püntener, K. A. Mack and M. S. Sigman, J. Am. Chem. Soc., 2023, 145, 110–121.
12. Y. T. Boni, R. C. Cammarota, K. Liao, M. S. Sigman and H. M. L. Davies, J. Am. Chem. Soc., 2022, 144, 15549–15561.
13. T. Williams, K. McCullough and J. A. Lauterbach, Chem. Mater., 2020, 32, 157–165.
14. H. Shalit Peleg and A. Milo, Angew. Chem., Int. Ed., 2023, 62, e202219070.
15. D. M. Hawkins, J. Chem. Inf. Comput. Sci., 2004, 44, 1–12.
16. B. C. Haas, D. Kalyani and M. S. Sigman, Sci. Adv., 2025, 11, eadt3013.
17. Z. Zhou, C. Qiu and Y. Zhang, Sci. Rep., 2023, 13, 22420.
18. S. Chowdhury, Y. Lin, B. Liaw and L. Kerby, in 2022 International Conference on Intelligent Data Science Technologies and Applications (IDSTA), IEEE, San Antonio, TX, USA, 2022, pp. 17–25.
19. A. Assis, J. Dantas and E. Andrade, Angew. Chem., Int. Ed., 2025, 11, 1.
20. L. Barreñada, P. Dhiman, D. Timmerman, A.-L. Boulesteix and B. Van Calster, Diagn. Progn. Res., 2024, 8, 14.
21. O. A. Montesinos López, A. Montesinos López and J. Crossa, in Multivariate Statistical Machine Learning Methods for Genomic Prediction, Springer International Publishing, Cham, 2022, pp. 109–139.
22. J. A Ilemobayo, O. Durodola, O. Alade, O. J. Awotunde, A. T. Olanrewaju, O. Falana, A. Ogungbire, A. Osinuga, D. Ogunbiyi, A. Ifeanyi, I. E Odezuligbo and O. E Edu, J. Eng. Res. Rep., 2024, 26, 388–395.
23. D. Dalmau and J. V. Alegre-Requena, WIREs Comput. Mol. Sci., 2024, 14, e1733.
24. P. Refaeilzadeh, L. Tang and H. Liu, in Encyclopedia of Database Systems, ed. L. Liu and M. T. Özsu, Springer, US, Boston, MA, 2009, pp. 532–538.
25. Z. Xiong, Y. Cui, Z. Liu, Y. Zhao, M. Hu and J. Hu, Comput. Mater. Sci., 2020, 171, 109203.
26. Z. Cao, L. Falivene, A. Poater, B. Maity, Z. Zhang, G. Takasao, S. B. Sayed, A. Petta, G. Talarico, R. Oliva and L. Cavallo, Cell Rep. Phys. Sci., 2025, 6, 102348.
27. D. R. Jones, M. Schonlau and W. J. Welch, J. Global Optim., 1998, 13, 455–492.
28. F. Nogueira, Bayesian Optimization: Open source constrained global optimization tool for Python, 2014, https://github.com/bayesian-optimization/BayesianOptimization.
29. N. Artrith, K. T. Butler, F.-X. Coudert, S. Han, O. Isayev, A. Jain and A. Walsh, Nat. Chem., 2021, 13, 505–508.
30. C. Fang, M. Fantin, X. Pan, K. De Fiebre, M. L. Coote, K. Matyjaszewski and P. Liu, J. Am. Chem. Soc., 2019, 141, 7486–7497.
31. V. Dhayalan, S. C. Gadekar, Z. Alassad and A. Milo, Nat. Chem., 2019, 11, 543–551.
32. S. H. Lau, M. A. Borden, T. J. Steiman, L. S. Wang, M. Parasram and A. G. Doyle, J. Am. Chem. Soc., 2021, 143, 15873–15881.
33. B. C. Haas, A. E. Goetz, A. Bahamonde, J. C. McWilliams and M. S. Sigman, Proc. Natl. Acad. Sci. U.S.A., 2022, 119, e2118451119.
34. P. S. Engl, C. B. Santiago, C. P. Gordon, W.-C. Liao, A. Fedorov, C. Copéret, M. S. Sigman and A. Togni, J. Am. Chem. Soc., 2017, 139, 13117–13125.
35. Y. Park, Z. L. Niemeyer, J.-Q. Yu and M. S. Sigman, Organometallics, 2018, 37, 203–210.
36. T. Piou, F. Romanov-Michailidis, M. Romanova-Michaelides, K. E. Jackson, N. Semakul, T. D. Taggart, B. S. Newell, C. D. Rithner, R. S. Paton and T. Rovis, J. Am. Chem. Soc., 2017, 139, 1296–1310.
37. G. C. Cawley and N. L. C. Talbot, J. Mach. Learn. Res., 2010, 11, 2079–2107.
38. V. Svetnik, A. Liaw, C. Tong, J. C. Culberson, R. P. Sheridan and B. P. Feuston, J. Chem. Inf. Comput. Sci., 2003, 43, 1947–1958.
39. L. Breiman, Mach. Learn., 2001, 45, 5–32.
40. C. Rücker, G. Rücker and M. Meringer, J. Chem. Inf. Model., 2007, 47, 2345–2357.
41. K. V. Chuang and M. J. Keiser, Science, 2018, 362, eaat8603.
42. https://robert.readthedocs.io .
43. L. S. Shapley, in The Shapley Value, ed. A. E. Roth, Cambridge University Press, 1st edn, 1988, pp. 31–40.
44. M. Lundberg and S.-I. Lee, in Advances in Neural Information Processing Systems, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, vol. 30.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00996k

---