Correlative analysis of Ni(II) coordination states in molten salts using a combination of X-ray and optical spectroscopies and simulations

Abstract

Understanding the factors that control the speciation of metal ions in molten salts is crucial for the successful deployment of molten salts in both concentrated solar power and nuclear energy applications. The speciation of the Ni(II) ion is of interest because it is a common corrosion product, and the distribution of coordination states it occupies is highly sensitive to the molten salt matrix. We employ in situ X-ray absorption spectroscopy (XAS), optical spectroscopy, and ab initio molecular dynamics (AIMD) simulations to investigate and understand the heterogeneities of Ni(II) coordination in LiCl–KCl, NaCl–MgCl_2, and LiCl–ZnCl₂ molten salt systems. The main challenge lies in identifying the population distribution of Ni(II) coordination states as a function of temperature and melt composition. We combined the multivariate curve resolution – alternating least squares (MCR-ALS) analysis of the XAS data and principal component analysis (PCA) of the optical spectra to determine the number of unique coordination states coexisting in the molten state, extract X-ray spectra for each state, and obtain their mixing fractions at different temperatures and for different salt mixtures. AIMD simulations were essential in identifying the coordination states corresponding to the deconvoluted spectra. The differences in the coordination states of Ni(II) in different salt systems are discussed in terms of the effects of the varying polarizing powers of the cations in the host salt matrix on chloride ion coordination to Ni(II). Such elucidation of the local structure adopted by metal ions enables a better understanding of the factors controlling the speciation of ions and their effect on molten salt properties.

---

Introduction

Molten chloride salts are attractive fluids for various applications including use as electrolytes for pyroprocessing of used nuclear fuel,¹ heat transfer fluids, thermal storage media for concentrating solar power plants,^2,3 and coolants for nuclear reactors^4,5 due to their good thermal conductivity, radiolytic stability, large specific heat, low viscosity, and low vapor pressure at operating conditions. LiCl–KCl is a commonly used electrolyte for nuclear fuel pyroprocessing,¹ while NaCl–MgCl₂ is attractive as a molten salt reactor coolant and energy storage medium due to its higher latent heat value and lower vapor pressure.^3,4 However, for the successful implementation of molten chloride salts in a broader range of applications, it is important to understand the chemical reactivity and speciation of metal ions, since the high abundance of chloride as a complexing ligand, coupled with trace impurities such as moisture and oxygen, can induce corrosion of structural materials.

Nickel-based alloys are candidate structural materials for nuclear applications due to their superior corrosion resistance and good mechanical properties.^6,7 Despite their corrosion resistance, Ni(II) is certain to corrode into the working molten salt, and its speciation and solubility in the particular salt will influence the corrosion process. Elucidating the heterogeneuous local coordination structures adopted by Ni(II) in relevant molten salt systems such as LiCl–KCl and NaCl–MgCl₂ over a range of temperatures can provide insights into the solute–solvent (Ni–molten salt) interactions that determine the speciation of metal ion complexes and the properties of metal–laden molten salts. This will advance the successful deployment of molten salts by providing the information needed to predict and manage the speciation and behavior of corrosion products, fission products, and fuel in reactor systems.

We have previously investigated the coordination states of Ni(II) in single-component ZnCl₂ ⁸ and bicomponent KCl–ZnCl₂ ⁹ systems as functions of temperature and solvent chemistry using a multi-modal approach of combining X-ray absorption spectroscopy (XAS) and optical spectroscopy with ab initio molecular dynamics (AIMD) simulations. We found that Ni(II) exhibits heterogeneous speciation in molten ZnCl₂ via the coexistence of several coordination environments, where the hexacoordinate, octahedral structure observed in pure solid NiCl₂ changes after melting to a temperature-dependent combination of pentacoordinate and tetracoordinate structures.⁸ We then explored the effects of varying the Lewis acidity/basicity of the salt medium on Ni(II) speciation by using two compositions of molten KCl–ZnCl₂.⁹ We found that the exchange dynamics of the chloride ions coordinated to Ni(II) varies with salt composition because of variations in the polarizing power of the melt cations and consequently influences the speciation of coexisting Ni(II) coordination states.

A major challenge in performing structural characterization of the coordination environments of metal ion solutes such as Ni(II) in molten salt media is the careful handling of the air and moisture-sensitive salts, as well as the evaluation of structural complexity at high temperatures and under controlled atmosphere. Because of such stringent requirements, the behavior of metal ions over a wide range of temperatures, from room temperature to the melting point, is not generally understood. For example, the optical absorption measurements performed on Ni(II) and Co(II) in ZnCl₂ medium⁸ and the theoretical modelling of those⁸ and related media (Ni(II) in KCl–ZnCl₂ mixtures)⁹ by AIMD were performed in the molten state only. As such, alternative analysis methods are needed to extend the temperature range and complete the speciation studies, both to complement the previous work and to obtain insights into the behavior of metal ions at the broad temperature range across the solid–liquid phase transition in molten salt systems.^10,11 X-ray absorption spectroscopy is the technique of choice for such purposes, but there are several challenges in the application of XAS to characterize metal ion speciation in molten salts. As has been recently demonstrated, there is a strong and dynamic structural heterogeneity present for Ni(II) in different molten salt media: the local coordination states of Ni(II) fluctuate dynamically between nominally 4-coordinate, 5-coordinate, and highly-distorted but nominally 6-coordinate states.^8,9 As a result of the strong and asymmetric bonding disorder inherent to this kind of dynamic behavior, the average coordination environment cannot reliably be understood by applying a conventional fitting approach to extended X-ray absorption fine structure (EXAFS) spectroscopy, as demonstrated previously.⁸ The limitations of EXAFS fitting approach for studying the structure and speciation of dilute metal ions in molten salts, as well as alternative strategies that rely on the use of machine learning – assisted analysis of EXAFS data, are discussed in a recent review.¹² On the other hand, X-ray absorption near edge structure (XANES) spectroscopy is a useful alternative to EXAFS because the information about the partial contribution to XANES from each coordination state is encoded in the XANES spectrum, and thus not only the types of coordination state but also their mixing fractions can in principle be decoded from the spectra. To the best of our knowledge, no reports are available showing how the speciation of these statically and dynamically distinct states adopted by metal ions in molten salt systems can be performed by XANES analysis.

In this study, we present a deconvolution of the coexisting coordination states of Ni(II) in several chloride molten salt systems (LiCl–KCl, NaCl–MgCl₂, LiCl–ZnCl₂) using a chemometric approach, namely multivariate curve resolution alternating least squares (MCR-ALS) analysis, to correlate the resultant structures that coexist in the molten state by using complementary optical absorption measurements and extend the speciation studies to the solid state of the salt solution, which was previously unexplored by theoretical or experimental methods. While linear combination fitting (LCF) has been commonly used for studying the composition of mixtures for several decades, it requires the use of known standards for the fitting, which is a limitation for solute speciation studies. MCR-ALS, on the other hand, can isolate the species and obtain their concentrations in the mixture automatically and without prior knowledge of standards or spectral components.^13–15 To determine the number of independent components in the MCR-ALS method, principal component analysis (PCA) is applied to the dataset as the initial step.^16–19 Then, an iterative procedure is performed to separate the distinct solute species from the series of spectra that are representative of a mixture of coordination states.

Experimental

XAS data were collected using a custom-built, high-temperature cell on the ISS (8-ID) beamline at the National Synchrotron Light Source II (NSLS-II) at Brookhaven National Laboratory and were analyzed by the Demeter package. The concentration of NiCl₂ was 1 wt% in all three solvents: LiCl–KCl (58–42 mol%, melting point (m.p.) 353 °C), NaCl–MgCl₂ (56–44 mol%, m.p. 450 °C) and LiCl–ZnCl₂ (22–78 mol%, m.p. 275 °C). Whereas 1 wt% NiCl₂ was fully soluble at all temperatures in LiCl–KCl and NaCl–MgCl₂, it exceeded the solubility limit of NiCl₂ in LiCl–ZnCl₂ according to our measurements (details in ESI Table S1 and Fig. S2†). Further details of sample preparation, cell design and XAS data processing and analysis are included in the ESI.†

Optical absorption spectroscopy (UV-Vis-near IR) was conducted on Ni(II) in the chloride melts using a custom-designed spectroscopy furnace setup at Idaho National Laboratory, following experimental and analysis procedures similar to previous works.^9,20 The NiCl₂ loading in the salt systems was 0.1 wt% in NaCl–MgCl₂ and LiCl–KCl, and 0.05 wt% in LiCl–ZnCl₂; the concentration range was adjusted to provide the highest signal-to-noise ratio possible without overwhelming the detection limits of the spectrophotometer. The samples were prepared using a glassy carbon crucible that was rinsed with isopropanol, dried overnight in a vacuum oven at 120 °C, followed by baking at 700 °C for 4 hours inside an argon-atmosphere glovebox. Sample weights were recorded to 0.1 mg precision using a Mettler-Toledo balance. A stock mixture of 1 wt% NiCl₂ in each chloride salt mixture was first prepared using a glassy carbon crucible. The NiCl₂-loaded salt mixture was melted and held at 500 °C for 3 hours to ensure complete homogeneity. The 1 wt% NiCl₂ stock mixture was then ground to a powder using an agate mortar and pestle and diluted to the desired concentration for optical spectroscopy measurements. For example, to prepare a mixture with 0.1 wt% NiCl₂ loading, 0.5 g of the 1 wt% stock mixture was placed in a quartz cuvette. Then, 4.5 g of the base salt was added to achieve a total mass of 5 g, resulting in a 0.1 wt% NiCl₂ loaded mixture. Because of the risk of thermal damage to the optical fibers used to transport analyzing light to and from the spectroscopy furnace, measurement temperatures were generally limited to 600 °C or below. For each measurement at a particular temperature, a reference scan with the base salt mixture was recorded. The spectra were baseline-corrected and analyzed using Spectrograph version 1.2.11 software. Further experimental and data analysis details are provided in the ESI.†

Comparatively long AIMD simulations (150 ps) were performed for all three salt systems containing two Ni(II) cations at 2 mol% (simulation box size: 19–21 Å). A simulation temperature of 600 °C was chosen to provide a direct comparison with the experimental EXAFS spectra and to make sure that various Ni(II) coordination states are fully equilibrated. Full computational details are provided in the ESI.†

Results and discussion

XANES analysis

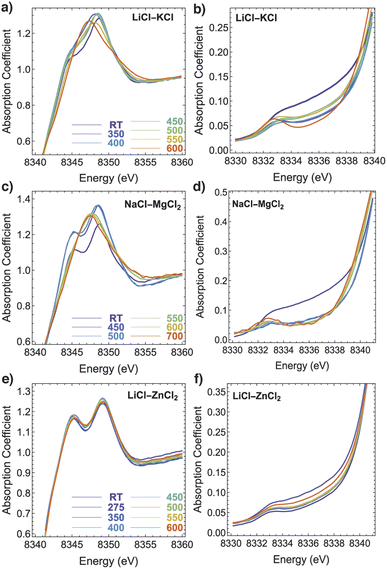
Fig. 1 shows two energy regions of the XANES spectra for all three salt mixtures. The first region (the edge rise and the main peak) is known as the white line (a, c, and e) and the second region is referred to as the pre-edge region (b, d, and f). The changes in the spectra for two systems, LiCl–KCl and NaCl–MgCl₂, are similar in nature. The white line region transforms from a bimodal shape (a peak and shoulder in Fig. 1a and two peaks in Fig. 1c) to a unimodal shape at elevated temperatures. In the LiCl–ZnCl₂ system, the bimodal shape persists at all temperatures.

Fig. 1 XANES features in the main edge and pre-edge regions at the Ni K edge of NiCl₂ in LiCl–KCl (a and b), NaCl–MgCl₂ (c and d) and LiCl–ZnCl₂ (e and f). The colors correspond to different temperatures (in °C).

Likewise, in the pre-edge region, the changes in the LiCl–KCl and NaCl–MgCl₂ systems are similar. The overall intensity of the signal between 8332 and 8340 eV decreases drastically at 350 °C and continues to evolve, albeit more gradually, to the highest temperatures. On the contrary, in the LiCl–ZnCl₂ system, the XANES spectra evolve very little with temperature between RT and 600 °C, which is consistent with the fact that the added 1 wt% NiCl₂ is not entirely dissolved (see Fig. S2†). The spectral changes are minor and are difficult to distinguish from those that may have been caused by thermal effects. Even at higher temperatures (550–600 °C) where at least half of the NiCl₂ is dissolved, the XANES spectra still resemble that of solid NiCl₂. It is worth noting that the double peaks in white line spectra for Ni(II) in LiCl–KCl and NaCl–MgCl₂ at room temperature are not as pronounced as they are for the regular O_h octahedral coordination geometry in solid NiCl₂ represented in Fig. 1e. Therefore, we infer that the Ni(II) ions dissolved in solid LiCl–KCl and NaCl–MgCl₂ exist in relatively distorted octahedral coordination sites within a solid salt solution.

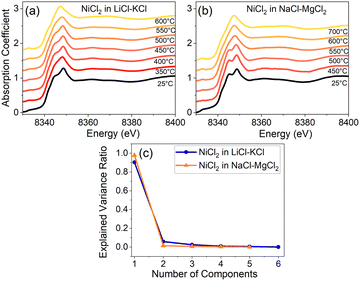
After applying principal component analysis (PCA) to the three data sets shown in Fig. 1, we obtained information about the minimum number of unique spectra required to represent the most important species in the samples. For the PCA analysis, we used the energy range between 8340 eV and 8400 eV for all the spectra, as seen, e.g., in Fig. 2a and b for Ni XANES in LiCl–KCl and NaCl–MgCl₂, respectively. To determine the number of principal components in the spectra shown in Fig. 2 we initially performed a scree test, and, later, validated these determinations by the results of AIMD simulations and optical absorption data analysis. The results (Fig. 2c) demonstrate that three unique spectral components exist for Ni(II) in the LiCl–KCl system, while two components dominate the spectra of Ni(II) in the NaCl–MgCl₂ mixture. For the LiCl–ZnCl₂ mixture, the XANES spectra in Fig. 1e show a similar shape, with a single peak dominating all the spectra.

Fig. 2 XANES spectra of NiCl₂ in (a) LiCl–KCl and (b) NaCl–MgCl₂ at different temperatures. The scree plot of the PCA analysis of the XANES spectra above the respective melting points in (a) and (b) is shown in (c).

To quantify the effect of solvent composition on the speciation of Ni(II) and the presence of various coordination states of Ni(II) in LiCl–KCl and NaCl–MgCl₂ melts, we performed multivariate curve resolution – alternating least square (MCR-ALS) analysis on the XAS spectra of Ni, as shown in Fig. 3a and b for LiCl–KCl and Fig. 3c and d for NaCl–MgCl₂, respectively. We performed MCR-ALS only for the data corresponding to the molten states to eliminate the contribution from the distorted octahedral environment of Ni(II) that exists in the solid state at 25 °C. Our MCR-ALS analysis follows a similar procedure to that described in previous work.^13–15 According to the PCA analysis (Fig. 2c), three components are required to describe all Ni(II) spectra in molten LiCl–KCl, and two components for Ni(II) in molten NaCl–MgCl₂. We applied the MCR-ALS analysis to isolate the spectra corresponding to different Ni(II) coordination states in each salt mixture (S1–S3 for Ni(II) in LiCl–KCl and S1–S2 for Ni(II) in NaCl–MgCl₂). The details of our procedure are described in the ESI.† The details of the local geometry of each unique state are not available from this analysis, but we hypothesize that species S1 for both salt mixtures, which are most abundant at lower to intermediate temperatures, are relatively higher coordinated due to the clear appearance of the split white line peak (Fig. 3b and d) that resembles the 25 °C data for both compounds (Fig. 2a and b). We hypothesize that these states are consistent with a highly distorted 6-coordinate environment, as discussed in greater detail below. The nature of the S2 state in each salt mixture is likely to be 4-coordinate, and this attribution will be examined by analysis of optical absorption data and AIMD simulations.

Fig. 3 XANES spectra corresponding to the three component states of Ni(II) (S1, S2, and S3, respectively) obtained by MCR-ALS analysis and their mixing fractions f in for Ni(II) in LiCl–KCl (a and b) and in NaCl–MgCl₂ (c and d).

The results shown in Fig. 3 offer new insights into the transformation between different coordination states for the two salt systems (LiCl–KCl and NaCl–MgCl₂). In the NaCl–MgCl₂ melt at temperatures between 400 and 600 °C, the transition from a relatively high (greater than 4)-coordinate geometry to the 4-coordinate one with increasing temperature is a single-step process (Fig. 3c). In contrast, the populations of Ni(II) in LiCl–KCl include two states with coordination numbers greater than 4 (Fig. 3a). We note that, at 350 °C, the contribution of S1 to XANES spectra of Ni(II) in LiCl–KCl is lower than at 400 and 450 °C (Fig. 3a), and the contribution from S3 is higher. This implies a complex relationship between the coordination number distribution and temperature in LiCl–KCl. To disentangle the factors responsible for the observed differences in the speciation between LiCl–KCl and NaCl–MgCl₂, theoretical simulations, such as those based on ab initio or machine learning-assisted molecular dynamics have been demonstrated to be effective tools.^9,21

Optical absorption spectroscopy

The optical absorption spectroscopy of Ni(II) in these molten salts is complementary to the Ni XANES data, providing independent insights into the electronic structure and coordination environments adopted by Ni(II). The optical absorption spectra for Ni(II) in the three solvent salt mixtures studied here: NaCl–MgCl₂, LiCl–KCl, and LiCl–ZnCl₂ are shown in Fig. 4a–c, respectively (note that NiCl₂ is fully soluble in LiCl–ZnCl₂ at the concentration used for the optical spectroscopy). In prior work,^8,9 our team investigated Ni(II) coordination in ZnCl₂ and in two KCl–ZnCl₂ mixtures as a function of composition and temperature, shown in Fig. 4d–f. In that study, the concentrations of NiCl₂ were 0.100 wt% in ZnCl₂, 0.116 wt% in KCl–ZnCl₂ (Comp 1), and 0.096 wt% in KCl–ZnCl₂ (Comp 2). Fig. 4 illustrates that Ni(II) exhibits a high degree of solvatochromism and thermochromism in molten chloride salts. These effects arise from the fact that Ni(II) can occupy a range of coordination states, depending on the atomic-scale structure and chlorobasicity of the salt medium, that varies with temperature. Each coordination state generates a characteristic splitting of the 3d-orbital manifold, which results in a specific spectroscopic signature from the d⁸ electronic occupancy. This feature of Ni(II) spectroscopy in molten salts has been known for several decades and numerous researchers have used it to probe the solvent properties of molten salts,^22–33 which is also our motivation along with the present-day advantage of taking a multimodal approach including X-ray spectroscopy and ab initio MD simulations.

Fig. 4 Optical absorption spectra in UV-Vis-NIR range for Ni(II) species in: (a) 56 : 44 mol% NaCl–MgCl₂, (b) 58 : 42 LiCl–KCl, (c) 22 : 78 LiCl–ZnCl₂ (note different vertical scale), (d) 45.3 : 55.7 KCl–ZnCl₂, (e) 52.5 : 47.5 KCl–ZnCl₂, and (f) neat ZnCl₂ as functions of temperature. Color-coded bands in each graph indicate the spectral regions where different coordination states have predominant absorption bands, as discussed in the text and labeled at the bottom of the figure. The regions are broadly defined and overlap to some extent.

Historically, the optical spectroscopy of Ni(II) in molten salts has been interpreted in terms of a temperature and salt-composition-dependent equilibrium between two coordination geometries with distinct optical signatures – 4-coordinate tetrahedral (“T”) and 6-coordinate octahedral (“O”).^29–31 The optical signature of the 4-coordinate state of Ni(II) is a two-peak feature in the 14 000–16 000 cm⁻¹ region (indicated in red in Fig. 4) that is well documented in the literature as a Jahn–Teller-distorted tetrahedral state.^{23,24,31,34,35} The canonical optical signature of the 6-coordinate state assigned as O has been attributed as an absorption band peaking sharply at ∼20 000 cm⁻¹ with a shoulder sloping towards lower energy.^{26,28–30,32} The region of this band is indicated in blue in Fig. 4. In attempting to fit all the observed data into this binary model, some researchers postulated that there could be other states that represent larger perturbations of the T and O coordination geometries,²⁶ but there were no examples of structurally-characterized solid-state analogues to model them, as were available for the T and O states.^24,31,36,37

In our previous studies of Ni(II) in ZnCl₂ and the KCl–ZnCl₂ system (in two compositions containing 45.3 and 52.5 mol% KCl), the lowest-temperature spectra above the melting points (Fig. 4d and e) indicated the presence of very distorted 6-coordinate Ni(II), which we now prefer to call 6*-coordinate to distinguish it from classical octahedral coordination (vide infra). As the temperature was increased in each case, this state transitioned in both mixtures to a combination of 4- and 5-coordinate states.⁹ A 5-coordinate, distorted square pyramidal (Sp) state of Ni(II), observed in molten KCl–ZnCl₂ between 320-700 °C, was interpreted for the first time in that work and analyzed with a combination of XAFS and AIMD simulations along with optical spectroscopy. The 5-coordinate Sp Ni(II) state is indicated by an absorption feature in the region around 18 000 cm⁻¹ (indicated by the green band).

Before discussing the spectroscopy of Ni(II) in the three salt mixtures that are the subject of this report, it is necessary to draw a distinction between the Ni(II) species historically assigned as octahedral (O) and Ni(II) in truly symmetric octahedral coordination (point group O_h) with six equidistant chloride ions in the first coordination sphere. The best example of the latter is the optical spectrum of single-crystal NiCl₂ reported by Kozielski et al.³⁸ where a sharp absorption band attributed to a ³T_1g transition appears at 22 000 cm⁻¹ at 300 K. Another example of a band around 22 000 cm⁻¹ was observed for Ni(II) in acidic 1-ethyl-3-methylimidazolium chloride/aluminum chloride (emim Cl/AlCl₃) ionic liquid mixtures.³³ In the NiCl₂ crystal structure³⁹ and an EXAFS study of Ni(II) in acidic emim Cl/AlCl₃,⁴⁰ the average Ni–Cl bond distance in the octahedral complex is about 2.4 Å.

In contrast, the state observed in molten salts that peaks around 20 000 cm⁻¹ has been assigned as octahedral (O) on the basis of single-crystal spectroscopy in systems of defined structures such as Ni(II)-doped CsCdCl₃,²⁴ where Ni(II) replaces Cd(II) host sites, and Ni(II)-doped KMgCl₃,³⁶ where Ni(II) replaces Mg(II). However, the Cd–Cl bond distance in CsCdCl₃ is 2.63 Å⁴¹ and the Mg–Cl distance in KMgCl₃ is 2.5 Å.³⁶ In both cases, the host site for Ni(II) is too large compared to the optimal 2.4 Å distance for a symmetric octahedral (O_h) nickel chloride complex, so the Ni(II) centers within these hosts will experience weaker ligand field splitting, leading to lower transition energies compared to those in NiCl₂ and acidic emim Cl/AlCl₃. Another possible consequence of an oversized host site is the likely displacement of the Ni(II) ion in the direction of some of the neighboring chlorides and away from others, leading to the formation of a distorted octahedral complex with some long Ni–Cl distances, having an effective coordination number (CN) slightly lower than 6. In fact, these Ni(II)-doped crystal systems are indeed spectroscopic models, but they are models of highly-distorted, nominally 6-coordinate states that we will call 6* to make it clear that they are far from octahedral (O_h) symmetry. Accordingly, references to CN 6 in our earlier work^8,9 should be equated with the 6* state rather than the O_h state, and states labelled as O in earlier literature (1950s–1960s) are generally consistent with 6*.

Having established the paradigm of 4-, 5- and 6*-coordinate states for Ni(II) in molten chloride salts, we can now interpret the optical absorption trends for Ni(II) in molten LiCl–KCl, NaCl–MgCl₂ and LiCl–ZnCl₂. The spectra in LiCl–KCl and NaCl–MgCl₂ evolve with temperature in ways that imply changes in the distribution of Ni(II) coordination states, while in LiCl–ZnCl₂, the 6* coordination state appears to dominate at all temperatures. In LiCl–KCl eutectic melt (Fig. 4b), at 450 °C and below, the coexistence of 4-, 5- and 6*-Ni(II) states is apparent based on the feature at ∼20 000 cm⁻¹ corresponding to CN 6* and broad absorption in the regions characteristic of 4- and 5-coordinate Ni(II). The signature of CN 6* gradually disappears with increasing temperature as the population distribution shifts to lower CN. Compared to the LiCl–KCl system, Ni(II) in NaCl–MgCl₂ shows a much larger spectral contribution from CN 5 over the temperature range studied for this system, 500–650 °C, with a gradual shift towards CN 4 as the temperature increases.

In LiCl–ZnCl₂, Ni(II) adopts a rather different coordination environment between 300 and 450 °C, featuring a very strong band around 20 000 cm⁻¹ characteristic of CN 6*, and weaker bands at 14 000 cm⁻¹ and 16 000 cm⁻¹ corresponding to CN 4. In this salt mixture and temperature regime, the proportions of CN 4 and CN 5 are relatively low compared to the other salts in Fig. 4. At 500 °C, there appears to be the beginning of a shift towards lower coordination numbers with increasing temperature, but volatility of the ZnCl₂ component limited our ability to measure at higher temperatures.

PCA analysis was applied to the temperature-dependent optical absorption spectra in Fig. 4a–c. The graph of explained variance ratios vs. the number of components in Fig. 5 indicates that all the data for Ni(II) in LiCl–KCl and NaCl–MgCl₂ salts over the measured temperature range can be represented by mixtures of three unique states, while for the LiCl–ZnCl₂ salt mixture, two states are required. These results agree qualitatively with the results of PCA/MCR-ALS analysis of XANES spectra. Quantitative analysis of the optical absorption data using MCR-ALS is currently in progress and will be published elsewhere.

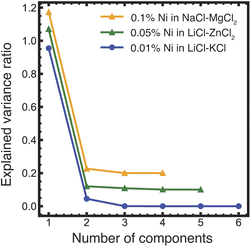Fig. 5 Results of the PCA analysis of the optical absorption data shown in Fig. 4a–c. The numbers of principal components (determined visually as the crossover between the constant slope of the eigenvalues at higher component numbers to the varying slope at the lower numbers, showing by a dashed vertical line) are three for LiCl–KCl and NaCl–MgCl₂ and two for LiCl–ZnCl₂ (the latter two data sets are displaced vertically by 0.2 and 0.1 units, respectively, for legibility).

When considering the effect of salt composition on the coordination states of Ni(II) in the six systems discussed here, it can be helpful to apply an empirical rule of thumb to estimate the polarizing power of the constituent cations of the salt. Polarizing power controls how much electron density the chloride ions can donate to the coordination of Ni(II). When the polarizing power of the salt cations is low, the chlorides donate more electron density, which favors lower coordination numbers. Highly polarizing cations withdraw chloride electron density from Ni(II) coordination, resulting in higher coordination numbers. Table 1 lists the polarizing powers of cations and weighted averages of polarizing powers for salt mixtures, calculated as the ionic charge divided by the square of the ionic radius. By this calculation, eutectic LiCl–KCl is the least polarizing salt system in this set, and pure ZnCl₂ is the most polarizing, followed by 22 : 78 LiCl–ZnCl₂. While this correlation generally agrees with the coordination number changes with composition, it is far from ideal. For example, Fig. 4c–e show that addition of a chloride salt of a monovalent cation with less polarizing power (Li⁺ or K⁺) to pure ZnCl₂ increases the average Ni(II) coordination number, sometimes substantially, while decreasing the empirical polarizing power of the mixture. A similar example was reported in CsCl–ZnCl₂ mixtures by Smith et al.³² where as little as 8 mol% CsCl loading dramatically changed the coordination environment of Ni(II) from CN 4 & 5 to CN 6*. As described by Smith³² and in our earlier work,⁸ ZnCl₂ is a highly networked liquid that favors a 4-coordinate geometry for solute ions sitting in zinc vacancies. Addition of monovalent salts such as alkali halides disrupts this network and permits the system to stabilize at higher Ni(II) coordination numbers. To understand the true nature of these changes on the molecular level, ab initio molecular dynamics simulations can be extremely helpful.

Table 1 Polarizing power (electronic charge)/(ionic radius)² (e Å⁻²) of the cations present in LiCl–KCl, KCl–ZnCl₂, NaCl–MgCl₂, and LiCl–ZnCl₂ salt mixtures and the weighted average cation polarizing powers of the mixtures. Values for the ionic radii were taken from the literature^42,43

Cation or salt mixture	Polarizing power (e Å^−2)	Ionic radius, Å
Na^+	0.96	1.02
Mg^2+	3.86	0.72
K^+	0.53	1.38
Li^+	1.73	0.76
Zn^2+/ZnCl2	3.65	0.74
58LiCl–42KCl	1.22	—
52.5KCl–47.5ZnCl2 (Comp 2)	2.01	—
45.3KCl–54.7ZnCl2 (Comp 1)	2.24	—
56NaCl–44MgCl2	2.24	—
22LiCl–78ZnCl2	3.23	—

---

Ab initio molecular dynamics simulations

To further probe how the distribution of Ni(II) coordination states changes in molten salt systems, AIMD simulations in the canonical ensemble (NVT) at 600 °C were employed. Fig. 6 shows free energy (W_(CN)) plots as a functions of the Ni(II) coordination number (CN) for the three salt mixtures. As mathematically defined in our previous work on Ni(II) speciation,⁹ CN varies smoothly with time (i.e., sampling fraction values), exploring transition paths between different metastable Ni–Cl coordination shells. W_(CN) in Fig. 6 represents the CN states as the free energy wells separated by the barriers between them. Based on the free energy minima and barrier locations, we assign CN 3 to CNs < 3.5, CN 4 to 3.5 < CNs < 4.5, CN 5 to 4.5 < CNs < 5.5, and CN 6* to CNs > 5.5. Comparing the relative depths of the free energy wells at 600 °C, we find a general trend of increasing average coordination number with increasing polarizing power of the solvent salt cations. For instance, in CN 5 and CN 6* are more populated (lower minima) in the LiCl–ZnCl₂ melt than in the NaCl–MgCl₂ melt. CN 5 is lowest-populated and CN 6* is practically nonexistent (very high free energy) in the LiCl–KCl melt. This trend is observed due to the reduction in the effective polarizing ability of the cations as we go from LiCl–ZnCl₂ (strong effects from both Li⁺ and Zn²⁺) to NaCl–MgCl₂ (strong effects from only Mg²⁺) to LiCl–KCl (strong effects from only Li⁺).

Fig. 6 Free energy plots of the coordination numbers of Ni(II) determined from the AIMD simulations at 600 °C as defined previously,^8,9 highlighting the influence of the polarizing power of the solvent salt cations on the distribution of the Ni(II) coordination geometries.

It is noticeable that in all cases the global free-energy minimum is centered at CN 4, suggesting that Ni(II) speciation at 600 °C in these melt mixtures is dominated by tetrahedral coordination. This is consistent with the experimental observations from the optical and XANES spectroscopy at that temperature. Furthermore, the aforementioned higher populations of the higher coordinated Ni(II) states, CN 5 and 6*, in the NaCl–MgCl₂ melt compared to the LiCl–KCl melt, are confirmed by the distribution of various coordination states deduced from the MCR-ALS analysis. Due to ZnCl₂ evaporation at high temperature we do not have optical spectra for Ni(II) in LiCl–ZnCl₂ at 600 °C to compare directly with the AIMD results. Nevertheless, the AIMD results are consistent with the trend of the LiCl–ZnCl₂ optical spectra with temperature, exhibiting a larger fraction of higher coordination states compared to the LiCl–KCl and NaCl–MgCl₂ melts.

To provide geometric insight into the CN states, we depict the Cl–Ni–Cl bond angle and Ni–Cl bond distance distributions computed from the AIMD simulations for CN 3, 4, 5 and 6* in Fig. 7. In terms of the bond angles, the geometries of the CN 3–6* states are approximately trigonal, tetrahedral, square pyramidal, and octahedral, respectively. However, the standard deviation and the presence of asymmetry in these distributions indicate their distorted nature. The systematic change in the bond distance distribution (shift in the most-likely bond length and its disorder/standard deviation) from CN 3 to CN 6* further confirms the observed distortion. The bond length distributions follow the expected trend of bond lengthening with increasing coordination number. Considering thermal effects, the most likely bond distance for CN 4 (2.30 Å) is consistent with those reported in a crystal structure of tetraethylammonium tetrachloronickelate (2.276 Å)³⁷ and by EXAFS analysis in a basic emim Cl/AlCl₃ melt (2.28 Å).⁴⁰ The most likely bond distance for CN 6* (2.43 Å) is consistent with the crystal structure of octahedral NiCl₂ (2.40 Å)³⁹ and EXAFS analysis in an acidic emim Cl/AlCl₃ melt (2.41 Å).⁴⁰ The bond length distributions become increasingly asymmetric towards longer distances with increasing coordination number, consistent with the effects of distortion observed in the optical spectroscopy.

Fig. 7 Normalized probability distributions of Cl–Ni–Cl bond angles (a–d) and Ni–Cl distances (e–h) for nominal chloride coordination numbers CN 3, 4, 5 and 6* surrounding Ni(II), obtained from the AIMD simulations at 600 °C in the LiCl–KCl (black), ZnCl₂–LiCl (red), and NaCl–MgCl₂ (green) mixtures. The most-likely bond angles and distances with standard deviations for each CN are given next to the peak heights. It should be noted that CN 6* is rarely sampled in the LiCl–KCl mixture, and therefore, the corresponding angle/distance distributions are not included in parts (d and h).

While AIMD is useful in predicting general trends of how Ni(II) speciation responds to changes in the melt composition, a direct comparison of the experimental EXAFS spectra and the computed ones based on the AIMD trajectories (Fig. 8) reveals some limitations of AIMD to accurately capture structural disorder under certain conditions. In particular, MD-EXAFS underestimates the amplitude of the k-space EXAFS spectra and the main peak in the Fourier-transformed R-space EXAFS spectra for Ni(II) in LiCl–KCl and NaCl–MgCl₂ melts at 600 °C (more details in ESI Fig. S3†). To our surprise, recomputing the EXAFS spectra with a subset of configurations limited to the coordination number 4 (CN = 3.85–4.15) reduces the discrepancy with the experimental spectra, but still underestimates the amplitude in the k-space and the magnitude in the R-space (Fig. S3†). Dividing this subset into two groups with structures closer to the ideal tetrahedral geometry and the ones that are more distorted reveal higher amplitudes of the EXAFS oscillation for more symmetric configurations. Thus, we conclude that AIMD slightly overestimates the degree of dynamic disorder (the EXAFS Debye–Waller factor) for the tetrahedral Ni centers at 600 °C, precluding a quantitative analysis of Ni(II) speciation from the EXAFS data and linear combination fitting based on AIMD simulations without additional assumptions. On a qualitative basis, good phase matching of the computed k-space spectra to the experimental spectra indicates that the dominant four-coordinate state of Ni(II) at 600 °C is given correctly by the AIMD simulations. Moreover, good phase matching at 500–550 °C can only be achieved by assuming a significant involvement of the five-coordinate state, further supporting significant structural transformation between 500 and 600 °C.

Fig. 8 Comparison of the experimental EXAFS spectra with the computed ones at 600 °C based on the statistical mechanical ensemble of all possible states sampled by AIMD simulations (MD-EXAFS) and a selection of states with coordination number around 4 (CN = 3.85–4.15).

Conclusions

In conclusion, we have shown that the combined interpretation of optical absorption and XANES spectra of metal ions in molten salts is a useful and novel approach that aids in resolving coexisting distributions of coordination states. The results of the PCA analysis of the optical absorption and XANES data are complementary, both pointing at the coexistence of several unique Ni complexes at different temperatures in solid and molten states in the LiCl–KCl and NaCl–MgCl₂ salt mixtures. MCR-ALS analysis of XANES spectra was used to obtain the number of distinct species and their spectra at all temperatures. We report that the speciation and local structural heterogeneity demonstrated by Ni(II) ions in various molten salts systems is directly related to the solvent composition and is related to the polarizing power of the solvent metal cations with some specific exceptions. Coordination number 6* dominates in LiCl–ZnCl₂ due to the strong polarizing power of divalent Zn ions, while in the case of LiCl–KCl and NaCl–MgCl₂ a shift from CN 5 to CN 4 is observed with increasing temperature. Compared to our previous work⁹ where we have combined molecular dynamics with linear combinations to clarify the speciation changes of Ni(II)-containing molten salts, our approach with MCR-ALS based analysis is a fast method that can be utilized over a broad temperature range, due to the high penetrating power of X-rays and relatively strong signal in the near-edge region of the absorption coefficient. One of the major advantages of this novel approach is that it can elucidate structural heterogeneity of metal solutes in solid solutions at room temperature, which is not possible using the ab initio methods such as molecular dynamics simulations that are limited to the molten state only. Additionally, it is much easier to execute as it utilizes only the optical absorption and XANES spectra and does not rely on computationally intensive AIMD calculations, greatly simplifying the analysis. Molecular level knowledge obtained through this approach is important to advance safe and efficient deployment of molten salt reactors and emerging concentrated solar power technologies. Further, this approach can be utilized to study speciation and chemistry in a wide variety of energy storage applications (where complex structural heterogeneity is expected) including, but not limited to, battery storage as well as thermal energy storage applications.

Data availability

The digital data for all figures, tables, charts, and any other media contained in this publication and its associated ESI† files will be made accessible in the MSEE Community of the Zenodo repository, under Digital Object Identifier (DOI): https://doi.org/10.5281/zenodo.14563516.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported as part of the Molten Salts in Extreme Environments Energy Frontier Research Center, funded by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences. BNL, INL, and ORNL are operated under DOE contracts DE-SC0012704, DE-AC07-05ID14517, and DE-AC05-00OR22725, respectively. This research used resources of the ISS (8-ID) and QAS (7-BM) beamlines at the National Synchrotron Light Source II operated by the Brookhaven National Laboratory under Contract No. DE-SC0012704, a U.S. Department of Energy (DOE), Office of Science User Facility. This research used resources of the Compute and Data Environment for Science (CADES) at the Oak Ridge National Laboratory and the National Energy Research Scientific Computing Center (NERSC), which are supported by the Office of Science of the U.S. Department of Energy under contracts DE-AC05-00OR22725 and DE-AC02-05CH11231, respectively.

References

1. Y.-Z. Cho, T.-K. Lee, H.-C. Eun, J.-H. Choi, I.-T. Kim and G.-I. Park, J. Nucl. Mater., 2013, 437, 47–54.
2. J.-W. Wang, C.-Z. Zhang, Z.-H. Li, H.-X. Zhou, J.-X. He and J.-C. Yu, Sol. Energy Mater. Sol. Cells, 2017, 164, 146–155.
3. M. M. Kenisarin, Renewable Sustainable Energy Rev., 2010, 14, 955–970.
4. D. Williams, Assessment of candidate molten salt coolants for the NGNP/NHI heat-transfer loop, Oak Ridge National Lab. (ORNL), Oak Ridge, TN (United States), 2006.
5. S. Guo, J. Zhang, W. Wu and W. Zhou, Prog. Mater. Sci., 2018, 97, 448–487.
6. K. Vignarooban, P. Pugazhendhi, C. Tucker, D. Gervasio and A. M. Kannan, Sol. Energy, 2014, 103, 62–69.
7. T. Tzvetkoff and P. Gencheva, Mater. Chem. Phys., 2003, 82, 897–904.
8. S. K. Gill, J. Huang, J. Mausz, R. Gakhar, S. Roy, F. Vila, M. Topsakal, W. C. Phillips, B. Layne, S. Mahurin, P. Halstenberg, S. Dai, J. F. Wishart, V. S. Bryantsev and A. I. Frenkel, J. Phys. Chem. B, 2020, 124, 1253–1258.
9. S. Roy, Y. Liu, M. Topsakal, E. Dias, R. Gakhar, W. C. Phillips, J. F. Wishart, D. Leshchev, P. Halstenberg, S. Dai, S. K. Gill, A. I. Frenkel and V. S. Bryantsev, J. Am. Chem. Soc., 2021, 143, 15298–15308.
10. D. H. Kerridge and I. A. Sturton, Inorg. Chim. Acta, 1974, 8, 27–30.
11. S. Roy, S. Sharma, W. V. Karunaratne, F. Wu, R. Gakhar, D. S. Maltsev, P. Halstenberg, M. Abeykoon, S. K. Gill, Y. Zhang, S. M. Mahurin, S. Dai, V. S. Bryantsev, C. J. Margulis and A. S. Ivanov, Chem. Sci., 2021, 12, 8026–8035.
12. K. Zheng, N. Patra, N. Marcella, A. S. Ivanov, J. F. Wishart, A. R. Ballesteros, R. Gakhar, S. Dai, S. Roy, V. Bryantsev, S. K. Gill and A. I. Frenkel, Chem. Methods, 2025 DOI:10.1002/cmtd.202400097.
13. J. Jaumot, R. Gargallo, A. de Juan and R. Tauler, Chemom. Intell. Lab. Syst., 2005, 76, 101–110.
14. F. Eveillard, C. Gervillié, C. Taviot-Guého, F. Leroux, K. Guérin, M. T. Sougrati, S. Belin and D. Delbègue, New J. Chem., 2020, 44, 10153–10164.
15. Y. Liu, A. Halder, S. Seifert, N. Marcella, S. Vajda and A. I. Frenkel, ACS Appl. Mater. Interfaces, 2021, 13, 53363–53374.
16. T. Ressler, J. Wong, J. Roos and I. L. Smith, Environ. Sci. Technol., 2000, 34, 950–958.
17. A. I. Frenkel, O. Kleifeld, S. R. Wasserman and I. Sagi, J. Chem. Phys., 2002, 116, 9449–9456.
18. Q. Wang, J. C. Hanson and A. I. Frenkel, J. Chem. Phys., 2008, 129, 234502.
19. A. Piovano, G. Agostini, A. I. Frenkel, T. Bertier, C. Prestipino, M. Ceretti, W. Paulus and C. Lamberti, J. Phys. Chem. C, 2011, 115, 1311–1322.
20. W. C. Phillips, R. Gakhar, G. P. Horne, B. Layne, K. Iwamatsu, A. Ramos-Ballesteros, M. R. Shaltry, J. A. LaVerne, S. M. Pimblott and J. F. Wishart, Rev. Sci. Instrum., 2020, 91, 083105.
21. S.-C. Lee, Y. Zhai, Z. Li, N. P. Walter, M. Rose, B. J. Heuser and Y. Z, J. Phys. Chem. B, 2021, 125, 10562–10570.
22. C. R. Boston and G. P. Smith, J. Phys. Chem., 1958, 62, 409–413.
23. D. M. Gruen and R. L. McBeth, J. Phys. Chem., 1959, 63, 393–398.
24. D. M. Gruen and R. L. McBeth, Pure Appl. Chem., 1963, 6, 23–48.
25. G. P. Smith and C. R. Boston, J. Chem. Phys., 1965, 43, 4051–4056.
26. C. A. Angell and D. M. Gruen, J. Phys. Chem., 1966, 70, 1601–1609.
27. G. P. Smith, C. R. Boston and J. Brynestad, J. Chem. Phys., 1966, 45, 829–834.
28. W. E. Smith, J. Brynestad and G. P. Smith, J. Am. Chem. Soc., 1967, 89, 5983–5984.
29. J. Brynestad, C. R. Boston and G. P. Smith, J. Chem. Phys., 1967, 47, 3179–3189.
30. J. Brynestad and G. P. Smith, J. Chem. Phys., 1967, 47, 3190–3193.
31. C. R. Boston, J. Brynestad and G. P. Smith, J. Chem. Phys., 1967, 47, 3193–3197.
32. W. E. Smith, J. Brynestad and G. P. Smith, J. Chem. Phys., 1970, 52, 3890–3903.
33. J. F. Parker, G. T. Cheek, D. F. Roeper and W. E. O'Grady, ECS Trans., 2012, 41, 23.
34. R. J. Gale, B. Gilbert and R. A. Osteryoung, Inorg. Chem., 1979, 18, 2723–2725.
35. S. P. Gou and I. W. Sun, Electrochim. Acta, 2008, 53, 2538–2544.
36. J. Brynestad, H. L. Yakel and G. P. Smith, J. Chem. Phys., 1966, 45, 4652–4664.
37. G. D. Stucky, J. B. Folkers and T. J. Kistenmacher, Acta Crystallogr., 1967, 23, 1064–1070.
38. M. Kozielski, I. Pollini and G. Spinolo, J. Phys. C: Solid State Phys., 1972, 5, 1253.
39. A. Ferrari, A. Braibanti and G. Bigliardi, Acta Crystallogr., 1963, 16, 846–847.
40. D. F. Roeper, K. I. Pandya, G. T. Cheek and W. E. O'Grady, J. Electrochem. Soc., 2011, 158, F21.
41. S. Siegel and E. Gebert, Acta Crystallogr., 1964, 17, 790.
42. B. Averill and P. Eldredge, General Chemistry: Principles, Patterns, and Applications, Saylor Foundation, 2011.
43. R. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.

---

Footnote

† Electronic supplementary information (ESI) available: The description of EXAFS experiment and analysis. Characterization of melting point. MCR-ALS analysis. AIMD simulations protocol. See DOI: https://doi.org/10.1039/d5sc01059d

---