Unveiling the covalency of versatile Pu(iii)-N bonds in a unique plutonium(iii) complex

Abstract

A trivalent plutonium–pyrazinyl–tetrazolate complex Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O (Pu_dtp, H₂dtp = 2,3-di-1H-tetrazol-5-ylpyrazine) was synthesized through metathesis reaction of plutonium bromide and Na₂(dtp)·2H₂O in water. This structure is particularly notable among complexes formed by trivalent f-elements and the dtp²⁻ ligand in aqueous media. In contrast to other trivalent f-elements, including all Ln³⁺ (with the exception of Pm³⁺) and Cm³⁺, preferentially coordinated with eight water molecules rather than the nitrogen donors of the dtp²⁻ ligand, Pu³⁺ exhibits a distinct affinity for nitrogen coordination. This observation provides strong evidence that the 5f electrons in Pu³⁺ are more delocalized than other studied trivalent f-elements. In Pu_dtp, three distinct Pu(III)–N bonds are present: one Pu(III)–N5 from pyrazinyl, one Pu(III)–N4 from the least electronegative nitrogen in the tetrazolate, and three Pu(III)–N1/N2/N3 from the most electronegative nitrogens in the tetrazolate. Experimental Pu(III)–N bond lengths, Wiberg bond indices (WBI), natural localized molecular orbitals (NLMO), quantum theory of atoms in molecules (QTAIM), and energy decomposition analysis (EDA), reveal a covalency trend: Pu(III)–N from the most electronegative nitrogen in tetrazolate > Pu(III)–N from the least electronegative nitrogen in tetrazolate > Pu(III)–N from pyrazinyl. This trend arises from the increased negative charge on the most electronegative nitrogen atoms in the tetrazolate ring, enhancing electrostatic Pu–N1/N2/N3 interactions. These stronger electrostatic interactions lead to shorter bond lengths, thereby enhancing orbital overlap and greater covalency, compared to the less electronegative nitrogen in tetrazolate (Pu–N4) and the neutral pyrazinyl nitrogen (Pu–N5).

---

Introduction

Understanding metal–ligand interactions remains a critical frontier in f-element chemistry, providing key insights into covalency,¹ electronic structure,² and potential Ln/An and An/An separations.³ Unlike the predominantly ionic bonding observed in most lanthanides, actinides, particularly early actinides with high oxidation states, exhibit significant covalent character due to more accessible radial extension of their 5f and 6d orbitals.⁴ The extent of metal–ligand orbital mixing is proportional to their spatial overlap and inversely proportional to their energy difference.⁵ Since covalency is generally associated with orbital mixing, actinides display a dual mechanism for covalent bonding, driven both by energy degeneracy and orbital overlap. For example, computational studies on An³⁺:(DPA²⁻)_n (An = Am, Cm, Bk, and Cf; n = 1–3) revealed that late actinides, with limited radial extension of their 5f orbitals, engage in covalent bonding primarily due to the energetic degeneracy between their 5f orbitals and ligand molecular orbitals, rather than spatial overlap.⁶ Furthermore, early actinides, where the 5f and 6d orbitals have similar energies, exhibit greater overlap between 6d orbitals and ligand orbitals than between 5f orbitals and ligand orbitals, as the 6d orbitals are more diffuse.⁵ A study on An–Cl covalency in AnCl₆²⁻ (An⁴⁺ = Th, U, Np, Pu) demonstrated substantial mixing between Cl 3p orbitals and An⁴⁺ 5f and 6d orbitals, with the 6d orbitals forming stronger covalent bonds than the 5f orbitals.⁷

A well-established trend in actinide-ligand bonding is the preference for softer ligands (e.g., N-, S-, or P-donors) to form more covalent bonds compared to harder ligands (e.g., F- and O-donors). This behaviour demonstrates that more itinerant 5f electrons in actinide ions exhibit greater affinity for softer donor atoms. For instance, Kaltsoyannis and coworkers found that in M[N(EPH₂)₂]₃ (M = U and Pu) complexes, covalency in M–E bonds increases in the order S < Se < Te.⁸ Leveraging this preference for ligands with high polarizability has also been explored as a strategy for improving the separation of minor actinides from lanthanides in used nuclear fuel processing. In particular, heterocyclic N-donor ligands have been successfully employed to selectively extract actinides(III) over lanthanides(III), offering a promising route for enhancing nuclear waste management.⁹

While the impact of different donor ligands on covalency has been extensively studied, the influence of the local electronic and steric environment of a single ligand type on actinide-ligand covalency remains less explored. The 5f orbitals of plutonium(III) are sufficiently extended to participate in bonding. However, the covalency of Pu(III)–N bonds is poorly understood, because early actinide and lanthanide separations are relatively straightforward.¹⁰ In addition, experimental research on covalency of Pu³⁺ remains scarce, due to the combined challenges of requiring specialized facilities for safe handling of radiological materials, limited isotope availability,^11,12 and the air-sensitive nature of Pu³⁺.¹³ To explore how the local electronic and steric environment of nitrogen-donor ligands influences covalent bonding with Pu³⁺, tetrazoles represent a promising class of ligands. These ligands offer unique advantages in coordination chemistry due to their versatile bonding modes and the ability to exist in both neutral and anionic forms, enabling fine-tuning of electronic properties and promoting structural diversity.^14–16 Herein, 2,3-di-1H-tetrazolate-5-ylpyrazine (dtp²⁻) was chosen, with multiple nitrogen donor atoms, two from the pyrazine ring and eight from two tetrazolate rings. This provides a variety of nitrogen atoms with differing electron density for metal coordination.

Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O (Pu_dtp) was synthesized from the reaction of Na₂(dtp)·2H₂O with Pu³⁺ salt in aqueous solution. Notably, Pu_dtp does not have a structural congener among other reported trivalent f-element dtp complexes.^17,18 Unlike other trivalent f-elements, including lanthanides (excluding Pm³⁺) and Cm³⁺ that preferentially coordinate with water rather than nitrogen atoms of this ligand, Pu³⁺ exhibits a distinct preference for nitrogen coordination. This observation indicates that 5f electrons in Pu³⁺ are more delocalized than the other studied trivalent f-elements.

As shown in Fig. S1.1,† this ligand exhibits three distinct coordination modes, forming three distinct Pu(III)–N bonds: three Pu(III)–N1/N2/N3 from the most negative charged nitrogens in tetrazolate, one Pu(III)–N4 from the least negative charged nitrogen in tetrazolate, and one Pu(III)–N5 from pyrazinyl, embedded in a resonance-stabilized aromatic ring. By integrating experimental bond length data with computational metrics—Wiberg bond indices (WBIs), natural localized molecular orbitals (NLMOs) analysis, the quantum theory of atoms in molecules (QTAIM), and energy decomposition analysis (EDA), covalent contributions to these five Pu(III)–N bonds were compared.

Experimental

General caution! Plutonium isotopes, including ²³⁹Pu (approximately 96% ²³⁹Pu, t_1/2 = 24110 years), and ²⁴⁰Pu (approximately 4%, t_1/2 = 6561 years) pose significant health hazards due to their α-particle emissions and the radiotoxicity of their decay products, α-, β-, and γ-emitting daughters. To address these risks, all plutonium-related reactions were carried out in a radiation laboratory featuring a high-efficiency particulate air (HEPA)-filtered fume hood. Additionally, to further reduce the potential for inhalation and exposure, plutonium materials were handled only under solvent or immersion oil. During all characterization processes, radiation levels were continuously and meticulously monitored using multiple instruments to ensure full compliance with established safety protocols.

H₂dtp (2,3-di-1H-tetrazol-5-ylpyrazine) is a high-energy material. While this ligand is thermally stable,^19,20 explosions can occur under specific conditions. Therefore, it is essential to implement appropriate safety measures during experiments involving this ligand.

Materials

2,3-Pyrazinedicarbonitrile (98%, Sigma-Aldrich), NaN₃ (99%, Sigma-Aldrich), DI H₂O, anhydrous ZnCl₂ (98%, Sigma-Aldrich), HCl (37%, Sigma-Aldrich), HBr_(aq) (48%, Sigma-Aldrich), diethyl ether (99%, Fisher Scientific), NH_3(aq) (32%, Sigma-Aldrich) are all used as received. Synthesis of Na₂(dtp)·2H₂O was carried out following a literature procedure developed by Bu et al. with minor modifications.²¹ For detailed experimental conditions, please refer to our previous report.¹⁸ The plutonium used in this experiment was utilized as a PuCl_x solution (10 mg mL⁻¹ of plutonium content in 1 M HCl).^22,23

Synthesis of Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O (Pu_dtp)

A 0.2 mL ²³⁹Pu stock solution (containing 2 mg ²³⁹Pu, 0.0083 mmol) evaporated to dryness in a 20 mL scintillation vial. The resulting residue was dissolved in 1 mL of water and transferred to a centrifuge tube. Plutonium hydroxide was precipitated by adding excess NH₄OH to the solution. The precipitate was centrifuged and washed three times with 1 mL of water to eliminate excess NH₄Cl. Excess HBr was then added to the precipitate, forming an aqueous solution of PuBr₃. This solution was gently evaporated to dryness under a heat lamp with a slow stream of nitrogen, yielding a hydrated PuBr₃ residue.

The hydrated ²³⁹PuBr₃·nH₂O solid was washed with diethyl ether (3 × 2 mL) to remove any embedded Br₂, formed due to the oxidation of HBr. The PuBr₃·nH₂O solid was then dissolved in 0.1 mL of DI water in a shell vial. A solution containing 8 mg (∼0.03 mmol) Na₂(dtp)·2H₂O, dissolved in 1.5 mL DI water, was added to the ²³⁹PuBr₃ solution. The mixture was allowed to stand at room temperature, leading to the formation of crystals suitable for single-crystal X-ray diffraction within a day. A small portion of the crystals was isolated for characterization using single-crystal X-ray diffraction and solid-state UV-vis-NIR spectroscopy.

Instrumentation

Crystallographic studies. Crystal suitable for single crystal X-ray diffraction was carefully selected under immersion oil, mounted on a MiTeGen MicroLoop, and oriented using a digital camera integrated with the APEX IV software on a Bruker D8 Quest X-ray diffractometer. Data collection strategies were calculated for Mo K_α X-ray radiation (λ = 0.71073 Å) at 100 K, maintained using a Cryo Industries Cryocool cold stream system. The diffraction data were evaluated, integrated, and reduced using Apex-V.² with absorption corrections applied via the multi-scan method implemented in SADABS.²⁴ The structure was solved and refined using direct methods within the SHELXTL suite, accessed through the OLEX2 software package.^25,26 Supplementary crystallographic data for this study have been deposited with the Cambridge Crystallographic Data Centre (CCDC) under deposition number 2421228.

Solid-state UV-vis-NIR spectroscopy

Selected crystals were placed on a glass slide under Paratone-N oil and positioned under the light source of a microspectrophotometer. The software optimized the data collection time, and spectra were recorded from 320 to 1700 nm using a 75 W xenon lamp as the light source.

Theory

All calculations were performed using the Amsterdam Density Functional (ADF) engine of the AMS 2024.106 software, utilizing the experimentally single crystal XRD determined crystal structures as a foundation. Wiberg bond indices (WBIs) and natural localized molecular orbitals (NLMOs) were carried out using NBO6.²⁷ The electron density distribution of Pu_dtp was examined on the quantum theory of atoms in molecules (QTAIM).²⁸ The numerical quality was set to “very good,” with the analysis level set as “Full”, source function and a grid spacing of 0.2 bohr. To compare the difference between those versatile Pu–N bonds, the energy of Pu_dtp was examined using energy decomposition analysis (EDA). We have calculated the EDA in terms of three reactions for which different fragments were defined to better capture the interaction of the different coordinating ligands (the details are shown in Section S8†):

Pu–N1/N5: [Pu(Hdtp)(dtp)(H₂O)₄] + dtp²⁻ → [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻

Pu–N2/N3: [Pu(Hdtp)(dtp)(H₂O)₄] + dtp²⁻ → [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻

Pu–N4: [Pu(dtp)₂(H₂O)₄]⁻ + Hdtp⁻ → [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻

All calculations were generated employing the PBE0 functional,²⁹ with no frozen-core approximation applied, paired with the TZ2P basis set.³⁰ Scalar relativistic effects were incorporated through the zero-order regular approximation (ZORA).³¹ To ensure high precision, the computational settings were configured to be a “very good” accuracy level. More details are shown in ESI.†

Results and discussion

Structural characterization

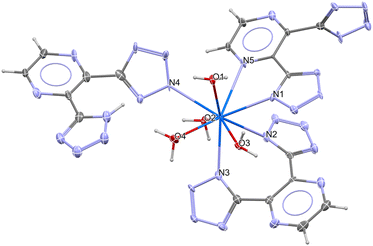
The compound, Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O (Pu_dtp) formed from the reaction of Na₂(dtp)·2H₂O and PuBr₃ in aqueous solution. Single-crystal X-ray diffraction analysis reveals Pu_dtp crystallizes in the triclinic space group P1̄ (#2) consisting of one [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻ anion and two Na⁺ cations to neutralize the charge as well as nine noncoordinated water molecules to form a hydrogen framework in the asymmetric unit, shown in Sections S2 and S3.† In the [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻ anion (Fig. 1), the Pu³⁺ cation exhibits a coordination environment comprising four water molecules and 5 nitrogen atoms. The five nitrogen donors arise from two distinct bidentate moieties of the dtp²⁻ dianion, a tetrazolate–tetrazolate (N^N, referring to a bidentate ligand with two nitrogen donor atoms) and a tetrazolate–pyrazinyl (N^N) as well as a monodentate Hdtp⁻ anion. This arrangement results in a spherical capped square antiprismatic geometry with a deviation value of 0.928, from the analysis via SHAPE software.^32,33 Additional structural information including coordination environment, hydrogen bonds, extended structures are shown in Sections S3 and S4.†

Fig. 1 Thermal ellipsoid plots of Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O, with probability 50% at 100 K. Non-coordinating H₂O molecules and two Na⁺ cations are omitted for clarity. (Pu³⁺, blue; O, red; N, light blue; C, grey, H light gray).

Bonding

Pu–H₂O bonds ranging from 2.468(5) Å to 2.499(5) Å, is comparable with those observed in previously reported water-containing Pu³⁺ complexes.^13,34–39 These three Pu–N1/N2/N3_tetrazolate bonds involving the most electronegative nitrogen in the tetrazolate ring have bond lengths of 2.572(6) Å, 2.586(6) Å, and 2.597(6) Å, respectively. Those bonds are much shorter than Pu–N4_tetrazolate (2.673(6) Å) from the least electronegative nitrogen in tetrazolate and Pu–N5 (2.757(6) Å) from pyrazinyl. They fall within the range of reported Pu–N bonds in recently reported Pu–tetrazolate complexes of [Pu(pmtz)₃(H₂O)₃]·8H₂O and [(Pu(pmtz)₂(H₂O)₃)₂(μ-pmtz)]₂(pmtz)₂·14H₂O (pmtz⁻ = 5-(pyrimidyl)tetrazolate).⁴⁰ Pu–N4 is 0.16 Å shorter than that in [Pu(Hdtb)(H₂O)₈](dtb)·11H₂O (dtb²⁻ = 1,3-di(tetrazolate-5-yl)benzene) with ^IXPu(III)–N, where IX refers to the coordination number, (2.8338(15) Å) from least electronegative nitrogen in tetrazolate, likely due to less steric hindrance.⁴¹

To further investigate the bonding of [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻, Wiberg bond indices (WBI) and natural localized molecular orbitals (NLMOs) approximation were conducted, since it offers a more realistic picture of the chemical bonding, as reported in several studies.^39,42–44 The Pu contribution to the NLMOs was decomposed into atomic orbital character, with detailed results provided in Section S8,† Fig. 2 and 3. The WBI analysis indicates that the Pu–N bonds, with average value of 0.2820 are stronger than Pu–H₂O, with average values of 0.2350. In general, the total Pu contribution for the one σ and one weak π bonds to NLMOs of all four Pu–H₂O interactions is less than 5.82% and average is 5.53%, that is observably less than plutonium contribution to NLMOs of five Pu–N interactions. This observation further supports the general trend that ligands with increased polarizability exhibit greater orbital overlap and stronger covalent interactions with actinide ions, consistent with previous studies.^45,46

Fig. 2 Selected α and β spin natural localized molecular orbitals (NLMOs) and metal contributions to the NLMOs along with their hybrid contributions showing the Pu–N bonding [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻.

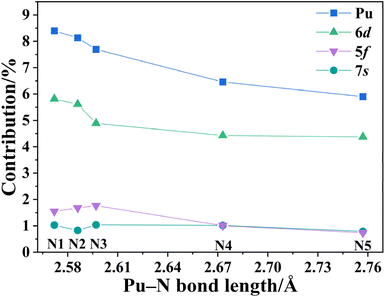Fig. 3 Average (α + β spin) plutonium and specific orbitals (6d, 5f and 7s) contributions to the Pu–N NLMOs vs. respective bond lengths.

A comparative analysis of these five Pu–N bonds reveals differences in their bonding characteristics. The WBI bond order analysis indicates that the Pu–N1/N2/N3 bonds are stronger than Pu–N4 bond (ΔWBI > 0.04) and are stronger than Pu–N5 bond (ΔWBI > 0.07), shown in Table 1. As illustrated in Fig. 3, further evaluation of the covalency in the Pu–N bonds using NLMO analysis, is consistent with the WBI findings. The results indicate that the contribution of plutonium to the bonding orbitals is inversely correlated with the Pu–N bond lengths. The average α + β spin contribution of Pu to the NLMOs is approximately 8% for Pu–N1/N2/N3 bonds, higher than the 6.46% for Pu–N4 and decreasing to 5.90% for Pu–N5. A breakdown of this metal contribution into 6d, 5f, and 7s components, with a negligible 6p contribution, reveals that all these NLMOs exhibit stronger 6d involvement than 5f due to the greater diffusivity of 6d orbitals. The 7s contribution remains relatively consistent across the five Pu–N bonds, while 6d and 5f contributions show a slight decrease from Pu–N1/N2/N3 to Pu–N4/5. These findings demonstrate a distinct trend in covalency: Pu–N1/N2/N3 from the most negative charged nitrogen in tetrazolate > Pu–N4 from the least negative charged nitrogen in tetrazolate > Pu–N5 from neutral pyrazinyl. Here, a hypothesis is proposed that this observed decrease in covalency correlates with the electronegativity of the respective nitrogen atoms, highlighting the influence of electronic charge distribution on the strength of covalent interactions.

Table 1 Wiberg bond indices (WBI) of Pu–N bonds

Bond	WBI
M–N1	0.3236
M–N2	0.3095
M–N3	0.2979
M–N4	0.2518
M–N5	0.2273

---

To further elucidate trends in covalency and investigate the underlying factors contributing to these trends, QTAIM analysis was employed including several metrics.⁴⁷ The electron density at the bond critical point (BCP), ρ(r), serves as an indicator of electron accumulation, with higher values signifying stronger bonding interactions. The potential energy density, V(r), is associated with attractive interactions, where more negative values reflect stabilization of electron density concentration. An excess of kinetic energy density, G(r), suggests pronounced closed-shell characteristics, while a more negative total energy density, H(r), is indicative of stronger covalent bonding. The bond strength parameter, H(r)/ρ(r), provides further insight into covalency, with more negative values corresponding to increased covalent character. The delocalization index, δ(r), quantifies electron delocalization between atomic basins, with higher values implying stronger bonding and enhanced electron sharing. The localization index, λ(M), represents the electron population assigned to an atom M based on QTAIM partitioning. It is used calculating the oxidation state, OS(M) through the equation OS(M) = Z(M) – λ(M), where Z(M) is the nuclear charge of atom M. A greater degree of covalent character can result in deviations from classical oxidation state values.⁴⁸ Table 2 summarizes the main QTAIM metrics for Pu–H₂O_average and five Pu–N interactions, while detailed metrics for individual Pu–H₂O bond are provided in Section S5.†

Table 2 Single crystal X-ray diffraction (SC-XRD) bond length of Pu–O_avg and Pu–N in Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O at 100 K and QTAIM metrics, including the electron density ρ(r) in e Å⁻³; potential (V), kinetic (G), and total (H) energy densities in kJ mol⁻¹ Å⁻³; delocalization indices, δ(r), and localization indices, λ(M); integrated oxidation state, OS, calculated from the equation OS(M) = Z(M) – λ(M), at the bond critical points (BCPs). Fully detailed metrics can be found in Section S6 in the ESI. Larger values of electron density (ρ(r)) tend to in part indicate greater covalent contributions. More negative values of the bond strength parameter (H(r)/ρ(r)) correspond to more covalent character. Higher values delocalization index (δ(r)) corresponds to stronger delocalization and bonding

	Pu–Oavg	Pu–N1	Pu–N2	Pu–N3	Pu–N4	Pu–N5
Distance/Å	2.484(5)	2.572(6)	2.586(6)	2.597(6)	2.673(6)	2.757(6)
ρ(r)	0.3276	0.3354	0.3273	0.3079	0.2584	0.2351
V(r)	−964.60	−905.97	−864.64	−804.37	−639.09	−529.51
G(r)	942.50	786.12	744.42	719.26	615.19	491.56
H(r)	−22.10	−119.85	−120.21	−85.11	−23.91	−37.94
H(r)/ρ(r)	−67.18	−357.28	−367.25	−276.38	−92.61	−161.36
δ(r)	0.2638	0.3053	0.2987	0.2852	0.2268	0.2217
λ(Pu)	90.4908
OS(Pu)	3.5

---

QTAIM analysis demonstrates that Pu–N bonds exhibit a greater degree of covalency compared to Pu–H₂O bonds. Being consistent with NLMO results, among five Pu–N bonds, Pu–N1/N2/N3, associated with the most electronegative nitrogen sites in tetrazolate, exhibit the stronger covalent character, as evidenced by their higher electron density ρ(r), more negative total energy density H(r), more negative bond strength parameter H(r)/ρ(r), and greater delocalization indices δ(r), compared with those of Pu–N4/N5. In addition, QTAIM analysis also reveals that Pu–N4 is slightly stronger than Pu–N5 due to slightly higher electron density (ρ(r) = 0.2584 vs. 0.2351 e Å⁻³) and slightly higher degree of electron delocalization (δ(r) = 0.2268 vs. 0.2217). However, Pu–N4 possess less negative total energy density H(r) (H(r) = −23.91 vs. −37.94 kJ mol⁻¹ Å⁻³) and less negative bond strength parameter (H(r)/ρ(r) = −92.61 vs. −161.36 kJ mol⁻¹ e⁻¹). The observed deviation in the total energy density for Pu–N4 and N5 can be rationalized by the chelate effect, that enhances the affinity of a chelating ligand Pu–N5 for a metal ion compared to its monodentate counterparts Pu–N4.

The observation of both potential energy density, V(r) and kinetic energy density G(r) of Pu–N1/N2/N3 are higher than that of Pu–N4/N5 and reveals that the negative charge from the tetrazolate ring enhances the electrostatic interaction of the ligand and Pu³⁺, that makes more Pu³⁺ preference to the ligand (shorter Pu–N bond length), that in turn lead to more orbital overlap and more covalency. Even though N4 is less negatively charged than N1/N2/N3 due to a resonance and charge distribution of tetrazolate, electronegativity of N4 from the delocalized change tetrazolate is more preferred for Pu³⁺ than neutral N5. Therefore, there are more potential energy density (V(r) = −639.09 vs. −529.51 kJ mol⁻¹ Å⁻³) and kinetic energy density (G(r) = 615.19 vs. 491.56 kJ mol⁻¹ Å⁻³) for N4 than that of neutral N5 with Pu³⁺. This corresponds to shorter bond length of Pu–N4 (2.673 Å vs. 2.757 Å for Pu–N5) further supports that Pu–N4, exhibits a greater degree of covalency than Pu–N5. This further affirms the covalency trend from NLMO data and experimental bond lengths.

In addition, the integrated oxidation state for Pu³⁺ is notably elevated to 3.5, that may be attributed to Pu^3+/4+ redox potentials (−1.04 V, 1 M HClO₄, vs. SHE),⁴⁹ leading to electron density donation from Pu(III) to the local environment. This increase in the integrated oxidation state is likely driven more by redox behaviour than by Pu–L bonding characteristics.

To further validate the hypothesis, a more comprehensive comparison of the electrostatic and orbital energy contributions between the Pu–N1/N2/N3_tetrazolate and Pu–N5_pyridinyl interactions was conducted using energy decomposition analysis (EDA), shown in Table 3.⁵⁰ This method divides the interaction energy (ΔE_int) of chemical bonds between two or more molecular fragments in a fixed geometry into four main components, as expressed in the following equation:⁵¹

ΔE_int = ΔE_elast + ΔE_Pauli + ΔE_orb + ΔE_disp

Table 3 Energy decomposition analysis (EDA), in kJ mol⁻¹, of Pu_dtp

kJ mol^−1	Pu–N1/N5	Pu–N2/N3	Pu–N4
Pauli repulsion	365.13	2260.17	191.53
Electrostatic	−506.76	−1067.58	−179.42
Orbital	−137.94	−2406.8	22.99
Solvation (el)	−1018.67	−1017.36	−1018.66
Total	−1283.81	−2217.15	−969.14

---

Electrostatic interaction (ΔE_elestat) represents the classical Coulomb attraction between the charge distributions of the interacting fragments. This term is dominant in ionic bonds and describes stabilization due to electrostatic forces. Pauli repulsion (ΔE_Pauli) accounts for the repulsive interactions caused by the overlap of occupied orbitals, due to the Pauli exclusion principle, that comprises the destabilizing interactions between electrons of the same spin on either fragment. Orbital interaction (ΔE_orb) describes the mixing of molecular orbitals, including covalent bonding effects, charge transfer, and polarization. This term plays a crucial role in covalent bonding and stabilizes the system beyond electrostatics. Dispersion energy (ΔE_disp) represents van der Waals interactions due to instantaneous dipole–induced dipole attractions, particularly significant for non-covalent interactions.

Comparing the EDA results for Pu–N1/N5 and Pu–N2/N3 reveals that the longer Pu–N_pyrazinyl bond length than Pu–N_tetrazolate results in a significant decrease in ΔE_Pauli. However, the negative charge of tetrazolate provides substantially greater electrostatic stabilization, particularly in the Pu–N2/N3 bonds. Additionally, the Pu–N_tetrazolate interactions exhibit stronger orbital contributions to the total bonding interactions than Pu–N_pyrazinyl. Therefore, in Pu_dtp, compared to the Pu–N_pyrazinyl interaction, the Pu–N_tetrazolate interaction is predominantly stabilized by stronger electrostatic interactions along with significant orbital contributions.

All these computational data on these three distinct Pu(III)–N bonds reveal a covalency strength trend: Pu(III)–N_tetrazolate from the most electronegative nitrogen in tetrazolate > Pu(III)–N_tetrazolate from the least electronegative nitrogen in tetrazolate > Pu(III)–N_pyrazinyl from pyrazinyl. This trend arises from the increased negative charge on the tetrazolate ring, enhancing their electrostatic interactions and shortening the bond lengths with Pu³⁺. This, in turn, promotes better orbital overlap and results in greater covalency compared to the neutral pyrazinyl nitrogen.

Solid-state UV-vis-NIR spectrum

The characteristic Laporte-forbidden 5f → 5f transition peaks observed in Pu_dtp are consistent with those reported for PuCl₃ thin films by Carnall and co-workers, and the following discussion is based on the spectral assignments for that compound.⁵² As illustrated in Fig. 4, the spectral profile exhibits three distinct electronic transition groups (L, M, and K), as diagnostic markers for the Pu³⁺ compounds: group L and M (18 822–16 828 cm⁻¹), namely these 5f → 5f transition peaks as ⁶H_5/2 → ⁴L_13/2, ⁴K_11/2, ⁴I_9/2, ⁴P_5/2, and group K (16 828–15 765 cm⁻¹), as ⁶H_5/2 → ⁴M_15/2. These 5f → 5f transition peaks align with prior observations in Pu³⁺ compounds, such as Pu₂[C₆(CO₂)₆](H₂O)₉·H₂O, Pu₂[C₆(CO₂)₆](H₂O)₈·2H₂O,³⁷ and [(H₃O)(18-crown-6)][Pu(H₂O)₄(18-crown-6)](ClO₄)₄·2H₂O.³⁹ Additionally, other high-intensity 5f → 5f transitions characteristic of Pu³⁺ are evident, including group H (15 424–14 637 cm⁻¹, ⁶H_5/2 → ⁶F_11/2), group F (13 323–11 714 cm⁻¹, ⁶H_5/2 →⁶H_15/2, ⁶F_9/2), group E (11 655–10 520 cm⁻¹, ⁶H_5/2 → ⁶H_13/2), group D (10 127–9541 cm⁻¹, ⁶H_5/2 → ⁶F_7/2), group C (9422–8397 cm⁻¹, ⁶H_5/2 → ⁶H_11/2), and group B (7400–6000 cm⁻¹, ⁶H_5/2 → ⁶F_3/2, ⁶H_5/2, ⁶H_9/2). Furthermore, as shown in Fig. S5.1,† compared with the solid-state absorption spectrum of [Pu(H₂O)₉]³⁺,³⁸ all these 5f → 5f transition peaks exhibit red shifts due to more covalency of Pu–N bonds than Pu–H₂O bonds. In addition, the broad band from 32 000 cm⁻¹ to 20 000 cm⁻¹, corresponding to the metal to ligand charge transfer due to the accessible Pu^3+/4+, (−1.04 V, 1 M HClO₄, vs. SHE),⁴⁹ has also been observed in other Pu³⁺ complexes, such as Pu₂[C₆(CO₂)₆](H₂O)₉·H₂O, Pu₂[C₆(CO₂)₆](H₂O)₈·2H₂O,³⁷ [Pu(pmtz)₃(H₂O)₃]·8H₂O and [(Pu(pmtz)₂(H₂O)₃)₂(μ-pmtz)]₂(pmtz)₂·14H₂O.⁴⁰

Fig. 4 Experimental solid-state UV-vis-NIR absorption spectrum of Pu_dtp.

Conclusions

In summary, [Pu(Hdtp)(dtp)₂(H₂O)₄]²⁻ has been synthesized and characterized by X-ray single crystal diffraction and solid-state UV-vis-NIR absorption spectroscopy. Analysis of experimental bond lengths, WBIs, NLMOs and QTAIM reveals that the negative charge on the most electronegative nitrogen atom within the tetrazolate ring enhances electrostatic interactions (Pu–N1, N2, and N3). These stronger electrostatic interactions result in shorter bond lengths that in turn enhance orbital overlap and increase covalency, compared to the interactions involving the less electronegative nitrogen atom of the tetrazolate ring (Pu–N4) and the neutral pyrazinyl nitrogen (Pu–N5). This observed trend highlights a direct correlation between the electronegativity of the coordinating nitrogen atoms and the degree of Pu–N covalency, demonstrating that the strength of Pu(III)–N bonding is influenced by the electronic properties of the nitrogen donors. These findings underscore the complexity of Pu–N bonding in Pu³⁺ complexes with nitrogen-containing ligands of varying electronic structures, providing valuable insights for the rational design of ligands to further investigate covalency and separation processes in actinide chemistry.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data for Pu_dtp has been deposited at the CCDC under 2421228.

Author contributions

Zhuanling Bai and Joseph M. Sperling carried out the synthesis and characterization of Pu_dtp. Zhuanling Bai and Madeline C. Martelles performed the computational studies. Zhuanling Bai, Joseph M. Sperling, and Thomas E. Albrecht jointly conceived and organized the project. Zhuanling Bai wrote the manuscript with input from all authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Heavy Elements Chemistry Program, under the award number DE-SC0023693.

Notes and references

1. L. I. Katzin, Nature, 1950, 166, 605.
2. S. K. Cary, M. Vasiliu, R. E. Baumbach, J. T. Stritzinger, T. D. Green, K. Diefenbach, J. N. Cross, K. L. Knappenberger, G. Liu, M. A. Silver, A. E. DePrince, M. J. Polinski, S. M. Van Cleve, J. H. House, N. Kikugawa, A. Gallagher, A. A. Arico, D. A. Dixon and T. E. Albrecht-Schmitt, Nat. Commun., 2015, 6, 6827.
3. K. L. Nash, C. Madic, J. N. Mathur and J. Lacquement, in The Chemistry of the Actinide and Transactinide Elements, ed. L. R. Morss, N. M. Edelstein and J. Fuger, Springer Netherlands, Dordrecht, 2006, pp. 2622–2798.
4. G. Schreckenbach, P. J. Hay and R. L. Martin, J. Comput. Chem., 1999, 20, 70–90.
5. M. L. Neidig, D. L. Clark and R. L. Martin, Coord. Chem. Rev., 2013, 257, 394–406.
6. M. P. Kelley, J. Su, M. Urban, M. Luckey, E. R. Batista, P. Yang and J. C. Shafer, J. Am. Chem. Soc., 2017, 139, 9901–9908.
7. J. Su, E. R. Batista, K. S. Boland, S. E. Bone, J. A. Bradley, S. K. Cary, D. L. Clark, S. D. Conradson, A. S. Ditter, N. Kaltsoyannis, J. M. Keith, A. Kerridge, S. A. Kozimor, M. W. Löble, R. L. Martin, S. G. Minasian, V. Mocko, H. S. La Pierre, G. T. Seidler, D. K. Shuh, M. P. Wilkerson, L. E. Wolfsberg and P. Yang, J. Am. Chem. Soc., 2018, 140, 17977–17984.
8. K. I. M. Ingram, M. J. Tassell, A. J. Gaunt and N. Kaltsoyannis, Inorg. Chem., 2008, 47, 7824–7833.
9. Z. Kolarik, Chem. Rev., 2008, 108, 4208–4252.
10. A. Kovács, C. Apostolidis and O. Walter, Inorganics, 2019, 7, 26.
11. J. Su, T. Cheisson, A. McSkimming, C. A. P. Goodwin, I. M. DiMucci, T. Albrecht-Schönzart, B. L. Scott, E. R. Batista, A. J. Gaunt, S. A. Kozimor, P. Yang and E. J. Schelter, Chem. Sci., 2021, 12, 13343–13359.
12. N. K. Gupta, J. Mol. Liq., 2018, 269, 72–91.
13. S. Wang, E. V. Alekseev, W. Depmeier and T. E. Albrecht-Schmitt, Inorg. Chem., 2011, 50, 2079–2081.
14. F. R. Benson, Chem. Rev., 1947, 41, 1–61.
15. J.-P. Zhang, Y.-B. Zhang, J.-B. Lin and X.-M. Chen, Chem. Rev., 2012, 112, 1001–1033.
16. P. Pachfule, R. Das, P. Poddar and R. Banerjee, Cryst. Growth Des., 2010, 10, 2475–2478.
17. Z. Bai, M. Redington, S. Haldar, N. B. Beck, J. M. Sperling, B. Scheibe, J. P. Brannon, E. Zurek, L. Gagliardi and T. E. Albrecht, J. Am. Chem. Soc., 2025, 147, 6137–6148.
18. Z. Bai, B. Scheibe, J. M. Sperling and T. E. Albrecht-Schönzart, Inorg. Chem., 2022, 61, 19193–19202.
19. D.-P. Chi, L. Yang, J.-M. Han, G.-Y. Zhang, J.-C. Liu, Z.-Z. Yan, J. Qin and W.-C. Tong, Main Group Chem., 2020, 19, 105–116.
20. C. Qiao, L. Lü, W. Xu, Z. Xia, C. Zhou, S. Chen and S. Gao, Acta Phys.-Chim. Sin., 2020, 36, 190508.
21. J.-R. Li, Y. Tao, Q. Yu, X.-H. Bu and S. Kitagawa, Chem.–Eur. J., 2008, 14, 2271–2776.
22. CrysAlisPro, Version 1.171.41.115a, Rigaku Oxford Diffraction, Oxford, UK, 2021.
23. APEX4, Version 2021.4-0, Bruker AXS Inc., Madison, Wisconsin, USA, 2021.
24. SADABS, Bruker AXS Inc., Madison, Wisconsin, USA 2016.
25. G. M. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8.
26. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
27. G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931–967.
28. J. I. Rodríguez, R. F. W. Bader, P. W. Ayers, C. Michel, A. W. Götz and C. Bo, Chem. Phys. Lett., 2009, 472, 149–152.
29. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
30. E. Van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142–1156.
31. E. Van Lenthe, E. J. Baerends and J. G. Snijders, J. Comput. Chem., 1994, 101, 9783–9792.
32. D. Casanova, M. Llunell, P. Alemany and S. Alvarez, Chem.–Eur. J., 2005, 11, 1479–1494.
33. A. Ruiz-Martínez, D. Casanova and S. Alvarez, Chem.–Eur. J., 2008, 1291–1303.
34. S. K. Cary, S. S. Galley, M. L. Marsh, D. L. Hobart, R. E. Baumbach, J. N. Cross, J. T. Stritzinger, M. J. Polinski, L. Maron and T. E. Albrecht-Schmitt, Nat. Chem., 2017, 9, 856–861.
35. R. G. Surbella, L. C. Ducati, K. L. Pellegrini, B. K. McNamara, J. Autschbach, J. M. Schwantes and C. L. Cahill, Chem. Commun., 2017, 53, 10816–10819.
36. W. Runde, L. F. Brodnax, G. Goff, A. C. Bean and B. L. Scott, Inorg. Chem., 2009, 48, 5967–5972.
37. J. M. Sperling, A. N. Gaiser, C. J. Windorff, B. E. Klamm, M. A. Whitefoot, A. T. Chemey, B. N. Long, J. G. Campbell and T. E. Albrecht-Schmitt, Inorg. Chem., 2020, 59, 3085–3090.
38. J. H. Matonic, B. L. Scott and M. P. Neu, Inorg. Chem., 2001, 40, 2638–2639.
39. K. Li, S. Hu, Q. Zou, Y. Zhang, H. Zhang, Y. Zhao, T. Zhou, Z. Chai and Y. Wang, Inorg. Chem., 2021, 60, 8984–8989.
40. Z. Bai, B. Scheibe, J. M. Sperling, N. B. Beck, J. P. Brannon, D. Gomez Martinez, B. M. Rotermund and T. E. Albrecht-Schönzart, Inorg. Chem., 2024, 63, 1266–1273.
41. Z. Bai, J. M. Sperling and T. E. Albrecht, Inorg. Chem., 2025, 64(16), 8164–8173.
42. Z. K. Huffman, J. M. Sperling, C. J. Windorff, B. N. Long, L. Cordova, H. Ramanantoanina, C. Celis-Barros and T. E. Albrecht-Schönzart, Chem. Commun., 2022, 58, 11791–11794.
43. B. N. Long, M. J. Beltrán-Leiva, C. Celis-Barros, J. M. Sperling, T. N. Poe, R. E. Baumbach, C. J. Windorff and T. E. Albrecht-Schönzart, Nat. Commun., 2022, 13, 201.
44. J. M. Sperling, E. J. Warzecha, C. Celis-Barros, D.-C. Sergentu, X. Wang, B. E. Klamm, C. J. Windorff, A. N. Gaiser, F. D. White, D. A. Beery, A. T. Chemey, M. A. Whitefoot, B. N. Long, K. Hanson, P. Kögerler, M. Speldrich, E. Zurek, J. Autschbach and T. E. Albrecht-Schönzart, Nature, 2020, 583, 396–399.
45. Y.-M. Chen, C.-Z. Wang, L. Zhang, Q.-Y. Wu, J.-H. Lan, Z.-F. Chai and W.-Q. Shi, Dalton Trans., 2024, 53, 7406–7413.
46. C. A. P. Goodwin, A. W. Schlimgen, T. E. Albrecht-Schönzart, E. R. Batista, A. J. Gaunt, M. T. Janicke, S. A. Kozimor, B. L. Scott, L. M. Stevens, F. D. White and P. Yang, Angew. Chem., Int. Ed., 2021, 60, 9459–9466.
47. Q.-R. Huang, J. R. Kingham and N. Kaltsoyannis, Dalton Trans., 2015, 44, 2554–2566.
48. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, Chem. Phys., 2002, 117, 5529–5542.
49. S. W. Rabideau and J. F. Lemons, J. Am. Chem. Soc., 1951, 73, 2895–2899.
50. D. Rodrigues Silva, L. De Azevedo Santos, M. P. Freitas, C. F. Guerra and T. A. Hamlin, Chem.–Asian J., 2020, 15, 4043–4054.
51. P. Jerabek, P. Schwerdtfeger and G. Frenking, J. Comput. Chem., 2019, 40, 247–264.
52. W. T. Carnall, P. R. Fields and R. G. Pappalardo, J. Chem. Phys., 1970, 53, 2922–2938.

---

Footnote

† Electronic supplementary information (ESI) available: Coordination modes of 2,3-di-1H-tetrazolate-5-ylpyrazine (dtp²⁻), images of reaction and crystals, additional crystal structures, crystallographic data, spectra of Na₂[Pu(Hdtp)(dtp)₂(H₂O)₄]·9H₂O and [Pu(H₂O)₉]³⁺, additional theory details, including WBI, QTAIM, NLMO, and EDA. CCDC 2421228. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5sc01808k

---