Electrochemical dechlorination promotes syngas production in N-heterocyclic carbene protected Au₁₃ nanoclusters

Abstract

Surface ligands play an important role in dictating the structure and catalytic properties of metal nanoclusters. Recently, a novel class of Au clusters protected by N-heterocyclic carbenes (NHCs) and halogens has been synthesized; however, the dynamic stability of the Au–NHCs/Au–halogen interface in real electrochemical environments as well as the influence of the ligand layer on the catalytic process remains obscure. Herein, we combined first-principles simulations with experiments to investigate the metal–ligand interface interaction of the classical [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster and its unique potential to promote electrocatalytic CO₂ reduction to syngas. Our simulations revealed the facile shedding of chlorine ligands from the surface of the Au₁₃ core upon electrochemical biasing, and the more negative the applied potential, the faster the kinetics of the Au–Cl bond cleavage. By contrast, the Au–NHC interface is highly stable, indicating the greater stability of Au–C bonds over the Au–Cl bonds under electrochemical conditions. Interestingly, the exposed icosahedral Au in dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster is capable of efficiently catalyzing electrochemical CO₂ reduction to generate CO and H₂ with comparable barriers in a wide potential range, showcasing its strong potential for syngas formation. Our predictions are further corroborated by experimental electrochemical data, where X-ray photoelectron spectroscopy (XPS) verified halogen stripping under acid or neutral media, and the activated Au₁₃ cluster demonstrated enhanced catalytic efficacy for syngas formation with a CO : H₂ ratio of approximately 0.8 to 1.2 across a broad potential range of −0.50 to −1.20 V. This work reveals an exciting frontier in the understanding of ligand etching dynamics in NHC-protected metal nanoclusters, and particularly, the catalytic preference for syngas production is revealed for the first time in gold-based nanoclusters, which is distinctive from previously reported Au nanoclusters that mainly produce CO.

---

1 Introduction

Atomically precise gold nanoclusters (AuNCs) passivated by organic ligands have emerged as a novel class of functional nanomaterials and received tremendous research interest recently as promising catalysts in various electrocatalytic reactions such as the hydrogen evolution reaction (HER) and electrocatalytic CO₂ reduction reaction (CO₂RR).^1–5 The well-defined molecular structure of AuNCs can be characterized by a multitude of techniques, including single crystal X-ray diffraction (SCXRD), nuclear magnetic resonance (NMR) spectroscopy, and mass spectrometry (MS).^6,7 The unique molecule-like and size-dependent properties of AuNCs coupled with their structural richness and diversity, present great opportunities to tailor their geometric structures and catalytic applications. Ligands, as the outermost protective layer, are closely related to the stability and physicochemical properties of AuNCs. Unlike nanoparticles, their presence not only prevents aggregation and facilitates nanocluster segregation, but also diversifies the structural functions of nanoclusters and generates important applications related to electronics, magnetism, optics, catalysis, biology and sensing.^8–11 It is typically assumed that the presence of an intact ligand shell leads to low catalytic activity in AuNCs.^12,13 Pretreatments such as thermal treatment, acid treatment and electrochemical etching^13–19 have been frequently employed to promote the catalytic activity of AuNCs by partially or entirely removing the stabilizing ligands from the cluster surface. Nevertheless, there exists a trade-off between catalytic activity and durability in ligand-protected AuNCs, and a crucial objective is to discover an appropriate treatment that stimulates the catalytic efficacy while preserving the stability of the cluster structure.²⁰

Among the numerous types of ligand-protected AuNCs, the structural and catalytic properties of AuNCs protected by thiolate, alkynyl and phosphine ligands have been extensively investigated, while the N-heterocyclic carbene (NHCs)-protected AuNCs are much less explored.^21–27 The NHC ligands exhibit strong σ-donating and moderate π-accepting abilities, and have been increasingly appreciated as a promising alternative to thiols for surface stabilization of metal surfaces and nanoclusters. In 2019, Crudden and co-workers made a seminal breakthrough in obtaining the first atomically precise [Au₁₃(NHC)₉Cl₃]²⁺ nanoclusters protected by NHCs and halogen ligands via the direct reduction of metal–carbene complexes.^28,29 Since then, great progress has been made in the experimental synthesis of other NHC-protected AuNCs with metal core sizes of Au₆, Au₁₀, Au₁₁, Au₁₆, Au₁₇, Au₂₃, Au₂₄, Au₂₅ and Au₄₄.^4,30,31 Particularly, in recent experimental studies, Au₁₃ clusters protected by bis-N-heterocyclic carbene (bisNHC) ligands, such as [Au₁₃(bisNHC)₄I₄]⁺ and [Au₁₃(bisNHC)₅Cl₂]³⁺, have also been characterized.^15,32 According to the superatom model,^33,34 the icosahedral Au₁₃⁵⁺ core has stable eight bonding electrons with a 1S²1P⁶ electronic structure. The stability of these Au₁₃ nanoclusters is enhanced by the presence of NHCs, but these ligands passivate the surface by imposing spatial constraints on the accessibility of the reactant molecules, thus blocking the availability of surface-active atoms. In this regard, the selective removal of ligands at local sites is considered to be crucial in boosting the catalytic activity of NHC-protected AuNCs. For example, Crudden et al. recently demonstrated that applying thermal treatment to the [Au₁₃(bisNHC)₅Cl₂]³⁺ nanocluster results in gradual and partial removal of bisNHC ligands and leads to improved catalytic efficiency in electrocatalytic CO₂ reduction compared to the diphosphine-stabilized analogues.¹⁵ This suggests that partial removal of the NHC ligand could effectively activate the Au₁₃ clusters.

Besides thermal annealing, electrochemical biasing is another promising strategy to partially etch the surface ligands and expose the catalytically active metal sites.³⁵ For example, recent studies have revealed that the thiolate-protected AuNCs such as Au₂₅(SR)₁₈ exhibit enhanced electrocatalytic activity after electrochemical activation,^11,13,16 where the surface thiolate ligands can be selectively removed under electrochemical reduction conditions.³⁶ Compared with the widely studied thiolate- and alkynyl ligand- protected AuNCs, the applications of emerging NHC-protected AuNCs in electrocatalysis have only recently become a topic of investigation. Particularly, the dynamic stability of the gold–NHCs interface in realistic electrochemical environments and the impact of the ligand layers on the active sites of the catalytic process have not been explored. To enhance the development of NHC-based AuNCs for future electrocatalytic applications, it is necessary to probe how the NHC-protected AuNCs interact with the electrolyte environment and provide a deep molecular-level understanding of the electrocatalytic mechanisms.

Motivated by these considerations, in this study, we selected the representative NHC and halogen co-protected [Au₁₃(NHC^Me)₉Cl₃]²⁺ (N,N′-dimethylbenzimidazolylidene, simplified as NHC^Me) cluster as our research model, where the side groups on the N atom of NHC were simplified to –CH₃ to reduce the computational cost. Considering solvation and potential effects, we first examined the dynamics of ligand etching on [Au₁₃(NHC^Me)₉Cl₃]²⁺ under electrochemical treatment, followed by identification of the active sites. After a series of ab initio molecular dynamics (AIMD) simulations, we found that the halogen chlorine atoms are favorably detached from the surface of the gold nucleus under applied reduction potential, such that the dechlorinated bare Au atoms serve as the active sites. In contrast, the Au–NHC interface is highly stable under electrochemical biasing, and the NHC ligands are stably bonded to the Au₁₃ core during the AIMD simulations. A strong dynamic preference for breaking the Au–Cl bond is also observed in the phosphine analogue [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster, where NHC ligands are replaced by phosphine ligands, indicating the stronger stability of Au–C or Au–P bonds over the Au–Cl bonds under electrochemical conditions. The catalytic properties of the dechlorinated Au₁₃ cluster under near neutral conditions (pH = 7) were further examined using constrained dynamic simulations with a slow-growth method. Surprisingly, the computational results demonstrated that the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster can effectively facilitate the electrochemical reduction of CO₂ to generate CO and H₂ with comparable energy barriers, indicating its great potential for syngas production. Our calculations are further supported by electrochemical experiments, where X-ray photoelectron spectroscopy (XPS) analysis revealed that the chlorine atoms in the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster were stripped off under electrocatalytic conditions. Furthermore, the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster, after ligand stripping at pH = 0 and U_RHE = −1.60 V, demonstrated enhanced catalytic efficacy for syngas formation in the CO₂RR across a broad electrochemical potential range of −0.50 to −1.20 V, exhibiting a stable CO : H₂ ratio of approximately 0.8 to 1.2. Our work provides unprecedented atomic-scale insights into the ligand etching dynamics occurring on the surface of novel [Au₁₃(NHC^Me)₉Cl₃]²⁺ clusters and offers an effective strategy to facilitate syngas production.

2 Computational methods

2.1 Ab initio molecular dynamics (AIMD) simulations

In order to investigate the dynamic stability of the Au–ligand interface in [Au₁₃(NHC^Me)₉Cl₃]²⁺ and [Au₁₃(PMe₃)₉Cl₃]²⁺ nanoclusters under electrochemical conditions, we performed constant potential AIMD simulations. The Quickstep module in the CP2K package (CP2K 9.1) was employed to conduct AIMD simulations.³⁷ For the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster, the periodic box size was set to 25 × 25 × 30 ų, where the local surface of the cluster contained 109 H₂O molecules and one H₃O⁺ along the Z-axis in the acidic system; while in the neutral system, 110 H₂O molecules were added. The box size for the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster was set to 20 × 20 × 28 ų, which contains 84 H₂O molecules plus one H₃O⁺ in the acidic system and 85 H₂O molecules in the neutral system. All the solvation models maintain a water density of about 1 g cm⁻³. The core electrons of all atoms are represented by the Goedecker–Teter–Hutter (GTH) pseudopotentials,³⁸ while their valence orbitals are expanded in the Gaussian and auxiliary plane-wave (GPW)-type double-ζ basis sets³⁹ with one set of polarization functions (DZVP)⁴⁰ and a plane wave cutoff for density expansion of 400 Ry. In all calculations, the electron exchange–correlation interactions were described using the Perdew–Berke–Ernzerhof (PBE) functional⁴¹ and the dispersion correction was applied using the DFT-D3 approximation⁴². The self-consistent field (SCF) convergence criteria and energy cutoff were set to 10⁻⁵ Ha and 300 Ry, respectively. AIMD simulations were performed in the canonical ensemble (NVT) employing the canonical sampling through a velocity rescaling (CSVR) thermostat⁴³ with a time step of 1 fs to control the temperature at 300 K.

2.2 Static calculations

All the static calculations were performed using spin-polarized density functional theory (DFT) with the Perdew–Burke–Ernzerhof (PBE) functional⁴¹ in the Vienna Ab initio Simulation Package (VASP 5.4.4).⁴⁴ The plane-wave cutoff energy was set to 450 eV, and the generalized gradient approximation (GGA)⁴⁵ is employed to describe the exchange–correlation energy, while the projector-augmented-wave (PAW)⁴⁶ method was used to describe the core electrons. The convergence criteria for energy and force were set as 10⁻⁴ eV and −0.025 eV Å⁻¹ for the maximal displacement. The k-point at the Gamma center only was used to sample the Brillouin zone. In addition, we utilized the empirical density functional dispersion (DFT-D3) method⁴⁷ to account for the van der Waals interactions between ligands and solvents. All atoms were unconstrained and fully relaxed during the simulation. Bader charges were obtained using the code developed by the Henkelman group.⁴⁸

2.3 Calculation of the catalytic performance

To evaluate the free energy barriers of the activated [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster in the CO₂RR and HER process, we conducted constrained AIMD simulations (cAIMD) using the “slow-growth” method in the VASP, sampling the free energy profile with a ∂ξ value of 0.0008 Å. The [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster with one halogen (Cl) atom removed was placed in a 22 × 22 × 28 ų box containing 90 water molecules. To achieve a superior equilibrium state, an AIMD simulation was conducted at 300 K for 3 ps using a Nose–Hoover thermostat with a 1 fs time step before constrained AIMD simulations. Fig. S8† depicts the choice of collective variable (CV) in each elementary reaction. During the cAIMD calculations, the plane-wave cutoff energy was set to 400 eV, and the simulation temperature was controlled at 300 K using a Nose–Hoover thermostat. To deal with the fluctuations in the work function in all AIMD simulations, we extracted at least 10 snapshots from the AIMD trajectories to determine the average work function.^49,50 The VASP-KIT code was used for post-processing of the computational data.⁵¹

3 Experimental methods

3.1 Materials

Sodium borohydride (NaBH₄, 99%), dichloromethane (DCM, 99%), ethanol (C₂H₅OH, 99%) and hydrochloric acid (HCl, 98%) were purchased from Sinopharm Chemical Reagent Co. Ltd (Shanghai, China). 1H-Benzo[d]imidazole (NHC, 97%) was purchased from Shanghai Acmec Biochemical Co., Ltd (Shanghai, China). (Dimethylsulfide)gold(I)chloride (Me₂SAuCl, 97%), and dibromo methane (CH₃BrCH₃, 99%) were purchased from Sigma-Aldrich (Germany). Benzyl bromide (C₇H₇Br, 99%) was purchased from Meryer (Shanghai, China). Benzene (C₆H₆, 99%), potassium carbonate (K₂CO₃, 99%), toluene (C₇H₈, 99.8%), acetonitrile (ACN, 99.8%) and sodium hexafluorophosphate (NaPF₆, 98%) were purchased from Macklin (Shanghai, China). [Au₁₃(NHC)₉Cl₃](PF₆)₂ was prepared by the method reported in the literature.^28,52

3.2 Ultraviolet-visible (UV-vis) spectroscopy

UV-vis spectra of [Au₁₃(NHC)₉Cl_l3](PF₆)₂ were acquired using a Shimadzu UV-2550 spectrophotometer at room temperature. The solution sample was measured in a quartz cuvette with a path length of 1 mm. The spectra were recorded in dichloromethane, and the signal from the solvent without the sample was subtracted.

3.3 Electrospray ionization mass spectrometry

Electrospray ionization mass data (ESI-MS) were obtained using an Agilent 6224 time-of-flight mass spectrometer in the positive mode. The cluster sample was initially dissolved in dichloromethane and subsequently filtered. The resulting solution was then directly infused into the spectrometer at a flow rate of 1.2 mL h⁻¹ using a syringe pump. The typical parameters for the measurements were as follows: capillary voltage: 4.0 kV; drying gas temperature: 150 °C; drying gas flow: 4 L min⁻¹; and nebulizer pressure: 20 psi.

3.4 Electrochemical etching of Au₁₃ clusters

The preparation of the working electrode involved dissolving 2 mg of [Au₁₃(NHC)₉Cl₃](PF₆)₂ in 1 mL of dichloromethane (DCM), dropping the solution onto a carbon paper of 1 cm × 2 cm, and drying it under vacuum conditions for 8 hours. The electrochemical measurements were performed using a CHI 760E electrochemical workstation (CH Instruments) with a conventional single-compartment three-electrode system. The working electrode was sandwiched between a glassy carbon electrode and an Ag/AgCl electrode and platinum foil were used as the reference and counter electrodes, respectively. The potential (U_Ag/AgCl) was converted to the reversible hydrogen electrode (RHE) scale (U_RHE) using the following equation:

U_RHE = U_Ag/AgCl + 0.197V + 0.0591 × pH

The electrochemical desorption of Cl ligands on [Au₁₃(NHC)₉Cl₃](PF₆)₂ NCs was conducted in 0.5 M H₂SO₄ electrolyte and 0.5 M Na₂SO₄ electrolyte. Chronopotentiometry tests were performed at voltages of U = −0.30 V (vs. RHE), U = −1.60 V (vs. RHE), U = −0.61 V (vs. RHE), and U = −1.30 V (vs. RHE), with each voltage test lasting for one hour.

3.5 Electrochemical measurements

Electrochemical CO₂ reduction was conducted on a CHI 600c electrochemical workstation in a three-channel flow cell, which comprises carbon paper with a gas-diffusion layer (GDL, YLS-30T), an anion exchange membrane (AEM, Fumasep, FAB-PK-130) and a platinum plate. In the electrochemical test, an Ag/AgCl electrode (immersed in saturated KCl solution) was used as the reference electrode, with an anion-exchange membrane and a platinum plate serving as the ion mobility channel and counter electrode, respectively. The working electrode was prepared as follows: 1 mg of carbon nanotubes and 3 mg of [Au₁₃(NHC^Me)₉Cl₃]²⁺ nanoclusters were dissolved in 0.5 mL of CH₂Cl₂ to achieve a uniform dispersion ink containing 20 μL of 0.25 wt% Nafion solution. The composite ink was then spread onto the GDL with a loading mass of 2 mg cm⁻².

In the electrocatalytic CO₂RR process, the cathode chamber and anode chamber were separated by an anion exchange membrane. The electrolyte (0.5 M NaHCO₃ or 1.0 M KOH) in both the cathode and anode compartments was recirculated using a peristaltic pump, with a rotation speed of 40 rpm. High-purity CO₂ (99.9999%) gas was continuously purged into the gas chamber behind the gas-diffusion layer. The gas flow rate was 24 sccm, controlled by a mass flow controller (D08-1F, Beijing Sevenstar Flow Co., Ltd). The gas products were analyzed quantitatively and qualitatively with the help of a gas chromatograph (GC, Huaai 9560). The faradaic efficiencies (FE) for the formation of the products (CO and H₂) were calculated as follows:

where Q_i is the charge required to form the gaseous product, Q_total is the total charge during the reaction, n_i is the number of moles of the product detected by gas chromatography, Z is the number of electrons transferred during the formation of the product (2 for both CO and H₂), and F is Faraday's constant (96 485C mol⁻¹). The partial current densities of CO (j_CO) and H₂ (j_H2) were calculated by multiplying the total current density (j_total) by the faradaic efficiencies of CO and H₂, respectively. The turnover frequency (TOF) was calculated as follow:
where j_i is the partial current density of the corresponding gas product, Z is the number of electrons transferred to form the product (2 for CO and 2 for H₂), F is the Faraday constant (96 485C mol⁻¹), m_i is the mass of the loaded catalyst, ω is the relative mass fraction of Au in the catalyst, and M is the relative atomic mass of Au.

Linear sweep voltammetry (LSV) of the CO₂RR was conducted in 1 M KOH or 0.5 M NaHCO₃ solution saturated with either N₂ or CO₂, using a scan rate of 50 mV s⁻¹. The electrochemical active surface area (ECSA) of the samples was quantified using C_dl obtained from cyclic voltammetry (CV) curves, with a scanning rate ranging from 40 to 120 mV s⁻¹ in a sealed and gas-circulated H-cell in a 0.5 M KHCO₃ solution.

3.6 X-ray photoelectron spectroscopy (XPS) analysis

The working electrode, subjected to electrochemical treatment at U = −0.30 V (vs. RHE) and U = −1.6 V (vs. RHE) at pH = 0 and U = −0.61 V (vs. RHE) and U = −1.30 V (vs. RHE) at pH = 7 was analyzed using XPS with a VG Scientific ESCALAB Mark II spectrometer equipped with two ultra-high vacuum (UHV) chambers. The spectra were calibrated using the C 1s peak (284.5 electron volts). The extent of Cl ligand detachment was tracked relative to the atomic ratio of Cl and Au.

4 Results and discussion

4.1 Ligand etching on Au₁₃ nanoclusters

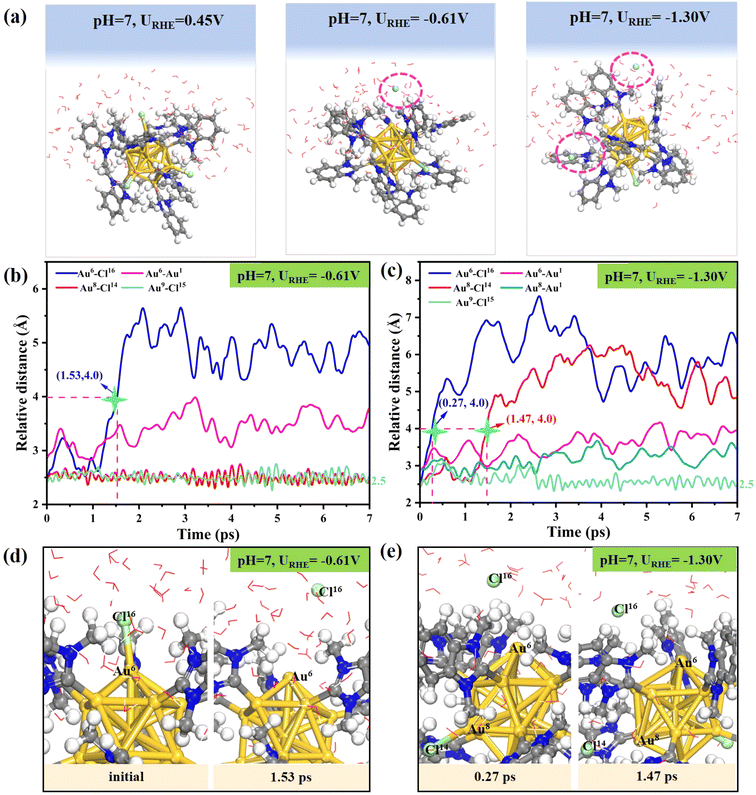
In order to detect the dynamic behavior of the gold–ligand interface at a given applied potential U_RHE, constant potential AIMD simulations were performed on [Au₁₃(NHC^Me)₉Cl₃]²⁺ and its hypothetical structural analogue [Au₁₃(PMe₃)₉Cl₃]²⁺ clusters under neutral and acidic conditions (approximately pH = 7 and pH = 0), respectively. Our computational model explicitly incorporates the electrode potential and solvation effect, where the applied potential U is introduced by manually adjusting the number of extra electrons in the presence of implicit and explicit water molecules. This model is based on the Poisson–Boltzmann function introducing a fractional charge at the implicit interface to continuously control the work function (Φ).⁵³ Given the fluctuations in the work function, we extracted at least 10 snapshots from the AIMD trajectories to determine the average work function.⁴⁹ Accordingly, the potential U can be derived by modifying the work function as follows: U_RHE = (Φ − 4.44)/e + 0.0592 × pH, where 4.44 is the work function of the standard hydrogen electrode (Φ_SHE) based on implicit solvation VASPsol calculations.⁵³

For the neutral model at pH = 7, about 0, 2 and 4 additional electrons are introduced to reach the U_RHE values of 0.45 V, −0.61 V, and −1.30 V, respectively. As illustrated in Fig. 1a, our AIMD snapshots demonstrate that the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster, when exposed to liquid water and potential at room temperature (300 K) undergoes spontaneous halogen shedding at lower reduction potentials. Moreover, the number of detached chlorine atoms increases under more negative potentials. In order to gain more detailed information of the ligand etching process, we focused on the atomic-level dynamics in the region surrounding the broken bond and labeled the key atoms involved (see Fig. S1 and S2a† for a detailed illustration of labelling). In the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster, the metal core is protected by nine NHC ligands and three halogen atoms (Au⁸–Cl¹⁴, Au⁶–Cl¹⁶, and Au⁹–Cl¹⁵). The structure of the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster remained unaltered after 7 ps of dynamic simulations at U_RHE = 0.45 V (Fig. 1a, left), which is consistent with the high stability of this cluster under solvation conditions at room temperature, as observed in the experiment.²⁸ Interestingly, as the potential shifts to a negative value of U_RHE = −0.61 V (Fig. 1a, middle), it takes about 1.53 ps to reach an elongated Cl¹⁶⋯Au⁶ distance of 4.0 Å from an initial Au–Cl bond of about 2.5 Å (marked by the green star in Fig. 1b), which can be considered as the complete detachment of the Cl¹⁶ atom from the cluster surface (Fig. 1d). As the potential further decreases to U_RHE = −1.31 V (Fig. 1a, right), the time required for the large separation between Au⁶ and Cl¹⁶ is dramatically reduced to 0.27 ps (Fig. 1c), and meanwhile, another halogen Cl¹⁴ atom subsequently detaches from the surface Au⁸ atom at a time of 1.47 ps (Fig. 1e). This interesting phenomenon highlights the critical role of applied potential in affecting the detachment dynamics of halogen ligands, where the more negative the applied potential, the easier and faster the Au–Cl bond breaks. The relative distance between the key atoms involved in the halogen leaching indicates that the detached Cl atom quickly migrates away from the surface Au to the water layer and that the structure of the resultant dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster remains essentially unchanged throughout the simulations. In addition, we investigated the possibility of re-adsorption of leached chlorine ligands onto Au atoms under pH = 7 and U_RHE = −0.16 V condition using the slow-growth method in constrained AIMD simulations (SG-MD). The free energy curve demonstrated that the energy barrier (E_a) to be surmounted for the entire migratory adsorption process was 0.99 eV (Fig. S3†), suggesting that re-coordination of the leached chlorine ligand with the Au atom is challenging.

Fig. 1 (a) Final snapshots of the [Au₁₃(NHC^Me)₉Cl₃]²⁺ nanocluster exposed to liquid water at three different potentials at pH = 7 after 7 ps AIMD simulations at 300 K. Statistics of the relative distance between representative atoms during the equilibrated AIMD simulation at (b) U_RHE = −0.61 V, and (c) U_RHE = −1.30 V for the neutral system. Detailed atomic structure evolution of chlorine leaching from the surface of Au₁₃ nuclei at (d) U_RHE = −0.61 V and (e) U_RHE = −1.30 V. Color modes: gray for C, white for H, green for Cl, blue for N, yellow for Au, and red for O. The same color scheme was used subsequently. For clarity, the water molecules are depicted in line modes.

Furthermore, to elucidate the influence of the electrolyte environment on the ligand leaching dynamics in the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster, we also performed constant potential AIMD simulations under acidic conditions (pH = 0) to monitor the structural evolution of the cluster at room temperature. Under acidic conditions, the introduction of 0e⁻, 2e⁻ and 4e⁻ would lead to electrode potentials (U_RHE) of around −0.09 V, −0.30 V and −1.60 V, respectively. The final snapshots after 7 ps of AIMD simulations at 300 K demonstrate that the cluster structure [Au₁₃(NHC^Me)₉Cl₃]²⁺ remains intact at U_RHE = −0.09 V (Fig. 2a, left), indicating the high structural stability of the cluster in the acid environment when the interfacial potential is small. However, upon the application of a more negative potential of −0.30 V and −1.60 V, it was observed that the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster undergoes halogen leaching from the gold core, resulting in the removal of one (Fig. 2a, middle) and two (Fig. 2a, right) chlorine atoms from the surface shell layer, respectively. The detailed dynamic process of halogen detachment can be traced from the change in the relative distance between the Au and Cl atoms (Fig. 2b–e). When U_RHE is −0.30 V (Fig. 2b), the proton (H²⁸⁶) from H₃O⁺ spontaneously attacks the electronegative Cl¹⁶ atom and weakens the interaction between Cl¹⁶ and Au⁶ atoms, separating the detached Cl¹⁶ atom from the Au₁₃ core to form an HCl molecule at 0.46 ps which subsequently diffuses into the aqueous solution (Fig. 2d). Note that the generated HCl molecule would then release the proton and be stably adsorbed on the exposed surface Au⁶ atom at about 1.43 ps with a Au–H bond length of 1.68 Å. This facile adsorption of protons can be attributed to the modification of the charge state of the exposed Au⁶ site after chlorine removal, which will be discussed later. When the potential decreases to U_RHE = −1.60 V (Fig. 2c), the Cl¹⁶ atom would be first detached in a shorter time of 0.43 ps compared to the 0.46 ps taken at U_RHE = −0.30 V, accompanied by proton adsorption at the exposed Au⁶ site at 1.39 ps (Fig. 2e). Moreover, the second Cl¹⁴ atom separates from the surface Au⁸ at 1.99 ps and was completely detached from the cluster at about 6.00 ps. Furthermore, the introduction of 5e⁻ in the acidic model resulted in an electrode potential of approximately −1.80 V. Following a 5 ps AIMD simulation, three chlorine ligands were found to completely detach from the surface of Au₁₃ nuclei at 0.25 ps, 0.45 ps, and 2.45 ps, respectively (Fig. S4†). The shedding dynamics are analogous to those at lower potentials, where H₃O⁺ in acidic solvents interacts with the chlorine atom to facilitate the leaching of the chlorine ligands. The process also involves proton transfer, with the excess proton finally adsorbed on the undercoordinated Au⁶ site. The above AIMD results under acidic conditions also revealed that the more negative the applied potential, the faster the kinetics of Au–Cl bond cleavage, where proton attack on halogens can accelerate the leaching process. Note that although the Cl ligands can be easily detached into solution, the NHC ligands remained tightly bound to the surface Au atoms of the Au₁₃ core throughout the AIMD simulations. This indicates that the interaction between Au and the NHC ligand is very strong and dynamically very stable under electrochemical conditions.

Fig. 2 (a) Final AIMD snapshots of the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster exposed to three different potentials at pH = 0 after 7 ps AIMD simulations at 300 K. Statistics of the relative distance between representative atoms during the equilibrated AIMD simulation at (b) U_RHE = −0.30 V, and (c) U_RHE = −1.60 V. Detailed atomic structural evolution of chlorine leaching from the surface of Au₁₃ nuclei at (d) U_RHE = −0.30 V and (e) U_RHE = −1.60 V. The transferred H from the proton during the evolution is highlighted in sky blue.

For comparison, we additionally carried out the constant potential AIMD simulations of the phosphine analogue cluster [Au₁₃(PMe₃)₉Cl₃]²⁺ at 300 K under both acidic (pH = 0) and neutral conditions (pH = 7), where the NHC ligands in the pristine [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster are replaced by the phosphine ligands. In neutral conditions, the dynamic process of ligand leaching from this cluster displays great similarities to that observed in [Au₁₃(NHC^Me)₉Cl₂]³⁺ (Fig. S2c, d and S5†). Specifically, at U_RHE = 0.28 V, the ligand remains stably attached to the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster. As the applied potential becomes increasingly negative, a gradual detachment of one Cl (U_RHE = −0.50 V) and two Cl atoms (U_RHE = −0.67 V) from the surface Au is observed. Under acidic conditions (pH = 0), the statistical analysis of relative distances between representative atoms in the equilibrium AIMD simulations indicate that the protons from H₃O⁺ can promote the leaching of Cl from the surface Au (Fig. S6a†). At U_RHE = −0.48 V, the proton (H³⁸⁹) first attacks Cl¹⁶, weakening the Au⁶–Cl¹⁶ bond and rapidly breaking it at 0.14 ps. Noteworthily, unlike what we have observed for the above [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster under acidic conditions, the proton does not transfer to the gold site (Au⁶) exposed by Cl removal in the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster but remains in the H₃O⁺ form in the water layer (Fig. S6b and S6d†). When the reduction potential increased to −1.09 V (Fig. S6c and S6e†), we observed the facile removal of two chlorine atoms (Cl¹⁶ and Cl¹⁴) from the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster at 0.29 and 0.39 ps, respectively. In this case, a sufficiently negative applied potential can facilitate the proton transfer to the activated Au⁶, ultimately leading to the proton adsorption on Au⁶ at 0.56 ps. Throughout the overall AIMD simulations, the structure of the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster remains intact, and no elongation in the distance between the P atom of the phosphine ligand and the surface Au is observed, indicating the high dynamic stability of the Au–P bonds.

Therefore, our constant-potential AIMD simulations of [Au₁₃(NHC^Me)₉Cl₂]³⁺ and [Au₁₃(PMe₃)₉Cl₃]²⁺ clusters indicate that there is a strong dynamic preference for breaking the Au–Cl bond rather than the Au–C or Au–P bonds under electrochemical conditions. Noteworthily, previous studies have indicated that the electron cloud overlap between the d orbitals of the peripheral Au atom and the coordinated P or C atom is greater than that between Au and Cl, suggesting that the Au–C and Au–P bonds are stronger than the Au–Cl bonds.³⁶ This also provides a rationale for the preferential removal of halogen over NHC and phosphine ligands. Moreover, under acidic conditions, the minimal spatial hindrance around the chlorine ligand allows enough space for protons to interact with Cl. Besides, the high electronegativity of chlorine also results in a strong affinity for proton. These, in turn, lead to the weakening of the Au–Cl bond, thereby promoting halogen shedding.

We further analyzed the changes in the Bader charge of the dechlorinated gold atoms after constant-potential AIMD simulations. Our analysis indicates that the protected gold atoms (Au⁶, Au⁸ and Au⁹) initially coordinated with chlorine exhibit a positive charge (0–0.1|e|), while the uncapped gold atoms, after the leaching of halogen ligands, undergo a charge transition from positive to negative (<−0.1|e|) (Fig. 3). This observation indicates that the dechlorinated gold atoms could serve as the catalytic active centers, potentially facilitating the activation of reactants in electrocatalytic processes such as the CO₂RR and HER. This also provides a logical rationale for the observed adsorption affinity of the dechlorinated gold for proton in under acidic conditions. The Bader charges of the other Au atoms are provided in Tables S1 and S2.† It is noteworthy that the Au atoms coordinated to the C atom of the NHC ligands in the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster are positively charged, whereas the Au atoms coordinated to the P atom of phosphine ligands in the [Au₁₃(PMe₃)₉Cl₃]²⁺ cluster are negatively charged. The difference in the charge states is consistent with the decreasing atomic electronegativity from C (2.5), Au (2.4), to P (2.1). Moreover, the Au¹ atom situated at the core of the icosahedral Au₁₃ nucleus exhibits a net negative charge under all electrochemical conditions. Overall, the electrochemical etching process results in a reduction in the coverage of surface Cl ligands and exposes the surface Au atoms, providing the possible catalytic sites. As Häkkinen et al. demonstrated, for the phosphine–halide-protected Au₁₁(PH₃)₇Cl₃ cluster, the removal of halogen atoms constitutes a pivotal step in the cluster activation process.⁵⁴ Following the identification of the active site, the effect of halogen chloride removal on the catalytic properties of the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster in hydrogen evolution and CO₂ electroreduction is of particular interest and will be the subject of our subsequent investigations.

Fig. 3 Changes in Bader charge on the surface gold atoms coordinated to Cl after 7 ps AIMD simulations of [Au₁₃(NHC^Me)₉Cl₃]²⁺ (a and b) and homologue [Au₁₃(PMe₃)₉Cl₃]²⁺ nanoclusters (c and d) at different potentials under neutral (pH = 7) and acidic (pH = 0) conditions. For the sake of clarity, the explicit aqueous layer, N-heterocyclic carbene ligands and phosphine ligands are depicted using line patterns.

4.2 Electrocatalytic properties of the [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster

We selected the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster, with one Cl atom removed, as the testing probe to explore its elctrocatalytic activity. We first conducted DFT calculations based on the computational hydrogen electrode (CHE) model to compare the catalytic selectivity between CO₂ electroreduction to CO and hydrogen evolution on the exposed Au sites. The step with the largest increase in free energy was defined as the rate-determining step (RDS) of the reaction. As illustrated in Fig. S7,† the free energy profile indicates that CO₂ activation is the most challenging step in the CO₂RR with a high reaction energy of 0.66 eV on the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster. Nevertheless, the RDS of the competitive HER occurs in the Volmer *H adsorption, H + * + e⁻ → *H (0.46 eV), which is 0.20 eV lower than the activation energy of CO₂, indicating a higher selectivity for hydrogen formation over CO₂ reduction. Note that the oversimplified thermodynamic predictions based on the conventional CHE model without explicitly considering the applied potential are inadequate for the accurate determination of reaction kinetics in practical electrocatalytic reactions. To address this limitation, we further investigate the kinetic performance of the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster using constant potential calculations.

To understand how the applied potential influences the CO₂ activation on the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ catalyst, we used constrained AIMD simulations by the slow-growth method (SG-MD) to construct the free energy profile of CO₂ adsorption at different electrode potentials (Fig. 4a) at pH = 7 (the collective variable (CV) setting for CO₂ activation was shown in Fig. S8a†). CO₂ activation was deemed to be complete when the O–C–O angle reached equilibrium throughout the simulations (Fig. S9†). The CO₂ molecule preferentially adsorbs at the top site of the exposed Au atom. Obviously, the energy barrier (ΔG^‡) of CO₂ adsorption has a strong dependence on the electrode potential. As the potential U shifted negatively from 0.48 V to −0.39 V, the energy barrier (ΔG^‡) decreased from 0.82 eV to 0.056 eV, indicating that the negative electrode potential could promote the kinetic adsorption of CO₂. In the inset of Fig. 4a, the conformation of adsorbed CO₂ deviates from its pristine linear shape, bending into a chemisorbed V-shaped conformation under the applied potential. Furthermore, since CO₂ activation entails the migration of reactants from the solvent to the Au surface, the difficulty of CO₂ activation can be assessed based on the position of the transition state (TS) (Fig. 4b). At a potential of 0.48 V, the C–Au bond length at the TS is 1.89 Å, indicating that CO₂ must move a long distance from solution to the active Au site to be activated. However, at a more negative potential of −0.39 V, the corresponding Au–C distance of TS increases to 2.56 Å, indicating that CO₂ can be activated farther from Au, which is possibly due to the higher electron density on the surface of the [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster at lower potentials. Interestingly, we fitted the corresponding potential U and the reaction energy barriers ΔG^‡ to get a linear correlation with R² = 0.90, whereas a higher R² value of 0.98 is achieved in a quadratic correlation (Fig. 4c). This observation could be ascribed to the configurational asymmetries in the potential energy surfaces (PES) of the initial and final states of CO₂ activation, resulting in a significant deviation from the typically anticipated linear potential dependence.⁵⁵ Such a quadratic type potential-dependent ΔG^‡ relationship indicates that CO₂ can be easily and effectively activated at potentials below −0.11 V, where the activation barrier is lower than 0.20 eV.

Fig. 4 (a) Potential-dependent free energy profiles of CO₂ adsorption on the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster at different electrode potentials (vs. RHE) at pH = 7. The inset depicts structural snapshots of the initial state (IS) and final state (FS) in the structural evolution of CO₂ activation. (b) Structure plots and location of the Au–C bond length at the transition state (TS) at different potentials. (c) Fitted correlation between applied potential U and reaction barriers (ΔG^‡) of CO₂ activation; the quantitative equation and the corresponding R² value are shown in the inset.

Similarly, we also examined the free energies of the subsequent CO₂RR steps at different applied potentials, including *COOH formation (*CO₂ + H₂O + e⁻ → *COOH + OH⁻, Fig. 5a), *CO formation (*COOH + e⁻ → *CO + OH⁻, Fig. 5b) and CO desorption (Fig. 5c). Unlike CO₂ activation, the conversion of *CO₂ to *COOH involves a solvent-mediated proton transfer. As illustrated in the inset of Fig. 5a, the neighboring water molecules are involved in the formation of *COOH under neutral conditions. The water-mediated proton transfer also occurs during the formation of *CO (Fig. 5b), which is analogous to the process observed in the *CO₂ to *COOH conversion. The CV settings along the reaction coordinate in *COOH and *CO formation are provided in Fig. S8b and S8c.† The last elementary step is the desorption of *CO from the active Au site, which determines its effective release from the active site and thus affects the overall catalytic performance. The corresponding CV setting of CO desorption in our calculation is defined as the distance between the center of mass of CO and the Au site (Fig. S8d†). In Fig. 5c, the length of the Au–C bond during steady-state CO adsorption is approximately 2.14 Å (IS). Throughout the free energy sampling, it was found that the free energy along the *CO desorption process increases with the elongation of the C–Au bond, which could be attributed to the diffusive resistance of the aqueous layer subsequent to CO desorption from the active site. Accordingly, an elongated C–Au bond length of 3 Å is deemed to signify the complete desorption of CO from the catalyst surface. The fitted potential-dependent energy barrier relationships for each elementary reaction are shown in Fig. 5d. Obviously, as the applied potential becomes more negative, the energy barriers for all the reaction steps reduce. Moreover, by considering all the reaction steps together, the critical rate-determining step and overall reaction difficulty of the CO₂RR process can be identified. Among the four elementary steps, the conversion of *COOH to *CO presents a significant energy barrier (ΔG^‡ > 0.8 eV) at typical working potentials (−1.5–0 V), making it a crucial rate-limiting step in the overall reaction process of CO₂ electroreduction.

Fig. 5 Potential-dependent free energy profiles of (a) *CO₂ to *COOH, (b) *COOH to *CO and (c) CO desorption on the dechlorinated [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster at different electrode potentials (vs. RHE) and pH = 7. The inset depicts structural snapshots of the initial state (IS) and final state (FS). The fitted quadratic curves for all elementary reactions in the CO₂RR are mapped in (d).

Furthermore, in competition with the CO₂ reduction reaction, the hydrogen evolution reaction (HER) significantly impacts the selectivity of the NHC-stabilized Au₁₃ catalyst. To probe this influence, an in-depth investigation of the free energy barrier for the HER under neutral conditions (pH = 7) was carried out using the same SG-MD approach. As shown in Fig. 6a, the energy barrier for proton adsorption from water cleavage in the Volmer step (H₂O + e⁻ + * → *H + OH⁻) shows a marked dependence on the applied potential. The free energy barrier, ΔG^‡, decreases progressively from 1.29 eV to 0.34 eV as the electrode potential shifts from −0.28 V to −1.09 V. Analysis of the FS snapshot reveals that hydrogen adsorbs at the top site of the unsaturated, dechlorinated gold atoms. A quadratic model (R² = 0.98) provides a better fit to the potential U and the energy barrier ΔG^‡ compared to a linear model (R² = 0.92) (Fig. 6b). Considering the involvement of water cleavage, the energy barrier for the initial Volmer step of *H formation is substantially higher than that observed for CO₂ adsorption. In neutral or alkaline environments, the subsequent Heyrovsky step in the HER involves the combination of H from water cleavage with the adsorbed hydrogen to form hydrogen gas (*H + H₂O + e⁻ → * + H₂ + OH⁻). The potential-dependent free energy change for the Heyrovsky step is illustrated in Fig. 6c. It is evident that as the applied potential becomes more negative, the activation barrier for this step decreases from 1.34 eV at 0.18 V to 0.77 eV at −1.73 V, indicating a direct correlation between the potential and the reaction kinetics. In this case, the quadratic correlation (R² = 0.99) also provides a better fit to the potential U and the energy barrier ΔG^‡ compared to the linear model (R² = 0.95) (Fig. 6d). Upon collating the fitted quadratic plots of the two elementary steps (Fig. 6e), the rate-determining step for the HER becomes evident. Interestingly, the Volmer step is identified as the rate-determining step when the applied potential is higher than −0.33 V, whereas the Heyrovsky step becomes as the rate-determining step when the potential is lower than −0.33 V. This transition underscores the pivotal role of electrode potential in modulating the catalytic mechanism of the HER on the [Au₁₃(NHC^Me)₉Cl₂]³⁺ cluster catalyst.

Fig. 6 Potential-dependent free energy profiles and location of the transition state (TS) barrier of the Volmer step (a) and Heyrovsky step (c) on [Au₁₃(NHC^Me)₉Cl₂]³⁺ at different electrode potentials (vs. RHE) at pH = 7. The inset depicts structural snapshots of the initial state (IS) and final state (FS). Correlation between the applied potential U and the reaction barriers (ΔG^‡) in the Volmer (b) and Heyrovsky (d) step, where the quantitative equation and the corresponding R² values are labeled. (e) The quadratic relationship curves for the HER. (f) The quadratic relationship curves for each elementary step in both the CO₂RR and HER.

Based on the established fitting quadratic relationships, a comparative analysis of the CO₂RR and HER at different potentials under neutral codition is illustrated in Fig. 6f. This analysis reveals a crossover potential at U_cross = −0.58 V, where the free energy barrier of the rate-determining step for the CO₂RR equals to that for the HER (ΔG^‡ (CO₂RR) = ΔG^‡ (HER)). At U_RHE > −0.58 V, the energy barrier of the rate-determining step in the CO₂RR is lower than that for the HER. While conversely, at U_RHE < −0.58 V, the energy barrier for the CO₂RR becomes higher than that of the HER. As the potential deviates further into the negative (U_RHE < −0.58 V) or extreme positive range (U_RHE > −0.33 V), the disparity in the energy barrier between these two reactions is exacerbated, indicating a higher selectivity for HER when U_RHE < −0.58 V and a higher selectivity for CO₂RR when U_RHE > −0.33 V. Intriguingly, we found that the energy barriers for CO₂ reduction and hydrogen evolution become comparable within a specific potential range, suggesting that the [Au₁₃(NHC^Me)₉Cl₂]³⁺ catalyst holds great promise for syngas production. By defining a threshold for the barrier difference between the CO₂RR and HER as |ΔG^‡ (CO₂RR) − ΔG^‡ (HER)| ≤ 0.15 eV, the corresponding potential is located roughly between −1.0 V and −0.26 V, as illustrated in the shaded region of Fig. 6f. Within this potential range, the selective production of syngas or a mixture of CO and H₂ can be precisely controlled by modulating the applied potential.

4.3 Experimental verification

To validate our theoretical predictions, we synthesized the [Au₁₃(NHC)₉Cl₃](PF₆)₂ nanocluster and confirmed its consistency with the literature through ESI-MS and UV-vis analysis.^28,52 The ESI-MS spectrum displayed distinct peaks in the positive ion mode (Fig. 7a), with the prominent peak at 2673 m/z attributed to [Au₁₃(NHC)₉Cl₃]²⁺. The simulated isotopic pattern matched perfectly with the experimental results. The cluster exhibits characteristic absorption peaks (234, 289, 330, 415 and 489 nm) in its UV-vis spectrum (Fig. 7b), which is in good agreement with the reported literature.²⁸ These results confirmed the successful synthesis of the [Au₁₃(NHC)₉Cl₃](PF₆)₂ nanocluster. Next, we investigated the ligand stripping of the [Au₁₃(NHC)₉Cl₃](PF₆)₂ nanocluster after 1 hour of reaction at different potentials in various electrolytes, similar to the catalyst activation treatment before electrocatalytic reactions. By measuring the Cl–Au elemental ratio using X-ray photoelectron spectroscopy (XPS) analysis, we calculated the average number of remaining ligands on the Au₁₃ cluster (Fig. 7c and d). It was observed that the number of remaining chloride ligands decreased when the potential became more negative, regardless of whether the electrolyte was neutral or acidic. The amount of Cl detached (about one third and two third surface chlorine ligands are lost as the applied potential decreases) was consistent with the results obtained from DFT calculations (one chlorine and two chlorine atoms are removed from the cluster surface with the decrease in reduction potential). Moreover, in both acidic and neutral electrolytes, the Au 4f_7/2 peaks shifted to lower binding energy regions, indicating the electron-rich nature of some gold atoms due to the dechlorination process, which was also in agreement with the DFT calculations (the Bader charge of Au shifts from positive to negative after electrochemical dechlorination). Furthermore, solid-state ¹³C NMR characterization of the original Au₁₃ cluster and those subjected to electrochemical treatment at −0.3 V (vs. RHE) at pH = 0 was performed (Fig. S10†), and it was found that the ¹³C NMR spectra before and after the electrochemical treatment were essentially identical. This finding clearly demonstrates that the Au–C bond remains intact even after the Au–Cl bond is broken during an electrochemical process.

Fig. 7 (a) ESI-MS spectrum of the [Au₁₃(NHC)₉Cl₃](PF₆)₂ cluster in the positive mode. The inset shows the comparison between experimental and simulated isotopic patterns of [Au₁₃(NHC)₉Cl₃]²⁺. (b) UV-vis absorption spectra of the [Au₁₃(NHC)₉Cl₃](PF₆)₂ cluster in dichloromethane. (c) Au 4f XPS spectra of Au₁₃ after a one-hour reaction at different potentials in media with pH = 0 and pH = 7. (d) Amount of Cl ligand in the Au₁₃ cluster after electrochemical treatment under different conditions.

Moreover, to further verify our theoretical predictions regarding syngas production, we investigated whether the synthesized [Au₁₃(NHC)₉Cl₃](PF₆)₂ cluster is efficient in the electrochemical reduction of CO₂ to generate CO and H₂. Fig. 8a shows the linear sweep voltammetry (LSV) curves of the [Au₁₃(NHC)₉Cl₃](PF₆)₂ cluster under CO₂ and N₂ gas saturation conditions before and after activation at different potentials in 0.5 M sulfuric acid for one hour. The LSV results showed that the pristine and activated [Au₁₃(NHC)₉Cl₃](PF₆)₂ clusters only facilitate the HER in a N₂-saturated environment, whereas a shifted onset potential is observed in a CO₂ atmosphere for both the unactivated and activated Au₁₃ clusters, suggesting their capability for electrocatalytic CO₂ reduction. The electrochemical tests were conducted in a 1 M KHCO₃ flow cell (pH = 7). Noteworthily, the pretreated Au₁₃ clusters at potentials of −0.30 V and −1.60 V under acidic conditions achieve significantly higher current density than that of the untreated one when tested in a CO₂-saturated KHCO₃ solution, indicating that the electrochemical activation may induce ligand removal to dramatically increase the catalytic activity. The gaseous products were analyzed by gas chromatography (GC), which demonstrated that CO and H₂ are the primary products, while no liquid product was identified from nuclear magnetic resonance (NMR) spectroscopy. Fig. 8b and c display the faradaic efficiencies (FE) of gaseous products, CO and H₂, at different potentials. The results indicate that Au₁₃ pre-activated under U_RHE = −1.60 V exhibits higher CO₂RR activity in the potential range of −0.70 to −1.20 V. In particular, compared to activation at U_RHE = −0.30 V, Au₁₃ activated at U_RHE = −1.60 V also demonstrates a more balanced activity for both HER and CO₂RR. Fig. 8d presents the CO : H₂ ratio distribution of CO₂RR for Au₁₃ treated at U_RHE = −1.60 V, where the stable CO : H₂ ratio was about 0.8 to 1.1 in the potential range of −0.70 to −1.20 V (the shaded area in Fig. 8d), which represents an ideal ratio of syngas for the hydroformylation reaction in the manufacture of fine chemicals. Moreover, the fractional current densities for CO (j_CO) and H₂ (j_H2) (Fig. 8e) clearly showed that H₂ vs. CO selectivity increases with decreasing reduction potential (more negative potential), and j_H2 gradually increases more rapidly than j_CO, indicating enhanced selectivity towards the HER, which is consistent with the computational results shown in Fig. 6f. Fig. S11† shows the turnover frequency (TOF) of CO and H₂ products. Notably, in the potential range of −0.7 to −1.1 V, the Au₁₃ cluster activated at U_RHE = −1.60 V exhibits similar TOF values for both CO and H₂. However, as the potential becomes more negative, the TOF of H₂ shows a more pronounced increase, indicating that hydrogen evolution gradually becomes the dominant process. The intrinsic properties of the catalyst were also measured as shown in Fig. S12,† where the electrochemical active surface area (ECSA) was determined from C_dl. Obviously, the Au₁₃ cluster treated at U_RHE = −1.60 V exhibits the largest C_dl value (0.99 mF cm⁻²), indicating a larger active surface area, which is consistent with its enhanced electrocatalytic performance. Additionally, the stability test (Fig. 8f) demonstrated that the Au₁₃ catalyst pre-activated at U_RHE = −1.60 V could maintain a stable current density and CO : H₂ ratio for over 10 h at −0.9 V without significant performance degradation. As evidenced by the transmission electron microscopy (TEM) analysis in Fig. S13,† the Au₁₃ nanocluster remained well-dispersed and stably anchored on the carbon nanotubes after prolonged reaction, also indicating the structural robustness of this nanocluster under the reaction conditions. Furthermore, the Au₁₃ cluster that had shed three chlorine ligands and was pre-treated at pH = 0 and U_RHE = −1.82 V was subjected to electrocatalytic testing in a 0.5 M KHCO₃ solution. As demonstrated in Fig. S14,† the HER activity of the catalyst enhanced by up to 90%, and the CO : H₂ ratio was significantly reduced to approximately 0.5. This suggests that the HER is more advantageous than CO₂ reduction under the condition of the removal of three chlorine ligands.

Fig. 8 Electrocatalytic CO₂RR performance in a CO₂ flow cell with 0.5 M KHCO₃ electrolyte. (a) LSV curves in N₂ and CO₂, and (b) FE_H2, (c) FE_CO and (d) CO : H₂ gas ratio at different potentials in unactivated and activated [Au₁₃(NHC)₉Cl₃](PF₆)₂ clusters under the conditions of pH = 0, U_RHE = −0.30 V and pH = 0, U_RHE = −1.60 V. (e) Fractional current density of H₂ and CO at different potentials. (f) Long-term stability test of the activated Au₁₃ cluster at pH = 0 and U_RHE = −1.60 V in the CO₂RR at −0.9 V (vs. RHE).

Besides the electrochemical performance in a near-neutral environment, the electrocatalytic activity of the Au₁₃ nanocluster under strong alkaline conditions was also investigated in 1 M KOH solution. Similarly, Fig. S15† shows that the Au₁₃ after activation at U_RHE = −1.60 V exhibits higher faradaic efficiency compared to the initial and treated cluster at U_RHE = −0.30 V, indicating the enhanced CO₂RR activity. The CO : H₂ ratio distribution shows that the Au₁₃ cluster activated at U_RHE = −1.60 V maintains a CO : H₂ ratio between 0.81 and 1.20 in the potential range of −0.50 to −1.10 V, making it suitable for syngas production in hydroformylation reactions. These electrochemical results under strong alkaline conditions are consistent with the performance under neutral conditions.

Overall, our experiments indicated that the activated [Au₁₃(NHC)₉Cl₃](PF₆)₂ cluster demonstrated enhanced CO₂RR activity towards syngas performance over a wide electrochemical potential, in good agreement with the theoretical predictions. Note that Au-based nanoclusters (e.g., Au₂₅, Au₃₈, and Au₁₄₄)^13,56 typically have high selectivity towards CO formation, often producing CO as the main reduction product in the electrocatalytic CO₂RR process. To our best knowledge, this work revealed, for the first time, the high catalytic preference for syngas production in the atomically precise Au₁₃ nanocluster. The distinctive electrocatalytic selectivity could be correlated to the unique icosahedral Au₁₃ core, where the exposed surface Au atoms after electrochemical dechlorination exhibit high curvature, enhancing their reactivity and facilitating water dissociation, thus leading to the facile formation of H₂ in addition to the typical CO product. In addition to the [Au₁₃(NHC)₉Cl₃]²⁺ prototype cluster explored in this work, other atomically and compositionally monodisperse NHC-protected gold nanoclusters with different core sizes and atomic arrangements have been reported, and the dependence of their electrocatalytic performance on factors such as size, structure, shape and composition as well as the mechanistic insights deserves future investigations.

5 Conclusions

In this study, we combined computational and experimental studies to reveal the interesting interface dynamics and unique electrocatalytic selectivity in the representative NHC protected [Au₁₃(NHC^Me)₉Cl₃]²⁺ cluster. The simulations demonstrated the higher stability of the Au–C or Au–P interface over the Au–Cl interface under electrochemical biasing, with the halogen ligand being preferentially detached from the surface of Au₁₃ core over the NHC or phosphine ligands when an adequate reduction potential is applied. Particularly, electrochemically induced dechlorination would expose the surface uncovered Au atoms that serve as the active sites, efficiently promoting the syngas (CO and H₂) production. In the CO₂RR, the conversion of *COOH to *CO is identified as the rate-determining step (RDS), whereas in the HER, the RDS transitions from the Volmer to the Heyrovsky step as the applied potential becomes more negative, highlighting the potential-dependent distinctive kinetics in electrocatalysis. Interestingly, the difference in the RDS barriers between the CO₂RR and HER is only less than 0.15 eV across a wide potential range between −1.0 V and −0.26 V, suggesting its great potential for electrocatalytic syngas formation. Our predictions were further confirmed by electrochemical activation experiments. The number of remaining Cl ligands decreases with the applied potential, and a stable CO : H₂ ratio between 0.8 and 1.1 is observed in a wide potential range, which is ideal for the hydroformylation reaction in fine chemical production. This study provides important atomic-scale insights into the electrocatalytic mechanism of NHC-protected gold nanoclusters, providing valuable implications for the development of efficient electrocatalysts for syngas production and contributing to the advancement of future sustainable energy technologies.

Data availability

The data supporting this article, including the simulation results and the electrochemical characterization data, have been included as part of the ESI.†

Author contributions

Z. C., D. Z. and L. Z. contributed equally to this work. Q. T. conceived the idea. Z. C. performed the theoretical calculations with help from Y. C. and F. S. D. Z. and L. Z. performed the experiments and analyzed the data under the guidance of H. S. and L. W. Z. C. wrote the manuscript with inputs from all authors. Q. T., H. S. and L. W. finalized the manuscript. All the authors approved the final version of the manuscript.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work was supported by the National Natural Science Foundation of China (no. 22473017) and the Chongqing Science and Technology Commission (CSTB2024NSCQ-MSX0250). L. K. Wang acknowledges the support from the National Natural Science Foundation of China (no. 21805170). H. S. acknowledges the support from the National Key R&D Program of China (2023YFB3507100), National Natural Science Foundation of China (22301149), Program for Young Talents of Science and Technology in Universities of Inner Mongolia Autonomous Region (NJYT23035) and start-up funding of Inner Mongolia University (10000-23112101/043).

References

1. M. H. Naveen, R. Khan and J. H. Bang, Gold Nanoclusters as Electrocatalysts: Atomic Level Understanding from Fundamentals to Applications, Chem. Mater., 2021, 33, 7595–7612.
2. X. Yuan and M. Zhu, Recent Advances in Atomically Precise Metal Nanoclusters for Electrocatalytic Applications, Inorg. Chem. Front., 2023, 10, 3995–4007.
3. W. Choi, H. Seong, V. Efremov, Y. Lee, S. Im, D.-H. Lim, J. S. Yoo and D. Lee, Controlled Syngas Production by Electrocatalytic CO₂ Reduction on Formulated Au₂₅(SR)₁₈ and PtAu₂₄(SR)₁₈ Nanoclusters, J. Chem. Phys., 2021, 155, 014305.
4. E. L. Albright, T. I. Levchenko, V. K. Kulkarni, A. I. Sullivan, J. F. DeJesus, S. Malola, S. Takano, M. Nambo, K. Stamplecoskie, H. Häkkinen, T. Tsukuda and C. M. Crudden, N-Heterocyclic Carbene-Stabilized Atomically Precise Metal Nanoclusters, J. Am. Chem. Soc., 2024, 146, 5759–5780.
5. L. Luo, X. Zhou, Y. Chen, F. Sun, L. Wang and Q. Tang, Ligand-induced Changes in the Electrocatalytic Activity of Atomically Precise Au₂₅ Nanoclusters, Chem. Sci., 2025, 16, 3598–3610.
6. K. Kwak and D. Lee, Electrochemistry of Atomically Precise Metal Nanoclusters, Acc. Chem. Res., 2019, 52, 12–22.
7. W. Jing, H. Shen, R. Qin, Q. Wu, K. Liu and N. Zheng, Surface and Interface Coordination Chemistry Learned from Model Heterogeneous Metal Nanocatalysts: From Atomically Dispersed Catalysts to Atomically Precise Clusters, Chem. Rev., 2023, 123, 5948–6002.
8. R. Jin, G. Li, S. Sharma, Y. Li and X. Du, Toward Active-Site Tailoring in Heterogeneous Catalysis by Atomically Precise Metal Nanoclusters with Crystallographic Structures, Chem. Rev., 2021, 121, 567–648.
9. Y.-M. Lei, D. Wu, M.-C. Pan, X.-L. Tao, W.-J. Zeng, L.-Y. Gan, Y.-Q. Chai, R. Yuan and Y. Zhuo, Dynamic Surface Reconstruction of Individual Gold Nanoclusters by Using a Co-Reactant Enables Color-Tunable Electrochemiluminescence, Chem. Sci., 2024, 15, 3255–3261.
10. S. Masuda, K. Sakamoto and T. Tsukuda, Atomically Precise Au and Ag Nanoclusters Doped with a Single Atom as Model Alloy Catalysts, Nanoscale, 2024, 16, 4514–4528.
11. F. Sun, L. Qin, Z. Tang and Q. Tang, Revisiting the Activity Origin of the PtAu₂₄(SR)₁₈ Nanocluster for Enhanced Electrocatalytic Hydrogen Evolution by Combining First-Principles Simulations with the Experimental in situ FTIR Technique, Chem. Sci., 2024, 15, 16142–16155.
12. N. Austin, S. Zhao, J. R. McKone, R. Jin and G. Mpourmpakis, Elucidating the Active Sites for CO₂ Electroreduction on Ligand-Protected Au₂₅ Nanoclusters, Catal. Sci. Technol., 2018, 8, 3795–3805.
13. H. Seong, V. Efremov, G. Park, H. Kim, J. S. Yoo and D. Lee, Atomically Precise Gold Nanoclusters as Model Catalysts for Identifying Active Sites for Electroreduction of CO₂, Angew. Chem., Int. Ed., 2021, 133, 14684–14691.
14. S. Chen, M. Li, S. Yu, S. Louisia, W. Chuang, M. Gao, C. Chen, J. Jin, M. B. Salmeron and P. Yang, Ligand Removal of Au₂₅ Nanoclusters by Thermal and Electrochemical Treatments for Selective CO₂ Electroreduction to CO, J. Chem. Phys., 2021, 155, 051101.
15. T. I. Levchenko, H. Yi, M. D. Aloisio, N. K. Dang, G. Gao, S. Sharma, C.-T. Dinh and C. M. Crudden, Electrocatalytic CO₂ Reduction with Atomically Precise Au₁₃ Nanoclusters: Effect of Ligand Shell on Catalytic Performance, ACS Catal., 2024, 14, 4155–4163.
16. F. Sun, L. Qin, Z. Tang, G. Deng, M. S. Bootharaju, Z. Wei, Q. Tang and T. Hyeon, SR Removal or –R Removal? A Mechanistic Revisit on the Puzzle of Ligand Etching of Au₂₅(SR)₁₈ Nanoclusters during Electrocatalysis, Chem. Sci., 2023, 14, 10532–10546.
17. P. Zhu, X. Zhu, X. Zhou, F. Sun, Y. Chen, L. Wang, Z. Tang and Q. Tang, Computational and Experimental Elucidation of the Charge-Dependent Acid-Etching Dynamics and Electrocatalytic Performance of Au₂₅(SR)₁₈^q (q=− 1, 0,+1) Nanoclusters, Small, 2025, 2411226.
18. Y. Fukumoto, T. Omoda, H. Hirai, S. Takano, K. Harano and T. Tsukuda, Diphosphine-Protected IrAu₁₂ Superatom with Open Site (s): Synthesis and Programmed Stepwise Assembly, Angew. Chem., Int. Ed., 2024, 63, e202402025.
19. Y. Ye, X. Zhou, Y. Chen, L. Wang and Q. Tang, Understanding the Ag–S Interface Stability and Electrocatalytic Activity of CO₂ Electroreduction in Atomically Precise Ag₂₅ Nanoclusters, Chem. Commun., 2025, 61, 2790–2793.
20. T. Kawawaki, Y. Kataoka, M. Hirata, Y. Iwamatsu, S. Hossain and Y. Negishi, Toward the Creation of High-Performance Heterogeneous Catalysts by Controlled Ligand Desorption from Atomically Precise Metal Nanoclusters, Nanoscale Horiz., 2021, 6, 409–448.
21. X. Li, S. Takano and T. Tsukuda, Ligand Effects on the Hydrogen Evolution Reaction Catalyzed by Au₁₃ and Pt@Au₁₂: Alkynyl vs. Thiolate, J. Phys. Chem. C, 2021, 125, 23226–23230.
22. J. Wang, F. Xu, Z. Y. Wang, S. Q. Zang and T. C. Mak, Ligand-Shell Engineering of a Au₂₈ Nanocluster Boosts Electrocatalytic CO₂ Reduction, Angew. Chem., Int. Ed., 2022, 61, e202207492.
23. Q.-L. Shen, L.-Y. Shen, L.-Y. Chen, L.-B. Qin, Y.-G. Liu, N. M. Bedford, F. Ciucci and Z.-H. Tang, Heterointerface of All-Alkynyl-Protected Au₂₈ Nanoclusters Anchored on NiFe-LDHs Boosts Oxygen Evolution Reaction: A Case to Unravel Ligand Effect, Rare Met., 2023, 42, 4029–4038.
24. J. Zhang, Y. Zhou, K. Zheng, H. Abroshan, D. R. Kauffman, J. Sun and G. Li, Diphosphine-Induced Chiral Propeller Arrangement of Gold Nanoclusters for Singlet Oxygen Photogeneration, Nano Res., 2018, 11, 5787–5798.
25. Y. Shichibu and K. Konishi, HCl-Induced Nuclearity Convergence in Diphosphine-Protected Ultrasmall Gold Clusters: A Novel Synthetic Route to “Magic-Number” Au₁₃ Clusters, Small, 2010, 6, 1216–1220.
26. M. R. Narouz, K. M. Osten, P. J. Unsworth, R. W. Y. Man, K. Salorinne, S. Takano, R. Tomihara, S. Kaappa, S. Malola, C.-T. Dinh, J. D. Padmos, K. Ayoo, P. J. Garrett, M. Nambo, J. H. Horton, E. H. Sargent, H. Häkkinen, T. Tsukuda and C. M. Crudden, N-Heterocyclic Carbene-Functionalized Magic-Number Gold Nanoclusters, Nat. Chem., 2019, 11, 419–425.
27. F. Sun, X. Zhou, L. Qin, Z. Tang, L. Wang and Q. Tang, Probing Temperature Effect on Enhanced Electrochemical CO₂ Reduction of Hydrophobic Au₂₅(SR)₁₈ Nanoclusters, ACS Catal., 2025, 15, 4605–4617.
28. M. R. Narouz, S. Takano, P. A. Lummis, T. I. Levchenko, A. Nazemi, S. Kaappa, S. Malola, G. Yousefalizadeh, L. A. Calhoun, K. G. Stamplecoskie, H. Häkkinen, T. Tsukuda and C. M. Crudden, Robust, Highly Luminescent Au₁₃ Superatoms Protected by N-Heterocyclic Carbenes, J. Am. Chem. Soc., 2019, 141, 14997–15002.
29. H. Shen, G. Deng, S. Kaappa, T. Tan, Y. Z. Han, S. Malola, S. C. Lin, B. K. Teo, H. Häkkinen and N. Zheng, Highly Robust but Surface-Active: An N-Heterocyclic Carbene-Stabilized Au₂₅ Nanocluster, Angew. Chem., Int. Ed., 2019, 131, 17895–17899.
30. H. Shen, Z. Xu, M. S. A. Hazer, Q. Wu, J. Peng, R. Qin, S. Malola, B. K. Teo, H. Häkkinen and N. Zheng, Surface Coordination of Multiple Ligands Endows N-Heterocyclic Carbene-Stabilized Gold Nanoclusters with High Robustness and Surface Reactivity, Angew. Chem., Int. Ed., 2021, 133, 3796–3802.
31. P. Luo, S. Bai, X. Wang, J. Zhao, Z. N. Yan, Y. F. Han, S. Q. Zang and T. C. Mak, Tuning the Magic Sizes and Optical Properties of Atomically Precise Bidentate N-Heterocyclic Carbene-Protected Gold Nanoclusters via Subtle Change of N-Substituents, Adv. Opt. Mater., 2021, 9, 2001936.
32. E. L. Albright, S. Malola, S. I. Jacob, H. Yi, S. Takano, K. Mimura, T. Tsukuda, H. Häkkinen, M. Nambo and C. M. Crudden, Enantiopure Chiral Au₁₃ Nanoclusters Stabilized by Ditopic N-Heterocyclic Carbenes: Synthesis, Characterization, and Electrocatalytic Reduction of CO₂, Chem. Mater., 2024, 36, 1279–1289.
33. M. Walter, J. Akola, O. Lopez-Acevedo, P. D. Jadzinsky, G. Calero, C. J. Ackerson, R. L. Whetten, H. Grönbeck and H. Häkkinen, A Unified View of Ligand-Protected Gold Clusters as Superatom Complexes, Proc. Natl. Acad. Sci. U.S.A., 2008, 105, 9157–9162.
34. O. Lopez-Acevedo, J. Akola, R. L. Whetten, H. Gronbeck and H. Hakkinen, Structure and Bonding in the Ubiquitous Icosahedral Metallic Gold Cluster Au₁₄₄(SR)₆₀, J. Phys. Chem. C, 2009, 113, 5035–5038.
35. Y. Chen, X. Zhou, X. Liu, Z. Tang, L. Wang and Q. Tang, Understanding the Role of Potential and Cation Effect on Electrocatalytic CO₂ Reduction in All-Alkynyl-Protected Ag₁₅ Nanoclusters, J. Am. Chem. Soc., 2025, 147, 2699–2713.
36. Z. Chen, F. Sun and Q. Tang, Thermal Stability and Electronic Properties of N-Heterocyclic Carbene-Protected Au₁₃ Nanocluster and Phosphine-Protected Analogues, J. Phys. Chem. Lett., 2023, 14, 10648–10656.
37. T. D. Kühne, M. Iannuzzi, M. Del Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, CP2K: An Electronic Structure and Molecular Dynamics Software Package-Quickstep: Efficient and Accurate Electronic Structure Calculations, J. Chem. Phys., 2020, 152, 194103.
38. S. Goedecker, M. Teter and J. Hutter, Separable Dual-Space Gaussian Pseudopotentials, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 1703.
39. G. Lippert, J. Hutter and M. Parrinello, The Gaussian and Augmented-Plane-Wave Density Functional Method for Ab Initio Molecular Dynamics Simulations, Theor. Chem. Acc., 1999, 103, 124–140.
40. J. VandeVondele and J. Hutter, Gaussian Basis Sets for Accurate Calculations on Molecular Systems in Gas and Condensed Phases, J. Chem. Phys., 2007, 127, 114105.
41. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865.
42. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate Ab Initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
43. G. Bussi, D. Donadio and M. Parrinello, Canonical Sampling through Velocity Rescaling, J. Chem. Phys., 2007, 126, 014101.
44. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
45. J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Atoms, Molecules, Solids, and Surfaces: Applications of the Generalized Gradient Approximation for Exchange and Correlation, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671.
46. P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
47. I. L. Garzon and A. Posada-Amarillas, Structural and Vibrational Analysis of Amorphous Au₅₅ Clusters, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11796.
48. W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys. Condens. Matter, 2009, 21, 084204.
49. K. Xie, F. Wang, F. Wei, J. Zhao and S. Lin, Revealing the Origin of Nitrogen Electroreduction Activity of Molybdenum Disulfide Supported Iron Atoms, J. Phys. Chem. C, 2022, 126, 5180–5188.
50. T. Cheng, H. Xiao and W. A. Goddard III, Reaction Mechanisms for the Electrochemical Reduction of CO₂ to CO and Formate on the Cu(100) Surface at 298 K from Quantum Mechanics Free Energy Calculations with Explicit Water, J. Am. Chem. Soc., 2016, 138, 13802–13805.
51. V. Wang, N. Xu, J.-C. Liu, G. Tang and W.-T. Geng, VASPKIT: A User-Friendly Interface Facilitating High-Throughput Computing and Analysis Using Vasp Code, Comput. Phys. Commun., 2021, 267, 108033.
52. H. Shen, S. Xiang, Z. Xu, C. Liu, X. Li, C. Sun, S. Lin, B. K. Teo and N. Zheng, Superatomic Au₁₃ Clusters Ligated by Different N-Heterocyclic Carbenes and their Ligand-Dependent Catalysis, Photoluminescence, and Proton Sensitivity, Nano Res., 2020, 13, 1908–1911.
53. T. Cheng, L. Wang, B. V. Merinov and W. A. Goddard III, Explanation of Dramatic pH-Dependence of Hydrogen Binding on Noble Metal Electrode: Greatly Weakened Water Adsorption at High pH, J. Am. Chem. Soc., 2018, 140, 7787–7790.
54. O. Lopez-Acevedo, K. A. Kacprzak, J. Akola and H. Häkkinen, Quantum Size Effects in Ambient CO Oxidation Catalysed By Ligand-Protected gold clusters, Nat. Chem., 2010, 2, 329–334.
55. H. Cao, Z. Zhang, J.-W. Chen and Y.-G. Wang, Potential-Dependent Free Energy Relationship in Interpreting the Electrochemical Performance of CO₂ Reduction on Single Atom Catalysts, ACS Catal., 2022, 12, 6606–6617.
56. S. Li, A. V. Nagarajan, X. Du, Y. Li, Z. Liu, D. R. Kauffman, G. Mpourmpakis and R. Jin, Dissecting Critical Factors for Electrochemical CO₂ Reduction on Atomically Precise Au Nanoclusters, Angew. Chem., Int. Ed., 2022, 134, e202211771.

---

Footnotes

† Electronic supplementary information (ESI) available: Additional simulation models, Bader charge analysis, reaction coordinates for SG-MD simulations, free energy profiles, and electrochemical characterization data. See DOI: https://doi.org/10.1039/d5sc00896d

‡ These three authors contributed equally to this work.

---