Open Access Article
Open Access ArticleDinitrogen reduction to ammonia with a pincer-Mo complex: new insights into the mechanism of nitride-to-ammonia conversion†
Souvik
Mandal
 a,
Xiaoguang
Zhou
a,
Xiaoguang
Zhou
 a,
Quinton J.
Bruch
a,
Quinton J.
Bruch
 bc,
Rachel N.
Allen
a,
Laurence W.
Giordano
a,
Nicholas J. I.
Walker
a,
Thomas J.
Emge
bc,
Rachel N.
Allen
a,
Laurence W.
Giordano
a,
Nicholas J. I.
Walker
a,
Thomas J.
Emge
 a,
Faraj
Hasanayn
a,
Faraj
Hasanayn
 d,
Alexander J. M.
Miller
d,
Alexander J. M.
Miller
 b,
Santanu
Malakar
b,
Santanu
Malakar
 *e and
Alan S.
Goldman
*e and
Alan S.
Goldman
 *a
*a
aDepartment of Chemistry and Chemical Biology, Rutgers, The State University of New Jersey, New Brunswick, New Jersey 08854, USA. E-mail: alan.goldman@rutgers.edu
bDepartment of Chemistry, University of North Carolina at Chapel Hill, Chapel Hill, North Carolina 27599, USA
cDepartment of Chemistry, Stony Brook University, Stony Brook, NY 11794, USA
dDepartment of Chemistry, American University of Beirut, Beirut 1107 2020, Lebanon
eDepartment of Chemistry, Rutgers University-Camden, Camden, New Jersey 08102, USA. E-mail: sm1792@chem.rutgers.edu
First published on 20th March 2025
Abstract
The thioether–diphosphine pincer-ligated molybdenum complex (PSP)MoCl3 (1-Cl3, PSP = 4,5-bis(diisopropylphosphino)-2,7-di-tert-butyl-9,9-dimethyl-9H-thioxanthene) has been synthesized as a catalyst-precursor for N2 reduction catalysis with a focus on an integrated experimental/computational mechanistic investigation. The (PSP)Mo unit is isoelectronic with the (PNP)Mo (PNP = 2,6-bis(di-t-butylphosphinomethyl)pyridine) fragment found in the family of catalysts for the reduction of N2 to NH3 first reported by Nishibayashi and co-workers. Electrochemical studies reveal that 1-Cl3 is significantly more easily reduced than (PNP)MoCl3 (with a potential ca. 0.4 eV less negative). The reaction of 1-Cl3 with two reducing equivalents, under N2 atmosphere and in the presence of iodide, affords the nitride complex (PSP)Mo(N)(I). This observation suggests that the N2-bridged complex [(PSP)Mo(I)]2(N2) is formed and undergoes rapid cleavage. DFT calculations predict the splitting barrier of this complex to be low, in accord with calculations of (PNP)Mo and a related (PPP)Mo complex reported by Merakeb et al. Conversion of the nitride ligand to NH3 has been investigated in depth experimentally and computationally. Considering sequential addition of H atoms to the nitride through proton coupled electron-transfer or H-atom transfer, formation of the first N–H bond is thermodynamically relatively unfavorable. Experiment and theory, however, reveal that an N–H bond is readily formed by protonation of (PSP)Mo(N)(I) with lutidinium chloride, which is strongly promoted by coordination of Cl− to Mo. Other anions, e.g. triflate, can also act in this capacity although less effectively. These protonations, coupled with anion coordination, yield MoIV imide complexes, thereby circumventing the difficult formation of the first N–H bond corresponding to a low BDFE and formation of the respective MoIII imide complexes. The remaining two N–H bonds required to produce ammonia are formed thermodynamically much more favorably than the first. Computations suggest that formation of the MoIV imide is followed by a second protonation, then a rapid and favorable one-electron reduction, followed by a third protonation to afford coordinated ammonia. This comprehensive analysis of the elementary steps of ammonia synthesis provides guidance for future catalyst design.
Introduction
The synthesis of ammonia from dinitrogen is perhaps the single most important industrially practiced chemical reaction, affording the fixed nitrogen for all synthetic fertilizer and thereby supporting approximately half of the world's food production.1,2 The current dominant process, based on fossil fuel reforming and Haber–Bosch catalysis is responsible for nearly 2% of the world's fossil fuel consumption and CO2 emissions.1–4 There is thus great interest in the development of electrochemically driven nitrogen reduction.5–18 Using a sustainable source of electrical energy, with water as the source of protons and electrons, such a process could in principle be essentially carbon-neutral. Such a process could also find applicability on a scale much larger even than the use of ammonia for fertilizer and chemicals, including the use of ammonia for storage and transportation of renewable energy or as a transportation fuel.4,15,16In 2003 Schrock reported that a (triamidoamine)Mo complex (Fig. 1a) catalyzed the reduction and protonation of N2 using Cp*2Cr (Cp* = η5-C5Me5) as the source of electrons, and lutidine·H+ (LutH+) as the proton source.19 This groundbreaking report represented the realization of a decades-old goal of a molecular catalyst for N2 fixation; however, turnover numbers were quite low, selectivity for ammonia formation was low, and a very slow addition of reagents was required to achieve even these modest results. Nishibayashi subsequently reported20,21 that the pincer-ligated dimeric Mo complex [(PNP)Mo(N2)2]2(μ-N2) (PNP = 2,6-bis(di-t-butylphosphinomethyl)pyridine) (Fig. 1b) catalyzed a similar reaction more efficiently, and later that the corresponding trihalides and nitridohalides were equally or more effective as catalyst precursors. Since then Nishibayashi and others have reported numerous other examples of pincer-ligated Mo catalysts, some of which yield extremely high turnovers, including systems that can utilize water as the proton source.22–37 Most of these catalysts share the “PYP pincer” motif in which two terminal dialkyl- or diarylphosphino groups are connected to a neutral coordinating group such as the pyridine group of PNP, a central phosphino group, or an N-heterocyclic carbene group. Other Mo-pincer complexes have also been found to effectively catalyze ammonia formation or, in some cases, to effect the key N2 cleavage step though not as part of a catalytic cycle for ammonia formation.12,17,20–55
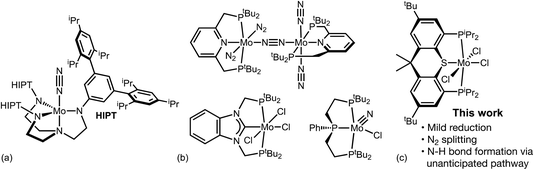 | ||
| Fig. 1 (a) Schrock's (triamidoamine)Mo catalyst.19,104 (b) (PYP)Mo catalysts or catalyst precursors reported by Nishibayashi.20–37 (c) (PSP)Mo complex reported in this work. | ||
These examples illustrate great progress in the development of molecular catalysts for N2 fixation, and in particular they indicate the promise of pincer-Mo complexes as catalysts for N2 reduction/protonation. Such complexes have very recently been found to be active catalysts for electrochemical reduction of N2 to NH3 as well, with48 or without54 a mediator. One of the challenges in the unmediated electrocatalysis is the need for highly negative applied potentials, which leads to competing H2 evolution and presumably a high electrochemical overpotential; the development of a system with practical utility requires minimizing both of these factors.11 Thus we have been particularly interested in designing new pincer Mo catalysts that are easier to reduce, while still maintaining good catalytic activity. More broadly, we have sought to expand the chemical space of (PYP)Mo-based catalysts while attempting to learn about the reaction mechanisms and the factors that govern the energetics of the numerous steps in any cycle catalyzed by such species. In this context, we report here the development of a (PSP)Mo-based system (PSP = 4,5-bis(diisopropylphosphino)-2,7-di-tert-butyl-9,9-dimethyl-9H-thioxanthene) for N2 reduction, the observation of several catalytically relevant intermediates and their reactions, and a computational study of this chemistry with comparison to Nishibayashi's archetypal (PNP)Mo catalysts.56
The family of catalysts exemplified by (PNP)Mo is typically proposed to operate via cleavage of N2 to give MoIV nitrides which then undergo sequential “H atom additions” (i.e. PCET, either concerted or non-concerted) to the nitride ligand to give coordinated NH3.35–37,57,58 Importantly, the “first” (imide) N–H BDFE is generally much smaller than that of the second (amide) and third (ammonia); formation of the first N–H bond through PCET is thus relatively unfavorable and may lead to the highest barrier in the overall reaction.35–37,57–61 The results presented herein, both experimental and computational, indicate that in fact this first N–H bond is not actually formed by PCET, but instead by protonation and addition of an anion, for both (PSP)Mo- and (PNP)Mo-based systems. This is then followed by PCET to the resulting MoIV imide, to form an amide; the energetics of this step correlate with a BDFE that is similar to that for the conventionally proposed MoIII imide intermediate. The third and final N–H BDFE, corresponding to PCET to the resulting MoIII amide, is similar to that for the MoII amide of the commonly proposed cycle. Thus, the formation of NH3 from nitride is achieved by “circumventing” the energetically unfavorable step of PCET to the nitride intermediate.
Experimental results and discussion
Synthesis and characterization of (PSP)MoCl3
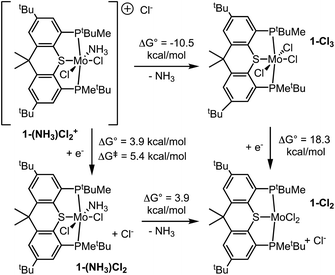
The pincer ligand PSP was synthesized as we have reported previously.62 Its reaction with MoCl3(THF)3 in THF solution gave 1-Cl3 in good yield (1 = (PSP)Mo; Scheme 1). The 1H NMR spectrum (THF-d8) was consistent with a single, paramagnetic species. Crystals were obtained by diffusion of pentane into a THF solution, and the molecular structure was determined by single-crystal X-ray diffraction (scXRD) (Fig. 2).The coordination sphere of Mo in 1-Cl3 is approximately octahedral, with the SMoCl3 unit being almost perfectly planar, although, as is typical with PXP-type pincer ligands, the X–M–P (S–Mo–P) angles are significantly less than 90°, at 76.5 ± 0.5°.
Reduction of 1-Cl3 and binding of N2
Cyclic voltammetry of 1-Cl3 in THF revealed a reversible reduction with a half-wave potential, E1/2 = −1.56 V vs. Fc+/0. This reduction is ca. 400 mV less negative than that of (PNP)MoCl3 (E1/2 = −1.94 V vs. Fc+/0),55 confirming our hypothesis that the PSP ligand would support milder reductions. Although no diamagnetic impurities or additional paramagnetic species were apparent by 1H NMR spectroscopy, an additional feature in the CV indicated a possible impurity at 10% or less. The major reduction peak was fully reversible at all scan rates studied, suggesting that chloride dissociation occurs relatively slowly. Chemical reductions were then attempted with sodium metal, which can assist in chloride abstraction via precipitation of NaCl.A THF solution of 1-Cl3 was stirred over Na/Hg amalgam (0.5% w/w Na; 3 equiv. Na) under N2 atmosphere. The predominant product exhibited broad signals in the 31P{1H} NMR spectrum; upon cooling, these resolved into an AB pattern of doublets at δ 80.8 and δ 79.1, 2JPP = 122.3 Hz (Fig. S1†). Crystals were obtained and scXRD revealed a dimolybdenum product analogous to Nishibayashi's Mo0 dimer [(PNP)Mo(N2)2]2(μ-N2),23,32,33i.e. [(PSP)Mo(N2)2]2(μ-N2) (2) (Fig. 3 and Scheme 2). Note that the bowl shape of the PSP ligand, in contrast with the planar PNP ligand, combined with the orthogonal relationship of the two PSP planes, results in the loss of mirror symmetry, rendering the P atoms of each PSP ligand inequivalent in accord with the predominant species observed in the 31P NMR spectrum.
In addition to the AB doublets, a sharp singlet at δ 78.2 (Fig. S1†) is seen in the 31P{1H} NMR spectrum of the solution under N2 atmosphere. We attribute this to an equilibrium between 2 and mononuclear product (PSP)Mo(N2)3 (3; Scheme 2); such an equilibrium is expected from complex 2 as its Mo(μ-N2)Mo core is a 12-π-electron system.63 Accordingly, increased N2 pressure led to an increased ratio of [3]![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [2] which was reversed upon decreasing N2 pressure. (The reaction kinetics were not measured, but it took approximately one week to reach apparent equilibrium, even with periodic rotation of the NMR tube to ensure gas-solution equilibration of N2.) At N2 pressures of 1.0 and 7.12 atm, Keq for the interconversion of 2 and 3, as shown in Scheme 2, was determined by 31P{1H} NMR spectroscopy to be 3.4(1) × 10−3 M atm−1 (see ESI†).
[2] which was reversed upon decreasing N2 pressure. (The reaction kinetics were not measured, but it took approximately one week to reach apparent equilibrium, even with periodic rotation of the NMR tube to ensure gas-solution equilibration of N2.) At N2 pressures of 1.0 and 7.12 atm, Keq for the interconversion of 2 and 3, as shown in Scheme 2, was determined by 31P{1H} NMR spectroscopy to be 3.4(1) × 10−3 M atm−1 (see ESI†).
The 31P{1H} NMR spectrum of the reaction solution additionally showed unidentified signals at ca. δ 77. Redissolving the crystals obtained as noted above affords a 31P{1H} NMR spectrum similar to that obtained before recrystallization. This leads us to speculate that the unidentified signals may be assigned to one or more isomers of 2 present in equilibrium in solution, e.g. isomers in which the bridging N2 is positioned cis to S in one or both of the (PSP)Mo units.22,64–66
Admitting a CO atmosphere to the solution of 2 and 3 resulted in a 31P NMR spectrum indicating formation of two species, one manifesting a very broad AB doublet (δ 88.8 and δ 88.0), and the other a sharp singlet at δ 91.0. Two products were crystallized from this mixture and both were characterized by scXRD (see ESI†). One was found to be (PSP)Mo(CO)3. The other was the N2-bridging dimer [(PSP)Mo(CO)2]2(μ-N2) (see ESI†), which is the analog of the product of the reaction of [(PNP)Mo(N2)2]2(μ-N2)20,23,32,33 with CO.20
Reduction of 1-Cl3 with cleavage of N2
The Mo0 dinitrogen complex 2 described above is stable with respect to the dissociative cleavage reaction to form metal nitrides, as expected based on the number of electrons in π-symmetry orbitals.67 A N2-bridged complex with one less e− per Mo would have the appropriate electronic structure for splitting, and iodide additives have previously been found to promote nitride formation in pincer Mo complexes.32,38,40,43,44,64 Accordingly, 1-Cl3 was treated with two reducing equivalents per Mo, rather than three as in the above examples, in the presence of added iodide. Under N2 atmosphere, Na/Hg amalgam (0.5% w/w Na; 2 equiv. Na) was added to a THF solution of 1-Cl3 and NaI (2 equiv.). The 31P{1H} NMR spectrum of the resulting solution showed a single resonance, at δ 79.8, and the 1H NMR spectrum was consistent with a single diamagnetic PSP-containing species with Cs symmetry.68 When the reaction was conducted under 15N2 atmosphere the resulting 15N NMR spectrum showed a single resonance at δ 446 (cf. δ 460 for (PNP)Mo(N)I28). These spectroscopic data are consistent with assignment as the product of N2-cleavage, (PSP)Mo(N)I (1-(N)I, Scheme 3). Crystals were grown from benzene/pentane, and scXRD afforded the structure shown in Fig. 4. The complex 1-(N)I has a coordination geometry that may be viewed as pseudo-square-pyramidal38 with nitride in the apical position and an N–Mo–L angle of ca. 100° with each of the four other Mo-coordinating atoms. This structural motif is well precedented among pincer-Mo38,69,70 and related nitride complexes.71,72Based on the modest reduction potential of 1-Cl3 (E1/2 = −1.56 V vs. Fc+/0), milder reductants should also be viable. Accordingly, under otherwise identical conditions, similar results were obtained with the use of 2 equiv. decamethylcobaltocene (Cp*2Co), which has an oxidation potential of −1.94 V vs. Fc+/0, as reductant in place of Na/Hg amalgam. However, no reaction was obtained with Cp2Co (−1.33 V vs. Fc+/0).
Thus, cleavage of N2 occurs upon reaction of two equivalents of reductant with 1-Cl3 while the addition of more than two equivalents leads to a stable bridging-N2 dimolybdenum(0) complex. This is consistent with the well-established principle that bimetallic cleavage of N2 to give nitrides is generally limited to bridging-N2 complexes with 10 electrons in the M(μ-N2)M π-system12,41,66,67,73–76 (Scheme 4).
 | ||
| Scheme 4 Reduction of 1-X3 by 2e− or 3e− under N2 atmosphere. Hypothetical pathways to 1-(N)X and 2. | ||
Protonation of the nitride ligand of 1-(N)I
Having observed cleavage of the N2 bond to give nitride complex 1-(N)I, we considered likely subsequent steps in a potential catalytic cycle for ammonia synthesis. As will be discussed in depth in following sections, formation of the initial N–H bond is indicated by DFT calculations to be the thermodynamically most challenging step in the conversion of the nitride to ammonia. Accordingly, 1-(N)I did not react with the H-atom donor TEMPO-H (up to 5 equiv.) even after 2 days at room temperature. Likewise it did not react with H-atom donors CpCr(CO)3H (Cr–H BDFE = 54.9 kcal mol−1 in MeCN77) or 1,4-cyclohexadiene (C–H BDFEs for benzene formation = 67.8 and 13.8 kcal mol−1 in gas phase77). Moreover, 1-(N)I did not undergo reaction with one-electron reductants Cp2Co or Cp*2Co (1 equiv.) in the absence of a proton source such as [LutH]Cl, and cyclic voltammetry revealed a significantly negative reduction potential (Epc < −2.7 V vs. Fc+/0; Fig. S36†). We therefore undertook investigation of protonation as the initial N–H bond formation step.The reaction of 1-(N)I with Brookhart's acid78 [H(Et2O)2][BArF4] (ArF = 3,5-bis(trimethyl)phenyl) in THF appears to result in complete protonation (eqn (1)). The 31P{1H} NMR spectrum shows a single broad signal upon addition of 1.0 equiv. [H(Et2O)2][BArF4] at δ 67.3. Addition of two more equiv. of the acid has no discernible effect on the chemical shift although the signal is then sharp. Reaction of [H(Et2O)2][BArF4] with 15N-labeled 1-(15N)I leads to a doublet (δ 51.0, 1JHN = 73 Hz) in the 15N NMR spectrum, which is well precedented in work by Schrock as a protonated nitride.79 The 31P{1H} NMR spectrum of 1-(15N)I shows a doublet with a small 31P–15N coupling, 2JPN = 5.8 Hz.
| (PSP)Mo(I)N + [H(Et2O)2][BArF4] → [(PSP)Mo(I)NH]+[BArF4]− + 2Et2O | (1) |
Upon addition of one equiv. of a weaker acid, [LutH][OTf] (the most commonly used proton source in the context of this chemistry32,33), the characteristic peak of 1-(N)I in the 31P{1H} NMR spectrum at δ 79.78 was broadened but only slightly shifted, to δ 79.2. An extremely broad peak appeared in the 1H NMR spectrum at ca. δ 14.9. Addition of two more equiv. [LutH][OTf] resulted in a shift of the 31P NMR signal to δ 77.8, while the downfield 1H NMR peak shifted to δ 14.8 and became more intense and sharper. With a total of 12 equiv. [LutH][OTf] added, the 31P NMR signal appeared at ca. δ 75.1 (see Fig. S2 and S3†) while the downfield 1H NMR signal, clearly exchanging with free [LutH][OTf], was at δ 14.04. These results are consistent with protonation of 1-(N)I, presumably at the nitride ligand, in a rapid equilibrium lying toward the left, either with the triflate anion coordinated to Mo (eqn (2a)) or ion-paired to the resulting cation (eqn (2b)). They are also consistent with an equilibrium in which the lutidinium cation is engaged in hydrogen bonding, again presumably with the nitride ligand (eqn (2c)).
| 1-(N)I + [LutH]+[OTf]− ⇌ (PSP)Mo(I)(NH)(OTf) + Lut | (2a) |
| 1-(N)I + [LutH]+[OTf]− ⇌ [(PSP)Mo(I)(NH)(Lut)]+[OTf]− | (2b) |
| 1-(N)I + [LutH]+[OTf]− ⇌ [(PSP)Mo(I)N⋯HLut]+[OTf]− | (2c) |
The addition of 4 equiv. lutidine to the solution with 12 equiv. [LutH][OTf] (with a 31P NMR signal at ca. δ 75.1) yielded a signal at δ 79.1, essentially the chemical shift of the solution with 1 equiv. [LutH][OTf] (δ 79.2, close to that of free 1-(N)I, δ 79.8). Since free lutidine participates only in the equilibrium of eqn (2a) this strongly supports eqn (2a), over eqn (2b) or (2c), as a description of the reaction of 1-(N)I with [LutH][OTf]. Note however that this does not offer insight into the configuration of (PSP)Mo(I)(NH)(OTf), and in particular does not distinguish between a complex with OTf− coordinated to Mo versus an ion pair (likely with OTf− hydrogen-bonding to the N-bound proton).
The above results indicate that a very strong acid, such as [H(Et2O)2][BArF4], is required to fully protonate 1-(N)I (to give 1-(NH)I+) while a moderately strong acid, [LutH][OTf], results in an equilibrium (likely with 1-(NH)I(OTf)) that lies toward the unprotonated form. Remarkably, however, in contrast with the reaction with [LutH][OTf], addition of the chloride salt of the same acid, [LutH]Cl (3 equiv.), resulted in complete protonation with no observable equilibrium. The 31P{1H} NMR spectrum indicates the presence of two species in a ca. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio with chemical shifts of δ 63.9 and δ 64.9 respectively. The 1H NMR spectrum contained signals at δ 6.40 and δ 6.49, also in a ca. 4
1 ratio with chemical shifts of δ 63.9 and δ 64.9 respectively. The 1H NMR spectrum contained signals at δ 6.40 and δ 6.49, also in a ca. 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, attributable to the protonated nitride ligand.
1 ratio, attributable to the protonated nitride ligand.
XRD of crystals grown by diffusion of pentane into a benzene solution yielded the molecular structure of trans-1-(NH)(Cl)(I) (Fig. 5). Apparently, by comparison with lutidinium triflate, in the case of lutidinium chloride coordination of the anion to molybdenum drives protonation of the nitride ligand fully to the protonated form (Scheme 5).
We propose that the minor species (with the 31P NMR chemical shift of δ 64.9 and 1H NMR shift of δ 6.49) is the corresponding dichloride complex, (PSP)MoCl2(NH). In accord with this proposal, the crystal was disordered and the structure was solved as 18% (PSP)MoCl2(NH).
[LutH]Cl (1.2 equiv.) was added to a THF-d8 solution 1-(15N)I to yield 1-(15NH)ICl, which gave a 31P{1H} NMR spectrum with signals, in a 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 ratio, at δ 63.5 and δ 64.4, both doublets with 2JPN = 6.1 Hz. The 1H NMR spectrum revealed a very sharp doublet of triplets at δ 6.31 with 1JNH = 73 Hz and 3JPH = 3.6 Hz attributable to the major species. In the 15N NMR spectrum a doublet appears at δ −2.5 (1JNH = 73 Hz) (the signals were too broad to observe P–N coupling). The HSQC spectrum showed strong correlation of this 15N NMR signal with the 1H NMR signal at δ 6.31.
1 ratio, at δ 63.5 and δ 64.4, both doublets with 2JPN = 6.1 Hz. The 1H NMR spectrum revealed a very sharp doublet of triplets at δ 6.31 with 1JNH = 73 Hz and 3JPH = 3.6 Hz attributable to the major species. In the 15N NMR spectrum a doublet appears at δ −2.5 (1JNH = 73 Hz) (the signals were too broad to observe P–N coupling). The HSQC spectrum showed strong correlation of this 15N NMR signal with the 1H NMR signal at δ 6.31.
Reaction of 1-(NH)ICl to yield ammonia, and the reverse reaction
In contrast with nitride 1-(N)I, imide 1-(NH)ICl was found to react with the H-atom donor TEMPO-H to give ammonia (Scheme 6). 1-(NH)ICl was generated in situ by addition of 5 equiv. [LutH]Cl to a THF solution (2 mL) of 1-(N)I; TEMPO-H (8 equiv.) was then added and after 24 h the volatiles were removed in vacuo. The residue was dissolved in DMSO-d6 and 1H NMR spectroscopy revealed formation of ammonia (free and/or bound) that was detected as NH4+ in 88% yield. While this reaction does not afford definitive information about the thermodynamics of H˙ transfer from TEMPO-H to 1-(NH)ICl (in part because the nature of the Mo product was not determined), it appears that transfer of H˙ from TEMPO-H to N does occur. Thus, although such H˙ transfer is likely endergonic, it is not so uphill as to preclude the reaction from occurring (slowly) at room temperature, despite the relatively high O–H BDFE of TEMPO-H (65.5 kcal mol−1 in THF77), and, importantly, in contrast with the lack of any reaction with nitride 1-(N)I.80Similarly, 1-(NH)ICl, generated as described above, reacted with H-atom donors CpCr(CO)3H (Cr–H BDFE = 54.9 kcal mol−1 in MeCN77) and 1,4-cyclohexadiene (C–H BDFEs for benzene formation = 67.8 and 13.8 kcal mol−1 in gas phase77); NH4+ was recovered in yields of 70% and 41% respectively (Scheme 6). As with TEMPO-H, 1-(N)I showed no reactivity toward these species.
To further investigate the apparent tendency of 1-(NH)ICl to react with H-atom donors, 1-(NH)ICl was generated by the addition of [LutH]Cl (3 equiv.) to a THF-d8 solution of 1-(N)I. Cp2Co (5 equiv.) was then added, over the course of 12 h. 1H NMR spectroscopy revealed appearance of the spectrum characteristic of paramagnetic 1-Cl3 (which would likely overlap with a mixed halide complex, 1-Cl2I) and a signal at δ −0.02 attributable to NH3 (Scheme 7). In a separate experiment (described in detail, S2.9.2†), volatiles from the resulting mixture were vacuum-transferred to a flask with HCl in diethyl ether; 1H NMR (DMSO-d6) revealed a 30% yield of ammonia (as NH4+). Thus, while 1-(NH)ICl undergoes no reaction with Cp2Co alone, it reacts with the PCET pair Cp2Co/[LutH]Cl as shown in Scheme 7.
 | ||
| Scheme 7 Reaction of 1-(NH)ICl with [LutH]Cl and Cp2Co to yield 1-Cl3 and NH3, followed by addition of KOtBu. | ||
Although the stoichiometry of the reaction of Scheme 7 would only require a single equivalent of Cp2Co, the reaction proceeded rapidly, but not to completion, even upon addition of excess (up to 5 equiv.) Cp2Co. Considering the possibility that an equilibrium had been reached, we investigated the possibility of driving the reaction in reverse. Consistent with our hypothesis, addition of base (KOtBu, 4 equiv.) to the mixture formed in this experiment resulted in the reappearance of some starting material 1-(N)I (Scheme 7; 17% yield).
The above experiments suggest, rather surprisingly, that the reaction of MoIV complex 1-(NH)ICl with Cp2Co/[LutH]Cl to give 1-MoCl3, Cp2Co+, and ammonia, is reversible (Scheme 7).81 Indeed, when [Cp2Co+][PF6−] (3 equiv.), NH3 (2 equiv.) and KOtBu (4 equiv.) were added to a fresh solution of 1-Cl3 in THF-d8, the formation of Cp2Co was clearly observed in the 1H NMR spectrum (δ −50.5) within 18 h (Scheme 8). A signal at δ 77.2 in the 31P NMR spectrum is attributed to 1-(N)Cl (identified by independent synthesis; see S2.11†) (ca. 25% of phosphorus-containing products). The presumed balanced equation is shown in Scheme 8. The major phosphorus-containing product, however, was the free PSP ligand (ca. 50%).
 | ||
| Scheme 8 Ideal balanced equation for reaction (oxidation) of 1-Cl3 with NH3, base, and Cp2Co+. (Actual reaction gives substantial decomposition/ligand-loss). | ||
Thus, individual steps of reduction, N2 cleavage (Schemes 2–5), and PCET or HAT, to give ammonium are demonstrated above. We have, however, thus far been unable to achieve catalysis to a significant extent with the (PSP)Mo unit. With 1-(N)I as a prospective catalyst or precursor, the use of various pyridinium hydrohalide derivatives with Cp*2Co was investigated. Slow addition (over 2 h) of 36 equiv. Cp*2Co to a solution of 1-(N)I and collidinium triflate (55 eq.) under N2 atmosphere gave 1.29 equiv. NH4+; other attempts generally gave significantly less than one equivalent NH4+. While this may be related to the apparent proclivity of the PSP ligand to dissociate, as illustrated above, efforts are ongoing to more fully characterize the decomposition pathway.
Computational results and discussion of mechanism
The observations described above suggest potential intermediates and reaction steps of a catalytic pathway for the synthesis of ammonia from dinitrogen, proceeding via bimetallic dinitrogen cleavage and subsequent reaction of the resulting metal nitride (Scheme 9; Y = S). Our observations implicate a mechanism for conversion of nitride to ammonia that is fundamentally distinct from commonly proposed views. Herein we describe a computational study integrated with our experimental observations. To evaluate the generalities of our findings on (PSP)Mo, we expand the calculations to include comparisons with the archetypal (PNP)Mo-based system reported by Nishibayashi. The calculations were done using Gaussian 16.82 The structures were optimized using the Minnesota-based hybrid metafunctional M06![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 83 and Pople's split valence basis set 6-31G(d,p)84,85 with the Stuttgart–Dresden effective core potential (SDD)86 for heavy atoms (Mo, Co, Br, and I). Improved potential energies and bulk solvation effects were obtained from single-point calculations of the gas phase optimized geometries employing the M06 functional, the all-electron Karlsruhe basis set Def2-QZVP86–90 for all atoms, and the SMD91 dielectric continuum (with benzene as solvent model). The PSP ligand was modeled with an asymmetric derivative bearing t-butylmethylphosphino groups instead of bis(isopropyl)phosphino groups to avoid multiple conformational possibilities, while maintaining the same ligand steric profile.92 Unless explicitly mentioned, this model has been used for all calculations pertinent to (PSP)Mo halide complexes. Bis(isopropyl)phosphino groups, however, were used for calculations involving the triflate anion to more precisely model the greater steric demands of the triflate ion and the absence of symmetry for triflate-coordinated and especially ion-paired triflate complexes. For the calculation of the inner-sphere reorganization energies associated with the calculation of kinetic barriers of electron transfer, the four-point method was used.93 The computational methodologies are also discussed, in further detail, in the ESI.†
83 and Pople's split valence basis set 6-31G(d,p)84,85 with the Stuttgart–Dresden effective core potential (SDD)86 for heavy atoms (Mo, Co, Br, and I). Improved potential energies and bulk solvation effects were obtained from single-point calculations of the gas phase optimized geometries employing the M06 functional, the all-electron Karlsruhe basis set Def2-QZVP86–90 for all atoms, and the SMD91 dielectric continuum (with benzene as solvent model). The PSP ligand was modeled with an asymmetric derivative bearing t-butylmethylphosphino groups instead of bis(isopropyl)phosphino groups to avoid multiple conformational possibilities, while maintaining the same ligand steric profile.92 Unless explicitly mentioned, this model has been used for all calculations pertinent to (PSP)Mo halide complexes. Bis(isopropyl)phosphino groups, however, were used for calculations involving the triflate anion to more precisely model the greater steric demands of the triflate ion and the absence of symmetry for triflate-coordinated and especially ion-paired triflate complexes. For the calculation of the inner-sphere reorganization energies associated with the calculation of kinetic barriers of electron transfer, the four-point method was used.93 The computational methodologies are also discussed, in further detail, in the ESI.†
 | ||
| Scheme 9 Proposed pathway (highly simplified) for catalytic synthesis of NH3via bimetallic cleavage of N2 and reduction/protonation. | ||
Cleavage of N2 by (PSP)Mo
Bimolecular cleavage of N2 by (PSP)MoX to yield the corresponding nitride complex is central to the mechanism of catalysis implied in this work, in analogy to previous proposals for (PNP)Mo and other (pincer)Mo complexes.12,17,32–36,52,66,94 In general, in the context of nitrogen fixation, cleavage of the strong N2 bond is often presented as the origin of the great challenge to achieving conversion under mild conditions.17,32,95–100 The barrier to bimolecular N2 cleavage, however, is not necessarily particularly high nor rate-determining. For example, Yoshizawa and Nishibayashi have calculated that the free energy barrier (ΔG‡) to N2 cleavage by the bridged complex [(PNP)MoI]2(μ-N2) is only 21.8 kcal mol−1, and that the reaction is exergonic by 27.6 kcal mol−1.28 Mézailles, Robert, and co-workers52 have likewise calculated a barrier of 21.1 kcal mol−1 for cleavage of [(PPP)MoI]2(μ-N2) (PPP = κ3-PhP[CH2CH2P(cy-C6H11)2]2); this reaction was calculated to be more exergonic (40.0 kcal mol−1).The activation free energy for N2 cleavage by [(PSP)MoI]2(μ-N2) (Scheme 10; X = I), ΔG‡ = 21.1 kcal mol−1, is essentially equal to that of [(PNP)MoI]2(μ-N2) and [(PPP)MoI]2(μ-N2), while the reaction energy (ΔG° = −33.7 kcal mol−1) is calculated to be intermediate between these two examples. The low calculated activation barrier is consistent with the rapid formation of 1-(N)I observed upon the addition of 2.0 equivalents Na/Hg to 1-Cl3 under N2 atmosphere in the presence of NaI (Scheme 3). Slightly greater barriers are calculated for X = Br and Cl (Scheme 10). The origin of this effect of varying the halide ligand is not obvious,101 and efforts are currently underway to elucidate it. In all cases the reaction is very exergonic.
 | ||
| Scheme 10 Calculated activation barriers and reaction energies of cleavage of the N2 bridge of [(PSP)MoX]2(μ-N2); X = Cl, Br, I. | ||
(PSP)MoN–H bond formation
It is typically presumed that the conversion of a nitride ligand to ammonia proceeds sequentially via H atom transfer (HAT) or PCET steps to yield the corresponding imide, amide, and ammonia complex (eqn (3)).35–37,57,58 | (3) |
As discussed above, within the class of complexes considered herein, the barriers to N2 cleavage to form nitride are low, and the reaction is very exergonic (i.e. the nitride products are “low-energy” species). Therefore it would not be unexpected that conversion of nitride to ammonia would comprise the rate-determining segment of a catalytic cycle. Thus, for example, Nishibayashi has proposed that N–H bond formation can be rate-determining in the (PNP)Mo-catalyzed reduction of N2 to NH3.35–37,57 More generally, insight into the reaction of nitride products to yield NH3 is critical to the rational design of energy-efficient catalysts based on bimetallic N2 splitting.17,25,29,59,60
Conversion of the nitride ligand to ammonia is also a key segment of catalytic pathways that are based on the so-called distal mechanism for N2 reduction, first envisioned by Chatt102,103 almost 50 years ago and many years later realized in practice by Yandulov and Schrock.19,104–106 Indeed, it appears that most molecular catalysts for N2 reduction based on molybdenum20–28,30–33,38,107,108 (and very possibly many or most other metals109,110) operate via either bimolecular N2-splitting or distal mechanisms; both classes require the conversion of a nitride ligand to ammonia.
| Product | [MoIII]X(N–H) | [MoII]X(NH–H) | [MoI]X(NH2–H) | [MoIII]X2(NH–H) | [MoII]X2(NH2–H) | [MoIII]X(NH–H)+ | [MoII]X(NH2–H)+ |
|---|---|---|---|---|---|---|---|
| a SMDbenzene/M06/Def2-QZVP//M06/SDD/6-31G(d,p). b Values in kcal mol−1. c Mo(IV) species have singlet spin states. s = singlet, d = doublet, t = triplet, q = quartet spin states. | |||||||
| [Mo] = (PSP)Mo | (PSP)MoX(NH n ) (n = 1, 2, 3) | (PSP)MoX 2 (NH n ) (n = 2, 3) | (PSP)MoX(NH n ) + (n = 2, 3) | ||||
| X = Cl | 33.0d | 56.3t | 51.2d | 50.0q | 55.9t | 47.0q | 60.7t |
| X = I | 31.6d | 58.2t | 49.3d | 49.1q | 58.3t | 45.7q | 47.7t |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||||
| [Mo] = (PNP)Mo | (PNP)MoX(NH n ) (n = 1, 2, 3) | (PNP)MoX 2 (NH n ) (n = 2, 3) | (PNP)MoX(NH n ) + (n = 2, 3) | ||||
| X = Cl | 31.2d | 45.0s | 52.9d | 50.7q | 50.7t | 47.8q | 54.0t |
| X = I | 31.9d | 45.8s | 51.3d | 50.6q | 51.5t | 47.8q | 52.7t |
In the case of (PNP)Mo(N)X it has been suggested that formation of the first N–H bond may proceed via an initial one-electron reduction.28 For 1-(N)X, however, we calculate that transfer of an electron from the strong reducing agent Cp*2Co, to give the ion-pair [Cp*2Co][(PSP)Mo(N)X], is highly endergonic, (ΔG° = 35.5, 36.7, and 35.5 kcal mol−1 for X = Cl, Br, I respectively). (See Computational section for discussion of ion-pairing effects, without which the electron transfer would be even much more endergonic, calculated as 52.5, 52.8, and 52.2 kcal mol−1 for X = Cl, Br, I respectively.) We also calculate that reduction of (PNP)Mo(N)X by Cp*2Co is similarly unfavorable (Table S7.15†).
The calculated thermodynamic barrier for this one-electron reduction (e.g. ΔG° = 35.5 kcal mol−1 for X = I) is prohibitively high for a reaction to occur at ambient conditions, even before considering the kinetic barrier. Nevertheless, we wished to investigate the kinetic barrier, at least to the extent that computational methods would allow. The reorganization energies (λ0) were calculated for Cp*2Co/[Cp*2Co +] and for (PSP)Mo(N)X/[(PSP)Mo(N)X−] and from these values the kinetic barriers to electron transfer could be calculated using the Marcus equation (eqn (4)).
 | (4) |
The values of ΔG‡ for reduction of 1-(N)X by Cp*2Co were determined, according to eqn (4), to be 53.3, 56.5, and 54.2 kcal mol−1 (X = Cl, Br, I respectively). Clearly these represent a prohibitively high kinetic barrier but, again, even absent any barrier in addition to the calculated endergonicity (e.g. ΔG° = 35.5 kcal mol−1 for X = Cl, I), the rate at ambient temperature would be extremely slow: 6 × 10−14 s−1 at 25 °C.
In agreement with these conclusions, as noted above, 1-(N)I underwent no reaction with Cp2Co or even Cp*2Co in the absence of a proton source such as [LutH]Cl, and cyclic voltammetry revealed a significantly negative reduction potential (Epc < −2.7 V vs. Fc+/0; S36†).
We therefore considered protonation, rather than reduction, following cleavage of N2.94 In the case of (PSP)Mo, as discussed above, experimentally we observed that the equilibrium for protonation of the N2 cleavage product 1-(N)(I) by [LutH][OTf] is slightly unfavorable, while [LutH]Cl readily reacted to afford an imide complex 1-(NH)(I)(Cl) without any indication of an observable equilibrium. Our DFT calculations are quite consistent with these observations. The reaction of 1-(N)(I) with [LutH]Cl to give trans-1-(NH)(Cl)(I) is calculated to be exergonic, ΔG° = −11.8 kcal mol−1 (eqn (5), X = Cl), whereas the analogous reaction with [LutH][OTf] is very slightly endergonic, ΔG° = 0.2 kcal mol−1.
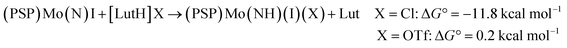 | (5) |
Note that even the calculated endergonic reaction with [LutH][OTf] is promoted by coordination of the corresponding anion (OTf−), although less so than is found for the more strongly coordinating chloride anion. The isomeric N-protonated species without Mo-coordinated triflate, but with triflate hydrogen-bonding to the NH ligand instead, was calculated to be higher in free energy, ΔG° = 7.1 kcal mol−1 (eqn (6)). 1-(N)(I) that is unprotonated, but acting as a H-bonding acceptor with [LutH][OTf], was calculated to be slightly lower in free energy, ΔG° = 5.1 kcal mol−1 (eqn (7)), but still higher in energy than the triflate-coordinated product of eqn (5). These results convey the favorability of N-protonation combined with anion coordination and the greater magnitude of this effect ( = 12.0 kcal mol−1) with chloride versus triflate anion (eqn (5)).
= 12.0 kcal mol−1) with chloride versus triflate anion (eqn (5)).
 | (6) |
 | (7) |
Thus, the calculated unfavorable thermodynamics of one-electron reduction of 1-(N)(I) are experimentally manifest by the lack of reaction with the strong reductant Cp*2Co. Likewise, the very low calculated N–H BDFE of 1-(NH)(I) is consistent with the failure of 1-(N)(I) to react with H-atom donors, TEMPO-H (O–H BDFE = 65.5 kcal mol−1 in THF77), 1,4-cyclohexadiene (C–H BDFEs = 67.8, gas phase77) or even CpCr(CO)3H (Cr–H BDFE = 54.9 kcal mol−1, MeCN77). Protonation, however, is achievable and kinetically very facile, assisted by coordination of an anion. Importantly, while protonation of course constitutes the formation of an N–H bond, it is not the reverse of the homolytic N–H bond dissociation that is implied to be so challenging based on the low N–H BDFE of 1-(NH)(I). Protonation does not represent a “full formation of the first N–H bond” in the sense of HAT or PCET as indicated in eqn (3).
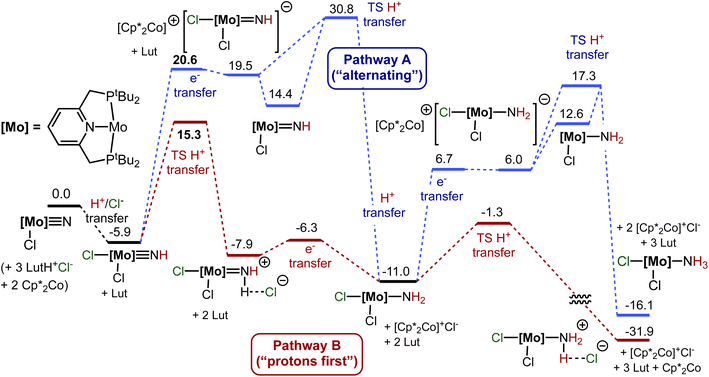
In a conventional protonation/reduction framework, in order to preserve charge balance, protonation of the nitride ligand would expectedly be followed by one-electron reduction. However, in the case of protonation of 1-(N)X this cannot be assumed, as charge balance is maintained by addition of a second halide. We therefore consider two pathways for the formation of the second N–H bond, following protonation: pathway A, beginning with reduction, and pathway B beginning with (a second) protonation. The energy profiles of the two pathways are illustrated in Fig. 6.
Following the net addition of HCl to 1-(N)Cl, transfer of an electron from Cp*2Co to 1-(NH)Cl2, to give the ion-pair [Cp*2Co][(PSP)Mo(NH)Cl2], is calculated to be highly unfavorable, ΔG° = 28.7 kcal mol−1 (eqn (8), and pathway A in Fig. 6). This is consistent with the failure of 1-(NH)ICl to undergo reaction with Cp*2Co in the absence of [LutH]Cl and cyclic voltammetry experiments on 1-(NH)ICl showing irreversible reductions only at very negative potentials (Fig. S37†).
| Cp*2Co + (PSP)Mo(NH)X2 → [Cp*2Co+][(PSP)Mo(NH)X2−], X = Cl; ΔG° = 28.7 kcal mol−1 | (8) |
Using the same Marcus-theory based approach as described above to estimate the kinetics of one-electron reduction of 1-(N)X, ΔG‡ for reduction of 1-(NH)Cl2 by Cp*2Co was determined to be 29.5 kcal mol−1 (Fig. 6, pathway A). Given the limitations of Marcus theory111,112 and assuming that the thermodynamic value of ΔG° = 28.7 kcal mol−1 must be viewed as a calculated lower limit, we suspect that the kinetics of the electron transfer step would be slower than are indicated by this calculated value of ΔG‡. Nevertheless even the rate predicted assuming that ΔG‡ = 29.5 kcal mol−1 would be prohibitively slow at ambient temperature (1.5 × 10−9 s−1 at 25 °C).
Subsequent loss of chloride from the hypothetical ion-paired product of electron-transfer, [Cp*2Co+][(PSP)MoIII(NH)Cl2−], is calculated to be exergonic by 5.0 kcal mol−1 (Fig. 6, pathway A; eqn (9b)), leading to the formation of (PSP)Mo(NH)Cl and [Cp*2Co]Cl. The resulting overall reduction of (PSP)MoIV(NH)Cl2 by Cp*2Co is shown in eqn (9c).
| (PSP)MoIV(NH)Cl2 + Cp*2Co → [Cp*2Co+][(PSP)MoIII(NH)Cl2−], ΔG° = 28.7 kcal mol−1 | (9a) |
| [Cp*2Co+][(PSP)MoIII(NH)Cl2−] → (PSP)MoIII(NH)Cl + [Cp*2Co+]Cl−, ΔG° = −5.0 kcal mol−1 | (9b) |
| (PSP)MoIV(NH)Cl2 + Cp*2Co → (PSP)MoIII(NH)Cl + [Cp*2Co+]Cl−, ΔG° = 23.7 kcal mol−1 | (9c) |
The product of eqn (9c), (PSP)MoIII(NH)Cl (1-(NH)Cl), is the net product of HAT/PCET to the starting nitride, 1-(N)Cl, formed via addition of H+/Cl− followed by reduction and loss of Cl− (pathway A, Fig. 6). While the barrier may be prohibitive (ΔG‡ = 29.5 kcal mol−1), we calculate that if 1-(NH)Cl were formed it could then react with [LutH]Cl, very exergonically, to undergo addition of H+Cl− across the MoIII![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) NH bond leading to amido complex (PSP)MoIII(NH2)Cl2 (eqn (10) and Fig. 6, pathway A). The TS for the proton transfer from lutidinium chloride could not be located but even assuming that there is a negligible enthalpic barrier, the entropic contribution of a bimolecular reaction is expected to be significant (and similar to the high barrier determined for the (PNP)Mo system which is discussed below). Thermodynamically, the reaction of 1-(NH)Cl with [LutH]Cl (eqn (10)) is calculated to be quite exergonic (ΔG° = −28.2 kcal mol−1; Fig. 6, pathway A). Combined with eqn (9c) (ΔG° = 23.7 kcal mol−1) this describes a reduction-first pathway for the thermodynamically favorable net addition of H-atom to the imide nitrogen of 1-(NH)Cl2 to give 1-(NH2)Cl2 (eqn (10), ΔG° = −4.5 kcal mol−1).
NH bond leading to amido complex (PSP)MoIII(NH2)Cl2 (eqn (10) and Fig. 6, pathway A). The TS for the proton transfer from lutidinium chloride could not be located but even assuming that there is a negligible enthalpic barrier, the entropic contribution of a bimolecular reaction is expected to be significant (and similar to the high barrier determined for the (PNP)Mo system which is discussed below). Thermodynamically, the reaction of 1-(NH)Cl with [LutH]Cl (eqn (10)) is calculated to be quite exergonic (ΔG° = −28.2 kcal mol−1; Fig. 6, pathway A). Combined with eqn (9c) (ΔG° = 23.7 kcal mol−1) this describes a reduction-first pathway for the thermodynamically favorable net addition of H-atom to the imide nitrogen of 1-(NH)Cl2 to give 1-(NH2)Cl2 (eqn (10), ΔG° = −4.5 kcal mol−1).
| (PSP)MoIV(NH)Cl2 + Cp*2Co + [LutH]Cl → (PSP)MoIII(NH2)Cl2 + [Cp*2Co+]Cl− + Lut, ΔG° = −4.5 kcal mol−1 | (10) |
The reduction of 1-(NH)Cl2 on pathway A would clearly encounter a prohibitive barrier. In contrast, proton transfer from [LutH]Cl to 1-(NH)Cl2 on pathway B is calculated to be kinetically facile and only slightly endergonic (eqn (11)). The kinetic barrier for this second protonation is calculated be ΔG‡ = 19.3 kcal mol−1 (mostly attributable to entropy; ΔE‡ is only 7.3 kcal mol−1), which would permit a rapid reaction at room temperature.
| 1-(NH)Cl2 + [LutH+]Cl− → [1-(NH2)Cl2+]Cl− + Lut, ΔG‡ = 19.3 kcal mol−1; ΔG° = 6.2 kcal mol−1 | (11) |
Subsequent reduction of the protonated complex [1-(NH2)Cl2]+Cl− is calculated to be exergonic (ΔG° = −10.7 kcal mol−1, eqn (12); Fig. 6, pathway B). Employing Marcus theory as discussed above, the kinetic barrier to electron transfer following this protonation is determined to be very low, ΔG‡ = 0.6 kcal mol−1.
| [1-(NH2)Cl2+]Cl− + Cp*2Co → [Cp*2Co+]Cl− + 1-(NH2)Cl2, ΔG‡ = 0.6 kcal mol−1; ΔG° = −10.7 kcal mol−1 | (12) |
Thus, our results strongly indicate that conversion of the N2-cleavage product, 1-(N)Cl, to 1-(NH2)Cl2, proceeds initially via N-protonation combined with addition of halide to Mo, as a rapid exergonic reaction to yield 1-(NH)Cl2. 1-(NH)Cl2 then undergoes a slightly endergonic protonation to give [1-(NH2)Cl2+]Cl− (eqn (11)). Reduction of this protonated complex by Cp*2Co is calculated to be exergonic with a very low kinetic barrier (eqn (12)). The net reaction, PCET to 1-(NH)Cl2 (eqn (10)) is exergonic by 4.5 kcal mol−1. Very similar results are obtained for the reactions of 1-(N)X and [LutH]X for X = Br and I (see ESI†).
Experimentally, consistent with the prediction of a very facile (and not rate-limiting) reduction of [1-(NH2)Cl2+]Cl− by Cp*2Co, even with use of the much weaker reductant, Cp2Co (Scheme 7), the formation of the second (as well as third) N–H bonds proceeds readily. By contrast, a hypothetical reduction of neutral 1-(NH)Cl2 by Cp2Co, prior to protonation, would be far more endergonic than with Cp*2Co (ΔE° = 0.78 eV = 18.1 kcal mol−1). The “protons-first” pathway (Fig. 6, pathway B) is thus strongly favored, by computation and experiment, for the formation of the first two N–H bonds on the path of the conversion of nitride ligand to ammonia.
Thus pathway B does not follow the paradigm of eqn (3), but instead circumvents the formation of a “first N–H bond” in the sense of HAT/PCET to 1-(N)Cl. Formation of MoIII imide 1-(NH)Cl or its Cl− adduct [1-(NH)Cl2−] are avoided. Instead, subsequent to the first protonation (and halide addition), a second protonation occurs, followed by a reduction. This comprises, overall, HAT/PCET to the MoIV imide 1-(NH)Cl2, forming an N–H bond with a BDFE of 49.1 kcal mol−1. This is much more favorable than HAT/PCET to the MoIV nitride 1-(N)Cl (corresponding to a BDFE of 31.6 kcal mol−1).
The underlying explanation for the much greater driving force (ΔΔG° = 17.5 kcal mol−1) for HAT/PCET to MoIV imide 1-(NH)Cl2, versus HAT/PCET to MoIV nitride 1-(N)Cl, is not obvious. Apparently, however, it can be primarily attributed to the added proton, rather than the coordinated halide. Thus HAT/PCET to the protonated MoIV nitride, i.e. the cationic imide 1-(NH)Cl+, has a driving force (45.7 kcal mol−1) similar to that for HAT/PCET to neutral 1-(NH)Cl2 (49.1 kcal mol−1) (Table 1). The major effect of the anion appears to be to favor this initial protonation of the nitride. It appears that HAT/PCET to nitride ligands may be inherently much less favorable than HAT/PCET to imides, independent of the oxidation state of the metal. It is perhaps notable, however, that coordination of the chloride anion even slightly favors (49.1 vs. 45.7 kcal mol−1) HAT/PCET – as this is formally a reduction of the molybdenum center.
The preference for pathway B versus pathway A is expected to apply even more strongly with a reducing agent weaker than Cp*2Co as the reduction step is not rate-determining. Importantly, this may be extrapolated to the case of an electrochemical system in which the cathodic overpotential is not very high, as would be required of a practical energy-efficient system.11
As discussed above in regard to formation of the second N–H bond, the experimental observation that formation of the third N–H bond proceeds readily even with the weak reducing agent Cp2Co instead of Cp*2Co, argues that a reduction step does not contribute to a rate-determining barrier. Again this is consistent with a “protons first” pathway (Fig. 6, pathway B). Beginning with (PSP)Mo(N)X (1-(N)X), the overall pathway to NH3 formation may therefore be described as addition of H+/X−/H+/e−/H+.
Subsequent to the very exergonic third protonation via pathway B, displacement of NH3 by Cl− (Scheme 11) is calculated to be exergonic by 10.5 kcal mol−1, giving 1-Cl3, the complex with which we began our study. In a catalytic cycle, if this displacement of ammonia by chloride occurs it would necessarily be followed by one-electron reduction and loss of a halide ion (Scheme 11) – the presumed initial step in the reactions of Schemes 2 and 3. An alternative to the replacement of NH3 by chloride (and subsequent reduction), would be direct one-electron reduction of the cationic species [1-(NH3)Cl2]+Cl− (Scheme 11). This step leads to the last species shown to be formed in pathway A in Fig. 6, i.e. the neutral MoII complex 1-(NH3)Cl2, but with an overall free energy of activation much lower than that of pathway A (which proceeds via one-electron reduction of neutral 1-(NH2)Cl2). Although beyond the scope of this work, further investigations are underway to determine in detail the pathways for reduction, with chemical reductants and electrochemically, which ultimately lead from MoIII complexes [1-(NH3)X2+] to the N2-bridging dimolybdenum(I) complexes [(PSP)MoX](μ-N2).
Comparison with the (PNP)MoN system
Extending our computational approach to the iconic PNP system yields results that are very similar to those obtained for PSP. As in the case of the PSP system, the initial N–H bond formation, using [LutH]Cl as the source of H+, is calculated to be exergonic (by 5.9 kcal mol−1) when coupled with chloride coordination. This reaction appears to have no barrier on the electronic energy surface. A subsequent hypothetical one-electron reduction by Cp*2Co is highly endergonic by 25.4 kcal mol−1 (pathway A, Fig. 7). For protonation of the resulting anion, in contrast with the case of the PSP analog ([(PSP)Mo(NH)Cl2]− anion), we successfully located a transition state; the free energy is 11.3 kcal mol−1 above the ion pair (fully attributable to entropy). The overall barrier to e−-transfer followed by protonation is therefore prohibitively high, 36.7 kcal mol−1. In contrast, protonation of (PNP)Mo(NH)Cl2 is slightly exergonic (ΔG° = −2.0 kcal mol−1) (pathway B, Fig. 7), with a relatively low barrier ΔG‡ = 21.2 kcal mol−1. One-electron reduction of the resulting [(PNP)Mo(NH2)Cl2+]Cl− ion pair is also slightly exergonic, and with a very low calculated kinetic barrier of ΔG‡ = 1.6 kcal mol−1 as determined using Marcus theory (pathway B).The “protons first” pathway B and the “alternating” pathway A reach the common intermediate (PNP)Mo(NH2)Cl2 analogously to the (PSP)Mo system. In the (PNP)Mo case our ability to locate a TS for the second protonation allows us to more quantitatively determine that the overall barrier for pathway A is significantly higher, by 15.5 kcal mol−1 (30.8 kcal mol−1versus 15.3 kcal mol−1), than that for pathway B (Fig. 7).
The intermediate common to both pathways A and B in Fig. 7, (PNP)Mo(NH2)Cl2, can undergo either protonation or reduction. As in the case of the (PSP)Mo system the barrier to reduction is not prohibitive, but protonation is much more favorable than reduction, kinetically (ΔG‡ = 9.7 kcal mol−1vs. 17.7 kcal mol−1) and especially thermodynamically (ΔG° = −20.9 kcal mol−1vs. 17.0 kcal mol−1). Moreover, as with formation of the second N–H bond, we have successfully located a TS for protonation subsequent to reduction (again, in contrast with the (PSP)Mo system) to form the third N–H bond. The overall barrier for the net addition of H-atom to (PNP)Mo(NH2)Cl2via the reduction/protonation pathway is 28.3 kcal mol−1 (pathway A). This compares with the much lower barrier of ΔG‡ = 9.7 kcal mol−1 for the very exergonic protonation yielding bound ammonia to afford the cationic complex [(PNP)Mo(NH3)Cl2+] (pathway B).
Our calculations with the PNP ligand thus serve to (a) reinforce the conclusions obtained with (PSP)Mo, by enabling identification of the TSs for the 2nd and 3rd protonation in an otherwise quite similar pathway, and (b) to demonstrate the broader applicability of the findings obtained with PSP.
Summary and conclusions
Pincer-molybdenum complexes, most notably Nishibayashi's (PNP)Mo-based and related catalysts, have demonstrated great promise for the formation of NH3 from N2 under mild conditions. As reported in this work, analogous (PSP)Mo complexes have been synthesized and their reactivity has been investigated, allowing us to observe intermediates and stoichiometric reactions directly relevant to this class of catalysts. In particular, our isolation of a nitride complex resulting from the cleavage of N2, and the formation and characterization of the corresponding imido complexes, may offer general mechanistic insight into N2 reduction pathways proceeding via such intermediates.Experimentally, the reaction of 1-Cl3 with an excess of reductant leads to the stable bridging-nitrogen complex 2, while reaction with only two equivalents Na/Hg per Mo in the presence of NaI leads to facile cleavage of N2 to give MoIV nitride complex 1-(N)(I). The very strong acid [H(Et2O)2][BArF4] protonates the nitride ligand of 1-(N)(I). Reaction with the moderately strong acid [LutH][OTf], which is often used for catalytic N2-to-NH3 conversion systems of this type, results in an equilibrium with a product that is not definitively characterized, but experimental evidence and DFT calculations indicate it to be 1-(NH)(OTf). [LutH]Cl, in contrast, fully reacts with 1-(N)(I), protonating the nitride ligand and adding chloride to the Mo center to give the fully characterized product 1-(NH)(I)(Cl). In the presence of additional [LutH]Cl, this MoIV imide complex can then be reduced with Cp*2Co resulting in the formation of NH3 and returning MoIII complex 1-Cl3. With the relatively weak reducing agent Cp2Co (Scheme 7) this reaction appears to reach equilibrium, and if base is added the reverse reaction is observed.
Results from DFT calculations are consistent with and shed light on various experimental observations, and their implications appear to apply to the (PNP)Mo analogs as well. Cleavage of N2 by the reduced MoI fragment to give the nitride complex 1-(N)(I) is calculated to be kinetically facile and thermodynamically favorable, in accord with experimental results and well precedented by calculations on other (pincer)Mo systems including (PNP)Mo and (PPP)Mo.
Conversion of nitride 1-(N)(I) to ammonia has been studied in depth. The N–H BDFE of the corresponding imide 1-(NH)(I), as in the case of other MoIV/MoIII nitride/imide couples, is particularly low, and its formation is intrinsically the least favorable of the three N–H bond formations leading to ammonia. Accordingly, H-atom transfer reagents such as TEMPO-H and CpCr(CO)3H do not undergo reaction with 1-(N)(I). Nor does 1-(N)(I) undergo reduction by Cp*2Co. However, in agreement with experiment, protonation of the nitride ligand of 1-(N)(I) by [LutH]Cl, in combination with addition of the chloride anion at the trans position to yield 1-(NH)(I)(Cl), is computed to be kinetically facile and thermodynamically favorable.
Thus a key conclusion of this work is that protonation of the nitride, assisted by anion coordination to MoIV, allows a pathway for nitride-to-ammonia conversion in which “formation of the first N–H bond” is circumvented. While N-protonation by definition results in formation of an N–H bond, it is, importantly, not the unfavorable HAT or PCET that corresponds to the low N–H BDFE of (PSP)Mo(X)(N–H).
Following protonation of the nitride, HAT or PCET to the imide ligand, to yield amide, is calculated to be thermodynamically more favorable, by ca. 15 kcal mol−1, than HAT or PCET to the nitride. This is the case whether or not the protonation is accompanied by anion coordination. Formation of this second N–H bond is calculated to proceed via a second protonation, followed by reduction (electron-transfer). Note than an initial reduction of the imide is necessarily unfavorable, since protonation followed by reduction would comprise a PCET to the nitride, and formation of the very low-BDFE “first” N–H bond. Thus the conventionally proposed pathway35–37,57,58 of sequential HAT/PCET to the MoIV nitride is not favorable, at least under conditions where reagents or potentials do not comprise a highly energy-inefficient system (e.g. very strong acids and reductants or very high overpotentials).
A final protonation by [LutH]X to give [1-(NH3)X2+]X−, is calculated to be kinetically facile and very exergonic. Thermodynamically, the overall reaction of 1-(NH)X2 with Cp*2Co and [LutH]X to yield this ammonia complex is calculated to be only slightly exergonic; this is consistent with the experiments indicating that the reaction of 1-(NH)(I)(Cl) with Cp2Co and [LutH]Cl, to give NH3 and Cp2Co+, is reversible.
Alternative pathways subsequent to the initial protonation of 1-(N)X certainly cannot be ruled out. Concerted PCET to 1-(NH)X2 or 1-(NH)X+ must be considered. However, the calculations – consistent with all relevant experimental observations – strongly indicate that net addition of H˙ (PCET, concerted or otherwise) to the MoIV N2-cleavage product 1-(N)X, is greatly favored by an initial protonation, accompanied by anion formation or not. Thus in the presence of sources of electron and proton sources of the type studied in this work, the lowest-energy overall sequence of N2 reduction by these catalysts appears to proceed through cleavage to yield nitride, followed by addition of H+/X−/H+/e−/H+, to yield coordinated NH3.
We note that thioethers and pyridines are not typically regarded as closely related ligands. Therefore, the strong mechanistic similarities between the PSP and PNP Mo complexes studied in this work suggest that the conclusions drawn from this study may be generally applicable to this important class of N2 reduction catalysts proceeding through MoIV nitrides.
Data availability
The authors confirm that the data supporting the findings of this study are available within the article and its ESI.†Author contributions
S. Man. and X. Z. conducted and analyzed the results of all synthetic and mechanistic experiments. S. Mal. and F. H. co-supervised and co-performed DFT calculations. R. N. A., L. W. G., and N. J. I. W. performed and analyzed DFT calculations. A. J. M. M. supervised electrochemical studies. Q. B. performed and analyzed electrochemical studies. T. J. E. and S. Man. collected and analyzed X-ray crystallographic data. A. S. G. supervised synthetic and mechanistic studies. S. Mal. and A. S. G. co-wrote the paper with significant contributions from S. Man., A. J. M. M., F. H. and Q. B. All authors read and approved the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported through the National Science Foundation Chemical Catalysis program under Grants No. CHE-2247259 and CHE-2247257, and through the NSF MRI Program, Award CHE-2117792. F. H. acknowledges support from the University Research Board of AUB (Award 104391). We thank Prof. Patrick Holland for helpful discussions and Prof. Jack Norton for a generous gift of CpCr(CO)3H.Notes and references
- V. Smil, Enriching the Earth: Fritz Haber, Carl Bosch, and the Transformation of World Food Production, MIT Press, Cambridge, MA, 2004 Search PubMed.
- J. W. Erisman, M. A. Sutton, J. Galloway, Z. Klimont and W. Winiwarter, How a century of ammonia synthesis changed the world, Nat. Geosci., 2008, 1(10), 636–639 CrossRef CAS.
- I. Rafiqul, C. Weber, B. Lehmann and A. Voss, Energy efficiency improvements in ammonia production—perspectives and uncertainties, Energy, 2005, 30(13), 2487–2504, DOI:10.1016/j.energy.2004.12.004.
- S. Giddey, S. P. S. Badwal, C. Munnings and M. Dolan, Ammonia as a Renewable Energy Transportation Media, ACS Sustain. Chem. Eng., 2017, 5(11), 10231–10239, DOI:10.1021/acssuschemeng.7b02219.
- T. J. Del Castillo, N. B. Thompson and J. C. Peters, A Synthetic Single-Site Fe Nitrogenase: High Turnover, Freeze-Quench 57Fe Mössbauer Data, and a Hydride Resting State, J. Am. Chem. Soc., 2016, 138(16), 5341–5350, DOI:10.1021/jacs.6b01706.
- A. R. Singh, B. A. Rohr, J. A. Schwalbe, M. Cargnello, K. Chan, T. F. Jaramillo, I. Chorkendorff and J. K. Nørskov, Electrochemical Ammonia Synthesis—The Selectivity Challenge, ACS Catal., 2017, 7(1), 706–709, DOI:10.1021/acscatal.6b03035.
- S. L. Foster, S. I. P. Bakovic, R. D. Duda, S. Maheshwari, R. D. Milton, S. D. Minteer, M. J. Janik, J. N. Renner and L. F. Greenlee, Catalysts for nitrogen reduction to ammonia, Nat. Catal., 2018, 1(7), 490–500, DOI:10.1038/s41929-018-0092-7.
- J. G. Chen, et al., Beyond fossil fuel-driven nitrogen transformations, Science, 2018, 360(6391), eaar6611, DOI:10.1126/science.aar6611.
- B. H. R. Suryanto, H.-L. Du, D. Wang, J. Chen, A. N. Simonov and D. R. MacFarlane, Challenges and prospects in the catalysis of electroreduction of nitrogen to ammonia, Nat. Catal., 2019, 2(4), 290–296, DOI:10.1038/s41929-019-0252-4.
- W. Guo, K. Zhang, Z. Liang, R. Zou and Q. Xu, Electrochemical nitrogen fixation and utilization: theories, advanced catalyst materials and system design, Chem. Soc. Rev., 2019, 48(24), 5658–5716, 10.1039/C9CS00159J.
- G. Hochman, et al., The Potential Economic Feasibility of Direct Electrochemical Nitrogen Reduction as a Route to Ammonia, ACS Sustain. Chem. Eng., 2020, 8(24), 8938–8948, DOI:10.1021/acssuschemeng.0c01206.
- Q. J. Bruch, G. P. Connor, N. McMillion, A. S. Goldman, F. Hasanayn, P. L. Holland and A. J. M. Miller, Considering Electrocatalytic Ammonia Synthesis via Bimetallic Dinitrogen Cleavage, ACS Catal., 2020, 10(19), 10826–10846, DOI:10.1021/acscatal.0c02606.
- M. J. Chalkley and J. C. Peters, Relating N-H Bond Strengths to the Overpotential for Catalytic Nitrogen Fixation, Eur. J. Inorg. Chem., 2020, 2020(15–16), 1353–1357, DOI:10.1002/ejic.202000232.
- M. J. Chalkley, M. W. Drover and J. C. Peters, Catalytic N2-to-NH3 (or -N2H4) Conversion by Well-Defined Molecular Coordination Complexes, Chem. Rev., 2020, 120(12), 5582–5636, DOI:10.1021/acs.chemrev.9b00638.
- D. R. MacFarlane, P. V. Cherepanov, J. Choi, B. H. R. Suryanto, R. Y. Hodgetts, J. M. Bakker, F. M. Ferrero Vallana and A. N. Simonov, A Roadmap to the Ammonia Economy, Joule, 2020, 4(6), 1186–1205, DOI:10.1016/j.joule.2020.04.004.
- N. Morlanés, S. P. Katikaneni, S. N. Paglieri, A. Harale, B. Solami, S. M. Sarathy and J. Gascon, A technological roadmap to the ammonia energy economy: current state and missing technologies, Chem. Eng. J., 2021, 408, 127310, DOI:10.1016/j.cej.2020.127310.
- S. J. K. Forrest, B. Schluschaß, E. Y. Yuzik-Klimova and S. Schneider, Nitrogen Fixation via Splitting into Nitrido Complexes, Chem. Rev., 2021, 121(11), 6522–6587, DOI:10.1021/acs.chemrev.0c00958.
- L. Merakeb and M. Robert, Advances in molecular electrochemical activation of dinitrogen, Curr. Opin. Electrochem., 2021, 29, 100834, DOI:10.1016/j.coelec.2021.100834.
- D. V. Yandulov and R. R. Schrock, Catalytic Reduction of Dinitrogen to Ammonia at a Single Molybdenum Center, Science, 2003, 301(5629), 76–78 Search PubMed.
- K. Arashiba, Y. Miyake and Y. Nishibayashi, A molybdenum complex bearing PNP-type pincer ligands leads to the catalytic reduction of dinitrogen into ammonia, Nat. Chem., 2011, 3(2), 120–125, DOI:10.1038/nchem.906.
- Y. Tanabe and Y. Nishibayashi, Developing more sustainable processes for ammonia synthesis, Coord. Chem. Rev., 2013, 257(17–18), 2551–2564, DOI:10.1016/j.ccr.2013.02.010.
- S. Kuriyama, K. Arashiba, K. Nakajima, H. Tanaka, N. Kamaru, K. Yoshizawa and Y. Nishibayashi, Catalytic formation of ammonia from molecular dinitrogen by use of dinitrogen-bridged dimolybdenum-dinitrogen complexes bearing PNP-pincer ligands: remarkable effect of substituent at PNP-pincer ligand, J. Am. Chem. Soc., 2014, 136(27), 9719–9731, DOI:10.1021/ja5044243.
- H. Tanaka, K. Arashiba, S. Kuriyama, A. Sasada, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Unique behaviour of dinitrogen-bridged dimolybdenum complexes bearing pincer ligand towards catalytic formation of ammonia, Nat. Commun., 2014, 5, 3737, DOI:10.1038/ncomms4737.
- K. Arashiba, E. Kinoshita, S. Kuriyama, A. Eizawa, K. Nakajima, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Catalytic Reduction of Dinitrogen to Ammonia by Use of Molybdenum–Nitride Complexes Bearing a Tridentate Triphosphine as Catalysts, J. Am. Chem. Soc., 2015, 137(17), 5666–5669, DOI:10.1021/jacs.5b02579.
- Y. Nishibayashi, Recent Progress in Transition-Metal-Catalyzed Reduction of Molecular Dinitrogen under Ambient Reaction Conditions, Inorg. Chem., 2015, 54(19), 9234–9247, DOI:10.1021/acs.inorgchem.5b00881.
- H. Tanaka, Y. Nishibayashi and K. Yoshizawa, Interplay between Theory and Experiment for Ammonia Synthesis Catalyzed by Transition Metal Complexes, Acc. Chem. Res., 2016, 49(5), 987–995, DOI:10.1021/acs.accounts.6b00033.
- A. Eizawa, K. Arashiba, H. Tanaka, S. Kuriyama, Y. Matsuo, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Remarkable catalytic activity of dinitrogen-bridged dimolybdenum complexes bearing NHC-based PCP-pincer ligands toward nitrogen fixation, Nat. Commun., 2017, 8, 14874, DOI:10.1038/ncomms14874.
- K. Arashiba, A. Eizawa, H. Tanaka, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Catalytic Nitrogen Fixation via Direct Cleavage of Nitrogen–Nitrogen Triple Bond of Molecular Dinitrogen under Ambient Reaction Conditions, Bull. Chem. Soc. Jpn., 2017, 90(10), 1111–1118, DOI:10.1246/bcsj.20170197.
- A. Eizawa and Y. Nishibayashi, Catalytic Nitrogen Fixation Using Molybdenum–Dinitrogen Complexes as Catalysts, Top. Organomet. Chem., 2017, 60, 153–169, DOI:10.1007/3418_2016_10.
- Y. Ashida, K. Arashiba, K. Nakajima and Y. Nishibayashi, Molybdenum-catalysed ammonia production with samarium diiodide and alcohols or water, Nature, 2019, 568(7753), 536–540, DOI:10.1038/s41586-019-1134-2.
- T. Itabashi, I. Mori, K. Arashiba, A. Eizawa, K. Nakajima and Y. Nishibayashi, Effect of substituents on molybdenum triiodide complexes bearing PNP-type pincer ligands toward catalytic nitrogen fixation, Dalton Trans., 2019, 48(10), 3182–3186, 10.1039/C8DT04975K.
- Y. Ashida and Y. Nishibayashi, Catalytic conversion of nitrogen molecule into ammonia using molybdenum complexes under ambient reaction conditions, Chem. Commun., 2021, 57(10), 1176–1189, 10.1039/d0cc07146c.
- Y. Tanabe and Y. Nishibayashi, Comprehensive insights into synthetic nitrogen fixation assisted by molecular catalysts under ambient or mild conditions, Chem. Soc. Rev., 2021, 50(8), 5201–5242, 10.1039/D0CS01341B.
- Y. Tanabe and Y. Nishibayashi, Recent advances in catalytic nitrogen fixation using transition metal-dinitrogen complexes under mild reaction conditions, Coord. Chem. Rev., 2022, 472, 214783, DOI:10.1016/j.ccr.2022.214783.
- Y. Ashida, T. Mizushima, K. Arashiba, A. Egi, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Catalytic production of ammonia from dinitrogen employing molybdenum complexes bearing N-heterocyclic carbene-based PCP-type pincer ligands, Nat. Synth., 2023, 2(7), 635–644, DOI:10.1038/s44160-023-00292-9.
- T. Mitsumoto, Y. Ashida, K. Arashiba, S. Kuriyama, A. Egi, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Catalytic Activity of Molybdenum Complexes Bearing PNP-Type Pincer Ligand toward Ammonia Formation, Angew. Chem., Int. Ed., 2023, 62(43), e202306631, DOI:10.1002/anie.202306631.
- Y. Tanabe and Y. Nishibayashi, Catalytic Nitrogen Fixation Using Well-Defined Molecular Catalysts under Ambient or Mild Reaction Conditions, Angew. Chem., Int. Ed., 2024, 63(33), e202406404, DOI:10.1002/anie.202406404.
- T. J. Hebden, R. R. Schrock, M. K. Takase and P. Muller, Cleavage of dinitrogen to yield a (t-BuPOCOP)molybdenum(IV) nitride, Chem. Commun., 2012, 48(13), 1851–1853, 10.1039/C2CC17634C.
- I. Klopsch, M. Finger, C. Würtele, B. Milde, D. B. Werz and S. Schneider, Dinitrogen Splitting and Functionalization in the Coordination Sphere of Rhenium, J. Am. Chem. Soc., 2014, 136(19), 6881–6883, DOI:10.1021/ja502759d.
- Q. Liao, A. Cavaillé, N. Saffon-Merceron and N. Mézailles, Direct Synthesis of Silylamine from N2 and a Silane: Mediated by a Tridentate Phosphine Molybdenum Fragment, Angew. Chem., Int. Ed., 2016, 55(37), 11212–11216, DOI:10.1002/anie.201604812.
- G. A. Silantyev, M. Förster, B. Schluschaß, J. Abbenseth, C. Würtele, C. Volkmann, M. C. Holthausen and S. Schneider, Dinitrogen Splitting Coupled to Protonation, Angew. Chem., Int. Ed., 2017, 56(21), 5872–5876, DOI:10.1002/anie.201701504.
- B. M. Lindley, R. S. van Alten, M. Finger, F. Schendzielorz, C. Würtele, A. J. M. Miller, I. Siewert and S. Schneider, Mechanism of Chemical and Electrochemical N2 Splitting by a Rhenium Pincer Complex, J. Am. Chem. Soc., 2018, 140(25), 7922–7935, DOI:10.1021/jacs.8b03755.
- M. F. Espada, S. Bennaamane, Q. Liao, N. Saffon-Merceron, S. Massou, E. Clot, N. Nebra, M. Fustier-Boutignon and N. Mezailles, Room-Temperature Functionalization of N2 to Borylamine at a Molybdenum Complex, Angew. Chem., Int. Ed., 2018, 57(39), 12865–12868, DOI:10.1002/anie.201805915.
- A. Eizawa, K. Arashiba, A. Egi, H. Tanaka, K. Nakajima, K. Yoshizawa and Y. Nishibayashi, Catalytic Reactivity of Molybdenum–Trihalide Complexes Bearing PCP-Type Pincer Ligands, Chem.–Asian J., 2019, 14(12), 2091–2096, DOI:10.1002/asia.201900496.
- Y. Ashida, S. Kondo, K. Arashiba, T. Kikuchi, K. Nakajima, S. Kakimoto and Y. Nishibayashi, A Practical Synthesis of Ammonia from Nitrogen Gas, Samarium Diiodide and Water Catalyzed by a Molybdenum-PCP Pincer Complex, Synthesis, 2019, 51(20), 3792–3795, DOI:10.1055/s-0039-1690151.
- A. Egi, H. Tanaka, A. Konomi, Y. Nishibayashi and K. Yoshizawa, Nitrogen Fixation Catalyzed by Dinitrogen-Bridged Dimolybdenum Complexes Bearing PCP- and PNP-Type Pincer Ligands: A Shortcut Pathway Deduced from Free Energy Profiles, Eur. J. Inorg. Chem., 2020, 2020(15–16), 1490–1498, DOI:10.1002/ejic.201901160.
- J. Y. Song, Q. Liao, X. Hong, L. Jin and N. Mezailles, Conversion of Dinitrogen into Nitrile: Cross-Metathesis of N2-Derived Molybdenum Nitride with Alkynes, Angew. Chem., Int. Ed., 2021, 60(22), 12242–12247, DOI:10.1002/anie.202015183.
- P. Garrido-Barros, J. Derosa, M. J. Chalkley and J. C. Peters, Tandem electrocatalytic N2 fixation via proton-coupled electron transfer, Nature, 2022, 609(7925), 71–76, DOI:10.1038/s41586-022-05011-6.
- Y. Ashida, Y. Onozuka, K. Arashiba, A. Konomi, H. Tanaka, S. Kuriyama, Y. Yamazaki, K. Yoshizawa and Y. Nishibayashi, Catalytic nitrogen fixation using visible light energy, Nat. Commun., 2022, 13(1), 7263, DOI:10.1038/s41467-022-34984-1.
- T. Itabashi, K. Arashiba, A. Egi, H. Tanaka, K. Sugiyama, S. Suginome, S. Kuriyama, K. Yoshizawa and Y. Nishibayashi, Direct synthesis of cyanate anion from dinitrogen catalysed by molybdenum complexes bearing pincer-type ligand, Nat. Commun., 2022, 13(1), 6161, DOI:10.1038/s41467-022-33809-5.
- T. Itabashi, K. Arashiba, S. Kuriyama and Y. Nishibayashi, Reactivity of molybdenum-nitride complex bearing pyridine-based PNP-type pincer ligand toward carbon-centered electrophiles, Dalton Trans., 2022, 51(5), 1946–1954, 10.1039/d1dt03952k.
- L. Merakeb, S. Bennaamane, J. De Freitas, E. Clot, N. Mezailles and M. Robert, Molecular Electrochemical Reductive Splitting of Dinitrogen with a Molybdenum Complex, Angew. Chem., Int. Ed., 2022, 61(40), e202209899, DOI:10.1002/anie.202209899.
- A. Coffinet, D. Specklin, Q. Le De, S. Bennaamane, L. Munoz, L. Vendier, E. Clot, N. Mezailles and A. Simonneau, Assessing Combinations of B(C6F5)3 and N2-Derived Molybdenum Nitrido Complexes for Heterolytic Bond Activation, Chem.–Eur. J., 2023, 29(26), e202203774, DOI:10.1002/chem.202203774.
- A. F. Ibrahim, P. Garrido-Barros and J. C. Peters, Electrocatalytic Nitrogen Reduction on a Molybdenum Complex Bearing a PNP Pincer Ligand, ACS Catal., 2023, 13(1), 72–78, DOI:10.1021/acscatal.2c04769.
- N. Ostermann, N. Rotthowe, A. C. Stückl and I. Siewert, (Electro)chemical N2 Splitting by a Molybdenum Complex with an Anionic PNP Pincer-Type Ligand, ACS Org. Inorg. Au, 2024, 4(3), 329–337, DOI:10.1021/acsorginorgau.3c00056.
- S. Malakar, S. Mandal, X. Zhou, Q. Bruch, R. Allen, L. Giordano, N. Walker; T. Emge, F. Hasanayn, A. Miller and A. Goldman, Mechanistic Insights into Key Steps of Dinitrogen Reduction to Ammonia with Pincer ligated Mo Complexes: Case Study of Easily Reduced PSP Mo Complexes, ChemRxiv, 2024, preprint, DOI:10.26434/chemrxiv-2024-2v9z2.
- A. Egi, H. Tanaka, T. Nakamura, K. Arashiba, Y. Nishibayashi and K. Yoshizawa, Computational screening of PCP-type pincer ligands for Mo-catalyzed nitrogen fixation, Bull. Chem. Soc. Jpn., 2024, 97(5), uoae041, DOI:10.1093/bulcsj/uoae041.
- Y. Yamazaki, K. Nakaya and Y. Nishibayashi, Synthesis of Molybdenum Complexes Bearing Pyridine-Based PNP-Type Pincer Ligands with Pendent Pyridyl Unit and Their Catalytic Activity for Ammonia Formation, Organometallics, 2024, 43(21), 2747–2754, DOI:10.1021/acs.organomet.4c00290.
- M. J. Bezdek, I. Pappas and P. J. Chirik, Determining and Understanding N-H Bond Strengths in Synthetic Nitrogen Fixation Cycles, Top. Organomet. Chem., 2017, 60, 1–21, DOI:10.1007/3418_2016_8.
- S. Kim, Y. Park, J. Kim, T. P. Pabst and P. J. Chirik, Ammonia synthesis by photocatalytic hydrogenation of a N2-derived molybdenum nitride, Nat. Synth., 2022, 1(4), 297–303, DOI:10.1038/s44160-022-00044-1.
- Chirik and co-workers have likewise calculated that for sequential addition of H atoms to the Mo(IV) nitride [(depe)2Mo
![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) N][BArF4] (depe = 1,2-bis(diethylphosphino)ethane) to give NH3, the first N–H BDFE is significantly weaker than the second and third (with an even more pronounced difference than found in this work for (PNP)MoX and (PSP)MoX nitrides); ref. 61.
N][BArF4] (depe = 1,2-bis(diethylphosphino)ethane) to give NH3, the first N–H BDFE is significantly weaker than the second and third (with an even more pronounced difference than found in this work for (PNP)MoX and (PSP)MoX nitrides); ref. 61. - X. Zhou, S. Malakar, T. Zhou, S. Murugesan, C. Huang, T. J. Emge, K. Krogh-Jespersen and A. S. Goldman, Catalytic Alkane Transfer Dehydrogenation by PSP-Pincer-Ligated Ruthenium. Deactivation of an Extremely Reactive Fragment by Formation of Allyl Hydride Complexes, ACS Catal., 2019, 9(5), 4072–4083, DOI:10.1021/acscatal.8b05172.
- L. S. Yamout, M. Ataya, F. Hasanayn, P. L. Holland, A. J. M. Miller and A. S. Goldman, Understanding Terminal versus Bridging End-on N2 Coordination in Transition Metal Complexes, J. Am. Chem. Soc., 2021, 143(26), 9744–9757, DOI:10.1021/jacs.1c01146.
- Q. Liao, N. Saffon-Merceron and N. Mezailles, N2 Reduction into Silylamine at Tridentate Phosphine/Mo Center: Catalysis and Mechanistic Study, ACS Catal., 2015, 5(11), 6902–6906, DOI:10.1021/acscatal.5b01626.
- S. Kuriyama, K. Arashiba, K. Nakajima, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Azaferrocene-Based PNP-Type Pincer Ligand: Synthesis of Molybdenum, Chromium, and Iron Complexes and Reactivity toward Nitrogen Fixation, Eur. J. Inorg. Chem., 2016, 2016(30), 4856–4861, DOI:10.1002/ejic.201601051.
- Q. J. Bruch, S. Malakar, A. S. Goldman and A. J. M. Miller, Mechanisms of Electrochemical N2 Splitting by a Molybdenum Pincer Complex, Inorg. Chem., 2022, 61(4), 2307–2318, DOI:10.1021/acs.inorgchem.1c03698.
- F. Hasanayn, P. L. Holland, A. S. Goldman and A. J. M. Miller, Lewis Structures and the Bonding Classification of End-on Bridging Dinitrogen Transition Metal Complexes, J. Am. Chem. Soc., 2023, 145(8), 4326–4342, DOI:10.1021/jacs.2c12243.
- In marked contrast with the reaction conducted in the presence of added I−, in the absence of added I− a complex mixture of products was observed by 31P and 1H NMR spectroscopy, including the “over-reduced” N2-bridged Mo(0) complex (2) as well as some remaining Mo(III) 1-Cl3.
- A. Katayama, T. Ohta, Y. Wasada-Tsutsui, T. Inomata, T. Ozawa, T. Ogura and H. Masuda, Dinitrogen-Molybdenum Complex Induces Dinitrogen Cleavage by One-Electron Oxidation, Angew. Chem., Int. Ed., 2019, 58(33), 11279–11284, DOI:10.1002/anie.201905299.
- G. Zhang, T. Liu, J. Song, Y. Quan, L. Jin, M. Si and Q. Liao, N2 Cleavage on d4/d4 Molybdenum Centers and Its Further Conversion into Iminophosphorane under Mild Conditions, J. Am. Chem. Soc., 2022, 144(6), 2444–2449, DOI:10.1021/jacs.1c11134.
- Y. Kani, T. Takayama, T. Sekine and H. Kudo, Crystal structures of nitridotechnetium(V) complexes of amine oximes differing in carbon chain lengths, J. Chem. Soc., Dalton Trans., 1999,(2), 209–214, 10.1039/A806245E.
- J. E. Weber, F. Hasanayn, M. Fataftah, B. Q. Mercado, R. H. Crabtree and P. L. Holland, Electronic and Spin-State Effects on Dinitrogen Splitting to Nitrides in a Rhenium Pincer System, Inorg. Chem., 2021, 60(9), 6115–6124, DOI:10.1021/acs.inorgchem.0c03778.
- C. E. Laplaza, M. J. A. Johnson, J. C. Peters, A. L. Odom, E. Kim, C. C. Cummins, G. N. George and I. J. Pickering, Dinitrogen Cleavage by Three-Coordinate Molybdenum(III) Complexes: Mechanistic and Structural Data, J. Am. Chem. Soc., 1996, 118(36), 8623–8638, DOI:10.1021/ja960574x.
- I. Klopsch, E. Y. Yuzik-Klimova and S. Schneider, in Nitrogen Fixation, ed. Y. Nishibayashi, Springer International Publishing, Cham, 2017, pp. 71–112 Search PubMed.
- B. Lindley, A. J. Miller and S. Schneider, Probing the mechanism of dinitrogen cleavage using electrochemical methods, in Abstracts, Southwest Regional and Rocky Mountain Regional Meeting of the American Chemical Society, El Paso, TX, United States, November, 2020 Search PubMed.
- R. S. van Alten, F. Waetjen, S. Demeshko, A. J. M. Miller, C. Wuertele, I. Siewert and S. Schneider, (Electro-)chemical Splitting of Dinitrogen with a Rhenium Pincer Complex, Eur. J. Inorg. Chem., 2020, 2020(15–16), 1402–1410, DOI:10.1002/ejic.201901278.
- R. G. Agarwal, et al., Free Energies of Proton-Coupled Electron Transfer Reagents and Their Applications, Chem. Rev., 2022, 122(1), 1–49, DOI:10.1021/acs.chemrev.1c00521.
- M. Brookhart, B. Grant and A. F. Volpe, [(3,5-(CF3)2C6H3)4B]−[H(OEt2)2]+: a convenient reagent for generation and stabilization of cationic, highly electrophilic organometallic complexes, Organometallics, 1992, 11(11), 3920–3922, DOI:10.1021/om00059a071.
- D. V. Yandulov, R. R. Schrock, A. L. Rheingold, C. Ceccarelli and W. M. Davis, Synthesis and reactions of molybdenum triamidoamine complexes containing hexaisopropylterphenyl substituents, Inorg. Chem., 2003, 42(3), 796–813, DOI:10.1021/ic020505l.
- In the absence of added [LutH]Cl, TEMPO-H (8.0 equiv.) was added to isolated (PSP)Mo(NH)(I)Cl (0.096 mmol) in THF. After 24 h at room temperature, volatiles were vacuum-transferred to a flask with HCl in diethyl ether. Ammonium chloride was only found in the receiving flask, in 41% yield. (See ESI†). (The low yield of NH4+ is attributed at least in part to some loss of NH3 during vacuum transfer).
- For a closely related example of an oxidative reaction of a pincer-Re complex with ammonia to yield a nitride complex, see: G. P. Connor, D. Delony, J. E. Weber, B. Q. Mercado, J. B. Curley, S. Schneider, J. M. Mayer and P. L. Holland, Facile conversion of ammonia to a nitride in a rhenium system that cleaves dinitrogen, Chem. Sci., 2022, 13(14), 4010–4018, 10.1039/D1SC04503B.
- M. J. Frisch, et al., Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford, CT, 2016 Search PubMed.
- H. S. Yu, X. He, S. L. Li and D. G. Truhlar, MN15: a Kohn–Sham global-hybrid exchange-correlation density functional with broad accuracy for multi-reference and single-reference systems and noncovalent interactions, Chem. Sci., 2016, 7(8), 5032–5051, 10.1039/C6SC00705H.
- M. M. Francl, W. J. Pietro, W. J. Hehre, J. S. Binkley, M. S. Gordon, D. J. DeFrees and J. A. Pople, Self-consistent molecular orbital methods XXIII A polarization-type basis set for second-row elements, J. Chem. Phys., 1982, 77(7), 3654–3665, DOI:10.1063/1.444267.
- M. S. Gordon, J. S. Binkley, J. A. Pople, W. J. Pietro and W. J. Hehre, Self-consistent molecular-orbital methods. 22. Small split-valence basis sets for second-row elements, J. Am. Chem. Soc., 1982, 104(10), 2797–2803, DOI:10.1021/ja00374a017.
- D. Andrae, U. Haeussermann, M. Dolg, H. Stoll and H. Preuss, Energy-adjusted ab initio pseudopotentials for the second and third row transition elements, Theor. Chim. Acta, 1990, 77(2), 123–141, DOI:10.1007/BF01114537.
- K. A. Peterson, D. Figgen, E. Goll, H. Stoll and M. Dolg, Systematically convergent basis sets with relativistic pseudopotentials. II. Small-core pseudopotentials and correlation consistent basis sets for the post-d group 16–18 elements, J. Chem. Phys., 2003, 119(21), 11113–11123, DOI:10.1063/1.1622924.
- D. Rappoport and F. Furche, Property-optimized Gaussian basis sets for molecular response calculations, J. Chem. Phys., 2010, 133(13), 134105, DOI:10.1063/1.3484283.
- F. Weigend and R. Ahlrichs, Balanced basis sets of split valence, triple zeta valence and quadruple zeta valence quality for H to Rn: design and assessment of accuracy, Phys. Chem. Chem. Phys., 2005, 7(18), 3297–3305, 10.1039/B508541A.
- F. Weigend, F. Furche and R. Ahlrichs, Gaussian basis sets of quadruple zeta valence quality for atoms H–Kr, J. Chem. Phys., 2003, 119(24), 12753–12762, DOI:10.1063/1.1627293.
- A. V. Marenich, C. J. Cramer and D. G. Truhlar, Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions, J. Phys. Chem. B, 2009, 113(18), 6378–6396, DOI:10.1021/jp810292n.
- D. Bezier, C. Guan, K. Krogh-Jespersen, A. S. Goldman and M. Brookhart, Experimental and Computational Study of Alkane Dehydrogenation Catalyzed by a Carbazolide-based Rhodium PNP Pincer Complex, Chem. Sci., 2016, 7(4), 2579–2586, 10.1039/C5SC04794C.
- B. Auer, L. E. Fernandez and S. Hammes-Schiffer, Theoretical Analysis of Proton Relays in Electrochemical Proton-Coupled Electron Transfer, J. Am. Chem. Soc., 2011, 133(21), 8282–8292, DOI:10.1021/ja201560v.
- K. Arashiba, H. Tanaka, K. Yoshizawa and Y. Nishibayashi, Cycling between Molybdenum-Dinitrogen and -Nitride Complexes to Support the Reaction Pathway for Catalytic Formation of Ammonia from Dinitrogen, Chem.–Eur. J., 2020, 26(59), 13383–13389, DOI:10.1002/chem.202002200.
- A. Katayama and H. Masuda, in Redox-based Catalytic Chemistry of Transition Metal Complexes, ed. T. Kojima, Royal Society of Chemistry, 2024, vol. 2, pp. 198–230 Search PubMed.
- T. Wang and F. Abild-Pedersen, Achieving industrial ammonia synthesis rates at near-ambient conditions through modified scaling relations on a confined dual site, Proc. Natl. Acad. Sci. U. S. A., 2021, 118(30), e2106527118, DOI:10.1073/pnas.2106527118.
- C. J. M. van der Ham, M. T. M. Koper and D. G. H. Hetterscheid, Challenges in reduction of dinitrogen by proton and electron transfer, Chem. Soc. Rev., 2014, 43(15), 5183–5191, 10.1039/C4CS00085D.
- S. Wang, F. Ichihara, H. Pang, H. Chen and J. Ye, Nitrogen Fixation Reaction Derived from Nanostructured Catalytic Materials, Adv. Funct. Mater., 2018, 28(50), 1803309, DOI:10.1002/adfm.201803309.
- M. Shao, et al., Efficient nitrogen fixation to ammonia on MXenes, Phys. Chem. Chem. Phys., 2018, 20(21), 14504–14512, 10.1039/C8CP01396A.
- Y. Liu, Y. Su, X. Quan, X. Fan, S. Chen, H. Yu, H. Zhao, Y. Zhang and J. Zhao, Facile Ammonia Synthesis from Electrocatalytic N2 Reduction under Ambient Conditions on N-Doped Porous Carbon, ACS Catal., 2018, 8(2), 1186–1191, DOI:10.1021/acscatal.7b02165.
- Effects of varying halides have been reported in the context of N2 cleavage by pincer-rhenium halide complexes, but these have been attributed to well-demonstrated effects of the halide on reduction potentials of several species involved in these reaction: R. S. van Alten, F. Waetjen, S. Demeshko, A. J. M. Miller, C. Wuertele, I. Siewert and S. Schneider, (Electro-)chemical Splitting of Dinitrogen with a Rhenium Pincer Complex, Eur. J. Inorg. Chem., 2020, 2020(15–16), 1402–1410, DOI:10.1002/ejic.201901278.
- J. Chatt, A. J. Pearman and R. L. Richards, The reduction of mono-coordinated molecular nitrogen to ammonia in a protic environment, Nature, 1975, 253, 39–40, DOI:10.1038/253039b0.
- J. Chatt, J. R. Dilworth and R. L. Richards, Recent advances in the chemistry of nitrogen fixation, Chem. Rev., 1978, 78(6), 589–625, DOI:10.1021/cr60316a001.
- R. R. Schrock, Catalytic reduction of dinitrogen to ammonia at a single molybdenum center, Acc. Chem. Res., 2005, 38(12), 955–962, DOI:10.1021/ar0501121.
- R. R. Schrock, Catalytic reduction of dinitrogen under mild conditions, Chem. Commun., 2003,(19), 2389–2391, 10.1039/B307784P.
- D. V. Yandulov and R. R. Schrock, Studies relevant to catalytic reduction of dinitrogen to ammonia by molybdenum triamidoamine complexes, Inorg. Chem., 2005, 44(4), 1103–1117, DOI:10.1021/ic040095w.
- R. R. Schrock, Catalytic reduction of dinitrogen to ammonia by molybdenum: theory versus experiment, Angew. Chem., Int. Ed., 2008, 47(30), 5512–5522, DOI:10.1002/anie.200705246.
- L. A. Wickramasinghe, T. Ogawa, R. R. Schrock and P. Müller, Reduction of Dinitrogen to Ammonia Catalyzed by Molybdenum Diamido Complexes, J. Am. Chem. Soc., 2017, 139(27), 9132–9135, DOI:10.1021/jacs.7b04800.
- J. S. Anderson, J. Rittle and J. C. Peters, Catalytic conversion of nitrogen to ammonia by an iron model complex, Nature, 2013, 501(7465), 84–87, DOI:10.1038/nature12435.
- S. E. Creutz and J. C. Peters, Catalytic reduction of N2 to NH3 by an Fe-N2 complex featuring a C-atom anchor, J. Am. Chem. Soc., 2014, 136(3), 1105–1115, DOI:10.1021/ja4114962.
- L. Jones and L. Lin, A theoretical study on the isomers of the B5TB heteroacene for improved semiconductor properties in organic electronics, Comput. Theor. Chem., 2017, 1115, 22–29, DOI:10.1016/j.comptc.2017.05.039.
- E. A. Buchanan and J. Michl, Optimal arrangements of 1,3-diphenylisobenzofuran molecule pairs for fast singlet fission, Photochem. Photobiol. Sci., 2019, 18(9), 2112–2124, 10.1039/c9pp00283a.
Footnote |
| † Electronic supplementary information (ESI) available: Complete experimental details and synthetic procedures, NMR data, computational details, computed energies and thermodynamic quantities. Optimized structures for calculated species. CCDC 2280371, 2329048 and 2340506–2340509. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d5sc00454c |
| This journal is © The Royal Society of Chemistry 2025 |