Open Access Article
Open Access ArticleModeling thermocatalytic systems for CO2 hydrogenation to methanol†
Jikai
Sun
and
Jianzhong
Wu
 *
*
Department of Chemical and Environmental Engineering, University of California, Riverside, CA 92521, USA. E-mail: jwu@engr.ucr.edu
First published on 10th March 2025
Abstract
The hydrogenation of CO2 to CH3OH over Cu-based catalysts holds significant potential for advancing carbon sequestration and sustainable chemical processes. While numerous studies have focused on catalyst development, the environmental effects on underlying reaction mechanisms have yet to be fully understood. In this work, we develop a grand potential theory for a comprehensive analysis of CO2 hydrogenation to CH3OH over Cu (111) and Cu (211) surfaces. By integrating electronic and classical density functional calculations to bridge the “pressure gap”, the theoretical results revealed that the HCOO* formation rate may vary by several orders of magnitude depending on reaction conditions. The grand potential theory enables us to elucidate the molecular mechanisms underlying the need for high H2 pressure, the prevalence of saturated CO2 adsorption, and the important roles of CO and H2O in hydrogenation. Moreover, this study addressed and clarified controversies over CO2versus CO adsorption and hydrogenation, the formate versus carboxy pathways, and the difference in HCOO* hydrogenation activity between Cu (111) and Cu (211) surfaces. The theoretical analysis offers a new perspective for optimizing reaction conditions and catalyst performance in methanol synthesis and can be generalized to enhance our understanding of heterogeneous catalysis under industrially relevant conditions.
1 Introduction
The hydrogenation of CO2 to CH3OH is of great significance, given potential applications in sustainable chemical processes and its important role in mitigating CO2 emissions.1,2 Cu-based catalysts have shown outstanding performance and are widely used in industrial applications.3–5 To optimize the catalytic efficiency, extensive research has been conducted to identify the active sites of copper species and understand the thermodynamic factors influencing the reaction kinetics, such as temperature, pressure and feedstock composition.6–8 First principles calculations have played a pivotal role in this fundamental research.9,10 The computational approach is highly effective in analyzing the interactions of various chemical species with the catalyst surface, locating active sites, exploring reaction pathways, and elucidating the underlying electronic structure and reaction mechanisms.11–13The hydrogenation of CO2 on metallic Cu has been extensively studied using electronic density functional theory (DFT).14–17 The theoretical work has helped establish a widely accepted reaction pathway for methanol synthesis, involving a series of intermediates such as HCOO, HCOOH, H2COOH, H2CO, H3CO, and H3COH.13,18 In addition to catalyst development, numerous studies have focused on investigating thermodynamic effects on CO2 hydrogenation, including the influence of temperature, pressure, and feed composition on the reaction rate and conversion efficiency.19–22 In general, the methanol yield can be maximized at low temperature, high pressure, high H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) COx and CO
COx and CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratios.23 However, different kinetic behaviors have been reported for the same catalyst under varying reaction conditions, and the underlying mechanisms remain not fully understood.20,24,25
CO2 ratios.23 However, different kinetic behaviors have been reported for the same catalyst under varying reaction conditions, and the underlying mechanisms remain not fully understood.20,24,25
The environmental effects on reaction rates can be investigated using Kinetic Monte Carlo (KMC) simulation, typically with the DFT results as input. To understand the kinetic behavior of CO2 hydrogenation to methanol under different conditions, Liu et al.26 employed DFT and KMC simulations to investigate the turnover frequencies (TOF) of methanol synthesis at various CO/CO2/H2 ratios on Cu (111) at 553 K and 80 bar. Their findings revealed that the CH3OH TOF initially increases with the CO2 to (CO2 + CO) ratio and then decreases beyond an optimal composition. Sauer and coworkers25 developed a three-site mean-field extended microkinetic model based on DFT calculations from the literature. They also demonstrated that methanol concentration initially increases and then decreases with the CO2 to (CO2 + CO) ratio on Cu (211) surfaces at 41 bar and temperatures ranging from 483 to 553 K. While these simulations accurately captured the reaction kinetics under certain conditions, discrepancies were noted when compared to experimental results. As reported by Sauer et al.,25 the experimental data indicated that methanol concentration only increases with the CO2 to (CO2 + CO) ratio when the temperature is reduced below 493 K. The optimal CO2/(CO2 + CO) ratio predicted by the micro kinetic model was not observed in experiments. This inconsistency likely stems from the interactions of reaction intermediates with gas molecules from the bulk, which are not adequately accounted for by conventional DFT calculations.
While first principles methods have achieved remarkable success in catalysis research, their applications for studying environmental factors, such as temperature, pressure, and gas-phase compositions, remain limited. Conventional DFT calculations typically assume a vacuum environment at 0 K. Although free-energy corrections are often applied to account for the bond vibrational entropy of the adsorbate, it ignores temperature effects on the thermodynamic properties of the entire system. Besides, conventional DFT calculations do not consider pressure and composition effects that influence the interaction of the adsorbate with gas molecules in the surroundings. Such interactions become increasingly significant at high pressure, leading to a “pressure gap” between theoretical predictions and experimental measurements.27 Because of the limitations of conventional DFT methods, many discrepancies have been reported in the hydrogenation activity of HCOO* on different Cu surfaces.11,12 The pressure gap is responsible for differences between DFT-calculated energy barriers and experimental apparent activation energies,18 the local reactant compositions, and uncertainties in reaction pathway selection.17,28
To bridge the pressure gap, we need to consider the interaction of catalyst and chemically adsorbed intermediates with gas molecules in an open environment. Toward that end, ab initio molecular dynamics (AIMD) simulations have been widely used to predict reaction processes under specific thermodynamic conditions.29–31 AIMD allows for the inclusion of environmental molecules, enabling a precise analysis of their interactions with the catalyst surface. However, the applicability of AIMD to thermocatalytic reactions is limited, not only by the computational intensity of first principles calculations but also by the relatively low number density of gas molecules in the bulk phase. For instance, at 503 K and 50 bar, the bulk density of CO2 is only about 1 molecule per nm3. Such a low density makes it challenging to simulate the gas composition near the catalyst surface accurately.
It should be noted that the impact of solvent effects in quantum chemical calculations is well established and is typically accounted for using either explicit or implicit solvent approaches. Implicit solvent models commonly employ the Poisson–Boltzmann equation to simulate the microenvironment around catalysts. Recently, Song et al. introduced a hybrid AIMD/cDFT model, demonstrating that classical DFT (cDFT) simulations can offer a more accurate description of solvent effects, thereby highlighting the potential of cDFT.32 At high pressure, similar effects are possible in gas-phase reactions; however, these effects remain largely underexplored in current computational studies.
In this work, we propose a grand potential theory that combines DFT for electronic structure calculations with cDFT to describe the thermodynamic properties of the entire reaction system. By embedding the catalytic sites in an open thermodynamic environment, the hybrid DFT allows for an explicit description of the inhomogeneous distributions of gas molecules as well as the grand potential of the heterogeneous system at different stages of chemical reactions. Equipped with this new theoretical capability, we have explored diverse thermodynamic factors influencing CO2 hydrogenation to methanol, including the effects of temperature, pressure, H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 and CO
CO2 and CO![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratios, and the impact of CO and H2O on HCOO* hydrogenation. Through the grand potential simulations, we uncovered the molecular mechanisms for the requirement of high H2 pressure and elucidated the intercorrelated roles of CO2, CO and H2O in the hydrogenation process. The theoretical framework can be readily generalized to account for environmental effects in other thermocatalytic systems.
CO2 ratios, and the impact of CO and H2O on HCOO* hydrogenation. Through the grand potential simulations, we uncovered the molecular mechanisms for the requirement of high H2 pressure and elucidated the intercorrelated roles of CO2, CO and H2O in the hydrogenation process. The theoretical framework can be readily generalized to account for environmental effects in other thermocatalytic systems.
2 Results and discussion
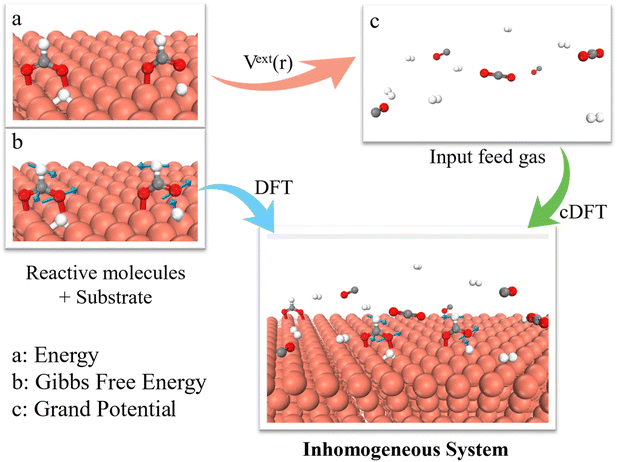
The theoretical details for our grand potential theory are described in ESI.† Briefly, Fig. 1 illustrates the hybrid DFT approach to simulate CO2 hydrogenation to CH3OH on Cu (111) and Cu (211) surfaces. The thermocatalytic process is governed by the grand potential of the entire system at different stages of the reaction, rather than the energy of individual intermediates (or the single molecular free energy) as used in conventional DFT calculations. To calculate the grand potential, we first identify the configuration of intermediate species at the catalyst surface through DFT calculations. The thermodynamic properties are then described using cDFT with a coarse-grained model for the surface species and environmental gas molecules. Notably, the grand potential simulations were conducted under a grand canonical (μVT) ensemble, allowing for the variation of gas molecules in alignment with experimental conditions. While conventional KS-DFT methods are used to evaluate the electronic energies of reaction intermediates, cDFT accounts for physical interactions among gas molecules and their adsorption on the catalyst surface under reaction conditions. The grand potential calculations thus consider both chemical bonding and the equilibrium between the catalyst surface (including chemically adsorbed species) and the gas phase, incorporating all intermolecular interactions including molecules in the near-surface region and bulk phase.2.1 Grand potential landscape
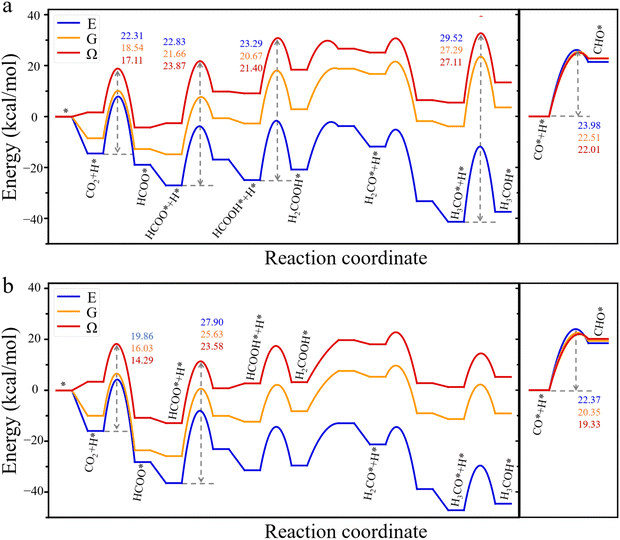
The grand-potential approach provides insight into the reaction mechanism from two distinct perspectives: the grand potential of the reactants and the catalyst as an open system and the local concentrations of molecular species near the catalyst surface. Specifically, Fig. 2 presents the grand-potential profile for CO2 hydrogenation to CH3OH as well as CO hydrogenation to CHO on Cu (111) and Cu (211) surfaces. For comparison, Fig. 2 also shows the corresponding energy (E) and free energy (G) landscapes calculated from conventional methods. It should be noted that in conventional DFT calculations, the energy E is defined as the difference between the surface with an adsorbate and the bare surface, along with a gas molecule in an isolated state (see eqn (S4)†). The free energy G corrects only the bond vibration entropy of individual intermediates. By contrast, the grand potential calculation naturally incorporates gas molecules in the environment at 503 K and 60 bar, with a feed gas composition of H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2
CO2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO = 6
CO = 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. This condition is commonly used in industrial applications of CO2 hydrogenation. Because the grand-potential corrected energy is defined relative to that of a bare surface in contact with the gas mixture under the reaction condition, it has a positive value for each intermediate. The positive energy does not imply exothermic adsorption of the intermediates, it only indicates that the adsorbates reduce the surface attraction for gas molecules in the bulk. In other words, the positively shifted energy profile originates from a negative energy in the reference state due to the strong attraction between Cu atoms and gas molecules.2,18,33
1. This condition is commonly used in industrial applications of CO2 hydrogenation. Because the grand-potential corrected energy is defined relative to that of a bare surface in contact with the gas mixture under the reaction condition, it has a positive value for each intermediate. The positive energy does not imply exothermic adsorption of the intermediates, it only indicates that the adsorbates reduce the surface attraction for gas molecules in the bulk. In other words, the positively shifted energy profile originates from a negative energy in the reference state due to the strong attraction between Cu atoms and gas molecules.2,18,33
As the electronic energy is significantly larger than the corrections for bond vibrations and intermolecular interactions, the conventional and hybrid DFT methods predict similar energy diagrams. Nevertheless, the thermodynamic effects are significant, particularly for predicting the intermediate steps of CO2 hydrogenation. Fig. 2 shows that grand potential corrections are as important as free energy corrections related to bond vibrations, with both being of the same order of magnitude. On the Cu (111) surface (Fig. 2a), both conventional DFT methods and the grand potential theory predict four high-energy barriers in the reaction pathway from CO2 to CH3OH. These include CO2 hydrogenation to HCOO*, HCOO* to HCOOH*, HCOOH* to H2COOH*, and H3CO* to H3COH*. Notably, KS-DFT predicts that the highest energy barrier, 29.52 kcal mol−1, occurs in the elementary step from H3CO* to H3COH*. This is the rate-determining step, mostly responsible for the low activity of CO2 hydrogenation at the Cu (111) surface. After applying the free-energy corrections of bond vibrations, the energy barriers decline for all four elementary steps. In particular, the energy barrier for CO2 hydrogenation falls to 18.54 kcal mol−1, implying that the adsorbed CO2 becomes more easily hydrogenated to form HCOO* at high temperature. These theoretical predictions are consistent with experimental results,34 showing HCOO* as the most prevalent species on Cu surfaces. With the grand-potential corrections, the reaction barriers for CO2 and H3CO* hydrogenation further decrease, while those for HCOO* and HCOOH* hydrogenation increase, narrowing the energy gap between HCOO* and H3CO* hydrogenation. Given the high concentration of HCOO* intermediate species, HCOO* plays a key role in the conversion of CO2 to CH3OH on the Cu (111) surface.
On the Cu (211) surface (Fig. 2b), all theoretical methods predict that HCOO* hydrogenation to HCOOH* is the most important rate-determining step. The energy barrier predicted by the KS-DFT decreases from 27.90 kcal mol−1 to 25.63 kcal mol−1 after the free-energy correction for bond vibrations. Nevertheless, this energy barrier is still much higher than 21.66 kcal mol−1, the energy barrier for HCOO* hydrogenation to HCOOH* on the Cu (111) surface. However, after applying grand-potential corrections, the energy barrier for HCOO* hydrogenation increases on the Cu (111) surface but decreases on the Cu (211) surface. Consequently, the grand-potential barrier on Cu (211) is slightly lower (23.58 kcal mol−1) than that on Cu (111) (23.87 kcal mol−1), indicating that the HCOO* hydrogenation on Cu (211) is comparable to that on Cu (111). While this slight difference is insufficient to explain why Cu (211) exhibits higher activity than Cu (111) for methanol production observed in experiment, the opposite trends in variation of the energy barriers on Cu (111) and Cu (211) surfaces underscore the importance of grand-potential corrections in understanding the reaction kinetics. As discussed later, the grand potential theory also provides information on the local concentrations of reactants, which have significant impacts on the reaction rate.12 For CO hydrogenation, the conventional and hybrid DFT methods predict a similar energy profile on both Cu (111) and Cu (211) surfaces, indicating that the reaction energy is relatively insensitive to vibrational entropy and grand-potential corrections. However, environmental effects can still play a significant role in the kinetics of CO hydrogenation because the reaction rate depends not only the energy barrier but also temperature and the local concentrations of reactants. In fact, temperature and gas composition are known to have strong influence on the water–gas shift (WGS) reaction.35
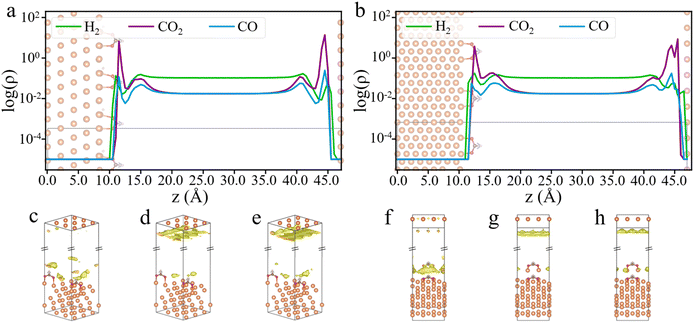
Through cDFT simulations, we have the density profiles of the feed gases near the catalyst surface. Fig. 3a and b show the gas density profiles on HCOO*-adsorbed Cu (111) and Cu (211) surfaces, while the profiles for bare Cu (111) and Cu (211) surfaces are presented in Fig. S2.† These figures reveal a significant disparity between the surface densities of the input gases and their bulk values. Notably, the surface density of CO2 is two orders of magnitude higher than its bulk density. Meanwhile, the surface densities of H2 and CO oscillate near the catalyst surface and show significant deviations from their respective bulk values. The local composition of gas molecules near the catalyst surface is markedly different from the input composition, with CO2 being much more prevalent than the other two gases. The H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio on the catalyst surface is much lower than the input ratio, implying that a higher H2
CO2 ratio on the catalyst surface is much lower than the input ratio, implying that a higher H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio in the feed gas is necessary to increase surface H2 density. Besides, CO2 adsorption is more favorable than CO, leading to CO2 the dominant carbon source in alignment with experimental observations.18
CO2 ratio in the feed gas is necessary to increase surface H2 density. Besides, CO2 adsorption is more favorable than CO, leading to CO2 the dominant carbon source in alignment with experimental observations.18
As will be discussed later, using surface reactant densities rather than their bulk densities provides a more accurate description of the hydrogenation kinetics. Fig. 3 shows that the first peak of the feed gas density occurs within about 5 Å of the surface, prompting us to define the gas concentration at the surface within this range. Additionally, by contrasting the differences between the HCOO*-adsorbed surface and the pristine surface, we observe that the presence of HCOO* reduces the surface density of CO2 and CO, while increasing the surface density of H2 (the bottom panel of Fig. S2b†). These differences are likely attributed to larger excluded volume effects due to the interactions of HCOO* with CO2 and CO molecules, whereas H2, with its smaller molecular size, is relatively less affected by the surface occupancy of the HCOO* species. Furthermore, from the 3D density maps of the feed gases on Cu (111) and Cu (211) surfaces (Fig. 3c–h), it is evident that H2 tends to accumulate around the HCOO* species rather than on the bare Cu surface. In contrast, CO2 and CO show greater adsorption on the bare Cu surfaces.
2.2 Effects of temperature and pressure
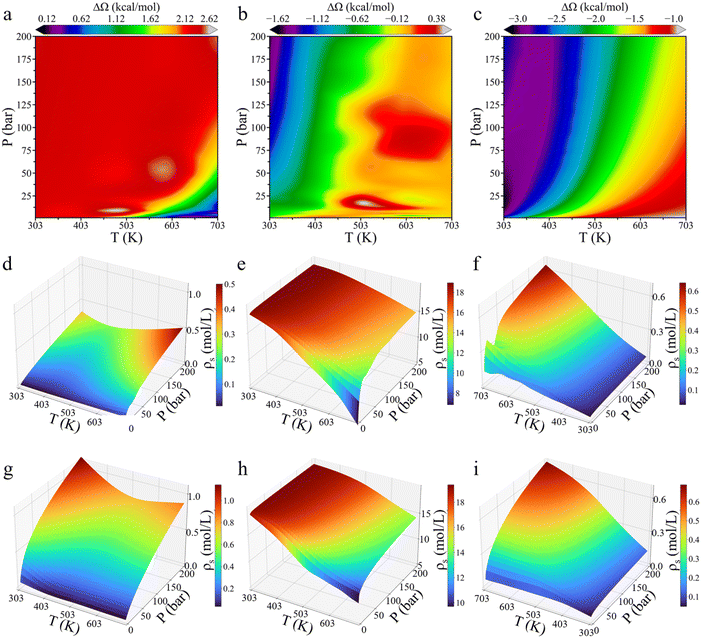
To investigate the environmental effects on CO2 hydrogenation to CH3OH, we calculated the grand potential barriers and surface gas densities over a wide range of temperatures and pressures. Fig. 4 presents the changes in the grand potential barrier (ΔΩ) for HCOO* and H3CO* hydrogenation on Cu (111), as well as HCOO* hydrogenation on Cu (211), while Fig. S3† shows the simulation data for HCOOH* hydrogenation on Cu (111). For HCOO* hydrogenation on the Cu (111) surface, the variation in the grand potential barrier is around 2.5 kcal mol−1, with the minimum appeared at high temperature and low pressure. In the case of HCOOH* hydrogenation, the grand potential barrier varies within the range of approximately 0.8 kcal mol−1 under most conditions. In contrast, for H3CO*, the grand potential correction is highly sensitive to both temperature and pressure, generally increasing with temperature and decreasing with pressure, with the changes ranging from −1.6 to 0.4 kcal mol−1. On the Cu (211) surface, HCOO* hydrogenation shows a similar trend, with the grand potential increasing with temperature but decreasing with pressure. At low temperature and high pressure, the grand potential correction can reduce the energy barrier by up to 3 kcal mol−1.The impact of temperature and pressure on the grand-potential corrected energy barrier is primarily driven by their influence on the surface-phase composition. Fig. 4d–i presents the surface densities of the feed gas at various temperatures and pressures. A higher gas-phase density results in stronger interactions between the gas-phase molecules and surface intermediates. While it is somewhat expected that the surface density of each gas increases with pressure and decreases with temperature, several noteworthy points emerge from the grand-potential simulation: first, CO2 adsorption becomes easily saturated due to its high concentration in the gas mixture. Second, the surface density of H2 initially decreases and then increases with temperature. At high pressure, the surface density of H2 on Cu (111) is greater at 703 K than at 303 K. This seemingly counterintuitive result can be attributed to CO2 saturation at low temperature, which inhibits hydrogen adsorption. Third, the surface densities of CO2 and CO on Cu (111) and Cu (211) surfaces are similar, while the H2 surface density on Cu (211) is approximately twice as high as that on Cu (111). The stepped Cu (211) surface is thus more favorable for H2 adsorption than the Cu (111) surface, further supporting that Cu (211) has a higher reactivity.
Based on the grand potential landscape and surface densities, we predicted the reaction rate of HCOO* hydrogenation using the transition state theory (TST). As shown in Fig. S4a and b,† the reaction rate increases monotonically with temperature, and it initially rises with pressure before reaching a plateau. Fig. S4c and d† present the ratio of reaction rates calculated via the grand potential theory to those calculated using the conventional DFT method (viz., through the free-energy barrier and bulk densities). After accounting for corrections of the surface densities and the grand potential, the reaction rate decreases by 1–2 orders of magnitude on the Cu (111) surface at most conditions. However, at 703 K and low pressure, the thermodynamic correction raises the reaction rate by almost 3 orders of magnitude. The drastic increase in the reaction rate can be attributed to the enhanced HCOO* coverage, which can be estimated from the quasi-equilibrium condition (see ESI†). As shown in Fig. S5,† the conventional approach predicts a small HCOO* coverage at high temperature and low pressure. The grand potential correction reduces the reaction energy for HCOO* formation. Besides, it predicts that the surface density of CO2 on Cu (111) significantly exceeds its bulk density. As a result, the grand-potential simulations yield an extremely high HCOO* coverage, close to 100%, explaining the drastic increase of the reaction rate. On the Cu (211) surface at low temperature and pressure, the grand potential theory predicts a reaction rate approximately 1–2 orders of magnitude higher than that calculated using the conventional method. At high temperature and pressure, the grand potential theory still predicts a higher reaction rate, but the relative difference between the two methods decreases. Because of the strong adsorption of HCOO* on Cu (211), the HCOO* coverage approaches near 100% according to both grand potential and free energy simulations. The high HCOO* coverage implies that the hydrogenation rate of HCOO* is independent of the surface concentration of CO2, challenging conventional understandings based on the CO2 pressure.
2.3 Effects of feed gas composition
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/b_char_2009.gif) CO2 ratio.
In this section, we explore the influence of the H2
CO2 ratio.
In this section, we explore the influence of the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio on the hydrogenation kinetics. Previous research suggests that a high H2
CO2 ratio on the hydrogenation kinetics. Previous research suggests that a high H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio favors the conversion of CO2 to CH3OH. For example, Lin and Bhan20 showed that, at a constant CO2 pressure, increasing H2 pressure linearly increases the methanol formation rate. Conversely, at 523 K and constant H2 pressure, the reaction exhibits Langmuir-type saturation kinetics with respect to CO2 pressure on Copper–Zinc–Alumina (CZA) catalysts. Nielsen et al.24 reported a similar Langmuir-type behavior concerning the effect of CO2 pressure on CH3OH formation rates on Cu/ZnO catalysts. These findings suggest that maintaining a high H2
CO2 ratio favors the conversion of CO2 to CH3OH. For example, Lin and Bhan20 showed that, at a constant CO2 pressure, increasing H2 pressure linearly increases the methanol formation rate. Conversely, at 523 K and constant H2 pressure, the reaction exhibits Langmuir-type saturation kinetics with respect to CO2 pressure on Copper–Zinc–Alumina (CZA) catalysts. Nielsen et al.24 reported a similar Langmuir-type behavior concerning the effect of CO2 pressure on CH3OH formation rates on Cu/ZnO catalysts. These findings suggest that maintaining a high H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio is crucial for optimizing the kinetics of methanol synthesis. This is often attributed to the dearth of surface H* and the saturation of HCOO* species on the catalyst surface. However, the upper limit of H2
CO2 ratio is crucial for optimizing the kinetics of methanol synthesis. This is often attributed to the dearth of surface H* and the saturation of HCOO* species on the catalyst surface. However, the upper limit of H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio remains uncertain. Lin and Bhan20 demonstrated that methanol production continues to increase linearly with H2 pressure, even when the H2
CO2 ratio remains uncertain. Lin and Bhan20 demonstrated that methanol production continues to increase linearly with H2 pressure, even when the H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio exceeds 10. This raises the question: why is such a high H2 pressure necessary? Moreover, even after the inflection point of the Langmuir-type curve, a further increase in the CO2 partial pressure can still raise the methanol production rate. This brings up another question: what role does CO2 partial pressure play once HCOO* saturation is reached?
CO2 ratio exceeds 10. This raises the question: why is such a high H2 pressure necessary? Moreover, even after the inflection point of the Langmuir-type curve, a further increase in the CO2 partial pressure can still raise the methanol production rate. This brings up another question: what role does CO2 partial pressure play once HCOO* saturation is reached?
The answers to these questions are related to the low H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
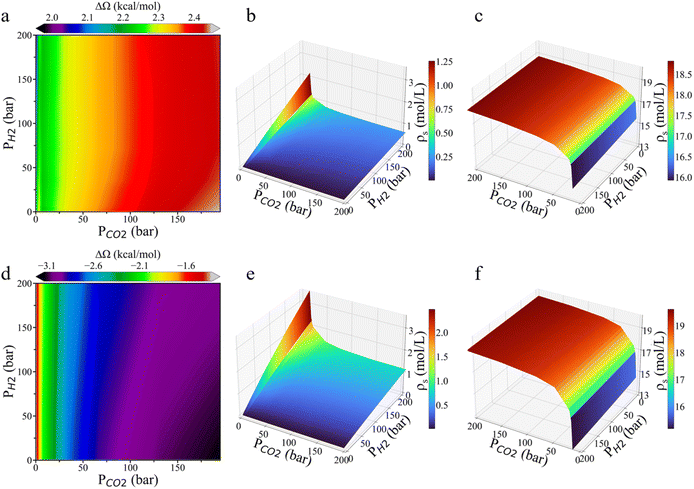
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio on the surface and the interactions between CO2 molecules and the reaction intermediates. As shown in Fig. 5, the grand potential barrier for HCOO* hydrogenation on the Cu (111) surface increases with rising CO2 pressure, while it remains nearly unchanged with varying H2 pressure. On the Cu (211) surface, however, the grand potential barrier falls with increasing CO2 pressure but increases with H2 pressure at higher CO2 pressure. Additionally, the surface density of H2 increases linearly as H2 pressure rises, with the increment being more pronounced at lower CO2 pressure. Notably, the surface density of H2 on Cu (211) is more than twice that on Cu (111). For CO2, the surface density rises sharply at low CO2 pressure before saturation. The inflection point occurs around 10 bar CO2 pressure, indicating that a further increase in CO2 pressure offers little additional benefit. As shown in Fig. S6,† at low CO2 pressure, the surface density of CO2 is two orders of magnitude higher than its bulk density, but the ratio of its surface density to the bulk density decreases sharply as the CO2 pressure increases to several bars. However, experimental results by Nielsen et al.24 indicate that the inflection point for the CO2 partial pressure in relation to CH3OH formation rate occurs at only 1–2 bar. This discrepancy can be attributed to the limited availability of active sites. As illustrated in Fig. S7,† HCOO* coverage becomes saturated even at low H2 and CO2 pressures, resulting the HCOO* coverage reaches a plateau before the CO2 surface concentration becomes saturated.
CO2 ratio on the surface and the interactions between CO2 molecules and the reaction intermediates. As shown in Fig. 5, the grand potential barrier for HCOO* hydrogenation on the Cu (111) surface increases with rising CO2 pressure, while it remains nearly unchanged with varying H2 pressure. On the Cu (211) surface, however, the grand potential barrier falls with increasing CO2 pressure but increases with H2 pressure at higher CO2 pressure. Additionally, the surface density of H2 increases linearly as H2 pressure rises, with the increment being more pronounced at lower CO2 pressure. Notably, the surface density of H2 on Cu (211) is more than twice that on Cu (111). For CO2, the surface density rises sharply at low CO2 pressure before saturation. The inflection point occurs around 10 bar CO2 pressure, indicating that a further increase in CO2 pressure offers little additional benefit. As shown in Fig. S6,† at low CO2 pressure, the surface density of CO2 is two orders of magnitude higher than its bulk density, but the ratio of its surface density to the bulk density decreases sharply as the CO2 pressure increases to several bars. However, experimental results by Nielsen et al.24 indicate that the inflection point for the CO2 partial pressure in relation to CH3OH formation rate occurs at only 1–2 bar. This discrepancy can be attributed to the limited availability of active sites. As illustrated in Fig. S7,† HCOO* coverage becomes saturated even at low H2 and CO2 pressures, resulting the HCOO* coverage reaches a plateau before the CO2 surface concentration becomes saturated.
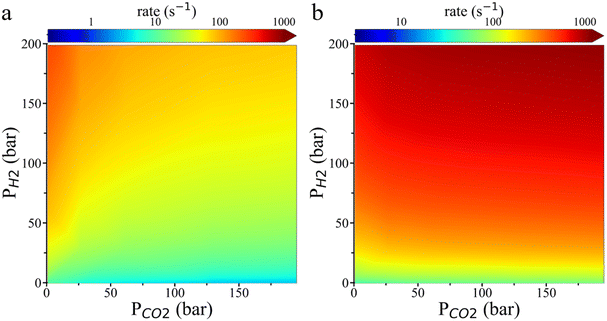
Fig. 6 shows the reaction rate for HCOO* hydrogenation predicted by the transition state theory. On the Cu (111) surface, the hydrogenation rate increases with H2 pressure while decreasing with CO2 pressure. The HCOO* hydrogenation rate is faster on the Cu (211) surface than on the Cu (111) surface. The theoretical result aligns well with the experimental observation that increasing H2 pressure significantly enhances the reaction rate, but increasing CO2 pressure has a minimal effect only when H2 pressure is high while CO2 pressure is low. Besides, as shown in Fig. S8,† the grand potential simulation indicates that the environmental effects become more pronounced on the rate of HCOO* hydrogenation on the Cu (211) surface at low H2 pressure and high CO2 pressure. The rate increase predicted by the grand potential theory agrees with the experimental finding that the CH3OH formation rate increases slightly with rising CO2 pressure, even when the surface coverage of HCOO* is saturated.
Based on the grand potential simulation, we found that the surface density of H2 is two orders of magnitude lower than the bulk density (Fig. 5b and e). This explains why the surface density of H2 increases linearly with bulk density without reaching saturation. In contrast, CO2 does not influence the HCOO* hydrogenation rate through surface concentration because the HCOO* coverage is already saturated. Instead, the HCOO* hydrogenation rate is influenced by both the energy barrier and the surface H2 concentration, these opposing effects cancel each other, leading to a stable HCOO* reaction rate with varying CO2 pressure. From this, we deduce that, at low temperature, the effect due to the reduction in energy barrier is more dominant, whereas at high H2 pressure, the reduction in surface H2 density has a greater impact. Therefore, the optimal H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio should decrease with temperature while increase with rising H2 pressure.
CO2 ratio should decrease with temperature while increase with rising H2 pressure.
Additionally, our grand-potential simulations may help resolve the ongoing debate regarding the formate pathway versus the carboxy pathway in CO2 hydrogenation.3,11,17,35 The reaction mechanism has been extensively debated over the past decade, with the formate pathway now widely accepted. However, certain observations continue to support the possibility of a carboxy pathway. For example, Yang et al.28 reported that surface reaction involving formate-containing adlayers on Cu (both supported on SiO2 and unsupported) failed to produce methanol in hydrogen atmospheres. Furthermore, some researchers questioned that surface HCOO* crowding at high coverages could enhance the reaction rate through the formate pathway.36 Based on the grand potential simulations, we observed that CO2 in the gas phase reduces the HCOO* hydrogenation energy barrier (Fig. 5d), indicating that HCOO* can hydrogenate more readily under a high-pressure atmosphere of CO2 gas. In contrast, without CO2 in the bulk gas, the grand potential theory predicts that HCOO* cannot undergo hydrogenation due to the high energy barrier (Fig. 5d), confirming that the HCOO* pathway is the dominant route for CO2 hydrogenation.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio favorable for methanol production.2,21,36,37 However, Kunkes et al.38 observed a continuous rise in methanol production rate with increasing the CO2 to (CO2 + CO) ratio on CZA at 413 K and 30 bar. Similar trends were reported by Liu et al.39 on CZA at 523 K and 50 bar. Meanwhile, Studt et al.33 noted that, while the intrinsic rate of methanol formation increases with the CO2 to (CO2 + CO) ratio on CZA, it decreases on Cu/MgO at 503 K and 30 bar. To minimize the effect of byproduct H2O, Nielsen et al.24 carried out experiment under low conversion conditions (<0.3 mol% methanol). They found that CO is purely inhibitory on RANEY® Cu and a variety of supported Cu-catalysts due to its competitive adsorption to the catalyst surface. However, as previously mentioned, when CO2 pressure exceeds 2 bar, the surface species HCOO* becomes saturated, suggesting that an additional increase of the CO2 pressure may not enhance methanol production significantly. This raises the question: why does CO still inhibit methanol formation even at high CO2 pressure? Moreover, recent experimental studies3,12,18 indicate that CO2 remains the dominant carbon source, even at low CO2 to (CO2 + CO) ratios, because CO tends to desorb more easily rather than undergo hydrogenation. This allows HCOO* derived from CO2 to reoccupy the active sites, as evidenced by the high coverage of HCOO*. This suggests that CO adsorption does not significantly poison the active sites or reduce TOF of methanol formation. Another question then arises: what is the precise role of CO in this process?
CO2 ratio favorable for methanol production.2,21,36,37 However, Kunkes et al.38 observed a continuous rise in methanol production rate with increasing the CO2 to (CO2 + CO) ratio on CZA at 413 K and 30 bar. Similar trends were reported by Liu et al.39 on CZA at 523 K and 50 bar. Meanwhile, Studt et al.33 noted that, while the intrinsic rate of methanol formation increases with the CO2 to (CO2 + CO) ratio on CZA, it decreases on Cu/MgO at 503 K and 30 bar. To minimize the effect of byproduct H2O, Nielsen et al.24 carried out experiment under low conversion conditions (<0.3 mol% methanol). They found that CO is purely inhibitory on RANEY® Cu and a variety of supported Cu-catalysts due to its competitive adsorption to the catalyst surface. However, as previously mentioned, when CO2 pressure exceeds 2 bar, the surface species HCOO* becomes saturated, suggesting that an additional increase of the CO2 pressure may not enhance methanol production significantly. This raises the question: why does CO still inhibit methanol formation even at high CO2 pressure? Moreover, recent experimental studies3,12,18 indicate that CO2 remains the dominant carbon source, even at low CO2 to (CO2 + CO) ratios, because CO tends to desorb more easily rather than undergo hydrogenation. This allows HCOO* derived from CO2 to reoccupy the active sites, as evidenced by the high coverage of HCOO*. This suggests that CO adsorption does not significantly poison the active sites or reduce TOF of methanol formation. Another question then arises: what is the precise role of CO in this process?
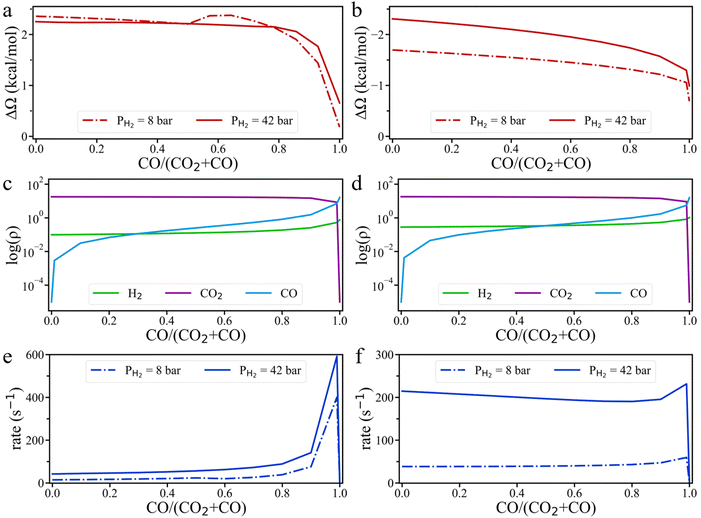
To address the above questions, we carried out grand-potential simulations at different ratios of CO to (CO2 + CO) while keeping the H2 pressure constant. As shown in Fig. 7, the grand potential correction of the energy barrier falls with increasing CO ratio for HCOO* hydrogenation on the Cu (111) surface, whereas the opposite trend is observed on the Cu (211) surface. This difference arises because the interaction between surface intermediates and CO is weaker than that with CO2. As the CO ratio increases, the absolute value of the grand-potential correction diminishes for both surfaces. Notably, the grand potential curve at 8 bar H2 pressure exhibits a distinct inflection point, likely due to a shift in the interaction of HCOO* at the Cu (111) surface with the input gas molecules—from H2 sub-dominance to CO sub-dominance—which causes an unexpected increase in the grand potential barrier. From Fig. 7c and d and S9,† we observe that the surface density of H2 increases slightly with the rising CO/(CO2 + CO) ratio, leading to the increase of the HCOO* hydrogenation rate on the Cu (111) surface. On the Cu (211) surface, the rate of *HCOO hydrogenation is nearly unchanged at 8 bar H2 partial pressure, until the CO/(CO2 + CO) ratio reaches above 0.7, at which point the rate increases (Fig. 7f). At 42 bar H2 pressure, however, the reaction rate first decreases and then increases with the CO/(CO2 + CO) ratio. The nonmonotonic trend corroborates the experimental observation that CO does not directly compete with CO2 for adsorption on the active sites.24 With the increasing CO/(CO2 + CO) ratio, the accumulation of CO on the Cu surface increases the energy barrier of HCOO* hydrogenation as well as H2 density on Cu (211) surface. These two opposing effects together control the HCOO* hydrogenation rate. At low H2 pressure, the increase in H2 surface density is the dominant factor, while at high H2 partial pressure, the effect on the energy barrier becomes more influential. Therefore, at low H2 pressure, the HCOO* hydrogenation rate increases with the CO ratio, but at high H2 pressure, the rate decreases with increasing CO ratio. This conclusion aligns well with the experimental findings that CH3OH formation rate remains unchanged with varying CO pressure at PCO2 = 4.7 bar and PH2 = 14 bar, but decreases with CO pressure at PCO2 = 4.7 bar and PH2 = 23 bar.20
Fig. 7f also shows that the HCOO* hydrogenation rate unexpectedly increases when the CO/(CO2 + CO) ratio reaches 0.99. In this case, the surface density of CO2 remains sufficiently high to form a substantial amount of HCOO* at the catalyst surface, while the surface density of H2 also increases significantly. The hydrogenation rate grows with the increasing H2 surface density because it has a favorable effect on HCOO* hydrogenation outweighing the negative effect due to the increased energy barrier. Experimental results from 40 years ago indicated that methanol formation rate in H2/CO mixtures is optimized when a small amount of CO2 is included in the feed, which supports our conclusion.40,41 However, the subsequent interpretation suggesting that ‘the RWGS reaction is likely autocatalyzed by water or water-derived species’ was incorrect and has largely been overlooked. Based on our proposed mechanism, CO undergoes both the water–gas shift (WGS) reaction and CO2 hydrogenation pathways to produce CH3OH. The fact that HCOO* is not readily detected can be explained by the prevalence of the Cu (111) surface, which is the most common facet for the Cu catalyst. When the CO/(CO2 + CO) ratio is greater than 0.9, the HCOO* hydrogenation rate on Cu (111) is hundreds of times faster than that at lower CO/(CO2 + CO) ratios. Therefore, HCOO* detected in experiments is likely presented on the Cu (111) surface, where it is rapidly converted to other intermediates at high CO/(CO2 + CO) ratios. This mechanism also explains why CO hydrogenation can be accelerated by the addition of H2O,28 and why CO hydrogenation on Cu/MgO oxide supports is significantly faster than CO2 hydrogenation.34
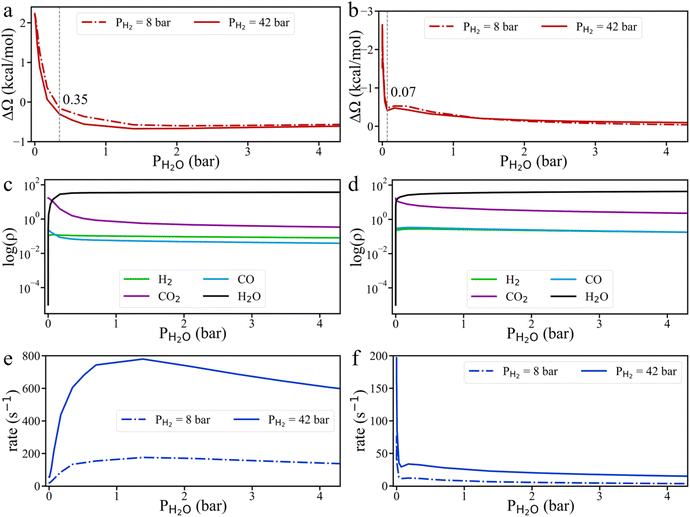
To resolve these conflicting observations, we conducted grand potential simulations to explore the effect of H2O pressure on HCOO* hydrogenation. As shown in Fig. 8 and S10,† H2O tends to accumulate more readily on the Cu surface than CO2. Even a small amount of H2O can significantly impact the grand potential barrier and the surface densities of gas compounds on both Cu (111) and Cu (211) surfaces. On the Cu (111) surface, the HCOO* hydrogenation rate initially increases before declining, while on the Cu (211) surface, the HCOO* hydrogenation rate sharply decreases with the addition of H2O, consistent with current understanding. However, due to the strong adsorption of H2O, even a small H2O pressure (0.07 bar) leads to surface saturation. Beyond this point, the HCOO* hydrogenation rate remains nearly unchanged, regardless of additional H2O. Therefore, when the methanol yield is high and CO is lacking, the byproduct H2O can reach its saturation point, meaning that further addition of H2O does not change the reaction rate. In fact, the strong interaction of H2O molecules with intermediate species might even positively influence the reaction under certain conditions. As a result, when the H2O pressure in the system is near zero, adding CO and H2O may reduce the CH3OH production rate. However, at high H2O partial pressure, the addition of CO and H2O could potentially increase the CH3OH production rate. Additionally, it should be noted that water can directly participate in the reaction. This effect should be explicitly captured through KS-DFT calculations involving H2O as a reactant in the reaction network.44,45
3 Conclusions
In this study, we combined electronic DFT and cDFT calculations to investigate the effects of various reaction conditions on CO2 hydrogenation to CH3OH over Cu (111) and Cu (211) surfaces. The grand potential approach enables to bridge the “pressure gap” between first principles calculations and experimental observations at conditions relevant to industrial practice. From the perspectives of grand potential landscape and surface concentrations, our findings provide several key insights into the kinetics of CO2 hydrogenation under the influence of temperature, pressure, and gas composition.First, the hybrid DFT calculations account for the thermodynamic effects on the grand potential barriers and local gas concentrations. The grand potential corrections have a significant impact on the formation of different intermediates, particularly at low temperature and high pressure, with the absolute values comparable to conventional corrections for the bond vibrational entropy. We demonstrated that the grand potential profiles align better with experimental data in terms of both surface composition and reaction kinetics. It is the surface density, rather than bulk concentration, determines the hydrogenation rates.
Our grand-potential simulations revealed that the surface density of H2 is lower than its bulk density, increasing linearly without reaching saturation, whereas the surface density of CO2 is two orders of magnitude higher than its bulk density and easily becomes saturated. CO2 does not influence the HCOO* hydrogenation rate through its surface concentration, as the HCOO* coverage is already saturated. Instead, two opposing effects—the reduction in the HCOO* hydrogenation energy barrier and the decrease in the surface H2 density—collectively influence the hydrogenation rate. This also explains why HCOO* could not continue to hydrogenate in a CO2-free gas atmosphere. Consequently, we conclude that the ideal H2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) CO2 ratio decreasing with temperature and increasing with H2 pressure.
CO2 ratio decreasing with temperature and increasing with H2 pressure.
We clarified that CO does not directly compete with CO2 for active sites but instead competes for physical adsorption on the Cu surface. On the Cu (211) surface, increasing the CO/(CO2 + CO) ratio leads to both an increased energy barrier for HCOO* hydrogenation and a higher H2 surface density. At low H2 pressure, the HCOO* hydrogenation rate is unaffected by the CO/(CO2 + CO) ratio. However, at high H2 pressure, the reaction rate falls as the CO/(CO2 + CO) ratio increases. Notably, the HCOO* hydrogenation rate rises significantly when the CO/(CO2 + CO) ratio reaches 0.99. From this, we infer that CO participates in both the water–gas shift (WGS) reaction and CO2 hydrogenation pathways to produce CH3OH.
While H2O is an inevitable byproduct of CO2 hydrogenation, it may exhibit either positive or negative effects on the hydrogenation rate. Although a small amount of H2O significantly reduces the reaction rate, H2O adsorption becomes saturated at very low partial pressures, after which the HCOO* hydrogenation rate remains nearly unchanged. Therefore, when the product yield is high and CO is scarce, the byproduct H2O can reach its saturation point, meaning that further addition of H2O does not reduce the reaction rate.
In summary, the grand-potential theory provides a comprehensive understanding of CO2 hydrogenation to CH3OH under industrially relevant conditions. By accounting for the influence of gas-phase interactions, surface adsorption effects, and variations in temperature and pressure, our study addresses inconsistencies between theoretical predictions with conventional DFT and experimental observations, offering new insights for optimizing catalyst performance in methanol synthesis. As the thermodynamic properties of inhomogeneous fluids can be systematically described using cDFT, the grand-potential framework can be readily extended to other gas-phase reactions involving heterogeneous catalysis, such as highly active CO2 hydrogenation catalysts like CuO and PdZn alloys.
Data availability
Additional data can be obtained from the authors upon request.Author contributions
J. S. and J. W. designed the research, discussed the results, and wrote the paper. J. S. performed the calculations.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research is made possible through financial support from the NSF-DFG Lead Agency Activity in Chemistry and Transport in Confined Spaces under Grant No. NSF 2234013. The authors thanks Musen Zhou for technical assistance in running the cDFT program.References
- M. A. Tedeeva, A. L. Kustov, A. M. Batkin, C. Garifullina, A. A. Zalyatdinov, D. Yang, Y. Dai, Y. Yang and L. M. Kustov, Mol. Catal., 2024, 566, 114403 CAS.
- P. Schwiderowski, H. Ruland and M. Muhler, Curr. Opin. Green Sustainable Chem., 2022, 38, 100688 CrossRef CAS.
- D. Zhao, S. Han and E. V. Kondratenko, ChemCatChem, 2023, 15, e202300679 CrossRef CAS.
- H. Zhang, J. Chen, X. Han, Y. Pan, Z. Hao, S. Tang, X. Zi, Z. Zhang, P. Gao, M. Li, J. Lv and X. Ma, Ind. Eng. Chem. Res., 2024, 63, 6210–6221 CAS.
- S. Saeidi, S. Najari, V. Hessel, K. Wilson, F. J. Keil, P. Concepción, S. L. Suib and A. E. Rodrigues, Prog. Energy Combust. Sci., 2021, 85, 100905 Search PubMed.
- M. Yang, J. Yu, A. Zimina, B. B. Sarma, L. Pandit, J.-D. Grunwaldt, L. Zhang, H. Xu and J. Sun, Angew. Chem., 2023, 135, e202216803 CrossRef.
- X. Jiang, X. Wang, X. Nie, N. Koizumi, X. Guo and C. Song, Catal. Today, 2018, 316, 62–70 CrossRef CAS.
- C. Wu, L. Lin, J. Liu, J. Zhang, F. Zhang, T. Zhou, N. Rui, S. Yao, Y. Deng, F. Yang, W. Xu, J. Luo, Y. Zhao, B. Yan, X.-D. Wen, J. A. Rodriguez and D. Ma, Nat. Commun., 2020, 11, 5767 CrossRef CAS PubMed.
- S. Kattel, P. J. Ramírez, J. G. Chen, J. A. Rodriguez and P. Liu, Science, 2017, 355, 1296–1299 CAS.
- J. Graciani, K. Mudiyanselage, F. Xu, A. E. Baber, J. Evans, S. D. Senanayake, D. J. Stacchiola, P. Liu, J. Hrbek, J. F. Sanz and J. A. Rodriguez, Science, 2014, 345, 546–550 CAS.
- P. S. Murthy, W. Liang, Y. Jiang and J. Huang, Energy Fuels, 2021, 35, 8558–8584 CAS.
- Y.-F. Shi, S. Ma and Z.-P. Liu, EES Catal., 2023, 1, 921–933 CAS.
- Y. Yang, J. Evans, J. A. Rodriguez, M. G. White and P. Liu, Phys. Chem. Chem. Phys., 2010, 12, 9909 RSC.
- X. Wang, H. Zhang, H. Qin, K. Wu, K. Wang, J. Ma and W. Fan, Fuel, 2023, 346, 128381 CrossRef CAS.
- I. Tezsevin, S. Senkan, I. Onal and D. Düzenli, J. Phys. Chem. C, 2020, 124, 22426–22434 CrossRef CAS.
- Y. Wang, M. Yu, X. Zhang, Y. Gao, J. Liu, X. Zhang, C. Gong, X. Cao, Z. Ju and Y. Peng, Molecules, 2023, 28, 2852 CrossRef CAS PubMed.
- X. Zhang, Nano Energy, 2018, 200–209 Search PubMed.
- Y.-F. Shi, P.-L. Kang, C. Shang and Z.-P. Liu, J. Am. Chem. Soc., 2022, 144, 13401–13414 CAS.
- Z. Chen, J. Wen, Y. Zeng, M. Li, Y. Tian, F. Yang, M. M.-J. Li, P. Chen, H. Huang, D. Ye and L. Chen, Appl. Catal., B, 2024, 340, 123192 CAS.
- T. C. Lin and A. Bhan, J. Catal., 2024, 429, 115214 CrossRef CAS.
- J. E. N. Swallow, E. S. Jones, A. R. Head, J. S. Gibson, R. B. David and M. W. Fraser, J. Am. Chem. Soc., 2023, 145(12), 6730–6740 CrossRef CAS.
- A. H. M. da Silva, L. H. Vieira, C. S. Santanta, M. T. M. Koper, E. M. Assaf, J. M. Assaf and J. F. Gomes, Appl. Catal., B, 2023, 324, 122221 CrossRef CAS.
- H.-X. Li, L.-Q.-Q. Yang, Z.-Y. Chi, Y.-L. Zhang, X.-G. Li, Y.-L. He, T. R. Reina and W.-D. Xiao, Catal. Lett., 2022, 152, 3110–3124 CrossRef CAS.
- N. D. Nielsen, A. D. Jensen and J. M. Christensen, J. Catal., 2021, 393, 324–334 CrossRef CAS.
- B. Lacerda De Oliveira Campos, K. Herrera Delgado, S. Wild, F. Studt, S. Pitter and J. Sauer, React. Chem. Eng., 2021, 6, 868–887 RSC.
- Y.-M. Liu, J.-T. Liu, S.-Z. Liu, J. Li, Z.-H. Gao, Z.-J. Zuo and W. Huang, J. CO2 Util., 2017, 20, 59–65 CAS.
- K. Gu, H. Guo and S. Lin, Angew. Chem., Int. Ed., 2024, e202405371 CAS.
- Y. Yang, C. A. Mims, D. H. Mei, C. H. F. Peden and C. T. Campbell, J. Catal., 2013, 298, 10–17 CAS.
- J. Sun, S. Jiang, Y. Zhao, H. Wang, D. Zhai, W. Deng and L. Sun, Phys. Chem. Chem. Phys., 2022, 24, 19938–19947 CAS.
- R. Yin, J. Xia, B. Jiang and H. Guo, ACS Catal., 2023, 13, 14103–14111 CrossRef CAS.
- X. Mao, T. He, G. Kour, H. Yin, C. Ling, G. Gao, Y. Jin, Q. Liu, A. P. O'Mullane and A. Du, Chem. Sci., 2024, 15, 3330–3338 CAS.
- D. Song, E. J. Bylaska, M. L. Sushko and K. M. Rosso, J. Chem. Phys., 2024, 160, 064112 CAS.
- F. Studt, M. Behrens, E. L. Kunkes, N. Thomas, S. Zander, A. Tarasov, J. Schumann, E. Frei, J. B. Varley, F. Abild-Pedersen, J. K. Nørskov and R. Schlögl, ChemCatChem, 2015, 7, 1105–1111 CAS.
- Y. Ren, K. Yuan, X. Zhou, H. Sun, K. Wu, S. L. Bernasek, W. Chen and G. Q. Xu, Chem.–Eur. J., 2018, 24, 16097–16103 CAS.
- Y. Yang, C. A. Mims, D. H. Mei, C. H. F. Peden and C. T. Campbell, J. Catal., 2013, 298, 10–17 CrossRef CAS.
- H. Liang, G. Zhang, Z. Li, Y. Zhang and P. Fu, Fuel Process. Technol., 2023, 252, 107995 CAS.
- A. Cao, Z. Wang, H. Li, A. O. Elnabawy and J. K. Nørskov, J. Catal., 2021, 400, 325–331 CAS.
- E. L. Kunkes, F. Studt, F. Abild-Pedersen, R. Schlögl and M. Behrens, J. Catal., 2015, 328, 43–48 CAS.
- Y. Liu, X. Liu, L. Xia, C. Huang, Z. Wu, H. Wang and Y. Sun, Acta Phys.-Chim. Sin., 2022, 38(3), 2002017 Search PubMed.
- K. Klier, J. Catal., 1982, 74, 343–360 CrossRef CAS.
- M. Sahibzada, I. S. Metcalfe and D. Chadwick, J. Catal., 1998, 174, 111–118 CrossRef CAS.
- J. Thrane, S. Kuld, N. D. Nielsen, A. D. Jensen, J. Sehested and J. M. Christensen, Angew. Chem., Int. Ed., 2020, 59, 18189–18193 CrossRef CAS.
- Z. Yan, Y. Wang, X. Wang, C. Xu, W. Zhang, H. Ban and C. Li, Catal. Lett., 2023, 153, 1046–1056 CrossRef CAS.
- Y. Kim, T. S. B. Trung, S. Yang, S. Kim and H. Lee, ACS Catal., 2016, 6, 1037–1044 CrossRef CAS.
- Y.-F. Zhao, Y. Yang, C. Mims, C. H. F. Peden, J. Li and D. Mei, J. Catal., 2011, 281, 199–211 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d5sc00211g |
| This journal is © The Royal Society of Chemistry 2025 |