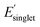Functional monomer design for synthetically accessible polymers

Abstract

Machine learning (ML) has emerged as a powerful tool to navigate polymer structure–property relationships. Despite recent progress, data sparsity is a major obstacle hindering the practical application of ML in polymer science. In this work, we explore functional monomer design by developing the first comprehensive database of monomer-level chemical and physical properties for approximately 12M synthetically accessible polymers. We generated diverse monomer-level properties by integrating quantum chemistry calculations with active learning to efficiently probe a vast chemical space of synthetically feasible polymers. Monomer-level property descriptors are benchmarked against both higher level computational predictions and experimental data to the extent possible, demonstrating their relevance to polymer design. Our results show that many monomer-level properties are weakly correlated, implying a strong freedom for functional design such that multiple physical properties can be simultaneously optimized by monomer selection. Moreover, the synthetically accessible nature of this chemical space allows targeted monomers to be considered by common polymerization mechanisms to facilitate their synthetic realization. Overall, this work opens new avenues for creating synthetically accessible polymers and provides new insights for designing next generation polymeric materials.

---

1 Introduction

A grand challenge in polymer science lies in establishing structure–property relationships that integrate monomer chemistry, topological structure, statistical heterogeneity, morphology, and processing within a single framework. Computational modeling strategies have previously focused on modulating polymer properties using coarse-grained representations of polymer chemistry to describe the effects of branching, molecular weight, and topology.^1–4 Such strategies have underscored the study of well-known olefin-based chemistries that continue to dominate the commercial landscape with precise stereochemical and topological properties combined with desired mechanical and thermal performance.^5–7 Although chemistry-agnostic approaches to polymer design have been useful, the modern era of materials discovery requires the integration of new chemistries to address critical issues in functional design and performance such as degradability, sustainability, synthetic cost, and electronic and optoelectronic properties.^8–13 Although top-down fitting of monomer specific parameters to experimental data is a powerful modeling approach, key knowledge gaps exist in using in silico methods to predict the monomer specific parameters that enter into coarse-grained theoretical approaches. Moving forward, computational methodologies that place monomer chemistry at the forefront of polymer design hold strong promise to offer powerful design strategies for polymeric materials.

The range of monomer chemistries currently used for common polymeric materials is relatively narrow compared to the vast chemical space for organic compounds. Many commercially relevant polymers such as polyolefins are prepared by chain-growth polymerization methods.^5–7 More chemically diverse polymer backbones can be prepared by step-growth polymerization methods, though many of these approaches have well-known limitations that practically reduces their chemical space.^14,15 In addition, sustainability is a major consideration in designing new polymer materials,^8–10 which motivates new and alternative polymer chemistries that allow for renewable feedstocks or enable circular lifecycle materials. To address these constraints, fundamental issues in functional design need to be considered across the entire hypothetical chemical space of polymeric materials. Polymer property prediction directly from monomer chemical structure is an exceedingly difficult task,^4,16 especially given that most practical polymer applications require the simultaneous optimization of multiple potentially correlated polymer properties.¹⁷ Successfully addressing the design challenge for polymer property prediction generally requires multiple disparate theoretical methods, e.g., quantum chemistry and continuum-level theories, to achieve specific design goals.^4,18 Consequently, alternative strategies are needed to understand the role of monomer chemistry on polymer properties across a broad chemical space.

Given sufficient experimental and computational data, complex polymer structure–property relationships can be effectively learned using machine learning (ML) methods. For example, polymer properties such as the radius of gyration or the end-to-end decorrelation time can be predicted based on a featurized representation of a polymer's molecular structure.¹⁹ Moreover, these learned structure–property relationships can be utilized to screen polymer candidates with desired functionality.^20–23 Transformer-based language models²⁴ have recently attracted attention by providing foundational numerical representations of polymer structures aimed at enabling general polymer property predictions.^25,26 Beyond polymer property prediction, new functional polymers can be discovered via generative ML approaches such as the popular variational autoencoder,²⁷ which allows polymer structure–property relationships to be learned from data.^28–31 Given the recent success of using ML in polymer science, data-driven approaches appear to hold strong promise for transforming polymer research.

Despite recent progress, however, a major obstacle hindering the practical implementation of data-driven ML for polymer design is the scarcity of openly available data in polymer science. Although several sub-disciplines of chemistry operate in data scarce regimes, this problem has been sufficiently offset in the small molecule design community^32–36via supplementation with abundant small organic molecule databases.^37–40 In recent years, the polymer science community has made significant efforts^{26,29,41–61} to address the data sparsity of polymeric materials. The review paper by Tran et al.⁶² provides a comprehensive summary of the current status of polymer informatics. However, existing polymer databases are limited by several factors including synthetic feasibility, lack of accessibility, or insufficient data quantities, which hinders their use in state-of-the-art and data-hungry ML algorithms. For example, millions of molecules are often required for data-driven molecular property prediction or generative molecular design via transformer-based chemical language models to achieve generalizable molecular representations for efficient knowledge adaptations,^25,26,63,64 and these data scales have yet to be robustly achieved for polymers.

In this paper, we explore functional monomer design via the development of the first comprehensive database of monomer-level chemical and physical properties for approximately 12M synthetically feasible polymers. We begin by providing a brief overview of ML-based monomer-level property generation integrating quantum chemistry calculations with active learning. Next, the performance of predictive ML models is evaluated with a focus on prediction accuracy and uncertainty. We then use our accurate ML models to label monomer-level chemical and physical properties that are intimately related to polymer properties across 12M synthetically accessible polymers within the Open Macromolecular Genome (OMG),²⁹ thereby elucidating the intrinsic nature of property design across polymer chemical space. The freedom in functional monomer design is then explored by examining the correlations between monomer-level properties and investigating functional monomer design with weakly correlated properties. Importantly, our work shows how diverse polymerization mechanisms can facilitate access to a wide range of functional properties. Broadly, our work highlights future directions for leveraging ML-based monomer-level properties in data-driven approaches to polymer science.

2 Methods

2.1 Selection of monomer-level properties

A comprehensive set of 25 monomer-level properties for OMG polymers was prepared, encompassing chemistry descriptors, molecular flexibility, geometry descriptors, electronic properties, optical properties, and phase behavior descriptors (Table 1). All geometric, electronic, and optical properties were derived via density functional theory (DFT) single point calculations, Boltzmann averaged over up to five distinct conformers of the methyl-terminated OMG constitutional repeating units (CRUs).⁶⁵ Flory–Huggins χ interaction parameters of polymer solutions were estimated from the distributions of the surface screening charges (i.e., σ-profiles⁶⁶) of the methyl-terminated OMG CRUs and averaged over up to five distinct conformers. Conformer searches⁶⁷ were performed with GFN2-xTB⁶⁸ (ESI,† generation of atomic coordinates for OMG CRUs). The optimized molecular conformer geometries are available at https://zenodo.org/records/13863778.

Table 1 Diverse monomer-level properties investigated for synthetically accessible polymers in the Open Macromolecular Genome (OMG). The symbol, description, unit, and property classification of monomer-level properties are provided. a₀ represents the atomic unit of length (Bohr radius)

	Symbol	Description	Unit	Property category
1	MW	Molecular weight	g mol^−1	Chemistry descriptor
2	Log P	Octanol–water partition coefficient	Unitless	Chemistry descriptor
3	QED	Quantitative estimate of drug-likeness	Unitless	Chemistry descriptor
4	TPSA	Functional group-based polar surface area	Å^2	Chemistry descriptor
5	Φ mon	Monomer structural flexibility	Unitless	Molecular flexibility
6	Φ bb	Backbone structural flexibility	Unitless	Molecular flexibility
7	Ω A	Asphericity to describe deviation from a spherical form	Unitless	Geometry descriptor
8	ε	Eccentricity to describe anisometry of a molecule	Unitless	Geometry descriptor
9	S I	Inertial shape factor based on principal moments of inertia	Å^−2 g^−1 mol	Geometry descriptor
10	R g	Radius of gyration	Å	Geometry descriptor
11	Ω S	Spherocity index to describe a resemblance of a shape to a perfect sphere	Unitless	Geometry descriptor
12	E HOMO−1	HOMO−1 energy	eV	Electronic property
13	E HOMO	HOMO energy	eV	Electronic property
14	E LUMO	LUMO energy	eV	Electronic property
15	E LUMO+1	LUMO+1 energy	eV	Electronic property
16	μ	Magnitude of dipole moment	e × a0	Electronic property
17	q	Isotropic quadrupole moment	e × a0^2	Electronic property
18	α	Isotropic polarizability	a 0 ^3	Electronic property
19	E S1	Energy of the lowest singlet excited state	eV	Optical property
20		Singlet excitation energy with the largest oscillator strength	eV	Optical property
21		Largest oscillator strength among the first 15 singlet transitions	Unitless	Optical property
22	E T1	Energy of the lowest triplet excited state	eV	Optical property
23	χ water	Flory–Huggins χ parameter of a polymer solution with water as a solvent (ε = 80.4)	Unitless	Phase behavior descriptors
24	χ ethanol	Flory–Huggins χ parameter of a polymer solution with ethanol as a solvent (ε = 24.3)	Unitless	Phase behavior descriptors
25	χ chloroform	Flory–Huggins χ parameter of a polymer solution with chloroform as a solvent (ε = 4.9)	Unitless	Phase behavior descriptors

---

A baseline set of essential cheminformatics-derived characterizations is included in the dataset to characterize molecular size (MW, molecular weight), lipophilicity (log P, log 10 of the partition coefficient between 1-octanol and water⁶⁹), drug-likeness (QED, quantitative estimate of drug-likeness⁷⁰) and lipid solubility (TPSA, topological polar surface area⁷¹) calculated using RDKit.⁷² Complementing these cheminformatics-derived descriptors is a set of essential three-dimensional structural characterizations including the monomer's asphericity (Ω_A), eccentricity (ε), inertial shape factor (S_I), radius of gyration (R_g), and spherocity index (Ω_S). These five geometry descriptors were computed with the principal moments of inertia and the gyration tensor of OMG CRUs (ESI,† mathematical definitions for geometry descriptors).

Given the critical importance of polymer structural flexibility in dictating polymer properties, we used a scalable monomer-level calculation of molecular conformational entropy via the Φ index.⁷³ Monomers with a high Φ index are more flexible than those with a low Φ index. To distinguish the contributions of polymer backbones and side chains to molecular flexibility, the Φ index was computed for both OMG CRUs (Φ_mon) as well as just the OMG CRU backbone (Φ_bb, where the backbone is defined by the shortest bonded path between polymerization sites of the CRU). Because the Φ index is an approximate characterization of flexibility derived by analysis of the molecular graph structure, we validated the calculation of this metric against experimental measurements (Fig. S1†). Specifically, our results show that the experimentally measured mean squared end-to-end distance per mass (〈h²〉₀/M) of polymers in the melt⁷⁴ can be estimated from Φ_mon and Φ_bb with high accuracy (Fig. S1a†). Given that Φ_mon and Φ_bb exhibit high predictive correlation with 〈h²〉₀/M, these results suggest that Φ_mon and Φ_bb can be further used to estimate the characteristic ratio (C_∞). This robust correlation implies that these molecular flexibility indices can provide semi-quantitative estimates of key polymer properties such as the plateau modulus, molecular weight between entanglements, and the reptation tube diameter of polymer melts.⁷⁴ In addition, Φ_mon exhibits a strong negative linear correlation with experimental glass transition temperatures (T_g),^75,76 further indicating that Φ_mon can capture the chain stiffness⁷⁷ (Fig. S1b†). These experimental correlations support that Φ_mon and Φ_bb can be useful descriptors to quantify polymer structural flexibility.

Electronic descriptors were also computed for the dataset to characterize the monomer's ionization potential, electron affinity, optical gap, and dielectric constant/refractive index, and several additional electronic descriptors. These properties include the highest occupied molecular orbital (HOMO) energy (E_HOMO), HOMO−1 energy (E_HOMO−1), lowest unoccupied molecular orbital (LUMO) energy (E_LUMO), LUMO+1 energy (E_LUMO+1), magnitude of dipole moment (μ), isotropic quadrupole moment (q), and isotropic polarizability (α). These seven electronic properties were calculated with DFT single point calculations at the revPBE-D3 (ref. 78 and 79)/def2-SVP level of theory using geometries optimized at the GFN2-xTB level of theory. The CPCM⁸⁰ implicit solvation model was employed with a dielectric constant ε = 2.4 to approximate the dielectric constant of conventional polymers at room temperature.⁸¹ Further, time-dependent DFT (TDDFT) was employed to compute optical properties of the monomers, including the energy of the lowest singlet excited state (E_S1), the singlet transition energy with the largest oscillator strength among the first 15 singlet transitions, the largest oscillator strength among the first 15 singlet transitions , and energy of the lowest triplet excited state (E_T1). These excited state properties are strongly correlated with experimental color⁸² and photostability^83–85 metrics. All calculations were performed using Orca.⁸⁶ Additional details are available in the ESI (ESI, DFT calculations).†

Flory–Huggins χ interaction parameters for OMG polymer solutions were estimated to describe phase behaviors of polymers with three different solvents of varying dielectric constants and included in the dataset: water (ε = 80.4), ethanol (ε = 24.3), and chloroform (ε = 4.9). Flory–Huggins χ interaction parameters^87–90 describe thermodynamics of polymer solutions of OMG CRUs with different solvents. We estimated Flory–Huggins χ parameters from COSMO-SAC⁹¹ calculations following the work of Aoki et al.⁹² using COSMO-RS calculations.⁹³ The estimated Flory–Huggins χ parameters from the COSMO-SAC calculations showed a strong linear correlation with experimental χ parameters (R² ≈ 0.75) (Fig. S2†).

2.2 Development of surrogate ML models for OMG CRU property prediction

To bypass the intractable computational cost of performing DFT calculations on all 12M OMG CRUs, we developed computationally efficient surrogate ML models via uncertainty-guided active learning targeting high prediction uncertainty chemistries.^94,95 Specifically, we combined evidential learning⁹⁶ with a directed message-passing 2D graph neural network (D-MPNN)⁹⁷ to predict monomer-level properties and corresponding prediction uncertainties. It is important to note that D-MPNN evidential networks predict monomer-level properties and corresponding prediction uncertainties directly from the molecular graph without needing to compute 3D molecular geometries of 12M OMG CRUs. Further details on the active learning campaign, including the active learning strategy benchmarked on QM9, are available in the ESI (ESI, details on active learning).†

Fig. 1 schematically illustrates the active learning campaign with D-MPNN evidential networks. Approximately 12 000 OMG CRUs (≈0.1% of the OMG chemical space) were randomly sampled for each polymerization mechanism (i.e., stratified random sampling) as an initial dataset incorporating diverse monomer chemistries to jumpstart the active learning campaign, as detailed in the ESI (Fig. S3).† DFT calculations were then applied to the sampled OMG CRUs to obtain monomer-level properties to train D-MPNN evidential networks. The trained D-MPNN evidential networks estimated prediction uncertainties for monomer-level properties for the unseen OMG CRUs. To sample OMG CRUs for the next round of active learning, we searched for non-dominated OMG CRUs located on the Pareto front of a high-dimensional prediction uncertainty space using a non-dominated sorting algorithm.⁹⁸ The Pareto front represents the set of non-dominated OMG CRUs where an increase in ML prediction uncertainty for given monomer-level property is only possible by reducing the ML prediction uncertainties associated with other properties. The active learning campaign continued with the sampled OMG CRUs from the Pareto front in the uncertainty space until the ML models stopped showing a significant improvement in prediction performance (Fig. S7†). After the active learning campaign, the trained D-MPNN evidential networks were used to predict monomer-level geometry descriptors, electronic properties, optical properties, and phase behavior descriptors for 12M OMG CRUs.

Fig. 1 Active learning campaign to obtain monomer-level properties for 12M synthetically accessible OMG polymers. (a) The 12M synthetically accessible OMG polymers are leveraged to develop ML models for monomer-level property predictions by adopting uncertainty-guided active learning. (b) The active learning campaign was initiated with randomly sampled OMG CRUs. Monomer-level properties are obtained using DFT calculations, followed by training ML models to predict monomer-level properties and corresponding prediction uncertainties. New OMG CRUs are then sampled for the next round of active learning by locating OMG CRUs on the Pareto front in a high-dimensional prediction uncertainty space. (c) At the conclusion of the active learning campaign, the trained ML models are utilized to predict monomer-level geometry descriptors, electronic properties, optical properties, and phase behavior descriptors for 12M OMG CRUs.

3 Results

3.1 Assessing surrogate ML model quality

We evaluated the ML prediction performance for 19 monomer-level properties for geometry descriptors, electronic properties, optical properties, and phase behavior descriptors in the active learning campaign. Chemistry descriptors and molecular flexibility were directly computed with RDKit⁷² due to their extremely low computational cost relative to DFT. Four D-MPNN evidential networks were trained on subsets of the 19 monomer-level properties. These ML models were evaluated on a test set of OMG CRUs (≈15 000) that were randomly sampled for each polymerization mechanism (i.e., stratified random sampling) (Fig. S3†). The D-MPNN evidential networks showed increasing averaged R² scores and achieved an average R² ≈ 0.807 at Round 3, as shown in Fig. S7.† The active learning campaign was stopped after Round 3 when the ML models exhibited saturation in the test set performance. We also assessed a different criterion for stopping the active learning process based on prediction accuracy of the sampled OMG CRUs,⁹⁹ but this analysis also indicated a saturation in the prediction performance after Round 3 (Fig. S8†). Our results show that there is a broad range of R² values for 19 monomer-level properties at Round 3. For example, the D-MPNN evidential networks predicted eccentricity (ε) with R² ≈ 0.342, whereas isotropic polarizability (α) was estimated with R² ≈ 0.996. The prediction performance was also relatively low for other geometry descriptors such as spherocity (Ω_S) and asphericity (Ω_A), as well as the magnitude of dipole moment (μ) which relies on molecular geometry. All monomer-level properties exhibiting low predictive performance were intimately tied to the 3D geometry of the molecule, which is consistent with the fact that D-MPNN evidential networks do not utilize molecular geometry for monomer-level property prediction. Moreover, incorporation of Boltzmann averaging via conformational searches induces an unavoidable noise on the prediction quality for characterizing the 3D geometry. However, all other monomer-level properties achieved R² values larger than 0.7 after Round 3 (Fig. S9†).

Fig. 2a–c show the test ML prediction performance after the active learning campaign for the radius of gyration (R_g), energy of the lowest singlet excited state (E_S1), and Flory–Huggins χ parameter of a polymer solution with water as a solvent (χ_water), respectively. For example, Fig. 2a shows that the ML model predicts R_g with R² ≈ 0.85 while also providing prediction uncertainties. The prediction uncertainty quantifies the standard deviation of a predictive Gaussian distribution of N(ŷ_i,prediction,σ²_{i,uncertainty}) where ŷ_i,prediction is a property prediction for given OMG CRU i, and σ_{i,uncertainty} is the corresponding prediction uncertainty. We calibrated our prediction uncertainties to obtain a better scale match of prediction uncertainty with absolute prediction errors, as detailed in the ESI (Fig. S10).† As anticipated, high prediction uncertainties tend to be associated with OMG CRUs in the regions with the least training data (i.e., large R_g values in the case of radius of gyration) or with a large prediction error. The rank correlations between prediction uncertainties and absolute prediction errors are available in the ESI (Fig. S10)† for all 19 monomer-level properties to quantify their ordinal association. Fig. 2b and c can be similarly interpreted as Fig. 2a, and the remaining monomer-level property predictions are provided in the ESI (Fig. S9).†

Fig. 2 Monomer-level property prediction for the test set of OMG CRUs after the active learning campaign. (a) Prediction for the radius of gyration (R_g). (b) Prediction for the energy of the lowest singlet excited state (E_S1). (c) Prediction for the Flory–Huggins χ parameter of a polymer solution with water as a solvent (χ_water). The colorbar indicates prediction uncertainties.

3.2 Structure of monomer-level property space via principal component analysis

To leverage this unprecedentedly large collection of monomer-level physical property data for synthetically accessible polymers, we focused on analyzing the intrinsic structure of the functional monomer design space. In particular, we used principal component analysis (PCA) to examine the distributions of ML-based monomer-level properties of OMG CRUs. Here, 100k OMG CRUs were randomly sampled from 12M OMG CRUs, and PCA was applied to their 25-dimensional monomer-level property vectors.

PCA results on the chemical space of OMG CRUs show correlations in OMG monomer-level properties, with a dominant role played by the size of the OMG CRU (e.g., R_g). Fig. 3a shows the two largest principal components where the color represents the R_g of methyl-terminated OMG CRUs, with Fig. 3b showing the top five monomer-level properties with their linear coefficients to the PC1 vector. This straightforward analysis of the property space shows that the PC1 vector has a strong contribution from R_g, correlating with the increasing size of the CRUs in Fig. 3c and suggesting that molecular size plays a dominant role in the distribution of the 25 monomer-level properties. The explained variance corresponding to Fig. 3b is available in the ESI (Fig. S11).†

Fig. 3 Principal component analysis (PCA) of ML-based monomer-level properties for the OMG CRUs. (a) PCA applied to the 25-dimensional monomer-level property vectors for 100k randomly sampled OMG CRUs. (b) The top five monomer-level properties with their linear coefficients to the PC1 vector. (c) The three methyl-terminated OMG CRUs marked in (a) with their top five monomer-level properties. The red color in molecules represents the functional groups for step-growth polymerization of dicarboxylic acid and diol.

The monomer size dependence similarly manifests in several intuitive ways in other computed physical properties. For example, Fig. 3b shows that isotropic polarizability (α) and molecular weight (MW) both have a negative contribution to the PC1 vector and are correlated with R_g. This indicates that both α and MW decrease as R_g decreases, an effect due to OMG CRUs with a small molecular size (i.e., smaller R_g) typically possessing fewer atoms, leading to decreased α and MW values.¹⁰⁰ Moreover, reduced α values are known to correlate with increasing HOMO–LUMO gap (E_gap) through an inverse relationship,^101–103 which is consistent with its relationship to R_g in Fig. 3b when considering E_gap as a proxy for . This set of correlations is consistent with the well known association between band gap and electron delocalization over larger molecular sizes. Similarly, decreased R_g values are anticipated to correlate with increased q values due to electrons having less negative quadratic contributions due to reduced molecular volumes.¹⁰⁴ Taken together, these results clearly show the intuitively sensible trend that many molecular properties exhibit a strong correlation with molecular size (i.e., R_g), and that molecular size is a natural structuring variable for variations in the computed property space, as shown in Fig. 3c. We also provide several chemical and physical properties normalized by the number of heavy atoms in OMG CRUs to approximately compensate for molecular size effects (Fig. S12 and S13†).

3.3 Exploring functional monomer design

We next analyzed pair correlations between all 25 monomer-level properties to understand the potential for functional monomer design across multiple property targets. In brief, the strength of these correlations will dictate the freedom for multi-target property optimization across polymer chemical space. For the pair correlation analysis, approximately 135k OMG polymers were randomly sampled across polymerization mechanisms (i.e. stratified random sampling) to incorporate diverse chemistries (Fig. S14†). Fig. 4 shows the pair correlations between 25 monomer-level properties and the histogram of Pearson correlation coefficients |ρ| between property pairs. To aid with visualization, we classified weak (|ρ| < 0.57), intermediate (0.57 ≤ |ρ| < 0.80), and strong (|ρ| ≥ 0.80) regimes of correlations based on three clusters identified in the histogram in Fig. 4 following the approach of Sandonas et al.¹⁰⁵

Fig. 4 Property pair correlations between 25 monomer-level properties. The histogram shows the distributions of Pearson correlation coefficients (|ρ|) between monomer-level property pairs. The three regimes are defined based on |ρ|: a weak regime (|ρ| < 0.57), an intermediate regime (0.57 ≤ |ρ| < 0.80), and a strong regime (|ρ| ≥ 0.80).

The histogram in Fig. 4 shows that most of the monomer-level property pairs exhibit weak linear correlations (|ρ| < 0.57). The abundant weak linear correlations suggest that multiple monomer-level properties relevant to functional monomer design can be simultaneously and orthogonally optimized. For instance, a practical multi-target polymer design campaign might target chain stiffness (Φ_mon, monomer structural flexibility), color (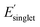, singlet excitation energy with the largest oscillator strength among the first 15 singlet transitions), and solubility (χ_water, Flory–Huggins χ parameter with water as a solvent). These three common properties exhibit weak linear pair correlations, which suggests that they can be tuned for functional monomer design, as explained below. Similar and potentially desirable sets of properties exhibiting quantitatively weak correlations with the potential for multi-target optimization include: (1) design of polymer dielectrics considering the dielectric constant (α, isotropic polarizability), and band gap (E_HOMO, HOMO energy and E_LUMO, LUMO energy) and (2) design of photostable polymers targeting photostability (E_T1, energy of the lowest triplet excited state) and solubility (χ_chloroform, Flory–Huggins χ parameter of a polymer solution with chloroform as a solvent). It is important to note that monomer-level properties provide insights into functional polymer design because several monomer-level properties are intimately related to polymer properties, including molecular flexibility (Fig. S1†), solubility (Fig. S2†), and electronic properties (Fig. S15†). In addition, the weakly correlated pair interactions persist even after incorporating several normalized properties to approximately account for molecular size effects (Fig. S16†). Overall, these results show that there exists a relative freedom of functional monomer design where practical property sets relevant to polymeric materials can be simultaneously optimized.

In addition to the general freedom of design exhibited by the weak property pair correlations, there are pairs of properties that exhibit strong correlations. Of all pair correlations, 256 pairs are classified as weak, whereas 30 pairs and 14 pairs are classified as intermediate and strong correlation, respectively. Within the intermediate and strongly correlated pairs, six of the most correlated pairs of features corroborate the PCA analysis of Fig. 3, reinforcing features that scale strongly with molecular size: α, , MW, q, and R_g. Many of these top five properties also exhibit intermediate correlations with QED, S_I, and TPSA, supporting the notion that a large molecular size can decrease QED and S_I while increasing TPSA (Fig. S11†).^70,71,106

Fig. 4 also shows pairs of properties exhibiting intermediate or strong correlations. Molecular size correlation is the strongest correlation across polymer property space, but several additional features emerge from these data. First, molecular flexibility correlates monomer structural flexibility (Φ_mon) and backbone structural flexibility (Φ_bb). Second, molecular geometry correlates asphericity (Ω_A), spherocity (Ω_S), and eccentricity (ε) by describing a molecular shape. Third, electronic structure correlates HOMO−1 energy (E_HOMO−1) and HOMO energy (E_HOMO). Fourth, optical transitions correlate LUMO energy (E_LUMO), LUMO+1 energy (E_LUMO+1), energy of the lowest singlet excited state (E_S1), singlet excitation energy with the largest oscillator strength , and energy of the lowest triplet excited state (E_T1). In addition, solubility is directly related to functional group-based polar surface area (TPSA), magnitude of dipole moment (μ), and Flory–Huggins χ parameter of a polymer solution with water as a solvent (χ_water) that is highly correlated with χ_ethanol. All of these sets of correlated features are physically consistent because they involve interrelated molecular features. For example, molecular flexibility is expected to be correlated with the flexibility of its subgroups, excitation energies are correlated with the single electron orbitals that compose them, and molecular polarity is a common proxy for molecular solubility.

Given the evidence for weakly correlated molecular properties within our database, we proceed to demonstrate the potential freedom for multi-property functional monomer design in a synthetically accessible chemical space. Specifically, we select three weakly correlated monomer-level properties previously mentioned: Φ_mon, , and χ_water. The randomly sampled ≈135k OMG polymers were then used for this analysis (Fig. S14†). Fig. 5a shows the distribution of χ_water from kernel density estimation over four different regimes of Φ_mon and . Each of the four regimes represents: (i) low Φ_mon and high , (ii) low Φ_mon and low , (iii) high Φ_mon and high 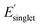, and (iv) high Φ_mon and low 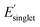, respectively. The low and high regimes were determined based on the mean and standard deviation of Φ_mon and 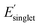for the sampled subset of OMG polymers. For instance, the low Φ_mon region includes values approximately one standard deviation below the mean Φ_mon value. Similarly, the high region includes values approximately one standard deviation above the mean 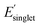value. Further details about the low and high regimes can be found in the ESI† (high and low Φ_mon, , and χ_water).

Fig. 5 Functional monomer design with three weakly correlated monomer-level properties. (a) The distributions of χ_water from kernel density estimation over four different regimes of Φ_mon and are plotted with the number of OMG CRUs within a range of χ_water. (b) Each box displays methyl-terminated OMG CRUs representing one of four different regimes of Φ_mon and with low χ_water and high χ_water. Colors denote functional groups for polymerization (red for step growth, green for chain growth, and purple for metathesis).

Fig. 5a shows a broad range of χ_water regardless of the low and high regimes of Φ_mon and . This reflects freedom of functional monomer design where χ_water is not significantly affected by the individual values or targeted optimization of Φ_mon and . Furthermore, Fig. 5a denotes that there are multiple OMG CRUs located within a range of low χ_water and high χ_water. For example, there are 28 OMG CRUs with low χ_water values that possess low Φ_mon and high . We also counted the number of OMG CRUs sharing multiple monomer-level properties that can provide additional flexibility for freedom of multi-target functional monomer design (Fig. S17†). Overall, this example demonstration indicates freedom of multi-target functional monomer design¹⁰⁵ for weakly correlated properties where a target monomer-level property (e.g., χ_water) can be pursued without being significantly affected by other monomer-level properties (e.g., Φ_mon and ).

Fig. 5b also shows the molecular structures of OMG CRUs in the four different regimes of Φ_mon and with low χ_water and high χ_water to extract monomer-structure property relationships. Each box in Fig. 5b displays methyl-terminated OMG CRUs with low χ_water (favorable to water solvation) and high χ_water (less favorable to water solvation) based on the mean and standard deviation of χ_water (ESI,† high and low Φ_mon, , and χ_water). Three monomer structure–property relationships can be identified in the multi-target optimization corresponding to Φ_mon, 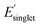, and χ_water. First, the OMG CRUs with high Φ_mon contain a large fraction of alkyl groups which enhances molecular flexibility. In contrast, the OMG CRUs with low Φ_mon generally contain a rigid ring structures which enhances molecular rigidity. Second, the OMG CRUs with low have extended π-conjugation¹⁰⁷ or a large molecular size (i.e., large isotropic polarizability α) that might lead to a narrow HOMO–LUMO gap contributing to low . On the contrary, the OMG CRUs with high generally have a small number of atoms with reduced π-conjugation. Third, the OMG CRUs with low χ_water exhibit hydrogen bonding, which enhances solvation with water, whereas the OMG CRUs of high χ_water do not exhibit hydrogen bonds. This molecular structure analysis suggests that ML-based monomer-level properties encode interpretable monomer structure–property relationships. Importantly, all example chemistries shown in Fig. 5b are derived via the known polymerization reactions and purchasable reactants that form the basis for the OMG dataset,²⁹ providing substantial synthetic viability for the chemical space examined.

We further investigated functional monomer design with a Pareto front search to simultaneously maximize two anti-correlated monomer properties within the synthetically accessible chemical space of OMG. Here, we further explore the relationships between isotropic polarizability (α) and HOMO–LUMO gap (E_gap) of the randomly sampled ≈135k OMG CRUs. Fig. 6a shows the distribution of α and E_gap of OMG CRUs possessing low χ_water with each color representing different polymerization reaction classes of step growth (red), chain growth (green), ring opening (blue), and metathesis (purple). Likewise, Fig. 6b shows the distribution of α and E_gap for the OMG CRUs with low χ_chloroform. The OMG CRUs with low χ_water and low χ_chloroform were determined based on the mean and standard deviation of χ_water and χ_chloroform for the sampled subset of OMG polymers (ESI,† low χ_water and χ_chloroform). Prior work has identified an inverse relationships between α and E_gap for a relatively narrow chemical space.^102,103 Although the OMG CRUs in Fig. 6a and b generally show a negative correlation between α and E_gap, considerable exceptions exist in the diverse chemical space of the OMG that do not follow a clear inverse relation.¹⁰⁵

Fig. 6 Functional monomer design with Pareto front search. The distribution of isotropic polarizability (α) and HOMO–LUMO gap (E_gap) of OMG CRUs possessing (a) low χ_water and (b) low χ_chloroform with each color representing different polymerization mechanisms of step growth (red), chain growth (green), ring opening (blue), and metathesis (purple). The solid line in the distribution plots is the fitting curve for the inverse relationship (i.e., α ∼E_gap⁻¹). The dashed line represents the Pareto front for α and E_gap.

We performed a Pareto front search to simultaneously maximize α and E_gap to gain insight into functional monomer design with opposing properties. The boxes in Fig. 6a and b show four of the methyl-terminated OMG CRUs on the Pareto front with colors representing methyl-terminated functional groups for polymerization (red for step growth, green for chain growth, and blue for ring opening). The methyl-terminated OMG CRUs in Fig. 6a have hydrogen bonds or polar atoms to favor solvation with water (low χ_water), whereas the methyl-terminated OMG CRUs in Fig. 6b contain a large portion of alkyl groups to favor solvation with chloroform (low χ_chloroform). In the Pareto front search, the molecular size of the OMG CRUs in Fig. 6a and b decreases as α decreases, which is consistent with the dependence of α on the number of atoms in a CRU.¹⁰⁰ Importantly, Fig. 6a and b show that the OMG CRUs from chain growth or ring opening polymerization can approach high E_gap by their relatively small monomer size during the Pareto front search. Overall, functional monomer design with Pareto front search provides interpretable monomer structure–property relationships while also showing that diverse polymerization mechanisms for OMG polymers can be useful for accessing various monomer functionality.

4 Discussion

We propose that the comprehensive monomer-level properties determined by accurate ML models in this work can be seamlessly integrated with data-driven approaches in polymer science to advance functional polymer design. The ML-based monomer-level properties offer useful insights into functional polymer design by establishing intimate correlations with polymer properties such as molecular flexibility (Fig. S1†), solubility (Fig. S2†), and electronic properties (Fig. S15†). Our work sets the stage for the discovery of next generation synthetic polymeric materials by leveraging data-driven approaches applied to tens of millions of monomer-level property data points serving as proxy properties for synthetically accessible polymers. Transformer-based language models^25,26 enable accurate predictions of polymer properties, facilitating the screening of potential polymer chemical spaces. Moreover, generative ML approaches with variational autoencoders³² can extract polymer structure–property relationships to enable inverse multi-target polymer design by linking low-dimensional polymer structure embeddings to polymer properties. These data-driven ML methods can significantly accelerate the transfer of knowledge from intrinsic monomer chemistries to polymer properties for functional polymer design. We also envision that our approach can be extended to other materials classes (e.g., inorganic crystals¹⁰⁸) by efficiently exploring their vast candidate space for materials discovery through accurate ML-based property prediction.

The present study possesses a few limitations. First, the ML prediction is not highly accurate for several monomer-level properties such as eccentricity (ε) and the magnitude of dipole moment (μ), both of which rely on the 3D molecular geometry. This is a result of the directed message-passing 2D graph neural networks (D-MPNN)⁹⁷ that only utilize 2D molecular graph of methyl-terminated OMG CRUs without 3D molecular geometry. To achieve higher prediction accuracy, 3D conformer geometries for the entire set of 12M OMG CRUs could be prepared with GFN2-xTB, but this would require a prohibitive computational cost at the present time (approximately 311 CPU years estimated from OMG CRUs with an average of 23 heavy atoms consisting of up to 15 conformers). Alternatively, automatic generation of 3D coordinates of molecules¹⁰⁹via atomistic neural network potentials could be employed to generate the molecular geometries of 12M OMG CRUs. However, this necessitates the verification of neural network potentials for a broad chemical space of OMG CRUs, which is outside of the scope of the present study. Second, the accuracy of ML-based monomer-level properties is limited by the accuracy of quantum chemistry calculations. We searched five distinct conformers for methyl-terminated OMG CRUs to estimate Boltzmann averaged values for most of 25 monomer-level properties to train ML models. We adopted a semi-empirical quantum mechanical method⁶⁸ for molecular geometry and a generalized gradient approximation (GGA) functional for DFT calculations (ESI,† DFT calculations) to reduce computational costs. However, a more comprehensive conformer search¹¹⁰ or a higher level of theory such as hybrid functionals¹¹¹ could be considered for more accurate calculations. Third, the ML-training performance can be increased by focusing solely on weakly correlated monomer-level properties. Fig. 4 shows the existence of intermediate or strong correlations between monomer-level properties. During active learning, however, we sampled the OMG CRUs located on the Pareto front of 19 monomer-level property prediction uncertainties ignoring possible property pair correlations. Overall, the property pair correlation analysis indicates that the ML models training can be improved by focusing only on the weakly correlated monomer-level properties to reduce the dimension of the uncertainty space and improve efficiency of Pareto front search (ESI,† details on active learning). Finally, although the OMG encodes a variety of synthetic accessibility constraints to form linear homopolymers detailed in our previous work,²⁹ the suggested chemistries do not necessarily guarantee synthetic viability. Future efforts automating an analogous discovery campaign across the OMG to understand reactivity could further help augment the synthetic viability of the chemistries considered in this work.

Overall, this work focuses on the diverse structural and chemical functionalities of monomers to provide new insights into the chemistry of synthetically accessible polymers. Ideally, a functional polymer design scheme should consider not only monomer chemistries but also additional factors that significantly influence polymer properties such as chain topology, solid-phase morphology, polydispersity, monomer compositions, and processing.¹⁶ However, the computational cost for addressing every possible permutation of polymer chain parameters using theoretical or computational methods would be intractable across a broad chemical space. We envision that the comprehensive monomer chemistries investigated in this work will provide a critical steppingstone to inclusion of the full complexity of the polymer representation and will complement and synergize with ongoing efforts in various aspects of polymer science to enable a unified framework for functional polymer design.

5 Conclusions

In this work, we explore the intrinsic nature of functional monomer design via the development of the first comprehensive database of monomer-level chemical and physical properties for 12M synthetically accessible polymers. We generated diverse ML-based monomer-level properties by integrating quantum chemistry calculations with active learning to efficiently navigate the vast chemical space of the synthetically feasible polymers within the Open Macromolecular Genome (OMG).²⁹ The diverse monomer-level properties encompass chemistry descriptors, molecular flexibility, geometry descriptors, electronic properties, optical properties, and phase behavior descriptors. Given comprehensive monomer structural and chemical functionalities labeled by accurate ML models, we demonstrate freedom of functional monomer design wherein multiple monomer-level properties can be simultaneously optimized, which is supported by the abundant weak property pair correlations. In addition, we illustrate how various polymerization mechanisms in OMG polymers can be leveraged and applied to a wide range of monomer functionalities. Overall, this work opens new avenues regarding intrinsic monomer chemistries of synthetically accessible polymers and provides valuable insights into the development of next generation of polymeric materials.

Data availability

The scripts used for active learning and data analysis in this work are available at https://github.com/TheJacksonLab/OMG_PhysicalProperties. The data and ML models can be found at https://zenodo.org/records/13863778 including (1) trained D-MPNN evidential networks, (2) 3D atomic geometries of methyl-terminated monomers from quantum chemistry calculations, and (3) ML-based monomer-level properties for 12M synthetically accessible polymers.

Author contributions

S. K. wrote the software to conduct the active learning campaign and analyze the data. C. M. S. and N. E. J. supervised and revised all stages of the work. All authors discussed the results and contributed to the final manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work is supported by the IBM-Illinois Discovery Accelerator Institute grant #114108. N. E. J. thanks the 3M Nontenured Faculty Award for support of this research.

References

1. M. Rubinstein and R. H. Colby, Polymer Physics, Oxford university press, 2003.
2. S. Dhamankar and M. A. Webb, J. Polym. Sci., 2021, 59, 2613–2643.
3. T. E. I. Gartner and A. Jayaraman, Macromolecules, 2019, 52, 755–786.
4. F. Schmid, ACS Polym. Au, 2023, 3, 28–58.
5. P. Galli and G. Vecellio, J. Polym. Sci., Part A: Polym. Chem., 2004, 42, 396–415.
6. C. M. Plummer, L. Li and Y. Chen, Macromolecules, 2023, 56, 731–750.
7. T. V. Tran and L. H. Do, Eur. Polym. J., 2021, 142, 110100.
8. M. Hong and E. Y.-X. Chen, Green Chem., 2017, 19, 3692–3706.
9. D. E. Fagnani, J. L. Tami, G. Copley, M. N. Clemons, Y. D. Getzler and A. J. McNeil, ACS Macro Lett., 2020, 10, 41–53.
10. S. A. Miller, ACS Macro Lett., 2013, 2, 550–554.
11. T. D. Huan, A. Mannodi-Kanakkithodi, C. Kim, V. Sharma, G. Pilania and R. Ramprasad, Sci. Data, 2016, 3, 160012.
12. A. Mannodi-Kanakkithodi, A. Chandrasekaran, C. Kim, T. D. Huan, G. Pilania, V. Botu and R. Ramprasad, Mater. Today, 2018, 21, 785–796.
13. R. J. Mortimer, A. L. Dyer and J. R. Reynolds, Displays, 2006, 27, 2–18.
14. S. Ito, Polym. J., 2016, 48, 667–677.
15. S. Oliver, L. Zhao, A. J. Gormley, R. Chapman and C. Boyer, Macromolecules, 2019, 52, 3–23.
16. J. S. Peerless, N. J. B. Milliken, T. J. Oweida, M. D. Manning and Y. G. Yingling, Adv. Theory Simul., 2019, 2, 1800129.
17. C. Kuenneth, J. Lalonde, B. L. Marrone, C. N. Iverson, R. Ramprasad and G. Pilania, Commun. Mater., 2022, 3, 96.
18. N. E. Jackson, J. Phys. Chem. B, 2021, 125, 485–496.
19. R. A. Patel, C. H. Borca and M. A. Webb, Mol. Syst. Des. Eng., 2022, 7, 661–676.
20. J. W. Barnett, C. R. Bilchak, Y. Wang, B. C. Benicewicz, L. A. Murdock, T. Bereau and S. K. Kumar, Sci. Adv., 2020, 6, eaaz4301.
21. S. Wu, Y. Kondo, M.-A. Kakimoto, B. Yang, H. Yamada, I. Kuwajima, G. Lambard, K. Hongo, Y. Xu, J. Shiomi, C. Schick, J. Morikawa and R. Yoshida, npj Comput. Mater., 2019, 5, 1–11.
22. C. Kuenneth, J. Lalonde, B. L. Marrone, C. N. Iverson, R. Ramprasad and G. Pilania, Commun. Mater., 2022, 3, 1–10.
23. H. Tran, K.-H. Shen, S. Shukla, H.-K. Kwon and R. Ramprasad, J. Phys. Chem. C, 2023, 127, 977–986.
24. A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. u. Kaiser and I. Polosukhin, Advances in Neural Information Processing Systems, 2017, vol. 30, https://papers.nips.cc/paper_files/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html.
25. C. Xu, Y. Wang and A. Barati Farimani, npj Comput. Mater., 2023, 9, 1–14.
26. C. Kuenneth and R. Ramprasad, Nat. Commun., 2023, 14, 4099.
27. D. P. Kingma and M. Welling, Auto-Encoding Variational Bayes, arXiv, 2013, preprint,  DOI:10.48550/arXiv.1312.6114, https://arxiv.org/abs/1312.6114.
28. R. Batra, H. Dai, T. D. Huan, L. Chen, C. Kim, W. R. Gutekunst, L. Song and R. Ramprasad, Chem. Mater., 2020, 32, 10489–10500.
29. S. Kim, C. M. Schroeder and N. E. Jackson, ACS Polym. Au, 2023, 3, 318–330.
30. S. Jiang, A. B. Dieng and M. A. Webb, npj Comput. Mater., 2024, 10, 1–13.
31. R. Gurnani, D. Kamal, H. Tran, H. Sahu, K. Scharm, U. Ashraf and R. Ramprasad, Chem. Mater., 2021, 33, 7008–7016.
32. R. Gómez-Bombarelli, J. N. Wei, D. Duvenaud, J. M. Hernández-Lobato, B. Sánchez-Lengeling, D. Sheberla, J. Aguilera-Iparraguirre, T. D. Hirzel, R. P. Adams and A. Aspuru-Guzik, ACS Cent. Sci., 2018, 4, 268–276.
33. B. Sanchez-Lengeling, C. Outeiral, G. L. Guimaraes and A. Aspuru-Guzik, Optimizing distributions over molecular space. An Objective-Reinforced Generative Adversarial Network for Inverse-design Chemistry (ORGANIC), 2017, https://chemrxiv.org/engage/chemrxiv/article-details/60c73d91702a9beea7189bc2.
34. R.-R. Griffiths and J. M. Hernández-Lobato, Chem. Sci., 2020, 11, 577–586.
35. J. Lim, S. Ryu, J. W. Kim and W. Y. Kim, J. Cheminf., 2018, 10, 31.
36. Z. Zhou, S. Kearnes, L. Li, R. N. Zare and P. Riley, Sci. Rep., 2019, 9, 10752.
37. R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, Sci. Data, 2014, 1, 140022.
38. J. J. Irwin, K. G. Tang, J. Young, C. Dandarchuluun, B. R. Wong, M. Khurelbaatar, Y. S. Moroz, J. Mayfield and R. A. Sayle, J. Chem. Inf. Model., 2020, 60, 6065–6073.
39. S. Kim, P. A. Thiessen, E. E. Bolton, J. Chen, G. Fu, A. Gindulyte, L. Han, J. He, S. He, B. A. Shoemaker, J. Wang, B. Yu, J. Zhang and S. H. Bryant, Nucleic Acids Res., 2016, 44, D1202–D1213.
40. M. Nakata and T. Shimazaki, J. Chem. Inf. Model., 2017, 57, 1300–1308.
41. D. J. Audus and J. J. de Pablo, ACS Macro Lett., 2017, 6, 1078–1082.
42. T. B. Martin and D. J. Audus, ACS Polym. Au, 2023, 3, 239–258.
43. A. J. Gormley and M. A. Webb, Nat. Rev. Mater., 2021, 6, 642–644.
44. R. Upadhya, S. Kosuri, M. Tamasi, T. A. Meyer, S. Atta, M. A. Webb and A. J. Gormley, Adv. Drug Delivery Rev., 2021, 171, 1–28.
45. C. Kim, A. Chandrasekaran, T. D. Huan, D. Das and R. Ramprasad, J. Phys. Chem. C, 2018, 122, 17575–17585.
46. P. Shetty, A. C. Rajan, C. Kuenneth, S. Gupta, L. P. Panchumarti, L. Holm, C. Zhang and R. Ramprasad, npj Comput. Mater., 2023, 9, 1–12.
47. S. Otsuka, I. Kuwajima, J. Hosoya, Y. Xu and M. Yamazaki, 2011 International Conference on Emerging Intelligent Data and Web Technologies, 2011, pp. 22–29.
48. Y. Hayashi, J. Shiomi, J. Morikawa and R. Yoshida, npj Comput. Mater., 2022, 8, 1–15.
49. M. Ohno, Y. Hayashi, Q. Zhang, Y. Kaneko and R. Yoshida, J. Chem. Inf. Model., 2023, 63, 5539–5548.
50. R. Ma and T. Luo, J. Chem. Inf. Model., 2020, 60, 4684–4690.
51. Polymer Property Predictor and Database, https://pppdb.uchicago.edu/.
52. MALDI Recipes, https://maldi.nist.gov/.
53. D. J. Walsh, W. Zou, L. Schneider, R. Mello, M. E. Deagen, J. Mysona, T.-S. Lin, J. J. de Pablo, K. F. Jensen, D. J. Audus and B. D. Olsen, ACS Cent. Sci., 2023, 9, 330–338.
54. T. Xie, H.-K. Kwon, D. Schweigert, S. Gong, A. France-Lanord, A. Khajeh, E. Crabb, M. Puzon, C. Fajardo, W. Powelson, Y. Shao-Horn and J. C. Grossman, APL Mach. Learn., 2023, 1, 046108.
55. L. C. Brinson, M. Deagen, W. Chen, J. McCusker, D. L. McGuinness, L. S. Schadler, M. Palmeri, U. Ghumman, A. Lin and B. Hu, ACS Macro Lett., 2020, 9, 1086–1094.
56. T.-S. Lin, C. W. Coley, H. Mochigase, H. K. Beech, W. Wang, Z. Wang, E. Woods, S. L. Craig, J. A. Johnson, J. A. Kalow, K. F. Jensen and B. D. Olsen, ACS Cent. Sci., 2019, 5, 1523–1531.
57. L. Schneider, D. Walsh, B. Olsen and J. d. Pablo, Digital Discovery, 2024, 3, 51–61.
58. S. P. Tiwari, W. Shi, S. Budhathoki, J. Baker, A. K. Sekizkardes, L. Zhu, V. A. Kusuma, D. P. Hopkinson and J. A. Steckel, J. Chem. Inf. Model., 2024, 64, 638–652.
59. B. S. Ferrari, M. Manica, R. Giro, T. Laino and M. B. Steiner, npj Comput. Mater., 2024, 10, 1–10.
60. J. Shi, D. Walsh, W. Zou, N. J. Rebello, M. E. Deagen, K. A. Fransen, X. Gao, B. D. Olsen and D. J. Audus, ACS Polym. Au, 2024, 4, 66–76.
61. T. Yue, J. He and Y. Li, PolyUniverse: Generation of a Large-scale Polymer Library Using Rule-Based Polymerization Reactions for Polymer Informatics, 2024, https://chemrxiv.org/engage/chemrxiv/article-details/669029525101a2ffa81c504e.
62. H. Tran, R. Gurnani, C. Kim, G. Pilania, H.-K. Kwon, R. P. Lively and R. Ramprasad, Nat. Rev. Mater., 2024, 9, 866–886.
63. W. Ahmad, E. Simon, S. Chithrananda, G. Grand and B. Ramsundar, ChemBERTa-2: Towards Chemical Foundation Models, arXiv, 2022, preprint,  DOI:10.48550/arXiv.2209.01712, https://arxiv.org/abs/2209.01712.
64. J. Born and M. Manica, Nat. Mach. Intell., 2023, 5, 432–444.
65. J. Kahovec, R. B. Fox and K. Hatada, Pure Appl. Chem., 2002, 74, 1921–1956.
66. E. Mullins, R. Oldland, Y. A. Liu, S. Wang, S. I. Sandler, C.-C. Chen, M. Zwolak and K. C. Seavey, Ind. Eng. Chem. Res., 2006, 45, 4389–4415.
67. N. M. O'Boyle, M. Banck, C. A. James, C. Morley, T. Vandermeersch and G. R. Hutchison, J. Cheminf., 2011, 3, 33.
68. C. Bannwarth, S. Ehlert and S. Grimme, J. Chem. Theory Comput., 2019, 15, 1652–1671.
69. S. A. Wildman and G. M. Crippen, J. Chem. Inf. Comput. Sci., 1999, 39, 868–873.
70. G. R. Bickerton, G. V. Paolini, J. Besnard, S. Muresan and A. L. Hopkins, Nat. Chem., 2012, 4, 90–98.
71. P. Ertl, B. Rohde and P. Selzer, J. Med. Chem., 2000, 43, 3714–3717.
72. RDKit, https://www.rdkit.org/.
73. L. B. Kier, Quant. Struct.-Act. Relat., 1989, 8, 221–224.
74. L. J. Fetters, D. J. Lohse, D. Richter, T. A. Witten and A. Zirkel, Macromolecules, 1994, 27, 4639–4647.
75. M. A. F. Afzal, A. R. Browning, A. Goldberg, M. D. Halls, J. L. Gavartin, T. Morisato, T. F. Hughes, D. J. Giesen and J. E. Goose, ACS Appl. Polym. Mater., 2020, 3, 620–630.
76. J. Bicerano, Prediction of Polymer Properties, cRc Press, 2002.
77. R. F. Boyer, Rubber Chem. Technol., 1963, 36, 1303–1421.
78. L. Goerigk and S. Grimme, Phys. Chem. Chem. Phys., 2011, 13, 6670–6688.
79. L. Goerigk, A. Hansen, C. Bauer, S. Ehrlich, A. Najibi and S. Grimme, Phys. Chem. Chem. Phys., 2017, 19, 32184–32215.
80. V. Barone and M. Cossi, J. Phys. Chem. A, 1998, 102, 1995–2001.
81. J.-W. Zha, M.-S. Zheng, B.-H. Fan and Z.-M. Dang, Nano Energy, 2021, 89, 106438.
82. D. T. Christiansen, A. L. Tomlinson and J. R. Reynolds, J. Am. Chem. Soc., 2019, 141, 3859–3862.
83. A. Distler, P. Kutka, T. Sauermann, H.-J. Egelhaaf, D. M. Guldi, D. Di Nuzzo, S. C. J. Meskers and R. A. J. Janssen, Chem. Mater., 2012, 24, 4397–4405.
84. K. McNeill and S. Canonica, Environ. Sci.: Processes Impacts, 2016, 18, 1381–1399.
85. I. Groeneveld, M. Kanelli, F. Ariese and M. R. van Bommel, Dyes Pigm., 2023, 210, 110999.
86. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
87. P. J. Flory, J. Chem. Phys., 1941, 9, 660.
88. P. J. Flory, J. Chem. Phys., 1942, 10, 51–61.
89. M. L. Huggins, J. Chem. Phys., 1941, 9, 440.
90. M. L. Huggins, J. Am. Chem. Soc., 1942, 64, 1712–1719.
91. S.-T. Lin and S. I. Sandler, Ind. Eng. Chem. Res., 2002, 41, 899–913.
92. Y. Aoki, S. Wu, T. Tsurimoto, Y. Hayashi, S. Minami, O. Tadamichi, K. Shiratori and R. Yoshida, Macromolecules, 2023, 56, 5446–5456.
93. A. Klamt, J. Phys. Chem., 1995, 99, 2224–2235.
94. J. S. Smith, B. Nebgen, N. Lubbers, O. Isayev and A. E. Roitberg, J. Chem. Phys., 2018, 148, 241733.
95. J. Vandermause, S. B. Torrisi, S. Batzner, Y. Xie, L. Sun, A. M. Kolpak and B. Kozinsky, npj Comput. Mater., 2020, 6, 1–11.
96. A. Amini, W. Schwarting, A. Soleimany and D. Rus, Adv. Neural Inf. Process. Syst., 2020, 14927–14937.
97. K. Yang, K. Swanson, W. Jin, C. Coley, P. Eiden, H. Gao, A. Guzman-Perez, T. Hopper, B. Kelley, M. Mathea, A. Palmer, V. Settels, T. Jaakkola, K. Jensen and R. Barzilay, J. Chem. Inf. Model., 2019, 59, 3370–3388.
98. M. Buzdalov and A. Shalyto, Parallel Problem Solving from Nature – PPSN XIII, Cham, 2014, pp. 528–537.
99. J. Zhu, H. Wang, E. Hovy and M. Ma, ACM Trans. Speech Lang. Process., 2010, 6, 1–24.
100. K. J. Miller, J. Am. Chem. Soc., 1990, 112, 8533–8542.
101. A. D. Buckingham, Advances in Chemical Physics, John Wiley & Sons, Ltd, 1967, pp. 107–142.
102. F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714.
103. D. M. Wilkins, A. Grisafi, Y. Yang, K. U. Lao, R. A. DiStasio and M. Ceriotti, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 3401–3406.
104. D. Zhao, X. He, P. W. Ayers and S. Liu, Molecules, 2023, 28, 2576.
105. L. Medrano Sandonas, J. Hoja, B. G. Ernst, Á. Vázquez-Mayagoitia, R. A. DiStasio and A. Tkatchenko, Chem. Sci., 2023, 14, 10702–10717.
106. R. Todeschini and V. Consonni, Handbook of Chemoinformatics, John Wiley & Sons, Ltd, 2003, pp. 1004–1033.
107. R. E. Larsen, J. Phys. Chem. C, 2016, 120, 9650–9660.
108. A. Merchant, S. Batzner, S. S. Schoenholz, M. Aykol, G. Cheon and E. D. Cubuk, Nature, 2023, 624, 80–85.
109. Z. Liu, T. Zubatiuk, A. Roitberg and O. Isayev, J. Chem. Inf. Model., 2022, 62, 5373–5382.
110. P. Pracht, F. Bohle and S. Grimme, Phys. Chem. Chem. Phys., 2020, 22, 7169–7192.
111. M. Bursch, J.-M. Mewes, A. Hansen and S. Grimme, Angew. Chem., 2022, 134, e202205735.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc08617a

---