 Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Point defect formation at finite temperatures with machine learning force fields†
Irea
Mosquera-Lois
a,
Johan
Klarbring
ab and
Aron
Walsh
 *a
*a
aThomas Young Centre & Department of Materials, Imperial College London, London SW7 2AZ, UK. E-mail: a.walsh@imperial.ac.uk
bDepartment of Physics, Chemistry and Biology (IFM), Linköping University, SE-581 83, Linköping, Sweden
First published on 8th April 2025
Abstract
Point defects dictate the properties of many functional materials. The standard approach to modelling the thermodynamics of defects relies on a static description, where the change in Gibbs free energy is approximated by the internal energy. This approach has a low computational cost, but ignores contributions from atomic vibrations and structural configurations that can be accessed at finite temperatures. We train a machine learning force field (MLFF) to explore dynamic defect behaviour using Te+1i and V+2Te in CdTe as exemplars. We consider the different entropic contributions (e.g., electronic, spin, vibrational, orientational, and configurational) and compare methods to compute the defect free energies, ranging from a harmonic treatment to a fully anharmonic approach based on thermodynamic integration. We find that metastable configurations are populated at room temperature and thermal effects increase the predicted concentration of Te+1i by two orders of magnitude — and can thus significantly affect the predicted properties. Overall, our study underscores the importance of finite-temperature effects and the potential of MLFFs to model defect dynamics at both synthesis and device operating temperatures.
1. Introduction
Point defects make or break material functionality.1 They limit photovoltaic efficiency by acting as non-radiative recombination centres, control ionic conductivity in batteries, provide active sites for catalytic reactions, and platforms for quantum information technologies. Despite their profound effect on the macroscopic properties of crystals, they are present in dilute concentrations and thus render experimental characterisation challenging. As a result, a combination of experiment and theory is needed to understand defect behaviour.The key factor when modelling defects is their concentration, which is determined by the free energy of defect formation, gf, at the synthesis or annealing temperature. Calculating gf is however computationally challenging, and is thus typically approximated by the formation internal energy, uf(0 K), i.e. gf(Tsynthesis) ≈ uf(0 K).2,3 Inherent in this approximation is the assumption of a static framework, where most studies only consider the defect ground state structure at 0 K, and thus neglect metastable configurations that may be populated at the device operating temperature. Since the properties of a defect strongly depend on its geometry,4–9 the predicted behaviour can be significantly affected when ignoring thermally accessible metastable configurations.10–16
With the development of better computational resources, more accurate studies that go beyond this static 0 K approximation are becoming possible using ab initio methods. In the last decades, many investigations have modelled entropic contributions for defects in elementary solids.17–30 Thermal effects are harder to model in multinary semiconductors due to the higher number of possible intrinsic charged defects and required level of theory,31–61 but have been included for specific defects.62–80 However, most of these studies adopt several approximations: (i) they only account for vibrational entropies, thereby neglecting other degrees of freedom (e.g., electronic, spin, orientational and configurational), and (ii) they adopt the (quasi)harmonic approximation to model vibrational effects (e.g., assuming a quadratic potential energy surface for the interatomic bonds). The limitations of these approximations are system-dependent and not well investigated, and demonstrate the lack of a reliable and affordable approach to model thermal effects for defects.
In this study, we target these limitations by considering all relevant entropic contributions and systematically comparing the different methods to calculate the defect formation free energy, ranging from a harmonic to a fully anharmonic approach based on thermodynamic integration (TI). To reduce the cost of these simulations, we use machine learning force fields as a surrogate model, which successfully map the defect energy surfaces (Section 2.1). We choose Te+1i and V+2Te in CdTe as exemplar systems since they display potential energy surfaces of different complexity (e.g., presence versus lack of low-energy metastable configurations12) (Section 2.2). By modelling the impact of thermal effects on their predicted defect concentrations, we find that these dominate when the defect undergoes symmetry-breaking structural reconstructions and has low-energy metastable configurations, thereby demonstrating the limitations of the idealised 0 K description (Section 2.3).
2. Results and discussion
2.1 Machine learning force fields for defects
Calculating the defect formation free energy, gf, requires modelling the defect formation reaction by computing the free energy difference between products and reactants at the synthesis temperature.2,3 For example, the formation of the positively charged tellurium interstitial, Te+1i, can be described by the defect reaction | (1) |
The corresponding formation free energy is defined from the sum of products (charged defect with an electron in the conduction band) minus the sum of reactants (pristine CdTe host and reservoir of Te). In the standard first-principles supercell formalism, this formation energy is given by
 | (2) |
To reduce the cost of free energy calculations, we employ machine learning force fields and train a separate MACE model83 for each system involved in the defect formation reaction, focussing on a single charge state of each defect. We target temperatures ranging from 100 K to the typical CdTe anneal temperature of 840 K.84 All models show good accuracies with low mean and root mean square errors on the test set (see Table 1 and further discussion in Methods and ESI†). The accuracy of the defect models is further confirmed by mapping the one-dimensional path between the stable defect structures, which shows good agreement despite the small energy difference between the distinct configurations of Te+1i (Fig. 1 and ESI Fig. S9†).
| System | Energy (meV per atom) | Force (meV Å−1) | Stress (meV Å−3) |
|---|---|---|---|
| CdTe | 0.3 (0.4) | 13 (17) | 0.2 (0.3) |
| Te+1i | 0.5 (0.7) | 21 (30) | 0.2 (0.3) |
| V +2Te | 0.4 (0.6) | 18 (24) | 0.2 (0.3) |
| Te | 1.6 (2.3) | 73 (102) | 0.9 (1.3) |
 | ||
| Fig. 1 Potential energy surfaces illustrating the defect configurations identified with defect structure searching,85 calculated with DFT (green circles) and MACE (pink triangles). The variable Q represents a mass-weighted displacement coordinate that tracks the structural change along the pathway between the defect configurations, as described in the Methods. (a) Te+1i is a bistable defect since the metastable configuration (split Te–Cd with Cs symmetry) is only 18 meV higher than the ground state (split Te–Te with C2v symmetry). Note that the differences between DFT and MACE are in meV per supercell, with the error in ΔE(C2v − Cs) only accounting to 0.1 meV per atom. (b) V+2Te, where the metastable configuration (C3v) is significantly higher in energy (1.8 eV above the ground state structure of Td symmetry). Te in brown, Cd in yellow, Te+1i in green and V+2Te in shaded grey. | ||
2.2 Defect dynamics at room temperature
We first investigate the limitations of the static framework by comparing the behaviour of the defects at 0 K and around the typical operating temperature for a solar cell (T = 300 K). The potential energy surface calculated at 0 K shows that Te+1i is a bistable defect with two accessible structures: a split configuration with either one or two Te–Te bonds,12 which have C2v and Cs site symmetries, respectively, and an energy difference of ΔE(Cs − C2v) = 18 meV (Fig. 1). In contrast, V+2Te only has one accessible structure at the device operating conditions since the metastable C3V configuration is 1.8 eV above the Td ground state (≫ kBT = 25 meV at 300 K).To validate these predictions, we perform molecular dynamics under the NPT ensemble (300 K, 1 atm, 1 ns), revealing three distinct motions for Te+1i (Fig. 2). The fastest process corresponds to changes in configuration between the C2v and Cs geometries, which is reflected by variations in the distances between Te+1i and its neighbouring Te atoms as it alternates between forming 1 and 2 Te–Te bonds. On a slower timescale, there are changes in the defect position (i.e., hopping between lattice sites) as well as changes in the orientation of the Te–Te bond, indicated by variation in the angle between the Te–Te bond(s) and the lattice axes. These three motions occur rapidly on the nanosecond timescale due to their low energy barriers relative to the thermal energy (Eb = 28 − 100 meV) with rates on the order of 1010 s−1 (configurational and hopping) and 108 s−1 (rotation) — and highlight the configurational, orientational and migration degrees of freedom that contribute to the defect formation and migration entropies, respectively. In contrast, this dynamic behaviour of Te+1i differs significantly from that of V+2Te, which remains stable in its Td ground state configuration, as depicted in ESI Fig. S12,† and is thus well-described by its static 0 K structure.
 | ||
| Fig. 2 Active degrees of freedom of Te+1i at 300 K and associated energy barriers. (a) Configurational change, reflected by changes in the Tei–Te distances. The narrow green peak illustrates the shortest Tei–Te bond, which shows little variation at around 2.8 Å, while the wider pink and orange distributions demonstrate the wide variation in the second and third shortest Te–Te distances (see ESI Fig. S11†). (b) Changes in the orientation of the Tei–Te bond with respect to the [100] direction. (c) Migration, illustrated by tracking the distance between the current and original position of the interstitial. | ||
2.3 Impact of defect entropy on predicted concentrations
The dynamic behaviour of Te+1i suggests that its formation entropy, sf, will be significant at the CdTe annealing temperature (≈840 K)84 and will thus affect the predicted equilibrium concentration. To verify this, we calculate sf and gf by considering the different degrees of freedom that change upon forming the defect at a fixed lattice site: electronic, spin, vibrational, orientational and structural (also referred to as configurational).2 While the first two terms can be estimated with analytical expressions (see Methods), the vibrational contribution is more challenging and typically requires approximations. By assuming a quadratic energy surface for the interatomic bonds, the harmonic vibrational gf can be calculated, which can be extended to account for thermal expansion with the quasiharmonic approximation.2,86 However, this harmonic assumption might be limited for defects at high temperatures, where anharmonic effects seem to be important – as suggested by the high anharmonicity scores87 observed for Te+1i relative to pristine CdTe (σ(840 K) = 4.5 versus 0.8, respectively, and σ typically ranging between 0–1; ESI Fig. S13†).To assess these limitations, we use non-equilibrium thermodynamic integration to account for anharmonic effects and compare the gf calculated with each approach. We do this by starting from the Einstein crystal (independent harmonic oscillators), integrating to the anharmonic crystal at 100 K, and finally integrating with respect to temperature up to 840 K (see Methods for further details). Since TI calculates the change in the total free energy described by the MACE potential (i.e., the ionic degrees of freedom), it already includes the vibrational, orientational and structural contributions, and thus we only have to add the electronic and spin terms to gTIf(T). We define three defect formation free energies with increasing accuracy:
 | (3) |
We follow the standard convention in defect chemistry and define gf as the change in free energy for forming a defect at a fixed lattice site (i.e., excluding entropic contributions from the mixing or site entropy‡). We calculate the equilibrium defect concentration with
 | (4) |
As demonstrated in Fig. 3b, for Te+1i thermal effects are significant at annealing temperature, with gf(840 K) differing by 0.5 eV from uf(0 K) − T(sspinf + sorientf). All methods are in good agreement, indicating that the harmonic approximation gives a reasonable estimate of gf, since anharmonic effects approximately cancel out between the bulk and the defect in this temperature range. This agreement also validates the decoupling approximation used to separate the different degrees of freedom (e.g., gTIf ≈ gvib,harmf − Tsorientf − Tsstrucf). Using this approximation, we find that their relative entropic contributions follow the expected trend, with the vibrational one dominating, followed by the structural, spin, orientational and electronic terms (with sf(840 K) of 4.2, 0.7, 0.7, −0.7 and 0.1 kB, respectively; Fig. 3a). However, we note that the structural term can become larger for defects that have many low-energy metastable configurations.25
Overall, the total entropic contribution is not negligible and significantly affects gf, increasing the predicted concentration by a factor of 500 (Fig. 3c). This importance of entropic effects contrasts with their role in V+2Te, where they are almost negligible (gf(840 K) − uf(0 K) = 0.08 eV; ESI Fig. S14†) due to (i) smaller magnitude of the vibrational entropy and (ii) lack of spin, orientational and structural entropies. As a result, we expect thermal effects to be important for defects which (i) introduce strong structural distortions (high svibf), (ii) break the host site symmetry (high sorientf), and (iii) have low-energy metastable configurations (high sstrucf).
3. Discussion
Overall, we have illustrated how to model thermal effects for point defects in crystals, demonstrating the dynamic character of Te+1i in CdTe, which rapidly changes between configuration, orientation and position at room temperature. These degrees of freedom increase the entropy upon defect formation, and can be computed from standard defect calculations as illustrated in this study. The computationally challenging term is the vibrational entropy. We have found that the harmonic approximation gives a reasonable and affordable description of the vibrational formation entropy at 840 K for a dynamic defect with a high anharmonicity score σanh. While this suggests the validity of the harmonic approximation for ‘simpler’ defects with single configurations that do not diffuse in this temperature regime, the impact of anharmonicity varies across different defects and host materials, as observed in several metals.18–20,22,23,26 This highlights the need for further calculations of ganhf and σanh on additional defects and host crystals to establish more general guidelines.By combining the different entropic contributions, we find that thermal effects increase the predicted concentration of Te+1i by two orders of magnitude, and can thus significantly affect the predicted behaviour by shifting the relative defect populations. Thermal effects will play a significant role for defects that undergo structural reconstructions, break the site symmetry of the host and have low-energy metastable configurations (high svibf, sorientf and sstrucf), as illustrated by comparing two defects with energy surfaces of different complexity. Beyond defect related factors, hosts with a soft and dynamic lattice or compositional disorder will also be more sensitive to thermal effects, since their defects typically lead to stronger reconstructions (e.g., rebonding or local octahedral rotations in perovskite structures88) and display many low-energy metastable configurations (e.g., Sb2Se3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8 or alloys89 like CdSexTe(1−x)90). A special case is materials where the phase relevant for applications is only stable at finite temperatures. Here, it can be key to model defects at the device operating temperature since their behaviour can be sensitive to their surrounding structure — as illustrated by the discrepancies when modelling the carrier capture behaviour of Ii in different phases of CsPbI3.91
8 or alloys89 like CdSexTe(1−x)90). A special case is materials where the phase relevant for applications is only stable at finite temperatures. Here, it can be key to model defects at the device operating temperature since their behaviour can be sensitive to their surrounding structure — as illustrated by the discrepancies when modelling the carrier capture behaviour of Ii in different phases of CsPbI3.91
Despite the importance of including thermal effects for accurate defect predictions, the current limitation is the computational cost. While the orientational, spin and electronic terms can be calculated from standard defect calculations using the doped Python package,92 the configurational term requires considering the different thermally-accessible structures of a defect, which can be identified through defect-structure searching methods like ShakeNBreak.85 More challenging is the vibrational term as it requires going beyond standard static defect calculations. In practice, accounting for this contribution will only be affordable for high-accuracy studies that target the low-energy defects; especially for applications with a high synthesis or operating temperature, like industrial thermoelectrics, thermochemical water splitting, exhaust automotive catalysts or solid-state fuel cells (Toperation ≈ 800–1900 K).93–95 In these high temperature applications, thermal effects will populate metastable configurations and could also affect the predicted position of the defect charge transition level (i.e., non-negligible entropic term of T × [sf(q,T) − sf(q′,T)]/(q − q′)) — especially when the change in charge state leads to significant differences in the defect structure and symmetry, spin state and position of the defect level within the bandgap.80Finally, based on the performance of our trained models, we note the promise of machine learning force fields for describing the thermal effects of defects. Beyond the prediction of more accurate concentrations, by learning the defect potential energy surface, they can also reduce the cost of modelling defect dynamics at the device operating temperature and on larger time and length scales, which can be key to predict complex processes like defect reactions or diffusion.96
4. Methodology
4.1 Density Functional Theory calculations
All reference calculations were performed with Density Functional Theory using the exchange-correlation functional PBEsol97 and the projector augmented wave method,98 as implemented in the Vienna Ab initio Simulation Package (VASP).99,100 We used the standard PAW PBE potentials (version 64) for Te (5s25p4) and Cd (4d105s2). Although hybrid functionals are typically required to accurately model the electronic behaviour of defects, we used a more affordable GGA functional for several reasons: (i) PBEsol has been found to accurately describe the vibrational properties of crystals;101 (ii) it correctly identifies the same defect configurations reported in a previous study using the HSE06 hybrid functional;12 and (iii) we aimed to benchmark how to properly train defect MLFFs to reach the high accuracies required to estimate gf, and as a result needed a functional that would allow a thorough exploration of the configurational landscape up to the CdTe synthesis temperature.We converged the plane wave energy cutoff and Γ-centered k-point mesh to 1 meV per atom, resulting in values of 450 eV and 4 × 4 × 4 for the conventional cell of CdTe. To minimise Pulay stress errors during molecular dynamics simulations, we increased the converged energy cutoff by 30% (585 eV). The threshold for electronic convergence was set to 10−5 eV.
4.2 Training of machine learning force fields
We used the structure similarity kernel implemented in VASP to generate the training sets of configurations using its on-the-fly molecular dynamics approach.102–105 This involved heating runs performed under the NPT ensemble with a pressure of 1 atm and from an initial temperature of 100 K up to 30% above our target temperature of 840 K. In addition, we generated a series of compressed and expanded structures (0.9–1.1 of the original cell volume) to ensure that the model could be used for the quasiharmonic approximation. For bulk CdTe and its defects, we used a 2 × 2 × 2 supercell of the conventional cell (13.0 Å in length and 64 atoms for bulk CdTe). For Te, we included all the low-energy phases available in the Materials Project106 (Ehull ≤ kBTsynthesis = kB × (840 K) = 0.08 eV), which were expanded to cubic supercells of at least 10 Å in length. For the liquid Te phase, we generated two models with the packmol code:107 two cubic boxes of 15 Å and 17.5 Å in length, containing 95 and 220 atoms, respectively, which gave densities matching the reported values in previous studies at our target temperatures (ρ = 0.027 atoms per Å3).108An independent model was trained for each system (bulk CdTe, Te+1i, V+2Te and Te), with the defect datasets only including one charge state (e.g. +1 for Tei and +2 for VTe). We note that the models for the charged defects were trained on the absolute DFT energies (e.g. without electrostatic corrections, which are applied a posteriori when calculating the defect formation energy, as described below). Training separate models for each system lead to higher accuracy models than training one joint model on the bulk and defect datasets. However, we have observed that training a model only on defect configurations should be avoided if the model will be applied to study the absolute energies of larger system sizes (e.g., defect formation energies). While models selectively trained on defect configurations achieve higher accuracy for defective supercells with the same number of atoms, these models lead to a systematic error in the total energies of larger supercells than the supercells used for training, as explained in detail in ESI Section 1C.†
After generating the training sets with VASP, we trained separate MACE83 force fields on these datasets to obtain models with higher accuracy and speed. 10% of the configurations in these datasets were used as validation sets to monitor the loss during training. We used a MACE model with Ziegler–Biersack–Littmark (ZBL) pair repulsion,109 2 message passing layers, 256 invariant messages, correlation order of 3, angular resolution of 3 and cutoff radius of 5 Å. The batch size was set to 2 and the Huber loss function was used, with weights of 1, 100 and 100 for the mean square errors in the energies, forces and stresses, respectively. For the last 20% of the training epochs, the weights were updated to values of 1000, 10 and 100 for energy, force and stress, respectively — following the recommended strategy of increasing the weight on the energy errors during the final training epochs. The models were trained until the validation loss converged, which required around 150–200 epochs. The reference energies were defined as the potential energies of isolated Cd and Te atoms.
4.3 Validation of machine learning force fields
To generate the test sets, we performed NPT molecular dynamics simulations with the trained models at three different temperatures (300, 550 and 900 K), running five independent 24 ps runs at each temperature. We then sampled 100–300 equally-spaced configurations from these trajectories, and performed DFT calculations on them, which were used to calculate the MAE and RMSE on the predicted properties (energy, forces and stresses) of each model (see distribution of sampled configurations and associated errors in Figs. ESI Fig. S1† to ESI Fig. S5†). The MAE and RMSE for the forces and stresses were calculated component wise, as defined in ref. 110. The predicted properties exhibited small absolute errors with no outliers, confirming that the models accurately describe the potential energy surfaces of each system up to 900 K. This extensive testing of the models is especially important for defective crystals, which exhibit more complex energy surfaces than the pristine hosts. In addition, we also validated that the model successfully described the phonons and vibrational free energy of bulk CdTe (see ESI Fig. S6†).4.4 Defect calculations
Defect calculations were setup and analysed using doped.92 To account for spurious finite-size supercell effects, the Kumagai–Oba111 (eFNV) charge correction scheme was used to calculate Ecorr, as automated in doped. The Fermi level was assumed to be located in the middle of the band gap.4.5 Spin degeneracy
The spin degeneracy was calculated with doped using | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(Ω)2.
ln(Ω)2.
4.6 Orientational degeneracy
The orientational degeneracy was also calculated with doped using | (6) |
For Te+1i, the C2v configuration has an initial site symmetry of Cs which becomes C2v when the atoms around the interstitial relax due to the formation of the Te–Te dimer. Similarly, the (metastable) Cs configuration has an initial C1 site symmetry which becomes Cs after the relaxation. As a result, for both configurations the orientational degeneracy Ωorient is 0.5 (e.g. the site symmetry increases upon relaxation of the atoms around the interstitial). The site multiplicities per primitive cell are 12 and 24 for the C2v and Cs configurations, respectively. These degeneracies are accounted for when predicting the defect concentration (eqn (4)) where the orientational entropy is included in gf.
4.7 Electronic entropy
The electronic entropy was calculated using the fixed density of states (DOS) approximation,56,112–115 that assumes a temperature-independent DOS. Since the electronic entropy is sensitive to the bandgap, and PBEsol significantly underestimates it, we performed self-consistent field HSE06 (α = 0.345 (ref. 13)) calculations on the 0 K structures optimised with PBEsol. The electronic entropy is then calculated using | (7) |
 | (8) |
• Te, CdTe and Cd32Te+133: The Fermi level is assumed to be located mid-gap between the highest occupied and lowest unoccupied state. Note that, in theory, the Fermi level of CdTe should correspond to the self-consistent value determined for a set of defects and charge states.116,117 Determining EF would require calculating the formation energies for all possible intrinsic defects in CdTe, which is beyond the scope of our study. Accordingly, we assume the Fermi level to be midgap.38 Te+1i introduces an empty state 0.75 eV above the valence band maximum (VBM), and thus EF is set to 0.75/2 = 0.37 eV above the VBM. Note that the electronic entropy is sensitive to the energy difference between EF and the lowest unoccupied state, thus requiring an accurate electronic structure.
• Extra electron: It is defined as the excess electronic entropy when one extra electron is added to the conduction band minimum (CBM) of the bulk system, i.e. selec(N + 1) − selec(N), where selec(N) denotes the electronic entropy of bulk CdTe with N and N + 1 electrons. To calculate the electronic entropy of the N + 1 system, we determine EF with118
 | (9) |
 | (10) |
 and h representing the electron effective mass and Planck constant, respectively. For the concentration of excess electrons donated by the defect, n, we assume a value of n = 1015 cm−3, which equals our predicted value for the equilibrium concentration of Te+1i at 840 K (thus making the reaction (CdTe)32 + Te → Cd32Te+133 + e− charge neutral). We note that if all possible point defects were considered, the value of n should be set to the excess electron concentration, as determined self-consistently.116
and h representing the electron effective mass and Planck constant, respectively. For the concentration of excess electrons donated by the defect, n, we assume a value of n = 1015 cm−3, which equals our predicted value for the equilibrium concentration of Te+1i at 840 K (thus making the reaction (CdTe)32 + Te → Cd32Te+133 + e− charge neutral). We note that if all possible point defects were considered, the value of n should be set to the excess electron concentration, as determined self-consistently.116
Finally, we note that the electronic entropy can become significant at elevated temperatures (T ≥ 1000 K, ESI Fig. S17†) if the defect i) introduces an (occupied) empty state close to the (CBM) VBM or ii) changes the occupation of localised d/f bands of nearby cations (e.g., V+2O reducing two Ce+4 to Ce+3 in CeO2), as demonstrated in previous studies.93,119
4.8 Structural entropy
The Python code ShakeNBreak was used to identify the defect ground state and metastable configurations.4,5,85 From these configurations, the structural or configurational entropy can be estimated using | (11) |
 | (12) |
 | (13) |
Beyond applying this analytical approach, we also calculated the structural entropy using the ‘inherent structures’ method (IS).25 Within this formalism, we performed NPT MD trajectories at 30 temperatures (equally spaced ranging from 100 to 840 K), then sampled 1600 equally-spaced configurations and performed conjugate gradient optimisations to quench the structures to the nearest local minima in the 0 K PES (ESI Fig. S16†). The configurational entropy was then calculated with
 | (14) |
 denotes the average potential energy of the inherent structures sampled at T, with the volume fixed to the optimal value for the 0 K ground state structure, and Ti and Tf set to 100 and 840 K, respectively. This method resulted in sstrucf(840 K) = 1.05 kB, in the same order of the value of 0.6 kB obtained with the analytical method. The slightly larger value of sstrucf estimated with the IS formalism likely stems from the additional intermediate configurations sampled with quenching.
denotes the average potential energy of the inherent structures sampled at T, with the volume fixed to the optimal value for the 0 K ground state structure, and Ti and Tf set to 100 and 840 K, respectively. This method resulted in sstrucf(840 K) = 1.05 kB, in the same order of the value of 0.6 kB obtained with the analytical method. The slightly larger value of sstrucf estimated with the IS formalism likely stems from the additional intermediate configurations sampled with quenching.
Finally, a third approach to account for the structural entropy involves coarse-graining the configurational degree of freedom, and calculating the total defect concentration as a sum over the different configurations i using2
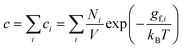 | (15) |
 | (16) |
4.9 Vibrational entropy
The harmonic and quasiharmonic vibrational free energies were calculated using phonopy.86,120 Within the quasiharmonic framework, which includes the effect of thermal expansion on the phonon frequencies, we generated 11 structures by scaling the supercell volume by factors ranging from 0.9 to 1.10 with a 0.02 increment.4.10 Thermodynamic integration
Fully anharmonic free energies were calculated using non-equilibrium TI in LAMMPS,121,122 as implemented in the code calphy.81 This involved two thermodynamic integration paths: first, we integrate from the Einstein crystal to the anharmonic one at 100 K (Frenkel Ladd method) and then we calculate the temperature variation of the free energy at constant pressure by integrating from 100 K to 840 K (commonly known as reversible scaling). These simulations were performed fixing the center of mass, as done in previous studies.18,81,122 For each path, we performed 10 independent TI runs to estimate the error, defined as the standard error of the mean free energy (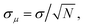 , where σ denotes the standard deviation in the individual free energies calculated from the N = 10 independent TI runs). The switching time was adjusted for each system until the error converged to an acceptable value (see ESI Fig. S15†), which must be very low (σμ < 0.25 meV per atom ≈ 20 meV per supercell) to get an accurate gf. Since gf is the difference between two large and similar numbers (the free energies of the bulk and defect supercells), small relative errors in either of these quantities can lead to a large error in gf. The convergence tests resulted in the switching times reported in Table 2.
, where σ denotes the standard deviation in the individual free energies calculated from the N = 10 independent TI runs). The switching time was adjusted for each system until the error converged to an acceptable value (see ESI Fig. S15†), which must be very low (σμ < 0.25 meV per atom ≈ 20 meV per supercell) to get an accurate gf. Since gf is the difference between two large and similar numbers (the free energies of the bulk and defect supercells), small relative errors in either of these quantities can lead to a large error in gf. The convergence tests resulted in the switching times reported in Table 2.
| Path | CdTe | Te+1i | V+2Te | Te |
|---|---|---|---|---|
| Einstein → anharmonic | 25, 100 | 25, 200 | 15, 150 | 25, 70 |
| 100 K → 840 K | 25, 170 | 25, 1000 | 25, 1000 | 25, 70 |
| 840 K → 500 K | — | — | — | 25, 70 |
We note that during the temperature scaling runs of the interstitial, defect diffusion occurs within the simulation timescale. This migration, which arises from the shape of the potential energy surface, contributes to the anharmonic free energy through the sampling of intermediate structures during site hopping. We expect that their contribution is small as the defects spend more time around their local minima configurations.
Finally, calculating the temperature dependence of the free energy for tellurium is slightly more challenging since it melts at 722 K.123 Accordingly, we performed two TI simulations:81 (i) Einstein crystal (100 K) → anharmonic crystal (100 K) → anharmonic crystal (840 K) and (ii) Uhlenbeck–Ford model (840 K) → liquid Te (840 K) → liquid Te (500 K). By comparing the free energies from both simulations, we determined the phase transition temperature and the variation of the free energy with temperature (ESI Fig. S19†). The calculated phase transition temperature is 704 K, which is in good agreement with the experimentally reported value of 722 K.123
4.11 Molecular dynamics
To model the behaviour of the defects at room temperature, we performed NPT molecular dynamics with LAMMPS121 using both a 65-atom (a = 13 Å) and 513-atom cubic supercells (a = 26 Å) to properly capture the dynamics and diffusion of the interstitial. The Nosé–Hoover thermostat and barostat were used (1 atm, 300 K and timestep of 2 fs) with equilibration and production times of 300 ps and 1 ns, respectively. These trajectories were analysed with Python using tools from the ase,124 pymatgen-analysis-defects,125,126 pymatgen,127–129 dscribe,130,131 umap,132 direct,133 matplotlib,134 and seaborn135 packages, and visualised with Ovito136 and CrystalMaker.137The energy barriers for the changes in configuration, orientation and position of Te+1i were calculated with the Nudged Elastic Band method,138,139 as implemented in ase.124 The associated rates for these processes were calculated using Transition State Theory (e.g. k(T) = ν![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eb/(kBT)) and approximating the attempt frequency ν by the curvature of the PES at the initial state. The reaction pathways between defect configurations were represented in one dimension using a generalised mass-weighted displacement coordinate Q, calculated using
exp(−Eb/(kBT)) and approximating the attempt frequency ν by the curvature of the PES at the initial state. The reaction pathways between defect configurations were represented in one dimension using a generalised mass-weighted displacement coordinate Q, calculated using
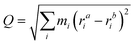 | (17) |
Data availability
The datasets and trained models are available from the Zenodo repository https://zenodo.org/records/15224961 (DOI: https://doi.org/10.1039/d4sc08582e).Author contributions
Conceptualisation & project administration: A. W., I. M.-L. Investigation, methodology and formal analysis: I. M.-L. Supervision: A. W. Writing – original draft: I. M.-L. Writing – review & editing: all authors. Resources and funding acquisition: A. W. These author contributions are defined according to the CRediT contributor roles taxonomy.Conflicts of interest
The authors declare no competing interests.Acknowledgements
We thank Seán R. Kavanagh for suggesting Te+1i as a test system and discussions regarding metastability. We also thank Venkat Kamil, Maurice de Koning, Talid Sinno, Blazej Grabowski, Sarath Menon and Luciano Colombo for useful discussions about thermodynamic integration. I. M.-L. thanks Imperial College London (ICL) for funding a President's PhD scholarship. J. K. acknowledges support from the Swedish Research Council (VR) program 2021-00486. We are grateful to the UK Materials and Molecular Modelling Hub for computational resources, which is partially funded by EPSRC (EP/P020194/1 and EP/T022213/1). This work used the ARCHER2 UK National Supercomputing Service (https://www.archer2.ac.uk) via our membership of the UK's HEC Materials Chemistry Consortium, funded by EPSRC (EP/L000202). We acknowledge the ICL High Performance Computing services for computational resources.References
- A. M. Stoneham, Theory of defects in solids, Oxford University Press, 1975 Search PubMed.
- I. Mosquera-Lois, S. R. Kavanagh, J. Klarbring, K. Tolborg and A. Walsh, Chem. Soc. Rev., 2023, 52, 5812–5826 RSC.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van De Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, npj Comput. Mater., 2023, 9, 1–11 CrossRef.
- I. Mosquera-Lois and S. R. Kavanagh, Matter, 2021, 4, 2602–2605 CrossRef.
- X. Wang, S. R. Kavanagh, D. O. Scanlon and A. Walsh, Phys. Rev. B, 2023, 108, 134102 CrossRef CAS.
- X. Wang, S. R. Kavanagh and A. Walsh, ACS Energy Lett., 2025, 10(1), 161–167 CrossRef CAS PubMed.
- X. Wang, S. R. Kavanagh, D. O. Scanlon and A. Walsh, Joule, 2024, 2105–2122 CrossRef CAS.
- A. G. Squires, L. Ganeshkumar, C. N. Savory, S. R. Kavanagh and D. O. Scanlon, ACS Energy Lett., 2024, 9, 4180–4187 CrossRef CAS PubMed.
- J.-H. Yang, L. Shi, L.-W. Wang and S.-H. Wei, Sci. Rep., 2016, 6, 21712 CrossRef CAS PubMed.
- A. Alkauskas, C. E. Dreyer, J. L. Lyons and C. G. Van de Walle, Phys. Rev. B, 2016, 93, 201304 CrossRef.
- S. R. Kavanagh, D. O. Scanlon, A. Walsh and C. Freysoldt, Faraday Discuss., 2022, 239, 339–356 RSC.
- S. R. Kavanagh, A. Walsh and D. O. Scanlon, ACS Energy Lett., 2021, 1392–1398 CrossRef CAS PubMed.
- S. R. Kavanagh, R. S. Nielsen, J. L. Hansen, R. S. Davidsen, O. Hansen, A. E. Samli, P. C. Vesborg, D. O. Scanlon and A. Walsh, Energy Environ. Sci., 2025 10.1039/D4EE04647A.
- D. Guo, C. Qiu, K. Yang and H.-X. Deng, Phys. Rev. Appl., 2021, 15, 064025 CrossRef CAS.
- W. B. Fowler, M. Stavola, A. Venzie and A. Portoff, J. Appl. Phys., 2024, 135, 170901 CrossRef CAS.
- A. S. Bochkarev, A. van Roekeghem, S. Mossa and N. Mingo, Phys. Rev. Mater., 2019, 3, 093803 CrossRef CAS.
- B. Cheng and M. Ceriotti, Phys. Rev. B, 2018, 97, 054102 CrossRef CAS.
- S. Chiesa, P. M. Derlet and S. L. Dudarev, Phys. Rev. B, 2009, 79, 214109 CrossRef.
- M. de Koning, C. R. Miranda and A. Antonelli, Phys. Rev. B, 2002, 66, 104110 CrossRef.
- M. De Koning, S. Ramos De Debiaggi and A. Monti, Defect Diffus. Forum, 2003, 224–225, 59–74 Search PubMed.
- A. Glensk, B. Grabowski, T. Hickel and J. Neugebauer, Phys. Rev. X, 2014, 4, 011018 CAS.
- B. Grabowski, L. Ismer, T. Hickel and J. Neugebauer, Phys. Rev. B, 2009, 79, 134106 CrossRef.
- G. Lucas and R. Schäublin, Nucl. Instrum. Methods Phys. Res., 2009, 267, 3009–3012 CrossRef CAS.
- J. Luo, C. Zhou, Y. Cheng, Q. Li, L. Liu, J. F. Douglas and T. Sinno, Phys. Rev. Mater., 2022, 6, 064603 CrossRef CAS.
- T. A. Mellan, A. I. Duff, B. Grabowski and M. W. Finnis, Phys. Rev. B, 2019, 100, 024303 CrossRef CAS.
- E. V. Safonova, Y. P. Mitrofanov, R. A. Konchakov, A. Y. Vinogradov, N. P. Kobelev and V. A. Khonik, J. Phys.: Condens. Matter, 2016, 28, 215401 CrossRef CAS PubMed.
- A. Satta, F. Willaime and S. de Gironcoli, Phys. Rev. B, 1998, 57, 11184–11192 CrossRef CAS.
- G. S. Smirnov and V. V. Stegailov, J. Phys.: Condens. Matter, 2019, 31, 235704 CrossRef CAS PubMed.
- D. Shin and C. Wolverton, Acta Mater., 2012, 60, 5135–5142 CrossRef CAS.
- Y. Gong, B. Grabowski, A. Glensk, F. Körmann, J. Neugebauer and R. C. Reed, Phys. Rev. B, 2018, 97, 214106 CrossRef CAS.
- D. Smirnova, S. Starikov, G. D. Leines, Y. Liang, N. Wang, M. N. Popov, I. A. Abrikosov, D. G. Sangiovanni, R. Drautz and M. Mrovec, Phys. Rev. Mater., 2020, 4, 013605 CrossRef CAS.
- X. Zhang, B. Grabowski, T. Hickel and J. Neugebauer, Comput. Mater. Sci., 2018, 148, 249–259 CrossRef CAS.
- L. Mathes, T. Gigl, M. Leitner and C. Hugenschmidt, Phys. Rev. B, 2020, 101, 134105 CrossRef CAS.
- T. Sinno, Z. K. Jiang and R. A. Brown, Appl. Phys. Lett., 1996, 68, 3028–3030 CrossRef CAS.
- O. K. Al-Mushadani and R. J. Needs, Phys. Rev. B, 2003, 68, 235205 CrossRef.
- E. Rauls and T. Frauenheim, Phys. Rev. B, 2004, 69, 155213 CrossRef.
- P. E. Blöchl, E. Smargiassi, R. Car, D. B. Laks, W. Andreoni and S. T. Pantelides, Phys. Rev. Lett., 1993, 70, 2435–2438 CrossRef PubMed.
- D. Maroudas and R. A. Brown, Phys. Rev. B, 1993, 47, 15562–15577 CrossRef CAS PubMed.
- M. I. Mendelev and Y. Mishin, Phys. Rev. B, 2009, 80, 144111 CrossRef.
- P. J. Ungar, T. Halicioglu and W. A. Tiller, Phys. Rev. B, 1994, 50, 7344–7357 CrossRef CAS PubMed.
- P. Wynblatt, J. Phys. Chem. Solids, 1969, 30, 2201–2211 CrossRef CAS.
- J. H. Harding, Physica B+C, 1985, 131, 13–26 CrossRef CAS.
- J. H. Harding and A. M. Stoneham, Philos. Mag. B, 1981, 43, 705–713 CAS.
- J. H. Harding, Phys. Rev. B, 1985, 32, 6861 CrossRef CAS PubMed.
- J. Luo, C. Zhou, Q. Li and L. Liu, J. Chem. Phys., 2022, 156, 214113 CrossRef CAS PubMed.
- J. Luo, C. Zhou, Q. Li and L. Liu, Materials, 2022, 15, 4026 CrossRef CAS PubMed.
- Y. Mishin, M. R. Sorensen and A. F. Voter, Philos. Mag. A, 2001, 81, 2591–2612 CAS.
- P. Wynblatt, Phys. Status Solidi B, 1969, 36, 797–808 CrossRef CAS.
- C. Lapointe, T. D. Swinburne, L. Proville, C. S. Becquart, N. Mousseau and M.-C. Marinica, Phys. Rev. Mater., 2022, 6, 113803 CrossRef CAS.
- P. W. M. Jacobs, J. Chem. Soc., Faraday Trans., 1990, 86, 1197–1201 RSC.
- J. Nam and R. Gómez-Bombarelli, arXiv, 2024, preprint, arXiv:2404.10746, DOI:10.48550/arXiv.2404.10746.
- S. Ramos de Debiaggi, M. de Koning and A. M. Monti, Phys. Rev. B, 2006, 73, 104103 CrossRef.
- K. M. Carling, G. Wahnström, T. R. Mattsson, N. Sandberg and G. Grimvall, Phys. Rev. B, 2003, 67, 054101 CrossRef.
- S. M. Foiles, Phys. Rev. B, 1994, 49, 14930–14938 CrossRef CAS PubMed.
- S. K. Estreicher, M. Sanati, D. West and F. Ruymgaart, Phys. Rev. B, 2004, 70, 125209 CrossRef.
- M. Sanati and S. K. Estreicher, Phys. B, 2003, 340–342, 630–636 CrossRef CAS.
- M. Sanati and S. K. Estreicher, Solid State Commun., 2003, 128, 181–185 CrossRef CAS.
- M. Sanati and S. K. Estreicher, Phys. Rev. B, 2005, 72, 165206 CrossRef.
- E. Smargiassi and R. Car, Phys. Rev. B, 1996, 53, 9760–9763 CrossRef CAS PubMed.
- C. Catlow, J. Corish, P. Jacobs and A. Lidiard, J. Phys. C:Solid State Phys., 1981, 14, L121 CrossRef CAS.
- P. Ágoston and K. Albe, Phys. Chem. Chem. Phys., 2009, 11, 3226–3232 RSC.
- T. Zacherle, P. C. Schmidt and M. Martin, Phys. Rev. B, 2013, 87, 235206 CrossRef.
- T. Smith, S. Moxon, J. S. Tse, J. M. Skelton, D. J. Cooke, L. J. Gillie, E. L. d. Silva, R. M. Harker, M. T. Storr, S. C. Parker and M. Molinari, J. Phys.: Energy, 2023, 5, 025004 Search PubMed.
- T. Zacherle, A. Schriever, R. A. De Souza and M. Martin, Phys. Rev. B, 2013, 87, 134104 CrossRef.
- A. Walsh, A. A. Sokol and C. R. A. Catlow, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 83, 224105 CrossRef.
- B. Baldassarri, J. He and C. Wolverton, Phys. Rev. Mater., 2024, 8, 055407 CrossRef CAS.
- S. L. Millican, J. M. Clary, C. B. Musgrave and S. Lany, Chem. Mater., 2022, 34, 519–528 CrossRef CAS.
- S. Moxon, J. Skelton, J. S. Tse, J. Flitcroft, A. Togo, D. J. Cooke, E. L. d. Silva, R. M. Harker, M. T. Storr, S. C. Parker and M. Molinari, J. Mater. Chem. A, 2022, 10, 1861–1875 RSC.
- Y. Sun, T. Liu, Q. Chang and C. Ma, J. Phys. Chem. Solids, 2018, 115, 228–232 CrossRef CAS.
- G. Miceli and A. Pasquarello, Phys. Rev. B, 2016, 93, 165207 CrossRef.
- S. Grieshammer, T. Zacherle and M. Martin, Phys. Chem. Chem. Phys., 2013, 15, 15935–15942 RSC.
- C. Cazorla, Phys. Rev. Appl., 2017, 7, 044025 CrossRef.
- J. M. Wynn, R. J. Needs and A. J. Morris, arXiv, 2016, preprint, arXiv:1609.04760, DOI:10.48550/arXiv.1609.04760.
- M. Youssef and B. Yildiz, Phys. Rev. B, 2012, 86, 144109 CrossRef.
- L. N. Holtzman, P. A. Vargas, R. G. Hennig and K. Barmak, J. Chem. Phys., 2024, 161, 144105 CrossRef CAS PubMed.
- A. Gorfer, R. Abart and C. Dellago, Phys. Rev. Mater., 2024, 8, 073602 CrossRef CAS.
- R. J. Tarento and J. H. Harding, J. Phys. C: Solid State Phys., 1987, 20, L677 CrossRef CAS.
- C. Zhang, F. Gygi and G. Galli, Phys. Rev. Mater., 2024, 8, 046201 CrossRef CAS.
- T. S. Bjørheim, M. Arrigoni, D. Gryaznov, E. Kotomin and J. Maier, Phys. Chem. Chem. Phys., 2015, 17, 20765–20774 RSC.
- S. Menon, Y. Lysogorskiy, J. Rogal and R. Drautz, Phys. Rev. Mater., 2021, 5, 103801 CrossRef CAS.
- V. Kapil, E. Engel, M. Rossi and M. Ceriotti, J. Chem. Theory Comput., 2019, 15, 5845–5857 CrossRef CAS PubMed.
- I. Batatia, D. P. Kovacs, G. Simm, C. Ortner and G. Csanyi, Adv. Neural Inf. Process. Syst., 2022, 35, 11423–11436 Search PubMed.
- W. K. Metzger, S. Grover, D. Lu, E. Colegrove, J. Moseley, C. L. Perkins, X. Li, R. Mallick, W. Zhang, R. Malik, J. Kephart, C.-S. Jiang, D. Kuciauskas, D. S. Albin, M. M. Al-Jassim, G. Xiong and M. Gloeckler, Nat. Energy, 2019, 4, 837–845 CrossRef CAS.
- I. Mosquera-Lois, S. R. Kavanagh, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2022, 7, 4817 CrossRef.
- A. Togo, L. Chaput, T. Tadano and I. Tanaka, J. Phys.:Condens. Matter, 2023, 35, 353001 CrossRef CAS PubMed.
- F. Knoop, T. A. R. Purcell, M. Scheffler and C. Carbogno, Phys. Rev. Mater., 2020, 4, 083809 CrossRef CAS.
- M. Choi, F. Oba, Y. Kumagai and I. Tanaka, Adv. Mater., 2013, 25, 86–90 CrossRef CAS PubMed.
- J. Park, B. Xu, J. Pan, D. Zhang, S. Lany, X. Liu, J. Luo and Y. Qi, npj Comput. Mater., 2023, 9, 1–13 CrossRef.
- I. Mosquera-Lois, S. R. Kavanagh, A. M. Ganose and A. Walsh, npj Comput. Mater., 2024, 10, 1–9 CrossRef.
- L. D. Whalley, J. Phys. Chem. C, 2023, 127, 15738–15746 CrossRef CAS.
- S. R. Kavanagh, A. G. Squires, A. Nicolson, I. Mosquera-Lois, A. M. Ganose, B. Zhu, K. Brlec, A. Walsh and D. O. Scanlon, J. Open Source Softw., 2024, 9, 6433 CrossRef.
- S. S. Naghavi, A. A. Emery, H. A. Hansen, F. Zhou, V. Ozolins and C. Wolverton, Nat. Commun., 2017, 8, 285 CrossRef PubMed.
- D. Sikstrom and V. Thangadurai, Ionics, 2024, 1, 1 Search PubMed.
- J. Gao, G. Tian, A. Sorniotti, A. E. Karci and R. Di Palo, Appl. Therm. Eng., 2019, 147, 177–187 CrossRef CAS.
- X. Zhong, F. Höfling and T. John, Geochem., Geophys., Geosyst., 2025, 26, e2024GC011951 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B, 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Hafner, Phys. Rev. B, 1994, 49, 14251–14269 CrossRef CAS PubMed.
- J. M. Skelton, D. Tiana, S. C. Parker, A. Togo, I. Tanaka and A. Walsh, J. Chem. Phys., 2015, 143, 064710 CrossRef PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- R. Jinnouchi, K. Miwa, F. Karsai, G. Kresse and R. Asahi, J. Phys. Chem. Lett., 2020, 11, 6946–6955 CrossRef CAS PubMed.
- P. Liu, C. Verdi, F. Karsai and G. Kresse, Phys. Rev. B, 2022, 105, L060102 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- J. Akola, R. O. Jones, S. Kohara, T. Usuki and E. Bychkov, Phys. Rev. B, 2010, 81, 094202 CrossRef.
- J. F. Ziegler and J. P. Biersack, in The Stopping and Range of Ions in Matter, ed. D. A. Bromley, Springer US, Boston, MA, 1985, pp. 93–129 Search PubMed.
- J. D. Morrow, J. L. A. Gardner and V. L. Deringer, J. Chem. Phys., 2023, 158, 121501 CrossRef CAS PubMed.
- Y. Kumagai and F. Oba, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 195205 CrossRef.
- O. Eriksson, J. M. Wills and D. Wallace, Phys. Rev. B, 1992, 46, 5221–5228 CrossRef CAS PubMed.
- X. Zhang, B. Grabowski, F. Körmann, C. Freysoldt and J. Neugebauer, Phys. Rev. B, 2017, 95, 165126 CrossRef.
- A. Metsue, A. Oudriss, J. Bouhattate and X. Feaugas, J. Chem. Phys., 2014, 140, 104705 CrossRef PubMed.
- F. Willaime, A. Satta, M. Nastar and O. Le Bacq, Int. J. Quantum Chem., 2000, 77, 927–939 CrossRef CAS.
- A. G. Squires, D. O. Scanlon and B. J. Morgan, J. Open Source Softw., 2023, 8, 4962 CrossRef.
- J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329–342 CrossRef CAS.
- A. H. M. Smets, K. Jäger, O. Isabella, R. A. v. Swaaij and M. Zeman, Solar energy : the physics and engineering of photovoltaic conversion, technologies and systems, UIT Cambridge Ltd, Cambridge, England, 2016 Search PubMed.
- S. Lany, J. Chem. Phys., 2018, 148, 071101 CrossRef PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- R. Freitas, M. Asta and M. de Koning, Comput. Mater. Sci., 2016, 112, 333–341 CrossRef CAS.
- F. C. Kracek, J. Am. Chem. Soc., 1941, 63, 1989–1990 CrossRef CAS.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, World J. Condens. Matter Phys., 2017, 29, 273002 CrossRef PubMed.
- J.-X. Shen and J. Varley, J. Open Source Softw., 2024, 9, 5941 CrossRef.
- J.-X. Shen, L. F. Voss and J. B. Varley, J. Appl. Phys., 2024, 135, 145102 CrossRef CAS.
- S. P. Ong, W. D. Richards, A. Jain, G. Hautier, M. Kocher, S. Cholia, D. Gunter, V. L. Chevrier, K. A. Persson and G. Ceder, Comput. Mater. Sci., 2013, 68, 314–319 CrossRef CAS.
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- S. P. Ong, S. Cholia, A. Jain, M. Brafman, D. Gunter, G. Ceder and K. A. Persson, Comput. Mater. Sci., 2015, 97, 209–215 CrossRef.
- L. Himanen, M. O. J. Jäger, E. V. Morooka, F. Federici Canova, Y. S. Ranawat, D. Z. Gao, P. Rinke and A. S. Foster, Comput. Phys. Commun., 2020, 247, 106949 CrossRef CAS.
- J. Laakso, L. Himanen, H. Homm, E. V. Morooka, M. O. Jäger, M. Todorović and P. Rinke, J. Chem. Phys., 2023, 158, 234802 CrossRef CAS PubMed.
- L. McInnes, J. Healy, N. Saul and L. Großberger, J. Open Source Softw., 2018, 3, 861 CrossRef.
- J. Qi, T. W. Ko, B. C. Wood, T. A. Pham and S. P. Ong, npj Comput. Mater., 2024, 10, 43 CrossRef.
- J. D. Hunter, Comput. Sci. Eng., 2007, 9, 90–95 Search PubMed.
- M. L. Waskom, J. Open Source Softw., 2021,(6), 3021 CrossRef.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- CrystalMaker®: a crystal and molecular structures program for Mac and Windows. CrystalMaker Software Ltd, Oxford, England (https://www.crystalmaker.com Search PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- F. Knoop, T. A. R. Purcell, M. Scheffler and C. Carbogno, J. Open Source Softw., 2020, 5, 2671 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc08582e |
| ‡ This mixing entropy arises from the different ways in which a defect can be arbitrarily placed at the symmetry-equivalent lattice sites and depends on the equilibrium defect concentration. Due to this dependence on c, it is separated from the free energy of forming the defect at a fixed site (gf, which is independent of c within the dilute limit) when deriving the expression for the defect concentration.2 |
| This journal is © The Royal Society of Chemistry 2025 |

