Open Access Article
Open Access ArticleSignatures of the quantum spin liquid state in triangular-based zig-zag polyaromatic hydrocarbon radicals†
Yongbing
Shen
 *a,
Mengxing
Cui
b,
Haitao
Zhang
b,
Hanjie
Guo
*a,
Mengxing
Cui
b,
Haitao
Zhang
b,
Hanjie
Guo
 c,
Jumpei G.
Nakamura
c,
Jumpei G.
Nakamura
 d,
Jan Peter
Embs
d,
Jan Peter
Embs
 e,
Jinkui
Zhao
cfg,
Masahiro
Yamashita
e,
Jinkui
Zhao
cfg,
Masahiro
Yamashita
 *bh and
Zhendong
Fu
*c
*bh and
Zhendong
Fu
*c
aDepartment of Chemistry, School of Science, The University of Tokyo, 7-3-1 Hongo, Bunkyo-ku, Tokyo, 113-0033, Japan. E-mail: shenyongbing17@gmail.com
bSchool of Chemical Science and Engineering, Tongji University, Siping Road 1239, Shanghai 200092, P. R. China. E-mail: yamasita.m@gmail.com
cSongshan Lake Materials Laboratory, Dongguan, Guangdong Province 523808, China. E-mail: zdfu@pku.edu.cn
dMuon Science Laboratory, Institute of Materials Structure Science, KEK, Tokai, Ibaraki 319-1106, Japan
eLaboratory for Neutron Scattering and Imaging, Paul Scherrer Institut (PSI), CH-5232 Villigen, Switzerland
fBeijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China
gSchool of Physical Sciences, Great Bay University, Dongguan 523808, China
hDepartment of Chemistry, Graduate School of Science, Tohoku University, 6-3 Aramaki-Aza-Aoba-Ku, Sendai 980-8578, Japan
First published on 6th March 2025
Abstract
Alkali-metal doped polyaromatic hydrocarbons (PAHs) have shown great potential in realizing exotic states of matter such as quantum spin liquids (QSLs). However, it is challenging to obtain new pure-phase candidates and perform experimental identifications accordingly. Here, we report the discovery and characterization of Cs(chrysene˙−)(THF)0.5·(THF)0.25 (1, THF = tetrahydrofuran), a pure-phase spin-½ organic magnet composed of triangular-based zig-zag magnetic layers, which give rise to strong spin frustration. Electron paramagnetic resonance and optical analyses show 1 is a Mott insulator. Despite the strong antiferromagnetic coupling, low-temperature specific heat and ac susceptibility demonstrate the absence of both long-range magnetic order and spin-glass phases down to 55 mK. Magnetic specific heat can be fitted to the power law, implying gapless spin excitation. Muon spin relaxation reveals constant spin fluctuation rates, suggesting persistent slow dynamics down to 0.3 K. Our results highlight PAHs as a promising avenue for exploring new QSLs.
Introduction
Quantum spin liquid (QSL) is a novel state of matter with neither long-range magnetic order (LRMO) nor spontaneous symmetry breaking of the crystal or magnetic lattice, where the spins persist in liquid-like disordered states even at absolute zero temperature.1–4 P. W. Anderson first proposed a resonating valence bond (RVB) model, where antiparallel spin pairs form spin singlets with zero total spin.5,6 The ground state of a QSL is a linear superposition of all possible singlets due to strong quantum fluctuations, showing high spin degeneracy.7 These features are similar to the Cooper pairs in conventional superconductivity and hold significant potential for advanced quantum technologies, such as quantum computing.8,9 Intensive investigations have been conducted to discover new QSL candidates with unique lattice topologies. Different kinds of organic and inorganic QSL candidates have been found so far, such as κ-(BEDT-TTF)2Cu2(CN)3 (ref. 10) and YbMgGaO4 (ref. 11) with two-dimensional (2D) triangular lattices, ZnCu3(OH)6Cl2 (ref. 12) and Cu3(HHTP)2 (ref. 13) with 2D kagome lattices, α-RuCl3 (ref. 14) and (NEt4)2[Co2(X2dhbq)3]15 with honeycomb lattices, and Yb2Ti2O7 (ref. 16) and Ce2Zr2O7 (ref. 17) with 3D pyrochlore lattices. Besides these simple idealized lattices, the QSL behavior can also be compatible with complex frustration mechanisms on distorted lattices. For example, the isotropic magnet Ca10Cr7O28 possesses several different ferromagnetic and antiferromagnetic interactions together with distorted kagome bilayers of Cr5+ ions, and still displays all the experimental features expected from a QSL magnet.18,19Despite that some promising QSL candidates have been reported, synthesizing and identifying QSLs experimentally remains challenging. For instance, the 2D spin-½ triangular QSL candidates, YbMgGaO4 and YbZnGaO4,20–24 might actually have spin-glass phases in their ground states due to Mg–Ga disorder.25–27 As for the well-known 2D triangular organic QSL candidates, κ-(BEDT-TTF)2Cu2(CN)3 and EtMe3Sb[Pd(dmit)2]2, whether itinerant spinons exist has been in dispute. The debate underlines the possible sample dependence in experimental characterization.28–32
Through effective crystal-engineering strategies, recent studies have identified metal–organic cooperative compounds as promising QSL candidates.15,33,34 In this context, polycyclic aromatic hydrocarbons (PAHs) with their unique packing preference via alkali intercalation turn out to be good playgrounds to search for new compounds hosting QSL states. PAHs are organic molecules composed of fused benzene rings and can crystallize into architectures with low-dimensionality and geometric frustration effects. However, the search for PAH-based QSL compounds has been largely impeded by the difficulty in obtaining pure-phase samples with good crystallinity because controlling the reaction of PAHs and alkali metals at high temperature is very hard. Recently, significant advances have been made by using a solution-based route under mild conditions, which prevent the PAH molecules from competing decomposition in the alkali reduction at high temperature. For instance, two binary cesium salts of phenanthrene, Cs(C14H10) and Cs2(C14H10), were isolated via the reaction of Cs and phenanthrene in tetrahydrofuran (THF) solution.35 Whereas Cs2(C14H10) is diamagnetic because of orbital polarization, Cs(C14H10) is a Heisenberg antiferromagnet with a gapped QSL state originating from a highly frustrated 3D spin topology of unequal-leg spin chains and distorted corner-sharing spin triangles. The reduction of triphenylene with potassium in 1,2-dimethoxyethane (DME) solution successfully yields single-phase K2(C18H12)2(DME) solids.36 Despite its strikingly strong nearest neighbor antiferromagnetic interactions, K2(C18H12)2(DME) shows no long-range magnetic order and resembles a gapped QSL state. The experimental identification of QSL states generally calls for a combination of macroscopic and microscopic techniques performed at ultralow temperatures down to a few tens of mK, which poses a great challenge.7 However, spin excitation and dynamics at ultralow temperatures, the key aspect of the QSL state, still remains unexplored in the alkali-doped PAH QSL candidates.
Here we report the experimental synthesis and characterization of a new alkali-intercalated PAH solid, Cs(chrysene˙−)(THF)0.5·(THF)0.25 (1), which is a Mott insulator. The S = 1/2 chrysene˙− radical anions are strongly antiferromagnetically coupled and form a novel triangular-based zig-zag magnetic structure. No LRMO is established down to 55 mK. The QSL-like behavior, originating from strong spin frustration, is probed using various characterization methods. This work highlights the importance of PAH molecules in the exploration of new QSL candidates.
Experimental
Synthetic procedures
Chrysene, cesium, dry THF, and dry n-hexane were purchased commercially and used as received. The glassware was used before being dried overnight. All reactions and treatments were performed in an argon-filled glovebox (the H2O and O2 levels are less than 1 ppm) or glassware with internal gas conditions. 1 mmol chrysene (228 mg), 1 mmol Cs (133 mg), and 10 mL dry THF were charged into a 50 mL vessel. The resulting mixture was sonicated for 4 hours and stirred for 24 hours at 50 °C. After cooling, the solution was filtered and layered with 30 mL of dry n-hexane for crystallization. Dark Olive crystals were obtained after 1 month by filtration. The crystals were washed with n-hexane and dried in a glove box. The yield was 46.7% based on chrysene.X-ray crystallography
Single-crystal X-ray crystallographic data were collected at 90 K on a Rigaku Saturn70 CCD Diffractometer (Rigaku, Tokyo, Japan) with graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) produced by a VariMax microfocus X-ray rotating anode source. Data processing was performed using the CrysAlisPro1.171.40.67a software. The structures were solved by using direct methods included in SHELXT2018/2 SIR-92,37 and refinement was carried out using SHELXL2018/3.38 The non-H atoms were refined anisotropically using weighted full-matrix least squares, and H atoms attached to the C atoms were positioned using idealized geometries and refined using a riding model. CCDC 2207133 contains the supplementary crystallographic data for this paper. These data can be obtained free of charge viahttps://www.ccdc.cam.ac.uk/conts/retrieving.html (or from the Cambridge Crystallographic Data Centre, 12 Union Road, Cambridge CB21EZ, UK; fax: (+44)1223-336-033; or E-mail: deposit@ccdc.cam.ac.uk). The Rietveld refinement of the powder XRD data was performed by using the Fullprof suite.39Spectroscopic measurements
The UV-vis-IR spectrum was acquired in the solid state as KBr pellets on a Shimadzu UV-3100pc (Shimadzu, Kyoto, Japan) and an FT-IR-6200YMS infrared spectrometer (JASCO, Tokyo, Japan) at room temperature. Raman spectroscopy was performed on single crystals using a Micro Laser Raman Spectrometer LabRam H-800 at an excitation of 532 nm at room temperature. EPR spectra were acquired by using a Bruker EMXplus spectrometer system from 5 to 300 K on the powder sample.DC and AC susceptibility measurements
DC magnetic susceptibility measurements were conducted on polycrystalline samples using a Quantum Design SQUID magnetometer MPMS-7L. The sample was sealed in a homemade glass tube by filling it with argon gas. AC magnetic susceptibility measurements were performed on a Quantum Design physical property measurement system (PPMS Dynacool) equipped with a 3He–4He dilution refrigerator. Polycrystalline samples were glued on standard quartz sample holders. The temperature range was from 0.055 to 23 K. At each temperature, the ac magnetic susceptibility was measured with various frequencies from 17.6 to 9984.0 Hz.Heat capacity measurements
Specific heat was acquired by using a Quantum Design PPMS-Dynacool system equipped with a 3He–4He dilution refrigerator. The HCDR option was used. A small crystal of about 1 mg was attached to the sample platform with Apiezon N grease. First, the heat capacity of the sample platform, the thermometer, the heater, and the Apiezon N grease was measured as addenda. Second, the heat capacity of the sample was determined by subtracting the addenda from the total heat capacity.Muon spin relaxation measurements
Muon spin relaxation (μSR) measurements were performed using the S1 instrument ARTEMIS in MLF, J-PARC. The incoming μ+ beam was nearly 100% spin-polarized with a full width at half-maximum of 100 ns and a momentum of 27 MeV/c. A 3He cryostat was used to provide a temperature range of 0.3–26.7 K. About 0.5 g of powder sample was pressed into a pellet and sealed in a cell made of Ag foils. Then the cell was attached to an Ag plate, which was mounted in the cryostat. μSR data were analyzed using the WiMDA program.40Results and discussion
Crystal structure and charge transfer integral calculation
The compound 1 is synthesized using a Cs-chrysene-THF incorporation method (details given in the Experimental Section). The reduction of chrysene by an equivalent amount of Cs metal in THF produced a single-phase, dark olive-colored solid (Fig. S1†). A single crystal was sealed in an argon-filled borosilicate glass capillary for structural determination using single-crystal X-ray diffraction. Phase purity was first checked by comparing the experimental and simulated powder XRD patterns (Fig. S2a†). The powder XRD pattern was refined (Fig. S2b†) using Rietveld analysis based on the structural parameters obtained from single-crystal XRD analysis. The observed and calculated profiles agreed well and no additional peaks from impurity phases were detected, confirming that the sample is phase-pure.The solid crystallizes in the P![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) space group with a complicated structural arrangement (detailed structure given in Fig. S3 and Table S1†), which is completely different from pristine chrysene (C2/c). In the symmetrical structural unit shown in Fig. 1a, a central THF molecule coordinates with two Cs+ ions, and each Cs+ ion is surrounded by three chrysene radicals with significant Cs+–Cπ interactions (dotted lines in Fig. 1a). Metal-bound solvent incorporation is a common phenomenon in organometallic compounds.41 The distances between neighbouring chrysene molecules fall in the range of 3.54–3.98 Å (Fig. S3†), indicating the existence of C–H⋯π interactions. To determine the strength of the intermolecular interactions and the dimensionalities of the electronic structures, we have calculated the charge transfer (CT) integrals (t) to estimate the interactions between neighbouring chrysene units. The energy splitting in the dimer method is applied:42
space group with a complicated structural arrangement (detailed structure given in Fig. S3 and Table S1†), which is completely different from pristine chrysene (C2/c). In the symmetrical structural unit shown in Fig. 1a, a central THF molecule coordinates with two Cs+ ions, and each Cs+ ion is surrounded by three chrysene radicals with significant Cs+–Cπ interactions (dotted lines in Fig. 1a). Metal-bound solvent incorporation is a common phenomenon in organometallic compounds.41 The distances between neighbouring chrysene molecules fall in the range of 3.54–3.98 Å (Fig. S3†), indicating the existence of C–H⋯π interactions. To determine the strength of the intermolecular interactions and the dimensionalities of the electronic structures, we have calculated the charge transfer (CT) integrals (t) to estimate the interactions between neighbouring chrysene units. The energy splitting in the dimer method is applied:42
| telectron = [ε(LUMO+1) − εLUMO]/2, | (1) |
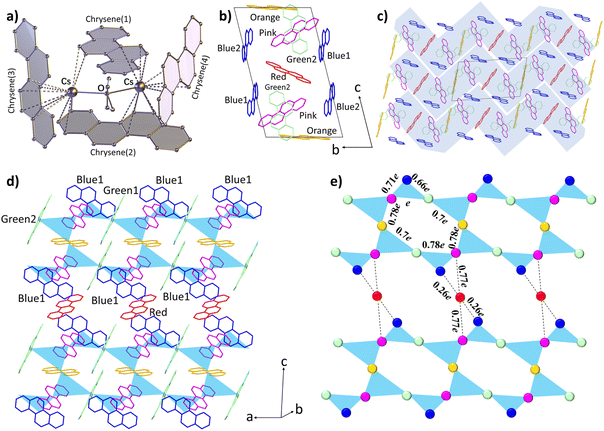 | ||
| Fig. 1 Molecular structure and crystal packing of compound 1. (a) Local structure unit of Cs2(chrysene)4(THF). The hydrogen atoms are omitted for clarity. (b) The arrangement of chrysene radicals in the unit cell. The THF molecules and Cs+ ions are omitted for clarity. (c) Stacking structure in the bc plane. Zig-zag layers are highlighted based on the charge transfer integral calculations. (d) The arrangement of chrysene molecules in a single zig-zag layer. The blue triangles represent the effective CT integrals between three nearest-neighbor chrysene radicals. (e) The diagram of the triangular-based zig-zag layer. The balls represent the chrysene spins, which are assumed at the centre of the chrysene radical. The color of the balls corresponds to those of the chrysene radicals in (d). The CT integrals (t) between chrysene radicals are summarized in Table 1. | ||
| 7 effective CT integrals (t) | |||||||
|---|---|---|---|---|---|---|---|
| Types | t(pink-green2) | t(green2-blue1) | t(blue1-pink) | t(pink-orange) | t(orange-green1) | t(green1-pink) | t(pink-red) |
| Energy (meV) | 98.9 (e) | 63.1 (0.66e) | 69.9 (0.71e) | 76.8 (0.78e) | 67.7 (0.7e) | 76.6 (0.78e) | 76.6 (0.77e) |
| 6 negligible CT integrals (t) | |||||||
|---|---|---|---|---|---|---|---|
| Types | t(blue2-red) | t(blue2-orange) | t(blue2-pink) | t(blue2-green1) | t(blue2-green2) | t(red-blue1) | — |
| Energy (meV) | 16.2 (0.16e) | 15.6 (0.16e) | 18.7 (0.19e) | 14.3 (0.14e) | 13.5 (0.14e) | 26.2 (0.26e) | — |
Spectroscopic properties
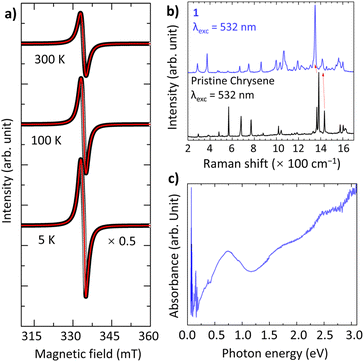
The drastic colour change in solution indicates that the CT from Cs to chrysene occurs. Solid-state electron paramagnetic resonance (EPR) spectra show a nearly ideal Lorentzian line at g = 2.0027 with linewidth ΔB = 21.3 mT at 297 K (Fig. 2a), consistent with g = 2.0023 for the organic free radical, confirming the presence of chrysene˙− radicals with a single electron fully transferred to chrysene. The g and ΔB decrease slightly to 2.0013 and 19.9 mT as the temperature decreases to 5 K. Although the spins are coupled antiferromagnetically, the EPR line at 5 K retains a Lorentzian character, indicating the spins are somehow affected by other factors, such as quantum entanglements. Remarkably, the EPR curves do not show any Dysonian line-shape asymmetry, indicating that 1 is not metallic.35 In addition, the electronic structure has been investigated by solid-state Raman and diffuse reflectance spectra. Compared to pristine chrysene, the key features of softening, splitting, and broadening provide favorable evidence for significant electron–phonon coupling in 1 (Fig. 2b).36 The red-shifting of Raman peaks, such as a 27 cm−1 shift in the skeletal ring vibration and a 19 cm−1 shift in the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C stretching vibration (Table S2†), are firm evidence of the reduction of chrysene molecules. Fig. 2c shows the diffuse reflectance spectrum, where the strong low-energy band around 0.74 eV is probably assigned to the intermolecular CT between chrysene radicals. Spectroscopic measurements imply that 1 is an insulator.
C stretching vibration (Table S2†), are firm evidence of the reduction of chrysene molecules. Fig. 2c shows the diffuse reflectance spectrum, where the strong low-energy band around 0.74 eV is probably assigned to the intermolecular CT between chrysene radicals. Spectroscopic measurements imply that 1 is an insulator.
Magnetic properties
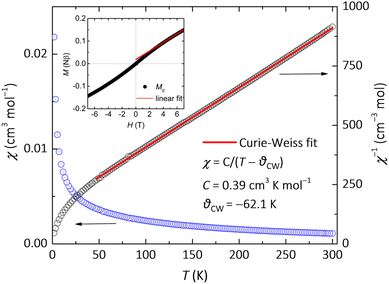
The magnetic behaviour of insulating 1 originates from the stacking of the chrysene radicals through Cs+–Cπ interactions. The dc magnetic susceptibility (χ) was measured in a field of 0.1 T and gradually increases as the sample is cooled as shown in Fig. 3. No peak or hump is observed down to 2 K, indicating the absence of LRMO or a spin-glass transition. The χ nicely follows the Curie–Weiss law between 50 and 300 K with a negative Curie–Weiss temperature θCW = −62.1 K and a Curie constant C = 0.39 cm3 K mol−1. The C value is close to the theoretical value of 0.375 for the system with free spins S = ½ and g = 2.0, indicating that the magnetic properties of 1 are derived from chrysene radicals. The negative θCW indicates dominant antiferromagnetic interactions. Here we invoke the mean-field formula, θCW = 2zS(S + 1)J/3kB, where J, z, S, and kB are the intermolecular interaction, the number of nearest-neighbour sites, the spin quantum number, and Boltzmann's constant, respectively. We can estimate the intermolecular exchange constant as |J/kB| = 3 × 62.1/(2 × 4 × 0.5 × 1.5) = 31.2 K, which is close to that found for the Cs-doped phenanthrene QSL candidate (J/kB= 30 K).35 The field-dependent magnetization (MH) curve at 1.8 K exhibits paramagnetic behavior (insert of Fig. 3), consistent with the χ–T and ESR data. The M increases linearly below 3 T but slowly above 4 T. At 7 T, M reaches 0.149 Nβ, which is significantly lower than the fully saturated value for free radical ions. The total M can be decomposed into defect-related (Md) and intrinsic Mi contributions, expressed as M = Md + Mi. At low fields (H < 3 T), the intrinsic component follows Mi = χH. The red dashed line represents a linear fit for H > 4 T, with a y-intercept of 0.018 Nβ and a slope of 0.0000195 Nβ.Low-temperature heat capacity
For a QSL, the origin of spin frustration is the competition of several magnetic exchange interactions that cannot be satisfied simultaneously. We expect spin frustration in 1 since the chrysene radicals form corner-sharing triangles with antiferromagnetically coupled spins in the zig-zag layers (Fig. 1e). The slightly-distorted antiferromagnetic interactions on these spin triangles destabilize the magnetic order and give rise to remarkable spin frustration, potentially leading to exotic phases. To identify the low-temperature magnetic phase, the temperature dependence of the specific heat (Cp–T) has been measured under various fields between 0 and 7 T from 0.055 to 3.0 K. The Cp–T plots in Fig. 4a show no sign of sharp lambda-shaped anomalies, indicating that no LRMO occurs over the investigated temperature range. The zero-field Cp values are 29.13 mJ K−1 mol−1 at 1 K and 225.96 mJ K−1 mol−1 at 3.0 K, which are quite large for an insulating system and similar to the reported values for {[Pd(dmit)2]0.5}− and [(BEDT-TTF)0.5]+-based organic QSLs, suggesting that magnetic entropy persists at low temperatures.44,45 Therefore, the magnetic susceptibility and specific heat data show no clear sign of LRMO down to 0.055 K, indicating that 1 is highly frustrated with a frustration parameter f = |θCW|/TN larger than 1100.When a magnetic field is applied, a clear upturn in specific heat can be seen in Fig. 4a at the lowest temperatures. As discussed in the ESI (Fig. S5†), we attribute the upturn to the high-T tail of the Schottky contribution from hydrogen nuclear spins, which is expressed as Chyp = αT−2.19 Lacking a non-magnetic isostructural reference, the lattice specific heat is approximated as Clat = βT3 within the investigated T range, where magnetic specific heat dominates. The lattice contribution is independent of the applied magnetic field. At 0 T, the Cp–T curve shows a small kink at ∼0.18 K, which shifts towards higher temperatures with increasing field and finally disappears at 5 and 7 T. Thus, the kink should be of magnetic origin, which still remains unclear at this point.
The magnetic specific heat Cmag is obtained by subtracting Chyp and Clat from Cp and the log–log Cmag–T curves are shown in Fig. 4b and S6.† The Cmag–T plots are fitted with the power-law expression Cmag = γTε. The power-law behaviour persists down to 0.055 K at 0 and 1 T. In Cmag–T data for 2–7 T, the deviations from the power law below 0.2 K are due to the subtraction of the strong Chyp contributions. The Cp–T curves are fitted with the expression, Cp = Chyp + Clat + Cmag = αT−2 + βT3 + γTε. Chyp is field-dependent and is omitted from the fit to the zero-field data because it is very weak. β is found to be 5.70(10) mJ K−4 mol−1 and keeps constant in all fit. For 0–3 T, the Cmag–T curves below and above the kink temperature (Tkink) can both be fitted with power-law terms with different γ and ε parameters. The data for 5 and 7 T show no kink and can be fitted with one power-law term. The fit to the zero-field data yields ε = 0.80 (above Tkink) and 1.19 (below Tkink), close to the reported values for the QSL candidates, ZnCu3(OH)6Cl2 (ε = 0.5–1.0) and Ca10Cr7O28 (ε = 1.2).12,19 Various ε values have been discovered in QSL materials. For example, ε is found to be 1 for organic QSL candidates κ-(BEDT-TTF)2Cu2(CN)3 (ref. 46) and EtMe3Sb{Pd(dmit)2}2 (ref. 45) as strong evidence for the gapless QSL state with a spinon Fermi surface, while ε = 2 for NaYbO2 (ref. 47) and YbZn2GaO5 (ref. 48) in agreement with the expectations for 2D Dirac QSLs. ε is reported to be 0.7 for YbMgGaO4, approaching the theoretical value of 2/3 reported in the triangular Heisenberg antiferromagnetic QSL with ring exchanges.49 Although a quadratic behaviour is predicted at the mean-field level for the U(1)-Dirac spin-liquid candidate ZnCu3(OH)6Cl2, the fit to heat capacity data yields ε values ranging from 0.5 to 1, depending on the considered temperature ranges.12 It is worth noting that the exponent ε can also deviate from simple integers or fractions, especially for the QSL candidates with complex magnetic structures, such as ε = 1.2 for Ca10Cr7O28.18 Thus we have observed a quasi-linear T dependence of magnetic heat capacity, indicative of gapless excitation. The field dependence of ε (Fig. S7a†) shows an increase with increasing field as the kink shifts upwards in temperature and finally disappears above 3 T. Such field dependence of the power-law exponent ε has also been observed in QSL candidates such as YbMgGaO4 (ref. 11) and NaRuO2,50 as a result of the gradual overcoming of the low-dimensional quantum spin correlations as the field increases.
The quasi-linear T dependence of specific heat observed in compound 1 is unusual for a Mott insulator, since such a linear term is typically expected in metals where the coefficient γ is proportional to the electronic density of states occupied at the Fermi level. For compound 1, the value of γ is estimated as 20.7 (above Tkink) and 44.7 (below Tkink) mJ K−2 mol−1 at zero field, which are quite large as compared with the small γ values of disordered insulators such as bulk TiO2 (0.1 mJ K−2 mol−1).51 The γ value above Tkink is comparable to those of other organic triangular QSL systems, such as 19.9 mJ K−2 mol−1 for EtMe3Sb[Pd(dmit)2]2 and 12 mJ K−2 mol−1 for κ-(BEDT-TTF)2Cu2(CN)3,45,46 while the γ value below Tkink is twice larger. Note that in a magnetically frustrated insulator, the linear term suggests the existence of a spinon Fermi surface and the coefficient γ is considered to be proportional to the spinon density of states with widely distributed energy in QSL.46 Therefore, the kink at Tkink may reflect an unusual thermodynamic transition to a low-T phase with enhanced short-range correlations and dense low-energy excitations, but still possessing slow spin dynamics persistent below Tkink. The field dependence of γ is plotted in Fig. S7b,† where γ shows a clear decrease as the field increases from 0 to 3 T. The variation of γ with field (especially below Tkink) seems largely affected by the shift of the anomaly at Tkink. For H ≥ 5 T, the anomaly is removed and γ stabilizes at about 15 mJ K−2 mol−1, indicating that there is a constant density of low-lying states consistent with a QSL state with spinon Fermi surfaces. The decreasing γ with increasing field may indicate part of the γ obtained below 3 T is induced by the quenched disorder.52 Interestingly, disorder can be relevant in the stabilization of QSL states in organic compounds, such as the layered EDT-BCO crystals.53 By inducing randomness or inhomogeneity, QSL behaviours are observed in an organic radical-based complex Zn(hfac)2(AxB1−x), which also displays reducing γ values with increasing fields.54 On the other hand, similar field dependence of γ can also exist with neither detectable structural disorder nor crystal-electric-field randomness as observed in the triangular QSL candidate NaYbO2.55
We have tried to fit the anomaly at Tkink in zero-field data with a gapped spectral function, which is expressed as C − (ΔE/T)2exp(ΔE/T)/[1 + exp(ΔE/T)]2. We find that the upper limit for the energy gap ΔE is about 0.5 K (0.8% of θCW) and the associated entropy release is about 0.012 J K−1 mol−1 (0.2% of Rln2). Therefore, even if there was freezing of disordered spins, its excitation gap is less than ∼|θCW|/100 and the freezing happens to a very small fraction of local moments. Such anomalies in specific heat have been observed in some other polycrystalline QSL candidates as well, such as Ca10Cr7O28,18 PbCuTe2O6,56 and Cu3V2O7(OH)2·2H2O,57,58 where the anomalies are all shifted towards high temperature and finally removed as the magnetic field increases. Specifically, the magnetic heat capacity of Cu3V2O7(OH)2·2H2O also shows different power-law dependence on temperature in the range above and below Tkink.57 The phase below Tkink is also found gapless with dense low-energy excitations and very slow spin fluctuations by using heat capacity, 51V NMR, μSR and inelastic neutron scattering methods.57–59 It is interesting to notice that all these systems exhibiting similar kinks are based on distorted corner-sharing triangles. Whether or not there is some kind of hidden phase, associated with frustration, short-range spin order and quantum fluctuation on the distorted corner-sharing triangle structure, remains an interesting and open issue.
AC magnetic susceptibility
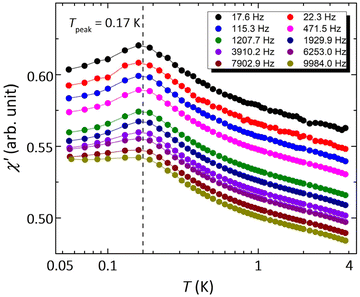
However, spin glass may also result in a linear-T dependence of Cmag and an absence of LRMO.25 When the temperature drops below the spin-glass temperature, the spins freeze into short-range ordered configurations with a broad distribution of relaxation times.60 Alternate current (AC) susceptibility is a powerful method to identify spin glass, which generally shows distinct frequency-dependent cusps at the crossover temperature where the observation time equals the relaxation time. Fig. 5 show the temperature dependence of the real component of the AC susceptibility (χ′–T) measured at various frequencies. The χ′ and χ′′ vs. T curves at higher temperatures are shown in Fig. S8.† There is a clear cusp at about 0.17 K, coinciding with Tkink–0.18 K in zero-field heat capacity data. The susceptibility χ′ decreases with temperature below the cusp, but still has a large value at 0.055 K, indicating substantial low-energy excitations. As shown by the χ′–T curves measured at various frequencies from 17.6 to 9984.0 Hz, the peak temperature of this cusp is independent of frequency, ruling out any spin freezing or spin glass transition down to 0.055 K. The AC susceptibility data indicate that 1 remains dynamic down to the lowest investigated temperatures, in spite of its relatively large antiferromagnetic interactions.Muon spin relaxation
Muon spin relaxation (μSR) is a powerful technique to clarify the static or dynamic nature of the magnetic ground state due to the sensitivity of muons to local magnetic fields. The spin-polarized positively charged muons are implanted within the sample and generally reside near negatively charged regions in the unit cell to minimize the electrostatic energy. The local magnetic fields (electronic and nuclear) strongly affect the evolution of muons, which decay into positrons emitted in the same direction of the muon spins. By measuring the time evolution of the muon spin polarization, one can tell whether the magnetic moments are ordered or fluctuating. To gain more insight into the low-T spin dynamics, we have collected zero-field (ZF) μSR data in the temperature range of 0.3–26 K.Fig. 6a shows a few representative ZF μSR spectra, evidencing a strong temperature dependence. Depolarization increases with the decreasing temperature. We observe a slow oscillation (Fig. S9†) at all investigated temperatures. Such oscillations in magnetic materials are often related to magnetic order, but it is clearly not the case because the oscillation persists up to 26.7 K where the sample is paramagnetic. Note that the coupling between a muon spin and a nearby nuclear spin can also cause such oscillations in ZF μSR spectra even in nonmagnetic or paramagnetic materials.61–63 Therefore, we attribute the oscillation to the coupling between the spin of a positive muon (S = 1/2) and the nuclear spin (I = 1/2) of a nearby hydride (H−) ion, which obtains one delocalized π electron of the chrysene˙− radical. The muon spin relaxation function for such an entangled two spin-1/2 system is described by
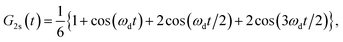 | (2) |
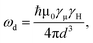 | (3) |
| A(t) = A1·G2S(t)·e−λ1t + A2·GKT(t)·e−λ2t + ABG, | (4) |
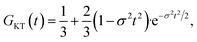 | (5) |
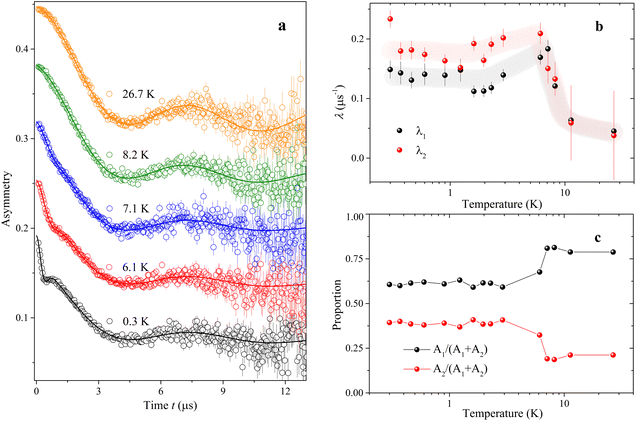 | ||
| Fig. 6 Representative zero-field μSR time spectra of compound 1. (a) Zero-field μSR time spectra measured at various temperatures from 0.3 to 26.7 K on S1, J-PARC. The solid lines are the best fits in terms of eqn (2)–(5) as described in the text. (b) Temperature dependence of λ1 and λ2 as obtained from the data fit. The light gray and the light pink lines are guide to the eye. (c) Proportions of A1 and A2 as obtained from the fit. | ||
Conclusions
The reduction of chrysene by Cs metal in THF solution produces a new QSL candidate, Cs(chrysene˙−)(THF)0.5·(THF)0.25, whose magnetic and thermodynamic properties have been studied by using spectroscopic properties, dc and ac susceptibility, heat capacity, and μSR measurements. Despite a large, negative Curie–Weiss temperature, heat capacity and ac susceptibility show no clear sign of both LRMO and spin-glass phases down to 0.055 K, implying a highly frustrated magnetic structure. The gapless low-energy excitations are evidenced by the power-law temperature dependence of magnetic specific heat and the significant magnetic susceptibility at low temperatures. The ZF μSR spectra indicate the absence of both static LRMO and spin freezing, and reveal slow and nearly T-independent spin fluctuations persistent down to 0.3 K. The origin of the kink in specific heat and ac susceptibility data is still unclear. By comparison between the literature and our results, we tentatively attribute the kink to a thermodynamic transition to an anomalous low-T phase with enhanced short-range correlations, dense low-energy excitations, and persistent spin fluctuations. Although the observed behaviours are compatible with a QSL candidate, we cannot discard the possibility that the kink represents the onset of LRMO, considering the samples used in experiments are either polycrystalline or powder. Whether the kink is related to an unknown phase in distorted corner-sharing triangular magnetic structure remains an interesting topic to explore. This work suggests that PAHs are promising in the search for exotic quantum states such as QSLs.Data availability
All data presented in this paper can be requested by contacting the corresponding authors.Author contributions
YS designed research, YS, ZF, MC, HZ, HG, JGN, and JPE performed research, YS synthesized samples, YS and ZF analysed data, MY, ZF, and JZ supervised the project, and YS and ZF wrote the manuscript with contributions from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Key R&D Program of China (Grant 2022YFA1603801), the Guangdong Basic and Applied Basic Research Foundation (Grant 2022B1515120070) and the National Natural Science Foundation of China (Grant 11875325). We thank Dr Masanori Wakizaka for the absorbance spectrum measurement. The μSR experiment at the Materials and Life Science Experimental Facility (MLF), J-PARC, was performed under the approved proposals (no. 2023B0111 and 2023B0148). The INS experiment at FOCUS, PSI, was performed under the approved proposal (No. 20230471).References
- C. Broholm, R. J. Cava, S. A. Kivelson, D. G. Nocera, M. R. Norman and T. Senthil, Science, 2020, 367, 263 CrossRef PubMed.
- L. Balents, Nature, 2010, 464, 199–208 CrossRef CAS PubMed.
- L. Savary and L. Balents, Rep. Prog. Phys., 2017, 80, 016502 CrossRef PubMed.
- Y. Zhou, K. Kanoda and T. K. Ng, Rev. Mod. Phys., 2017, 89, 025003 CrossRef.
- P. W. Anderson, Science, 1987, 235, 1196–1198 CrossRef CAS PubMed.
- P. W. Anderson, Mater. Res. Bull., 1973, 8, 153–160 CrossRef CAS.
- J. Wen, S.-L. Yu, S. Li, W. Yu and J.-X. Li, npj Quantum Mater., 2019, 4, 12 CrossRef.
- K. Yang, S. H. Phark, Y. Bae, T. Esat, P. Willke, A. Ardavan, A. J. Heinrich and C. P. Lutz, Nat. Commun., 2021, 12, 993 CrossRef CAS PubMed.
- G. Semeghini, H. Levine, A. Keesling, S. Ebadi, T. T. Wang, D. Bluvstein, R. Verresen, H. Pichler, M. Kalinowski, R. Samajdar, A. Omran, S. Sachdev, A. Vishwanath, M. Greiner, V. Vuletic and M. D. Lukin, Science, 2021, 374, 1242–1247 CrossRef CAS PubMed.
- Y. Shimizu, K. Miyagawa, K. Kanoda, M. Maesato and G. Saito, Phys. Rev. Lett., 2003, 91, 107001 CrossRef CAS PubMed.
- Y. Li, H. Liao, Z. Zhang, S. Li, F. Jin, L. Ling, L. Zhang, Y. Zou, L. Pi, Z. Yang, J. Wang, Z. Wu and Q. Zhang, Sci. Rep., 2015, 5, 16419 CrossRef CAS PubMed.
- J. S. Helton, K. Matan, M. P. Shores, E. A. Nytko, B. M. Bartlett, Y. Yoshida, Y. Takano, A. Suslov, Y. Qiu, J. H. Chung, D. G. Nocera and Y. S. Lee, Phys. Rev. Lett., 2007, 98, 107204 CrossRef CAS PubMed.
- Y. Misumi, A. Yamaguchi, Z. Zhang, T. Matsushita, N. Wada, M. Tsuchiizu and K. Awaga, J. Am. Chem. Soc., 2020, 142, 16513–16517 CrossRef CAS PubMed.
- K. Ran, J. Wang, S. Bao, Z. Cai, Y. Shangguan, Z. Ma, W. Wang, Z.-Y. Dong, P. Cermak, A. Schneidewind, S. Meng, Z. Lu, S.-L. Yu, J.-X. Li and J. Wen, Chin. Phys. Lett., 2022, 39, 027501 CrossRef CAS.
- S. Zhang, X. Yang, B. L. Wooten, R. Bag, L. Yadav, C. E. Moore, S. Parida, N. Trivedi, Y. Lu, J. P. Heremans, S. Haravifard and Y. Wu, J. Am. Chem. Soc., 2024, 146, 15061 CrossRef CAS PubMed.
- K. A. Ross, L. Savary, B. D. Gaulin and L. Balents, Phys. Rev. X, 2011, 1, 021002 Search PubMed.
- B. Gao, T. Chen, D. W. Tam, C.-L. Huang, K. Sasmal, D. T. Adroja, F. Ye, H. Cao, G. Sala, M. B. Stone, C. Baines, J. A. T. Verezhak, H. Hu, J.-H. Chung, X. Xu, S.-W. Cheong, M. Nallaiyan, S. Spagna, M. B. Maple, A. H. Nevidomskyy, E. Morosan, G. Chen and P. Dai, Nat. Phys., 2019, 15, 1052–1057 Search PubMed.
- C. Balz, B. Lake, J. Reuther, H. Luetkens, R. Schönemann, T. Herrmannsdörfer, Y. Singh, A. T. M. Nazmul Islam, E. M. Wheeler, J. A. Rodriguez-Rivera, T. Guidi, G. G. Simeoni, C. Baines and H. Ryll, Nat. Phys., 2016, 12, 942–949 Search PubMed.
- J. Sonnenschein, C. Balz, U. Tutsch, M. Lang, H. Ryll, J. A. Rodriguez-Rivera, A. T. M. Nazmul Islam, B. Lake and J. Reuther, Phys. Rev. B, 2019, 100, 174428 CrossRef CAS.
- Y. Shen, Y. D. Li, H. Wo, Y. Li, S. Shen, B. Pan, Q. Wang, H. C. Walker, P. Steffens, M. Boehm, Y. Hao, D. L. Quintero-Castro, L. W. Harriger, M. D. Frontzek, L. Hao, S. Meng, Q. Zhang, G. Chen and J. Zhao, Nature, 2016, 540, 559–562 CrossRef CAS PubMed.
- Y. Li, D. Adroja, R. I. Bewley, D. Voneshen, A. A. Tsirlin, P. Gegenwart and Q. Zhang, Phys. Rev. Lett., 2017, 118, 107202 CrossRef PubMed.
- Y. Li, G. Chen, W. Tong, L. Pi, J. Liu, Z. Yang, X. Wang and Q. Zhang, Phys. Rev. Lett., 2015, 115, 167203 CrossRef PubMed.
- M. Klanjšek, A. Zorko, R. Žitko, J. Mravlje, Z. Jagličić, P. K. Biswas, P. Prelovšek, D. Mihailovic and D. Arčon, Nat. Phys., 2017, 13, 1130–1134 Search PubMed.
- Y. Li, D. Adroja, P. K. Biswas, P. J. Baker, Q. Zhang, J. Liu, A. A. Tsirlin, P. Gegenwart and Q. Zhang, Phys. Rev. Lett., 2016, 117, 097201 CrossRef PubMed.
- Z. Ma, J. Wang, Z. Y. Dong, J. Zhang, S. Li, S. H. Zheng, Y. Yu, W. Wang, L. Che, K. Ran, S. Bao, Z. Cai, P. Cermak, A. Schneidewind, S. Yano, J. S. Gardner, X. Lu, S. L. Yu, M. Liu, S. Li, J. X. Li and J. Wen, Phys. Rev. Lett., 2018, 120, 087201 CrossRef CAS PubMed.
- Z. Zhu, P. A. Maksimov, S. R. White and A. L. Chernyshev, Phys. Rev. Lett., 2017, 119, 157201 CrossRef PubMed.
- Q. Luo, S. Hu, B. Xi, J. Zhao and X. Wang, Phys. Rev. B, 2017, 95, 165110 CrossRef.
- Y. Kurosaki, Y. Shimizu, K. Miyagawa, K. Kanoda and G. Saito, Phys. Rev. Lett., 2005, 95, 177001 Search PubMed.
- T. Furukawa, K. Kobashi, Y. Kurosaki, K. Miyagawa and K. Kanoda, Nat. Commun., 2018, 9, 307 CrossRef PubMed.
- M. Yamashita, N. Nakata, Y. Kasahara, T. Sasaki, N. Yoneyama, N. Kobayashi, S. Fujimoto, T. Shibauchi and Y. Matsuda, Nat. Phys., 2008, 5, 44–47 Search PubMed.
- Y. Xu, J. Zhang, Y. S. Li, Y. J. Yu, X. C. Hong, Q. M. Zhang and S. Y. Li, Phys. Rev. Lett., 2016, 117, 267202 CrossRef CAS PubMed.
- P. Bourgeois-Hope, F. Laliberté, E. Lefrançois, G. Grissonnanche, S. R. de Cotret, R. Gordon, S. Kitou, H. Sawa, H. Cui, R. Kato, L. Taillefer and N. Doiron-Leyraud, Phys. Rev. X, 2019, 9, 041051 CAS.
- M. G. Yamada, H. Fujita and M. Oshikawa, Phys. Rev. Lett., 2017, 119, 057207 CrossRef PubMed.
- E. Burzurí, M. J. Martínez-Pérez, C. Martí-Gastaldo, M. Evangelisti, S. Mañas-Valero, E. Coronado, J. I. Martínez, J. R. Galan-Mascaros and F. Luis, Chem. Sci., 2023, 14, 3899 RSC.
- Y. Takabayashi, M. Menelaou, H. Tamura, N. Takemori, T. Koretsune, A. Stefancic, G. Klupp, A. J. C. Buurma, Y. Nomura, R. Arita, D. Arcon, M. J. Rosseinsky and K. Prassides, Nat. Chem., 2017, 9, 635–643 CrossRef CAS PubMed.
- A. Štefančič, G. Klupp, Y. D. S. Knaflič, G. Tavčar, A. Potočnik, A. Beeby and D. Arčon, J. Phys. Chem. C, 2017, 121, 14864–14871 CrossRef.
- A. Altomare, M. C. Burla, M. Camalli, G. L. Cascarano, C. Giacovazzo, A. Guagliardi, A. G. G. Moliterni, G. Polidori and R. Spagna, J. Appl. Crystallogr., 1991, 32, 115–119 CrossRef.
- G. M. Sheldrick, Acta Crystallogr. C, 2015, 71, 3–8 CrossRef PubMed.
- J. Rodriguez-Carvajal, Phys. B Condens. Matter, 1993, 192, 55 CrossRef CAS.
- F. L. Pratt, Phys. B Condens. Matter, 2000, 289–290, 710 Search PubMed.
- A. V. Zabula and M. A. Petrukhina, Adv. Organomet. Chem., 2013, 61, 375–462 CrossRef CAS.
- E. F. Valeev, V. Coropceanu, D. A. da Silva, S. Salman and J. L. Bredas, J. Am. Chem. Soc., 2006, 128, 9882–9886 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, Jr. J. A. Montgomery, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C. 01, Wallingford, CT, 2016 Search PubMed.
- S. Yamashita, T. Yamamoto and Y. Nakazawa, Phys. B: Condens. Mat., 2010, 405, 240–243 Search PubMed.
- S. Yamashita, T. Yamamoto, Y. Nakazawa, M. Tamura and R. Kato, Nat. Commun., 2011, 2, 275 CrossRef PubMed.
- S. Yamashita, Y. Nakazawa, M. Oguni, Y. Oshima, H. Nojiri, Y. Shimizu, K. Miyagawa and K. Kanoda, Nat. Phys., 2008, 4, 459–462 Search PubMed.
- M. M. Bordelon, E. Kenney, C. Liu, T. Hogan, L. Posthuma, M. Kavand, Y. Lyu, M. Sherwin, N. P. Butch, C. Brown, M. J. Graf, L. Balents and S. D. Wilson, Nat. Phys., 2019, 15, 1058 Search PubMed.
- R. Bag, S. Xu, N. E. Sherman, L. Yadav, A. I. Kolesnikov, A. A. Podlesnyak, E. S. Choi, I. da Silva and J. E. Moore, Phys. Rev. Lett., 2024, 133, 266703 CrossRef CAS PubMed.
- J. A. M. Paddison, M. Daum, Z. Dun, G. Ehlers, Y. Liu, M. B. Stone, H. Zhou and M. Mourigal, Nat. Phys., 2017, 13, 117 Search PubMed.
- B. R. Ortiz, P. M. Sarte, A. H. Avidor, A. Hay, E. Kenney, A. I. Kolesnikov, D. M. Pajerowski, A. A. Aczel, K. M. Taddei, C. M. Brown, C. Wang, M. J. Graf, R. Seshadri, L. Balents and S. D. Wilson, Nat. Phys., 2023, 19, 943 Search PubMed.
- S. J. Smith, R. Stevens, S. Liu, G. Li, A. Navrotsky, J. B. Goates and B. F. Woodfield, Am. Mineral., 2009, 94, 236 Search PubMed.
- I. Kimchi, A. Nahum and T. Senthil, Phys. Rev. X, 2018, 8, 031028 CAS.
- P. Szirmai, C. Mézière, G. Bastien, P. Wzietek, P. Batail, E. Martino, K. Mantulnikovs, A. Pisoni, K. Riedl, S. Cottrell, C. Baines, L. Forró and B. Náfrádi, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 29555 CrossRef CAS PubMed.
- H. Yamaguchi, M. Okada, Y. Kono, S. Kittaka, T. Sakakibara, T. Okabe, Y. Iwasaki and Y. Hosokoshi, Sci. Rep., 2017, 7, 16144 Search PubMed.
- L. Ding, P. Manuel, S. Bachus, F. Grußler, P. Gegenwart, J. Singleton, R. D. Johnson, H. C. Walker, D. T. Adroja, A. D. Hillier and A. A. Tsirlin, Phys. Rev. B, 2019, 100, 144432 CrossRef CAS.
- B. Koteswararao, R. Kumar, P. Khuntia, S. Bhowal, S. K. Panda, M. R. Rahman, A. V. Mahajan, I. Dasgupta, M. Baenitz, K. H. Kim and F. C. Chou, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 035141 CrossRef CAS.
- S. Yamashita, T. Moriura, Y. Nakazawa, H. Yoshida, Y. Okamoto and Z. Hiroi, J. Phys. Soc. Jpn., 2010, 79, 083710 CrossRef.
- H. Yoshida, Y. Okamoto, T. Tayama, T. Sakakibara, M. Tokunaga, A. Matsuo, Y. Narumi, K. Kindo, M. Yoshida, M. Takigawa and Z. Hiroi, J. Phys. Soc. Jpn., 2009, 78, 043704 CrossRef.
- M. Yoshida, M. Takigawa, H. Yoshida, Y. Okamoto and Z. Hiroi, Phys. Rev. Lett., 2009, 103, 077207 CrossRef CAS PubMed.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, Taylor and Francis, 1993 Search PubMed.
- J. H. Brewer, S. R. Kreitzman, D. R. Noakes, E. J. Ansaldo, D. R. Harshman and R. Keitel, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 7813 CrossRef CAS PubMed.
- J. S. Lord, S. P. Cottrell and W. G. Williams, Phys. B Condens. Matter, 2000, 289–290, 495–498 CrossRef.
- P. Mendels, F. Bert, M. A. de Vries, A. Olariu, A. Harrison, F. Duc, J. C. Trombe, J. S. Lord, A. Amato and C. Baines, Phys. Rev. Lett., 2007, 98, 077204 CrossRef CAS PubMed.
- R. Kubo, Hyperfine Interact., 1981, 8, 731–738 CrossRef CAS.
- T. U. Ito, A. Koda, K. Shimomura, W. Higemoto, T. Matsuzaki, Y. Kobayashi and H. Kageyama, Phys. Rev. B, 2017, 95, 020301 CrossRef.
- R. Sarkar, Ph. Schlender, V. Grinenko, E. Haeussler, P. J. Baker, Th. Doert and H.-H. Klauss, Phys. Rev. B, 2019, 100, 241116 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2207133. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc08462d |
| This journal is © The Royal Society of Chemistry 2025 |