Switchable colossal anisotropic thermal expansion in a spin crossover framework

Abstract

Advanced materials with tunable thermal expansion properties have garnered significant attention due to their potential applications in thermomechanical sensing and resistance to thermal stress. Here, switchable colossal anisotropic thermal expansion (ATE) behaviors are realized in a Hofmann-type framework [Fe(bpy-NH₂){Au(CN)₂}₂]·ⁱPrOH (Fe·ⁱPrOH, bpy-NH₂ = [4,4′-bipyridin]-3-amine) through a three-in-one strategy: a vibrational mechanism, an electronic mechanism and molecular motion. Spin crossover (SCO) centers coordinate with dicyanoaurate linkers to form flexible wine-rack frameworks, which exhibit structural deformations driven by host–guest interactions with ⁱPrOH molecules. By means of the vibrational mechanism, a scissor-like motion driven by the rotation of dicyanoaurate is observed within the rhombic grids, resulting in the emergence of colossal ATE in the high temperature region. When the spin transition comes into play, the electronic mechanism is predominant to form reverse ATE behavior, which is associated with host–guest cooperation involving significant molecular motion of the ⁱPrOH guest and adaptive deformation of the host clathrate. A remarkably high negative thermal expansion coefficient up to −7.49 × 10⁵ M K⁻¹ accompanied by abrupt SCO behavior is observed. As a proof of concept, this study provides a novel perspective for designing dynamic crystal materials with tunable thermomechanical properties by integrating various ATE-related elements into a unified platform.

---

Introduction

Thermal expansion, referring to the changes in size with response to temperature fluctuations, is an inherent characteristic of matter. Due to the increasing atomic vibrations upon heating, crystalline materials commonly experience modest positive thermal expansions (PTEs) with thermal expansion coefficients (α) less than 20 M K⁻¹ along all principal axes.¹ In rare cases, materials can demonstrate anisotropic thermal expansion (ATE) in the lattice where expansion occurs in one direction while contraction takes place in another.^2–6 Unusual thermal expansions, such as colossal ATE (α > 100 M K⁻¹), have emerged as a hot topic in solid-state chemistry and functional materials for their potential applications in thermomechanical sensing and resistance against thermal stress.^4,7–11

Chemical diversity enables versatile crystal engineering strategies for the design of materials exhibiting colossal ATE. As shown in Fig. 1a, flexible structures (cyanides,^2,12–14 metal oxides/fluorides,^15–17 metal–organic frameworks^18–20etc.) featuring wine-rack or hinge-like scaffolds can facilitate ATE via a vibrational mechanism involving transverse vibrational displacement of bridging atoms.²¹ In addition, the couplings of geometric deformations in lattices and phase transitions (such as spin crossover (SCO),^22–24 charge transfer^25,26 and electric polarization^27,28) can significantly enhance ATE performance within a narrow temperature window through the electronic mechanism (Fig. 1b). Besides, considerable ATE behavior can also be induced by collective rotation/reorientation in dynamic molecular crystals (Fig. 1c).^11,29–31 However, the efficacy of this strategy is limited since molecular motions are always constrained by intermolecular interactions and steric hindrance in crystalline materials.

Fig. 1 Schematics of ATE regimes. (a) ATE via the vibrational mechanism in a wine-rack framework; (b) ATE via the electronic mechanism in an SCO complex; (c) ATE via collective motion in a dynamic molecular crystal; (d) three-in-one strategy for switchable ATE in this work.

Advanced materials with tunable thermal expansion capabilities are of great interest for high-tech scenarios. However, delicate design of ATE structures and efficient control of lattice deformations are still challenging.^32–36 By integrating multiple potential ATE-involving elements (e.g., flexible structures, phase transitions, molecular motion, etc.) into a unified crystalline material, switchable thermomechanical properties can potentially be manipulated via both vibrational and electronic mechanisms. Herein, a Hofmann-type framework [Fe(bpy-NH₂){Au(CN)₂}₂]·ⁱPrOH (Fe·ⁱPrOH, bpy-NH₂ = [4,4′-bipyridin]-3-amine) was constructed by a three-in-one strategy: a vibrational mechanism, an electronic mechanism and molecular motion (Fig. 1d). Specifically, spin crossover centers are assembled with cyanometallate linkers to form the flexible wine-rack framework, while ⁱPrOH molecules are incorporated into the lattice and exhibit deformation driven by host–guest synergy. In the high temperature region, flexing motions within rhombic grids are dominated by the vibrational mechanism, leading to a linear ATE phenomenon. During SCO at lower temperature, reverse ATE is induced by the electronic mechanism, where the host framework and ⁱPrOH guest undergo adaptive deformations in response to variations in internal stress. Note that the reorientation of ⁱPrOH molecules plays an important role in modulating the SCO/ATE kinetics; in turn, the structural transformations caused by spin transition facilitate molecular motions in the lattice.

Results and discussion

Synthesis and structural characterization

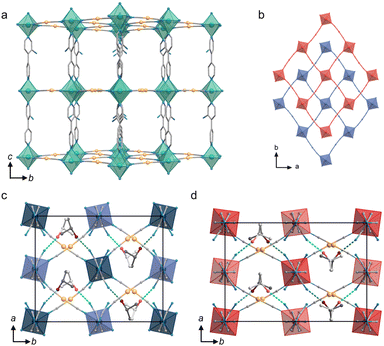
Fe·ⁱPrOH was prepared stoichiometrically via slow diffusion of KAu(CN)₂ and bpy-NH₂ ligands into Fe(ClO₄)₂·6H₂O in a ⁱPrOH/H₂O mixture. Single crystal X-ray diffraction (SC-XRD) measurements indicated that Fe·ⁱPrOH crystalizes in an orthorhombic Ibca space group (Table S1†). The asymmetric unit contains only one half of the formula. A C₂ rotation axis along the c-axis is present within the bpy-NH₂ ligand, where the amino group displays positional disorder with an occupation ratio of 1 : 1. Additionally, the ⁱPrOH guest molecule is associated with a C₂ rotation axis along the b-axis and exhibits two-fold disorder with an occupation ratio of 1 : 1 at all measured temperatures (Fig. S1†). As shown in Fig. 2a, each Fe^II ion equatorially coordinates to four [Au(CN)₂]⁻ linkers in the ab-plane to form an [Fe{Au(CN)₂}₂]_n layer. The almost-linear Fe–NC–Au–CN–Fe linkages lie parallel to the crystallographic 〈1̄10〉 and 〈1̄1̄0〉 directions. The adjacent heterometallic cyanido-bridged layers are connected by bpy-NH₂ ligands along the c-axis, giving rise to a sub-lattice framework with pcu topology. The potential pores of this framework enable double interpenetration of identical frameworks which are related to each other by weak aurophilic interactions (Fig. 2b). The pore space for each formula unit is occupied by one two-fold disordered ⁱPrOH molecule which interacts with the interpenetrating skeletons with H-bonding.

Fig. 2 The perspective view (a) and double interpenetration (b) of the Fe·ⁱPrOH framework. The lattice conformation of Fe·ⁱPrOH at 100 K (c) and 298 K (d) viewed along the c-axis. The two-fold disordered ⁱPrOH molecules are marked in distinct shades of color and the green dashed lines stand for the host–guest H-bonding interactions. The black boxes indicate the unit cell dimensions. Hydrogen atoms are omitted for clarity.

Variable temperature SC-XRD measurements reveal structural evolution of Fe·ⁱPrOH. Typically, the average Fe–N bond length alters from 2.167(4) Å at 298 K to 1.948(5) Å at 100 K, hinting at the spin transition from HS to LS states (Table S4†). Accordingly, the unit cell volume decreases by 6.5% with colossal anisotropic thermal expansion (Δa = −0.834 Å, Δb = 1.637 Å, and Δc = 0.776 Å). The decline in the c axis can be attributed to the shrinkage of Fe–N_py bonds mediated by rigid bpy-NH₂ pillars. By contrast, the thermal variations in the ab-plane are due to scissor-like motion of the flexible [Fe{Au(CN)₂}₂]_n layer (Fig. 2c and d). Amid the spin transition from HS to LS, massive strain accumulated due to the significant contraction in the b direction must be compensated for by negative thermal expansion along the a-axis to ensure the structural integrity. This situation is also accompanied by the reorientations of [Au(CN)₂]⁻ linkers and ⁱPrOH molecules. The Fe1–N1≡C1/Fe1–C2≡N2 angles change from 171.0°/160.8° at 298 K to 177.4°/169.4° at 100 K (Table S4†). On the other hand, ⁱPrOH undergoes an adaptive molecular rotation and deformation to match the more condensed packing with enhanced H-bonding interactions.

Anisotropic thermal expansion and SCO behavior

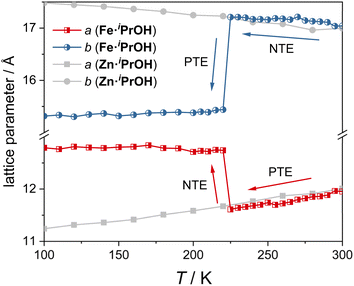
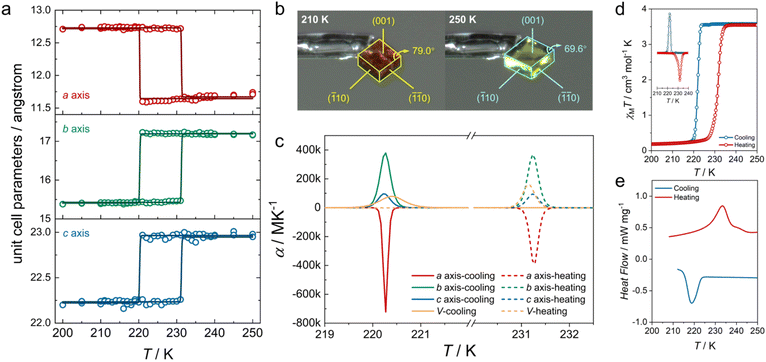
To investigate the ATE behavior in Fe·ⁱPrOH, temperature-dependent unit cell parameters are monitored at 100–300 K (Fig. 3). Within the temperature range of 225–300 K, the a-axis and b-axis of Fe·ⁱPrOH exhibit nearly linear PTE and NTE, respectively, with coefficients of thermal expansion (CTEs) calculated to be α_a = 463(14) M K⁻¹ and α_b = −166(14) M K⁻¹ using the PASCal web tool^37,38 (Fig. S32 and Table S8†). This ATE can be well described by the vibrational mechanism commonly reported in wine-rack framework materials. Further proof comes from the Zn-analogue (Zn·ⁱPrOH) wherein the a-axis and b-axis undergo similar PTE and NTE in the same temperature range. The CTEs for Zn·ⁱPrOH are α_a = 337(8) M K⁻¹ and α_b = −157(9) M K⁻¹ (Table S11†), comparable to those observed in Ag₃[Co(CN)₆]² and KMn[Ag(CN)₂]₃.¹³ At around 225 K, the ATE of the a-axis and b-axis switches to NTE and PTE owing to the abrupt spin transition. Below 220 K, thermal expansion behavior is imperceptible in Fe·ⁱPrOH, which is due to the closer packing and the void-free structure in the LS state (Fig. S37 and Table S10†). In contrast, the linear ATE is maintained over the whole temperature range in Zn·ⁱPrOH due to the absence of SCO capability.

Fig. 3 Temperature-dependent unit cell vectors (a-axis and b-axis) in Fe·ⁱPrOH and its Zn-analogue.

To get further insight into the ATE originated from the spin transition, detailed unit cell parameters were recorded for the single crystal of Fe·ⁱPrOH with an interval of 1 K upon heating and cooling modes (210–240 K). As depicted in Fig. 4a, an abrupt and hysteretic event was detected for crystallographic axes with critical temperatures (T_c) of T^cool_c = 220 K and T^heat_c = 231 K. The related principal axis parameters were modelled using the sigmoidal function,^23,39 and the best-fit results indicate that the spin transitions take place within extremely narrow temperature regions (<0.1 K, Table S9†). Significant variations of the lattice parameters imply evident deformation of crystal shape in response to the rearrangement of electronic configuration. Fig. 4b reveals the crystal images recorded at 210 K and 250 K. The obvious volume contraction and color change from yellow to red indicate the spin transition from HS to LS states. The anisotropic transformation can be checked from the crystallographic (001) plane with the angle altering from 69.6° to 79.0°, in line with the scissor-like motion of the rhombic Hofmann-type clathrate (vide infra). The CTEs are extracted from the sigmoidal function with maxima α^cool_a = −7.49 × 10⁵ M K⁻¹, α^cool_b = 3.79 × 10⁵ M K⁻¹, and α^cool_c = 9.36 × 10⁴ M K⁻¹ and α^heat_a = −3.89 × 10⁵ M K⁻¹, α^heat_b = 3.67 × 10⁵ M K⁻¹, and α^heat_c = 9.54 × 10⁴ M K⁻¹ (Fig. 4c). The uniaxial NTE is four orders of magnitude higher than that in prototypical NTE materials (such as Cd(CN)₂ (ref. 40) and ZrW₂O₈ (ref. 15)) and two orders of magnitude higher than the record in SCO materials.²⁴ Note that the huge CTEs in Fe·ⁱPrOH are caused by the abrupt SCO behavior within the extremely narrow temperature range. The crystals tend to crack after undergoing three cycles of the cooling and heating process, which is attributed to the significant structural changes associated with the abrupt SCO behavior.

Fig. 4 (a) Crystallographic axis parameters (circle) for Fe·ⁱPrOH in the temperature range of 200–250 K. Solid lines indicate the best-fitting results using the sigmoidal function. (b) The crystal images of Fe·ⁱPrOH recorded at 210 and 250 K. (c) The calculated thermal expansion coefficients according to unit cell parameters. (d) Variable-temperature molar magnetic susceptibility measured in the settle mode for Fe·ⁱPrOH. (e) The DSC curves of Fe·ⁱPrOH at 10 K min⁻¹.

Variable-temperature molar magnetic susceptibility for Fe·ⁱPrOH was measured in settle mode (Fig. 4d). Upon cooling, the χ_MT value changes from 3.99 cm³ mol⁻¹ K to 0.26 cm³ mol⁻¹ K, hinting at a HS-to-LS transition. Upon warming, the steep SCO profile shifts toward a higher temperature region. The 1st derivative curves of magnetic data reveal a thermal hysteresis with T^cool_c = 222 K and T^heat_c = 232 K (Fig. 4d, inset). The entropy-driven SCO behavior was further verified by differential scanning calorimetry (DSC) measurement with a pair of exothermic/endothermic peaks lying at 219/233 K (Fig. 4e). The variations of enthalpy are −12.20/11.54 kJ mol⁻¹ in the cooling/heating modes, in accordance with the spin transition of Fe(II) complexes.⁴¹ The hysteretic loops of in-phase dielectric constant ε′ also prove the SCO behavior in Fe·ⁱPrOH (Fig. S27†). The kinetic phenomenon of SCO profiles is negligible at 1–10 K min⁻¹ scanning rates, confirming the significant cooperative interactions in this system (Fig. S28†).

Mechanisms for ATE

To understand the switching regimes of the linear ATE and sigmoidal ATE in Fe·ⁱPrOH, the flexing motions within the rhombic grid [M{Au(CN)₂}₂]_n are studied in this system and clues are drawn from the rotations of [Au(CN)₂]⁻ motifs and/or the host–guest cooperation.

For the linear ATE, the vibrational mechanism can be explored by comparing the variable-temperature crystal structures of the diamagnetic Zn-analogue (Fig. 5a). First, the Zn⋯Zn distance (10.4 Å) linked by one [Au(CN)₂]⁻ remains almost unchanged at both 103 and 300 K in Zn·ⁱPrOH, revealing that the scissor-like motion within the rhombic grid is merely derived from atomic displacements and reorientations of the [Au(CN)₂]⁻ bridging motifs since the [Au(CN)₂]⁻ motifs prefer transverse vibrational displacement rather than the stretching one within the ab-plane. Upon heating from 103 to 300 K, [Au(CN)₂]⁻ linkers undergo rotations away from the b-axis with the related angle increasing from 24.9° to 28.4° (more details in Fig. S18 and Table S7†). The Zn1–N1≡C1/Zn1–N2≡C2 angles alter from 168.0°/158.1° to 171.7°/159.3° because of the more linear linkages of Zn–NC–Au–CN–Zn (Table S5†). Accordingly, the octahedral distortion parameter (∑) defined as the sum of the deviations from 90° for twelve cis-bond angles alters from 16.76° to 8.8°. These conformational changes lead to a “close” scissor-like motion with expansion along the a-axis and contraction along the b-axis. As a result, the Zn⋯Zn⋯Zn angle of the rhombic grid increases from 65.9° to 70.5° (Fig. 5a inset). Similarly, the Fe⋯Fe⋯Fe angle in HS Fe·ⁱPrOH increases from 67.7° at 225 K to 69.7° at 298 K (Table S4†).

Fig. 5 The lattice deformations within heterometallic cyanido-bridged rhombic grids for Zn·ⁱPrOH (a) and Fe·ⁱPrOH (b). Inset: schematic representations of the ab-plane geometric deformations caused by vibrational/electronic mechanisms.

For the sigmoidal ATE, the electronic mechanism is revealed by checking the structural transformation of Fe·ⁱPrOH at the same temperature but with distinct spin states (Fig. 5b). Amid the spin transition from LS to HS states, the radius of Fe(II) significantly increases from 75 pm to 92 pm due to the electron population at the higher e_g orbital.^42,43 Concomitantly, the expansion of each Fe–N length by ∼0.2 Å gives rise to an increase in the Fe⋯Fe distance from 10.0 to 10.4 Å. Driven by the internal stress caused by the thermal expansion of spin centers, the [Au(CN)₂]⁻ motifs reorientate to approach the b-axis (opposite to Zn·ⁱPrOH) with the angle changing from 26.4° to 36.3° to ensures minimize lattice energy under constraint. Upon the LS-to-HS transition, the Fe1–N1≡C1/Fe1–N2≡C2 angles decrease from 177.8°/168.5° to 169.3°/160.0°, and Fe(II) adopts a more distorted octahedral geometry (∑Fe = 9.2°/16.48° in the LS/HS states). These conformational changes result in an “open” scissor-like motion with contraction along the a-axis and expansion along the b-axis. And the Fe⋯Fe⋯Fe angle of the rhombic grid significantly decreases from 79.3° to 67.7° (Fig. 5b inset).

The geometric deformation in the SCO lattice is also involved with the host–guest synergistic effect^44,45 and commonly observed in amino-functionalized frameworks with asymmetric strong H-bonds.^46,47 The conformations of guest molecules and related H-bonding interactions in this system are described in Fig. 6a–d. For Zn·ⁱPrOH, H-bonds are formed between two-fold disordered ⁱPrOH molecules and the double interpenetrating frameworks. The pyridyl moieties of bpy-NH₂ ligands retain two-fold disorder at both 103 and 300 K, while the ⁱPrOH molecules undergo a slight slippage and deformation with the angle of isopropyl altering from 99.5° to 111.7° in response to the ATE translation. For Fe·ⁱPrOH, the HS structure (including the conformations of isopropyl from ⁱPrOH and pyridyl from bpy-NH₂) at 225 K is similar to those in Zn·ⁱPrOH. Upon the HS-to-LS transition, significant molecular rotation and deformation take place in the ⁱPrOH molecule with the angle of isopropyl altering from 97.6° to 123.4° (Fig. 6g). This flattening distortion of the guest operates in favor of the contraction of the host framework along the b-axis, and in turn, the pyridyl moieties in the host framework become ordered on account of the closer packing in the LS state. Variable temperature Raman spectra show strong correlation with SCO behavior and give a clue for the related conformational changes. Switchable stretching vibrations of the cyano group were detected near spin transition temperature (Fig. S25†). On the other hand, the vibrations of ⁱPrOH, such as –CH₃ bending (1431 cm⁻¹)⁴⁸ and C–C stretching (872/813 cm⁻¹)⁴⁹ modes, are nearly smeared out in the LS state, possibly due to the vibrational restraint in the shrunken lattice (Fig. 6h). When converting to the HS state, the corresponding vibrations of ⁱPrOH recovered as expected (Fig. S26†). Therefore, the geometric deformation in the lattice is mediated by host–guest cooperation.

Fig. 6 The selected structures in the bc-plane of Fe·ⁱPrOH (a) and (b), Zn·ⁱPrOH (c) and (d) and Fe·^tBuOH (e) and (f). The green/orange dashed lines stand for the host–guest H-bonding interactions and aurophilic interactions between pcu networks. Color code: cyaneous/carmine, Fe(LS/HS state); orange, Au; purple, I; red, Br; grey, C; blue, N; red, O. The H atoms are omitted for clarity. (g) The ⁱPrOH and ^tBuOH viewed along the C–O bond. The numbers demonstrate the angles of isopropyl and tert-butyl moieties. (h) The selected Raman spectra of Fe·ⁱPrOH recorded at 210 and 240 K.

Generally, the interplay between host–guest chemistry and spin-state change has an impact on the SCO behavior.^50–52 To evaluate the utility of the deformation in ⁱPrOH toward collective SCO properties, a control experiment was conducted by introducing the guest molecule with a larger substituent to hamper the conformational deformation in the lattice. An analogue Fe·^tBuOH was constructed with a similar framework except that ⁱPrOH is replaced by a ^tBuOH molecule. As expected, no remarkable molecular deformation was observed in ^tBuOH during the spin transition taking advantage of the steric hindrance of the tert-butyl group (Fig. 6g). Meanwhile, the pyridyl moieties are crystallographically ordered in the HS and LS states (Fig. 6e and f). Magnetic measurement indicates that Fe·^tBuOH displays a gradual and stepwise SCO behavior (Fig. S29†). Variable temperature SC-XRD experiments reveal ATE in unit cell parameters with maxima α^cool_a = −671 M K⁻¹, α^cool_b = 1267 M K⁻¹, and α^cool_c = 543 M K⁻¹ and α^heat_a = −752 M K⁻¹, α^heat_b = 1494 M K⁻¹, and α^heat_c = 615 M K⁻¹ within the temperature range of 100–250 K (Fig. S41†). The values of ATE coefficients in Fe·^tBuOH are almost three orders of magnitude smaller than those in Fe·ⁱPrOH, confirming the vital role of molecular motion of the guest in accelerating the spin transition and lattice deformation.

Conclusions

In summary, a Hofmann-type framework was constructed by the assembly of SCO centers, flexible cyanometallate linkers and deformable isopropanol guests. Notably, switchable colossal ATE behaviors were observed with a record-high negative thermal expansion coefficient up to −7.49 × 10⁵ M K⁻¹. Geometric transformations were found to be influenced either by vibrational or electronic mechanisms during structural deciphering. Moreover, it was discovered that the deformation of guest molecules in the lattice significantly impacted the collective magnetic and thermomechanical properties. These findings highlight that the multi-coupled relations between the ATE lattice and physicochemical properties (such as the spin transition and host–guest synergy) provide novel insights for functionalizing dynamic crystal materials and exploring ATE mechanisms.

Experimental

Materials and methods

All the reagents and solvents were commercially available and used without further purification. The elemental analyses were performed on an Elementar Vario-ELCHNS elemental analyzer with fresh samples. The Fourier transform infrared (FT-IR) spectra were recorded using KBr tablets in the range of 4000–400 cm⁻¹ on a Thermo Scientific Nicolet 6700. The powder X-ray diffraction (PXRD) patterns were recorded on a Rigaku D-MAX 2200 VPC X-ray diffractometer using Cu-K_α (λ = 1.54178 Å) radiation. The thermogravimetric analyses (TGA) were performed on a Netzsch TG209 F1 Libra under a N₂ flow with a heating rate of 10 K min⁻¹ from ambient temperature to 900 °C. Differential Scanning Calorimetry (DSC) was carried out on fresh samples soaked in a little mother liquor and performed in an aluminium crucible using a NETZSCH5 with a sweeping rate of 10 K min⁻¹ under a N₂ atmosphere.

Magnetic measurement. The variable-temperature magnetic susceptibility data were recorded at 1–10 K min⁻¹ or in settle mode using a Quantum Design MPMS3 magnetometer with a correction based on Pascal's constants.

X-ray crystallography. For Fe·ⁱPrOH (100/298 K) and Zn·ⁱPrOH (103 K), single-crystal X-ray diffraction (SC-XRD) measurements were carried out with a Bruker D8 QUEST diffractometer (Mo-K_α radiation, λ = 0.71073 Å). The data indexing and integrations were accomplished using Bruker APEX4 software. For Zn·ⁱPrOH (300 K) and Fe·^tBuOH (120/300 K), SC-XRD measurements were carried out with a Rigaku XtaLAB Synergy R diffractometer (Cu-K_α radiation, λ = 1.54184 Å), and the data reduction was carried out with the CrysAlisPro program. Using Olex2,⁵³ crystal structures were solved with the SHELXT program⁵⁴ using the intrinsic phasing method and all non-hydrogen atoms were refined with anisotropic displacement parameters by least squares on weighted F² values. The hydrogen atoms were constrained to the idealized geometry using a riding model. Due to the disordered nature of both the guest molecule and the bpy-NH₂ ligand, SIMU and/or DFIX restraints were applied to control the bond lengths and the thermal vibrations of atoms. Furthermore, ISOR restraints were utilized to ensure that individual atoms in the host framework remained positive-definite.

Variable-temperature SC-XRD measurements. For Fe·ⁱPrOH, the temperature change rates in the range of 100–210/240–300 K were 6 K min⁻¹ and structural data were collected at an interval of 10/5 K. In the temperature region of 210–240 K, structural data were collected at an interval of 1 K with the temperature change rate of 2 K min⁻¹. For Zn·ⁱPrOH, the temperature change rate in the range of 100–300 K was 6 K min⁻¹ and structural data were collected at an interval of 10 K. For Fe·^tBuOH, the temperature change rates in the range of 100–200/200–250 K were 6/4 K min⁻¹ and structural data were collected at an interval of 5/10 K.

Calculation of coefficients of thermal expansion. When the anisotropic thermal expansion is dominated by the vibrational mechanism (for example 100–200/225–300 K in Fe·ⁱPrOH and 100–300 K in Zn·ⁱPrOH), the coefficients of thermal expansion of crystallographic parameters were calculated using the web tool PASCal.^37,38

When the anisotropic thermal expansion is dominated by the electronic mechanism, the coefficients of thermal expansion of crystallographic parameters were calculated using the sigmoidal function:³⁹

The sigmoidal function is usually used for empirical fitting of the spin crossover trasnition.^23,24 The equation parameters represent A, the change of lattice parameters amid spin transitions (negative for NTE and positive for PTE); B, the sigmoidal center, equal to the critical temperature of the spin transition; C, the sigmoidal width, equal to the abruptness of SCO behavior; D, the momentum transfer value of the low-spin state.

The thermal expansion coefficients α are proportional to the 1st derivative of L(T) and can be calculated using eqn (2):

Synthesis of [Fe{Au(CN)₂}(bpy-NH₂)]·ⁱPrOH (Fe·ⁱPrOH). [4,4′-Bipyridin]-3-amine (0.1 mmol) and K[Au(CN)₂] (0.2 mmol) were placed at the bottom of a 10 mL vial. Then, 3 mL mixed solution of ⁱPrOH and H₂O (v:v = 1 : 2) was added carefully. 5 mL ⁱPrOH containing 0.1 mmol Fe(ClO₄)₂·6H₂O was laid on the top. Yellow single crystals suitable for X-ray diffraction were isolated after two weeks. Yield: ∼20%. Elemental analysis: Calcd for C₁₇H₁₇Au₂FeN₇O: C 26.01, H 2.18, N 12.49; found: C 25.92, H 2.18, N 12.56.

Synthesis of [Zn{Au(CN)₂}(bpy-NH₂)]·ⁱPrOH (Zn·ⁱPrOH). The synthetic procedure is similar to that of Fe·ⁱPrOH except for replacing Fe(ClO₄)₂·6H₂O by Zn(ClO₄)₂·6H₂O. Yield: ∼15%. Calcd for C₁₇H₁₇Au₂ZnN₇O: C 25.69, H 2.16, N 12.34; found: C 25.30, H 2.05, N 12.05.

Synthesis of [Fe{Au(CN)₂}(bpy-NH₂)]·^tBuOH (Fe·^tBuOH). [4,4′-Bipyridin]-3-amine (0.1 mmol) and K[Au(CN)₂] (0.2 mmol) were dissolved in 3 mL solution of ^tBuOH and H₂O (v:v = 1 : 2) and then transferred into a test tube. 5 mL solution of ^tBuOH and H₂O (v:v = 4 : 1) was added as the buffer layer. 2 mL ^tBuOH containing 0.1 mmol Fe(ClO₄)₂·6H₂O was laid on the top. Yield: ∼60%. Elemental analysis: calcd for C₁₈H₁₉Au₂FeN₇O: C 27.05, H 2.40, N 12.27; found: C 27.19, H 2.46, N 12.26.

Author contributions

S. G. W., Z. P. N. and M. L. T. designed the study and wrote the manuscript. S. G. W. and W. C. synthesized the materials and performed the experimental measurements. Z. Y. R. performed the magnetic measurements. M. L. T. supervised the research. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Data availability

The data supporting this article have been included as part of the ESI.† The crystallography data have been deposited at the Cambridge Crystallographic Data Centre (CCDC). CCDC 2386640–2386647 contain the supplementary crystallographic data for this paper. These data can be obtained free from The Cambridge Crystallographic Data Centre viahttps://www.ccdc.cam.ac.uk/structures/.

Acknowledgements

This work was supported by the NSFC (grant no. 22488101, 22075323 and 21773316), the Fundamental Research Funds for the Central Universities, Sun Yat-sen University (23ptpy73 and 24xkjc003), and the Science and Technology Program of Guangzhou, China (2024A04J4433).

Notes and references

1. R. S. Krishnan, R. Srinivasan and S. Devanarayanan, Thermal Expansion of Crystals, Pergamon, New York, 1979.
2. A. L. Goodwin, M. Calleja, M. J. Conterio, M. T. Dove, J. S. O. Evans, D. A. Keen, L. Peters and M. G. Tucker, Science, 2008, 319, 794–797.
3. Q. Li, K. Lin, Z. Liu, L. Hu, Y. Cao, J. Chen and X. Xing, Chem. Rev., 2022, 122, 8438–8486.
4. D. Das, T. Jacobs and L. J. Barbour, Nat. Mater., 2010, 9, 36–39.
5. X. G. Zheng, H. Kubozono, H. Yamada, K. Kato, Y. Ishiwata and C. N. Xu, Nat. Nanotechnol., 2008, 3, 724–726.
6. A. D. Fortes, E. Suard and K. S. Knight, Science, 2011, 331, 742–746.
7. L. Zhang, J. B. Bailey, R. H. Subramanian, A. Groisman and F. A. Tezcan, Nature, 2018, 557, 86–91.
8. P. Naumov, S. Chizhik, M. K. Panda, N. K. Nath and E. Boldyreva, Chem. Rev., 2015, 115, 12440–12490.
9. C. Lind, Materials, 2012, 5, 1125–1154.
10. B. B. Rath, G. Gallo, R. E. Dinnebier and J. J. Vittal, J. Am. Chem. Soc., 2021, 143, 2088–2096.
11. Z.-S. Yao, H. Guan, Y. Shiota, C.-T. He, X.-L. Wang, S.-Q. Wu, X. Zheng, S.-Q. Su, K. Yoshizawa, X. Kong, O. Sato and J. Tao, Nat. Commun., 2019, 10, 4805.
12. A. L. Goodwin, K. W. Chapman and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 17980–17981.
13. A. B. Cairns, A. L. Thompson, M. G. Tucker, J. Haines and A. L. Goodwin, J. Am. Chem. Soc., 2012, 134, 4454–4456.
14. Q. Gao, J. Wang, A. Sanson, Q. Sun, E. Liang, X. Xing and J. Chen, J. Am. Chem. Soc., 2020, 142, 6935–6939.
15. T. A. Mary, J. S. O. Evans, T. Vogt and A. W. Sleight, Science, 1996, 272, 90–92.
16. L. Hu, J. Chen, J. Xu, N. Wang, F. Han, Y. Ren, Z. Pan, Y. Rong, R. Huang, J. Deng, L. Li and X. Xing, J. Am. Chem. Soc., 2016, 138, 14530–14533.
17. D. Wendt, E. Bozin, J. Neuefeind, K. Page, W. Ku, L. Wang, B. Fultz, A. V. Tkachenko and I. A. Zaliznyak, Sci. Adv., 2019, 5, eaay2748.
18. S. Henke, A. Schneemann and R. A. Fischer, Adv. Funct. Mater., 2013, 23, 5990–5996.
19. C. Yang, X. Wang and M. A. Omary, Angew. Chem., Int. Ed., 2009, 48, 2500–2505.
20. S. J. Baxter, A. Schneemann, A. D. Ready, P. Wijeratne, A. P. Wilkinson and N. C. Burtch, J. Am. Chem. Soc., 2019, 141, 12849–12854.
21. A. L. Goodwin and C. J. Kepert, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 140301.
22. H. J. Shepherd, T. Palamarciuc, P. Rosa, P. Guionneau, G. Molnár, J.-F. Létard and A. Bousseksou, Angew. Chem., Int. Ed., 2012, 51, 3910–3914.
23. B. R. Mullaney, L. Goux-Capes, D. J. Price, G. Chastanet, J.-F. Létard and C. J. Kepert, Nat. Commun., 2017, 8, 1053.
24. H.-Y. Sun, Y.-S. Meng, L. Zhao, N.-T. Yao, P.-D. Mao, Q. Liu, F.-F. Yan, H. Oshio and T. Liu, Angew. Chem., Int. Ed., 2023, 62, e202302815.
25. M. Azuma, W.-t. Chen, H. Seki, M. Czapski, S. Olga, K. Oka, M. Mizumaki, T. Watanuki, N. Ishimatsu, N. Kawamura, S. Ishiwata, M. G. Tucker, Y. Shimakawa and J. P. Attfield, Nat. Commun., 2011, 2, 347.
26. J.-X. Hu, Y. Xu, Y.-S. Meng, L. Zhao, S. Hayami, O. Sato and T. Liu, Angew. Chem., Int. Ed., 2017, 56, 13052–13055.
27. J. Chen, L. Hu, J. Deng and X. Xing, Chem. Soc. Rev., 2015, 44, 3522–3567.
28. P. Hu, J. Chen, J. Deng and X. Xing, J. Am. Chem. Soc., 2010, 132, 1925–1928.
29. O. Sato, Nat. Chem., 2016, 8, 644–656.
30. Z.-S. Yao, M. Mito, T. Kamachi, Y. Shiota, K. Yoshizawa, N. Azuma, Y. Miyazaki, K. Takahashi, K. Zhang, T. Nakanishi, S. Kang, S. Kanegawa and O. Sato, Nat. Chem., 2014, 6, 1079.
31. X. Ding, D. K. Unruh, L. Ma, E. J. van Aalst, E. W. Reinheimer, B. J. Wylie and K. M. Hutchins, Angew. Chem., Int. Ed., 2023, 62, e202306198.
32. I. Grobler, V. J. Smith, P. M. Bhatt, S. A. Herbert and L. J. Barbour, J. Am. Chem. Soc., 2013, 135, 6411–6414.
33. Z. Chen, G. D. Stroscio, J. Liu, Z. Lu, J. T. Hupp, L. Gagliardi and K. W. Chapman, J. Am. Chem. Soc., 2023, 145, 268–276.
34. H.-L. Zhou, Y.-B. Zhang, J.-P. Zhang and X.-M. Chen, Nat. Commun., 2015, 6, 6917.
35. Q. Gao, J. Chen, Q. Sun, D. Chang, Q. Huang, H. Wu, A. Sanson, R. Milazzo, H. Zhu, Q. Li, Z. Liu, J. Deng and X. Xing, Angew. Chem., Int. Ed., 2017, 56, 9023–9028.
36. J. Chen, Q. Gao, A. Sanson, X. Jiang, Q. Huang, A. Carnera, C. G. Rodriguez, L. Olivi, L. Wang, L. Hu, K. Lin, Y. Ren, Z. Lin, C. Wang, L. Gu, J. Deng, J. P. Attfield and X. Xing, Nat. Commun., 2017, 8, 14441.
37. M. J. Cliffe and A. L. Goodwin, J. Appl. Crystallogr., 2012, 45, 1321–1329.
38. M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, J. Open Source Softw., 2023, 8, 5556.
39. R. M. van der Veen, O.-H. Kwon, A. Tissot, A. Hauser and A. H. Zewail, Nat. Chem., 2013, 5, 395–402.
40. K. W. Chapman, P. J. Chupas and C. J. Kepert, J. Am. Chem. Soc., 2005, 127, 15630–15636.
41. P. Gütlich, A. Hauser and H. Spiering, Angew. Chem., Int. Ed., 1994, 33, 2024–2054.
42. R. Shannon, Acta Crystallogr., Sect. A, 1976, 32, 751–767.
43. X. Li, D. Zhang, Y. Qian, W. Liu, C. Mathonière, R. Clérac and X. Bao, J. Am. Chem. Soc., 2023, 145, 9564–9570.
44. J.-P. Xue, Y. Hu, B. Zhao, Z.-K. Liu, J. Xie, Z.-S. Yao and J. Tao, Nat. Commun., 2022, 13, 3510.
45. P. D. Southon, L. Liu, E. A. Fellows, D. J. Price, G. J. Halder, K. W. Chapman, B. Moubaraki, K. S. Murray, J.-F. Létard and C. J. Kepert, J. Am. Chem. Soc., 2009, 131, 10998–11009.
46. W. Liu, Y.-Y. Peng, S.-G. Wu, Y.-C. Chen, M. N. Hoque, Z.-P. Ni, X.-M. Chen and M.-L. Tong, Angew. Chem., Int. Ed., 2017, 56, 14982–14986.
47. R. Turo-Cortés, C. Bartual-Murgui, J. Castells-Gil, M. C. Muñoz, C. Martí-Gastaldo and J. A. Real, Chem. Sci., 2020, 11, 11224–11234.
48. Y. Yu, Y. Wang, N. Hu, K. Lin, X. Zhou and S. Liu, J. Raman Spectrosc., 2014, 45, 259–265.
49. B. Yang, X. Cao, S. Wang and C. Sun, Optik, 2020, 204, 163544.
50. Z.-P. Ni, J.-L. Liu, M. N. Hoque, W. Liu, J.-Y. Li, Y.-C. Chen and M.-L. Tong, Coord. Chem. Rev., 2017, 335, 28–43.
51. M. Ohba, K. Yoneda, G. Agustí, M. C. Muñoz, A. B. Gaspar, J. A. Real, M. Yamasaki, H. Ando, Y. Nakao, S. Sakaki and S. Kitagawa, Angew. Chem., Int. Ed., 2009, 48, 4767–4771.
52. M. J. Murphy, K. A. Zenere, F. Ragon, P. D. Southon, C. J. Kepert and S. M. Neville, J. Am. Chem. Soc., 2017, 139, 1330–1335.
53. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
54. G. Sheldrick, Acta Crystallogr., Sect. C:Cryst. Struct. Commun., 2015, 71, 3–8.

---

Footnote

† Electronic supplementary information (ESI) available: Additional crystal data (Fig. S1–S18 and Tables S1–S7), powder X-ray diffraction patterns (Fig. S19 and S21), thermogravimetric analysis (Fig. S22 and S23), infrared and Raman spectra (Fig. S24–S26), dielectric properties (Fig. S27), magnetic properties (Fig. S28 and S29) and thermal expansion properties (Fig. S30–S47 and Tables S8–S13). CCDC 2386640–2386647. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc08032g

---