Dynamics and kinetics exploration of the oxygen reduction reaction at the Fe–N₄/C–water interface accelerated by a machine learning force field

Abstract

Understanding the oxygen reduction reaction (ORR) mechanism and accurately characterizing the reaction interface are essential for improving fuel cell efficiency. We developed an active learning framework combining machine learning force fields and enhanced sampling to explore the dynamics and kinetics of the ORR on Fe–N₄/C using a fully explicit solvent model. Different possible reaction paths have been explored and the O₂ adsorption process is confirmed as the rate-determining step of the ORR at the Fe–N₄/C–water interface, which needs to overcome a free energy barrier of 0.39 eV. By statistical analysis of solvent configurations for proton-coupled electron transfer (PCET) processes, it is revealed that the configurations of interface water remarkably influence the reaction efficiency. More hydrogen bonds and longer lifetimes facilitate the PCET reactions and even make them barrierless. Our theoretical framework highlights the significance of solvent configurations in determining free energy barriers, and offers new insights into the reaction mechanism of the ORR on Fe–N₄/C catalysts.

---

Introduction

Renewable energy technologies, such as fuel cells, play a pivotal role in advancing low-carbon, sustainable development goals when humanity is confronted with significant energy and environmental challenges.¹ Central to the efficiency of fuel cells is the electrocatalytic oxygen reaction reduction (ORR) occurring at the cathode, a critical process with sluggish kinetics that directly impacts the power output.^2,3 A deep understanding of the kinetic reaction mechanism during the ORR process and the intricate interactions between catalyst surfaces, reaction intermediates and solvent molecules at the electrode–liquid interface is essential for revealing the reaction mechanisms and developing novel catalysts.^4–6 Due to the complexity of the interfacial and electrochemical environments, atomic-scale insights revealed from experiments are limited, and traditional computational methods often overlook the solvent's influence and the interface effects on electrochemical reactions.⁷ Implicit solvation computational models attempt to address this limitation by representing solvent molecules with continuously polarized media,^8–10 but some models suffer from multinomial approximations leading to inaccurate interface description. Most of the structural models fail to account for proton exchange between reactants and solvent molecules, and static calculations of interface structures based on lowest-energy configurations ignore structural fluctuations along reaction coordinates. Moreover, the discrepancy between vacuum/continuously polarized media environments and realistic environments significantly affects reaction energies and the rate determining step (RDS). Therefore, developing computational methods that closely describe the ORR process in realistic electrochemical environments is urgently needed.

The rapid development of computing power in recent years has enabled a series of studies describing the catalyst–solvent interface using ab initio molecular dynamics (AIMD) with explicit solvation models, revealing new insights.^11,12 As for the ORR on the Fe–N₄/C catalyst, Liu et al. used constant potential AIMD with a hybrid solvent model and found that the competitive adsorption of O₂ and H₂O at the Fe site was the rate-determining step of the ORR.¹³ Wang et al. investigated the ORR at the same interface using AIMD simulations with a fully explicit solvent model, and they observed ions in solution formed pseudo-adsorption states on the reaction sites.¹⁴ These methods achieved a more detailed description of the complex environment at the ORR interface, but it is also a challenge to observe the crucial reaction mechanism in such short-time dynamics, and the AIMD simulations with large length-scale and long time-scale simulations are extremely expensive and time-consuming.

Integrating artificial intelligence into chemistry offers a promising solution to this challenge. In recent years, machine learning (ML) has been employed to make fast predictions across various scales, from microscopic to macroscopic in spatial scope and also from static to dynamic in temporal dimensions.^15–17 Particularly, machine learning force fields (MLFF) have shown great promise in predicting complex catalytic systems and enabling large-scale and long-time dynamics simulations with first-principles accuracy,¹⁸ which has been applied to the rapid identification of transition states for organic molecules on Pt surfaces,^19,20 exploration of proton transfer mechanisms at the TiO₂–water interface,²¹ examination of water dissociation in interfacial environments,²² analysis of the dynamic ORR mechanism on the Au–water surface²³ and NH₃ decomposition on the Li₂NH surface.²⁴

A deep understanding of the electrocatalytic reactions in realistic environments is crucial for designing and optimizing electrocatalysts with both high stability and activity. An important catalyst for the ORR is single atom Fe embedded in N-doped graphene (Fe–N₄/C), and extensive efforts have been made to improve its ORR activity and explore its reaction mechanism.^{7,9,14,25–30} Given the importance of the solid–liquid–gas interface in understanding ORR fundamentals, we constructed an active learning workflow to conduct fully explicit solvent simulations at the Fe–N₄/C–water interface using MLFFs and metadynamics. Our exploration of the dynamics and kinetic properties of the four-electron ORR revealed that the O₂ adsorption onto Fe active sites is the RDS, rather than the proton-coupled electron transfer (PCET) process, which was consistent with the previous constant-potential AIMD simulations.¹³ Long time-scale and fully explicit solvent simulations showed that the arrangement of water molecules at the solid–liquid–gas interface plays a crucial role in determining adsorption free energies of reaction intermediates and the free energy barriers. The statistical results of the interface solvent configuration based on MLFF-MD provide a microscopic explanation for the macroscopic energies of various ORR steps. Our theoretical framework reveals new insights into the reaction mechanism of the ORR on Fe–N₄/C, and emphasizes the significance of atomic-scale kinetic studies in heterogeneous electrocatalysis.

Computational details

MLFF was trained using the DeepMD-kit^31,32 employing a radial cutoff of 6 Å and the se_e2_a descriptor. The training set data were obtained from spin-polarized DFT calculations conducted with the Vienna ab initio simulation package (VASP).³³ The Perdew–Burke–Ernzerhof (PBE) exchange–correlation functional³⁴ with van der Waals correction was used to describe the electronic interaction. MD simulations utilizing the MLFF were performed with the Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS).³⁵ All enhanced sampling simulations were performed with a well-tempered metadynamics approach implemented in PLUMED.³⁶ More computational details on DFT calculations, model training and validation, molecular dynamics and enhanced sampling, and trajectory result analysis can be found in the ESI.†

Results and discussion

Activate learning workflow

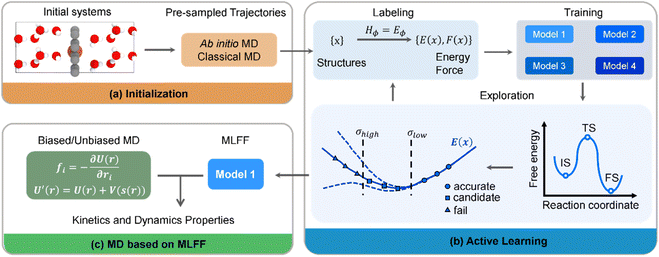
Our MLFF simulations were developed and implemented through a workflow framework, as illustrated in Fig. 1. To comprehensively and accurately describe the ORR interfacial environment, we gathered a wide range of possible structures to explore the configuration space. Initially, 3374 structures were generated through a series of AIMD and classical molecular dynamics (MD) simulations (Fig. 1a). These initial configurations were categorized into various groups, including different densities of bulk water, graphene, Fe–N₄/C, graphene–water interface, Fe–N₄/C–water interface, and Fe–N₄/C–adsorbate–water interface. The details are summarized in Table S1 of ESI.†

Fig. 1 Schematic diagram of the activate learning workflow. (a) Collection of initial configurations; (b) an active learning strategy based on committee queries and metadynamics; (c) MD simulations based on MLFFs to study the kinetics and dynamic properties of the ORR.

Subsequently, additional structures for the training set were acquired via an active learning iteration framework, as depicted in Fig. 1b. This framework employed a committee query strategy, where a structure was predicted by four models based on MLFFs-MD with only random seed variations, and their maximum deviation was calculated, denoted as “model deviation”. Configurations with model deviations below the designated minimum value were considered to adequately describe by the current force field. Configurations falling within the defined range of model deviations were labeled. In contrast to the conventional single-interval model deviation strategy of DPGEN,³⁷ a multi-interval model deviation strategy was adopted, dividing the model deviation interval into multiple subintervals. Within each subinterval, a higher proportion of configurations was selected for relatively large model deviation and a lower proportion of configurations was selected for relatively small model deviation facilitating the comprehensive consideration of configurations and accelerating the convergence of the iteration process because configurations with larger model deviation are more worthy of learning than those with smaller model deviation. Additionally, to avoid the similarity of configurations within the training set, only the configurations with residual values surpassing the specified threshold were selected to expand the training set. A total of 6008 configurations were collected in our work, which is significantly fewer (less than a half) than the previous studies,^23,38 underscoring the efficiency of our configuration selection strategy. Furthermore, the metadynamics method was employed in the active learning MD simulations to thoroughly sample transition state configurations for calculating the free energy barrier. The composition of the specific system corresponding to metadynamics is shown in Table S1.† Finally, a long-term model training was performed for all configurations to obtain a higher-precision MLFF. This force field was subsequently utilized to conduct biased/unbiased MD for evaluating the kinetics and dynamic properties of the ORR on the Fe–N₄/C catalyst (Fig. 1c).

Validation of our MLFF model

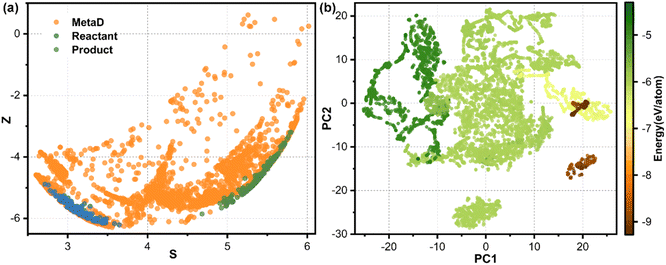
Fig. 2a–d show the accuracy of our trained MLFFs. In the validation set, the mean absolute errors (MAE) in energy and force are 3.4 meV per atom and 0.07 eV Å⁻¹, respectively, indicating our trained MLFF could provide accurate predictions for both energies and forces during MD simulations. Besides energetics, the configurations were also compared between our MLFF-MD and AIMD simulations. For water molecule description, the radial distribution function generated by MLFF-MD simulations agrees well with the results from AIMD simulations, as shown in Fig. 2e, indicating the accurate capture of both intra- and intermolecular structures of water molecules by our MLFF. In addition, the accuracy of MLFF was also verified in predicting the adsorption energy. After 10 iterations of active learning iterations, the adsorption energies of O₂ and H₂O predicted by MLFF are basically consistent with the values from density functional theory (DFT) (Fig. 2f). Therefore, the above comparisons confirm our trained MLFF achieved the accuracy of ab initio calculations.

Fig. 2 Comparison of model accuracy for the training set and validation set. (a and b) Comparisons between energies and forces derived from DFT calculations and MLFF predictions for the training set and (c and d) validation set. (e) Comparison between the radial distribution function of O–H in pure water obtained from AIMD and MLFF-MD. (f) Adsorption energies of O₂ and H₂O by the active learning workflow.

The reactants and products can be well described from our MLFF model by using the active learning strategy, while the transition states should be described by enhanced sampling. The metadynamics simulations employed the reaction path as the collective variable (CV). The reaction path was expressed by a series of well-designed reference structures, effectively distinguishing different intermediate and transition state structures, as shown in Fig. 3a. The full spatial configurations of the reaction path were fully sampled by combining active learning and enhanced sampling, covering a broader configuration space which could not be achieved by using unbiased MD.

Fig. 3 Richness of configuration space. (a) Configuration distribution of reactant, product and metadynamics simulation with path collective variables. The S represents the progress along the reaction pathway, while Z represents the distance between the structure and the reaction pathway specified by the reference configuration (similarly hereinafter). (b) Visualization of the t-distributed stochastic neighbor embedding results of structures for all training sets. PC1 and PC2 represent the first and second principal component, respectively. The two principal component values obtained after dimensionality reduction don't have specific physical and chemical meanings, but only represent the relative positions of the features of each structure in low dimensional space, reflecting the nearest neighbor relationship between data points.

To validate our model's ability to distinguish the different chemical environments of configurations, we employed the t-distributed stochastic neighbor embedding (t-SNE) method to visualize the structural features of all training sets, as shown in Fig. 3b. Configurations with similar chemical environments tended to aggregate together, while those with different chemical environments distribute distinctively from each other. Water molecules, water clusters and bulk water structures represented by dark green dots are distributed in the upper left of the graph. The catalysts, including Fe–N₄/C and pristine graphene, are distributed in the bottom right of the graph, shown in brown. Catalyst–water interface structures colored by green color are located in the middle of the graph, since they contained both water molecules and catalysts. Isolated dot clusters colored by green at the bottom represent the Fe–N₂/C–water configuration (Fig. S3b†), which is distinctive with the Fe–N₄/C–water configuration (Fig. S3a†), indicating that our strategy can successfully distinguish configurations with different Fe–N coordinated environments. Moreover, this model can also distinguish different adsorbates on the active site (Fig. S3a†) and different chemical environments of water molecules (Fig. S3b†). The numerous structures and continuous distribution in the energy plot indicate sufficient sampling of both stable and metastable structures in the configuration space.

In addition to validating the accuracy of our MLFF model, we have also compared the computational efficiency between our MLFF model and AIMD calculations. The number of steps required for metadynamics sampling convergence was tested to determine the minimum steps required for simulations. The free energies under different steps are shown in Fig. S4,† by using O₂ adsorption as a representative. The free energy no longer changes significantly after 500 000 steps, indicating that the sampling has converged. The Fe–N₄/C–water system calculated by AIMD with metadynamics requires at least 500 000 steps to achieve convergence for enhanced sampling, costing approximately 500 days on a 24-core CPU (Dual Intel Xeon Gold 6126) or 250 days on a V100 GPU. In contrast, for the same system, the trained MLFF model requires only 4 hours for 1 ns MD simulations on a V100 GPU or 12 hours on a 24-core CPU. The computational speed of the MLFF method is approximately 1000 times faster than AIMD simulations without considering the time consumed for training the MLFF model (see Fig. S1.2 and S4 in ESI†), and the speedup could be even more pronounced for larger-size systems due to the non-linear computational complexity of DFT with respect to the system size.

Dynamics and kinetic properties of the ORR

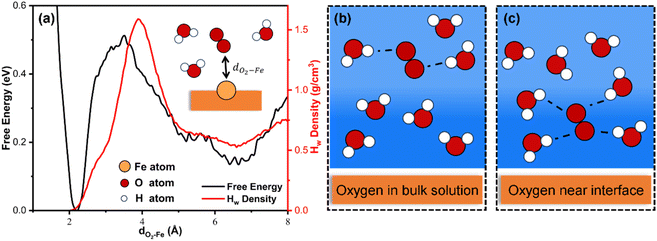
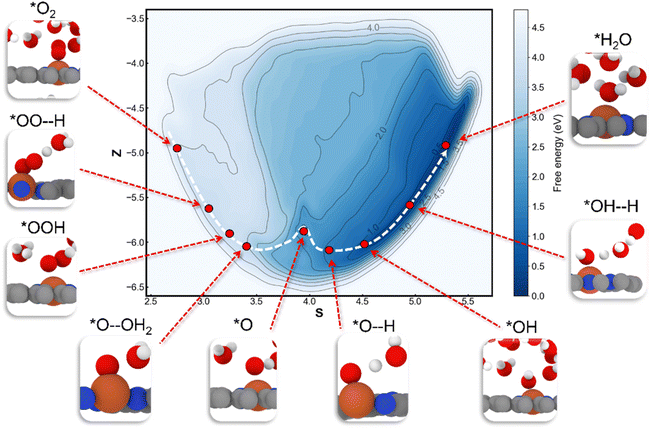
The well-trained MLFF is utilized to investigate the dynamics and kinetic properties of the ORR on the Fe–N₄/C catalyst. The dimensions and relative positions of the configuration are shown in Fig. S1.† The first step of the ORR on Fe–N₄/C involves the adsorption of O₂, regarded as a “thermal process”.¹³ Using MLFF-MD with metadynamics simulations, a meta-stable configuration of O₂ ∼ 6.5 Å away from the Fe–N₄/C–water interface was determined, which needs to overcome a significant free energy barrier of 0.39 eV to adsorb on the active Fe site (Fig. 4a black line). The high free energy barrier is attributed to the higher density of water at the catalyst–solvent interface than that in bulk solvent (red line in Fig. 4a). In bulk solvent with lower density, there are fewer hydrogen bonds between O₂ and water molecules (Fig. 4b). At the catalyst–water interface water with higher density, the hydrogen bonds between O₂ and the surrounding water molecules increase (Fig. 4c), requiring more energy to overcome these bonds for adsorption. In addition, before the O₂ adsorption, the H₂O adsorbed on the Fe site is also observed in our work, which agrees well with the previous AIMD simulations.¹³

Fig. 4 Free energies of O₂ at different positions. (a) Free energy profile of O₂ adsorption. The free energy was calculated by using MLFF-MD with metadynamics. The d_O2–Fe was employed as collective variables, representing the distance from the Fe site to the mass center of O₂. (b) Illustration of the configuration that O₂ locates in the bulk solvent. (c) Illustration of the configuration that O₂ locates at the catalyst–water interface. Dashed lines highlight the hydrogen bonds surrounding O₂.

The free energy profile for the ORR process on the Fe–N₄/C–water interface at 300 K has been extensively investigated, as shown in Fig. 5. The global free energy profile includes an initial state of *O₂ and a final state of *H₂O, delineated by two shallower basins (*OOH and *O) and one deeper basin (*H₂O). The global minimum energy reaction path, including reactants, intermediates, transition states, and products, is also illustrated in Fig. 5. Additionally, the probability of the reaction occurring along the other paths is very low due to the rapid increase in free energies with the direction perpendicular to the reaction path. The free energy barriers for each elementary reaction are calculated and compared, as shown in Fig. S6.† The results indicate that the RDS corresponds to the process of O₂ adsorption to the active site rather than the four PCET steps, which is consistent with the AIMD simulations.¹³

Fig. 5 The global reaction free energy as a function of path CV S and Z, revealed by the MLFF-MD with metadynamics. The global minimum energy path is marked by a white dashed line, with red dots indicating the reactants, transition states, and products present on the reaction path.

For the reaction process of *O₂ + 2H⁺ + 2e⁻ → *O + H₂O (abbreviated as PCET 1 & 2), our enhanced sampling algorithm reveals two possible paths (path 1 and path 2) for the formation of *O from *OOH, as displayed in Fig. 6a. In path 1, the O–O bond in *OOH breaks, and then the detached OH undergoes protonation in solution (Fig. 6b). A free energy barrier of 0.32 eV needs to be overcome in the breakage of the O–O bond, while the protonation process is barrierless. In path 2, *OOH first receives a proton from solution, then the O–O bond breaks, resulting in the desorption of H₂O (Fig. 6c). The free energy barrier of this path exists in the PCET process with 0.60 eV, while the O–O bond breaking is barrierless. Thus, path 1 is preferred for the formation of the *O intermediate. Then, the subsequent reaction processes of *O + H⁺ + e⁻ → *OH and *OH + H⁺ + e⁻ → *H₂O (abbreviated as PCET 3 & 4) are calculated, which are barrierless (Fig. S7†). Finally, the adsorbed water desorbs from the catalyst surface with a small desorption barrier of 0.15 eV.

Fig. 6 Free energy profile and configurations for *O₂ + 2H⁺ + 2e⁻ → *O + H₂O. (a) Free energy calculated by MLFF-MD with metadynamics. CN O²–H and CN O¹–O² are employed as collective variables, where CN O²–H is the O–H coordination number between the O² atom in *O₂ with Fe, CN O¹–O² describes the bonding interaction of the two O atoms in *O₂. (b) and (c) Illustrations of path 1 and path 2. Hydrogen bonds between O and H atoms are highlighted with black dashed lines. Oxygen and hydrogen atoms are shown in red and white, respectively.

Crucial role of interfacial solvent structures

Previous studies have demonstrated the critical role of hydrogen bonds in the PCET processes,^39–41 since interfacial water molecules act as proton donors, significantly influencing the reaction barriers in different PCET processes. To address this, we extensively analyzed the water configurations at the interface. Our results show that solvent environments for PCET 1 & 2 and PCET 3 & 4 are different. A greater number and longer lifetime of hydrogen bonds between the solvent and adsorbate exist for PCET 3 & 4, facilitating the PCET process with lower free energy barriers (Fig. 7f and g). The radial distribution function of O atoms in *O₂ and H atoms has been calculated, indicating that there are significantly more H atoms around the O atom in the first layer of solvent for PCET 3 & 4 (Fig. 7a). It implies that more hydrogen bonds will be formed in PCET 3 & 4. The density of H atoms in H₂O along the z-direction is statistically analyzed. The results show that water molecules prefer to aggregate at the interface with a higher density than the bulk solvent (Fig. 7b). Furthermore, the density of H atoms at the interface for PCET 3 & 4 is higher than that of PCET 1 & 2 (Fig. 7e), also facilitating the formation of more hydrogen bonds.

Fig. 7 Interface microenvironment for different PCET processes. (a) Radial distribution function between O²–H and O¹–H, where O² represents the O atom far away from Fe in *O₂ and O¹ represents the O atom near Fe. The range of the first peak is marked with a purple band. (b) Distribution of the H density in water (H_w) along the surface normal (z axis) for different PCET processes. PCET 1 & 2 refer to the first and second PCET processes and PCET 3 & 4 refer to the third and fourth PCET processes. (c) Probability density distribution of the angle (φ) between the surface normal (n̄) and the angular bisector of interfacial water (d̄). Interfacial water is defined as within 4 Å from the catalyst surface. (d) Life time of hydrogen bonds with O² and O¹. (e) Probability distribution of the number of hydrogen bonds. (f and g) Schematic diagrams of hydrogen bonds between O² and interface water for PCET 1 & 2 and PCET 3 & 4 processes, respectively. Dashed lines between O and H atoms represent hydrogen bonds.

To better understand the role of hydrogen bonds in different PCET processes, we have analyzed the directional tendency of water (angle φ) at the interface.^39,40 As shown in Fig. 7c, PCET 3 & 4 have a larger angle (92° for the first peak and 119° for the second peak) compared to PCET 1 & 2 (90° for the only peak), indicating a tendency of water molecules to adopt an H-down configuration where more H atoms point towards the adsorbed O atom. This results in the formation of more hydrogen bonds at the interface (Fig. 7c and e). Consequently, the proton transfer process of PCET 1 & 2 with fewer hydrogen bonds is more challenging and thus has a free energy barrier (Fig. 7f), whereas the proton transfer process of PCET 3 & 4 with more hydrogen bonds is easier without any barrier (Fig. 7g). Statistical analysis of the number of hydrogen bonds is also performed in a larger supercell. The same result is remarkably observed with the formation of more hydrogen bonds in PCET 3 & 4, strongly supporting the conclusions related to the free energy barrier.

Additionally, the lifetime of hydrogen bonds also influences the PCET process.⁴² The longer the lifetime of hydrogen bonds, the less possibility of hydrogen bond breakage, facilitating the PCET process. As shown in Fig. 7d, in PCET 3 & 4 there is still a small residual amount of hydrogen bonds after 1 ps, while the hydrogen bonds in PCET 1 & 2 decay more rapidly and almost none is left after 1 ps. Thus, it is more difficult for PCET 1 & 2 with shorter hydrogen bond lifetimes to occur than PCET 3 & 4 (Fig. 7f). The above statistical results strongly support the opinion that the interfacial water configurations and the formation of hydrogen bonds remarkably influence the reaction barriers in different PCET processes of the ORR. Our strategy combining MLFF and metadynamics could well describe it from a long time-scale and fully explicit solvent, providing a statistical explanation for the macroscopic energies of various PCETs.

To validate the efficiency and scalability of the MLFF, the small system was expanded to a 4 × 4 supercell, consisting of a total of 1984 atoms. The free energy barrier of O₂ adsorption is 0.375 eV, which agrees well with that from the original small cell (0.39 eV), confirming it to be the RDS of the ORR. Also, PCET 3 & 4 are barrierless (Fig. S9a†). Statistical results of solvent configurations for all PCET processes reveal that the RDF of O–H in PCET 3 & 4 exhibits a higher first peak compared to PCET 1 & 2 (Fig. S9b†). This corresponds to the formation of a larger number of hydrogen bonds at the interface for PCET 3 & 4 (Fig. S9c†). The increased hydrogen bonds facilitate proton transfer and dramatically reduce the free energy barrier for the PCET process. A more remarkable comparison between PCET 1 & 2 and PCET 3 & 4 could be seen from a relatively larger system.

Conclusions

In summary, we propose a strategy to explore the dynamic and kinetic mechanisms of the ORR at the catalyst–solvent interface by combining MLFF and enhanced sampling methods, significantly increasing the speed of MD simulations with ab initio accuracy, resolving the dilemma between “precision” and “efficiency” in describing complex electrochemical processes. Our results confirm that the RDS of the ORR at the Fe–N₄/C–water interface is the O₂ adsorption process with a free energy barrier of 0.39 eV rather than the PCET process. This is because O₂ forms more hydrogen bonds with the surrounding water at the interface than that in bulk solvent, requiring more energy to overcome for adsorption. By statistical analysis of water solvent configurations for different PCET processes, it is found that the interfacial water configurations remarkably change during the reaction progress. The density of H atoms at the interface for PCET 3 & 4 is higher than that of PCET 1 & 2, and there are more H-down configurations in water molecules. Thus, a greater number and longer lifetime of hydrogen bonds between the solvent and adsorbate exist for PCET 3 & 4, facilitating the PCET process with lower free energy barriers. Our study combining MLFF and metadynamics not only verifies the energetic conclusions of the previous AIMD simulations, but also reveals new statistical insights into the reaction mechanism of the ORR on Fe–N₄/C. Our work highlights the significance of kinetic studies with considering atomic-scale solvent configurations in heterogeneous electrocatalysis.

Data availability

The data supporting this article have been included as part of the ESI.†

Author contributions

L. W. conceived and designed the research. Q. Y. performed the calculations, plotted the figures and prepared the original draft. P. L. directed the machine learning force field calculations. Q. Y., X. N., P. L. and L. W. revised the manuscript. P. L., Y. L. and L. W. supervised the research. All authors discussed and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the support from National Key Research and Development Program of China (2022YFA1503101), National Natural Science Foundation of China (22373072), Collaborative Innovation Center of Suzhou Nano Science & Technology, 111 Project, and Joint International Research Laboratory of Carbon-Based Functional Materials and Devices.

References

1. S. Chu, Y. Cui and N. Liu, The path towards sustainable energy, Nat. Mater., 2017, 16, 16–22.
2. K. Jiao, J. Xuan, Q. Du, Z. Bao, B. Xie, B. Wang, Y. Zhao, L. Fan, H. Wang and Z. Hou, Designing the next generation of proton-exchange membrane fuel cells, Nature, 2021, 595, 361–369.
3. L. Gao, X. Cui, C. D. Sewell, J. Li and Z. Lin, Recent advances in activating surface reconstruction for the high-efficiency oxygen evolution reaction, Chem. Soc. Rev., 2021, 50, 8428–8469.
4. Y. Wang, L. Huang, P. Zhang, Y. Qiu, T. Sheng, Z. Zhou, G. Wang, J. Liu, M. Rauf, Z. Gu, W. Wu and S. Sun, Constructing a Triple-Phase Interface in Micropores to Boost Performance of Fe/N/C Catalysts for Direct Methanol Fuel Cells, ACS Energy Lett., 2017, 2, 645–650.
5. Q. Ma, H. Jin, J. Zhu, Z. Li, H. Xu, B. Liu, Z. Zhang, J. Ma and S. Mu, Stabilizing Fe–N–C Catalysts as Model for Oxygen Reduction Reaction, Adv. Sci., 2021, 8, 2102209.
6. X. Tian, X. F. Lu, B. Y. Xia and X. W. D. Lou, Advanced electrocatalysts for the oxygen reduction reaction in energy conversion technologies, Joule, 2020, 4, 45–68.
7. Z. Jin, P. Li, Y. Meng, Z. Fang, D. Xiao and G. Yu, Understanding the inter-site distance effect in single-atom catalysts for oxygen electroreduction, Nat. Catal., 2021, 4, 615–622.
8. S. Ringe, N. G. Hormann, H. Oberhofer and K. Reuter, Implicit solvation methods for catalysis at electrified interfaces, Chem. Rev., 2021, 122, 10777–10820.
9. X. Hu, S. Chen, L. Chen, Y. Tian, S. Yao, Z. Lu, X. Zhang and Z. Zhou, What is the real origin of the activity of Fe–N–C electrocatalysts in the O₂ reduction reaction? Critical roles of coordinating pyrrolic N and axially adsorbing species, J. Am. Chem. Soc., 2022, 144, 18144–18152.
10. X. Zhao, Z. H. Levell, S. Yu and Y. Liu, Atomistic Understanding of Two-dimensional Electrocatalysts from First Principles, Chem. Rev., 2022, 122, 10675–10709.
11. Y. Li and Z.-F. Liu, Solvated proton and the origin of the high onset overpotential in the oxygen reduction reaction on Pt(111), Phys. Chem. Chem. Phys., 2020, 22, 22226–22235.
12. T. Ikeshoji and M. Otani, Toward full simulation of the electrochemical oxygen reduction reaction on Pt using first-principles and kinetic calculations, Phys. Chem. Chem. Phys., 2017, 19, 4447–4453.
13. S. Yu, Z. Levell, Z. Jiang, X. Zhao and Y. Liu, What Is the Rate-Limiting Step of Oxygen Reduction Reaction on Fe–N–C Catalysts?, J. Am. Chem. Soc., 2023, 145, 25352–25356.
14. J.-W. Chen, Z. Zhang, H.-M. Yan, G.-J. Xia, H. Cao and Y.-G. Wang, Pseudo-adsorption and long-range redox coupling during oxygen reduction reaction on single atom electrocatalyst, Nat. Commun., 2022, 13, 1734.
15. Z. Fan, Z. Zeng, C. Zhang, Y. Wang, K. Song, H. Dong, Y. Chen and T. Ala-Nissila, Neuroevolution machine learning potentials: combining high accuracy and low cost in atomistic simulations and application to heat transport, Phys. Rev. B, 2021, 104, 104309.
16. A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Gaussian approximation potentials: the accuracy of quantum mechanics, without the electrons, Phys. Rev. Lett., 2010, 104, 136403.
17. K. Bi, L. Xie, H. Zhang, X. Chen, X. Gu and Q. Tian, Accurate medium-range global weather forecasting with 3D neural networks, Nature, 2023, 619, 533–538.
18. J. Behler and M. Parrinello, Generalized neural-network representation of high-dimensional potential-energy surfaces, Phys. Rev. Lett., 2007, 98, 146401.
19. S. Huang, C. Shang, P. Kang, X. Zhang and Z. Liu, LASP: fast global potential energy surface exploration, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1415.
20. X. Li, L. Chen, G. Wei, C. Shang and Z. Liu, Sharp increase in catalytic selectivity in acetylene semihydrogenation on Pd achieved by a machine learning simulation-guided experiment, ACS Catal., 2020, 10, 9694–9705.
21. M. F. C. Andrade, H.-Y. Ko, L. Zhang, R. Car and A. Selloni, Free energy of proton transfer at the water–TiO₂ interface from ab initio deep potential molecular dynamics, Chem. Sci., 2020, 11, 2335–2341.
22. Y. Zhuang, R. Bi and J. Cheng, Resolving the odd–even oscillation of water dissociation at rutile TiO₂(110)–water interface by machine learning accelerated molecular dynamics, J. Chem. Phys., 2022, 157, 164701.
23. X. Yang, A. Bhowmik, T. Vegge and H. A. Hansen, Neural network potentials for accelerated metadynamics of oxygen reduction kinetics at Au–water interfaces, Chem. Sci., 2023, 14, 3913–3922.
24. M. Yang, U. Raucci and M. Parrinello, Reactant-induced dynamics of lithium imide surfaces during the ammonia decomposition process, Nat. Catal., 2023, 6, 829–836.
25. T. Marshall-Roth, N. J. Libretto, A. T. Wrobel, K. J. Anderton, M. L. Pegis, N. D. Ricke, T. V. Voorhis, J. T. Miller and Y. Surendranath, A pyridinic Fe-N₄ macrocycle models the active sites in Fe/N-doped carbon electrocatalysts, Nat. Commun., 2020, 11, 5283.
26. D. Eisenberg, T. K. Slot and G. Rothenberg, Understanding Oxygen Activation on Metal- and Nitrogen-Codoped Carbon Catalysts, ACS Catal., 2018, 8, 8618–8629.
27. A. Kumar, S. Ibraheem, T. A. Nguyen, R. K. Gupta, T. Maiyalagan and G. Yasin, Molecular-MN₄ vs atomically dispersed M−N₄−C electrocatalysts for oxygen reduction reaction, Coord. Chem. Rev., 2021, 446, 214122.
28. W. Liang, J. Chen, Y. Liu and S. Chen, Density-Functional-Theory Calculation Analysis of Active Sites for Four-Electron Reduction of O₂ on Fe/N-Doped Graphene, ACS Catal., 2014, 4, 4170–4177.
29. K.-M. Zhao, S. Liu, Y.-Y. Li, X. Wei, G. Ye, W. Zhu, Y. Su, J. Wang, H. Liu, Z. He, Z.-Y. Zhou and S.-G. Sun, Insight into the Mechanism of Axial Ligands Regulating the Catalytic Activity of Fe–N₄ Sites for Oxygen Reduction Reaction, Adv. Energy Mater., 2022, 12, 2103588.
30. W. Li, C. Liu, C. Gu, J.-H. Choi, S. Wang and J. Jiang, Interlayer Charge Transfer Regulates Single-Atom Catalytic Activity on Electride/Graphene 2D Heterojunctions, J. Am. Chem. Soc., 2023, 145, 4774–4783.
31. J. Zeng, D. Zhang, D. Lu, P. Mo, Z. Li, Y. Chen, M. Rynik, L. a. Huang, Z. Li and S. Shi, DeePMD-kit v2: a software package for deep potential models, J. Chem. Phys., 2023, 159, 054801.
32. H. Wang, L. Zhang, J. Han and E. Weinan, DeePMD-kit: a deep learning package for many-body potential energy representation and molecular dynamics, Comput. Phys. Commun., 2018, 228, 178–184.
33. J. Hafner, Ab initio simulations of materials using VASP: density‐functional theory and beyond, J. Comput. Chem., 2008, 29, 2044–2078.
34. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett., 1996, 77, 3865.
35. A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. In't Veld, A. Kohlmeyer, S. G. Moore and T. D. Nguyen, LAMMPS-a flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales, Comput. Phys. Commun., 2022, 271, 108171.
36. G. A. Tribello, M. Bonomi, D. Branduardi, C. Camilloni and G. Bussi, PLUMED 2: new feathers for an old bird, Comput. Phys. Commun., 2014, 185, 604–613.
37. Y. Zhang, H. Wang, W. Chen, J. Zeng, L. Zhang, H. Wang and W. E, DP-GEN: a concurrent learning platform for the generation of reliable deep learning based potential energy models, Comput. Phys. Commun., 2020, 253, 107206.
38. M. Yang, L. Bonati, D. Polino and M. Parrinello, Using metadynamics to build neural network potentials for reactive events: the case of urea decomposition in water, Catal. Today, 2022, 387, 143–149.
39. X. Yang, H. Ding, S. Li, S. Zheng, J.-F. Li and F. Pan, Cation-Induced Interfacial Hydrophobic Microenvironment Promotes the C–C Coupling in Electrochemical CO₂ Reduction, J. Am. Chem. Soc., 2024, 5532–5542.
40. P. Li, Y. Jiao, Y. Ruan, H. Fei, Y. Men, C. Guo, Y. Wu and S. Chen, Revealing the role of double-layer microenvironments in pH-dependent oxygen reduction activity over metal-nitrogen-carbon catalysts, Nat. Commun., 2023, 14, 6936.
41. H. Cao, G.-J. Xia, J.-W. Chen, H.-M. Yan, Z. Huang and Y.-G. Wang, Mechanistic Insight into the Oxygen Reduction Reaction on the Mn–N₄/C Single-Atom Catalyst: The Role of the Solvent Environment, J. Phys. Chem. C, 2020, 124, 7287–7294.
42. J. Lentz and S. H. Garofalini, Role of the hydrogen bond lifetimes and rotations at the water/amorphous silica interface on proton transport, Phys. Chem. Chem. Phys., 2019, 21, 12265–12278.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc06422d

---