Kinetics and dynamics of atomic-layer dissolution on low-defect Ag

Abstract

Electrochemical metal dissolution reaction is a fundamental process in various critical technologies, including metal anode batteries and nanofabrication. However, experimentally revealing the kinetics and dynamics of active sites of metal dissolution reactions is challenging. Herein, we investigate metal dissolution on near-perfect single-crystal surfaces of Ag within regions of a few hundred nanometers isolated by scanning electrochemical cell microscopy (SECCM). Potential oscillation is observed under constant current conditions for dissolution. The one-to-one correspondence between the dissolution charge and the geometry of the dissolution pit from colocalized imaging allows ambiguous correlation, which suggests that each oscillation cycle corresponds to the dissolution of one atomic layer. The oscillation behavior is further explained in a kinetic model, which reveals that the oscillation comes from the dynamic evolution of the number of different active sites as the dissolution progresses on each atomic layer. In addition to the fundamental interest, the ability to observe layer-by-layer dissolution in electrochemical measurements suggests a potential pathway for developing electrochemical atomic layer etching for fabricating structures and devices with atomic precision.

---

Introduction

Herein, we study the electrochemical metal dissolution behavior on low-defect single-crystal Ag (100) and Ag (111) surfaces isolated by scanning electrochemical cell microscopy (SECCM). The different dissolution rate at the step edge vs. basal plane causes potential oscillation under different dissolution currents, consistent with a layer-by-layer mechanism of dissolution. The ability to measure the metal dissolution reaction one atomic layer at a time helps to isolate the kinetics and mechanism at specific sites in electrochemical measurements.

Electrochemical metal dissolution reaction is one of the elementary reactions in many important technical processes, such as corrosion,^1–3 sensors,^4–6 material synthesis,^7,8 and battery technology.^9–11 Kinetics and rate-determining steps of metal dissolution reaction can be studied electrochemically.^12–15 However, in conventional electrochemical experiments, the electrode surface is not an ideal homogeneous surface. It inevitably exhibits diverse surface structures, such as grains with different crystal orientations and defects, including grain boundaries, dislocations, and point defects. These surface characteristics significantly affect thermodynamics, kinetics, and mechanism of metal dissolution reactions. Building the microscopic structure–activity relationship of metal dissolution reaction at different surface structures and sites is crucial in understanding the dissolution behavior at complex metal surfaces.

Silver is a model system for studying metal dissolution reactions. Despic and Bockris examined the kinetics of metal dissolution and highlighted the role of surface diffusion and adatom concentrations,¹⁶ which is also confirmed by Gerischer and coworkers.^17,18 Hackerman studied this reaction on a polycrystalline silver electrode using electrochemical impedance spectroscopy (EIS) and concluded the reaction is controlled by adatom diffusion.¹⁹ In all previous examples, electrochemical kinetics were measured using ensemble approaches on surfaces with unknown distributions of surface structures, including different local densities of dislocations. Because the measured activity is an ensemble average over the entire electrode surface, it is difficult to develop a site-specific mechanism that can be directly verified by experiments.

To better define the relationship between surface structure and the activity of metal dissolution, a local electrochemical method is desirable because it allows the isolation of specific surface structures. One emerging technique that allows such isolation is SECCM, which was developed by the Unwin group.²⁰ Several studies have investigated metal dissolution and its relationship with crystal orientations.^21–25 The influence of different electrolytes on metal dissolution kinetics and mechanisms has also been explored.^26–28 Mauzeroll and coworkers applied SECCM to study the electrochemical metal dissolution and passivation on different alloys and interpreted the results using a high-field model.^26–28 Our group have previously shown that the heterogeneity of metal dissolution at different surface structures can be elucidated using SECCM.²⁹ Combined with colocalized structural characterization using SEM, EBSD, and FIB-assisted TEM, we have explained the origin of heterogeneity in the metal dissolution reactions on different grain boundaries.³⁰ In addition, the effect of local oxide layer thickness on the local breakdown potential was also obtained via combined SECCM and TOF-SIMS. At low-defect crystal planes, however, the atomistic mechanisms of metal dissolution remain elusive.³¹

In this report, we demonstrated the SECCM approach to study the kinetics and mechanism of Ag dissolution at the low-defect single crystal (100) and (111) surfaces. The low-defect single crystal surface was prepared using Budewski's electrodeposition method.³² In galvanostatic experiments, potential oscillation is observed during the anodic dissolution. A model based on site-specific kinetics of dissolution on kink vs. edge sites was developed, which explains how the potential oscillation stems from layer-by-layer dissolution, with each oscillation cycle corresponding to monolayer dissolution. The preparation of high-quality electrode surface coupled with shrinking of electrode area under investigation by SECCM provide a unique design that allows us to link new experimental data with atomistic dissolution process, allowing new insight into metal dissolution reactions at low-defect surfaces.

Experimental section

HClO₄ (70%, certified ACS, Fisher) was used as received. All solutions were prepared using deionized water (18.2 MΩ cm, Synergy). Glassy carbon plate (SPI-Glas 22 grade, 100 mm × 100 mm) was purchased from SPI supplies and cut to smaller plates of ∼5 cm². The GC plate was polished on a polishing cloth (PSA Backing, Buehler) with slurries of γ-alumina particles (50 nm diameter, Electron Microscopy Sciences) and sonicated in deionized water for 10 min before electrodeposition.

Ag microparticles were deposited using constant potential in 6.0 M AgNO₃ (99.9+% metal basis, Thermo Scientific) and 100 mM HNO₃ (Trace Grade, Spectrum Chemical). The electrodeposition procedures are described in ESI Section 1.†

The SECCM was performed in a home-built scanning probe system which was covered by a thermally insulated Faraday cage, similar to our previous report.^29,30 The nanopipette was fabricated using a laser puller (Sutter, P-2000) and characterized using a scanning electron microscope. A silver wire (0.127 mm dia, 99.9% metals basis, Thermo Scientific) was used as a reference electrode for all SECCM experiments and microparticle deposition. The constant current Ag dissolution experiment is described in the ESI Section 2.† All SEM images were obtained on a FEI Quanta 650 ESEM system with the 10 keV accelerate voltage and 10 mm working distance.

Results and discussion

We studied the anodic dissolution of Ag⁰ to Ag⁺ (aq) in acid on Ag (111) and Ag (100) facets from Ag microparticles via SECCM as illustrated in Fig. 1a. A quartz nanopipette with an opening of ∼250 nm diameter was used as the probe, which was characterized under SEM as shown in Fig. 1b. An example microparticle shown in Fig. 1c contains square and triangular surfaces, corresponding to (100) and (111) facets, respectively. The microparticles were deposited under electrolyte conditions similar to those used by Budevski and coworkers³³ to obtain low-defect Ag at the sub-millimeter scale. AFM measurements of the basal plane revealed an RMS roughness of 977 pm (see ESI Section 3†). In addition, SECCM allows the isolation of a circular area about 250 nm in radius on a microparticle, as illustrated in Fig. 1a. The isolation of a smaller area allows a high probability of locating a low-defect area within a specific facet of interest.

Fig. 1 (a) Schematic of SECCM study of metal dissolution reaction on well-defined facets of Ag microparticle on glassy carbon substrate. SEM images of (b) the opening of a nanopipette and (c) an electrodeposited Ag microparticle. The nanopipette contains 1 mM AgClO₄ and 10 mM HClO₄.

A zero current was applied between the substrate and the Ag quasi-reference counter electrode (QRCE) inside the nanopipette when the nanopipette approached the microparticle. When the droplet was in contact with the substrate, the circuit was closed, resulting in an abrupt change in potential. This served as feedback to pause the pipette and prevent it from crashing onto the surface. A constant anodic current was then applied to induce Ag dissolution while a potential transient was recorded. After an electrochemical measurement of dissolution at one location was complete, the nanopipette was retracted and moved to a new location for a subsequent experiment.

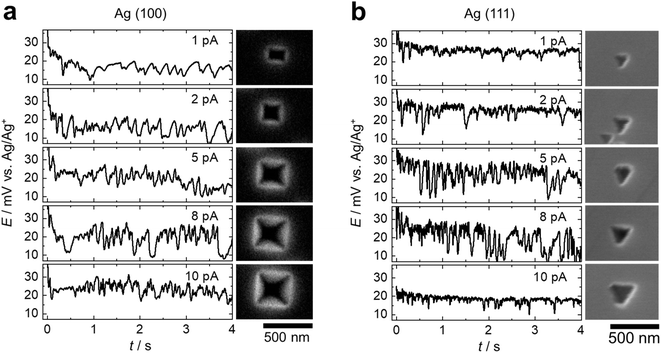
When dissolution occurs at different crystallographic facets, the geometries of the dissolution pits vary. As shown in the SEM images in Fig. 2, the pits exhibit projected shapes of near-squares on (100) facets (Fig. 2a), and triangles on (111) facets (Fig. 2d). The 3-fold and 4-fold symmetries of the (111) and (100) facets are reflected on these projected geometries of the dissolution pits. The potential transients at 2 pA applied current in Fig. 2c and f show that at t = 0, the potential quickly drops initially, then oscillates with a peak-to-peak amplitude of a few mV. The average period of oscillation is on the orders of 100 to 200 ms, and varies slightly from cycle to cycle. Conveniently, this potential is measured vs. the equilibrium potential of Ag/Ag⁺ due to the use of Ag QRCE, and therefore represents the overpotential for Ag dissolution.

Fig. 2 Example SEM image of a dissolution pit after 2 pA for 2 s on (a) Ag (100) and (d) Ag (111). Colocalized AFM topography on (b) Ag (100) and (e) Ag (111). Atomic models showing the (111) planes inside the dissolution pits are shown as insets. Topography profiles along the marked blue arrows are shown at the bottom. Representative E–t curves during Ag dissolution on (c) Ag (100) and (f) Ag (111). The electrolyte contains 1 mM Ag ClO₄ and 10 mM HClO₄.

We hypothesize that the dissolution in this isolated low-defect region operates in a layer-by-layer dissolution mechanism, with each oscillation cycle corresponding to the dissolution of one atomic layer of Ag. This layer-by-layer mechanism would have several predictions: first, dissolution predominantly occurs along a direction parallel to a certain crystal plane. Because the surface atoms on the (111) plane have the highest coordination number, the preferred dissolution direction should be parallel to (111). Second, the charge associated with each oscillation corresponds to a monolayer of Ag. Third, the frequency of oscillation increases with the applied current. This is because increasing current means a faster dissolution rate, therefore reducing the time to dissolve a specific monolayer.

The first prediction on the geometry is consistent with the triangle cross-section of the dissolution pit left on Ag(100) and Ag(111). On (100) surfaces, the geometry of the dissolution pits is confirmed as square-pyramidal by AFM (Fig. 2b). On (111) surfaces, the dissolution pit assumes a triangular prism shape with a flat bottom face parallel to the (111) surface of the microparticle (Fig. 2e). Both geometries are consistent with the preferred dissolution along the (111) plane. The deviation of the cross-section from a perfect square in some samples is attributed to dissolution starting from two positions on the surface and fusing together during the simultaneous dissolution and the tilting of our probe with respect to the normal of the sample surface. In addition, an oscillation in potential was observed during the dissolution on both Ag (100) (Fig. 2c) and Ag (111) (Fig. 2f). More examples of potential transients during dissolution of (111) and (100) are shown in ESI Section 4† and at different times with 10 pA of applied current in ESI Section 5.†

To investigate the second prediction, the charge from dissolution at different applied currents is compared with that calculated from AFM topography as described in ESI Section 6.† The charge agrees with that calculated using the volume of the dissolution pit (Fig. S6†). Note that the colocalization between the AFM and the SECCM allows us to associate each local E–t curve for dissolution to the exact dissolution pit under the AFM, which greatly reduces the error in the analysis from the variation at different locations. Furthermore, the charge associated with a single potential oscillation cycle is calculated from the average oscillation cycle duration and the applied current. This charge obtained from electrochemical measurement is compared with the expected charge of the monolayer based on the geometry of the dissolution pit. As shown in ESI Section 7,† the monolayer charge for dissolution on the Ag(100) surface is calculated using the area of the four (111) faces of the square pyramidal dissolution pit, which is obtained by the AFM after the SECCM dissolution experiment (Fig. S6†). The surface area of the dissolution pit on Ag (100) continues to grow vs. charge, so the “monolayer” charge also increases as more Ag layers are dissolved (Fig. S7†). We observed that the monolayer charge measured electrochemically and derived from the AFM topography both increase with the applied current (the dissolution time is fixed), as shown in Fig. S8.† When the dissolution current is <6 pA, the expected charge calculated from AFM topography agrees with the electrochemically measured charge, supporting the mechanism of layer-by-layer dissolution. At higher applied currents (>6 pA), the agreement becomes worse, likely due to the simultaneous stripping of multiple monolayers or overlapping of the potential transients. We speculate that this effect is ultimately responsible for the absence of visible oscillations in bulk electrochemical measurements on polycrystalline Ag.^15,16,34

To test the third prediction of the layer-by-layer mechanism, we measured the potential transient as a function of applied current. The potential oscillations become denser as the applied current increases on both Ag (100) and Ag (111), as shown in Fig. 3a and b, respectively. This trend qualitatively agrees with the prediction. Fast Fourier Transform (FFT) analysis of the E–t curves during dissolution shows no prevalent frequency, indicating that the potential oscillations are not periodic (Fig. S9†).

Fig. 3 Representative E–t curves during the local dissolution on (a) Ag (100) and (b) Ag (111) at various applied currents. The corresponding SEM images of the dissolution pits after the experiment are shown beside each E–t trace.

The duration of each oscillation (Δt) was further analyzed by obtaining its distribution following a peak-finding procedure described in ESI Section 8.† As shown in Fig. 4a and b, the distribution of Δt shifts to a shorter time as the applied current increases on both Ag (100) and Ag (111). On Ag (100), Δt decreases from 150 ± 6 to 49 ± 1 ms (mean ± standard deviation) when the current increases from 1 to 10 pA (Fig. 4c), which qualitatively consistent with the third prediction. We note that an increase of current by 10× does not lead to a 10× decrease in Δt. This is attributed to two reasons: (1) the area of active dissolving (111) planes is larger at a higher current as expected for the expansion of the pyramidal pit, which can also be observed in the SEM images in Fig. 3. The larger area of active (111) planes at a higher current means more charge to completely dissolve a monolayer, and therefore, the frequency will decrease. (2) The potential oscillation overlaps at a higher applied current, leading to an underestimation of Δt. On Ag (111) planes, the average oscillation duration decreases from 360 ± 30 to 30 ± 10 ms when the current decreases from 1 to 10 pA (Fig. 4d). We did not attempt to quantitatively compare the difference of Δt between Ag (100) and Ag (111) because different nanopipettes were used, and the variations in the pipette/droplet size lead to changes in the absolute charge associated with (111) monolayers exposed at the electrode/electrolyte interface. We also note that the size of the pits can be larger than the pipette opening, which is attributed to droplet wetting on Ag, and the variation of the pipette size.

Fig. 4 Distribution of oscillation duration (Δt) in E–t curves at various applied currents (i_app) for metal dissolution on (a) Ag (100) and (b) Ag (111). Average peak width (Δt) vs. applied current on (c) Ag (100) and (d) Ag (100). Each error bar represents the standard deviation from n = 10 E–t traces.

We also showed that similar potential oscillation behavior is observed under N₂ and O₂ environments (ESI Section 9†), suggesting O₂ is not involved in the oscillation. To further elucidate the dynamics of Ag dissolution on a low-defect surface, we simulate the E–t traces using a model that considers the site-specific kinetics and double-layer charging during galvanostatic electro-dissolution. The most reactive surface sites are the ones with fewer neighboring interactions. Therefore, kink sites (6 neighboring atoms) should dissolve faster than edge sites (7 neighboring atoms). The dynamics of formation and annihilation between kink sites and edge sites are shown in Fig. 5b–d, which are considered in the simulation. Typically, edge dissolution creates two new kink sites (Fig. 5b), while kink dissolution does not change the number of kink sites (Fig. 5c) unless two neighboring kink sites are annihilated (Fig. 5d). Other sites, such as adatoms or atoms within a perfect layer (coordination number of 9), are neglected for simplicity. The geometry of the dissolution pits and the number of atoms in dissolution in each layer are also considered in the model as illustrated in Fig. S14.† A description of the mathematical model is presented in ESI Section 11.†

Fig. 5 (a) Schematic showing a two-layer Ag (111) with kink and edge sites. Schematics of (b) edge dissolution, (c) kink dissolution, and (d) kink annihilation. (e) Simulated potential transient at different currents showing overpotential oscillation from layer-by-layer dissolution on Ag (100).

Simulated potential transients at different applied currents are presented in Fig. 5e, which shows the oscillation behavior. From the model, the oscillation in the current comes from the dynamic oscillation in the number of kink and edge sites as the dissolution progresses in each layer (vide infra). The average duration of the peak increases as the current increases, consistent with the experiments. On Ag (100), the frequency of the potential oscillation decreases as more layers are dissolved as required by the expansion of the pyramidal dissolution pit (Fig. S7†). The frequency stabilizes once the dissolution pits become sufficiently large. This trend in the frequency of oscillation is also observed experimentally on Ag (100) at a low dissolution current (e.g., 1 pA in Fig. 3a). At higher applied currents, the pits quickly become large enough that the oscillation frequency appears constant.

We observe several differences between the experiment and simulation. First, the duration of each oscillation is more erratic in the experiment compared to the simulation. This is likely due to the neglect of dissolution at sites other than kink or edge. Second, the potential overall increases with the applied current in the simulation, and significant heterogeneity in the current oscillation is observed at higher current (see also Fig. S4†). This discrepancy is attributed to the simplified assumptions in our model: the simulation considers sublayer dissolution only occurring after top layer is completely dissolved. Simultaneous dissolution of both top layer and sub-layers becomes important at higher applied current, which causes overlap of current contributions from multiple layers and deviation from our model prediction. Some shape variations in the potential transients can also be attributed to an induction mechanism, where the potential rises slowly until the activation barrier for the next layer is overcomed, followed by a sharp decrease. The details of this possible mechanism are discussed in ESI Section S12.† A more sophisticated model considering this phenomenon is beyond the scope of this current paper and will be explored in future work.

Combining simulation and experimental results, the potential oscillation can be understood through the following mechanism. As a monolayer starts dissolving, the number of kink atoms (i.e., active sites) increases through edge dissolution, which lowers the potential required to sustain the same current. This is because the kinetics (e.g., exchange current) is proportional to the number of atoms at the active sites. As the dissolution continues the monolayer, kink annihilation decreases the number of active sites, causing the overpotential to increase. The potential increases until a layer of atoms is completely dissolved and then decreases again as the next layer begins to dissolve.

Conclusions

We studied the kinetics and dynamics of metal dissolution reaction on low-defect Ag (111) and (100) isolated by SECCM. Potential oscillations were observed during the galvanostatic dissolution, consistent with a layer-by-layer dissolution mechanism. A microscopic model with site-specific kinetics was developed, showing that the dynamics of edge and kink sites on the electrode surface during dissolution contribute to the potential oscillation behavior, with each potential oscillation cycle corresponding to one atomic layer Ag dissolution. The experiment provides direct electrochemical evidence of the relevance of the layer-by-layer mechanism in metal dissolution reactions, offering new insights into the kinetics and dynamics of metal dissolution on low-defect surfaces at the nanoscale.

The insights into the metal dissolution reaction have broad applicability. The selective etching demonstrated in this work is directly relevant to nanofabrication techniques, including nanostructure sculpting for tuning plasmonic resonance,^34,35 and controlled layer dissolution for lithography fabrication.³⁶ Extending of the kinetic and mechanistic studies to 2D materials, such as transition metal dichalcogenides (e.g. MoS₂), can establish the foundational knowledge required to precisely control 2D material layers through etching, which hold promise for next-generation electronics.^37,38

This study can be extended to polycrystalline materials, where techniques such as Electron Backscatter Diffraction (EBSD) can map crystallographic orientations and correlate them with local dissolution behavior to reveal how different facets and grain boundaries influence etch rates. The site-specific insights from local electrochemistry can inform processes like atomic layer etching (ALE) in polycrystalline films, helping to address uniformity challenges in nanofabrication and semiconductor applications.

Data availability

The data supporting this article have been included as part of the ESI.† Other relevant data can be provided by the authors upon reasonable request.

Author contributions

Y. W. and R. G. C. contributed equally to this work. Conceptualization: H. R.; funding acquisition: H. R.; investigation: Y. W., R. G. C.; data analysis: Y. W. and R. G. C.; resources: H. R.; visualization: Y. W., R. G. C.; writing—original draft preparation: Y. W., R. G. C.; writing—review and editing: Y. W., R. G. C., H. R.; supervision: H. R. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors would like to acknowledge support from National Science Foundation (NSF) under the Chemical Measurement & Imaging (CMI) Program (CHE-2240113) and the Sloan Research Foundation (FG-2023-20317). We also acknowledge the Center for Electrochemistry, University of Texas at Austin, for providing partial financial support for this work through the Bard CEC Student Scholar Fellowship under Grant no. HF-0037 from the Welch Foundation. We acknowledge Alex Schmeltzer for the discussion and assistance on peak finding.

References

1. L. Liu, Y. Li and F. Wang, Electrochemical Corrosion Behavior of Nanocrystalline Materials—A Review, J. Mater. Sci. Technol., 2010, 26(1), 1–14.
2. M. Pourbaix, Electrochemical Corrosion of Metallic Biomaterials, Biomaterials, 1984, 5(3), 122–134.
3. N. Li, Y. Li, S. Wang and F. Wang, Electrochemical Corrosion Behavior of Nanocrystallized Bulk 304 Stainless Steel, Electrochim. Acta, 2006, 52(3), 760–765.
4. S. Głab, A. Hulanicki, G. Edwall and F. Ingman, Metal-Metal Oxide and Metal Oxide Electrodes as pH Sensors, Crit. Rev. Anal. Chem., 1989, 21(1), 29–47.
5. E. Katz, I. Willner and J. Wang, Electroanalytical and Bioelectroanalytical Systems Based on Metal and Semiconductor Nanoparticles, Electroanalysis, 2004, 16(1–2), 19–44.
6. Q. Ding, C. Li, H. Wang, C. Xu and H. Kuang, Electrochemical Detection of Heavy Metal Ions in Water, Chem. Commun., 2021, 57(59), 7215–7231.
7. Z. X. Cai, Z. L. Wang, J. Kim and Y. Yamauchi, Hollow Functional Materials Derived from Metal–Organic Frameworks: Synthetic Strategies, Conversion Mechanisms, and Electrochemical Applications, Adv. Mater., 2019, 31(11), 1804903.
8. A. Martinez Joaristi, J. Juan-Alcañiz, P. Serra-Crespo, F. Kapteijn and J. Gascon, Electrochemical Synthesis of Some Archetypical Zn²⁺, Cu²⁺, and Al³⁺ Metal Organic Frameworks, Cryst. Growth Des., 2012, 12(7), 3489–3498.
9. C. Zhan, T. Wu, J. Lu and K. Amine, Dissolution, Migration, and Deposition of Transition Metal Ions in Li-ion Batteries Exemplified by Mn-Based Cathodes–A Critical Review, Energy Environ. Sci., 2018, 11(2), 243–257.
10. T. Joshi, K. Eom, G. Yushin and T. F. Fuller, Effects of Dissolved Transition Metals on the Electrochemical Performance and SEI Growth in Lithium-Ion Batteries, J. Electrochem. Soc., 2014, 161(12), A1915–A1921.
11. J. Desilvestro and O. Haas, Metal Oxide Cathode Materials for Electrochemical Energy Storage: a Review, J. Electrochem. Soc., 1990, 137(1), 5C–22C.
12. M. Stefanoni, U. M. Angst and B. Elsener, Kinetics of Electrochemical Dissolution of Metals in Porous Media, Nat. Mater., 2019, 18(9), 942–947.
13. J. M. Kolotyrkin, Effects of Anions on the Dissolution Kinetics of Metals, J. Electrochem. Soc., 1961, 108(3), 209–216.
14. H. Lee and K. Nobe, Kinetics and Mechanisms of Cu Electrodissolution in Chloride Media, J. Electrochem. Soc., 1986, 133(10), 2035–2043.
15. E. Mattsson and J. M. Bockris, Galvanostatic Studies of the Kinetics of Deposition and Dissolution in the Copper⁺ Copper Sulphate System, Trans. Faraday Soc., 1959, 55, 1586–1601.
16. A. Despic and J. O. M. Bockris, Kinetics of the Deposition and Dissolution of Silver, J. Chem. Phys., 1960, 32(2), 389–402.
17. H. Gerischer and R. P. Tischer, Zum Mechanismus der elektrolytischen Abscheidung und Auflösung fester Metalle I. Vorgänge bei der stationären Auflösung von Silberelektroden und die Geschwindigkeit der Durchtrittsreaktion, Z. Elektrochem., 1957, 61(9), 1159–1162.
18. H. Gerischer, Mechanism of Electrolytic Deposition and Dissolution of Metals, Anal. Chem., 1959, 31(1), 33–39.
19. D. Larkin and N. Hackerman, The Ag⁺-Ag Exchange Reaction in Aqueous Acidic Nitrate Electrolyte, J. Electrochem. Soc., 1977, 124(3), 360–363.
20. N. Ebejer, M. Schnippering, A. W. Colburn, M. A. Edwards and P. R. Unwin, Localized High Resolution Electrochemistry and Multifunctional Imaging: Scanning Electrochemical Cell Microscopy, Anal. Chem., 2010, 82(22), 9141–9145.
21. V. Shkirskiy, L. Yule, E. Daviddi, C. Bentley, J. Aarons, G. West and P. Unwin, Nanoscale Scanning Electrochemical Cell Microscopy and Correlative Surface Structural Analysis to Map Anodic and Cathodic Reactions on Polycrystalline Zn in Acid Media, J. Electrochem. Soc., 2020, 167(4), 041507.
22. E. Daviddi, V. Shkirskiy, P. M. Kirkman, M. P. Robin, C. L. Bentley and P. R. Unwin, Nanoscale Electrochemistry in a Copper/Aqueous/Oil Three-phase System: Surface Structure–Activity-Corrosion Potential Relationships, Chem. Sci., 2021, 12(8), 3055–3069.
23. L. C. Yule, C. L. Bentley, G. West, B. A. Shollock and P. R. Unwin, Scanning Electrochemical Cell Microscopy: A Versatile Method for Highly Localized Corrosion-Related Measurements on Metal Surfaces, Electrochim. Acta, 2019, 298, 80–88.
24. L. C. Yule, V. Shkirskiy, J. Aarons, G. West, B. A. Shollock, C. L. Bentley and P. R. Unwin, Nanoscale Electrochemical Visualization of Grain-Dependent Anodic Iron Dissolution from Low-Carbon Steel, Electrochim. Acta, 2020, 332, 135267.
25. M. Bernal, D. Torres, S. S. Parapari, M. Čeh, K. Ž. Rožman, S. Šturm and J. Ustarroz, A Microscopic View on the Electrochemical Deposition and Dissolution of Au with Scanning Electrochemical Cell Microscopy—Part I, Electrochim. Acta, 2023, 445, 142023.
26. H. Zhou, D. Chhin, A. Morel, D. Gallant and J. Mauzeroll, Potentiodynamic Polarization Curves of AA7075 at High Scan Rates Interpreted Using the High Field Model, npj Mater. Degrad., 2022, 6(1), 20.
27. Y. Li, A. Morel, D. Gallant and J. Mauzeroll, Oil-Immersed Scanning Micropipette Contact Method Enabling Long-Term Corrosion Mapping, Anal. Chem., 2020, 92(18), 12415–12422.
28. L. Grandy, S. R. Yassine, R. Lacasse and J. Mauzeroll, Selective Initiation of Corrosion Pits in Stainless Steel Using Scanning Electrochemical Cell Microscopy, Anal. Chem., 2024, 96(19), 7394–7400.
29. Y. Wang, M. Li, E. Gordon, Z. Ye and H. Ren, Nanoscale Colocalized Electrochemical and Structural Mapping of Metal Dissolution Reaction, Anal. Chem., 2022, 94(25), 9058–9064.
30. Y. Wang, M. Li and H. Ren, Interfacial Structure and Energy Determine the Heterogeneity in the Electrochemical Metal Dissolution Activity at Grain Boundary, Chem. Mater., 2023, 35(11), 4243–4249.
31. R. Kang, Y. Zhao, D. Hait, J. A. Gauthier, P. A. Kempler, K. A. Thurman, S. W. Boettcher and M. Head-Gordon, Understanding Ion-Transfer Reactions in Silver Electrodissolution and Electrodeposition from First-Principles Calculations and Experiments, Chem. Sci., 2024, 15(13), 4996–5008.
32. E. Budewski, W. Bostanoff, T. Witanoff, Z. Stoinoff, A. Kotzewa and R. Kaischew, Keimbildungserscheinungen an Versetzungsfreien (100)-Flächen von Silbereinkristallen, Electrochim. Acta, 1966, 11(12), 1697–1707.
33. E. Budewski and W. Bostanoff, Galvanostatische Einschaltkurven an Einkristallelektroden, Electrochim. Acta, 1964, 9(4), 477–482.
34. J. S. Huang, V. Callegari, P. Geisler, C. Brüning, J. Kern, J. C. Prangsma, X. Wu, T. Feichtner, J. Ziegler, P. Weinmann, M. Kamp, A. Forchel, P. Biagioni, U. Sennhauser and B. Hecht, Atomically Flat Single-crystalline Gold Nanostructures for Plasmonic Nanocircuitry, Nat. Commun., 2010, 1, 150.
35. R. T. Hill, J. J. Mock, A. Hucknall, S. D. Wolter, N. M. Jokerst, D. R. Smith and A. Chilkoti, Plasmon Ruler with Angstrom Length Resolution, ACS Nano, 2012, 6(10), 9237–9246.
36. Y. You, J. Park and J. Kim, Editors' Choice—Atomic Layer Etching of Tungsten Disulfide Using Remote Plasma-Induced Oxidation and Wet Etching, ECS J. Solid State Sci. Technol., 2023, 12(7), 075009.
37. M. Chhowalla, H. S. Shin, G. Eda, L.-J. Li, K. P. Loh and H. Zhang, The Chemistry of Two-Dimensional Layered Transition Metal Dichalcogenide Nanosheets, Nat. Chem., 2013, 5(4), 263–275.
38. W. Zhou, X. Zou, S. Najmaei, Z. Liu, Y. Shi, J. Kong, J. Lou, P. M. Ajayan, B. I. Yakobson and J.-C. Idrobo, Intrinsic Structural Defects in Monolayer Molybdenum Disulfide, Nano Lett., 2013, 13(6), 2615–2622.

---

Footnotes

† Electronic supplementary information (ESI) available: Experimental and simulation details; additional electrochemistry data; and additional simulation data. See DOI: https://doi.org/10.1039/d4sc05954a

‡ These authors contributed equally to this work.

---