Slow magnetic relaxation and strong magnetic coupling in the nitroxyl radical complexes of lanthanide(III) with diamagnetic ground state (Ln = Lu, Eu)

Abstract

Radical lanthanide complexes are appealing platforms to investigate the possibility to engineer relevant magnetic couplings between the two magnetic centers by exploiting the strongly donating magnetic orbitals of the radical. In this paper, we report a spectroscopic and magnetic study on [LnRad(NO₃)₃], where Ln = Eu³⁺ or Lu³⁺ and Rad is the tridentate tripodal nitroxyl radical 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl. A thorough magnetic investigation by Electron Paramagnetic Resonance (EPR) spectroscopy and magnetometry, fully supported by ab initio calculations, allowed us to unravel an unprecedentedly large antiferromagnetic coupling between the Eu³⁺ and the radical (J₁₂ = +19.5 cm⁻¹, +J₁₂S₁S₂ convention). Remarkably, both europium and lutetium complexes showed slow magnetization dynamics below 20 K. The field and temperature dependent relaxation dynamics, dominated by Raman and direct processes were modelled simultaneously, allowing us to assess that the Raman process is field dependent.

---

Introduction

The development of molecule-based materials with specific functional properties^1–4 requires the understanding of the electronic structure of molecular complexes, and how their fundamental properties can be manipulated. Lanthanide(III) (Ln) coordination compounds are unique in this respect due to their combination of magnetic, redox,⁵ photophysical and catalytic properties.^6–13 Due to the synergic effects of strong spin orbit coupling and a moderate ligand field, which can lead to a magnetic anisotropy barrier, mononuclear Ln complexes often manifest Single Molecule Magnet (SMM) behaviour, i.e. slow relaxation of the magnetization below a blocking temperature.¹⁴

Among the means to increase the height of the magnetic anisotropy barrier, the coupling of the magnetic moment of the lanthanide with another spin carrier is one of the most interesting possibilities.^15–17 However, this coupling is difficult to achieve due to the shielded nature of the 4f orbitals. The most successful strategies to achieve magnetic communication between a lanthanide and another spin are the use of large donor bridging atoms^18–20 and the exploitation of the orbitals of organic radical ligands, with strongly donating magnetic orbitals providing effective overlap with the inner 4f orbitals of the lanthanide. Among them, tetrazine and pyrazine radicals have recently been highly exploited.^21–28

More recently, it has been shown that, due to inefficient spin-phonon coupling, an effective S = 1/2 coupled to a Ln characterized by a diamagnetic ground state might provide slow relaxation of the magnetization in an external applied field^29,30 in analogy to the slow relaxation detected for S = 1/2 molecular spin qubits.^31–34 If the lanthanide chosen is Eu³⁺, widely known for its rich photophysical properties, this provides a means to obtain a luminescent, slowly relaxing species. Diamagnetic lanthanides are exploited in heteronuclear coordination compounds^29,35–38 or complexes with redox active or radical ligands.^9,39–41 Nevertheless, magnetic studies of complexes encompassing diamagnetic Lu³⁺,^42–46 Y³⁺,^41,47–60 La³⁺ (ref. 50, 56, 59, 61 and 62) and poorly magnetic Eu³⁺ ions^{46,50,59,61,63,64} are rare and often undertaken only to evaluate inter-radical interactions in diradical lanthanide complex {Ln^III(radical)₂} species. To the best of our knowledge, no determination of the Ln³⁺–radical exchange interaction in Eu³⁺–radical systems has ever been reported. This lack of information probably stems from the assumption that the coupling is weak and should be, therefore, active only at low temperature, where only the ground J = 0 state of the ⁷F_J of Eu³⁺ is populated, thus being hardly detectable. However, this approach hides a misconception, since the exchange coupling involves the two spins, S = 1/2 and S = 3 for the radical and the Eu³⁺, respectively. The effects of the exchange coupling should then be visible at any temperature if the interaction is strong enough.

In order to improve our understanding of the nature of the coupling between radical spins and poorly magnetic lanthanides, we investigated the magnetic and luminescent properties of an Eu³⁺–radical system in which the magnetic exchange interaction, estimated by the corresponding Gd³⁺ derivative,⁶⁵ is expected to be strong. In this approach, the Lu³⁺ derivative provides the ideal closed-shell reference to derive the influence of the Eu³⁺ presence on the radical behavior. We then selected for the present study [EuRad(NO₃)₃] and [LuRad(NO₃)₃], where Rad is a tridentate tripodal nitroxyl radical—4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl (Scheme 1). For this paramagnetic tripod, strong magnetic exchange interactions were recorded with 3d metal ions^66,67 and gadolinium(III)⁶⁵ and field-induced slow magnetic relaxation for the cobalt(II)⁶⁸ and terbium(III)⁶⁵ complexes. The europium(III) derivative showed the expected luminescence, and both studied complexes exhibit field-induced slow magnetic relaxation (SMR) below 20 K. In addition, dc-magnetic measurements and EPR spectroscopy clearly demonstrated the presence of a large and antiferromagnetic Eu–Rad exchange interaction, the latter being modelled by ab initio theoretical calculations, which also provided indications on the coupling mechanism between paramagnetic centres.

Scheme 1 Tridentate radical – 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl (Rad).

Results and discussion

Tripodal ligands possess a predictable coordination mode, which is essential for molecular and crystal engineering. Tripodal binding mode of the paramagnetic ligand (Rad) is ensured by the set of the donor atoms, i.e. an oxygen of the nitroxyl group and the two nitrogen atoms from 2-pyridyl substituents; and by the presence of an sp³ hydridized carbon, which fulfils the role of a bridgehead atom. In all previously studied metal complexes only the tripodal mode of coordination, i.e. with Rad occupying the three sites on the vertices of a triangle in the coordination sphere of a central atom, has been reported.^65–74 In this context, Ln³⁺ nitrate salts turned out to be suitable precursors, because the three nitrate anions block six coordination sites leaving a space only for one Rad ligand, resulting in a neutral species without solvent molecules. The synthesis of [LnRad(NO₃)₃], where Ln = Eu³⁺ or Lu³⁺ and Rad is the tridentate tripodal nitroxyl radical 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine-3-oxyl thus followed the procedure, previously reported for the other Ln³⁺ derivatives.⁶⁵ The phase purity of the obtained bulk polycrystalline samples was ascertained by elemental and PXRD analyses as shown in Fig. S1†.

Crystal structures

The powder diffractograms indicate that all the complexes from the series: [LnRad(NO₃)₃] (Ln = Gd, Dy, Tb, Tm, Y, Eu and Lu), studied to date, are isostructural.⁶⁵ The crystal cell parameters and powder diffraction patterns for europium and lutetium complexes are presented in Table S1 and Fig. S1†, respectively. According to the stereochemical analysis⁷⁵ (see Table S2†), the LnO₇N₂ polyhedron for the whole series⁶⁵ is best defined as a spherical tricapped trigonal prism geometry, with an idealized D_3h point group symmetry. In the neutral complexes, the paramagnetic ligand is coordinated to the central atom in a tridentate tripodal manner through two nitrogen atoms of the pyridyl groups and one oxygen of NO moiety (Fig. 1), and three nitrate anions acts as bidentate anionic ligands compensating the tripositive charge of the central atom. The donor atoms of Rad compose a triangular face of the prism. The Ln–O_Rad bond distances are 2.425(2) and 2.343(5) Å for Eu and Lu, respectively. N–O bond length of the nitroxide moiety is 1.275(3) and 1.247(8) Å for Eu and Lu, respectively. Noteworthy, both these bond lengths, and the angles are in the anticipated range (see Table S3†). The packing of molecules and distances between lanthanide ions correspond to those for the previously published complexes.⁶⁵

Fig. 1 Molecular structure of [LnRad(NO₃)₃], hydrogen atoms are omitted for clarity.

Fluorescence of [EuRad(NO₃)₃]

Ordinarily, under UV irradiation, the emission of europium(III) complexes of diamagnetic ligands display the spectral transitions from emitting level ⁵D₀ to ground levels ⁷F_J (J = 0–4).^13,76 However, the photophysical properties of europium(III) compounds with radical ligands were poorly investigated previously. For this reason, it was of great interest to probe the emission photoluminescence of [EuRad(NO₃)₃]. Fig. 2 shows a cascade of emission bands to five different multiplets using an excitation source at wavelength of 397 nm. Since the spectrum was recorded at room temperature, the peaks corresponding to ⁵D₀ → ⁷F_J (J = 0–5) transitions are usually broadened compared to those for low-temperature spectra. Consequently, peaks of weak intensity may be poorly distinguishable at a broad background line. A simple Gaussian fit of the emission reveals the following barycentres of the states: 16 892 cm⁻¹ (592 nm), 16 234 cm⁻¹ (616 nm), 15 349 cm⁻¹ (651.5 nm), 14 286 (700 nm), and 13 736 (728 nm) corresponding to the ⁵D₀ → ⁷F_J (J = 1–5) transitions as reported in Table 1. The luminescence to the ground ⁷F₀ state is not clearly observed, in agreement with expectations from Judd–Ofelt theory.⁷⁶ Remarkably, the absence of ⁵D₀ → ⁷F₀ in the emission spectrum supports the SHAPE analysis in indicating a high local symmetry around the Eu³⁺ ion since this transition should be observed for sites of symmetry C_s, C_n or C_nv.^76,77 Interestingly, this transition appears as a very weak peak in [Eu(Tpm)(NO₃)₃] (Tpm is tris(3,5-dimethylpyrazolyl) methane),⁷⁸ which can be considered as the congener of [EuRad(NO₃)₃] but with a diamagnetic tripod, given the similarity of their coordination polyhedra. The first observed transition in [EuRad(NO₃)₃] at 592 nm is the ⁵D₀ → ⁷F₁ transition, which possesses a moderate emission intensity. It is a magnetic dipole (MD) allowed transition, the integral intensity of which is substantially unaffected by the metal ion environment. On the other hand, the absence of a structure of this peak indicates that at this temperature we do not have enough resolution to observe the different components due to crystal-field splitting of the ⁷F₁ multiplet. The ⁵D₀ → ⁷F₂ transition, most affected by the local symmetry of the Eu³⁺ ion and the nature of the ligands, appears in the spectrum as the main peak at 616 nm, being responsible for red light release by the complex. The presence of this intense peak indicates that the Eu³⁺ is not at a centrosymmetric site. The ⁵D₀ → ⁷F₃ transition has a maximum intensity at 652 nm. Usually this ED transition is very weak, since it is also forbidden according to the Judd–Ofelt theory, and can be strengthened by strong J-mixing. Remarkably, for our complex we observe the peaks at 700 and 730 nm, corresponding to the ⁷F₄ and ⁷F₅ multiplets, usually very weak. This is also related to a strong J-mixing.

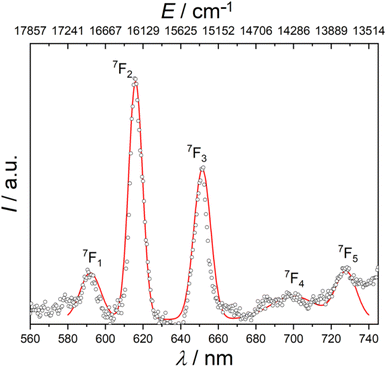Fig. 2 Room temperature photoluminescence emission spectrum for solid [EuRad(NO₃)₃] at excitation wavelength of 397 nm. The red line is a simple fit using a sum of five gaussian curves.

Table 1 Photoluminescence data for Eu³⁺ in [EuRad(NO₃)₃] and [Eu(Tpm)(NO₃)₃] (left). Energy levels of [EuRad(NO₃)₃] from ab initio calculations and magnetic data simulation (right)

Transitions	Common range^76	EuRad	EuTpm^78	Energy levels ^7FJ (J = 0–5) of [EuRad(NO3)3]/cm^−1
	λ, nm			Eu^3+ (ref. 79)^b	CASSCF-SOC^c	NEVPT2-SOC^c	Magnetism^c
a Very weak. b Calculated energies of Eu^3+ free-ion levels.^79 c Barycentre.
^5D0 → ^7F0	570–585	—^a	580^a	0	0	0	0
^5D0 → ^7F1	585–600	592	594	379	322/352/414 (362)	332/366/436 (378)	314.6/324.6/508.8 (383)
^5D0 → ^7F2	610–630	616	616	1043	998/1021/1049/1068/1102 (1048)	1025/1054/1087/1109/1150 (1085)	1044/1066/1156/1166/1212 (1029)
^5D0 → ^7F3	640–660	652	653	1896	1945/1958/1962/1971/2003/2041/2059/(1991)	1993/2005/2013/2032/2064	2179/2212/2226/2252/2253/2275
						2112/2131(2050)	2284.8 (2240)
^5D0 → ^7F4	680–710	700	700	2869	2966/2977/3083/3116/3165/3192/3223/3231/3335 (3143)	3012/3025/3148/3186/3254	3687/3692/3701/3709/3728/3732/3740/3748/3756 (3721)
						3281/3319/3332/3450 (3223)
^5D0 → ^7F5	740–770	728	—	3912	4284/4329/4345/4394/4406	4348/4406/4425/4474/4500	5478/5493/5523/5530/5545/5567
					4466/4483/4502/4539/4552	4566/4585/4613/4651/4665	5572/5611/5623/5657/5695 (5573)
					4559 (4442)	4685 (4538)

---

We note that despite the same idealized symmetry (D_3h) and similarity of the coordination spheres with [Eu(Tpm)(NO₃)₃] there are obvious differences in the intensity and structure of the spectral bands of the two complexes. These might be attributed to differences in J-mixing;⁷⁶ it is tempting to attribute these differences to the presence of an exchange coupling interaction between the radical spin and the Eu³⁺ centre. Additional photophysical studies at low temperatures are, however, necessary to understand exactly how the spin coupling of Eu³⁺ and radical affects the electronic structure comparatively to the related complex of formally diamagnetic analogue of Rad. This is beyond the scope of the present study, mainly focused on the resultant magnetic properties (see below).

DC magnetic properties and EPR spectroscopy. Direct current (dc) magnetic susceptibilities for the polycrystalline samples were measured in the temperature range of 2–300 K under an applied magnetic field of 1000 Oe. The room temperature χT value of 1.541 emu K mol⁻¹ is lower than the sum of the Curie constants of a free radical and a typical Eu³⁺ complex (0.375 + 1.251 = 1.626 emu K mol⁻¹, where 1.251 emu K mol⁻¹ is a reference value found for the [Eu(Tpm)(NO₃)₃] complex mentioned above),⁸⁰ (Fig. 3a). The χT value steadily decreases to reach 0.23 emu K mol⁻¹ at T = 2 K, in agreement with reported values for most Eu³⁺–radical complexes.^63,81–83 Such a low value is often ascribed to the presence of diamagnetic impurities or non-radical ligands.⁸³ In the present case, however, both elemental and phase analyses (Fig. S1†) unambiguously confirm the product purity. Moreover, the χT value of [Lu(Rad)(NO₃)₃] is almost constant in the entire temperature range and matches well the value corresponding to one unpaired electron (0.375 emu K mol⁻¹) (insert in Fig. S2†). Therefore, we attribute the observed low values of χT at low temperature for [Eu(Rad)(NO₃)₃] to a strong antiferromagnetic coupling between Eu³⁺ and the radical spins. This hypothesis is confirmed by the field dependent magnetization curves reported in Fig. 3b, for which the highest value measured at T = 2 K (ca. 0.67 mB) is lower than the one of [Lu(Rad)(NO₃)₃] (ca. 1μ_B, see Fig. S2†).

Fig. 3 Magnetic behaviour of [EuRad(NO₃)₃]: (a) temperature dependence of χT product at B = 0.1 T; (b) magnetization curve measured at 1.8 K (blue), 5 K (green) and 10 K (red). Black continuous lines are the best fits obtained with the model described in the text. The dashed red line is the SA-CASSCF(7,8)/NEVPT2/QDPT calculated χT curve.

To obtain more information on this point, we performed a low temperature EPR study. Indeed, while for the few Eu³⁺–radical systems investigated by this technique up to now the resulting spectrum could simply be attributed to the isolated radical spin,^63,84 we considered that a relatively large antiferromagnetic coupling should bring in the anisotropy induced on Eu³⁺ by the ligand field acting on its angular orbital momentum.

Indeed, the EPR study of a microcrystalline powder, recorded at low temperature (Fig. 4), showed for [Eu(Rad)(NO₃)₃] a spectrum which strongly contrasts with the one of [Lu(Rad)(NO₃)₃], that can be simply simulated with an isotropic g = 1.998(1), as expected for a simple radical (Fig. S3†). The spectral features of [Eu(Rad)(NO₃)₃] are typical for a strongly anisotropic effective doublet, with g_⊥ < g_∥ and both principal values (g_∥ ≃ 1.75, g_⊥ ≃ 1.46) are much lower than the free electron g factor (g = 2.0023).

Fig. 4 Experimental X-band EPR spectra (continuous lines) and their simulations (dotted lines) for [EuRad(NO₃)₃] at the temperatures of 5, 10, 30 and 50 K obtained using parameters and Hamiltonian reported in the text.

To understand the origin of such peculiar behaviour, which is to the best of our knowledge unreported for Eu³⁺ complexes, we made a survey of simulated spectra by using Hamiltonian⁸⁵(1):

Here, the first term describes the spin–orbit coupling of Eu³⁺-ion; the second one takes into account the ligand field, acting on the orbital component of the metal centre, and is described by a second-order axial operator based on the analysis of the coordination polyhedron; the third one is the Zeeman interaction of the two different spins and the orbital moment existing in the system; the final term defines the isotropic coupling between the europium spin and the radical one, positive values of J₁₂ corresponding to antiferromagnetic coupling. The results, reported in Fig. S4a†, clearly show that, if no ligand field is considered, an antiferromagnetic coupling between the spin component of the Eu³⁺ and the radical spin results in an isotropic signal with g < 2.00, while the opposite is true for a ferromagnetic coupling. On the other hand, if one also includes the ligand field (Fig. S4b–d†), an axial spectrum is observed: this has g_⊥ < g_∥ if C⁰₂·J₁₂ > 0, whereas the opposite holds for C⁰₂·J₁₂ < 0.

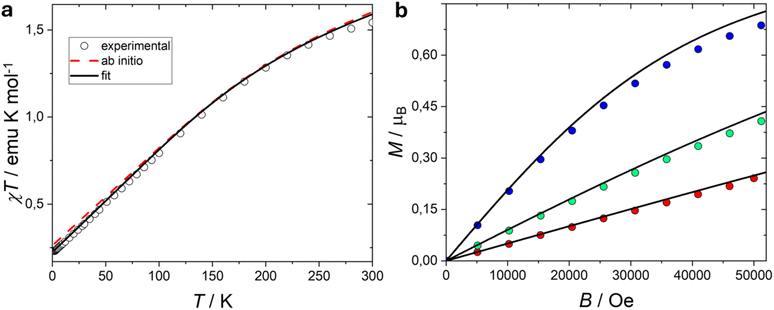
On these bases, the observed spectrum, centred at an average g < g_e can be directly attributed to the antiferromagnetic nature of the exchange coupling between europium(III) and the radical, of non-negligible magnitude compared to the spin–orbit coupling of europium ion. On the basis of the survey of the simulated spectra the observation of an easy axis anisotropy further indicates that the parameter describing the axial ligand field acting on the L = 3 angular momentum of the europium(III) must be positive. This behaviour can be rationalized by considering that the projection of the orbital momentum on the first excited J = 1 state for the ⁷F multiplet has a negative coefficient (−45/10).⁸⁶ Following these premises, we attempted a combined simulation of the EPR and the static magnetic measurements by means of the Hamiltonian (1). A very satisfactory simulation of both magnetic (solid lines in Fig. 3) and EPR data (dotted lines in Fig. 4) was achieved by using the following values: λ_Eu = 370 cm⁻¹, C⁰₂ = 14 cm⁻¹, J₁₂ = +19.5 cm⁻¹, and fixed g_L = 1, g_S = 2.0023, g_Rad = 1.998 (the complete spin system structure is reported in the ESI†). With these parameters, the low-lying energy structure is the one reported in the last column of Table 1. The ground and first excited multiplet are also reported in Fig. S6† to provide a better comparison with ab initio calculations (vide infra).

Notably, the value of 19.5 cm⁻¹ for Eu³⁺–radical exchange coupling is comparable with that of 23 cm⁻¹ found for its Gd³⁺ congener,⁶⁵ which is the largest among the nitroxide complexes of Ln studied to date.^87–89 As a comparison, we note that for the complexes involving a single nitronyl nitroxide,^90–95 the exchange coupling is even lower (|J₁₂| = 0.77–8.35 cm⁻¹). For the monoradical complexes of the closest congeners of our Rad-ligand, the derivatives of the six-membered hetero-cyclic Tempo (2,2,6,6-tetramethylpiperidin-1-yl)oxidanyl, is coupled to Gd³⁺ with J₁₂ = 2.43 and 9.25 cm⁻¹.^96,97 For the semiquinonate complex, [Gd(HBTp₃)₂SQ], |J₁₂| is 11.4 cm⁻¹.⁹⁸

For the complexes of organic radicals and europium(III), for which the ground spin state is usually considered to be diamagnetic,⁹⁹ such a strong magnetic interaction is unprecedented, as is the observation of an EPR spectrum.

The cause of this robust coupling in the Eu/Gd–Rad trinitrate complexes is most likely determined by the favorable superposition of the Ln and radical magnetic orbitals. In contrast to the greatly investigated complexes with nitronyl and imino nitroxyl radicals, in which the spin density is mainly delocalized over four or three atoms (O–N⋯N–O, N⋯N–O),^100–102 in Rad, one unpaired electron is delocalized only in two atoms: nitrogen and oxygen. Therefore, the spin density on the donor O atom in Rad is greater than that in a nitroxyl radical. In order to get more insight into the origin of the magnetic coupling and on the experimentally obtained energy level structure, we performed DFT and ab initio calculations, which are reported below.

Ab initio calculations: magnetic behaviour simulation and electronic structure of Eu specie. The calculations of the temperature dependence of magnetic susceptibility was performed at SA-CASSCF(7,8)/NEVPT2/QDPT level, and the results are presented in Fig. 3a. In order to emphasize the key role of the dynamic correlation to correctly reproduce the experiments we report in Fig. S5† the χT curve obtained before and after this correction. Based on the electronic structure calculations, the level splitting between octets and sextets (Fig. 5 and Table S4†) is larger in the case of account of dynamic correlation, which corresponds to a larger value of effective exchange interaction between Eu³⁺ and radical spins.

Fig. 5 The lowest spin multiplets (seven octets and sextets) calculated for [EuRad(NO₃)₃] at SA-CASSCF(7,8) (CASSCF) and SA-CASSCF(7,8)/NEVPT2 (NEVPT2) and SO-multiplets after account of SOC at QDPT level (CASSCF-SOC and NEVPT2-SOC). Kramers doublets appearing after account of SOC are roughly presented as a result of interaction between Eu³⁺ states with assigned full moment J (purple) and ligand doublet state interaction.

The lowest spin multiplets of the [EuRad(NO₃)₃] are presented in Fig. S6 and S7,† to highlight the different electronic structure terms involved in the calculations. Based on the result of interaction between europium ⁷F and ⁵D terms and radical ²S term, only seven, twelve and five roots for the multiplicities 8, 6 and 4 were taken in consideration. The corresponding MOs involved in the active space are depicted in Fig. S8† and the full electronic structure is presented in Fig. S9† after the calculations at different levels of theory. The splitting can be defined within the framework of the effective spin-Hamiltonian approach as exchange interaction between europium and radical spins. The ground state of the complex is the sextet state with the next first excited octet state at 54.1 cm⁻¹. The account of dynamic correlation leads to a larger splitting between sextets and octets. The effective value of exchange parameter J₁₂ = 14.9 cm⁻¹ extracted from the splitting between each of seven octets and sextets pairs is in a good agreement with the one obtained from the magnetometric and EPR data.

Additionally, the main magnetic axis (MMA) of the ground doublet state was calculated and reported in Fig. S10†. The angles between it and MMA of the next eight excited states are reported in Table S5†. The principal values of the g-tensor of the lowest nine Kramers doublets and corresponding directions of the main magnetic axes for each component are presented in the Table S6†. Fig. S11 and S12† present the spin density map calculated for the ground sextet state at DFT level using B3LYP functional. According to the calculation results, the spin density for the [EuRad(NO₃)₃] compound is concentrated on the Eu-center and radical NO group, with almost equal negative density on nitrogen and oxygen atoms (|0.485| and |0.454| μ_B on N and O, respectively). The latter result is in agreement with the spin density previously reported for tempone,¹⁰² and is consistent with our hypothesis of radical tripod being more “compact” compared to the nitronyl and imino-nitroxyl radicals, which have magnetic orbitals spread over four or three atoms.^100–103 This favours a stronger exchange for the tripodal nitroxyl radical than for nitronyl and imino-nitroxyl ones.

The C⁰₂ parameter describing the ligand field and acting on the orbital component of the metal center, obtained using SINGLE-ANISO module after account of dynamic correlation, is 15.9 cm⁻¹ and correlates well with the value obtained from the fit of the experimental data. According to the AILFT calculations, the resulting value of effective SOC constant is ζ = 1378.6 cm⁻¹, and the corresponding λ = +ζ/2S (S = 3) is equal to 229.8 cm⁻¹. This value is slightly lower than the one obtained experimentally, however it must be kept in mind that the experimentally determined value is an effective value, which also includes the effect of other free ion terms.

The ab initio analysis of [EuRad(NO₃)₃] evidences a surprising similitude with the magnetic behaviour reported for heterometallic complex [Cu(SB)Eu(NO₃)₃].²⁹ The distance between Cu²⁺ and Eu³⁺ ions in that complex is about 2.4 Å, close to 2.42 Å found between europium and oxygen of NO-group of Rad in [EuRad(NO₃)₃]. Conceivably, in square-pyramidal environment, the SOMO d-orbital of Cu²⁺ is oriented with respect to the 4f-orbitals of Eu³⁺ by the same manner as the SOMO p,π*-orbital of Rad, leading to a comparable exchange interaction.

Bonding mechanisms between Eu³⁺ and ligand. To inquire into the mechanisms of bonding between paramagnetic ligand and Eu³⁺ cation, we performed calculations using Natural Bonding Orbital (NBO)¹⁰⁴ analysis and Natural Energy Decomposition Analysis (NEDA).^105,106 The results were compared with those obtained for extended transition state scheme combined with the natural orbitals for chemical valence (ETS-NOCV)¹⁰⁷ method, and Quantum Theory of Atoms in Molecules (QTAIM)¹⁰⁸ analysis. To elucidate the specificity in bonding patterns in the case of paramagnetic ligand, Rad, the same analyses were performed for diamagnetic congener of our complex, [Eu(Tpm)(NO₃)₃]⁸⁰ which has a closely similar coordination polyhedron (see above). It is important to note that all these methods can give only qualitative representation of the bounding nature in the complexes and should be considered with caution.

The topological properties of the electron density computed at the bond critical points (BCP) for both complexes using QTAIM are presented in the Tables S7 and S8†. Compared to the complex of Tpm, the complex of Rad has shorter bonding distances for all coordination bonds. This observation is partially attributed to the higher temperature of the SCXRD data collection for the complex of Tpm (150 K versus 100 K for the radical complex). However, the Mayer bonding order, P, correlates with this observation being two times larger in the case of radical tripod than for the diamagnetic one. It should be noted that both the extremely low value of the electron density, ρ(r), and the quite positive value of the Laplacian of the electronic density (∇²ρ(r)) at BCPs indicate the depletion of the electronic density in the region between atoms for both systems. The vanishingly small values of total energy density, H(r), and the ratio of absolute value of potential energy density to Lagrangian kinetic energy density, |V(r)|/G(r), being close to one for every presented bonding point indicate the non-covalent character of bonding.¹⁰⁹ Natural charges obtained from NBO procedure (Fig. S13 and S14†) tend to be attributed to the ionic type of bonding. Another parameter to establish the nature of the interaction is the bonds ellipticity, ε, whose small values allow to conclude that all bonds are close to cylindrical symmetry.¹¹⁰ The value of the last analysed parameter, η ≪ 1, allows to conclude that the bonds have a closed-shell nature.¹¹¹

The results of the comparative NBO analysis for the complexes [Eu(Rad)(NO₃)₃] and [Eu(Tpm)(NO₃)₃] are presented in Table 2, Fig. 6 and S15.† According to the stabilization energy values in both complexes (Table 2), the electron donation is predominantly from the ligand to the Eu³⁺ ion. The individual components of the stabilization energies E⁽²⁾ for α and β orbital sets appear from the donations from sp-orbitals (lone pairs, LP) of the coordinated oxygen and two nitrogen atoms of the paramagnetic tripod, or three nitrogen atoms of diamagnetic tripod, to the orbitals of Eu center. They are the combination of 5d, 6s and, in a few instances, 4f orbitals (virtual Lewis orbitals) with admixture of more diffuse orbitals of the same type. The nitrogen sp-orbitals are directed towards Eu with prevailing orbital density concentrated in the space in between. Nitroxyl oxygen is presented by two sp-orbitals, the first of which is also directed towards Eu, while the second is perpendicular to the first, and its orbital density is concentrated mainly outside the radical ligand. Here is the difference with the Tpm coordination pattern (Fig. S15†), where only one orbital type is present for all three nitrogen centres. The presence of p oxygen orbital largely influences the nature of the exchange interaction between the radical and Eu centres. While looking at the results of ETS-NOCV calculations (Table S9, Fig. 7 and S16†), a similar situation is observed. The bonding is mostly defined by the interaction of 5d- and 6s-orbitals for Eu³⁺ and sp-orbitals for a tripodal ligand in the case of both complexes in α and β sets. The first three pairs of NOCV orbitals represent σ-type bonding where tripod acts through sp-orbitals of nitrogen atoms or nitroxyl oxygen, and metal is presented by d-orbitals mostly in the first two pairs and s-orbital in the third pair. Next three pairs, 4–6, repeat the scheme of orbital contribution for Eu and increase the number of the tripod orbitals by including the sp-orbitals of aromatic carbons. The orbitals of these last three NOCV pairs belong to π-type bonding with less contribution from the metal orbitals in comparison with the first three pairs.

Table 2 The stabilization energies (kJ mol⁻¹) derived from the NBO analysis for the [EuRad(NO₃)₃] and [Eu(Tpm)(NO₃)₃] complexes with accent to Eu–Rad and Eu–Tpm bonds, respectively^a

	E ^2nbo = E^αnbo + E^βnbo	E ^αnbo = ∑E^2α	E ^2α,main	E ^βnbo = ∑E^2β	E ^2β,main
a The electron donations in two directions are shown with the individual components of the stabilization energies E^(2) for α and β orbital sets (symbol “→” denotes direction of donation) and their cumulative values with smaller contributions.
Eu → Rad	−4.6	−4.4	—	−0.2	—
Rad → Eu	−1362.2	−722.6	O: −17.8 (1sp → 5d4f)	−639.6	O: −16.7 (1sp → 5d)
			−44.0 (1sp → 6s5d)		−21.0 (1sp → 6s5d)
			−9.5 (1sp → 5d)		−12.6 (1sp → 5d)
			−15.2 (2sp → 5d4f)		−33.6 (2sp → 6s5d)
			−41.8 (2sp → 6s5d)		−35.5 (2sp → 5d)
			−26.7 (2sp → 5d)		N1: −49.3 (sp → 5d)
			N1: −55.6 (sp → 5d4f)		−48.9 (sp → 5d)
			−54.3 (sp → 5d4f)		−13.6 (sp → 6s5d)
			−17.0 (sp → 5d6s4f)		N2: −45.9 (sp → 5d)
			−11.2 (sp → 6s5d)		−24.4 (sp → 5d)
			N2: −29.4 (sp → 5d4f)		−22.6 (sp → 6s5d)
			−75.1 (sp → 5d6s4f)		−16.9 (sp → 5d6s)
			−10.8 (sp → 5d)
Eu → Ldia	−0.6	−0.6	—	—	—
Ldia → Eu	−1038.1	−556.1	N1: −95.8 (sp → 5d6s)	−482.0	N1: −70.3 (sp → 6s5d)
			N2: −71.5 (sp → 6s5d)		N2: −70.7 (sp → 5d6s)
			N3: −92.5 (sp → 5d6s)		N3: −94.1 (sp → 5d6s)

---

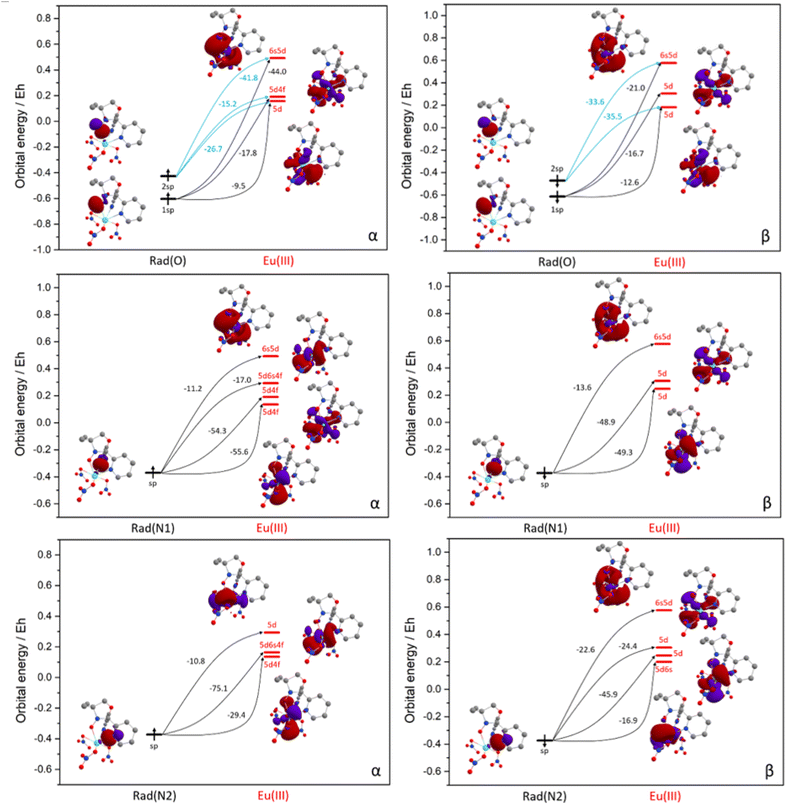Fig. 6 Orbital energy diagrams for the Eu–Rad bond formation in [EuRad(NO₃)₃] and the main electron donation paths. The values of the individual components are shown in Table 2.

Fig. 7 The most important pairs of α and β NOCVs responsible for σ (top row) and π (bottom row) type bonding with their eigenvalues. Each pair of NOCVs corresponds to two orbitals with positive and negative eigenvalues of the same magnitude.

This observation correlates with the observed contribution of the pair energies to the total orbital interaction energy (ΔE_orb, Table S9†), the energies of orbitals 1–3 being several times greater than the energies of orbitals 4–6 and their sum making up most of the whole ΔE_orb. All the information about the energies responsible for the bonding interaction and stabilization of the complexes is presented in Table 3. The energies obtained in NBO and NEDA procedures, namely, charge transfer energy, E_CT, total bonding energy, E_NEDA, and full stabilization energy, E²_nbo, are consistent with the orbital stabilization energy, ΔE_orb, obtained in ETS-NOCV. Based on these results, we conclude that the charge transfer from the occupied orbitals tripod-based to the virtual orbitals of europium is a relevant factor in bonding formation.

Table 3 The total bonding energy ENEDA, charge transfer energy ECT, full stabilization energy, E_nbo², obtained by NBO calculations, and orbital stabilization energy ΔE_orb with α and β orbital contributions obtained by means of ETS-NOCV calculations for the complexes [EuRad(NO₃)₃] and [Eu(Tpm)(NO₃)₃] (2) in kJ mol⁻¹

	−ENEDA	−ECT	−E^2nbo	−ΔEorb	−ΔEorb,α	−ΔEorb,β
a Number in α part, given in parenthesis, corresponds to an artefact of transition between two 4f-orbitals of Eu in ETS-NOCV procedure. Its value changes depending on the functional type, namely the amount of HF exchange. It was added in ΔEorb.
B3LYP	277.8	969.0	1366.8	255.6 (777.8)^a	132.5 (522.2)^a	123.1
PBE0	—	—	—	273.2 (953.5)	142.3 (680.3)	130.8
TPSSh	—	—	—	238.6 (454.5)	124.2 (215.9)	114.4
M06-2X	—	998.7	—	—	—	—
B3LYP, (2)	378.2	850.9	1038.7	243.8 (653.3)	123.8 (533.3)	120.0

---

To sum up, the SA-CASSCF(7,8)/NEVPT2/QDPT calculation results demonstrate that an agreement between the calculated magnetic properties and the experimental ones can be achieved if dynamic correlation is accounted for. At the same time, the magnetic parameters obtained from ab initio calculations correlate well with those obtained by fitting experimental data. Calculations evidence that the largest contribution to the resulting energy states comes from a combination of electronic configurations with electron transfer from the occupied orbital space to the virtual space. The analysis of the bonding patterns for [EuRad(NO₃)₃] complex highlights the importance of charge transfer from ligand occupied orbitals to metal virtual orbitals, namely, 5d and 6s, with corresponding energy stabilization of the considered states. This is reflected in the quite large value of the effective exchange interaction between europium ion and the radical.

Dynamic magnetic properties. AC magnetic studies were carried out to elucidate the magnetization dynamics of the compounds. Intriguingly, both complexes show slow relaxation of the magnetization in an applied field (Fig. 8 and 9). This is unusual, given the diamagnetic electronic configuration of Lu³⁺ and the quasi-diamagnetic nature of Eu³⁺.

Fig. 8 Field evolution of the imaginary component of the magnetic susceptibility for [LnRad(NO₃)₃] at T = 5 K: (a) Lu; (b) Eu. The lines are the best fits discussed in the text.

Fig. 9 Temperature evolution of the imaginary component of the magnetic susceptibility for LnRad(NO₃)₃ at B = 0.1 T: (a) Lu; (b) Eu. The lines are the best fits discussed in text.

A field scan at T = 5 K (Fig. 8) reveals a similar field dependence of the relaxation behaviour for both complexes. The relative in-phase susceptibilities are reported in Fig. S17†. The relaxation time (Fig. 10a) reaches a maximum around 2–2.5 T, and then it starts decreasing. A temperature scan at B = 0.1 T, Fig. 9 displays peaks in the imaginary component of the magnetic susceptibility up to 17 and 20 K for Eu and Lu species, respectively. The relative in-phase susceptibilities are reported in Fig. S18†. The relaxation time values are comparable for both complexes at all the investigated temperatures. Notably, since the field of the temperature scan was identical to the one found in the dc measurements, we can straightforwardly compare the value of the χ_dc and the values of the isothermal ac susceptibility (χ_T) to quantify the amount of sample taking part to the slow relaxation, Fig. S19†. For lutecium complex the two values coincide, i.e. 100% of the sample is slowly relaxing, while for europium one, we get approximately 80% of the sample. This excludes that the relaxation dynamics might be related to impurities.

Fig. 10 Field (a) and thermal (b) evolution of the relaxation time of Lu species (blue squares) and Eu one (red circles). The lines are the best fits discussed in the text.

The field dependence of the relaxation time for S = ½ systems, is usually fitted using the Brons-Van Vleck equation.¹¹² This formula contains two terms: the direct mechanism, responsible for the relaxation between the two states of the system resulted from Zeeman splitting, and a term that accounts for internal fields promoting fast relaxation in zero field. However, the equation cannot be used to simultaneously reproduce the field and temperature evolution of the relaxation time of the studied complexes. More specifically, the decrease of relaxation time with temperature is more rapid than the 1/T dependence expected for a simple direct process. Therefore, we have modified the equation introducing a temperature dependence on the second term, analogously to a Raman process:

where c is the direct mechanism coefficient, R is the Raman coefficient, the e parameter, strongly dependent on the spin concentration, accounts the field effects on the relaxation of interacting spins and f takes into account the ability of the field to suppress this process. Using eqn (2) we were able to reproduce the field and temperature dependence of the relaxation time for both complexes, and the obtained parameters are summarized in Table 4. The results that we obtain deserve some comments. We can immediately notice that most of the parameters are very similar. For example, the e parameter that accounts for the spin density in the lattice is virtually indistinguishable between the two derivatives. The two most different parameters are c and f. The first one suggests that the direct mechanism is more effective for [EuRad(NO₃)₃], while the second one hints towards the fact that the magnetic field suppresses more efficiently the relaxation in lutetium congener than in europium one. Our analysis highlights that the relaxation of the radical in europium complex is indeed affected by the coupling with Eu³⁺ ion that creates a sort of “effective” magnetic field.

Table 4 Best fit parameters for the [LnRad(NO₃)₃] complexes, extracted from the temperature and field dependence of the ac relaxation times using eqn (2)

Parameter	Lu	Eu
c/s^−1 T^−4	0.158(7)	0.702(8)
R/s^−1 K^−n	876(51)	855(44)
n	1.41(2)	1.39(2)
e/T^−2	1.77(9)	1.76(5)
f/T^−2	32(1)	18(3)

---

Conclusions

In this paper we reported a spectroscopic and magnetic study on two tripodal radical-containing lanthanide complexes involving the poorly magnetic Eu³⁺ or the diamagnetic Lu³⁺ ion. The exchange coupling of the radical with Eu³⁺ was found to provide characteristic shape and resonance fields of the EPR spectrum, which is clearly visible at temperature as high as 50 K. This surprising result prompts a reassessment of the magnetic behaviour of the many Eu³⁺–radical complexes reported in the literature, for which the coupling is usually neglected due to the formally diamagnetic ground state of this ion (⁷F₀).^81,113 Further specific features of the magnetic behaviour allowed us to obtain a value of the exchange-coupling between the radical S = ½ and the S = 3 of the Eu³⁺ ion, which is completely consistent with the results obtained for the Gd³⁺ congener.⁶⁵ The observed antiferromagnetic coupling is among the largest ever reported between a lanthanide and a radical, only outcompeted by few families of compounds such as the low-yield endohedral dilanthanofullerenes,¹¹⁴ the air sensitive mixed-valence (Cp^iPr5)₂Ln₂I₃ (ref. 18) and the N₂³⁻ bridged¹⁶ dilanthanide complexes. The combined DFT and ab initio calculations yielded results in excellent agreement with the experiments, providing further insight in the mechanism leading to the strong exchange. Finally, the ac magnetometric characterization evidenced slow relaxation of the magnetization in an applied field at temperatures below 20 K. By comparing the behaviour of the two complexes we could demonstrate that the exchange coupling of the radical with Eu³⁺ has a non-negligible influence on the field dependence of the slow relaxation. More importantly, the observation of this slow relaxation, seldomly observed in complexes containing only poorly magnetic ions and radicals, suggests a relative inefficiency of the field-dependent Raman and direct processes. This demonstrates that non-Orbach processes are not very detrimental in promoting the relaxation and is thus of much relevance in the design of new air stable building blocks for complexes displaying slow relaxation of the magnetization at high temperature.

Experimental section

The common chemical reagents used in this work were obtained from commercial sources and utilized as received. The 4,4-dimethyl-2,2-bis(pyridin-2-yl)-1,3-oxazolidine N-oxyl radical (Rad) was synthesized according to known procedure.⁶⁶ Ln(NO₃)₃·6H₂O (Ln = Eu, Lu) were obtained upon dissolution of Eu₂O₃ or Lu₂(CO₃)₃·xH₂O in diluted HNO₃ at 50 °C with subsequent vaporization of all volatiles and recrystallization from acetonitrile solution to remove the HNO₃ traces. Elemental analysis was done using a Eurovector EuroEA3000 analyser. IR spectra were registered in KBr pellets using FT-801 Fourier spectrometer (Simex). A Shimadzu XRD-7000 diffractometer (CuKα radiation, Ni filter, 2θ angle range from 5° to 30°, Dectris MYTHEN2 R 1K detector) was used to perform a powder XRD investigation. X-band EPR spectra were recorded on a Bruker Elexsys E500 spectrometer equipped with an ESR900 (Oxford Instruments) continuous-flow 4He cryostat to work at low temperature and a SHQ resonator. The crystalline powder of each sample was ground, pressed in pellet to avoid preferential orientation, and then placed in 4 mm diameter quartz tubes. The luminescence measurements were carried out on a Horiba Fluorolog spectro-fluorometer.

Synthesis of the compounds

[LnRad(NO₃)₃] were prepared according to the procedure described for Eu congener.

To a solution of Eu(NO₃)₃·6H₂O (0.113 mmol) in CH₃CN (2 mL), a solution of Rad (0.11 mmol) in CH₃CN (1.5 mL) was added. The reaction mixture was stirred for one hour at heating about 60 °C until the solution volume was reduced by half. The solution was left in peace overnight. The resultant yellow crystalline product was separated from the supernatant, washed with a small amount of cold acetonitrile and then with ether and air-dried. Yield: 80%. Anal. Calcd (%) for C₁₅H₁₆EuN₆O₁₁: C, 29.6; H, 2.6; N, 13.8. Found: C, 29.8; H, 2.5; N, 13.8. IR (KBr): ν (cm⁻¹) 3127 (w), 2984 (w), 2934 (w), 2892 (w), 1599 (m), 1507 (s), 1491 (s), 1472 (s), 1437 (s), 1379 (m), 1368 (sh), 1287 (sh), 1264 (s), 1192 (w), 1163 (m), 1148 (m), 1103 (w), 1074 (m), 1063 (m), 1022 (s), 1003 (m), 980 (w), 960 (w), 941 (sh), 930 (w), 912 (w), 903 (w), 876 (w), 833 (w), 814 (m), 772 (s), 758 (w), 743 (s), 708 (w), 679 (sh), 664 (m), 638 (m), 621 (m), 567 (m), 513 (w), 419 (w).

[LuRad(NO₃)₃]

Lu(NO₃)₃·6H₂O – 0.154 mmol, L – 0.152 mmol. Yield: 70%. Anal. Calcd (%) for C₁₅H₁₆LuN₆O₁₁: C, 28.5; H, 2.5; N, 13.3. Found: C, 28.4; H, 2.2; N, 13.3. IR (KBr): ν (cm⁻¹) 3134 (w), 2986 (w), 2941 (w), 2897 (w), 1621 (sh), 1605 (s), 1570 (w), 1536 (s), 1518 (s), 1504 (s), 1491 (s), 1476 (sh), 1464 (sh), 1441 (s), 1385 (s), 1300 (s), 1288 (sh), 1277 (s), 1260 (sh), 1227 (w), 1194 (w), 1150 (w), 1103 (w), 1078 (m), 1063 (m), 1028 (s), 1020 (sh), 1005 (m), 982 (w), 958 (w), 939 (sh), 932 (w), 912 (w), 902 (w), 837 (sh), 814 (m), 772 (s), 748 (m), 708 (m), 664 (m), 643 (m), 638 (m), 621 (w), 569 (w), 515 (m), 424 (w), 415 (sh).

X-ray structure determination

Single-crystal XRD data for [EuRad(NO₃)₃] and [LuRad(NO₃)₃] were collected a APEX-II CCD and Bruker Apex X8 diffractometers equipped with a 4K CCD area detector using the graphite-monochromated Mo Kα radiation (λ = 0.71073 Å) (Table S1†) at 100 and 150 K respectively. The φ- and ω-scan techniques were employed to measure intensities. Absorption corrections were applied with the use of the SADABS program_ENREF_50.¹¹⁵ The crystal structures were solved using the SHELXT¹¹⁶ and were refined using SHELXL¹¹⁷ programs with OLEX2 GUI.¹¹⁸ Atomic displacement parameters for non-hydrogen atoms were refined anisotropically.

Magnetic measurements

To avoid preferential orientation of the crystallites, DC magnetic measurements were carried out on the polycrystalline samples pressed in Teflon pellets, using a QD MPMS SQUID magnetometer in the temperature range 1.9–300 K with applied field up to 5.5 T AC magnetic measurements were performed on the same samples using the ACMS module of a QD PPMS working in the frequency range 10–10 000 Hz. The intrinsic diamagnetic contributions of the samples have been estimated using Pascal's Constants.¹¹⁹

Computational details

The electronic structure calculations at DFT and ab initio SA-CASSCF/NEVPT2/QDPT level were performed using the ORCA 5.0.3 program package.^120–122 DFT calculation with the following NBO¹⁰⁴ and NEDA^105,106 analysis were performed using Gaussian 16 (ref. 123) and NBO 7.0 (ref. 124) program packages. The DFT calculations were performed using B3LYP,¹²⁵ PBE0 (ref. 126 and 127) TPSSh,¹²⁸ and M06-2X^107,129 functionals. The QTAIM and ETS-NOCV analysis were performed using the Multiwfn package¹⁰⁸ (version 3.8, released 2023-06-04). The electronic structure of [EuRad(NO₃)₃] was studied at SA-CASSCF(7,8)/NEVPT2 level.^130–133 Active space was constructed with seven 4f-orbitals of Eu and one SOMO of radical ligand. Relativistic effects were taken into account with use of DKH2 Hamiltonian.^134,135 Active space was constructed with seven 4f-orbitals of Eu and one SOMO of radical ligand. Relativistic effects were taken into account with use of DKH2 Hamiltonian. SARC2-DKH-QZVP¹³⁶ basis set for Eu and DKH-def2-TZVP(-f)^137,138 basis set for other atoms were used for calculations and JK auxiliary basis sets for RI-JK approximation to the Coulomb and exchange integrals.^139,140 Spin–orbit coupling effects were included using quasi-degenerate perturbation theory (QDPT) with mixing CASSCF states in the spin–orbit mean field.¹⁴¹ The temperature dependence of magnetic susceptibility was calculated by differentiation of the QDPT Hamiltonian with respect to magnetic field. Electronic structure of the [EuRad(NO₃)₃] complex was calculated using state-averaged (SA) CASSCF calculations and taking into account dynamic correlation using NEVPT2. Active space of CASSCF(7,8) consisted of seven 4f-orbitals of europium and one SOMO of radical ligand (Fig. S8†). Seven, twelve and five roots for the multiplicities 8, 6 and 4 were taken in consideration, correspondingly, based on the result of interaction between europium ⁷F and ⁵D terms and radical ²S term. The full electronic structure is presented in Fig. S9† after the calculations at different levels of theory. Spin–orbit coupling (SOC) was accounted for using the quasi-degenerate perturbation theory (QDPT) approach after SA-CASSCF(7,8) and SA-CASSCF(7,8)/NEVPT2 (NEVPT2-SOC) calculations. To determine the values of SOC constant the Ab initio Ligand Field Theory (AILFT)^142,143 calculations on the base of SA-CASSCF(6,7)/NEVPT2 calculations with 7 septets and 140 quintets for cation and anion forms of [EuRad(NO₃)₃] complex were performed.

Data availability

The data supporting this article have been included as part of the ESI.† Crystallographic data has been deposited at the CCDC under CCDC numbers 2373742, 2373744 for [EuRad(NO₃)₃] and [LuRad(NO₃)₃] respectively and can be obtained directly from https://www.ccdc.cam.ac.uk/products/csd/request/

Author contributions

The work was designed and carried out by K. V. The magnetic and EPR characterization and modelling were performed by L. S. and M. P. The quantum theoretical calculations were performed by A. A. D. The manuscript was written through contributions and continuous discussion of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was funded by the Russian Science Foundation, Grant No. 23-23-00437. M. Perfetti and L. Sorace acknowledge the MUR – Dipartimenti di Eccellenza 2023–2027 (DICUS 2.0 – CUP B97G22000740001) to the Department of Chemistry “Ugo Schiff” of the University of Florence for the financial support to perform the AC magnetic measurements and spectroscopic characterization. A. Dmitriev acknowledges the Supercomputer Centre of Novosibirsk State University for the computational resources.

References

1. A. Raza and M. Perfetti, Coord. Chem. Rev., 2023, 490, 215213.
2. E. Coronado, Nat. Rev. Mater., 2019, 5, 87–104.
3. A. J. Heinrich, W. D. Oliver, L. M. K. Vandersypen, A. Ardavan, R. Sessoli, D. Loss, A. B. Jayich, J. Fernandez-Rossier, A. Laucht and A. Morello, Nat. Nanotechnol., 2021, 16, 1318–1329.
4. O. Sato, Nat. Chem., 2016, 8, 644–656.
5. N. Bajaj, N. Mavragani, A. A. Kitos, D. Chartrand, T. Maris, A. Mansikkamäki and M. Murugesu, Chem, 2024, 10, 2484–2499.
6. Y.-X. Qu, P.-Y. Liao, Y.-C. Chen and M.-L. Tong, Coord. Chem. Rev., 2023, 475, 214880.
7. X. Yi, K. Bernot, F. Pointillart, G. Poneti, G. Calvez, C. Daiguebonne, O. Guillou and R. Sessoli, Chem.–Eur. J., 2012, 18, 11379–11387.
8. R. Marin, G. Brunet and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 1728–1746.
9. M. A. Hay and C. Boskovic, Chem.–Eur. J., 2021, 27, 3608–3637.
10. J.-H. Jia, Q.-W. Li, Y.-C. Chen, J.-L. Liu and M.-L. Tong, Coord. Chem. Rev., 2019, 378, 365–381.
11. R. Jankowski, M. Wyczesany and S. Chorazy, Chem. Commun., 2023, 59, 5961–5986.
12. D. J. Bell, L. S. Natrajan and I. A. Riddell, Coord. Chem. Rev., 2022, 472, 214786.
13. A. Virender, A. Chauhan, A. Kumar, G. Singh, A. A. Solovev, J. Xiong, X. Liu and B. Mohan, J. Rare Earths, 2024, 42, 16–27.
14. V. Vieru, S. Gómez-Coca, E. Ruiz and L. F. Chibotaru, Angew. Chem., 2024, 136, e202303146.
15. Y.-N. Guo, G.-F. Xu, W. Wernsdorfer, L. Ungur, Y. Guo, J. Tang, H.-J. Zhang, L. F. Chibotaru and A. K. Powell, J. Am. Chem. Soc., 2011, 133, 11948–11951.
16. J. D. Rinehart, M. Fang, W. J. Evans and J. R. Long, Nat. Chem., 2011, 3, 538–542.
17. S. Demir, I.-R. Jeon, J. R. Long and T. D. Harris, Coord. Chem. Rev., 2015, 289–290, 149–176.
18. C. A. Gould, K. R. McClain, D. Reta, J. G. C. Kragskow, D. A. Marchiori, E. Lachman, E.-S. Choi, J. G. Analytis, R. D. Britt, N. F. Chilton, B. G. Harvey and J. R. Long, Science, 2022, 375, 198–202.
19. P. Zhang, R. Nabi, J. K. Staab, N. F. Chilton and S. Demir, J. Am. Chem. Soc., 2023, 145, 9152–9163.
20. H. Kwon, K. R. McClain, J. G. C. Kragskow, J. K. Staab, M. Ozerov, K. R. Meihaus, B. G. Harvey, E. S. Choi, N. F. Chilton and J. R. Long, J. Am. Chem. Soc., 2024, 146, 18714–18721.
21. S. Demir, M. I. Gonzalez, L. E. Darago, W. J. Evans and J. R. Long, Nat. Commun., 2017, 8, 2144.
22. F. Benner, L. La Droitte, O. Cador, B. Le Guennic and S. Demir, Chem. Sci., 2023, 14, 5577–5592.
23. N. Mavragani, A. A. Kitos, J. L. Brusso and M. Murugesu, Chem.–Eur. J., 2021, 27, 5091–5106.
24. N. Mavragani, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Inorg. Chem. Front., 2023, 10, 259–266.
25. N. Mavragani, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Chem. Sci., 2024, 15, 16234–16242.
26. H.-D. Li, S.-G. Wu and M.-L. Tong, Chem. Commun., 2023, 59, 6159–6170.
27. N. Mavragani, D. Errulat, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, Angew. Chem., Int. Ed., 2021, 60, 24206–24213.
28. N. Mavragani, A. A. Kitos, J. Hrubý, S. Hill, A. Mansikkamäki, J. O. Moilanen and M. Murugesu, Inorg. Chem. Front., 2023, 10, 4197–4208.
29. M. Dolai, M. Ali, C. Rajnák, J. Titiš and R. Boča, New J. Chem., 2019, 43, 12698–12701.
30. J. Wang, Z.-Y. Ruan, Q.-W. Li, Y.-C. Chen, G.-Z. Huang, J.-L. Liu, D. Reta, N. F. Chilton, Z.-X. Wang and M.-L. Tong, Dalton Trans., 2019, 48, 1686–1692.
31. K. Bader, D. Dengler, S. Lenz, B. Endeward, S.-D. Jiang, P. Neugebauer and J. van Slageren, Nat. Commun., 2014, 5, 5304.
32. J. M. Zadrozny, J. Niklas, O. G. Poluektov and D. E. Freedman, ACS Cent. Sci., 2015, 1, 488–492.
33. L. Tesi, E. Lucaccini, I. Cimatti, M. Perfetti, M. Mannini, M. Atzori, E. Morra, M. Chiesa, A. Caneschi, L. Sorace and R. Sessoli, Chem. Sci., 2016, 7, 2074–2083.
34. L. C. de Camargo, M. Briganti, F. S. Santana, D. Stinghen, R. R. Ribeiro, G. G. Nunes, J. F. Soares, E. Salvadori, M. Chiesa, S. Benci, R. Torre, L. Sorace, F. Totti and R. Sessoli, Angew. Chem., Int. Ed., 2021, 60, 2588–2593.
35. C. Aronica, G. Chastanet, G. Pilet, B. Le Guennic, V. Robert, W. Wernsdorfer and D. Luneau, Inorg. Chem., 2007, 46, 6108–6119.
36. A. C. Rizzi, R. Calvo, R. Baggio, M. T. Garland, O. Peña and M. Perec, Inorg. Chem., 2002, 41, 5609–5614.
37. K. Manseki, O. Nakamura, K. Horikawa, M. Sakamoto, H. Sakiyama, Y. Nishida, Y. Sadaoka and H. Okawa, Inorg. Chem. Commun., 2002, 5, 56–58.
38. I. V. Kurganskii, E. S. Bazhina, A. A. Korlyukov, K. A. Babeshkin, N. N. Efimov, M. A. Kiskin, S. L. Veber, A. A. Sidorov, I. L. Eremenko and M. V. Fedin, Molecules, 2019, 24, 4582.
39. D. Luneau and P. Rey, Coord. Chem. Rev., 2005, 249, 2591–2611.
40. I. V. Ershova, A. V. Piskunov and V. K. Cherkasov, Russ. Chem. Rev., 2020, 89, 1157.
41. P. Zhang, M. Perfetti, M. Kern, P. P. P. Hallmen, L. Ungur, S. Lenz, M. R. R. Ringenberg, W. Frey, H. Stoll, G. Rauhut and J. van Slageren, Chem. Sci., 2018, 9, 1221–1230.
42. N. Zhou, Y. Ma, C. Wang, G.-F. Xu, J. Tang, S.-P. Yan and D.-Z. Liao, J. Solid State Chem., 2010, 183, 927–932.
43. H. Yan, J. Wei and W.-X. Zhang, Organometallics, 2021, 40, 3245–3252.
44. H. Yan, B. Wu, J. Wei and W.-X. Zhang, Inorg. Chem., 2023, 62, 8052–8057.
45. H. Yan, B. Wu, X.-K. Zhao, C. Yu, J. Wei, H.-S. Hu, W.-X. Zhang and Z. Xi, CCS Chem., 2021, 3, 2772–2781.
46. D. Mouchel Dit Leguerrier, R. Barré, M. Bryden, D. Imbert, C. Philouze, O. Jarjayes, D. Luneau, J. K. Molloy and F. Thomas, Dalton Trans., 2020, 49, 8238–8246.
47. N. Claiser, M. Souhassou, C. Lecomte, B. Gillon, C. Carbonera, A. Caneschi, A. Dei, D. Gatteschi, A. Bencini, Y. Pontillon and E. Lelièvre-Berna, J. Phys. Chem. B, 2005, 109, 2723–2732.
48. H. Li, C. Jin, J. Han, L. Xi and Z. Song, Cryst. Growth Des., 2023, 23, 612–619.
49. C. V. Sarmiento, T. A. Araujo, S. G. Reis, M. S. de Souza, R. A. Allão Cassaro, M. A. Novak and M. G. F. Vaz, RSC Adv., 2019, 9, 30302–30308.
50. X.-H. Lv, S.-L. Yang, Y.-X. Li, C.-X. Zhang and Q.-L. Wang, RSC Adv., 2017, 7, 38179–38186.
51. F. Benner and S. Demir, Chem. Sci., 2022, 13, 5818–5829.
52. F. Delano, S. Deshapriya and S. Demir, Inorg. Chem., 2024, 63, 9659–9669.
53. L. Duan, Y.-B. Jia, X.-G. Li, Y.-M. Li, H. Hu, J. Li and C. Cui, Eur. J. Inorg. Chem., 2017, 2017, 2231–2235.
54. S. Ito, R. Takano, S. Hatanaka and T. Ishida, Inorg. Chem., 2022, 61(28), 10619–10623.
55. A. Dei, D. Gatteschi, J. Pécaut, S. Poussereau, L. Sorace and K. Vostrikova, C. R. Acad. Sci., Ser. IIc: Chim., 2001, 4, 135–141.
56. R. Murakami, T. Nakamura and T. Ishida, Dalton Trans., 2014, 43, 5893–5898.
57. J. Jung, M. Puget, O. Cador, K. Bernot, C. J. Calzado and B. Le Guennic, Inorg. Chem., 2017, 56, 6788–6801.
58. T. Nakamura and T. Ishida, Polyhedron, 2015, 87, 302–306.
59. J. Sutter, M. L. Kahn, S. Golhen, L. Ouahab and O. Kahn, Chem.–Eur. J., 1998, 4, 571–576.
60. X. Wang, P. Hu, L. Li and J.-P. Sutter, Inorg. Chem., 2015, 54, 9664–9669.
61. C. Lescop, D. Luneau, G. Bussière, M. Triest and C. Reber, Inorg. Chem., 2000, 39, 3740–3741.
62. C. Lescop, E. Belorizky, D. Luneau and P. Rey, Inorg. Chem., 2002, 41, 3375–3384.
63. J. W. Buchler, A. De Cian, J. Fischer, M. Kihn-Botulinski and R. Weiss, Inorg. Chem., 1988, 27, 339–345.
64. S. V. Klementyeva, A. N. Lukoyanov, M. Y. Afonin, M. Mörtel, A. I. Smolentsev, P. A. Abramov, A. A. Starikova, M. M. Khusniyarov and S. N. Konchenko, Dalton Trans., 2019, 48, 3338–3348.
65. M. Perfetti, A. Caneschi, T. S. Sukhikh and K. E. Vostrikova, Inorg. Chem., 2020, 59, 16591–16598.
66. A. Ito, Y. Nakano, M. Urabe, K. Tanaka and M. Shiro, Eur. J. Inorg. Chem., 2006, 2006, 3359–3368.
67. I. A. Gass, M. Asadi, D. W. Lupton, B. Moubaraki, A. M. Bond, S.-X. Guo and K. S. Murray, Aust. J. Chem., 2014, 67, 1618.
68. I. A. Gass, S. Tewary, A. Nafady, N. F. Chilton, C. J. Gartshore, M. Asadi, D. W. Lupton, B. Moubaraki, A. M. Bond, J. F. Boas, S.-X. Guo, G. Rajaraman and K. S. Murray, Inorg. Chem., 2013, 52, 7557–7572.
69. I. A. Gass, J. Lu, R. Ojha, M. Asadi, D. W. Lupton, B. L. Geoghegan, B. Moubaraki, L. L. Martin, A. M. Bond and K. S. Murray, Aust. J. Chem., 2019, 72, 769–777.
70. I. A. Gass, S. Tewary, G. Rajaraman, M. Asadi, D. W. Lupton, B. Moubaraki, G. Chastanet, J.-F. Létard and K. S. Murray, Inorg. Chem., 2014, 53, 5055–5066.
71. A. H. Pedersen, B. L. Geoghegan, G. S. Nichol, D. W. Lupton, K. S. Murray, J. Martínez-Lillo, I. A. Gass and E. K. Brechin, Dalton Trans., 2017, 46, 5250–5259.
72. I. A. Gass, J. Lu, M. Asadi, D. W. Lupton, C. M. Forsyth, B. L. Geoghegan, B. Moubaraki, J. D. Cashion, L. L. Martin, A. M. Bond and K. S. Murray, Chempluschem, 2018, 83, 658–668.
73. P. Rey, A. Caneschi, T. S. Sukhikh and K. E. Vostrikova, Inorganics, 2021, 9, 91.
74. K. E. Vostrikova, Inorganics, 2023, 11, 307.
75. M. Llunell, D. Casanova, J. Cirera, P. Alemany and S. Alvarez, Program for the Stereochemical Analysis of Molecular Fragments by Means of Continuous ShapeMeasures and Associated Tools, SHAPE, Version 2, Universitat de Barcelona, Spain, 2013.
76. K. Binnemans, Coord. Chem. Rev., 2015, 295, 1–45.
77. D. E. Barry, D. F. Caffrey and T. Gunnlaugsson, Chem. Soc. Rev., 2016, 45, 3244–3274.
78. D. M. Lyubov, T. V. Mahrova, A. V. Cherkasov, G. K. Fukin, Y. V. Fedorov and A. A. Trifonov, Eur. J. Inorg. Chem., 2023, 26, e202300292.
79. W. T. Carnall, G. L. Goodman, K. Rajnak and R. S. Rana, J. Chem. Phys., 1989, 90, 3443–3457.
80. K. E. Vostrikova, T. S. Sukhikh and A. N. Lavrov, Inorganics, 2023, 11, 418.
81. A. Caneschi, A. Dei, D. Gatteschi, S. Poussereau and L. Sorace, Dalton Trans., 2004, 1048–1055.
82. J.-X. Xu, Y. Ma, D. Liao, G.-F. Xu, J. Tang, C. Wang, N. Zhou, S.-P. Yan, P. Cheng and L.-C. Li, Inorg. Chem., 2009, 48, 8890–8896.
83. S. V. Klementyeva, N. P. Gritsan, M. M. Khusniyarov, A. Witt, A. A. Dmitriev, E. A. Suturina, N. D. D. Hill, T. L. Roemmele, M. T. Gamer, R. T. Boeré, P. W. Roesky, A. V. Zibarev and S. N. Konchenko, Chem.–Eur. J., 2017, 23, 1278–1290.
84. L. Sorace, PhD thesis, University of Florence, 2001, https://hdl.handle.net/2158/1363972.
85. S. Stoll and A. Schweiger, J. Magn. Reson., 2006, 178, 42–55.
86. A. Bencini and D. Gatteschi, Electron Paramagnetic Resonance of Exchange Coupled Systems, Springer Berlin Heidelberg, Berlin, Heidelberg, 1990.
87. T. Ishida, R. Murakami, T. Kanetomo and H. Nojiri, Polyhedron, 2013, 66, 183–187.
88. T. Kanetomo and T. Ishida, Inorg. Chem., 2014, 53, 10794–10796.
89. T. Kanetomo, T. Yoshitake and T. Ishida, Inorg. Chem., 2016, 55, 8140–8146.
90. P. Hu, M. Zhu, X. Mei, H. Tian, Y. Ma, L. Li and D. Liao, Dalton Trans., 2012, 41, 14651.
91. X. Wang, M. Zhu, J. Wang and L. Li, Dalton Trans., 2015, 44, 13890–13896.
92. J. Wang, H. Miao, Z.-X. Xiao, Y. Zhou, L.-D. Deng, Y.-Q. Zhang and X.-Y. Wang, Dalton Trans., 2017, 46, 10452–10461.
93. C. Benelli, A. Caneschi, D. Gatteschi and L. Pardi, Inorg. Chem., 1992, 31, 741–746.
94. P. Hu, Z. Sun, X. Wang, L. Li, D. Liao and D. Luneau, New J. Chem., 2014, 38, 4716–4721.
95. P. Y. Chen, M. Z. Wu, X. J. Shi and L. Tian, RSC Adv., 2018, 8, 15480–15486.
96. T. Nakamura and T. Ishida, AIP Conf. Proc., 2016, 1709, 020016.
97. T. Nakamura, T. Kanetomo and T. Ishida, Inorg. Chem., 2021, 60, 535–539.
98. A. Caneschi, A. Dei, D. Gatteschi, L. Sorace and K. Vostrikova, Angew. Chem., Int. Ed., 2009, 39, 246–248.
99. L. Sorace and D. Gatteschi, in Lanthanides and Actinides in Molecular Magnetism, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015, pp. 1–26.
100. A. Zheludev, V. Barone, M. Bonnet, B. Delley, A. Grand, E. Ressouche, P. Rey, R. Subra and J. Schweizer, J. Am. Chem. Soc., 1994, 116, 2019–2027.
101. K. E. Vostrikova, E. Belorizky, J. Pécaut and P. Rey, Eur. J. Inorg. Chem., 1999, 1181–1187.
102. J. Schweizer and E. Ressouche, in Magnetism: Molecules to Materials I, ed. J. S. Miller and M. Drillon, Wiley-VCH Verlag GmbH & Co. KGaA, 2001, pp. 325–355.
103. E. V. Tretyakov, V. I. Ovcharenko, A. O. Terent’ev, I. B. Krylov, T. V. Magdesieva, D. G. Mazhukin and N. P. Gritsan, Russ. Chem. Rev., 2022, 91, RCR5025.
104. E. D. Glendening, C. R. Landis and F. Weinhold, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 1–42.
105. E. D. Glendening, J. Phys. Chem. A, 2005, 109, 11936–11940.
106. G. K. Schenter and E. D. Glendening, J. Phys. Chem., 1996, 100, 17152–17156.
107. M. Walker, A. J. A. Harvey, A. Sen and C. E. H. Dessent, J. Phys. Chem. A, 2013, 117, 12590–12600.
108. T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592.
109. E. Espinosa, I. Alkorta, J. Elguero and E. Molins, J. Chem. Phys., 2002, 117, 5529–5542.
110. R. F. W. Bader, T. S. Slee, D. Cremer and E. Kraka, J. Am. Chem. Soc., 1983, 105, 5061–5068.
111. N. J. M. Amezaga, S. C. Pamies, N. M. Peruchena and G. L. Sosa, J. Phys. Chem. A, 2010, 114, 552–562.
112. J. H. Van Vleck, Phys. Rev., 1940, 57, 1052.
113. M. L. Kahn, J.-P. Sutter, S. Golhen, P. Guionneau, L. Ouahab, O. Kahn and D. Chasseau, J. Am. Chem. Soc., 2000, 122, 3413–3421.
114. F. Liu, D. S. Krylov, L. Spree, S. M. Avdoshenko, N. A. Samoylova, M. Rosenkranz, A. Kostanyan, T. Greber, A. U. B. Wolter, B. Büchner and A. A. Popov, Nat. Commun., 2017, 8, 16098.
115. Apex3 Software Suite: Apex3, SADABS-2016/2 and SAINT 8.40a, Publisher: Bruker AXS Inc., Madison, WI, USA, 2017.
116. G. M. Sheldrick, Acta Crystallogr., Sect. A:Found. Adv., 2015, 71, 3–8.
117. G. M. Sheldrick, Acta Crystallogr., Sect. C:Struct. Chem., 2015, 71, 3–8.
118. O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341.
119. G. A. Bain and J. F. Berry, J. Chem. Educ., 2008, 85, 532.
120. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606,  DOI:10.1002/wcms.1606.
121. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
122. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
123. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev C.01/C.02, Gaussian, Inc., Wallingford CT, 2016.
124. E. D. Glendening, C. R. Landis and F. Weinhold, J. Comput. Chem., 2019, 40, 2234–2241.
125. A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652.
126. C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170.
127. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
128. J. P. Perdew, J. Tao, V. N. Staroverov and G. E. Scuseria, J. Chem. Phys., 2004, 120, 6898–6911.
129. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
130. B. O. Roos, P. R. Taylor and P. E. M. Sigbahn, Chem. Phys., 1980, 48, 157–173.
131. C. Angeli, B. Bories, A. Cavallini and R. Cimiraglia, J. Chem. Phys., 2006, 124, 054108.
132. C. Angeli, R. Cimiraglia, S. Evangelisti, T. Leininger and J.-P. Malrieu, J. Chem. Phys., 2001, 114, 10252–10264.
133. C. Angeli, R. Cimiraglia and J.-P. Malrieu, Chem. Phys. Lett., 2001, 350, 297–305.
134. B. A. Hess, Phys. Rev. A, 1986, 33, 3742–3748.
135. A. Wolf, M. Reiher and B. A. Hess, J. Chem. Phys., 2002, 117, 9215–9226.
136. D. Aravena, F. Neese and D. A. Pantazis, J. Chem. Theory Comput., 2016, 12, 1148–1156.
137. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297.
138. D. A. Pantazis, X.-Y. Chen, C. R. Landis and F. Neese, J. Chem. Theory Comput., 2008, 4, 908–919.
139. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
140. F. Weigend, J. Comput. Chem., 2008, 29, 167–175.
141. F. Neese, J. Chem. Phys., 2005, 122, 034107.
142. M. Atanasov, D. Ganyushin, K. Sivalingam and F. Neese, A Modern First-Principles View on Ligand Field Theory through the Eyes of Correlated Multireference Wavefunctions, in Molecular Electronic Structures of Transition Metal Complexes II, ed. D. M. P. Mingos, P. Day and J. P. Dahl, Springer Berlin Heidelberg, Berlin, Heidelberg, 2012, pp. 149–220.
143. L. Lang, M. Atanasov and F. Neese, J. Phys. Chem. A, 2020, 124, 1025–1037.

---

Footnote

† Electronic supplementary information (ESI) available: Structural information in detail, powder XRD spectra, and additional magnetic and theoretical results figures. CCDC 2373742 and 2373744. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4sc05035e

---