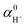Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Absolute standard hydrogen electrode potential and redox potentials of atoms and molecules: machine learning aided first principles calculations†
Ryosuke
Jinnouchi
 *a,
Ferenc
Karsai
b and
Georg
Kresse
bc
*a,
Ferenc
Karsai
b and
Georg
Kresse
bc
aToyota Central R&D Labs., Inc., Yokomichi 41-1, Nagakute, Aichi, Japan. E-mail: jryosuke@mosk.tytlabs.co.jp
bVASP Software GmbH, Berggasse 21, A-1090 Vienna, Austria
cUniversity of Vienna, Faculty of Physics, Kolingasse 14-16, A-1090 Vienna, Austria
First published on 23rd December 2024
Abstract
Constructing a self-consistent first-principles framework that accurately predicts the properties of electron transfer reactions through finite-temperature molecular dynamics simulations is a dream of theoretical electrochemists and physical chemists. Yet, predicting even the absolute standard hydrogen electrode potential, the most fundamental reference for electrode potentials, proves to be extremely challenging. Here, we show that a hybrid functional incorporating 25% exact exchange enables quantitative predictions when statistically accurate phase-space sampling is achieved via thermodynamic integrations and thermodynamic perturbation theory calculations, utilizing machine-learned force fields and Δ-machine learning models. The application to seven redox couples, including molecules and transition metal ions, demonstrates that the hybrid functional can predict redox potentials across a wide range of potentials with an average error of 140 mV.
1 Introduction
The absolute standard hydrogen electrode potential (ASHEP) is the foundation for the thermodynamic measurement of redox potentials. It is defined as the chemical potential of electrons, referenced to the vacuum level, that equilibrates the redox reaction of hydrogen, ½H2 ↔ H+ + e−, in its standard state (0.1 MPa for H2 and 1 mol L−1 for H+). In many electrochemical experiments, the half-cell potential is scaled to a selected reference electrode, making ASHEP not always a necessary property. However, the absolute potential is a fundamental property that becomes essential when comparing redox potentials to the band edges of metal and semiconductor electrodes or the chemical potential of electrons calculated in electronic structure calculations. ASHEP is also closely related to the absolute value of the real potential of a single ion, which is defined as the free energy change associated with the transfer of an ion from the gas phase to the liquid phase under the standard state. Based on the Born–Haber cycle, the free energy change (ΔatG0) of the hydrogen dissociation reaction, H2 ↔ 2H, and the ionization potential (ΔionG0) of an H atom, allow ASHEP to be converted to the real potential of a proton , which is also referred to as the work function of a proton (here, we use the notations from ref. 1). The real potential is further related to the solvation free energy. The real potential includes the contribution of the electrostatic potential difference across the vacuum–solute interface; by subtracting this so-called surface potential contribution, the solvation free energy can be obtained.2,3 However, in experiments, the surface potential always exists at the vacuum–liquid interface. To separate the surface potential contribution from the real potential, a definition of the solution phase without the surface potential is required, which has been a topic of debate for years in the cluster-pair-based approach.2,3 However, since the effect of the surface potential is always involved in the ASHEP, which we focus on in this study, we place our emphasis on the real potential.
, which is also referred to as the work function of a proton (here, we use the notations from ref. 1). The real potential is further related to the solvation free energy. The real potential includes the contribution of the electrostatic potential difference across the vacuum–solute interface; by subtracting this so-called surface potential contribution, the solvation free energy can be obtained.2,3 However, in experiments, the surface potential always exists at the vacuum–liquid interface. To separate the surface potential contribution from the real potential, a definition of the solution phase without the surface potential is required, which has been a topic of debate for years in the cluster-pair-based approach.2,3 However, since the effect of the surface potential is always involved in the ASHEP, which we focus on in this study, we place our emphasis on the real potential.
Despite its importance, determining the ASHEP is challenging. The most reliable experimental value is considered to be −4.44 ± 0.02 V recommended by Trasatti and by the International Union of Pure and Applied Chemistry (IUPAC).1 The value was determined from the potential difference of a voltaic battery.4,5 However, experimental studies using other methods, such as the Kelvin work function measurement,6 UHV measurements,7 and cluster-ion solvation data,2 have reported scattered results of −4.80 to −4.28 V.
A first-principles (FP) prediction of the ASHEP is also highly challenging. The redox potential Uredox is determined by the free energy difference ΔA between the reduced and oxidized states:
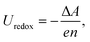 | (1) |
To mitigate the problems, Sprik and co-workers12,19–21 introduced a restraining potential that fixes protons to specific water molecules during short, approximately 5–20 picosecond, FPMD simulations to achieve stable and convergent results through TI calculations. They also used localized Gaussian basis sets22 and norm-conserving pseudopotentials.23 Ambrosio and co-workers24,25 used a similar approach with the rVV10 van der Waals functional26,27 to calculate the ASHEP at −4.56 V, a value that closely matches the Trasatti's experimental results. However, the use of localized basis sets can introduce basis set superposition errors. Additionally, the restraining potential used to suppress diffusion in solution might also introduce errors in the entropy of the protons. Finally, the long first principles calculations remain even today computationally very demanding, limit the statistical accuracy, require state of the art parallel computing facilities, and make routine calculations challenging.
Recently, methods have been proposed to accelerate time-consuming TI using machine learning (ML) surrogate models to calculate free energy changes and redox potentials. For example, Wang and co-workers28,29 proposed a method to train deep neural network potentials during TI calculations. Although they still employed restraining potentials and localized Gaussian basis sets, they devised a way to calculate free energy changes and redox potentials via TI using these potentials. Additionally, we13 developed a method that utilizes machine learning force fields (MLFFs) to achieve highly accurate statistical averaging and further corrects the errors in MLFFs through TI. We reported that this approach can accurately predict the redox potentials of electron transfer reactions for three transition metal redox couples, Fe3+/Fe2+, Cu2+/Cu+, and Ag2+/Ag+, using the PBE0 functional with 25% exact exchange, the all-electron projector augmented wave (PAW) method, and plane waves.30–33 However, there are no reports on calculating ASHEP using the PAW method with plane-wave basis sets, without applying restraining potentials. This is the main goal of the present work.
To achieve sufficient statistics for accurate predictions, we extend the machine learning (ML)-aided thermodynamic integration (TI) developed in our previous study,13 which enabled electron insertion into aqueous solutions, to also allow for proton insertion into aqueous solutions. Using a hybrid functional that includes 25% exact exchange and dispersion corrections (PBE0+D3),34–36 this method predicts the ASHEP and the real potential of the proton as −4.52 ± 0.09 V and −11.12 ± 0.09 eV, respectively. These values are very close to the IUPAC recommended values of −4.44 ± 0.02 V and −11.28 ± 0.02 eV, as shown in Table 1. In addition to the ASHEP and the three redox couples Fe3+/Fe2+, Cu2+/Cu+, and Ag2+/Ag+ from our previous study,13 we extend applications to the electron transfer reactions of three redox couples, V3+/V2+, Ru3+/Ru2+, and O2/O2−. The redox couple Ru3+/Ru2+ forms a rigid first solvation shell composed of six water molecules, similar to the Fe3+/Fe2+ couple. Past density functional theory calculations using a continuum solvation model37 have shown that the calculated redox potentials vary by more than 1 V depending on whether the second solvation shell is explicitly included or not, demonstrating the challenges in non-empirically determining solvation structures through static calculations. The redox couple V3+/V2+ is involved in a half-cell reaction of the redox flow battery.38 The non-catalytic electron transfer reaction, O2 + e− → O2−, serves as a foundation for elucidating the formation mechanism of the superoxide ion, which is considered the initial precursor in the oxygen reduction reaction in alkaline conditions.39–41 Thus, their FP modeling is considered to be of practical importance. The calculations across these seven redox potentials over a wide range of potentials are expected to demonstrate that our ML-assisted FP method provides a universal framework for accurately predicting redox potentials.
 (eV), ASHEP (V) and relevant free energies (eV) calculated by five exchange–correlation functionals (RPBE+D3, PBE0, PBE0+D3, HSE06 and B3LYP) compared with the experimental values recommended by the International Union of Pure and Applied Chemistry (IUPAC).1 ΔatE and ΔatG0 represent the atomization energy and dissociation free energy of the H2 molecule, respectively. ΔionG0 is the ionization potential of an H atom in vacuum. MLFF denotes the machine-learned force field trained on the RPBE+D3 data. The specified modeling error bars correspond to 2σ, estimated by block averaging analysis8
(eV), ASHEP (V) and relevant free energies (eV) calculated by five exchange–correlation functionals (RPBE+D3, PBE0, PBE0+D3, HSE06 and B3LYP) compared with the experimental values recommended by the International Union of Pure and Applied Chemistry (IUPAC).1 ΔatE and ΔatG0 represent the atomization energy and dissociation free energy of the H2 molecule, respectively. ΔionG0 is the ionization potential of an H atom in vacuum. MLFF denotes the machine-learned force field trained on the RPBE+D3 data. The specified modeling error bars correspond to 2σ, estimated by block averaging analysis8
| ΔatE | ΔatG0 | ΔionG0 | ASHEP | ||
|---|---|---|---|---|---|
| MLFF | 4.58 | 4.04 | 13.75 | −10.98 ± 0.05 | −4.78 ± 0.05 |
| RPBE+D3 | 4.58 | 4.04 | 13.75 | −11.02 ± 0.06 | −4.75 ± 0.05 |
| PBE0 | 4.53 | 3.99 | 13.64 | −11.06 ± 0.09 | −4.58 ± 0.09 |
| PBE0+D3 | 4.53 | 3.99 | 13.64 | −11.12 ± 0.09 | −4.52 ± 0.09 |
| HSE06 | 4.53 | 3.99 | 13.63 | −11.06 ± 0.09 | −4.57 ± 0.09 |
| B3LYP | 4.78 | 4.25 | 13.67 | −10.94 ± 0.08 | −4.86 ± 0.09 |
| Exp. | 4.73 | 4.21 | 13.62 | −11.28 ± 0.02 | −4.44 ± 0.02 |
2 Overview of method
2.1 ASHEP and real potential of proton
We provide a brief overview of our computational methodology for ASHEP. Details are given in Section S1.† To facilitate the calculation of the free energy, we divide the hydrogen oxidation reaction into three steps, as in previous studies:20,42 dissociation, H2(g) → 2H(g), ionization, 2H(g) → 2H+ + 2e−(g), and solvation, 2H+(g) → 2H+(aq), where (g) and (aq) denote species in vacuum and in the aqueous phase, respectively. The corresponding free energy changes are ΔatG0 in the dissociation, 2ΔionG0 in the ionization, and in the solvation. The free energy of the entire redox reaction per electron (defined as −ΔA) is written as follows:
in the solvation. The free energy of the entire redox reaction per electron (defined as −ΔA) is written as follows: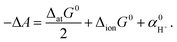 | (2) |
Among the three free energies, ΔionG0 can be easily calculated by a single-point FP calculation. The dissociation free energy ΔatG0 can also be easily computed using the ideal gas model. The remaining quantity, the real potential of the proton,  , can be computed by a TI simulation from the non-interacting proton in the gas phase to the interacting proton in the aqueous phase:
, can be computed by a TI simulation from the non-interacting proton in the gas phase to the interacting proton in the aqueous phase:
 | (3) |
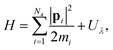 | (4) |
| Uλ = λ(U1 + eΔϕ) + (1 − λ)U0, | (5) |
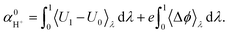 | (6) |
In practice, computing Δϕ and the TI in eqn (3) is highly challenging, as relaxation times in water are slow and require expensive ns-scale FP MD simulations that consume millions to tens of millions of core hours. Here, we address these issues by extending the ML-aided scheme developed in our previous study13 from electron insertion to proton insertion.
2.2 Local potential gap
The local potential gap Δϕ needs to be determined to correctly fix the reference potential for charges to a point just outside a water surface. This reference level is usually determined in a separate slab calculation involving an interface between water and the vacuum. But then, how does one align the so determined vacuum level with the periodic slab calculation? There are several conceivable options for this procedure. Considering the procedures generally used for semi-conductors,43,44 one might be inclined to use the valence band edge (highest occupied orbitals) of water as reference. This choice is not ideal, as the valence band edges are global quantities and might be difficult to identify unambiguously in a finite system. The averaged local potential19–21,42 has also been suggested as reference level. However, a natural point of alignment are the O 1s levels far from the reactant in the considered periodic cells at any coupling and at the middle of water slabs, respectively.13 Similar procedures—reference points far away from defects—were also suggested to account for most of the finite size effects,43 oblivating the need for additional finite size corrections. We also note that the chosen concentration almost agrees with the experimental proton concentration (1 mol L−1 for H+). As depicted in Fig. 1 (see the green arrow), the local potential gap 〈Δϕ〉λ is then determined by:| e〈Δϕ〉λ = μ − 〈ε1s,slab〉 + 〈ε1s,bulk〉λ, | (7) |
2.3 Thermodynamic integration
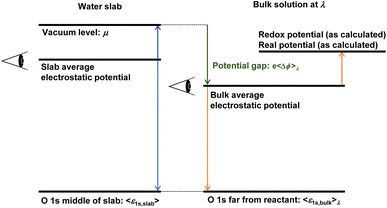
The TI in the first term on the right-hand side of eqn (6) is performed by the modified λ-MLFF scheme, which allows for insertion of atoms and molecules.46,47 As in our previous study, the TI is decomposed into two steps: (1) TI using the MLFFs from the non-interacting proton and pure liquid water to the fully interacting aqueous solution containing the proton (or vice versa), and (2) TI from the MLFF potential to the FP potential. Step (1) is further decomposed into two steps (I) and (II) as shown in Fig. 2(a) to yield a reversible thermodynamic pathway between two endpoints. In the first step, a Gaussian soft-repulsive potential is gradually introduced between the proton and other atoms along the coupling parameter λI to form a cavity in water similar to the previous FP calculation of solvation free energies of Li+ and F− ions.48 Subsequently, in the second step, the soft-repulsive potential is replaced with the full interaction represented by the MLFF model along the coupling parameter λII. A point worth noting is that, unlike the TI approach used by Sprik and co-workers,19,20 no restraining potential is introduced in the final state where the MLFF is applied. For a system with 64 water molecules, we estimate that the neglected entropy contribution with a restraining potential is typically 1/β![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln(64) ≈ 100 meV. In our simulations, the free energy of the freely diffusing protons is accurately represented in the final state. It has been found that achieving a good convergence in the TI leading to fully diffusing protons requires simulations on the nanosecond scale. The MLFF makes this possible by accelerating these MD simulations by several orders of magnitude. Details of these two TI simulations are explained in Section S2.† We refer to this improved method as the soft landing λ-MLFF scheme.
ln(64) ≈ 100 meV. In our simulations, the free energy of the freely diffusing protons is accurately represented in the final state. It has been found that achieving a good convergence in the TI leading to fully diffusing protons requires simulations on the nanosecond scale. The MLFF makes this possible by accelerating these MD simulations by several orders of magnitude. Details of these two TI simulations are explained in Section S2.† We refer to this improved method as the soft landing λ-MLFF scheme.
While the TI step (1) provides a statistically accurate free energy for the MLFF, the MLFF model may introduce a non-negligible error. This error is corrected by the TI step (2). In this step, the potential energy transitions seamlessly from the MLFF to the FP potential. One of the main advantages of our ML-aided scheme is that the initial TI step from the non-interacting to the interacting system is done using the MLFF model. This initial step, which requires the use of an infinitesimally small interaction between the inserted atom and other atoms, becomes extremely challenging as the yet non-interacting atom approaches or even overlaps with other atoms and hence experiences a significant repulsive potential. Additionally, it is highly challenging to perform adequate configurational sampling of the proton, which diffuses through the Grotthuss mechanism, requiring multiple ns to tens of ns of simulations along the coupling parameter with the FP method. The MLFF accelerates these computations by several orders of magnitude. Another major advantage is that the accurate reproduction of FP structures by the MLFF results in small and nearly linear integrands with respect to the coupling parameter for the TI step (2), facilitating the convergence of this integral after a few tens of ps of MD simulations, thus reducing the high computational costs associated with FP calculations.
However, directly applying the final TI step (2) to an expensive FP method, like the hybrid functional used in this study, remains highly costly. Therefore, as in our previous study,13 we correct the free energy calculated with the computationally inexpensive FP method, that is a semi-local functional in our case, through using thermodynamic perturbation theory (TPT) and a scheme akin to Δ-ML.49–56 Specifically, the free energy difference is calculated using:
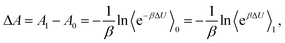 | (8) |
2.4 Correction to vibrational free energy
Another obstacle in computational studies is the integration of nuclear quantum effects, which cannot be accounted for in the classical thermodynamic integration (TI) and thermodynamic perturbation theory (TPT) simulations described previously. Specifically, the contributions of zero-point energy cannot be neglected due to the high frequency of the O–H bond.19,20,24,25 In this study, nuclear quantum effects were estimated to be 0.30 eV by calculating the free energy difference between the quantum harmonic oscillator model and the classical model for three experimentally measured vibrational frequencies of 1250, 1760, and 3020 cm−1,57 which were attributed to the solvation of a single proton by water (details in Section S3†). Our estimated value is slightly smaller than the previously reported value of 0.36 eV,24 which was calculated solely from the contribution of zero-point energies, excluding entropy contributions and the subtraction of classical vibrational contributions. The discrepancy, as explained in Section S3,† stems from whether these additional contributions are accounted for. To examine the sensitivity of the correction to the model and frequencies, the correction was also calculated for H3O+ and H2O molecules in vacuum. The results indicate that the correction is insensitive to details of the model and frequencies (see also Section S3†).2.5 Redox potentials of other electron transfer reactions
Finally, to demonstrate that the hybrid functional consistently predicts the redox potentials of a wide range of redox couples with high precision, we calculated the redox potentials for electron transfer reactions, Ox + e− ↔Red, of three redox couples, V3+/V2+, Ru3+/Ru2+, and O2/O2−, in addition to the three redox couples, Fe3+/Fe2+, Cu2+/Cu+, and Ag2+/Ag+, that were calculated in our previous study.13 The redox potentials were calculated from the free energy changes computed via the ML-aided TI and TPT calculations from the oxidized state to the reduced state. Details of the computational method are explained in our previous publication.13 Details of the models are described in Section S1.†2.6 Computational method
All simulations were carried out using the Vienna Ab initio Simulation Package (VASP).31–33 For the MLFF models, we utilized the algorithm described in our previous publications.45,58 Similar to the pioneering ML approaches,59,60 the potential energy is approximated as a sum of local energies, which are further approximated as a weighted sum of a sparse set of kernel basis functions. The Bayesian framework allows for accurate predictions of energies, forces, and their uncertainties, enabling efficient on-the-fly sampling of reference structures during FPMD simulations of target systems. For the proton insertion calculations performed to compute ASHEP, a single MLFF was trained on both the reactant and product states. Additionally, to generate a stable and reversible thermodynamic pathway, the MLFF was also trained on the fly during the TI simulation along the coupling constant λII prior to the production run. For other electron transfer reactions, individual MLFF models were trained separately on the reactant and product states and were further trained on the fly during the TI simulation along the coupling constant. Exchange–correlation interactions between electrons were modeled using the modified Perdew–Burke–Ernzerhof semi-local functional,61 augmented with Grimme's dispersion interaction with zero-damping (RPBE+D3).35,36 Details of the equations, parameters, and training conditions are summarized in Section S1.† The same formulation was applied to the Δ-ML model. A Δ-ML model was generated for each reactant and product state. The training was conducted based on the differences in energies and forces between the semi-local RPBE+D3 functional and a selected functional from among the following: a non-local hybrid functional with 25% exact exchange (with or without Grimme's dispersion interaction, PBE0+D3 or PBE0),34 a hybrid functional with screened exchange (HSE06),62,63 and the B3LYP functional.64 Among the five functionals, we primarily focus on the RPBE+D3, PBE0, and PBE0+D3 functionals, guided by previous calculations of redox potentials,11–13,28,29 band alignments,25,65 and structural properties of liquid water.66–68 As reported in previous studies,11,12 incorrectly aligned band edges of liquid water can hybridize with redox levels, leading to significant errors in redox potentials. A previous study25 showed that the PBE0 functional with 25% exact exchange [PBE0 (x = 0.25)] provides a band gap closer to experimental results than the HSE06 functional, and that even better agreement can be achieved by increasing the exact exchange to 45% [PBE0 (x = 0.45)]. However, it is also known that thermochemical properties are calculated with better balance at x = 0.25,34 and our previous study13 demonstrated that for three redox couples—Fe3+/Fe2+, Cu2+/Cu+, and Ag2+/Ag+—PBE0 (x = 0.25) achieves more balanced accuracy in redox potentials than PBE0 (x = 0.50). Furthermore, a recent evaluation of common density functionals68 showed that, while better functionals do exist, RPBE+D3 and PBE0+D3 yield reasonable isobaric density profiles for water. As described below, we focus on the results from these three functionals; however, for reference, we also performed calculations using the HSE06 and B3LYP functionals, which are commonly used in the fields of solid-state physics and quantum chemistry.All aqueous solutions were modeled using a unit cell containing 64 water molecules, which is close to the ion concentration at the standard state (56 water molecules per ion). Our previous study13 on the size effect demonstrated that the impact of this slight deviation in concentration is negligible.
3 Results and discussion
3.1 Accuracy of MLFF and Δ-ML models
The MLFF models for seven redox couples achieve root mean square errors (RMSEs) of 1–2 meV per atom, 40–80 meV Å−1, and 0.40–1.1 kbar, as shown in Table S3† (error distributions are also presented in Fig. S2 to S8†). These RMSEs are comparable to those of MLFFs in previous studies.45,46,69,70 Due to their accuracy, the MLFFs reproduce the solvation structure surrounding the redox couples, as demonstrated by the radial distribution functions (RDFs) shown in Fig. 3. Consistent with the previous FPMD simulation,71 H+ forms an H3O+ ion coordinated by three water molecules on average. Similarly, Fe and Ru form rigid first solvation shells composed of six water molecules, regardless of the oxidation state, in alignment with previous computational results.37,72–74 Vanadium also forms a rigid first solvation shell composed of six water molecules. In contrast, as reported in previous studies,13,75 the coordination number for Cu changes from 5–6 in the oxidized state (Cu2+) to 1–2 in the reduced state (Cu+), and for Ag, it changes from 5–6 in the oxidized state (Ag2+) to 4–5 in the reduced state (Ag+). Notable H-bonds are not formed between the neutral O2 and other water molecules, while its reduced state, O2−, is coordinated by roughly three water molecules on average. Although the MLFF models reproduce the solvation structures observed in our FPMD calculations and previous calculations, non-negligible deviations are present in the RDFs calculated by the MLFF models compared to those calculated by the FP method. The error in the MLFF models can be corrected through the TI simulation from the MLFF potential to the FP potential, as illustrated by the transition of the radial distribution function (RDF) shown in Fig. 2(c).Thanks to the smooth energy difference between the semi-local and hybrid functionals, the Δ-ML models accurately represent the energy difference with only 40 configurations, achieving RMSEs more than an order of magnitude smaller than those of the MLFFs, as shown in Table S4 and Fig. S2 to S8.† Due to this remarkable accuracy, the Δ-ML models can provide exceedingly accurate free energy changes via TPT calculations without further correction.13
3.2 Real potential of proton
As illustrated in Fig. 2(b), thermodynamic integration (TI) simulations using the MLFF trained on the semi-local RPBE+D3 functional generate smooth and reversible integrands along the coupling parameters, within the range of statistical errors. At the endpoint of TI (λI = 1 and λII = 1), as shown in Fig. 2(c), the MLFF well reproduces the RDF calculated using the RPBE+D3 functional. Owing to this high precision, as shown in Fig. 2(d), TI from MLFF to the RPBE+D3 functional yields nearly linear and relatively small integrands along the coupling path η. Consequently, this TI induces only slight modifications to the real potential of the proton (40 meV). The calculated value shown in Table 1 (−11.02 ± 0.06 eV) is already close to the experimental result (−11.28 ± 0.02 eV) and also closely matches a previously calculated value of −11.00 eV. This earlier calculated value was derived by adding 0.08 eV to the tabulated value of WH+ = −11.08 eV reported by Ambrosio et al.25 This adjustment was made to account for the dilution of the hydrogen atom in the gas phase from a concentration of 1 mol L−1 to 0.1 MPa (1/24.45 mol L−1), to make it comparable with Trasatti's value. The agreement with experiment is further improved through hybrid functional calculations (PBE0 and PBE0+D3) facilitated by TPT calculations utilizing the Δ-ML scheme. The TPT calculations demonstrate that the probability distributions of energy differences between the hybrid functional (PBE0 or PBE0+D3) and RPBE+D3 are accurately represented by Gaussian distributions, as depicted in Fig. 2(e). This implies that the second cumulant expansion equation [eqn (S9)†] provides a reasonable approximation. The computed value for PBE0+D3 (−11.12 ± 0.09 eV) is in very good agreement with the experimental results. In addition to these hybrid functionals, HSE06 produces an accurate real potential nearly identical to that of the PBE0 functional. In contrast, the B3LYP functional provides relatively less stabilization for protons in water.
(40 meV). The calculated value shown in Table 1 (−11.02 ± 0.06 eV) is already close to the experimental result (−11.28 ± 0.02 eV) and also closely matches a previously calculated value of −11.00 eV. This earlier calculated value was derived by adding 0.08 eV to the tabulated value of WH+ = −11.08 eV reported by Ambrosio et al.25 This adjustment was made to account for the dilution of the hydrogen atom in the gas phase from a concentration of 1 mol L−1 to 0.1 MPa (1/24.45 mol L−1), to make it comparable with Trasatti's value. The agreement with experiment is further improved through hybrid functional calculations (PBE0 and PBE0+D3) facilitated by TPT calculations utilizing the Δ-ML scheme. The TPT calculations demonstrate that the probability distributions of energy differences between the hybrid functional (PBE0 or PBE0+D3) and RPBE+D3 are accurately represented by Gaussian distributions, as depicted in Fig. 2(e). This implies that the second cumulant expansion equation [eqn (S9)†] provides a reasonable approximation. The computed value for PBE0+D3 (−11.12 ± 0.09 eV) is in very good agreement with the experimental results. In addition to these hybrid functionals, HSE06 produces an accurate real potential nearly identical to that of the PBE0 functional. In contrast, the B3LYP functional provides relatively less stabilization for protons in water.
3.3 ASHEP and other redox potentials
The ASHEP values calculated by RPBE+D3, PBE0, and PBE0+D3 are −4.75 ± 0.05, −4.58 ± 0.09, and −4.52 ± 0.09 V, respectively. While error cancellation between the hydrogen dissociation free energy ΔatG0 and the other two properties is a partial cause, the PBE0+D3 functional shows excellent agreement with the IUPAC recommended experimental ASHEP value of −4.44 ± 0.02 V. Furthermore, the PBE0+D3 functional accurately reproduces experimental values of the redox potentials of five transition metal redox couples, Ag2+/Ag+, Fe3+/Fe2+, Cu2+/Cu+, V3+/V2+, Ru3+/Ru2+, and the molecular redox couple O2/O2− as shown in Fig. 4 (all relevant data are in Fig. S9 and Table S6†). Comparison with experimental data demonstrates that the PBE0+D3 functional consistently reproduces experimental redox potentials across a broad range of potentials with a small RMSE of 140 mV. The HSE06 functional also yields accurate redox potentials almost identical to those calculated by the PBE0 functional. In contrast, the B3LYP functional leads to the largest error among the five functionals. These results suggest that, for calculating redox potentials in extended systems with explicit treatment of both solute and solvent, the hybrid functionals PBE0 or HSE06 are preferable. The B3LYP was designed to optimally reproduce experimental atomization energies, electron and proton affinities, and ionization potentials of atomic and molecular species composed of light elements taken from Pople's G2 test set.64 However, it was not calibrated for properties of heavy elements as well as properties of condensed matter, such as band alignments in extended systems. In addition, B3LYP fails to attain the exact homogeneous electron gas limit.77 On the other hand, while PBE0 and HSE06 also have parameters optimized to reproduce experimental values, they satisfy certain constraints met by the PBE functional.34,62,63 For instance, these functionals fulfill the uniform electron gas limit. These properties of PBE0 and HSE06 may contribute to the accurate calculation of redox potentials.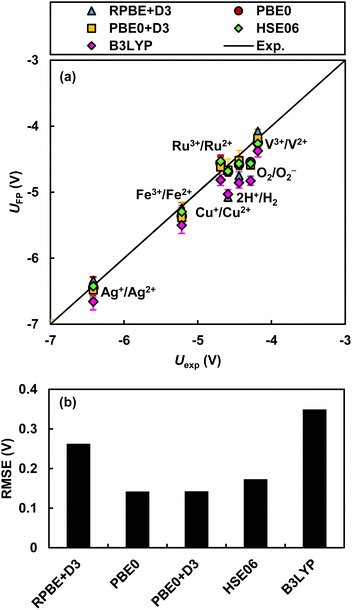 | ||
| Fig. 4 Redox potentials: (a) comparison of the absolute redox potentials of seven redox couples determined by three functionals with their experimental values76 and (b) RMSE. Data for transition metals, Fe3+/Fe2+, Cu2+/Cu+, and Ag2+/Ag+, were taken from our previous publication.13 | ||
4 Conclusions
We have developed an ML-aided FP method that allows for statistically accurate computation of the free energy change associated with proton insertion into aqueous solutions through TI and TPT calculations. In this approach, most of the energetic contributions to the free energy change were obtained through TI simulations using MLFF models trained on semi-local exchange–correlation functionals. Small residual errors in the MLFF models were corrected via subsequent TI simulations transitioning from the MLFF potential to the FP potential. Moreover, the Δ-ML model, which learned the potential energy difference between semi-local and hybrid functionals, enabled efficient TPT calculations of free energy changes for the expensive hybrid functional. Overall, our scheme accelerates free energy computations by about two orders of magnitude, enabling the calculation of redox potentials for seven redox couples on an absolute scale, including the ASHEP. This application has shown that when combined with a hybrid functional (PBE0), the method can predict redox potentials with an exceptional average accuracy of 140 mV. In condensed-matter, highly accurate beyond density functional theory methods, such as the random phase approximation78,79 and coupled-cluster approaches,80 are being adopted, and these methods may achieve accuracy surpassing that of PBE0 used in this study. The ML surrogate models we propose, which enable proton and electron insertions, are expected to provide a flexible, accurate, and efficient framework for predicting free energy changes and redox potentials on an absolute scale for any proton and electron transfer reactions, utilizing such high-precision electronic structure theories.Data availability
We have provided all relevant data in the ESI† of the paper. The datasets used to produce the machine-learned force fields in this work can be freely accessed at https://doi.org/10.5281/zenodo.14503891.Author contributions
R. J. developed the ML-aided TI and TPT calculation method. F. K. and G. K. developed the MLFF and VASP code. G. K. suggested the alignment method using the oxygen 1s levels. All authors participated in preparing and editing the manuscript.Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
This research was funded in part by the Austrian Science Fund (FWF) 10.55776/COE5. For open access purposes, the author has applied a CC BY public copyright license to any author accepted manuscript version arising from this submission.Notes and references
- S. Trasatti, Pure Appl. Chem., 1986, 58, 955–966 CrossRef CAS.
- M. D. Tissandier, K. A. Cowen, W. Y. Feng, E. Gundlach, M. H. Cohen, A. D. Earhart, J. V. Coe and T. R. Tuttle, J. Phys. Chem. A, 1998, 102, 7787–7794 CrossRef CAS.
- A. A. Isse and A. Gennaro, J. Phys. Chem. B, 2010, 114, 7894–7899 CrossRef CAS PubMed.
- J. E. B. Randles, Trans. Faraday Soc., 1956, 52, 1573–1581 RSC.
- J. R. Farrell and P. McTigue, J. Electroanal. Chem. Interfacial Electrochem., 1982, 139, 37–56 CrossRef CAS.
- W. Hansen and D. Kolb, J. Electroanal. Chem. Interfacial Electrochem., 1979, 100, 493–500 CrossRef CAS.
- P. A. Thiel and T. E. Madey, Surf. Sci. Rep., 1987, 7, 211–385 CrossRef CAS.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, 1987 Search PubMed.
- R. W. Zwanzig, J. Chem. Phys., 1954, 22, 1420–1426 CrossRef CAS.
- J. G. Kirkwood, J. Chem. Phys., 1935, 3, 300–313 CrossRef CAS.
- C. Adriaanse, J. Cheng, V. Chau, M. Sulpizi, J. VandeVondele and M. Sprik, J. Phys. Chem. Lett., 2012, 3, 3411–3415 CrossRef CAS PubMed.
- X. Liu, J. Cheng and M. Sprik, J. Phys. Chem. B, 2015, 119, 1152–1163 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai and G. Kresse, npj Comput. Mater., 2024, 10, 107 CrossRef CAS.
- T. S. Hofer and P. H. Hünenberger, J. Chem. Phys., 2018, 148, 222814 CrossRef PubMed.
- V. Tripkovic, M. E. Björketun, E. Skúlason and J. Rossmeisl, Phys. Rev. B:Condens. Matter Mater. Phys., 2011, 84, 115452 CrossRef.
- C.-G. Zhan and D. A. Dixon, J. Phys. Chem. A, 2001, 105, 11534–11540 CrossRef CAS.
- C. P. Kelly, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2006, 110, 16066–16081 CrossRef CAS PubMed.
- R. Jinnouchi, T. Hatanaka, Y. Morimoto and M. Osawa, Phys. Chem. Chem. Phys., 2012, 14, 3208–3218 RSC.
- J. Cheng, M. Sulpizi and M. Sprik, J. Chem. Phys., 2009, 131, 154504 CrossRef PubMed.
- F. Costanzo, M. Sulpizi, R. G. D. Valle and M. Sprik, J. Chem. Phys., 2011, 134, 244508 CrossRef PubMed.
- J. Cheng and M. Sprik, Phys. Chem. Chem. Phys., 2012, 14, 11245–11267 RSC.
- T. D. Kühne, M. Iannuzzi, M. D. Ben, V. V. Rybkin, P. Seewald, F. Stein, T. Laino, R. Z. Khaliullin, O. Schütt, F. Schiffmann, D. Golze, J. Wilhelm, S. Chulkov, M. H. Bani-Hashemian, V. Weber, U. Borštnik, M. Taillefumier, A. S. Jakobovits, A. Lazzaro, H. Pabst, T. Müller, R. Schade, M. Guidon, S. Andermatt, N. Holmberg, G. K. Schenter, A. Hehn, A. Bussy, F. Belleflamme, G. Tabacchi, A. Glöβ, M. Lass, I. Bethune, C. J. Mundy, C. Plessl, M. Watkins, J. VandeVondele, M. Krack and J. Hutter, J. Chem. Phys., 2020, 152, 194103 CrossRef PubMed.
- S. Goedecker, M. Teter and J. Hutter, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 1703–1710 CrossRef CAS PubMed.
- F. Ambrosio, G. Miceli and A. Pasquarello, J. Chem. Phys., 2015, 143, 244508 CrossRef PubMed.
- F. Ambrosio, Z. Guo and A. Pasquarello, J. Phys. Chem. Lett., 2018, 9, 3212–3216 CrossRef CAS PubMed.
- O. A. Vydrov and T. Van Voorhis, J. Chem. Phys., 2010, 133, 244103 CrossRef PubMed.
- G. Miceli, S. de Gironcoli and A. Pasquarello, J. Chem. Phys., 2015, 142, 034501 CrossRef PubMed.
- F. Wang and J. Cheng, J. Chem. Phys., 2022, 157, 024103 CrossRef CAS PubMed.
- F. Wang, Z. Ma and J. Cheng, J. Am. Chem. Soc., 2024, 146, 14566–14575 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15 CrossRef CAS.
- G. Kresse and D. Joubert, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef PubMed.
- S. Grimme, Wiley Interdiscip. Rev.:Comput. Mol. Sci., 2011, 1, 211–228 CAS.
- P. Jaque, A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. C, 2007, 111, 5783–5799 CrossRef CAS.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164 CrossRef CAS.
- N. Anastasijević, V. Vesović and R. Adžić, J. Electroanal. Chem. Interfacial Electrochem., 1987, 229, 305–316 CrossRef.
- C. Hartnig and M. T. Koper, J. Electroanal. Chem., 2002, 532, 165–170 CrossRef CAS.
- X. Ge, A. Sumboja, D. Wuu, T. An, B. Li, F. W. T. Goh, T. S. A. Hor, Y. Zong and Z. Liu, ACS Catal., 2015, 5, 4643–4667 CrossRef CAS.
- J. Le, M. Iannuzzi, A. Cuesta and J. Cheng, Phys. Rev. Lett., 2017, 119, 016801 CrossRef PubMed.
- S. Lany and A. Zunger, Phys. Rev. B:Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2019, 100, 014105 CrossRef CAS.
- R. Jinnouchi, F. Karsai and G. Kresse, Phys. Rev. B, 2020, 101, 060201 CrossRef CAS.
- R. Jinnouchi, F. Karsai, C. Verdi and G. Kresse, J. Chem. Phys., 2021, 154, 094107 CrossRef CAS PubMed.
- T. T. Duignan, M. D. Baer, G. K. Schenter and C. J. Mundy, Chem. Sci., 2017, 8, 6131–6140 RSC.
- R. M. Balabin and E. I. Lomakina, J. Chem. Phys., 2009, 131, 074104 CrossRef PubMed.
- R. Ramakrishnan, P. O. Dral, M. Rupp and O. A. von Lilienfeld, J. Chem. Theory Comput., 2015, 11, 2087–2096 CrossRef CAS PubMed.
- A. P. Bartók, M. J. Gillan, F. R. Manby and G. Csányi, Phys. Rev. B:Condens. Matter Mater. Phys., 2013, 88, 054104 CrossRef.
- S. Chmiela, H. E. Sauceda, K.-R. Müller and A. Tkatchenko, Nat. Commun., 2018, 9, 3887 CrossRef PubMed.
- H. E. Sauceda, S. Chmiela, I. Poltavsky, K.-R. Müller and A. Tkatchenko, J. Chem. Phys., 2019, 150, 114102 CrossRef PubMed.
- P. Liu, C. Verdi, F. Karsai and G. Kresse, Phys. Rev. B, 2022, 105, L060102 CrossRef CAS.
- C. Verdi, L. Ranalli, C. Franchini and G. Kresse, Phys. Rev. Mater., 2023, 7, L030801 CrossRef CAS.
- P. Liu, J. Wang, N. Avargues, C. Verdi, A. Singraber, F. Karsai, X.-Q. Chen and G. Kresse, Phys. Rev. Lett., 2023, 130, 078001 CrossRef CAS PubMed.
- J. Kim, U. W. Schmitt, J. A. Gruetzmacher, G. A. Voth and N. E. Scherer, J. Chem. Phys., 2002, 116, 737–746 CrossRef CAS.
- R. Jinnouchi, S. Minami, F. Karsai, C. Verdi and G. Kresse, J. Phys. Chem. Lett., 2023, 14, 3581–3588 CrossRef CAS PubMed.
- J. Behler and M. Parrinello, Phys. Rev. Lett., 2007, 98, 146401 CrossRef PubMed.
- A. P. Bartók, M. C. Payne, R. Kondor and G. Csányi, Phys. Rev. Lett., 2010, 104, 136403 CrossRef PubMed.
- B. Hammer, L. B. Hansen and J. K. Nørskov, Phys. Rev. B:Condens. Matter Mater. Phys., 1999, 59, 7413–7421 CrossRef.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2003, 118, 8207–8215 CrossRef CAS.
- J. Heyd, G. E. Scuseria and M. Ernzerhof, J. Chem. Phys., 2006, 124, 219906 CrossRef.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- T. A. Pham, C. Zhang, E. Schwegler and G. Galli, Phys. Rev. B:Condens. Matter Mater. Phys., 2014, 89, 060202 CrossRef.
- T. Morawietz, A. Singraber, C. Dellago and J. Behler, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 8368–8373 CrossRef CAS PubMed.
- P. Montero de Hijes, C. Dellago, R. Jinnouchi, B. Schmiedmayer and G. Kresse, J. Chem. Phys., 2024, 160, 114107 CrossRef CAS PubMed.
- P. Montero de Hijes, C. Dellago, R. Jinnouchi and G. Kresse, J. Chem. Phys., 2024, 161, 131102 CrossRef CAS PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- R. Jinnouchi, F. Karsai, C. Verdi, R. Asahi and G. Kresse, J. Chem. Phys., 2020, 152, 234102 CrossRef CAS PubMed.
- M. Tuckerman, K. Laasonen, M. Sprik and M. Parrinello, J. Chem. Phys., 1995, 103, 150–161 CrossRef CAS.
- T. Remsungnen and B. M. Rode, Chem. Phys. Lett., 2004, 385, 491–497 CrossRef CAS.
- J. Blumberger and M. Sprik, J. Phys. Chem. B, 2005, 109, 6793–6804 CrossRef CAS PubMed.
- S. A. Bogatko, E. J. Bylaska and J. H. Weare, J. Phys. Chem. A, 2010, 114, 2189–2200 CrossRef CAS PubMed.
- J. Blumberger, L. Bernasconi, I. Tavernelli, R. Vuilleumier and M. Sprik, J. Am. Chem. Soc., 2004, 126, 3928–3938 CrossRef CAS PubMed.
- A. Bard, R. Parsons and J. Jordan, Standard Potentials in Aqueous Solution, Taylor & Francis, 1985 Search PubMed.
- J. Paier, M. Marsman and G. Kresse, J. Chem. Phys., 2007, 127, 024103 CrossRef PubMed.
- J. Harl, L. Schimka and G. Kresse, Phys. Rev. B:Condens. Matter Mater. Phys., 2010, 81, 115126 CrossRef.
- M. Macher, J. Klimeš, C. Franchini and G. Kresse, J. Chem. Phys., 2014, 140, 084502 CrossRef CAS PubMed.
- G. H. Booth, A. Grüneis, G. Kresse and A. Alavi, Nature, 2013, 493, 365–370 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4sc03378g |
| This journal is © The Royal Society of Chemistry 2025 |